Математика 5 класс страница 45 номер 200: Номер №200 — ГДЗ по Математике 5 класс: Никольский С.М.

Математика Алдамуратова 5 класс 2017 Упражнение 200 ГДЗ(дүж) решебник KZGDZ.COM

Глава II. ДЕЛИМОСТЬ НАТУРАЛЬНЫХ ЧИСЕЛ 2.2. Простые числа. Составные числа Упражнение 200

← Предыдущий Следующий →

Глава I. НАТУРАЛЬНЫЕ ЧИСЛА И НУЛЬ

1.1. Натуральные числа и нуль

Упражнение

134567891011121314151617

1.2. Координатный луч. Изображение натуральных чисел и числа нуль на координатном луче

Упражнение

18192021222324252627

1.3. Сравнение натуральных чисел. Двойное неравенство

Упражнение

282930313233343536373839

1.4. Сложение и вычитание натуральных чисел

Упражнение

4041424344454647484950

1.5. Умножение и деление натуральных чисел. Основное свойство частного

Упражнение

5152535455565758596061

1.

6. Свойства арифметических действий

Упражнение

6263646566676869707172

1.7. Арифметические действия над натуральными числами

Упражнение

73747576777879

1.8. Числовые выражения. Буквенные выражения

Упражнение

80

81828384858687888990

1.9. Упрощение выражений

Упражнение

919293949596979899100101102103

1.10. Уравнение

Упражнение

104105106107108109110111112113114115116117118119120121

1.11. Формулы. Вычисление по формулам

Упражнение

122123124125126127128129130131132133134135136137138139140

1.12. Числовые последовательности

Упражнение

141142143144145146147148149150

Упражнения для повторения главы I

Упражнение

151152153154155156157158159160

161162163164165166

2.

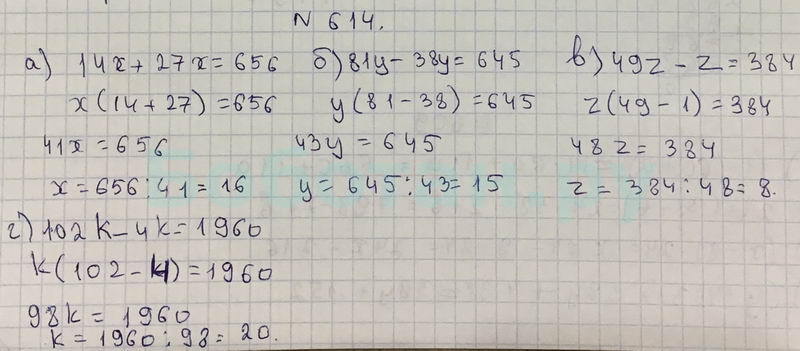1. Делители натурального числа. Кратные натурального числа

Упражнение

167168169170171172173174175176177178179180181182183184185186187188

Глава II. ДЕЛИМОСТЬ НАТУРАЛЬНЫХ ЧИСЕЛ

2.2. Простые числа. Составные числа

Упражнение

189190191192193194195196197198199200

2.3. Основные свойства делимости

Упражнение

201202203204205206207208209210211212213214

2.4. Признаки делимости натуральных чисел на 2, 5 и 10

Упражнение

215216217218219220221222223224225226227

2.5. Признаки делимости натуральных чисел на 3 и на 9

Упражнение

228229230231232233234235236237238239

2.6. Степень числа

Упражнение

240

241242243244245246247248249250251252253254255256257258259260261262

2.

7. Разложение составных чисел на простые множители

Упражнение

263264265266267268269270271272273274275

2.8. Наибольший общий делитель. Взаимно простые числа.

Упражнение

276277278279280281282283284285286287288290291292293294295

2.9. Наименьшее общее кратное

Упражнение

296297298299300301302303304305306307308309310311312313314315

Упражнения для повторения главы II

Упражнение

316317318319320321

322323324325326327

2.10. Движение по реке

Упражнение

328329330331332333334335336337338339340341342343344345346347348

Глава III. ОБЫКНОВЕННЫЕ ДРОБИ И ДЕЙСТВИЯ НАД НИМИ

3.1. Обыкновенная дробь. Чтение и запись обыкновенных дробей

Упражнение

349350351352353354355356357358359360361362363364365366367368369370371373374

3.

2. Основное свойство дроби. Сокращение дробей

Упражнение

375376377378379380381382383384385386387388389390391392393394395

3.3. Правильные дроби. Неправильные дроби

Упражнение

396397398399400401402

403404405406407408409410411412413414

3.4. Смешанные числа

Упражнение

415416417418419420421422423424425426427428429430431432433434435436

3.5. Изображение обыкновенных дробей и смешанных чисел на координатном луче

Упражнение

437438439440441442443444445446447448449450451452453454455456

3.6. Приведение обыкновенных дробей и смешанных чисел к наименьшему общему знаменателю

Упражнение

457458459460461462463464465466467468469470471472473474475476477

3.7. Сравнение обыкновенных дробей. Сравнение смешанных чисел

Упражнение

478479480481482

483484485486487488489490491492493494495496497498499

3.

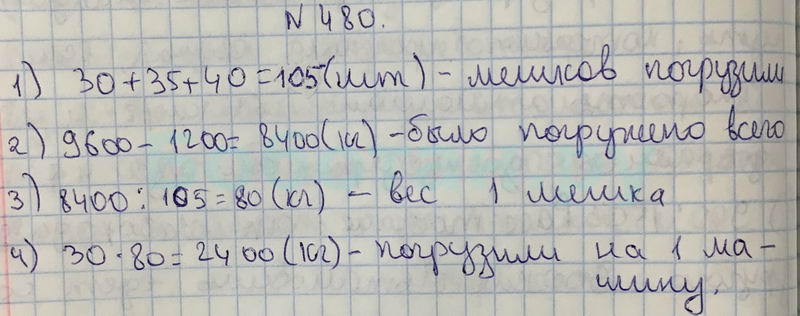8. Сложение и вычитание обыкновенных дробей

Упражнение

500501502503504506507508509510511512513514515516517518519520521522523524525526527528529530531

3.9. Сложение и вычитание смешанных чисел

Упражнение

532533534535536537538539540541542543544545546547548549550551552553554555556557558559

3.10. Аликвотные дроби

Упражнение

560561562563

564565566567568569570571572

3.11. Умножение обыкновенных дробей и смешанных чисел

Упражнение

573574575576577578579580581582583584585586587588589590591592593594595596597598599600601602

3.12. Взаимно обратные числа

Упражнение

603604605

3.13. Деление обыкновенных дробей и смешанных чисел

Упражнение

606607608609610611612613614615616617618619620621622623624625626627628629630631632633634635636637638639640641642643

644645646647648649650651652653654655656657658659660661662663664665

3.

14. Нахождение дроби от числа. Нахождение числа по его дроби

Упражнение

666667668669670671672673674675676677678679680681682683684685686687688689690691692693

3.15. Задачи на совместную работу

Упражнение

694695696697698699700701702703704705706707708709710711712713714

Глава IV. ДЕСЯТИЧНЫЕ ДРОБИ. ДЕЙСТВИЯ НАД ДЕСЯТИЧНЫМИ ДРОБЯМИ

4.1. Десятичная дробь. Чтение и запись десятичных дробей.

Упражнение

715716717718719720721722723

724725726727728729730731732733734

4.2. Перевод десятичной дроби в обыкновенную, обыкновенной дроби — в десятичную

Упражнение

735736737738739740741742743744745746747748749750751752753754

4.3. Изображение десятичной дроби на координатном луче. Сравнение десятичных дробей

Упражнение

755756757758759760761762763764765766767768769770771772773774775776777

4.

4. Сложение и вычитание десятичных дробей

Упражнение

778779780781782783784785786787788789790791792793794795796797798799800801802803

804805806807808809810

4.5. Умножение десятичной дроби на натуральное число

Упражнение

811812813814815816817818819820821822823824825826827828829830831832833834835836837838839840

4.6. Умножение десятичных дробей

Упражнение

841842843844845846847848849850851852853854855856857858859860861862863864865866867868869870871872

4.7. Деление десятичной дроби на натуральное число

Упражнение

873874875876877878879880881882883

884885886887888889890891892893894895896897898899900901902903

4.8. Деление десятичной дроби на десятичную дробь

Упражнение

904905906907908909910911912913914915916917918919920921922923924925926927928929930931932933934

4.

9. Умножение и деление десятичной дроби на 10, 100, 1000 и на 0,1; 0,01; 0,001;

Упражнение

935936937938939940941942943944945946947948949950951952953954955

4.10. Арифметические действия над обыкновенными и десятичными дробями.

Упражнение

956957958959960961962963

964965966967968969970971972973974975976977978979980981

4.11. Округление десятичных дробей

Упражнение

98298398498598698798898999099199299399499599699799899910001001100210031004

4.12. Числовые последовательности, составленные из дробей.

Упражнение

1005100610071008100910101011101210131014

Глава V. МНОЖЕСТВА

5.1. Множество. Элементы множества. Изображения множеств

Упражнение

101510161017101810191020102110221023102410251026102710281029103010311032

5.

2. Подмножество

Упражнение

10331034103510361037103810391040104110421043

1044104510461047104810491050

5.3. Пересечение множеств. Объединение множеств

Упражнение

105110521053105410551056105710581059106010611062106310641065106610671068

5.4. Задачи на множества

Упражнение

1069107010711072107310741075107610771078107910801081108210831084

Глава VI. ПРОЦЕНТЫ

6.1. Проценты

Упражнение

10851086108710881089109010911092109310941095109610971098109911001101110211031104110511061107110811091110111111121113

6.2. Нахождение процентов от данного числа

Упражнение

1114111511161117111811191120112111221123

112411251126112711281129113011311132113311341135113611371138113911401141

6.

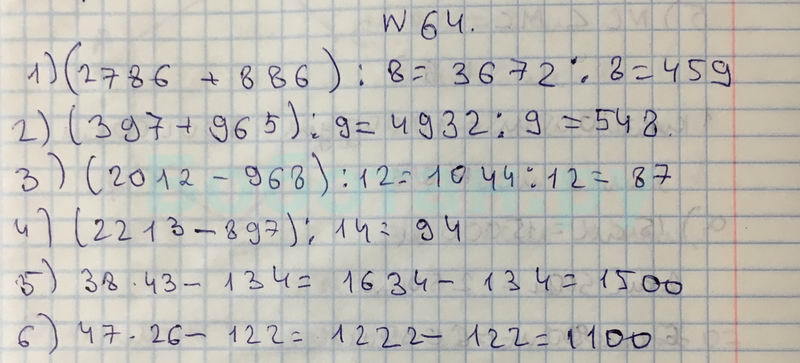3. Нахождение числа по его процентам

Упражнение

1142114311441145114611471148114911501151115211531154115511561157115811591160116111621163116411651166116711681169

Упражнения для повторения главы VI.

Упражнение

117011711172117311741175117611771178117911801181118211831184

Глава VII. УГЛЫ. МНОГОУГОЛЬНИКИ

7.1. Угол. Градусная мера угла Краткие сведения о градусе

Упражнение

118511861187118811891190119111921193119411951196119711981199

7.2. Транспортир. Измерение и построение углов

Упражнение

1200120112021203

120412051206120712081209121012111212121312141215

7.3. Сравнение углов. Виды углов. Чертежный треугольник

Упражнение

121612171218121912201221122212231224122512261227122812291230

7.4. Многоугольники

Упражнение

12311232123312341235123612371238123912401241124212431244124512461247

Упражнения для повторения главы VII

Упражнение

1248124912501251125212531254

Глава VIII.

ДИАГРАММЫ

8.1. Окружность. Круг

Упражнение

125512561257125812591260126112621263126412651266126712681269127012711272127312741275

8.2 Круговой сектор

Упражнение

12761277127812791280128112821283

128412851286128712881289

8.3.Способы представления статистических данных. Столбчатые, линейные, круговые и графические диаграммы. Таблицы

Упражнение

129012911292129312941295129612971298129913001301

Глава IX. РАЗВЕРТКИ ПРОСТРАНСТВЕННЫХ ФИГУР

9.1. Прямоугольный параллелепипед и его развертка

Упражнение

13021303130413051306130713081309131013111312

9.2. Задачи на разрезание фигур Задачи на склеивание фигур

Упражнение

1313131413151316

Упражнения для повторения пройденного за год

1. Натуральные числа и нуль

Упражнение

13171318131913201321132213231324132513261327

2.

Делимость натуральных чисел

Упражнение

1328132913301331133213331334

3. Обыкновенные дроби и действия над ними

Упражнение

133513361337133813391340134113421343

4. Десятичные дроби и действия над ними

Упражнение

1344134513461347134813491350

5. Множества

Упражнение

1351135213531354

6. Проценты

Упражнение

13551356135713581359

7. Углы. Многоугольники

Упражнение

136013611362

8. Диаграммы. Развертка прямоугольного параллелепипеда

Упражнение

1363

13641365

200. а) У Васи было 46 марок. За год его коллекция увеличилась на 230 марок. Во сколько раз… 5 класс Математика Никольский С.М. – Рамблер/класс

200. а) У Васи было 46 марок. За год его коллекция увеличилась на 230 марок. Во сколько раз… 5 класс Математика Никольский С.М. – Рамблер/класс

Интересные вопросы

Школа

Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?

Новости

Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?

Школа

Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?

Школа

Когда в 2018 году намечено проведение основного периода ЕГЭ?

Новости

Будет ли как-то улучшаться система проверки и организации итоговых сочинений?

Вузы

Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?

200.
а)   У Васи было 46 марок. За год его коллекция увеличилась на 230 марок. Во сколько раз увеличилась коллекция?
б)   У Коли было 42 р., он потратил 36 р. Во сколько раз у Коли стало меньше денег?

ответы

а) 1) 46 + 230 = 276 (м.) — стало у Васи;
2)       276 : 46 = 6 (р.) — во столько раз увеличилась коллекция Васи. Ответ: 6 раз.
б) 1) 42 — 36 = 6 (р.) — осталось у Коли;
2)       42 : 6 = 7 (р.) — во столько раз стало меньше денег у Коли.
Ответ: 7 р.

ваш ответ

Можно ввести 4000 cимволов

отправить

дежурный

Нажимая кнопку «отправить», вы принимаете условия  пользовательского соглашения

похожие темы

3 класс

Репетитор

Химия

Алгебра

похожие вопросы 5

В четырёхугольнике ABCD проведена диагональ AC так, что угол ACB=CAD,ACD=CAB.Докажите,что четырёхугольник ABCD — параллелограмм

ГДЗ

Хело! У кого есть ответ к уравнению? Вариант 29. Часть 2. Задание 21. ОГЭ 36 вариантов ответов по Математике 9 класс Ященко.

Решите уравнение х3 + 2х2 — х — 2 = 0.

ГДЗМатематикаОГЭ9 классЯщенко И.В.

111. Запишите произведение в виде разности… Математика 5 класс Никольский С.М.

111.
Запишите произведение в виде разности: (Подробнее…)

ГДЗМатематика5 классНикольский С.М.

Задание 152 Изменение по падежам имён существительных. Русский язык.4 класс. Канакина В.П., Горецкий В.Г. ГДЗ

Как правильно указать падеж?
Прочитайте. Запишите, вставляя пропущенные слова метро и радио. Укажите падеж неизменяемых (Подробнее…)

ГДЗРусский языкКанакина В.П.Горецкий В.Г.4 класс

169. Запишите число в виде произведения одинаковых чисел… Никольский С.М. Математика 5 класс

169.
Запишите число в виде произведения одинаковых чисел:
а) 4; б) 1; в) 27; г) 256.

ГДЗМатематика5 классНикольский С. М.

Умножение × | Основы арифметики

На этой странице рассматриваются основы умножения (×) .

См. другие наши арифметические страницы для обсуждения и примеров: сложение (+), вычитание (-) и деление ( ÷ ).

Умножение

При записи общий знак умножения — « × ». В электронных таблицах и некоторых других компьютерных приложениях символ « * » (или звездочка) используется для обозначения операции умножения.

Чтобы выполнять вычисления по умножению без калькулятора или электронной таблицы, вам необходимо знать, как складывать числа. См. нашу страницу «Добавление» для помощи в добавлении.

Когда вы «умножаете» или «умножаете» число, вы добавляете его само к себе несколько раз, например, 4 умножить на 3 — это то же самое, что сказать 4 + 4 + 4 = 12. Таким образом, умножение — это более быстрый способ сложения. одно и то же число много раз, например 3 × 4 = 12. Этот расчет аналогичен утверждению, если у меня есть 3 мешка с 4 яблоками, сколько яблок у меня всего?

Основные правила умножения:

---

• Любое число, умноженное на 0, равно 0.  200 × 0 = 0
• Любое число, умноженное на 1, остается прежним. 200 × 1 = 200,
• Когда число умножается на два, мы удваиваем число. 200 × 2 = 400.
• Когда целое число умножается на 10, мы можем просто написать 0 в конце (в 10 один ноль, потому что это 1 × 10). 200 × 10 = 2000. 
• При умножении на 100 пишем в конце два нуля, при тысяче пишем в конце три нуля и так далее. 4 × 2000 например 4 × 2 = 8 с 3 нулями: 8000.

Для простого и быстрого умножения полезно запомнить умножение или «таблицу умножения на », как показано ниже. Эта таблица дает ответы на все умножения до 10 × 10. Чтобы получить ответ на 4 × 6, например, найдите 4 в верхней (заштрихованной красным) строке и найдите 6 в левом (заштрихованном красным) столбце – точка пересечения двух прямых и есть ответ: 24 .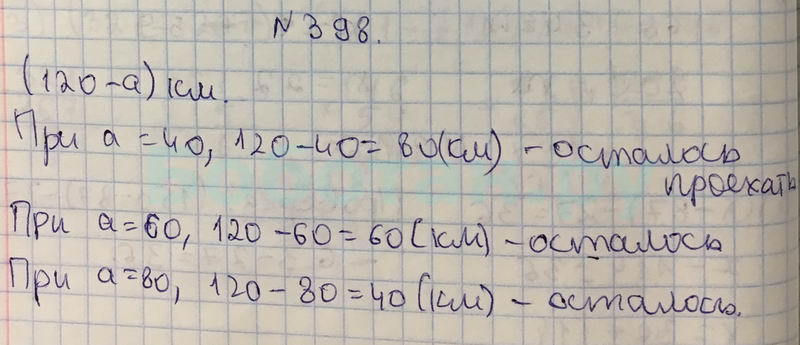

Не имеет значения, с какой стороны вы ищете номера; если вы найдете 4 в первом столбце и 6 в первой строке, вы получите тот же ответ, 24.

Таблица умножения

×	1	2	3	4	5	6	7	8	9	10
1	1	2	3	4	5	6	7	8	9	10
2	2	4	6	8	10	12	14	16	18	20
3	3	6	9	12	15	18	21	24	27	30
4	4	8	12	16	20	24	28	32	36	40
5	5	10	15	20	25	30	35	40	45	50
6	6	12	18	24	30	36	42	48	54	60
7	7	14	21	28	35	42	49	56	63	70
8	8	16	24	32	40	48	56	64	72	80
9	9	18	27	36	45	54	63	72	81	90
10	10	20	30	40	50	60	70	80	90	100

Приведенная выше таблица может помочь нам быстро вычислить ответ на следующую задачу. Меган ведет трех своих братьев в кино, всего ей нужно купить 4 билета, и каждый билет стоит 8 фунтов стерлингов. Сколько будет полная стоимость поездки? Нам нужно рассчитать 4 лота по £8, что записывается 4 × 8.

Найдите 4 в вертикальном красном столбце и 8 в горизонтальном красном столбце, ответ находится в ячейке, где две линии пересекаются: 32 . Таким образом, стоимость похода в кино составит £32 .

Часто бывает необходимо умножать числа больше 10. В этом случае приведенная выше таблица умножения не может дать немедленный ответ. Тем не менее, мы все еще можем использовать его, чтобы упростить вычисления.

Лиза занимается ресторанным бизнесом. Ей приходится доставлять бутерброды на 23 предприятия, в каждом из которых работает по 14 сотрудников. Если предположить, что каждый сотрудник съедает один бутерброд, сколько бутербродов должна приготовить Лиза?

Каждому из 23 предприятий нужно по 14 бутербродов, что составляет 23 лота из 14 или, другими словами, 23, умноженное на 14. Как мы уже обнаружили, мы могли бы записать расчет наоборот. 14×23. Ответ будет таким же.

Нам нужно найти ответ на вычисление 23 × 14.

Сначала напишите свои числа в столбцах, представляющих сотни, десятки и единицы (см. нашу страницу Числа ).

Сотни	Десятки	шт.
	2	3
	1	4

Шаг 1: Начиная с правого столбца (единицы), умножьте 4 и 3. При необходимости вы можете обратиться к приведенной выше таблице умножения. Запишите ответ (12) под своим расчетом, поставив 1 в столбце десятков и 2 в столбце единиц.

Синие числа — это те, над которыми мы сейчас работаем, а розовые числа — это первая часть нашего ответа.

Сотни	Десятки	шт.
	2	3
	1	4
	1	2

Шаг 2: Затем мы умножаем 4 на следующее число, которое равно 2 (или 20, потому что оно находится в столбце десятков). Запишите свой ответ внизу в столбце десятков: Мы пишем 8 в столбце десятков (4 умножить на 2 десятка) и ноль в столбце единиц (4 умножить на 2 десятка равно 4 × 20 = 80).

Сотни	Десятки	шт.
	2	3
	1	4
	1	2
	8	0

Шаг 3: В предыдущих шагах мы умножили единицы нижнего числа (4) на верхнее число (23). Далее нам нужно умножить десятки в нижнем числе (1) на верхнее число (23). Теперь мы работаем с цифрой в столбце десятков нижнего числа и повторяем шаги, описанные выше. Оглядываясь назад на наши основные правила умножения выше, мы знаем, что когда мы умножаем число на 10, мы пишем ноль в конце. На этом шаге, поскольку мы перешли столбец и работаем с десятками, мы должны не забыть записать нули в первом столбце (единицы).

Решите 1 × 3. Как и выше, мы записываем наш ответ (3) в столбце десятков и (0) в столбце единиц.

Сотни	Десятки	шт.
	2	3
	1	4
	1	2
	8	0
	3	0

Шаг 4: Последнее умножение, которое нам нужно выполнить, это 1 × 2. Оба числа находятся в столбце десятков, поэтому мы умножаем один набор из 10 на два набора из 10. Используя правила, которые мы изучили в предыдущие шаги, нам нужно написать ноль в столбце единиц и ноль в столбце десятков. Наш ответ (1 × 2 = 2) записан в столбце сотен, потому что мы фактически вычислили 10 × 20 = 200.

Сотни	Десятки	шт.
	2	3
	1	4
	1	2
	8	0
	3	0
2	0	0

Этап 5: На этом этапе мы закончили умножение; осталось только сложить все наши ответы (розовые числа), чтобы найти общее количество необходимых бутербродов. См. нашу страницу Дополнение  , если вам нужна помощь в сложении чисел.

	Сотни	Десятки	шт.
		2	3
		1	4
		1	2
		8	0
		3	0
	2	0	0
Итого:	3	2	2

12 + 80 + 30 + 200 = 322. Мы подсчитали, что Лизе нужно сделать всего 322 бутерброды.

В приведенном выше примере показано, как выполнить умножение, разделенное на все возможные части, но по мере повышения уверенности шаги можно пропускать.

Мы могли бы, например, умножить 4 на 23, разбив сумму на части:

4 × 20 = 80
4 × 3 = 12
80 + 12 = 92

Сотни	Десятки	шт.
	2	3
	1	4
	9	2

То же самое для второго столбца:

10 × 23 = 230

Сотни	Десятки	шт.
	2	3
	1	4
	9	2
2	3	0

Наконец, мы добавляем два наших ответа:

	Сотни	Десятки	шт.
		2	3
		1	4
		9	2
	2	3	0
Итого:	3	2	2

92 + 230 = 322.

---

---

Умножение более двух чисел умножьте следующее число на первую сумму. Например, если бы Джо хотел подсчитать, сколько часов он проработал за четыре недели, расчет будет выглядеть так:

Джо работает по 7 часов в день, 5 дней в неделю в течение четырех недель.

Шаг первый:

7 × 5 = 35 (количество часов, которые Джо работает в неделю).

Шаг второй:

Чтобы найти, сколько часов Джо работает за четыре недели, мы можем умножить этот ответ (35) на 4. 35 × 4 = 140.

Если мы знаем, что Джо получает 12 фунтов стерлингов в час. , тогда мы можем подсчитать, сколько денег он заработал за четыре недели: 12 × 140.

Быстрый способ вычислить это — вычислить:
10 × 140 = 1400 (помните, что если мы умножаем на 10, мы просто добавляем ноль в конец числа, на которое умножаем).
2 × 140 = 280 то же, что 2 × 14 (с нулем на конце) или 140 + 140.

Складываем наши ответы вместе: 1400 + 280 = 1680. недельный период.

Умножение отрицательных чисел

---

Умножение отрицательного числа на положительное всегда дает отрицательный ответ:

15 × (−4) = −60

Умножение отрицательного числа на другое отрицательное число всегда дает положительный ответ:

(−15) × (−4) = 60

---

Руководство по навыкам счета

Это руководство, состоящее из четырех частей, знакомит вас с основами счета от арифметики до алгебры, с промежуточными остановками на дробях, десятичных знаках, геометрии и статистике.

Если вы хотите освежить свои знания или помочь своим детям в обучении, эта книга для вас.

---

Составные числа — определение, список, свойства и примеры

В математике составные числа — это числа, имеющие более двух делителей. Эти номера также называются составными . Составные числа — это полная противоположность простым числам, у которых есть только два делителя, то есть 1 и само число. Все натуральные числа, не являющиеся простыми, являются составными числами, так как их можно разделить более чем на два числа. Например, 6 является составным числом, потому что делится на 1, 2, 3 и даже на 6. В этой статье мы узнаем определение составных чисел, свойства, наименьшее составное число, четные и нечетные составные числа, список составные числа и разница между простыми и составными числами, а также множество решенных примеров в деталях.

Содержание: Определение Примеры Свойства Список составных чисел Как найти составное число Типы составных номеров Нечетный Четный Наименьшее составное число Разница между простыми и составными числами Прост-факторизация составного числа Решенные примеры Практические вопросы Часто задаваемые вопросы

Что такое составные числа в математике?

Определение 1: В математике составными числами называются числа, имеющие более двух делителей.

Определение 2: Числа, которые могут быть получены путем умножения двух наименьших положительных целых чисел и содержат хотя бы один делитель, отличный от числа «1» и самого себя, называются составными числами. Эти числа всегда имеют более двух множителей.

Факт: Любое четное число, большее 2, является составным числом.

Является ли 0 составным числом?

Ноль (0) не считается ни простым, ни составным числом, поскольку у него нет делителей.

Примеры составных чисел

Примерами составных чисел являются 6, 14, 25, 30, 52 и т. д., например:

Составные номера	Факторы
6	1, 2, 3, 6
14	1, 2, 7, 14
25	1, 5, 25
30	1, 2, 3, 5, 6, 10, 15, 30
52	1, 2, 4, 13, 26, 52

Во всех приведенных выше примерах составные числа имеют более двух делителей. Есть ряд составных чисел, которые мы можем перечислить из набора натуральных чисел от 1 до 1000 и более. Давайте посмотрим список составных чисел в следующем разделе.

Свойства составных чисел

Свойства составных чисел легко запомнить.

• Составные числа имеют более двух делителей
• Составные числа делятся без остатка на свои множители
• Каждое составное число само по себе является множителем
• Наименьшее составное число 4
• Каждое составное число будет включать как минимум два простых числа в качестве своих делителей (например, 10 = 2 x 5, где 2 и 5 — простые числа)
• Составные числа также делятся на другие составные числа

Список составных номеров

Вот список составных чисел от 1 до 100 по математике. Учащиеся могут записать это, а также попытаться написать числа после 100 для практики, такие как составные от 1 до 200 или до 500.

Таблица составных чисел

Составные числа от 1 до 200

Целые положительные числа, имеющие более двух делителей, являются составными числами. Список составных чисел от 1 до 200 приведен ниже в таблице.

4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, 22, 24, 25, 26, 27, 28, 30, 32, 33, 34, 35, 36, 38, 39, 40, 42, 44, 45, 46, 48, 49, 50, 51, 52, 54, 55, 56, 57, 58, 60, 62, 63, 64, 65, 66, 68, 69, 70, 72, 74, 75, 76, 77, 78, 80, 81, 82, 84, 85, 86, 87, 88, 90, 91, 92, 93, 94, 95, 96, 98, 99, 100, 102, 104, 105, 106, 108, 110, 111, 112, 114, 115, 116, 117, 118, 119, 120, 121, 122, 123, 124, 125, 126, 128, 129, 130, 132, 133, 134, 135, 136, 138, 140, 141, 142, 143, 144, 145, 146, 147, 148, 150, 152, 154, 155, 156, 157, 158, 159, 160, 162, 164, 165, 166, 168, 170, 172, 174, 175, 176, 177, 178, 180, 182, 184, 185, 186, 187, 188, 189, 190, 192, 194, 195 , 196 и 198.

Как найти составной номер?

Процедуры определения того, является ли заданное число простым или составным:

• Найти все делители натурального числа
• Число называется простым, если оно имеет только два делителя: 1 и само
.
• Если число имеет более двух делителей, то оно составное

Пример: Найдите, является ли 14 составным числом. Найдем множители числа 14. 14÷1 = 14 14÷2 = 7 14÷7 = 2 14÷14 = 1 Как мы видим, множители 14 равны 1,2,7 и 14, так что это составное число.

Типы составных чисел

В математике есть два основных типа составных чисел:

• Нечетные составные числа или составные нечетные числа
• Четные составные числа или Составные четные числа

Нечетные составные числа

Все нечетные целые числа, не являющиеся простыми, являются нечетными составными числами. Примеры составных нечетных чисел: 9, 15, 21, 25, 27, 31 и т. д.

Четные составные числа

Все четные целые числа, не являющиеся простыми, являются четными составными числами. Примеры четных составных чисел: 4, 6, 8, 10, 12, 14, 16 и т. д.

Наименьшее составное число

4 — наименьшее составное число.

Почему?

1 не является составным числом, потому что единственный делитель 1 равен 1. Целые положительные числа 2 и 3 являются простыми числами, потому что их можно разделить только на два множителя: единицу и само себя. Значит 2 и 3 не составные.

Но в случае с числом 4 у нас больше двух множителей. Делители 4 равны 1,2,4. Таким образом, это число удовлетворяет условию составного числа, как указано выше. После 4 6 является следующим составным положительным целым числом, которое имеет делители 1, 2, 3 и 6.

Следовательно, 4 — наименьшее составное число (доказано).

Важные примечания по составным номерам Наименьшее составное число = 4 Наименьшее простое число = 2 Наименьшее нечетное составное число = 9 Двузначное наименьшее составное число = 10

Разница между простыми и составными числами

Различия между простыми и составными числами в математике перечислены ниже:

Простые числа	Составные номера
Делится только на 1 и на себя, поэтому имеет только два множителя.	Имеет более двух факторов (1 и саму себя).
Можно записать только как произведение двух чисел	Можно записать как произведение двух или более чисел
Пример: 5 имеет делители 1 и 5	Пример: 4 имеет коэффициенты 1, 2 и 4

Простая факторизация составных чисел

Здесь приведен список составных числительных от 1 до 50 с их разложением на простые множители. Здесь вы можете увидеть, как составные части разложены на простые числа. Проверьте приведенную ниже таблицу, чтобы лучше понять. С помощью этой таблицы вы также можете найти составные числа за пределами 50 с их простой факторизацией.

Составные номера	Факторизация простых чисел
4	2 × 2
6	2 × 3
8	2 × 2 × 2
9	3 × 3
10	2 × 5
12	2 × 2 × 3
14	2 × 7
15	3 × 5
16	2 × 2 × 2 × 2
18	2 × 3 × 3
20	2 × 2 × 5
21	3 × 7
22	2 × 11
24	2 × 2 × 2 × 3
25	5 × 5
26	2 × 13
27	3 × 3 × 3
28	2 × 2 × 7
30	2 × 3 × 5
32	2 × 2 × 2 × 2 × 2
33	3 × 11
34	2 × 17
35	5 × 7
36	2 × 2 × 3 × 3
38	2 × 19
39	3  × 13
40	2 × 2 × 2 × 5
42	2 × 3 × 7
44	2 × 2 × 11
45	3 × 3 × 5
46	2 × 23
48	2 × 2 × 2 × 2 × 3
49	7 × 7
50	2 × 5 × 5

Видеоурок о числах

Связанные статьи

• Простые и составные числа
• Факторизация простых чисел
• Простые, составные и четные, нечетные числа

Решенные задачи на составные числа

Пример 1:

Определите, является ли 328 составным числом.

Решение:

Делители числа 328 равны 1, 2, 4, 8, 41, 82, 164, 328.

Следовательно, 328 — составное число.

Пример 2:

Какова простая факторизация числа 60?

Решение:

Разложение числа 60 на простые множители:

60 = 2 × 2 × 3 × 5.

Пример 3:

Перечислите составные числа из заданного набора чисел.

2, 4, 9, 11, 21, 31, 44, 53, 67, 88, 101, 108.

Решение:

Составные числа: 4, 9, 21, 44, 88, 108.

Пример 4:

Найдите произведение первых 5 составных чисел.

Решение:

Первые 5 составных чисел: 4, 6, 8, 9, 10.

Следовательно, произведение первых 5 составных чисел = 4 × 6 × 8 × 9 × 10

= 17280

Следовательно, произведение первых пяти составных чисел равно 17280.

Практические вопросы (рабочий лист)

1. Список составных чисел от 20 до 30.
2. Определите, является ли 85 составным числом.
3. Каковы простые делители числа 99?
4. Чему равна сумма делителей составного числа 18?
5. Найдите составные числа среди следующего набора чисел в данной таблице.

7	18	33	11
6	13	90	21
98	5	63	19
61	52	2	81

Чтобы узнать больше о различных типах чисел, загрузите BYJU’S -The Learning App из магазина Google Play и посмотрите интерактивные видеоролики.

Часто задаваемые вопросы о составных номерах

Что такое составной номер?

Составное число — это натуральное или положительное целое число, имеющее более двух делителей. Например, 15 имеет делители 1, 3, 5 и 15, следовательно, это составное число.

Является ли 2 составным числом?

Нет, 2 не является составным числом, потому что оно имеет только два делителя, то есть 1 и 2. Следовательно, это простое число.

Является ли 9 составным числом?

Да, 9 — составное число, поскольку оно имеет более двух делителей, например 1, 3 и 9.

Какие составные числа бывают от 1 до 100?

Список составных чисел от 1 до 100:
4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, 22, 24, 25, 26, 27, 28, 30, 32, 33, 34, 35, 36, 38, 39, 40, 42, 44, 45, 46, 48, 49, 50, 51, 52, 54, 55, 56, 57, 58, 60, 62, 63, 64, 65, 66, 68, 69, 70, 72, 74, 75, 76, 77, 78, 80, 81,82, 84, 85, 86, 87, 88, 90, 91, 92, 93, 94, 95, 96, 98, 99, 100.

Является ли число 19 простым или составным?

19 — простое число, потому что оно имеет только два делителя, то есть 1 и 19.

Является ли 1 составным числом?

Нет, потому что 1 не имеет более двух множителей, а имеет только 1 множитель.