Математика Алдамуратова 5 класс 2017 Упражнение 246 ГДЗ(дүж) решебник KZGDZ.COM
Глава II. ДЕЛИМОСТЬ НАТУРАЛЬНЫХ ЧИСЕЛ 2.6. Степень числа Упражнение 246
← Предыдущий Следующий →
Глава I. НАТУРАЛЬНЫЕ ЧИСЛА И НУЛЬ
1.1. Натуральные числа и нуль
Упражнение
134567891011121314151617
1.2. Координатный луч. Изображение натуральных чисел и числа нуль на координатном луче
Упражнение
18192021222324252627
1.3. Сравнение натуральных чисел. Двойное неравенство
Упражнение
282930313233343536373839
1.4. Сложение и вычитание натуральных чисел
Упражнение
4041424344454647484950
1.5. Умножение и деление натуральных чисел. Основное свойство частного
Упражнение
5152535455565758596061
1.
 6. Свойства арифметических действий
6. Свойства арифметических действийУпражнение
6263646566676869707172
1.7. Арифметические действия над натуральными числами
Упражнение
73747576777879
1.8. Числовые выражения. Буквенные выражения
Упражнение
80
81828384858687888990
1.9. Упрощение выражений
Упражнение
919293949596979899100101102103
1.10. Уравнение
Упражнение
104105106107108109110111112113114115116117118119120121
1.11. Формулы. Вычисление по формулам
Упражнение
122123124125126127128129130131132133134135136137138139140
1.12. Числовые последовательности
Упражнение
141142143144145146147148149150
Упражнения для повторения главы I
Упражнение
151152153154155156157158159160
161162163164165166
2.
 1. Делители натурального числа. Кратные натурального числа
1. Делители натурального числа. Кратные натурального числаУпражнение
167168169170171172173174175176177178179180181182183184185186187188
Глава II. ДЕЛИМОСТЬ НАТУРАЛЬНЫХ ЧИСЕЛ
2.2. Простые числа. Составные числа
Упражнение
189190191192193194195196197198199200
2.3. Основные свойства делимости
Упражнение
201202203204205206207208209210211212213214
2.4. Признаки делимости натуральных чисел на 2, 5 и 10
Упражнение
215216217218219220221222223224225226227
2.5. Признаки делимости натуральных чисел на 3 и на 9
Упражнение
228229230231232233234235236237238239
2.6. Степень числа
Упражнение
240
241242243244245246247248249250251252253254255256257258259260261262
2.
 7. Разложение составных чисел на простые множители
7. Разложение составных чисел на простые множителиУпражнение
263264265266267268269270271272273274275
2.8. Наибольший общий делитель. Взаимно простые числа.
Упражнение
276277278279280281282283284285286287288290291292293294295
2.9. Наименьшее общее кратное
Упражнение
296297298299300301302303304305306307308309310311312313314315
Упражнения для повторения главы II
Упражнение
316317318319320321
322323324325326327
2.10. Движение по реке
Упражнение
328329330331332333334335336337338339340341342343344345346347348
Глава III. ОБЫКНОВЕННЫЕ ДРОБИ И ДЕЙСТВИЯ НАД НИМИ
3.1. Обыкновенная дробь. Чтение и запись обыкновенных дробей
Упражнение
349350351352353354355356357358359360361362363364365366367368369370371373374
3.
 2. Основное свойство дроби. Сокращение дробей
2. Основное свойство дроби. Сокращение дробейУпражнение
375376377378379380381382383384385386387388389390391392393394395
3.3. Правильные дроби. Неправильные дроби
Упражнение
396397398399400401402
403404405406407408409410411412413414
3.4. Смешанные числа
Упражнение
415416417418419420421422423424425426427428429430431432433434435436
3.5. Изображение обыкновенных дробей и смешанных чисел на координатном луче
Упражнение
437438439440441442443444445446447448449450451452453454455456
3.6. Приведение обыкновенных дробей и смешанных чисел к наименьшему общему знаменателю
Упражнение
457458459460461462463464465466467468469470471472473474475476477
3.7. Сравнение обыкновенных дробей. Сравнение смешанных чисел
Упражнение
478479480481482
483484485486487488489490491492493494495496497498499
3.
 8. Сложение и вычитание обыкновенных дробей
8. Сложение и вычитание обыкновенных дробейУпражнение
500501502503504506507508509510511512513514515516517518519520521522523524525526527528529530531
3.9. Сложение и вычитание смешанных чисел
Упражнение
532533534535536537538539540541542543544545546547548549550551552553554555556557558559
3.10. Аликвотные дроби
Упражнение
560561562563
564565566567568569570571572
3.11. Умножение обыкновенных дробей и смешанных чисел
Упражнение
573574575576577578579580581582583584585586587588589590591592593594595596597598599600601602
3.12. Взаимно обратные числа
Упражнение
603604605
3.13. Деление обыкновенных дробей и смешанных чисел
Упражнение
606607608609610611612613614615616617618619620621622623624625626627628629630631632633634635636637638639640641642643
644645646647648649650651652653654655656657658659660661662663664665
3.
 14. Нахождение дроби от числа. Нахождение числа по его дроби
14. Нахождение дроби от числа. Нахождение числа по его дробиУпражнение
666667668669670671672673674675676677678679680681682683684685686687688689690691692693
3.15. Задачи на совместную работу
Упражнение
694695696697698699700701702703704705706707708709710711712713714
Глава IV. ДЕСЯТИЧНЫЕ ДРОБИ. ДЕЙСТВИЯ НАД ДЕСЯТИЧНЫМИ ДРОБЯМИ
4.1. Десятичная дробь. Чтение и запись десятичных дробей.
Упражнение
715716717718719720721722723
724725726727728729730731732733734
4.2. Перевод десятичной дроби в обыкновенную, обыкновенной дроби — в десятичную
Упражнение
735736737738739740741742743744745746747748749750751752753754
4.3. Изображение десятичной дроби на координатном луче. Сравнение десятичных дробей
Упражнение
755756757758759760761762763764765766767768769770771772773774775776777
4.
 4. Сложение и вычитание десятичных дробей
4. Сложение и вычитание десятичных дробейУпражнение
778779780781782783784785786787788789790791792793794795796797798799800801802803
804805806807808809810
4.5. Умножение десятичной дроби на натуральное число
Упражнение
811812813814815816817818819820821822823824825826827828829830831832833834835836837838839840
4.6. Умножение десятичных дробей
Упражнение
841842843844845846847848849850851852853854855856857858859860861862863864865866867868869870871872
4.7. Деление десятичной дроби на натуральное число
Упражнение
873874875876877878879880881882883
884885886887888889890891892893894895896897898899900901902903
4.8. Деление десятичной дроби на десятичную дробь
Упражнение
904905906907908909910911912913914915916917918919920921922923924925926927928929930931932933934
4.
 9. Умножение и деление десятичной дроби на 10, 100, 1000 и на 0,1; 0,01; 0,001;
9. Умножение и деление десятичной дроби на 10, 100, 1000 и на 0,1; 0,01; 0,001;Упражнение
935936937938939940941942943944945946947948949950951952953954955
4.10. Арифметические действия над обыкновенными и десятичными дробями.
Упражнение
956957958959960961962963
964965966967968969970971972973974975976977978979980981
4.11. Округление десятичных дробей
Упражнение
98298398498598698798898999099199299399499599699799899910001001100210031004
4.12. Числовые последовательности, составленные из дробей.
Упражнение
1005100610071008100910101011101210131014
Глава V. МНОЖЕСТВА
5.1. Множество. Элементы множества. Изображения множеств
Упражнение
101510161017101810191020102110221023102410251026102710281029103010311032
5.
 2. Подмножество
2. ПодмножествоУпражнение
10331034103510361037103810391040104110421043
1044104510461047104810491050
5.3. Пересечение множеств. Объединение множеств
Упражнение
105110521053105410551056105710581059106010611062106310641065106610671068
5.4. Задачи на множества
Упражнение
1069107010711072107310741075107610771078107910801081108210831084
Глава VI. ПРОЦЕНТЫ
6.1. Проценты
Упражнение
10851086108710881089109010911092109310941095109610971098109911001101110211031104110511061107110811091110111111121113
6.2. Нахождение процентов от данного числа
Упражнение
1114111511161117111811191120112111221123
112411251126112711281129113011311132113311341135113611371138113911401141
6.
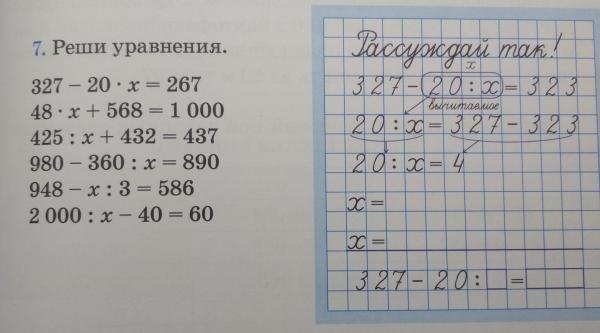 3. Нахождение числа по его процентам
3. Нахождение числа по его процентамУпражнение
1142114311441145114611471148114911501151115211531154115511561157115811591160116111621163116411651166116711681169
Упражнения для повторения главы VI.
Упражнение
117011711172117311741175117611771178117911801181118211831184
Глава VII. УГЛЫ. МНОГОУГОЛЬНИКИ
7.1. Угол. Градусная мера угла Краткие сведения о градусе
Упражнение
118511861187118811891190119111921193119411951196119711981199
7.2. Транспортир. Измерение и построение углов
Упражнение
1200120112021203
120412051206120712081209121012111212121312141215
7.3. Сравнение углов. Виды углов. Чертежный треугольник
Упражнение
121612171218121912201221122212231224122512261227122812291230
7.4. Многоугольники
Упражнение
12311232123312341235123612371238123912401241124212431244124512461247
Упражнения для повторения главы VII
Упражнение
1248124912501251125212531254
Глава VIII.
 ДИАГРАММЫ
ДИАГРАММЫ8.1. Окружность. Круг
Упражнение
125512561257125812591260126112621263126412651266126712681269127012711272127312741275
8.2 Круговой сектор
Упражнение
12761277127812791280128112821283
128412851286128712881289
8.3.Способы представления статистических данных. Столбчатые, линейные, круговые и графические диаграммы. Таблицы
Упражнение
129012911292129312941295129612971298129913001301
Глава IX. РАЗВЕРТКИ ПРОСТРАНСТВЕННЫХ ФИГУР
9.1. Прямоугольный параллелепипед и его развертка
Упражнение
13021303130413051306130713081309131013111312
9.2. Задачи на разрезание фигур Задачи на склеивание фигур
Упражнение
1313131413151316
Упражнения для повторения пройденного за год
1. Натуральные числа и нуль
Упражнение
13171318131913201321132213231324132513261327
2.
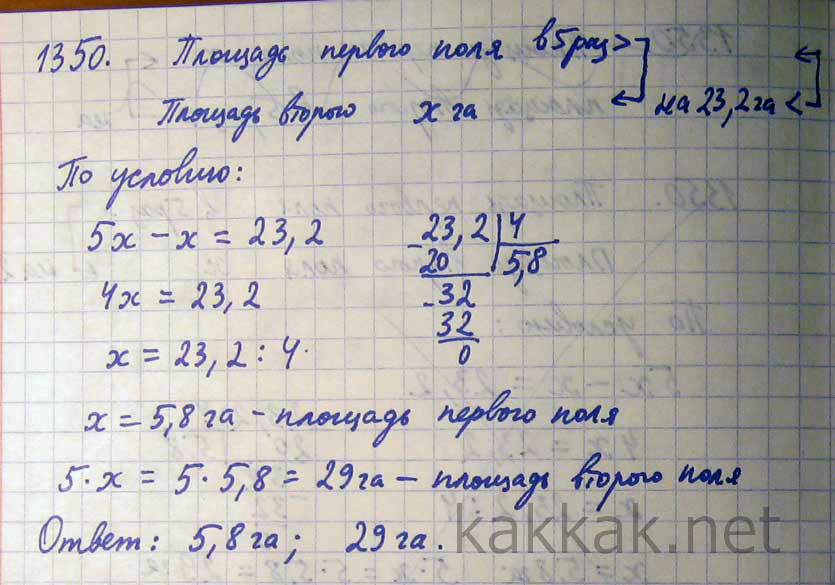 Делимость натуральных чисел
Делимость натуральных чиселУпражнение
1328132913301331133213331334
3. Обыкновенные дроби и действия над ними
Упражнение
133513361337133813391340134113421343
4. Десятичные дроби и действия над ними
Упражнение
1344134513461347134813491350
5. Множества
Упражнение
1351135213531354
6. Проценты
Упражнение
13551356135713581359
7. Углы. Многоугольники
Упражнение
136013611362
8. Диаграммы. Развертка прямоугольного параллелепипеда
Упражнение
1363
13641365
Номер 246 — ГДЗ по Математике 5 класс Учебник Виленкин, Жохов, Чесноков, Шварцбурд 2021. Часть 2 (решебник)
Номер 246 — ГДЗ по Математике 5 класс Учебник Виленкин, Жохов, Чесноков, Шварцбурд 2021. Часть 2 (решебник) — GDZwow
Часть 2 (решебник) — GDZwowПерейти к содержанию
Search for:
Авторы: Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И.
Издательство: Мнемозина
Тип: Учебник
Новая версия
1 ЧАСТЬ
Выберите номер
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139140141142143144145146147148149150151152153154155156157158159160161162163164165166167168169170171172173174175176177178179180181182183184185186187188189190191192193194195196197198199200201202203204205206207208209210211212213214215216217218219220221222223224225226227228229230231232233234235236237238239240241242243244245246247248249250251252253254255256257258259260261262263264265266267268269270271272273274275276277278279280281282283284285286287288289290291292293294295296297298299300301302303304305306307308309310312313314315316317318319320321322323324325326327328329330331332333334335336337338339340341342343344345346347348349350351352353354355356357358359360361362363364365366367368369370371372373374375376377378379380381382383384385386387388389390391392393394395396397398399400401402403404405406407408409410411412413414415416417418419420421422423424425426427428429430432433434435436437438439440441442443444445446447448449450451452453454455456457458459460461462463464465466467468469470471472473474475476477478479480481482483484485486487488489490491492493494495496497498499500501502503504505506507508509510511512513514515516517518519520521522523524525526527528529530531532533534535536537538539540541542543544545546547548549550551552553554555556557558559560561562563564565566567568569570571572573574575576577578579580581582583584585586587588589590591592593594595596597598599600601602603604605606607608609610611612613614615616617618619620621622623624625626627628629630631632633634635636637638639640641642643644645646647648649650651652653654655656657658659660661662663664665666667668669670671672673674675676677678679680681682683684686687688689690691692693694695696697698698699701702703704705706707708709710711712713714715716717718719720721722723724725726727728729730731732733734735736737738739740741742743744745746747748749750751752753754755756757758759760761762763764765766767768769770771772773774775776777778779780781782783784785786787788789790791792793793794795797798799800801802803804805806807808809810811812813814815816817817819820821822823824825826827828829830831832833834835836837838839840841842843844845846847848849850851852
2 ЧАСТЬ
Выберите номер
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273747576777879808182838485868788899091929394959697989910010110210310410510610710810911011111211311411511611711811912012112212312412512612712812913013113213313413513613713813914014114214314414514614714814915015115215315415515615715815916016116216316416516616716816917017117217317417517617717817918018118218318418518618718818919019119219319419519619719819920020120220320420520620720820921021121221321421521621721821922022122222322422522622722822923023123223323423523623723823924024124224324424524624724824925025125225325425525625725825926026126226326426526626726826927027127227327427527627727827928028128228328428528628728828929029129229329429529629729829930030130230330430530630730830931031131231331431531631731831932032132232332432532632732832933033133233333433533633733833934034134234334434534634734834935035135235335435535635735835936036136236336436536636736836937037137237337437537637737837938038138238338438538638738838939039139239339439539639739839940040140240340440540640740840941041141241341441541641741841942042142242342442542642742842943043143243343443543643743843944044144244344444544644744845045145245345445545645745845946046146246346446546646746846947047147247347447547647747847948048148248348448548648748848949049149249349449549649749849950050150250350450550650750850951051151251351451551651751851952052152252352452552652752852953053153253353453553653753853954054154254354454554654754854955055155255355455555655755855956056156256356456556656756856957057157257357457557657757857958058158258358458558658758858959059159259359459559659759859960060160260360460560660760860961061161261361461561661761861962062162262362462562662762862963063163263363463563663763863964064164264364464564664764864965065165465565665765865966066166266366466566666766866967067167267367467567667767867968068168268368468568668768868969069169269369469569669769869970070170270370470570670770870971071171271371471571671771871972072172272372472572672772872973073173273373473573673773873974074174274374474574674774874975075175275375475575675775875976076176276376476576676776876977077177277377477577677777877978078178278378478578678778878979079179279379479579679779879980080180280380480580680780880981081181281381481581681781881982082182282382482582682782882983083183283383483583683783883984084184284384484584684784884985085185285385485585685785885986086186286386486586686786886987087187287387487587687787887988088188288388488588688788888989089189289389489589689789889990090190290390490590690790890991091191291391491591691791891992092192292392492592692792892993093193293393493593693793893994094194294394494594694794894995095195295395495595695795895996096196296396496596696796896997097197297397497597697797897998098198298398498598698798898999099199299399499599699799899910001001100210031004100510061007100810091010101110121013101410151016101710181019102010211022102310241025102610271028102910301031103210331034103510361037103810391040104110421043104410451046104710481049105010511052105310541055105610571058105910601061106210631064106510661067106810691070107110721073107410751076107710781079108010811082108310841085108610871088108910901091109210931094109510961097109810991100110111021103110411051106110711081109111011111112111311141115111611171118111911201121112211231124112511261127112811291130113111321133113411351136113711381139114011411142114311441145114611471148114911501151115211531154115511561157115811591160116111621163116411651166116711681169117011711172117311741175117611771178117911801181118211831184118511861187118811891190119111921193119511961197119811991200120112021203120412051206120712081209121012111212121312141215121612171218121912201221122212231224122512261227122812291230123112321233123412351236123712381239124012411242124312441245124612471248124912501251125212531254125512561257125812591260126112621263126412651266126712681269127012711272127312741275127612771278127912801281128212831284128512861287128812891290129112921293129412951296129712981299130013011302130313041305130613071308130913101311131213131314131513161317131813191320132113221323132413251326132713281329133013311332133313341335133613371338133913401341134213431344134513461347134813491350135113521353135413551356135713581359136013611362136313641365136613671368136913701371137213731374137513761377137813791380138113821383138413851386138713881389139013911392139313941395139613971398139914001401140214031404140514061407140814091410141114121413141414151416141714181419142014211422142314241425142614271428142914301431143214331434143514361437143814391440144114421443144414451446144714481449145014511452145314541455145614571458145914601461146214631464146514661467146814691470147114721473147414751476147714781479148014811482148314841485148614871488148914901491149214931494149514961497149814991500150115021503150415051506150715081509151015111512151315141515151615171518151915201521152215231524152515261527152815291530153115321533153415351536153715381539154015411542154315441545154615471548154915501551155215531554155515561557155815591560156115621563156415651566156715681569157015711572157315741575157615771578157915801581158215831584158515861587158815891590159115921593159415951596159715981599160016011602160316041605160616071608160916101611161216131614161516161617161816191620162116221623162416251626162716281629163016311632163316341635163616371638163916401641164216431644164516461647164816491650165116521653165416551656165716581659166016611662166316641665166616671668166916701671167216731674167516761677167816791680168116821683168416851686168716881689169016911692169316941695169616971698169917001701170217031704170517061707170817091710171117121713171417151716171717181719172017211722172317241725172617271728172917301731173217331734173517361737173817391740174117421743174417451746174717481749175017511752175317541756175717581759176017611762176317641765176617671768176917701771177217731774177517761777177817791780178117821783178417851786178717881789179017911792179317941795179617971798179918001801180218031804180518061807180818091810181118121813181418151816181718181819182018211822182318241825182618271828182918301831183218331834183518361837183818391840184118421843184418451846184718481849
Adblockdetector
дайын үй жұмыстары Математика Алдамуратова 5 класс 2017 Упражнение 246 2021
Глава I.
 НАТУРАЛЬНЫЕ ЧИСЛА И НУЛЬ
НАТУРАЛЬНЫЕ ЧИСЛА И НУЛЬ1.1. Натуральные числа и нуль
134567891011121314151617
1.2. Координатный луч. Изображение натуральных чисел и числа нуль на координатном луче
18192021222324252627
1.3. Сравнение натуральных чисел. Двойное неравенство
282930313233343536373839
1.4. Сложение и вычитание натуральных чисел
4041424344454647484950
1.5. Умножение и деление натуральных чисел. Основное свойство частного
5152535455565758596061
1.6. Свойства арифметических действий
6263646566676869707172
1.7. Арифметические действия над натуральными числами
73747576777879
1.8. Числовые выражения. Буквенные выражения
8081828384858687888990
1.9. Упрощение выражений
919293949596979899100101102103
1.
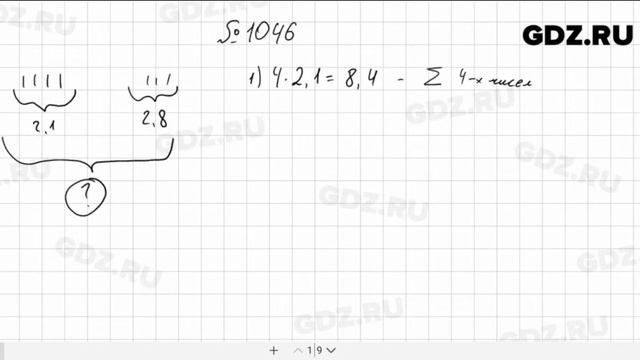 10. Уравнение
10. Уравнение104105106107108109110111112113114115116117118119120
121
1.11. Формулы. Вычисление по формулам
122123124125126127128129130131132133134135136137138139140
1.12. Числовые последовательности
141142143144145146147148149150
Упражнения для повторения главы I
151152153154155156157158159160161162163164165166
2.1. Делители натурального числа. Кратные натурального числа
167168169170171172173174175176177178179180181182183184185186187188
Глава II. ДЕЛИМОСТЬ НАТУРАЛЬНЫХ ЧИСЕЛ
2.2. Простые числа. Составные числа
189190191192193194195196197198199200
2.3. Основные свойства делимости
201202203204205206207208209210211212213214
2.4. Признаки делимости натуральных чисел на 2, 5 и 10
215216217218219220221222223224225226227
2.
 5. Признаки делимости натуральных чисел на 3 и на 9
5. Признаки делимости натуральных чисел на 3 и на 9228229230231232233234235236237238239
2.6. Степень числа
240
241242243244245246247248249250251252253254255256257258259260261262
2.7. Разложение составных чисел на простые множители
263264265266267268269270271272273274275
2.8. Наибольший общий делитель. Взаимно простые числа.
276277278279280281282283284285286287288290291292293294295
2.9. Наименьшее общее кратное
296297298299300301302303304305306307308309310311312313314315
Упражнения для повторения главы II
316317318319320321322323324325326327
2.10. Движение по реке
328329330331332333334335336337338339340341342343344345346347348
Глава III. ОБЫКНОВЕННЫЕ ДРОБИ И ДЕЙСТВИЯ НАД НИМИ
3.
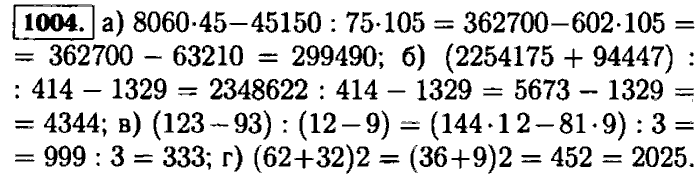 1. Обыкновенная дробь. Чтение и запись обыкновенных дробей
1. Обыкновенная дробь. Чтение и запись обыкновенных дробей349350351352353354355356357358359360361
362363364365366367368369370371373374
3.2. Основное свойство дроби. Сокращение дробей
375376377378379380381382383384385386387388389390391392393394395
3.3. Правильные дроби. Неправильные дроби
396397398399400401402403404405406407408409410411412413414
3.4. Смешанные числа
415416417418419420421422423424425426427428429430431432433434435436
3.5. Изображение обыкновенных дробей и смешанных чисел на координатном луче
437438439440441442443444445446447448449450451452453454455456
3.6. Приведение обыкновенных дробей и смешанных чисел к наименьшему общему знаменателю
457458459460461462463464465466467468469470471472473474475476477
3.
 7. Сравнение обыкновенных дробей. Сравнение смешанных чисел
7. Сравнение обыкновенных дробей. Сравнение смешанных чисел478479480481482
483484485486487488489490491492493494495496497498499
3.8. Сложение и вычитание обыкновенных дробей
500501502503504506507508509510511512513514515516517518519520521522523524525526527528529530531
3.9. Сложение и вычитание смешанных чисел
532533534535536537538539540541542543544545546547548549550551552553554555556557558559
3.10. Аликвотные дроби
560561562563564565566567568569570571572
3.11. Умножение обыкновенных дробей и смешанных чисел
573574575576577578579580581582583584585586587588589590591592593594595596597598599600601602
3.12. Взаимно обратные числа
603
604605
3.13. Деление обыкновенных дробей и смешанных чисел
606607608609610611612613614615616617618619620621622623624625626627628629630631632633634635636637638639640641642643644645646647648649650651652653654655656657658659660661662663664665
3.
 14. Нахождение дроби от числа. Нахождение числа по его дроби
14. Нахождение дроби от числа. Нахождение числа по его дроби666667668669670671672673674675676677678679680681682683684685686687688689690691692693
3.15. Задачи на совместную работу
694695696697698699700701702703704705706707708709710711712713714
Глава IV. ДЕСЯТИЧНЫЕ ДРОБИ. ДЕЙСТВИЯ НАД ДЕСЯТИЧНЫМИ ДРОБЯМИ
4.1. Десятичная дробь. Чтение и запись десятичных дробей.
715716717718719720721722723
724725726727728729730731732733734
4.2. Перевод десятичной дроби в обыкновенную, обыкновенной дроби — в десятичную
735736737738739740741742743744745746747748749750751752753754
4.3. Изображение десятичной дроби на координатном луче. Сравнение десятичных дробей
755756757758759760761762763764765766767768769770771772773774775776777
4.4. Сложение и вычитание десятичных дробей
778779780781782783784785786787788789790791792793794795796797798799800801802803804805806807808809810
4.
 5. Умножение десятичной дроби на натуральное число
5. Умножение десятичной дроби на натуральное число811812813814815816817818819820821822823824825826827828829830831832833834835836837838839840
4.6. Умножение десятичных дробей
841842843
844845846847848849850851852853854855856857858859860861862863864865866867868869870871872
4.7. Деление десятичной дроби на натуральное число
873874875876877878879880881882883884885886887888889890891892893894895896897898899900901902903
4.8. Деление десятичной дроби на десятичную дробь
904905906907908909910911912913914915916917918919920921922923924925926927928929930931932933934
4.9. Умножение и деление десятичной дроби на 10, 100, 1000 и на 0,1; 0,01; 0,001;
935936937938939940941942943944945946947948949950951952953954955
4.10. Арифметические действия над обыкновенными и десятичными дробями.
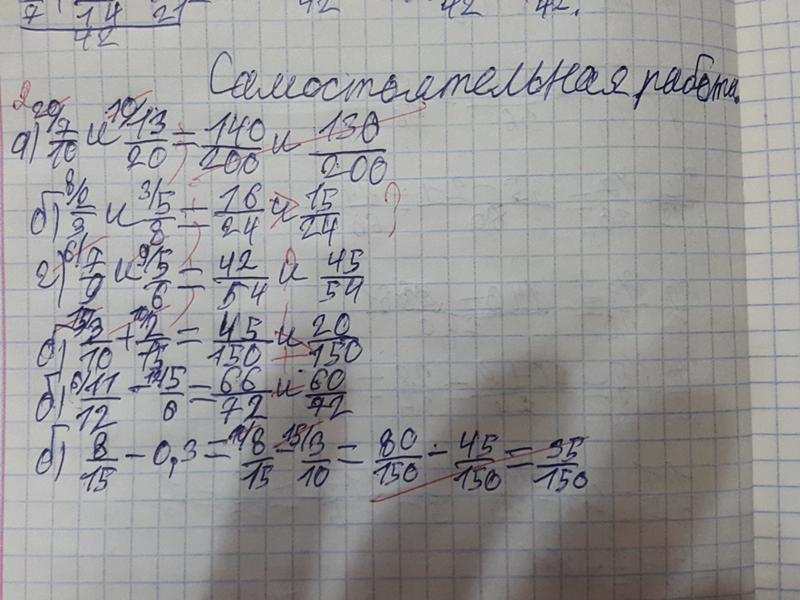
956957958959960961962963
964965966967968969970971972973974975976977978979980981
4.11. Округление десятичных дробей
98298398498598698798898999099199299399499599699799899910001001100210031004
4.12. Числовые последовательности, составленные из дробей.
1005100610071008100910101011101210131014
Глава V. МНОЖЕСТВА
5.1. Множество. Элементы множества. Изображения множеств
101510161017101810191020102110221023102410251026102710281029103010311032
5.2. Подмножество
103310341035103610371038103910401041104210431044104510461047104810491050
5.3. Пересечение множеств. Объединение множеств
105110521053105410551056105710581059106010611062106310641065106610671068
5.4. Задачи на множества
106910701071107210731074107510761077107810791080108110821083
1084
Глава VI.
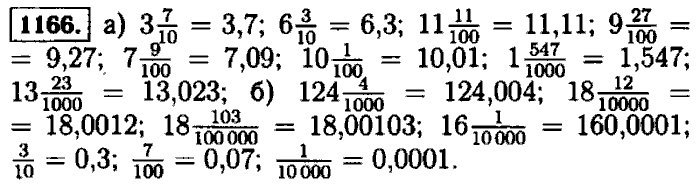 ПРОЦЕНТЫ
ПРОЦЕНТЫ6.1. Проценты
10851086108710881089109010911092109310941095109610971098109911001101110211031104110511061107110811091110111111121113
6.2. Нахождение процентов от данного числа
1114111511161117111811191120112111221123112411251126112711281129113011311132113311341135113611371138113911401141
6.3. Нахождение числа по его процентам
1142114311441145114611471148114911501151115211531154115511561157115811591160116111621163116411651166116711681169
Упражнения для повторения главы VI.
117011711172117311741175117611771178117911801181118211831184
Глава VII. УГЛЫ. МНОГОУГОЛЬНИКИ
7.1. Угол. Градусная мера угла Краткие сведения о градусе
118511861187118811891190119111921193119411951196119711981199
7.2. Транспортир. Измерение и построение углов
1200120112021203
120412051206120712081209121012111212121312141215
7.
 3. Сравнение углов. Виды углов. Чертежный треугольник
3. Сравнение углов. Виды углов. Чертежный треугольник121612171218121912201221122212231224122512261227122812291230
7.4. Многоугольники
12311232123312341235123612371238123912401241124212431244124512461247
Упражнения для повторения главы VII
1248124912501251125212531254
Глава VIII. ДИАГРАММЫ
8.1. Окружность. Круг
125512561257125812591260126112621263126412651266126712681269127012711272127312741275
8.2 Круговой сектор
12761277127812791280128112821283128412851286128712881289
8.3.Способы представления статистических данных. Столбчатые, линейные, круговые и графические диаграммы. Таблицы
129012911292129312941295129612971298129913001301
Глава IX. РАЗВЕРТКИ ПРОСТРАНСТВЕННЫХ ФИГУР
9.1. Прямоугольный параллелепипед и его развертка
13021303130413051306130713081309131013111312
9.
 2. Задачи на разрезание фигур Задачи на склеивание фигур
2. Задачи на разрезание фигур Задачи на склеивание фигур1313131413151316
Упражнения для повторения пройденного за год
1. Натуральные числа и нуль
1317131813191320132113221323
1324132513261327
2. Делимость натуральных чисел
1328132913301331133213331334
3. Обыкновенные дроби и действия над ними
133513361337133813391340134113421343
4. Десятичные дроби и действия над ними
1344134513461347134813491350
5. Множества
1351135213531354
6. Проценты
13551356135713581359
7. Углы. Многоугольники
136013611362
8. Диаграммы. Развертка прямоугольного параллелепипеда
136313641365
Математика 5 класс
‹›
|
Аннотация к рабочей программе учебного предмета «Математика» для учащихся 5-го класса (базовый уровень)
Рабочая программа учебного предмета учебного предмета «Математика» для учащихся 5-го класса (базовый уровень)
Рабочая программа учебного предмета учебного предмета «Математика» для учащихся 5-го класса (базовый уровень) составлена на основе Программы: Математика. Сборник рабочих программ. 5 – 6 классы: пособие для учителей общеобразовательных организаций / ( сост. Т.А. Бурмистрова). – 3е изд,- М.: Просвещение, 2014г. Основной образовательной программы основного общего образования МБОУ «СОШ № 41» ( протокол педсовета № 8 от 10.04.2014г., приказ директора школы № 268/1 от 18.04.2014г.), а также согласно Положению о рабочей программе учебного предмета (курса) по ФГОС ООО школы. Содержание образования соотнесено с Федеральным государственным стандартом основного общего образования по математике.
Сборник рабочих программ. 5 – 6 классы: пособие для учителей общеобразовательных организаций / ( сост. Т.А. Бурмистрова). – 3е изд,- М.: Просвещение, 2014г. Основной образовательной программы основного общего образования МБОУ «СОШ № 41» ( протокол педсовета № 8 от 10.04.2014г., приказ директора школы № 268/1 от 18.04.2014г.), а также согласно Положению о рабочей программе учебного предмета (курса) по ФГОС ООО школы. Содержание образования соотнесено с Федеральным государственным стандартом основного общего образования по математике.
Учебная литература:
- Агаханов Н.Х. Математика. Всероссийские олимпиады. 5-11 классы /Н.Х. Агаханов. – М.: Просвещение, 2010г.
- Арутюнян Е. Б. Математические диктанты для 5-9 классов: книга для учителя /Е.Б. Арутюнян. – М.: Просвещение, 2010г.
- Фарков, А.В. Математические олимпиады в школе. 5-11 классы / А.В. Фарков. – М.:Айрис-Пресс, 2010г.
- Жохов В.И. Математика.

- Жохов В.И. Математические диктанты. 5 класс: пособие для учителей и учащихся/ В.И. Жохов, И.М. Митяева. – М.: Мнемозина, 2011г.
- Жохов В.И. Математический тренажёр. 5 класс: пособие для учителей и учащихся/В.И. Жохов, В.Н. Погодин. – М. : Мнемозина,2011г.
- Чесноков, А.С. Дидактические материалы по математике для 5 класса / А.С. Чесноков, К.И. Нешков. – М.: Классик Стиль, 2010
- Я иду на урок математики: 5 класс: книга для учителя / сост. И.Л. Соловейчик. – М.: Первое сентября, 2010. – (Библиотека «Первого сентября»)
- в направлении личностного развития
Цели курса
Целями изучения курса математики в 5 классе являются систематическое развитие понятия числа, выработка умений выполнять устно и письменно арифметические действия над числами, переводить практические задачи на язык математики, подготовка учащихся к изучению систематических курсов алгебры и геометрии.
Курс строится на индуктивной основе с привлечением элементов дедуктивных рассуждений. Теоретический материал курса излагается на наглядно-интуитивном уровне, математические методы и законы формулируются в виде правил.
В ходе изучения курса учащиеся развивают навыки вычислений с натуральными числами, овладевают навыками действий с обыкновенными и десятичными дробями, получают начальные представления об использовании букв для записи выражений и свойств арифметических действий, составлении уравнений, продолжают знакомство сгеометрическими понятиями, приобретают навыки построения геометрических фигур и измерения геометрических величин.
Изучение математики в направлено на достижение целей не только в предметном направлении, но и:
- формирование у учащихся интеллектуальной честности и объективности, способности к преодолению мыслительных стереотипов, вытекающих из обыденного опыта;
- воспитание качеств личности, обеспечивающих социальную мобильность, способность принимать самостоятельные решения;
- формирование качеств мышления, необходимых для адаптации в современном информационном обществе;
- развитие интереса к математическому творчеству и математических способностей;
- в метапредметном направлении
- формирование представлений о математике как части общечеловеческой культуры, о значимости математики в развитии цивилизации и современного общества;
- развитие представлений о математике как форме описания и методе познания действительности, создание условий для приобретения первоначального опыта математического моделирования;
- формирование общих способов интеллектуальной деятельности, характерных для математики и являющихся основой познавательной культуры, значимой для различных сфер человеческой деятельности.

Основные темы курса:
1. Натуральные числа и шкалы(15 часов)
2.Сложение и вычитание натуральных чисел (21 час)
3.Умножение и деление натуральных чисел (27часов)
4.Площади и объемы (12часов)
5. Обыкновенные дроби (25 часа)
6.Десятичные дроби. Сложение и вычитание десятичных дробей (13часов)
7.Умножение и деление десятичных дробей (26 часов)
8. Инструменты для вычислений и измерений (17 часов)
9.Повторение. Решение задач. (18 часов)
Количество часов:
Согласно Федеральном базисному учебному плану для образовательных учреждений Российской Федерации на изучение математики на ступени основного общего образования отводится не менее 875 часов из расчёта 5 часов в неделю в 5-9 классах. Рабочая программа для 5 класса рассчитана на 5 часов в неделю, общий объём 170 часов.
Контрольных работ за год – 14
Разработчики:
5 класс: учитель математики первой квалификационной категории Ульянова О. В.
В.
- Подробности
- Опубликовано: 03 декабря 2015
- Назад
- Вперёд
Полезные ссылки
Это полный урок с инструкциями и упражнениями для 5-го класса об умножении десятичных дробей на десятичные дроби. Интерпретация умножения десятичного числа на десятичное состоит в том, чтобы думать об этом как о взятии дробной части десятичного числа (символ × переводится как «из»). Урок сравнивает умножение на десятичную дробь с масштабированием и сжатием палочки. Наконец, он показывает распространенный способ десятичного умножения (умножить, как если бы десятичных точек не было; в ответе столько десятичных знаков, сколько множителей в сумме). В видео ниже я объясняю правило умножения десятичных дробей (поставьте в ответ столько десятичных цифр, сколько их в множителях). Я объясняю, откуда взялось это правило, используя умножение дробей. Урок продолжается под видео.
1. Запишите как умножение с использованием десятичной дроби и
решать. Помните, что «из» переводится как «×». Используйте верхнюю задачу
2. Решить. Используйте верхнюю задачу в каждом блоке, чтобы
Помогите решить нижний.
3. Ответ. Вам не нужно рассчитывать. а. Вы узнали, что 0,1 ×
246 означает одну десятую
246. б. Кроме того, 0,1 × 0,8 означает одну десятую
0,8. в. Будет ли результат 1,9 × 928 больше или меньше 928?
4. Палка в усадке . Сколько это будет в пикселях? Сравните проблемы.
5. Красная палочка 50 пикселей длинный. Это расширенный или сжатый . Заполнить бланки.
6. Скажите, получилась ли палочка после «умножения» будет короче или длиннее оригинала.
7.
8. Умножить сначала как будто там были НЕТ десятичных точек. Затем добавьте к ответу десятичную точку.
9. Умножить.
10. Решить.
11. Найдите общую стоимость. Напишите умножение. а. Лента стоит 1,10 доллара за метр, а вы покупаете 0,4 метров. б. Гайки стоимость 8 долларов за фунт. Вы покупаете 0,3 фунта. c. Телефон звонок стоит 7 долларов в час. Вы разговариваете 1,2 часа. d. Кружево стоит 2,20 доллара за метр, и вы покупаете 1,5 метров. Здесь вы можете сделать рабочие листы для десятичного умножения. Этот урок взят из книги Марии Миллер Math Mammoth Decimals 2 и размещен на сайте www.HomeschoolMath.net с разрешения автора. Авторское право © Мария Миллер. Он соответствует Общему базовому стандарту для 5-го класса 5.NBT.7. Mammoth Decimals 2 Учебник для самообучения для 5-6 классов, который охватывает четыре действия с десятичными числами до трех десятичных цифр, уделяя особое внимание десятичному умножению и делению. Скачать ($6,25) . Также доступен в виде печатной копии. => Узнайте больше и посмотрите бесплатные образцы! Меню уроков математики | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Множители числа 246 — Найти простые факторизации/Множители числа 246 , 123, 246. Сумма всех множителей числа 246 равна 504, а его множители в парах равны (1, 246), (2, 123), (3, 82), (6, 41).
- Все множители 246: 1, 2, 3, 6, 41, 82, 123 и 246
- Отрицательные коэффициенты числа 246: -1, -2, -3, -6, -41, -82, -123 и -246
- Простые множители числа 246: 2, 3, 41
- Факторизация числа 246: 2 1 × 3 1 × 41 1
- Сумма множителей 246: 504
1.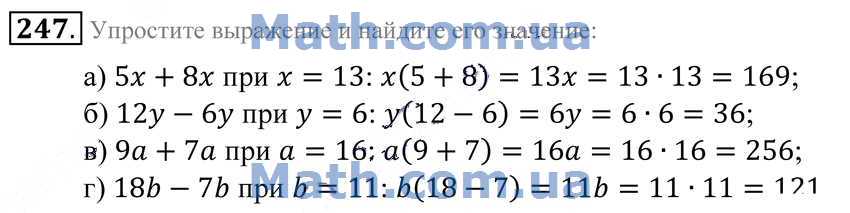 | Каковы делители числа 246? |
| 2. | Коэффициенты 246 с помощью простой факторизации |
| 3. | Коэффициенты 246 в парах |
| 4. | Часто задаваемые вопросы о факторах 246 |
Что такое множители числа 246?
Множители 246 — это пары тех чисел, произведение которых дает 246. Эти множители являются либо простыми, либо составными числами.
Как найти делители числа 246?
Чтобы найти делители числа 246, нам нужно найти список чисел, которые делят 246 без остатка.
- 246/2 = 123; следовательно, 2 — это множитель 246, а 123 — тоже множитель 246.
- 246/6 = 41; следовательно, 6 — это множитель 246, а 41 — тоже множитель 246.
Точно так же мы можем найти и другие факторы. Следовательно, делители числа 246 равны 1, 2, 3, 6, 41, 82, 123, 246.
☛ Также проверьте:
- Факторы 5 — Делители 5 равны 1, 5
- Множители 56 — Множители 56 равны 1, 2, 4, 7, 8, 14, 28, 56
- Множители числа 91 — Множители числа 91 равны 1, 7, 13, 91
- Множители 65 — Множители 65 равны 1, 5, 13, 65
- Множители 98 — Множители 98 равны 1, 2, 7, 14, 49, 98
Факторизация числа 246 множителями
Число 246 составное, поэтому оно имеет простые делители. Теперь давайте научимся вычислять простые множители числа 246.
Первый шаг — разделить число 246 на наименьший простой множитель, здесь это 2. Продолжаем делить, пока не получится ненулевой остаток.
Теперь давайте научимся вычислять простые множители числа 246.
Первый шаг — разделить число 246 на наименьший простой множитель, здесь это 2. Продолжаем делить, пока не получится ненулевой остаток.
- 246 ÷ 2 = 123
Дальнейшее деление 123 на 2 дает ненулевой остаток. Поэтому мы останавливаем процесс и продолжаем делить число 123 на следующий наименьший простой множитель. В конце концов мы останавливаемся, если следующего простого множителя не существует или когда мы не можем дальше делить.
Итак, разложение числа 246 на простые множители можно записать как 2 1 × 3 1 × 41 1 , где 2, 3, 41 — простые числа.
Коэффициенты 246 в парах
Парные множители 246 — это пары чисел, которые при умножении дают произведение 246. Парные множители 246:
- 1 × 246 = (1, 246)
- 2 × 123 = (2, 123)
- 3 × 82 = (3, 82)
- 6 × 41 = (6, 41)
Отрицательные парные множители числа 246:
- -1 × -246 = (-1, -246)
- -2 × -123 = (-2, -123)
- -3 × -82 = (-3, -82)
- -6 × -41 = (-6, -41)
ПРИМЕЧАНИЕ: Если (a, b) является парным множителем числа, то (b, a) также является парным множителем этого числа.
Коэффициенты 246 решенных примеров
Пример 1: Сколько множителей существует для числа 246?
Решение:
Делители числа 246 равны 1, 2, 3, 6, 41, 82, 123, 246. Следовательно, число 246 имеет 8 делителей.
Пример 2. Нахождение наименьшего общего кратного и наибольшего общего делителя (НОД) чисел 246 и 22.
Решение:
Делители числа 246 равны 1, 2, 3, 6, 41, 82, 123, 246, а числа 22 равны 1, 2, 11, 22.
Следовательно, наименьшее общее кратное 246 и 22 равно 2706, а наибольший общий делитель (GCF) 246 и 22 равен 2.
Пример 3. Найдите, являются ли 2, 6, 123, 202 и 246 делителями 246.
Решение:
При делении 246 на 202 остается остаток. Следовательно, число 202 не является делителем 246. Все числа, кроме 202, являются делителями 246.
Пример 4.
 Найдите произведение всех простых делителей числа 246.
Найдите произведение всех простых делителей числа 246. Решение:
Так как простые делители числа 246 равны 2, 3, 41. Следовательно, произведение простых делителей = 2 × 3 × 41 = 246,
перейти к слайдуперейти к слайдуперейти к слайдуперейти к слайду
Готовы увидеть мир глазами математика?
Математика лежит в основе всего, что мы делаем. Наслаждайтесь решением реальных математических задач на живых уроках и станьте экспертом во всем.
Записаться на бесплатный пробный урок
перейти к слайдуперейти к слайдуперейти к слайдуперейти к слайдуперейти к слайду
Часто задаваемые вопросы о факторах числа 246
Что такое факторы числа 246?
Множители числа 246 равны 1, 2, 3, 6, 41, 82, 123, 246, а его отрицательные множители равны -1, -2, -3, -6, -41, -82, -123, -246. .
Чему равна сумма множителей числа 246?
Сумма всех делителей 246 = (2 1 + 1 — 1)/(2 — 1) × (3 1 + 1 — 1)/(3 — 1) × (41 1 + 1 — 1)/(41 — 1) = 504
Какие числа являются простыми делителями числа 246?
Простые делители числа 246 равны 2, 3, 41.
Каков наибольший общий делитель чисел 246 и 81?
Множители 246 и 81 равны 1, 2, 3, 6, 41, 82, 123, 246 и 1, 3, 9, 27, 81 соответственно.
Общие делители 246 и 81: [1, 3].
Следовательно, наибольший общий делитель чисел 246 и 81 равен 3.
Сколько делителей числа 246 также являются делителями числа 128?
Так как множители 246 равны 1, 2, 3, 6, 41, 82, 123, 246, а множители 128 равны 1, 2, 4, 8, 16, 32, 64, 128.
Следовательно, [ 1, 2] — общие делители чисел 246 и 128.
Правила делимости на 2, 3, 4, 5, 6, 9 и 10
Число a делится на число b, если a \div b имеет остаток от нуля (0). Например, 15 разделить на 3 равно 5, а это означает, что его остаток равен нулю. Затем мы говорим, что 15 делится на 3.
В другом нашем уроке мы обсуждали правила делимости для 7, 11 и 12. На этот раз мы рассмотрим правила или тесты делимости для 2 , 3 , 4 , 5 , 6 , 9 и 10 .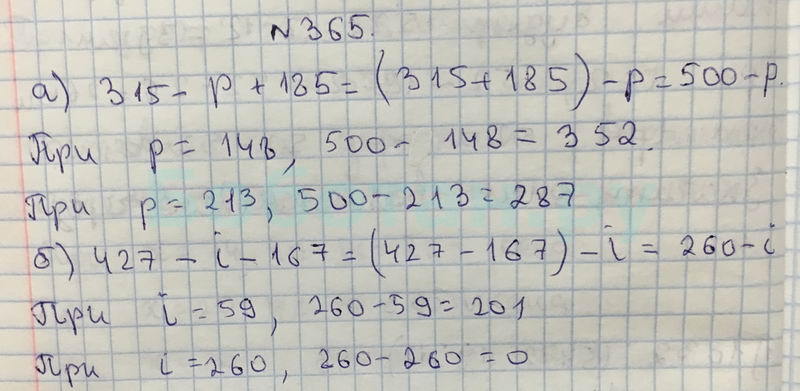 Поверьте мне, вы сможете выучить их очень быстро, потому что вы можете не знать, что у вас уже есть базовое и интуитивное понимание этого. Например, очевидно, что все четные числа делятся на 2. Это в значительной степени правило делимости для 2 . Цель этого урока правил делимости — формализовать то, что вы уже знаете.
Поверьте мне, вы сможете выучить их очень быстро, потому что вы можете не знать, что у вас уже есть базовое и интуитивное понимание этого. Например, очевидно, что все четные числа делятся на 2. Это в значительной степени правило делимости для 2 . Цель этого урока правил делимости — формализовать то, что вы уже знаете.
Правила делимости помогают нам определить, делится ли одно число на другое, не прибегая к фактическому процессу деления, такому как метод деления в длинное число. Если рассматриваемые числа численно достаточно малы, нам может не понадобиться использовать правила для проверки делимости. Однако для чисел, значения которых достаточно велики, мы хотим иметь некоторые правила, которые служили бы «ярлыками», чтобы помочь нам выяснить, действительно ли они делятся друг на друга.
Число делится на 2, если его последняя цифра 0, 2, 4, 6 или 8.
Пример 1. Делится ли число 246 на 2?
Решение: Поскольку последняя цифра числа 246 оканчивается на 6, это означает, что оно делится на 2.
Пример 2. Какие из чисел 100, 514, 309 и 768 делятся на 2?
Решение: Если мы рассмотрим все четыре числа, то только число 309 не оканчивается на 0, 2, 4, 6 или 8. Мы можем сделать вывод, что все числа выше, кроме 309делятся на 2.
Число делится на 3, если сумма цифр этого числа делится на 3.
Пример 1. Делится ли число 111 на 3?
Решение: Сложим цифры числа 111. Получим 1 + 1 + 1 = 3. Так как сумма цифр делится на 3, то и число 111 делится на 3.
Пример 2: Какое из двух чисел 522 и 713 делится на 3?
Решение: Сумма цифр числа 522 (5+2+2=9) равно 9, которое делится на 3. Это делает 522 делящимся на 3. Однако число 713 имеет 11 в виде суммы его цифр, что явно не делится на 3, поэтому 713 не делится на 3. Следовательно, только 522 делится на 3.
Число делится на 4, если две последние цифры числа делятся на 4.
Пример 1. Какое единственное число в приведенном ниже наборе делится на 4?
{945, 736, 118, 429}
Решение: Обратите внимание на последние две цифры четырех чисел в наборе. Обратите внимание, что 736 — единственное число, в котором две последние цифры (36) делятся на 4. Мы можем заключить, что 736 — единственное число в наборе, которое делится на 4.
Обратите внимание, что 736 — единственное число, в котором две последние цифры (36) делятся на 4. Мы можем заключить, что 736 — единственное число в наборе, которое делится на 4.
Пример 2: Правда или Ложь. Число 5,554 делится на 4.
Решение: Последние две цифры числа 5,554 равны 54, что не делится на 4. Это означает, что данное число НЕ делится на 4, поэтому ответ false .
Число делится на 5, если последняя цифра числа 0 или 5.
Пример 1. Множественный выбор. Какое число делится на 5.
А) 68
B) 71
C) 20
D) 44
Решение. Чтобы число делилось на 5, его последняя цифра должна быть либо 0, либо 5. варианты, только число 20 делится на 5, так что ответ выбор C .
Пример 2. Выберите все числа, которые делятся на 5.1103 343
E) 600
Решение. И 105, и 600 делятся на 5, потому что либо оканчиваются на 0, либо на 5. Таким образом, варианты B и E являются правильными ответами.
Таким образом, варианты B и E являются правильными ответами.
Число делится на 6, если оно делится и на 2, и на 3.
Пример 1. Делится ли число 255 на 6?
Решение. Чтобы число 255 делилось на 6, оно должно делиться на 2 и 3. Давайте сначала проверим, делится ли оно на 2. Обратите внимание, что 255 не является четным числом (любое число, оканчивающееся на 0, 2, 4). , 6 или 8), что делает его неделимым 2. Дальше проверять не нужно. Теперь мы можем сделать вывод, что это число не делится на 6. Ответ: 9.0767 НЕТ .
Пример 2. Делится ли число 4608 на 6?
Решение. Число является четным, поэтому оно делится на 2. Теперь проверьте, делится ли оно на 3. Сделаем это, сложив все цифры числа 4 608, что равно 4 + 6+ 0 + 8 = 18. Очевидно, сумма цифр делится на 3, потому что 18 ÷ 3 = 6. Поскольку число 4608 делится и на 2, и на 3, оно должно делиться и на 6. Ответ: ДА .
Число делится на 9если сумма цифр делится на 9.
Пример 1. Делится ли число 1764 на 9?
Решение: Чтобы число делилось на 9, сумма его цифр также должна делиться на 9. Для числа 1764 мы получаем 1 + 7 + 6 + 4 = 18. Поскольку сумма цифр равна 18 и делится на 9, поэтому 1764 должно делиться на 9.
Пример 2. Выберите все числа, которые делятся на 9.
A) 7,065
B) 3 512
C) 8,874
D) 22,778
E) 48,069
Решение: . 7,065, 7 + 0 + 6 + 5 = 18, которое делится на 9.
Число делится на 10, если его последняя цифра равна 0.
Числа 20, 40, 50, 170 и 990 делятся на 10, потому что их последняя цифра равна нулю, 0 С другой стороны, 21, 34, 127 и 468 не делятся на 10, так как они не оканчиваются нулем.
Вам также могут быть интересны:
Правила делимости на 7, 11 и 12 T E X A S E D U C A T I O N A G E N C Y Страница 1 Название округа: HARMONY ISD Система показателей академического превосходства Всего учащихся: 246 Название кампуса: HARMONY MIDDLE 1991–92 Диапазон успеваемости в кампусе: 05–08 Кампус №: 230
 5 Предыдущий год (90/91)
___________
Чтение % Успешно 62,7% 46,7% ? 46,7% — * 48,3% 47,6%
% мастерства 18,7% 8,3% ? 8,3% — * 8,6% 4,8%
Написание % прохождения 74,9% 56,9% ? 56,9% — * 58,9% 52,4%
% мастерства 24,4% 13,8% ? 13,8% — * 14,3% 9,5%
Математика % Успешно 55,9% 37,7% ? 37,7% — * 39,0% 42,9%
% мастерства 15.0% 4.9% ? 4,9% — * 5,1% 9,5%
ТААС Груп. 7 Текущий год (91/92)
___________
Чтение % прохождения {90%} 50,1% 56,0% 68,4% 56,0% (-) — — 56,0% (-) 58,3% (-)
% Мастерство 9,4% 10,0% 14,2% 10,0% — — 10,0% 0,0%
Написание % Прохождение {90%} 59,6% 67,3% 75,5% 67,3% (-) — — 67,3% (-) 75,0% (-)
% мастерства 19,4% 22,4% 27,3% 22,4% — — 22,4% 25,0%
Математика % прохождения {90%} 50,9% 52,0% 68,3% 52,0% (-) — — 52,0% (-) 58,3% (-)
% Мастерство 10,0% 8,0% 15,7% 8,0% — — 8,0% 8,3%
ТААС Груп. 7 Предыдущий год (90/91)
___________
Чтение % Успешно 44,2% 56,6% 55,2% 56,6% — * 57,7% 50,0%
% мастерства 9,4% 13,2% 12,5% 13,2% — * 13,5% 0,0%
Написание % прохождения 61,9% 73,6% 72,8% 73,6% — * 75,0% 75,0%
% мастерства 19,5% 13,2% 25,7% 13,2% — * 13,5% 12,5%
Математика % Успешно 50,3% 62,3% 62,5% 62,3% — * 61,5% 75,0%
% мастерства 12,1% 3,8% 15,9% 3,8% — * 3,8% 0,0%
T E X A S E D U C A T I O N A G E N C Y Страница 2
Название округа: HARMONY ISD Система показателей академического превосходства Всего учащихся: 246
Название кампуса: HARMONY MIDDLE 1991–92 Диапазон успеваемости в кампусе: 05–08
Кампус №: 230
5 Предыдущий год (90/91)
___________
Чтение % Успешно 62,7% 46,7% ? 46,7% — * 48,3% 47,6%
% мастерства 18,7% 8,3% ? 8,3% — * 8,6% 4,8%
Написание % прохождения 74,9% 56,9% ? 56,9% — * 58,9% 52,4%
% мастерства 24,4% 13,8% ? 13,8% — * 14,3% 9,5%
Математика % Успешно 55,9% 37,7% ? 37,7% — * 39,0% 42,9%
% мастерства 15.0% 4.9% ? 4,9% — * 5,1% 9,5%
ТААС Груп. 7 Текущий год (91/92)
___________
Чтение % прохождения {90%} 50,1% 56,0% 68,4% 56,0% (-) — — 56,0% (-) 58,3% (-)
% Мастерство 9,4% 10,0% 14,2% 10,0% — — 10,0% 0,0%
Написание % Прохождение {90%} 59,6% 67,3% 75,5% 67,3% (-) — — 67,3% (-) 75,0% (-)
% мастерства 19,4% 22,4% 27,3% 22,4% — — 22,4% 25,0%
Математика % прохождения {90%} 50,9% 52,0% 68,3% 52,0% (-) — — 52,0% (-) 58,3% (-)
% Мастерство 10,0% 8,0% 15,7% 8,0% — — 8,0% 8,3%
ТААС Груп. 7 Предыдущий год (90/91)
___________
Чтение % Успешно 44,2% 56,6% 55,2% 56,6% — * 57,7% 50,0%
% мастерства 9,4% 13,2% 12,5% 13,2% — * 13,5% 0,0%
Написание % прохождения 61,9% 73,6% 72,8% 73,6% — * 75,0% 75,0%
% мастерства 19,5% 13,2% 25,7% 13,2% — * 13,5% 12,5%
Математика % Успешно 50,3% 62,3% 62,5% 62,3% — * 61,5% 75,0%
% мастерства 12,1% 3,8% 15,9% 3,8% — * 3,8% 0,0%
T E X A S E D U C A T I O N A G E N C Y Страница 2
Название округа: HARMONY ISD Система показателей академического превосходства Всего учащихся: 246
Название кампуса: HARMONY MIDDLE 1991–92 Диапазон успеваемости в кампусе: 05–08
Кампус №: 230 _____ ________ _____ ______ ________ ________ _____ _______
% посещаемости студентов
____________________
Текущий год (91/92) {97%} 95,1% 97,0% 96,2% 97,4% (+) н/д н/д н/д н/д
Предыдущий год (90/91) 95,7% 96,5% 96,4% 96,9% н/д н/д н/д н/д
Уровень отчисления
____________
Текущий год (90/91) { 1%} 3,9% 0,0% 0,0% 0,0% (+) — * 0,0% (+) 0,0% (+)
Предыдущий год (89/90) 5,1% 0,3% 0,9% — * — — н/д
Т Е Х А С Е Д У К А Ц И Я Г Е Н Ц И Я Стр. 3
Название округа: HARMONY ISD Система показателей академического превосходства Всего учащихся: 246
Название кампуса: HARMONY MIDDLE 1991–92 Диапазон успеваемости в кампусе: 05–08
Кампус №: 230
_____ ________ _____ ______ ________ ________ _____ _______
% посещаемости студентов
____________________
Текущий год (91/92) {97%} 95,1% 97,0% 96,2% 97,4% (+) н/д н/д н/д н/д
Предыдущий год (90/91) 95,7% 96,5% 96,4% 96,9% н/д н/д н/д н/д
Уровень отчисления
____________
Текущий год (90/91) { 1%} 3,9% 0,0% 0,0% 0,0% (+) — * 0,0% (+) 0,0% (+)
Предыдущий год (89/90) 5,1% 0,3% 0,9% — * — — н/д
Т Е Х А С Е Д У К А Ц И Я Г Е Н Ц И Я Стр. 3
Название округа: HARMONY ISD Система показателей академического превосходства Всего учащихся: 246
Название кампуса: HARMONY MIDDLE 1991–92 Диапазон успеваемости в кампусе: 05–08
Кампус №: 230 5 Текущий год (91/92)
___________
Показания % Удовлетворительно {90%} 71,2% (-) 72,0% (-) 70,4% (-) 62,5% — — — —
% мастерства 21,2% 16,0% 25,9% 12,5% — — — —
Написание % Прохождение {90%} 76,9% (-) 68,0% (-) 85,2% (-) 28,6% — — — —
% мастерства 15,4% 12,0% 18,5% 0,0% — — — —
Математика % прохождения {90%} 62,3% (-) 61,5% (-) 63,0% (-) 37,5% — — — —
% мастерства 11,3% 11,5% 11,1% 0,0% — — — —
ТААС Груп. 5 Предыдущий год (90/91)
___________
Чтение % Успешно 46,7% 40,7% 51,5% 14,3% — — — —
% мастерства 8,3% 3,7% 12,1% 0,0% — — — —
Написание % прохождения 56,9% 46,2% 65,6% 23,1% — — — —
% мастерства 13,8% 7,7% 18,8% 0,0% — — — —
Математика % Успешно 37,7% 25,9% 47,1% 7,1% — — — —
% мастерства 4,9% 0,0% 8,8% 0,0% — — — —
ТААС Груп. 7 Текущий год (91/92)
___________
Чтение % прохождения {90%} 56,0% (-) 56,0% (-) 56,0% (-) 50,0% — — — —
% Мастерство 10.0% 8.
5 Текущий год (91/92)
___________
Показания % Удовлетворительно {90%} 71,2% (-) 72,0% (-) 70,4% (-) 62,5% — — — —
% мастерства 21,2% 16,0% 25,9% 12,5% — — — —
Написание % Прохождение {90%} 76,9% (-) 68,0% (-) 85,2% (-) 28,6% — — — —
% мастерства 15,4% 12,0% 18,5% 0,0% — — — —
Математика % прохождения {90%} 62,3% (-) 61,5% (-) 63,0% (-) 37,5% — — — —
% мастерства 11,3% 11,5% 11,1% 0,0% — — — —
ТААС Груп. 5 Предыдущий год (90/91)
___________
Чтение % Успешно 46,7% 40,7% 51,5% 14,3% — — — —
% мастерства 8,3% 3,7% 12,1% 0,0% — — — —
Написание % прохождения 56,9% 46,2% 65,6% 23,1% — — — —
% мастерства 13,8% 7,7% 18,8% 0,0% — — — —
Математика % Успешно 37,7% 25,9% 47,1% 7,1% — — — —
% мастерства 4,9% 0,0% 8,8% 0,0% — — — —
ТААС Груп. 7 Текущий год (91/92)
___________
Чтение % прохождения {90%} 56,0% (-) 56,0% (-) 56,0% (-) 50,0% — — — —
% Мастерство 10.0% 8. 0% 12.0% 0.0% — — — —
Написание % Прохождение {90%} 67,3% (-) 62,5% (-) 72,0% (-) 44,4% — — — —
% мастерства 22,4% 16,7% 28,0% 22,2% — — — —
Математика % Успешно {90%} 52,0% (-) 60,0% (-) 44,0% (-) 50,0% — — — —
% Мастерство 8.0% 8.0% 8.0% 10.0% — — — —
ТААС Груп. 7 Предыдущий год (90/91)
___________
Чтение % Успешно 56,6% 52,4% 59,4% 27,3% — — — —
% мастерства 13,2% 9,5% 15,6% 0,0% — — — —
Написание % Прохождение 73,6% 57,1% 84,4% 72,7% — — — —
% мастерства 13,2% 4,8% 18,8% 0,0% — — — —
Математика % Успешно 62,3% 57,1% 65,6% 27,3% — — — —
% мастерства 3,8% 4,8% 3,1% 0,0% — — — —
T E X A S E D U C A T I O N A G E N C Y Страница 4
Название округа: HARMONY ISD Система показателей академического превосходства Всего учащихся: 246
Название кампуса: HARMONY MIDDLE 1991–92 Диапазон успеваемости в кампусе: 05–08
Кампус №: 230
0% 12.0% 0.0% — — — —
Написание % Прохождение {90%} 67,3% (-) 62,5% (-) 72,0% (-) 44,4% — — — —
% мастерства 22,4% 16,7% 28,0% 22,2% — — — —
Математика % Успешно {90%} 52,0% (-) 60,0% (-) 44,0% (-) 50,0% — — — —
% Мастерство 8.0% 8.0% 8.0% 10.0% — — — —
ТААС Груп. 7 Предыдущий год (90/91)
___________
Чтение % Успешно 56,6% 52,4% 59,4% 27,3% — — — —
% мастерства 13,2% 9,5% 15,6% 0,0% — — — —
Написание % Прохождение 73,6% 57,1% 84,4% 72,7% — — — —
% мастерства 13,2% 4,8% 18,8% 0,0% — — — —
Математика % Успешно 62,3% 57,1% 65,6% 27,3% — — — —
% мастерства 3,8% 4,8% 3,1% 0,0% — — — —
T E X A S E D U C A T I O N A G E N C Y Страница 4
Название округа: HARMONY ISD Система показателей академического превосходства Всего учащихся: 246
Название кампуса: HARMONY MIDDLE 1991–92 Диапазон успеваемости в кампусе: 05–08
Кампус №: 230 (b) В знаменателе для этого расчета используются только учащиеся, которые предоставили информацию о мобильности в отчетах TAAS.
Т Е Х А С Е Д У К А Ц И Я Н А Г Е Н Ц И Я Раздел II — 2
Название округа: HARMONY ISD Система показателей академического превосходства Всего учащихся: 246
Название кампуса: HARMONY MIDDLE 1991–92 Профиль кампуса Диапазон оценок: 05–08
Кампус №: 230
(b) В знаменателе для этого расчета используются только учащиеся, которые предоставили информацию о мобильности в отчетах TAAS.
Т Е Х А С Е Д У К А Ц И Я Н А Г Е Н Ц И Я Раздел II — 2
Название округа: HARMONY ISD Система показателей академического превосходства Всего учащихся: 246
Название кампуса: HARMONY MIDDLE 1991–92 Профиль кампуса Диапазон оценок: 05–08
Кампус №: 230 США 22 868 долл. США 20 398 долл. США 22 833 долл. США
6-10 лет опыта $24 610 $26 157 $24 484 $26 180
11-20 лет опыта $27 166 $30 06926 227 долларов 29 989 долларов
0ver 20 лет опыта $29 106 $34 016 $29 106 $34 258
Средняя фактическая заработная плата:
Учителя 25 087 долларов 27 455 долларов 24 459 долларов 27 557 долларов
Профессиональная поддержка 30 603 долл. США 33 102 долл. США 28 508 долл. США 33 491 долл. США
Администрация кампуса $40 257 $44 13938 623 долл. США 43 933 долл. США
? Указывает, что данные для этого элемента вышли за пределы разумного диапазона.
Т Е Х А С Е Д У К А Ц И Я Н А Г Е Н Ц И Я Раздел II — 3
Название округа: HARMONY ISD Система показателей академического превосходства Всего учащихся: 246
Название кампуса: HARMONY MIDDLE 1991–92 Профиль кампуса Диапазон оценок: 05–08
Кампус №: 230
США 22 868 долл. США 20 398 долл. США 22 833 долл. США
6-10 лет опыта $24 610 $26 157 $24 484 $26 180
11-20 лет опыта $27 166 $30 06926 227 долларов 29 989 долларов
0ver 20 лет опыта $29 106 $34 016 $29 106 $34 258
Средняя фактическая заработная плата:
Учителя 25 087 долларов 27 455 долларов 24 459 долларов 27 557 долларов
Профессиональная поддержка 30 603 долл. США 33 102 долл. США 28 508 долл. США 33 491 долл. США
Администрация кампуса $40 257 $44 13938 623 долл. США 43 933 долл. США
? Указывает, что данные для этого элемента вышли за пределы разумного диапазона.
Т Е Х А С Е Д У К А Ц И Я Н А Г Е Н Ц И Я Раздел II — 3
Название округа: HARMONY ISD Система показателей академического превосходства Всего учащихся: 246
Название кампуса: HARMONY MIDDLE 1991–92 Профиль кампуса Диапазон оценок: 05–08
Кампус №: 230 США 2 683 долл. США 3 771 долл. США 3 742 долл. США
% Расходы по функциям:
Обучение 86,2% 74,3% 60,8% 61,3%
Учебное администрирование — 0,1% — 2,4%
Администрация кампуса 11,5% 8,2% 7,0% 5,7%
Прочие расходы кампуса 2,4% 17,5% 32,1% 30,5%
Операционные расходы на обучение $500 332 $135 101,991 1 667 942 долл. США 7 941 370 265 долл. США
Операционные расходы на обучение на одного учащегося 2 034 долл. США 1 993 долл. США 2 294 долл. США 2 295 долл. США
_____________________________________________________________________________________________________________________________
ИНФОРМАЦИЯ О ПРОГРАММЕ |——-Кампус——-| Кампус Район Штат
Подсчет процентной группы
Зачисление студентов по программам:
Специальное образование 33 13,4% 90,7% 12,2% 9,9%
Профессиональное образование 0 — 9,1% 20,1% 13,0%
Двуязычное образование/ESL образование 4 1,6% 0,7% 1,4% 8,9%
Образование для одаренных и талантливых 22 8,9% 13,2% 7,8% 7,4%
Учителя по программам (обслуживаемое население):
Обычное образование 14,4 88,1% 790,6% 81,6% 71,5%
Специальное образование 1,0 6,1% 9,6% 5,9% 9,0%
Компенсационное образование 0,6 3,9% 3,2% 5,4% 5,4%
Профессиональное образование 0,0 — 1,9% 3,7% 4,0%
Двуязычное образование/ESL образование 0,0–0,3% 1,0% 6,1%
Образование для одаренных и талантливых 0,3 1,9% 3,1% 2,4% 2,2%
Другое 0,0 — 2,4% — 1,8%
Операционные расходы на обучение по программам:
Обычное образование $432 989 86,5% 82,5% 79,3% 69,9%
Специальное образование $26 320 5,3% 10,5% 5,9% 10,7%
Компенсационное образование $30 575 6,1% 3,7% 7,3% 10,7%
Профессиональное образование $0 — 1,3% 5,0% 4,1%
Двуязычное/ESL образование $250 — 0,3% 0,5% 2,7%
Обучение для одаренных и талантливых $10,198 2,0% 1,7% 2,1% 1,7%
Другое $0 — — — 0,2%
США 2 683 долл. США 3 771 долл. США 3 742 долл. США
% Расходы по функциям:
Обучение 86,2% 74,3% 60,8% 61,3%
Учебное администрирование — 0,1% — 2,4%
Администрация кампуса 11,5% 8,2% 7,0% 5,7%
Прочие расходы кампуса 2,4% 17,5% 32,1% 30,5%
Операционные расходы на обучение $500 332 $135 101,991 1 667 942 долл. США 7 941 370 265 долл. США
Операционные расходы на обучение на одного учащегося 2 034 долл. США 1 993 долл. США 2 294 долл. США 2 295 долл. США
_____________________________________________________________________________________________________________________________
ИНФОРМАЦИЯ О ПРОГРАММЕ |——-Кампус——-| Кампус Район Штат
Подсчет процентной группы
Зачисление студентов по программам:
Специальное образование 33 13,4% 90,7% 12,2% 9,9%
Профессиональное образование 0 — 9,1% 20,1% 13,0%
Двуязычное образование/ESL образование 4 1,6% 0,7% 1,4% 8,9%
Образование для одаренных и талантливых 22 8,9% 13,2% 7,8% 7,4%
Учителя по программам (обслуживаемое население):
Обычное образование 14,4 88,1% 790,6% 81,6% 71,5%
Специальное образование 1,0 6,1% 9,6% 5,9% 9,0%
Компенсационное образование 0,6 3,9% 3,2% 5,4% 5,4%
Профессиональное образование 0,0 — 1,9% 3,7% 4,0%
Двуязычное образование/ESL образование 0,0–0,3% 1,0% 6,1%
Образование для одаренных и талантливых 0,3 1,9% 3,1% 2,4% 2,2%
Другое 0,0 — 2,4% — 1,8%
Операционные расходы на обучение по программам:
Обычное образование $432 989 86,5% 82,5% 79,3% 69,9%
Специальное образование $26 320 5,3% 10,5% 5,9% 10,7%
Компенсационное образование $30 575 6,1% 3,7% 7,3% 10,7%
Профессиональное образование $0 — 1,3% 5,0% 4,1%
Двуязычное/ESL образование $250 — 0,3% 0,5% 2,7%
Обучение для одаренных и талантливых $10,198 2,0% 1,7% 2,1% 1,7%
Другое $0 — — — 0,2% Математические науки | Smith College
Математика – одна из старейших учебных дисциплин. Однако, несмотря на всю свою древность, это современная, быстро развивающаяся область. Всего 70 лет назад можно было бы сказать, что математика состоит из алгебры, анализа, теории чисел и геометрии. Сегодня появилось так много новых областей, что термин «математика» кажется почти неадекватным. Новое словосочетание «математические науки» вошло в моду для описания широкой дисциплины, включающей бурно развивающиеся области статистики, исследования операций, биоматематики и информатики, а также традиционные разделы чистой и прикладной математики.
Однако, несмотря на всю свою древность, это современная, быстро развивающаяся область. Всего 70 лет назад можно было бы сказать, что математика состоит из алгебры, анализа, теории чисел и геометрии. Сегодня появилось так много новых областей, что термин «математика» кажется почти неадекватным. Новое словосочетание «математические науки» вошло в моду для описания широкой дисциплины, включающей бурно развивающиеся области статистики, исследования операций, биоматематики и информатики, а также традиционные разделы чистой и прикладной математики.
На этой странице
- Требования
- Курсы
- События
- Факультет
- Возможности
- Постбакалавриат
наверх
Объявления
Объявление основного или дополнительного образования по математике
Вот несколько слайдов из нашей последней презентации основного предмета:
Если вы хотите объявить основной или дополнительный предмет, первым делом заполните эту форму запроса консультанта.
Требования
Цели обучения математическим наукам
- Учитывая проблему, распознать ее математические аспекты и создать абстрактную математическую модель проблемы.
- Базовые математические навыки (через дискретную математику, курс исчисления и линейную алгебру).
- Чтобы эффективно писать математику:
- Математическое направление: Понимать и писать математические доказательства.
- Отслеживание статистики: для написания профессионального технического отчета.
- Эффективно говорить математические или статистические термины в устных презентациях.
- Правильно использовать технологии для изучения и понимания математики.
Главная
Консультанты : Пау Атела, Бенджамин Баумер, Дженнифер Бейхман, Патрисия Кан, Лука Капонья, Кристоф Голе, Раджан Мехта, Геремиас Поланко, Кэндис Прайс, Даниэль Шультейс, Илеана Стрейну, Джулианна Тимочко
Если вы хотите объявить математическую специальность или второстепенную специализацию, первым делом заполните здесь форму предпочтения консультанта.
У специальности математика есть базовые требования, основные требования, требования к глубине и общие требования к кредитам.
Базовые требования состоят из 111 мес., 112 мес., 153 мес., 211 мес. и 212 мес. Некоторые из этих требований могут быть отменены для хорошо подготовленного учащегося.
Основное требование состоит из одного курса алгебры (MTH 233 или MTH 238) и одного курса анализа (MTH 280 или MTH 281). В качестве альтернативы учащиеся, выбравшие математическую специальность до осени 22 года, могут сосредоточиться на статистике; студенты, изучающие этот трек по специальности, не обязаны проходить курс алгебры, а вместо этого должны пройти MTH 220, MTH 246, MTH 320 или либо MTH 29.1 или MTH 290. Студенты, намеревающиеся объявить специальность после осени 22 года, не имеют этой возможности, и им рекомендуется выбрать специальность MST (математическая статистика).
Для получения специальности необходимо пройти хотя бы один курс повышения квалификации. Это требование глубины. Продвинутый курс — это курс математики в Smith под номерами от 310 до 390.
Это требование глубины. Продвинутый курс — это курс математики в Smith под номерами от 310 до 390.
- В общей сложности, по специальностям необходимо набрать не менее 36 кредитов среди курсов с номером 153 или выше, за следующими исключениями:
- С одобрения факультета до 8 кредитов могут быть удовлетворены за курсы, пройденные вне факультета математики и статистики.
- Курсы, изучаемые вне факультета, должны содержать либо существенное математическое содержание на уровне более продвинутом, чем MTH 211 и 212, либо статистическое содержание на уровне более продвинутом, чем MTH 220. Как правило, такому курсу с 4 кредитами дается 2 кредита на математику. главный.
- Обратите внимание, что курсы, включенные в перекрестный список с математикой и другим факультетом (CSC 250, ECO 220, PHI 202, PHI 203, PHI 220 и SDS 292), считаются курсами математики и получают полный зачет по основной специальности математики. Следующие курсы соответствуют критериям для получения 2 кредитов по специальности «математика»: AST 337, AST 351, AST 352, CHM 331, CHM 332, CSC 240, CSC 252, CSC 274, CSC 334, ECO 240, ECO 255, EGR 220, EGR.
 315, рециркуляция ОГ 320, рециркуляция ОГ 326, рециркуляция ОГ 374, рециркуляция ОГ 389, LOG 100, PHY 210, PHY 317, PHY 318, PHY 319, PHY 327 и SDS 293. Студент может подать прошение в отдел, если он желает получить зачет по любому курсу, не указанному в этом списке.
315, рециркуляция ОГ 320, рециркуляция ОГ 326, рециркуляция ОГ 374, рециркуляция ОГ 389, LOG 100, PHY 210, PHY 317, PHY 318, PHY 319, PHY 327 и SDS 293. Студент может подать прошение в отдел, если он желает получить зачет по любому курсу, не указанному в этом списке.
Обычно все курсы, которые засчитываются как основные, так и дополнительные, должны быть сданы для получения буквенной оценки.
Несовершеннолетние
Специальность по математическим наукам
Дополнительная программа по математике состоит из 211 и 16 кредитов, взятых из следующих: 153, 205 и курсов с номерами выше 211, включая два курса с номерами выше 218. Четыре кредита могут быть заменены восемью кредиты из списка утвержденных курсов засчитываются за 2 кредита по направлению MTH Major в описании основных требований, приведенных выше.
Дополнительное образование в области прикладной статистики
Дополнительное дополнительное обучение в области прикладной статистики предлагает студентам возможность изучать статистику в контексте интересующей их области применения. Несовершеннолетний разработан с достаточной гибкостью, чтобы позволить студенту выбирать из множества возможных областей применения. Минор состоит из пяти курсов. Среди курсов, используемых для удовлетворения основного требования учащегося, максимум два курса могут засчитываться в качестве второстепенного. Обычно не более одного курса с оценкой S/U засчитывается в несовершеннолетний. Дополнительную информацию см. на веб-сайте статистики и наук о данных.
Несовершеннолетний разработан с достаточной гибкостью, чтобы позволить студенту выбирать из множества возможных областей применения. Минор состоит из пяти курсов. Среди курсов, используемых для удовлетворения основного требования учащегося, максимум два курса могут засчитываться в качестве второстепенного. Обычно не более одного курса с оценкой S/U засчитывается в несовершеннолетний. Дополнительную информацию см. на веб-сайте статистики и наук о данных.
Награды
Проект с отличием состоит из направленного чтения, исследования и диссертации. Это возможность заниматься стипендией на высоком уровне. Студенту любого уровня, рассматривающему проект с отличием, рекомендуется проконсультироваться с директором с отличием и любым членом отдела, чтобы получить совет и дополнительную информацию.
Дипломные проекты факультета математики и статистики оцениваются в 8–12 кредитов. В идеале ваша программа должна быть одобрена департаментом весной перед выпускным годом. (Вы также можете подать заявку на летний исследовательский грант от Смита, чтобы вы могли провести лето перед выпускным годом в Нортгемптоне, начав работу над своим проектом.)
(Вы также можете подать заявку на летний исследовательский грант от Смита, чтобы вы могли провести лето перед выпускным годом в Нортгемптоне, начав работу над своим проектом.)
Право на участие
Обычно учащийся, который подает заявку на работу с отличием, должен иметь общий средний балл 3.0 для курсов до первого года обучения и средний балл 3.3 для курсов по специальности. Студент может подать заявление либо во втором семестре младшего курса, либо ко второй неделе первого семестра старшего курса; мы настоятельно рекомендуем первое.
Финансовая помощь
Мемориальный фонд Томлинсона оказывает финансовую помощь дипломным проектам. Если вы заинтересованы в получении средств, вы должны заполнить форму заявки «Финансовая помощь для ведомственных наград» и отправить ее вместе с заявкой на получение награды. Эту форму заявления можно получить у директора почетных званий или в деканате класса.
Хронология*
Как правило, вы встречаетесь со своим консультантом по проекту несколько раз в неделю.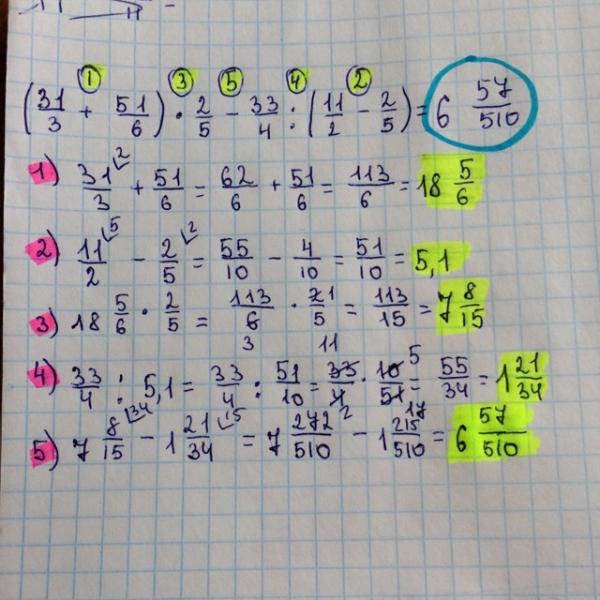 Обычно проект фокусируется на одной области и включает в себя чтение статей и книг по математике на продвинутом уровне. Написанная вами дипломная работа будет ассимиляцией и экспозицией области. Иногда проект будет включать новый вклад студента. К началу весны большая часть ваших исследований должна быть завершена, и вы начнете писать. Документ должен быть готов в середине апреля. Его читает группа преподавателей, а в начале мая вы представляете кафедре доклад о своей работе.
Обычно проект фокусируется на одной области и включает в себя чтение статей и книг по математике на продвинутом уровне. Написанная вами дипломная работа будет ассимиляцией и экспозицией области. Иногда проект будет включать новый вклад студента. К началу весны большая часть ваших исследований должна быть завершена, и вы начнете писать. Документ должен быть готов в середине апреля. Его читает группа преподавателей, а в начале мая вы представляете кафедре доклад о своей работе.
Презентация диссертации
Правила колледжа Смита предусматривают, что окончательный вариант вашей диссертации должен быть представлен вашему научному руководителю (первому читателю) и второму читателю до 15 апреля*. Этот окончательный вариант будет подвергнут оценке первым и вторым читателями. Кандидаты с отличием делают 45-минутную устную презентацию своего исследования с отличием для математического факультета, которая будет открыта для всех заинтересованных членов сообщества Smith College и других лиц по приглашению.
Вы должны ожидать вопросов от аудитории во время и после презентации. После открытой презентации будет дополнительный период вопросов только для факультета математики. Эта презентация будет запланирована на последнюю неделю занятий или периода чтения, но не позднее последнего дня периода предэкзаменационного обучения.
Оценка
- 60% тезис
- 20% устное выступление
- 20% оценок по специальности
Ваша оценка за проект (зачет, отличие, высокая оценка, высшая оценка) определяется комбинацией ваших оценок за работу, презентацию и ваши курсы по математике. Презентация имеет наименьший вес в вашей оценке, но она дает всем нам возможность услышать о том, что вы сделали. Мы также приглашаем вас выступить с вашими коллегами по специальности, хотя это не является частью официального процесса.
*Расписание для выпускников мая. Проконсультируйтесь с вашим консультантом о датах, если вы планируете получить высшее образование в январе.
Курсы
Наметьте свой майор
Обратитесь к Каталогу курсов колледжа Смит для получения информации о текущих курсах по математике и статистике.
Есть также несколько курсов, которые доступны для кредита на других факультетах, включая искусство, психологию и другие. Обратитесь к каталогу.
Какие занятия вам следует посещать, во многом зависит от того, что вы считаете наиболее интересным и каковы ваши цели. Обсудите свои варианты с вашим консультантом, а также поговорите с преподавателями конкретных курсов, которые вас интересуют.
Если вы интересуетесь наукой
Департамент предлагает различные курсы, чтобы дать вам солидный математический опыт. Исчисление III и линейная алгебра являются фундаментальными курсами. Вы также можете рассмотреть возможность изучения одного или нескольких из следующих предметов: Введение в теорию вероятностей и статистику, Дифференциальные уравнения, Дифференциальные уравнения и численные методы, Дискретная математика, Дополнительные темы непрерывной прикладной математики.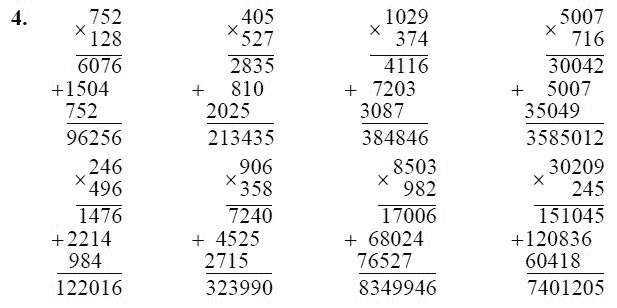
Если вы интересуетесь информатикой
Попробуйте взять некоторые из них: Исчисление III, Линейная алгебра, Современная алгебра, Дискретная математика. Многие из наших студентов имеют двойную специализацию по математике и информатике.
Если вы интересуетесь экономикой
Расчет даст вам хороший базовый опыт. Вы можете рассмотреть и другие курсы, поэтому обязательно обсудите свои варианты со своим консультантом. Если вы подумываете о поступлении в аспирантуру по экономике, экономический факультет рекомендует вам пройти MTH 211, 212, 280 и 281. Также хорошей идеей будет пройти солидный курс статистики (любой из MTH 220, 246, 29).0, 291 и 320). Многие специалисты в области экономики также хотят получить MTH 264 . Двойная специализация по математике и экономике — хороший выбор.
Если вы интересуетесь прикладной математикой
Следующие курсы работают специально с приложениями: MTH 205, 264, 353 и 364. Другие курсы, которые содержат много приложений и важны для тех, кто хочет поступить в аспирантуру по прикладной математике: MTH 220, 246, 254, 255, 280, 290, 291 и 320.
Если вы интересуетесь теоретической математикой
Следующие курсы работают с абстрактными структурами: MTH 233, 238, 246, 254, 255, 280, 281, 333, 370, 381 и 382.
Если вам понравилось исчисление
Есть много причин любить исчисление. Например, если вам нравится геометрия, вам следует рассмотреть MTH 270, 280, 370 и 382. Если вам понравилась сила исчисления для описания и понимания мира, вы захотите пройти MTH 264. Если вы очарованы представления о пределе и бесконечности и хотите докопаться до них, вам следует взять МТН 281.
Если вам понравилась линейная алгебра
Вам очень понравится MTH 233, а также MTH 238 и 333.
Если вам понравилась дискретная математика
Естественным продолжением дискретной математики будет MTH 254 или 255, а затем 353 , Кроме того, вас могут заинтересовать MTH 246 и CSC 252 (засчитывается 2 кредита к основной математике).
Если вы заинтересованы в аспирантуре по математике
Пройдите множество курсов, но обязательно пройдите MTH 233, 254 и 281 и как можно больше MTH 264, 333, 370, 381 и 382 . Вам также следует подумать о поступлении в аспирантуру Массачусетского университета.
Вам также следует подумать о поступлении в аспирантуру Массачусетского университета.
Если вы заинтересованы в аспирантуре по статистике
Совместная специальность MST по математической статистике между MTH и SDS специально разработана как подготовка к аспирантуре по статистике.
Если вы заинтересованы в аспирантуре в области исследования операций
Исследование операций — это относительно новая область математики, объединяющая математические идеи и методы, которые применяются в крупных организациях, таких как предприятия, компьютеры и правительства. Вам следует пройти MTH 211 и по крайней мере некоторые из перечисленных выше курсов по статистике, некоторые курсы по комбинаторике (MTH 254) и некоторые по информатике. Рассмотрим также разделы прикладной математики и численного анализа.
Если вы хотите стать учителем
Требования к сертификации сильно различаются в зависимости от штата. Если вы заинтересованы в преподавании в средней школе, для начала может быть достаточно специальности по математике плюс практика преподавания. В штате Массачусетс основная специальность должна включать MTH 233 или 238 и один из MTH 220 или 246. Также полезен курс, включающий геометрию, например MTH 270 или MTH 370. Вы также должны иметь некоторое представление о компьютерах. Рекомендации см. в списке курсов, перечисленных в программе MAT. Наконец, в то время как MTH 307 Topics in Mathematics Education редко предлагается, что-то эквивалентное преподается в качестве специального предмета всякий раз, когда есть студенты MAT.
В штате Массачусетс основная специальность должна включать MTH 233 или 238 и один из MTH 220 или 246. Также полезен курс, включающий геометрию, например MTH 270 или MTH 370. Вы также должны иметь некоторое представление о компьютерах. Рекомендации см. в списке курсов, перечисленных в программе MAT. Наконец, в то время как MTH 307 Topics in Mathematics Education редко предлагается, что-то эквивалентное преподается в качестве специального предмета всякий раз, когда есть студенты MAT.
Если вы заинтересованы в преподавании в начальной школе, большинство необходимых вам курсов будет проходить в отделе образования. На математическом факультете мы заботимся о том, чтобы вам было комфортно с математикой, вы видели ее разнообразие и, самое главное, чтобы она вам нравилась. При всем при этом вы должны пройти те курсы математики, которые вам больше всего нравятся. Что касается образовательных курсов, последняя информация заключается в том, что вы должны пройти EDC 235, 238, 346, 347, 404 (практика преподавания) и один факультативный для получения сертификата. Обратите внимание, что в течение семестра, когда вы проходите практику преподавания EDC 404, вы, скорее всего, не сможете пройти курс математики. Планируйте заранее и консультируйтесь с отделом образования.
Обратите внимание, что в течение семестра, когда вы проходите практику преподавания EDC 404, вы, скорее всего, не сможете пройти курс математики. Планируйте заранее и консультируйтесь с отделом образования.
Если вы хотите стать врачом
У вас все хорошо, потому что вы специализируетесь на математике. Курс по статистике был бы очень хорошей идеей. Другими полезными областями математики являются дифференциальные уравнения и комбинаторика.
Если вы хотите стать актуарием
Сдайте MTH 246, 290, 291 и 320 и актуарные экзамены, которые предлагаются периодически. Продвижение в качестве актуария достигается путем сдачи ряда экзаменов. Часто формируются неформальные студенческие учебные группы (поспрашивайте!).
Если вы хотите получить хорошую работу после выпуска
Специальность по математике хорошо подготовит вас, независимо от того, какой курс вы выберете. Студенты-математики учатся думать на ходу; они не боятся чисел и чувствуют себя как дома с абстрактными идеями. Часто это единственное, что ищут работодатели. Тем не менее, мы должны добавить, что знание компьютерного программирования очень полезно, как и некоторое знакомство со статистикой.
Часто это единственное, что ищут работодатели. Тем не менее, мы должны добавить, что знание компьютерного программирования очень полезно, как и некоторое знакомство со статистикой.
Если вам нужно что-то, чего Смит не предлагает
Если вас интересует предмет, который мы не предлагаем, вам следует поговорить с профессорами, чьи области интересов ближе всего к предмету, как к специальным исследованиям. Договоренность должна быть одобрена отделом, но обоснованные просьбы не отклоняются. Если ваш интерес особенно силен, вы можете рассмотреть проект с отличием или летнюю исследовательскую работу. Вам также следует подумать о прохождении курса (или курсов) в одной из школ консорциума.
Программы магистратуры
Программа постбакалавриата
Спонсируемая Центром женщин-математиков программа постбакалавриата предназначена для женщин со степенью бакалавра, которые не изучали математику или чья специальность математики была легкой. Эта программа открыта для всех женщин, окончивших колледж, проработавших курс по математике выше уровня исчисления и проявляющих серьезный интерес к дальнейшему изучению математики. Более подробную информацию о программе предоставляет Центр женщин в математике.
Эта программа открыта для всех женщин, окончивших колледж, проработавших курс по математике выше уровня исчисления и проявляющих серьезный интерес к дальнейшему изучению математики. Более подробную информацию о программе предоставляет Центр женщин в математике.
Магистр педагогических наук
Департамент математики и статистики в сотрудничестве с Департаментом образования и детского образования предлагает годовую программу магистра педагогических наук (MAT).
В течение одного лета и двух семестров кандидаты на получение MAT проходят три курса по математике и всю курсовую работу, необходимую для сертификации учителей средней школы в штате Массачусетс. Программа включает семестровую стажировку в местной школе. Кандидаты на программу MAT по математике должны иметь степень бакалавра по математике. Выпускники колледжей с другой специальностью будут рассматриваться, если их высшее образование включало прочную основу в области математики.
Пятый курс магистра наук в области статистики
Квалифицированные выпускники факультета математики и статистики могут подать заявление в Университет Массачусетса в Амхерсте, чтобы получить степень магистра статистики на пятом курсе. Узнайте больше о программе.
Узнайте больше о программе.
События
- Ведомственные мероприятия
- Конференция «Женщины в математике»
- Региональные собрания и конференции
Разговоры за обедом по четвергам
Большинство четвергов во время обеда проводятся беседы отдела (при условии, что вы приносите свой напиток). Выступление на кафедре — это возможность для преподавателей, студентов и друзей услышать интересное выступление и обсудить математику. Несколько разговоров происходят вечером, часто им предшествует чай или ужин.
Женщины-математики в Новой Англии (WiMiN)
23 сентября 2023 г.
Ежегодная конференция «Наши женщины-математики в Новой Англии» (WiMiN) посвящена женщинам-математикам. Мы публикуем доклады десятков студентов, аспирантов и приглашенных гостей, работающих в различных областях математики.
Зарегистрируйтесь
Зайдите позже, чтобы получить регистрационную информацию.
Smith Mathematicians (SMath)
SMath — это собрание, на котором нынешние студенты, выпускники и преподаватели могут обсудить свои проекты. На этой конференции представлены еда, выступления преподавателей и студентов, а также различные панели.
Joint Mathematics Meetings (JMM)
JMM — это национальная конференция, организованная Математической ассоциацией Америки (MAA) и Американским математическим обществом. Бывшие студенты исследовательского класса Центра (MTH 300) присутствовали, чтобы представить доклады о своей работе, а также узнать о последних достижениях в различных математических темах.
Конференция студентов по математике на реке Гудзон (HRUMC)
HRUMC — это однодневная конференция по математике, которая проводится ежегодно каждый весенний семестр в чередующихся учебных заведениях и посещается студентами и преподавателями различных университетов, колледжей и муниципальных колледжей Нью-Йорка и Новой Англии. . На конференции представлены короткие доклады студентов и преподавателей, а также более подробное выступление известного математика. Подается обед и другие легкие закуски. 9{2}}\]
Посмотреть решение play_arrowвопрос_ответ 4)
Третья сторона треугольника, если периметр треугольника равен 20 м, а две его стороны 5 м и 4 м, равна
А)
11 м
Б)
10м
В)
12м
Г)
5 м
Посмотреть решение play_arrowвопрос_ответ 5)
Найдите недостающую сторону на приведенном ниже рисунке, если его периметр равен 28 м.
А)
12м
Б)
3м
В)
9м
Г)
6м 9{2}}\]
Посмотреть решение play_arrowвопрос_ответ 7)
Длина и ширина прямоугольника равны (3а + 2) и (2а — 1). Что из следующего представляет его периметр?
А)
2(5а — 1)
Б)
(5а + 1)
В)
(5а — 1)
Г)
2(5а + 1)
Посмотреть решение play_arrowвопрос_ответ 8)
Разница между длиной и шириной прямоугольника составляет 8 см, а периметр равен 64 см. Что из следующего может быть длиной и шириной этого прямоугольника?
Что из следующего может быть длиной и шириной этого прямоугольника?
А)
Д = 12 см, В = 4 см
В)
Д = 20 см, В = 8 см
В)
Д = 20 см, В = 12 см
Г)
Д = 12 см, В = 8 см
Посмотреть решение play_arrowвопрос_ответ 9)
Площадь треугольника, основание которого равно 12 см, а высота, удвоенная основанием, равна
А)
144кв.см
B)
288 кв.см
В)
289 кв.см
Г)
Невозможно определить
Посмотреть решение play_arrowвопрос_ответ 10)
Площадь квадрата 100 кв. см. Если стороны этого квадрата увеличить на 10%, то какова будет площадь нового квадрата?
см. Если стороны этого квадрата увеличить на 10%, то какова будет площадь нового квадрата?
А)
121 кв. см
B)
101 кв. см
C)
81 кв.см
D)
169 кв. см
Посмотреть решение play_arrowвопрос_ответ 11)
Ширина прямоугольника увеличилась на 2 единицы. Его периметр теперь увеличен на ?
А)
2 шт.
Б)
4 шт.
В)
8 шт.
Г)
16 шт.
Посмотреть решение play_arrowвопрос_ответ 12)
Площадь квадрата равна площади прямоугольника I = 8 см и b = 2 см. Чему равна сторона квадрата?
Чему равна сторона квадрата?
А)
6 см
Б)
4 см
В)
3 см
Г)
8 см
Посмотреть решение play_arrowвопрос_ответ 13)
Сколько маленьких кубиков со стороной 2 см можно положить в кубическую коробку со стороной 6 см?
А)
9
Б)
12
В)
27
Г)
6
Посмотреть решение play_arrowquestion_answer 14)
Кубоид имеет размеры \[24м\х12м\х10м. \]сколько кубов со стороной 3м может поместиться в коробке?
\]сколько кубов со стороной 3м может поместиться в коробке?
А)
9
Б)
16
В)
15
Г)
24
Посмотреть решение play_arrowвопрос_ответ 15)
Площадь квадрата:
А)
произведение всех сторон
Б)
сумма всех сторон
C)
\[сторона\раз сторона\]
Г)
\[2\раз сторона\]
Посмотреть решение play_arrow 9{2}}\]A)
B)
C)
D)
Посмотреть решение play_arrow вопрос_ответ 9{2}}. \] Если длина 8 м, то ширина = ________
\] Если длина 8 м, то ширина = ________
А)
20м
Б)
4м
В)
10м
Г)
12м
Посмотреть решение play_arrowвопрос_ответ 19)
Сопоставьте следующее: A B C D
A)
2 4 3 1
Б)
2 4 1 3
В)
3 4 1 2
D)
4 1 2 3
Посмотреть решение play_arrowвопрос_ответ 20)
Если у фигуры стороны 4 м, 2 м, 4 м и 2 м, то какая это фигура?
А)
Круг
Б)
Прямоугольник
В)
Квадрат
Г)
Треугольник
Посмотреть решение 9{2}}\] Посмотреть решение play_arrowвопрос_ответ 22)
Какое из следующих утверждений верно или неверно? Выберите верный вариант. Периметр треугольника = \[2\times\] сумма трех сторон. Площадь квадрата = \[сторона\умножить на сторону\] Если мы хотим оградить площадь, мы вычисляем периметр этого места. У прямоугольника все четыре стороны равны.
Периметр треугольника = \[2\times\] сумма трех сторон. Площадь квадрата = \[сторона\умножить на сторону\] Если мы хотим оградить площадь, мы вычисляем периметр этого места. У прямоугольника все четыре стороны равны.
А)
ТТТТ
Б)
TFFT
В)
FTTF
Г)
TFFT
Посмотреть решение play_arrowвопрос_ответ 23)
Указания: Заполните пропуски в данном отрывке, выбрав правильный вариант ответа. У Джаянта есть сад размером 20 на 25 футов. Он хочет, чтобы на какой-то его части был газон. Он хочет, чтобы газон был размером 10 на 13 футов. Чтобы найти площадь травяного газона, он должен использовать формулу ____ (23) ____ он также хочет огородить весь сад. Для этого муравью-сойке нужно будет вычислить ____ (24)____ сада, что равно ____ (25) ____. Таким образом, у него будет травяной газон площадью ____(26)____кв. футов.
Таким образом, у него будет травяной газон площадью ____(26)____кв. футов.
A)
\[сторона\раз сторона\]
Б)
л + б
C)
\[l\times b\]
D)
ни один из этих
Посмотреть решение play_arrowвопрос_ответ 24)
Указания: Заполните пропуски в данном отрывке, выбрав правильный вариант ответа. У Джаянта есть сад размером 20 на 25 футов. Он хочет, чтобы на какой-то его части был газон. Он хочет, чтобы газон был размером 10 на 13 футов. Чтобы найти площадь травяного газона, он должен использовать формулу ____ (23) ____ он также хочет огородить весь сад. Для этого муравью-сойке нужно будет вычислить ____ (24)____ сада, что равно ____ (25) ____. Таким образом, у него будет травяной газон площадью ____(26)____кв. футов.
футов.
А)
область
Б)
периметр
В)
оба
D)
ни один из этих
Посмотреть решение play_arrowвопрос_ответ 25)
Указания: Заполните пропуски в данном отрывке, выбрав правильный вариант ответа. У Джаянта есть сад размером 20 на 25 футов. Он хочет, чтобы на какой-то его части был газон. Он хочет, чтобы газон был размером 10 на 13 футов. Чтобы найти площадь травяного газона, он должен использовать формулу ____ (23) ____ он также хочет огородить весь сад. Для этого муравью-сойке нужно будет вычислить ____ (24)____ сада, что равно ____ (25) ____. Таким образом, у него будет травяной газон площадью ____(26)____кв. футов.
А)
2л+б
Б)
2б+л
В)
2(л + б)
Г)
2 л
Посмотреть решение play_arrowвопрос_ответ 26)
Указания: Заполните пропуски в данном отрывке, выбрав правильный вариант ответа. У Джаянта есть сад размером 20 на 25 футов. Он хочет, чтобы на какой-то его части был газон. Он хочет, чтобы газон был размером 10 на 13 футов. Чтобы найти площадь травяного газона, он должен использовать формулу ____ (23) ____ он также хочет огородить весь сад. Для этого муравью-сойке нужно будет вычислить ____ (24)____ сада, что равно ____ (25) ____. Таким образом, у него будет травяной газон площадью ____(26)____кв. футов.
У Джаянта есть сад размером 20 на 25 футов. Он хочет, чтобы на какой-то его части был газон. Он хочет, чтобы газон был размером 10 на 13 футов. Чтобы найти площадь травяного газона, он должен использовать формулу ____ (23) ____ он также хочет огородить весь сад. Для этого муравью-сойке нужно будет вычислить ____ (24)____ сада, что равно ____ (25) ____. Таким образом, у него будет травяной газон площадью ____(26)____кв. футов.
А)
130
Б)
140
В)
124
Г)
80
Посмотреть решение play_arrowquestion_answer 27)
Рима хочет распространить; ковер на полу размером \[13 м\х 14 м.\]Если стоимость укладки ковра составляет рупий. 14 за кв.м. рассчитать стоимость коврового покрытия площади.
А)
2455
Б)
2548
В)
2344
Г)
500
Посмотреть решение play_arrowвопрос_ответ 28)
Найдите площадь и периметр фигуры; 9{2}},P=68м\]
D)
Ничего из перечисленного
Посмотреть решение play_arrowquestion_answer 29)
Найдите площадь заштрихованной части.
9{2}}\] Посмотреть решение play_arrowвопрос_ответ 30)
Какое из следующих утверждений верно или неверно? Выберите верный вариант. {2}}.\] Утверждение C: Прямоугольник всегда можно разделить на несколько квадратов, каждый из которых имеет единичную площадь. Утверждение D: При нахождении площади прямоугольника его длину и ширину следует брать в одних и тех же единицах длины.
{2}}.\] Утверждение C: Прямоугольник всегда можно разделить на несколько квадратов, каждый из которых имеет единичную площадь. Утверждение D: При нахождении площади прямоугольника его длину и ширину следует брать в одних и тех же единицах длины.
А)
ТТФФ
Б)
ФФФФ
С)
ТТТТ
Г)
ПФТТ
Посмотреть решение play_arrowвопрос_ответ 31)
Какое из следующих утверждений верно или неверно? Выберите верный вариант. Утверждение A: Объем прямоугольного параллелепипеда = длина + ширина + высота Утверждение B: Мера количества пространства, занимаемого твердым телом, называется его m-объемом. Утверждение C: Объем куба = \[(сторона\умножить на сторону\умножить на сторону)\] кубических единиц Утверждение D: Каждое твердое тело занимает определенное пространство.
А)
FTFT
Б)
ФТТТ
В)
ТФТТ
Г)
ТТФТ
Посмотреть решение play_arrowquestion_answer 32)
Рассмотрим следующие два утверждения. Утверждение A: Периметр определяется как длина граничной линии близкой геометрической фигуры. Утверждение B: Вместимость контейнера называется объемом. Какой из следующих вариантов правилен в отношении приведенных выше утверждений?
А)
Верно только А.
B)
Верно только B
C)
Оба варианта A и B верны.
D)
Ни A, ни B неверны.
Посмотреть решение play_arrowquestion_answer 33)
Рассмотрим следующие два утверждения. Утверждение A: Если ребро куба имеет размеры 25 м и I = 20 м, b = 20 м, h = 30 м являются мерами прямоугольного параллелепипеда, то кубоид имеет больший объем. Утверждение Б: Дилип разбивает стержень длиной 90 см на четыре равные части. Взяв три части, он делает треугольник, соединяя конец к концу. Периметр треугольника равен 67,5 см. Какой из следующих вариантов правилен в отношении приведенных выше утверждений?
Утверждение A: Если ребро куба имеет размеры 25 м и I = 20 м, b = 20 м, h = 30 м являются мерами прямоугольного параллелепипеда, то кубоид имеет больший объем. Утверждение Б: Дилип разбивает стержень длиной 90 см на четыре равные части. Взяв три части, он делает треугольник, соединяя конец к концу. Периметр треугольника равен 67,5 см. Какой из следующих вариантов правилен в отношении приведенных выше утверждений?
A)
Утверждение A неверно, а B верно.
B)
Утверждение A верно, а B ложно.
C)
Оба утверждения верны.
D)
Оба утверждения неверны.
Посмотреть решение play_arrowвопрос_ответ 34)
На основании следующих признаков определите правильную форму. Его длина и ширина равны. Его площадь сторона х сторона. Его периметр в 4 раза больше его стороны. Это четырехсторонний многоугольник.
Его длина и ширина равны. Его площадь сторона х сторона. Его периметр в 4 раза больше его стороны. Это четырехсторонний многоугольник.
А)
Прямоугольник
Б)
Параллелограмм
В)
Квадрат
D)
Трапеция
Посмотреть решение play_arrowвопрос_ответ 35)
На основании следующих признаков определите правильную форму. Это четырехугольник, у которого противоположные стороны равны. Его периметр в два раза больше суммы длины и ширины. Его площадь вычисляется путем умножения его длины на ширину.
А)
Прямоугольник
Б)
Параллелограмм
В)
Квадрат
D)
Трапеция
Посмотреть решение play_arrowвопрос_ответ 36)
Периметр равностороннего треугольника и квадрата одинаковы. Что из нижеперечисленного может быть мерой стороны равностороннего треугольника и квадрата?
Что из нижеперечисленного может быть мерой стороны равностороннего треугольника и квадрата?
А)
Равносторонний треугольник = 9 см; квадрат = 12 см
B)
Равносторонний треугольник = 12 см; квадрат = 9 см
C)
Равносторонний треугольник = 15 см; квадрат = 10см
D)
Равносторонний треугольник = 6 см; квадрат = 4 см
Посмотреть решение play_arrowвопрос_ответ 37)
Найдите площадь и периметр данной фигуры.
А)
Зона 40; Периметр 40
Б)
Зона 36; Периметр 28
В)
Зона 28; Периметр 36
Г)
Зона 30; Периметр 40
Посмотреть решение play_arrowвопрос_ответ 38)
Найдите площадь и периметр данной фигуры.
А)
Зона 19; Периметр 20
Б)
Зона 20; Периметр 20
В)
Зона 19; Периметр 19
Г)
Зона 20; Периметр 19
Посмотреть решение play_arrowquestion_answer 39)
Найдите недостающую длину стороны, когда площадь равна 90 квадратных единиц.
А)
10
Б)
8
В)
9
Г)
7
Посмотреть решение play_arrowвопрос_ответ 40)
Прочитайте утверждение и выберите правильный вариант. Утверждение А: сторона квадрата равна 3. Следовательно, его площадь равна 9 квадратных единиц. Утверждение B: Периметр квадрата равен 12, а длина стороны 3.
Утверждение А: сторона квадрата равна 3. Следовательно, его площадь равна 9 квадратных единиц. Утверждение B: Периметр квадрата равен 12, а длина стороны 3.
А)
Утверждение А верно Б неверно,
B)
Утверждение B верно A неверно.
C)
Оба утверждения неверны,
D)
Оба утверждения верны.
Посмотреть решение play_arrowвопрос_ответ 41)
Площадь квадрата 25 квадратных единиц, а его сторона 5. Найдите его периметр.
А)
25
Б)
20
В)
50
Г)
40
Посмотреть решение play_arrowвопрос_ответ 42)
Чему равен периметр квадрата, если длина каждой стороны 8,2 см?
А)
64,16 см
Б)
67,24 см
В)
32,8 см
D)
16,2 см
Посмотреть решение play_arrowвопрос_ответ 43)
9{2}}\]. Тогда его периметр равен
Тогда его периметр равенА)
64 см
В)
32 см
С)
46 см
Г)
48 см
Посмотреть решение play_arrowвопрос_ответ 44)
Периметр двух квадратов равен 12 см и 24 см. Во сколько раз площадь большего квадрата больше площади меньшего?
А)
5 раз
Б)
2 раза
В)
3 раза
Г)
4 раза
Посмотреть решение play_arrowвопрос_ответ 45)
На рисунке сторона каждого квадрата равна 1 см.


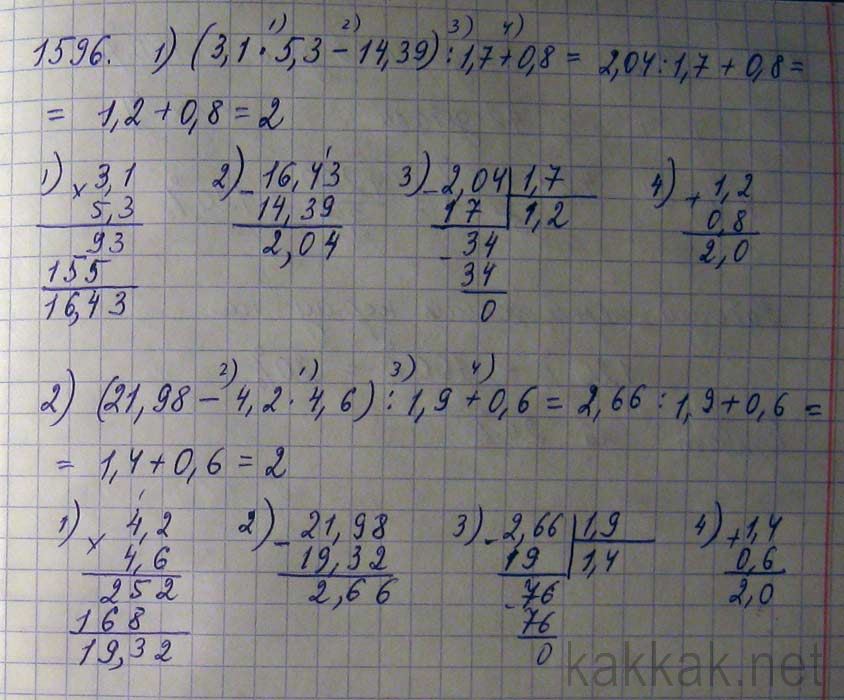

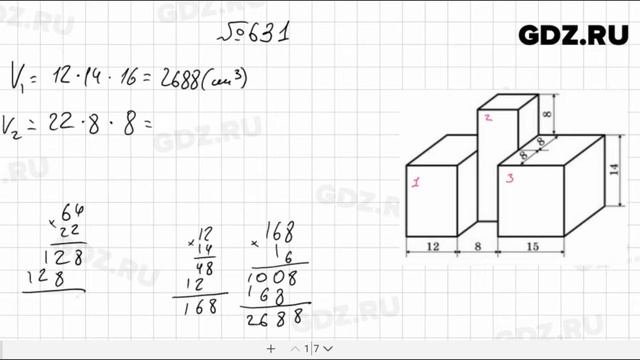

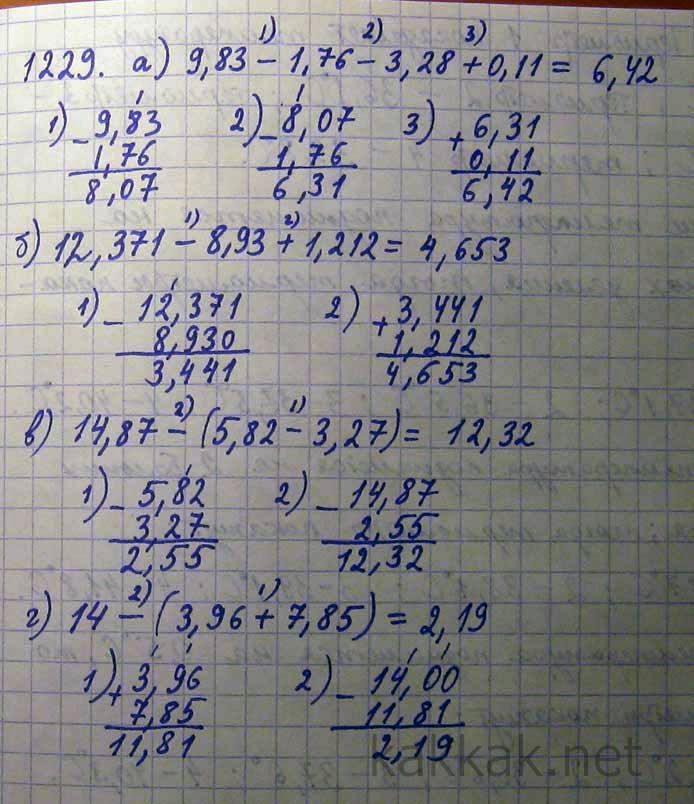
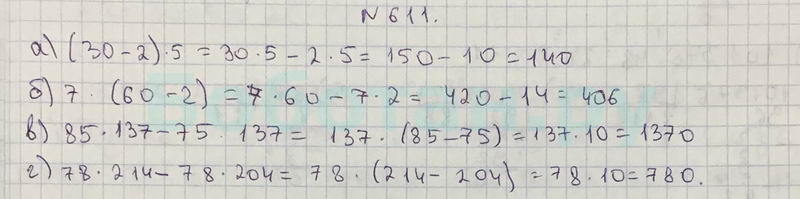

 3,1 ×
будет длиннее/короче
3,1 ×
будет длиннее/короче Заполните аргументацию Аниты.
Заполните аргументацию Аниты.
 0,4 × 0,08 =
________
0,4 × 0,08 =
________ 0,4 × 4
× 0,2 =
_________
0,4 × 4
× 0,2 =
_________ 0,4 × 0,5 =
_______
0,4 × 0,5 =
_______
 Книга также охватывает разрядность, сравнение, округление, сложение и вычитание десятичных знаков. Есть много умственных математических задач.
Книга также охватывает разрядность, сравнение, округление, сложение и вычитание десятичных знаков. Есть много умственных математических задач. Найдите произведение всех простых делителей числа 246.
Найдите произведение всех простых делителей числа 246.  315, рециркуляция ОГ 320, рециркуляция ОГ 326, рециркуляция ОГ 374, рециркуляция ОГ 389, LOG 100, PHY 210, PHY 317, PHY 318, PHY 319, PHY 327 и SDS 293. Студент может подать прошение в отдел, если он желает получить зачет по любому курсу, не указанному в этом списке.
315, рециркуляция ОГ 320, рециркуляция ОГ 326, рециркуляция ОГ 374, рециркуляция ОГ 389, LOG 100, PHY 210, PHY 317, PHY 318, PHY 319, PHY 327 и SDS 293. Студент может подать прошение в отдел, если он желает получить зачет по любому курсу, не указанному в этом списке.