ГДЗ По Математике 4 Класс Развивайка – Telegraph
➡➡➡ ПОДРОБНЕЕ ЖМИТЕ ЗДЕСЬ!
ГДЗ По Математике 4 Класс Развивайка
Развивайка . Сайт для детей и любящих родителей . 09 . Авг 18 . 0 . Математика . 4 класс . Ответы к заданиям . ГДЗ .
Развивайка . Сайт для детей и любящих родителей . 4 класс . Учебник . 1 часть . Моро М .И ., Бантова М .А ., Бельтюкова М .А ., Волкова С .И ., Степанова С .В .
ВКонтакте – универсальное средство для общения и поиска друзей и одноклассников, которым ежедневно пользуются десятки миллионов человек . Мы хотим, чтобы друзья, однокурсники, одноклассники, соседи и коллеги всегда оставались в контакте .
Убедись в правильности решения задачи вместе с ГДЗ по Математике за 4 класс Г .Л . Муравьева, М .А . Урбан часть 1 . Ответы сделаны к книге 2019 года от Национальный институт образования .
Г .Л . Муравьева, М .А . Урбан . Решебник (ГДЗ ) по Математике за 4 (четвертый ) класс авторы: Муравьева, Урбан издательство Национальный институт образования, 2019 год, часть 1 .
.
ГДЗ Решебник Математика за 4 класс Г .Л . Муравьева . Авторы: Г .Л . Муравьева, М .А . Урбан . Идеальный сборник ГДЗ по математике для 4 класса Г .Л . Муравьёва, составленный лучшими педагогами на легкодоступном языке, не содержит ни единой ошибки и способен оказать . .
Онлайн решебники 4 класс по всем предметам, гдз и ответы к домашним заданиям . Математика 1-4 класс контрольные работы Волкова С .И .
ГДЗ по математике для 4 класса — Чеботаревская (Часть 1, 2) . С нашими ГДЗ вы повторите пройденный в 3-ем классе материал, ознакомитесь с многозначными числами от 1000 до 1 000 000, узнаете о классах и разрядах, квадратных единицах измерения, научитесь складывать . .
ГДЗ решебники и ответы 4 класс , Математика . Готовые домашние задания . 4 класс Математика Моро М .И . Волкова С .И . Степанова С .В . Бантова М .А . Бельтюкова Г .В . Учебник часть 1 .
Смотрите любимые видео, слушайте любимые песни, загружайте собственные ролики и делитесь ими с друзьями, близкими и целым миром .
ГДЗ . Математика . Русский язык . 4 класс . Учебник . 1 часть . Моро М .И ., Бантова М .А ., Бельтюкова М .А ., Волкова С .И ., Степанова С .В .
ГДЗ и ответы по математике . ГДЗ и ответы к учебнику математики за 4 класс (Часть 1 – 2) Моро, Бантова, Волкова . Часть 1 Страницы учебника .
Математика . 4 класс . Часть 1 . Допущено Министерством образования Республики Беларусь . Нарушение авторских прав преследуется по закону . Описание . Учебное пособие для 4 класса учреждений общего среднего образования с русским языком обучения .
Учебник по математике 4 класс разработан авторами Моро, Бантовой, Бельтюковой и выпущен в свет с помощью книгоиздательства Преимущества ГДЗ . Четвертый класс завершается сдачей первого в жизни школьников настоящего экзамена: Всероссийских проверочных работ .
ГДЗ : Спиши готовые домашние задания по математике за 4 класс, решебник и ответы онлайн на GDZ .RU . ГДЗ по математике позволит исправить ситуацию . В сборнике вы найдете не просто численные ответы, которые можно переписать тетрадь .
Развивайка . Сайт для детей и любящих родителей . 09 . Авг 18 . 0 . Математика . 4 класс . Ответы к заданиям . ГДЗ .
Развивайка . Сайт для детей и любящих родителей . 4 класс . Учебник . 1 часть . Моро М .И ., Бантова М .А ., Бельтюкова М .А ., Волкова С .И ., Степанова С .В .
ВКонтакте – универсальное средство для общения и поиска друзей и одноклассников, которым ежедневно пользуются десятки миллионов человек . Мы хотим, чтобы друзья, однокурсники, одноклассники, соседи и коллеги всегда оставались в контакте .
Убедись в правильности решения задачи вместе с ГДЗ по Математике за 4 класс Г .Л . Муравьева, М .А . Урбан часть 1 . Ответы сделаны к книге 2019 года от Национальный институт образования .
Г .Л . Муравьева, М .А . Урбан . Решебник (ГДЗ ) по Математике за 4 (четвертый ) класс авторы: Муравьева, Урбан издательство Национальный институт образования, 2019 год, часть 1 . .
ГДЗ Решебник Математика за 4 класс Г .Л . Муравьева . Авторы: Г .Л . Муравьева, М .
А . Урбан . Идеальный сборник ГДЗ по математике для 4 класса Г .Л . Муравьёва, составленный лучшими педагогами на легкодоступном языке, не содержит ни единой ошибки и способен оказать . .
Онлайн решебники 4 класс по всем предметам, гдз и ответы к домашним заданиям . Математика 1-4 класс контрольные работы Волкова С .И .
ГДЗ по математике для 4 класса — Чеботаревская (Часть 1, 2) . С нашими ГДЗ вы повторите пройденный в 3-ем классе материал, ознакомитесь с многозначными числами от 1000 до 1 000 000, узнаете о классах и разрядах, квадратных единицах измерения, научитесь складывать . .
ГДЗ решебники и ответы 4 класс , Математика . Готовые домашние задания . 4 класс Математика Моро М .И . Волкова С .И . Степанова С .В . Бантова М .А . Бельтюкова Г .В . Учебник часть 1 .
Смотрите любимые видео, слушайте любимые песни, загружайте собственные ролики и делитесь ими с друзьями, близкими и целым миром .
ГДЗ . Математика . Русский язык . 4 класс . Учебник . 1 часть .
Моро М .И ., Бантова М .А ., Бельтюкова М .А ., Волкова С .И ., Степанова С .В .
ГДЗ и ответы по математике . ГДЗ и ответы к учебнику математики за 4 класс (Часть 1 – 2) Моро, Бантова, Волкова . Часть 1 Страницы учебника .
Математика . 4 класс . Часть 1 . Допущено Министерством образования Республики Беларусь . Нарушение авторских прав преследуется по закону . Описание . Учебное пособие для 4 класса учреждений общего среднего образования с русским языком обучения .
Учебник по математике 4 класс разработан авторами Моро, Бантовой, Бельтюковой и выпущен в свет с помощью книгоиздательства Преимущества ГДЗ . Четвертый класс завершается сдачей первого в жизни школьников настоящего экзамена: Всероссийских проверочных работ .
ГДЗ : Спиши готовые домашние задания по математике за 4 класс, решебник и ответы онлайн на GDZ .RU . ГДЗ по математике позволит исправить ситуацию . В сборнике вы найдете не просто численные ответы, которые можно переписать тетрадь .
Английский Книга ГДЗ 5 Класса Афанасьева
ГДЗ Лол 2020
Решебник Мордкович 8
ГДЗ История России Артасов
ГДЗ По Алгебре Анализ 10 11
Русский Язык 7 Класс Упражнение 14 ГДЗ
Решебник По Белорусскому 8
ГДЗ Прописи 1 Класс Климанова
ГДЗ Матем 4 Учебник 2 Часть
ГДЗ По Математике 6 Дидактический Материал Кузнецова
ГДЗ По Белорусской Литературе 7 Класс 2020
ГДЗ По Русскому 6 Класс Чесноков
Решебник По Физике 7 Перышкин Сборник
ГДЗ Решебник По Физике 10
Англий Язык 7 Класс Ваулина Учебник ГДЗ
ГДЗ Английский Перспектива
Решебник Английский Язык 3 Класс Дули
ГДЗ Английский Язык З Класс Биболетова
Решебник По Русскому 2 Класс Шклярова
Решебник По Алгебре Атанасян
ГДЗ По Математике 45 Класс
ГДЗ Пасечник 9 Рабочая Тетрадь
Физике Марон Решебник
Решебник По Английскому 6 Класс Алла Несвит
ГДЗ По Задачнику 8 Класс
Решебник Мерзляк Полонский 7
ГДЗ По Литературе Кубасова 4 Часть
ГДЗ По Математике 5 Класс Алгоритм Успеха
Русск 4 Кл Канакина Решебник ГДЗ
Spotlight 7 Огэ ГДЗ
ГДЗ Математика 2 Часть Вентана Граф
Решебник По Физике 7 Класс Грачев
Английский Язык 8 Класс Дули Учебник ГДЗ
ГДЗ По Русской Речи 6 Класс Никитина
ГДЗ Онлайн По Русскому 6 Класс Баранов
Решебник По Истории России 9
ГДЗ По Русскому Языку 2кл Упр 9
ГДЗ По Английскому Языку 9 Класс Валиуллина
ГДЗ Плешаков 3 Класс Проверочные Работы
ГДЗ По Математике 5 Класс Сборник Задач
ГДЗ По Географии 6 Герасимов
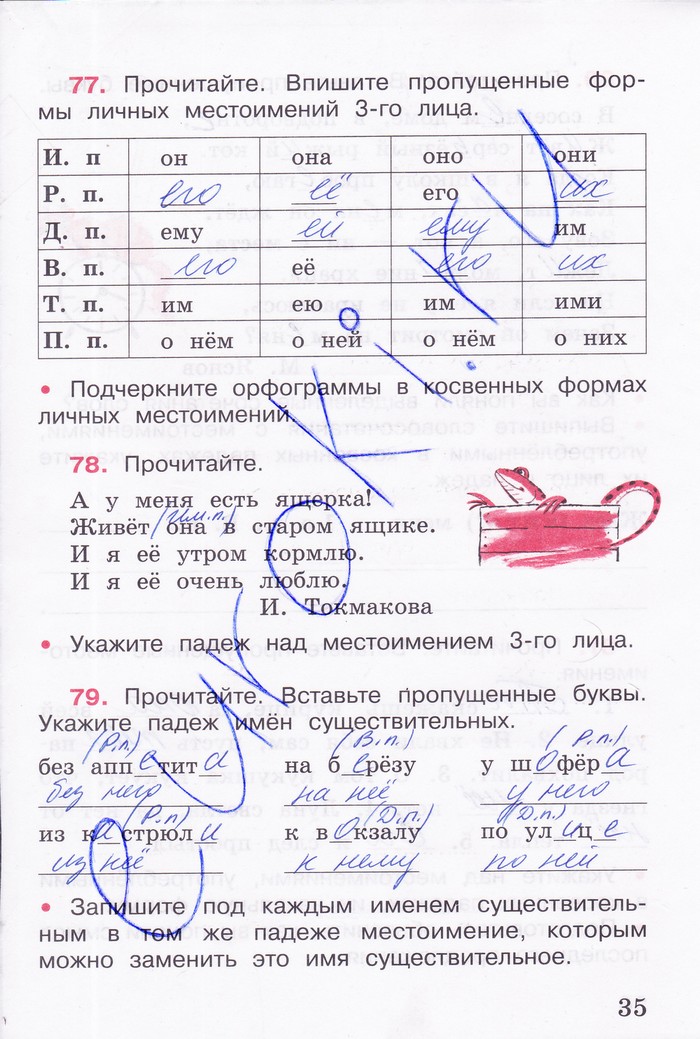
Spotlight 6 Класс ГДЗ
Спотлайт 6 Класс Решебник
ГДЗ По Немецкому 9 Класс Горизонты Учебник
ГДЗ По Химии 11 Класс Габриелян Рт
ГДЗ По Русскому 3 Класс Рт Канакина
ГДЗ Атанасян Рабочая Тетрадь 7 Класс
ГДЗ По Математике 7 Кл
Spotlight Student Book 7 Класс ГДЗ
ГДЗ По Математике Дидактический
ГДЗ Рабочая Тетрадь Вентана Граф
ГДЗ По Математике 4 Класс Учебник Демидова
ГДЗ По Жохову 8 Класс
ГДЗ Комарова 10 Класс
ГДЗ Еремеева 9
Летние математические программы для классов K-12
Зарегистрируйтесь сегодня
Учащиеся K-12 могут выбрать один из множества онлайновых или очных математических курсов — укрепить свои знания или найти дополнительные задачи!
Последние избранные
Наши курсы помогут учащимся, независимо от их целей на лето и предстоящий учебный год.
Учащиеся классов K–12 могут выбирать из множества математических курсов, в том числе курсов, которые укрепят их знания и подготовят к предстоящему учебному году, или конкурсов по математике, которые доставят им дополнительные трудности. Также доступны курсы подготовки к экзаменам, включая SAT I, ISEE и другие.
Могут быть доступны как онлайн-занятия (преподавание в живом, интерактивном, виртуальном классе), так и очные занятия.
Ознакомьтесь с предложениями класса ниже.
Летние математические курсы K-12 начинаются в июне!
Предлагаемые онлайн и очные курсы представлены ниже. Чтобы просмотреть конкретные расписания и стоимость обучения, выберите филиал на странице наших местоположений или нажмите «Начать» выше, чтобы запросить встречу с преподавателем для более подробного ознакомления с нашей программой.
Курсы открываются в июне и в основном предлагаются в течение 6 недель, по 2 занятия в неделю.
Grade K Prep
Этот курс использует уникальную методологию RSM для работы с подрастающими детсадовцами над развитием их абстрактного мышления и способности рассуждать.
Мы пробуждаем ранний интерес к математике, изучая числа и связи между ними, изучая геометрические фигуры, практикуя развитие математического языка и развивая навыки решения задач.
Выберите отделение для просмотра расписания
Подготовка к 1 классу
В этом курсе используется уникальная методология RSM для работы с подрастающими первоклассниками над развитием их абстрактного мышления и способности рассуждать. Мы пробуждаем ранний интерес к математике, изучая числа и связи между ними, изучая геометрические фигуры, практикуя развитие математического языка и развивая навыки решения задач.
Подготовка ко 2-му классу
В этом курсе используется уникальная методология RSM для работы с подрастающими второклассниками над развитием их абстрактного мышления и способности рассуждать. Мы пробуждаем ранний интерес к математике, изучая числа и связи между ними, изучая геометрические фигуры, практикуя развитие математического языка и развивая навыки решения задач.
Подготовка к 3 классу
Этот курс позволяет учащимся 3-го класса интуитивно изучать абстрактные понятия. Учащиеся начнут развивать навыки рассуждения, а также исследовать и создавать основу для математических понятий, таких как операции с числами и связи между ними, стратегии решения задач и геометрические фигуры.
Выберите отделение для просмотра расписания
Подготовка к 4 классу
В этом курсе используется уникальный подход RSM к работе с учащимися четвертого класса для развития их способности использовать логику для решения задач. Студенты будут расширять и применять свои знания об операциях, открывать секреты вычислений в уме, и им будет предложено применить свои базовые знания о работе с числами к составным задачам и задачам со словами.
Это можно рассматривать как отдельный летний курс повышения квалификации для студентов, не обучающихся в RSM; сильные учащиеся, продолжающие изучение RSM осенью, могут иметь возможность перейти на продвинутый уровень.
Выберите отделение для просмотра расписания
Подготовка к 4 классу с отличием
Этот курс является продолжением нашего класса 3 класса, проводимого в течение учебного года. Он предназначен для закрепления их знаний об основных понятиях, рассмотренных в этом году, и подготовки их к 4-му классу. Студенты, не являющиеся RSM, должны пройти оценку, чтобы присоединиться.
Выберите отделение для просмотра расписания
Advanced Topics & Competitions 2
Бросьте вызов и подготовьте своего ребенка, поступающего во 2-й класс, к таким соревнованиям, как математический кенгуру. Получайте удовольствие от нестандартных задач, требующих умных решений. Этот курс идеально подходит для тех студентов, которые любят и ищут математические задачи и хотят исследовать нестандартные вопросы.
Выберите отделение для просмотра расписания
Advanced Topics & Competitions 3/4
Бросьте вызов и подготовьте своего ребенка, поступающего в 3-4 классы, к национальным и международным математическим соревнованиям, таким как Math Kangaroo.
Получайте удовольствие от нестандартных задач, требующих умных решений. Этот курс идеально подходит для тех студентов, которые любят и ищут математические задачи и хотят исследовать нестандартные вопросы.
Подготовка к 5 классу
Этот курс разработан, чтобы научить подрастающих 5-классников использовать логику для решения задач. Учащиеся опережают отслеживание, которое ждет их в средней школе, развивая свои навыки рассуждения, продвигаясь в эффективных умственных вычислениях, оперируя числами и дробями со знаком и изучая начальную алгебру. Особое внимание уделяется текстовым задачам.
Выберите отделение для просмотра расписания
Подготовка к 5 классу с отличием
Этот курс является продолжением курса 4 класса, проводимого в течение учебного года. Он предназначен для закрепления их знаний об основных понятиях, рассмотренных в этом году, и подготовки их к 5-му классу.
Студенты, не являющиеся RSM, должны пройти оценку, чтобы присоединиться.
Выберите отделение для просмотра расписания
Предварительная алгебраическая подготовка
Этот курс рекомендуется для подрастающих 6-х классов и будет развивать стратегии решения задач учащихся, работая с различными текстовыми задачами, которые часто недостаточно представлены в традиционных школьных программах. Общие понятия, охватываемые этим курсом, включают делимость, выражения с дробями, решение и моделирование с помощью уравнений, рациональные числа, упрощение и введение в теорию чисел.
Выберите отделение для просмотра расписания
Предварительная подготовка к алгебре с отличием
Этот курс является продолжением нашего класса пятого класса, проводимого в течение учебного года. Он предназначен для закрепления их знаний об основных понятиях, рассмотренных в этом году, и подготовки их к 6-му классу.
Выберите отделение для просмотра расписания
Подготовка к алгебре I
Рекомендуется для подрастающих семиклассников. Этот курс охватывает ключевые темы основ алгебры (необходим для изучения алгебры I осенью). Рассматриваемые темы включают понятие и применение соотношений, пропорций и процентов. Учащиеся начинают изучать алгебраические понятия, включая линейные уравнения и уравнения с абсолютными значениями. Особое внимание уделяется работе с текстовыми задачами, часто недостаточно представленными в традиционных школьных программах, и моделированию с помощью уравнений.
Выберите отделение для просмотра расписания
Algebra I Prep Honors
Этот курс является продолжением курса для 6-го класса, проводимого в течение учебного года. Он предназначен для закрепления их знаний об основных понятиях, рассмотренных в этом году, и подготовки их к 7-му классу.
Выберите отделение для просмотра расписания
Подготовка к геометрии II
Рекомендуется для подрастающих 7-х классов. Это первый курс в нашей трехлетней последовательности геометрии, которая служит для развития глубокого понимания геометрических понятий. Этот вводный курс охватывает основные геометрические утверждения и включает подробное изучение треугольников. Студенты, не являющиеся RSM, должны пройти оценку, чтобы присоединиться (требуется знание предварительной алгебры).
Выберите отделение для просмотра расписания
Подготовка к алгебре II
Этот курс рекомендуется для учащихся 8-х классов и охватывает ключевые темы основ алгебры I. Рассматриваемые темы включают многочлены, факторинг, уравнения и неравенства, в том числе уравнения и неравенства с абсолютными значениями, а также системы линейных уравнений.
Учащиеся освоят применение алгебраических инструментов для решения текстовых задач.
Выберите отделение для просмотра расписания
Преподавание по алгебре II с отличием
Этот курс является продолжением курса для 7-го класса, проводимого в течение учебного года. Он предназначен для закрепления их знаний об основных понятиях, рассмотренных в этом году, и подготовки их к 8-му классу. Студенты, не являющиеся RSM, должны пройти оценку, чтобы присоединиться.
Выберите отделение для просмотра расписания
Подготовка к геометрии III
Подготовьтесь к поступлению на школьный курс геометрии с прочной базой. Студенты, посещающие этот класс, будут ознакомлены с основными понятиями геометрии и теоремами. Они узнают о доказательствах и о том, как использовать законы формальной логики. Это чрезвычайно важно для тех студентов, которые планируют сдать ранний тест SAT в рамках программы Johns Hopkins CTY.
Рассматриваемые темы включают геометрию треугольников, окружностей и четырехугольников со всеми соответствующими теоремами и доказательствами.
Этот курс рекомендуется для повышения 8 и 9й классники.
Выберите отделение для просмотра расписания
Расширенные темы и конкурсы 5/6
Бросьте вызов и подготовьте своего ребенка, поступающего в 5-й и 6-й классы, к математическим конкурсам, таким как Math Kangaroo и MOEMS E, и приобретите необходимые навыки, чтобы начать подготовку к AMC-8. Охватывая многие темы, основное внимание уделяется обучению студентов тому, как подходить к комбинаторике, словесным и логическим задачам. Особое внимание уделяется развитию математических способностей учащихся в уме, что является жизненно важным навыком для успеха в различных математических олимпиадах. Учебная программа включает конкурсы, игры и другие мероприятия в классе, чтобы сделать обучение активным и увлекательным для учащихся.
Ограничения по времени добавляются часто, чтобы учащиеся могли практиковаться в быстром и умном мышлении, как и ожидается от них на реальном математическом соревновании.
Выберите отделение для просмотра расписания
Advanced Topics & AMC 8 Prep
Бросьте вызов и подготовьте своего ребенка, поступающего в 7–8 классы, к математическим соревнованиям, таким как AMC-8, MOEMS M, Math Kangaroo и т. д. Класс фокусируется на темах, которые имеют первостепенное значение для учащихся. прогресс в соревнованиях, включая теорию чисел, комбинаторику и вероятность, геометрию и многое другое. Студенты практикуются с задачами из реальных математических соревнований. Курс подходит для целеустремленных студентов, которые могут работать самостоятельно (под руководством учителя на протяжении всего урока).
Подготовка к ISEE/SSAT для средней школы
Ознакомьтесь с основными темами, необходимыми для подготовки к математическому разделу вступительного экзамена в частную/независимую школу.
Развивайте навыки сдачи тестов, выполняя практические тесты и анализируя свои ошибки с нашими опытными преподавателями.
Выберите отделение для просмотра расписания
ISEE/SSAT Prep for High School
Ознакомьтесь с основными темами, необходимыми для подготовки к математическому разделу вступительного экзамена в частную/независимую школу. Развивайте навыки сдачи тестов, выполняя практические тесты и анализируя свои ошибки с нашими опытными преподавателями.
Выберите отделение для просмотра расписания
High School Math Prep
Этот курс рекомендуется для учащихся 9-х и 10-х классов и охватывает основы алгебры I и алгебры II, чтобы подготовить учащихся к поступлению на курс математики в средней школе. Рассматриваемые темы включают многочлены и факторинг, алгебраические дроби, введение в функции, уравнения квадратного корня и квадратные уравнения.
Курс также включает в себя основы тригонометрии.
Это можно рассматривать как отдельный летний курс повышения квалификации для студентов, не обучающихся в RSM; сильные учащиеся, продолжающие изучение RSM осенью, могут иметь возможность перейти на продвинутый уровень Precalculus I.
Выберите отделение для просмотра расписания
Подготовка к геометрии в средней школе
Подготовьтесь к поступлению на школьный курс геометрии с прочной базой. Студенты, посещающие этот класс, будут ознакомлены с основными понятиями геометрии и теоремами. Они узнают о доказательствах и о том, как использовать законы формальной логики. Рассматриваемые темы включают геометрию треугольников, окружностей и четырехугольников со всеми соответствующими теоремами и доказательствами.
Выберите отделение для просмотра расписания
Предварительное исчисление II, подготовка
Этот курс предназначен для тех учащихся, которые хотят подготовиться к предстоящему курсу Pre-Calc в старшей школе.
Курс охватывает полиномиальные, рациональные, логарифмические и экспоненциальные функции, комплексные числа и основы тригонометрии.
Предпосылка: Алгебра I. Оценка требуется для новых студентов.
Это можно рассматривать как отдельный летний курс повышения квалификации для студентов, не обучающихся в RSM; сильные учащиеся, продолжающие изучение RSM осенью, могут иметь возможность перейти на продвинутый уровень.
Выберите отделение для просмотра расписания
Algebra II / Trig Honors
Наш полный аккредитованный курс Algebra II, позволяющий учащимся выполнить требования школы за одно лето. Обратите внимание, что обязательным условием является либо курс алгебры RSM I, либо курс геометрии средней школы государственной или частной школы, либо эквивалентные курсы! Студенты, не являющиеся RSM, должны будут пройти оценку в RSM, чтобы попасть на этот курс.
Выберите отделение для просмотра расписания
Pre Calc I Part A
Алгебра II для подготовки к математическому анализу и Sat 2 IIC.
Этот курс является продолжением нашего первого занятия по алгебре, которое проводилось в течение учебного года. Студенты, не являющиеся RSM, должны будут пройти оценку в RSM, чтобы попасть на этот курс. Успешное завершение этого курса может соответствовать требованиям курса студентов. Пожалуйста, обратитесь в свою школу для получения дополнительной информации.
Выберите отделение для просмотра расписания
Pre Calc I Part B (Trig)
Тригонометрия для Precalculus и Sat 2 IIC. Студенты, не являющиеся RSM, должны будут пройти оценку в RSM, чтобы попасть на этот курс. Успешное завершение этого курса может соответствовать требованиям курса студентов. Пожалуйста, обратитесь в свою школу для получения дополнительной информации.
Это можно рассматривать как отдельный летний курс повышения квалификации для студентов, не обучающихся в RSM; сильные учащиеся, продолжающие изучение RSM осенью, могут иметь возможность перейти на продвинутый уровень.
Выберите отделение для просмотра расписания
Pre-Calc Part C (геометрия)
Geometry for Pre-Calculus and Math Subject test. Этот курс включает темы аналитической геометрии, геометрии твердых тел и вводной линейной алгебры. Студенты, не являющиеся RSM, должны будут пройти оценку в RSM, чтобы попасть на этот курс. Успешное завершение каждого из этих курсов может соответствовать требованиям курса студентов. Пожалуйста, обратитесь в свою школу для получения дополнительной информации.
Выберите отделение для просмотра расписания
Precalculus I & II (полный курс)
Подготовка учащихся к успешному прохождению школьного курса Precalculus или исчисления.
Выберите отделение для просмотра расписания
Подготовка к исчислению, часть A
Предварительное исчисление для подготовки к исчислению и SAT II IIC.
Успешное завершение этого курса может соответствовать требованиям курса студентов. Пожалуйста, обратитесь в свою школу для получения дополнительной информации.
Студенты, не являющиеся RSM, требуют оценки.
Выберите отделение для просмотра расписания
Подготовка к исчислению, часть B (Trig)
Тригонометрия для исчисления и Sat 2 IIC. Успешное завершение каждого из этих курсов может соответствовать требованиям курса студентов. Пожалуйста, обратитесь в свою школу для получения дополнительной информации. Студенты, не являющиеся RSM, требуют оценки.
Выберите отделение для просмотра расписания
Подготовка к исчислению (полный курс)
Предварительное исчисление и тригонометрия для подготовки к исчислению. Успешное завершение этого курса может соответствовать требованиям курса дневной школы. Пожалуйста, обратитесь в свою школу для получения дополнительной информации.
Студенты, не являющиеся RSM, требуют оценки.
Выберите отделение для просмотра расписания
ISEE/SSAT Math Prep for High School
Ознакомьтесь с основными темами, необходимыми для подготовки к математическому разделу вступительного экзамена в частную/независимую школу. Развивайте навыки сдачи тестов, выполняя практические тесты и анализируя свои ошибки с нашими опытными преподавателями.
Выберите отделение для просмотра расписания
Advanced Topics & AMC 10 Prep
Предназначен для тех учащихся, которые хотят подготовиться к AMC 10. Наши преподаватели конкурсов охватят основные темы AMC 10 и проведут учащиеся через практические тесты для подготовки к предстоящему конкурсу.
Выберите отделение для просмотра расписания
6 недель: 2 занятия в неделю
Большинство наших онлайн-курсов будут проводиться в течение 6 недель, по 2 занятия в неделю.
Продолжительность занятий зависит от класса. Проверьте филиал для конкретных графиков.
Класс
Все онлайн-занятия проводятся в реальном виртуальном классе. Классы состоят из 12 учеников и опытного преподавателя, который ведет интерактивный урок.
Для кого наша летняя программа?
Мы предлагаем занятия для тех учащихся, которые хотят укрепить свои знания основ, подготовиться к предстоящему учебному году или испытать дополнительные трудности.
Уникальная учебная программа
Наша учебная программа, совершенствовавшаяся в течение двух десятилетий нашей командой талантливых ученых, вдохновлена элитными математическими школами бывшего Советского Союза и адаптирована для образовательной среды США.
Развитие конкретных навыков, компетенций и точек зрения, необходимых профессионалам в области, наиболее тесно связанной с этим курсом
Редактор серии : Michael Theall, Университет штата Янгстаун
Автор : Нэнси МакКлюр, Университет штата Fairmont
youtube.com/embed/aN7qnngmaAQ?feature=oembed» frameborder=»0″ allow=»accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»> Навыки, компетентность и точка зрения профессионала влияют на его или ее работу на рабочем месте. Когда вы выбираете профессиональные услуги, вы понимаете, что вам нужен профессионал, у которого есть все: навыки, компетентность и правильная точка зрения или характер. Как профессионалы приобретают эти качества? Согласно Венгеру (1), обучение такого рода предполагает участие в практическом сообществе, термин, который «…относится не только к местным событиям или участию в определенных мероприятиях с определенными людьми, но и к более охватывающий процесс активного участия в практиках социальных сообществ и конструирования идентичностей по отношению к этим сообществам» (с. 4). Хотя Лаве и Венгер (2) ввели термин «практикующее сообщество», чтобы обеспечить основу для своих наблюдений во время изучения различных типов ученичества, эта концепция не нова для образования.
Его корни восходят к ранним работам Льва Выготского, русского психолога, связавшего когнитивное развитие с культурой. Выготский сформулировал идею о том, что обучение по своей сути является социальным и встроено в определенную культурную среду (3). С тех пор исследователи, изучающие познание, развили эту идею в теоретической структуре, известной как ситуативное обучение. В целом они согласны с тем, что со временем учащиеся в практикующем сообществе становятся более способными участвовать в функциях группы и использовать ее инструменты. По сути, учащиеся аккультурируются, делая нормы, поведение, навыки, убеждения, язык и установки своего конкретного сообщества своими собственными (4, 5, 6, 7, 8, 9).). Возможно, Клэнси (10) выразился лучше всех: «Учиться, чтобы стать членом сообщества профессионалов, нельзя путем передачи правил и инструментов. Знания профессионала концептуальны, воплощены в способах видения, ролях, способах взаимодействия. А поскольку концепции — это не слова, обучение не может быть достигнуто путем простого описания или рассказа».
К счастью, задача определения наилучших способов помочь учащимся стать полноценными членами практического сообщества возлагается не только на учителя. Многочисленные исследования дают направление. В расширенной версии Как люди учатся , Брансфорд, Браун и Кокинг (11) сосредоточены на исследованиях человеческого обучения и потенциала обучения всех людей. Исследование объясняет структуру знаний и определяет восемь факторов, влияющих на развитие компетентности и компетентность. Они перефразируются следующим образом.
- Если знания актуальны, люди могут их систематизировать и сохранить.
- Учащиеся должны соотносить свои знания с новыми задачами, делая их полезными знаниями, которыми обладают эксперты.
- Наличие соответствующих знаний позволяет учащимся мыслить с точки зрения решения проблем, делать выводы и делать выводы.
- Знания влияют на представление учащимся проблемы, что может повлиять на легкость, с которой учащийся может решить проблему.
- Эксперты обладают высокоорганизованными структурами знаний, связанными с представлением проблем, что позволяет легко получать доступ к соответствующим знаниям и использовать их.
- Поскольку разные дисциплины обладают разными организационными свойствами, учащиеся должны знать как содержание, так и организацию предмета.
- Лучшие ученики и специалисты по решению проблем понимают, как они учатся, и способны корректировать стратегии для удовлетворения новых потребностей. У них есть «метакогнитивные» навыки.
- Как и эксперты, люди в повседневных обстоятельствах и в определенных контекстах действуют в соответствии с социальными нормами и используют наборы инструментов, которые позволяют им выполнять задачи, которые они не смогли бы выполнить в других ситуациях.
Основываясь на этом исследовании обучения, преподавания и учебной среды, Bransford et al. предложить, чтобы среда обучения была ориентирована на учащегося, обеспечивала среду, ориентированную на знания, которая проясняет содержание, причины изучения содержания и целевое мастерство.
Эти среды должны постоянно оценивать обучение учащихся (формативно) и охватывать подход, ориентированный на сообщество.
Полезные советы
Чтобы создать среду обучения, подобную той, которую предложили Брансфорд и его коллеги, вы можете следовать предложениям Веймера (12). Она описывает среду, ориентированную на учащегося, с точки зрения пяти практических изменений, которые включают в себя все компоненты, предложенные Bransford et al. а также исследованием сообществ практики. Первые четыре изменения кратко изложены здесь, а пятое изменение обсуждается в Оценке
. Первое изменение на практике требует перехода от точки зрения, согласно которой учитель отвечает за обучение, к точке зрения, согласно которой учителя и ученики разделяют возможности обучения. Когда учащиеся имеют право голоса в своем обучении, они более заинтересованы в том, чтобы оставаться вовлеченными в задачу (см. Документ IDEA № 41). Например, когда учащиеся ставят перед собой высокие цели и работают над их достижением (см.
примечание Центра POD-IDEA № 15), это побуждает учащихся брать на себя ответственность за свое обучение.
Второе практическое изменение касается содержания. В содержательно-ориентированном классе учителя «раскрывают» содержание, а учащиеся «усваивают» его. Напротив, учителя и ученики в классе, ориентированном на учащихся, используют контент для создания знаний (3, 13, 14). В результате на первый план выходят предварительные знания учащихся, учащиеся используют различные формы знаний, а формирование знаний становится социальным предприятием (15). Когда учащиеся работают над формированием знаний, они проявляют интерес к получению дополнительных знаний, задавая собственные вопросы и ища ответы (цель IDEA 12).
Третье изменение в практике связано с ролью учителя. Как упоминалось ранее, учителя и ученики делят власть в классе, ориентированном на ученика. Это приводит к переопределению роли учителя с поставщика информации на фасилитатора, который помогает учащимся продуктивно взаимодействовать с контентом.
Два лучших способа для учителя помочь учащимся продуктивно использовать содержание (т. е. развивать навыки, компетенции и склонности профессионалов в данной области) — продемонстрировать важность предмета и соотнести учебный материал с реальной жизнью. ситуациях (см. примечания POD-IDEA Center #4 и #11). Эти две стратегии тесно связаны с достижением цели IDEA 4. Учителя часто используют аутентичные проблемные задачи (16) и тематические исследования для достижения этой цели.
Четвертое изменение в практике — это шаг к тому, чтобы помочь ученику стать самостоятельным учеником. Учащиеся, которые знают и контролируют свои когнитивные ресурсы или являются метакогнитивными, являются учащимися, которые являются «активными, планирующими учениками». Учителя могут помочь учащимся стать более самостоятельными, проявляя личный интерес к ним и их обучению (см. примечание Центра POD-IDEA № 1). Учителя, которые знают сильные и слабые стороны учеников, могут работать с учениками на более личном уровне, чтобы помочь им более продуктивно использовать свои сильные стороны и найти способы превратить слабые стороны в сильные.
Кроме того, учителя могут помочь учащимся стать более независимыми, находя способы помочь им ответить на свои собственные вопросы (см. примечание Центра POD-IDEA № 2). По мере того, как учащиеся учатся брать на себя ответственность за свое обучение и задавать свои собственные вопросы, учителя лучше понимают, кем является учащийся как ученик, и могут лучше направлять его или ее поиск ответов.
Подводя итог, можно сказать, что учащиеся развивают навыки, компетенции и точки зрения, необходимые профессионалам, становясь активными участниками среды, ориентированной на учащихся. Преподаватели и студенты в этой среде образуют сообщество практики, где они учатся друг у друга посредством межличностного общения, связанного с проектом или работой, взаимодействия с окружающей средой и использования инструментов, представляющих работу группы. Со временем активное участие в сообществе практиков улучшает изучение содержания и помогает участникам перейти от новичка к статусу эксперта.
Проблемы с оцениванием
Последнее изменение в практике, предложенное Веймером (12), заключается во включении различных типов оценивания и привлечении учащихся к самооценке.
Это изменение вытекает из пересмотренного взгляда на цель оценки. В то время как раньше оценивание было способом выставления оценок, новая цель не только выставляет оценки, но и способствует обучению. Основываясь на этом новом описании оценивания, традиционные оценивания (например, тесты, викторины и т. д.) или любой инструмент, с помощью которого учащиеся0021 выбрать ответов) следует заменить или дополнить альтернативными методами оценивания, такими как вопросы с краткими ответами, эссе, оценки успеваемости, демонстрации, портфолио или любые формы, в которых учащиеся создают ответов (17, см. также Документы IDEA № 16 и № 17). Когда учащиеся имеют возможность построить ответы на ряд конкретных критериев, у учителя появляется больше возможностей не только увидеть, что учащиеся изучают, но и предоставить обратную связь, связанную с критериями. Этот тип обратной связи способствует более глубокому обучению, особенно когда у учащихся есть возможность переоценить и пересмотреть свою работу (см.
Документы IDEA № 39).и № 42).
Стратегии, которые вы используете для оценки приобретения учащимися навыков, компетенций и точек зрения, отражают ваше суждение как практикующего профессионала. Вы наиболее квалифицированы, чтобы знать, чего ждут от вашей профессии. Независимо от того, полагаетесь ли вы на стандарты аккредитации или какие-либо другие рекомендации для вашей профессии, вы знаете важные критерии. Эти критерии помогут вам выбрать стратегии оценки. После того, как вы определили конкретные критерии для навыков, компетенций и точек зрения, вы рассмотрите, какие стратегии оценивания дают наилучшую картину достижений ваших студентов в вашем сообществе практики. (См. Walvoord and Anderson (18), чтобы узнать больше о том, как связать оценку/выставление оценок с результатами обучения.)
Например, в педагогическом образовании вы хотите убедиться, что ваши ученики могут планировать и проводить уроки в соответствии с возрастом, ежедневно управлять загруженными классами и хорошо ладить как с детьми, так и со взрослыми.
Студенты-инженеры должны выйти за рамки математических расчетов, чтобы разработать работоспособные решения или продукты. Начинающие музыканты должны овладеть теорией музыки, но также должны уметь создавать и исполнять новые произведения. Будущие философы должны знать Аристотеля, но также должны демонстрировать привычки мышления в этой дисциплине и развивать личные философии. В конечном счете, вовлечение и оценка ваших студентов в выполнении аутентичных задач в конкретных практических сообществах помогает им создать идентичность по отношению к этим сообществам и поддерживает их профессиональный рост.
Ссылки и ресурсы
- Венгер, Э. (1999). Сообщества практики: обучение, значение и идентичность . Кембридж: Издательство Кембриджского университета.
- Лав, Дж., и Венгер, Э. (1991). Ситуативное обучение: легитимное периферийное участие . Кембридж: Издательство Кембриджского университета.
- Выготский Л.С. (1993). Собрание сочинений Л. С. Выготского: Том 2 (Дж. Нокс и К. Стивенс, пер.) Нью-Йорк: Пленум.
- Группа познания и технологий в Вандербильте. (1990). Закрепленное обучение и его отношение к ситуативному познанию. Исследователь в области образования, 19(6) , 2-10.
- Группа познания и технологий в Вандербильте. (1993). Пересмотр закрепленного обучения и ситуативного обучения. Образовательные технологии, 33(3) , 52-70.
- Дерри, С.Дж. (1992). Помимо символической обработки: расширение горизонтов педагогической психологии. Журнал педагогической психологии, 84, 413-419.
- Гаррисон, Дж. (1995). Дьюианский прагматизм и эпистемология современного социального конструктивизма. Американский журнал исследований в области образования, 32, 716-741.
- Грино, Дж. Г., Коллинз, А. М., и Резник, Л. Б. (1996). Познание и обучение. В D. Berliner & R. Calfee (Eds.), Справочник по педагогической психологии (стр. 15-46). Нью-Йорк: Макмиллан.
- Смарт, Дж. К., и Фельдман, К. А. (1998). Эффекты акцентуации разнородных академических отделов: применение и исследование теории Холланда. Research in Higher Education, 39 (4), 385–418.
- Клэнси, В. Дж. (1995). Учебник по ситуативному обучению. [Электронная версия]. In Self, J. (Eds.) Proceedings of the International Conference on Computers and Education (Taiwan) Charlottesville, VA: AACE.
- Брансфорд, Дж., Браун, А., и Кокинг, Р. (ред.). (2000). Как люди учатся: мозг, разум, опыт и школа. Вашингтон: Издательство Национальной академии.
- Веймер, М. (2002). Обучение, ориентированное на учащегося . Сан-Франциско: Джосси-Басс.
- Дьюи, Дж. (1933). Как мы думаем. Бостон: Хит.
- Пиаже, Дж. (1997). Нравственное суждение ребенка. Нью-Йорк: Free Press.
- Лейнхардт, Г. (1992). Что исследования в области обучения говорят нам о преподавании. Управление образования , 49, 20-25.
С. Выготского: Том 2 (Дж. Нокс и К. Стивенс, пер.) Нью-Йорк: Пленум.
