Страница 59 — ГДЗ Математика 4 класс. Моро, Бантова. Учебник часть 2
- Главная
- ГДЗ
- 4 класс
- Математика
- Моро, Бантова. Учебник
- Числа, которые больше 1000. Деление на двузначное и трёхзначное число
- Страница 59. Часть 2
Вернуться к содержанию учебника
Числа, которые больше 1000. Деление на двузначное и трёхзначное число
Вопрос
Объясняй, как выполнено деление. по плану:
1) Выделяю первое неполное делимое.
2) Нахожу первую цифру частного.
3) Образую второе неполное делимое.
4) Нахожу вторую цифры частного.
Проверь, правильно ли найдено частное.
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
219.
| 768 : 24 | 2688 : 32 | 2000 — 450 • 342 : 900 |
| 4088 : 73 | 3392 : 53 | 4010 — 106 • 150 : 300 |
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
220. На стройку дома доставили 3360 т строительных материалов. Десятую их часть составляла известь, двенадцатую часть — цемент. На сколько больше доставлено тонн извести, чем цемента?
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
221. Масса слона 5 т. Это на 4 т 500 кг больше, чем масса лошади. Во сколько раз слон тяжелее лошади? (Вырази массу в килограммах. )
)
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
222. На одной пасеке было 47 ульев, а на другой — 52 улья. С первой пасеки собрали на 350 кг мёда меньше, чем со второй. Сколько килограммов мёда собрали с каждой пасеки, если считать, что с каждого улья получили одно и то же количество мёда?
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
223. Сколько метров в 9 км? в 900 дм? в 9000 см?
Сколько квадратных метров в 400 дм2? в 8 км2?
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
224.
| m | 250 | 340 | |||
| k | 4 | 120 | 2 | 20 | 90 |
| m • k | 600 | 1000 | 720 |
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
225. Реши уравнения.
• 802 = 0 | : 163 = 1 | — 342 = 0 |
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
Вычисли.
| 1702 : 74 | 1131 : 87 |
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
Ребус
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
Начерти и раскрась такой узор.
Ответ
Поделись с друзьями в социальных сетях:
Вернуться к содержанию учебника
ГДЗ по математике 4 класс учебник Моро, Бантова 2 часть
- Тип: ГДЗ, Решебник.
- Автор: Моро М. И., Волкова С. И., Бантова М.
 А.
А. - Год: 2020.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.
❤️️Ответ к странице 59. Математика 4 класс учебник 2 часть. Авторы: М.И. Моро, М.А. Бантова.
Решебник — страница 59Готовое домашнее задание
Задание вверху страницы
Объясни, как выполнено деление по плану:
2) Нахожу первую цифру частного.
3) Образую второе неполное делимое.
4) Нахожу вторую цифру частного.
Ответ:
828 : 36
1) 82 (десятка).
2) 82 : 36 = 2 (десятка).
3) 36 ∙ 2 = 72, 82 − 72 = 10 (десятков).
Добавляю оставшиеся 8 единиц – 108.
4) 108 : 36 = 3 (единицы).
Получилось частное 23.
Проверка:
Деление выполнено верно, без остатка.
4725 : 63
1) 472 (десятка).
2) 472 : 63 = 7 (десятков). 3) 63 ∙ 7 = 441, 472 − 441 = 31 (десяток).
Добавляю оставшиеся 5 единиц – 315.
4) 315 : 63 = 5 (единиц).
Получилось частное 75.
Проверка:
3) 63 ∙ 7 = 441, 472 − 441 = 31 (десяток).
Добавляю оставшиеся 5 единиц – 315.
4) 315 : 63 = 5 (единиц).
Получилось частное 75.
Проверка:
Деление выполнено верно, без остатка.
Номер 219.
Ответ:
Номер 220.
На стройку дома доставили 3360 т строительных материалов. Десятую их часть составляла известь, двенадцатую часть – цемент. На сколько больше доставлено тонн извести, чем цемента?
Ответ:
1) 3360 : 10 = 336 (т) – извести привезли на стройку.
2) 3360 : 12 = 280 (т) – цемента привезли на стройку.
3) 336 − 280 = 56 (т) – на столько больше доставили извести, чем цемента.
Ответ: на 56 тонн.
Номер 221.
Масса слона 5 т. Это на 4 т 500 кг больше, чем масса лошади. Во сколько раз слон тяжелее лошади? (Вырази массу в килограммах.)
Ответ:
5 т = 5000 кг; 4 т 500 кг = 4500 кг.
1) 5000 − 4500 = 500 (кг) – масса лошади. 2) 5000 : 500 = 10 (раз) – во столько раз слон тяжелее лошади.
Ответ: в 10 раз.
2) 5000 : 500 = 10 (раз) – во столько раз слон тяжелее лошади.
Ответ: в 10 раз.
Номер 222.
На одной пасеке было 47 ульев, а на другой – 52 улья. С первой пасеки собрали на 350 кг мёда меньше, чем со второй. Сколько килограммов мёда собрали с каждой пасеки, если считать, что с каждого улья получили одно и то же количество мёда?
Ответ:
1) 52 − 47 = 5 (ул.) – на столько больше ульев на 2-ой пасеке.
2) 350 : 5 = 70 (кг) – мёда, собирают с одного улья.
3) 70 ∙ 47 = 3290 (кг) – мёда, собрали с 1ой пасеке.
4) 70 ∙ 52 = 3640 (кг) – мёда, собрали со 2ой пасеке.
Ответ: 3290 кг и 3640 кг.
Номер 223.
Сколько метров в 9 км? в 900 дм? в 9000 см? Сколько квадратных метров в 400 дм²? в 8 км²?
Ответ: 9 км = 9000 м; 900 дм = 90 м; 9000 см = 90 м; 400 дм² = 4 м², 8 км² = 8000000 м².
Номер 224.
Ответ:
Номер 225.
Реши уравнения.
Ответ:
Задание внизу страницы
Вычисли.
Ответ:
Задание на полях страницы
Ребус.
Ответ:
Рейтинг
Выберите другую страницу
1 часть
| Учебник Моро | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 | 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 | 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 | 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 | 111 |
|---|
2 часть
| 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 | 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 | 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 | 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 | 111 | 112 | 113 | 114 | 115 | 116 | 117 | 118 | 119 | 120 | 121 | 122 | 123 | 124 | 125 | 126 | 127 |
|---|
Ваше сообщение отправлено!
+
Сайт vpr-klass.
 com — впр-класс.ком : гдз, решебник, гиа, егэ, решение задач, задания, варианты, подготовка к экзамену, тесты, презентации.
com — впр-класс.ком : гдз, решебник, гиа, егэ, решение задач, задания, варианты, подготовка к экзамену, тесты, презентации.Error in links file
Сайт vpr-klass.com — впр-класс.ком : гдз, решебник, гиа, егэ, решение задач, задания, варианты, подготовка к экзамену, тесты, презентации. У нас вы найдете много учебных материалов: решебники, ГДЗ, тестовые задания, видео уроки, генераторы задач, решения упражнений гиа и егэ.
| Расскажи друзьям vpr-klass или впр-класс Презентации Детские презентации Презентации по математике Презентации по астрономии Демо-варианты: Математика Русский язык Физика Обществознание Английский язык Информатика История Биология Химия Литература География Математика Русский язык |  com (впр-класс) com (впр-класс) Последние новости ГИА и ЕГЭ 2017. Сайт Vpr-klass.com — это учебный-образовательно-познавательный сайт для школьников! Приветствуем на уникальном сайте помощи всем ученикам 1-11 классов. На образовательном ресурсе полно полезной, учебной информации от способов решения заданий по математике до разных генераторов задач по алгебре и онлайн калькуляторов по геометрии, которые облегчат жизнь школьника. В частности, сделан больший уклон на решебники и ГДЗ, ведь правильная домашняя работа — это хорошие оценки и учеба в школе. | Интересно Много разных решений Тесты ГИА онлайн. Видео — ГИА 2013: геометрия Видео — ГИА 2012 Видео — Демо-вариант 2012. Решение Демо-варианта 2013 года (2014 года). Задача №1, Вычислить. Задача №2, Числа и прямая. Задача №3, Сравнение чисел. Задача №4, Уравнения. Задача №5, Графики и формулы. Задача №6, Прогрессии. Задача №7, Упростить выражение. Задача №8, Неравенства, системы неравенств. Задача №9, Задания по геометрии. Генератор вариантов ГИА 2014 Много разных решений. Онлайн тесты. Видео уроки ЕГЭ по математике. Генератор вариантов ЕГЭ 2014 Книги, справочники Решение демо варианта ЕГЭ по математике 2014 Задания B1, задача. Задания B2, диаграммы. Задания B5, уравнения. Задания B8, производная. Задания B10, вероятность. Видео уроки |
Copyright © 2017 vpr-klass.com | Если какой-либо из материалов нарушает ваши авторские права, просим немедленно связаться с Администрацией!!! Наш e-mail: [email protected] | Правообладателям |
sitemap. xml
xml
Математика 222: Описание курса
- Учебник:
Исчисление, 3-е издание , Роберт Смит и Роланд Минтон.
Мы рассмотрим примерно главы 6-10. Темы могут меняться в зависимости от успеваемости класса, а некоторые темы могут быть пропущены из-за нехватки времени.
Обратите внимание, что мы будем работать над развитием ваших навыков самостоятельного чтения по математике. Я, конечно, не смогу охватить в классе весь материал, который вам потребуется изучить. В результате от вас ожидают, что вы будете много читать. Вы должны прочитать разделы учебника, которые соответствуют материалу, пройденному на лекциях. Чтение позволит вам ответить на мои вопросы и задать свои собственные целенаправленные вопросы во время лекции и поможет вам лучше понять материал.
- Технология:
Мы будем использовать калькуляторы TI-89.
 Поэтому, вероятно, в ваших интересах иметь его.
Поэтому, вероятно, в ваших интересах иметь его.Может быть полезно периодически использовать математические программы, такие как MATLAB, Maple или Mathematica. Они доступны в большинстве студенческих компьютерных лабораторий на территории кампуса.
Описание курса:Охвачено тем: Темы включают трансцендентные и обратные функции, различные методы интегрирования, несобственные интегралы, дифференциальные уравнения, последовательности и ряды, ряды Тейлора, параметрические уравнения, полярные координаты и различные приложения.
Math 222, Исчисление II, является курсом второго семестра серии исчисления и задуман как продолжение развития исчисления с одной переменной. Мы охватим дифференциальное исчисление трансцендентных функций (экспоненты, логарифмы, обратные тригонометрические функции и т. д.), а также продолжим интегральное исчисление, которое мы начали в Math 221, Исчисление I.
 Мы познакомимся с методами интегрирования, такими как интегрирование по частям, тригонометрическое замещение и разложение на неполные дроби.
Мы познакомимся с методами интегрирования, такими как интегрирование по частям, тригонометрическое замещение и разложение на неполные дроби.Мы также рассмотрим математику последовательностей и рядов. То есть мы будем изучать списки чисел и суммы этих чисел. При добавлении бесконечного списка чисел вас может удивить, что сумма на самом деле может быть конечной. Таким образом, мы изучим «тесты» для определения того, «сходится» ли ряд к конечному числу или действительно ли он «расходится» до бесконечности. Наконец, мы также узнаем о параметрических уравнениях и полярных координатах, а также о таких вещах. На протяжении всего курса мы будем обсуждать приложения этих тем к задачам из других дисциплин.
Экзамены и оценки:Ваша общая оценка будет определяться следующим образом:
- 20% — WeBWorK, викторины и участие в занятиях
- 20% — Экзамен 1
- 20% — Экзамен 2
- 20% — Экзамен 3
- 20% — выпускной экзамен
Ваша общая оценка за курс будет отражать успехи класса и будет высокой, если все усердно работают над домашним заданием и хорошо сдают экзамены.
 Практически все вопросы на экзаменах будут в том же духе, что и домашние задания. Поэтому понимание того, как выполнять все домашние задания, позволит вам хорошо сдать экзамены.
Практически все вопросы на экзаменах будут в том же духе, что и домашние задания. Поэтому понимание того, как выполнять все домашние задания, позволит вам хорошо сдать экзамены.Домашнее задание: Большая часть домашних заданий выполняется через систему домашних заданий в Интернете под названием WeBWorK. Однако иногда могут возникать проблемы, которые вы должны написать и передать мне. Все задания должны быть выполнены к установленному сроку.
Более того, хотя выполнение рукописной версии заданий WeBWorK не обязательно, это настоятельно рекомендуется. Написание задачи от руки, показ всех шагов расчета и сохранение их в блокноте очень поможет вам при подготовке к экзаменам.
Экзамены: Будет три промежуточных экзамена и один итоговый экзамен. Экзамены — это закрытая книга, закрытые заметки, закрытые друзья и открытый мозг. Мобильные телефоны, iPod и другие электронные устройства НЕ допускаются к экзаменам.
Расписание экзаменов следующее: Вопрос о том, разрешены ли калькуляторы на экзамене, будет определен позднее.
Вопрос о том, разрешены ли калькуляторы на экзамене, будет определен позднее.- Экзамен 1: Пятница, 18 сентября*, В КЛАССЕ
- Экзамен 2: Четверг, 15 октября*, В КЛАССЕ
- Экзамен 3: Пятница, 20 ноября*, В КЛАССЕ
- Выпускной экзамен:
- РАЗДЕЛ 2: пятница, 18 декабря, с 8:00 до 11:00, в классе
- РАЗДЕЛ 5: пятница, 18 декабря, с 12:00 до 15:00, в классе
Викторины и участие в занятиях: Время от времени в классе будут проводиться необъявленные викторины, чтобы убедиться, что учащиеся понимают материал курса и не отстают от него. Тесты будут основаны на материалах домашних заданий и предыдущих лекций. Также обязательно, чтобы вы не отставали от чтения учебника.
 ВИКТОРИНЫ ПО МАКИЯЖУ НЕ ПРОВОДЯТСЯ. Участие в занятиях будет основываться на вашей готовности ЗАДАВАТЬ и ОТВЕЧАТЬ на вопросы в классе.
ВИКТОРИНЫ ПО МАКИЯЖУ НЕ ПРОВОДЯТСЯ. Участие в занятиях будет основываться на вашей готовности ЗАДАВАТЬ и ОТВЕЧАТЬ на вопросы в классе.
Дополнительная помощь:Важно не отставать, потому что каждая лекция основана на предыдущей работе. Если у вас возникли проблемы с каким-либо материалом, НЕМЕДЛЕННО ОБРАЩАЙТЕСЬ ЗА ПОМОЩЬЮ одним из следующих способов:
- СПРОСИТЕ МЕНЯ! (в классе или в частном порядке),
- Отправляйтесь в Учебный центр математики в Южном зале 332. В нем работают однокурсники, которые ответят на ваши вопросы по очереди.
- Одним из самых лучших ресурсов могут быть ваши сокурсники!
Если у вас возникли трудности, немедленно обратитесь за помощью — не ждите пока не станет слишком поздно оправиться от отставания или непонимания концепция!
Math Tricks — Behavioral Sciences Research Core
Меню страницЭта веб-страница посвящена
невероятно крутой
идее о том, что математика может быть интересной!
Попробуйте эти трюки:
- Дополнение Easy Magic
- Магический квадрат #15
- Волшебный квадрат #34
- Создайте свой собственный магический квадрат
- Перевернутый магический квадрат
- Антимагический квадрат
- Выиграйте ставки с этим квадратом
- Фокус с картами
- Калькулятор молний
- Таблицы забавных чисел
- Знаете ли вы.
 ..?
..? - Уловка на этот год
- Где струна?
- Огромный магический квадрат
Вот несколько интересных ссылок:
- Список книг по хитрой математике для чтения, большинство из которых я использовал для этого сайта.
- Узнайте об оригинальном компьютере: The Abacus (http://www.ee.ryerson.ca:8080/~elf/abacus/)
- Сыграйте в математическую игру (http://dev.eyecon.com/marcia) — для одного или двух игроков. (Если вы используете Netscape, Не прокручивать страницу вниз, пока загружается .
- Играйте в Shoot Balls (http://www.fi.uu.nl/wisweb/en/applets/bollen/Welcome.html).
- Играйте в Flippo 24 (http://www.fi.uu.nl/wisweb/en/applets/bollen/Welcome.html).
- Проверьте свои знания таблицы умножения (http://www.fi.uu.nl/wisweb/en/applets/tafels/Welcome.html)
- Попробуйте свои силы в оценке (http://www.fi.uu.nl/wisweb/en/applets/bollen/Welcome.html).
- Исследуйте геометрию в увлекательной интерактивной форме.

- Попробуйте загадку «Ханойская башня» (http://www.eng.auburn.edu/~fwushan/Hanoi1.html).
- Посмотрите, что такое Spriographis (http://www.mainstrike.com/mstservices/handy/Spiro/).
- Посмотрите, что такое набор Мандельброта (http://www.franceway.com/java/fractale/mandel_b.htm).
- Если вы хотите больше математических задач , попробуйте новый сайт PBS MATHLINE MATH CHALLENGES. Попробуйте, вам понравится. (Но помните, что мы были первыми.)
Magic Addition Trick #1
Удивите батраков этим трюком. Все просто. Это эффективно. Он получает их каждый раз.
- Спросите свою оценку по номеру выберите три (3) разных номеров между 1 и 9.
- Скажите ему или ей (или ей, или ему) записать три числа рядом друг с другом, начиная с наибольшего и заканчивая наименьшим, чтобы получилось одно трехзначное число. Скажите ему/ей, чтобы он не говорил вам, что это за числа.
- Затем попросите ее или его составить новое трехзначное число, переставив цифры местами, поставив наименьшее первым, а самое большое последним.
 И напишите это число прямо под первым числом.
И напишите это число прямо под первым числом. - Теперь попросите его или ее вычесть меньшее (и меньшее) трехзначное число из старшего (и большего) трехзначного числа. Скажи им, чтобы они не говорили тебе, каков результат.
- Теперь у вас есть выбор оберток:
- Попросите вашего друга сложить три цифры числа, которое получается в результате вычитания меньшего из большего трехзначного числа. Затем удивите его или ее, сказав, какова сумма этих трех чисел. Сумма трехзначного ответа всегда будет 18!
- Скажите своему другу, что если он или она скажет вам, какая первая ИЛИ последняя цифра ответа, вы скажете ей или ему, какие две другие цифры. Это возможно, потому что средняя цифра всегда будет 9, а сумма двух других цифр всегда будет 9! Итак, чтобы получить цифру, отличную от средней (которая равна 9) и отличную от цифры, которую сказал вам ваш друг, просто вычтите цифру, которую ваш друг сказал вам, из 9, и это будет неизвестная цифра.

Вернуться к началу
Магический квадрат #15
Каждая строка и столбец в этом магическом квадрате в сумме дают 15. Так сделайте обе диагонали!
| 8 | 3 | 4 |
| 1 | 5 | 9 |
| 6 | 7 | 2 |
Вернуться к началу
Магический квадрат #34
Каждая строка и столбец в этом магическом квадрате в сумме дают 34. Так сделайте обе диагонали!
| 1 | 15 | 14 | 4 |
| 12 | 6 | 7 | 9 |
| 8 | 10 | 11 | 5 |
| 13 | 3 | 2 | 16 |
Вернуться к началу
Рецепт собственного магического квадрата 3 X 3
Вот рецепт изготовления собственного магического квадрата 3 X 3. Этот рецепт и оба вышеупомянутых магических квадрата взяты из одной чертовски большой книги под названием « Математика на миллион » Ланселота Хогбена, изданной Norton and Company. Я очень рекомендую это. Вам совсем не нужно много математики, чтобы погрузиться в приключения чисел, описанные в этой классической книге.
Этот рецепт и оба вышеупомянутых магических квадрата взяты из одной чертовски большой книги под названием « Математика на миллион » Ланселота Хогбена, изданной Norton and Company. Я очень рекомендую это. Вам совсем не нужно много математики, чтобы погрузиться в приключения чисел, описанные в этой классической книге.
Некоторые необходимые правила и определения:
- Пусть буквы a , b и c обозначают целые числа (то есть целые числа).
- Всегда выбирайте a так, чтобы оно было больше суммы b и c . То есть a > b + c . Это гарантирует отсутствие записи в магический квадрат отрицательного числа.
- Не допускайте 2 X b = c . Это гарантирует, что вы не получите одно и то же число в разных ячейках.
- Используя формулы, приведенные в таблице ниже, вы можете составить магический квадрат, в котором сумма строк, столбцов и диагоналей равна 3 X независимо от и .

Чтобы создать первый магический квадрат #15 выше, пусть a будет равно 5, пусть b будет равно 3, и пусть c равны 1. Вот некоторые другие:
- a = 6, b = 3, c = 2
- а = 6, б = 3, в = 1
- а = 7, б = 3, в = 2
- а = 7, б = 4, в = 2
- а = 8, б = 6, в = 1
- а = 8, б = 5, в = 2
- а = 8, б = 4, в = 3
Попробуйте придумать что-нибудь свое.
Вернуться к началу
Перевернутый магический квадрат
Вот магический квадрат, который не только дает в сумме 264 во всех направлениях, но и делает это, даже когда он перевернут! Если не веришь мне, посмотри на это, стоя на голове! (Или просто скопируйте его и переверните.)
| 96 | 11 | 89 | 68 |
| 88 | 69 | 91 | 16 |
| 61 | 86 | 18 | 99 |
| 19 | 98 | 66 | 81 |
Вернуться к началу
Антимагический квадрат
Вот магический квадрат с максимально возможным количеством различных сумм .
| 5 | 1 | 3 |
| 4 | 2 | 6 |
| 8 | 7 | 9 |
Эта таблица дает 8 различных итоговых значений.
Вернуться к началу
Выиграть ставки с помощью этого волшебного квадрата
Вот отличный способ выиграть ставки с помощью волшебного квадрата. Позвоните другу по телефону. Пусть он или она возьмет карандаш и бумагу и поднесет их к телефону, чтобы он или она могли записывать числа от 1 до 9.. Скажите своему другу, что вы будете по очереди называть числа от 1 до 9. Ни один из вас не может повторить число, которое называет другой. Затем вы оба записываете числа от 1 до 9. Затем, когда ваш друг называет одно из чисел, он или она обводит это число кружком, и вы тоже. Когда вы называете число, вы рисуете квадрат вокруг этого числа, и ваш друг делает то же самое. Выигрывает тот, кто первым наберет три числа, сумма которых точно равна 15.
Допустим, вы идете первым и называете 8. Ваш друг может назвать 6. Затем вы называете 2. Ваш друг называет 5, и вы называете 4. Ваш друг называет 7, а вы называете 3. Затем вы говорите своему другу, что вы только что выиграли, потому что назвали 8, 3 и 4, что в сумме дает 15.
Ваш друг снова захочет поиграть. Так что на этот раз вы можете поспорить с ним, что выиграете, с условием, что в случае ничьей (когда вы используете числа от 1 до 9, но ни один из вас не получает в сумме 15) никто ничего не должен.
Если вы знаете хитрость, вы никогда не проиграете, и, вероятно, проиграете в большинстве случаев.
Фокусы На самом деле фокус основан как на крестиках-ноликах, так и на магическом квадрате. Магический квадрат выглядит так:
| 8 | 1 | 6 |
| 3 | 5 | 7 |
| 4 | 9 | 2 |
Поскольку это магический квадрат, каждая строка, каждый столбец и каждая диагональ в сумме дают 15. Поэтому, если этот квадрат находится перед вами с вашим другом по телефону, вы можете поставить X в квадраты числа, которое вы называете, и O в квадратах чисел, которые называет ваш друг. Затем, как и в крестиках-ноликах, вы пытаетесь поставить три крестика подряд, потому что в сумме это всегда будет 15.
Затем, как и в крестиках-ноликах, вы пытаетесь поставить три крестика подряд, потому что в сумме это всегда будет 15.
Итак, в приведенном выше примере, когда вы называете 8, вы ставите X в верхнем левом углу. Когда ваш друг говорит 6, вы ставите ) в правом верхнем углу. И так далее.
Наверх
Математический фокус с картами
Для этого задания вам понадобится обычная колода карт. Никаких причудливых перетасовок не требуется. Просто следуйте этим простым шагам:
- Перемешайте карты, чтобы тщательно их перемешать.
- Разложите 36 карт стопкой.
- Попросите друга выбрать одну из 36 карточек, посмотреть на нее и запомнить, а затем положить ее обратно в стопку, не показывая ее вам.
- Перемешайте 36 карт.
- Разложите 36 карт в 6 рядов по 6 карт в каждом. Обязательно сдавайте верхний ряд слева направо. Затем нанесите второй ряд под ним слева направо. И так далее, каждый последующий ряд кладется под предыдущий.
- Попросите друга посмотреть на карточки и сказать, в каком ряду находится выбранная карточка.
 Запомните номер ряда.
Запомните номер ряда. - Аккуратно поднимите карты в том же порядке, в котором вы их положили . Таким образом, первая карта слева в верхнем ряду находится наверху стопки, а последняя карта справа в нижнем ряду — внизу стопки.
- Теперь разложите карты в 6 рядов по 6 карт в каждом, но на этот раз разложите карты по одному столбцу за раз . Вместо того, чтобы переходить от одной строки к другой, переходите от одного столбца к другому. Разложите первые шесть карт в столбик сверху вниз в крайнее левое положение. Затем выложите следующие шесть карт во второй столбец из шести карт справа от первого столбца из шести карт. Продолжайте делать это, пока у вас не будет 6 столбцов по 6 карт в каждом (что выглядит так же, как 6 рядов по 6 карт в каждом, потому что это 9).0150 это то же самое).
- Еще раз спросите у друга, в каком ряду находится выбранная карта.
- Когда ваш друг скажет вам, в каком ряду находится карта, вы можете сказать, какая именно выбранная карта.
 Как? Если ваш друг сказал, что карта была в строке 2 в первый раз, а в строке 5 во второй раз, то выбранная карта — это карта во втором столбце пятой строки. Это связано с тем, что при расположении карточек то, что в первый раз было строками, во второй раз становится столбцами.
Как? Если ваш друг сказал, что карта была в строке 2 в первый раз, а в строке 5 во второй раз, то выбранная карта — это карта во втором столбце пятой строки. Это связано с тем, что при расположении карточек то, что в первый раз было строками, во второй раз становится столбцами.
Вернуться к началу
Калькулятор молнии
Вот уловка, чтобы удивлять их каждый раз! Попросите кого-нибудь записать свой номер социального страхования. Затем попросите их переписать его так, чтобы все было перемешано. (Если у них нет номера социального страхования, попросите их записать любые 9 цифр от 1 до 9.) Если есть нули, попросите заменить их на любую другую цифру от 1 до 9. Затем попросите их скопировать свои девять цифр. числа в том же порядке рядом с исходными девятью числами. Это даст им число с 18 цифрами, первая половина которого такая же, как вторая половина. Далее измените вторую цифру на 7, и измените одиннадцатую цифру (это будет то же число, что и вторая цифра, но во вторых девяти цифрах) также на 7. Тогда поспорьте с ними, что вы сможете сказать им, что останется после деления числа на 7, быстрее, чем они сообразят это вручную. Ответ: 0 — 7 делится на это новое число ровно без остатка!
Тогда поспорьте с ними, что вы сможете сказать им, что останется после деления числа на 7, быстрее, чем они сообразят это вручную. Ответ: 0 — 7 делится на это новое число ровно без остатка!
Вернуться к началу
Таблицы забавных чисел
Следующие забавные таблицы взяты из одной из моих любимых книг всех времен, Recreations in the Theory of Numbers , Альберт Х. Бейлер, опубликовано Dover Publications. Эта книга на самом деле объясняет математические причины, по которым эти трюки работают.
987654 9 + 2 = 888888888
987654 9 + 2 = 888888888
987654. 9 + 0 = 888888888
9 + 0 = 888888888
 д.
д.Наверх
Знаете ли вы…?
Каждое двузначное число, оканчивающееся на 9, является суммой двух цифр плюс сумма двух цифр. Так, например, 29 = (2 х 9) + (2 + 9). 2 X 9 = 18. 2 + 9 = 11. 18 + 11 = 29.
40 — уникальное число, потому что, когда его записывают как «сорок», это единственное число, буквы которого расположены в алфавитном порядке.
А простой число — это целое число больше 1, которое не делится без остатка ни на какое другое целое число, кроме самого себя (и 1). 2, 3, 5, 7, 11, 13 и 17 являются примерами простых чисел.
139 и 149 — первые последовательные простые числа, отличающиеся на 10.
69 — единственное число, в квадрате и кубе которого между ними используются все цифры от 0 до 9 по одному разу:
69 2 = 4761 и 69 3 = 328 509.
Один фунт железа содержит примерно 4 891 500 000 000 000 000 000 000 атомов.
Существует около 318 979 564 000 возможных способов сыграть первые четыре хода с каждой стороны в игре в шахматы.
Земля проходит более полутора миллионов миль каждый день.
В Эйфелевой башне 2 500 000 заклепок.
Если бы все кровеносные сосуды в человеческом теле были сложены встык, они растянулись бы на 100 000 миль.
Вернуться к началу
Математический трюк для этого года
Предполагается, что этот трюк будет работать только в 1998 году, но на самом деле одно изменение позволит ему работать в течение любого года.
1. Выберите количество дней в неделю, когда вы хотели бы выходить на улицу (1-7).
2. Умножьте это число на 2.
3. Прибавьте 5.
4. Умножьте полученную сумму на 50.
5. В 1998 году, если у вас уже был день рождения в этом году, прибавьте 1748. Если нет , добавьте 1747. В 1999 году просто добавьте 1 к этим двум числам (поэтому добавьте 1749, если у вас уже был день рождения, и добавьте 1748, если нет). В 2000 году номер меняется на 1749 и 1748. И так далее.
6. Вычтите из четырех цифр год вашего рождения (19ХХ).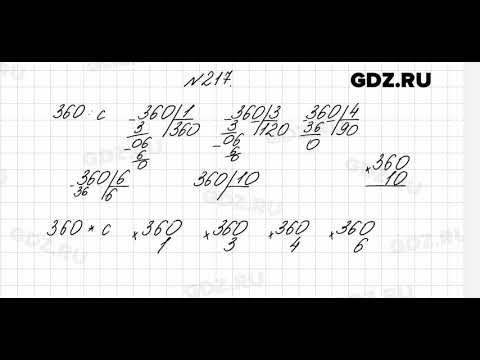
Результаты:
У вас должно быть трехзначное число.
Первая цифра этого числа означала количество дней, в течение которых вы хотите выходить на улицу каждую неделю (1–7).
Последние две цифры — ваш возраст.
(Спасибо, что передали мне это, Джуди.)
Вернуться к началу
Где нить?
В следующий раз, когда вы будете с группой людей и захотите произвести на них впечатление своими экстрасенсорными способностями, попробуйте это. Пронумеруйте всех в группе от 1 до любого числа. Возьмите кусок веревки и скажите, чтобы он привязал ее кому-нибудь к пальцу, пока вы выходите из комнаты или поворачиваетесь спиной. Затем скажите, что вы можете сказать им не только, у кого он есть, но и на какой руке и на каком пальце он находится, если они просто посчитают за вас и дадут вам ответы. Затем попросите одного из них ответить на следующие вопросы:
1. Умножьте номер человека со строкой на 2.
2. Прибавьте 3.
3. Умножьте результат на 5.
4. Если строка справа, прибавьте 8.
Если струна находится на левой руке, добавьте 9.
5. Умножьте на 10.
6. Добавьте номер пальца (большой палец = 1).
7. Добавить 2.
Попросите их сказать вам ответ. Затем мысленно вычтите 222. Остаток дает ответ, начиная с правой цифры ответа.
Например, предположим, что струна находится на безымянном пальце левой руки Игрока №6:
1. Умножить на 2 = 12.
2. Прибавить 3 = 15.
3. Умножить на 5 = 75
4. Поскольку струна находится на левой руке, прибавляем 9 = 84.
5. Умножаем на 10 = 840.
6. Прибавляем номер пальца (3) = 843.
7. Прибавляем 2 = 845.
Теперь мысленно вычтите 222 = 623. Цифра справа (3) говорит вам, что струна находится на безымянном пальце. Средняя цифра говорит о том, что он находится на левой руке (правая рука = 1). Цифра слева говорит о том, что строка принадлежит Игроку №6.
Кстати, когда номер человека больше 9, вы получите ЧЕТЫРЕХзначное число, а ДВЕ левые цифры будут номером Игрока.
В чем секрет?
(Это из замечательной книги Шейлы Энн Барри Giant Book of Puzzles & Games, . Опубликовано Sterling Publishing Co., Inc., Нью-Йорк, 1978 г., недавно переиздано в мягкой обложке.)
Следите за новостями. больше математических трюков. Они будут добавляться время от времени, так что не забудьте проверить снова.
Что такое восходящий порядок? Значение, Решенные примеры, Факты
Что такое Восходящий порядок?
Восходящий порядок означает расположение чисел в порядке возрастания, то есть от меньшего к большему.
Чтобы расположить числа в любом порядке, нам сначала нужно их сравнить.
Сначала Сравните , затем Закажите
Расположите числа в порядке возрастания:
- Подсчитайте количество цифр в каждом числе. Число с наименьшим количеством цифр является наименьшим. Напишите это первым. Продолжайте до тех пор, пока все числа, оставшиеся для сравнения, не будут иметь одинаковое количество цифр.

- Для чисел с одинаковым количеством цифр начните со сравнения чисел, начиная с самой левой цифры. Запишите число с наименьшей цифрой.
- Если крайние левые цифры совпадают, перейдите к цифрам справа и сравните их. Напишите число с меньшей цифрой.
- Продолжайте делать это с оставшимися числами, пока мы не упорядочим все числа.
Пример : Расположите 22554, 231, 22, 245, 22354 в порядке возрастания.
Число 22 имеет наименьшее количество цифр. Итак, запишите его первым, так как это наименьшее число.
Далее, 231 и 245 — трехзначные числа. У обоих по 2 на сотне. Итак, переходим к цифре справа. Сравните 2 3 1 и 2 4 5 Поскольку 3 < 4; Итак, 231 < 245
Затем сравните 22554 и 22354, так как оба имеют 5 цифр. Сравнивая 22 5 54 и 22 3 54, мы находим 3 < 5
Таким образом, 22354 < 22554
Затем мы можем расположить числа на числовой прямой следующим образом:
Упорядочивание дробей по возрастанию
- Упорядочивание дробей с одинаковыми знаменателями
У дробей с одинаковым знаменателем наименьшей является дробь с наименьшим числителем.
Пример : Организатор 3 ⁄ 7 , 2 ⁄ 7 , 5 ⁄ 7 , 1⁄ 7 в ASCNDEND.
Сравнивая числители, получаем 1 < 2 < 3 < 5
Therefore, 1⁄ 7 < 2 ⁄ 7 < 3 ⁄ 7 < 5 ⁄ 7
- Ordering fractions with same numerators
When the fractions have тот же числитель, дробь с большим знаменателем наименьшая.
Пример : Расставить 3 ⁄ 7 , 3 ⁄ 8 , 5 9 8
⁄ 51159 , 3 ⁄ 4 в порядке возрастания.Здесь числитель 3 во всех дробях. Итак, сравним знаменатель.
При сравнении знаменателей мы получаем: 4 <5 <7 <8
Следовательно, 3 ⁄ 8 < 3 ⁄ 7 < 3 стран 5 999996 3 6 3 6 3 6 3 6 3 919996 3 919996 39996 39996 3 6 3 6 3 6 3 6 3 6 3 6 3 6 3 6 3 6 3 6 3 6 3 6 3 6 3 6 3 6 3 6. 4
4
- Упорядочивание дробей с разными числителями и знаменателями
Приведите дроби к одинаковым знаменателям (или числителям), а затем сравните и упорядочите их.
Пример : Организатор 2 ⁄ 5 , 4 ⁄ 6 , 3 ⁄ 5 и 1
ón 3 .Знаменатели 5, 6 и 3.
Упорядочивание десятичных знаков по возрастанию- Сначала сравните целую часть числа в каждом десятичном разряде. Число с наименьшим целым числом является наименьшим.
- Если целые части числа одинаковы, сравнивайте десятичные части так же, как мы сравниваем целые числа.
Пример : Расположите 22.44, 22.04, 22.40 и 2.45 в порядке возрастания.
Сначала сравните целые числа:
22,44, 22,04, 22,40 и 2,45
2 — самый маленький, пишем его первым.
| 2,45 |
22,44, 22,04, 22. 40 All All 22.
40 All All 22.
SO, Compare The Demimal The Demimal.
0.04 < 0.40 < 0.44
Therefore, 22.04 < 22.40 < 22.44
The ascending order is:
| 2.45 | 22.04 | 22.40 | 22.44 |
| Забавные факты – Чтобы запомнить порядок возрастания, вспомните полет «самолета» от низкого к высокому. |
Десятичные числа сравниваются так же, как и многозначные числа, сохраняя количество цифр одинаковым с помощью завершающих нулей.
3/5 < 3/7 < 3/9 < 3/11
3/11 < 3/7 < 3/5 < 3/9
3/11 < 3/9 < 3/7 < 3/ 5
3/7 < 3/11 < 3/9 < 3/7
Правильный ответ: 3/11 < 3/9 < 3/7 < 3/5
Для дробей с одинаковыми числителями дробь с наименьший знаменатель — наибольшая дробь, а дробь с наибольшим числителем — наименьшая дробь.
2/9 < 3/9 < 5/9 < 7/9
7/9 < 5/9 < 3/9< 2/9
2/9 < 7/9 < 5/9 < 3/9
7/9 < 5/9 < 2/9 < 3/9
Правильный ответ: 2/9 < 3/ 9 < 5/9 < 7/9
Для дробей с одинаковыми знаменателями дробь с наименьшим числителем является наименьшей дробью, а дробь с наибольшим числителем — наибольшей дробью.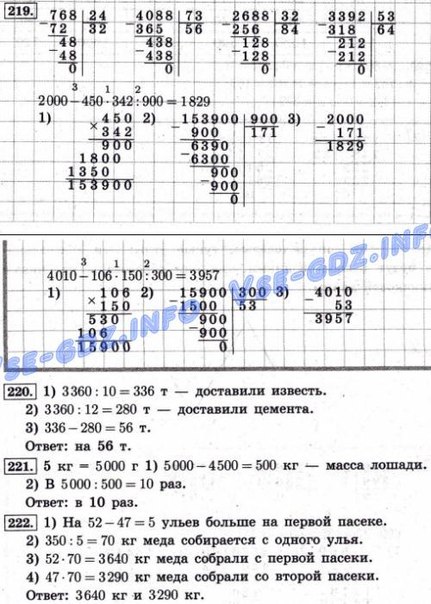
22 < 222 < 2322 < 2222
22 < 222 < 2222 < 2322
22 < 2222 < 222 < 2322
2322 < 2222 < 2 2292 < 20015
Правильный ответ: 22 < 222 < 2222 < 2322
При сравнении многозначных чисел первыми идут числа с наименьшим количеством цифр. Для многозначных чисел с одинаковым количеством цифр мы сравниваем цифры слева направо.
Часто задаваемые вопросы
В порядке убывания от меньшего к большему?
Нет. В порядке убывания от большего к меньшему. Наибольшее количество или число помещается первым, а наименьшее количество или число помещается в последнюю позицию.
Можно ли расположить дроби в порядке возрастания или убывания?
Да. Как и целые числа, дроби можно расположить в порядке возрастания или убывания.
Какие символы используются при расположении чисел в порядке возрастания и убывания?
Символы < (меньше) и > (больше) используются при расположении чисел в порядке возрастания и убывания.

 А.
А.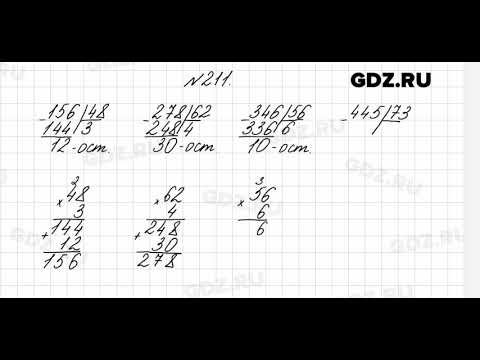 Также имеется достаточно материалов, которые пригодятся к экзаменам в 9-ых и 11-ых классах. Есть много готовых решенных задач ЕГЭ (ГИА, ОГЭ) и упражнений для отличной самоподготовки к экзаменам. Имеются демонстрационные варианты разных лет и онлайн тесты на основе КИМов для качественной самопроверки знаний. Также есть уникальные генераторы заданий, которые помогут учителям создать карточки для учеников. Есть разделы посвещенные контрольным и самостоятельным и проверочным работам для 3-4-ых и 5-6 классов. Помимо прочего имеются полезные презентации для учителей по разным школьным предметам — биология, обж, информатика, кубановедение, химия и другие. Кроме того есть обучающие видео уроки по математике (ЕГЭ, ГИА, КДР) и информатике (ОГЭ), которые принесут огромную пользу старшеклассникам в подготовке к экзаменам 2018 учебного года.
Также имеется достаточно материалов, которые пригодятся к экзаменам в 9-ых и 11-ых классах. Есть много готовых решенных задач ЕГЭ (ГИА, ОГЭ) и упражнений для отличной самоподготовки к экзаменам. Имеются демонстрационные варианты разных лет и онлайн тесты на основе КИМов для качественной самопроверки знаний. Также есть уникальные генераторы заданий, которые помогут учителям создать карточки для учеников. Есть разделы посвещенные контрольным и самостоятельным и проверочным работам для 3-4-ых и 5-6 классов. Помимо прочего имеются полезные презентации для учителей по разным школьным предметам — биология, обж, информатика, кубановедение, химия и другие. Кроме того есть обучающие видео уроки по математике (ЕГЭ, ГИА, КДР) и информатике (ОГЭ), которые принесут огромную пользу старшеклассникам в подготовке к экзаменам 2018 учебного года. 

 Поэтому, вероятно, в ваших интересах иметь его.
Поэтому, вероятно, в ваших интересах иметь его. Мы познакомимся с методами интегрирования, такими как интегрирование по частям, тригонометрическое замещение и разложение на неполные дроби.
Мы познакомимся с методами интегрирования, такими как интегрирование по частям, тригонометрическое замещение и разложение на неполные дроби. Практически все вопросы на экзаменах будут в том же духе, что и домашние задания. Поэтому понимание того, как выполнять все домашние задания, позволит вам хорошо сдать экзамены.
Практически все вопросы на экзаменах будут в том же духе, что и домашние задания. Поэтому понимание того, как выполнять все домашние задания, позволит вам хорошо сдать экзамены. Вопрос о том, разрешены ли калькуляторы на экзамене, будет определен позднее.
Вопрос о том, разрешены ли калькуляторы на экзамене, будет определен позднее. ВИКТОРИНЫ ПО МАКИЯЖУ НЕ ПРОВОДЯТСЯ. Участие в занятиях будет основываться на вашей готовности ЗАДАВАТЬ и ОТВЕЧАТЬ на вопросы в классе.
ВИКТОРИНЫ ПО МАКИЯЖУ НЕ ПРОВОДЯТСЯ. Участие в занятиях будет основываться на вашей готовности ЗАДАВАТЬ и ОТВЕЧАТЬ на вопросы в классе.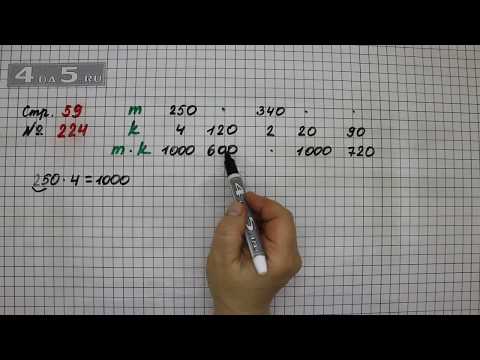 ..?
..?
 И напишите это число прямо под первым числом.
И напишите это число прямо под первым числом.

 Запомните номер ряда.
Запомните номер ряда. Как? Если ваш друг сказал, что карта была в строке 2 в первый раз, а в строке 5 во второй раз, то выбранная карта — это карта во втором столбце пятой строки. Это связано с тем, что при расположении карточек то, что в первый раз было строками, во второй раз становится столбцами.
Как? Если ваш друг сказал, что карта была в строке 2 в первый раз, а в строке 5 во второй раз, то выбранная карта — это карта во втором столбце пятой строки. Это связано с тем, что при расположении карточек то, что в первый раз было строками, во второй раз становится столбцами.