ГДЗ по математике 2 класс учебник Петерсон 1 часть
- Тип: ГДЗ, Решебник.
- Автор: Л. Г. Петерсон.
- Год: 2021.
- Серия: Учись Учиться.
- Издательство: Просвещение/Бином.
Подготовили готовое домашнее задание к упражнениям на 61 странице по предмету математика за 2 класс. Ответы на задания: 6, 7, 8, 9 и 10.
Учебник 1 часть — Страница 61.
Ответы 2021 года.
Номер 6.
а) Чебурашка для строительства Дома дружбы привёз 524 белых кирпича и 316 красных. Сколько всего кирпичей привёз Чебурашка? На сколько красных кирпичей меньше, чем белых?
б) Крокодил Гена привёз на строительство 275 л краски. Жёлтой краски было 96 л, а зелёной – на 38 л меньше, чем жёлтой. Сколько было литров краски других цветов?
Ответ:
а) Чтобы узнать, сколько всего кирпичей привёз Чебурашка (целое), нужно сложить две части.
Чтобы узнать, на сколько красных кирпичей меньше, чем белых, нужно от числа белых отнять число красных (разностное сравнение).
Задачу можно оформить с помощью краткой записи или чертежа:
б) Чтобы узнать, сколько литров краски других цветов (часть), нужно от всей краски (целого) отнять две части: жёлтую и зелёную краску. Сразу этого мы сделать не можем. Жёлтой краски 96 литров, а зелёной на 38 л меньше, то есть 96 – 38.
Задачу можно решить разными способами.
Оформить можно с помощью краткой записи или чертежа:
Номер 7.
Составь задачи, которые решаются так: 642 – 396 587 – 94 – 238 453 + 49 + 306
Ответ:
а) До обеда в магазине продали 642 тетради, после обеда 396. На сколько тетрадей меньше продали после обеда?
б) Петя читает книгу, в которой 587 страниц. На первой неделе он прочитал 95 страницы, на второй – 238. Сколько страниц ему осталось еще прочитать?
в) В школе объявили сбор макулатуры. 2 «А» сдал 453 кг, 2 «Б» – 49 кг, 2 «В» – 306 кг. Сколько килограммов сдали три класса вместе?
Номер 8.
Сравни.
Ответ:
Любое трехзначное число больше любого двузначного числа и любого однозначного числа, а из двух трехзначных чисел больше то, у которого больше цифра в старшем из несовпадающих разрядов.
Если одно слагаемое одинаковое, а второе больше, то результат этой суммы больше.
При одинаковом уменьшаемом значение той разности больше, в которой вычитаемое меньше.
При одинаковом вычитаемом значение той разности больше, в которой уменьшаемое больше.
58 и 126 207 и 720
111 и 9 340 и 35
0 и 532 814 и 418
а + 25 и а + 125
b – 602 и b – 62
456 – с и 356 – с
Номер 9.
В какой из фигур больше клеток? Как легче сосчитать?
Ответ:
Надо узнать, в какой фигуре больше клеток, то есть сравнить их по площади.
Когда предметов много, то счетные единицы удобно укрупнять. Маленькие клетки считать неудобно.
Лучше считать большие клетки, состоящие из 4 маленьких. Разбивая фигуры на большие клетки, устанавливаем, что в первой фигуре их содержится 10, во второй – 11, а в третьей – тоже 10. Таким образом, во второй фигуре больше всего больших клеток, а значит, и маленьких.
Номер 10.
5 рыбаков за 5 часов выпотрошили 5 судаков. За сколько часов 100 рыбаков выпотрошат 100 судаков? (Все рыбаки работают с постоянной и одинаковой скоростью.)
Ответ:
Из условия следует, что один рыбак потрошит одну рыбу за 5 часов. Каждому из 100 рыбаков надо распотрошить всего по 1 рыбе. Значит, им тоже потребуется для этого 5 часов.
Рейтинг
← Выбрать другую страницу ←
ГДЗ по математике 2 класс учебник Петерсон 1 часть
- Тип: ГДЗ, Решебник.
- Автор: Л. Г. Петерсон.
- Год: 2021.
- Серия: Учись Учиться.
- Издательство: Просвещение/Бином.
Подготовили готовое домашнее задание к упражнениям на 23
странице по предмету математика за 2 класс.
Ответы на задания: 5, 6, 7, 8, 9 и 10.
Учебник 1 часть — Страница 23.
Ответы 2021 года.
Номер 5.
Запиши примеры в столбик и вычисли:
Ответ:
В примерах второй строки одно из слагаемых на несколько десятков больше или меньше, чем в первой. Соответственно, на столько же десятков будет больше или меньше и вся сумма.
5 + 28 = 33 34 + 29 = 63
28 + 45 = 73 59 + 34 = 93
58 + 17 = 75 47 + 36 = 83
Номер 6.
В пачке 25 листов бумаги красного цвета, 13 – жёлтого цвета и 10 – синего. Объясни, что узнаешь, выполнив действия: 25 + 13 13 + 10 25 + 10 + 13 25 – 10
Найди значения выражений.
Ответ:
25 + 13 = 38
Сколько листов бумаги красного и желтого цвета?
13 + 10 = 23
Сколько листов бумаги желтого и синего цвета?
25 + 10 + 13 = 48
Сколько всего листов бумаги в пачке?
25 – 10 = 15
На сколько листов бумаги красного цвета больше, чем синего?
Номер 7.
Прочитай задачи. Чем они похожи и чем отличаются? Составь схемы к этим задачам и реши их.
а) Саша и Гена помогали в саду собирать яблоки. Саша собрал 28 кг яблок, а Гена – 15 кг. Сколько килограммов яблок собрали Саша и Гена вместе?
б) Саша и Гена помогали в саду собирать яблоки. Саша собрал 28 кг яблок, а Гена – на 15 кг больше. Сколько килограммов яблок собрали Саша и Гена вместе?
Ответ:
В обеих задачах одинаковые сюжеты, числовые значения величин. Однако в первой задаче сказано, что «Гена собрал 15 кг яблок», а во второй – что «Гена собрал на 15 кг яблок больше, чем Саша». Отсюда и разница в решении.
а)
– Чтобы узнать, сколько килограммов яблок собрали Саша и Гена вместе, надо сложить массу яблок, которые собрал каждый из них. (Ищем целое.) По условию известно, что Саша собрал 28 кг, а Гена – 15 кг.
28 + 15 = 43 (кг)
Ответ: Саша и Гена собрали вместе 43 кг яблок.
б)
– Чтобы узнать, сколько килограммов яблок собрали Саша и Гена вместе, надо сложить массу яблок, которые собрал каждый из них.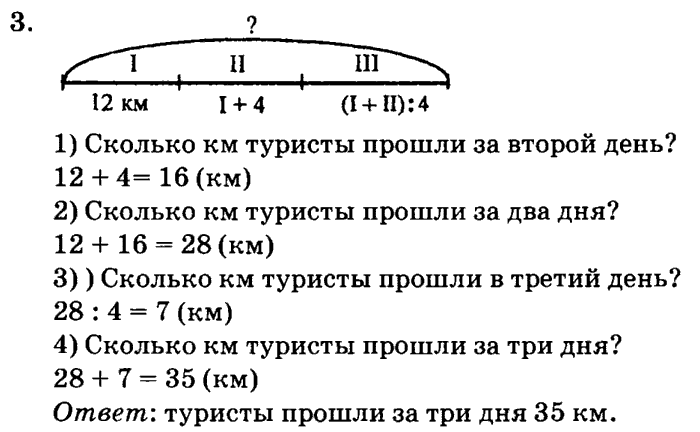
(Ищем целое.) По условию известно, что Саша собрал 28 кг. Масса яблок, собранных Геной, не известна, но сказано, что Гена собрал на 15 кг яблок больше, чем Саша. Значит, мы можем ее найти, увеличив 28 кг на 15 кг.
2) 28 + 43 = 71 (кг)
Ответ: Саша и Гена вместе собрали 71 кг яблок.
Номер 8.
Сравни, если возможно:
Ответ:
23 кг > 5 кг 68 см < 86 см 3 дм > 16 см
18 л < 37 л 51 дм < 57 дм 7 м 8 кг
Сравнивать, складывать и вычитать величины можно только тогда, когда они выражены в одних и тех же единицах измерения. Поэтому прежде, чем сравнить 3 дм и 16 см, надо выразить их в сантиметрах: 3 дм = 30 см, 30 см > 16 см, значит, 3 дм > 16 см.
Сравнить 7 м и 8 кг нельзя, так как они выражают значения разных величин.
Номер 9.
Вычисли:
Ответ:
14 – 8 + 5 = 6 + 5 = 11
9 + 3 – 7 = 12 – 7 = 5
20 – 4 – 9 = 16 – 9 = 7
26 + 12 – 8 = 38 – 8 = 30
78 – 4 + 16 = 74 + 16 = 90
95 – 72 + 40 = 23 + 40 = 63
50 – 35 + 18 = 15 + 18 = 33
46 + 7 – 24 = 53 – 24 = 29
Номер 10.
Какое слово в каждом ряду лишнее:
а) окно, волк, коза, бежать, берёза;
б) гора, холм, река, лес, трамвай, поле;
в) трамвай, такси, автобус, корова, грузовик;
г) книга, тетрадь, арбуз, ластик, велосипед?
Ответ:
а) Лишний глагол «бежать», остальные слова – существительные; может быть лишним слово «берёза», так как в нем три слога, а в остальных словах – два;
б) «трамвай» – он создан человеком, а все остальное – природой;
в) «корова» – это животное, а все остальное – неодушевленные предметы; лишним может быть «автобус» по признаку «начинается с гласной»;
г) «арбуз» – он съедобный, а остальные предметы – нет. Может быть лишним слово «велосипед», так как в нем четыре слога, а в остальных словах – два.
Рейтинг
← Выбрать другую страницу ←
Дэйв Петерсон — Страница 15 — The Math Doctors
(Доктор Петерсон)
Бывший инженер-программист со степенью в области математики, я нашел свой опыт работы доктором математики, начавшийся в 1998 году, настолько стимулирующим, что в 2004 году я устроился на новую работу преподавателем математики в местном колледже, чтобы помогать таким же людям лицом к лицу.
У меня трое взрослых детей, и я живу недалеко от Рочестера, штат Нью-Йорк. Я являюсь автором и инициатором всего на сайте, что не приписывается кому-либо другому.
Статистика / 10 ноября 2020 г. 9 ноября 2020 г.
В нашей серии средних значений на прошлой неделе мы представили идею средневзвешенного значения (или средневзвешенного значения), где каждому элементу присваивается вес. Все классические примеры по-разному связаны со средними оценками. На этот раз мы рассмотрим, как возникают средневзвешенные значения, когда вам нужно усреднить несколько средних вместе, что-то, что мы коснулись …
Средневзвешенные значения: усреднение средних или коэффициентов Подробнее »
NQOTW, тригонометрия / 6 ноября 2020 г. 5 ноября 2020 г.
(Новый вопрос недели) Сентябрьский вопрос о построении графика косинуса по горизонтали привел к долгому разговору. Между опечаткой в задаче и некоторыми мыслями наизнанку эта удивительно нестандартная задача привела к хорошему напряжению ума! Я значительно сократил это, убрав отвлекающие факторы от основных идей, но это…
Упражнение на растяжку ума с растянутым косинусом Подробнее »
Статистика / 3 ноября 2020 г.
2 ноября 2020 г.
В нашей серии средних мы рассмотрели среднее/медиану/моду, затем детали (арифметического) среднего, а затем различные виды среднего (арифметическое, геометрическое, гармоническое, квадратичное). Далее я хочу рассмотреть концепцию средневзвешенного значения. Проверяя то, что мы говорили об этом, я нашел полезную серию объяснений одного применения…
(Новый вопрос недели) Давайте рассмотрим короткий вопрос из середины сентября, на который было несколько разных ответов. В некотором смысле это простой вопрос; но мы пойдем немного дальше, так что продолжайте читать до конца. Можно ли умножить дробь и десятичную дробь? Азраф спросил: Могу ли я умножить …
Умножение дробей и десятичных дробей Подробнее »
Статистика / 27 октября 2020 г. 27 октября 2020 г.
На прошлой неделе мы рассмотрели, что именно представляет собой среднее, имея в виду конкретно среднее арифметическое, то, которое мы сначала узнаем как «среднее».
Но так же, как мы видели ранее, что есть несколько вещей, называемых «средним» (среднее, медиана, мода), на самом деле существует несколько различных видов «среднего». Посмотрим здесь на арифметику, …
Четыре вида «средних» Подробнее »
Algebra, Calculus, NQOTW / 23 октября 2020 г. 23 октября 2020 г.
(новый вопрос недели) Я часто говорил, что на уроках математического анализа многие студенты, наконец, изучают алгебру, потому что теперь алгебра является важным инструментом, а не только что-то, чтобы узнать для экзамена. Это особенно верно в отношении нетрадиционных учащихся, которые, возможно, недавно не изучали математику или даже изучают …
Предел: правильное знание алгебры Подробнее »
Статистика / 20 октября 2020 г. 19 октября 2020 г.
На прошлой неделе мы начали серию средних значений, рассматривая общий список трех видов средних значений: среднее значение, медиана и мода. На этот раз мы сосредоточимся на (арифметическом) среднем, думая о том, почему оно подходит для многих приложений; это приведет к обсуждению на следующей неделе того, когда другие виды среднего значения …
Как сделать среднее значение более значимым Подробнее »
Алгебра, геометрия, NQOTW / 16 октября 2020 г.
15 октября 2020 г.
Одна из вещей, которую мы любим делать, — это направлять ученика в процессе решения задач. Вот задача от августа, которая иллюстрирует, как продумывать сложное геометрическое доказательство. В частности, здесь используются некоторые теоремы о кругах, включающие хорды, секущие и касательные, а также немного алгебры. Проблема Вот проблема (у меня есть…
Задача-доказательство: аккорды и касательные Подробнее »
Статистика / 13 октября 2020 г. 12 октября 2020 г.
Есть три различных статистики, которые обычно преподают как «средние» или «меры центральной тенденции» набора чисел: среднее, медиана и мода. (Есть и другие, о которых мы поговорим позже.) Каковы они? Чем они отличаются? Как вы их используете? Мы рассмотрим подобные вопросы как…
Три вида «средних» Подробнее »
Алгебра, NQOTW / 9 октября 2020 г. 8 октября 2020 г.
(Новый вопрос недели) Вопрос, заданный в конце августа, поставил перед студентом и доктором математики дополнительную задачу из-за очевидной опечатки в вопросе проблема.
Нам особенно нравится работать со студентами, которые готовы взять на себя дополнительную работу, чтобы узнать больше, чем им нужно…
Тренировка конечной серии Подробнее »
Есть вопрос? Спроси здесь!
Мы — группа опытных волонтеров, главная цель которых — помочь вам, ответив на ваших вопросов по математике. Чтобы задать вопрос, просто нажмите здесь.
Последние сообщения в блоге
Архив блога
Категории
Теги
Об этом сайте
The Math Doctors полностью управляется добровольцами, которым нравится делиться своими математическими знаниями с людьми всех возрастов. У нас более 20 лет опыта работы в качестве группы, и мы заслужили уважение педагогов. Чтобы узнать о нашей прошлой истории, см. О программе Спросите доктора Математики. Если вы хотите стать волонтером или внести свой вклад другим способом, пожалуйста, свяжитесь с нами.
Математика | Edutopia
Джордж Лукас Образовательный фонд
EdutopiaEdutopia
Search
Сорт:Рекомендованные
Рекомендованные.
для усвоения материала.
Джозеф Манфре
896
Создание среды, в которой все учащиеся видят, что они могут быть хороши в математике
Когда учителя направляют учащихся не ограничиваться узкими показателями успеха в математике, больше учащихся увидят свой потенциал в обучении.
Кристал Фроммерт
737
5 способов перестать думать за учащихся
Слишком часто учащиеся-математики полагаются на учителей, чтобы они думали за них, но есть несколько простых способов научить их думать самостоятельно.
Crystal Frommert
4.1k
Использование тестовых поправок в качестве инструмента обучения
Назначение исправлений в качестве классной работы, а затем повторное тестирование учащихся позволяет учителю точно оценить, усвоили ли они материал.
Margaret McDade
2,8k
Развивайте сильные математические навыки, используя эти простые стратегии
Изучение новых слов является фундаментальной частью понимания математических понятий.
Используйте эти стратегии, чтобы добиться как беглости речи, так и вовлеченности.
Стивен Нуну
3.6k
Не стоит недооценивать силу оценки
Эти развлекательные онлайн-инструменты помогут учащимся старших классов научиться оценивать, что является полезным навыком сейчас и в будущем.
Джон Янг
530
Альтернатива задачам на разминку
Начинать урок математики с задачи на разминку — обычное дело. Вот как один учитель вместо этого начинает с небольшого разговора, прежде чем перейти к математике.
Джей Вамстед
2.7k
Подкрепление элементарных уроков математики движением
Сочетание простых упражнений с обучением математике может помочь учащимся начальной школы запомнить эти уроки.
Элизабет Петерсон
5,4k
Почему учащиеся должны писать по всем предметам
Письмо улучшает обучение, закрепляя информацию в долговременной памяти, объясняют исследователи.
Плюс пять увлекательных письменных заданий по всем предметам.
Юки Терада
16.5k
Учим ли мы детей математике?
Каждый ребенок обладает огромным математическим потенциалом, говорит Джо Боулер, профессор математики Стэнфордского университета и автор бестселлеров.
Sarah Gonser
10,6k
4 способа сделать упражнения на беглую математику увлекательными
Эффективные упражнения на беглость речи могут предложить учащимся момент игры, а их активное участие помогает закрепить математические факты в их сознании.
Kurt Stielow
642
11 математических приложений и онлайн-инструментов, рекомендуемых учителями
Независимо от того, преподаете ли вы этой осенью онлайн или очно, эти цифровые математические инструменты могут пригодиться в классах от дошкольного до 12-го.
Emelina Minero
11,8k
3 фразы, которые могут демотивировать учащихся на уроке математики
На первый взгляд безобидные утверждения могут усугубить тревожность учащихся по поводу математики, а избегание этих фраз может помочь всем учащимся увидеть себя «математиками».