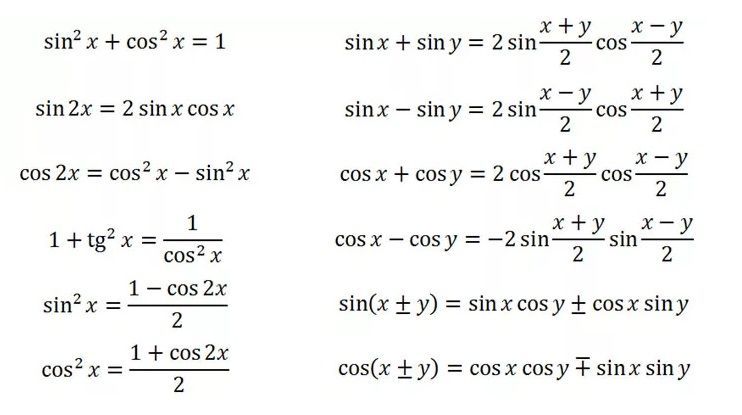Таблицы по алгебре 10 11 класс: Справочник по алгебре 10-11 класс: в таблицах и схемах

Справочник по алгебре. 10-11 класс

Все формулы по алгебре за 11 класс

Удобный справочник по алгебре, позволит учащимся 10-11 классов более глубоко осваивать включенный в школьную программу материал, подробно разбирать различные темы при самостоятельной работе. С его помощью можно самостоятельно проработать теоретическую часть предмета более детально, чем с использованием исключительно учебника.

В справочник включены уроки в последовательности, соответствующей утверждено образовательной программе. Это позволит систематически изучать новый материал, чтобы повысить свою успеваемость и лучше усваивать знания по предмету, переходя последовательно от одной темы к следующей.

С его помощью можно самостоятельно проработать теоретическую часть предмета более детально, чем с использованием исключительно учебника.

Reshator. com

07.02.2019 11:05:17

2019-02-07 11:05:17

Источники:

Https://reshator. com/sprav/algebra/10-11-klass/

Шпаргалки по математике — формулы, таблицы, шпаргалки по алгебре, геометрии, тригонометрии. » /> » /> .keyword { color: red; }

Все формулы по алгебре за 11 класс

Математика принадлежит к числу тех наук, которые ясны сами по себе.

Войти

Интересные статьи

Новые образовательные стандарты и школьные учебники по ним Олимпиада по информатике «Отличник» Олимпиада по математике «Отличник» Олимпиада по английскому языку «Отличник» Самообразование учителя математики Особенности студенческой визы в США Частный репетитор английского языка – как не потеряться в изобилии предложений

Как Вы оцениваете сайт?

Новые материалы

Рабочая программа по алгебре для 10 класса. Колягин. Рекомендуемые ресурсы сети интернет для подготовки к ЕГЭ Построение графика квадратичной функции Таблицы квадратов и степеней Справочные материалы 7-9 классы. Алгебра Справочные материалы 6 класс Справочные материалы 5 класс

Подписка на новые материалы

Вы здесь: Главная Шпаргалки по математике

На этой странице собраны полезные шпаргалки по математике, алгебре и геометрии для учащихся 5-11 классов. Среди них часто используемые математические формулы, таблицы значений и многое другое.

Таблицы квадратов и степеней

Таблицы квадратов и степеней

Основные формулы планиметрии

Справочные материалы по тригонометрии

Справочные материалы по тригонометрии для 10 класса.

Шпаргалка по математике для 4 класса

Таблица производных элементарных функций

Формулы сокращенного умножения

Таблица двоичных логарифмов целых чисел от 1 до 64

Основные тригонометрические формулы

Таблица синусов, косинусов, тангенсов и котангенсов

© 2012-2020 «Уроки математики» — сайт учителя математики Соколовой А. А.

Все права на материалы сайта охраняются в соответствии с законодательством РФ.

Любое использование материалов с сайта Запрещено без письменного разрешения администрации сайта.

Вы здесь: Главная Шпаргалки по математике

Таблицы квадратов и степеней

Таблицы квадратов и степеней

Справочные материалы по тригонометрии для 10 класса.

© 2012-2020 «Уроки математики» — сайт учителя математики Соколовой А. А.

Все права на материалы сайта охраняются в соответствии с законодательством РФ.

Любое использование материалов с сайта Запрещено без письменного разрешения администрации сайта.

Основные формулы планиметрии.

Sokolova-aa. ru

15.11.2019 22:02:29

2019-11-15 22:02:29

Источники:

Http://sokolova-aa. ru/cribs

Все формулы по математике » /> » /> .keyword { color: red; }

Все формулы по алгебре за 11 класс

На этой странице собраны все формулы, необходимые для сдачи контрольных и самостоятельных работ, экзаменов по по алгебре, геометрии, тригонометрии, стереометрии и другим разделам математики.

Здесь вы можете скачать или посмотреть онлайн все основные тригонометрические формулы, формулу площади круга, формулы сокращенного умножения, формула длины окружности, формулы приведения и многие другие.

Можно так же распечатать необходимые сборники математических формул.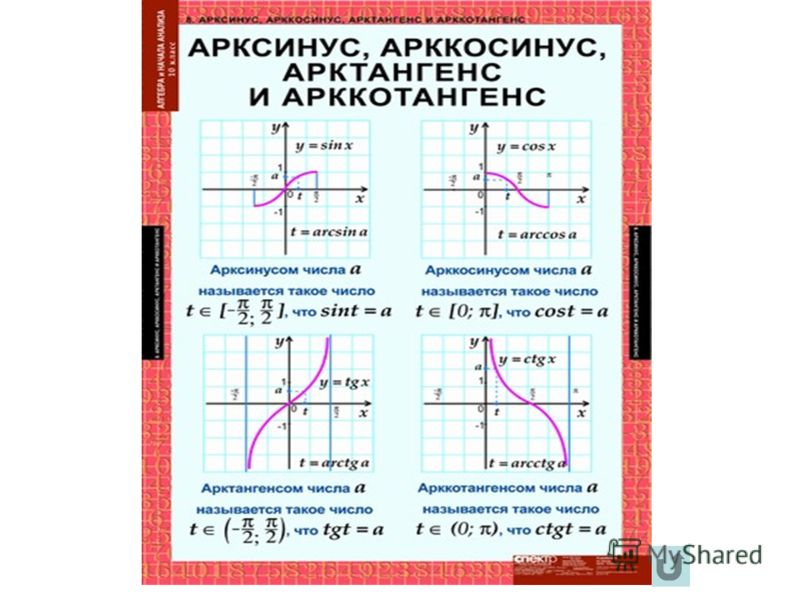

Успехов в учебе!

Формулы Арифметики:

Формулы Алгебры:

Геометрические Формулы:

Арифметические формулы:

Законы действий над числами

Переместительный закон сложения: a + b = b + a.

Сочетательный закон сложения: (a + b) + с = a + (b + c).

Переместительный закон умножения: ab = ba.

Сочетательный закон умножения: (ab)с = a(bc).

Распределительный закон умножения относительно сложения: (a + b)с = aс + bс.

Распределительный закон умножения относительно вычитания: (a — b)с = aс — bс.

Некоторые математические обозначения и сокращения:

Признаки делимости

Признаки делимости на «2»

Число, делящееся на «2» без остатка называется Чётным, не делящееся – Нечётным. Число делится на «2» без остатка, если его последняя цифра чётная (2, 4, 6, 8) или ноль

Признаки делимости на «4»

Число делится на «4» без остатка, если две последние его цифры нули или в сумме образуют число, делящееся без остатка на «4»

Признаки делимости на «8»

Число делится на «8» без остатка, если три последние его цифры нули или в сумме образуют число, делящееся без остатка на «8» (Пример: 1 000 — три последние цифры «00», а при делении 1 000 на 8 получается 125; 104 — две последние цифры «12» делятся на 4, а при делении 112 на 4 получается 28; и. т.д.)

Признаки делимости на «3» и на «9»

Без остатка на «3» делятся только те числа, у которых сумма цифр делится без остатка на «3»; на «9» — только те, у которых сумма цифр делится без остатка на «9»

Признаки делимости на «5»

Признаки делимости на «25»

Без остатка на «25» делятся числа, две последние цифры которых нули или в сумме образуют число, делящееся без остатка на «25» (т. е. числа, оканчивающиеся на «00», «25», «50», «75»

Признаки делимости на «10», «100» и на «1 000»

Без остатка на «10» делятся только те числа, последняя цифра которых ноль, на «100» — только те числа, у которых две последние цифры нули, на «1000» — только те числа, у которых три последние цифры нули

Признаки делимости на «11»

Без остатка на «11» делятся только те числа, у которых сумма цифр, занимающих нечётные места, либо равна сумме цифр, занимающих чётные места, либо отличается от неё на число, делящееся на «11»

Абсолютная величина — формулы ( модуль)

|a| ? 0, Причём |a| = 0 только если a = 0; |-a|=|a| |a2|=|a|2=a2 |ab|=|a|*|b| |a/b|=|a|/|b|, Причём b? 0; |a+b|?|a|+|b| |a-b|?|a|-|b|

Формулы Действия с дробями

Формула обращения конечной десятичной дроби в рациональную дробь:

Пропорции

Два равных отношения образуют Пропорцию:

Основное свойство пропорции

Ad = bc

Нахождение членов пропорции

Средние величины

Среднее арифметическое

Среднее геометрическое (среднее пропорциональное)

Среднее квадратичное

Среднее гармоническое

Некоторые конечные числовые ряды

Тождественные преобразования алгебраических и тригонометрических выражений

Свойства степеней

Свойства арифметических корней

Многочлены

Свойства числовых неравенств

1) Если a

2) Если a 0, то aс

3) Если a bс.

4) Если a 1/b.

5) Если a

6) Если a 0, b > 0, c > 0, d > 0, то ac

7) Если a 0, b > 0, то

8) Если, то

Соотношения между тригонометрическими функциями одного и того же аргумента

Формулы сложения:

Формулы двойного аргумента:

Формулы тройного аргумента:

Формулы половинного аргумента:

(для функций sin и cos – формулы понижения степени)

Формулы третьей и четвертой степени:

Формулы преобразования суммы в произведение:

Формулы преобразования произведения в сумму:

Формула приведения для преобразования выражений вида а) перед приведенной функцией ставиться тот знак, который имеет исходная функция;б) функция меняется на «кофункцию», если n нечетно; функция не меняется, если n четно. (Кофункциями синуса, косинуса, тангенса и котангенса называются соответственно косинус, синус, котангенс и тангенс. ) Например:

Формулы нахождения угла:

ТАБЛИЦА ЗНАЧЕНИЙ

Единичная окружность:

Формулы Прогрессии:

Арифметическая прогрессия

(a1 – первый член; d – разность; n – число членов; an – n-й член; Sn – сумма n первых членов):

Геометрическая прогрессия

(b1 – первый член; q – знаменатель; n – число членов; bn – n-й член; Sn – сумма n первых членов, S – сумма бесконечной геом. прогрессии):

Производная

Основные правила дифференцирования:

Производная сложной функции:

Если функция f имеет производную в точке xo, а функция g имеет производную в точке yo = f(xo), то сложная функция h(x) = g(f(x)) также имеет производную в точке xo, причем:

Производные тригонометрической функции:

Производная логарифмической функции:

Уравнение касательной к графику функции:

1. Расстояние между точками A1(x1;y1) и A2(x2;y2) находится по формуле:

2. Координаты (x;y) середины отрезка с концами A1(x1;y1) и A2(x2;y2) находится по формулам:

3. Уравнение прямой с угловым коэффициентом и начальной ординатой имеет вид:

Угловой коэффициент k представляет собой значение тангенса угла, образуемого прямой с положительным направлением оси Ox, а начальная ордината q – значение ординаты точки пересечения прямой с осью Oy.

4. Общее уравнение прямой имеет вид: ax + by + c = 0.

5. Уравнения прямых, параллельных соответственно осям Oy и Ox, имеют вид:

6. Условия параллельности и перпендикулярности прямых y1=kx1+q1 и y2=kx2+q2 соответственно имеют вид:

7. Уравнения окружностей с радиусом R и с центром соответственно в точках O(0;0) и C(xo;yo) имеют вид:

Представляет собой уравнение параболы с вершиной в точке, абсцисса которой

1. Расстояние между точками A1(x1;y1;z1) и A2(x2;y2;z2) находится по формуле:

2. Координаты (x;y;z) середины отрезка с концами A1(x1;y1;z1) и A2(x2;y2;z2) находятся по формулам:

3. Модуль вектора заданного своими координатами, находится по формуле:

4. При сложении векторов их соответствующие координаты складываются, а при умножении вектора на число все его координаты умножаются на это число, т. е. справедливы формулы:

5. Единичный вектор сонаправленный с вектором находится по формуле:

6. Скалярным произведением векторов называется число:

Где — угол между векторами.

7. Скалярное произведение векторов

8. Косинус угла между векторами и находится по формуле:

9. Необходимое и достаточное условие перпендикулярности векторов и имеет вид:

10. Общее уравнение плоскости, перпендикулярной вектору имеет вид:

Ax + by + cz + d = 0.

11. Уравнение плоскости, перпендикулярной вектору и проходящей через точку (xo;yo;zo), имеет вид:

A(x — xo) + b(y — yo) + c(z — zo) = 0.

12. Уравнение сферы с центром O(0;0;0) записывается в виде:

1) Число перестановок из n элементов находится по формуле:

2) Число размещений из n элементов по m находится по формуле:

3) Число сочетаний из n элементов по m находится по формуле:

4) Справедливы следующие свойства сочетаний:

5) Формула бинома Ньютона имеет вид:

Сумма показателей чисел a и b равна n.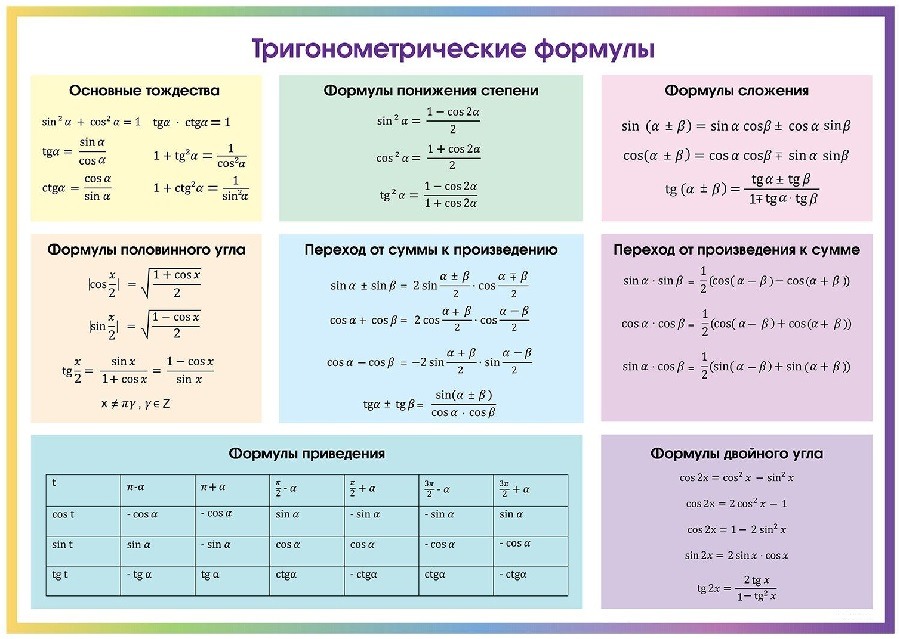

6) (k+1)-й член находится по формуле:

7) Число сочетаний также можно найти по треугольнику Паскаля.

Треугольник Паскаля (до n=7):

8) Сумма биномиальных коэффициентов равна 2n.

9) Чтобы найти биномиальный коэффициент следующего члена, нужно биномиальный коэффициент предыдущего члена умножить на показатель числа a и разделить на кол-во предыдущих членов.

Центр описанной окружности – точка пересечения серединных перпендикуляров. Центр вписанной окружности – точка пересечения биссектрис. (a, b,c – стороны: — противолежащие им углы; p – полупериметр; R – радиус описанной окружности; r – радиус вписанной окружности; S – площадь; ha – высота, проведенная к стороне a):

2. Прямоугольный треугольник:

Центр описанной окружности совпадает с центром гипотенузы. (a, b – катеты; c – гипотенуза; ac, bc – проекции катетов на гипотенузу):

3. Равносторонний треугольник:

Медиана = биссектрисе. OR = Or.

4. Произвольный выпуклый четырехугольник

(d1 и d2 – диагонали; – угол между ними; S — площадь):

5. Параллелограмм

(a и b – смежные стороны; – угол между ними; ha – высота, проведенная к стороне a):

6. Ромб:

В любой ромб можно вписать окружность.

7. Прямоугольник:

Около любого прямоугольника можно описать окружность.

8. Квадрат

9. Трапеция

(a и b – основания; h – расстояние между ними; l – средняя линия):

10. Описанный многоугольник

(p – полупериметр; r – радиус вписанной окружности):

S = pr. 11. Правильный многоугольник

(an – сторона правильного n-угольника; R – радиус описанной окружности; r – радиус вписанной окружности):

12. Окружность, круг

(r — радиус; C – длина окружности; S – площадь круга):

13. Сектор

(l – длина дуги, ограничивающей сектор; — градусная мера центрального угла; — радианная мера центрального угла):

(l – боковое ребро; P – периметр основания; S – площадь основания; H – высота; Pсеч – периметр перпендикулярного сечения; Sбок – площадь боковой поверхности; V — объем):

2. Прямая призма: 3. Прямоугольный параллелепипед

(a, b,c – его измерения; V — диагональ):

4. Куб

5. Произвольная пирамида

(S – площадь основания; H – высота; V — объем):

6. Правильная пирамида

(P – периметр основания; l – апофема; Sбок – площадь боковой поверхности):

7. Произвольная усеченная пирамида

(S1 и S1 – площади оснований; h – высота; V — объем):

8. Правильная усеченная пирамида

(P1 и P2 – периметры оснований; l – апофема; Sбок – площадь боковой поверхности):

9. Цилиндр

(R – радиус основания; H – высота; Sбок – площадь боковой поверхности; V — объем):

10. Конус

(R – радиус основания; H – высота; l – образующая; Sбок – площадь боковой поверхности; V — объем):

11. Шар, сфера

(R – радиус шара; S – площадь сферической поверхности; V — объем):

12. Шаровой сегмент

(R – радиус шара; h – высота сегмента; S – площадь сферической поверхности сегмента; V — объем):

13. Шаровой сектор

(R – радиус шара; h – высота сегмента; V — объем):

Полезности

Цитаты и афоризмы

“ Если хочешь узнать человека, не слушай, что о нём говорят другие, послушай, что он говорит о других.” —

Два равных отношения образуют Пропорцию: Основное свойство пропорции ad = bc

Формулы Арифметики:

Законы действий над числами

Переместительный закон сложения: a + b = b + a.

Сочетательный закон сложения: (a + b) + с = a + (b + c).

Переместительный закон умножения: ab = ba.

Сочетательный закон умножения: (ab)с = a(bc).

Распределительный закон умножения относительно сложения: (a + b)с = aс + bс.

Распределительный закон умножения относительно вычитания: (a — b)с = aс — bс.

1) Если a 0, то aс bс. 4) Если a 1/b. 5) Если a 0, b > 0, c > 0, d > 0, то ac 0, b > 0, то 8) Если, то

Формула приведения для преобразования выражений вида а) перед приведенной функцией ставиться тот знак, который имеет исходная функция;б) функция меняется на «кофункцию», если n нечетно; функция не меняется, если n четно. (Кофункциями синуса, косинуса, тангенса и котангенса называются соответственно косинус, синус, котангенс и тангенс.) Например:

Абсолютная величина формулы модуль.

Advice-me. ru

04.06.2020 3:22:47

2020-06-04 03:22:47

Источники:

Http://advice-me. ru/vse-formuly-po-matematike/

Справочник по алгебре. 10-11 класс

Таблица по алгебре 10

Удобный справочник по алгебре, позволит учащимся 10-11 классов более глубоко осваивать включенный в школьную программу материал, подробно разбирать различные темы при самостоятельной работе. С его помощью можно самостоятельно проработать теоретическую часть предмета более детально, чем с использованием исключительно учебника.

В справочник включены уроки в последовательности, соответствующей утверждено образовательной программе. Это позволит систематически изучать новый материал, чтобы повысить свою успеваемость и лучше усваивать знания по предмету, переходя последовательно от одной темы к следующей.

С его помощью можно самостоятельно проработать теоретическую часть предмета более детально, чем с использованием исключительно учебника.

Reshator. com

05.04.2020 8:39:59

2020-04-05 08:39:59

Источники:

Https://reshator. com/sprav/algebra/10-11-klass/

Таблицы демонстрационные Алгебра 10 класс — Edustrong » /> » /> .keyword { color: red; }

Таблица по алгебре 10

Тригонометрические функции. Синус, косинус, тангенс и котангенс. Свойства синуса, косинуса, тангенса и котангенса. Основные тригонометрические тождества. Формулы сложения. Формулы суммы и разности синусов (косинусов). Формулы двойного аргумента. Формулы половинного аргумента. Графики функций синус и косинус. Преобразование графиков функций синус и косинус. Графики функций тангенс и котангенс. Преобразование графиков функций тангенс и котангенс. Арксинус, арккосинус, арктангенс и арккотангенс. Решение тригонометрических уравнений. Решение тригонометрических неравенств. Свойство периодичности функции. Периодичность тригонометрических функций. Приращение функции. Понятие о производной. Правила вычисления производных. Производная сложной функции. Производные тригонометрических функций. Применения непрерывности и производной. Касательная к графику функции. Критические точки функции, максимумы и минимумы. Сложная функция.

Формулы суммы и разности синусов косинусов.

Edustrong. ru

23.09.2017 18:11:27

2017-09-23 18:11:27

Источники:

Https://edustrong. ru/3334_Matematika/6495_Tablitsi_demonstratsionnie_Algebra_10_klass

Алгебра и начало анализа 10 класс таблицы купить » /> » /> .keyword { color: red; }

Таблица по алгебре 10

Алгебра и начало анализа 10 класс таблицы

Учебное пособие выполнено на плотном полиграфическом картоне размером 68х98 см. В комплект входит брошюра с методическими рекомендациями для учителя.

Пособие состоит из 17 таблиц:

Тригонометрические функции. Синус, косинус, тангенс и котангенс. Свойства синуса, косинуса, тангенса и котангенса. Основные тригонометрические тождества. Формулы сложения. Формулы суммы и разности синусов (косинусов). Формулы двойного аргумента. Формулы половинного аргумента. Графики функций синус и косинус. Преобразование графиков функций синус и косинус. Графики функций тангенс и котангенс. Преобразование графиков функций тангенс и котангенс. Арксинус, арккосинус, арктангенс и арккотангенс. Решение тригонометрических уравнений. Решение тригонометрических неравенств. Свойство периодичности функции. Периодичность тригонометрических функций. Приращение функции. Понятие о производной. Правила вычисления производных. Производная сложной функции. Производные тригонометрических функций. Применения непрерывности и производной. Касательная к графику функции. Критические точки функции, максимумы и минимумы. Сложная функция.

«Алгебра и начало анализа» 10 класс таблицы в наличии на складе. Доставка во все регионы России и страны СНГ. Возможен самовывоз со склада в Москве

Учебное пособие выполнено на плотном полиграфическом картоне размером 68х98 см. В комплект входит брошюра с методическими рекомендациями для учителя.

Пособие состоит из 17 таблиц:

Тригонометрические функции. Синус, косинус, тангенс и котангенс. Свойства синуса, косинуса, тангенса и котангенса. Основные тригонометрические тождества. Формулы сложения. Формулы суммы и разности синусов (косинусов). Формулы двойного аргумента. Формулы половинного аргумента. Графики функций синус и косинус. Преобразование графиков функций синус и косинус. Графики функций тангенс и котангенс. Преобразование графиков функций тангенс и котангенс. Арксинус, арккосинус, арктангенс и арккотангенс. Решение тригонометрических уравнений. Решение тригонометрических неравенств. Свойство периодичности функции. Периодичность тригонометрических функций. Приращение функции. Понятие о производной. Правила вычисления производных. Производная сложной функции. Производные тригонометрических функций. Применения непрерывности и производной. Касательная к графику функции. Критические точки функции, максимумы и минимумы. Сложная функция.

«Алгебра и начало анализа» 10 класс таблицы в наличии на складе. Доставка во все регионы России и страны СНГ. Возможен самовывоз со склада в Москве

Формулы половинного аргумента.

Skale. ru

02.07.2018 5:08:40

2018-07-02 05:08:40

Источники:

Https://skale. ru/magazin/product/tablitsy-algebra-i-nachalo-analiza

Учебники по алгебре за 10 класс в электронном виде



Учебники по по алгебре за все классы:

Учебники по алгебре за 10 класс в электронном виде. Чтобы не носить с собой тяжелые учебники, их можно скачать себе на планшет. Так как не всегда есть электронная версия учебника, то можно скачать фотографии страниц, сохраненные в форматах pdf или djvu. Вы можете добавить свой учебник, так сказать поделиться с другими, или же найти и скачать нужный Вам учебник Алгебра 10 класс

Показано 1 — 20 из 20

Пособие содержит таблицы по всем наиболее важным разделам школьного курса арифметики, алгебры, начал анализа. В таблицах кратко изложена теория по каждой теме, приведены основные формулы, графики, примеры решений типовых задач. В конце книги помещен …

Книга предназначена для более глубокого изучения курса математики в 10-м классе средней школы — как самостоятельно, так и в классах и школах с углубленным теоретическим и практическим изучением математики и ее приложений. Она может быть использована …

Пособие содержит основные теоретические вопросы курса алгебры 10 класса в соответствии с действующей программой. Рассмотрены решения типовых задач каждой темы. Подобраны тренировочные упражнения , самостоятельные и контрольные работы ко всем разделам …

Предлагаемый задачник по курсу «Алгебра и начала анализа» в 10—11 классах соответствует одноименному учебнику. В каждом параграфе задачника представлена разнообразная система упражнений, включающая четыре уровня — по степени нарастания трудности. …

Учебник дает цельное и полное представление о школьном курсе алгебры и начал анализа, отвечает требованиям обязательного минимума содержания образования. Отличительная особенность учебника — более доступное для школьников изложение материала по сравн …

Пособие содержит контрольные работы для 8-11 классов, задания выпускных экзаменов по математике в 9 и 11 классах с углубленным и профильным изучением математики, а также практикум для поступающих в вузы. Ко всем заданиям даны ответы. Книга может испо …

Учебник соответствуют базовому и профильному уровням. Материал учебника для 10 класса посвящен изучению элементарной математики: элементарных функций, многочленов, уравнений, неравенств и их систем. Материал первой главы предназначен для повторения к …

Учебник Ю.М.Колягина «Алгебра и начала анализа.10 класс» полностью соответствует программе Ш.А.Алимова для старших классов и является органичным продолжением учебников алгебры для 7-9 классов, подготовленных авторским коллективом в составе: Ш.А.Алимо …

Учебник представляет собой первую часть комплекта из двух книг, предназначенных для изучения курса алгебры и начал математического анализа в 10-м классе с профильной подготовкой по математике (вторая часть — задачник). ОГЛАВЛЕНИЕ Предисловие …

Задачник представляет собой вторую часть комплекта из двух книг, предназначенных для изучения курса алгебры и начал анализа в 10-м классе с профильной подготовкой по математике (первая часть — учебник). ОГЛАВЛЕНИЕ Предисловие для учителя 3 З . ..

Учебник предназначен для классов с профильным уровнем изучения математики, в которых на изучение алгебры и начал математического анализа отведено не менее 4 часов в неделю. Содержание учебника полностью охватывает все разделы и темы, предусмотренные …

Учебник соответствует федеральным компонентам государственного стандарта общего образования по математике и содержит материал как для базового, так и для профильного уровня. По нему можно работать независимо от того, по каким учебникам учились школьн …

Учебник дает цельное и полное представление о школьном курсе алгебры и начал математического анализа. Отличительные особенности учебника — более доступное для школьников изложение материала по сравнению с традиционными учебными пособиями, наличие бол …

Предлагаемый задачник по курсу «Алгебра и начала математического анализа» в 10—11-м классах соответствует одноименному учебнику. В каждом параграфе задачника представлена разнообразная система упражнений, включающая четыре уровня — по степени нараста . ..

Учебник для общеобразовательных учреждений. Базовый уровень. Рекомендован Министерством образования и науки Российской Федерации. ОГЛАВЛЕНИЕ Глава 1. Действительные числа § 1. Целые и рациональные числа 3 § 2. Действительные числа 7 § 3. Беск …

Учебник написан на высоком научном уровне, основные теоретические положения иллюстрируются конкретными примерами. Каждый пункт книги содержит образцы решения типичных задач, соответствующих обязательному уровню подготовки по данной теме, и более труд …

Учебное пособие для профильной школы. Книга содержит: 1) задачи по школьному курсу алгебры и математического анализа для профильных классов, в первую очередь для классов с углублённым изучением математики; 2) ответы ко всем задачам; 3) решения зад …

Учебник для 10 класса является частью учебно-методического комплекта для старших классов школ с углубленным изучением математики. Представлены разделы: элементы математической логики, числовые множества, рациональные функции и графики, многочлены и с . ..

Задачник для 10-11 классов является частью учебно-методического комплекта для старших классов школ с углубленным изучением математики. Главы задачника соответствуют главам учебников для 10 и 11 классов. Задачи по каждой теме расположены в порядке воз …

Мордкович

Показано 1 — 20 из 20

Алгебра

Таблица умножения на 11 — Выучить таблицу 11

LearnPracticeDownload

Таблица умножения на 11 — это таблица умножения 11, где мы получаем произведение умножения 11 на целые числа. Изучение таблицы умножения на 11 сравнительно легче. Кратные всегда представляют собой повторение одной и той же цифры, например, 11 × 1 = 11, 11 × 2 = 22, 11 × 5 = 55, 11 × 79 = 99 и т. д. В этом мини-уроке вы можете найти умножение 11 с целыми числами до 10.

11 Таблица умножения Таблица умножения:

1.	Таблица умножения 11
2.	Советы по таблице 11 раз
3.	Часто задаваемые вопросы о таблице умножения на 11

Таблица умножения 11

Таблица умножения 11 — важный навык при решении математических задач, основанных на умножении и делении. Очень полезно находить числа, кратные 11. Просмотрите приведенную ниже таблицу умножения на 11 для быстрых вычислений.

11 Таблица умножения

11 Таблица умножения до 10
11 × 1 = 11	11 × 6 = 66
11 × 2 = 22	11 × 7 = 77
11 × 3 = 33	11 × 8 = 88
11 × 4 = 44	11 × 9 = 99
11 × 5 = 55	11 × 10 = 110

Вы можете распечатать или сохранить таблицу 11 в формате PDF, нажав на ссылку ниже.

☛ Таблица умножения на 11

Советы для 11-кратного стола

• Первые девять кратных 11 очень легко запомнить. Когда 11 умножается на любое однозначное натуральное число, произведение этого натурального числа записывается дважды. Например, 11 × а = аа; здесь а — натуральное число. Таким образом, мы получили первые девять кратных 11 и, следовательно, таблицу умножения на 11.
• Чтобы рассчитать таблицу умножения на 11 для двузначных чисел, есть хитрость. Когда двузначное число умножается на 11, возьмите сумму цифр этого числа и поместите эту сумму между двумя цифрами исходного двузначного числа. Например, при умножении 11 на 16 возьмите сумму 1 и 6, то есть 7. Теперь поместите сумму 7 между 1 и 6. Получившееся число равно 176. Произведение 11 и 16 равно 176, т. е. 11 × 16 = 176,

Таблица от 11 до 20

11 × 11 = 121	11 × 16 = 176
11 × 12 = 132	11 × 17 = 187
11 × 13 = 143	11 × 18 = 198
11 × 14 = 154	11 × 19 = 209
11 × 15 = 165	11 × 20 = 220

 

11 Примеры таблицы умножения

1. Пример 1: Используя таблицу умножения на 11, оцените 11 умножить на 7 минус 2 плюс 4.

   Решение:

   Сначала мы математически напишем 11 умножить на 7 минус 2 плюс 4.

   Используя таблицу умножения на 11, мы имеем: 11 умножить на 7 минус 2 плюс 4 = 11 × 7 — 2 + 4 = 77 + 2 = 79

   Следовательно, 11 умножить на 7 минус 2 плюс 4 равно 79.

2. Пример 2: Мэри пошла в детский дом и раздала там детям по 5 кексов. В детском доме было 11 детей. Используя Таблицу 11, найдите, сколько всего кексов было роздано?

   Решение:

   Было 11 детей, и она раздала детям по 5 кексов.

   Следовательно, из таблицы 11 5 × 11= 55 кексов

   Следовательно, всего было роздано 55 кексов.

3. Пример 3: Используя таблицу умножения на 11, вычислите 7 минус 6 плюс 3 умножить на 11.

   Решение:

   Сначала мы математически запишем 7 минус 6 плюс 3 умножить на 11.

   Из таблицы умножения на 11 имеем: 7 минус 6 плюс 3 умножить на 11 = 7 — 6 + 3 × 11 = 1 + 33 = 34

   Следовательно, 7 минус 6 плюс 3 умножить на 11 равно 34.

4. Пример 4: Используя таблицу умножения 11, найдите число, которое при умножении на 11 дает 11?

   Решение:

   Мы знаем, что при умножении числа на 1 получается одно и то же число.

   Итак, если мы умножим 11 на 1, мы получим: 1 × 11 = 11

перейти к слайдуперейти к слайдуперейти к слайдуперейти к слайду

Хотите заложить прочный фундамент в математике?

Выйдите за рамки запоминания формул и поймите «почему», стоящее за ними. Испытайте Cuemath и приступайте к работе.

Забронировать бесплатный пробный урок

Часто задаваемые вопросы о таблице умножения на 11

Что такое Таблица умножения на 11?

Таблица умножения на 11 кратна 11, как показано ниже:

11 × 1 = 11	11 × 6 = 66
11 × 2 = 22	11 × 7 = 77
11 × 3 = 33	11 × 8 = 88
11 × 4 = 44	11 × 9 = 99
11 × 5 = 55	11 × 10 = 110

Каково правило таблицы умножения на 11?

Один из приемов или правил, которые следует помнить при вычислении таблицы умножения на 11, заключается в том, что когда двузначное число умножается на 11, сумма цифр помещается между двумя цифрами исходного двузначного числа. Например, если 11 умножить на 15, сумма 1 и 5 будет 6. Поместите сумму 6 между 1 и 5. Следовательно, в результате получится 165.

Сколько кратно 11?

В таблице умножения на 11 можно увидеть числа, кратные 11, т. е. 11, 22, 33, 44, 55, 66, 77, 88, 99, 110.

Как объяснить таблицу умножения на 11?

Таблицу умножения на 11 можно запомнить, умножив каждую цифру на 11, т. е. 11 × 11 = 121 и 12 × 11 = 132, поскольку сумма внешних цифр каждого ответа дает среднюю цифру. Другой способ запомнить таблицу 11 — просто повторять цифры от 1 до 9.

Таблицы умножения

Загрузить БЕСПЛАТНЫЕ учебные материалы

Рабочие листы по таблице умножения

Рабочие листы по математике и
наглядный учебный план

Шкала оценок Оценки штата | ОСПИ

Перейти к основному содержанию

Вы находитесь здесь

Главная » Успехи учащихся » Тестирование » Тестирование штата » Баллы и отчеты » Баллы по шкале Оценка штата

Сокращенные (или пороговые) баллы для Уровней 1, 2, 3 и 4 в диапазоне баллов по шкале, были первоначально разработаны консорциумом Smarter Balanced Assessment Consortium при участии тысяч преподавателей и членов сообщества. Государства-члены Smarter Balanced утвердили эти оценки. Затем баллы были утверждены Государственным советом по образованию в январе 2015 года. ESHB 2224 (принятый в июле 2017 года) переместил оценку тестирования средней школы с 11 класса на 10 класс. Сокращенные баллы 10 класса были приняты Государственным советом по образованию в январе 2018 года. Выпускные баллы по английскому языку и математике, принятые Государственным советом в августе 2015 года, не изменились.

Ниже приведены диапазоны баллов по шкале для всех уровней достижений в тестах Smarter Balanced.

Smarter Balanced ELA	Уровень 1	Уровень 2	Уровень 3	Уровень 4
3 класс	<2367	2367-2431	2432-2489	>2489
Класс 4	<2416	2416-2472	2473-2532	>2532
Класс 5	<2442	2442-2501	2502-2581	>2581
6 класс	<2457	2457-2530	2531-2617	>2617
7 класс	<2479	2479-2551	2552-2648	>2648
8 класс	<2487	2487-2566	2567-2667	>2667
10 класс*	<2491	2491-2576	2577-2677	>2677

*5 августа 2015 г. Совет по образованию штата (State Board of Education, SBE) установил минимальные баллы по экзаменам средней школы, необходимые для выполнения требований к выпускным экзаменам. Посмотрите эти сокращенные баллы.

Умная сбалансированная математика	Уровень 1	Уровень 2	Уровень 3	Уровень 4
3 класс	<2381	2381-2435	2436-2500	>2500
Класс 4	<2411	2411-2484	2485-2548	>2548
Класс 5	<2455	2455-2527	2528-2578	>2578
6 класс	<2473	2473-2551	2552-2609	>2609
7 класс	<2484	2484-2566	2567-2634	>2634
8 класс	<2504	2504-2585	2586-2652	>2652
10 класс*	<2533	2533-2613	2614-2696	>2696

* 05. 08.2015 Государственный совет по образованию (SBE) установил минимальные баллы по аттестациям в средней школе, необходимые для выполнения требований к выпускным экзаменам. Просмотрите эти партитуры.

Комплексная оценка науки штата Вашингтон (WCAS)

Предельные (или пороговые) баллы для уровней 1, 2, 3 и 4 были разработаны преподавателями штата Вашингтон. Эти сокращенные баллы были утверждены Государственным советом по образованию в августе 2018 г.

WCAS	Уровень 1	Уровень 2	Уровень 3	Уровень 4
5 класс	375-649	650-699	700-784	785-1060
8 класс	345-649	650-699	700-764	765-1060
11 класс	390-649	650-699	700-790	791-1190

Диапазоны баллов по исторической шкале

Ниже приведены диапазоны баллов по шкале для оценок, которые не проводились в 2017-18 учебном году. Они включают в себя все уровни в 3-8 классах (чтение, математика и письмо), измерения успеваемости учащихся (MSP), Smarter Balanced Assessments 11 класса, экзамен на знание средней школы (HSPE) и выпускные экзамены (EOC). . HSPE и MSP представляют собой те же диапазоны баллов по шкале, что и Вашингтонская оценка обучения учащихся (WASL), которая была заменена в 2009 г.-10 учебный год. Диапазоны баллов по шкале включают наименьший и наивысший достижимый балл по каждому тесту (чтение, письмо, математика и естествознание).

Чтение	Уровень 1	Уровень 2	Уровень 3	Уровень 4
3 класс	275-374	375-399	400-425	426-500
4	275-374	375-399	400-423	424-475
5	275-374	375-399	400-421	422-475
6	275-374	375-399	400-424	425-475
7	275-374	375-399	400-417	418-475
8	250-374	375-399	400-418	419-500
Средняя школа (HSPE)	225-374	375-399	400-426	427-525

 

Математика	Уровень 1	Уровень 2	Уровень 3	Уровень 4
3 класс	200-374	375-399	400-435	436-575
4	200-374	375-399	400-446	447-575
5	200-374	375-399	400-439	440-575
6	200-374	375-399	400-441	442-575
7	200-374	375-399	400-443	444-575
8	200-374	375-399	400-436	437-575

 

Письмо	Уровень 1	Уровень 2	Уровень 3	Уровень 4
4 класс	0-6	7-8	9-10	11-12
7	0-6	7-8	9-10	11-12
Средняя школа (HSPE)	0-12	13-16	17-20	21-24

 

MSP Science	Уровень 1	Уровень 2	Уровень 3	Уровень 4
5 класс	200-374	375-399	400-431	432-550
8	250-374	375-399	400-430	431-550

 

Smarter Balanced ELA	Уровень 1	Уровень 2	Уровень 3	Уровень 4
11 класс*	<2493	2493-2582	2583-2681	>2681

 

Умная сбалансированная математика	Уровень 1	Уровень 2	Уровень 3	Уровень 4
11 класс*	<2543	2543-2627	2628-2717	>2717

 

EOC Math	Уровень 1	Уровень 2	Уровень 3	Уровень 4
Алгебра/Интеграция 1	200-374	375-399	400-442	443-675
Геометрия/встроенная 2	200-374	375-399	400-435	436-600

 

Выпускные экзамены EOC по математике	Уровень 1	Уровень 2	Уровень 3	Уровень 4
Алгебра/Интеграция 1	200-374	375-399	400-439	440-675
Геометрия/встроенная 2	200-374	375-399	400-426	427-600

 

EOC Science	Уровень 1	Уровень 2	Уровень 3	Уровень 4
Биология	275-374	375-399	400-422	423-525

Таблица значений линейных уравнений.

Примеры, инструкции и график

Часть I. Как линейные уравнения соотносятся с таблицами значений

Уравнения как отношения

Уравнение прямой выражает отношение между значениями x и y на координатной плоскости. Например, уравнение $$y = x$$ выражает отношение, в котором каждое значение x имеет точно такое же значение y. Уравнение $$ y = 2x $$ выражает соотношение, в котором каждое значение y в два раза превышает значение x, а $$ y = x + 1 $$ выражает соотношение, в котором каждое значение y на 1 больше, чем значение x.

А как насчет таблицы значений?

Поскольку, как мы только что написали, каждое линейное уравнение представляет собой отношение значений x и y, мы можем создать таблицу значений для любой строки. Это просто значения $$ x $$ и $$ y $$, которые верны для данной строки. Другими словами, таблица значений — это просто некоторые точки, находящиеся на прямой.

Пример 1

Уравнение: $$ \red y = \blue x + 1 $$

Таблица значений

$$ \синий х \текст {значение} $$	Уравнение	$$ \red y \text{значение} $$
	у = х + 1
$$ \ синий 3 $$	$$y = (\синий 3) + 1$$	$$ \ красный 4 $$
$$ \ синий 4 $$	у = ($$ \синий 4 $$ ) + 1	$$ \ красный 5 $$
$$ \ синий 5 $$	$$ у = (\синий 5 ) + 1$$	$$ \ красный 6 $$
$$ \ синий 6 $$	$$ у = (\синий 6) + 1 $$	$$ \ красный 7 $$

Пример 2

Уравнение: у = 3х + 2

Таблица значений

X Значение	Уравнение	Значение Y
	у = 3х + 2
1	у = 3(1) + 2	5
2	у = 3(2) + 2	7
3	у = 3(3) + 2	11
4	у = 3(4) + 2	14

Таким образом, чтобы создать таблицу значений для строки, просто выберите набор значений x, подставьте их в уравнение и оцените, чтобы получить значения y.

Практика Создание таблицы значений

Проблема 1

• Исходная проблема
• Шаг 1
• Шаг 2
• Шаг 3
• Шаг 4

Создайте таблицу значений уравнения y = 5x + 2.

Создайте таблицу и выберите набор значений x.

X Значение	Уравнение	Значение Y
	у = 5х + 2
1
2
3
4

Подставьте каждое значение x (левый столбец) в уравнение.

X Значение	Уравнение	Значение Y
	у = 5х + 2
1	у = 5(1) + 2
2	у = 5(2) + 2
3	у = 5(3) + 2
4	у = 5(4) + 2

Оцените уравнение (средний столбец), чтобы получить значение y.

X Значение	Уравнение	Значение Y
	у = 5х + 2
1	у = 5(1) + 2	7
2	у = 5(2) + 2	12
3	у = 5(3) + 2	17
4	у = 5(4) + 2	22

Необязательный шаг, если вы хотите, вы можете опустить средний столбец из своей таблицы, поскольку таблица значений на самом деле представляет собой только пары x и y.
(Мы использовали средний столбец просто для получения значений y)

X Значение	Y Значение
1	7
2	12
3	17
4	22

Проблема 2

• Исходная проблема
• Шаг 1
• Шаг 2
• Шаг 3
• Шаг 4

Создайте таблицу значений уравнения y = −6x + 2.

Создайте таблицу и выберите набор значений x.

X Значение	Уравнение	Значение Y
	у = -6х + 2
1
2
3
4

Подставьте каждое значение x (левый столбец) в уравнение.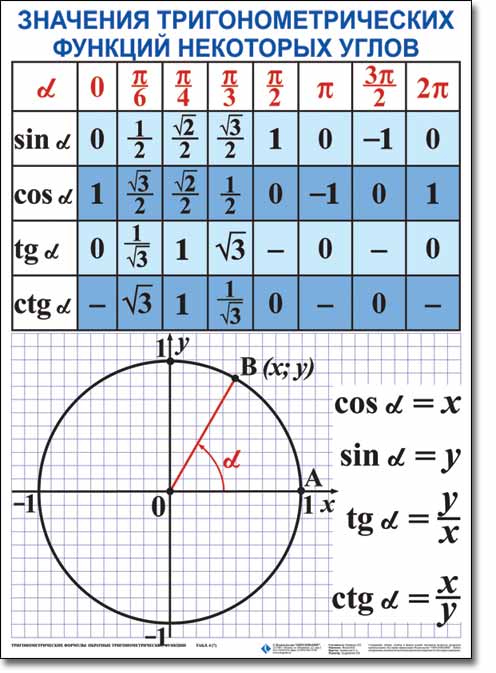

X Значение	Уравнение	Значение Y
	у = -6х + 2
1	у = -6(1) + 2
2	у = -6(2) + 2
3	г = -6(3) + 2
4	у = -6(4) + 2

Оцените уравнение (средний столбец), чтобы получить значение y.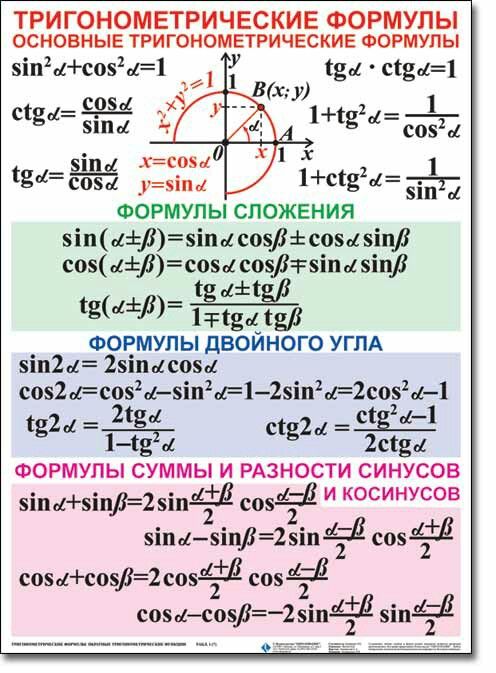

X Значение	Уравнение	Значение Y
	у = -6х + 2
1	г = -6(1) + 2	-4
2	у = -6(2) + 2	-10
3	у = -6(3) + 2	-16
4	у = -6(4) + 2	-22

Необязательный шаг, если вы хотите, вы можете опустить средний столбец из своей таблицы, поскольку таблица значений на самом деле представляет собой только пары x и y. (Мы использовали средний столбец просто для получения значений y)

X Значение	Значение Y
1	-4
2	-10
3	-16
4	-22

Проблема 3

• Исходная проблема
• Шаг 1
• Шаг 2
• Шаг 3
• Шаг 4

Создайте таблицу значений уравнения y = −6x − 4

Создайте таблицу и выберите набор значений x

X Значение	Уравнение	Значение Y
	у = -6х — 4
1
2
3
4

Подставьте каждое значение x (левый столбец) в уравнение.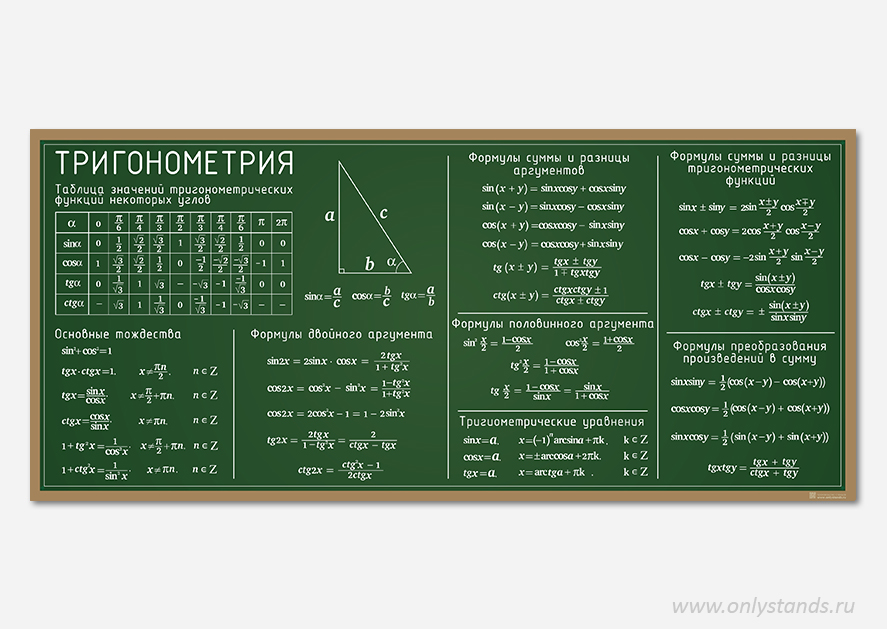

X Значение	Уравнение	Значение Y
1	г = -6(1) — 4
2	г = -6(2) — 4
3	г = -6(3) — 4
4	г = -6(4) — 4

Оцените уравнение (средний столбец), чтобы получить значение y.

X Значение	Уравнение	Значение Y
1	г = -6(1) — 4	-10
2	г = -6(2) — 4	-16
3	г = -6(3) — 4	-22
4	г = -6(4) — 4	-28

Необязательный шаг, если вы хотите, вы можете опустить средний столбец из своей таблицы, поскольку таблица значений на самом деле представляет собой только пары x и y. (Мы использовали средний столбец просто для получения значений y)

X Значение	Значение Y
1	-10
2	-16
3	-22
4	-28

Часть II.

Запись уравнения из таблицы значений

Часто студентов просят написать уравнение прямой из таблицы значений. Чтобы решить такую ​​задачу, просто выберите любые 2 точки на столе и выполните обычные шаги для написания уравнения прямой из 2 точек.

Проблема 4

• Исходная проблема
• Шаг 1
• Шаг 2
• Шаг 3
• Шаг 4

Напишите уравнение линии из таблицы значений ниже.

X Значение	Значение Y
0	3
1	7
2	11
3	15

Выберите любые две пары x, y из таблицы и рассчитайте наклон. Так как я люблю работать с легкими маленькими числами, я выбрал (0, 3) и (1, 7).

X Значение	Значение Y
0	3
1	7
2	11
3	15

Подставьте наклон в форму пересечения наклона линии.

у = мх + б
у = 4х + б

Найдите значение ‘b’ в уравнении пересечения наклона.

у = мх + б
у = 4х + б

Поскольку наша таблица дала нам точку (0, 3), мы знаем, что «b» равно 3. Помните, что «b» — это точка пересечения с осью y, которая, к счастью, была предоставлена ​​нам в таблице.

Ответ: у = 4x + 3

При желании вы можете проверить свой ответ, подставив значения из таблицы в уравнение. Каждая пара x, y из таблицы должна работать с вашим ответом.

Проблема 5

• Исходная проблема
• Шаг 1
• Шаг 2
• Шаг 3
• Шаг 4

Напишите уравнение из приведенной ниже таблицы значений.

X Значение	Значение Y
2	8
4	9
6	10

Выберите любые две пары x, y из таблицы и рассчитайте наклон. Я выбрал (2, 8) и (4, 9).

Х	Д
2	8
4	9
6	10

Подставьте наклон в форму пересечения наклона линии.

у = мх + б
у = ½х + б

Найдите значение ‘b’ в уравнении пересечения наклона.

Теперь, когда мы знаем значение b, мы можем подставить его в наше уравнение.

Ответ: у = ½x + 7

При желании вы можете проверить свой ответ, подставив значения из таблицы в уравнение. Каждая пара x, y из таблицы должна работать с вашим ответом.

Проблема 6

• Исходная проблема
• Шаг 1
• Шаг 2
• Шаг 3
• Шаг 4

Напишите уравнение из приведенной ниже таблицы значений.

X Значение	Значение Y
3	2
6	0
9	-2

Выберите любые две пары x, y из таблицы и рассчитайте наклон. Я выбрал (2, 8) и (4, 9).

Х	Д
3	2
6	0
9	-2

Подставьте наклон в форму пересечения наклона линии.