ГДЗ по алгебре 7 класс Макарычев, Миндюк, Нешков
При переходе учеников в 7-ой класс, математика разделяется на два направления — алгебру и геометрию. В свою очередь алгебра добавляет в обучение множество новых формул, задач, уравнений. Объем которых ученики не всегда успевают усвоить. Даже не из-за нового материала, а его количества. Чтобы быть уверенным в правильности самого решения и его последовательности, стоит обратиться к решебнику, созданному на основе учебника алгебры за 7 класс, авторами которого являются Макарычев и Миндюк. В готовых домашних заданиях этих авторов, собраны не только ответы на задания по предмету, а и логический ход решения каждого уравнения и задачи, заданного в книге. Хотелось также бы развеять стереотип, связанный со сборниками готовых домашних заданий по школьным предметам. Якобы их используют только для списания заданного материала. Отнюдь, это не так. Многим ученикам они помогают разобраться в подаче решения. Ведь новые программы отличаются от тех, которые изучали родители, а значит их помощь может и не понадобится.
А если учитывать и тот факт, что не каждым родителям по карману репетиторы или ребенок не настроен в будущем связать свою деятельность с математикой, то решебник даст шанс разобраться в вопросах домашнего задания, помогая не испортить общую оценку знаний в аттестате.
Способы эффективной самоподготовки по предмету
Начав изучать в седьмом классе алгебру, учащиеся должны изначально настроиться на серьезную и скрупулезную работу. Дело не только в достаточной сложности самой дисциплины, но и в том, что задания по этому предмету составляют основной блок на итоговых испытаниях по математике. А их предстоит сдавать всем без исключения выпускникам школ. Для организации подготовки необходимы качественные учебные материалы и решебники к ним. Выбор пособий может осуществляться как самими семиклассниками, так и педагогами-предметниками, репетиторами, руководителями математических курсов и кружков.
Для того, чтобы работа по ГДЗ принесла желаемый и ожидаемый результат, необходимо подходить к её реализации:
— системно, заранее разработав эффективный план подготовки, исходя из базового уровня знания семиклассника, его ответственности и целеустремленности, а также поставленных задач. Они могут быть не только долгосрочными — подготовиться к ОГЭ/ЕГЭ, но и связанными с получением результата в ближайшем будущем. Например, повышение балла в четверти, году или участие, победа в математических, алгебраических предметных олимпиадах;
Они могут быть не только долгосрочными — подготовиться к ОГЭ/ЕГЭ, но и связанными с получением результата в ближайшем будущем. Например, повышение балла в четверти, году или участие, победа в математических, алгебраических предметных олимпиадах;
— комплексно, подобрав оптимальный комплект учебной литературы. В основе — базовый учебник, который надо выбирать особенно тщательно;
— периодически контролируя достигнутые результаты и меняя, корректируя планы по мере необходимости.
В числе полезной, эффективной литературы можно назвать базовый учебник по алгебре за 7 класс, составленный Макарычевым Ю. Н. В нем разбираются подробно и полно основные разделы этой дисциплины, вызывающие у семиклассников наибольшее число вопросов и трудностей. В частности:
— числовые выражения, уравнения и тождества;
— формулы сокращенного умножения;
— функции и их графики;
— проценты и текстовые задачи на проценты;
— текстовые задачи на движение и другие.
Для того, чтобы подготовка проходила максимально результативно и интересно для семиклассников, в комплект к базовому учебнику можно предложить использовать другие пособия этого же автора. В их числе — рабочие тетради по алгебре, тестовые, дидактические, контрольно-проверочные материалы, домашние работы. Для находящихся на домашнем/семейном обучении семиклассников рекомендуются поурочные разработки, рабочие программы и дидактические материалы по предмету.
В их числе — рабочие тетради по алгебре, тестовые, дидактические, контрольно-проверочные материалы, домашние работы. Для находящихся на домашнем/семейном обучении семиклассников рекомендуются поурочные разработки, рабочие программы и дидактические материалы по предмету.
ГДЗ Алгебра 7 класс Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова (2013 год). Ответы и решения
ГЛАВА 1. ВЫРАЖЕНИЯ, ТОЖДЕСТВА, УРАВНЕНИЯ № 1-257 ↑
§ 1. ВЫРАЖЕНИЯ № 1-69 ↑
1. Числовые выражения № 1-18 ↑
2. Выражения с переменными № 19-46 ↑
3. Сравнение значений выражений № 47-69 ↑
§ 2. ПРЕОБРАЗОВАНИЕ ВЫРАЖЕНИЙ № 70-110 ↑
4. Свойства действий над числами № 70-84 ↑
5. Тождества. Тождественные преобразования выражений № 85-110 ↑
§ 3. УРАВНЕНИЯ С ОДНОЙ ПЕРЕМЕННОЙ № 111-166 ↑
6. Уравнение и его корни № 111-125 ↑
7. Линейное уравнение с одной переменной № 126-142 ↑
8.
 Решение задач с помощью уравнений № 143-166 ↑
Решение задач с помощью уравнений № 143-166 ↑
§ 4. СТАТИСТИЧЕСКИЕ ХАРАКТЕРИСТИКИ № 167-195 ↑
9. Среднее арифметическое, размах и мода № 167-185 ↑
10. Медиана как статистическая характеристика № 186-195 ↑
Для тех, кто хочет знать больше № 196-205 ↑
Дополнительные упражнения к главе 1 № 206-257 ↑
ГЛАВА 2. ФУНКЦИИ № 258-373 ↑
§ 5. ФУНКЦИИ И ИХ ГРАФИКИ № 258-296 ↑
12. Что такое функция № 258-266 ↑
13. Вычисление значений функции по формуле № 267-282 ↑
14. График функции № 283-296 ↑
§ 6. ЛИНЕЙНАЯ ФУНКЦИЯ № 297-338 ↑
15. Прямая пропорциональность и её график № 297-312 ↑
16. Линейная функция и её график № 313-338 ↑
Для тех, кто хочет знать больше № 339-347 ↑
17. Задание функции несколькими формулами № 339-347 ↑
Дополнительные упражнения к главе 2 № 348-373 ↑
ГЛАВА 3.
§ 7. СТЕПЕНЬ И ЕЁ СВОЙСТВА № 374-454 ↑
18. Определение степени с натуральным показателем № 374-402 ↑
19. Умножение и деление степеней № 403-427 ↑
20. Возведение в степень произведения и степени № 428-454 ↑
§ 8. ОДНОЧЛЕНЫ № 455-499 ↑
21. Одночлен и его стандартный вид № 455-466 ↑
22. Умножение одночленов. Возведение одночлена в степень № 467-483 ↑
23. Функции у=х2 и у=х3 и их графики № 484-499 ↑
Для тех, кто хочет знать больше № 500-510 ↑
24. О простых и составных числах № 500-510 ↑
Дополнительные упражнения к главе 3 № 511-566 ↑
ГЛАВА 4. МНОГОЧЛЕНЫ № 567-798 ↑
§ 9. СУММА И РАЗНОСТЬ МНОГОЧЛЕНОВ № 567-613 ↑
25. Многочлен и его стандартный вид № 567-584 ↑
26. Сложение и вычитание многочленов № 585-613 ↑
§ 10.
 ПРОИЗВЕДЕНИЕ ОДНОЧЛЕНА И МНОГОЧЛЕНА № 614-676 ↑
ПРОИЗВЕДЕНИЕ ОДНОЧЛЕНА И МНОГОЧЛЕНА № 614-676 ↑§ 11. ПРОИЗВЕДЕНИЕ МНОГОЧЛЕНОВ № 677-721 ↑
29. Умножение многочлена на многочлен № 677-707 ↑
30. Разложение многочлена на множители способом группировки № 708-721 ↑
Для тех, кто хочет знать больше № 722-733 ↑
31. Деление с остатком № 722-733 ↑
Дополнительные упражнения к главе 4 № 734-798 ↑
ГЛАВА 5. ФОРМУЛЫ СОКРАЩЁННОГО УМНОЖЕНИЯ № 799-1024 ↑
§ 12. КВАДРАТ СУММЫ И КВАДРАТ РАЗНОСТИ № 799-853 ↑
32. Возведение в квадрат и в куб суммы и разности двух выражений № 799-832 ↑
33. Разложение на множители с помощью формул квадрата суммы и квадрата разности № 833-853 ↑
§ 13. РАЗНОСТЬ КВАДРАТОВ. СУММА И РАЗНОСТЬ КУБОВ № 854-917 ↑
34. Умножение разности двух выражений на их сумму № 854-882 ↑
35. Разложение разности квадратов на множители № 883-904 ↑
36.
 Разложение на множители суммы и разности кубов № 905-917 ↑
Разложение на множители суммы и разности кубов № 905-917 ↑
§ 14. ПРЕОБРАЗОВАНИЕ ЦЕЛЫХ ВЫРАЖЕНИЙ № 918-956 ↑
37. Преобразование целого выражения в многочлен № 918-933 ↑
38. Применение различных способов для разложения на множители № 934-956 ↑
Для тех, кто хочет знать больше № 957-965 ↑
Дополнительные упражнения к главе 5 № 966-1024 ↑
ГЛАВА 6. СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ № 1025-1183 ↑
§ 15. ЛИНЕЙНЫЕ УРАВНЕНИЯ С ДВУМЯ ПЕРЕМЕННЫМИ И ИХ СИСТЕМЫ № 1025-1067 ↑
40. Линейное уравнение с двумя переменными № 1025-1044 ↑
41. График линейного уравнения с двумя переменными № 1045-1055 ↑
42. Системы линейных уравнений с двумя переменными № 1056-1067 ↑
§ 16. РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ № 1068-1127 ↑
Для тех, кто хочет знать больше № 1128-1136 ↑
46. Линейные неравенства с двумя переменными и их системы № 1128-1136 ↑
Дополнительные упражнения к главе 6 № 1137-1183 ↑
Задачи повышенной трудности № 1184-1231 ↑
Контрольные задания и вопросы № 1-16 ↑
ГДЗ оказывают огромное положительное влияние на успеваемость школьников и на их развитие, поэтому данные книги и заслужили такое уважение, а также очень быстро стали популярными среди детей и взрослых.
Структура, которой обладают решебники по алгебре на VIPGDZ
Наш портал VIPGDZ.ru не обошел стороной такую полезную книгу, как ГДЗ по алгебре 7 класс Макарычев, и выложил ее на своих страницах. Если говорить о строении данного учебного пособия, то оно достаточно понятное и удобное.
Начнем с того, что, как и любая другая книга, решебники начинаются из содержания. Роль этого элемента состоит в том, чтобы помогать ученикам в поисках необходимых им номеров заданий. Это значительно экономит время и избавляет от бессмысленного листания страниц. После выбора упражнения, идут правильные процессы его решения. Выполнение задачи расписывается подробно и поэтапно, чтобы ученик смог проследить как нужно применять правило на практике.
 Эти компоненты справочника помогают подросткам самостоятельно осуществлять проверку своей домашней работы и исправлять допущенные ошибки. Кроме того, с помощью ответов в ГДЗ Макарычева, ученик всегда будет уверен в своих силах. Не стоит беспокоиться о поиске данного пособия. Чтобы воспользоваться им, достаточно просто посетить наш сайт VIPGDZ.
Эти компоненты справочника помогают подросткам самостоятельно осуществлять проверку своей домашней работы и исправлять допущенные ошибки. Кроме того, с помощью ответов в ГДЗ Макарычева, ученик всегда будет уверен в своих силах. Не стоит беспокоиться о поиске данного пособия. Чтобы воспользоваться им, достаточно просто посетить наш сайт VIPGDZ.VIPGDZ – ресурс, где находятся лучшие правильные решения по алгебре
Наш образовательный портал VIPGDZ сделал так, чтобы все нужные Вам ответы по алгебре всегда были под рукой и помогали с решением даже самых сложных упражнений. Во-первых, ученики 7 класса могут пользоваться материалами на сайте без каких-либо ограничений. Все дело в том, что книги Макарычева находятся на наших страницах в открытом доступе круглосуточно. Работать с ними можно бесплатно, кроме того, без предварительных регистраций. На этом плюсы, которые мы дарим нашим пользователям, не заканчиваются.
Ученик 7 класса не будет иметь никаких трудностей во время сотрудничества с ГДЗ на VIPGDZ. ru. Это становится возможным, благодаря очень удобному интерфейсу нашего сайта, который делает поиск нужных книг быстрым и легким. Также, добавив страницу портала в закладки, Вы сможете приступать к сотрудничеству с решебниками в считанные мгновения.
ru. Это становится возможным, благодаря очень удобному интерфейсу нашего сайта, который делает поиск нужных книг быстрым и легким. Также, добавив страницу портала в закладки, Вы сможете приступать к сотрудничеству с решебниками в считанные мгновения.
Еще одним бонусом VIPGDZ является то, что мы создали мобильную версию нашего сайта. Эта инновация позволит Вам просматривать ГДЗ по алгебре в режиме онлайн, независимо от места нахождения. Теперь работать со справочниками такого типа можно с любого современного гаджета. Наслаждайтесь изучением точных дисциплин в седьмом классе вместе с нашим сайтом VIPGDZ!
ГДЗ Алгебра 7 класс Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков 2009
Функция ГДЗ — придать ученикам уверенность во время подготовки к своим урокам. Школьники будут лучше справляться с домашними заданиями, если воспользуются помощью решебника по нужному предмету. У них будет возможность взглянуть на образец решения домашнего задания, ознакомиться с порядком выполнения действий. И все это для того, чтобы получить правильные ответы. ГДЗ по алгебре 7 класс имеет большую популярность в интернете, потому что этот учебный год считается самым сложным и насыщенным в школьном процессе.
И все это для того, чтобы получить правильные ответы. ГДЗ по алгебре 7 класс имеет большую популярность в интернете, потому что этот учебный год считается самым сложным и насыщенным в школьном процессе.
Во время уроков школьники не всегда успевают усвоить весь новый материал, которые им преподают учителя. Все работают в разных ритмах и в зависимости от своих способностей. И очень хорошо, что дома семиклассникам можно в удобное время позаниматься с решебником онлайн.
Огромным спросом пользуется ГДЗ по алгебре за 7 класс Макарычева Ю.Н. и других авторов. У данного решебника есть важные преимущества:
- -материал излагается последовательно от простого к сложному,
- — включает задания для учеников с различной степенью освоения знаний, поэтому с ним интересно работать ученикам со слабой и сильной подготовкой,
- -дается развернутое решение каждого задания, поэтому родители могут протестировать усвоения школьником знаний по алгебре.

-
- 1. Выражения, тождества, уравнения;
- 2. Функции;
- 3. Степень с натуральным показателем;
- 4. Многочлены;
- 5. Формулы сокращенного выражения;
- 6. Системы линейных выражений.
-
С помощью решебника по алгебре 7 класс можно не просто переписать верный ответ, но и развить математические навыки работы с такими выражениями как раскрывание скобок, решение системы уравнений, подмены одного выражения другим и т.д. Главная их задача — это правильное применение алгебраических формул для решения практических вопросов.
Учебник представлен разделами, которые отвечают требованиям общеобразовательной подготовки:
Описание УМК Алгебра. Макарычев Ю.Н. (7-9) — Группа компаний «Просвещение»
Авторы: Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков и др. / Под ред. Теляковского С.А.
В состав УМК входят:
- учебники
- Ю.
 Н. Макарычев, Н. Г. Миндюк, К. И. Нешков и др. / Под ред. Теляковского С.А. Алгебра. 7 класс;
Н. Макарычев, Н. Г. Миндюк, К. И. Нешков и др. / Под ред. Теляковского С.А. Алгебра. 7 класс; - Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков и др. / Под ред. Теляковского С.А. Алгебра. 8 класс;
- Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков и др. / Под ред. Теляковского С.А. Алгебра. 9 класс;
- Ю.
- рабочие программы;
- рабочая тетрадь;
- дидактические материалы;
- тематические тесты;
- книги для учителя;
- методические рекомендации.
Учебники соответствуют Федеральному государственному образовательному стандарту основного общего образования. Учебники содержат теоретический материал, написанный на высоком научном уровне и систему упражнений, органически связанную с теорией. В каждом пункте учебников выделяются задания обязательного уровня, которые варьируются с учётом возможных случаев. В системе упражнений специально выделены задания для работы в парах, задачи-исследования, старинные задачи. Приводимые образцы решения задач, пошаговое нарастание сложности заданий, сквозная линия повторения – всё это позволяет учащимся успешно овладеть новыми умениями. Каждая глава учебников заканчивается пунктом рубрики «Для тех, кто хочет знать больше». Этот материал предназначен для учащихся, проявляющих интерес к математике, и может быть использован для исследовательской и проектной деятельности.
Приводимые образцы решения задач, пошаговое нарастание сложности заданий, сквозная линия повторения – всё это позволяет учащимся успешно овладеть новыми умениями. Каждая глава учебников заканчивается пунктом рубрики «Для тех, кто хочет знать больше». Этот материал предназначен для учащихся, проявляющих интерес к математике, и может быть использован для исследовательской и проектной деятельности.
Электронные приложения к учебникам включают сведения из истории предмета, биографии учёных, решения задач и указания к решениям, тренажёры, тесты и др.
Рабочие тетради предназначены для работы в школе и дома. Каждая работа состоит из двух разделов. В первом содержатся несложные задания, способствующие усвоению нового материала, во втором – более сложные задания.
Тематические тесты помогут учителю в организации текущего контроля и подготовке к ГИА. Формулировки многих заданий, их форма предъявления идентичны тем, которые даются в сборниках для государственной итоговой аттестации.
Книги для учителя «Уроки алгебры» содержат тексты устных упражнений, уроков заключительного повторения, самостоятельных и контрольных работ, примерное тематическое планирование.
Методические рекомендации содержат не только указания к упражнениям учебника, но и к упражнениям из рабочей тетради. Авторы подробно разбирают решения упражнений рубрики «Для тех, кто хочет знать больше» и из раздела «Задачи повышенной трудности».
Особенности линии УМК:
- последовательное изложение теории с привлечением большого числа примеров, способствующее эффективной организации учебного процесса;
- создание условий для глубокого усвоения учащимися теории и овладения математическим аппаратом благодаря взаимосвязи и взаимопроникновению содержательно-методических линий курса;
- обеспечение усвоения основных теоретических знаний и формирования необходимых умений и навыков с помощью системы упражнений;
- выделение заданий обязательного уровня в каждом пособии, входящем в УМК;
- рекомендуются к использованию в линиях по математике (5-6) М.
 В. Ткачевой
В. Ткачевой
ГДЗ по Алгебре за 7 класс: Макарычев (Решебник)
ГДЗ по алгебре за 7 класс Макарычев – это решебник, т.е. сборник готовых домашних заданий по одноименному учебнику, составленному коллективом авторитетных российских авторов: Ю.Н. Макарычевым, Н.Г. Миндюком, К.И. Нешковым, С.Б. Суворовым. Он станет помощником родителям и ученикам, желающим разобраться в практическом выполнении математических примеров.
Решебник по алгебре за 7 класс Макарычева – контроль за успеваемостью школьников
Большинство родителей желают контролировать учебные успехи своих чад. Однако адекватно проверить задание по такому сложному предмету как алгебра под силу далеко не всем. Для того чтобы определить правильность выполнения того или иного примера можно воспользоваться решебником по алгебре за 7 класс Макарычев.
Пособие будет чрезвычайно полезно и для школьников, которые не сумели разобраться с правилами выполнения примера в классе: благодаря тому, что в сборнике приводятся не только онлайн-ответы, но и пошаговый алгоритм их расчета.
Наш сайт позаботился об экономии времени пользователей:
- Найти ответ на тот или иной пример можно, воспользовавшись строкой быстрого поиска, куда можно вбить номер задания или цитату из его условия – и легко выбрать из предложенного списка нужный вариант;
- Не отвлекаться от текущих дел и садиться за компьютер, а зайти в систему с любого электронного гаджета – ноутбука, планшета, смартфона.
На сайте представлены самые актуальные решебники к учебным пособиям, используемым в российских общеобразовательных школах. По отдельным примерам приводится несколько вариантов ответа из разных сборников
Гдз по алгебре в 7 классе: Макарычев, Миндюк, Нешков, Суворова — учебник 2013 года
Все решения, собранные в сборнике онлайн-ответов на нашем сайте составлены на базе заданий учебника по алгебре выпущенного в 2013 году под редакцией Макарычева Ю.Н. Пособие включает в себя 46 тем, разделенных на 16 крупных параграфов. Представленный в учебнике материал знакомит учащихся 7 классов с такими темами, как:
- Преобразование математических выражений и решение уравнений с одной переменной;
- Понятием и типами функций, а также особенностями построения их графиков;
- Формулами сокращенного умножения и практическими основами их использования;
- Порядком совершения математических действий со степенями, одночленами и многочленами;
- Простыми системами линейных уравнений и способами их решения.

Разобраться в столь внушительном массиве информации поможет наш сайт, который позволяет научиться выполнять алгебраические задачи самостоятельно, без привлечения репетитора.
Решебник алгебра 9 клас а.г мерзляк в.б полонський м.с якір
Скачать решебник алгебра 9 клас а.г мерзляк в.б полонський м.с якір EPUB
Решебник (ГДЗ) Алгебра 9 клас А.Г. Мерзляк, В.Б. Полонський, М.С. Якір ( рік). Авторы: А.Г. Мерзляк, В.Б. Полонський, М.С. Якір. Год: |. Класс: 9 |. Основные функции решений. В достижении превосходной успеваемости школьникам всегда готовы прийти на помощь решебники. Предназначение этих справочников как раз и состоит в том, чтобы способствовать выполнению сложных упражнений и чтобы делать их проверку более эффективной. Особенно сильно вмешательство данных пособий нужно девятиклассникам, которым для изучения алгебры нужно встречаться с серьезными объемами заданий из учебника года.
Дети в любой необходимый момент могут воспользоваться решениями на Vshkole. ГДЗ з алгебри для 9 класу за підручником автора Мерзляк та інших. О решебнике А.Г. Мерзляк, В.Б. Полонський, М. Якир. Другие решебники по алгебре для 9 классa. А.Г. Мордкович Мордкович А.Г. и др. — 10 изд.
ГДЗ з алгебри для 9 класу за підручником автора Мерзляк та інших. О решебнике А.Г. Мерзляк, В.Б. Полонський, М. Якир. Другие решебники по алгебре для 9 классa. А.Г. Мордкович Мордкович А.Г. и др. — 10 изд.
— М.:Мнемозина, г. Ю.Н. Макарычев «Алгебра: Учебник для 9 класса» Ю.Н. Макарычев и др. — 14 изд. М.:Просвещение, — М.: Просвещение, / г. Ю.Н. Макарычев Макарычев Ю. Н. А.Г. Мордкович, Т.Н. Мишустина, Е.Е. Тульчинская А.Г. Мордкович, Т.Н. Мишустина, Е.Е. Тульчинская. — 5-е изд. — М.: Мнемозина, Ш.А. Алимов, Ю.М. Колягин, Ю.В. Сидоров Ш.А. Алимов, Ю.М. Колягин, Ю.В.
Сидоров и др. — 6-е изд. — М.: «Просвещение», г. ГДЗ Алгебра 9 клас Мерзляк Авторы:Мерзляк А. Г., Полонський В. Б., Якір М. Ц. Издательство:Гімназія, Харьков. Год издания Язык обучения:Украинский. Відповіді до:Підручника. Похожие ГДЗ и учебники. Відповіді Збірник задач Алгебра 9 клас Мерзляк ГДЗ. Ответы к учебнику Алгебра 9 класс Мерзляк — решебник новая программа. Смотреть ГДЗ (решебник) онлайн: § 1. Нерівності№ — 1.
Числові нерівності — 2. Властивості числових нерівностей№ — 3. Додавання і множення нерівностей — 4. Нерівності з однією змінною№ — 5. Розв’язування нерівностей — 6. Системи нерівносте№ — § 2. Квадратична функція№ — Бесплатный решебник (ГДЗ) к учебнику по алгебре за 9 класс, авторы: А.Г.
Мерзляк, В.Б. Полонский, М.С. Якир. В состав учебного пособия Алгебра. 9 класс вошли задания нескольких уровней сложности, теоретический материал и контрольные вопросы по каждой пройденной теме.
Подходит для общеобразовательных школ. В процессе обучения, каждый школьник вспомнить материал предыдущих классов и изучит новые правила. Поможет ориентироваться во вновь изучаемых темах помогут готовые домашние задания к учебнику по алгебре для 9 класса авторов Мерзляк, Полонский, Якир.
Повні відповіді та гдз на вправи з алгебри для 9 класу до підручника авторів Мерзляк, Полонський, Якір, за новою програмою Бесплатный решебник (ГДЗ) к учебнику по алгебре за 9 класс, авторы: А.Г.
Мерзляк, В.Б. Полонский, М.С. Якир. В состав учебного пособия Алгебра. 9 класс вошли задания нескольких уровней сложности, теоретический материал и контрольные вопросы по каждой пройденной теме.
Подходит для общеобразовательных школ. В процессе обучения, каждый школьник вспомнить материал предыдущих классов и изучит новые правила. Поможет ориентироваться во вновь изучаемых темах помогут готовые домашние задания к учебнику по алгебре для 9 класса авторов Мерзляк, Полонский, Якир. «Алгебра 9 класс: учебник для учащихся общеобразовательных организаций». В пособии решены и в большинстве случаев подробно разобраны задачи и упражнения из учебника «Мерзляк А.Г.
Алгебра: 8 класс: учебник для учащихся общеобразовательных организаций / А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. — М.: Вентана-Граф, — с.». Пособие адресовано родителям, которые смогут проконтролировать правильность решения, а в случае необходимости помочь детям в выполнении домашней работы по геометрии. Учебник находится здесь: crystal-zvon. ru
ru
Похожее:
▶▷▶▷ гдз по алгебре 9 класс 1028
▶▷▶▷ гдз по алгебре 9 класс 1028| Интерфейс | Русский/Английский |
| Тип лицензия | Free |
| Кол-во просмотров | 257 |
| Кол-во загрузок | 132 раз |
| Обновление: | 15-09-2019 |
гдз по алгебре 9 класс 1028 — ГДЗ по алгебре для 9 класса ЮН Макарычев — номер 1028 reshebamegdzalgebra 9 -klassmakarychev 1028 Cached Гдз дидактические материалы по Алгебре за 9 класс можно найти тут предыдущее Следующее 1028 Номер 1028 — гдз по алгебре 9 класс Макарычев, Миндюк, Нешков gdzplusme 9 -klassalgebramakarychevzadacha- 1028 Cached ГДЗ 9 класс Алгебра Макарычев, Миндюк, Нешков Задача 1028 9 класс Задача 1028 , ГДЗ по алгебре за 9 класс к учебнику Макарычева Гдз По Алгебре 9 Класс 1028 — Image Results More Гдз По Алгебре 9 Класс 1028 images Номер задания 1028 — ГДЗ по Алгебре 9 класс: Макарычев ЮН gdzputinainforeshebniki 9 -klassalgebra Cached Номер задания 1028 Назад к содержанию Ответ на Номер задания 1028 из ГДЗ по Алгебре 9 класс : Макарычев ЮН ГДЗ по алгебре для 7 класса ЮН Макарычев — номер 1028 reshebamegdzalgebra7-klassmakarychevnomer- 1028 Cached Подробное решение номер 1028 по алгебре для учащихся 7 класса, авторов ЮН Макарычев, НГ Решебник (ГДЗ) Алгебра 9 класс ОС Істер 2017 Вшколе vshkolecom 9 -klassreshebnikialgebraos-ister-2017 Cached ГДЗ по алгебре 9 класс Істер пользуются огромным спросом, как среди подростков, так и среди родителей, качественно помогая в эффективной проверке домашних работ Решебник (ГДЗ) по алгебре 9 класс Макарычев megareshebarupublreshebnikalgebra 9 _klass Cached Авторы учебника ЮН Макарычев и другие — 17 — 19 издание Издательство Просвещение 2016 год Пользуясь этим ГДЗ , делать домашнюю работу по алгебре в 9 классе станет проще Решебник (ГДЗ) по алгебре за 9 класс megareshebarupublgdzalgebra 9 _klass97-1-0-1267 Cached Подробный решебник ( гдз ) по Алгебре за 9 класс к учебнику школьной программы ГДЗ по алгебре за 9 класс, решебник и ответы онлайн gdzruclass- 9 algebra Cached ГДЗ : Спиши готовые домашние задания по алгебре за 9 класс , решебник и ответы онлайн на gdzru Номер задания 1028 — ГДЗ по Алгебре 8 класс: Макарычев ЮН gdzputinainfomakarychevnomer-zadaniya- 1028 Cached Назад к содержанию Ответ на Номер задания 1028 из ГДЗ по Алгебре 8 класс : Макарычев ЮН Номер 3327(1028) — ГДЗ по алгебре 7 класс Мордкович uchimorggdzpo-algebre-7-klass-mordkovich2137 Cached Решение задания номер 3327( 1028 ) ГДЗ по алгебре 7 класс Мордкович поможет в выполнении и проверке Promotional Results For You Free Download Mozilla Firefox Web Browser wwwmozillaorg Download Firefox — the faster, smarter, easier way to browse the web and all of 1 2 3 4 5 Next 223,000
- Ответы по алгебре.
 Введите в строку поиска только фамилию автора и класс. Добавить книги в список П
Введите в строку поиска только фамилию автора и класс. Добавить книги в список П - о запросу не найдено ни одной книги. ГДЗ бесплатно по всем предметам. ГДЗ по алгебре 7 класс Мордкович — онлайн решебник. Вы открыли задание номер 1028 из решебника на uchim.org. Предмет: Алгебра.
- кович — онлайн решебник. Вы открыли задание номер 1028 из решебника на uchim.org.
Предмет: Алгебра. 2011-2016 УРОКУ.НЕТ — Бесплатные ГДЗ решебники, ответы, онлайн решения задач. Похожих решений по Алгебра 9 класс Бевз не найдено.
Домашние задание по алгебре за 7 класс: Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова задание 1028 — решебник, ответы и онлайн гдз.
ГДЗ по алгебре 7 кл. Никольский М.К. разработаны с целью помочь семикласснику усвоить шаблоны алгебраических действий.
Автор расписал решебник по алгебре настолько доступно, что разберётся даже тот ученик, который пропустил занятия и не слышал объяснений педагога.
ГДЗ по алгебре 9 класс Кравчук — поможет любому ученику досконально усвоить и изучить алгебраическую науку! Да, страшное слово алгебра снилось, снится и будет сниться в страшном сне не одному поколению школьников.
 ГДЗ по алгебре. 12-річна програма, Бевз Г. П. Бевз В. Г. Сайт гдз-класс.рф принадлежит группе сайтов УРОКУ.НЕТ.
ГДЗ по алгебре. 12-річна програма, Бевз Г. П. Бевз В. Г. Сайт гдз-класс.рф принадлежит группе сайтов УРОКУ.НЕТ.
страшное слово алгебра снилось
Н.Г. Миндюк
- качественно помогая в эффективной проверке домашних работ Решебник (ГДЗ) по алгебре 9 класс Макарычев megareshebarupublreshebnikalgebra 9 _klass Cached Авторы учебника ЮН Макарычев и другие — 17 — 19 издание Издательство Просвещение 2016 год Пользуясь этим ГДЗ
- smarter
- решебник и ответы онлайн gdzruclass- 9 algebra Cached ГДЗ : Спиши готовые домашние задания по алгебре за 9 класс
гдз по алгебре класс Все результаты ГДЗ номер алгебра класс ЮН Макарычев, НГ ГДЗ класс Алгебра Макарычев ЮН Подробное решение номер по алгебре для учащихся класса , авторов ЮН Макарычев, НГ Миндюк, КИ Нешков, СБ Суворова Задача ГДЗ решебник Алгебра класс Макарычев gdzreshebnik algebraklass makarychev Решение задания по алгебре Макарычев класс Ответ на Номер задания из ГДЗ по Алгебре класс algebra makarychevyan nomerzadaniya ГДЗ готовое домашние задание из решебника на Номер задания по учебнику Алгебра класс учебник для общеобразовательных ГДЗ по алгебре класс Макарычев, Миндюк номер gdz _class algebra makarichev Решение задачизадания номер к учебнику по алгебре за класс авторов Макарычев, Миндюк ГДЗ по алгебре класс Макарычев ЮН упражнение exercises На сайте представлено решение по предмету Алгебра за класс автора Макарычев ЮН упражнение Это гдз поможет вам решить или ГДЗ по алгебре для класса ЮН Макарычев номер ГДЗ класс Алгебра Макарычев Подробное решение номер по алгебре для учащихся класса , авторов ЮН Макарычев, НГ Миндюк, КИ Нешков, СБ Суворова ГДЗ номер , список задач по алгебре класс gdz algebra makarychev ГДЗ , готовое домашнее задание по алгебре класс , автор учебника Макарычев ЮН На Решунове ты всегда найдешь полный список всех Задача Алгебра класс Макарычев Рамблеркласс temyalgebra ktopomozhetpostroitzadachaal Ответы на вопрос Кто поможет построить? Задача Алгебра класс Макарычев читайте на Рамблеркласс Постройте график функции VIPGDZcom klass algebra makarychev zadanie решебника ГДЗ на Задание по учебнику ЮН Макарычев, НГ Миндюк, КИ Нешков, СБ Суворова Учебник по алгебре класса е издание Задание ГДЗ по алгебре класс Макарычев zadaniealgebraklassmakarychev Задание Алгебра класс Макарычев Видео решение задания Алгебра класс Макарычев Письменное решение задания Алгебра ГДЗ алгебра класс Макарычев, Миндюк, Нешков gdz algebra _klass zadanie Решебник по алгебре за класс авторы Макарычев, Миндюк, Нешков издательство Просвещение Задание Видео Задание Геометрия класс Атанасян UrokiTV YouTube сент г Номер Геометрия класс Атанасян Алексей Подлесов YouTube апр г Все результаты ГДЗ по алгебре, Алгебра класс Макарычев wwwmygdzcom ГДЗ по алгебре Алгебра класс Макарычев ГДЗ по алгебре , Алгебра класс Макарычев Готовое домашнее задание mygdzcom ГДЗ по алгебре класс Макарычев учебник г класс макарычев г онлайн ГДЗ по алгебре класс Макарычев учебник г подходит к г онлайн Номер гдз по алгебре класс Макарычев, Миндюк klass algebra makarychev zadacha Разбор задания по алгебре за класс Макарычев, Миндюк Картинки по запросу гдз по алгебре класс Показать все Другие картинки по запросу гдз по алгебре класс Жалоба отправлена Пожаловаться на картинки Благодарим за замечания Пожаловаться на другую картинку Пожаловаться на содержание картинки Отмена Пожаловаться Все результаты Номер гдз по алгебре класс Мерзляк, Полонский klass algebra merzlyak zadacha Разбор задания по алгебре за класс Мерзляк Задание Алгебра, класс, Макарычев ЮА ГДЗ domashkasu gdz klass algebra book Решение задания Учебник Алгебра , класс , Макарычев ЮА Предмет Алгебра , класс Номер Решебник по алгебре класс Макарычев gdz poalgebreklassmakarychev Решение задания номер Решебник по алгебре класс Макарычев поможет в выполнении и проверке Ответ на задачу Страница ГДЗ Алгебра nikoljaru ГДЗ Алгебра класс Никольский СМ Ответ на задачу ГДЗ Зеленый учебник русский язык класс Баранов, Ладыженская Предыдущая Решебник по алгебре класс Макарычев, Миндюк, Нешков algebraklassmakarychevmindyukneshkovsuvorova Пособие ГДЗ по алгебре , Макарычев ЮН, Миндюк НГ, Нешков КИ, Суворова СБ, задание Номер ГДЗ по Алгебре класс Макарычев Где Гдз klass algebra makarychev nomer Номер из решебника ГДЗ на учебник по Алгебре класса от авторов ЮН Макарычев, НГ Миндюк, КИ Нешков, СБ Суворова Готовое ГДЗ по алгебре класс ЮН Макарычев, НГ Миндюк, КИ wwwggdzru class algebra otvetykuprazhneniyam list Спиши ГДЗ по алгебре класс юн макарычев, нг миндюк, ки нешков, сб суворова Ответы к упражнениям, ответ на вопрос с, найди ответ ГДЗ по Алгебре класс ЮН Макарычев, НГ Миндюк, КИ reshebniki algebra class makarychev Здравствуйте школьники и дорогие читатели решебника к учебнику Алгебра класс авторов Макарычев, Миндюк Поздравляем вас с началом нового ГДЗ по геометрии для классов Атанасян ЛС Номер godozru gdzgeometriya klassatanasyanls nomer Главная Алгебра Геометрия Русский Физика Химия ГДЗ по геометрии для классов Атанасян ЛС Номер ГДЗ онлайн Godozru ГДЗ по математике класс упражнение Зубарева ИИ dzokru gdz book unit Готовое Домашнее Задание по математике для класса упражнение Зубарева ИИ, Мордкович АГ Решебник Математика упр ответы на Задание Алгебра класс Макарычев OrtCams заданиеалгебраклассмакарычев_ae янв г Другие решения смотри тут Пройти тесты по учебнику и посмотреть сам материал тут algebraklassmakarychevyunmindyukng Категория ГДЗ алгебра класс Макарычев Задание Геометрия класс Атанасян Задание ГДЗ Алгебра класс Бевз Г П, Бевз В Г gdzometrby bookresh Задание Задание Задание Задание Задание Задание Задание Задание Содержание Закрыть Математика класс Мерзляк, Полонский, Якир Номер uchebniki klass matematika merzlyak Выполните действия , , , ,; , , , ,; , , ,; Алгебра класс Макарычев ГДЗ, решебник на Gdzlife klass algebra makarichev Рейтинг , голоса Подробные ГДЗ от GDZ life по алгебре класса Макарычев ЮН, Миндюк ГДЗ к учебнику от Макарычева ЮН для класса поможет справиться с РешеноУпр ГДЗ Мерзляк Полонский класс по otvet reshebniki otvet Упр из учебника по алгебре Мерзляк Полонский класс бесплатно с пояснениями ГДЗ по Алгебре класс Макарычев Решебник онлайн class algebra makarychev Проверяй домашнюю работу с помощью пособия ГДЗ по Алгебре для класса ГДЗ по Алгебре класс ЮН Макарычев, НГ Миндюк Решебник по Алгебре за класс ЮН Макарычев, НГ reshebnik class algebra makarychev Данное пособие содержит решебник ГДЗ по Алгебре за класс ГДЗ рабочая тетрадь по алгебре класс Макарычев предлагает Решебник ГДЗ по алгебре класс Макарычев ГДЗ класс Алгебра ЮН Макарычев Похожие Подробный гдз и решебник по алгебре для класса , авторов ЮН ГДЗ Дидактические материалы алгебра класс ЮН Макарычев Ответы НГде можно скачать учебник по алгебре класс Домашние задания Другие предметы Алгебра Учебник для класса общеобразовательных учреждений, г Макарычев ЮН, Миндюк НГ, Суворова СБ только не старый учебник,а Упражнение Математика класс Виленкин НЯ watch февр г Добавлено пользователем ГДЗ Математика класс Упражнение Математика Published on Feb , Наша группа ВК ГДЗ Канал на YouTube ГДЗ Алгебра класс В параллелограмме ABCD ADм, BD, м, A node В параллелограмме ABCD ADм, BD, м, A Найдите BDC и DBC Источник Решебник по геометрии за класс к учебнику гдз по алгебре класс макарычев юн миндюк нг wwwtaurusgruppru img gdzpoalgebreklassmakarycheviu_nm янв г гдз по алгебре класс макарычев юн миндюк нг Yahoo Search г Алгебра класс Макарычев GDZ Ru YouTube Алгебра класс Макарычев Vcevceru vcevceru Похожие Главная Алгебра класс Мордкович Алгебра класс Макарычев Русский язык класс Ладыженская Геометрия класс Атанасян Физика ГДЗ по алгебре класс Макарычев, Миндюк, Нешков ️ класс ️ Решебник по алгебре за класс хорошо подходит для проверки домашних заданий В ГДЗ собраны ответы к учебнику по алгебре ЮН Макарычев, НГ ГДЗ по Алгебра класс Макарычев номер решебник gdz otvet Подробное решение номер ГДЗ Алгебра класс Макарычев номер Решебник Лучшие бесплатные решебники и готовое домашнее задание Решебник ГДЗ Алгебра, класс Ю Н DocBazaru resh Решебник по учебнику Домашняя работа по алгебре за класс к учебнику Алгебра класс ЮН Макарычев и др, М Просвещение, XXXX г Мегарешеба ГДЗ по Алгебре за класс ЮН Макарычев gdzalgebra class makarychev ГДЗ идет к рабочей тетради по алгебре за класс Миндюк НГ Школьник может решать упражнения , кропотливо прорабатывая каждую задачу ГДЗ по алгебре для класса ЮН Макарычев poalgebre klass makarychev Похожие Но очень подробный гдз по алгебре за класс ЮН Макарычев, НГ ГДЗ к рабочей тетради по алгебре за класс Миндюк НГ можно скачать здесь ; ; ; ; ; ; ; ; ; ; ; ; Решение номера Математика класс ГДЗ matematika klass petersondorofeevchast На странице представлено онлайн решение номера по учебнику Математика класс Петерсон часть Если вы нашли ошибку или у вас Алгебра класс ЮН Макарычев ГДЗ Решебник Niglus gdz Алгебра Макарычев ЮН Алгебра класс ЮН Макарычев ГДЗ Решебник Также гг гг Задание не найдено Показать задания ГДЗ по Алгебре класс Макарычев ЮН gdz class algebra makarichev ГДЗ Готовые домашние задания по Алгебре класс , решебник Макарычев ЮН ГДЗ по алгебре класс Макарычев решебник онлайн gdzonlinecom klass algebra makarychev ГДЗ к учебнику по алгебре за класс Макарычев, Миндюк, Нешков, Суворова онлайн ГДЗ и решебник по алгебре для класса Макарычев ответы spishi _gdz_i_reshebnik_po_alg Спиши готовую домашнюю работу ГДЗ из онлайн решебника по алгебре для класса Макарычев Смотри бесплатные ответы на Домашка мигом! Учебник по алгебре, класс Макарычев domashkamigomru gdz uchebnik_po_algebre___klass___god_ Учебник по алгебре , класс Макарычев ЮА, год О сайте domashka migomru Готовые домашние задания Пояснения к фильтрации результатов В ответ на официальный запрос мы удалили некоторые результаты с этой страницы Вы можете ознакомиться с запросом на сайте LumenDatabaseorg В ответ на официальный запрос мы удалили некоторые результаты с этой страницы Вы можете ознакомиться с запросом на сайте LumenDatabaseorg В ответ на жалобу, поданную в соответствии с Законом США Об авторском праве в цифровую эпоху, мы удалили некоторые результаты с этой страницы Вы можете ознакомиться с жалобой на сайте LumenDatabaseorg Вместе с гдз по алгебре класс часто ищут гдз по алгебре класс макарычев алгебра класс алгебра класс учебник алгебра класс алгебра класс номер книга по алгебре класс макарычев алгебра класс номер алгебра класс номер Документы Blogger Duo Hangouts Keep Jamboard Подборки Другие сервисы Приложения
Ответы по алгебре. Введите в строку поиска только фамилию автора и класс. Добавить книги в список По запросу не найдено ни одной книги.
ГДЗ бесплатно по всем предметам. ГДЗ по алгебре 7 класс Мордкович — онлайн решебник. Вы открыли задание номер 1028 из решебника на uchim.org.
Предмет: Алгебра. 2011-2016 УРОКУ.НЕТ — Бесплатные ГДЗ решебники, ответы, онлайн решения задач. Похожих решений по Алгебра 9 класс Бевз не найдено.
Домашние задание по алгебре за 7 класс: Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова задание 1028 — решебник, ответы и онлайн гдз.
ГДЗ по алгебре 7 кл. Никольский М.К. разработаны с целью помочь семикласснику усвоить шаблоны алгебраических действий.
Автор расписал решебник по алгебре настолько доступно, что разберётся даже тот ученик, который пропустил занятия и не слышал объяснений педагога.
ГДЗ по алгебре 9 класс Кравчук — поможет любому ученику досконально усвоить и изучить алгебраическую науку! Да, страшное слово алгебра снилось, снится и будет сниться в страшном сне не одному поколению школьников.
Введите в строку поиска только фамилию автора и класс. Добавить книги в список По запросу не найдено ни одной книги.
ГДЗ бесплатно по всем предметам. ГДЗ по алгебре 7 класс Мордкович — онлайн решебник. Вы открыли задание номер 1028 из решебника на uchim.org.
Предмет: Алгебра. 2011-2016 УРОКУ.НЕТ — Бесплатные ГДЗ решебники, ответы, онлайн решения задач. Похожих решений по Алгебра 9 класс Бевз не найдено.
Домашние задание по алгебре за 7 класс: Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова задание 1028 — решебник, ответы и онлайн гдз.
ГДЗ по алгебре 7 кл. Никольский М.К. разработаны с целью помочь семикласснику усвоить шаблоны алгебраических действий.
Автор расписал решебник по алгебре настолько доступно, что разберётся даже тот ученик, который пропустил занятия и не слышал объяснений педагога.
ГДЗ по алгебре 9 класс Кравчук — поможет любому ученику досконально усвоить и изучить алгебраическую науку! Да, страшное слово алгебра снилось, снится и будет сниться в страшном сне не одному поколению школьников. ГДЗ по алгебре. 12-річна програма, Бевз Г. П. Бевз В. Г. Сайт гдз-класс.рф принадлежит группе сайтов УРОКУ.НЕТ.
ГДЗ по алгебре. 12-річна програма, Бевз Г. П. Бевз В. Г. Сайт гдз-класс.рф принадлежит группе сайтов УРОКУ.НЕТ.
Алгебра. 7 класс. Учебник Норы Миндюк, Светланы Суворовой, Юрия Макарычева, Константина Нешкова: новинка (2018)
Изображение запасаИздательство Просвещение, 2018
Новый Состояние: новый Твердый переплет
Об этом товаре
Страниц: 256 Язык: Русский.Данный учебник является первой частью трехлетнего курса алгебры для общеобразовательных школ. Новое издание учебника дополнено и переработано. Его математическое содержание позволяет достичь достаточных планируемых результатов обучения, предусмотренных Федеральным государственным образовательным стандартом основного общего образования. В задачный материал включены новые по форме задания: задачи для работы в парах и задачи-исследования. В конце учебника приводится список литературы, дополняющей его.97850
В задачный материал включены новые по форме задания: задачи для работы в парах и задачи-исследования. В конце учебника приводится список литературы, дополняющей его.97850275. Опись продавца книг № 10-1326028
Задайте вопрос продавцу
Библиографические данные
Название: Алгебра. 7 класс. Учебник
Издательство: Просвещение
Дата публикации: 2018
Переплет: Твердый переплет
Состояние книги: новый
Об этом заголовке
Сводка: Русская книга.Издательство: Просвещение. Страниц: 256. Год: 2018. Обложка: Твердая обложка.
«Об этом заголовке» может принадлежать другой редакции этого заголовка.
Описание магазина
Руслания — один из крупнейших оптовых продавцов и дистрибьюторов российских книг, фильмов, музыки и периодических изданий. Компания ведет, пожалуй, самый большой в мире каталог продаж нот на русском языке.Руслания занимается распространением русской продукции, в основном письменной. В ассортименте есть товары и на других языках, но основное внимание уделяется России. Благодаря узкой направленности «Руслания» может предложить очень высокий уровень обслуживания как корпоративным, так и частным клиентам, интересующимся Россией.Посетить витрину продавца
Условия продажи:
Условия доставки:
Список книг продавца
Способы оплаты
принимает продавец
% PDF-1. 4
% 1505 0 объект
>
endobj xref
1505 87
0000000044 00000 н.
0000003256 00000 н.
0000003558 00000 н.
0000003620 00000 н.
0000003771 00000 н.
0000004451 00000 п.
0000005648 00000 н.
0000006112 00000 н.
0000006325 00000 н.
0000015649 00000 п.
0000016304 00000 п.
0000017507 00000 п.
0000017841 00000 п.
0000018033 00000 п.
0000022261 00000 п.
0000023058 00000 п.
0000024254 00000 п.
0000024683 00000 п.
0000024895 00000 п.
0000033016 00000 п.
0000033619 00000 п.
0000034816 00000 п.
0000035204 00000 п.
0000035423 00000 п.
0000042825 00000 п.
0000043189 00000 п.
0000044383 00000 п.
0000044604 00000 п.
0000058549 00000 п.
0000059746 00000 п.
0000060192 00000 п.
0000060412 00000 п.
0000070794 00000 п.
0000071214 00000 п.
0000072411 00000 п.
0000072814 00000 п.
0000073034 00000 п.
0000080478 00000 п.
0000080856 00000 п.
0000081890 00000 п.
0000082100 00000 п.
0000084950 00000 п.
0000086146 00000 п.
0000086547 00000 п.
0000086746 00000 п.
0000089557 00000 п.
4
% 1505 0 объект
>
endobj xref
1505 87
0000000044 00000 н.
0000003256 00000 н.
0000003558 00000 н.
0000003620 00000 н.
0000003771 00000 н.
0000004451 00000 п.
0000005648 00000 н.
0000006112 00000 н.
0000006325 00000 н.
0000015649 00000 п.
0000016304 00000 п.
0000017507 00000 п.
0000017841 00000 п.
0000018033 00000 п.
0000022261 00000 п.
0000023058 00000 п.
0000024254 00000 п.
0000024683 00000 п.
0000024895 00000 п.
0000033016 00000 п.
0000033619 00000 п.
0000034816 00000 п.
0000035204 00000 п.
0000035423 00000 п.
0000042825 00000 п.
0000043189 00000 п.
0000044383 00000 п.
0000044604 00000 п.
0000058549 00000 п.
0000059746 00000 п.
0000060192 00000 п.
0000060412 00000 п.
0000070794 00000 п.
0000071214 00000 п.
0000072411 00000 п.
0000072814 00000 п.
0000073034 00000 п.
0000080478 00000 п.
0000080856 00000 п.
0000081890 00000 п.
0000082100 00000 п.
0000084950 00000 п.
0000086146 00000 п.
0000086547 00000 п.
0000086746 00000 п.
0000089557 00000 п. 0000089905 00000 п.
00000
0000089905 00000 п.
00000
Labo J.
 -V. Браслет: Н.Верещагин Labo J. -V. Браслет: Н.Верещагин
-V. Браслет: Н.Верещагин Labo J. -V. Браслет: Н.ВерещагинИсследователь в Лаборатории с февраля 2005 г.
Навсегда место работы:
Кафедра математической логики и теории алгоритмов, Механико-математический факультет, МГУ, Москва, 119899 Россия.
ФАКС: +7 095 939 3031
Эл. Почта: ver AT mech.math.msu.su
Общие
Личный
Родился 27.10.1958 г. в г. Москва, Россия.
Текущая аффилированность
Профессор МГУ им. М.В. Ломоносова Механико-математический факультет Кафедра математической логики и теории алгоритмов
Текущее направление исследований
Вычислительная сложность, Колмогоровская сложность
Прочая деятельность
Член Программного комитета 18-я конференция IEEE по вычислительной сложности, 2003 г., Орхус (Дания) и
18-й Международный симпозиум по теоретическим аспектам Компьютерные науки, 2001, Дрезден (Германия).
Вклады в конференцию
- 2004
- 31-й Международный коллоквиум по автоматам, языкам и Программирование, ICALP, Турку, Финляндия
- 2005, 2004, 1999
- Симпозиум по теоретическим аспектам компьютерных наук, STACS
- 2002
- 47-й симпозиум IEEE по основам компьютерных наук,
FOCS.

- 2001, 2000, 1999, 1998, 1997, 1993, 1992
- Ежегодная конференция IEEE по вычислительной сложности.
- 2003, 1996
- Дагштуль-семинары «Структура и сложность» и «Колмогоровская сложность и приложения», Schloß Dagstuhl, Германия
- 1995
- Восьмая ежегодная конференция по вычислительному обучению Theory, Санта-Крус, Калифорния, США
- 1995
- Третий Израильский симпозиум по теории вычислений и систем, Тель-Авив, Израиль (Два разговора)
- 1994
- Мастерская COLORET, Амстердам, Нидерланды
- 1992
- Конференция по логическим основам информатики.Тверь, Россия.
- 1991
- Суслинская мемориальная конференция. Саратов, Россия.
- 1988
- 9-я Всесоюзная конференция по математической логике, Ленинград, Россия.
- 1985
- 18-я Всесоюзная алгебраическая конференция, Кишинев, Молдова
- 1982
- 6-я Всесоюзная конференция по математической логике,
Тбилиси, Грузия.

Международный опыт
- 2005, 2004, 2003, 2002, 2001
- Месячный исследовательский визит в CWI, Амстердам.По приглашению Х. Бурмана и П. Витаньи.
- 2004, 2003, 2002, 2001, 2000
- Месячный исследовательский визит в Университет Прованса, Франция. Приглашает Бруно Дюран.
- 2003
- Конференция IEEE по вычислительной сложности, Орхус (Дания). Член программного комитета.
- 2003
- Дагштуль-семинар «Колмогоровская сложность и ее применение»
- 2004, 2002
- Дагштуль-семинар «Алгебраические методы в квантовых и классические вычисления »
- 2001
- 18-й Международный симпозиум по теоретическим аспектам Компьютерные науки, Дрезден, Германия.Член Программного комитета.
- 1999
- 3-месячный исследовательский визит в Ecole Normale Supérieure в Лионе, Франция. Приглашает Бруно Дюран.
- 1998
- 13-я ежегодная конференция IEEE по вычислительной технике
Сложность, Буффало, США.

- 1998
- Трехмесячный исследовательский визит в Вюрцбургский университет, Германия. Приглашает Клаус Вагнер.
- 1997/1998
- 6-месячный исследовательский визит в Ecole Normale Supérieure в Лионе, Франция.
- 1997
- Месячный исследовательский визит в Университет Рутгерса, США.Приглашает Эрик Аллендер.
- 1997
- 12-я ежегодная конференция IEEE по вычислительной технике Теория сложности, Ульм, Германия.
- 1997
- Месячный исследовательский визит в Амстердамский университет. По приглашению П. ван Эмде Боаса и П.М.Б. Витани.
- 1997
- 10-дневный исследовательский визит в Университет Йоханнеса Гутенберга, Майнц, Германия. Приглашает Клеменс Лаутеманн.
- 1996
- Дагштуль-семинар «Структура и сложность»
- 1995
- Третий Израильский симпозиум по теории вычислений и системы, Тель-Авив, Израиль, янв.1995 г.
- 1994
- Двухнедельная исследовательская поездка в Рочестерский университет, штат Нью-Йорк, США.
 Приглашает Лейн Хемаспандра.
Приглашает Лейн Хемаспандра. - 1994
- Мастерская COLORET, г. Амстердам, Нидерланды
- 1994
- 9-я ежегодная конференция IEEE по структуре сложности Theory, Амстердам, Нидерланды
Семинары проходят
МГУ, механико-математический факультет
- Колмогоровский семинар по сложности описания и сложности вычислений (с А.Л.Семенов, А.Х. Шен), 1984-, выпускник.
- Профессиональный семинар по математической логике и теории алгоритмов (совместно с В. А. Успенским, А. Л. Семеновым, А. Х. Шен, А. А. Разборовым), 1984-, бакалавр.
Последние публикации
Учебники
- А. Шен, Н. Верещагин.
Математическая логика и теория вычислений. Элементы теории множеств.
Московский центр непрерывного математического образования, 1999, 127 стр.
(Русский)
Английский перевод: Основная теория множеств.Американское математическое общество. Студенческая математическая библиотека, т. 17. 2002
Студенческая математическая библиотека, т. 17. 2002 - А. Шен, Н. Верещагин. Математическая логика и теория вычислений.
Вычислимые функции.
Московский центр непрерывного математического образования, 1999, 174 стр.
(Русский)
Английский перевод: Вычислимые функции. Американское математическое общество. Студенческая математическая библиотека, т. 19. 2003 г. - А. Шен, Н. Верещагин. Математическая логика и теория вычислений. Языки и исчисления.Московский центр непрерывного математического образования, 1999, 286 стр. (Русский)
- В.А. Успенский, Н. Верещагин, В. Плиско. Введение в математическую логику. Издательство МГУ, 1991, Наука, 2004, 136 с.
Глава в книге
- Н. Верещагин. Релятивизируемость в теории сложности. Глава в книге Л.Д. Беклемишева, М. Пентуса и Н. Верещагин, Доказуемость, сложность, грамматики, AMS Translations, Series 2, v. 192 , 1999, стр.87—172.
Реферируемые журнальные публикации
- Н.
 Верещагин и П. Витани.
«Колмогоровский
Структурные функции с приложением
к основам выбора модели »
IEEE Transactions по теории информации 50:12 (2004) 3265-3290.
Предварительная версия:
Proc. 47-я конференция IEEE Symp. Найденный. Comput. Наук,
2002, 751-760.
Верещагин и П. Витани.
«Колмогоровский
Структурные функции с приложением
к основам выбора модели »
IEEE Transactions по теории информации 50:12 (2004) 3265-3290.
Предварительная версия:
Proc. 47-я конференция IEEE Symp. Найденный. Comput. Наук,
2002, 751-760. - Б. Дюран, Н. Верещагин. «Стохастичность Колмогорова-Ловленда для конечных строк ». Информационные письма, 91 (2004) 263-269.
- О. Митина и Н. Верещагин. «Как использовать несколько шумных каналов с неизвестной вероятностью ошибки » Информация и вычисления 182 (2003) 229-241. Предварительный версия появилась под заголовком «Как пользоваться советом специалиста в случае, когда актуальные значения предполагаемых событий остаются неизвестно «. Proc. Восьмая ежегодная конференция по вычислительному обучению Теория (5-8 июля), 1995, Санта-Крус, Калифорния, 91-97.
- Н.К. Верещагин, Д. Скворцов, Э. Скворцова, А. Чернов.Варианты реализуемости пропозициональных формул
и логика слабого закона исключенного среднего.
 Труды Математического института им. В. А. Стеклова 242 (2003) 67-85.
Предварительная версия появилась в:
Труды Computer Science Logic’02,
Конспект лекций по информатике,
2002, т. 2471, с. 74-88.
Труды Математического института им. В. А. Стеклова 242 (2003) 67-85.
Предварительная версия появилась в:
Труды Computer Science Logic’02,
Конспект лекций по информатике,
2002, т. 2471, с. 74-88. - Б. Дюран, В. Кановей, В. Успенский, Н. Верещагин. «Делай сильнее существуют определения случайности? » Теоретическая информатика 290: 3 (2003) 1987–1996.
- К.Макарычев, Ю. Макарычев, А. Ромащенко, Н. Верещагин. «Новый класс неравенства нешенноновского типа для энтропий Коммуникации в информации и системах, 2: 2 (2002) 147-166.
- Н. Верещагин. «Колмогоровская сложность, обусловленная большими целыми числами». Теоретическая информатика 271 (2002) 59-67.
- Н. Верещагин и М. Вьюгин. «Независимые программы минимальной длины для перевода между данные строки «. Теоретическая информатика 271 (2002) 131-143. Предварительная версия в: Proc.15-го ежегодного IEEE Конференция по вычислительной сложности, Флоренция, июль 2000 г., стр. 138—144.
- А.
 Ромащенко, А. Шен, Н. Верещагин.
«Комбинаторная интерпретация колмогоровской сложности»,
Теоретическая информатика 271 (2002) 111—123.
Предварительная версия в:
Proc. 15-й ежегодной конференции IEEE по вычислительной сложности,
Флоренция, июль 2000 г., стр. 131-137.
Ромащенко, А. Шен, Н. Верещагин.
«Комбинаторная интерпретация колмогоровской сложности»,
Теоретическая информатика 271 (2002) 111—123.
Предварительная версия в:
Proc. 15-й ежегодной конференции IEEE по вычислительной сложности,
Флоренция, июль 2000 г., стр. 131-137. - А. Чернов, Ан. Мучник, А. Ромащенко, А. Шен, Н. Верещагин. Верхняя полурешетка двоичных строк с соотношением «x просто условно для y».Теоретическая информатика 271 (2002) 69–95}. Предварительная версия в: 14-я ежегодная конференция IEEE по вычислительной сложности, Атланта, 4-6 мая, 1999, 114—122.
- А. Шен и Н. Верещагин. «Логические операции и колмогоровская сложность». Теоретическая информатика 271 (2002) 125-129.
- Д. Хаммер, А. Ромащенко, А. Шен, Н. Верещагин. «Неравенства для энтропии Шеннона и колмогоровской сложности». Журнал компьютерных и системных наук 60 (2000) 442-464.
- Р. Раз, Г. Тардос, О. Вербицкий, Н. Верещагин. «Игры Артура-Мерлина в булевых деревьях решений». Журнал компьютерных систем наук 59 (1999) 346-372,
- Б.
 Дюран, А. Шен, Н. Верещагин.
«Описательная сложность вычислимых последовательностей».
Теоретическая информатика 171 (2001), стр. 47-58;
Предварительная версия: Учеб. 16-й Ann. Symp. на
Теоретические аспекты компьютерных наук, Трир, Германия, март
1999, LNCS 1563, с. 153—162.
Дюран, А. Шен, Н. Верещагин.
«Описательная сложность вычислимых последовательностей».
Теоретическая информатика 171 (2001), стр. 47-58;
Предварительная версия: Учеб. 16-й Ann. Symp. на
Теоретические аспекты компьютерных наук, Трир, Германия, март
1999, LNCS 1563, с. 153—162.
Публикации в трудах выборных конференций
- H.Бурман, Х. Клаук, Н. Верещагин, П. Витаньи. «Сложность индивидуального общения». 21-й ежегодный симпозиум по теоретическим аспектам компьютерных наук, STACS 2004, Монпелье, Франция, 25-27 марта, 2004, Известия. Серия: Конспект лекций по информатике, Vol. 2996, г. страницы 19-30.
- Б.Дуран, Н.К. Верещагин, М.А.Ушаков. «Экологические» вычисления ». В: Proc. 31-й Международный коллоквиум по автоматам, языкам и Программирование, ICALP 2004, Турку, Финляндия, июль 12–16, 2004 г.Серия: Конспект лекций по информатике, Vol. 3142 Diaz, J .; Karhumaki, J .; Леписта, А .; Саннелла, Д. (ред.) страницы 457-468.
- An. Мучник и Н.
 Верещагин.
«Логические операции и колмогоровская сложность II».
Proc. 16-го ежегодного IEEE
Конференция по вычислительной сложности, Чикаго, июнь 2001 г., стр. 256—265.
Верещагин.
«Логические операции и колмогоровская сложность II».
Proc. 16-го ежегодного IEEE
Конференция по вычислительной сложности, Чикаго, июнь 2001 г., стр. 256—265.
MATH / CMSC 38405: Арифметическая комбинаторика
Весна 20 : Вторник, четверг 14: 00–15: 20- Приемные часы. По предварительной записи (напишите мне по электронной почте).
- Литература. Значительную часть материала можно найти в монографии [1]. Для более старых результатов
особенно в первой части курса, см. также [2]. Ссылки на более конкретные источники по отдельным темам будут
быть также размещенным здесь, поскольку мы делаем успехи.
- Т. Тао и В. Х. Ву, Additive Combinatorics , Cambridge University Press, 2009.
- М. Б. Натансон, Аддитивная теория чисел: обратные задачи и геометрия сумм , Springer-Verlag, 1996.
- P. Frankl, Новое короткое доказательство теоремы Крускала-Катоны , Discrete
Математика , 48, 1984, 327-329.

- Н. Н. Боголюбов, О некоторых арифметических свойствах квазипериодов (французский и украинский), Ann. Chaire Phys. Математика. Акад. Sci. Украина (Киев) , 4, 1939, 195-205.
- Г. Петридис, Новые доказательства оценок типа Плуннеке для продуктовых множеств в группах , Combinatorica , 32, № 6, 2012, 721-733.
- С. Ловетт, Экспозиция квазиполинома Сандерса Теорема Фреймана-Ружа, Теория вычислений , Обзоры выпускников 6 (2015), стр. 1-14
- Р. О’Доннелл, Анализ булевых функций , Cambridge University Press, 2014.
- А. Разборов, Теорема произведения в свободных группах , Анналы математики , 179, № 2, 2014, 405-429.
- Б. Грин, Заметки о полиномиальной гипотезе Фреймана-Ружи.
- Т.Сандерс, О лемме Боголюбова-Ружи , Анализ и PDE , 5 (3): 627-655, 2012.
- Шакан Г. О высших энергетических разложениях и суммированном произведении.
 явление.
явление. - Б. Барак, Р., Импальяццо, А. Вигдерсон, Извлечение случайности с использованием нескольких независимых источников , Журнал SIAM по вычислениям , 36 (4): 1095-1118, 2006.
- Б. Барак, Г. Киндлер, Р. Шалтиэль, Б. Судаков, А. Вигдерсон, Моделирование независимости: новые конструкции конденсаторов, диаграмм Рамсея, диспергаторов и экстракторов , Journal of the ACM , 57 (4), апрель 2010 г.
- M.-C. Чанг, Теоремы о произведении в SL_2 и SL_3 , J. Inst. Математика. Jussieu , 7: 1-25, 2008.
- М. Браверман, К. Макарычев, Ю. Макарычев, А. Наор, Константа Гротендика строго меньше, чем оценка Кривина, Forum of Mathematics, Pi , 2013.
- I. Ruzsa и A. Szemeredi, Тройная система без шести точек, несущих три треугольника , Коллок. Математика. Soc. J. Bolyai 18 (1978), 939-945.
- J. Fox, Новое доказательство леммы об удалении графа , Annals of Mathematics , 174,
2011, 561-579.

- Н. Алон, Э. Фишер, М. Кривелевич и М. Сегеди, Эффективное тестирование больших графов , Combinatorica , 20 (4), 2000, 451-476.
- Дж. Фокс, Л. М. Ловаш, Точная нижняя оценка леммы Семереди о регулярности , Combinatorica , 37 (5), 2017, 911-951.
- Б. Грин, Т. Тао, Простые числа содержат произвольно длинные арифметические прогрессии , Анналы математики , 167, 2008, 481-547.
- Д. Конлон, Дэвид, Дж. Фокс, Я. Чжао, Теорема Грина-Тао: описание , Обзоры EMS в Математические науки , 1 (2), 2014, 249–282.
- Л., Бабай, Н. Нисан, М. Сегеди, Многосторонние протоколы, псевдослучайные генераторы для лог-пространства и компромиссы времени и пространства , Journal of Computer and System Sciences , 45 (2), 1992, 204–232,
- Э. Виола, Границы корреляции для многочленов от {0,1} , ACM SIGACT News , 40 (1), 2009.
- Ф. Чанг, Р. Грэм и Р.
 Уилсон, Квазислучайные графы , Combinatorica , 9 (4),
1989, 345-362.
Уилсон, Квазислучайные графы , Combinatorica , 9 (4),
1989, 345-362. - L. Lovasz, Большие сети и пределы графов , Американское математическое общество, 2012.
- А. Разборов, Алгебры флагов , Журнал символической логики , 72 (4), 2007, 1239-1282.
- Л. Корельяно, А. Разборов, Semantic Пределы плотных комбинаторных объектов, 2019.
- Текущая программа и дополнительные ссылки. Этот раздел будет регулярно обновляться, обычно в конце
неделя.
- Первая неделя: введение. | A + B |> = | A | + | B | -1 по целым числам: [1, лемма 5.3]. Обратный результат: [1,
Предложение 5.8]. е-преобразования и их свойства: [1, лемма 5.2]. Теорема Коши-Дэвенпорта: [1,
Теорема 5.4]. Теорема Кнезера (без доказательства): [1, теорема 5.5]. Теорема Воспера (без
доказательство): [1, теорема 5.9]. (3k-3) теорема (без доказательства): [1, теорема 5.11]. Доказательство Франкла
Теорема Крускала-Катоны: [3].
 Константы удвоения: [1, Глава 2.2].
Константы удвоения: [1, Глава 2.2]. - Вторая неделя: Теорема Фреймана: обсуждение. Константы удвоения и многомерные арифметические прогрессии,
правильные прогрессии. «Собственность» («внешний» вариант, без доказательства): [1, теорема 3.40]. Теорема Фреймана
(утверждения): случай без кручения [1, теорема 5.32], случай кручения [1, теорема 5.27]. Граница измерения:
[1, лемма 5.13]. Оценки Плуннеке-Ружи (утверждение): [1, следствие 6.29]; для старомодного доказательства
прочтите [1, раздел 6.5] или [2, Раздел 7]. Идея леммы Боголюбова-Ружи восходит к [4]. Покрытие Ружи
лемма: [1, лемма 2.14]. Неравенство треугольника Ружи: [1, лемма 2.6]. Расстояние Ружи: [1,
Определение 2.5]. Оценки Плуннеке-Ружи (доказательство Петридиса): [5]. Изоморфизмы Фреймана: [1, раздел 5.3].
Сведение к лемме Боболюбова-Ружи. Изоморфизмы Фреймана сохраняют структуру
«объекты»: [1, предложение 5.24] (торсионный случай аналогичен и проще). Хорошая (плотная) лепка:
[6, раздел 3.2] (торсионный случай), [1, лемма 5.
 26] (случай без кручения).
26] (случай без кручения). - Третья неделя: хороший модельный cntd. Для общей двойственности Понтрягина
см. например Статья Википедии, но мы будем использовать
Анализ Фурье только на конечных группах. Несколько другие системы обозначений для него можно найти в [1, раздел 4.1].
и [7] (характеристика 2). Оба источника также содержат все основные факты.
мы рассмотрели. Очень важные персонажи: [1, Определение 4.34]. Множества Бора: [1, раздел 4.4]. Наборы Бора находятся в 2A-2A:
[1, предложение 4.39]; обратите внимание, что мы работали с более сильным предположением о хорошем моделировании, поэтому наше доказательство
намного проще.Геометрия чисел: [1, разделы 3.1.1, 3.1.2, 3.5]. Вторая теорема Минковского:
[1, теорема 3.30]. Множества Бора содержат большие обобщенные арифметические прогрессии: [1, предложение 4.23]. Столкновение
числа (также известные как аддитивная энергия): [1, определение 2.8]. Статистическая версия оценок Плуннеке-Ружи (без доказательства):
[8, Раздел 6].
 n $ близко следует изложению в [6].
n $ близко следует изложению в [6]. - Четвертая неделя: квазиполиномиальное исследование Фреймана-Руши. Наш рассказ об истории Эрдоша-Семереди гипотеза ([1, гипотеза 8.13]) и связанные вопросы следуют [1] довольно близко. Оценка Элекеса: [1, теорема 8.14]. Теорема Семереди-Троттера: [1, теорема 8.3]. Нижние оценки числа перекрестков: [1, теорема 8.1]. Самая известная дорога на Эрдош-Семереди гипотеза: [11]. Теорема Бургейна-Каца-Тао (оценки сумм-произведений в конечных полях): [1, теорема 2.55]. Лемма Кац-Тао: [1, лемма 2.53].Фактор-множество: [1, определение 2.49]. Наборы коэффициентов представляют собой подполя: [1, следствие 2.52]. Разработаны приложения к псевдослучайности и конструктивным теоремам Рамсея. в серии статей, начиная с [12]; последний из них, кажется, [13] и содержит все соответствующие ссылки.
- Пятая неделя: Построение обычных графов Рамсея из двудольных. Некоммутативные аналоги:
[1, Раздел 2.7]; частичное обобщение теории Плуннеке-Руша: [1, предложение 2.
 40]. Обратный
теоремы (без доказательств): в $ SL_2 (\ mathbb C) $ [14] и в свободной группе [8]. Теорема Семереди
и его различные доказательства представлены в двух разделах [1]: Разделе 11 и Разделе 12. Пример Беренда:
[1, упражнение 10.1.4]. Лемма об удалении треугольника: [1, лемма 10.46]. Наши прямые (т.е. в обход [1,
Предложение 10.45]) сведение случая $ k = 3 $ к этому утверждению кажется частью фольклора. Наши
определение $ \ epsilon $ -регулярных (известных в определенных кругах как квазислучайных ) двудольных графов является
немного отличается от [1, определение 10.41], но эквивалентен последнему с точностью до полиномиального увеличения
$ \ epsilon $. Последней статьей о неравенстве Гротендика является [15]. Лемма Семереди о регулярности (без
доказательство): [1, лемма 10.42], доказательство можно найти в любой продвинутой книге по теории графов. Доказательство
Лемма об удалении треугольника (а также большая часть следующего материала) взята из основополагающей статьи [16].
40]. Обратный
теоремы (без доказательств): в $ SL_2 (\ mathbb C) $ [14] и в свободной группе [8]. Теорема Семереди
и его различные доказательства представлены в двух разделах [1]: Разделе 11 и Разделе 12. Пример Беренда:
[1, упражнение 10.1.4]. Лемма об удалении треугольника: [1, лемма 10.46]. Наши прямые (т.е. в обход [1,
Предложение 10.45]) сведение случая $ k = 3 $ к этому утверждению кажется частью фольклора. Наши
определение $ \ epsilon $ -регулярных (известных в определенных кругах как квазислучайных ) двудольных графов является
немного отличается от [1, определение 10.41], но эквивалентен последнему с точностью до полиномиального увеличения
$ \ epsilon $. Последней статьей о неравенстве Гротендика является [15]. Лемма Семереди о регулярности (без
доказательство): [1, лемма 10.42], доказательство можно найти в любой продвинутой книге по теории графов. Доказательство
Лемма об удалении треугольника (а также большая часть следующего материала) взята из основополагающей статьи [16]. Больше
недавнее доказательство с несколько лучшей оценкой: [17]. Теорема индуцированных паросочетаний: [1, предложение 10.45].
(6,3) -теорема: [1, Упражнение 10.6.2].
Больше
недавнее доказательство с несколько лучшей оценкой: [17]. Теорема индуцированных паросочетаний: [1, предложение 10.45].
(6,3) -теорема: [1, Упражнение 10.6.2]. - Шестая неделя: (6,3) -теорема cntd. Леммы об индуцированном удалении и проверка свойств: [18]. Нижняя
оценки леммы Семереди о регулярности: [19] и цитируемая там литература. Наш набросок доказательства
общая версия теоремы Семереди следует аргументу Гауэрса [1, разделы 11.1-11.4], скорее
внимательно. Мы определили норму равномерности Гауэрса с помощью развернутой формулы [1, (11.1)]. Рекурсивное определение
Нормы Гауэрса: [1, определение 11.2]. Внутреннее произведение Гауэрса, неравенство Гауэрса-Коши-Шварца и Гауэрса
Неравенство треугольника: [1, страницы 419-420].3 $ (без доказательства): [1, теорема 11.9]. «Гипотеза Эрдоша-Турана»: Википедия
статья. Теорема Грина-Тао об арифметических прогрессиях в простых числах: [20], см. Также изложение в [21].
Сложность многосторонней связи: [22], см.
 Также Википедию.
статья и цитируемая в ней литература. Обзор границ полиномиальной корреляции: [23].
Квазислучайность: [24].
Также Википедию.
статья и цитируемая в ней литература. Обзор границ полиномиальной корреляции: [23].
Квазислучайность: [24]. - Восьмая неделя: квазислучайность cntd. Пределы графика: [25]. Алгебры флагов: [26]. Единая теория для общих комбинаторных объектов: [27].Проекты: Тестирование свойств монотонного графа (Ю.).
- Девятая неделя (короткая): Проекты. Основные результаты с использованием флаговых алгебр (Аснесс). Вторая теорема Минковского (Гецельман).
- Первая неделя: введение. | A + B |> = | A | + | B | -1 по целым числам: [1, лемма 5.3]. Обратный результат: [1,
Предложение 5.8]. е-преобразования и их свойства: [1, лемма 5.2]. Теорема Коши-Дэвенпорта: [1,
Теорема 5.4]. Теорема Кнезера (без доказательства): [1, теорема 5.5]. Теорема Воспера (без
доказательство): [1, теорема 5.9]. (3k-3) теорема (без доказательства): [1, теорема 5.11]. Доказательство Франкла
Теорема Крускала-Катоны: [3].
Документы
Документы- Топология и сопряжение в удовлетворении ограничений обещаний
- Алгебраический подход к удовлетворению ограничений обещаний
- Робастные алгоритмы с полиномиальными потерями для CSP с почти единогласием
В. Далмау, М. Козик, А. Крохин, К. Макарычев, Ю. Макарычев, Я. Опршал.
Журнал SIAM по вычислениям, 48 (6), 1763-1795, 2019.
Версия конференции в SODA’17, 340-357, 2017. - К характеристике аппроксимируемых постоянным фактором конечнозначных CSP
V.Далмау, А. Крохин, Р. Манокаран
Журнал компьютерных и системных наук, 97, 14-27, 2018.
Версия конференции в SODA’15, 847-857, 2015. - Бинаризация для задач удовлетворения ценностных ограничений
Д. Коэн, М. Купер, П. Дживонс, А. Крохин, Р. Пауэлл и С. Живны.
Журнал СИАМ по дискретной математике, 31 (4), 2279–2300, 2017. - Полиморфизмы и как их использовать
Л. Барто, А. Крохин и Р. Виллард.
Обзор. В: Проблема удовлетворения ограничений: сложность и приближаемость, 1-44, 2017. - Сложность оцененных ССП
А. Крохин, С. Живны.
Обзор. В: Проблема удовлетворения ограничений: сложность и приближаемость, 233-266, 2017.
- Сложность общезначных CSP
В. Колмогоров, А. Крохин, М. Ролинек.
Журнал SIAM по вычислениям, 46 (3), 1087-1110, 2017.
Версия конференции в FOCS’15, 1246-1258, 2015. - Об алгебрах со многими симметрическими операциями
К. Карвалью и А. Крохин.
Международный журнал алгебры и вычислений, 26 (5), 1019-1032, 2016. - Характеристики некоторых условий Мальцева
М. Козик, А. Крохин, М. Валериот, Р. Виллард.
Универсальная алгебра, 73 (3-4), 205-224, 2015. - Сложность удовлетворения оценочных ограничений
П. Явонс, А. Крохин, С. Живны.
Обзор. Столбец «Алгоритмика» Вестника EATCS, 113, 21-55, 2014. (Errata) - Оракульная управляемость косых бисубмодульных функций
А. Хубер и А. Крохин.
Журнал СИАМ по дискретной математике, 28 (4), 1828-1837, 2014. - Косая бисубмодулярность и оцененные CSP
А. Хубер, А. Крохин, Р. Пауэлл.
Журнал SIAM по вычислениям, 43 (3), 1064–1084, 2014.
Версия конференции в SODA’13, 1296-1305, 2013.
- Робастная выполнимость для CSP: надежность и алгоритмические результаты
В. Далмау, А. Крохин.
Транзакции ACM по теории вычислений, 5 (4), статья 15, 2013. - Сложность проблемы гомоморфизма списков для графов
Л. Эгри, А. Крохин, Б. Лароз, П. Тессон.
Теория вычислительных систем, 51 (2), 143-178, 2012.
Версия конференции в STACS’10, LIPIcs 5, 335-346, 2010. - О жесткости похудения
А. Крохин и Д. Маркс.
Транзакции ACM на алгоритмах, 8 (2), Статья No 19, 2012.
Версия конференции в ICALP’08, LNCS 5125, 662-673, 2008. - Две новые двойственности гомоморфизмов и решеточные операции
К. Карвалью, В. Далмау и А. Крохин.
Журнал логики и вычислений, 21 (6), 1065-1092, 2011.
Версия конференции (части статьи) в LICS’08, 307-316, 2008. - Двойственность CSP и деревья ограниченной ширины пути
К. Карвалью, В. Далмау и А. Крохин.
Теоретическая информатика, 411 (34-36), 3188-3208, 2010. - Ретракции в псевдолеса
Т. Федер, П. Хелл, П. Йонссон, А. Крохин, Г. Норд.
Федер, П. Хелл, П. Йонссон, А. Крохин, Г. Норд.
Журнал СИАМ по дискретной математике, 24 (1), 101-112, 2010. - Проблемы удовлетворения жестких ограничений имеют жесткие пробелы в местоположении 1
P. Jonsson, A.Крохин и Ф. Куйвинен.
Теоретическая информатика, 410 (38-40), 3856-3874, 2009.
Версия конференции в CSR’07, LNCS 4649, 2007, 182-193. - Сложность игр удовлетворения ограничений и QCSP.
Ф. Бурнер, А. Булатов, Х. Чен, П. Дживонс и А. Крохин.
Информация и вычисления, 207 (9), 923-944, 2009.
Версия конференции (часть этой статьи) в CSL’03, LNCS 2803, 2003, 58-70. - Дуальности для задач удовлетворения ограничений
А. Булатов, А.Крохин и Б. Лароз. Обзор
, В: Сложность ограничений, LNCS 5250, 93-124, 2008. (Исправления) - Аппроксимируемость Max CSP с фиксированными ограничениями
В. Дейнеко, П. Йонссон, М. Классон и А. Крохин
Журнал АКМ, 55 (4), статья № 16, 2008 г.
Версия конференции в Eurocomb’05, DMTCS Proceedings, volume AE, 51-56, 2005.
- Вычислительная сложность аудита дискретных атрибутов в статистических базах данных
П. Йонссон и А. Крохин.
Журнал компьютерных и системных наук, 74 (5), 898-909, 2008. - Ограничения большинства имеют ограниченную двойственность ширины пути
В. Далмау и А. Крохин.
Европейский журнал комбинаторики, 29 (4), 821-837, 2008. - Максимизация супермодульных функций на решетках продуктов с применением к максимальному удовлетворению ограничений
А. Крохин и Б. Лароз.
Журнал SIAM по дискретной математике, 22 (1), 312-328, 2008.
Версия конференции (часть этой статьи) в CP’05, LNCS 3709, 2005, 388-402. - Ретракции на последовательно-параллельные позы.
В. Далмау, А. Крохин, Б. Ларос.
Дискретная математика, 308 (11), 2104-2114, 2008. - Сложность клаузальных ограничений над цепями
Н. Крейну, М. Герман, А. Крохин, Г. Зальцер.
Теория вычислительных систем, 42 (2), 239-255, 2008. - Заметка о супермодулярных подрешетках в конечных относительно дополняемых решетках
А. Крохин, Б. Лароз.
Крохин, Б. Лароз.
Algebra Universalis, 59 (1-2), 2008, 237-241. - Максимум H-раскрашиваемых поддиографов и оптимизация ограничений с произвольными весами
P.Йонссон и А. Крохин.
Журнал компьютерных и системных наук, 73 (5), 691-702, 2007. - Определимые задачи ретракции первого порядка для множеств и рефлексивных графов
В. Далмау, А. Крохин и Б. Ларос.
Журнал логики и вычислений, 17 (1), 31-51, 2007.
Версия конференции в LICS’04, 2004, 232-241. - Сложность выполнения мягких ограничений
Д. Коэн, М. Купер, П. Дживонс и А. Крохин.
Журнал искусственного интеллекта, 170 (11), 983-1016, 2006.
Версия конференции (части этой статьи) в CP’03, LNCS 2833, 2003, 244—258. - Аппроксимируемость трехзначного Max CSP
П. Йонссон, М. Классон и А. Крохин.
Журнал SIAM по вычислениям, 35 (6), 1329-1349, 2006. - Моноидальный интервал клонов самодуальных функций
А. Крохин и И. Г. Розенберг.
Журнал автоматов, языков и комбинаторики, 11 (2), 2006, 189-208.
- Супермодульные функции и сложность Max CSP
Д. Коэн, М.Купер, П. Дживонс и А. Крохин.
Дискретная прикладная математика, 149 (1-3), 53-72, 2005.
Версия для конференции в STACS’04, LNCS 2996, 2004, 152-163. - Сложность удовлетворения ограничений: алгебраический подход
А. Крохин, А. Булатов, П. Дживонс. Обзор
, В: Структурная теория автоматов, полугрупп и универсальная алгебра (Монреаль, 2003 г.),
НАТО Science Seiries II: математика, физика, химия, том 207, 181-213, 2005. - Классификация сложности ограничений с использованием конечных алгебр
A.Булатов, П. Дживонс и А. Крохин.
Журнал SIAM по вычислениям, 34 (3), 720-742, 2005.
Версия конференции в ICALP’00, LNCS 1853, 2000, 272-282. - Классификация сложности в рассуждении качественных временных ограничений
П. Йонссон и А. Крохин.
Журнал искусственного интеллекта, 160 (1-2), 35-51, 2004.
Версия конференции в TIME’02, 2002, 28-35. - Распознавание замороженных переменных в задачах удовлетворения ограничений
П. Йонссон и А. Крохин.
Йонссон и А. Крохин.
Теоретическая информатика, 160 (1-3), 93-113, 2004. - Максимально управляемый класс мягких ограничений
Д. Коэн, М. Купер, П. Дживонс, А. Крохин.
Журнал исследований искусственного интеллекта, 22, 2004, 1-22.
Версия конференции в IJCAI’03 2003, 209-214. - Задачи удовлетворения ограничений на интервалах и длинах
А. Крохин, П. Дживонс, П. Йонссон.
Журнал СИАМ по дискретной математике, 17 (3), 2004, 453-477.
Версия для конференций в STACS’02, LNCS 2285, 2002, 443-454. - Рассуждения о временных отношениях: трактуемые подалгебры интервальной алгебры Аллена
A.Крохин, П. Дживонс и П. Йонссон.
Журнал ACM, 50 (5), 2003, 591-640.
Версия конференции в IJCAI’01, 2001, 83-88. - Функции многозначной логики и сложность выполнения ограничений: краткий обзор
А. Крохин, А. Булатов, П. Дживонс.
в ISMVL’03, 2003, 343-351. - Решение порядковых ограничений в логарифмическом пространстве
А. Крохин и Б. Лароз.
Крохин и Б. Лароз.
в STACS’03, LNCS 2607, 2003, 379-390. - Количественные ограничения и сюръективные полиморфизмы
F.Бурнер, А. Крохин, А. Булатов, П. Дживонс.
Технический отчет PRG-RR-02-11, Оксфордский университет, 2002 г., 25 стр. - Моноидальный интервал изотонных клонов на конечной цепи
А. Крохин, Б. Лароз.
Acta Sci. Математика. (Сегед), 68 (1-2), 2002, 37-62. - Сложность языков с максимальными ограничениями
А. Булатов, А. Крохин, П. Дживонс.
в STOC’01, 2001, 667-674. - О структуре решеток клонов, II
А. Булатов, А. Крохин, К. Сафин, А. Семигродских, Э.Суханов.
Многозначная логика, 7 (5-6), 2001, 379-389. - Конгруэнции решеток клонов, II
А. Крохин. Приказ
, 18 (2), 2001, 151-159. - О клонах, моноидах преобразований и конечных булевых алгебрах
А. Крохин.
Универсальная алгебра, 46 (1-2), 2001, 231-236. - О клонах, сохраняющих рефлексивную бинарную связь
А. Крохин и Д. Швайгерт.
Крохин и Д. Швайгерт.
Acta Sci. Математика. (Сегед), 67 (3-4), 2001, 461-473. - Конгруэнции решеток клонов, I
A.Крохин и А. Семигродских.
Contributions to General Algebra, 11, Verlag Johannes Heyn, Klagenfurt, 1999, 137-150. - Максимальные клоны в моноидальных интервалах, I
А. Крохин.
Сиб. Мат. Журнал, 40 (3), 1999, 619-631. англ.перевод: Сибирский математический журнал, 40 (3), 1999, 528-538] - О структуре решетки замкнутых классов многочленов
А. Крохин, К. Сафин, Е. Суханов.
Дискретная математика, 9 (2), 1997, 24-39.[Русский; англ.пер .: Дискретная математика и приложения, 7 (2), 131-146] - Булевы решетки как интервалы в решетках клонов
А. Крохин.
Многозначная логика, 2 (3), 1997, 263-271. - О клонах, трансформационных моноидах и ассоциативных кольцах
А. Крохин.
Algebra Universalis, 37 (4), 1997, 527-540. - Моноидальные и распределительные интервалы в решетках клонов
А. Крохин.
Крохин.
Алгебра (Красноярск, 1993). Ред .: Ю. Л. Ершов и др., de Gruyter Verlag, Берлин, 1996, 153–159. - О строении решеток клонов
А. Булатов, А. Крохин, К. Сафин, Э. Суханов.
Общая алгебра и дискретная математика, ред .: К. Денеке, О. Людерс, Heldermann Verlag, Берлин, 1995, 27-34. - Моноидальные интервалы в решетках клонов
А. Крохин.
Алгебра и логика, 34 (3), 1995, 282-310. [Русский; англ.transl .: Algebra and Logic, 34 (3), 155-168]
Расширенная версия объединенных бумаг FOCS’19 и SODA’20.
Отправлено для публикации в журнале.
Версия конференции в STOC’19, 602-613, 2019. (больше подходит для первого чтения)
Отправлено для публикации в журнале.

SIAM — Книжный магазин
{{viewProduct.Код товара}} Скидка {{viewProduct.Discount}}% {{viewProduct. Rating | номер 1}}
{{viewProduct.Rating | номер 1}}
Rating | номер 1}}
{{viewProduct.Rating | номер 1}}
{{viewUmbrellSelectProduct.Rating | номер 1}}
ОГРАНИЧЕННОЕ КОЛИЧЕСТВО НА ЗАКАЗЕ ПРЕДВАРИТЕЛЬНЫЙ ЗАКАЗ ДОСТУПЕН НА ЗАКАЗЕ ПРОДАЕТСЯ {{viewUmbrellProducts.SubProductOption01 [0] .OptionDescription}}
Выберите {{viewUmbrellProducts.SubProductOption01 [0] .OptionDescription}}
{{viewUmbrellProducts.SubProductOption02 [0] .OptionDescription}}
Выберите {{viewUmbrellProducts.SubProductOption02 [0] .OptionDescription}}
Прейскурантная цена: {{viewProduct.Цена | валюта}}
Стоимость участника: {{viewProduct.MemberPrice | валюта}}Прейскурантная цена: {{viewProduct.MinListPrice | currency}} на {{viewProduct.MaxListPrice | валюта}}
Стоимость участника: {{viewProduct.MinMemberPrice | currency}} на {{viewProduct.MaxMemberPrice | валюта}} Цена: {{viewUmbrellSelectProduct. Цена | валюта}}
Стоимость участника: {{viewUmbrellSelectProduct.MemberPrice | валюта}}
Цена | валюта}}
Стоимость участника: {{viewUmbrellSelectProduct.MemberPrice | валюта}}
Эта книга доступна для предзаказа.
Эта книга доступна для предварительного заказа.
На складе осталось меньше или равно {{viewProduct.StockAvailable}} книг.
Количество Добавить в корзину
Все скидки применяются при окончательном оформлении заказа
Эта книга доступна в виде электронной книги в GooglePlay.
Эта книга недоступна. {o (log n)} — Time Breaks ETH.
{o (log n)} — Time Breaks ETH.
1 декабря 2014 г.
Коллоквиум по CS: Боаз Барак. Доказательства алгоритмов, алгоритмы из доказательств.
1 декабря 2014 г.
Сет Петти. Рандомизированное нарушение симметрии и конструктивная локальная лемма Ловаса
24 ноября 2014 г.
Ян Вондрак. Быстрые алгоритмы оптимизации субмодульных функций
20 ноября 2014 г.
Коллоквиум по CS: Кристофер Мур. Основанные на физике алгоритмы и фазовые переходы в обнаружении сообщества.
17 ноября 2014 г.
Коллоквиум по CS: Яэль Тауман Калаи.Делегирование вычислений.
17 ноября 2014 г.
Гиллат Кол. Экспоненциальное разделение информации и коммуникации.
17 ноября 2014 г.
Обед-семинар CRCS: Бабис Цуракакис. Разработка алгоритмов для крупномасштабных наборов данных.
14 ноября 2014 г.
Ави Вигдерсон. Очки, линии и ранги расчетных матриц
13-14 ноября 2014 г.
Альфорс Лекции: Ави Вигдерсон. Случайность / постоянство и детерминантность: неидентичные близнецы
10 ноября 2014 г.
Коллоквиум CS: Мадху Судан.Общение в условиях неопределенности.
10 ноября 2014 г.
Крис Муско. Разрезание графа в потоковой модели.
6 ноября 2014 г.
Коллоквиум по CS: Майкл Кернс. Игры, сети и люди.
3 ноября 2014 г.
Пранджал Авасти. Изучение полупространств с шумом.
30 октября 2014 г.
Коллоквиум по CS: Ричард Баранюк. Изучение почти изометрических линейных вложений.
27 октября 2014 г.
Софья Расходникова. Постоянное время тестирования и алгоритмов обучения свойств изображения.
24 октября 2014 г.
Семинар EconCS: Рафаэль Фронгилло. Динамика рисков в торговых сетях.
16 октября 2014 г.
Коллоквиум по CS: Анкур Моитра. Новые алгоритмы факторизации неотрицательной матрицы и не только.
9 октября 2014 г.
Коллоквиум по CS: Рон Феджин. Применение теории к практике (и практики к теории).
8 октября 2014 г.
Коллоквиум CMSA: Салил Вадхан. Вычислительная сложность конфиденциальности данных.
6 октября 2014 г.
Аарон Сидфорд.Методы поиска пути для линейного программирования.
29 сентября 2014 г.
Коллоквиум по прикладной математике: Рэйчел Уорд. Уменьшение линейной размерности с помощью случайных проекций.
29 сентября 2014 г.
Эли Гафни. Возвращение к проблеме скоординированной атаки.
29 сентября 2014 г.
Обед-семинар CRCS: Or Sheffet. Утилитарные модели потери конфиденциальности и социального выбора.
22 сентября 2014 г.
Эмануэле Виола. Местные скидки.
15 сентября 2014 г.
Обед-семинар CRCS: Итаи Ишлаги.Несбалансированные совпадающие рынки.
12 сентября 2014 г.
Семинар EconCS: Моше Бабайофф. Bertrand Networks.
16 мая 2014 г.
Сьорд Дирксен. Единый подход к уменьшению размерности с помощью субгауссовских матриц.
6 мая 2014 г., вторник
Венкат Гурусвами. Полярные коды: надежная связь с полиномиальным масштабированием сложности в промежутке до пропускной способности Шеннона.-reshenie-137.jpg)
Вторник, 22 апреля 2014 г.
Or Sheffet. Метод энтропии, который скоро будет.
8 апреля 2014 г.
Raef Bassily.Каналы причинного стирания.
3 апреля 2014 г.
Коллоквиум по CS: Давид Соловейчик. Инженерные интеллектуальные молекулярные системы.
25 марта 2014 г.
Николов Александр. Аппроксимация наследственной несовпадения с помощью эллипсоидов малой ширины.
24 марта 2014 г.
Обед-семинар CRCS: Дэвид Сяо. Понимание стимулов для лиц, заботящихся о конфиденциальности.
11 марта 2014 г.
Майкл Форбс. Наборы совпадений для полилинейных программ алгебраического ветвления с однократным чтением в любом порядке.
27 февраля 2014 г.
Коллоквиум по CS: Ралука Ада Попа. Создание систем, вычисляющих зашифрованные данные.
25 февраля 2014 г.
Марк Жандры. Многосторонний обмен ключами, эффективное отслеживание предателей и многое другое от обфускации неразличимости.
14 февраля 2014 г.

 Решение задач с помощью уравнений № 143-166 ↑
Решение задач с помощью уравнений № 143-166 ↑ ПРОИЗВЕДЕНИЕ ОДНОЧЛЕНА И МНОГОЧЛЕНА № 614-676 ↑
ПРОИЗВЕДЕНИЕ ОДНОЧЛЕНА И МНОГОЧЛЕНА № 614-676 ↑ Разложение на множители суммы и разности кубов № 905-917 ↑
Разложение на множители суммы и разности кубов № 905-917 ↑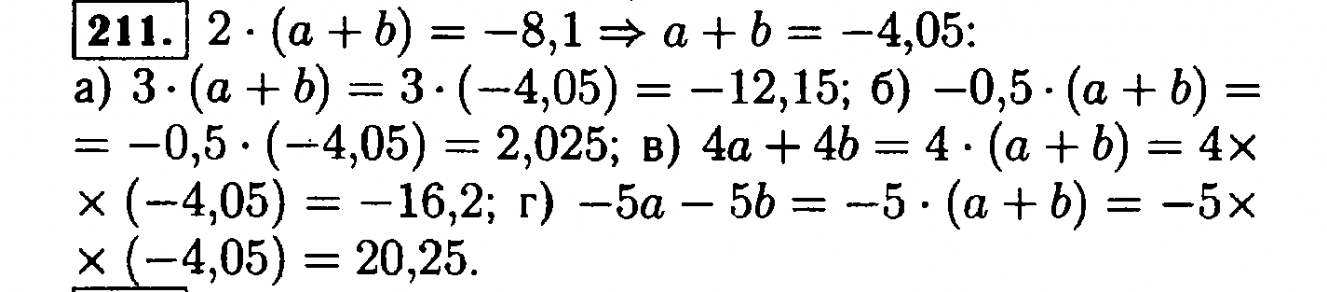
 Н. Макарычев, Н. Г. Миндюк, К. И. Нешков и др. / Под ред. Теляковского С.А. Алгебра. 7 класс;
Н. Макарычев, Н. Г. Миндюк, К. И. Нешков и др. / Под ред. Теляковского С.А. Алгебра. 7 класс; В. Ткачевой
В. Ткачевой
 Введите в строку поиска только фамилию автора и класс. Добавить книги в список П
Введите в строку поиска только фамилию автора и класс. Добавить книги в список П ГДЗ по алгебре. 12-річна програма, Бевз Г. П. Бевз В. Г. Сайт гдз-класс.рф принадлежит группе сайтов УРОКУ.НЕТ.
ГДЗ по алгебре. 12-річна програма, Бевз Г. П. Бевз В. Г. Сайт гдз-класс.рф принадлежит группе сайтов УРОКУ.НЕТ.


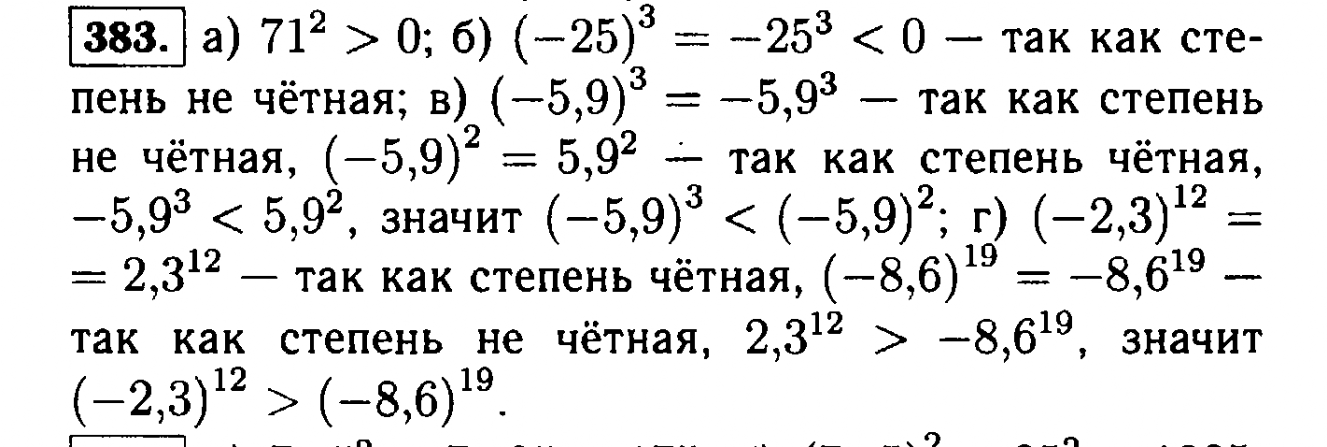 Приглашает Лейн Хемаспандра.
Приглашает Лейн Хемаспандра.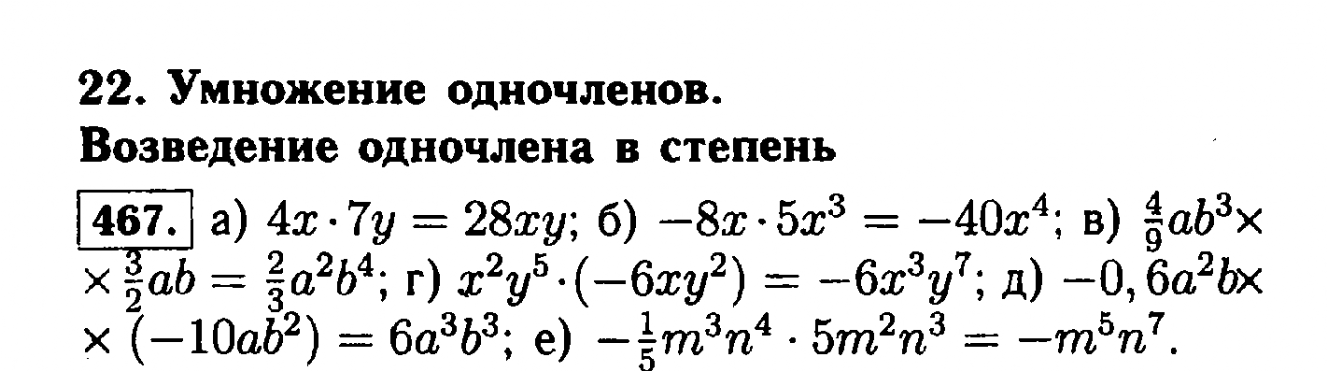 Студенческая математическая библиотека, т. 17. 2002
Студенческая математическая библиотека, т. 17. 2002 Верещагин и П. Витани.
«Колмогоровский
Структурные функции с приложением
к основам выбора модели »
IEEE Transactions по теории информации 50:12 (2004) 3265-3290.
Предварительная версия:
Proc. 47-я конференция IEEE Symp. Найденный. Comput. Наук,
2002, 751-760.
Верещагин и П. Витани.
«Колмогоровский
Структурные функции с приложением
к основам выбора модели »
IEEE Transactions по теории информации 50:12 (2004) 3265-3290.
Предварительная версия:
Proc. 47-я конференция IEEE Symp. Найденный. Comput. Наук,
2002, 751-760. Труды Математического института им. В. А. Стеклова 242 (2003) 67-85.
Предварительная версия появилась в:
Труды Computer Science Logic’02,
Конспект лекций по информатике,
2002, т. 2471, с. 74-88.
Труды Математического института им. В. А. Стеклова 242 (2003) 67-85.
Предварительная версия появилась в:
Труды Computer Science Logic’02,
Конспект лекций по информатике,
2002, т. 2471, с. 74-88. Ромащенко, А. Шен, Н. Верещагин.
«Комбинаторная интерпретация колмогоровской сложности»,
Теоретическая информатика 271 (2002) 111—123.
Предварительная версия в:
Proc. 15-й ежегодной конференции IEEE по вычислительной сложности,
Флоренция, июль 2000 г., стр. 131-137.
Ромащенко, А. Шен, Н. Верещагин.
«Комбинаторная интерпретация колмогоровской сложности»,
Теоретическая информатика 271 (2002) 111—123.
Предварительная версия в:
Proc. 15-й ежегодной конференции IEEE по вычислительной сложности,
Флоренция, июль 2000 г., стр. 131-137. Дюран, А. Шен, Н. Верещагин.
«Описательная сложность вычислимых последовательностей».
Теоретическая информатика 171 (2001), стр. 47-58;
Предварительная версия: Учеб. 16-й Ann. Symp. на
Теоретические аспекты компьютерных наук, Трир, Германия, март
1999, LNCS 1563, с. 153—162.
Дюран, А. Шен, Н. Верещагин.
«Описательная сложность вычислимых последовательностей».
Теоретическая информатика 171 (2001), стр. 47-58;
Предварительная версия: Учеб. 16-й Ann. Symp. на
Теоретические аспекты компьютерных наук, Трир, Германия, март
1999, LNCS 1563, с. 153—162. Верещагин.
«Логические операции и колмогоровская сложность II».
Proc. 16-го ежегодного IEEE
Конференция по вычислительной сложности, Чикаго, июнь 2001 г., стр. 256—265.
Верещагин.
«Логические операции и колмогоровская сложность II».
Proc. 16-го ежегодного IEEE
Конференция по вычислительной сложности, Чикаго, июнь 2001 г., стр. 256—265.
 явление.
явление.
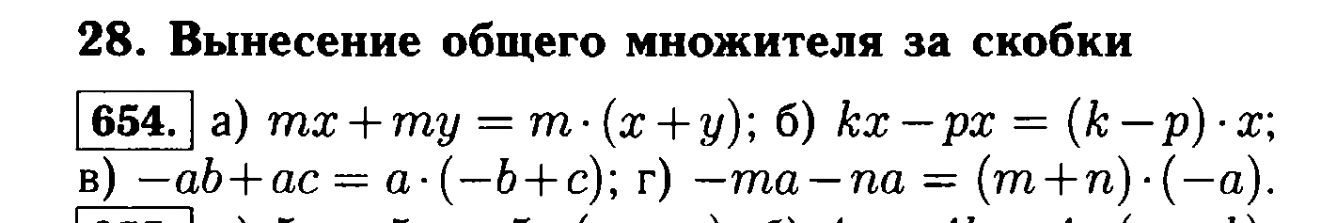 Уилсон, Квазислучайные графы , Combinatorica , 9 (4),
1989, 345-362.
Уилсон, Квазислучайные графы , Combinatorica , 9 (4),
1989, 345-362. Константы удвоения: [1, Глава 2.2].
Константы удвоения: [1, Глава 2.2]. 26] (случай без кручения).
26] (случай без кручения). n $ близко следует изложению в [6].
n $ близко следует изложению в [6]. 40]. Обратный
теоремы (без доказательств): в $ SL_2 (\ mathbb C) $ [14] и в свободной группе [8]. Теорема Семереди
и его различные доказательства представлены в двух разделах [1]: Разделе 11 и Разделе 12. Пример Беренда:
[1, упражнение 10.1.4]. Лемма об удалении треугольника: [1, лемма 10.46]. Наши прямые (т.е. в обход [1,
Предложение 10.45]) сведение случая $ k = 3 $ к этому утверждению кажется частью фольклора. Наши
определение $ \ epsilon $ -регулярных (известных в определенных кругах как квазислучайных ) двудольных графов является
немного отличается от [1, определение 10.41], но эквивалентен последнему с точностью до полиномиального увеличения
$ \ epsilon $. Последней статьей о неравенстве Гротендика является [15]. Лемма Семереди о регулярности (без
доказательство): [1, лемма 10.42], доказательство можно найти в любой продвинутой книге по теории графов. Доказательство
Лемма об удалении треугольника (а также большая часть следующего материала) взята из основополагающей статьи [16].
40]. Обратный
теоремы (без доказательств): в $ SL_2 (\ mathbb C) $ [14] и в свободной группе [8]. Теорема Семереди
и его различные доказательства представлены в двух разделах [1]: Разделе 11 и Разделе 12. Пример Беренда:
[1, упражнение 10.1.4]. Лемма об удалении треугольника: [1, лемма 10.46]. Наши прямые (т.е. в обход [1,
Предложение 10.45]) сведение случая $ k = 3 $ к этому утверждению кажется частью фольклора. Наши
определение $ \ epsilon $ -регулярных (известных в определенных кругах как квазислучайных ) двудольных графов является
немного отличается от [1, определение 10.41], но эквивалентен последнему с точностью до полиномиального увеличения
$ \ epsilon $. Последней статьей о неравенстве Гротендика является [15]. Лемма Семереди о регулярности (без
доказательство): [1, лемма 10.42], доказательство можно найти в любой продвинутой книге по теории графов. Доказательство
Лемма об удалении треугольника (а также большая часть следующего материала) взята из основополагающей статьи [16]. Больше
недавнее доказательство с несколько лучшей оценкой: [17]. Теорема индуцированных паросочетаний: [1, предложение 10.45].
(6,3) -теорема: [1, Упражнение 10.6.2].
Больше
недавнее доказательство с несколько лучшей оценкой: [17]. Теорема индуцированных паросочетаний: [1, предложение 10.45].
(6,3) -теорема: [1, Упражнение 10.6.2]. Также Википедию.
статья и цитируемая в ней литература. Обзор границ полиномиальной корреляции: [23].
Квазислучайность: [24].
Также Википедию.
статья и цитируемая в ней литература. Обзор границ полиномиальной корреляции: [23].
Квазислучайность: [24].
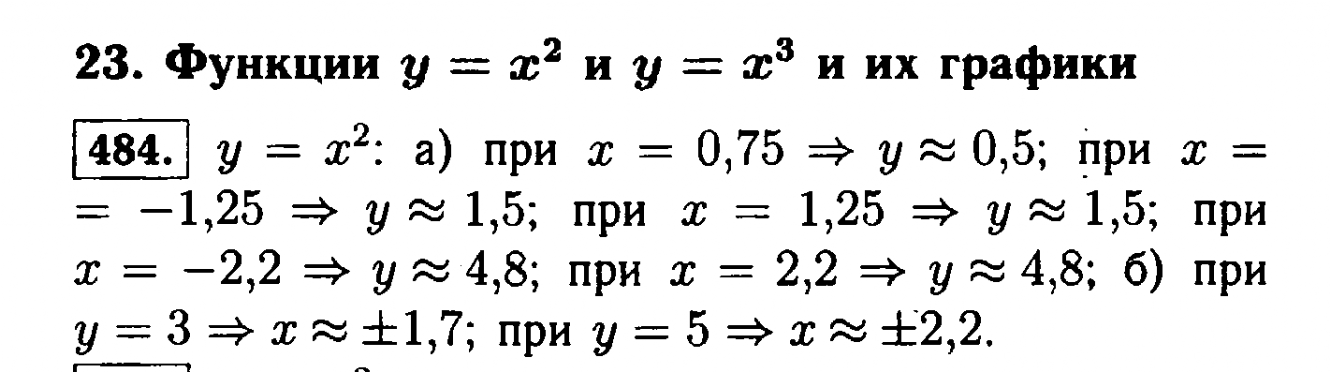
 Федер, П. Хелл, П. Йонссон, А. Крохин, Г. Норд.
Федер, П. Хелл, П. Йонссон, А. Крохин, Г. Норд. .png)
 Крохин, Б. Лароз.
Крохин, Б. Лароз. 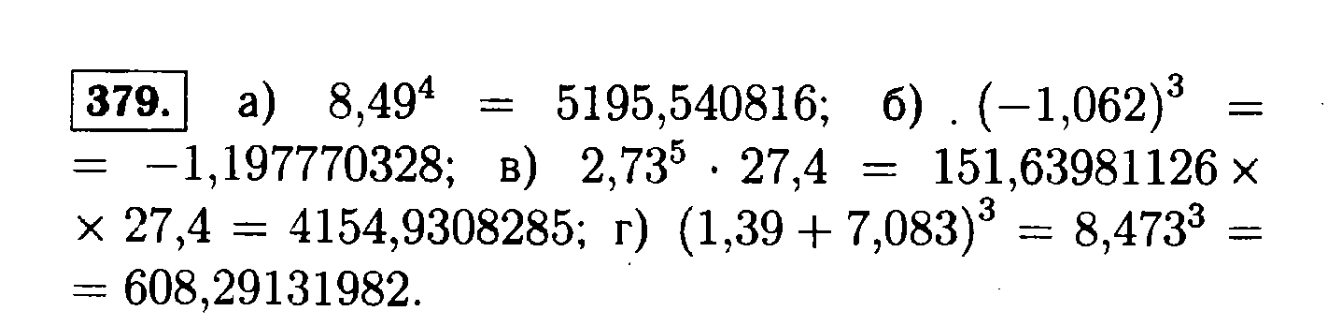
 Йонссон и А. Крохин.
Йонссон и А. Крохин.  Крохин и Б. Лароз.
Крохин и Б. Лароз.  Крохин и Д. Швайгерт.
Крохин и Д. Швайгерт.  Крохин.
Крохин.