135 – Джозеф Гуаданьи
Канал доктора Г. на YouTube
Математический факультет – Политика и расписание занятий по математике 135
Математический факультет – Обзор курса математики 135
Учебник: Исчисление, ранние трансцендентальные, третье издание. Бриггс, Кокран, Гилетт и Шульц. Pearson, 2018.
Чтобы преуспеть в математике 135, вам нужна эффективная стратегия обучения. Мы рекомендуем следующий общий цикл обучения по каждой теме:
- Просмотрите список воспроизведения видео перед лекцией по следующей теме.
- Посещайте лекции и делайте заметки.
- Начните с домашней работы MyLab по этой теме, стремясь закончить ее до следующей лекции.
- Обратитесь к инструктору за помощью с любыми особенно сложными домашними заданиями. Мы рекомендуем посещать рабочие часы с конкретными вопросами.
- Закончите домашнее задание по этой теме перед следующей лекцией.
- Проработайте практический лист по этой теме.
- Повторите шаги с 1 по 6 для каждой темы экзамена.
- После того, как ваш инструктор закончил изучение тем экзамена, а вы выполнили последнее домашнее задание, проработайте предыдущие экзамены.
Ваша основная цель — шаг №8 (проработка предыдущих экзаменов). Но чтобы достичь этого и сделать это время эффективным, вы должны пройти шаги №1–№7.
На этой странице вы найдете следующие ресурсы:
- Списки воспроизведения видео перед лекцией (организованные по отдельным темам)
- Лекционные видеоролики (организованные по отдельным темам)
- Конспект лекций (один основной документ по всем темам)
- Практические рабочие листы (один основной документ по всем темам с решениями)
- Предыдущие промежуточные экзамены (один основной документ по всем темам с решениями)
- Предыдущие выпускные экзамены (один основной документ по всем темам с решениями)
Основные ресурсы
Все примечания к лекциям по теме
Примечания к дополнительным темам
Раздел 2.
6: Теорема промежуточного значенияРазделы 3.1/3.2: Среднее значение теоремы
Разделы 5.1/5.2: Сумма Riemann — Проработанный пример
ВСЕ рабочие листы по темам… Решения
Упражнения для дополнительной задачи
Сложные упражнения для повторения
Обратите внимание, что формат курса, включая количество экзаменов и темы, затрагиваемые каждым из них, быстро изменился за последние несколько лет. Экзамены в предыдущем семестре могут существенно отличаться от экзаменов в текущем семестре.
ВСЕ предыдущие промежуточные экзамены (с осени 2017 г.
)… РешенияSELECTED Предыдущие выпускные экзамены… Решения
Обратите внимание, что каждый лектор по математике 135 готовит свои собственные тесты, и они основаны на конкретном расписании их лекций. Так что ваши викторины могут существенно отличаться от тех, что здесь, как по сложности, так и по охвату темы.
ИЗБРАННЫЕ Тесты… Решения
6: Теорема промежуточного значения
)… РешенияВидео по теме
01:640:356 — Теория чисел
Общие сведения (описание в каталоге)
Приоритеты натуральных чисел, сравнения, дизофантиновые уравнения и элементарные арифметические функции.
Необходимое условие: CALC3 и Math 300 или разрешение отдела.
Math 300 (Математическое мышление) или очень хороший опыт математических доказательств.
Учащиеся с хорошими результатами в своих курсах математики, которые не прошли курс Math 300, но хотят пройти курс теории чисел, должны запросить отмену предварительного условия у главного консультанта ([email protected]).
- Предлагаемый учебник
- Предлагаемая программа
- разделов, преподаваемых в этом семестре
- Предыдущие семестры
Предлагаемый учебник
Преподаватели в 356 иногда используют другой текст и следуют программе, отличной от показанной.
Учебник: Текущий учебник см. на странице со списком основных учебников. Однако все, что размещено на странице в текущем семестре, заменяет эту программу.
| Номер лекции | Раздел в тексте | Предлагаемые упражнения |
|---|---|---|
| 1 | 1,2 | 8, 12, 20, 30. |
| 1,3 | 6, 8. | |
| 2 | 1,4 | 4, 8, 20, 22. |
| 3 | 2,1 | 2, 6, 12, 28. |
| 4 | 2,2 | 4, 6, 12. |
| 2,3 | 2, 4, 14, 18. | |
| 5 | 3.1 | 2, 4, 6, 8, 12, 14, 16, 20. |
| 6 | 3,2 | 4, 6, 8, 14, 22. |
| 3,3 | 2, 8, 9, 10, 14, 15. | |
| 7 | 3,4 | 2, 4, 8, 10, 14, 15, 16. |
| 8 | 3,6 | 2, 4, 8, 14. |
| 9 | 4.1 | 4, 5, 10, 12, 14, 16, 22, 28. |
| 10 | 4.2: | 2, 6, 8, 10, 16, 18. |
| 11 | 4,3 | 2, 4, 6, 8, 34. |
| 12 | 4,4 | 2, 4, 6, 8, 10. |
| 4,6 | 2. | |
| 13 | экзамен | |
| опционально | 5,1 | 2, 4, 12, 24. |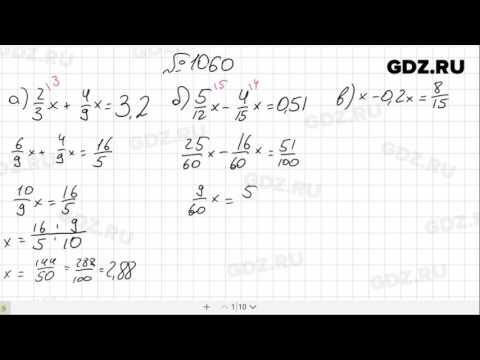
| 5,2 | 2, 6. | |
| 5,5 | 2, 6, 8, 12, 14, 16. | |
| 6,1 | 2, 6, 8, 10, 14, 20. | |
| 6,2 | 8, 12, 16д. | |
| 15 | 6,3 | 1(все), 2, 4, 16, 18. |
| 16 | 7,1 | 2(все), 4(все), 6, 8, 12, 14, 34. |
| 17 | 7,2 | 2(все), 4, 6с, 8, 10, 12. |
| 18 | 7,3 | 4, 8, 10, 14. |
| 7,4 | 2 (все), 6, 8, 10, 13, 14. | |
| 19 | 11,1 | 2, 4, 5, 11, 12, 14. |
| 20 | 11,2 | 1(все), 2, 4. |
| 21 | 11,3 | 1(все), 2, 5, 6. |
| 22 | 9,1 | 2(все), 4(все), 6, 8, 14. |
| 9,2 | 1(все), 2(все), 4, 6, 8, 12. | |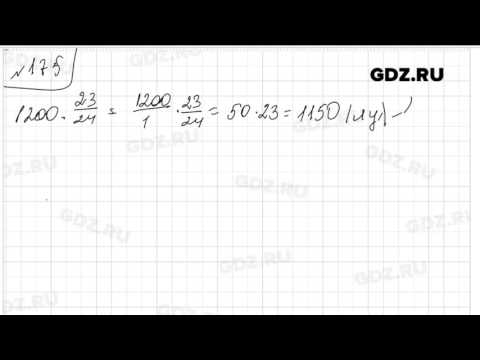
| 23 | 9,3 | 2, 4(все), 6(все), 8(все), 10. |
| 24 | 12,1 | 1(все), 6(все), 8, 9, 12. |
Один промежуточный экзамен и выпускной экзамен подходят для этого курса. Выбор необязательных тем в середине таблицы может быть вставлен, если предыдущий материал будет пройден до того, как можно будет сдать экзамен. Темы, перечисленные для лекции 14, должны быть представлены , а не до промежуточного экзамена. Эта программа предусматривает две недели в конце курса для изучения дополнительных тем. Такие темы должны быть продиктованы интересами класса.
Расписание секций:
Предыдущие семестры
- Осень 2016 г.: проф. Таннелл
- Осень 2013: Дорон Зейлбергер
- Лето 2011: Джеррольд Таннелл
- Осень 2010: Андерс Бух
- Лето 2010: Том Тиррелл
- Осень 2009 г.: проф. Вайбель
- Лето 2009 г.
