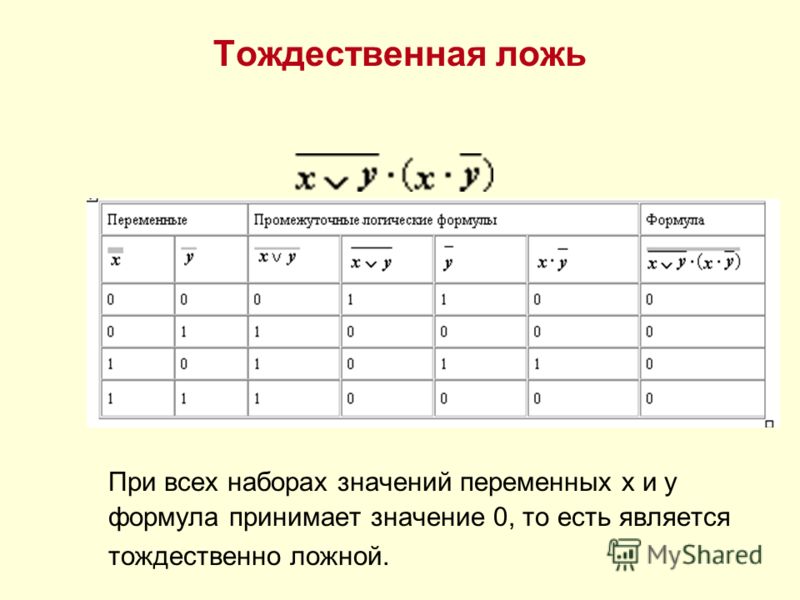
Тождественно равные выражения: определение, примеры
После того, как мы разобрались с понятием тождеств, можно переходить к изучению тождественно равных выражений. Цель данной статьи – объяснить, что это такое, и показать на примерах, какие выражения будут тождественно равными другим.
Тождественно равные выражения: определение
Понятие тождественно равных выражений обычно изучается вместе с самим понятием тождества в рамках школьного курса алгебры. Приведем основное определение, взятое из одного учебника:
Определение 1Тождественно равными друг другу будут такие выражения, значения которых будут одинаковы при любых возможных значениях переменных, входящих в их состав.
Также тождественно равными считаются такие числовые выражения, которым будут отвечать одни и те же значения.
Это достаточно широкое определение, которое будет верным для всех целых выражений, смысл которых при изменении значений переменных не меняется. Однако позже возникает необходимость уточнения данного определения, поскольку помимо целых существуют и другие виды выражений, которые не будут иметь смысла при определенных переменных. Отсюда возникает понятие допустимости и недопустимости тех или иных значений переменных, а также необходимость определять область допустимых значений. Сформулируем уточненное определение.
Отсюда возникает понятие допустимости и недопустимости тех или иных значений переменных, а также необходимость определять область допустимых значений. Сформулируем уточненное определение.
Тождественно равные выражения – это те выражения, значения которых равны друг другу при любых допустимых значениях переменных, входящих в их состав. Числовые выражения будут тождественно равными друг другу при условии одинаковых значений.
Фраза «при любых допустимых значениях переменных» указывает на все те значения переменных, при которых оба выражения будут иметь смысл. Это положение мы объясним позже, когда будем приводить примеры тождественно равных выражений.
Можно указать еще и такое определение:
Определение 3Тождественно равными выражениями называются выражения, расположенные в одном тождестве с левой и правой стороны.
Примеры выражений, тождественно равных друг другу
Используя определения, данные выше, рассмотрим несколько примеров таких выражений.
Для начала возьмем числовые выражения.
Пример 1 Так, 2+4 и 4+2 будут тождественно равными друг другу, поскольку их результаты будут равны (6 и 6). Пример 2Точно так же тождественно равны выражения 3 и 30:10, (22)3 и 26(для вычисления значения последнего выражений нужно знать свойства степени).
Пример 3А вот выражения 4-2 и 9-1 равными не будут, поскольку их значения разные.
Перейдем к примерам буквенных выражений. Тождественно равными будут a+b и b+a, причем от значений переменных это не зависит (равенство выражений в данном случае определяется переместительным свойством сложения).
Пример 4Например, если a будет равно 4, а b – 5, то результаты все равно будут одинаковы.
Еще один пример тождественно равных выражений с буквами – 0·x·y·z и 0. Какими бы ни были значения переменных в этом случае, будучи умноженными на 0, они дадут 0. Неравные выражения – 6·x и 8·x, поскольку они не будут равны при любом x.
В том случае, если области допустимых значений переменных будут совпадать, например, в выражениях a+6 и 6+a или a·b·0 и 0, или x4 и x, и значения самих выражений будут равны при любых переменных, то такие выражения считаются тождественно равными.
Но область допустимого значения в одном выражении может отличаться от области другого.
Пример 5Например, возьмем два выражения: x−1 и x-1·xx. Для первого из них областью допустимых значений x будет все множество действительных чисел, а для второго – множество всех действующих чисел, за исключением нуля, ведь тогда мы получим 0 в знаменателе, а такое деление не определено. У этих двух выражений есть общая область значений, образованная пересечением двух отдельных областей. Можно сделать вывод, что оба выражения x-1·xx и x−1 будут иметь смысл при любых действительных значениях переменных, за исключением 0.
Основное свойство дроби также позволяет нам заключить, что x-1·xx и x−1 будут равными при любом x, которое не является 0. Значит, на общей области допустимых значений эти выражения будут тождественно равны друг другу, а при любом действительном x говорить о тождественном равенстве нельзя.
Если мы заменяем одно выражение на другое, которое является тождественно равным ему, то этот процесс называется тождественным преобразованием. Это понятие очень важно, и подробно о нем мы поговорим в отдельном материале.
Решение задач
от 1 дня / от 150 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Автор: Ирина Мальцевская
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Тождественно равные выражения. Тождества / Алгебра / Справочник по математике 5-9 класс
- Главная
- Справочники
- Справочник по математике 5-9 класс
- Алгебра
- Тождественно равные выражения. Тождества
| Два выражения, значения которых равны при любых значениях переменных, называют тождественно равными. |
Рассмотрим две пары выражений:
1) и Найдем их значения при Мы получили один и тот же результат. | 2) Найдем их значения при Мы получили один и тот же результат. Однако, можно указать такие значения и , при которых значения этих выражений не будут иметь равные значения. Например, если , то Мы получили разные результаты. |
Следовательно, выражения и являются тождественно равными, а выражения не являются тождественно равными.
| Равенство, верное при любых значениях переменных, называется тождеством. |
Равенство — тождество, т.к. оно верно при любых значениях и .
Также к тождествам можно отнести равенства, выражающие свойства сложения и умножения чисел:
Можно привести и другие примеры тождеств:
Тождествами считают и верные числовые равенства.
Очень часто при вычислении значений выражений, легче сначала упростить имеющееся выражение, а затем выполнять вычисления.
| Замену одного выражения другим, тождественно равным ему выражением, называют тождественным преобразованием или просто преобразованием выражения. |
К тождественным преобразованиям можно отнести приведение подобных слагаемых и раскрытие скобок.
Примеры:
1) , мы преобразовали выражение в выражение .
2) , мы преобразовали выражение в выражение .
Для того, чтобы доказать, что данное равенство является тождеством (или доказать тождество), используют следующие методы: 1) тождественно преобразуют одну из частей данного 2) тождественно преобразуют каждую из частей данного равенства, получая одно и то же выражение; 3) доказывают, что разность левой и правой частей данного равенства тождественно равна нулю. |
Также, чтобы доказать, что равенство не является тождеством, достаточно привести контрпример, т.е. указать такое значение переменной (или переменных, если их несколько), при котором данное равенство не выполняется.
Пример: Докажите, что равенство не является тождеством.
Решение: Приведем контрпример. Если , то
, следовательно, равенство не является тождеством.
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Введение в алгебру
Линейное уравнение с одной переменной
Решение задач с помощью уравнений
Степень с натуральным показателем
Свойства степени с натуральным показателем
Одночлены
Многочлены
Сложение и вычитание многочленов
Умножение одночлена на многочлен
Умножение многочлена на многочлен
Разложение многочленов на множители
Формулы сокращенного умножения
Функции
Системы линейных уравнений с двумя переменными
Алгебра
Правило встречается в следующих упражнениях:
7 класс
Номер 133, Мерзляк, Полонский, Якир, Учебник
Номер 142, Мерзляк, Полонский, Якир, Учебник
Номер 295, Мерзляк, Полонский, Якир, Учебник
Номер 302, Мерзляк, Полонский, Якир, Учебник
Номер 336, Мерзляк, Полонский, Якир, Учебник
Номер 412, Мерзляк, Полонский, Якир, Учебник
Номер 420, Мерзляк, Полонский, Якир, Учебник
Номер 421, Мерзляк, Полонский, Якир, Учебник
Номер 675, Мерзляк, Полонский, Якир, Учебник
Номер 948, Мерзляк, Полонский, Якир, Учебник
Тождества.
 Тождественные преобразования выражений. (7 класс)
Тождественные преобразования выражений. (7 класс)Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
1. Тождества. Тождественные преобразования выражений.
7 класс.2. Найдем значение выражений при х=5 и у=4
3(х+у)=3(5+4)=3*9=273х+3у=3*5+3*4=27
Найдем значение выражений
при х=6 и у=5
3(х+у)=3(6+5)=3*11=33
3х+3у=3*6+3*5=33
3. ВЫВОД:
Мы получили один и тот же результат.Из распределительного свойства
следует, что вообще при любых
значениях переменных значения
выражений 3(х+у) и 3х+3у равны.

3(х+у) = 3х+3у
4. Рассмотрим теперь выражения 2х+у и 2ху.
при х=1 и у=2 они принимают равныезначения:
2х+у=2*1+2=4
2ху=2*1*2=4
при х=3, у=4 значения выражений
разные
2х+у=2*3+4=10
2ху=2*3*4=24
5. ВЫВОД:
Выражения 3(х+у) и 3х+3у являютсятождественно равными, а выражения
2х+у и 2ху не являются тождественно
равными.
Определение:
Два выражения, значения которых равны
при любых значениях переменных,
называются тождественно равными.
6. ТОЖДЕСТВО
Равенство 3(х+у) и 3х+3у верно прилюбых значениях х и у. Такие равенства
называются тождествами.
Определение: Равенство, верное при
любых значениях переменных,
называется тождеством.
Тождествами считают и верные числовые
равенства. С тождествами мы уже
встречались.
617 238 238 617
38 150 173 38 150 38 173
315 961 961 315
8. Тождествами являются равенства, выражающие основные свойства действий над числами.
 a+b=b+a
a+b=b+aab = ba
(a + b) + c = a + (b + c)
(ab)c = a(bc)
a(b + c) = ab + ac
9. Можно привести и другие примеры тождеств:
а+0=аа*1=а
а + (-а) = 0
а * (-b) = — ab
а-b = a + (-b)
(-a) * (-b) = ab
• Замену одного
выражения другим,
тождественно
равным ему
выражением,
называют
тождественным
преобразованием
или просто
преобразованием
выражения.
10. Запомним:
• ВЫРАЖЕНИЯ, СООТВЕТСВЕННЫЕЗНАЧЕНИЯ КОТОРЫХ РАВНЫ ПРИ ЛЮБЫХ
ДОПУСТИМЫХ ЗНАЧЕНИЯХ ПЕРЕМЕННЫХ,
НАЗЫВАЮТСЯ
ТОЖДЕСТВЕННО РАВНЫМИ.
Например: (a²)³ и a6
ab∙(-a²b) и –a³b²
• ЗАМЕНУ ОДНОГО ВЫРАЖЕНИЯ ДРУГИМ,
ТОЖДЕСТВЕННО РАВНЫМ ЕМУ,
НАЗЫВАЮТ ТОЖДЕСТВЕННЫМ
ПРЕОБРАЗОВАНИЕМ
11. Запиши:
Способы доказательстватождеств:
1. Преобразование левой части
тождества так, чтобы получилась её
правая часть
(если после преобразования левой
части, выражение получится как в
правой части , то данное выражение
является тождеством)
12.
 Проверьте, данное выражение – тождество?a(b x) x(a b) b(a x)
Проверьте, данное выражение – тождество?a(b x) x(a b) b(a x)13. Решение:
Преобразуем левую частьравенства:
а(в — х) + х(а + в) =
= ав – ах + ах + хв =
= ав + хв = в(а + х)
14. Вывод:
В результате тождественногопреобразования левой части
равенства, мы получили его
правую часть и тем самым
доказали,
что данное равенство является
тождеством.
15. В теорию (способы доказательства тождеств):
2. Преобразование правой частитождества так, чтобы получилась её
левая часть
16. Проверьте, данное выражение – тождество?
a 7a 10 (a 2)(a 5)2
17. Решение:
Преобразуем правую частьравенства
(а+2)(а+5)=
= а² + 5а + 2а+ + 10 =
= а² + 7а + 10
18. Вывод:
В результате тождественногопреобразования правой части
равенства, мы получили его
левую часть и тем самым
доказали, что данное равенство
является тождеством.
19. В теорию (способы доказательства тождеств):
3. Преобразование обеих частей
Преобразование обеих частейтождества…..(должны получится
одинаковые выражения)
20. Докажите тождество:
16 (a 3)( a 2) 4 (6 a)( a 1)21. Решение:
Упростим обе части равенства1)16 (a 3)( a 2) 16 (a 2a 3a 6)
2
16 a 5a 6 a 5a 10.
2
2
2)4 (6 a)( a 1) 4 (6a 6 a a)
2
4 5a a 6 a 5a 10.
2
2
22. Вывод:
Так как левая и правая частиданного равенства равны одному и
тому же выражению, то они
тождественно равны между собой.
Значит исходное равенство –
тождество.
23. В теорию (способы доказательства тождеств):
4. Найти разность между правой и левойчастями выражения. (если эта разность
равна нулю, то данное выражение тождество)
24. Докажите тождество:
(m-a)(m-b) = m²- (a+b)m +ab
25. Решение: (найдем разность между левой и правой частями выражения)
(m-a)(m-b) – [m² — (a+b)m + ab] ==m² — mb – ma + ab — [m² — am – bm + ab ]
= m² — mb – ma + ab — m² + am + bm — ab =
=0
26.
 Вывод:Так как разность между
Вывод:Так как разность междулевой и правой частями
выражения равна нулю,
то данное выражения
является
тождеством
27. Работаем по задачнику:
№ 36.6 (а) — № 36.10 (а)English Русский Правила
Урок по математике в 7 классе «Тождества»
«Тождества. Тождественные преобразования выражений».
Цели урока
Образовательные:
·ознакомить и первично закрепить понятия «тождественно равные выражения», «тождество», «тождественные преобразования»;
·рассмотреть способы доказательства тождеств, способствовать выработке навыков доказательства тождеств;
·проверить усвоение учащимися пройденного материала, сформировывать умения применения изученного для восприятия нового.
Развивающая: развивать мышление, речь учащихся.
Воспитательная: воспитывать трудолюбие, аккуратность, правильность записи решения упражнений.
Тип урока: изучение нового материала
Оборудование: проектор, презентация, доска, учебник, рабочая тетрадь.
План урока
1.Организационный момент (нацелить учащихся на урок)
2.Проверка домашнего задания (коррекция ошибок)
3.Устные упражнения
4.Изучение нового материала (Ознакомление и первичное закрепление понятий «тождество», «тождественные преобразования»).
5.Тренировочные упражнения (Формирование понятий «тождество», «тождественные преобразования»).
6.Подведение итогов урока (Обобщить теоретические сведения, полученные на уроке).
7.Сообщение домашнего задания (Разъяснить содержание домашнего задания)
Ход урока
I. Организационный момент.
Проверка домашнего задания.
Вопросы по домашнему заданию.
Разбор решения у доски.
Математика нужна
Без нее никак нельзя
Учим, учим мы, друзья,
Что же помним мы с утра?
II.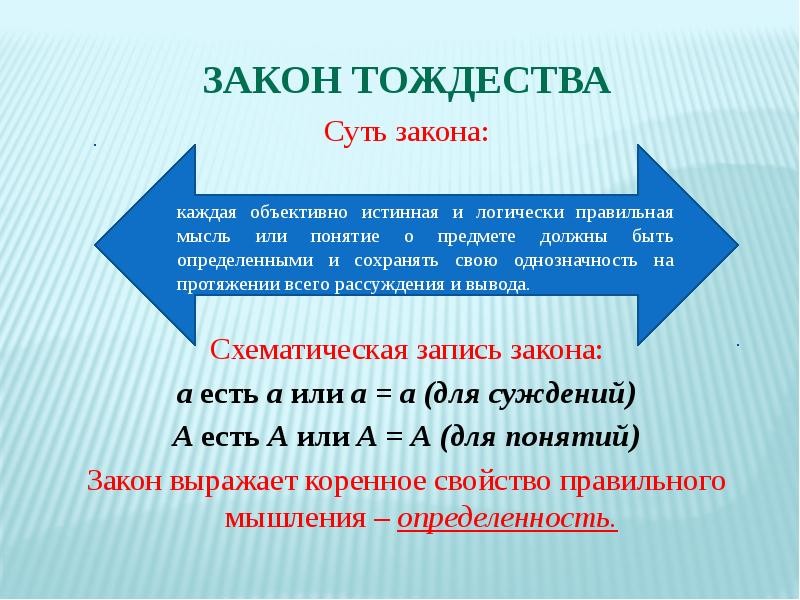 Устные упражнения.
Устные упражнения.
Сделаем разминку.
1.Результат сложения. (Сумма)
2.Сколько цифр вы знаете? (Десять)
3.Сотая часть числа. ( Процент)
4.Результат деления? (Частное)
5.Наименьшее натуральное число? (1)
6.Можно ли при делении натуральных чисел получить ноль? (нет)
7.Чему равна сумма чисел от -200 до 200? (0)
8.Назовите наибольшее целое отрицательное число. (-1)
9.На какое число нельзя делить? (0)
10.Результат умножения? (Произведение)
11.Наибольшее двузначное число? (99)
12.Чему равно произведение от -200 до 200? (0)
13.Результат вычитания. (Разность)
14.Сколько граммов в килограмме? (1000)
15.Переместительное свойство сложения. (От перестановки мест слагаемых сумма не изменяется)
16.Переместительное свойство умножения. (От перестановки мест множителей произведение не изменяется)
17.Сочетательное свойство сложения. (Чтобы к сумме двух чисел прибавить какое-нибудь число, можно к первому числу прибавить сумму второго и третьего)
18. Сочетательное свойство умножения. (чтобы произведение двух чисел умножить на третье число, можно первое число умножить на произведение второго и третьего)
Сочетательное свойство умножения. (чтобы произведение двух чисел умножить на третье число, можно первое число умножить на произведение второго и третьего)
19.Распределительное свойство. (Чтобы число умножить на сумму двух чисел, можно умножить это число на каждое слагаемое и сложить полученные результаты)
III. Изучение нового материала.
Учитель. (Слайд 2,3)
Найдем значение выражений при х=5 и у=4
3(х+у)=3(5+4)=3*9=27
3х+3у=3*5+3*4=27
Мы получили один и тот же результат. Из распределительного свойства следует, что вообще при любых значениях переменных значения выражений 3(х+у) и 3х+3у равны.
(Слайд 4,5)
Рассмотрим теперь выражения 2х+у и 2ху. При х=1 и у=2 они принимают равные значения:
2х+у=2*1+2=4
2ху=2*1*2=4
Однако можно указать такие значения х и у, при которых значения этих выражений не равны. Например, если х=3, у=4, то
2х+у=2*3+4=10
2ху=2*3*4=24
Определение: Два выражения, значения которых равны при любых значениях переменных, называются тождественно равными.
(Слайд 6,7)
Выражения 3(х+у) и 3х+3у являются тождественно равными, а выражения 2х+у и 2ху не являются тождественно равными.
Равенство 3(х+у) и 3х+3у верно при любых значениях х и у. Такие равенства называются тождествами.
Определение: Равенство, верное при любых значениях переменных, называется тождеством.
(Слайд 8,9)
Тождествами считают и верные числовые равенства. С тождествами мы уже встречались. Тождествами являются равенства, выражающие основные свойства действий над числами (Учащиеся комментируют каждое свойство, проговаривая его).
a + b = b + a
ab = ba
(a + b) + c = a + (b + c)
(ab)c = a(bc)
a(b + c) = ab + ac
Можно привести и другие примеры тождеств (Учащиеся комментируют каждое свойство, проговаривая его).
а + 0 = а
а * 1 = а
а + (-а) = 0
а * (-b) = — ab
a—b=a + (-b)
(-a) * (-b) = ab
Определение: Замену одного выражения другим, тождественно равным ему выражением, называют тождественным преобразованием или просто преобразованием выражения.
Учитель:
Тождественные преобразования выражений с переменными выполняются на основе свойств действий над числами.
Тождественные преобразования выражений широко применяются при вычислении значений выражений и решении других задач. Некоторые тождественные преобразования вам уде приходилось выполнять, например приведение подобных слагаемых, раскрытие скобок. Напомним правила этих преобразований:
Учащиеся:
1.(Слайд 10) Чтобы привести подобные слагаемые, надо сложить их коэффициенты и результат умножить на общую буквенную часть;
2.( Слайд 11) Если перед скобками стоит знак «плюс», то скобки можно опустить, сохранив знак каждого слагаемого, заключенного в скобки;
3.(Слайд 12) Если перед скобками стоит знак «минус», то скобки можно опустить, изменив знак каждого слагаемого, заключенного в скобки.
Учитель:
Пример 1. Приведем подобные слагаемые
5х +2х-3х=х(5+2-3)=4х
Каким правилом мы воспользовались?
Ученик:
Мы воспользовались правилом приведения подобных слагаемых. Это преобразование основано на распределительном свойстве умножения.
Это преобразование основано на распределительном свойстве умножения.
Учитель:
Пример 2. Раскроем скобки в выражении 2а + (b-3c) = 2a + b – 3c
Применили правило раскрытия скобок, перед которыми стоит знак «плюс».
На каком свойстве основано данное преобразование?
Ученик:
Проведенное преобразование основано на сочетательном свойстве сложения.
Учитель:
Пример 3. Раскроем скобки в выражении а – (4b – с) = a – 4b + c
Воспользовались правилом раскрытия скобок, перед которыми стоит знак «минус».
определение, примеры. Примеры выражений, тождественно равных друг другу
Получив представление о тождествах , логично перейти к знакомству с . В этой статье мы ответим на вопрос, что такое тождественно равные выражения, а также на примерах разберемся, какие выражения являются тождественно равными, а какие – нет.
Навигация по странице.
Что такое тождественно равные выражения?
Определение тождественно равных выражений дается параллельно с определением тождества. Это происходит на уроках алгебры в 7 классе. В учебнике по алгебре для 7 классов автора Ю. Н. Макарычев приведена такая формулировка:
Это происходит на уроках алгебры в 7 классе. В учебнике по алгебре для 7 классов автора Ю. Н. Макарычев приведена такая формулировка:
Определение.
– это выражения, значения которых равны при любых значениях входящих в них переменных. Числовые выражения, которым отвечают одинаковые значения, также называют тождественно равными.
Это определение используется вплоть до 8 класса, оно справедливо для целых выражений , так как они имеют смысл для любых значений входящих в них переменных. А в 8 классе определение тождественно равных выражений уточняется. Поясним, с чем это связано.
В 8 классе начинается изучение других видов выражений, которые, в отличие от целых выражений, при некоторых значениях переменных могут не иметь смысла. Это заставляет ввести определения допустимых и недопустимых значений переменных, а также области допустимых значений ОДЗ переменной, и как следствие — внести уточнение в определение тождественно равных выражений.
Определение.
Два выражения, значения которых равны при всех допустимых значениях входящих в них переменных, называются тождественно равными выражениями . Два числовых выражения, имеющие одинаковые значения, также называются тождественно равными.
Два числовых выражения, имеющие одинаковые значения, также называются тождественно равными.
В данном определении тождественно равных выражений стоит уточнить смысл фразы «при всех допустимых значениях входящих в них переменных». Она подразумевает все такие значения переменных, при которых одновременно имеют смысл оба тождественно равных выражения. Эту мысль разъясним в следующем пункте, рассмотрев примеры.
Определение тождественно равных выражений в учебнике Мордковича А. Г. дается немного иначе:
Определение.
Тождественно равные выражения – это выражения, стоящие в левой и правой частях тождества.
По смыслу это и предыдущее определения совпадают.
Примеры тождественно равных выражений
Введенные в предыдущем пункте определения позволяют привести примеры тождественно равных выражений .
Начнем с тождественно равных числовых выражений. Числовые выражения 1+2
и 2+1
являются тождественно равными, так как им соответствуют равные значения 3
и 3
. Также тождественно равны выражения 5
и 30:6
, как и выражения (2 2) 3
и 2 6
(значения последних выражений равны в силу ). А вот числовые выражения 3+2
и 3−2
не являются тождественно равными, так как им соответствуют значения 5
и 1
соответственно, а они не равны.
Также тождественно равны выражения 5
и 30:6
, как и выражения (2 2) 3
и 2 6
(значения последних выражений равны в силу ). А вот числовые выражения 3+2
и 3−2
не являются тождественно равными, так как им соответствуют значения 5
и 1
соответственно, а они не равны.
Теперь приведем примеры тождественно равных выражений с переменными. Таковыми являются выражения a+b и b+a . Действительно, при любых значениях переменных a и b записанные выражения принимают одинаковые значения (что следует из чисел). К примеру, при a=1 и b=2 имеем a+b=1+2=3 и b+a=2+1=3 . При любых других значениях переменных a и b мы также получим равные значения этих выражений. Выражения 0·x·y·z и 0 тоже тождественно равны при любых значениях переменных x , y и z . А вот выражения 2·x и 3·x не являются тождественно равными, так как, к примеру, при x=1 их значения не равны. Действительно, при x=1 выражение 2·x равно 2·1=2 , а выражение 3·x равно 3·1=3 .
Когда области допустимых значений переменных в выражениях совпадают, как, например, в выражениях a+1
и 1+a
, или a·b·0
и 0
, или и , и значения этих выражений равны при всех значениях переменных из этих областей, то тут все понятно – эти выражения тождественно равны при всех допустимых значениях входящих в них переменных. Так a+1≡1+a
при любых a
, выражения a·b·0
и 0
тождественно равны при любых значениях переменных a
и b
, а выражения и тождественно равны при всех x
из ; под ред. С. А. Теляковского. — 17-е изд. — М. : Просвещение, 2008. — 240 с. : ил. — ISBN 978-5-09-019315-3.
Так a+1≡1+a
при любых a
, выражения a·b·0
и 0
тождественно равны при любых значениях переменных a
и b
, а выражения и тождественно равны при всех x
из ; под ред. С. А. Теляковского. — 17-е изд. — М. : Просвещение, 2008. — 240 с. : ил. — ISBN 978-5-09-019315-3.
Обе части которого являются тождественно равными выражениями. Тождества делятся на буквенные и числовые.
Тождественные выражения
Два алгебраических выражения называются тождественными (или тождественно равными ), если при любых численных значениях букв они имеют одинаковую численную величину. Таковы, например, выражения:
Таковы, например, выражения:
x (5 + x ) и 5x + x 2
Оба представленных выражения, при любом значении x будут равны друг другу, поэтому их можно назвать тождественными или тождественно равными.
Так же тождественными можно назвать и числовые выражения, равные между собой. Например:
20 — 8 и 10 + 2
Буквенные и числовые тождества
Буквенное тождество — это равенство, которое справедливо при любых значениях входящих в него букв. Другими словами, такое равенство, у которого обе части являются тождественно равными выражениями, например:
(a + b )m = am + bm
(a + b ) 2 = a 2 + 2ab + b 2
Числовое тождество — это равенство, содержащее только числа, выраженные цифрами, у которого обе части имеют одинаковую численную величину. Например:
4 + 5 + 2 = 3 + 8
5 · (4 + 6) = 50
Тождественные преобразования выражений
Все алгебраические действия представляют собой преобразование одного алгебраического выражения в другое, тождественное первому.
При вычислении значения выражения, раскрытии скобок, вынесении общего множителя за скобки и в ряде других случаев одни выражения заменяются другими, тождественно равными им. Замену одного выражения другим, тождественно равным ему, называют тождественным преобразованием выражения или просто преобразованием выражения . Все преобразования выражений выполняются на основе свойств действий над числами.
Рассмотрим тождественное преобразование выражения на примере вынесения общего множителя за скобки:
10x — 7x + 3x = (10 — 7 + 3)x = 6x
Рассмотрим две равенства:
1. a 12 *a 3 = a 7 *a 8
Это равенство будет выполняться при любых значениях переменной а. Областью допустимых значений для того равенства будет все множество вещественных чисел.
2. a 12: a 3 = a 2 *a 7 .
Это неравенство будет выполняться для всех значений переменной а, кроме а равного нулю. Областью допустимых значений для этого неравенства будет все множество вещественных чисел, кроме нуля. 2*b) и -a 3 *b 2 ;
2*b) и -a 3 *b 2 ;
3. ((x 3 *x 8)/x) и x 10 .
Мы всегда можем заменить одно выражение любым другим выражением, тождественно равным первому. Такая замена будет являться тождественным преобразованием.
Примеры тождеств
Пример 1: являются ли тождествами следующие равенства:
1. a + 5 = 5 + a;
2. a*(-b) = -a*b;
3. 3*a*3*b = 9*a*b;
Не все представленные выше выражения будут являться тождествами. Из этих равенств тождествами являются лишь 1,2 и 3 равенства. Какие бы числа мы в них не подставили, вместо переменных а и b у нас все равно получатся верные числовые равенства.
А вот 4 равенство уже не является тождеством. Потому что не при всех допустимых значениях это равенство будет выполняться. Например, при значениях a = 5 и b = 2 получится следующий результат:
Данное равенство не верно, так как число 3 не равняется числу -3.
После того, как мы разобрались с понятием тождеств, можно переходить к изучению тождественно равных выражений. Цель данной статьи – объяснить, что это такое, и показать на примерах, какие выражения будут тождественно равными другим.
Цель данной статьи – объяснить, что это такое, и показать на примерах, какие выражения будут тождественно равными другим.
Тождественно равные выражения: определение
Понятие тождественно равных выражений обычно изучается вместе с самим понятием тождества в рамках школьного курса алгебры. Приведем основное определение, взятое из одного учебника:
Определение 1
Тождественно равными друг другу будут такие выражения, значения которых будут одинаковы при любых возможных значениях переменных, входящих в их состав.
Также тождественно равными считаются такие числовые выражения, которым будут отвечать одни и те же значения.
Это достаточно широкое определение, которое будет верным для всех целых выражений, смысл которых при изменении значений переменных не меняется. Однако позже возникает необходимость уточнения данного определения, поскольку помимо целых существуют и другие виды выражений, которые не будут иметь смысла при определенных переменных. Отсюда возникает понятие допустимости и недопустимости тех или иных значений переменных, а также необходимость определять область допустимых значений.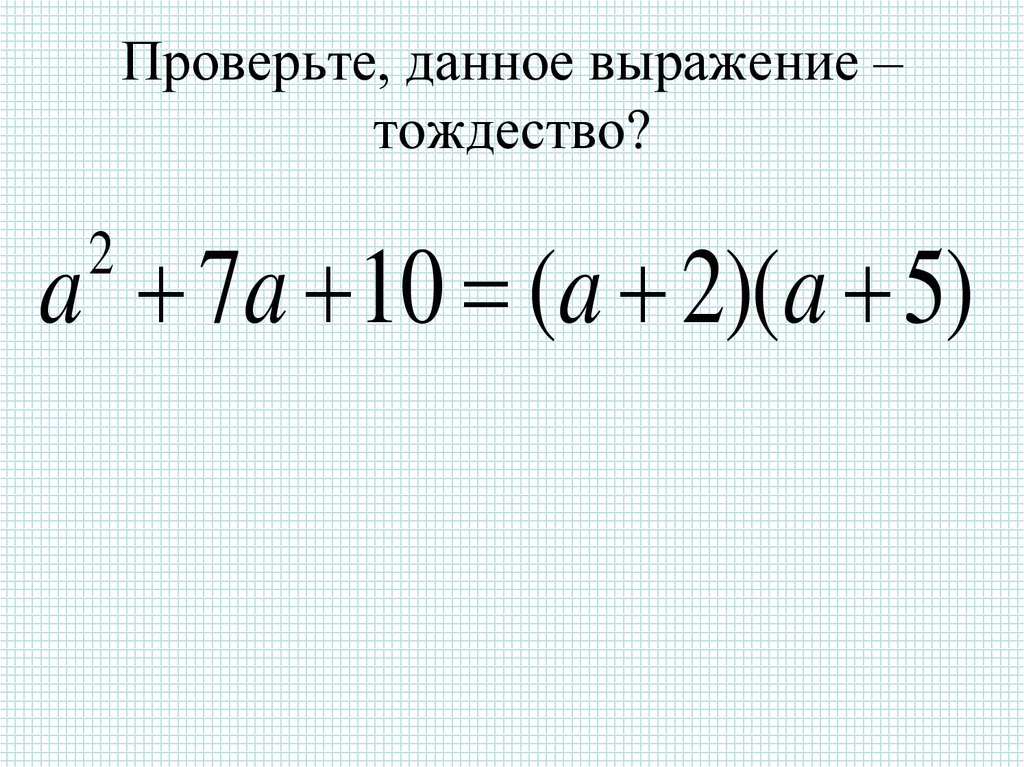 Сформулируем уточненное определение.
Сформулируем уточненное определение.
Определение 2
Тождественно равные выражения – это те выражения, значения которых равны друг другу при любых допустимых значениях переменных, входящих в их состав. Числовые выражения будут тождественно равными друг другу при условии одинаковых значений.
Фраза «при любых допустимых значениях переменных» указывает на все те значения переменных, при которых оба выражения будут иметь смысл. Это положение мы объясним позже, когда будем приводить примеры тождественно равных выражений.
Можно указать еще и такое определение:
Определение 3
Тождественно равными выражениями называются выражения, расположенные в одном тождестве с левой и правой стороны.
Примеры выражений, тождественно равных друг другу
Используя определения, данные выше, рассмотрим несколько примеров таких выражений.
Для начала возьмем числовые выражения.
Пример 1
Так, 2 + 4 и 4 + 2 будут тождественно равными друг другу, поскольку их результаты будут равны (6 и 6).
Пример 2
Точно так же тождественно равны выражения 3 и 30: 10 , (2 2) 3 и 2 6 (для вычисления значения последнего выражений нужно знать свойства степени).
Пример 3
А вот выражения 4 — 2 и 9 — 1 равными не будут, поскольку их значения разные.
Перейдем к примерам буквенных выражений. Тождественно равными будут a + b и b + a , причем от значений переменных это не зависит (равенство выражений в данном случае определяется переместительным свойством сложения).
Пример 4
Например, если a будет равно 4 , а b – 5 , то результаты все равно будут одинаковы.
Еще один пример тождественно равных выражений с буквами – 0 · x · y · z и 0 . Какими бы ни были значения переменных в этом случае, будучи умноженными на 0 , они дадут 0 . Неравные выражения – 6 · x и 8 · x , поскольку они не будут равны при любом x .
В том случае, если области допустимых значений переменных будут совпадать, например, в выражениях a + 6 и 6 + a или a · b · 0 и 0 , или x 4 и x , и значения самих выражений будут равны при любых переменных, то такие выражения считаются тождественно равными. Так, a + 8 = 8 + a при любом значении a , и a · b · 0 = 0 тоже, поскольку умножение на 0 любого числа дает в итоге 0 . Выражения x 4 и x будут тождественно равными при любых x из промежутка [ 0 , + ∞) .
Так, a + 8 = 8 + a при любом значении a , и a · b · 0 = 0 тоже, поскольку умножение на 0 любого числа дает в итоге 0 . Выражения x 4 и x будут тождественно равными при любых x из промежутка [ 0 , + ∞) .
Но область допустимого значения в одном выражении может отличаться от области другого.
Пример 5
Например, возьмем два выражения: x − 1 и x — 1 · x x . Для первого из них областью допустимых значений x будет все множество действительных чисел, а для второго – множество всех действующих чисел, за исключением нуля, ведь тогда мы получим 0 в знаменателе, а такое деление не определено. У этих двух выражений есть общая область значений, образованная пересечением двух отдельных областей. Можно сделать вывод, что оба выражения x — 1 · x x и x − 1 будут иметь смысл при любых действительных значениях переменных, за исключением 0 .
Основное свойство дроби также позволяет нам заключить, что x — 1 · x x и x − 1 будут равными при любом x, которое не является 0 . Значит, на общей области допустимых значений эти выражения будут тождественно равны друг другу, а при любом действительном x говорить о тождественном равенстве нельзя.
Если мы заменяем одно выражение на другое, которое является тождественно равным ему, то этот процесс называется тождественным преобразованием. Это понятие очень важно, и подробно о нем мы поговорим в отдельном материале.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Два выражения называются тождественно равными на множестве, если они на этом множестве имеют смысл и все их соответственные значения равны.
Равенство, в котором левая и правая части — тождественно равные выражения, называется тождеством.
Замена одного выражения другим, тождественно равным ему на данном множестве, называется тождественным преобразованием выражения.
Задача. Найти область определения выражения .
Решение. Так как выражение представляет собой дробь, то для нахождения его области определения нужно найти те значения переменной х , при которых знаменатель обращается в нуль, и исключить их. Решив уравнение х 2 — 9 = 0, находим, что х = -3 и х = 3. Следовательно, область определения данного выражения состоит из всех чисел, отличных от -3 и от 3. Если обозначить ее через Х , то можно записать:
Решив уравнение х 2 — 9 = 0, находим, что х = -3 и х = 3. Следовательно, область определения данного выражения состоит из всех чисел, отличных от -3 и от 3. Если обозначить ее через Х , то можно записать:
Х = (-¥; -3) È (-3; 3) È (3; +¥).
Задача. Являются ли выражения и х — 2 тождественно равными: а) на множестве R ; б) на множестве целых чисел, отличных от нуля?
Решение. а) На множестве R эти выражения не являются тождественно равными, так как при х = 0 выражение не имеет значения, а выражение х — 2 имеет значение -2.
б) На множестве целых чисел, отличных от нуля, эти выражения являются тождественно равными, так как = .
Задача. При каких значениях х являются тождествами следующие равенства:
а) ; б) .
Решение. а) Равенство является тождеством, если ;
б) Равенство является тождеством, если .
Тождества. Тождественные преобразования выражений.
 (7 класс) презентация, доклад
(7 класс) презентация, докладТождества.
Тождественные преобразования выражений.
7 класс.
Найдем значение выражений
при х=5 и у=4
3(х+у)=3(5+4)=3*9=27
3х+3у=3*5+3*4=27
Найдем значение выражений при х=6 и у=5
3(х+у)=3(6+5)=3*11=33
3х+3у=3*6+3*5=33
ВЫВОД:
Мы получили один и тот же результат.
Из распределительного свойства следует, что вообще при любых значениях переменных значения выражений 3(х+у) и 3х+3у равны.
3(х+у) = 3х+3у
Рассмотрим теперь выражения 2х+у и 2ху.
при х=1 и у=2 они принимают равные значения:
2х+у=2*1+2=4
2ху=2*1*2=4
при х=3, у=4 значения выражений разные
2х+у=2*3+4=10
2ху=2*3*4=24
ВЫВОД:
Выражения 3(х+у) и 3х+3у являются тождественно равными, а выражения 2х+у и 2ху не являются тождественно равными.
Определение:
Два выражения, значения которых равны при любых значениях переменных, называются тождественно равными.
ТОЖДЕСТВО
Равенство 3(х+у) и 3х+3у верно при любых значениях х и у. Такие равенства называются тождествами.
Определение: Равенство, верное при любых значениях переменных, называется тождеством.
Тождествами считают и верные числовые равенства. С тождествами мы уже встречались.
Тождествами являются равенства, выражающие основные свойства действий над числами.
a + b = b + a
ab = ba
(a + b) + c = a + (b + c)
(ab)c = a(bc)
a(b + c) = ab + ac
Можно привести и другие примеры тождеств:
а + 0 = а
а * 1 = а
а + (-а) = 0
а * (-b) = — ab
а-b = a + (-b)
(-a) * (-b) = ab
Замену одного выражения другим, тождественно равным ему выражением, называют тождественным преобразованием или просто преобразованием выражения.
Запомним:
ВЫРАЖЕНИЯ, СООТВЕТСВЕННЫЕ ЗНАЧЕНИЯ КОТОРЫХ РАВНЫ ПРИ ЛЮБЫХ ДОПУСТИМЫХ ЗНАЧЕНИЯХ ПЕРЕМЕННЫХ, НАЗЫВАЮТСЯ
ТОЖДЕСТВЕННО РАВНЫМИ.
Например: (a²)³ и a6
ab∙(-a²b) и –a³b²
ЗАМЕНУ ОДНОГО ВЫРАЖЕНИЯ ДРУГИМ, ТОЖДЕСТВЕННО РАВНЫМ ЕМУ, НАЗЫВАЮТ ТОЖДЕСТВЕННЫМ ПРЕОБРАЗОВАНИЕМ
Запиши:
Способы доказательства тождеств:
Преобразование левой части тождества так, чтобы получилась её правая часть
(если после преобразования левой части, выражение получится как в правой части , то данное выражение является тождеством)
Проверьте, данное выражение – тождество?
Решение:
Преобразуем левую часть равенства:
а(в — х) + х(а + в) =
= ав – ах + ах + хв =
= ав + хв = в(а + х)
Вывод:
В результате тождественного преобразования левой части равенства, мы получили его
правую часть и тем самым доказали,
что данное равенство является тождеством.
В теорию (способы доказательства тождеств):
2. Преобразование правой части тождества так, чтобы получилась её левая часть
Проверьте, данное выражение – тождество?
Решение:
Преобразуем правую часть равенства
(а+2)(а+5)=
= а² + 5а + 2а+ + 10 =
= а² + 7а + 10
Вывод:
В результате тождественного преобразования правой части равенства, мы получили его левую часть и тем самым доказали, что данное равенство является тождеством.
В теорию (способы доказательства тождеств):
Преобразование обеих частей тождества…..(должны получится одинаковые выражения)
Докажите тождество:
Решение:
Упростим обе части равенства
Вывод:
Так как левая и правая части данного равенства равны одному и тому же выражению, то они тождественно равны между собой.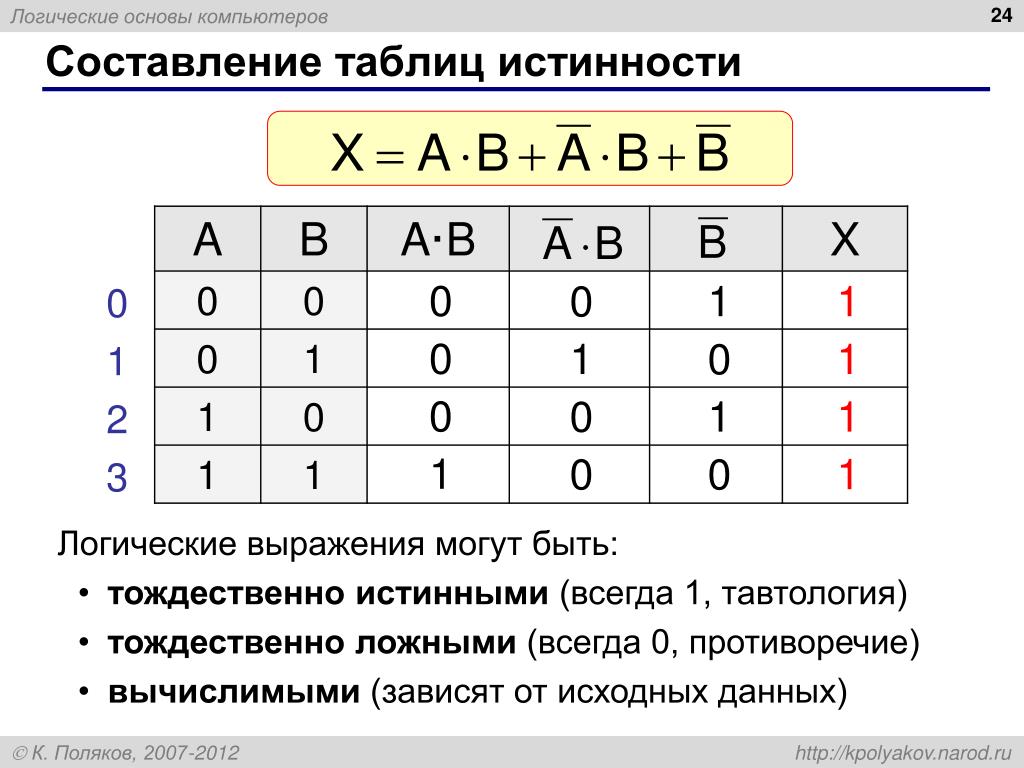
Значит исходное равенство –
тождество.
В теорию (способы доказательства тождеств):
4. Найти разность между правой и левой частями выражения. (если эта разность равна нулю, то данное выражение — тождество)
Докажите тождество:
(m-a)(m-b) = m²- (a+b)m + ab
Решение:
(найдем разность между левой и правой частями выражения)
(m-a)(m-b) – [m² — (a+b)m + ab] =
=m² — mb – ma + ab — [m² — am – bm + ab ] =
= m² — mb – ma + ab — m² + am + bm — ab =
= 0
Вывод:
Так как разность между левой и правой частями выражения равна нулю,
то данное выражения является
тождеством
Работаем по задачнику:
№ 36. 6 (а) — № 36.10 (а)
6 (а) — № 36.10 (а)
Скачать презентацию
определение, примеры Одинаково равные значения следующих выражений a4
Обе части которых являются тождественно равными выражениями. Идентификаторы делятся на буквенные и числовые.
Тождественные выражения
Два алгебраических выражения называются тождественными (или тождественно равными ), если при любых числовых значениях букв они имеют одинаковое числовое значение. Это, например, выражения:
х (5 + х ) и 5 х + х 2
Оба представленных выражения при любом значении х будут равны между собой, поэтому их можно назвать тождественными или тождественно равными.
Числовые выражения, равные друг другу, также можно назвать идентичными. Например:
20 — 8 и 10 + 2
Тождества букв и цифр
Тождества букв — это равенство, которое справедливо для любых значений входящих в него букв. Другими словами, такое равенство, при котором обе части являются тождественно равными выражениями, например:
( a + b ) m = am + bm
( a + b ) 2 = a 2 + 2 ab + b 2
Числовое тождество — равенство, содержащее только числа, выраженные цифрами, в котором обе части имеют одинаковое числовое значение. Например:
Например:
4 + 5 + 2 = 3 + 8
5 (4 + 6) = 50
Преобразования идентичных выражений
Все алгебраические действия представляют собой преобразование одного алгебраического выражения в другое, идентичное первому.
При вычислении значения выражения, раскрытии скобок, вынесении за скобки общего множителя и в ряде других случаев одни выражения заменяются другими, тождественно равными им. Замена одного выражения другим, тождественно равным ему, называется тождественным преобразованием выражения или просто преобразованием выражения . Все преобразования выражений выполняются на основе свойств действий над числами.
Рассмотрим тождественное преобразование выражения на примере вынесения общего множителя за скобки:
10 х — 7 х + 3 х = (10 — 7 + 3) х = 6 x
После того, как мы разобрались с понятием тождеств, можно перейти к изучению тождественно равных выражений. Цель этой статьи — объяснить, что это такое, и показать на примерах, какие выражения будут тождественно равны другим.
Тождественно равные выражения: определение
Понятие тождественно равных выражений обычно изучается вместе с самим понятием тождества в рамках школьного курса алгебры. Вот основное определение, взятое из одного учебника:
Определение 1
Тождественно равными друг другу будут такие выражения, значения которых будут одинаковыми при любых возможных значениях переменных, входящих в их состав .
Также тождественно равными считаются такие числовые выражения, которым будут соответствовать одинаковые значения.
Это достаточно широкое определение, которое будет правильным для всех целочисленных выражений, смысл которых не меняется при изменении значений переменных. Однако позже возникает необходимость уточнить это определение, так как помимо целых чисел существуют и другие типы выражений, которые не будут иметь смысла для тех или иных переменных. Отсюда возникает понятие допустимости и недопустимости тех или иных значений переменных, а также необходимость определения диапазона допустимых значений. Сформулируем более точное определение.
Сформулируем более точное определение.
Определение 2
Тождественно равные выражения — это те выражения, значения которых равны друг другу при любых допустимых значениях переменных, входящих в их состав. Числовые выражения будут тождественно равны друг другу, если они имеют одинаковые значения.
Фраза «для любых допустимых значений переменных» относится ко всем тем значениям переменных, для которых оба выражения будут иметь смысл. Мы объясним это положение позже, когда приведем примеры тождественно равных выражений.
Можно также указать следующее определение:
Определение 3
Равно равные выражения — это выражения, расположенные в одном и том же идентификаторе слева и справа.
Примеры выражений, тождественно равных друг другу
Используя определения, данные выше, рассмотрим несколько примеров таких выражений.
Начнем с числовых выражений.
Пример 1
Итак, 2 + 4 и 4 + 2 будут тождественно равны друг другу, так как их результаты будут равны (6 и 6).
Пример 2
Точно так же тождественно равны выражения 3 и 30: 10, (2 2) 3 и 2 6 (чтобы вычислить значение последнего выражения, нужно знать свойства степени).
Пример 3
Но выражения 4 — 2 и 9 — 1 не будут равны, так как их значения различны.
Перейдем к примерам литеральных выражений. A+b и b+a будут тождественно равны, и это не зависит от значений переменных (равенство выражений в данном случае определяется свойством смещения сложения).
Пример 4
Например, если a равно 4, а b равно 5, результаты останутся теми же.
Другой пример тождественно равных выражений с буквами — 0 x y z и 0. Какими бы ни были значения переменных в этом случае, при умножении на 0 они дадут 0. Неравные выражения — 6 x и 8 x, так как они не будет равным ни для какого x.
В случае совпадения диапазонов допустимых значений переменных, например, в выражениях а + 6 и 6 + а или а b 0 и 0, или х 4 и х, и значений сами выражения будут равны для любых переменных, то такие выражения считаются тождественно равными. Итак, a + 8 = 8 + a для любого значения a, и a b 0 тоже = 0, так как умножение любого числа на 0 дает в конце 0. Выражения x 4 и x будут тождественно равны для любого x из интервала [0, +∞).
Итак, a + 8 = 8 + a для любого значения a, и a b 0 тоже = 0, так как умножение любого числа на 0 дает в конце 0. Выражения x 4 и x будут тождественно равны для любого x из интервала [0, +∞).
Но диапазон достоверности одного выражения может отличаться от диапазона другого.
Пример 5
Например, возьмем два выражения: x — 1 и x — 1 x x. Для первого из них диапазоном допустимых значений х будет все множество действительных чисел, а для второго множество всех действительных чисел, за исключением нуля, потому что тогда мы получим 0 в знаменателе , и такое деление не определено. Эти два выражения имеют общий диапазон значений, образованный пересечением двух отдельных областей. Можно сделать вывод, что оба выражения x — 1 x x и x — 1 будут иметь смысл при любых действительных значениях переменных, кроме 0,9.0003
Основное свойство дроби также позволяет сделать вывод, что х — 1 х х и х — 1 будут равны для любого х, отличного от 0. Это означает, что в общем диапазоне допустимых значений эти выражения будут тождественно равны между собой, и ни для какого действительного х нельзя говорить об тождественном равенстве.
Если заменить одно выражение другим, тождественно равным ему, то этот процесс называется тождественным преобразованием. Это понятие очень важно, и мы подробно поговорим о нем в отдельной статье.
Если вы заметили ошибку в тексте, выделите ее и нажмите Ctrl + Enter
Говорят, что два выражения тождественно равны на множестве, если они имеют смысл на этом множестве и все их соответствующие значения равны.
Равенство, в котором левая и правая части являются тождественно равными выражениями, называется тождеством.
Замена одного выражения другим, тождественно равным ему на данном множестве, называется идентичное преобразование выражения.
Задача. Найти область выражения.
Раствор. Так как выражение является дробью, то для нахождения его области определения нужно найти те значения переменной NS , при которых знаменатель обращается в нуль и исключить их. Решая уравнение НС 2 — 9 = 0, находим, что НС = -3 и НС = 3. Следовательно, область определения этого выражения состоит из всех чисел, кроме -3 и 3. Если обозначить его к NS , то можно написать:
Следовательно, область определения этого выражения состоит из всех чисел, кроме -3 и 3. Если обозначить его к NS , то можно написать:
NS = (- ¥; -3) È (-3; 3) È (3; + ¥).
Задача. Выражения и NS — 2 тождественно равны: а) на множестве R ; б) на множестве ненулевых целых чисел?
Раствор. а) На множестве R эти выражения не тождественно равны, так как для NS = 0 выражение несущественно, а выражение NS — 2 имеет значение -2.
б) На множестве ненулевых целых чисел эти выражения тождественно равны, так как = .
Задача. При каких значениях НС следующие равенства являются тождествами:
а) ; б).
Раствор. а) Равенство есть тождество, если;
б) Равенство есть тождество, если.
Получив представление об идентичностях, логично перейти к знакомству с . В этой статье мы ответим на вопрос, что такое тождественно равные выражения, а также на примерах разберемся, какие выражения тождественно равны, а какие нет.
Навигация по страницам.
Что такое тождественно равные выражения?
Определение тождественно равных выражений дается параллельно с определением тождества. Это происходит на уроках алгебры в 7 классе. В учебнике по алгебре для 7 классов автора Ю.Н. Макарычева дана следующая формулировка:
Определение.
Являются выражениями, значения которых равны при любых значениях входящих в них переменных. Числовые выражения, имеющие одинаковые значения, также называются тождественно равными.
Это определение используется до 8 класса, оно справедливо для целочисленных выражений, так как они имеют смысл при любых значениях входящих в них переменных. А в 8 классе уточняется определение тождественно равных выражений. Поясним, с чем это связано.
В 8 классе начинается изучение других видов выражений, которые, в отличие от целочисленных выражений, при некоторых значениях переменных могут не иметь смысла. Это заставляет ввести определения допустимых и недопустимых значений переменных, а также диапазона допустимых значений ОДЗ переменной и, как следствие, уточнить определение тождественно равных выражений.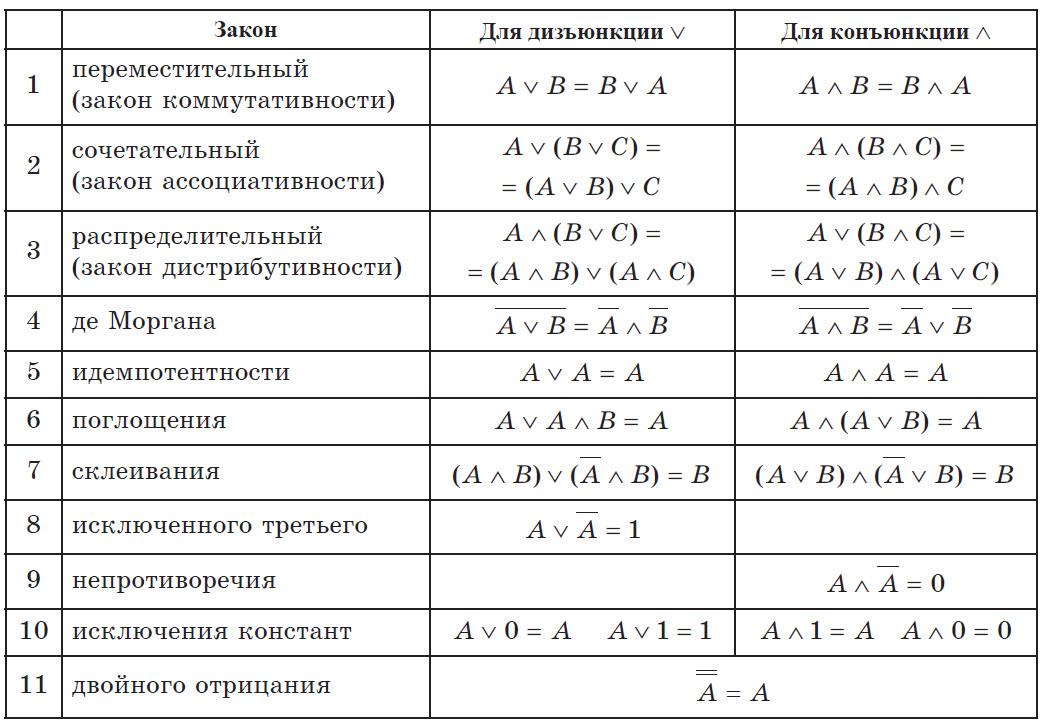
Определение.
Два выражения, значения которых равны при всех допустимых значениях входящих в них переменных, называются тождественно равными выражениями . Два числовых выражения, имеющих одинаковое значение, также называются тождественно равными.
В этом определении тождественно равных выражений стоит уточнить смысл фразы «для всех допустимых значений входящих в них переменных». Под ним подразумеваются все такие значения переменных, для которых оба тождественно равных выражения имеют смысл одновременно. Мы проясним эту идею в следующем параграфе, рассматривая примеры.
Определение тождественно равных выражений в учебнике А.Г. Мордковича дано несколько иначе:
Определение.
Тождественно равные выражения Выражения слева и справа от тождества.
Значение этого и предыдущего определений совпадают.
Примеры тождественно равных выражений
Определения, введенные в предыдущем абзаце, позволяют нам привести примеров тождественно равных выражений .
Начнем с тождественно равных числовых выражений. Числовые выражения 1 + 2 и 2 + 1 тождественно равны, так как им соответствуют равные значения 3 и 3. Также тождественно равны выражения 5 и 30:6, как и выражения (2 2) 3 и 2 6 (т.е. значения последних выражений равны по силе). Но числовые выражения 3+2 и 3−2 тождественно не равны, так как им соответствуют значения 5 и 1 соответственно, и они не равны.
Теперь приведем примеры тождественно равных выражений с переменными. Это выражения a + b и b + a. Действительно, при любых значениях переменных a и b написанные выражения принимают одинаковые значения (что следует из цифр). Например, для a = 1 и b = 2 имеем a + b = 1 + 2 = 3 и b + a = 2 + 1 = 3. При любых других значениях переменных a и b также получаем равные значения этих выражений. Выражения 0 x y z и 0 также тождественно равны при любых значениях переменных x, y и z. Но выражения 2 х и 3 х не тождественно равны, так как, например, при х = 1 их значения не равны. Действительно, при x = 1 выражение 2 x равно 2 1 = 2, а выражение 3 x равно 3 1 = 3,
Когда диапазоны допустимых значений переменных в выражениях совпадают, как, например, в выражениях а + 1 и 1 + а, или а б 0 и 0, или и, и значения этих выражений равны для всех значений переменных из этих областей, то тут все ясно — эти выражения тождественно равны для всех допустимых значений переменных, входящих в них. Итак, а + 1≡1 + а для любого а, выражения а · b · 0 и 0 тождественно равны при любых значениях переменных а и b, а выражения и тождественно равны при всех х из; изд. С. А. Теляковский. — 17-е изд. – М.: Просвещение, 2008. – 240 с. : больной. — ИСБН 978-5-09-019315-3.
Итак, а + 1≡1 + а для любого а, выражения а · b · 0 и 0 тождественно равны при любых значениях переменных а и b, а выражения и тождественно равны при всех х из; изд. С. А. Теляковский. — 17-е изд. – М.: Просвещение, 2008. – 240 с. : больной. — ИСБН 978-5-09-019315-3.
Рассмотрим два равенства:
1.a 12 * a 3 = a 7 * a 8
Это равенство будет выполняться при любых значениях переменной a. Диапазоном допустимых значений для этого равенства будет весь набор действительных чисел.
2.а 12: а 3 = а 2 * а 7.
Это неравенство будет выполняться для всех значений переменной а, кроме а равного нулю. Диапазоном допустимых значений этого неравенства будет весь набор действительных чисел, кроме нуля.
Каждое из этих равенств можно считать верным для любых допустимых значений переменных a. Такие равенства в математике называются тождествами .
Концепция тождества
Тождество — это равенство, истинное для любых допустимых значений переменных. Если в это равенство вместо переменных подставить какие-либо допустимые значения, то должно получиться правильное числовое равенство.
Стоит отметить, что истинные числовые равенства также являются тождествами. Тождества, например, будут свойствами действий над числами. 92*б) и -а 3*б 2;
3. ((x 3 * x 8) / x) и x 10.
Мы всегда можем заменить одно выражение любым другим выражением, тождественно равным первому. Такая замена будет тождественной трансформацией.
Примеры тождеств
Пример 1: равны ли следующие равенства:
1. а + 5 = 5 + а;
а + 5 = 5 + а;
2.а * (- б) = -а * б;
3,3 * а * 3 * Ь = 9 * а * Ь;
Не все приведенные выше выражения будут тождествами. Из этих равенств только 1, 2 и 3 равенства являются тождествами. Какие бы числа мы в них не подставляли, вместо переменных a и b мы все равно получим правильные числовые равенства.
Но 4 равенство больше не тождество. Потому что это равенство не будет выполняться для всех допустимых значений. Например, для значений a = 5 и b = 2 вы получите следующий результат:
Это равенство неверно, так как число 3 не равно числу -3.
Как преобразовать выражение в тождественно равное. Тождества, определение, обозначения, примеры
Тема « Доказательства личности » 7 класс (КРО)
Учебник Макарычев Ю.Н., Миндюк Н.Г.
Цели занятия
Образовательные:
познакомить и первоначально закрепить понятия «тождественно равные выражения», «тождество», «тождественные преобразования»;
рассмотреть способы подтверждения личности, способствовать развитию навыков для подтверждения личности;
для проверки усвоения учащимися изученного материала, формирования навыков применения изученного для восприятия нового.
Проявление:
Развивать грамотную математическую речь учащихся (обогащать и усложнять словарный запас при использовании специальных математических терминов),
развивать мышление,
Воспитательная: воспитывать трудолюбие, аккуратность, правильность записи решения упражнений.
Тип урока: изучение нового материала
Во время занятий
1 . Организация времени.
Проверка домашнего задания.
Вопросы по домашнему заданию.
Подведение итогов на доске.
Математика нужна
Без нее нельзя
Учим, учим, друзья,
Что вспоминаем с утра?
2 . Давайте сделаем разминку.
Результат сложения. (Сумма)
Сколько чисел вы знаете? (Десять)
Сотая часть числа. (проценты)
результат деления? (Частный)
Наименьшее натуральное число? (один)
Можно ли при делении натуральных чисел получить нуль? (Нет)
Какое наибольшее отрицательное целое число? (-один)
На какое число нельзя разделить? (0)
Результат умножения? (Работа)
Результат вычитания.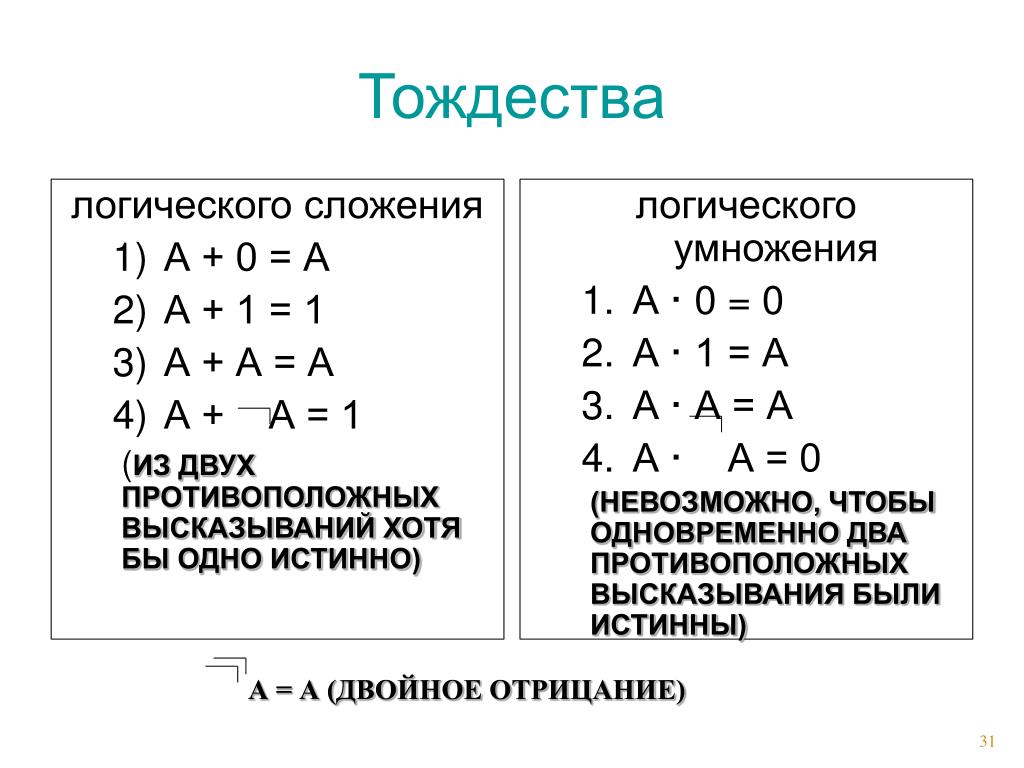 (Разность)
(Разность)
Коммутативное свойство сложения. (Сумма не меняется от перестановки членов местами)
Коммутативное свойство умножения. (Произведение не меняется от перестановки мест множителей)
Изучение новой темы(определение с записью в тетради)
Найдите значение выражений при x=5 и y=4
3(x+y)=3(5+4)=3*9=27
3x+3y=3*5+3*4 =27
Мы получили тот же результат. Из дистрибутивного свойства следует, что, вообще говоря, при любых значениях переменных значения выражений 3(x + y) и 3x + 3y равны.
Теперь рассмотрим выражения 2x + y и 2xy. Для x=1 и y=2 они принимают равные значения:
Однако можно указать значения x и y так, что значения этих выражений не равны. Например, если x=3, y=4, то
Определение : Два выражения, значения которых равны для любых значений переменных, называются тождественно равными.
Выражения 3(x+y) и 3x+3y тождественно равны, но выражения 2x+y и 2xy не тождественно равны.
Равенство 3(x + y) и 3x + 3y верно для любых значений x и y. Такие равенства называются тождествами.
Определение: Равенство, истинное для любых значений переменных, называется тождеством.
Истинные числовые равенства также считаются тождествами. Мы уже встречались с тождествами. Тождества – это равенства, выражающие основные свойства действий над числами (учащиеся комментируют каждое свойство, произнося его).
a + b = b + a
ab=ba
(a + b) + c = a + (b + c)
(ab)c = a(bc)
a(b + c) = ab + ac
Приведите другие примеры тождеств
Определение : Замена одного выражения другим, тождественно равным ему, называется тождественным преобразованием или просто преобразованием выражения.
Идентичные преобразования выражений с переменными выполняются на основе свойств операций над числами.
Тождественные преобразования выражений широко используются при вычислении значений выражений и решении других задач. Вам уже приходилось производить некоторые одинаковые преобразования, например, сокращение однотипных терминов, раскрытие скобок.
Вам уже приходилось производить некоторые одинаковые преобразования, например, сокращение однотипных терминов, раскрытие скобок.
5 . №691, №692 (с произношением правил раскрытия скобок, умножения отрицательных и положительных чисел)
Тождества для выбора рационального решения: (фронтальная работа)
6 . Подведение итогов урока.
Учитель задает вопросы, а ученики отвечают на них по своему желанию.
Какие два выражения называются тождественно равными? Приведите примеры.
Какое равенство называется тождеством? Приведите пример.
Какие одинаковые превращения вы знаете?
7. Домашнее задание. Выучите определения, Приведите примеры идентичных выражений (не менее 5), запишите их в тетрадь
В этой статье представлено начальное понятие идентичности . Здесь мы определяем тождества, вводим используемые обозначения и, конечно же, приводим различные примеры тождеств
Навигация по страницам.
Что такое личность?
Логично начать изложение материала с тождественных определений . В Ю. Учебник Н. Макарычева, алгебра для 7 классов, определение тождества дано так:
Определение.
Identity — равенство верно для любых значений переменных; любое истинное числовое равенство также является тождеством.
При этом автор сразу оговаривается, что в дальнейшем это определение будет уточнено. Это уточнение происходит в 8 классе, после ознакомления с определением допустимых значений переменных и ОДЗ. Определение становится следующим:
Определение.
Тождества являются истинными числовыми равенствами, а также равенствами, истинными для всех допустимых значений входящих в них переменных.
Так почему же при определении тождества в 7 классе мы говорим о любых значениях переменных, а в 8 классе начинаем говорить о значениях переменных с их ДПВ? До 8 класса работа ведется исключительно с целочисленными выражениями (в частности, с мономами и многочленами), причем они имеют смысл при любых значениях входящих в них переменных. Поэтому в 7 классе мы говорим, что тождество — это равенство, истинное при любых значениях переменных. А в 8 классе появляются выражения, которые уже имеют смысл не для всех значений переменных, а только для значений из их ОДЗ. Поэтому тождествами начнем называть равенства, верные для всех допустимых значений переменных.
Поэтому в 7 классе мы говорим, что тождество — это равенство, истинное при любых значениях переменных. А в 8 классе появляются выражения, которые уже имеют смысл не для всех значений переменных, а только для значений из их ОДЗ. Поэтому тождествами начнем называть равенства, верные для всех допустимых значений переменных.
Итак, тождество — это особый случай равенства. То есть любое тождество есть равенство. Но не всякое равенство есть тождество, а только равенство, истинное для любых значений переменных из диапазона их допустимых значений.
Знак тождества
Известно, что при записи равенств используется знак равенства вида «=», слева и справа от которого стоят некоторые числа или выражения. Если мы добавим к этому знаку еще одну горизонтальную черту, то получим тождественных знаков 9.0008 «≡», или как его еще называют знак равенства .
Знак тождества обычно используется только тогда, когда необходимо подчеркнуть, что перед нами не просто равенство, а именно тождество. В остальных случаях представления тождеств по форме не отличаются от равенств.
В остальных случаях представления тождеств по форме не отличаются от равенств.
Примеры тождеств
Пришло время привести примеров тождеств . В этом нам поможет определение идентичности, данное в первом абзаце.
Числовые равенства 2=2 являются примерами тождеств, так как эти равенства истинны, а любое истинное числовое равенство по определению является тождеством. Их можно записать как 2≡2 и .
Числовые равенства вида 2+3=5 и 7−1=2·3 также являются тождествами, поскольку эти равенства верны. То есть 2+3≡5 и 7−1≡2 3 .
Перейдем к примерам тождеств, которые содержат в своей записи не только числа, но и переменные.
Рассмотрим равенство 3·(x+1)=3·x+3 . При любом значении переменной x записанное равенство верно в силу дистрибутивного свойства умножения по отношению к сложению, поэтому исходное равенство является примером тождества. Вот еще один пример тождества: y(x−1)≡(x−1)x:x y 2:y, здесь областью допустимых значений переменных x и y являются все пары (x, y), где x и y — любые числа, кроме нуля.
Но равенства x+1=x−1 и a+2 b=b+2 a не являются тождествами, так как существуют значения переменных, при которых эти равенства будут неверны. Например, при x=2 равенство x+1=x−1 превращается в неверное равенство 2+1=2−1 . Более того, равенство x+1=x−1 вообще не достигается ни при каких значениях переменной x. А равенство a+2 b=b+2 a превращается в неверное равенство, если мы берем переменные a и b в различных значениях. Например, при a=0 и b=1 мы придем к неверному равенству 0+2 1=1+2 0 . Равенство |x|=x , где |x| — переменная x , также не является тождеством, так как неверна для отрицательных значений x .
Примерами наиболее известных тождеств являются sin 2 α+cos 2 α=1 и a log a b =b .
В заключение этой статьи хотелось бы отметить, что при изучении математики мы постоянно сталкиваемся с тождествами. Записи свойств числовых действий являются тождествами, например, a+b=b+a , 1 a=a , 0 a=0 и a+(−a)=0 . Также тождества
Основные свойства сложения и умножения чисел.
Коммутативное свойство сложения: при перестановке членов значение суммы не меняется. Для любых чисел a и b верно равенство
Ассоциативное свойство сложения: чтобы к сумме двух чисел прибавить третье число, нужно прибавить к первому числу сумму второго и третьего. Для любых чисел a, b и c справедливо равенство
Коммутативное свойство умножения: перестановка множителей не меняет значения произведения. Для любых чисел a, b и c верно равенство
Ассоциативное свойство умножения: чтобы умножить произведение двух чисел на третье число, нужно умножить первое число на произведение второго и третьего.
Для любых чисел a, b и c справедливо равенство
Распределительное свойство: Чтобы умножить число на сумму, вы можете умножить это число на каждый член и сложить результаты. Для любых чисел a, b и c верно равенство
Из коммутативных и ассоциативных свойств сложения следует, что в любой сумме можно как угодно переставлять члены и объединять их в группы произвольным образом.
Пример 1 Подсчитаем сумму 1,23+13,5+4,27.
Для этого удобно объединить первое слагаемое с третьим. Получаем:
1,23+13,5+4,27=(1,23+4,27)+13,5=5,5+13,5=19.
Из коммутативных и ассоциативных свойств умножения следует: в любом произведении можно как угодно переставлять множители и произвольно объединять их в группы.
Пример 2 Найдем стоимость произведения 1,8 0,25 64 0,5.
Объединив первый множитель с четвертым, а второй с третьим, получим:
1,8 0,25 64 0,5 = (1,8 0,5) (0,25 64) = 0,9 16 = 14,4.
Свойство распределения также действует, когда число умножается на сумму трех или более членов.
Например, для любых чисел a, b, c и d верно равенство
a(b+c+d)=ab+ac+ad.
Мы знаем, что вычитание можно заменить сложением, прибавив к уменьшаемому число, противоположное вычитаемому:
Это позволяет числовое выражение типа a-b рассматривать сумму чисел a и -b, рассматривать числовое выражение вида a +b-c-d как суммы чисел a, b, -c, -d и т. д. Рассмотренные свойства действий справедливы и для таких сумм.
д. Рассмотренные свойства действий справедливы и для таких сумм.
Пример 3 Найдем значение выражения 3,27-6,5-2,5+1,73.
Это выражение представляет собой сумму чисел 3,27, -6,5, -2,5 и 1,73. Применяя свойства сложения, получаем: 3,27-6,5-2,5+1,73=(3,27+1,73)+(-6,5-2,5)=5+(-9) = -4.
Пример 4 Вычислим произведение 36·().
Множитель можно представить как сумму чисел и -. Используя распределительное свойство умножения, получаем:
36()=36-36=9-10=-1.
Личности
Определение. Два выражения, соответствующие значения которых равны при любых значениях переменных, называются тождественно равными.
Определение. Равенство, истинное при любых значениях переменных, называется тождеством.
Найдем значения выражений 3(x+y) и 3x+3y для x=5, y=4:
3(x+y)=3(5+4)=3 9=27 ,
3x+3y=3 5+3 4=15+12=27.
Мы получили тот же результат. Из дистрибутивного свойства следует, что, вообще говоря, при любых значениях переменных соответствующие значения выражений 3(x+y) и 3x+3y равны.
Теперь рассмотрим выражения 2x+y и 2xy. Для x=1, y=2 они принимают равные значения:
Однако можно указать значения x и y так, что значения этих выражений не равны. Например, если x=3, y=4, то
Выражения 3(x+y) и 3x+3y тождественно равны, но выражения 2x+y и 2xy не тождественно равны.
Равенство 3(x+y)=x+3y, верное для любых значений x и y, является тождеством.
Истинные числовые равенства также считаются тождествами.
Итак, тождества — это равенства, выражающие основные свойства действий над числами:
a+b=b+a, (a+b)+c=a+(b+c),
ab=ba, (ab) с=а(bc), а(b+c)=ab+ac.
Можно привести и другие примеры тождеств:
a+0=a, a+(-a)=0, a-b=a+(-b),
a 1=a, a (-b)=-ab, (-а)(-б)=аб.
Тождественные преобразования выражений
Замена одного выражения другим, тождественно равным ему, называется тождественным преобразованием или просто преобразованием выражения.
Идентичные преобразования выражений с переменными выполняются на основе свойств операций над числами.
Чтобы найти значение выражения xy-xz по заданным значениям x, y, z, нужно выполнить три шага. Например, при x=2,3, y=0,8, z=0,2 получаем:
xy-xz=2,3 0,8-2,3 0,2=1,84-0,46=1,38.
Этот результат можно получить всего за два шага, используя выражение x(y-z), которое тождественно равно выражению xy-xz:
xy-xz=2,3(0,8-0,2)=2,3 0,6=1,38.
Мы упростили вычисления, заменив выражение xy-xz тождественно равным выражением x(y-z).
Тождественные преобразования выражений широко используются при вычислении значений выражений и решении других задач. Некоторые идентичные преобразования уже были выполнены, например, сокращение однородных терминов, раскрытие скобок. Напомним правила выполнения этих преобразований:
чтобы привести одинаковые члены, нужно сложить их коэффициенты и умножить результат на общую буквенную часть;
если перед скобками стоит знак плюс, то скобки можно опустить, сохранив знак каждого члена, заключенного в скобки;
если перед скобками стоит знак минус, то скобки можно опустить, изменив знак каждого члена, заключенного в скобки.
Пример 1 Сложим одинаковые члены в сумме 5x+2x-3x.
Используем правило сокращения подобных членов:
5x+2x-3x=(5+2-3)x=4x.
Это преобразование основано на распределительном свойстве умножения.
Пример 2 Раскроем скобки в выражении 2a+(b-3c).
Применение правила раскрытия квадратных скобок, которым предшествует знак плюс:
2a+(b-3c)=2a+b-3c.
Выполненное преобразование основано на ассоциативном свойстве сложения.
Пример 3 Раскроем скобки в выражении a-(4b-c).
Воспользуемся правилом раскрытия скобок, которым предшествует знак минус:
a-(4b-c)=a-4b+c.
Выполненное преобразование основано на распределительном свойстве умножения и ассоциативном свойстве сложения. Давайте покажем это. Представим второй член -(4b-c) в этом выражении как произведение (-1)(4b-c): 92-2x)$,$\ \frac(x-y)(y-x)$ и др.) Сходство этих понятий состоит в том, что и в многочленах, и в алгебраических дробях присутствуют переменные и числовые значения, арифметические операции: сложение, вычитание, умножение , возведение в степень. Отличие этих понятий в том, что деление на переменную не производится в многочленах, а деление на переменную может производиться в алгебраических дробях.
Отличие этих понятий в том, что деление на переменную не производится в многочленах, а деление на переменную может производиться в алгебраических дробях.
И многочлены, и алгебраические дроби в математике называются рациональными алгебраическими выражениями. Но многочлены — это целочисленные рациональные выражения, а алгебраические дроби — дробно-рациональные выражения. 92-4x+4)(x-2)$ и $x-2\$ можно считать одинаковыми не для всех значений переменной, так как для существования дробно-рационального выражения и для приведения к чтобы многочлен $x-2$ был возможен, знаменатель дроби не должен быть равен $0$ (как и множитель, на который мы уменьшаем. В данном примере знаменатель и множитель совпадают, но это не всегда случай).
Значения переменных, для которых будет существовать алгебраическая дробь, называются допустимыми значениями переменных. 92-4x+4)(x-2)$ и $x-2$ идентичны для всех значений переменной, кроме $2$.
Определение 1
тождественно равные Выражения — это такие, которые равны для всех возможных значений переменной.
Тождественное преобразование — это любая замена исходного выражения тождественно равным. К таким преобразованиям относятся следующие действия: сложение, вычитание, умножение, приведение круглых скобок, приведение алгебраических дробей к общему знаменателю, приведение алгебраических дробей, приведение однородных членов и т. д. Необходимо учитывать, что ряд преобразований, таких как приведение, сокращение подобных терминов, может изменить допустимые значения переменной.
Методы, используемые для подтверждения тождества
Преобразование левой части тождества в правую или наоборот с помощью преобразования тождества
Свести обе части к одному выражению с помощью идентичных преобразований
Перенесите выражения из одной части выражения в другую и докажите, что полученная разность равна $0$
Какой из вышеперечисленных методов использовать для подтверждения данной личности, зависит от исходной личности. 92$
Обратите внимание, что полученное выражение показывает, что исходное тождество верно.
Обратите внимание, что в исходной идентичности разрешены все значения переменной, а это значит, что мы доказали идентичность с помощью одинаковых преобразований, и она верна для всех допустимых значений переменной.
определение, примеры Что означает тождественное выражение
Обе части которого являются тождественно равными выражениями. Тождества делятся на буквы и цифры.
Тождественные выражения
Два алгебраических выражения называются тождественными (или тождественно равными ), если при любых числовых значениях букв они имеют одинаковое числовое значение. Это, например, выражения:
х (5 + х ) и 5 х + х 2
Оба представленных выражения, при любом значении х будут равны между собой, поэтому их можно назвать тождественными или тождественно равными.
Числовые выражения, равные друг другу, также можно назвать идентичными. Например:
20 — 8 и 10 + 2
Тождества букв и цифр
Тождества букв есть равенство, справедливое для любых значений входящих в него букв. Другими словами, такое равенство, в котором обе части являются тождественно равными выражениями, например:
Другими словами, такое равенство, в котором обе части являются тождественно равными выражениями, например:
( а + б ) м = ам + бм
( a + b ) 2 = a 2 + 2 ab + b 2
Числовой идентификатор — это равенство, содержащее только числа, в обеих частях выраженные цифрами одинаковое числовое значение. Например:
4 + 5 + 2 = 3 + 8
5 (4 + 6) = 50
Тождественные преобразования выражений
Все алгебраические операции представляют собой преобразование одного алгебраического выражения в другое, идентичное первому.
При вычислении значения выражения, раскрытии скобок, вынесении общего множителя за скобки и в ряде других случаев одни выражения заменяются другими, тождественно равными им. Замена одного выражения другим, тождественно равным ему, называется выражением преобразования тождества или просто преобразованием выражения . Все преобразования выражений выполняются на основе свойств операций над числами.
Рассмотрим тождественное преобразование выражения на примере выноса общего множителя за скобки:
10 х — 7 х + 3 х = (10 — 7 + 3) х = 6 x
Получив представление об тождествах, логично перейти к знакомству с . В этой статье мы ответим на вопрос, что такое тождественно равные выражения, а также на примерах разберемся, какие выражения тождественно равны, а какие нет.
Навигация по страницам.
Что такое тождественно равные выражения?
Определение тождественно равных выражений дается параллельно с определением тождества. Это происходит на уроке алгебры в 7 классе. В учебнике по алгебре для 7 классов автор Ю. Н. Макарычев дает следующую формулировку:
Определение.
— это выражения, значения которых равны при любых значениях входящих в них переменных. Числовые выражения, соответствующие одинаковым значениям, также называются тождественно равными.
Это определение используется до класса 8, оно справедливо для целочисленных выражений, так как они имеют смысл при любых значениях входящих в них переменных. А в 8 классе уточняется определение тождественно равных выражений. Поясним, с чем это связано.
А в 8 классе уточняется определение тождественно равных выражений. Поясним, с чем это связано.
В 8 классе начинается изучение других видов выражений, которые, в отличие от целочисленных выражений, могут не иметь смысла для некоторых значений переменных. Это заставляет ввести определения допустимых и недопустимых значений переменных, а также диапазона допустимых значений ОДВ переменной и, как следствие, уточнить определение тождественно равных выражений.
Определение.
Два выражения, значения которых равны при всех допустимых значениях их переменных, называются тождественно равными выражениями . Два числовых выражения, имеющие одинаковое значение, также называются тождественно равными.
В этом определении тождественно равных выражений стоит уточнить смысл фразы «для всех допустимых значений входящих в них переменных». Под ним подразумеваются все такие значения переменных, для которых одновременно имеют смысл оба тождественно равных выражения. Эта идея будет разъяснена в следующем разделе на примерах.
Определение тождественно равных выражений в учебнике А. Г. Мордковича дано несколько иначе:
Определение.
Идентичные равные выражения — это выражения слева и справа от тождества.
По смыслу это и предыдущее определения совпадают.
Примеры тождественно равных выражений
Определения, введенные в предыдущем подразделе, позволяют привести примеров тождественно равных выражений .
Начнем с тождественно равных числовых выражений. Числовые выражения 1+2 и 2+1 тождественно равны, потому что они соответствуют равным значениям 3 и 3. Выражения 5 и 30:6 также тождественно равны, как и выражения (2 2) 3 и 2 6 (значения последних выражений равны благодаря ). Но числовые выражения 3+2 и 3−2 не тождественно равны, так как они соответствуют значениям 5 и 1 соответственно, но они не равны.
Теперь приведем примеры тождественно равных выражений с переменными. Это выражения a+b и b+a . Действительно, при любых значениях переменных a и b записанные выражения принимают одни и те же значения (что следует из цифр). Например, с a=1 и b=2 мы имеем a+b=1+2=3 и b+a=2+1=3 . При любых других значениях переменных a и b мы также получим равные значения этих выражений. Выражения 0·x·y·z и 0 также тождественно равны при любых значениях переменных x, y и z. Но выражения 2 х и 3 х не тождественно равны, так как, например, при х=1 их значения не равны. Действительно, при x=1 выражение 2 x равно 2 1=2 , а выражение 3 x равно 3 1=3 .
Например, с a=1 и b=2 мы имеем a+b=1+2=3 и b+a=2+1=3 . При любых других значениях переменных a и b мы также получим равные значения этих выражений. Выражения 0·x·y·z и 0 также тождественно равны при любых значениях переменных x, y и z. Но выражения 2 х и 3 х не тождественно равны, так как, например, при х=1 их значения не равны. Действительно, при x=1 выражение 2 x равно 2 1=2 , а выражение 3 x равно 3 1=3 .
Когда области допустимых значений переменных в выражениях совпадают, как, например, в выражениях а+1 и 1+а , или а б 0 и 0 , или и , и значения этих выражений равны равны для всех значений переменных из этих областей, то здесь все ясно — эти выражения тождественно равны для всех допустимых значений переменных, входящих в них. Итак, a+1≡1+a для любого a , выражения a b 0 и 0 тождественно равны при любых значениях переменных a и b , а выражения и тождественно равны при всех x из ; изд. С. А. Теляковский. — 17-е изд. — М. : Просвещение, 2008. — 240 с. : больной. — ИСБН 978-5-09-019315-3.
Разобравшись с понятием тождеств, можно перейти к изучению тождественно равных выражений. Цель этой статьи — объяснить, что это такое, и показать на примерах, какие выражения будут тождественно равны другим.
Тождественно равные выражения: определение
Понятие тождественно равных выражений обычно изучается вместе с самим понятием тождества в рамках школьного курса алгебры. Вот основное определение, взятое из одного учебника:
Определение 1
тождественно равны друг другу будут такие выражения, значения которых будут одинаковыми при любых возможных значениях переменных, входящих в их состав.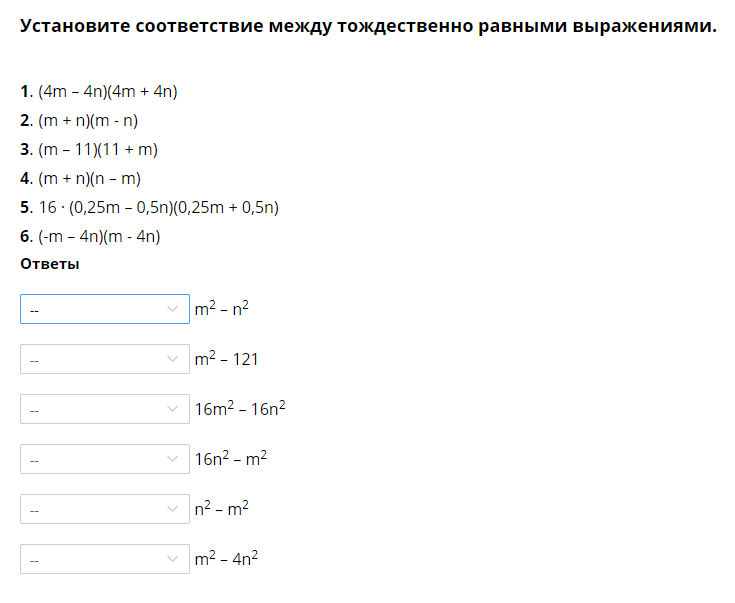
Также тождественно равными считаются такие числовые выражения, которым будут соответствовать одинаковые значения.
Это достаточно широкое определение, которое будет верным для всех целочисленных выражений, смысл которых не меняется при изменении значений переменных. Однако позже возникает необходимость уточнить это определение, поскольку существуют и другие виды выражений, помимо целых чисел, которые не будут иметь смысла с некоторыми переменными. Отсюда возникает понятие допустимости и недопустимости тех или иных значений переменных, а также необходимость определения диапазона допустимых значений. Сформулируем уточненное определение.
Определение 2
Идентичные равные выражения — это те выражения, значения которых равны друг другу при любых допустимых значениях переменных, входящих в их состав. Числовые выражения будут тождественно равны друг другу при условии, что значения совпадают.
Фраза «при любых допустимых значениях переменных» указывает на все те значения переменных, при которых оба выражения будут иметь смысл. Мы поясним это положение позже, когда приведем примеры тождественно равных выражений.
Мы поясним это положение позже, когда приведем примеры тождественно равных выражений.
Можно также указать следующее определение:
Определение 3
Идентичные равные выражения — это выражения, расположенные в одном и том же идентификаторе слева и справа.
Примеры выражений, тождественно равных друг другу
Используя определения, данные выше, рассмотрим несколько примеров таких выражений.
Начнем с числовых выражений.
Пример 1
Таким образом, 2 + 4 и 4 + 2 будут тождественно равны друг другу, так как их результаты будут равны (6 и 6).
Пример 2
Точно так же тождественно равны выражения 3 и 30: 10 , (2 2) 3 и 2 6 (для вычисления значения последнего выражения нужно знать свойства степени) .
Пример 3
Но выражения 4 — 2 и 9 — 1 не будут равны, так как их значения различны.
Перейдем к примерам литеральных выражений. A + b и b + a будут тождественно равны, и это не зависит от значений переменных (равенство выражений в данном случае определяется коммутативным свойством сложения).
Пример 4
Например, если a равно 4, а b равно 5, результаты останутся теми же.
Другой пример тождественно равных выражений с буквами: 0 · x · y · z и 0 . Какими бы ни были значения переменных в этом случае, при умножении на 0 они дадут 0. Неравные выражения — это 6 x и 8 x, потому что они не будут равны ни для какого x.
В том случае, если диапазоны допустимых значений переменных будут совпадать, например, в выражениях а + 6 и 6 + а или а b 0 и 0, или х 4 и х, и значения сами выражения будут равны для любых переменных, то такие выражения считаются тождественно равными. Итак, a + 8 = 8 + a для любого значения a, и a · b · 0 тоже = 0, так как при умножении любого числа на 0 получается 0. Выражения x 4 и x будут тождественно равны для любого x из интервал [ 0 , + ∞) .
Но область допустимого значения в одном выражении может отличаться от области действия другого.
Пример 5
Например, возьмем два выражения: x — 1 и x — 1 · x x . Для первого из них областью допустимых значений х будет все множество действительных чисел, а для второго — множество всех действительных чисел, кроме нуля, потому что тогда мы получим 0 в знаменателе, и такие деление не определено. Эти два выражения имеют общий диапазон, образованный пересечением двух отдельных диапазонов. Можно сделать вывод, что оба выражения x — 1 · x x и x — 1 будут иметь смысл при любых действительных значениях переменных, кроме 0 .
Эти два выражения имеют общий диапазон, образованный пересечением двух отдельных диапазонов. Можно сделать вывод, что оба выражения x — 1 · x x и x — 1 будут иметь смысл при любых действительных значениях переменных, кроме 0 .
Основное свойство дроби также позволяет нам заключить, что x-1 x x и x-1 будут равны для любого x, отличного от 0. Так что при допустимых значениях общей площади эти выражения будут тождественно равны друг другу, и при любом вещественном x нельзя говорить об тождественном равенстве.
Если заменить одно выражение другим, тождественно равным ему, то этот процесс называется тождественным преобразованием. Это понятие очень важно, и мы подробно поговорим о нем в отдельной статье.
Если вы заметили ошибку в тексте, выделите ее и нажмите Ctrl+Enter
Рассмотрим два равенства:
1. a 12 * a 3 = a 7 * a 8
Это равенство выполняется при любом значении переменная а. Диапазоном допустимых значений для этого равенства будет весь набор действительных чисел.
2. а 12: а 3 = а 2 * а 7 .
Это неравенство будет выполняться для всех значений переменной а, кроме а равного нулю. Диапазоном допустимых значений этого неравенства будет весь набор действительных чисел, кроме нуля.
О каждом из этих равенств можно утверждать, что оно будет верным при любых допустимых значениях переменных a. Такие уравнения в математике называются тождествами .
Понятие тождества
Тождество есть равенство, истинное при любых допустимых значениях переменных. Если в это равенство вместо переменных подставить какие-либо допустимые значения, то должно получиться правильное числовое равенство.
Стоит отметить, что истинные числовые равенства также являются тождествами. Тождества, например, будут свойствами действий над числами. 92*b) и -a 3 *b 2 ;
3. ((x 3 *x 8)/x) и x 10 .
Мы всегда можем заменить одно выражение любым другим выражением, тождественно равным первому. Такая замена будет тождественной трансформацией.
Примеры тождеств
Пример 1: Имеют ли место следующие равенства тождеств:
1. а + 5 = 5 + а;
2. а*(-б) = -а*б;
3. 3*а*3*б = 9*а*б;
Не все приведенные выше выражения будут тождествами. Из этих равенств только 1,2 и 3 равенства являются тождествами. Какие бы числа мы в них не подставляли, вместо переменных a и b мы все равно получаем правильные числовые равенства.
Но 4 равенство больше не тождество. Потому что не для всех допустимых значений это равенство будет выполняться. Например, при значениях a = 5 и b = 2 вы получите следующий результат:
Это равенство неверно, так как число 3 не равно числу -3.
Два выражения называются тождественно равными в наборе, если они имеют смысл в этом наборе и все их соответствующие значения равны.
Равенство, в котором левая и правая части тождественно равны, называется тождество.
Замена одного выражения другим, тождественно равным ему на данном множестве, называется тождественным преобразованием выражения.
Задание. Найти область выражения.
Решение. Так как выражение является дробью, то для нахождения его области действия нужно найти те значения переменной X , у которых знаменатель равен нулю, и исключить их. Решая уравнение X 2 — 9 = 0, мы находим, что X = -3 и X = 3. Следовательно, область определения этого выражения состоит из всех чисел, кроме -3 и 3. Если мы обозначим его через X , то можно написать:
X = (-¥; -3) È (-3; 3) È (3; +¥).
Задание. Являются ли выражения и X — 2 тождественно равными: а) на множестве R ; б) на множестве ненулевых целых чисел?
Решение. а) на комплекте Р эти выражения не тождественно равны, так как при X = 0 выражение не имеет значения, а выражение X — 2 имеет значение -2.
б) На множестве целых чисел, отличных от нуля, эти выражения тождественно равны, так как = .
Задание. При каких значениях X следующие равенства являются тождествами:
а) ; б) .
Решение. а) Равенство есть тождество, если ;
б) Равенство есть тождество, если .
Эквивалентные выражения
Рассмотрим выражения 3 2 + 1 а также 5 × 2 . Оба равны 10 . То есть это эквивалентные выражения.
Теперь давайте рассмотрим некоторые выражения, включающие переменные, например 5 Икс + 2 .
Выражение можно переписать как 5 Икс + 2 знак равно Икс + Икс + Икс + Икс + Икс + 1 + 1 .
Мы можем перегруппировать правую часть уравнения, чтобы
2
Икс
+
3
Икс
+
1
+
1
или же
Икс
+
4
Икс
+
2
или какая-то другая комбинация. Все эти выражения имеют одно и то же значение всякий раз, когда одно и то же значение подставляется вместо
Икс
. То есть это эквивалентные выражения.
Все эти выражения имеют одно и то же значение всякий раз, когда одно и то же значение подставляется вместо
Икс
. То есть это эквивалентные выражения.
Говорят, что два выражения эквивалент если они имеют одинаковое значение независимо от значения переменной (переменных) в них.
Пример 1:
Являются ли два выражения 2 у + 5 у − 5 + 8 а также 7 у + 3 эквивалент? Поясните свой ответ.
Объедините подобные члены первого выражения.
Здесь условия
2
у
а также
5
у
похожи на термины. Итак, складываем их коэффициенты.
2
у
+
5
у
знак равно
7
у
.
Также, − 5 а также 8 можно комбинировать, чтобы получить 3 .
Таким образом, 2 у + 5 у − 5 + 8 знак равно 7 у + 3 .
Следовательно, эти два выражения эквивалентны.
Пример 2:
Являются ли два выражения 6 ( 2 а + б ) а также 12 а + 6 б эквивалент? Поясните свой ответ.
Использовать Распределительное право расширить первое выражение.
6 ( 2 а + б ) знак равно 6 × 2 а + 6 × б знак равно 12 а + 6 б
Следовательно, эти два выражения эквивалентны.
Пример 3:
Проверить, являются ли два выражения 2 Икс + 3 у а также 2 у + 3 Икс эквивалент.
Первое выражение представляет собой сумму 2 Икс ‘песок 3 у , тогда как второй является суммой 3 Икс ‘песок 2 у с.
Оценим выражения для некоторых значений Икс а также у . Брать Икс знак равно 0 а также у знак равно 1 .
2 ( 0 ) + 3 ( 1 ) знак равно 0 + 3 знак равно 3 2 ( 1 ) + 3 ( 0 ) знак равно 2 + 0 знак равно 2
Итак, существует хотя бы одна пара значений переменных, для которых два выражения не совпадают.
Следовательно, два выражения нет эквивалент.
Пример 4:
Проверить, являются ли два выражения 3 × м × м м а также м + м + м эквивалент.
Рассмотрим первое выражение для любых ненулевых значений переменной.
Отменить общие условия.
3 × м × м м знак равно 3 м
Соедините подобные члены второго выражения.
м + м + м знак равно 3 м
Так,
3
×
м
×
м
м
знак равно
м
+
м
+
м
когда
м
≠
0
.
Когда м знак равно 0 , выражение 3 × м × м м не определено.
То есть выражения эквивалентны, за исключением случаев, когда м знак равно 0 . Они есть нет эквивалент в общем.
Какое эквивалентное выражение идентично. Преобразования идентичности выражений, их типы
Преобразования идентичности — это работа, которую мы выполняем с числовыми и буквенными выражениями, а также с выражениями, содержащими переменные. Все эти преобразования проведем для того, чтобы привести исходное выражение к виду, удобному для решения задачи. Основные виды тождественных преобразований мы рассмотрим в этой теме.
Яндекс. РТБ Р-А-339285-1
РТБ Р-А-339285-1
Преобразование тождества выражения. Что это?
Впервые с понятием тождественно преобразованные мы встречаемся на уроках алгебры в 7 классе. Тогда мы впервые знакомимся с понятием тождественно равные выражения. Давайте разберемся с понятиями и определениями, чтобы облегчить усвоение темы.
Определение 1
Преобразование тождества выражения — это действия, выполняемые для замены исходного выражения выражением, которое будет тождественно равно исходному.
Часто это определение используется в сокращенной форме, в которой опущено слово «идентичный». Предполагается, что в любом случае мы проводим преобразование выражения таким образом, чтобы получить выражение, идентичное исходному, и это не нужно подчеркивать отдельно.
Проиллюстрируем это определение примерами.
Пример 1
Если заменить выражение x + 3 — 2 на тождественно равное выражение x+1 , то проводим идентичное преобразование выражения x + 3 — 2 .
Пример 2
Замена выражения 2 a 6 выражением a 3 является тождественным преобразованием, а замена выражения x выражением x 2 не является тождественным преобразованием, поскольку выражения x и x2 не тождественно равны.
Обращаем ваше внимание на форму записи выражений при проведении идентичных преобразований. Обычно мы записываем исходное выражение и результирующее выражение в виде равенства. Итак, запись x + 1 + 2 = x + 3 означает, что выражение x + 1 + 2 было приведено к форме x + 3.
Последовательное выполнение действий приводит нас к цепочке равенств, представляющей собой несколько последовательных одинаковых преобразований. Итак, мы понимаем запись х + 1 + 2 = х + 3 = 3 + х как последовательную реализацию двух преобразований: сначала выражение х + 1 + 2 приводилось к виду х + 3, а оно приводилось к форма 3 + х.
Преобразования тождеств и ОДЗ
Ряд выражений, которые мы начинаем изучать в 8 классе, не имеют смысла ни при каких значениях переменных. Проведение одинаковых преобразований в этих случаях требует обратить внимание на область допустимых значений переменных (ОДВ). Выполнение идентичных преобразований может оставить ОДЗ без изменений или сузить ее.
Проведение одинаковых преобразований в этих случаях требует обратить внимание на область допустимых значений переменных (ОДВ). Выполнение идентичных преобразований может оставить ОДЗ без изменений или сузить ее.
Пример 3
При переходе от выражения a + (−b) к выражению a-b диапазон допустимых значений переменных a и b остается прежним.
Пример 4
Переход от выражения х к выражению х 2 х приводит к сужению диапазона допустимых значений переменной х от множества всех действительных чисел к множеству всех действительных чисел, из которого ноль исключен.
Пример 5
Преобразование тождества выражения x 2 x выражение x приводит к расширению диапазона допустимых значений переменной x от множества всех действительных чисел, кроме нуля, до множества всех действительных чисел .
Сужение или расширение диапазона допустимых значений переменных при проведении идентичных преобразований имеет важное значение при решении задач, так как может повлиять на точность вычислений и привести к ошибкам.
Основные преобразования идентичности
Давайте теперь посмотрим, что такое идентичные преобразования и как они выполняются. Выделим в основную группу те виды тождественных преобразований, с которыми нам приходится иметь дело чаще всего.
В дополнение к основным преобразованиям идентификаторов существует ряд преобразований, относящихся к выражениям определенного типа. Для дробей это методы редукции и приведения к новому знаменателю. Для выражений с корнями и степенями — все действия, которые выполняются на основе свойств корней и степеней. Для логарифмических выражений действия, которые выполняются на основе свойств логарифмов. Для тригонометрических выражений все действия с использованием тригонометрических формул. Все эти частные преобразования подробно обсуждаются в отдельных темах, которые можно найти на нашем ресурсе. По этой причине мы не будем останавливаться на них в этой статье.
Перейдем к рассмотрению основных тождественных преобразований.
Перестановка слагаемых, множители
Начнем с перестановки слагаемых.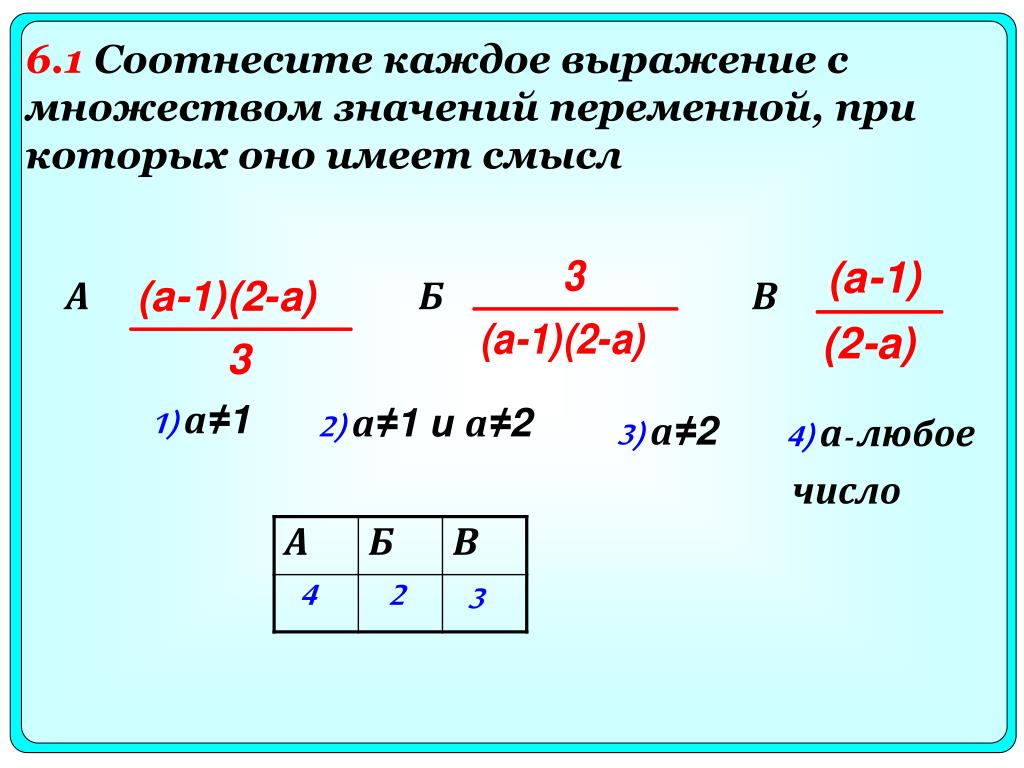 С этим тождественным преобразованием мы имеем дело чаще всего. И главным правилом здесь можно считать следующее утверждение: в любой сумме перестановка слагаемых местами не влияет на результат.
С этим тождественным преобразованием мы имеем дело чаще всего. И главным правилом здесь можно считать следующее утверждение: в любой сумме перестановка слагаемых местами не влияет на результат.
Это правило основано на коммутативных и ассоциативных свойствах сложения. Эти свойства позволяют переставлять термы местами и при этом получать выражения, тождественно равные исходным. Поэтому перестановка членов местами в сумме есть тождественное преобразование.
Пример 6
У нас есть сумма трех слагаемых 3 + 5 + 7 . Если поменять местами слагаемые 3 и 5, то выражение примет вид 5+3+7. Вариантов перестановки слагаемых в этом случае несколько. Все они приводят к получению выражений, тождественно равных исходному.
В качестве слагаемых в сумме могут выступать не только числа, но и выражения. Их так же, как и числа, можно переставлять, не влияя на конечный результат вычислений.
Пример 7
В сумме трех слагаемых 1 а + b, а 2 + 2 а + 5 + а 7 а 3 и — 12 а вида 1 а + b + а 2 + 2 а + 5 + а 7 a 3 + (- 12) a члены можно переставить, например, так (- 12) a + 1 a + b + a 2 + 2 a + 5 + a 7 a 3 . В свою очередь можно переставить члены в знаменателе дроби 1 а + b, при этом дробь примет вид 1 b + а. И выражение под знаком корня а 2 + 2 а + 5 тоже является суммой, в которой члены можно поменять местами.
В свою очередь можно переставить члены в знаменателе дроби 1 а + b, при этом дробь примет вид 1 b + а. И выражение под знаком корня а 2 + 2 а + 5 тоже является суммой, в которой члены можно поменять местами.
Так же, как и члены, в исходных выражениях можно поменять местами множители и получить одинаково правильные уравнения. Это действие регулируется следующим правилом:
Определение 2
В произведении перестановка множителей местами не влияет на результат расчета.
Это правило основано на коммутативных и ассоциативных свойствах умножения, подтверждающих правильность тождественного преобразования.
Пример 8
Работа 3 5 7 Перестановка факторов может быть представлена в одной из следующих форм: 5 3 7 , 5 7 3 , 7 3 5 , 7 5 3 или 3 7 5 .
Пример 9
Перестановка множителей в произведении x + 1 x 2 — x + 1 x даст x 2 — x + 1 x x + 1
Расширение скобок
Скобки могут содержать записи числовых выражений и выражений с переменными . Эти выражения можно преобразовать в тождественно равные выражения, в которых скобок не будет вообще или их будет меньше, чем в исходных выражениях. Этот способ преобразования выражений называется расширением скобок.
Эти выражения можно преобразовать в тождественно равные выражения, в которых скобок не будет вообще или их будет меньше, чем в исходных выражениях. Этот способ преобразования выражений называется расширением скобок.
Пример 10
Выполним действия со скобками в выражении вида 3 + x − 1 x , чтобы получить тождественно истинное выражение 3 + x − 1 x .
Выражение 3 · x — 1 + — 1 + x 1 — x можно преобразовать в тождественно равное выражение без скобок 3 · x — 3 — 1 + x 1 — x .
Подробно правила преобразования выражений со скобками мы обсуждали в теме «Раскрытие скобок», которая размещена на нашем ресурсе.
Группировка терминов, коэффициенты
В случаях, когда мы имеем дело с тремя и более терминами, можно прибегнуть к такому виду тождественных преобразований, как группировка термов. Под этим способом преобразования понимается объединение нескольких терминов в группу путем их перестановки и заключения в скобки.
При группировке термины меняются местами таким образом, что сгруппированные термины находятся в записи выражения рядом друг с другом. После этого их можно заключить в скобки.
После этого их можно заключить в скобки.
Пример 11
Возьмем выражение 5 + 7 + 1 . Если мы сгруппируем первый член с третьим, мы получим (5 + 1) + 7. .
Группировка факторов осуществляется аналогично группировке терминов.
Пример 12
В работе 2 3 4 5 можно сгруппировать первый множитель с третьим, а второй множитель с четвертым, в этом случае придем к выражению (2 4) (3 5) . А если бы мы сгруппировали первый, второй и четвертый факторы, то получили бы выражение (2 3 5) 4 .
Сгруппированные термины и факторы могут быть представлены как простыми числами, так и выражениями. Правила группировки подробно обсуждались в теме «Термины и факторы группировки».
Замена разностей суммами, частичными произведениями и наоборот
Замена разностей суммами стала возможной благодаря нашему знакомству с противоположными числами. Теперь вычитание из числа a числа b можно рассматривать как сложение с числом a числа −b . Равенство a − b = a + (− b) можно считать справедливым и на его основании осуществить замену разностей суммами.
Равенство a − b = a + (− b) можно считать справедливым и на его основании осуществить замену разностей суммами.
Пример 13
Возьмем выражение 4 + 3 − 2 , в котором разница чисел 3 − 2 можно записать в виде суммы 3 + (− 2) . Получить 4 + 3 + (− 2) .
Пример 14
Все различия в выражении 5 + 2 x — x 2 — 3 x 3 — 0, 2 можно заменить такими суммами, как 5 + 2 x + (− x 2) + (− 3 x 3) + (− 0 , 2) .
Суммировать можно из любых разностей. Точно так же мы можем сделать обратную замену.
Замена деления умножением на обратную величину делителя стала возможной благодаря понятию обратных чисел. Это преобразование можно записать как a: b = a (b − 1) .
Это правило легло в основу правила деления обыкновенных дробей.
Пример 15
Частный 1 2: 3 5 можно заменить товаром вида 1 2 5 3 .
Точно так же по аналогии деление можно заменить умножением.
Пример 16
В случае выражения 1+5:x:(x+3) заменить деление на x можно умножить на 1 x . Деление на х + 3 можно заменить умножением на 1 х + 3 . Преобразование позволяет получить выражение, идентичное исходному: 1 + 5 1 x 1 x + 3 .
Замена умножения делением осуществляется по схеме a b = a: (b − 1) .
Пример 17
В выражении 5 х х 2 + 1 — 3 умножение можно заменить делением на 5: х 2 + 1 х — 3.
Выполнение действий с числами
Выполнение действий с числами подлежит правило порядка действий. Во-первых, операции выполняются со степенями чисел и корнями чисел. После этого заменяем логарифмы, тригонометрические и другие функции их значениями. Затем выполняются действия в скобках. А потом уже можно проводить все остальные действия слева направо. Важно помнить, что умножение и деление выполняются раньше, чем сложение и вычитание.
Операции с числами позволяют преобразовать исходное выражение в идентичное ему равное.
Пример 18
Преобразуем выражение 3 · 2 3 — 1 · a + 4 · x 2 + 5 · x, выполнив все возможные действия с числами.
Раствор
Сначала посмотрим на степень 2 3 и корень 4 и вычислить их значения: 2 3 = 8 и 4 = 2 2 = 2 .
Подставляем полученные значения в исходное выражение и получаем: 3 (8 — 1) а + 2 (х 2 + 5 х) .
Теперь расставим скобки: 8 − 1 = 7 . И перейдем к выражению 3 7 а + 2 (х 2 + 5 х).
Нам просто нужно умножить 3 и 7 . Получаем: 21 а + 2 (х 2 + 5 х).
Ответ: 3 2 3 — 1 а + 4 х 2 + 5 х = 21 а + 2 (х 2 + 5 х)
Операциям с числами могут предшествовать другие виды преобразования идентичности, такие как группировка чисел или раскрытие скобок.
Пример 19
Возьмем выражение 3 + 2 (6:3) x (y 3 4) − 2 + 11 .
Раствор
Прежде всего изменим частное в скобках 6:3 по своему значению 2 .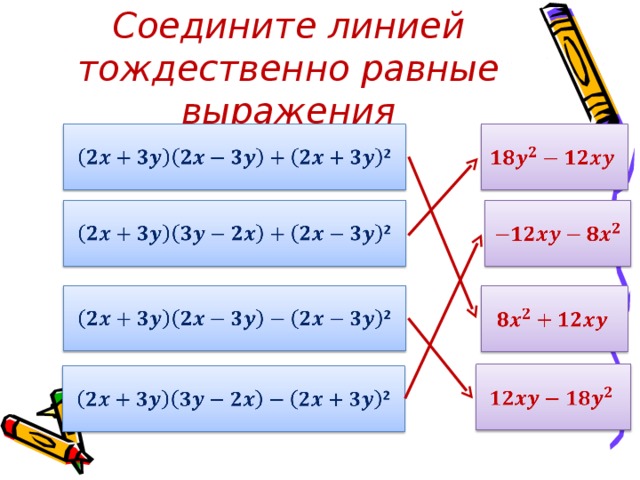 Получаем: 3 + 2 2 х (у 3 4) — 2 + 11 .
Получаем: 3 + 2 2 х (у 3 4) — 2 + 11 .
Раскроем скобки: 3 + 2 2 х (у 3 4) — 2 + 11 = 3 + 2 2 х у 3 4 — 2 + 11 .
Сгруппируем числовые множители в произведении, а также слагаемые, являющиеся числами: (3 − 2 + 11) + (2 2 4) х у 3 .
Раскроем скобки: (3 − 2 + 11) + (2 2 4) x y 3 = 12 + 16 x y 3
Ответ: 3 + 2 (6: 3) x (y 3 4 ) − 2 + 11 = 12 + 16 x y 3
Если мы работаем с числовыми выражениями, то целью нашей работы будет нахождение значения выражения. Если мы преобразуем выражения с переменными, то целью наших действий будет упрощение выражения.
Брекетинг общего множителя
В случаях, когда члены в выражении имеют одинаковый множитель, то этот общий множитель можно вынести за скобки. Для этого сначала нужно представить исходное выражение в виде произведения общего множителя и выражения в скобках, состоящего из исходных членов без общего множителя.
Пример 20
Численно 2 7 + 2 3 мы можем вынести общий множитель 2 вне скобок и получим тождественно правильное выражение вида 2 (7 + 3) .
Освежить в памяти правила вынесения общего множителя за скобки можно в соответствующем разделе нашего ресурса. В материале подробно рассматриваются правила вынесения общего множителя за скобки и приводятся многочисленные примеры.
Приведение подобных членов
Теперь перейдем к суммам, которые содержат подобные члены. Здесь возможны два варианта: суммы, содержащие одинаковые члены, и суммы, члены которых отличаются числовым коэффициентом. Операции с суммами, содержащими одинаковые члены, называются приведением подобных членов. Осуществляется это следующим образом: выносим за скобки общую буквенную часть и вычисляем в скобках сумму числовых коэффициентов.
Пример 21
Рассмотрим выражение 1 + 4 x − 2 x . Мы можем вынести буквальную часть x за скобки и получить выражение 1 + x (4 − 2) . Вычислим значение выражения в скобках и получим сумму вида 1 + x · 2 .
Замена чисел и выражений тождественно равными выражениями
Числа и выражения, составляющие исходное выражение, могут быть заменены тождественно равными им выражениями. Такое преобразование исходного выражения приводит к выражению, тождественно равному ему.
Такое преобразование исходного выражения приводит к выражению, тождественно равному ему.
Пример 22 Пример 23
Рассмотрим выражение 1 + a5 , в котором можно заменить степень a 5 на тождественно равное ей произведение, например, вида a 4 . Это даст нам выражение 1 + a 4 .
Выполненное преобразование является искусственным. Это имеет смысл только при подготовке к другим преобразованиям.
Пример 24
Рассмотрим преобразование суммы 4 x 3 + 2 x 2 . Здесь термин 4×3 мы можем представить как продукт 2 x 2 x 2 x . В результате исходное выражение принимает вид 2 x 2 2 x + 2 x 2 . Теперь мы можем выделить общий делитель 2×2 и вынести его за скобки: 2 x 2 (2 x + 1) .
Сложение и вычитание одного и того же числа
Одновременное сложение и вычитание одного и того же числа или выражения является методом искусственного преобразования выражения.
Пример 25
Рассмотрим выражение х 2 + 2 х . Мы можем прибавить или вычесть из него единицу, что позволит нам впоследствии провести еще одно идентичное преобразование — выбрать квадрат бинома: х 2 + 2 х = х 2 + 2 х + 1 — 1 = (х + 1 ) 2-1 .
Мы можем прибавить или вычесть из него единицу, что позволит нам впоследствии провести еще одно идентичное преобразование — выбрать квадрат бинома: х 2 + 2 х = х 2 + 2 х + 1 — 1 = (х + 1 ) 2-1 .
Если вы заметили ошибку в тексте, выделите ее и нажмите Ctrl+Enter
Основные свойства сложения и умножения чисел.
Коммутативное свойство сложения: при перестановке членов значение суммы не меняется. Для любых чисел a и b верно равенство
Ассоциативное свойство сложения: чтобы к сумме двух чисел прибавить третье число, нужно прибавить к первому числу сумму второго и третьего. Для любых чисел a, b и c справедливо равенство
Коммутативное свойство умножения: перестановка множителей не меняет значения произведения. Для любых чисел a, b и c верно равенство
Ассоциативное свойство умножения: чтобы умножить произведение двух чисел на третье число, нужно умножить первое число на произведение второго и третьего.
Для любых чисел a, b и c справедливо равенство
Распределительное свойство: Чтобы умножить число на сумму, вы можете умножить это число на каждый член и сложить результаты.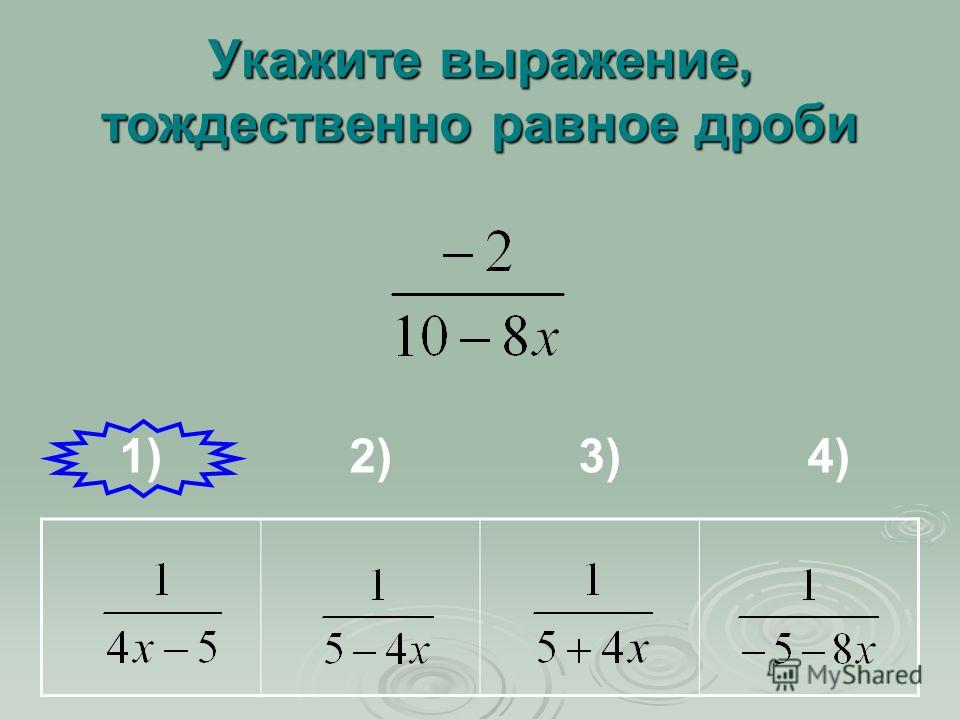 Для любых чисел a, b и c верно равенство
Для любых чисел a, b и c верно равенство
Из коммутативных и ассоциативных свойств сложения следует, что в любой сумме можно как угодно переставлять члены и объединять их в группы произвольным образом.
Пример 1 Подсчитаем сумму 1,23+13,5+4,27.
Для этого удобно объединить первое слагаемое с третьим. Получаем:
1,23+13,5+4,27=(1,23+4,27)+13,5=5,5+13,5=19.
Из коммутативных и ассоциативных свойств умножения следует: в любом произведении можно как угодно переставлять множители и произвольно объединять их в группы.
Пример 2 Найдем стоимость произведения 1,8 0,25 64 0,5.
Объединив первый множитель с четвертым, а второй с третьим, получим:
1,8 0,25 64 0,5 = (1,8 0,5) (0,25 64) = 0,9 16 = 14,4.
Свойство распределения также действует, когда число умножается на сумму трех или более членов.
Например, для любых чисел a, b, c и d верно равенство
a(b+c+d)=ab+ac+ad.
Мы знаем, что вычитание можно заменить сложением, прибавив к уменьшаемому число, противоположное вычитаемому:
Это позволяет рассматривать числовое выражение вида a-b как сумму чисел a и -b, форму a + b-c-d считать суммой чисел a, b, -c, -d и т. д. Рассмотренные свойства действий справедливы и для таких сумм.
д. Рассмотренные свойства действий справедливы и для таких сумм.
Пример 3 Найдем значение выражения 3,27-6,5-2,5+1,73.
Это выражение представляет собой сумму чисел 3,27, -6,5, -2,5 и 1,73. Применяя свойства сложения, получаем: 3,27-6,5-2,5+1,73=(3,27+1,73)+(-6,5-2,5)=5+(-9) = -четыре.
Пример 4 Вычислим произведение 36·().
Множитель можно представить как сумму чисел и -. Используя распределительное свойство умножения, получаем:
36()=36-36=9-10=-1.
Тождества
Определение. Два выражения, соответствующие значения которых равны при любых значениях переменных, называются тождественно равными.
Определение. Равенство, истинное при любых значениях переменных, называется тождеством.
Найдем значения выражений 3(x+y) и 3x+3y для x=5, y=4:
3(x+y)=3(5+4)=3 9=27 ,
3x+3y=3 5+3 4=15+12=27.
Мы получили тот же результат. Из дистрибутивного свойства следует, что, вообще говоря, при любых значениях переменных соответствующие значения выражений 3(x+y) и 3x+3y равны.
Теперь рассмотрим выражения 2x+y и 2xy. Для x=1, y=2 они принимают равные значения:
Однако можно указать значения x и y так, что значения этих выражений не равны. Например, если x=3, y=4, то
Выражения 3(x+y) и 3x+3y тождественно равны, но выражения 2x+y и 2xy не тождественно равны.
Равенство 3(x+y)=x+3y, верное для любых значений x и y, является тождеством.
Истинные числовые равенства также считаются тождествами.
Итак, тождества — это равенства, выражающие основные свойства действий над числами:
a+b=b+a, (a+b)+c=a+(b+c),
ab=ba, (ab) с=а(bc), а(b+c)=ab+ac.
Можно привести и другие примеры тождеств:
a+0=a, a+(-a)=0, a-b=a+(-b),
a 1=a, a (-b)=-ab, (-а)(-б)=аб.
Тождественные преобразования выражений
Замена одного выражения другим, тождественно равным ему, называется тождественным преобразованием или просто преобразованием выражения.
Идентичные преобразования выражений с переменными выполняются на основе свойств операций над числами.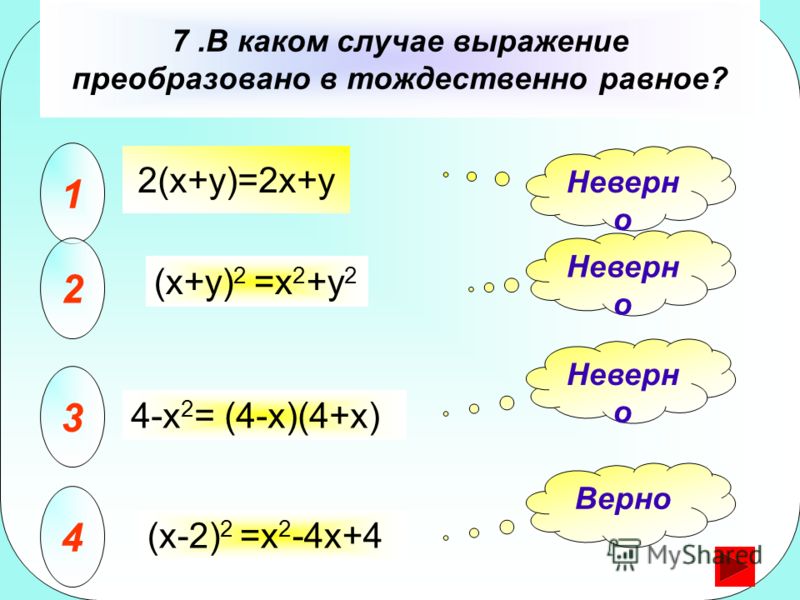
Чтобы найти значение выражения xy-xz по заданным значениям x, y, z, нужно выполнить три шага. Например, при x=2,3, y=0,8, z=0,2 получаем:
xy-xz=2,3 0,8-2,3 0,2=1,84-0,46=1,38.
Этот результат можно получить всего за два шага, используя выражение x(y-z), которое тождественно равно выражению xy-xz:
xy-xz=2,3(0,8-0,2)=2,3 0,6=1,38.
Мы упростили вычисления, заменив выражение xy-xz тождественно равным выражением x(y-z).
Тождественные преобразования выражений широко используются при вычислении значений выражений и решении других задач. Некоторые идентичные преобразования уже были выполнены, например, сокращение однородных терминов, раскрытие скобок. Напомним правила выполнения этих преобразований:
чтобы привести одинаковые члены, нужно сложить их коэффициенты и умножить результат на общую буквенную часть;
если перед скобками стоит знак плюс, то скобки можно опустить, сохранив знак каждого члена, заключенного в скобки;
если перед скобками стоит знак минус, то скобки можно опустить, изменив знак каждого члена, заключенного в скобки.
Пример 1 Сложим одинаковые члены в сумме 5x+2x-3x.
Используем правило сокращения подобных членов:
5x+2x-3x=(5+2-3)x=4x.
Это преобразование основано на распределительном свойстве умножения.
Пример 2 Раскроем скобки в выражении 2a+(b-3c).
Применение правила раскрытия квадратных скобок, которым предшествует знак плюс:
2a+(b-3c)=2a+b-3c.
Выполненное преобразование основано на ассоциативном свойстве сложения.
Пример 3 Раскроем скобки в выражении a-(4b-c).
Воспользуемся правилом раскрытия скобок, которым предшествует знак минус:
a-(4b-c)=a-4b+c.
Выполненное преобразование основано на распределительном свойстве умножения и ассоциативном свойстве сложения. Давайте покажем это. Представим второй член -(4b-c) в этом выражении как произведение (-1)(4b-c): 92-2x)$,$\ \frac(x-y)(y-x)$ и т. д.) Сходство этих понятий состоит в том, что и в многочленах, и в алгебраических дробях присутствуют переменные и числовые значения, арифметические действия: сложение, вычитание, умножение, возведение в степень Отличие этих понятий в том, что деление на переменную не производится в многочленах, а деление на переменную может производиться в алгебраических дробях.
И многочлены, и алгебраические дроби в математике называются рациональными алгебраическими выражениями. Но многочлены — это целочисленные рациональные выражения, а алгебраические дробные выражения — это дробно-рациональные выражения. 92-4x+4)(x-2)$ и $x-2\$ можно считать одинаковыми не для всех значений переменной, потому что для существования дробно-рационального выражения и приведения к многочлену $ x-2$ можно, знаменатель дроби не должен быть равен $0$ (как и множитель на который уменьшаем. В данном примере знаменатель и множитель совпадают, но это не всегда так) .
Значения переменных, для которых будет существовать алгебраическая дробь, называются допустимыми значениями переменных. 92-4x+4)(x-2)$ и $x-2$ идентичны для всех значений переменной, кроме $2$.
Определение 1
тождественно равные Выражения — это такие, которые равны для всех возможных значений переменной.
Тождественное преобразование — это любая замена исходного выражения тождественно равным. К таким преобразованиям относятся выполнение действий: сложение, вычитание, умножение, вынесение общего множителя за скобки, приведение алгебраических дробей к общему знаменателю, приведение алгебраических дробей, приведение однородных членов и т. д. Необходимо учитывать, что ряд преобразований , такие как сокращение, сокращение однородных членов, может изменять допустимые значения переменной.
К таким преобразованиям относятся выполнение действий: сложение, вычитание, умножение, вынесение общего множителя за скобки, приведение алгебраических дробей к общему знаменателю, приведение алгебраических дробей, приведение однородных членов и т. д. Необходимо учитывать, что ряд преобразований , такие как сокращение, сокращение однородных членов, может изменять допустимые значения переменной.
Методы, используемые для подтверждения тождества
Преобразование левой части тождества в правую или наоборот с помощью преобразования тождества
Свести обе части к одному выражению с помощью идентичных преобразований
Перенесите выражения из одной части выражения в другую и докажите, что полученная разность равна $0$
Какой из вышеперечисленных методов использовать для подтверждения данной личности, зависит от исходной личности. 92$
Обратите внимание, что полученное выражение показывает, что исходное тождество верно.
Обратите внимание, что в исходной идентичности разрешены все значения переменной, а это значит, что мы доказали идентичность с помощью одинаковых преобразований, и она верна для всех допустимых значений переменной.
Рассмотрим два равенства:
1. a 12 * a 3 = a 7 * a 8
Это равенство выполняется при любом значении переменной a. Диапазоном допустимых значений для этого равенства будет весь набор действительных чисел.
2. а 12: а 3 = а 2 * а 7 .
Это неравенство будет выполняться для всех значений переменной а, кроме а равного нулю. Диапазоном допустимых значений этого неравенства будет весь набор действительных чисел, кроме нуля.
О каждом из этих равенств можно утверждать, что оно будет верным при любых допустимых значениях переменных а. Такие уравнения в математике называются тождествами .
Понятие тождества
Тождество есть равенство, истинное при любых допустимых значениях переменных. Если в это равенство вместо переменных подставить какие-либо допустимые значения, то должно получиться правильное числовое равенство.
Стоит отметить, что истинные числовые равенства также являются тождествами. Тождества, например, будут свойствами действий над числами.
3. а + b = b + а;
4. а + (б + в) = (а + б) + в;
6. а*(б*с) = (а*б)*с;
7. а*(б + с) = а*б + а*с;
11. а*(-1) = -а.
Если два выражения для любых допустимых переменных соответственно равны, то такие выражения называются тождественно равными . Ниже приведены несколько примеров тождественно равных выражений: 92*b) и -a 3 *b 2 ;
3. ((x 3 *x 8)/x) и x 10 .
Мы всегда можем заменить одно выражение любым другим выражением, тождественно равным первому. Такая замена будет тождественной трансформацией.
Примеры тождеств
Пример 1: Имеют ли место следующие равенства тождеств:
1. а + 5 = 5 + а;
2. а*(-б) = -а*б;
3. 3*а*3*б = 9*а*б;
Не все приведенные выше выражения будут тождествами. Из этих равенств только 1,2 и 3 равенства являются тождествами. Какие бы числа мы в них не подставляли, вместо переменных a и b мы все равно получаем правильные числовые равенства.
Но 4 равенство больше не тождество. Потому что не для всех допустимых значений это равенство будет выполняться. Например, при значениях a = 5 и b = 2 вы получите следующий результат:
Потому что не для всех допустимых значений это равенство будет выполняться. Например, при значениях a = 5 и b = 2 вы получите следующий результат:
Это равенство неверно, так как число 3 не равно числу -3.
Получив представление об идентичностях, логично перейти к знакомству с . В этой статье мы ответим на вопрос, что такое тождественно равные выражения, а также на примерах разберемся, какие выражения тождественно равны, а какие нет.
Навигация по страницам.
Что такое тождественно равные выражения?
Определение тождественно равных выражений дается параллельно с определением тождества. Это происходит на уроке алгебры в 7 классе. В учебнике по алгебре для 7 классов автор Ю. Н. Макарычев дает следующую формулировку:
Определение.
— это выражения, значения которых равны при любых значениях входящих в них переменных. Числовые выражения, соответствующие одинаковым значениям, также называются тождественно равными.
Это определение используется до класса 8, оно справедливо для целочисленных выражений, так как они имеют смысл при любых значениях входящих в них переменных. А в 8 классе уточняется определение тождественно равных выражений. Поясним, с чем это связано.
А в 8 классе уточняется определение тождественно равных выражений. Поясним, с чем это связано.
В 8 классе начинается изучение других видов выражений, которые, в отличие от целочисленных выражений, могут не иметь смысла для некоторых значений переменных. Это заставляет ввести определения допустимых и недопустимых значений переменных, а также диапазона допустимых значений ОДВ переменной и, как следствие, уточнить определение тождественно равных выражений.
Определение.
Два выражения, значения которых равны при всех допустимых значениях их переменных, называются тождественно равными выражениями . Два числовых выражения, имеющие одинаковое значение, также называются тождественно равными.
В этом определении тождественно равных выражений стоит уточнить смысл фразы «для всех допустимых значений входящих в них переменных». Под ним подразумеваются все такие значения переменных, для которых одновременно имеют смысл оба тождественно равных выражения. Эта идея будет разъяснена в следующем разделе на примерах.
Определение тождественно равных выражений в учебнике А. Г. Мордковича дано несколько иначе:
Определение.
Идентичные равные выражения — это выражения слева и справа от тождества.
По смыслу это и предыдущее определения совпадают.
Примеры тождественно равных выражений
Определения, введенные в предыдущем подразделе, позволяют привести примеров тождественно равных выражений .
Начнем с тождественно равных числовых выражений. Числовые выражения 1+2 и 2+1 тождественно равны, потому что они соответствуют равным значениям 3 и 3. Выражения 5 и 30:6 также тождественно равны, как и выражения (2 2) 3 и 2 6 (значения последних выражений равны благодаря ). Но числовые выражения 3+2 и 3−2 не тождественно равны, так как они соответствуют значениям 5 и 1 соответственно, но они не равны.
Теперь приведем примеры тождественно равных выражений с переменными. Это выражения a+b и b+a . Действительно, при любых значениях переменных a и b записанные выражения принимают одни и те же значения (что следует из цифр). Например, с a=1 и b=2 мы имеем a+b=1+2=3 и b+a=2+1=3 . При любых других значениях переменных a и b мы также получим равные значения этих выражений. Выражения 0·x·y·z и 0 также тождественно равны при любых значениях переменных x, y и z. Но выражения 2 х и 3 х не тождественно равны, так как, например, при х=1 их значения не равны. Действительно, при x=1 выражение 2 x равно 2 1=2 , а выражение 3 x равно 3 1=3 .
Например, с a=1 и b=2 мы имеем a+b=1+2=3 и b+a=2+1=3 . При любых других значениях переменных a и b мы также получим равные значения этих выражений. Выражения 0·x·y·z и 0 также тождественно равны при любых значениях переменных x, y и z. Но выражения 2 х и 3 х не тождественно равны, так как, например, при х=1 их значения не равны. Действительно, при x=1 выражение 2 x равно 2 1=2 , а выражение 3 x равно 3 1=3 .
Когда области допустимых значений переменных в выражениях совпадают, как, например, в выражениях а+1 и 1+а , или а б 0 и 0 , или и , и значения этих выражений равны равны для всех значений переменных из этих областей, то здесь все ясно — эти выражения тождественно равны для всех допустимых значений переменных, входящих в них. Итак, a+1≡1+a для любого a , выражения a b 0 и 0 тождественно равны при любых значениях переменных a и b , а выражения и тождественно равны при всех x из ; изд. С. А. Теляковский. — 17-е изд. — М. : Просвещение, 2008. — 240 с. : больной. — ИСБН 978-5-09-019315-3.
Алгебраические выражения
Алгебраические выражения — это выражения, составленные из целочисленных констант, переменных и алгебраических операций.
Например, следующее выражение является алгебраическим выражением:
a + b + 4
Алгебраические выражения можно использовать для записи законов, формул и уравнений. Умение манипулировать алгебраическими выражениями – залог хорошего знания алгебры и высшей математики.
Любая серьезная задача по математике сводится к решению уравнений. А чтобы уметь решать уравнения, нужно уметь работать с алгебраическими выражениями.
А чтобы уметь решать уравнения, нужно уметь работать с алгебраическими выражениями.
Для работы с алгебраическими выражениями необходимо изучить основы арифметики: сложение, вычитание, умножение, деление, основные законы математики, дроби, действия с дробями, пропорции. И не просто выучить, а понять досконально.
Переменные
Буквы, содержащиеся в алгебраических выражениях, называются переменных .
Например, в выражении a + b + 4 буквы a и b являются переменными. Если вместо этих переменных подставить какие-либо числа, то алгебраическое выражение a + b + 4 превратится в числовое выражение, значение которого можно найти.
Числа, подставляемые вместо переменных, называются значениями переменных .
Значение переменной – константа, представляющая собой число, которое выражается как.
Например, измените значения переменных a и b. Знак равенства используется для замены переменных их значениями.
a = 2 , b = 3
Переменной a присвоено значение 2, а переменной b присвоено значение 3. В результате алгебраическое выражение a + b + 4 превращается в обычное числовое выражение 2 + 3 + 4, значение которого можно найти:
2 + 3 + 4 = 9
: Когда переменные перемножаются, они записываются вместе.
Например, запись ab означает то же самое, что запись a × b. Если мы подставим числа 2 и 3 вместо переменных a и b, то получим 6
2 × 3 = 6
. Вы также можете написать умножение числа на выражение в скобках.
Например, вместо a × (b + c) вы можете написать a(b + c). Применяя распределительный закон умножения, получаем a(b + c) = ab + ac.
Коэффициенты
В алгебраических выражениях часто встречаются обозначения, в которых число и переменная записываются вместе, например ‘ 3a’ . На самом деле это короткая запись умножения числа 3 на переменную a, и эта запись выглядит как 3 × a.
Другими словами, выражение 3a является произведением числа 3 и переменной a. Число 3 в этом продукте называется коэффициентом . Этот коэффициент показывает, во сколько раз будет увеличена переменная а. Это выражение можно прочитать как «трижды а» или «увеличить значение а в три раза».
Например, если переменная a равна 5, то значение выражения 3a равно 15.
3 × 5 = 15
Проще говоря, частное — это число, стоящее перед переменной ).
Переменных может быть несколько, например 5abc. Здесь коэффициентом является число 5. Этот коэффициент показывает, что произведение переменных abc увеличивается на пять. Это выражение можно прочитать как «пять раз абв».
Если мы подставим числа 2, 3 и 4 вместо переменных abc, то значение выражения 5abc будет 120
5 × 2 × 3 × 4 = 120
Вы можете мысленно представить, что сначала умножаете числа 2, 3 и 4, а полученное значение умножаете на пять:
Знак коэффициента относится только к коэффициенту, а не к переменным!
Рассмотрим выражение -6b. Минус перед коэффициентом 6 относится только к коэффициенту 6 и не относится к переменной b. Понимание этого факта поможет вам не ошибиться с приметами в будущем.
Минус перед коэффициентом 6 относится только к коэффициенту 6 и не относится к переменной b. Понимание этого факта поможет вам не ошибиться с приметами в будущем.
Пример 1. Найдите значение выражения -6b, когда b = 3.
-6b — это краткая форма -6 × b. Для наглядности запишем выражение -6b в развернутом виде и подставим значение переменной b
−6 b = −6 × b = −6 × 3 = −18
Пример 2. Найдите значение выражения -6b при b = -5
Запишем выражение -6b в развернутом виде
−6 b 919Пример 3. Найдите значение выражения -5a + b, если a = 3 и b = 2
-5a + b является краткой формой -5 × a + b, поэтому для ясности запишем выражение -5 × a + b в развернутом виде и подставить значения переменных a и b
−5 a + b = −5 × a + b = −5 × 3 + 2 = −15 + 2 = −13
Иногда переменные записывают без коэффициента , например a или ab. В этом случае коэффициент равен 1:
В этом случае коэффициент равен 1:
1 a , 1 ab
но единицу обычно не записывают, поэтому пишут просто a или ab.
Если перед переменной стоит минус, коэффициент равен -1.
Например, выражение -a на самом деле выглядит как -1a. Это произведение минус единицы и переменной а. Получается следующим образом:
−1 × a = −1 a
Здесь есть небольшая загвоздка. В выражении -a минус перед переменной a на самом деле относится к невидимой единице, а не к переменной a. Поэтому следует быть осторожным при решении проблем.
Например, если дано выражение -а и нас просят найти его значение при а = 2, то в школе мы подставляли два вместо переменной а и получали ответ -2, не особо задумываясь, как так получилось . На самом деле мы умножили минус один на положительное число 2.
−a = −1 × a
−1 × a = −1 × 2 = −2
Если задано выражение -a и мы хотим найти его значение для a = -2 , подставим -2 вместо переменной a
−a = −1 × a
−1 × a = −1 × (−2) = 2
Во избежание ошибок первое время невидимо единицы могут быть записаны явно.
Пример 4. Вычислите выражение abc для a=2, b=3 и c=4
Выражение abc представляет собой краткую форму 1×a×b×c. Для наглядности запишем abc в развернутом виде и подставим значения переменных a, b, c
1 × a × b × c = 1 × 2 × 3 × 4 = 24
Пример 5. Вычислите выражение abc для a=-2, b=-3 и c=-4
Запишите выражение abc в развернутом виде и подставьте значения переменных a, b и c
1 × a × b × c = 1 × (−2) × (−3) × (−4) = −24
Пример 6. Вычислить выражение -abc для a=3, b=5 и c=7
Выражение -abc представляет собой краткую форму -1×a×b×c. Для наглядности напишем выражение -abc в развернутом виде и подставим значения переменных a, b и c
−abc = −1 × a × b × c = −1 × 3 × 5 × 7 = −105
Пример 7. Вычислить выражение -abc для a=-2, b=-4 и c=-3
Запишите выражение -abc в расширенной форме:
−abc = −1 × a × b × c
Подставим значения переменных a, b и c
−abc = −1 × a × b × c = −1 × (−2) × (−4) × (−3) = 24
Как вычислить коэффициент
Иногда вам нужно решить задачу, в которой вы хотите вычислить коэффициент выражения. В принципе, эта проблема очень проста. Достаточно уметь правильно умножать числа.
В принципе, эта проблема очень проста. Достаточно уметь правильно умножать числа.
Чтобы вычислить частное выражения, умножьте числа в выражении отдельно и перемножьте переменные отдельно. Полученный числовой множитель и будет коэффициентом.
Пример 1. Вычислить коэффициент в выражении: 7m×5a×(-3)×n
Выражение состоит из нескольких множителей. Это хорошо видно, если записать выражение в развернутом виде. То есть, запишите произведения 7m и 5a в виде 7×m и 5×a
7 × m × 5 × a × (−3) × n
Примените ассоциативный закон умножения, который позволяет нам умножайте множители в любом порядке. А именно, умножать отдельно числа и отдельно умножать буквы (переменные):
−3 × 7 × 5 × m × a × n = −105man
Коэффициент равен -105. После завершения желательно расположить переменную часть в алфавитном порядке:
−105amn
Пример 2. Вычислим коэффициент в выражении: -a×(-3)×2
Умножим числа и переменные отдельно:
−a × (−3) × 2 = −3 × 2 × (−a) = −6 × (−a) = 6a
Коэффициент равен 6,
Пример 3. Рассчитаем коэффициент в выражении:
Рассчитаем коэффициент в выражении:
Перемножим числа и переменные отдельно:
Коэффициент равен -1. Обратите внимание, единицу не пишут, потому что коэффициент 1 принято не писать.
Эти, казалось бы, простые задачи могут сыграть с нами очень злую шутку. Часто оказывается, что знак у частного неправильный: либо отсутствует знак минус, либо, наоборот, он поставлен зря. Чтобы избежать этих досадных ошибок, тему умножения целых чисел нужно изучить на хорошем уровне.
Слагаемые в алгебраических выражениях
При сложении нескольких чисел получается сумма чисел. Добавляемые числа называются слагаемыми. Может быть более одного слагаемого, например:
1 + 2 + 3 + 4 + 5
Когда выражение состоит из слагаемых, его гораздо легче вычислить, потому что сложение проще, чем вычитание. Но выражение может содержать не только сложение, но и вычитание, например:
1 + 2 − 3 + 4 − 5
В этом выражении числа 3 и 5 являются вычитателями, а не слагаемыми. Но ничто не мешает нам заменить вычитание сложением. Тогда снова получаем выражение, состоящее из слагаемых:
Но ничто не мешает нам заменить вычитание сложением. Тогда снова получаем выражение, состоящее из слагаемых:
1 + 2 + (−3) + 4 + (−5)
Неважно, что числа -3 и -5 теперь со знаком минус. Главное, чтобы все числа в этом выражении были соединены знаком сложения, то есть выражение представляло собой сумму.
Оба выражения 1 + 2 — 3 + 4 — 5 и 1 + 2 + (-3) + 4 + (-5) равны одному и тому же значению — минус один:
1 + 2 — 3 + 4 — 5 = -1
1 + 2 + (-3) + 4 + (-5) = -1
Таким образом, значение выражения не изменится, если мы подставим сложение для вычитания где-то.
Вы также можете заменить вычитание сложением в алгебраических выражениях. Например, рассмотрим следующее выражение:
7a + 6b − 3c + 2d − 4s
По возможности заменить вычитание сложением:
7a + 6b + (−3c) + 2d + (−4s)
Для любых значений переменных a, b, c, d и s выражения 7a + 6b — 3c + 2d — 4s и 7a + 6b + (-3c) + 2d + (-4s) будут равны ценность.
Будьте готовы к тому, что учитель в школе или преподаватель в институте может назвать даже те числа (или переменные), которые не являются слагаемыми.
Например, если на доске написана разница a — b, учитель не скажет, что a — это уменьшаемое, а b — это вычитаемое. Он будет называть обе переменные одним общим словом — слагаемые. Это потому, что математик видит выражение формы a — b как сумму a + (-b). В этом случае выражение становится суммой, а переменные a и (-b) становятся слагаемыми.
Похожие термины
Подобные термины (аналогичные термины) — это термины, которые имеют одинаковые переменные .
Например, рассмотрим выражение 7a + 6b + 2a. Слагаемые 7а и 2а имеют одни и те же переменные — переменную а. Таким образом, слагаемые 7а и 2а подобны.
Обычно подобные члены добавляются для упрощения выражения или решения уравнения. Это действие называется , объединяющим подобные термины .
Чтобы объединить одинаковые члены, просуммируйте все коэффициенты этих членов и умножьте результат на одну и ту же переменную часть.
Например, объедините одинаковые термины в выражении 3a + 4a + 5a. В этом случае все слагаемые одинаковы. Сложите их коэффициенты и умножьте результат на общую переменную часть — на переменную а
3а + 4а + 5а = (3 + 4 + 5)×а = 12а
Такие термины обычно объединяют в уме и результат записывается сразу:
3а + 4а + 5а = 12а
Также можно рассуждать так:
Было 3 переменных и , добавлены еще 4 переменные и и еще 5 переменных и . В результате получилось 12 переменных a
Давайте рассмотрим несколько примеров комбинирования подобных терминов. Учитывая, что эта тема очень важная, сначала подробно распишем каждую деталь. Несмотря на то, что здесь все очень просто, большинство людей допускают массу ошибок. В основном по невнимательности, а не по незнанию.
Пример 1. Объедините одинаковые члены в выражение 3a + 2a + 6a + 8a
Сложите коэффициенты в этом выражении и умножьте результат на ту же переменную часть:
3 а + 2 а + 6 а + 8 а = (3 + 2 + 6 + 8) × a = 19 a
Построение (3 + 2 + 6 + 8) × a можно не записывать, поэтому сразу записываем ответ
3 a + 2 a + 6 а + 8 а = 19 а
Пример 2. Объединить одинаковые члены в выражении 2a + a
Второе слагаемое a написано без коэффициента, но на самом деле ему предшествует коэффициент 1, которого мы не видим, потому что он не записан. Таким образом, выражение выглядит следующим образом:
2а + 1а
Теперь соединим подобные члены. То есть складываем коэффициенты и результат умножаем на общую переменную часть:
2а + 1а = (2 + 1) × а = 3а
Запишем решение вкратце:
2a + a = 3a
Соединяя одинаковые члены в выражении 2a+a, можно рассуждать иначе:
Были 2 переменные a , мы добавили еще одну переменную и , так что мы получили 3 переменные и .
Пример 3. Объединить одинаковые члены в выражении 2a − a
Заменить вычитание сложением:
2a + (−a)
Второе слагаемое (-a) записывается без коэффициента, но на самом деле выглядит как (-1a). Коэффициент -1 снова невидим, потому что не записывается. Следовательно, выражение выглядит так:
2a + (−1a)
Теперь объединим одинаковые члены. Сложите коэффициенты и умножьте результат на равную переменную часть:
2а + (−1а) = (2 + (−1)) × а = 1а = а
Обычно записывают короче:
2a − a = a
Соединяя одинаковые слагаемые в выражении 2a−a , можно рассуждать иначе: оставив одну переменную a
Пример 4. Объедините одинаковые члены в выражении 6a − 3a + 4a − 8a
Замените вычитание сложением, где это возможно: 8а = 6а + (-3а) + 4а + (-8а)
Теперь давайте объединим одинаковые термины. Складываем коэффициенты и результат умножаем на равную переменную часть
Складываем коэффициенты и результат умножаем на равную переменную часть
(6 + (−3) + 4 + (−8)) × a = −1a = −a
Запишем решение кратко:
6a − 3a + 4a − 8a = −a
Существуют выражения, содержащие несколько различных одинаковых членов.
Например, 3а + 3б + 7а + 2б. Для таких выражений действуют те же правила, что и для остальных, а именно сложение коэффициентов и умножение результата на общую переменную часть. Но во избежание ошибок удобно подчеркивать разные группы слагаемых разными чертами.
Например, в выражении 3a + 3b + 7a + 2b те термины, которые содержат переменную a , можно подчеркнуть одной чертой, а те термины, которые содержат переменную b , можно подчеркнуть двумя черточками:
Теперь давайте объединим одинаковые термины. То есть сложить коэффициенты и умножить результат на общую переменную часть. Сделайте это для обеих групп слагаемых: для слагаемых, содержащих переменную и , и для слагаемых, содержащих переменную 9. 1974 б .
1974 б .
3a + 3b + 7a + 2b = (3+7)×a + (3 + 2)×b = 10a + 5b
Опять же, выражение несложное, и подобные термины можно комбинировать в уме:
3A + 3B + 7A + 2B = 10A + 5B
Пример 5. Объединение, как термины в выражении 5A — 6A -7B + B
Заменить субтракцию с добавлением, где это возможно:
7479Заменить с добавлением с добавлением:
7474. 5a − 6a −7b + b = 5a + (−6a) + (−7b) + b
Подчеркнем одинаковые термины разными черточками. Одной чертой подчеркните термы, содержащие переменные a , а двумя черточками подчеркните термы, содержащие переменные b :
Теперь объединим одинаковые термы. Сложите коэффициенты и умножьте результат на общую переменную часть:
5a + (−6a) + (−7b) + b = (5 + (−6))×a + ((−7) + 1) ×b = −a + (−6b)
Если выражение содержит обычные числа без каких-либо переменных множителей, они складываются отдельно.
Пример 6. Объедините одинаковые члены в выражение 4a + 3a − 5 + 2b + 7
Замените вычитание сложением, где это возможно:
4a + 3a − 5 + 2b + 7 = 4a + 3a + (−5) + 2b + 7
Теперь давайте объединим одинаковые члены. Числа -5 и 7 не имеют буквенных множителей, но они подобны слагаемым — вам просто нужно их сложить. А терм 2b останется неизменным, потому что это единственный член в выражении, имеющий буквальный множитель 9.1974 b
, и добавить не к чему:4a + 3a + (−5) + 2b + 7 = (4 + 3)×a + 2b + (−5) + 7 = 7a + 2b + 2
Запишем решение вкратце:
4a + 3a − 5 + 2b + 7 = 7a + 2b + 2
Термы можно расположить так, чтобы в одна и та же часть выражения.
Пример 7. Объединение одинаковых членов в выражение 5t+2x+3x+5t+x
Поскольку выражение представляет собой сумму нескольких членов, это позволяет нам вычислять его в любом порядке. Следовательно, мы можем записать термы, содержащие переменную t , в начало выражения, а термы, содержащие переменную x , в конец выражения:
Следовательно, мы можем записать термы, содержащие переменную t , в начало выражения, а термы, содержащие переменную x , в конец выражения:
5t + 5t + 2x + 3x + x
Теперь можно комбинировать подобные члены:
5t + 5t + 2x + 3x + x = (5+5)×t + (2+3+1)×x = 10t + 6x
Запишем решение коротко:
5t + 2x + 3x + 5t + x = 10t + 6x
Сумма противоположных чисел равна нулю. Это правило работает и для алгебраических выражений. Если в выражении есть одинаковые слагаемые, но с противоположными знаками, от них можно избавиться на этапе объединения однотипных слагаемых . Другими словами, просто вычеркните их из выражения, так как их сумма равна нулю.
Пример 8. Объединить одинаковые члены в выражение 3t − 4t − 3t + 2t
По возможности заменить вычитание сложением:
3t − 4t − 3t + 2t = 3t + (−4t) + (−3t) + 2t противоположный. Сумма противоположных членов равна нулю. Если мы удалим этот ноль из выражения, значение выражения не изменится, поэтому мы его удалим. И убираем его, просто зачеркнув слагаемые 3t и (-3t)
Сумма противоположных членов равна нулю. Если мы удалим этот ноль из выражения, значение выражения не изменится, поэтому мы его удалим. И убираем его, просто зачеркнув слагаемые 3t и (-3t)
В итоге у нас осталось выражение (-4t)+2t. В этом выражении мы можем объединить одинаковые члены и получить окончательный ответ:
(−4t) + 2t = ((−4) + 2)×t = −2t
Кратко запишем решение:
Упрощение выражений
» упростить выражение » , а затем дает выражение, которое вы хотите упростить. Упростить выражение означает сделать его проще и короче.
На самом деле, мы уже упрощали выражения, когда сокращали дроби. После сокращения дробь становится короче и понятнее.
Рассмотрим следующий пример. Упростите выражение.
Это назначение можно буквально понимать как: « Примените любые возможные действия к этому выражению, но упростите его «.
В этом случае можно уменьшить дробь, а именно разделить числитель и знаменатель дроби на 2:
Что еще можно сделать? Мы можем вычислить полученную дробь. Тогда получаем десятичную дробь 0,5
Тогда получаем десятичную дробь 0,5
В итоге дробь упростили до 0,5.
Первый вопрос, который вы должны задать себе при решении подобных задач, должен быть: «Что можно сделать?» Потому что есть действия, которые можно совершить, и есть действия, которые нельзя совершить.
Еще одна важная вещь, о которой следует помнить, это то, что значение выражения не должно меняться после упрощения выражения. Вернемся к выражению. Это выражение представляет собой деление, которое можно выполнить. Выполнив это деление, мы получим значение этого выражения, равное 0,5
Но мы упростили выражение и получили новое упрощенное выражение. Значение нового упрощенного выражения по-прежнему равно 0,5
Таким образом, как бы мы ни упрощали выражение, значение полученных выражений по-прежнему равно 0,5. Таким образом, упрощение было выполнено правильно на каждом шаге. Это то, к чему мы должны стремиться при упрощении выражений — на значение выражения не должны влиять наши действия.
Часто бывает необходимо упростить переменные выражения. К ним применяются те же правила упрощения, что и к числовым выражениям. Любые допустимые действия могут быть выполнены до тех пор, пока значение выражения не изменится.
Давайте рассмотрим несколько примеров.
Пример 1. Упростите выражение 5,21s × t × 2,5
Чтобы упростить это выражение, вы можете умножать числа отдельно и умножать переменные отдельно. Эта задача очень похожа на ту, которую мы рассматривали, когда учились определять коэффициент:
5,21s × t × 2,5 = 5,21 × 2,5 × s × t = 13,025 × st = 13,025st
Таким образом, выражение 5,21с×т×2,5 упрощается до 13,025ст.
Пример 2. Упростим выражение -0,4 × (-6,3b) × 2
Второе произведение (-6,3b) можно перевести в понятный нам вид, а именно записать в виде ( -6,3)×b, затем перемножить числа отдельно и перемножить переменные отдельно:
− 0,4 × (−6,3b) × 2 = − 0,4 × (−6,3) × b × 2 = 5,04b
Таким образом, выражение -0,4 × (-6,3b) × 2 упрощается до 5,04b
Пример 3. Упростим выражение
Упростим выражение
Давайте разберем это выражение более подробно, чтобы ясно видеть, где числа и где переменные:
Теперь умножьте числа отдельно и умножьте переменные отдельно:
Таким образом, выражение упрощается до -abc. Это решение можно записать в более короткой форме:
При упрощении выражений дроби можно сокращать в процессе их решения, а не в самом конце, как мы это делали с правильными дробями.
Например, если мы встретимся с выражением типа при его решении, то не обязательно вычислять числитель и знаменатель и сделать примерно так:
Дроби можно сократить, выбрав в числителе множитель и множитель в знаменателе и уменьшив эти множители на их наибольший общий делитель. Другими словами, используйте краткий вариант сокращения дроби, в котором мы не описываем подробно, на что были разделены числитель и знаменатель.
Например, в числителе множитель 12, а в знаменателе множитель 4 можно уменьшить на 4. Четверку держим в уме, и после деления 12 и 4 на эту четверку записываем ответы рядом с этими чисел, предварительно зачеркнув их
Четверку держим в уме, и после деления 12 и 4 на эту четверку записываем ответы рядом с этими чисел, предварительно зачеркнув их
Тогда в числителе множитель 9, а в знаменателе множитель 3 можно уменьшить на 3
Тогда в числителе множитель 6, а в знаменателе множитель 2 уменьшить к 2
Теперь можно умножить полученные маленькие множители. В данном случае их немного и их можно перемножать в уме:
Со временем вы можете обнаружить, что при решении той или иной задачи выражения начинают «укорачиваться», поэтому желательно привыкнуть к быстрым вычислениям. То, что вы можете просчитать в своей голове, вы должны просчитать в своей голове. То, что можно быстро сократить, должно быть сокращено быстро.
Пример 4. Упростим выражение
Умножим числа отдельно и переменные отдельно:
Таким образом, выражение упростится до
Пример 5. Упростим выражение
Умножим числа отдельно и переменные отдельно: 3
Таким образом, выражение упрощается до млн .
Пример 6. Упростим выражение
Распишем это выражение подробнее, чтобы было понятно, где числа, а где переменные:
Теперь умножьте числа отдельно и переменные отдельно. Для удобства десятичное -6,4 и смешанное число можно преобразовать в дроби:
Таким образом, выражение упростится до -6,4stx
Решение для этого примера можно записать в гораздо более короткой форме. Это будет выглядеть следующим образом:
Пример 7. Упростить выражение
Перемножить числа и переменные отдельно. Для удобства смешанное число и десятичные дроби 0,1 и 0,6 можно преобразовать в дроби:
Таким образом, выражение упрощается до abcd. Если опустить детали, это решение можно записать намного короче:
Обратите внимание, как сокращается дробь. Новые множители, полученные в результате уменьшения предыдущих множителей, также могут быть уменьшены.
Теперь поговорим о том, чего делать не следует. При упрощении выражений совершенно нельзя умножать числа и переменные, если выражение представляет собой сумму, а не произведение.
Например, если вы хотите упростить выражение 5a + 4b, вы не можете написать так:
Это эквивалентно тому, как если бы нас попросили сложить два числа, и мы бы умножили их вместо сложения.
При подстановке любых значений переменных a и b выражение 5a +4b превращается в обычное числовое выражение. Предположим, что переменные a и b имеют следующие значения:
a = 2, b = 3
Тогда значение выражения будет 22
5a + 4b = 5 × 2 + 4 × 3 = 10 + 12 = 22
Сначала выполняется умножение, а затем результаты суммируются. А если бы мы попытались упростить это выражение, перемножив числа и переменные, то получили бы следующее:
5a + 4b = 5 × 4 × a × b = 20ab
20ab = 20 × 2 × 3 = 120
Получается совсем другое значение выражения. В первом случае это 22, во втором случае 120. Это означает, что упрощение выражения 5a + 4b было сделано неправильно .
В первом случае это 22, во втором случае 120. Это означает, что упрощение выражения 5a + 4b было сделано неправильно .
После упрощения выражения его значение не должно меняться при тех же значениях переменных. Если подстановка любых значений переменных в исходное выражение дает одно значение, то после упрощения выражения значение должно быть таким же, как и до упрощения.
Вы ничего не можете сделать с выражением 5a + 4b. Это не упрощенно.
Если выражение содержит одинаковые члены, их можно добавить, если наша цель — упростить выражение.
Пример 8. Упростите выражение 0,3a-0,4a+a
Чтобы упростить это выражение, вы можете объединить подобные члены:
0,3a − 0,4a + a = 0,3a + (−0,4a) + a = (0,3 + (−0,4) + 1)×a = 0,9a
или меньше: 0,3a − 0,4a + a = 0,9a
Таким образом, выражение 0,3a-0,4a +a упрощается до 0,9a
Пример 9. Упростите выражение −7,5a − 2,5b + 4a
Упростите выражение −7,5a − 2,5b + 4a
Чтобы упростить это выражение, вы можете объединить подобные члены:
−7,5a − 2,5b + 4a = −7,5a + (−2,5b) + 4a = ((−7,5) + 4)×a + (−2,5b) = −3,5a + (−2,5b)
или короче: −7,5a − 2,5b + 4a = −3,5a + (−2,5b)
Слагаемое (-2,5b) осталось неизменным, поскольку к нему нечего было добавить.
Пример 10. Упростите выражение
Чтобы упростить это выражение, вы можете объединить подобные члены:
Коэффициент был преобразован в неправильную дробь для простоты вычисления.
Таким образом, выражение упростится до
Пример 11. Упростите выражение
Чтобы упростить это выражение, вы можете объединить подобные члены:
Таким образом, выражение упростится до .
В этом примере было бы разумнее сначала добавить первый и последний коэффициенты. В этом случае мы получим короткое решение. Это будет выглядеть так:
Это будет выглядеть так:
Пример 12. Упростим выражение
Чтобы упростить это выражение, вы можете комбинировать подобные термины:
Таким образом, выражение упрощается до .
Слагаемое осталось без изменений, потому что к нему нечего было добавить.
Это решение можно записать гораздо короче. Это будет выглядеть следующим образом:
В кратком решении отсутствуют этапы замены вычитания сложением и подробная запись того, как дроби приводились к общему знаменателю.
Другое отличие состоит в том, что в подробном решении ответ выглядит как , а в кратком — как . По сути, это одно и то же выражение. Отличие состоит в том, что в первом случае вычитание заменено сложением, потому что в начале, когда мы записывали решение в развернутой форме, мы везде, где это возможно, заменяли вычитание сложением, и эта замена сохраняется для ответ.
Личность. Эквивалентные выражения
После упрощения выражения оно становится проще и короче. Чтобы проверить правильность упрощения выражения, просто подставьте любые значения переменных сначала в предыдущее выражение, которое нужно упростить, а затем в новое упрощенное выражение. Если значение в обоих выражениях одинаковое, это означает, что выражение упрощено правильно.
Чтобы проверить правильность упрощения выражения, просто подставьте любые значения переменных сначала в предыдущее выражение, которое нужно упростить, а затем в новое упрощенное выражение. Если значение в обоих выражениях одинаковое, это означает, что выражение упрощено правильно.
Рассмотрим простой пример. Пусть выражение 2a × 7b упростится. Чтобы упростить это выражение, мы можем перемножить числа и переменные отдельно:
2 a × 7 b = 2 × 7 × a × b = 14 ab
Проверим, правильно ли мы упростили выражение. Для этого подставляем любые значения переменных a и b сначала в первое выражение, которое мы хотели упростить, а затем во второе выражение, которое мы упростили.
Пусть значения переменных a, b будут следующими:
a = 4
b = 5
Подставим их в первое выражение которое получается в результате упрощения выражения 2a × 7b, а именно в выражении 14ab
14 ab = 14 × 4 × 5 = 280
Мы видим, что при a = 4 и b = 5 значение первого выражения 2a × 7b, а значение второго выражения 14ab равно
2 a × 7 b = 2 × 4 × 7 × 5 = 280
14 ab = 14 × 4 × 5 = 280
То же самое произойдет для любых других значений. Например, пусть a = 1 и b = 2
Например, пусть a = 1 и b = 2
2 a × 7 b = 2 × 1 × 7 × 2 = 28
14 × 7 × 1 = 1 827 1 949 919
Таким образом, выражения 2a × 7b и 14ab равны одному и тому же значению для всех значений переменных. Такие выражения называются эквивалентных выражения .
Делаем вывод, что между выражениями 2a × 7b и 14ab можно поставить знак равенства, так как они равны одному и тому же значению: любое выражение, соединенное знаком равенства (=).
Равенство формы 2a × 7b = 14ab называется уравнением тождества .
Тождество — это равенство, истинное для всех значений переменных. 9
a(b + c) = ab + ac законы математики, которые мы изучали, тождественны.
Истинные числовые уравнения также являются тождествами. Например:
2 + 2 = 4
3 + 3 = 5 + 1
10 = 7 + 2 + 1
При решении сложной задачи для упрощения расчета сложное выражение заменяется на более простое выражение, тождественно равное предыдущему.
Например, мы упростили выражение 2a × 7b и получили более простое выражение 14ab. Это упрощение можно назвать преобразованием идентичности .
Вы часто будете видеть задание, в котором говорится « доказать равенство уравнения», за которым следует равенство, которое вы хотите доказать. Обычно это равенство состоит из двух частей: левой и правой частей равенства. Наша задача — произвести тождественные преобразования с одной частью равенства и получить другую часть. Или выполните преобразования идентичности для обеих частей равенства и сделайте так, чтобы обе части равенства имели одинаковые выражения.
Например, докажите, что равенство 0,5a × 5b = 2,5ab является тождеством.
Упростим левую часть этого равенства. Для этого перемножьте числа и переменные по отдельности:
0,5 × 5 × a × b = 2,5ab
2,5ab = 2,5ab
В результате небольшого тождественного преобразования левая часть равенство стало равным правой части равенства. Итак, мы доказали, что равенство 0,5a × 5b = 2,5ab является тождеством.
Итак, мы доказали, что равенство 0,5a × 5b = 2,5ab является тождеством.
Из тождественных преобразований мы научились складывать, вычитать, умножать и делить числа, сокращать дроби, добавлять одинаковые термины и упрощать некоторые выражения.
Но это не все тождественные преобразования, существующие в математике. Есть еще много одинаковых преобразований. Мы еще не раз увидимся в будущем.
Упражнения:
Вычислите выражение 2xy для и
Показать решение
Оцените выражение -xy для
Показать решение
Оцените выражение -xyz для и и
Показать решение
Вычислите выражение -0.02ab для и
Показать решение
Задание 5. Запишите следующую последовательность действий в виде алгебраического выражения:
- умножьте на на три и из этого произведения вычтите пятнадцать
- умножьте т на девять, и прибавьте к произведению тридцать пять.

Показать решение
Задание 6. Объедините одинаковые члены в следующее выражение:
Показать решение
Задание 7. Объединить одинаковые члены в следующее выражение:
Показать решение
Задание 8. Объединить одинаковые члены в следующее выражение:
Показать решение
9.51 9.50402 9 похожие члены в следующем выражении:Показать решение
Задача 10. Объединить одинаковые члены в следующем выражении:
Показать решение
Задача 11. Упростить выражение:
Показать решение
Задача 12. Упростить выражение:
Показать решение
Задача 13. Упростить выражение:
Покажите решение
Задача 14. Упрощение экспрессии:
Покажите решение
4.Задача 15. Упростите выражение:
Показать решение
Задача 16.