Способ подстановки в решении систем: Решение систем уравнений — метод как решить систему линейных уравнений

Решение системы линейных уравнений. Метод подстановки, сложения, графический. Особые случаи, тесты

Математика->Система уравнений->решение системы линейных уравнений->

Тестирование онлайн

• Система линейных уравнений

Система линейных уравнений

Обычно уравнения системы записывают в столбик одно под другим и объединяют фигурной скобкой

Система уравнений такого вида, где a, b, c — числа, а x, y — переменные, называется системой линейных уравнений.

При решении системы уравнений используют свойства, справедливые для решения уравнений.

Решение системы линейных уравнений способом подстановки

Рассмотрим пример

1) Выразить в одном из уравнений переменную. Например, выразим y в первом уравнении, получим систему:

2) Подставляем во второе уравнение системы вместо y выражение 3х-7:

3) Решаем полученное второе уравнение:

4) Полученное решение подставляем в первое уравнение системы:

Система уравнений имеет единственное решение: пару чисел x=1, y=-4. Ответ: (1; -4), записывается в скобках, на первой позиции значение x, на второй — y.

Решение системы линейных уравнений способом сложения

Решим систему уравнений из предыдущего примера методом сложения.

1) Преобразовать систему таким образом, чтобы коэффициенты при одной из переменных стали противоположными. Умножим первое уравнение системы на «3».

2) Складываем почленно уравнения системы. Второе уравнение системы (любое) переписываем без изменений.

3) Полученное решение подставляем в первое уравнение системы:

Решение системы линейных уравнений графическим способом

Графическое решение системы уравнений с двумя переменными сводится к отыскиванию координат общих точек графиков уравнений.

Графиком линейной функции является прямая. Две прямые на плоскости могут пересекаться в одной точке, быть параллельными или совпадать. Соответственно система уравнений может: а) иметь единственное решение; б) не иметь решений; в) иметь бесконечное множество решений.

2) Решением системы уравнений является точка (если уравнения являются линейными) пересечения графиков.

Графическое решение системы

Метод введения новых переменных

Замена переменных может привести к решению более простой системы уравнений, чем исходная.

Рассмотрим решение системы

Введем замену , тогда

Переходим к первоначальным переменным

Особые случаи

Не решая системы линейных уравнений, можно определить число ее решений по коэффициентам при соответствующих переменных.

Пусть дана система

1) Если , то система имеет единственное решение.

2) Если , то система решений не имеет. В этом случае прямые, являющиеся графиками уравнений системы, параллельны и не совпадают.

3) Если , то система имеет бесконечное множество решений. В этом случае прямые совпадают друг с другом.

§ Системы уравнений. Как решать системы уравнений

Прежде чем перейти к разбору как решать системы уравнений, давайте разберёмся, что называют системой уравнений с двумя неизвестными.

Запомните!

Системой уравнений называют два уравнения с двумя неизвестными (чаще всего неизвестные в них называют «x» и «y»), которые объединены в общую систему фигурной скобкой.

Например, система уравнений может быть задана следующим образом.

	x + 5y = 7
	3x − 2y = 4

Чтобы решить систему уравнений, нужно найти и «x», и «y».

Существуют два основных способа решения систем уравнений. Рассмотрим оба способа решения.

Способ подстановки

или
«железобетонный» метод

Первый способ решения системы уравнений называют способом подстановки или «железобетонным».

Название «железобетонный» метод получил из-за того, что с помощью этого метода практически всегда можно решить систему уравнений. Другими словами, если у вас не получается решить систему уравнений, всегда пробуйте решить её методом подстановки.

Разберем способ подстановки на примере.

	x + 5y = 7
	3x − 2y = 4

Выразим из первого уравнения «x + 5y = 7» неизвестное «x».

Важно!

Чтобы выразить неизвестное, нужно выполнить два условия:

• перенести неизвестное, которое хотим выразить, в левую часть уравнения;
• разделить и левую и правую часть уравнения на нужное число так, чтобы коэффициент при неизвестном стал равным единице.

Перенесём в первом уравнении «x + 5 y = 7» всё что содержит «x» в левую часть, а остальное в правую часть по правилу переносу.

При «x» стоит коэффициент равный единице, поэтому дополнительно делить уравнение на число не требуется.

	x = 7 − 5y
	3x − 2y = 4

Теперь, вместо «x» подставим во второе уравнение полученное выражение
«x = 7 − 5y» из первого уравнения.

	x = 7 − 5y
	3(7 − 5y) − 2y = 4

Подставив вместо «x» выражение «(7 − 5y)» во второе уравнение, мы получили обычное линейное уравнение с одним неизвестным «y». Решим его по правилам решения линейных уравнений.

Чтобы каждый раз не писать всю систему уравнений заново, решим полученное уравнение «3(7 − 5y) − 2y = 4» отдельно. Вынесем его решение отдельно с помощью обозначения звездочка (*).

	x = 7 − 5y
	3(7 − 5y) − 2y = 4  (*)

 (*)   3(7 − 5y) − 2y = 4
21 − 15y − 2y = 4
− 17y = 4 − 21
                 − 17y = − 17     | :(−17)
y = 1

Мы нашли, что «y = 1». Вернемся к первому уравнению «x = 7 − 5y» и вместо «y» подставим в него полученное числовое значение. Таким образом можно найти «x».

Запишем в ответ оба полученных значения.

	x = 7 − 5y
	y = 1

	x = 7 − 5 · 1
	y = 1

	x = 2
	y = 1

Ответ: x = 2; y = 1

Способ сложения

Рассмотрим другой способ решения системы уравнений. Метод называется способ сложения. Вернемся к нашей системе уравнений еще раз.

	x + 5y = 7
	3x − 2y = 4

По правилам математики уравнения системы можно складывать. Наша задача в том, чтобы сложив исходные уравнения, получить такое уравнение, в котором останется только одно неизвестное.

Давайте сейчас сложим уравнения системы и посмотрим, что из этого выйдет.

Запомните!

При сложения уравнений системы левая часть первого уравнения полностью складывается с левой частью второго уравнения, а правая часть полностью складывается с правой частью.

	x + 5y = 7		(x + 5y) + (3x − 2y) = 7 + 4
		+          =>	x + 5y + 3x − 2y = 11
	3x − 2y = 4		4x + 3y = 11

При сложении уравнений мы получили уравнение «4x + 3y = 11». По сути, сложение уравнений в исходном виде нам ничего не дало, так как в полученном уравнении мы по прежнему имеем оба неизвестных.

Вернемся снова к исходной системе уравнений.

	x + 5y = 7
	3x − 2y = 4

Чтобы при сложении неизвестное «x» взаимноуничтожилось, нужно сделать так, чтобы в первом уравнении при «x» стоял коэффициент «−3».

Для этого умножим первое уравнение на «−3».

Важно!

При умножении уравнения на число, на это число умножается каждый член уравнения.

	x + 5y = 7 | ·(−3)
	3x − 2y = 4

	x ·(−3) + 5y · (−3) = 7 · (−3)
	3x − 2y = 4

	−3x −15y = −21
	3x − 2y = 4

Теперь сложим уравнения.

	−3x −15y = −21		(−3x −15y ) + (3x − 2y) = −21 + 4
		+          =>	−3x −15y + 3x − 2y = −21 + 4
	3x − 2y = 4		−17y = −17 |:(−17)
			y = 1

Мы нашли «y = 1». Вернемся к первому уравнению и подставим вместо «y» полученное числовое значение и найдем «x».

	x = 7 − 5y
	y = 1

	x = 7 − 5 · 1
	y = 1

	x = 2
	y = 1

Ответ: x = 2; y = 1

Пример решения системы уравнения

способом подстановки

	x − 3y = 17
	x − 2y = −13

Выразим из первого уравнения «x».

	x = 17 + 3y
	x − 2y = −13

Подставим вместо «x» во второе уравнение полученное выражение.

	x = 17 + 3y
	(17 + 3y) − 2y = −13 (*)

(*) (17 + 3y) − 2y = −13
17 + 3y − 2y = −13
17 + y = −13
y = −13 − 17
y = −30

Подставим в первое уравнение полученное числовое значение «y = −30» и найдем «x».

	x = 17 + 3y
	y = −30

	x = 17 + 3 · (−30)
	y = −30

	x = 17 −90
	y = −30

	x = −73
	y = −30

Ответ: x = −73; y = −30

Пример решения системы уравнения

способом сложения

Рассмотрим систему уравнений.

	3(x − y) + 5x = 2(3x − 2)
	4x − 2(x + y) = 4 − 3y

Раскроем скобки и упростим выражения в обоих уравнениях.

	3x − 3y + 5x = 6x − 4
	4x − 2x − 2y = 4 − 3y

	8x − 3y = 6x − 4
	2x −2y = 4 − 3y

	8x − 3y − 6x = −4
	2x −2y + 3y = 4

	2x − 3y = −4
	2x + y = 4

Мы видим, что в обоих уравнениях есть «2x». Наша задача, чтобы при сложении уравнений «2x» взаимноуничтожились и в полученном уравнении осталось только «y».

Для этого достаточно умножить первое уравнение на «−1».

	2x − 3y = −4      |·(−1)
	2x + y = 4

	2x · (−1) − 3y · (−1) = −4 · (−1)
	2x + y = 4

	−2x + 3y = 4
	2x + y = 4

Теперь при сложении уравнений у нас останется только «y» в уравнении.

	−2x + 3y = 4		(−2x + 3y ) + (2x + y) = 4 + 4
		+          =>	−2x + 3y + 2x + y = 4 + 4
	2x + y = 4		4y = 8         | :4
			y = 2

Подставим в первое уравнение полученное числовое значение «y = 2» и найдем «x».

	−2x + 3y = 4
	y = 2

	−2x + 3 · 2 = 4
	y = 2

	−2x + 6 = 4
	y = 2

	−2x = −2       | :(−2)
	y = 2

	x = 1
	y = 2

Ответ: x = 1; y = 2

Метод замены | Решение системы уравнений подстановкой

Одним из методов алгебраического решения системы линейных уравнений с двумя переменными является метод подстановки. В этом методе мы находим значение любой из переменных, изолируя ее с одной стороны и беря все остальные члены с другой стороны уравнения. Затем подставляем это значение во второе уравнение. Он включает в себя простые шаги, чтобы найти значения переменных системы линейных уравнений методом подстановки. Давайте узнаем об этом подробно в этой статье.

1.	Что такое метод замещения?
2.	Решение систем уравнений методом подстановки
3.	Разница между методом исключения и замены
4.	Часто задаваемые вопросы о методе замены

Что такое метод замены?

Метод подстановки — это простой способ алгебраического решения системы линейных уравнений и поиска решений переменных. Как следует из названия, он включает в себя нахождение значения переменной x через переменную y из первого уравнения, а затем подстановку или замену значения переменной x во втором уравнении. Таким образом, мы можем решить и найти значение переменной y.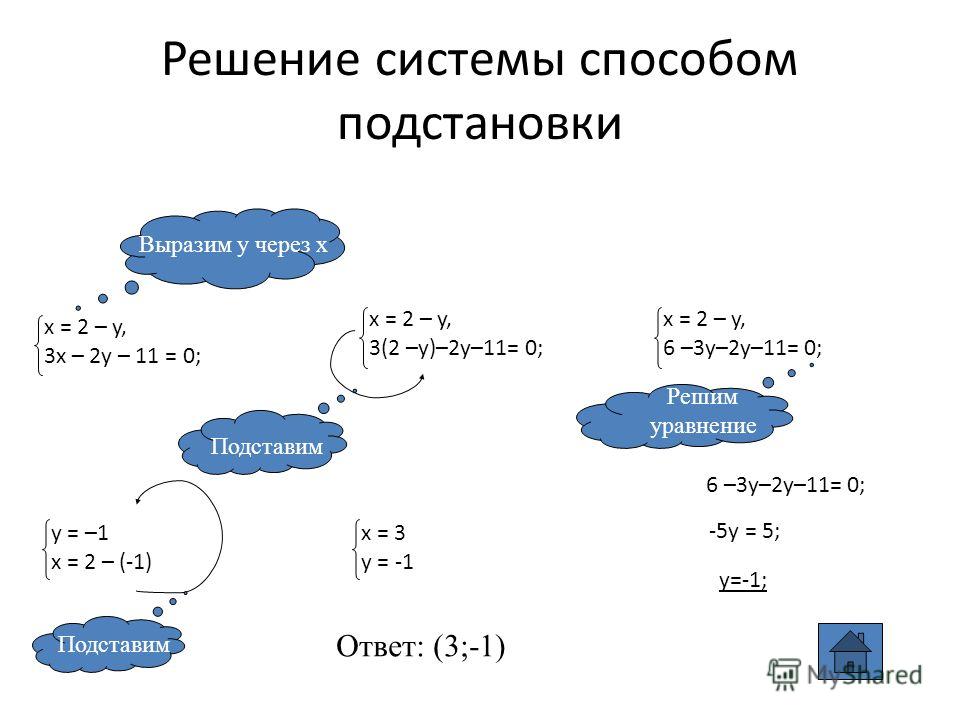 И, наконец, мы можем подставить значение y в любое из данных уравнений, чтобы найти x. Этот процесс также можно поменять местами, когда мы сначала находим x, а затем находим y.

Определение метода подстановки

Метод подстановки — это один из алгебраических методов решения одновременных линейных уравнений. Он включает в себя подстановку значения любой из переменных из одного уравнения в другое уравнение. Двумя другими алгебраическими методами решения линейных уравнений являются метод исключения и метод перекрестного умножения. Помимо алгебраического метода, мы также можем решить систему линейных уравнений графически.

Рассмотрим пример решения двух уравнений x-2y=8 и x+y=5 методом подстановки.

Решение систем уравнений методом подстановки

Шаги по применению или использованию метода подстановки для решения системы уравнений приведены ниже:

• Шаг 1:  Упростите данное уравнение, при необходимости расширив скобки.
• Шаг 2: Решите любое уравнение для любой из переменных. Вы можете использовать любую переменную, исходя из простоты расчета.
• Шаг 3: Подставьте полученное значение x или y в другое уравнение.
• Шаг 4: Теперь упростим новое уравнение, полученное с помощью арифметических операций, и решим уравнение для одной переменной.
• Шаг 5: Теперь подставьте значение переменной из  Шаг 4  в любое из приведенных уравнений, чтобы найти другую переменную.

Вот пример решения системы уравнений методом подстановки: 2x+3(y+5)=0 и x+4y+2=0.

Решение:

Шаг 1:  Итак, здесь мы можем упростить первое уравнение, чтобы получить 2x + 3y + 15 = 0. Теперь у нас есть два уравнения:

2x + 3y + 15 = 0 _____ ( 1)

x + 4y + 2 = 0 ______ (2)

Шаг 2: Решаем уравнение (2) относительно x. Итак, получаем x = -4y — 2.

Шаг 3: Подставляем полученное значение x в уравнение (1). т. е. подставляя x = -4y-2 в уравнение 2x + 3y + 15 = 0, получаем 2(-4y-2) + 3y + 15 = 0,

Шаг 4: Теперь упростим новое уравнение. Получаем -8y-4+3y+15=0

-5y + 11 = 0

-5y = -11

y = 11/5

Шаг 5: Теперь подставим значение y в любое из приведенных уравнений. Подставим значение y в уравнение (2).

x + 4y + 2 = 0

x + 4 × (11/5) + 2 = 0

x + 44/5 + 2 = 0

x + 54/5 = 0

x = -54 /5

Следовательно, решив данную систему уравнений методом подстановки, получим x = -54/5 и y= 11/5.

Разница между методом исключения и замены

И метод исключения, и метод подстановки являются способами алгебраического решения линейных уравнений. Когда метод подстановки становится немного трудным для применения в уравнениях, содержащих большие числа или дроби, мы можем использовать метод исключения, чтобы облегчить наши вычисления. Давайте поймем разницу между этими двумя методами с помощью приведенной ниже таблицы:

Метод замены	Метод исключения
Здесь мы находим значение любой из переменных и подставляем его значение в другое уравнение.	В этом методе мы умножаем или делим одно или оба уравнения на число, чтобы сделать коэффициенты переменной x или переменной y одинаковыми в обоих уравнениях. Затем мы добавляем или вычитаем уравнения, чтобы исключить переменную с тем же коэффициентом. Таким образом, мы находим значение одной переменной, которое можно подставить в любое из уравнений, чтобы найти и другую переменную.
Метод подстановки лучше использовать, когда уравнения либо заданы в виде, либо могут быть приведены в виде x = ay + b и y = mx + n.	Лучше использовать метод исключения, когда коэффициент любого из слагаемых одинаков. Например, Ax+By+C=0 и Px+By+R=0.

Важные примечания к методу подстановки:

• Чтобы начать с метода подстановки, сначала выберите уравнение с коэффициентом 1 хотя бы для одной из переменных и решите для той же переменной (с коэффициентом 1). Это упрощает процесс.
• Перед тем, как начать использовать метод подстановки, объедините все одинаковые термины (если они есть).
• После решения для одной переменной мы можем выбрать любое из заданных уравнений или любое уравнение во всем процессе, чтобы найти другую переменную.
• Если при решении методом подстановки мы получаем какое-либо верное утверждение, например, 3 = 3, 0 = 0 и т. д., то это означает, что система имеет бесконечно много решений.
• Если мы получим какое-либо ложное утверждение типа 3 = 2, 0 = 1 и т. д. при решении методом подстановки, то это означает, что система не имеет решения.

☛  Похожие темы:

Ознакомьтесь с этими статьями, посвященными методу замены.

• Калькулятор метода замены
• Калькулятор метода замены
• Решатель системы уравнений

 

Примеры методов замены

1. Пример 1: Шон получил два уравнения 5m−2n=17 и 3m+n=8. Можете ли вы помочь ему найти решение этих уравнений методом подстановки?

   Решение: Даны два уравнения:

   5m−2n=17 ____ (1)

   3m+n=8 _____ (2)

   Решение данных двух уравнений можно найти, выполнив следующие действия. :

   • Из уравнения 2 мы можем найти значение n через m, где n = 8 — 3m
   • Подставляем значение n в уравнение 1. Получаем, 5m — 2(8-3m)=17

   5м — 2(8-3м)=17

   5м — 16 + 6м =17

   11м = 17 + 16

   11m=33

   m = 3

   • Подставляем значение m в уравнение 2, получаем 3×3+n=8

   9+n=8

   n=8-9

   n=-1

   Ответ:  Следовательно, методом подстановки мы выяснили, что m=3 и n=-1.

2. Пример 2: У Джеки есть два числа, сумма которых равна 20, а разница между ними равна 10. Найдите числа, используя метод подстановки решения линейных уравнений.

   Решение: Пусть два числа будут x и y такими, что x>y. Дано, что x+y=20 ___ (1) и x−y=10 ___ (2). Из уравнения 1 получаем x = 20-y. Подставьте это значение в уравнение 2, чтобы найти значение y.

   x−y=10

   20-y-y=10

   20-2y=10

   20-10=2y

   10=2y

   y=10/2 = 5 9000 y в уравнении 1, мы получаем, x+5=20, что дает нам x=15.

   Ответ: Следовательно, эти два числа — 15 и 5.

3. Пример 3: Решить данную систему линейных уравнений методом подстановки:

   — 2x — 5 + 3x + y = 0 ___ (1)

   3x + y = 11 ___ (2)

   Решение: Как мы видим, первое уравнение можно еще больше упростить, комбинируя подобные члены. После упрощения получаем x+y-5=0. Из этого уравнения найдем значение x через y, то есть x = 5-y. Теперь подставляем это значение в уравнение 2, получаем 3(5-y)+y=11.

   15-3y+y=11

   15-2y=11

   15-11=2y

   4=2y

   y=4/2=2

   Теперь подставим значение y в уравнение 1. Получаем x+2-5=0, что можно упростить до x = 3.

   Ответ:  Следовательно, методом подстановки имеем x=3 и y=2.

перейти к слайдуперейти к слайдуперейти к слайду

Разбивайте сложные концепции с помощью простых визуальных эффектов.

Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.

Записаться на бесплатный пробный урок

Практические вопросы по методу замены

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы о методе замены

Что такое метод подстановки в алгебре?

В алгебре метод подстановки является одним из способов решения линейных уравнений с двумя переменными. В этом методе мы подставляем значение переменной, найденное одним уравнением, во второе уравнение. Его очень легко использовать, когда у нас есть меньшие числа, но в случае больших чисел или дробных коэффициентов применять метод подстановки становится утомительно.

Когда следует использовать метод подстановки?

Метод подстановки можно применить к любой паре линейных уравнений с двумя переменными. Метод подстановки целесообразно использовать, когда мы имеем меньшие коэффициенты в терминах или когда уравнения заданы в виде x = ay+c и y=bx+p.

Что мы заменяем в методе замещения?

В методе подстановки мы подставляем значение одной переменной, найденное путем упрощения уравнения, в другое уравнение. Например, если в уравнениях m и n две переменные, то мы можем сначала найти значение m через n из любого из уравнений, а затем подставить это значение во второе уравнение, чтобы получить ответ n . Затем снова подставляем значение n в любое из данных уравнений.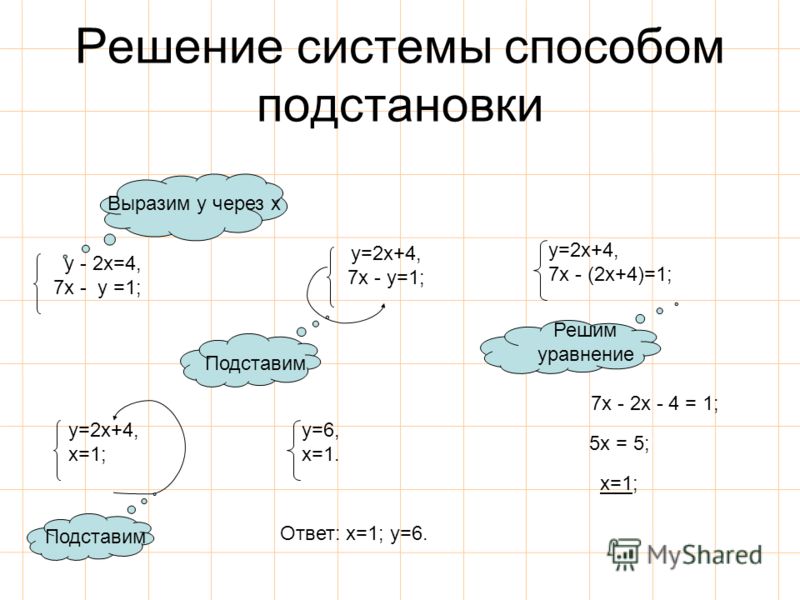

Что общего между методом замены и методом исключения?

Оба метода включают процесс замены. В обоих методах мы сначала находим значение одной переменной, а затем подставляем его в любое из заданных уравнений. Таким образом, это характерно как для метода исключения, так и для метода замены.

Что такое первый шаг в методе замещения?

Первым шагом в методе подстановки является нахождение значения любой из переменных в одном уравнении через другую переменную. Например, если есть два уравнения x+y=7 и x-y=8, то из первого уравнения можно найти, что x=7-y. Это первый шаг применения метода замещения.

Каковы шаги метода замены?

Ниже приведены три простых шага метода подстановки :

• Найдите значение любой переменной из любого уравнения через другую переменную.
• Подставьте его в другое уравнение и решите.
• Снова подставьте значение второй переменной в любое из уравнений.

Как использовать метод подстановки с двумя переменными?

Имея две переменные, скажем, x и y, мы сначала находим значение x через y из любого из приведенных уравнений. Затем мы подставляем это значение в другое уравнение, чтобы найти значение y. Наконец, мы снова подставляем значение y в любое данное уравнение, чтобы найти x.

Является ли метод замены только для линейных уравнений?

Нет, метод подстановки можно применять для любого типа уравнений. Например, уравнения y = x ²  и y = 3x + 4 можно решить методом подстановки.

Скачать БЕСПЛАТНЫЕ учебные материалы

ЛИСТКИ

Решение систем линейных уравнений с помощью подстановки

Горячая математика

Системы линейных уравнений:

А система линейные уравнения представляет собой просто набор из двух или более линейных уравнений.

В двух переменных ( Икс и у ) , график системы двух уравнений представляет собой пару прямых на плоскости.

Есть три возможности:

• Линии пересекаются в нулевых точках. (Прямые параллельны.)
• Линии пересекаются ровно в одной точке. (Большинство случаев.)
• Прямые пересекаются в бесконечном числе точек. (Два уравнения представляют одну и ту же прямую.)

Как решить систему с помощью Метод замены

• Шаг 1 : Сначала решим одно линейное уравнение относительно у с точки зрения Икс .
• Шаг 2 : Затем подставьте это выражение вместо у в другом линейном уравнении. Вы получите уравнение в Икс .
• Шаг 3 : Решите это, и вы получите Икс -координата перекрестка.
• Шаг 4 : Затем подключите Икс к любому уравнению, чтобы найти соответствующее у -координата.

Запись 1 : Если проще, можно начать с решения уравнения для Икс с точки зрения у , а также – такая же разница!

Пример:

Решите систему { 3 Икс + 2 у знак равно 16 7 Икс + у знак равно 19

Решите второе уравнение для у .

у знак равно 19 − 7 Икс

Заменять 19 − 7 Икс за у в первом уравнении и решить Икс .

3 Икс + 2 ( 19− 7 Икс ) знак равно 16 3 Икс + 38 − 14 Икс знак равно 16 − 11 Икс знак равно − 22 Икс знак равно 2

Заменять 2 за Икс в у знак равно 19 − 7 Икс и решить для у .

у знак равно 19 − 7 ( 2 ) у знак равно 5

Решение ( 2 , 5 ) .

No related posts.