Самостоятельная работа «Умножение и деление обыкновенных дробей». Математика 6 класс
Главная / Старшие классы / Алгебра
Скачать
19.61 КБ, 494962.docx Автор: Галустян Светлана Леоновна, 21 Мар 2015
Самостоятельная работа «Умножение и деление обыкновенных дробей». Математика 6 класс
Автор: Галустян Светлана Леоновна
Похожие материалы
| Тип | Название материала | Автор | Опубликован |
|---|---|---|---|
| документ | Самостоятельная работа «Умножение и деление обыкновенных дробей». Математика 6 класс | Галустян Светлана Леоновна | 21 Мар 2015 |
| документ | Самостоятельная работа «Умножение и деление» 3 класс | Урясьева Александра Сергеевна | 6 Дек 2015 |
| разное | Урок — сказка » Умножение и деление обыкновенных дробей», математика 6 класс | Бацева Ольга Анатольевна | 1 Апр 2015 |
| документ | Умножение и деление обыкновенных дробей (математика 6 класс) | Севрюгина Марина Александровна | 21 Мар 2015 |
| документ | Контрольная работа по математике в 6 классе на тему «Деление и умножение обыкновенных дробей» | Игнатьева Анастасия Геннадьевна | 25 Апр 2015 |
| разное | Обобщающий урок по теме «Умножение и деление обыкновенных дробей», 6 класс | Эдольф Светлана Викторовна | 1 Апр 2015 |
| презентация, документ | Обобщающий урок по теме «Умножение и деление обыкновенных дробей», 6 класс | Ризатдинова Гульнар Хасановна | 1 Апр 2015 |
| документ | Методическая разработка (6 класс) по теме:»Умножение и деление обыкновенных дробей» | 8 Апр 2015 | |
| презентация, документ | Методическая разработка урока математики «В мире необыкновенных животных» ( умножение и деление обыкновенных дробей, 6 класс). | Руженцева Наталья Викторовна | 15 Окт 2015 |
| документ | Самостоятельная работа по теме «Умножение и деление десятичных дробей» 5 класс | Бердникова Елена Леопольдовна | 1 Фев 2016 |
| разное | Урок «Деление обыкновенных дробей» 6 класс | Домрычева Марина Николаевна | 1 Апр 2015 |
| презентация | Урок с презентацией «Деление обыкновенных дробей». Математика. 6 класс. | Красавина Юлия Алексеевна | 21 Мар 2015 |
| документ | Методическая разработка: «Деление обыкновенных дробей». Математика 6 класс. Конспект урока. Математика 6 класс. Конспект урока. | Коровкина Валентина Николаевна | 20 Мар 2015 |
| разное | Конспект и презентация к уроку математики в 6 классе на тему » Деление и умножение обыкновенных дробей» | Денисова Любовь Владимировна | 21 Мар 2015 |
| документ | Урок математики в 6 классе на тему «Умножение и деление обыкновенных дробей» | Голюшова Клара Витальевна | 20 Мар 2015 |
| документ | Урок математики в 6 классе по теме «Умножение и деление обыкновенных дробей» УМК Мордковича А. Г. (ФГОС) Г. (ФГОС) | Дьяченкова Надежда Анатольевна | 21 Мар 2015 |
| документ | Конспект урока по математике в 6 классе по теме «Умножение и деление обыкновенных дробей» | Барабанова Ольга Алексеевна | 1 Апр 2015 |
| документ | Методическая разработка урока по математике «Умножение и деление обыкновенных дробей » в 6 классе | Иванова Надежда Мефодьевна | 1 Апр 2015 |
| документ | «Умножение и деление обыкновенных дробей» в 6 классе. | Крякина Надежда Александровна | 8 Фев 2016 |
| документ | Конспект урока по математике 6 класс «Деление обыкновенных дробей» Давыденко Наталья Борисовна Урок в 6-м классе «Деление обыкновенных дробей» | Давыденко Наталья Борисовна | 1 Апр 2015 |
| разное | Урок «Деление дробей» 6 класс Урок «Деление обыкновенных дробей» | Денейко Екатерина Сергеевна | 1 Апр 2015 |
| документ | Урок математики. 6 класс. Тема: Умножение и деление обыкновенных дробей. 6 класс. Тема: Умножение и деление обыкновенных дробей. | сайфутдинова лариса григорьевна | 9 Июл 2015 |
| документ | Самостоятельная работа по математике 6 класс по теме «Деление дробей» | Ласая Ольга Николаевна | 21 Мар 2015 |
| презентация | Устная работа»Умножение обыкновенных дробей» | Павленко Ольга Юрьевна | 6 Дек 2015 |
| документ | контрольная работа по математике по теме «Табличное умножение и деление» 2 класс программа «Перспектива» | Прелова Елена Анатольевна | 6 Дек 2015 |
| документ | Контрольная работа «Умножение и деление» 2 класс | Cтепанова Инна Анатольевна | 14 Апр 2015 |
| документ | Контрольная работа 3 класс по теме «Табличное умножение и деление» | Храмова Евгения Юрьевна | 6 Дек 2015 |
| разное | Конспект урока по математике » Табличное умножение и деление» 2 класс | Москалева Анжела Александровна | 6 Июн 2015 |
| документ | Урок алгебры по теме «Деление обыкновенных дробей» (6 класс) | Рябошапко Галина Николаевна | 21 Мар 2015 |
| презентация | Презентация к уроку по математике 6 класс «Деление обыкновенных дробей» | Давыденко Наталья Борисовна | 1 Апр 2015 |
| презентация | Презентация для интерактивной доски «Деление обыкновенных дробей» 6 класс Диск | Шапков Виктор Петрович | 1 Апр 2015 |
| документ | Технологическая карта по теме «Деление обыкновенных дробей», 6 класс | Лукина Лариса Николаевна | 26 Окт 2015 |
| документ | Умножение и деление дробей (математика 6 класс) | Применко Анастасия Сергеевна | 21 Мар 2015 |
| презентация | Самостоятельные работы «Сложение и вычитание обыкновенных дробей» и «Деление и умножение» | Неровнова Вера Владимировна | 7 Апр 2016 |
| презентация | Устная работа»Деление обыкновенных дробей» | Павленко Ольга Юрьевна | 15 Дек 2015 |
| презентация | Урок математики 5 класс «Деление обыкновенных дробей» | Кузьмина Елена Владимировна | 8 Июл 2015 |
| разное | Урок соревнование по математике «Умножение и деление обыкновенных дробей» | Кальянова Наталья Михайловна | 21 Мар 2015 |
| разное | Использование ИКТ-технологии при изучении темы «Умножение и деление обыкновенных дробей на натуральное число» | Демидова Инна Раисовна | 31 Мар 2015 |
| презентация | Презентация «Координатная плоскость. Умножение и деление обыкновенных дробей» Умножение и деление обыкновенных дробей» | Басинских Любовь Алексеевна | 1 Апр 2015 |
| документ | Разработка открытого урока «Умножение и деление обыкновенных дробей» | Васина Олеся Анатольевна | 4 Ноя 2015 |
Сведения об общеобразовательной организации
Сведения об общеобразовательной организацииЦвет:C C C
Изображения Вкл. Выкл.
Обычная версия сайта
- Телефон доверия: 8 800 200-01-22
Ошибка 404
К сожалению запрашиваемая страница не найдена.
Но вы можете воспользоваться поиском или картой сайта ниже
|
|
Методическая разработка урока «Умножение обыкновенных дробей»
- org/Person»>
Малиева Виктория Викторовна, Учитель математики
Разделы: Математика
Класс: 5
Ключевые слова: умножение дробей
Тип урока: Урок открытия нового знания.
Учебное оборудование: мультимедийный проектор, компьютер, экран, раздаточный материал.
Цели: >
- Деятельностная цель: формирование у учащихся способностей к самостоятельному построению новых способов действия на основе метода рефлексивной самоорганизации.
- Образовательная цель: расширение понятийной базы по теме «Действия с обыкновенными дробями»: вывести правило умножения дробей, сформировать умение умножать обыкновенные дроби.

В ходе урока учащиеся смогут применить правило при решении упражнений.
Планируемые результаты:
- Личностные результаты: формировать устойчивый познавательный интерес, выражают положительное отношение к процессу познания; адекватно оценивают свою учебную деятельность; применяют правила делового сотрудничества.
- Метапредметные результаты.
- Коммуникативные УУД: вступают в обсуждение, аргументируя свою точку зрения, используя адекватные языковые средства ; развивают умение договариваться и приходить к общему решению; оформляют мысли в устной и письменной речи с учетом речевых ситуаций.
- Регулятивные: определяют цель учебной деятельности, осуществляют поиск средства её достижения; ставят учебную задачу на основе соотнесения того, что уже известно и усвоено, и того, что еще неизвестно.
- Познавательные: передают содержание в сжатом (развернутом) виде, выводы в виде правил.

Предметные результаты:
- Формулировать правило умножения обыкновенных дробей.
- Применять правило умножения обыкновенных дробей при решении заданий.
Ресурсы:
- Алгоритм умножения обыкновенных дробей.
- Задание на карточках.
- Презентация «Умножение обыкновенных дробей».
Этап (учебная ситуация) | Деятельность учителя | Деятельность учащихся | ||||||
1. Этап мотивации. | — Здравствуйте! Садитесь. | Демонстрируют готовность к уроку | ||||||
| 2. Актуализация знаний. Цель этапа: повторение изученного материала, необходимого для «открытия нового знания», и выявление затруднений в индивидуальной деятельности каждого учащегося | Устная работа. — Как называется число, записанное на доске? Что вы о нем знаете? — Какая часть фигуры закрашена? | Дают ответы: — Обыкновенные дроби. | ||||||
— Как называются данные числа? 2/3, 4/9, 11/8, 12/5. — Как называются первые две дроби? Какие дроби называются правильными? Другие две дроби. | — Правильные дроби. Это дроби, у которых числитель меньше знаменателя. — Неправильные дроби. Это дроби, у которых числитель больше или равен знаменателю. | |||||||
| — Сократить дроби: (Что означает «Сократить дробь»? А каким свойством мы пользуемся при сокращении дробей?) 14/21, 10/30, 18/36, 5/10. | ||||||||
| — Сравнить дроби: (Повторяем правила сравнения дробей — комментарии) ½ и ¼, 5/7 и 5/9, 7/8 и 5/8, 11/15 и 4/15. (рассмотреть другие случаи) | — Если числители одинаковые, то больше та дробь, знаменатель которой меньше. — Если знаменатели одинаковые, то больше та дробь, знаменатель которой больше. | |||||||
— Вычислить (решаем с комментариями) | — Выполняют сложение, вычитание Умножение 1/3*5/6. | |||||||
| 3. Постановка проблемы. Цель этапа: сформулировать проблему, тему и цели урока. | — Почему не смогли решить задачу? — Почему не смогли выполнить умножение дробей? | — Не умеем умножать обыкновенные дроби. | ||||||
— Как вы думаете, какая тема урока сегодня будет? | Умножение обыкновенных дробей. Записывают тему урока в тетради. | |||||||
4. | — Чтобы вывести правило умножения дробей, вспомним, как найти площадь прямоугольника. S= 4см*5см =20 см2. — Рассмотрим квадрат. Разделим его на равные квадраты. Длина этого квадрата равна 1, ее разделили на 5 частей и закрасили 4 части. Значит, длина прямоугольника составляет 4/5 от длины квадрата. А какую часть от ширины квадрата составляет ширина прямоугольника? (3/5) А как найти площадь этого прямоугольника? S=3/5*4/5, но мы получили, что площадь равна12/25. Значит, 3/5*4/5=12/25. (Мы умножаем две дроби. Как в числителе получить 12? Как в знаменателе получить 25? | Выполняют задания. | ||||||
Давайте попробуем сформулировать правило умножения дробей: чтобы умножить две дроби, надо_______________. Прочитать правило в учебнике вслух. Ещё раз расскажите правило своему соседу. | Читают правило в учебнике. Записывают формулу в тетради. | |||||||
| Физминутка Цель этапа: снять напряжение у учащихся путем переключения на другой вид деятельности. | Физминутка А теперь представим, детки, | |||||||
5. | А сейчас мы будем работать по правилу. Решим №889. (Решение с комментариями детей.) | Учащиеся решают задания у доски с комментарием. | ||||||
6. Найдите ошибку в решении. Самостоятельная работа с самопроверкой | 1. Найдите ошибку в решении * = > Самостоятельная работа с самопроверкой 2. | |||||||
Выставите себе оценку за самостоятельную работу. | Выполняют самостоятельную работу с самопроверкой. | |||||||
7.Этап контроля и оценки. Итог урока (рефлексия деятельности) Цель этапа: осознание уч-ся своей учебной деятельности, самооценка результатов деятельности своей и всего класса | Научились умножать дроби? Тогда, оцените свою работу на уроке, зажгите светофор. | Дают ответы на вопросы. | ||||||
Зажгите светофор: Выставление оценок. | Анализируют работу на уроке через самооценку | |||||||
Домашнее задание | 1.Выучить правило умножения обыкновенных дробей. Запасное задание. | Записывают домашнее задание |
Деление дробей
6i9DOPwHZWwПереверните вторую дробь вверх ногами и умножьте.
Есть 3 простых шага для деления дробей:
Шаг 1. Переверните вторую дробь (ту, на которую хотите разделить) вверх ногами Шаг 2. Умножьте первую дробь на обратную Шаг 3. Упростите дробь (при необходимости) |
Пример:
1 2 ÷ 1 6
Шаг 1. Переверните вторую дробь вверх ногами (она станет обратной ):
1 6 становится 6 1
Шаг 2. Умножить первую дробь на обратную :
(умножить вершины …)
1 2 × 6 1 знак равно 1 × 6 2 × 1 знак равно 6 2
(… умножить основания)
Шаг 3. Упростите дробь:
6 2 = 3
С ручкой и бумагой
А вот как это сделать ручкой и бумагой (нажмите кнопку воспроизведения):
Чтобы помочь вам запомнить:
♫ «Делить дроби проще простого,
Переверни вторую дробь, затем умножь.
И не забудь упростить,
Пока не пришло время прощаться» ♫
Другой способ запомнить: «оставь меня, измени меня, переверни меня» |
Сколько?
20 разделить на 5 спрашивает «сколько 5 в 20?» (=4) и так:
1 2 ÷ 1 6 действительно спрашивает:
сколько 1 6 с в 1 2 ?
Теперь посмотрите на пиццу ниже… сколько «1/6 кусочков» помещается в «1/2 кусочка»?
| Сколько | в | ? | Ответ: 3 |
Итак, теперь вы понимаете, почему 1 2 ÷ 1 6 = 3
Другими словами: «У меня есть половина пиццы, если я разделю ее на одну шестую часть, сколько получится частей?»
Другой пример:
1 8 ÷ 1 4
Шаг 1. Переверните вторую дробь вверх ногами ( обратную ):
Переверните вторую дробь вверх ногами ( обратную ):
1 4 становится 4 1
Шаг 2. Умножьте первую дробь на обратную :
1 8 × 4 1 знак равно 1 × 4 8 × 1 знак равно 4 8
Шаг 3. Упростите дробь:
4 8 знак равно 1 2
Дроби и целые числа
Как насчет деления с дробями и целых чисел?
Превратите целое число в дробь, положив его на 1.
Пример: 5 тоже 5 1
Дальше продолжайте как раньше.
Пример:
2 3 ÷ 5
Превратите 5 в 5 1 :
2 3 ÷ 5 1
Продолжайте, как раньше.
Шаг 1. Переверните вторую дробь вверх ногами ( обратное ):
5 1 становится 1 5
Шаг 2. Умножьте первую дробь на обратную :
2 3 × 1 5 знак равно 2 × 1 3 × 5 знак равно 2 15
Шаг 3. Упростите дробь:
Дробь уже настолько проста, насколько это возможно.
Ответ = 2 15
Пример:
3 ÷ 1 4
Превратите 3 в 3 1 :
3 1 ÷ 1 4
Затем продолжайте, как раньше.
Шаг 1. Переверните вторую дробь вверх ногами ( обратное ):
1 4 становится 4 1
Шаг 2. Умножьте первую дробь на обратную :
Умножьте первую дробь на обратную :
3 1 × 4 1 знак равно 3 × 4 1 × 1 знак равно 12 1
Шаг 3. Упростите дробь:
12 1 = 12
И помните…
Вы можете переписать вопрос типа «20 разделить на 5» на «сколько 5 в 20»
Таким образом, вы также можете переписать «3 разделить на ¼» в «сколько ¼ в 3» (=12)
Зачем переворачивать дробь вверх ногами?
Потому что деление противоположно умножению!
| Дробь говорит: | ||
|
Но для ОТДЕЛ мы:
- делим на большее число
- умножить на нижнее число
Пример: деление на
5 / 2 — это то же самое, что умножение на 2 / 5, вместо того, чтобы делить на фронт, это легче, чтобы разделиться, что это будет легче, чтобы разделиться, что это будет легче, чтобы разделиться, что это будет легче, чтобы разделиться, что это будет легче на фронт. вниз, затем выполните умножение.
вниз, затем выполните умножение.
937 938 939, 1411, 1412, 1413, 3575, 3576, 3577, 3578
Умножение смешанных чисел
(«Смешанные дроби» также называются «смешанными числами»)
Чтобы умножить смешанные дроби:
- преобразовать в неправильные дроби
- Умножение дробей
- преобразовать результат обратно в смешанные дроби
Пример: Что такое 1
3 8 × 3?Подумайте о пицце.
| 1 3 8 это 1 пицца и 3 восьмых части другой пиццы. |
Сначала преобразуем смешанную дробь (1 3 8 ) в неправильную дробь ( 11 8 ):
Разрежьте всю пиццу на восемь частей и сколько всего у вас будет восьмерок? 1 партия из 8 плюс 3 восьмых = 8+3 = 11 восьмых. |
Теперь умножьте это на 3:
| | 1 3 8 × 3 = 11 8 × 3 1 = 33 8 |
И, наконец, преобразовать в смешанную дробь (только потому, что исходная дробь была в таком виде):
| | 33 восьмых — это 4 целых пиццы (4×8=32) и 1 восьмая осталась. |
And this is what it looks like in one line:
1 3 8 × 3 = 11 8 × 3 1 = 33 8 = 4 1 8
Другой пример: Что такое 1
1 2 × 2 1 5 ?Выполните действия, описанные выше:
- преобразовать в неправильные дроби
- Умножение дробей
- преобразовать результат обратно в смешанные дроби
Step, by step it is:
Convert Mixed to Improper Fractions:
1 1 2 = 2 2 + 1 2 = 3 2
2 1 5 = 10 5 + 1 5 = 11 5
Multiply the fractions (multiply the top numbers, multiply bottom numbers):
3 2 × 11 5 = 3 × 11 2 × 5 = 33 10
Преобразование в смешанное число
33 10 = 3 3 10 30005 If you are clever you can do it all in one line like this: 1 1 2 × 2 1 5 = 3 2 × 11 5 = 33 10 = 3 3 10 Преобразование смешанных дробей в неправильные: 3 1 4 = 13 4 3 1 3 = 10 3 Multiply 13 4 × 10 3 = 130 12 Convert to a mixed number: 130 12 = 10 10 12 And simplify: 10 10 12 = 10 5 6 Here it is in one line: 3 1 4 × 3 1 3 = 13 4 × 10 3 = 130 12 = 10 10 12 = 10 5 6 Преобразование смешанных дробей в неправильные: 1 5 9 = 9 9 + 5 9 = 14 9 , затем умножьте неправильные фракции (Примечание: отрицательное время дает положительный результат) : —14 × –15 3333333333330 годы = Еще один пример:
Что такое 3
1 4 × 3 1 3 ? У этого есть негативы: что -1
5 9 × 2 1 7 3333333 × –2 1 7 3333333?
2 1 7 = 14 7 + 1 7 = 15 7  −15 9 × 7 = 210 63
−15 9 × 7 = 210 63
Теперь мы можем упростить. Здесь мы используем два шага, сначала по 7 (21 и 63 оба кратны 7), затем снова по 3. Но это можно сделать за один шаг, разделив на 21:
210 63 = 30 9 = 10 3
И, наконец, преобразовать в смешанную дробь (потому что это был стиль вопроса):
10 3 = (9 + 1) 3 = 3 + 1 3 = 3 1 3
9005.
Умножение дробей начинается с умножения заданных числителей, за которым следует умножение знаменателей. Затем полученная дробь еще больше упрощается и при необходимости сокращается до наименьших членов. Узнайте все об умножении дробей в этой статье. 1. | Как умножать дроби? |
| 2. | Правила умножения дробей |
| 3. | Умножение дробей с одинаковым знаменателем |
| 4. | Умножение дробей с разными знаменателями |
| 5. | Умножение дробей на целые числа |
| 6. | Умножение дробей со смешанными числами |
| 7. | Умножение неправильных дробей |
| 8. | Часто задаваемые вопросы об умножении дробей |
Как умножать дроби?
Умножение дробей не похоже на сложение или вычитание дробей, где знаменатель должен быть одинаковым. Здесь можно легко перемножить любые две дроби с разными знаменателями. Единственное, что нужно иметь в виду, это то, что дроби не должны быть в смешанной форме, они должны быть либо правильными дробями, либо неправильными дробями. Давайте научимся умножать дроби, выполнив следующие шаги:
- Шаг 1: Умножьте числители.

- Шаг 2: Умножьте знаменатели.
- Шаг 3: Сократите полученную дробь до наименьшего значения.
Давайте разберем эти шаги на примере.
Пример: Умножьте следующие дроби: 1/3 × 3/5.
Решение: Начнем с умножения числителей: 1 × 3 = 3, затем умножим знаменатели: 3 × 5 = 15. Это можно записать как: (1 × 3)/(3 × 5) = 3 /15. Теперь уменьшите это значение до самой низкой формы. 3 — это наибольший общий делитель (НОД) 3 и 15, поэтому разделите и 3, и 15 на 3, чтобы упростить дробь. Следовательно, 1/3 × 3/5 = 1/5.
Правила умножения дробей
При умножении дробей следует помнить о следующих правилах:
- Правило 1: Первое правило состоит в преобразовании смешанных дробей в неправильные дроби, если таковые имеются. Затем умножьте числители данных дробей.
- Правило 2: Умножьте знаменатели отдельно.

- Правило 3: Упростите полученное значение до наименьшего члена.
Эти три правила можно применить к любым двум дробям, чтобы найти их произведение. Теперь давайте изучим отдельные случаи умножения дробей с разными типами дробей.
Умножение дробей с одинаковым знаменателем
Умножение дробей с одинаковыми знаменателями не меняет правила умножения дробей. Дроби, имеющие одинаковые знаменатели, называются дробями. Хотя сложение и вычитание одинаковых дробей отличается от сложения и вычитания разнородных дробей, в случае умножения и деления метод остается тем же. Мы умножаем числители, затем знаменатели, а затем дробь сокращается до наименьших членов.
Пример: Умножить 1/3 × 5/3
Решение: Мы можем умножить эти дроби, используя следующие шаги.
- Шаг 1: Умножьте числители, 1 × 5 = 5.
- Шаг 2: Умножьте знаменатели, 3 × 3 = 9.

- Шаг 3: Произведение, которое мы получаем, равно 5/9. Это не может быть уменьшено дальше, поэтому ответ 5/9.
Умножение дробей с разными знаменателями
Умножение дробей с разными знаменателями точно такое же, как умножение одинаковых дробей. Давайте разберемся в этом на примере.
Пример: Умножьте 4/12 × 16/24.
Мы можем умножить эти дроби, используя следующие шаги:
- Шаг 1: Умножьте числители, 4 × 16 = 64.
- Шаг 2: Умножьте знаменатели, 12 × 24 = 288.
- Шаг 3: Произведение, которое мы получаем, равно 64/288. Это может быть уменьшено до 2/9. Таким образом, 2/9 является ответом.
Альтернативный метод
Те же дроби можно умножить другим методом, в котором мы упрощаем дроби между собой, а затем умножаем числители, затем знаменатели, чтобы получить конечный продукт.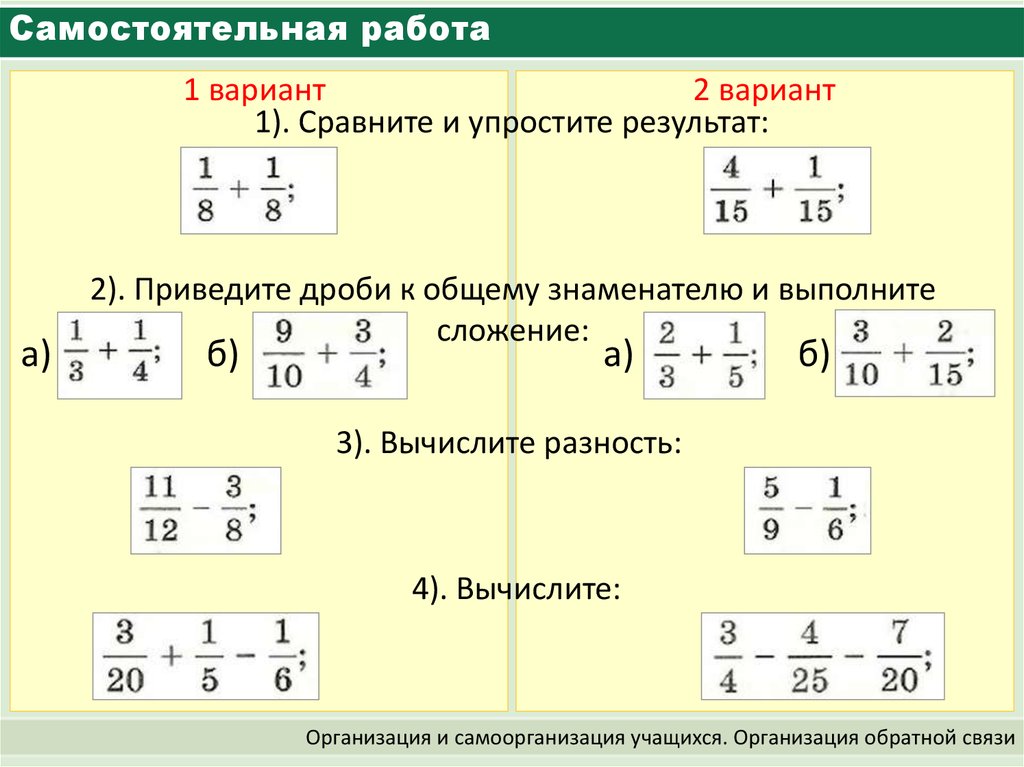
Пример: Умножьте 4/12 × 16/24.
Умножим данные дроби, используя следующие шаги:
- Шаг 1: Упростим данные дроби между собой. Другими словами, эти дроби можно сократить до 1/3 × 2/3.
- Шаг 2: Умножим числители, 1 × 2 = 2.
- Шаг 3: Теперь умножим знаменатели, 3 × 3 = 9.
- Шаг 4: Следовательно, произведение, которое мы получаем, равно 2/9.
Умножение дробей на целые числа
Умножение дробей на целые числа — простая идея. Поскольку мы знаем, что умножение — это многократное сложение одного и того же числа, этот факт можно применить и к дробям.
Умножение дробей на целые числа Визуальная модель
Рассмотрим следующий пример: 4 × 2/3. Это означает, что 2/3 добавляется 4 раза. Представим этот пример с помощью визуальной модели. Четырежды две трети представлены как:
Шаги умножения дробей на целые числа
Чтобы умножать дроби с целыми числами, мы используем простое правило умножения числителей, затем умножения знаменателей, а затем сокращения их до наименьших членов. Однако в случае целых чисел мы запишем их в дробной форме, поставив «1» в знаменателе. Давайте разберемся в этом на примере.
Однако в случае целых чисел мы запишем их в дробной форме, поставив «1» в знаменателе. Давайте разберемся в этом на примере.
Пример: Умножить: 5 × 3/4.
Решение: Давайте используем следующие шаги, чтобы умножить данную дробь на целое число.
- Шаг 1: Здесь 5 — это целое число, которое можно записать как 5/1, а затем его можно умножить, как мы умножаем обычные дроби.
- Шаг 2: Это означает, что нам нужно умножить 5/1 × 3/4.
- Шаг 3: Умножьте числители, 5 × 3 = 15.
- Шаг 4: Умножьте знаменатели, 1 × 4 = 4.
- Этап 5: Полученное произведение равно 15/4, и его дальнейшее уменьшение невозможно.
- Шаг 6: Поскольку 15/4 — неправильная дробь, мы изменим ее на смешанную дробь, 15/4 = \(3\frac{3}{4}\).
Умножение дробей со смешанными числами
Смешанные числа или смешанные дроби — это дроби, состоящие из целого числа и правильной дроби, например \(2\frac{3}{4}\), где 2 — целое число, а 3/4 — правильная дробь. Для умножения смешанных дробей нам нужно преобразовать смешанные дроби в неправильную дробь перед умножением. Например, если число равно \(2\frac{2}{3}\), нам нужно изменить его на 8/3. Давайте разберемся в этом с помощью примера.
Для умножения смешанных дробей нам нужно преобразовать смешанные дроби в неправильную дробь перед умножением. Например, если число равно \(2\frac{2}{3}\), нам нужно изменить его на 8/3. Давайте разберемся в этом с помощью примера.
Пример: Умножьте \(2\frac{2}{3}\) и \(3\frac{1}{4}\).
Решение: Следующие шаги можно использовать для умножения дробей со смешанными числами.
- Шаг 1: Измените заданные смешанные дроби на неправильные, т. е. (8/3) × (13/4).
- Шаг 2: Умножьте числители неправильных дробей, а затем умножьте знаменатели. Это даст 104/12.
- Шаг 3: Теперь уменьшите полученную дробь до наименьшего значения, что сделает ее равной 26/3.
- Шаг 4: Далее, преобразуйте ответ обратно в смешанную дробь, которая будет \(8\frac{2}{3}\).
Умножение неправильных дробей
Теперь давайте разберемся с умножением неправильных дробей. Мы уже знаем, что неправильная дробь — это та, у которой числитель больше знаменателя. При умножении двух неправильных дробей часто получается неправильная дробь. Например, чтобы умножить 3/2 × 7/5, две неправильные дроби, нам нужно выполнить следующие шаги:
Мы уже знаем, что неправильная дробь — это та, у которой числитель больше знаменателя. При умножении двух неправильных дробей часто получается неправильная дробь. Например, чтобы умножить 3/2 × 7/5, две неправильные дроби, нам нужно выполнить следующие шаги:
- Шаг 1: Умножьте числители и знаменатели. (3 × 7)/(2 × 5) = 21/10.
- Шаг 2: Дробь 21/10 не может быть сокращена до наименьшего члена.
- Шаг 3: Следовательно, ответ равен 21/10, что можно записать как \(2\frac{1}{10}\).
Советы и приемы умножения дробей
Вот несколько важных советов и приемов, которые помогут при умножении дробей.
- Обычно учащиеся упрощают дробь после умножения. Однако, чтобы упростить расчеты, проверьте, не находятся ли две дроби, которые нужно умножить, в младших формах. Если нет, сначала упростите их, а затем умножьте. Например, 4/12 × 5/13 будет сложно умножить напрямую.

- Теперь, если мы сначала упростим дробь, мы получим: 1/3 × 5/13 = 5/39.
- Упрощение также можно выполнить для двух дробей. Если между числителем одной из дробей и знаменателем другой дроби есть общий множитель, можно их упростить и продолжить. Например, 5/28 × 7/9можно упростить до 5/4 × 1/9 перед умножением.
☛ Похожие темы
- Калькулятор умножения дробей
- Обратное число дробей
- Умножение десятичных дробей
- Умножение и деление целых чисел
- Сложение дробей
- Вычитание дробей
- Деление дробей
Умножение дробей Примеры
Пример 1: Умножьте данные дроби: 1/4 × 5/8.
Решение:
Для умножения дробей с разными знаменателями, как указано в 1/4 × 5/8, мы начинаем с умножения числителей: 1 × 5 = 5. После этого мы умножаем знаменатели: 4 × 8 = 32. Это можно записать как: (1 × 5)/(4 × 8) = 5/32.
 Теперь эту результирующую дробь нельзя упростить, поэтому ответ равен 5/32.
Теперь эту результирующую дробь нельзя упростить, поэтому ответ равен 5/32.Пример 2: Изменяет ли правило умножения дробей умножение дробей на целые числа? Обоснуйте свой ответ, умножив 4 × 6/5.
Решение:
Нет, умножение дробей на целые числа не меняет правила умножения дробей. Нам просто нужно записать целое число в форме дроби. В этом случае 4 будет записано как 4/1, и тогда мы будем использовать тот же метод. Итак, мы будем умножать 4/1 × 6/5. При умножении числителей мы получаем 4 × 6 = 24. При умножении знаменателей мы получаем 1 × 5 = 5. Следовательно, результирующее произведение равно 24/5, которое нельзя уменьшить дальше. Поэтому мы изменим эту неправильную дробь 24/5 на смешанную дробь, чтобы представить ее как ответ, который равен 24/5 = \(4\frac{4}{5}\).
Пример 3: Каким будет произведение 5/4 × 5/2 × 5/3?
Решение:
Чтобы умножить три дроби, мы сначала умножим все три числителя, а затем все три знаменателя.
 Затем мы упростим окончательный ответ.
Затем мы упростим окончательный ответ.⇒ 5/4 × 5/2 × 5/3
⇒ (5×5×5)/(4×2×3)
⇒ 125/24
Следовательно, 5/4 × 5/2 × 5/3 = 125/24 или \(5\frac{5}{24}\)
перейти к слайдуперейти к слайдуперейти к слайду
Готовы увидеть мир глазами математика?
Математика — это жизненный навык. Помогите своему ребенку усовершенствовать его с помощью реального приложения.
Записаться на бесплатный пробный урок
Практические вопросы по умножению дробей
перейти к слайдуперейти к слайду
Часто задаваемые вопросы по умножению дробей
Как умножать дроби?
Умножение дробей означает нахождение произведения двух или более дробей. Метод, используемый для умножения дробей, отличается от сложения и вычитания дробей. Чтобы умножить любые две дроби, мы следуем шагам, указанным ниже. Давайте умножим 7/8 × 2/6, чтобы понять шаги.
- Умножьте числители. Итак, 7 × 2 = 14, .
- Умножьте знаменатели. Это означает, что 8 × 6 = 48, .
- Полученная дробь равна 14/48. Упростите полученную дробь до наименьших членов. Упрощение дроби 14/48 дает нам 7/24. Следовательно, ответ 7/24.

Каковы правила умножения дробей?
Есть три простых правила умножения дробей. Сначала умножьте числители, а затем знаменатели обеих дробей, чтобы получить результирующую дробь. Затем нам нужно упростить полученную дробь, чтобы получить окончательный ответ. Это можно понять на простом примере → 2/6 × 4/7 = (2 × 4)/(6 × 7) = 8/42 = 4/21.
Как умножать дроби со смешанными числами?
Следующие шаги можно использовать для умножения смешанных дробей. Умножим 1/4 × \(3\frac{1}{2}\).
- Замените смешанную дробь на неправильную. Здесь \(3\frac{1}{2}\) станет 7/2. Итак, теперь нам нужно умножить 1/4 × 7/2.
- Умножьте числители, а затем знаменатели. Это означает, что (1 × 7)/(4 × 2) = 7/8.
- Убедитесь, что ответ указан в самом низком выражении.
 Поскольку 7/8 нельзя уменьшить дальше, ответом будет 7/8.
Поскольку 7/8 нельзя уменьшить дальше, ответом будет 7/8.
Как умножать дроби на целые числа?
Чтобы понять умножение дроби на целое число, мы можем взять простой числовой пример 2/7 × 3. Начните с перезаписи целого числа (3 в этом примере) в виде дроби 3/1. Теперь мы можем применить шаги, которые мы используем для умножения дробей. Это означает, что 2/7 × 3/1 = (2 × 3)/(7 × 1) = 6/7.
Как умножать дроби с одинаковыми знаменателями?
Умножение дробей с одинаковыми знаменателями аналогично умножению других правильных дробей. Давайте разберемся в этом на примере. Умножим 4/5 × 3/5. Умножаем числители, то есть 4 × 3 = 12. Затем умножаем знаменатели, то есть 5 × 5 = 25. Это даст нам произведение как 12/25. Поскольку это нельзя уменьшить дальше, ответом будет 12/25.
Как умножать дроби с разными знаменателями?
Умножение дробей с разными знаменателями не меняет правила умножения дробей. Давайте разберемся в этом на примере. Умножьте 2/6 × 3/4. Мы можем умножить эти дроби, используя следующие шаги:
Мы можем умножить эти дроби, используя следующие шаги:
- Умножить числители, 2 × 3 = 6.
- Умножьте знаменатели, 6 × 4 = 24.
- Продукт, который мы получаем, это 6/24. Это можно уменьшить до 1/4, следовательно, ответ 1/4.
Как умножить дробь на дробь?
Умножение двух дробей — простейшая форма арифметических операций между двумя дробями. Сначала умножаются числители обеих дробей, а затем умножаются знаменатели. Затем полученная дробь при необходимости упрощается до наименьших членов.
Чем умножение дробей отличается от сложения дробей?
Сложение дробей отличается от умножения дробей. При умножении сначала умножаются числители двух дробей, затем умножаются знаменатели, чтобы получить результирующую дробь. Однако в процессе сложения дробей нам сначала нужно сделать знаменатели обеих дробей равными, а затем сложить числители, чтобы получить результирующую дробь. Кроме сложения или вычитания дробей, мы не складываем и не вычитаем знаменатели отдельно.
Как умножать десятичные дроби?
Чтобы умножить дроби на десятичные, мы преобразуем десятичное число в дробь, а затем используем те же правила умножения дробей. Например, давайте умножим 5/7 × 0,6.
- Здесь мы преобразуем 0,6 в дробную форму, что даст 6/10.
- Теперь умножим 5/7 × 6/10 обычным способом.
- Умножим числители, 5 × 6 = 30.
- Умножим знаменатели, 7 × 10 = 70.
- Таким образом, результирующая дробь будет 30/70.
- Упростив полученную дробь, мы получим произведение как 3/7.
Как научить умножению дробей?
Умножению дробей можно научиться так же, как умножению целых чисел. Важным аспектом перед умножением дробей является преобразование смешанной дроби в неправильную дробь. После этого шага мы умножаем числители обеих дробей, а затем знаменатели обеих дробей, чтобы получить результирующую дробь. Для обучения умножению дробей можно использовать следующие способы:
- Максимально используйте визуальные модели для представления концепции.


 Педагогический (научно-педагогический) состав
Педагогический (научно-педагогический) состав Курсы/ Кружки/ Факультативы
Курсы/ Кружки/ Факультативы

 Запишите число. Сегодня у нас не совсем обычный урок. Пожелайте удачи друг другу. Хочу начать урок со слов: «Дорогу осилит — идущий, математику — мыслящий!». А это значит, что мы на уроке будем думать и продолжим путь изучения математики.
Запишите число. Сегодня у нас не совсем обычный урок. Пожелайте удачи друг другу. Хочу начать урок со слов: «Дорогу осилит — идущий, математику — мыслящий!». А это значит, что мы на уроке будем думать и продолжим путь изучения математики. Какие две дроби называются неправильными?
Какие две дроби называются неправильными?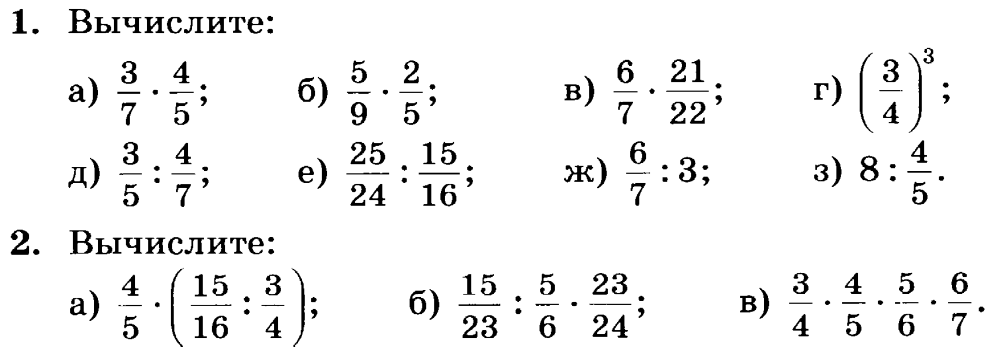
 Открытие учениками нового знания.
Открытие учениками нового знания. 
 Этап закрепления изученного материала. Первичное закрепление.
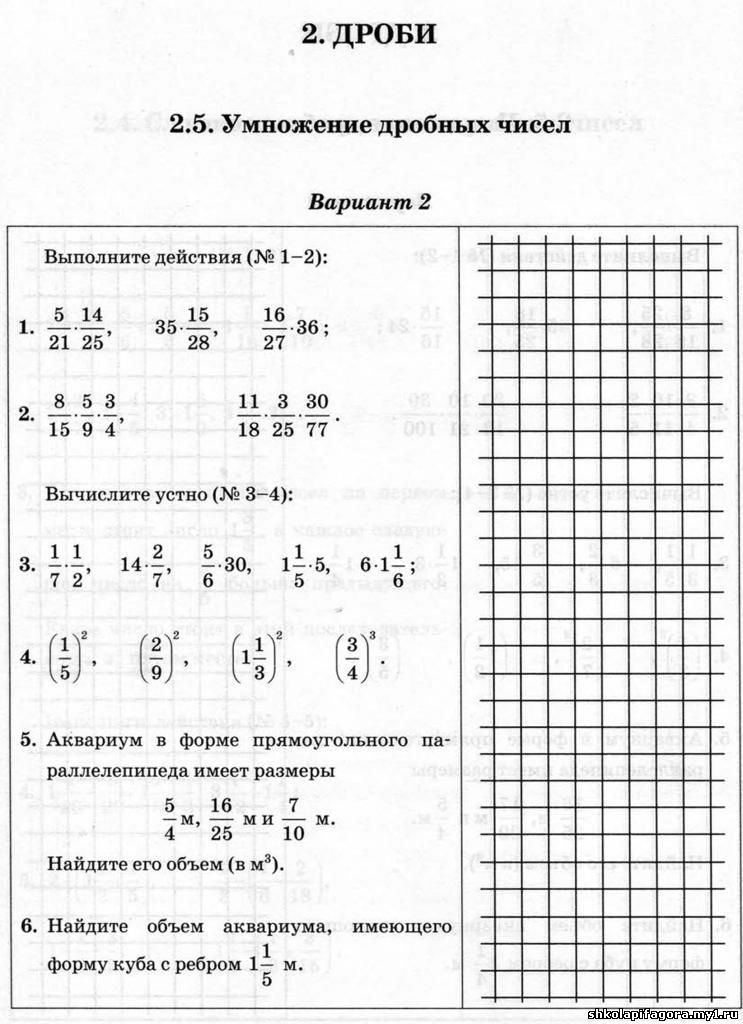
Этап закрепления изученного материала. Первичное закрепление.  Используя правило, выполните умножение обыкновенных дробей.
Используя правило, выполните умножение обыкновенных дробей.






 Теперь эту результирующую дробь нельзя упростить, поэтому ответ равен 5/32.
Теперь эту результирующую дробь нельзя упростить, поэтому ответ равен 5/32. Затем мы упростим окончательный ответ.
Затем мы упростим окончательный ответ. Поскольку 7/8 нельзя уменьшить дальше, ответом будет 7/8.
Поскольку 7/8 нельзя уменьшить дальше, ответом будет 7/8.