Краткий обзор алгебры в геометрии
Вы думали, что закончили с алгеброй. К сожалению, математика постоянно строит сама себя, как бесконечный танец Hokey Pokey, и геометрия не является исключением. Теперь встряхните все это.
Нас могут попросить найти меру угла или отрезка, и в дополнение к пониманию геометрических отношений между частями изображения нам также потребуется выставить напоказ наши навыки алгебры (если у вас есть это, выставлять напоказ!) чтобы покончить с проблемой навсегда.
Обычно наш план атаки выглядит примерно так:
- Нарисуйте картинку (если у нас ее еще нет).
- Используйте геометрию, чтобы выяснить взаимосвязь между некоторыми неизвестными величинами.
- Составьте уравнение или два (или семь), используя это соотношение.
- Решите уравнения для любых переменных. Вот где алгебра прокрадывается в картину. Какой крипер.
- При необходимости подключите переменные, чтобы получить то, о чем нас просит вопрос.
Одна из часто упускаемых из виду, но очень важных вещей — это ответьте на заданный вопрос .
- Проверьте, действительно ли наши ответы имеют смысл в рамках геометрических соотношений. Это позволит убедиться, что наш ответ правильный.
Одна из часто упускаемых из виду, но очень важных вещей — это ответьте на заданный вопрос . Вооружившись этой стратегией, мы можем рассмотреть несколько примеров.
Пример задачи
На рисунке m∠ ABC = 2 x + 7 и m∠ DBE = 4 x – 14. Чему равно ∠ ABC 9024?
Теперь вы могли бы быть нахальным и сказать: «Ух! Угол ABC равен 2 x + 7», но этот ответ, вероятно, не принесет вам много очков. Кто знает, что такое x ? Если вы скажете плотнику отрезать кусок дерева под углом 2 x + 7 градусов, плотник может отрезать вам большие пальцы ножовкой. Вместо этого мы, вероятно, должны решить проблему.
Поскольку ∠ ABC и ∠ DBE противоположны друг другу и исходят из пересекающихся прямых, они представляют собой вертикальные (и, следовательно, конгруэнтные) углы.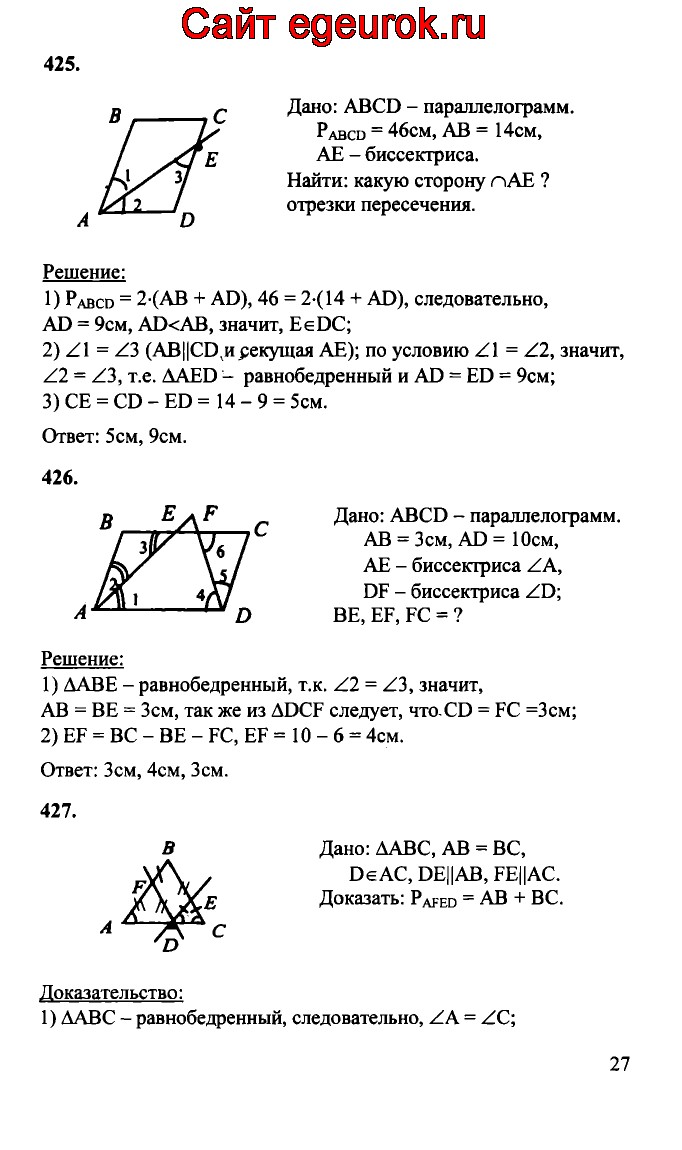
Это означает, что m∠ ABC = м∠ DBE . Теперь мы к чему-то пришли: мы можем подставить то, что мы знаем об углах, чтобы получить:
2 x + 7 = 4 x – 14
Теперь мы перемещаем все переменные в одну сторону, а числа к другому, чтобы получить:
21 = 2 x
Разделив обе стороны на 2, мы получим:
x = 10,5
. . Мы закончили. Но отвечает ли это на вопрос? Мы хотели найти меру угла ∠ АВС . Это означает, что мы должны подставить x = 10,5 обратно в 2 x + 7. 28°
Просто чтобы убедиться, что все имеет смысл, мы должны вычислить m∠ DBE , подставив найденное x в 4 x – 14.
m∠ DBE = 4(10,5) – 14,5 = 28°
Их меры равны, как и должно быть. Это наш ответ.
Пример задачи
Угол на 25 градусов больше своего дополнения. Какова его мера?
Так как эта задача даже не позволила нам нарисовать картинку, мы можем нарисовать свою собственную.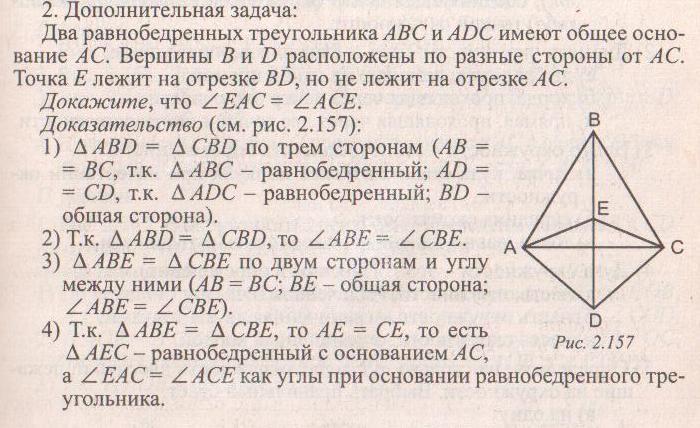
У нас должно быть два дополнительных угла, поэтому давайте нарисуем его как прямой угол, разделенный на две части (помните, это правильно , чтобы сделать комплиментов ):
Что еще мы знаем? Единственная дополнительная информация состоит в том, что один из углов на 25° больше другого. Если обозначить меньший угол x , больший должен быть x + 25.
Мы знаем, что сумма дополнительных углов составляет 90°, поэтому это означает:
x + ( x + 9025) =
Мы можем сложить эти x вместе.
2 x + 25 = 90
Решение для x дает нам:
x = 32,5
Теперь мы можем исправить нашу картину, чтобы включить фактические измерения углов: 9 0002
:4
0004Итак, что за вопрос? Сформулируйте проблему: «Никогда».
Ой. Мы имели в виду, цитирует задачу, «Угол измеряется на 25 градусов больше, чем его дополнение. Какова его мера?» Поскольку угол, о котором идет речь, больше, чем его дополнение, это означает, что ответ на вопрос равен 32,5 + 25 = 57,5 °.
Наконец, мы быстро проверяем, что 32,5 + 57,5 = 90°, так что углы на самом деле являются дополнительными.
Ученые CMU решили геометрическую задачу 90-летней давности — Новости
05 октября 2020 г.
Компьютерщики и математики из Университета Карнеги-Меллона решили последнюю и упрямую часть гипотезы Келлера, геометрическую задачу, над которой ученые ломали голову 90 лет.
Структурируя головоломку как то, что ученые-компьютерщики называют проблемой выполнимости, исследователи решили эту проблему за четыре месяца лихорадочного компьютерного программирования и всего за 30 минут вычислений на кластере компьютеров.
«Я был очень счастлив, когда мы ее решили, но потом мне было немного грустно, что проблема исчезла», — сказал Джон Макки, преподаватель факультета компьютерных наук (CSD) и факультета математических наук, который преследовал задачу Келлера. предположение, так как он был аспирантом 30 лет назад.
«Но потом я снова почувствовал себя счастливым. Просто это чувство удовлетворения».
Решение стало еще одним успехом подхода, предложенного Марин Хеуле, адъюнкт-профессором компьютерных наук, который присоединился к CSD в августе прошлого года. Хеуле использовал решатель SAT — компьютерную программу, использующую логику высказываний для решения задач выполнимости (SAT), — чтобы справиться с несколькими застарелыми математическими задачами, в том числе с проблемой пифагорейских троек и числом Шура 59.0004
«Эта проблема интересовала многих людей на протяжении десятилетий, почти века», — сказал Хеуле о гипотезе Келлера. «Это действительно демонстрация того, что можно сделать сейчас, что было невозможно раньше».
Гипотеза, выдвинутая немецким математиком Эдуардом Оттом-Генрихом Келлером, связана с замощением — в частности, как покрыть площадь плитками одинакового размера без каких-либо промежутков или перекрытий. Гипотеза состоит в том, что по крайней мере две плитки должны иметь общее ребро, и это верно для пространств любого измерения.
Легко доказать, что это верно для двумерных плиток и трехмерных кубов. К 1940 году гипотеза подтвердилась для всех измерений до шести. Однако в 1990 году математики доказали, что это не работает в размерности 10 и выше.
Именно тогда гипотеза Келлера захватила воображение Макки, в то время студента Гавайского университета. Имея офис рядом с вычислительным кластером университета, он был заинтригован тем, что проблема может быть переведена с использованием теории дискретных графов в форму, которую могут исследовать компьютеры. В этой форме, называемой графом Келлера, исследователи могли искать «клики» — подмножества элементов, которые соединяются, не имея общей грани, тем самым опровергая гипотезу.
В 2002 году Макки сделал именно это, обнаружив клику в восьмом измерении. Тем самым он доказал, что гипотеза неверна в этом измерении и, соответственно, в девятом измерении.
Это оставило гипотезу о седьмом измерении нерешенной.
Когда в прошлом году Хеул прибыл в CMU из Техасского университета, он уже имел репутацию специалиста, использующего SAT-решатель для решения давних открытых математических задач.
«Я подумал про себя, может быть, мы сможем использовать его технику», — вспоминал Макки. Вскоре он начал обсуждать, как использовать решатель SAT для гипотезы Келлера, с Хеуле и Джошуа Бракензиком, двумя специальностями в области математических наук и компьютерных наук, которые сейчас получают докторскую степень. по информатике в Стэнфордском университете.
Решатель SAT требует структурирования проблемы с помощью пропозициональной формулы — (A или не B) и (B или C) и т. д. — чтобы решатель мог проверить все возможные комбинации переменных, которые будут удовлетворять всем условиям.
«Существует много способов сделать эти переводы, и качество перевода обычно влияет на вашу способность решить проблему, — сказал Хеул.
Обладая 15-летним опытом, Heule отлично справляется с выполнением этих переводов. Одной из целей его исследований является разработка автоматизированных рассуждений, чтобы этот перевод мог выполняться автоматически, позволяя большему количеству людей использовать эти инструменты для решения своих проблем.
Даже при качественном переводе количество комбинаций, которые нужно проверить в седьмом измерении, было ошеломляющим — число из 324 цифр — решения не видно даже с помощью суперкомпьютера. Но Хеуле и другие применили ряд уловок, чтобы уменьшить размер проблемы. Например, если одна конфигурация данных оказалась неработоспособной, они могли автоматически отклонить другие комбинации, которые на нее полагались. А поскольку большая часть данных была симметричной, программа могла исключить зеркальные отражения конфигурации, если она заходила в тупик в одном расположении.
Используя эти методы, они сократили свой поиск примерно до миллиарда конфигураций. В этих усилиях к ним присоединился Дэвид Нарваез, доктор философии. студент Рочестерского технологического института, который был приглашенным исследователем осенью 2019 года.
После того, как они запустили свой код на кластере из 40 компьютеров, они, наконец, получили ответ: гипотеза верна в седьмом измерении.
«Причина нашего успеха в том, что у Джона есть многолетний опыт и понимание этой проблемы, и мы смогли преобразовать его в компьютерный поиск», — сказал Хеул.
Доказательство результата полностью вычисляется компьютером, сказал Хеул, в отличие от многих публикаций, которые комбинируют проверенные компьютером части доказательства с ручными описаниями других частей. Он отметил, что это затрудняет понимание читателями. Компьютерное доказательство решения Келлера включает в себя все аспекты решения, в том числе часть, нарушающую симметрию, предоставленную Нарваэсом, подчеркнул Хеуле, так что ни один аспект доказательства не должен полагаться на ручное усилие.
«Мы можем быть уверены в правильности этого результата», сказал он. Статья, описывающая резолюцию Хеуле, Макки, Бракензика и Нарваеса, получила награду за лучшую статью на Международной объединенной конференции по автоматизированному мышлению в июне.
Решение гипотезы Келлера имеет практическое применение, сказал Макки. Те клики, которые ученые ищут, чтобы опровергнуть гипотезу, полезны для создания нелинейных кодов, которые могут ускорить передачу данных. Таким образом, решатель SAT можно использовать для поиска нелинейных кодов более высокой размерности, чем это было возможно ранее.