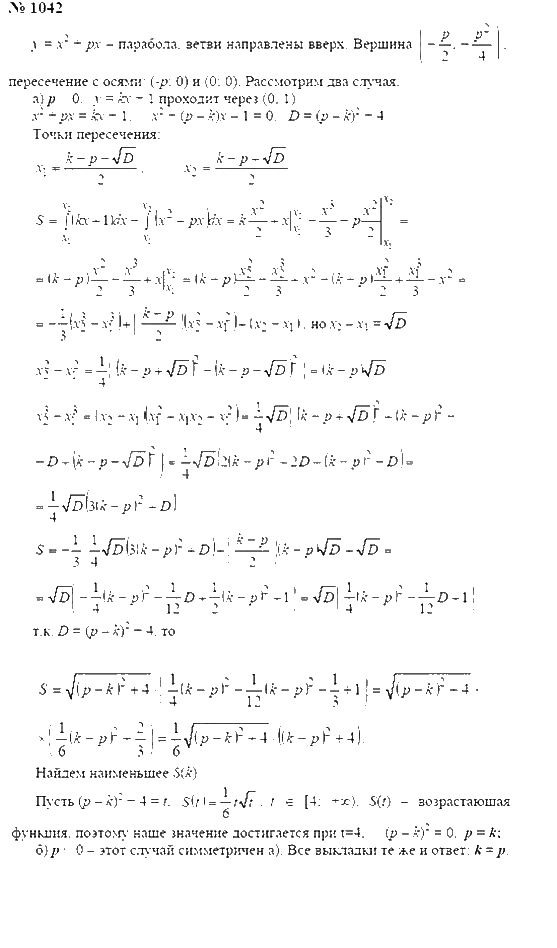Решебник по математике 10 11 алимов: ГДЗ Алгебра 10-11 класс Алимов, Колягин, Сидоров

ГДЗ По Алгебре 10 22 Алимов – Telegraph

➡➡➡ ПОДРОБНЕЕ ЖМИТЕ ЗДЕСЬ!

ГДЗ По Алгебре 10 22 Алимов

Если просто списываете ответы или проверяете свои решения, сборник ГДЗ Алимов 10-11 классы станет для Вас замечательным другом и помощником . Не важно как Вы используете решебники: просто списываете ответы или проверяете свои решения, сборник «ГДЗ . Алимов .

Это ГДЗ по алгебре за 10 -11 класс Алимов разбирает все тринадцать глав из учебника . Здесь найдутся ответы и на упражнения по действительным числам, и на задания из темы степенная функция . Полностью решены все примеры на темы показательная и логарифмическая функции . .

Ш .А . Алимов , Ю .М . Колягин, М .В . Ткачева . Решебник (ГДЗ ) по Алгебре за 10 ‐11 (десятый‐одиннадцатый) класс авторы: Алимов, Колягин, Ткачева издательство Просвещение, год .
Убедись в правильности решения задачи вместе с ГДЗ по Алгебре за 10 ‐11 класс Ш .А . Алимов, Ю .М . Колягин, М . В . Ткачева . Однако порой такая схема попросту не представляется возможной . Особенно, когда дело касается алгебры . Это один из самых сложных предметов . .

Издание ГДЗ к учебнику по алгебре для 10 -11 классов Ш . А . Алимова содержит полный свод правильных ответов ко всем приведенным упражнениям . Учебник по алгебре и началам математического анализа включает в себя семь разделов . Согласно всем разделам составлено . .

Разбор задания № 22 по алгебре за 10 -11 класс из учебника Алимова . ГДЗ 10 класс Алгебра Алимов , Колягин, Сидоров Номер №22 . Упражнения для итогового повторения курса алгебры и начал математического анализа (Задания с 1228 по 1559) .

Доскональность решений в ГДЗ по алгебре 10-11 класс способствует тому, что даже малейшие нюансы не ускользнут от внимания подростков, а данный предмет уже не будет глава 1 глава 2 глава 3 глава 4 глава 5 глава 6 глава 7 глава 8 глава 9 глава 10 глава 11 глава 12 глава 13 .

Ответы к учебнику по алгебре и началу анализа для 10 -11 класса Алимов . Добавить книги в список » По зосу «» не найдено ни одной книги . Алгебра и начала анализа . 10 -11 класс Алимов Ш . А .

Алимов , Колягин, Сидоров . «Просвещение» . 2007- год . ГДЗ (решебник) по алгебре 10 -11 класс Алимов, Колягин, Сидоров . Искать ответы к математическим задачам в старшей школе все труднее, ведь от простых операций с числами и выражениями дети переходят к сложным . .

ГДЗ (решебник) по алгебре за 10 -11 класс Алимов, Колягин, Сидоров — ответы онлайн . Все ответы на домашние задания составляются тем же коллективом авторов, который и создал сам учебник . ГДЗ – это не просто возможность беззаботно списать для запущенного троечника, это . .

ГДЗ алгебра и начала математического анализа 10 класс Алимов Просвещение . Похожие решебники по алгебре 10 класс .

Изучение алгебры в старших классах процесс невероятно сложный и помощь ГДЗ по алгебре 10 -11 класс Алимов будет просто необходима . Решебник имеет в своём содержании подробные и верные ответы, которые легко и просто отыскать по номеру задания . Они помогут

22 . О решебнике Ш .А . Алимов 2007 . Данное пособие рассчитано на школьников, учащихся в 10-11 классах общеобразовательных учреждений . Комплект из учебника и решебника помогает ученикам овладеть полным курсом алгебры и начал анализа в 10-11 классах и . .

Данное пособие содержит решебник (ГДЗ ) по Алгебре за 10 ‐11 класс . Автора: Ш .А . Алимов, Ю .М . Колягин, М .В . Ткачева Издательство: Просвещение . Решебник по алгебре для 10 и 11 класса от Ш .А . Алимов, Ю .М . Колягин, М .В . Ткачева станет лучшим другом школьника в период . .

Данный решебник Алимов по алгебре в 10 -11 класс позволяет всем слабым ученикам списывать все решения абсолютно бесплатно и онлайн . Наслаждайтесь ответами . Кроме того, данное ГДЗ помогает и начинающим учителям, которые сами еще не решили сборник Алимова .

Ш .А . Алимов , Ю .М . Колягин, М .В . Ткачева . Решебник (ГДЗ ) по Алгебре за 10 ‐11 (десятый‐одиннадцатый) класс авторы: Алимов, Колягин, Ткачева издательство Просвещение, год .
Убедись в правильности решения задачи вместе с ГДЗ по Алгебре за 10 ‐11 класс Ш .А . Алимов, Ю .М . Колягин, М .В . Ткачева . Однако порой такая схема попросту не представляется возможной . Особенно, когда дело касается алгебры . Это один из самых сложных предметов . .

Учебник ГДЗ Музыка 5
Решебник Сборника Задач По Химии 8
Рабочая Тетрадь По Географии 7 Класс ГДЗ
Решебник 6 Класс Математика Тетрадь Мерзляк
ГДЗ Путина 8 Класс Макарычев
ГДЗ Литература 9 Коровина 2
Решебник Муравьевой 4 Класс
Математика 6 Полонский ГДЗ
ГДЗ По Французскому 9 Класс Селиванова
ГДЗ Химии 11 Углубленный Уровень
ГДЗ Математики 6 Клас Якір
ГДЗ По Математике Второй Класс Тетрадь
ГДЗ Starlight 5 Сборник Упражнений
ГДЗ По Математике 1 Часть Номер
ГДЗ По Математике Виленкин Жохов Шварцбург
ГДЗ По Алгебре 7 Класс Беларусь
ГДЗ По Русскому Седьмой Класс Баранова
Контрольные Самостоятельные Работы 4 Класс Решебник
ГДЗ Русский Язык 1 Язык Климанова
Решебник По Биологии 8 Класс Сухорукова
ГДЗ Spotlight Девятый Класс Задание Номер Шесть
Решебник По Математике 5 Самостоятельные Работы
ГДЗ По Математике 6 Класса Виленкин Жохов
ГДЗ По Физике 9 Класс Кабардин Бесплатно
ГДЗ По Английскому 6 Класс Биболетова Денисенко
ГДЗ По Русскому 8 Класса 2007
ГДЗ Английский 2 Класс Рабочая Форвард
ГДЗ По Математике 2 Класс Проверочные
Starlight Сборник Упражнений ГДЗ
Букварь Гармония 1 Класс Решебник Соловейчик Ответы
ГДЗ Окружающий Мир 4 Поглазова
ГДЗ По Алгебре 7 Класс Никольский Скачать
Решебник Львов
ГДЗ По Русскому Языку Николина
Звездный Английский 5 Класс Рабочая Тетрадь ГДЗ
ГДЗ Алгебра 11 Класс Мордкович Часть 2
ГДЗ Петерсон Третий Класс Первая Часть
ГДЗ По Алгебре 9 Класс Мешков
ГДЗ По Русскому 2 Класс Барковская
ГДЗ По Алгебре 7 Класс Никольский 28
Решебник Математика 4 Класс Чеботаревская 2
ГДЗ По Математике Г Класс
Решебник Лунгу 1 Курс
ГДЗ По Математике 5 Класс Автор Дорофеев
Физика Класс Рымкевич Задачник ГДЗ
ГДЗ По Англ Яз Тетр 5
ГДЗ Рыбченкова 6 Класс Тетрадь
ГДЗ Алиев 10 11 Класс Алгебра
ГДЗ По Алгебре 7 9 Класс Дорофеев
ГДЗ Путина По Английскому 4

ГДЗ Русский Язык 2 Класс Страница 18

ГДЗ Чтение 4 Класс Учебник Ответы

Гдз Захарова Математика Тетрадь 1 Часть

ГДЗ Седьмой Класс Мордкович

ГДЗ Торкунова 6 Класс 2 Часть

Решебник Алгебра Алимов Ш.

А. 11 класс гдз

Задание не найдено

Глава 1. Действительные числа

§ 1. Целые и рациональные числа

§ 2. Действительные числа

§ 3. Бесконечно убывающая геометрическая прогрессия

§ 4. Арифметический корень натуральной степени

§ 5. Степень с рациональным и действительным показателями

Упражнения к главе I

100

101

102

103

104

105

106

107

108

109

110

111

112

113

114

115

116

117

118

Глава II. Степенная функции

§ 6. Степенная функция, её свойства и график

119

120

121

122

123

124

125

126

127

128

129

130

§ 7. Взаимно обратные функции

131

132

133

134

135

136

137

§ 8. Равносильные уравнения и неравенства

138

139

140

141

142

143

144

145

146

147

148

149

150

§ 9. Иррациональные уравнения

151

152

153

154

155

156

157

158

159

160

161

162

163

164

§ 10. Иррациональные неравенства

165

166

167

168

169

170

171

172

173

174

Упражнения к главе II

175

176

177

178

179

180

181

182

183

184

185

186

187

188

189

190

191

Глава III. Показательная функция

§11. Показательная функция, её свойства и график

192

193

194

195

196

197

198

199

200

201

202

203

204

205

206

207

§ 12. Показательные уравнения

208

209

210

211

212

213

214

215

216

217

218

219

220

221

222

223

224

225

226

227

§ 13. Показательные неравенства

228

229

230

231

232

233

234

235

236

237

238

239

§ 14. Системы показательных уравнений и неравенств

240

241

242

243

244

245

Упражнения к главе III

246

247

248

249

250

251

252

253

254

255

256

257

258

259

260

261

262

263

264

265

Глава IV. Логарифмическая функция

§ 15. Логарифмы

266

267

268

269

270

271

272

273

274

275

276

277

278

279

280

281

282

283

284

285

286

287

288

289

§ 16. Свойства логарифмов

290

291

292

293

294

295

296

297

298

299

300

§ 17. Десятичные и натуральные логарифмы

301

302

303

304

305

306

307

308

309

310

311

312

313

314

315

316

317

§ 18. Логарифмическая функция, её свойства и график

318

319

320

321

322

323

324

325

326

327

328

329

330

331

332

333

334

335

§ 19. Логарифмические уравнения

336

337

338

339

340

341

342

343

344

345

346

347

348

349

350

351

352

353

§ 20. Логарифмические неравенства

354

355

356

357

358

359

360

361

362

363

364

365

366

367

Упражнения к главе IV

368

369

370

371

372

373

374

375

376

377

378

379

380

381

382

383

384

385

386

387

388

389

390

391

392

393

394

395

396

397

398

399

400

401

402

403

404

405

406

Глава V . Тригонометрические формулы

§ 21. Радианная мера угла

407

408

409

410

411

412

413

414

415

§ 22. Поворот точки вокруг начала координат

416

417

418

419

420

421

422

423

424

425

426

427

428

§ 23. Определение синуса, косинуса и тангенса угла

429

430

431

432

433

434

435

436

437

438

439

440

441

§ 24. Знаки синуса, косинуса и тангенса

442

443

444

445

446

447

448

449

450

451

452

453

454

455

§ 25. Зависимость между синусом, косинусом и тангенсом одного и того же угла

456

457

458

459

460

461

462

463

464

§ 26. Тригонометрические тождества

465

466

467

468

469

470

471

472

473

474

§ 27. Синус, косинус и тангенс углов α и -α

475

476

477

478

479

480

§ 28. Формулы сложения

481

482

483

484

485

486

487

488

489

490

491

492

493

494

495

496

497

§ 29. Синус, косинус и тангенс двойного угла

498

499

500

501

502

503

504

505

506

507

508

509

510

511

512

§ 30. Синус, косинус и тангенс половинного угла

513

514

515

516

517

518

519

520

521

522

523

§ 31. Формулы приведения

524

525

526

527

528

529

530

531

532

533

534

535

536

§ 32. Сумма и разность синусов. Сумма и разность косинусов

537

538

539

540

541

542

543

544

545

Упражнения к главе V

546

547

548

549

550

551

552

553

554

555

556

557

558

559

560

561

562

563

564

565

566

567

Глава VI. Тригонометрические уравнения

§ 33. Уравнение cos х = а

568

569

570

571

572

573

574

575

576

577

578

579

580

581

582

583

584

585

§ 34. Уравнение sin х = а

586

587

588

589

590

591

592

593

594

595

596

597

598

599

600

601

602

603

604

605

606

§ 35. Уравнение tg х = а

607

608

609

610

611

612

613

614

615

616

617

618

619

§ 36. Решение тригонометрических уравнений

620

621

622

623

624

625

626

627

628

629

630

631

632

633

634

635

636

637

638

639

640

641

642

643

644

645

646

647

§ 37. Примеры решения простейших тригонометрических неравенств

648

649

650

651

652

653

654

Упражнения к главе VI

655

656

657

658

659

660

661

662

663

664

665

666

667

668

669

670

671

672

673

674

675

676

677

678

679

680

681

682

683

684

685

686

687

688

689

690

Глава VII. Тригонометрические функции

§ 38. Область определения и множество значений тригонометрических функций

691

692

693

694

695

696

697

698

699

§ 39. Чётность, нечётность, периодичность тригонометрических функций

700

701

702

703

704

705

706

707

§ 40. Свойства функции у = cos x и её график

708

709

710

711

712

713

714

715

716

717

718

719

§ 41. Свойства функции у = sin x и её график

720

721

722

723

724

725

726

727

728

729

730

731

732

§ 42. Свойства функции у = tg x и её график

733

734

735

736

737

738

739

740

741

742

743

744

745

746

747

748

749

§ 43. Обратные тригонометрические функции

750

751

752

753

754

755

756

757

Упражнения к главе VII

758

759

760

761

762

763

764

765

766

767

768

769

770

771

772

773

774

775

Начально-краевая задача для уравнения субдиффузии с дробным временем с произвольным эллиптическим дифференциальным оператором

Список журналов
Коллекция чрезвычайных ситуаций в области общественного здравоохранения Nature
PMC8101089

Лобачевский Ж. Матем. 2021; 42(3): 517–525.

Опубликовано онлайн 2021 мая 6. DOI: 10.1134/S1995080221030070

PMCID: PMC8101089

^и

Авторская информация. Замечания. Статья. Замечание. рассмотрено дробное уравнение субдиффузии с эллиптическим дифференциальным оператором произвольного порядка. Единственность и существование классического решения поставленной задачи доказывается классическим методом Фурье. Указаны достаточные условия на начальную функцию и на правую часть уравнения, при которых соответствующие ряды Фурье сходятся абсолютно и равномерно. В случае начально-краевой задачи на -мерном торе легко видеть, что эти условия не только достаточны, но и необходимы.

Ключевые слова: Уравнение субдиффузии с дробным временем, начально-краевая задача, метод Фурье, регулярное решение, пространства Соболева

Теория дифференциальных уравнений с дробными производными за последние несколько лет приобрел значительную популярность и значение десятилетия, в основном из-за его применения в многочисленных, казалось бы, отдаленные области науки и техники (см. пример, [1–8]). В качестве наиболее важных применений этого теории можно рассмотреть недавние исследования по моделированию COVID-19вспышки [2, 3]. Данные [9], представленные Johns Hopkins Университет о вспышках из разных стран, кажется, показывает динамические процессы дробного порядка.

В свою очередь, заслуженная популярность теории привлекла внимание специалистов, вызывая большое количество расследований по математическим аспектам дробных дифференциальных уравнений и методы их решения (см., например, [1] и литературу там же, [10–13]). Интересные результаты были получены в работах [14–16]. Метод Фурье широко используется в современных исследованиях парциальных дифференциальные уравнения и оптимальное управление (см., например, [17–21]).

В данной работе мы будем исследовать методом Фурье разрешимость (в классическом смысле) начально-краевого значения задачи для уравнения субдиффузии с дробным временем с эллиптическими дифференциальные операторы любого порядка, определенные на произвольном -мерная ограниченная область с гладкой границей . Дробная часть нашего уравнения будет Дробная производная Римана – Лиувилля заказ .

Многие частные случаи этой задачи были рассмотрены количество авторов, использующих различные методы. Это было в основном рассмотрен случай одной пространственной переменной и уравнение субдиффузии с «эллиптической частью» (см. например, справочник [1], книга А.А. Килбас и др. [6] и монография А.В. Псху [11] и ссылки в этих работах). В многомерный случай () вместо дифференциальное выражение считалось либо оператор Лапласа [6, 22], или эллиптический дифференциал, или псевдодифференциальный оператор во всем пространстве с постоянными коэффициентами [10]. В обоих случаях авторы исследовал задачи типа Коши, применяя либо Лапласов преобразование или преобразование Фурье. В своей недавней статье [23] Псху рассмотрена начально-краевая задача для субдиффузии уравнение с оператором Лапласа и областью определения — a многомерная прямоугольная область. Автору удалось построить функцию Грина. Естественно, исходя из физ.

смысла проблемы, интересно рассмотреть аналогичные задачи для произвольных ограниченных пространственных областей.

В произвольной области начально-краевые задачи для уравнений субдиффузии (дробная часть уравнения многочлен и начальные условия нелокальны) с капуто дериваты исследовали М. Ружанский с соавт. [24]. авторы доказали существование и единственность обобщенного Решение проблемы.

Лет — произвольная положительная формально самосопряженная (симметричная) эллиптическая дифференциальный оператор порядка с достаточно гладким коэффициенты в , где — многоиндексные и , . Напомним, оператор эллиптичен по , если для всех и у одного

Дробное интегрирование порядка функции определенное на в смысле Римана–Лиувилля, есть определяется формулой

при условии существования правой части. Вот Гамма-функция Эйлера. Используя это определение, можно определить Дробная производная Римана–Лиувилля порядка , , , as (см., например, [11, п. 14])

Заметим, если , то дробная производная совпадает с обычный классический вывод: .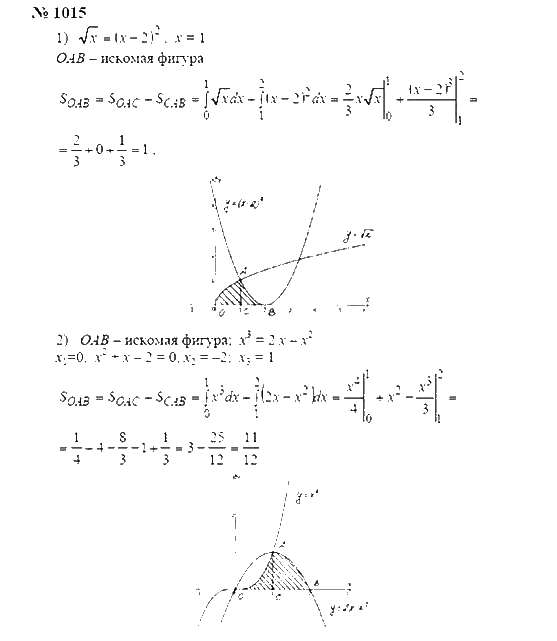

Позвольте быть постоянным числом. Рассмотрим дифференциальное уравнение

с начальными

и граничными

условиями, где и коэффициенты – заданные функции.

Определение 1. Функция А с свойства , и удовлетворяющий всем условия задачи (1)–(3) в классическом смысле называется регулярное решение начально-краевого значения задача (1)–(3).

Обращаем внимание на то, что в этом определении требование непрерывности в замкнутой области всех производных решения, входящего в уравнение (1), не обусловлено достоинства. Однако, с одной стороны, уникальность именно такого решение доказывается достаточно просто, а с другой стороны, решение найденное методом Фурье, удовлетворяет указанным выше условиям.

Обычное решение также будем называть просто раствором краевая задача.

Применение метода Фурье к задаче (1)–(3) приводит к рассмотрим следующую спектральную задачу

С. Агмон [25] нашел необходимые условия для граничного домена и для коэффициентов операторы и , гарантирующие компактность обратный оператор, т.е. существование полного в система ортонормированных собственных функций и счетный набор положительных собственных значений спектральная задача (4)–(5). Мы будем называть эти условия как состояние .

В соответствии с методом Фурье будем искать решение к задаче (1)–(3) в виде ряда

где функции являются решениями задачи типа Коши

Здесь мы обозначили и Фурье коэффициенты функций и относительно системе собственных функций соответственно, определяется как скалярное произведение на , т. е., например, . Единственное решение задачи (6) имеет вид (см., например, [11, с. 16])

где – функция Миттаг-Леффлера вида

Результат единственности решения задачи (1)–(3) может быть формулируется как

Теорема 1. Пусть условие быть доволен и и . Тогда задача (1)–(3) может иметь только одно обычное решение.

В дальнейшем мы предполагаем, что выполняется условие доволен.

Чтобы сформулировать теорему существования, нам нужно ввести для любого реальное число оператор, действующий в следующим образом

Очевидно, что оператор с областью определения

является самосопряженным. Если обозначить оператором в , действует как и с областью определения , то нетрудно показать, что оператор является самосопряженным расширением оператора .

Теорема 2. Пусть и . Более того, пусть для всех и функция быть непрерывным по пространственной норме для всех . Тогда существует решение начально-краевой задачи (1)–(3) и имеет вид серия

, которое абсолютно и равномерно сходится к . и за каждый .

Обратите внимание, когда эта теорема утверждает существование единственного решение задачи, когда уравнение и начальное условие иметь форму

и граничное условие такое же, как (3).

Следует отметить, что Ш. А. Алимов в своей статье [27] представляет достаточные условия принадлежности данной функции области определения определения оператора в терминах различных классы дифференцируемых функций. В конце этой статьи мы рассмотрим начально-краевую задачу (1)–(3) в торе когда оператор имеет постоянные коэффициенты. Мы увидим, что в этом случае область определения совпадает с соответствующими пространствами Соболева.

В этом разделе мы докажем теорему 1. Предположим, что все условия этой теоремы выполнены, и пусть начально-краевая задачи значений (1)–(3) имеют два регулярных решения и . Наша цель доказать, что . Так как задача линейная, то имеем следующую однородную задачу для :

Пусть – регулярное решение задачи (9)–(11) и — произвольная собственная функция задачи (4)–(5) с соответствующее собственное значение . Рассмотрим функцию

По определению регулярного решения можно записать

или, интегрируя по частям,

Поскольку условие (2) можно переписать в виде (см. , например, [11, п. 104])

то, используя в (12) однородное начальное условие (10) в этом В форме имеем следующую задачу Коши для :

Эта задача имеет единственное решение; следовательно, функция определяемый (12), тождественно равен нулю: (см. (7)). От полноты в системе собственные функции , мы имеем для всех и . Следовательно, теорема 1 доказана.

Здесь мы позаимствовали некоторые оригинальные идеи из метода развитые в работе М. А. Красносельского с соавт. [26]. ключевую роль в этом методе играет следующая лемма [26, с. 453].

Лемма. Пусть . Тогда для любого оператора (полностью) непрерывно сопоставляется с в и, кроме того, следующие оценка верна

Используя эту лемму, мы доказываем, что можно справедливо применить операторы с и к ряду (8) почленно.

Для функции Миттаг-Леффлера с отрицательным аргументом имеем оценка (см. например, [11], с. 13). Следовательно, поскольку все собственные значения положительны,

где . Действительно, пусть , то

, а если , то

Заметим, что ряд (8) на самом деле является суммой двух рядов. Рассмотрим первый ряд:

и пусть эта функция удовлетворяет условию Теорема 2, т.е. для некоторых

Выберем малое так, чтобы . С , мы можем переписать сумма (16) как

Следовательно, в силу леммы 1 имеем

Используя ортонормированность системы , будем иметь

Применение неравенства (15) дает

Следовательно, оценку (18) можно переписать в виде

Отсюда следует равномерно сходимость дифференцированная сумма (16) по переменным для каждый . С другой стороны, сумма (17) сходится при любая перестановка его членов, так как эти термины взаимно ортогональны. Отсюда следует абсолютная сходимость дифференцированная сумма (16) на том же интервале .

Теперь рассмотрим вторую часть ряда (8):

и предположим, что функция удовлетворяет всем условиям теоремы 2, т. е. следующий ряд сходится равномерно на для некоторых :

Имеем

Тогда в силу леммы 1 имеем

Используя ортонормированность системы , будем иметь

Теперь воспользуемся оценкой (15) и применим обобщенную формулу Минковского неравенство. Тогда

Следовательно, используя те же рассуждения, что и выше, мы видим, что дифференцированная сумма (19) по переменным сходится абсолютно и равномерно на .

Нетрудно видеть, что

Абсолютная и равномерная сходимость последнего ряда может быть доказано, как указано выше.

Очевидно, что функция (8) удовлетворяет граничным условиям (3). Учитывая начальное условие, как в (13), нетрудно убедиться, что это условие также выполняется.

Таким образом, теорема 2 полностью доказана.

Обратите внимание, принимая во внимание приведенные выше оценки, можно получить оценку для , которая дает устойчивость решения задачи (1)–(3).

В доказательстве теоремы 2 мы используем только тот факт, что эллиптические оператор имеет полный набор ортонормированных собственных функций и лемма 1.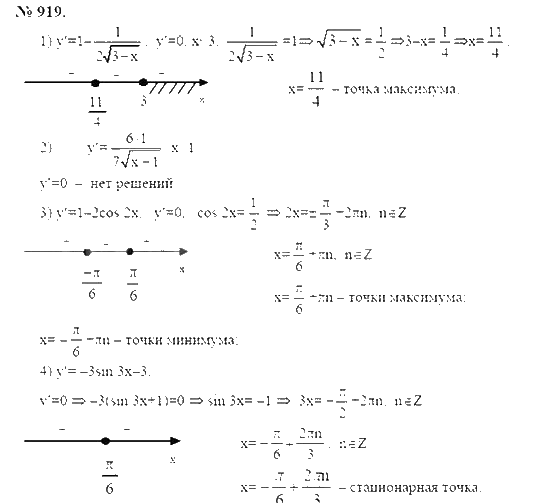 Эта лемма сводит к изучению равномерной сходимости к изучению сходимости в , где равенство Парсеваля сразу дает решение задачи. Следовательно, аналогично теореме 2 утверждение справедливо для любого оператор с этими свойствами. В качестве примера мы можем рассмотреть дифференциальный оператор с инволюцией и оператор Бесселя (см. статья М. Ружанского и соавт. [24]), или начальная граница задача о значениях в -мерном торе: .

Рассмотрим последний случай. Так что давайте быть однородным симметричный положительный эллиптический дифференциальный оператор с константой коэффициенты. Пусть дифференциальное уравнение и начальное условие имеют вид ()

Вместо граничных условий (3) рассмотрим -периодические в каждом аргументе функции и предположим, что и также являются -периодическими функциями в .

Пусть обозначает оператор , определенный на -периодическом функции из . Закрытие этого оператор in является самосопряженным. это не трудно видим, что оператор имеет полное (в ) множество собственных функций , и соответствующие собственные значения .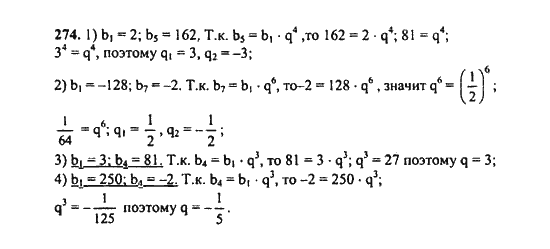 Следовательно, в силу теоремы Дж. фон Нимана для любого оператор действует как , где – коэффициенты Фурье . область определения этого оператора определяется из состояние и имеет форма

Для определения области определения оператора в терминах пространств Соболева, напомним определение этих пространств (см., например, [28]): мы говорим, что функция принадлежит пространству Соболева с действительным числом , если норма

ограничена. Когда не целое, то это пространство также называется пространством Лиувилля.

Нетрудно показать существование констант и такой, что

Следовательно, .

Дословно повторяя доказательство теоремы 2, следующее утверждение доказано.

Теорема 3. Пусть и . Более того, пусть для любого и функция быть непрерывным по пространственной норме для всех . Тогда существует решение начально-краевой задачи (21)–(22) и имеет форма

, которое абсолютно и равномерно сходится к . и за каждый , где и — соответствующие коэффициенты Фурье.

Заметим, когда по вложению Соболева теореме, все функции в -периодические непрерывные функции. Выполнение обратное неравенство , допускает существование неограниченных функций в (см., для например, [28]). Поэтому условие этого теоремы не только достаточно, чтобы утверждение было верным, но и это также необходимо.

А — периодическая непрерывная функция, определенная на , называется непрерывной по Гёльдеру с показатель степени, если для некоторой константы

Мы определяем пространство Гёльдера -периодические функции по , есть целая часть , все производные , , из которых непрерывны по Гёльдеру с показателем . Из теоремы вложения следует , , что условия теоремы 3 можно сформулировать в терминах гёльдеровы пространства, заменяющие классы по классам. Опять же, условие является точным: если , то существует функция в , ряд Фурье которого в некоторой точке расходится (см. , например, [28]).

Авторы выражают благодарность Ш. А. Алимову и С.Р. Умарову за обсуждения этих результатов. Хотим также поблагодарить Б. Турметова за то, что ознакомили нас с работой М. Ружанского и соавт. [24].

(Представил Юлдашев Т.К.)

Ашуров Р.Р., Email: moc.liamg@rvoruhsa.

Мухиддинова О.Т., Email: ur.liam@2991aliqo.

1. Мачадо Дж. А. Т. Справочник по дробному исчислению с приложениями . Берлин: Де Грюйтер; 2019. [Google Академия]

2. C. Xu, Y. Yu, Y. Q. Chen и Z. Lu, «Прогнозный анализ эпидемической тенденции COVID-19 в Соединенных Штатах с помощью обобщенной модели SEIR дробного порядка», arXiV: 2004.12541v1 (2020). [Бесплатная статья PMC] [PubMed]

3. М. А. Хан и А. Атангана, «Моделирование динамики нового коронавируса (2019-nCov) с дробной производной», Alexandria J. Eng. (2020, в печати).

4. Горенфло Р., Килбас А. А., Майнарди Ф., Рогозин С. В. Функции Миттаг-Леффлера, родственные темы и приложения . Берлин: Спрингер; 2014. [Google Scholar]

5. Ю. Чжан, Д. А. Бенсон, М. М. Меершарт, Э. М. Лаболль, Х. П. Шеффлер, «Аппроксимация случайного блуждания дробного порядка многомасштабной аномальной диффузии», Phys. Ред. E 74 , 026706 (2006 г.). [PubMed]

6. Килбас А. А., Сривастава Х. М., Трухильо Дж. Дж. Теория и приложения дробных дифференциальных уравнений . Амстердам: Эльзевир; 2006. [Google Scholar]

7. Умаров С., Хан М., Кобаяши К. За пределами треугольника: броуевское движение, расчеты Ито и дробные обобщения уравнения Фоккера–Планка . Сингапур: Мировой научный; 2017. [Google Scholar]

8. Хилфер Р. Приложения дробного исчисления в физике . Сингапур: Мировой научный; 2000. [Google Scholar]

9. https://www.worldometers.info/coronavirus/.

10. Умаров С. Введение в дробные и псевдодифференциальные уравнения с сингулярными символами . Берлин: Спрингер; 2015. [Google Академия]

11. Псху А. В. Уравнения в частных производных дробного порядка . Москва: Наука; 2005. [Google Scholar]

12. Агравал О. П. Решение дробного диффузионно-волнового уравнения, заданного в ограниченной области. Нонлин. Динам. 2002; 29: 145–155. doi: 10.1023/A:101653

92. [CrossRef] [Google Scholar]

13. Ашуров Р., Кабада А., Турметов Б. Операторный метод построения решений линейных дробно-дифференциальных уравнений с постоянными коэффициентами. Фракт. Расчет. заявл. Анальный. 2016;1:229–252. [Google Scholar]

14. Ахмед Х. М., Эль-Овайди Х. М., Аль-Наххас М. А. Нелинейная дробно-интегро-частная дифференциальная система Гильфера. Лобачевский Ю. Матем. 2019;40:115–126. doi: 10.1134/S19950802121. [CrossRef] [Google Scholar]

15. Дамаг Ф. Х., Килисман А., Ибрагим Р. В. Смешанные решения монотонного итерационного метода для гибридных дробно-дифференциальных уравнений. Лобачевский Ю. Матем. 2019;40:156–165. doi: 10.1134/S19950802169. [Перекрестная ссылка] [Академия Google]

16. Тайеб А. Устойчивость сингулярных дробных систем нелинейных интегро-дифференциальных уравнений. Лобачевский Ю. Матем. 2019;40:219–229. doi: 10.1134/S19950802148. [CrossRef] [Google Scholar]

17. Ильин В. А. Единственность обобщенных решений смешанных задач для волнового уравнения с нелокальными краевыми условиями. Отличаться. Экв. 2008; 44: 692–700. doi: 10.1134/S001226610805011X. [CrossRef] [Google Scholar]

18. Ильин В. А., Моисеев Е. И. Оценка сверху по диагонали спектральной функции многомерного оператора Шрёдингера с потенциалом, удовлетворяющим условию Като. Отличаться. Экв. 1998;34:358–368. [Google Scholar]

19. Капустин Н. Ю., Моисеев Е. И. Спектральная задача для оператора Лапласа в квадрате со спектральным параметром в граничном условии. Отличаться. Экв. 1998; 34: 663–668. [Google Scholar]

20. Юлдашев Т. К. Об одной краевой задаче для нелинейного интегро-дифференциального уравнения типа Буссинеска с отражающим аргументом. Лобачевский Ю. Матем. 2020;41:111–123. doi: 10.1134/S1995080220010151. [CrossRef] [Google Scholar]

21. Юлдашев Т. К. Нелинейное оптимальное управление тепловыми процессами в нелинейной обратной задаче. Лобачевский Ю. Матем. 2020; 41: 124–136. дои: 10.1134/S1995080220010163. [CrossRef] [Google Scholar]

22. Псху А. В. Начальная задача для линейного обыкновенного дифференциального уравнения нецелого порядка. Сб.: Матем. 2011; 202: 571–582. [Google Scholar]

23. Псху А. В. Функция Грина первой краевой задачи для дробного диффузионно-волнового уравнения в многомерной прямоугольной области. Математика. 2020;8:464. doi: 10.3390/math8040464. [CrossRef] [Google Scholar]

24. Ружанский М., Токмагамбетов Н., Торебек Б.Т. О нелокальной задаче для многочленного дробного диффузионно-волнового уравнения. arXiv:1812.01336v2 [math. АП] (2018).

25. Агмон С. О собственных функциях и собственных значениях общих эллиптических краевых задач. коммун. Чистое приложение Мат. 1962; 15: 119–147.

Решебник по математике 10 11 алимов: ГДЗ Алгебра 10-11 класс Алимов, Колягин, Сидоров

ГДЗ По Алгебре 10 22 Алимов – Telegraph

Решебник Алгебра Алимов Ш.

Начально-краевая задача для уравнения субдиффузии с дробным временем с произвольным эллиптическим дифференциальным оператором

Добавить комментарий Отменить ответ

Рубрики