ГДЗ решебник Алгебра за 7 класс Арефьева, Пирютко (Учебник) «Народная асвета»
Алгебра 7 классУчебникАрефьева, Пирютко«Народная асвета»
Ребенок теряется в обилии нового учебного материала? Все никак не может вникнуть в учебный процесс, из-за чего испытывает дискомфорт, неуверенность в себе и своих знаниях? Мы крайне рекомендуем попробовать вам решебник к учебнику «Алгебра 7 класс Учебник Арефьева, Пирютко Народная асвета», написанный специально с учётом программы по алгебре для седьмого класса.
Что насчёт содержания
В этой книге есть материалы, как для изучения, так и для сотворения. Так же, определенным плюс является наличие тестовых заданий, поделенных на подразделы и темы. Ко все непонятным терминам в пособии есть пояснения.
У данного пособия имеется много плюсов
Преимущества готовых домашних заданий неоспоримы, а именно:
- Самостоятельная проверка своих домашних заданий даёт ребенку уверенность в себе и своих силах.

- Теперь вам не нужно тратить долгие часы на самостоятельное решение всех заданий.
- Все пояснительные тексты внутри книги написаны понятным, лаконичным языком.
Что ж, подводя итог, определенно стоит упомянуть, что готовые домашние задания в большинстве случаев крайне положительно сказываются не только на учебном процессе, но и на воспитании ребенка, его самостоятельности и самооценке.
Задания. Глава 1
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139140141142143144145146147148149150151152153154155156157158159160161162163164165166167168169170171172173174175176177178179180181182183184185186187188189190191192193194195196197198199200201202203204205206Задания. Глава 2
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139140141142143144145146147148149150151152153154155156157158159160161162163164165166167168169170171172173174175176177178179180181182183184185186187188189190191192193194195196197198199200201202203204205206207208209210211212213214215216217218219220221222223224225226227228229230231232233234235236237238239240241242243244245246247248249250251252253254255256257258259260261262263264265266267268269270271272273274275276277278279280281282283284285286287288289290291292293294295296297298299300301302303304305306307308309310311312313314315316317318319320321322323324325326327328329330331332333334335336337338339340341342343344345346347348349350351352353354355356357358359360361362363364365366367368369370371372373374375376377378379380381382383384385386387388389390391392393394395396397398399400401402403404405406407408409410411412413414415416417418419420421422423424425426427428429430431432433434435436437438439440441442443444445446447448449Задания.
 Глава 3123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139140141142143144145146147148149150151152153154155156157158159160161162163164165166167168169170171172173174175176177178179180181182183184185186187188189190191192193194195196197198199200201202203204205206207208209210211212213214215216217218219220221222223224225226227228229230231232233234235236237238239240241242243244245246247248249250251252253254255256257258259260261262263264265266267268269270271272273274275276277278279280281282283284285286287288289290291292293294295296297298299300301302303304305306307308309310311312313314315316317318319320321322323324325326327328329330331332333334335336337338339340341342343344345346347348349350351352353354355356357358359360361362363364365366367368369370371372373374375376377378379380381382383384385386387388389390391392393394395396
Глава 3123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139140141142143144145146147148149150151152153154155156157158159160161162163164165166167168169170171172173174175176177178179180181182183184185186187188189190191192193194195196197198199200201202203204205206207208209210211212213214215216217218219220221222223224225226227228229230231232233234235236237238239240241242243244245246247248249250251252253254255256257258259260261262263264265266267268269270271272273274275276277278279280281282283284285286287288289290291292293294295296297298299300301302303304305306307308309310311312313314315316317318319320321322323324325326327328329330331332333334335336337338339340341342343344345346347348349350351352353354355356357358359360361362363364365366367368369370371372373374375376377378379380381382383384385386387388389390391392393394395396Задания.
 Глава 4123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139140141142143144145146147148149150151152153154155156157158159160161162163164165166167168169170171172173174175176177178179180181182183184185186
Глава 4123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139140141142143144145146147148149150151152153154155156157158159160161162163164165166167168169170171172173174175176177178179180181182183184185186Я проверяю свои знания
стр. 42стр. 143стр. 251стр. 302Задания. Глава 1: 1
◄ Предыдущий
Следующий ►
Условие
Решение
◄ Предыдущий
Следующий ►
ГДЗ решебник по алгебре 7 класс Арефьева, Пирютко учебник Народная асвета
Алгебра 7 класс
Тип пособия: Учебник
Авторы: Арефьева, Пирютко
Издательство: «Народная асвета»
Дружба с алгеброй
«ГДЗ по алгебре учебник для 7 класса Арефьева (Народная асвета)» – пособие, создано для помощи в выполнении домашних заданий и осваивания предмета. Авторы разработали его не только с целью списывания школьниками верных ответов, как предполагают большинство родителей, но и для того, чтобы сделать учебный процесс проще и понятнее. Алгебра – довольно сложная дисциплина, точная наука, имеющая непростую программу. А ведь есть и другие предметы, не менее громоздкие и безусловно важные. Решебник значительно упростит изучение, и сократит время для понимания. Ученик часто сталкивается с трудностями в школе и родители либо пытаются помочь сами, либо нанять репетиторов для ребенка, но это довольно дорого и не всегда дает те результаты, которые способны оправдать ожидания, ведь репетитор должен не только объяснять тему, но и найти правильный подход к школьнику, а учитывая сложности возраста семиклассников этого не всегда можно добиться. Так почему же готовые домашние задания не смогут выполнить эту функцию?
Авторы разработали его не только с целью списывания школьниками верных ответов, как предполагают большинство родителей, но и для того, чтобы сделать учебный процесс проще и понятнее. Алгебра – довольно сложная дисциплина, точная наука, имеющая непростую программу. А ведь есть и другие предметы, не менее громоздкие и безусловно важные. Решебник значительно упростит изучение, и сократит время для понимания. Ученик часто сталкивается с трудностями в школе и родители либо пытаются помочь сами, либо нанять репетиторов для ребенка, но это довольно дорого и не всегда дает те результаты, которые способны оправдать ожидания, ведь репетитор должен не только объяснять тему, но и найти правильный подход к школьнику, а учитывая сложности возраста семиклассников этого не всегда можно добиться. Так почему же готовые домашние задания не смогут выполнить эту функцию?
Особенности ГДЗ
Учебник может похвастаться множеством плюсов и преимуществ. Он позволит:
- проверить правильность выполнения уроков;
- провести работу над ошибками;
- вернуться к повторению менее понятных или трудных тем;
- детально разобраться в ответах и их решениях;
- получить примеры готовых верных ответов и применять их при написании самостоятельных или контрольных работ;
- улучшить оценки в дневнике.

Также само пособие может похвастаться своей доступностью. Школьник легко найдет нужные номера онлайн-ответов в интернете, на специальных площадках с ГДЗ.
Тематика решебника
Книга содержит четыре главы и в конце контрольные вопросы, которые помогают проверить и закрепить пройденный материал. В комплекс упражнений авторы включили наглядные иллюстрации, схемы, примеры решений, таблицы, повышающие удобство изучения предмета. «ГДЗ по алгебре учебник для 7 класса И.Г. Арефьева, О.Н. Пирютко (Народная асвета)» затрагивает темы учебной программы за 7 класс:
- Работа с дробями.
- Степени: простые арифметические действия.
- Линейные уравнения и функции.
Таким образом семиклассник сможет подготовить себя к старшей школе и изучению сложных задач и упражнений по более широким и непростым темам, развить логику, аналитическое мышление, потренировать память и обнаружить наклонности к точным наукам. Кто знает, возможно в будущем ребенок станет великим математиком, а решебник в этом поможет.
Первая глава. Задания
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139140141142143144145146147148149150151152153154155156157158159160161162163164165166167168169170171172173174175176177178179180181182183184185186187188189190191192193194195196197198199200201202203204205206Вторая глава. Задания
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139140141142143144145146147148149150151152153154155156157158159160161162163164165166167168169170171172173174175176177178179180181182183184185186187188189190191192193194195196197198199200201202203204205206207208209210211212213214215216217218219220221222223224225226227228229230231232233234235236237238239240241242243244245246247248249250251252253254255256257258259260261262263264265266267268269270271272273274275276277278279280281282283284285286287288289290291292293294295296297298299300301302303304305306307308309310311312313314315316317318319320321322323324325326327328329330331332333334335336337338339340341342343344345346347348349350351352353354355356357358359360361362363364365366367368369370371372373374375376377378379380381382383384385386387388389390391392393394395396397398399400401402403404405406407408409410411412413414415416417418419420421422423424425426427428429430431432433434435436437438439440441442443444445446447448449Задания: Я проверяю свои знания
12345678910Третья глава.
 Задания123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139140141142143144145146147148149150151152153154155156157158159160161162163164165166167168169170171172173174175176177178179180181182183184185186187188189190191192193194195196197198199200201202203204205206207208209210211212213214215216217218219220221222223224225226227228229230231232233234235236237238239240241242243244245246247248249250251252253254255256257258259260261262263264265266267268269270271272273274275276277278279280281282283284285286287288289290291292293294295296297298299300301302303304305306307308309310311312313314315316317318319320321322323324325326327328329330331332333334335336337338339340341342343344345346347348349350351352353354355356357358359360361362363364365366367368369370371372373374375376377378379380381382383384385386387388389390391392393394395396
Задания123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139140141142143144145146147148149150151152153154155156157158159160161162163164165166167168169170171172173174175176177178179180181182183184185186187188189190191192193194195196197198199200201202203204205206207208209210211212213214215216217218219220221222223224225226227228229230231232233234235236237238239240241242243244245246247248249250251252253254255256257258259260261262263264265266267268269270271272273274275276277278279280281282283284285286287288289290291292293294295296297298299300301302303304305306307308309310311312313314315316317318319320321322323324325326327328329330331332333334335336337338339340341342343344345346347348349350351352353354355356357358359360361362363364365366367368369370371372373374375376377378379380381382383384385386387388389390391392393394395396Четвертая глава.
 Задания123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139140141142143144145146147148149150151152153154155156157158159160161162163164165166167168169170171172173174175176177178179180181
Задания123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139140141142143144145146147148149150151152153154155156157158159160161162163164165166167168169170171172173174175176177178179180181Первая глава. Задания: 1
Решебник По Алгебре 7 Класс Арефьева – Telegraph
>>> ПОДРОБНЕЕ ЖМИТЕ ЗДЕСЬ <<<
Решебник По Алгебре 7 Класс Арефьева
Арефьева И .Г ., Пирютко О .Н . Решебник (ГДЗ) по Алгебре за 7 (седьмой ) класс авторы: Арефьева, Пирютко издательство Народная асвета, 2019 год .
Подробный решебник по алгебре для 7 класса , авторов Арефьева, Пирютко . Благодаря нашему решебнику , каждый школьник сможет изучить курс алгебры 7 класса, а подробные ответы помогут разобрать непонятные моменты из программы и подтянуть слабые стороны .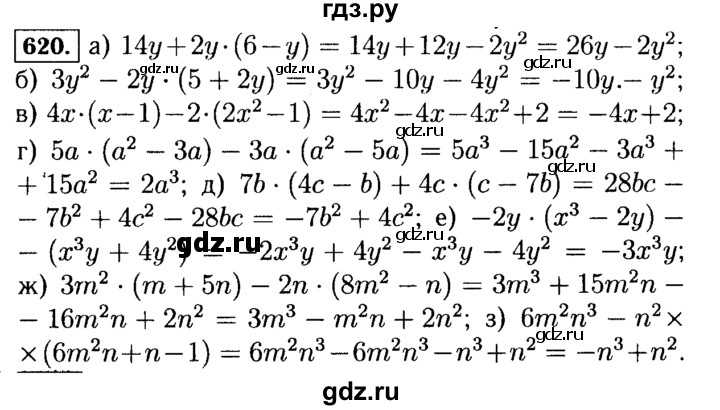
ГДЗ Арефьева , Пирютко за 7 класс по Алгебре . Авторы: Арефьева И .Г ., Пирютко О .Н . Тип: Учебник . Издатель: Народная асвета 2019 год . Белорусские ГДЗ и Решебник за 7 класс по Алгебре поможет Вам найти верный ответ на самый сложный номер задания онлайн .
ГДЗ по алгебре 7 класс , авторы: , Арефьева И .Г ., Пирютко О .Н ., Народная асвета 2020-2021 год . Глава 1 . Упражнения .
Онлайн решебник и ГДЗ по алгебре для 7 -го класса к новому учебнику 2020 года, авторов Арефьева И . Г ., Пирютко О . Н . с подробными Решеба по алгебре за 7 класс включает в себя несколько разделов, один из которых – блок для самостоятельной подготовки к грядущим . .
Готовые домашние задания по алгебре 7 класса под авторством Арефьева И .Г . и Пирютко О .Н . 2019-2020 . Решебник по алгебре авторов Арефьева и Пирютко — это эффективная настольная книга, в котором указаны все правильные ответы на любые вопросы .
Ответы к пособию «Алгебра . 7 класс . Самостоятельные и контрольные работы» .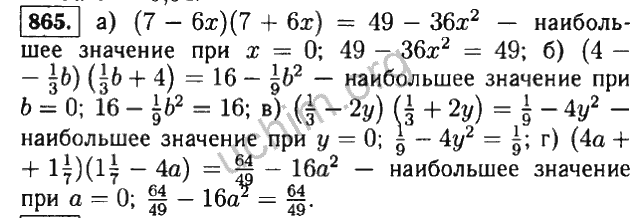 В приложении приведены ответы ко всем заданиям, предложенным в последнем издании пособия «Алгебра . 7 класс .
В приложении приведены ответы ко всем заданиям, предложенным в последнем издании пособия «Алгебра . 7 класс .
Смотрите любимые видео, слушайте любимые песни, загружайте собственные ролики и делитесь ими с друзьями, близкими и целым миром .
Арефьева И .Г ., Пирютко О .Н . Алгебраические выражения вызывают затруднение у многих старшеклассников . Ориентироваться в пространстве и соотносить величины друг с другом бывает нелегко даже взрослому .
Заходите, не пожалеете! Тут отличные гдз по алгебре для 7 класса , Арефьева И .Г ., Пирютко О .Н . от Путина . ГДЗ по алгебре 7 класс Арефьева И .Г . Тип: Учебник . Авторы: Арефьева И .Г ., Пирютко О .Н . Издательство: Народная асвета .
Так же ГДЗ по алгебре 7 класс Арефьева является прекрасным помощником при подготовке к контрольным работам . Зачастую они обращаются за помощью к решебнику к учебнику «Алгебра 7 класс » Арефьева, где и получают доскональные ответы на свои вопросы .
Решебники , ГДЗ . 11 Класс . ГДЗ — поможет Вам сверить ответы к домашнему заданию по Алгебре Арефьева И .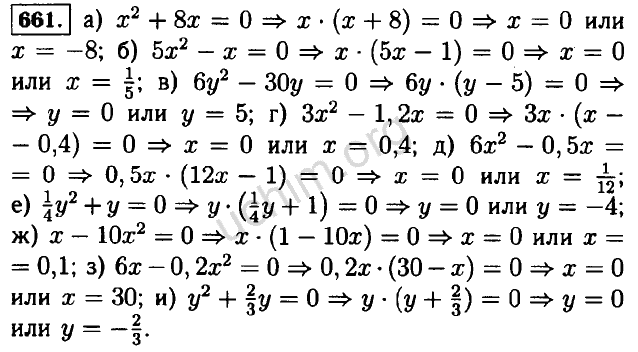 Г ., Пирютко О .Н . 7 класс .
Г ., Пирютко О .Н . 7 класс .
Алгебра . 7 класс . Учебное пособие для 7 класса учреждений общего среднего образования с русским языком обучения . Допущено Министерством образования Республики Беларусь . По этой книге вы начнете изучать раздел математики, который называется алгебра .
Алгебра . 7 класс . Арефьева И .Г ., Пирютко О .Н . Минск: 2019 . — 312 с . Учебное пособие для 7 класса учреждений общего среднего образования с русским По этой книге вы начнете изучать раздел математики, который называется алгебра . Эта наука изучает операции с различными . .
Алгебра . 7 класс . Авторы: Арефьева И . Г ., Пирютко О . Н . Предмет: Математика . 7 класс . Учебное пособие для 7 класса учреждений общего среднего образования с русским языком обучения .
Арефьева И .Г ., Пирютко О .Н . Решебник (ГДЗ) по Алгебре за 7 (седьмой ) класс авторы: Арефьева, Пирютко издательство Народная асвета, 2019 год .
Подробный решебник по алгебре для 7 класса , авторов Арефьева, Пирютко . Благодаря нашему решебнику , каждый школьник сможет изучить курс алгебры 7 класса, а подробные ответы помогут разобрать непонятные моменты из программы и подтянуть слабые стороны .
Благодаря нашему решебнику , каждый школьник сможет изучить курс алгебры 7 класса, а подробные ответы помогут разобрать непонятные моменты из программы и подтянуть слабые стороны .
ГДЗ Арефьева , Пирютко за 7 класс по Алгебре . Авторы: Арефьева И .Г ., Пирютко О .Н . Тип: Учебник . Издатель: Народная асвета 2019 год . Белорусские ГДЗ и Решебник за 7 класс по Алгебре поможет Вам найти верный ответ на самый сложный номер задания онлайн .
ГДЗ по алгебре 7 класс , авторы: , Арефьева И .Г ., Пирютко О .Н ., Народная асвета 2020-2021 год . Глава 1 . Упражнения .
Онлайн решебник и ГДЗ по алгебре для 7 -го класса к новому учебнику 2020 года, авторов Арефьева И . Г ., Пирютко О . Н . с подробными Решеба по алгебре за 7 класс включает в себя несколько разделов, один из которых – блок для самостоятельной подготовки к грядущим . .
Готовые домашние задания по алгебре 7 класса под авторством Арефьева И .Г . и Пирютко О .Н . 2019-2020 . Решебник по алгебре авторов Арефьева и Пирютко — это эффективная настольная книга, в котором указаны все правильные ответы на любые вопросы .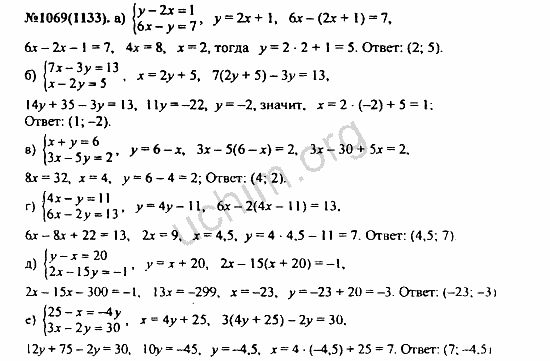
Ответы к пособию «Алгебра . 7 класс . Самостоятельные и контрольные работы» . В приложении приведены ответы ко всем заданиям, предложенным в последнем издании пособия «Алгебра . 7 класс .
Смотрите любимые видео, слушайте любимые песни, загружайте собственные ролики и делитесь ими с друзьями, близкими и целым миром .
Арефьева И .Г ., Пирютко О .Н . Алгебраические выражения вызывают затруднение у многих старшеклассников . Ориентироваться в пространстве и соотносить величины друг с другом бывает нелегко даже взрослому .
Заходите, не пожалеете! Тут отличные гдз по алгебре для 7 класса , Арефьева И .Г ., Пирютко О .Н . от Путина . ГДЗ по алгебре 7 класс Арефьева И .Г . Тип: Учебник . Авторы: Арефьева И .Г ., Пирютко О .Н . Издательство: Народная асвета .
Так же ГДЗ по алгебре 7 класс Арефьева является прекрасным помощником при подготовке к контрольным работам . Зачастую они обращаются за помощью к решебнику к учебнику «Алгебра 7 класс » Арефьева, где и получают доскональные ответы на свои вопросы .
Решебники , ГДЗ . 11 Класс . ГДЗ — поможет Вам сверить ответы к домашнему заданию по Алгебре Арефьева И .Г ., Пирютко О .Н . 7 класс .
Алгебра . 7 класс . Учебное пособие для 7 класса учреждений общего среднего образования с русским языком обучения . Допущено Министерством образования Республики Беларусь . По этой книге вы начнете изучать раздел математики, который называется алгебра .
Алгебра . 7 класс . Арефьева И .Г ., Пирютко О .Н . Минск: 2019 . — 312 с . Учебное пособие для 7 класса учреждений общего среднего образования с русским По этой книге вы начнете изучать раздел математики, который называется алгебра . Эта наука изучает операции с различными . .
Алгебра . 7 класс . Авторы: Арефьева И . Г ., Пирютко О . Н . Предмет: Математика . 7 класс . Учебное пособие для 7 класса учреждений общего среднего образования с русским языком обучения .
ГДЗ По Истории Данилов Тетрадь 6
ГДЗ По Геометрии 7 Класс Макарычев Миндюк
ГДЗ По Русскому 7 Класс Ладыженская 20
Математика 7 Класс Бунимович Учебник ГДЗ
ГДЗ По Истории Рабочая Тетрадь Кочегарова
ГДЗ По Английскому Языку 6 Класс Рабочая
ГДЗ По Математике 6 Класс Ладыженская Баранов
ГДЗ По Математике Учебник Страница 90
Рыбченкова 6 Класс Учебник 2020 ГДЗ
ГДЗ Геометрия 7 Класс Афанасьева Михеева Баранова
ГДЗ По Математике 6 Истомин
История 5 Класс Никитина Решебник
ГДЗ Алгебра 7 Класс Мордкович Александрова Мишустина
Решебник Рус 5
ГДЗ 3 Русский Язык Канакина 2 Часть
ГДЗ По Истории Египет
ГДЗ По Биологии 9 Данилов Романова
ГДЗ По Русскому 2 Класс Стр 17
ГДЗ По Математике 5 Ерина
ГДЗ По Алгебре 11 Класс Мордкович Углубленный
ГДЗ По Сборнику 7 Физика
ГДЗ По Англ 5 Рабочая
Решебник Данилова Рабочая Тетрадь
ГДЗ Русский Язык 4 Класс Нечаева
ГДЗ По Впр 7 Класс История
Истомина Математика 4 Класс Решебник 1 Часть
ГДЗ Четвертый Класс Математика Муравин Муравина
Решебник Чеботаревская 4 Класс 2 Часть
ГДЗ Ломакович 3 Класс Часть 2
ГДЗ По Биологии 8 Класс Колесов Беляев
Решебник По Биологии 7 Класс Константинов Учебник
ГДЗ 3класс Русский Канакина Учебник
ГДЗ По Алгебре Алимова Класс
ГДЗ Англ 8 Spotlight Учебник
Решебник По Геометрии Зив
ГДЗ По Обж 11 Класс Смирнов
ГДЗ По Белорусскому Языку 7
Элифба 1 Класс Мияссарова Решебник Первая Часть
Решебник Балаян Геометрия 7 9
Решебник Геометрия 10 Атанасян Бутузов
ГДЗ По Английскому 5 Класс Дули
Бесплатный Решебник По Алгебре 10
ГДЗ Русский Язык 2013 Год
ГДЗ Химия 10 Класс Еремин Базовый Уровень
ГДЗ 5 Класса Ладыженская 2 Часть
ГДЗ Математика Страница 90
Решебник За Шестой Класс
ГДЗ По Математике 2 Демидова Тонких
ГДЗ По Новой Истории 8 Класс Юдовская
Решебник По Географии 7 Класс Учебник Дронов
ГДЗ По Самостоятельной Мордкович 9 Класс
Гдз Русский 5 Класс Ладыженская Зеленый Учебник
ГДЗ Путина По Английскому Языку Кузовлев
ГДЗ По Алгебре 11 Класс Колмогоров 2008
ГДЗ По Русскому Упражнение 19
Ключ к ответу Глава 7 — Колледж Алгебра
Попытайся
7.
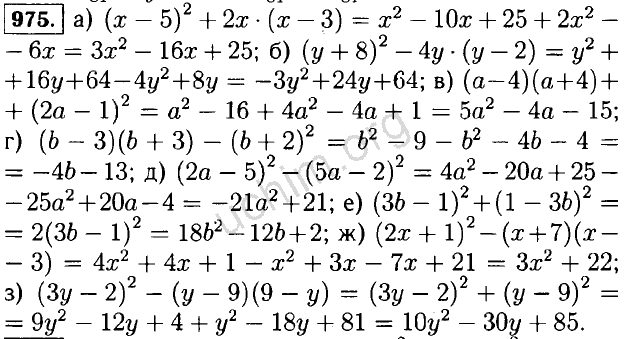 1
Системы линейных уравнений: две переменные
1
Системы линейных уравнений: две переменные1.
Не решение.
2.
Решением системы является упорядоченная пара (−5,3).(−5,3).
(-2,-5)(-2,-5)
4.
(-6,-2)(-6,-2)
5.
(10,−4)(10,−4)
6.
Нет решения. Это непоследовательная система.
7.
Система зависима, поэтому существует бесконечное число решений вида (x,2x+5).(x,2x+5).
8.
700 детей, 950 взрослых
7.2 Системы линейных уравнений: три переменные
1.
(1,−1,1)(1,−1,1)
2.
Нет решения.
3.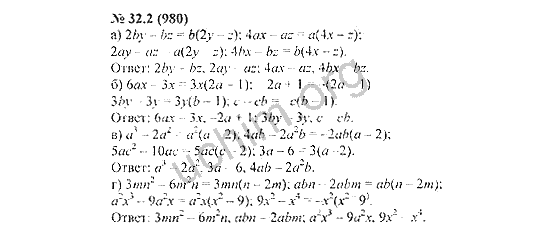
Бесконечное число решений вида (x,4x−11,−5x+18).(x,4x−11,−5x+18).
7.3 Системы нелинейных уравнений и неравенств: две переменные
1.
(−12,12)(−12,12) и (2,8)(2,8)
2.
(−1,3)(−1,3)
3.
{(1,3),(1,−3),(−1,3),(−1,−3)}{(1,3),(1,−3),(−1,3 ),(−1,−3)}
4.
7.4 Частичные дроби
1.
3x-3-2x-23x-3-2x-2
2.
6x-1-5(x-1)26x-1-5(x-1)2
3.
3x−1+2x−4×2+13x−1+2x−4×2+1
4.
х-2х2-2х+3+2х+1(х2-2х+3)2х-2х2-2х+3+2х+1(х2-2х+3)2
7,5 Матрицы и матричные операции
1.
A+B=[21160−3]+[31−4−253]A+B=[21160–3]+[31−4−253]
2.
−2B=[−8−2−6−4]−2B=[−8−2−6−4]
7.6 Решающие системы с исключением Гаусса
1.
[4−332|114][4−332|114]
2.
x−y+z=52x−y+3z=1y+z=−9x−y+z=52x−y+3z=1y+z=−9
3.
(2,1)(2,1)
4.
[1−5252015001|17292][1−5252015001|17292]
5.
(1,1,1)(1,1,1)
6.
150 000 долларов США под 7 %, 750 000 долларов США под 8 %, 600 000 долларов США под 10 %
7.7 Решающие системы с инверсиями
1.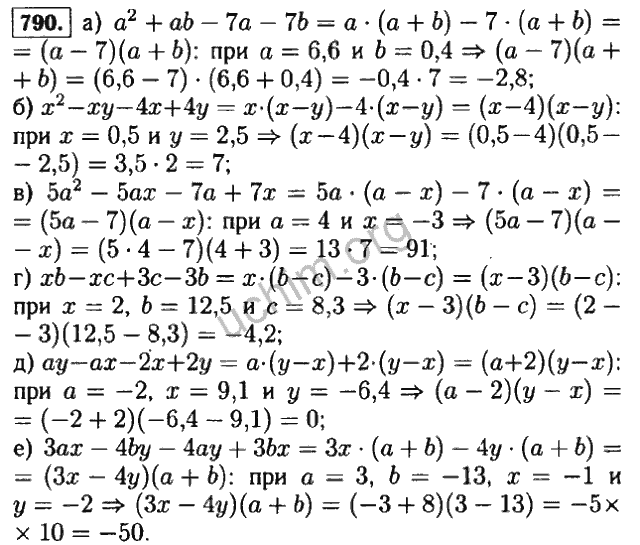
AB=[14−1−3][−3−411]=[1(−3)+4(1)1(−4)+4(1)−1(−3)+−3(1 )−1(−4)+−3(1)]=[1001]BA=[−3−411][14−1−3]=[−3(1)+−4(−1)−3( 4)+-4(-3)1(1)+1(-1)1(4)+1(-3)]=[1001]AB=[14-1-3][-3-411]= [1(−3)+4(1)1(−4)+4(1)−1(−3)+−3(1)−1(−4)+−3(1)]=[1001] BA=[−3−411][14−1−3]=[−3(1)+−4(−1)−3(4)+−4(−3)1(1)+1(−1 )1(4)+1(−3)]=[1001]
2.
А-1=[3515-2515]А-1=[3515-2515]
3.
А-1=[11224-336-5]А-1=[11224-336-5]
4.
Х=[43858]Х=[43858]
7,8 Решающие системы с правилом Крамера
1.
(3,−7)(3,−7)
2.
−10−10
3.
(-2,35,125)(-2,35,125)
7.1 Секционные упражнения
1.
Нет, их может быть ноль, единица или бесконечно много.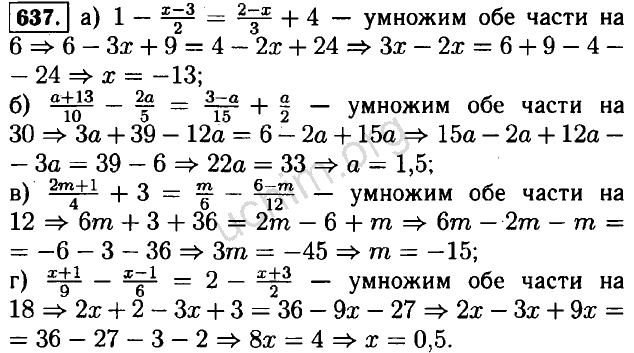 Изучите графики.
Изучите графики.
3.
Это означает, что реальной точки безубыточности не существует. К тому времени, когда компания производит одну единицу, они уже получают прибыль.
5.
Можно решить подстановкой (вычленением xx или yy ), графически или сложением.
7.
Да
9.
Да
11.
(−1,2)(−1,2)
13.
(−3,1)(−3,1)
15.
(−35,0)(−35,0)
17.
Решений не существует.
19.(725,1325)(725,1325)
21.
(6,−6)(6,−6)
23.
(−12 110)(−12 110)
25.
Решений не существует.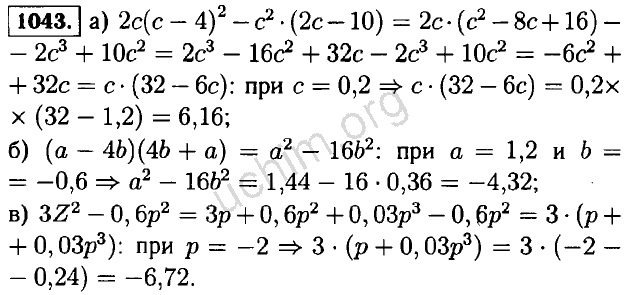
27.
(−15,23)(−15,23)
29.
(х,х+32)(х,х+32)
31.
(−4,4)(−4,4)
33.
(12,18)(12,18)
35.
(16,0)(16,0)
37.
(х, 2 (7х-6)) (х, 2 (7х-6))
39.
(−56,43)(−56,43)
41.
В соответствии с одним решением
43.
45.
Зависимый с бесконечным числом решений
47.
(-3,08,4,91)(-3,08,4,91)
49.
(-1,52,2,29)(-1,52,2,29)
51.
(А+В2,А-В2)(А+В2,А-В2)
53.
(-1A-B,AA-B)(-1A-B,AA-B)
55.
(CE-BFBD-AE,AF-CDBD-AE)(CE-BFBD-AE,AF-CDBD-AE)
57.
Они никогда не приносят прибыли.
59.
(1 250 100 000)(1 250 100 000)
61.
Цифры 7,5 и 20,5.
63.
24 000
65.790 второкурсники, 805 первокурсники
67.
56 мужчин, 74 женщины
69.
10 галлонов 10% раствора, 15 галлонов 60% раствора
71.
Лебединый пик: 750 000 долларов, Риверсайд: 350 000 долларов
73.
12 500 долларов на первый счет, 10 500 долларов на второй счет.
75.
Высокие: 45, Низкие: 15
77.
Бесконечное множество решений. Нам нужно больше информации.
7.2 Секционные упражнения
1.
Нет, решений может быть только одно, ноль или бесконечно много.
3.
Не обязательно. Решений может быть ноль, одно или бесконечно много. Например, (0,0,0)(0,0,0) не является решением приведенной ниже системы, но это не означает, что она не имеет решения.
2x+3y-6z=1-4x-6y+12z=-2x+2y+5z=102x+3y-6z=1-4x-6y+12z=-2x+2y+5z=10
5.
Любую систему уравнений можно решить графически, подстановкой и сложением. Однако системы из трех уравнений становятся очень сложными для графического решения, поэтому другие методы обычно предпочтительнее.
9.
Да
11.
(−1,4,2)(−1,4,2)
13.
(-85107,312107,1
)(-85107,312107,1
)
15.
(1,12,0)(1,12,0)
17.(4,−6,1)(4,−6,1)
19.
(х,127(65-16х),х+2827)(х,127(65-16х),х+2827)
21.
(-4513,1713,-2)(-4513,1713,-2)
23.
Решений не существует
25.
(0,0,0)(0,0,0)
27.
(47,−17,−37)(47,−17,−37)
29.
(7,20,16)(7,20,16)
31.
(−6,2,1)(−6,2,1)
33.
(5,12,15)(5,12,15)
35.
(-5,-5,-5)(-5,-5,-5)
37.
(10,10,10)(10,10,10)
39.
(12,15,45)(12,15,45)
41.
(12,25,45)(12,25,45)
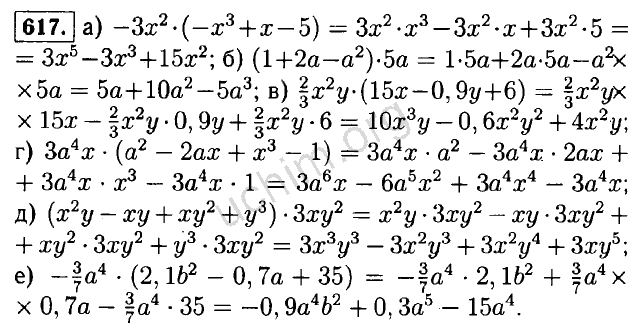
(2,0,0)(2,0,0)
45.
(1,1,1)(1,1,1)
47.
(128557,23557,28557)(128557,23557,28557)
49.
(6,−1,0)(6,−1,0)
51.
24, 36, 48
53.
70 бабушек и дедушек, 140 родителей, 190 детей
55.
Ваша доля составила 19,95 долларов, доля Сары — 40 долларов, а доля другой вашей соседки по комнате — 22,05 доллара.
57.
Существует бесконечно много решений; нам нужна дополнительная информация
59.
500 учащихся, 225 детей и 450 взрослых
61.
BMW стоил 49 636 долларов, джип — 42 636 долларов, а Toyota — 47 727 долларов.
63.
400 000 долларов на счете с выплатой 3%, 500 000 долларов на счете с выплатой 4% и 100 000 долларов на счете с выплатой 2%.
65.
США потребляли 26,3%, Япония 7,1% и Китай 6,4% мировой нефти.
67.
Саудовская Аравия импортировала 16,8%, Канада импортировала 15,1% и Мексика 15,0%
69.
Птицы 19,3%, рыбы 18,6%, млекопитающие 17,1% исчезающих видов
7.3 Секционные упражнения
1.
Нелинейная система может представлять собой две окружности, которые перекрываются и пересекаются в двух местах, следовательно, два решения. Нелинейная система может представлять параболу и окружность, где вершина параболы встречается с окружностью, а ветви также пересекают окружность, следовательно, три решения.
3.
Нет. Достижимая область не требуется. Рассмотрим систему, ограниченную двумя параллельными прямыми. Одно неравенство представляет область выше верхней линии; другой представляет область ниже нижней линии. В этом случае в обеих областях нет точек на плоскости; следовательно, нет допустимой области.
В этом случае в обеих областях нет точек на плоскости; следовательно, нет допустимой области.
5.
Выберите любое число из каждого решения и подставьте его в C(x)C(x) и R(x).R(x). Если C(x)
7.
(0,−3),(3,0)(0,−3),(3,0)
9.
(−322 322),(322,−322)(−322 322),(322,−322)
11.
(-3,0),(3,0)(-3,0),(3,0)
13.
(14,−628),(14 628)(14,−628),(14 628)
15.
(−3984,1994),(3984,1994)(−3984,1994),(3984,1994)
17.
(0,2),(1,3)(0,2),(1,3)
19.
(−12(5−1),12(1−5)),(12(5−1),12(1−5))(−12(5−1),12(1−5)) ,(12(5−1),12(1−5))
21.
(5,0)(5,0)
23.
(0,0)(0,0)
25.
(3,0)(3,0)
27.
Решений не существует
29.
Решений не существует
31.
(-22,-22),(-22,22),(22,-22),(22,22)(-22,-22),(-22,22),(22,-22) ,(22,22)
33.
(2,0)(2,0)
35.
(-7,-3),(-7,3),(7,-3),(7,3)(-7,-3),(-7,3),(7,-3) ,(7,3)
37.
(−12(73−5),12(7−73)),(12(73−5),12(7−73))(−12(73−5),12(7−73)) ,(12(73−5),12(7−73))
39.
41.
43.
45.
47.
49.
(-270383,-23529),(-270383,23529),(270383,-23529),(270383,23529)(-270383,-23529),(-270383,23529),(270383,-23529) ,(270383,23529)
51.
Решение не существует
53.
x=0,y>0x=0,y>0 и 0
55.
12, 288
57.
2–20 компьютеров
7.4 Секционные упражнения
1.
Нет, частное полиномов можно разложить только в том случае, если знаменатель можно разложить на множители. Например, 1×2+11×2+1 нельзя разложить, потому что знаменатель нельзя разложить на множители.
3.
Изобразите обе стороны и убедитесь, что они равны.
5.
Если мы выберем x=−1,x=−1, то B -член исчезнет, давая нам немедленно понять, что A=3.A=3. В качестве альтернативы мы могли бы подставить x=−53x=−53, что дало бы нам B — значение −2,−2.
7.
8x+3-5x-88x+3-5x-8
9.
1x+5+9x+21x+5+9x+2
11.
35x−2+44x−135x−2+44x−1
13.
52(х+3)+52(х-3)52(х+3)+52(х-3)
15.
3x+2+3x−23x+2+3x−2
17.
95(х+2)+115(х-3)95(х+2)+115(х-3)
19.
8x-3-5x-28x-3-5x-2
21.
1x−2+2(x−2)21x−2+2(x−2)2
23.
−64x+5+3(4x+5)2−64x+5+3(4x+5)2
25.
−1x−7−2(x−7)2−1x−7−2(x−7)2
27.
4x−32(x+1)+72(x+1)24x−32(x+1)+72(x+1)2
29.
4x+2×2−33x+2+72(3x+2)24x+2×2−33x+2+72(3x+2)2
31.
х+1х2+х+3+3х+2х+1х2+х+3+3х+2
33.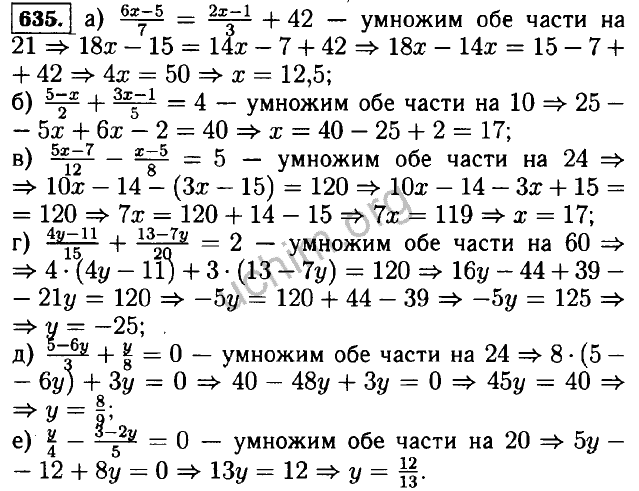
4−3xx2+3x+8+1x−14−3xx2+3x+8+1x−1
35.
2x−1×2+6x+1+2x+32x−1×2+6x+1+2x+3
37.
1×2+x+1+4x-11×2+x+1+4x-1
39.
2×2−3x+9+3x+32×2−3x+9+3x+3
41.
−14×2+6x+9+12x−3−14×2+6x+9+12x−3
43.
1x+1x+6-4xx2-6x+361x+1x+6-4xx2-6x+36
45.
х+6х2+1+4х+3(х2+1)2х+6х2+1+4х+3(х2+1)2
47.
х+1х+2+2х+3(х+2)2х+1х+2+2х+3(х+2)2
49.
1×2+3x+25-3x(x2+3x+25)21×2+3x+25-3x(x2+3x+25)2
51.
18x−x8(x2+4)+10−x2(x2+4)218x−x8(x2+4)+10−x2(x2+4)2
53.
−16x−9×2+16x−1−7(x−1)2−16x−9×2+16x−1−7(x−1)2
55.
1x+1−2(x+1)2+5(x+1)31x+1−2(x+1)2+5(x+1)3
57.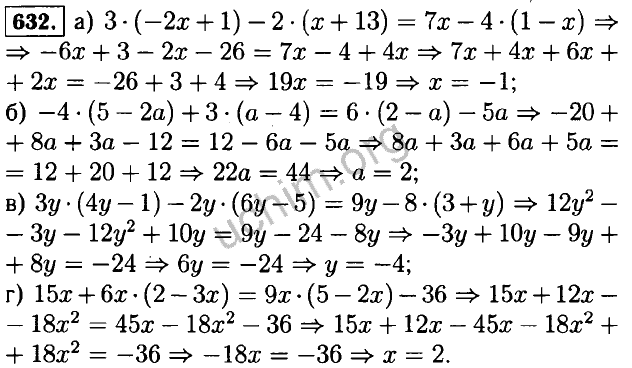
5x-2-310(x+2)+7x+8-710(x-8)5x-2-310(x+2)+7x+8-710(x-8)
59.
−54x−52(x+2)+112(x+4)+54(x+4)−54x−52(x+2)+112(x+4)+54(x+4)
7.5 Секционные упражнения
1.
Нет, они должны иметь одинаковые размеры. Пример может включать две матрицы разных размеров. Следующие две матрицы нельзя сложить, потому что первая — это матрица 2 × 22 × 2, а вторая — матрица 2 × 32 × 3. [1234]+[654321][1234]+[654321] не имеет суммы.
3.
Да, если размеры AA равны m×nm×n, а размеры BB равны n×m,n×m, оба продукта будут определены.
5.
Не обязательно. Чтобы найти AB,AB, мы умножаем первую строку AA на первый столбец BB, чтобы получить первую запись AB.AB. Чтобы найти BA,BA, мы умножаем первую строку BB на первый столбец AA, чтобы получить первую запись BA.BA. Таким образом, если они не равны, то умножение матриц не коммутирует.
7.
[111
1767][111
1767]
9.
[-4281][-4281]
11.
Неизвестно; размеры не совпадают
13.
[92763360192][92763360192]
15.
[-64-12-28-72-360-20-12-116][-64-12-28-72-360-20-12-116]
17.
[1,8001,2001,3008001,4006007004002,100][1,8001,2001,3008001,4006007004002,100]
19.
[201022828][201022828]
21.
[60412-16120-216][60412-16120-216]
23.
[-6824136-54-1264-5730128][-6824136-54-1264-5730128]
25.
Не определено; размеры не совпадают.
27.
[-841-340-15-1442742][-841-340-15-1442742]
29.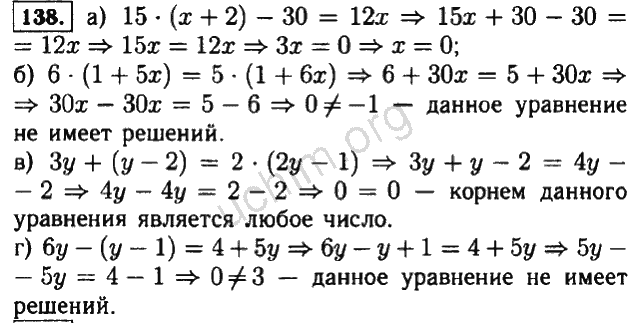
[-840650-530330360250-10
0][-840650-530330360250-100]31.
[−3501,050350350][−3501,050350350]
33.
Не определено; внутренние размеры не совпадают.
35.
[1,400700-1,400700][1,400700-1,400700]
37.
[332 500927 500−227 50087 500][332 500927 500−227 50087 500]
39.
[490 00000490 000][490 00000490 000]
41.
[-234-79-7][-234-79-7]
43.
[-42921-27-31][-42921-27-31]
45.
[-3-2-2-285946-4167][-3-2-2-285946-4167]
47.
[1-18-9-198505369-7212691][1-18-9-198505369-7212691]
49.
[01,69−1][01,69−1]
51.
[224−4,51232−9−86461][224−4,51232−9−86461]
53.
[0,530,521210710][0,530,521210710]
55.
[100010001][100010001]
57.
[100010001][100010001]
59.
Bn={[100010001], neven,[100001010], nodd.Bn={[100010001], neven,[100001010], nodd.
7.6 Секционные упражнения
1.
Да. Для каждой строки коэффициенты при переменных записываются поперек соответствующей строки и ставится вертикальная черта; то константы располагаются справа от вертикальной черты.
3.
Нет, существует множество правильных методов использования строковых операций над матрицей. Возможны следующие два пути: (1) Поменять местами строки 1 и 2. Тогда R2=R2−9R1.R2=R2−9R1. (2) R2=R1-9R2.R2=R1-9R2. Затем разделите строку 1 на 9.
5.
Нет. Матрица с 0 элементами для всей строки будет иметь либо ноль, либо бесконечно много решений.
7.
[0169−1|42][0169−1|42]
9.
[1581230349|164−7][1581230349|164−7]
11.
−2x+5y=56x−18y=26−2x+5y=56x−18y=26
13.
3x+2y=3−x−9y+4z=−18x+5y+7z=83x+2y=3−x−9y+4z=−18x+5y+7z=8
15.
4x+5y-2z=12 y+58z=28x+7y-3z=-54x+5y-2z=12 y+58z=28x+7y-3z=-5
17.
Нет решений
19.
(-1,-2)(-1,-2)
21.
(6,7)(6,7)
23.
(3,2)(3,2)
25.
(15,12)(15,12)
27.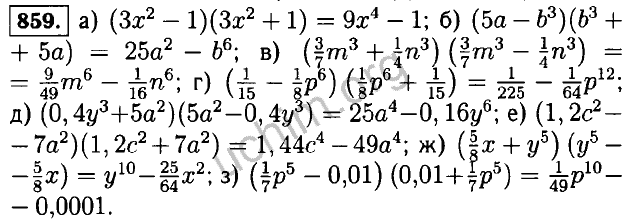
(x,415(5x+1))(x,415(5x+1))
29.
(3,4)(3,4)
31.
(19639,−513)(19639,−513)
33.
(31,−42,87)(31,−42,87)
35.
(2140,120,98)(2140,120,98)
37.
(1813,1513,−1513)(1813,1513,−1513)
39.
(x,y,12(1−2x−3y))(x,y,12(1−2x−3y))
41.
(х,-х2,-1)(х,-х2,-1)
43.
(125,−25,0)(125,−25,0)
45.
(8,1,−2)(8,1,−2)
47.
(1,2,3)(1,2,3)
49.
(x,3128-3×4,128(-7x-3))(x,3128-3×4,128(-7x-3))
51.
Решений не существует.
53.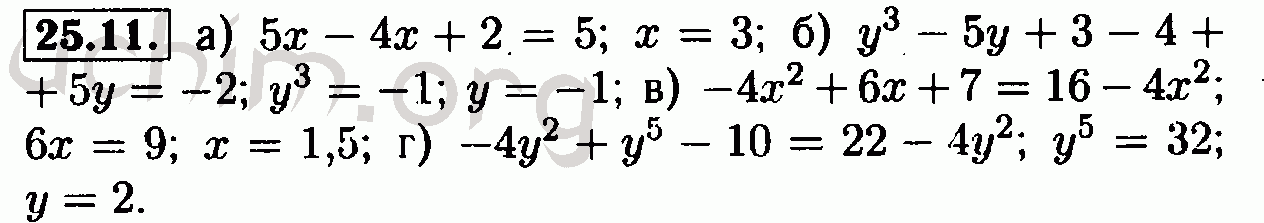
860 красный бархат, 1340 шоколад
55.
4% на счет 1, 6% на счет 2
57.
126 долларов
59.
Банан 3%, тыква 7%, каменистая дорога 2%
61.
100 миндаля, 200 кешью, 600 фисташек
7.7 Секционные упражнения
1.
Если A-1A-1 обратна A,A, то AA-1=I,AA-1=I, единичная матрица. Поскольку AA также является обратным к A−1, A−1A=IA−1,A−1A=I. Вы также можете проверить это, доказав это для матрицы 2×22×2.
3.
Нет, потому что adad и bcbc оба равны 0, поэтому ad-bc=0,ad-bc=0, что требует от нас деления на 0 в формуле.
5.
Да. Рассмотрим матрицу [0110].[0110]. Обратное находится с помощью следующего вычисления: A−1=10(0)−1(1)[0−1−10]=[0110].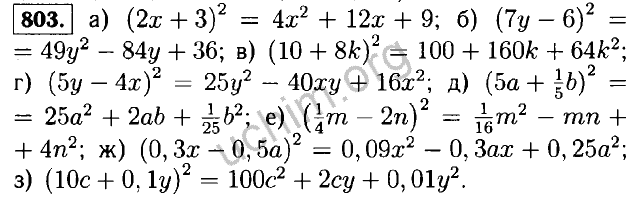 A−1=10(0)−1(1)[0− 1-10]=[0110].
A−1=10(0)−1(1)[0− 1-10]=[0110].
7.
AB=BA=[1001]=IAB=BA=[1001]=I
9.
AB=BA=[1001]=IAB=BA=[1001]=I
11.
AB=BA=[100010001]=IAB=BA=[100010001]=I
13.
129[92−13]129[92−13]
15.
169[−2793]169[−2793]
17.
Нет обратного
19.
47[0,51,51−0,5]47[0,51,51−0,5]
21.
117[−55−320−3121−14]117[−55−320−3121−14]
23.
1209[47-576
-12-2438-13]1209[47-576
-12-2438-13]
25.
[1860-168-56-1404484080-280][1860-168-56-1404484080-280]
27.
(−5,6)(−5,6)
29.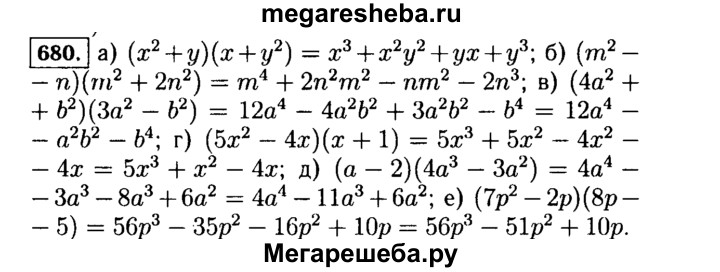
(2,0)(2,0)
31.
(13,−52)(13,−52)
33.
(-23,-116)(-23,-116)
35.
(7,12,15)(7,12,15)
37.
(5,0,−1)(5,0,−1)
39.
134(-35,-97,-154)134(-35,-97,−154)
41.
1690(65,-1136,-229)1690(65,-1136,-229)
43.
(−3730 815)(−3730 815)
45.
(10123,−1,25)(10123,−1,25)
47.
12[21-1-1011-10-11101-11]12[21-1-1011-10-11101-11]
49.
139[321-718-53321024-36219-946-16-5]139[321-718-53321024-36219-946-16-5]
51.
[100000010000001000000100000010−1−1−1−1−11][100000010000001000000100000010−1−1−1−1−11]
53.
Бесконечные решения.
55.
50% апельсины, 25% бананы, 20% яблоки
57.
10 соломенных шляп, 50 шапочек, 40 ковбойских шляп
59.
Том съел 6, Джо съел 3 и Альберт съел 3.
61.
124 апельсина, 10 лимонов, 8 гранатов
7.8 Секционные упражнения
1.
Определитель — это сумма и произведение элементов матрицы, поэтому вы всегда можете оценить это произведение, даже если в итоге оно будет равно 0,9.0007
3.
Обратное не существует.
5.
−2−2
9.
−4−4
11.
00
13.
−7 990,7−7 990,7
15.
33
17.
−1−1
19.
224224
21.
1515
23.
−17.03−17.03
25.
(1,1)(1,1)
27.
(12,13)(12,13)
29.
(2,5)(2,5)
31.
(-1,-13)(-1,-13)
33.
(15,12)(15,12)
35.
(1,3,2)(1,3,2)
37.
(−1,0,3)(−1,0,3)
39.
(12,1,2)(12,1,2)
41.
(2,1,4)(2,1,4)
43.
Бесконечные решения
45.
2424
47.
11
49.
Да; 18, 38
51.
Да; 33, 36, 37
53.
7000 долларов на первый счет, 3000 долларов на второй счет.
55.
120 детей, 1080 взрослых
57.
4 галлона желтого цвета, 6 галлона синего цвета
59.
13 зеленых помидоров, 17 красных помидоров
61.
Клубника 18%, апельсины 9%, киви 10%
63.
100 для фильма 1, 230 для фильма 2, 312 для фильма 3
65.
20–29: 2100, 30–39: 2600, 40–49: 825
67.
300 миндаля, 400 клюквы, 300 кешью
Обзор упражнений
3.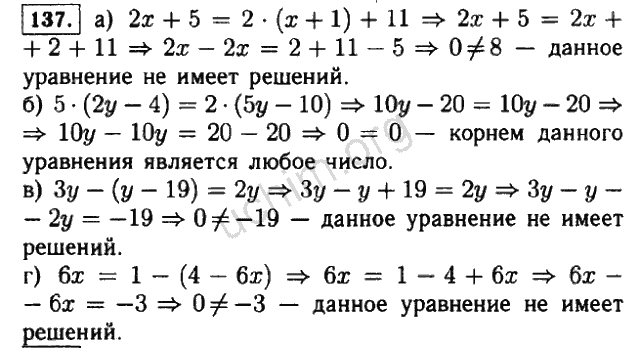
(−2,3)(−2,3)
5.
(4,−1)(4,−1)
7.
Решений не существует.
9.
(300,60,000)(300,60,000)
11.
Бесконечные решения
13.
Решений не существует.
15.
(-1,-2,3)(-1,-2,3)
17.
(х,8х5,14х5)(х,8х5,14х5)
19.
11, 17, 33
21.
(2,−3),(3,2)(2,−3),(3,2)
23.
Нет решения
25.
Нет решения
27.
29.
31.
2x+2,−4x+12x+2,−4x+1
33.
7x+5,−15(x+5)27x+5,−15(x+5)2
35.
3x−5,−4x+1×2+5x+253x−5,−4x+1×2+5x+25
37.
х-4(х2-2),5х+3(х2-2)2х-4(х2-2),5х+3(х2-2)2
39.
[-168-4-12][-168-4-12]
41.
не определено; размеры не совпадают
43.
не определено; внутренние размеры не соответствуют
45.
[11328104481−418498−42][11328104481−418498−42]
47.
[-127-74176-21140287738][-127-74176-21140287738]
49.
не определено; внутренние размеры не соответствуют
51.
x−3z=7y+2z=−5x−3z=7y+2z=−5 с бесконечными решениями
53.
[−2212−8519−1022|703][−2212−8519−1022|703]
55.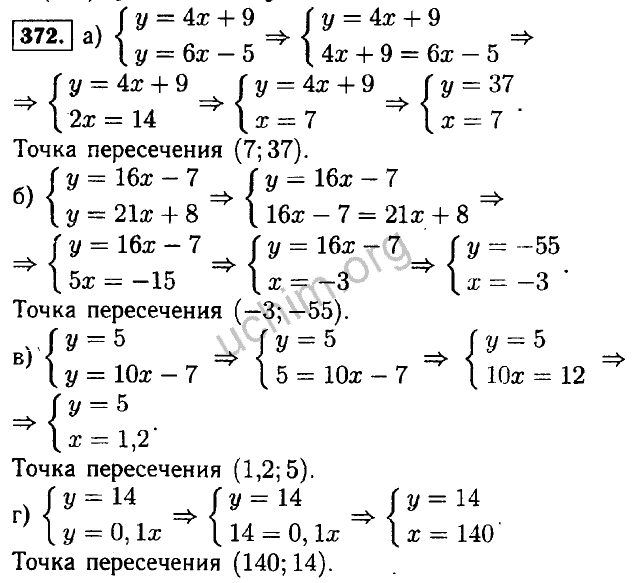
[103−140012|120−7][103−140012|120−7]
57.
Решений не существует.
59.
Решений не существует.
61.
18[2761]18[2761]
63.
Обратного не существует.
65.
(−20,40)(−20,40)
67.
(-1,0,2,0,3)(-1,0,2,0,3)
69.
17% апельсины, 34% бананы, 39% яблок
75.
(6,12)(6,12)
77.
( х , 5 х + 3)
79.
(0,0,−12)(0,0,−12)
Практический тест
1.
Да
3.
Решений не существует.
5.
120(10,5,4)120(10,5,4)
7.
(x,16×5-13×5)(x,16×5-13×5)
9.
(-22,-17),(-22,17),(22,-17),(22,17)(-22,-17),(-22,17),(22,-17) ,(22,17)
11.
13.
53x+1−2x+3(3x+1)253x+1−2x+3(3x+1)2
15.
[1751−811][1751−811]
17.
[12-20-1530][12-20-1530]
19.
−18−18
21.
[14-213-23-61-512|140-111][14-213-23-61-512|140-111]
23.
Решений не существует.
25.
(100,90)(100,90)
27.
(1100,0)(1100,0)
29.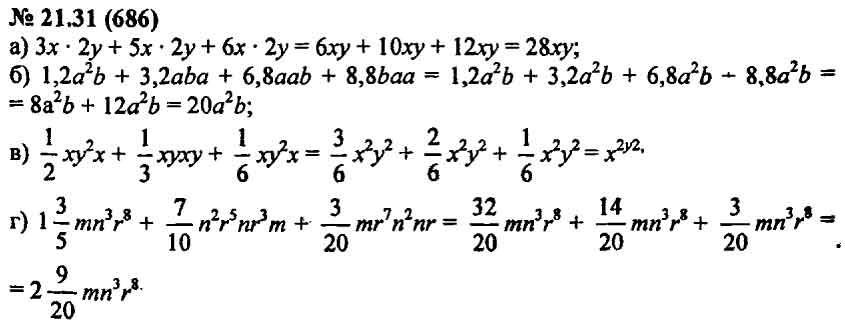
8. Решение: См. «Линейная алгебра — правильное решение» Глава 7 Задача 3 (a).
9. Решение: См. «Линейная алгебра — правильное решение» Глава 7 Задача 3 (b).
10. Решение: См. «Линейная алгебра — правильное решение», глава 7, Задача 5.
11. Решение: См. «Линейная алгебра — правильное решение», глава 7, Задача 4.
12. Решение: Пусть $u$ будет единичный собственный вектор (т. е. $\|u\|=1$) $T$, соответствующий собственному значению 3, тогда $Tu=3u$. Пусть $w$ — единичный собственный вектор (т. е. $\|w\|=1$) оператора $T$, соответствующий собственному значению 4, тогда $Tv=4w$. 9*v = 0, $$ для всех $v \in V$. Можно считать, что $u$ и $x$ отличны от нуля (иначе нечего доказывать). Принятие $v = u$ заставляет $\langle v, u \rangle \neq 0$, показывая, что $x$ и $u$ линейно зависимы.
Обратно, предположим, что $x$ и $u$ линейно зависимы. Можно считать, что $x$ и $u$ не равны нулю, иначе $T$ равнялось бы $0$, что уже является самосопряженным. *$. 92-5T+6I\ne 0$.
*$. 92-5T+6I\ne 0$.
4. Решение: Предположим, что $T$ нормальна, согласно 7.22 все пары собственных векторов, соответствующие различным собственным значениям $T$, ортогональны. По 7.24 и 5.41 имеем \[V=E(\lambda_1,T)\oplus\cdots\oplus E(\lambda_m,T),\], где $\lambda_1$, $\cdots$, $\lambda_m$ обозначают различные собственные значения $T$.
Предположим, что все пары собственных векторов, соответствующие различным собственным значениям $T$, ортогональны и \[V=E(\lambda_1,T)\oplus\cdots\oplus E(\lambda_m,T),\], где $\lambda_1$ , $\cdots$, $\lambda_m$ обозначают различные собственные значения $T$, то $V$ имеет ортонормированный базис, состоящий из собственных векторов $T$. Фактически этот базис можно выбрать как объединение ортонормированных базисов $E(\lambda_i,T)$, $i=1,\cdots,m$. Опять же к 7.24 у нас $T$ в норме.
5. Решение: Пусть $T$ самосопряженная, $v$ и $u$ — собственные векторы $T$, соответствующие собственным значениям $\lambda$ и $\xi$ соответственно, где $\lambda\ne \ xi$. Тогда $T$ является самосопряженным \[ \langle Tv,u\rangle=\langle v,Tu\rangle, \]отсюда \[ \lambda \langle v,u\rangle=\xi\langle v,u\rangle . \]Это означает $\langle v,u\rangle=0$, поскольку $\lambda\ne \xi$. По 7.29 и 5.41 имеем \[V=E(\lambda_1,T)\oplus\cdots\oplus E(\lambda_m,T),\], где $\lambda_1$, $\cdots$, $\lambda_m$ обозначают различные собственные значения $T$.
Тогда $T$ является самосопряженным \[ \langle Tv,u\rangle=\langle v,Tu\rangle, \]отсюда \[ \lambda \langle v,u\rangle=\xi\langle v,u\rangle . \]Это означает $\langle v,u\rangle=0$, поскольку $\lambda\ne \xi$. По 7.29 и 5.41 имеем \[V=E(\lambda_1,T)\oplus\cdots\oplus E(\lambda_m,T),\], где $\lambda_1$, $\cdots$, $\lambda_m$ обозначают различные собственные значения $T$.
Предположим, что все пары собственных векторов, соответствующие различным собственным значениям $T$, ортогональны и \[V=E(\lambda_1,T)\oplus\cdots\oplus E(\lambda_m,T),\], где $\lambda_1$ , $\cdots$, $\lambda_m$ обозначают различные собственные значения $T$, то $V$ имеет ортонормированный базис, состоящий из собственных векторов $T$. Фактически этот базис можно выбрать как объединение ортонормированных базисов $E(\lambda_i,T)$, $i=1,\cdots,m$. Снова по 7.29 мы имеем, что $T$ самосопряжен.
6. Решение: См. «Линейная алгебра: правильное решение» Глава 7 Задача 92\n т$.
9. Решение: См. «Линейная алгебра — правильное решение» Глава 7.


