ГДЗ по геометрии для 9 класса Казаков В.В.
Авторы: Казаков В.В.
Решебник по геометрии для 9 класса , Казаков В.В. . Подробные и качественные решения задач онлайн от Спиши фан.
Задания
Задачи. Решения
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281 282 283 284 285 286 287 288 289 290 291 292 293 294 295 296 297 298 299 300 301 302 303 304 305 306 307 308 309Моделирование. Решения
§1 §2 §10 §12 §18 Решения»> Реальная геометрия. Решения §1 §3 §6 §9 §13 §18 §19Гимнастика ума. Параграфы. Решения
§2 §4 §8 §14 §16 §17 §18 §19Геометрия 3D. Решения
§3 §6 §8 §10 §13 §19 Решения»> Повторение. Решения Страница 44Подготовка к контрольной работе. Решения
№1 №2 №3 №4Экспресс-повторение. Решения
Глава 3Дополните базу знаний. Решения
7 класс 8 класс 9 классГеометрия Солтан 9 класс 2020 Упражнение 108 ГДЗ(дүж) решебник KZGDZ.COM
I. Векторы 6. Угол между векторами.
 Скалярное произведение двух векторов. Упражнение 108
Скалярное произведение двух векторов. Упражнение 108← Предыдущий Следующий →
Повторение курса геометрии 8 класса.
Упражнение
6789101112131415171920212223242526272829
I. Векторы
1. Понятие вектора. Коллинеарные векторы
Упражнение
3334353637383941
2. Сложение и вычитание векторов
Упражнение
4345464950515253545556
3. Умножение вектора на число. Критерий коллинеарности двух векторов
Упражнение
6162636466676869707172
4. Разложение вектора по двум неколлинеарным векторам.
Упражнение
737475767778798081828384
5. Координаты вектора.
Упражнение
87889093949596979899100101
6. Угол между векторами. Скалярное произведение двух векторов.
Упражнение
103104105
106107108109110112113114115116117118119120
7. Применение векторов при решении задач
Упражнение
121122124126127128
8. Упражнения на повторение раздела «Векторы»
Упражнение
129131132133134135136138139140141142144145
Проверь себя!
Упражнение
148 3B148 4B148 5C
II. Преобразования плоскости.
9. Преобразование плоскости. Движение и его виды
Упражнение
149150151153154155157
10. Применение движений к решению задач
Упражнение
158159160161164165
11. Преобразования гомотетии и подобия, их свойства
Упражнение
166167168169170171172
12. Подобные треугольники
Упражнение
174175176177178179180181182183184185186187188189190
13.
 Подобные многоугольники
Подобные многоугольникиУпражнение
192193194195196197
198199200
14. Применение гомотетии и подобия при решении задач.
Упражнение
202203204205206207208
15. Упражнения на повторение раздела «Преобразования плоскости»
Упражнение
209210211212213214215216217218219220221222223224
Проверь себя!
Упражнение
225 4B225 5С
III. Решение треугольников.
16. Теорема синусов
Упражнение
226227228229230231232233234235
17. Теорема косинусов
Упражнение
236237238239240241242243244245246
18. Решение треугольников
Упражнение
247248249250251253254255256257258259
19. Углы, вписанные в окружность, и их свойства
Упражнение
260262263264265266267268269
20.
 Свойства касательной и секущей, пересекающихся хорд окружности
Свойства касательной и секущей, пересекающихся хорд окружностиУпражнение
270271272273274275276277278279
21. Применение тригонометрии к выводу формул площадей треугольника и решению задач
Упражнение
280281282283284285286287288289290291292293294295296297298299300301302303
22. Упражнения на повторение раздела «Решение треугольников»
Упражнение
304305306307308309310311312313
Проверь себя!
Упражнение
314 4В
IV. Окружность. Многоугольники
23. Вписанные в окружность четырехугольники
Упражнение
316317318319320321
24. Описанные около окружности четырехугольники
Упражнение
322323324325326327328329330331332333334
25. Правильные многоугольники. Окружности, описанная около правильного многоугольника и вписанная в него
Упражнение
336337338339340341342
26.
 Нахождение длин сторон и площадей правильных многоугольников.
Нахождение длин сторон и площадей правильных многоугольников.Упражнение
343344345346347348349
27. Длина окружности и ее дуги
Упражнение
351352353354355356357358359360361362
363364365366367368
28. Площадь круга, его сектора и сегмента
Упражнение
370371372373374375376377378379380381382383384385
29. Упражнения на повторение раздела «Окружность. Многоугольники»
Упражнение
386387388389390391392393394395396397398399400401402403404405406407408409
Повторение курса геометрии 9 класса
Упражнение
411412413414415416417418419420421422423424425426427428430431433434435436437438439440441442443444445446
447448449450451452
ГДЗ по Геометрии для 10 класса Смирнов В.А.
 , Туяков Е.А. на 5 ГДЗ по Геометрии для 10 класса Смирнов В.А., Туяков Е.А. на 5
, Туяков Е.А. на 5 ГДЗ по Геометрии для 10 класса Смирнов В.А., Туяков Е.А. на 5Часто ищут
- Биология 10 класс
- Авторы: Каменский А.А., Криксунов Е.А., Пасечник В.В.
- Издательство: Дрофа 2014
- Химия 10 класс Базовый уровень
- Автор: О.
 С. Габриелян
С. Габриелян - Издательство: Дрофа 2015
- Геометрия 10 класс Базовый и углубленный уровень
- Авторы: Александров А. Д., Вернер А.Л., Рыжик В.И.
- Издательство: Просвещение 2014
- Английский язык 10 класс Starlight Углубленный уровень
- Авторы: В.
 Эванс, Д. Дули, К. Баранова, В. Копылова, Р. Мильруд
Эванс, Д. Дули, К. Баранова, В. Копылова, Р. Мильруд - Издательство: Просвещение 2017
- Химия 10 класс Углубленный уровень
- Авторы: Габриелян О.С., Остроумов И.Г., Пономарев С.Ю.
- Издательство: Дрофа 2014
- Русский язык 10 класс
- Авторы: Власенков А.
 И., Рыбченкова Л.М.
И., Рыбченкова Л.М. - Издательство: Просвещение 2009
- История 10 класс
- Авторы: Данилов А. А., Брандт М. Ю., Горинов М. М.
- Издательство: Просвещение 2013
- Алгебра 10 класс Задачник Базовый уровень
- Автор: А.
 Г. Мордкович
Г. Мордкович - Издательство: Мнемозина 2015-2020
- Алгебра 10 класс Базовый и углубленный уровень
- Авторы: Ш.А. Алимов, Ю.М. Колягин, М.В. Ткачева
- Издательство: Просвещение 2015
Образовательный минимум — МЕЖДУНАРОДНАЯ Лингвистическая Школа
Образовательный минимум – это образовательные единицы (понятия, правила, формулы, теоремы, алгоритмы, лексика и т. д.), которые учащиеся должны освоить в 1,2,3,4 четверти. Единственное и неукоснительное требование – дословное заучивание всего теоретического материала, входящего в минимум.
д.), которые учащиеся должны освоить в 1,2,3,4 четверти. Единственное и неукоснительное требование – дословное заучивание всего теоретического материала, входящего в минимум.
В 5-6,11 классах учитель сам планирует и выбирает формы проверки «Образовательного минимума» (далее – ОМ). В 7-9,10 классах – администрация присутствует при проверке. Сдача ОМ планируется не позднее чем за 2 недели до окончания четверти. Без зачета по образовательному минимуму отметка за четверть не может быть выставлена.
Русский язык
- Образовательный минимум по русскому языку для 5 класса, 1 четверть
- Образовательный минимум по русскому языку для 5 класса, 2 четверть
- Образовательный минимум по русскому языку для 5 класса, 3 четверть
- Образовательный минимум по русскому языку для 5 класса, 4 четверть
- Образовательный минимум по русскому языку для 6 класса, 1 четверть
- Образовательный минимум по русскому языку для 6 класса, 2 четверть
- Образовательный минимум по русскому языку для 6 класса, 3 четверть
- Образовательный минимум по русскому языку для 7 класса, 1 четверть
- Образовательный минимум по русскому языку для 7 класса, 2 четверть
- Образовательный минимум по русскому языку для 7 класса, 3 четверть
- Образовательный минимум по русскому языку для 7 класса, 4 четверть
- Образовательный минимум по русскому языку для 8 класса, 1 четверть
- Образовательный минимум по русскому языку для 8 класса, 2 четверть
- Образовательный минимум по русскому языку для 8 класса, 3 четверть
- Образовательный минимум по русскому языку для 9 класса, 1 четверть
- Образовательный минимум по русскому языку для 9 класса, 2 четверть
- Образовательный минимум по русскому языку для 10 класса
- Образовательный минимум по русскому языку для 10 класса, 2 четверть
- Образовательный минимум по русскому языку для 11 класса
Математика
- Образовательный минимум по математике для 5 класса, 1 четверть
- Образовательный минимум по математике для 5 класса, 2 четверть
- Образовательный минимум по математике для 5 класса, 3 четверть
- Образовательный минимум по математике для 5 класса, 4 четверть
- Образовательный минимум по математике для 6 класса, 1 четверть
- Образовательный минимум по математике для 6 класса, 2 четверть
- Образовательный минимум по математике для 6 класса, 3 четверть
- Образовательный минимум для 6 класса, 4 четверть
- Образовательный минимум по математике для 7 класса
- Образовательный минимум по математике для 7 класса, 2 четверть
- Образовательный минимум по математике для 7 класса, 3 четверть
- Образовательный минимум по математике для 7 класса, 4 четверть
- Образовательный минимум по алгебре и геометрии для 8 класса, 1 четверть
- Образовательный минимум по алгебре и геометрии для 8 класса, 2 четверть
- Образовательный минимум по геометрии для 8 класса, 3 четверть
- Образовательный минимум по математике для 8 класса, 4 четверть
- Образовательный минимум по алгебре для 9 класса
- Образовательный минимум по геометрии для 9 класса
- Образовательный минимум по математике для 9 класса, 2 четверть
- Образовательный минимум по математике для 9 класса, 3 четверть
- Образовательный минимум по алгебре для 9 класса, 3 четверть
- Образовательный минимум по геометрии для 9 класса, 3 четверть
- Образовательный минимум по алгебре для 10-11 классов
Физика
- Образовательный минимум по физике для 7 класса
- Образовательный минимум по физике для 7 класса, 2 четверть
- Образовательный минимум по физике для 7 класса, 3 четверть
- Образовательный минимум по физике для 8 класса, 1 четверть
- Образовательный минимум по физике для 8 класса, 2 четверть
- Образовательный минимум по физике для 8 класса, 3 четверть
- Образовательный минимум по физике для 9 класса, 1 четверть
- Образовательный минимум по физике для 9 класса, 2 четверть
- Образовательный минимум по физике для 9 класса, 3 четверть
Химия
- Образовательный минимум по химии для 8 класса
- Образовательный минимум по химии для 9 класса
- Образовательный минимум по химии для 10 класса
Биология
- Образовательный минимум по биологии для 5 класса
- Образовательный минимум по биологии для 6 класса
- Образовательный минимум по биологии для 7 класса
- Образовательный минимум по биологии для 8 класса
- Образовательный минимум по биологии для 9 класса
- Образовательный минимум по биологи для 10 класса
- Образовательный минимум по биологии для 11 класса, 1 полугодие
История
- Образовательный минимум по истории для 5 класса
- Образовательный минимум по истории для 6 класса
- Образовательный минимум по истории для 7 класса
- Образовательный минимум по истории для 8 класса
- Образовательный минимум по историяя для 9 класса
- Образовательный минимум по истории для 10 класса (базовый)
- Образовательный минимум по истории для 10 класса (углубленный уровень)
- Образовательный минимум по истории для 11 класса (базовый уровень)
- Образовательный минимум по истории для 11 класса (углубленный уровень)
Литература
- Образовательный минимум по литературе для 5 класса
- Образовательный минимум по литературе для 5 класса, 3 четверть
- Образовательный минимум по литературе для 5 класса, 4 четверть
- Образовательный минимум по литературе для 6 класса
- Образовательный минимум по литературе для 7 класса
- Образовательный минимум по литературе для 7 класса, 3 четверть
- Образовательный минимум по литературе для 7 класса, 4 четверть
- Образовательный минимум по литературе для 8 класса
- Образовательный минимум по литературе для 8 класса, 2 четверть
- Образовательный минимум по литературе для 8 класса, 3 четверть
- Образовательный минимум по литературе для 9 класса
- Образовательный минимум по литературе для 10 класса
- Образовательный минимум по литературе для 11 класса
Обществознание
- Образовательный минимум по обществознанию для 5 класса
- Образовательный минимум по обществознанию для 6 класса
- Образовательный минимум по обществознанию для 7 класса, 1 четверть
- Образовательный минимум по обществознанию для 7 класса, 2 четверть
- Образовательный минимум по обществознанию для 7 класс, 3 четверть
- Образовательный минимум по обществознанию для 8 класса
- Образовательный минимум по обществознанию для 9 класса
- Образовательный минимум по обществознанию для 10 класса
- Образовательный минимум по обществознания для 11 класса, 1 полугодие
География
- Образовательный минимум по географии, 5 класс 1-2 четверти
- Образовательный минимум по географии 6 класс, 1-2 четверти
- Образовательный минимум по географии для 7 класса
- Образовательный минимум по географии для 8 класса
- Образовательный минимум по географии для 9 класса
- Образовательный минимум по географии для 10 класса ( I полугодие)
- Образовательный минимум по географии для 10 класса ( II полугодие)
Информатика
- Образовательный минимум по информатике
Корейский язык
- Образовательный минимум по корейскому языка для 6 класса, 1 четверть
- Образовательный минимум по корейскому языку для 6 класса, 2 четверть
- Образовательный минимум по корейскому языку для 6 класса, 3 четверть
- Образовательный минимум по корейскому языку для 6 класса, 4 четверть
- Образовательный минимум по корейскому языку для 7 класса, 1 четверть
- Образовательный минимум по корейскому языку для 7 класса, 2 четверть
- Образовательный минимум по корейскому языку для 7 класса, 3 четверть
- Образовательный минимум по корейскому языку для 7 класса, 4 четверть
- Образовательный минимум по корейскому языку для 8 класса, 1 четверть
- Образовательный минимум по корейскому языку для 8 класса, 2 четверть
- Образовательный минимум по корейскому языку для 8 класса, 3 четверть
- Образовательный минимум по корейскому языку для 8 класса, 4 четверть
- Образовательный минимум по корейскому языку для 9 класса, 1 четверть
- Образовательный минимум по корейскому языку для 9 класса, 2 четверть
- Образовательный минимум по корейскому языку для 9 класса, 3 четверть
- Образовательный минимум по корейскому языку для 9 класса, 4 четверть
Китайский язык
- Образовательный минимум по китайскому языку для 6 класса
- Образовательный минимум по китайскому языку для 7 класса
- Образовательный минимум ко китайскому языку для 8 класса
- Образовательный минимум по китайскому языку для 9 класса
- Образовательный минимум по китайскому языку для 9 (2) класса
Японский язык
- Образовательный минимум по японскому языку для 9 класса
Cultural Studies
- Образовательный минимум по Cultural Studies для 6 класса
- Образовательный минимум по Cultural Studies для 6 класса, 2 четверть
- Образовательный минимум по Cultural Studies для 6 класса, 3 четверть
Экономика
- Образовательный минимум по экономике для 8 класса, 1 четверть
- Образовательный минимум по экономике для 8 класса, 2 четверть
- Образовательный минимум по экономике для 8 класса, 3 четверть
- Образовательный минимум по экономике для 8 класса, 4 четверть
- Образовательный минимум по экономике для 9 класса, 1 четверть
- Образовательный минимум по экономике для 9 класса, 2 четверть
- Образовательный минимум по экономике для 9 класса, 3 четверть
Естествознание
- Образовательный минимум по естествознанию для 10 класса
- Образовательный минимум по естествознанию для 11 класса
Теория познания
- Теория познания
- Теория познания 10 класс, 2 четверть
- Теория познания, 10 класс, 3 четверть
- Теория познания, 10 класс, 4 четверть
Изобразительное искусство
- Образовательный минимум по изобразительному искусству для 5 класса
- Образовательный минимум по изобразительному искусству для 6 класса
Английский язык
I четверть II четверть III четверть IV четверть elementary 5 класс Introductory Unit
Unit1
Unit 2
Unit 3
Unit 4
Unit 5
Unit 6
Unit 7
pre intermediate 6
класс
Unit 1 Unit 2
Unit 3
Unit 4
Unit 5
Unit 6
Unit 7
pre intermediate 7
класс
Unit 8 Unit 9
Unit 10
intermediate 7 класс Unit 1 Vocabulary
Unit 2 Vocabulary
Unit 3 Vocabulary
Unit 4 Vocabulary
intermediate 8 класс Unit 5 Vocabulary Unit 6 Vocabelary
Unit 7 Vocabulary
Unit 8
Unit 9
Unit 10 upper Intermediate 9
класс
Unit 1 Unit 2
Unit 3
Unit 4
Unit 5
Unit 6
Unit 7
advanced 10 класс Vocabulary Unit 1
Vocabulary Unit 2
Vocabulary Unit 3
Vocabulary Unit 4
Vocabulary Unit 5
advanced 11 класс Unit 6 Vocabulary
Vocabulary Unit 5
Демонстрационные варианты (демоверсии) ОГЭ по математике
Демонстрационные варианты по математике (алгебре) 2010 года представлены в двух видах: демонстрационный вариант 1 и демонстрационный вариант 2. Отличие между ними заключается в том, что первая часть демонстрационного варианта 2 содержит на две задачи больше, чем первая часть демонстрационного варианта 1 (задачи 17 и 18) Эти задачи относятся к теории вероятностей и статистике. Других отличий нет.
Отличие между ними заключается в том, что первая часть демонстрационного варианта 2 содержит на две задачи больше, чем первая часть демонстрационного варианта 1 (задачи 17 и 18) Эти задачи относятся к теории вероятностей и статистике. Других отличий нет.
Демонстрационный вариант ОГЭ по математике (алгебре) 2011 года почти полностью совпадает с демонстрационным вариантом 2 ОГЭ по математике (алгебре) 2010 года. Отличие заключается лишь в заданиях №10 и №22.
В 2011 году в ряде регионов в порядке эксперимента для проведения ОГЭ-9 по математике была использована перспективная модель КИМов, проект демонстрационного варианта которой мы также размещаем.
В 2012 году в демонстрационный вариант ОГЭ по математике были включены не только задания по алгебре, теории вероятностей и статистике, но также и задания по геометрии.
Демонстрационные варианты ОГЭ по математике 2013-2017 годов отличаются от вариантов предыдущих лет. В них
В них
- Работа состоит из трёх модулей: «Алгебра», «Геометрия», «Реальная математика». Модули «Алгебра» и «Геометрия» состоят из двух частей: во второй части задачи более сложные по сравнению с первой частью.
- За каждое правильно выполненное задание части 1 выставляется 1 балл. В каждом модуле части 2 задания расположены по нарастанию сложности и оцениваются в 2 балла (в 2, 3 и 4 балла в демонстрационных вариантах по математике 2013-2015 годов).
- Рекомендуемый минимальный порог выполнения экзаменационной работы – 8 баллов, набранные в сумме за выполнение заданий всех трёх модулей, при условии, что по модулю «Алгебра» набрано не менее 3 баллов, по модулю «Геометрия» набрано не менее 2 баллов и по модулю «Реальная математика»набрано не менее 2 баллов.

Демонстрационный вариант ОГЭ по математике 2014 годапрактически полностью совпадает с демонстрационным вариантом ОГЭ по математике 2013 года. Небольшое отличие имеется лишь в задаче №13, где требуется указать номера верных утверждений: в 2013 году условие этой задачи содержало 3 утверждения, а 2014 году к этим трем утверждениям было добавлено еще одно.
В демонстрационном варианте ОГЭ по математике 2015 года по сравнению с демонстрационным вариантом 2014 года были заменены задачи 1, 2, 3, 4, 6, 7, 10 и 17 на другие по той же тематике. Задачи 8 и 12 претерпели лишь косметические изменения. Из чертежа задачи 11 по геометрии удалены лишние данные. Остальные задачи были оставлены без изменений. Кроме того, в 2015 году была изменена форма записи ответа в задачах с выбором ответа: ответ стало нужно записывать цифрой с номером правильного ответа (а не обводить кружком).
В демонстрационных вариантах ОГЭ по математике 2016-2017 годов по сравнению с демонстрационным вариантом 2015 года изменений нет. Снижен максимальный первичный балл за всю работу с 38 до 32 за счет того, что правильное выполнение каждого из заданий части 2 в демонстрационных вариантах ОГЭ по математике 2016-2017 годов оценивается в 2 балла.
В демонстрационный вариант ОГЭ по математике 2018 года по сравнению с демонстрационным вариантом 2017 года были внесены следующие изменения: из демонстрационного варианта был исключен модуль «Реальная математика», а задания, входившие в этот модуль, были распределены по модулям «Алгебра» и «Геометрия». При этом общее количество заданий и максимальный балл за всю работу не изменились.
В демонстрационном варианте ОГЭ по математике 2019 года по сравнению с демонстрационным вариантом 2018 года изменений не было.
В демонстрационном варианте ОГЭ по математике 2020 года по сравнению с демонстрационным вариантом 2019 года были заменены задания 2, 5, 7, 8, 15 на блок практико-ориентированных заданий 1-5, объединенных единым сюжетом.
В демонстрационный вариант ОГЭ по математике 2021 года по сравнению с демонстрационным вариантом 2020 года были внесены следующие изменения:
- Были объединены в одно задания 13 и 8 на преобразование выражений
- Задание 12 заменено на задание с практическим содержанием, направленное на проверку умения применять знания о последовательностях и прогрессиях в прикладных ситуациях
- Изменен порядок заданий в соответствии с тематикой и сложностью
- Максимальный балл уменьшен с 32 до 31
В демонстрационных вариантах ОГЭ по математике 2022 и 2023 годов по сравнению с демонстрационным вариантом 2021 года изменений не было.
NCERT Solutions Class 9 Math Chapter 5 Introduction to Euclid’s Geometry
NCERT Solutions Class 9 Math Chapter 5 – Free PDF Download
Решения NCERT для класса 9 по математике Глава 5 Введение в геометрию Евклида приведены здесь для ознакомления учащихся. Геометрия Евклида — это фундаментальная концепция, которая формирует основу для гораздо более сложных тем. Поэтому одним из руководств, которые помогут вам понять эту концепцию, являются решения NCERT для математики класса 9, глава 5 — Введение в геометрию Евклида. Он разработан знающими учителями с многолетним соответствующим опытом. NCERT Solutions — одно из лучших руководств, которое вы можете использовать для своих учебных нужд.
Кроме того, мы также обновляем контент в соответствии с предписаниями CBSE и разрабатываем решения таким образом, чтобы упростить изучение.
Загрузить PDF-файл NCERT Solutions for Class 9 Math Chapter 5 — Introduction to Euclid’s Geometry
Список упражнений по математике для 9 класса, глава 5
Упражнение 5. 1 Решения — 7 вопросов
1 Решения — 7 вопросов
Упражнение 5.2 Решения — 2 вопроса
Access Answers of Science NCERT Класс 9 Математика Глава 5 – Введение в геометрию Евклида
Упражнение 5.1 Страница: 85
1. Какие из следующих утверждений верны, а какие нет? Обоснуйте свои ответы.
(i) Только одна линия может проходить через одну точку.
(ii) Существует бесконечное число прямых, проходящих через две различные точки.
(iii) Линия с заделкой может производиться неограниченное количество раз с обеих сторон.
(iv) Если две окружности равны, то их радиусы равны.
(v) На рис. 5.9, если AB = PQ и PQ = XY, то AB = XY.
Решение:
(i) Ложь
Через одну точку можно провести бесконечное количество линий. Следовательно, упомянутое утверждение является ложным
.(ii) Ложь
Через две различные точки можно провести только одну линию. Следовательно, упомянутое утверждение является ложным
Следовательно, упомянутое утверждение является ложным
(iii) Правда
Завершенная линия может бесконечно производиться с обеих сторон, так как линия может бесконечно удлиняться с обеих сторон. Следовательно, упомянутое утверждение верно.
(iv) Правда
Радиусы двух окружностей равны, если они равны. Окружность и центр обеих окружностей совпадают; и, таким образом, радиусы двух кругов должны быть равны. Следовательно, упомянутое утверждение верно.
(v) Правда
Согласно аксиоме Евклида 1 st : «Вещи, равные одной и той же вещи, также равны друг другу». Следовательно, упомянутое утверждение верно.
2. Дайте определение каждому из следующих терминов. Существуют ли другие термины, которые необходимо определить в первую очередь? Что это такое и как вы можете их определить?
(i) параллельные линии
(ii) перпендикулярные линии
(iii) сегмент линии
(iv) радиус окружности
(в) квадратный
Решение:
Да, есть и другие термины, которые необходимо определить в первую очередь. Они следующие:
Они следующие:
Плоскость: Плоские поверхности, на которых можно рисовать геометрические фигуры, называются плоскостями. Плоская поверхность – это поверхность, ровно лежащая с прямыми линиями на ней.
Точка: безразмерная точка, нарисованная на плоской поверхности, называется точкой. Точка есть то, что не имеет частей.
Линия: совокупность точек, имеющих только длину и не имеющих ширины, называется линией. Его можно расширить в обе стороны. Линия – это длина без ширины.
(i) Параллельные линии. Параллельные линии — это линии, которые никогда не пересекаются друг с другом и всегда находятся на постоянном перпендикулярном расстоянии друг от друга. Параллельные линии могут состоять из двух или более линий.
(ii) Перпендикулярные линии – Перпендикулярные линии – это линии, которые пересекают друг друга в плоскости под прямым углом. Говорят, что прямые перпендикулярны друг другу.
(iii) Отрезок линии. Когда линия не может быть продлена дальше из-за наличия у нее двух конечных точек, тогда линия называется сегментом линии. Отрезок имеет 2 конечные точки.
Отрезок имеет 2 конечные точки.
(iv) Радиус окружности. Радиусом окружности называется линия, проходящая от любой точки окружности окружности до центра окружности.
(v) Квадрат – Четырехугольник, у которого все четыре стороны равны, а каждый из его внутренних углов прямой, называется квадратным.
3. Рассмотрим два «постулата», приведенных ниже:
(i) Для любых двух различных точек A и B существует третья точка C, которая находится между A и B.
(ii) Существуют по крайней мере три точки, не лежащие на одной прямой.
Содержат ли эти постулаты какие-либо неопределенные термины? Соответствуют ли эти постулаты? Вытекают ли они из постулатов Евклида? Объяснять.
Решение:
Да, эти постулаты содержат неопределенные термины. Неопределенные термины в постулатах следующие:
— На плоскости лежит много точек. Но в приведенных здесь постулатах не указано положение точки С, независимо от того, лежит ли она на отрезке, соединяющем АВ, или нет.
— Кроме того, нет информации о том, находятся ли точки в одной плоскости или нет.
и
Да, эти постулаты непротиворечивы, когда мы имеем дело с этими двумя ситуациями:
– Точка C лежит на отрезке AB между A и B.
– Точка C не лежит на отрезке AB.
Нет, они не следуют из постулатов Евклида. Они следуют аксиомам.
4. Если точка C лежит между двумя точками A и B так, что AC = BC, то докажите, что AC = ½ AB. Объясните, нарисовав рисунок.
Решение:
Учитывая, что AC = BC
Теперь добавляем переменный ток с обеих сторон.
Л.В.С+АС = П.С.С+АС
АС+АС = ВС+АС
2АС = ВС+АС
Мы знаем, что BC+AC = AB (поскольку он совпадает с отрезком AB)
∴ 2 AC = AB (Если равные прибавляются к равным, целые равны.)
⇒ АС = (½)АВ.
5. В вопросе 4 точка C называется серединой отрезка AB. Докажите, что каждый отрезок имеет одну и только одну середину.
Решение:
Пусть AB будет отрезком
Предположим, что точки P и Q являются двумя различными средними точками AB.
Сейчас,
∴ P и Q — середины отрезка AB.
Следовательно,
AP = PB и AQ = QB.
также,
PB+AP = AB (поскольку совпадает с отрезком AB)
Аналогично, QB+AQ = AB.
Сейчас,
Добавление AP к левой и правой сторонам уравнения AP = PB
Получаем, АР+АР = РВ+АР (Если к равным прибавить равные, то и целые равны.)
⇒ 2АП = АВ — (i)
Аналогично,
2 AQ = AB — (ii)
Из (i) и (ii), поскольку правая сторона одинакова, мы приравниваем левую сторону
2 AP = 2 AQ (Вещи, которые равны одной и той же вещи, равны друг другу.)
⇒ AP = AQ (Вещи, которые удваивают одни и те же вещи, равны друг другу.)
Таким образом, мы заключаем, что P и Q — это одни и те же точки.
Это противоречит нашему предположению, что P и Q — две разные средние точки AB.
Таким образом, доказано, что каждый отрезок имеет одну и только одну середину.
Следовательно Доказано.
6. На рис. 5.10, если AC = BD, то докажите, что AB = CD.
Решение:
Дано, AC = BD
Из данной цифры получаем,
АС = АВ+ВС
БД = БК+КД
⇒ AB+BC = BC+CD [AC = BD, дано]
Мы знаем, что, согласно аксиоме Евклида, при вычитании равных из равных остатки также равны.
Вычитая BC из левой и правой сторон уравнения AB+BC = BC+CD, мы получаем,
АВ+ВС-ВС = ВС+CD-ВС
АВ = CD
Следовательно Доказано.
7. Почему аксиома 5 в списке аксиом Евклида считается «универсальной истиной»? (Обратите внимание, что вопрос не о пятом постулате.)
Решение:
Аксиома 5: Целое всегда больше, чем часть.
Например: Торт. Когда он целый или полный, предположим, что он весит 2 фунта, но когда его часть вынимают и измеряют, его вес будет меньше, чем в предыдущем измерении. Итак, пятая аксиома Евклида верна для всех материалов во Вселенной. Следовательно, аксиома 5 в списке аксиом Евклида считается «универсальной истиной».
Итак, пятая аксиома Евклида верна для всех материалов во Вселенной. Следовательно, аксиома 5 в списке аксиом Евклида считается «универсальной истиной».
Упражнение 5.2 Страница: 88
1. Как бы вы переписали пятый постулат Евклида, чтобы его было легче понять?
Решение:
Пятый постулат Евклида: если прямая, падающая на две прямые, образует внутренние углы по одну и ту же сторону, взятые вместе, меньше двух прямых, то две прямые, если их провести бесконечно, пересекутся с той стороны, на которой сумма углов меньше двух прямых.
То есть пятый постулат Евклида о параллельных прямых.
Параллельные прямые — это прямые, которые никогда не пересекаются друг с другом и всегда находятся на постоянном перпендикулярном расстоянии друг от друга. Параллельные линии могут состоять из двух или более линий.
A: Если X не лежит на прямой A, то мы можем провести линию через X, которая будет параллельна линии A.
B: через точку X можно провести только одну прямую, параллельную прямой A.
2. Предполагает ли пятый постулат Евклида существование параллельных прямых? Объяснять.
Решение:
Да, пятый постулат Евклида действительно подразумевает существование параллельных линий.
Если сумма внутренних углов равна сумме прямых углов, то две прямые не пересекутся ни в одной точке, следовательно, они параллельны друг другу.
∠1+∠3 = 180 или
Или ∠3+∠4 = 180 или
Решения NCERT для математики класса 9 Глава 5 Введение в геометрию Евклида
Глава 5. Введение в геометрию Евклида относится к Разделу 4: Геометрия. Этот конкретный блок имеет 28 баллов из 100. Поэтому очень важно тщательно изучить эту главу. В этой главе рассматриваются следующие важные темы:
- Определения Евклида
- Аксиомы и постулаты
Евклидова геометрия — это система, введенная александрийско-греческим математиком Евклидом около 300 г. до н.э. Спустя более 2000 лет вклад Евклида все еще остается в силе. Он имеет практическое применение в нескольких областях, от инженерии до теоретической физики. Это даже имеет академическое значение и значение в различных дисциплинах математики и естественных наук.
до н.э. Спустя более 2000 лет вклад Евклида все еще остается в силе. Он имеет практическое применение в нескольких областях, от инженерии до теоретической физики. Это даже имеет академическое значение и значение в различных дисциплинах математики и естественных наук.
Узнайте, как работает евклидова геометрия, и откройте для себя различные теоремы. Найдите более важные решения NCERT для класса 9Математика, чтобы помочь вам практиковать.
Ключевые особенности решений NCERT для математики класса 9 Глава 5 Введение в геометрию Евклида
- Продуманное и подробное содержание
- Формулы выделены
- Объяснения представлены на понятном языке
- Разработано квалифицированными учителями
- Включает последние вопросы из установленной программы
- Обширный анализ экзаменационных листов предыдущего года
- Ознакомьтесь с дополнительными учебными ресурсами, такими как образцы документов и т. д.
Для лучшего понимания концепций, связанных с геометрией Евклида, учащиеся могут получить доступ к другим учебным материалам, предоставленным BYJU’S. Высококвалифицированные преподаватели разрабатывают решения с особой тщательностью, чтобы помочь студентам решить сложные вопросы без особых усилий.
Высококвалифицированные преподаватели разрабатывают решения с особой тщательностью, чтобы помочь студентам решить сложные вопросы без особых усилий.
- RD Sharma Solutions for Math Class 9 Глава 7 Введение в геометрию Евклида
Отказ от ответственности:
Отброшенные темы – 5.3 Эквивалентные версии пятого постулата Евклида.
Часто задаваемые вопросы о решениях NCERT для математики 9 класса, глава 5
Подходят ли решения NCERT для математики 9 класса, глава 5, для учащихся CBSE?
Решения NCERT в течение многих лет предписывались студентам CBSE как полный источник информации для развития их аналитических навыков. Они доказали свою важность для изучения учебной программы и развития уверенности, необходимой для сдачи экзаменов. Решения NCERT для класса 9Математика Глава 5 объясняет шаги с точностью, не упуская при этом существенных аспектов решения вопроса.
Где я могу скачать решения NCERT для математики класса 9, глава 5?
NCERT Решения по математике для 9-го класса Глава 5 представлены на веб-сайте BYJU и считаются одним из наиболее важных учебных материалов для учащихся 9-го класса. Решения, предоставляемые BYJU’S, сформулированы таким образом, что каждый шаг объясняется четко и подробно. Решения для класса 9Математика NCERT подготовлена нашими предметными экспертами, чтобы помочь студентам в подготовке к экзамену на доске. Очень важно, чтобы учащиеся хорошо разбирались в этих решениях, чтобы получить хороший балл на экзамене в 9 классе.
В чем смысл евклидовой геометрии в соответствии с решениями NCERT для математики класса 9, глава 5?
Евклидова геометрия — это изучение геометрических форм и фигур, основанное на различных аксиомах и теоремах. Он в основном вводится для плоских поверхностей. Это лучше объясняется специально для форм геометрических фигур и плоскостей. Ссылаясь на NCERT Solutions for Class 9 Maths Chapter 5, учащиеся могут хорошо сдать экзамены.
Ссылаясь на NCERT Solutions for Class 9 Maths Chapter 5, учащиеся могут хорошо сдать экзамены.
Многоракурсная геометрия в компьютерном зрении Глава 9 Решения — Эпиполярная геометрия и фундаментальная матрица
Вот краткий указатель всех проблем в этой главе.
я II III IV ви viii ix
Основной индекс можно найти здесь.
I. Крепление камер. Предположим, что две камеры фиксируются в точке пространства так, что их главные оси пересекаются в этой точке. Покажите, что если координаты изображения нормированы так, что начало координат совпадает с главной точкой, то элемент $F_{33}$ фундаментальной матрицы равен нулю. 9Т$. Следовательно ограничение на $F$ становится $$\begin{pmatrix}0 & 0 & 1 \end{pmatrix} F \begin{pmatrix}0 \\ 0 \\ 1 \end{pmatrix}= 0$$ откуда следует, что $F_{33} = 0$.
II. Зеркальные изображения. Предположим, что камера смотрит на объект и его отражение в плоском зеркале. Покажите, что эта ситуация эквивалентна двум видам объекта и что фундаментальная матрица кососимметрична.
 {-1}}$, где $\mathtt{H_e}$ — евклидово преобразование
$\mathtt{\begin{pmatrix}R & \bf{t} \\ \bf{0} & 1 \end{pmatrix}}$ и
$\mathtt{\Lambda} = diag(-1, 1, 1)$. Доказательство этого утверждения приведено на
конец этого решения. 9Tt]_{\times}}$ — матрица
формы
$$\begin{pmatrix}
0 и 0 и 0
\\ 0 & 0 & -x
\\ 0 & x & 0 \end{pmatrix}$$
{-1}}$, где $\mathtt{H_e}$ — евклидово преобразование
$\mathtt{\begin{pmatrix}R & \bf{t} \\ \bf{0} & 1 \end{pmatrix}}$ и
$\mathtt{\Lambda} = diag(-1, 1, 1)$. Доказательство этого утверждения приведено на
конец этого решения. 9Tt]_{\times}}$ — матрица
формы
$$\begin{pmatrix}
0 и 0 и 0
\\ 0 & 0 & -x
\\ 0 & x & 0 \end{pmatrix}$$Это также означает, что $F$ автоэпиполярна.
Так же, как и в случае перевода, где эпиполь был точкой схода направления перевода, в данном случае эпиполь — исчезающий точка направления отражения, т.е. нормаль к плоскости отражения или направление линии симметрии, соединяющей точку и ее отражение ($\mathtt{X}$ и $\mathtt{X’}$ на рисунке ниже). 9T & 1 \end{pmatrix}$ и $\mathtt{\Lambda’} = диаг(-1, 1, 1, 1)$.
III. Покажите, что если линия схода плоскости содержит эпиполь, то плоскость параллельна базовой линии.
Эпиполь — это точка схода базовой линии. Параллельные плоскости
в трехмерном пространстве пересекают $\Pi_\infty$ по общей прямой и образ этой прямой
линия схода плоскости. Итак, если точка схода базовой линии
лежит на этой линии схода, то базовая линия должна лежать в плоскости, параллельной
данный самолет.
Итак, если точка схода базовой линии
лежит на этой линии схода, то базовая линия должна лежать в плоскости, параллельной
данный самолет.
IV. Покажите, что поляра $\textbf{x}_a$ пересекает конику Штейнера $F_s$ в эпиполях (рис. 9.10а). Подсказка: начните с $F\textbf{e} = F_s\textbf{e} + F_a\textbf{e} = 0$. Так как $\textbf{e}$ лежит на конике $F_s$, то $\textbf{l}_1 = F_s\textbf{e}$ является касательной в $\textbf{e}$, а $\textbf{ l}_2 = F_a\textbf{e} = [x_\textbf{a}]_{\times}\textbf{e} = x_\textbf{a} \times \textbf{e}$ — это строка, проходящая через $\ textbf{x}_a$ и $\textbf{e}$.
$$\mathtt{F\textbf{e} = F_s\textbf{e} + F_a\textbf{e} = 0}$$ $$\mathtt{\ подразумевает F_s\textbf{e} = -F_a\textbf{e}}$$
Это означает, что $\mathtt{F_s\textbf{e}}$ и $\mathtt{F_a\textbf{e}}$ одинаковы
линии, далее подразумевающие, что линия через $\mathtt{\textbf{x}_a}$ и
$\mathtt{\textbf{e}}$ касается $\mathtt{F_s}$ в точке $\mathtt{\textbf{e}}$.
Применяя аналогичную логику к $\mathtt{\textbf{e}’ }$, становится ясно, что строки
касательные через $\mathtt{\textbf{x}_a}$ к $\mathtt{F_s}$ пересекаются
$\mathtt{F_s}$ в $\mathtt{\textbf{e}}$ и $\mathtt{\textbf{e}’ }$. Следовательно
$\mathtt{\textbf{e}}$ и $\mathtt{\textbf{e}’ }$ лежат на поляре
$\mathtt{\textbf{x}_a}$. 9{-1}}$$
Следовательно
$\mathtt{\textbf{e}}$ и $\mathtt{\textbf{e}’ }$ лежат на поляре
$\mathtt{\textbf{x}_a}$. 9{-1}}$$
Это уравнение нельзя привести к более простому виду из-за асимметричности компонентов и, следовательно, мы ничего не можем сказать о ранге $\mathtt{F_s}$.
Я думаю, что этот вопрос неправильно поставлен в этой главе, так как мы не действительно узнал о реконструкциях еще. Я мог бы вернуться к этому после узнать больше о реконструкции в последующих главах.
IX. Следуя аналогии с разделом 9.2.2, выведите форму фундаментальной матрицы для двух линейных камер с веерным сканированием. Подробности этой матрицы приведены в [Gupta-97], где показано, что аффинная реконструкция возможна по паре изображений.
Так как в данный момент меня не интересуют щеточные камеры, я пропущу эту.
- Манди, Джозеф Л. и Эндрю Зиссерман. Повторяющиеся структуры: ограничения соответствия изображения и восстановление трехмерной структуры. Совместный европейско-американский семинар по применению инвариантности в компьютерном зрении.
 Спрингер, Берлин, Гейдельберг, 1993. [возврат]
Спрингер, Берлин, Гейдельберг, 1993. [возврат]
Включите JavaScript для просмотра комментариев на платформе Disqus.comments на базе Disqus
Глава 11 Трехмерная геометрия — класс 12
Вы учитесь…
Получите решения NCERT класса 12 Трехмерная геометрия, глава 11 книга НЦЭРТ. Решения всех вопросов и примеры с объяснением формул.
В 11 классе мы изучали основы трехмерной геометрии — Формула расстояния, Формула сечения
В этой главе «Трехмерная геометрия класса 12» мы узнаем о трехмерных линиях и плоскостях, а также находим уравнения в векторной форме — с помощью главы 10 «Векторы».
Специальные темы включают —
- Косинусы направлений и отношения направлений — Как найти с помощью различных методов — когда задан угол , когда задана сторона , когда заданы две точки
- Уравнение прямой — Составляем уравнение прямой в разных случаях — одна точка и 1 параллельная линия , 2 точки заданы.
 Мы также узнаем, как преобразовать векторную форму уравнения в декартову форму .
Мы также узнаем, как преобразовать векторную форму уравнения в декартову форму . - Угол между двумя линиями — Мы находим угол между двумя линиями, используя векторную формулу, декартову формулу, используя направляющие косинусы и отношения
- Кратчайшее расстояние между двумя прямыми — Нахождение кратчайшего расстояния между двумя параллельными и двумя наклонными прямыми
- Уравнение плоскости — Нахождение уравнения плоскости в нормальной форме , при задании перпендикуляра и проходящей через него точки , при прохождении через 3 неколлинеарных точек. Мы также находим уравнение плоскости, используя форму пересечения , и когда плоскость проходит через пересечение плоскостей
- Компланарность двух линий — Проверка компланарности двух линий
- Угол между двумя плоскостями — Нахождение угла между двумя плоскостями векторным и декартовым методом
- Расстояние между точкой и плоскостью — Вектор и декартова формула
- Угол между линией и плоскостью — Только векторная формула
- Уравнение прямой при условии плоскости — Нахождение уравнения прямой при заданном условии между двумя плоскостями
- Точка с линиями и плоскостями — Поиск координат точки при пересечении прямой через плоскость или Поиск точки при пересечении прямой и плоскости
Чтобы узнать больше, нажмите на любую концептуальную тему или выполните упражнение NCERT.
Серийный заказ
Пример 11.1
Пример 11.2
Пример 11.3
Примеры
Разное
Вопросы, основанные на конкретных случаях (MCQ)
Концептуальные вопросы
Направленные косинусы и отношения
Уравнение прямой — заданная точка и //вектор
Уравнение прямой — учитывая 2 точки
Угол между двумя линиями — вектор
Угол между двумя линиями — Картизиан
Угол между двумя линиями — Отношения направлений или косинусы
Кратчайшее расстояние между двумя наклонными линиями
Кратчайшее расстояние между двумя параллельными линиями
Уравнение плоскости — в нормальной форме
Уравнение плоскости — препендикулярно вектору и проходящей через точку
Уравнение плоскости — прохождение через 3 точки, не лежащие на одной прямой
Уравнение плоскости — форма Intercept
Уравнение плоскости — прохождение через пересечение плоскостей
Копланарность 2 линий
Угол между двумя плоскостями
Расстояние точки от плоскости
Угол между линией и плоскостью
Уравнение прямой в условиях плоскостей
Точка с линиями и плоскостями
Teachoo дает вам лучший опыт, когда вы вошли в систему. Пожалуйста, войдите 🙂
Пожалуйста, войдите 🙂
Логин
Teachoo ответит на все ваши вопросы, если вы черный пользователь!
Присоединиться к Teachoo Черный
NCERT Solutions for Class 9 Math Chapter 5 Introduction to Euclid Geometry
NCERT Solutions for Class 9 Math Chapter 5 Introduction to Euclid Geometry Ex 5.1 являются частью NCERT Solutions for Class 9 Maths. Здесь мы дали решения NCERT для математики класса 9 Глава 5 Введение в геометрию Евклида Ex 5.1.
Решения NCERT для класса 9Математика Глава 5 Введение в геометрию Евклида Упр. 5.1
Упр. 5.1 Класс 9 Математика Вопрос 1.
Какие из следующих утверждений верны, а какие нет? Обоснуйте свои ответы.
(i) Только одна линия может проходить через одну точку.
(ii) Существует бесконечное число прямых, проходящих через две различные точки.
(iii) Конечная линия может производиться неограниченное количество раз с обеих сторон.
(iv) Если две окружности равны, то их радиусы равны.
(v) На рисунке, если AB – PQ и PQ = XY, то AB = XY.
Решение:
(i) Неверно
Причина: Если мы отметим точку O на поверхности бумаги. Используя карандаш и масштаб, мы можем провести бесконечное количество прямых линий, проходящих через точку
.
(ii) Неверно
Q. Но есть одна и только одна линия, которая проходит через P так же, как и через Q.
(iii) Верно
Причина: Постулат 2 говорит, что «конечную линию можно производить бесконечно».
(iv) Верно
Причина: Накладывая области одного круга на другой, мы находим их совпадающими. Значит, их центры и границы совпадают.
Таким образом, их радиусы будут совпадать или равны.
(v) Истинно
Причина: Согласно аксиоме Евклида, вещи, равные одной и той же вещи, равны друг другу.
Упр. 5.1 Класс 9 Математика Вопрос 2.
Дайте определение каждому из следующих терминов. Существуют ли другие термины, которые необходимо определить в первую очередь? Что это такое и как вы можете их определить?
(i) Параллельные прямые
(ii) Перпендикулярные прямые
(iii) Отрезок
(iv) Радиус круга
(v) Квадрат
Решение:
Да, нам нужно иметь представление о таких терминах, как точка, линия , луч, угол, плоскость, окружность и четырехугольник и т. д., прежде чем определять необходимые термины.
д., прежде чем определять необходимые термины.
Определения необходимых терминов приведены ниже:
(i) Параллельные прямые:
Две прямые l и m на плоскости называются параллельными, если они не имеют общей точки и мы записываем их как l ॥ м.
(ii) Перпендикулярные прямые:
Две прямые p и q, лежащие в одной плоскости, называются перпендикулярными, если они образуют прямой угол, и мы записываем их как p ⊥ q.
(iii) Отрезок линии:
Отрезок линии является частью линии и имеет определенную длину. Он имеет два конца. На рисунке показан отрезок с концами A и B. Он записывается как \(\overline { AB }\) или \(\overline { BA }\).
(iv) Радиус окружности :
Расстояние от центра до точки на окружности называется радиусом окружности. На рисунке P — центр, Q — точка на окружности, тогда PQ — радиус.
(v) Квадрат :
Четырехугольник, в котором все четыре угла прямые и все четыре стороны равны, называется квадратом. Дана фигура, PQRS представляет собой квадрат.
Дана фигура, PQRS представляет собой квадрат.
Упр. 5.1 Класс 9 Математика Вопрос 3.
Рассмотрим два «постулата», приведенных ниже
(i) Для любых двух различных точек A и B существует третья точка C, которая находится между A и B.
(ii) Существуют по крайней мере три точки, не лежащие на одной прямой.
Содержат ли эти постулаты какие-либо неопределенные термины? Соответствуют ли эти постулаты? Вытекают ли они из постулатов Евклида? Объяснять.
Решение:
Да, эти постулаты содержат неопределенные термины, такие как «точка и линия». Кроме того, эти постулаты непротиворечивы, потому что они имеют дело с двумя разными ситуациями, как
(i) говорит, что если даны две точки A и B, то на прямой между ними лежит точка C. Тогда как
(ii) говорит, что при заданных точках А и В можно взять точку С, не лежащую на прямой, проходящей через А и В.
Нет, эти постулаты не следуют из постулатов Евклида, однако они следуют из аксиомы: две различные точки, через них проходит единственная линия».
Упр. 5.1 Математика 9 класса Вопрос 4.
Если точка C лежит между двумя точками A и B так, что AC = BC, то докажите, что AC = \(\frac { 1 }{ 2 }\) AB, объясните рисуя фигуру.
Решение:
У нас есть,
AC = BC [Дано]
∴ AC + AC = BC + AC
[Если равные прибавить к равным, тогда целые равны]
или 2AC = AB [∵ AC + BC = AB]
или AC = \(\frac { 1 }{ 2 } AB\)
Упр. 5.1 Класс 9 Математика Вопрос 5.
В вопросе 4 точка C называется серединой отрезка AB. Докажите, что каждый отрезок имеет одну и только одну середину.
Решение:
Пусть данная линия AB имеет две средние точки C и D.
AC = \(\frac { 1 }{ 2 } AB\) ……(i)
и AD = \(\frac { 1 }{ 2 } AB\) ……(ii)
Вычитая (i) из (ii), мы получаем
AD – AC = \(\frac { 1 }{ 2 } AB -\frac { 1 }{ 2 } AB\)
или AD – AC = 0 или CD = 0
∴ C и D совпадают.
Таким образом, каждый отрезок имеет одну и только одну среднюю точку.
Упр. 5.1 Математика 9 класса Вопрос 6.
На рисунке, если AC = BD, то докажите, что AB = CD.
Решение:
Дано: AC = BD
⇒ AB + BC = BC + CD
Вычитая BC с обеих сторон, получаем
AB + BC – BC = BC + CD – BC
[Когда равные вычитаются из равных, остатки равны]
⇒ AB = CD
Пример 5.1 Класс 9 Математика Вопрос 7.
Почему аксиома 5 в списке аксиом Евклида считается «универсальной истиной»? (Обратите внимание, что вопрос не о пятом постулате.)
Решение:
Поскольку утверждение истинно во всех ситуациях. Следовательно, это считается «универсальной истиной».
NCERT Solutions for Class 9 Maths Chapter 5 Introduction to Euclid’s Geometry0011
NCERT Solutions for Class 9 Math Chapter 5 Introduction to Euclid Geometry Ex 5.2
Ex 5.2 Class 9 Maths Вопрос пятый, чтобы понять, что было бы легче постулировать, что было бы легче переписать Euclid ?
Решение:
Пятый постулат Евклида можно записать так: «Две различные пересекающиеся прямые не могут быть параллельны одной прямой». Объяснять.
Объяснять.
Решение:
Да. Если прямая l падает на две прямые m и n так, что сумма внутренних углов по одну сторону от l равна двум прямым углам, то по пятому постулату Евклида прямые m и n не пересекутся по эту сторону от l. Кроме того, мы знаем, что сумма внутренних углов по другую сторону прямой l тоже будет двумя прямыми углами. Таким образом, они не встретятся и на другой стороне.
∴ Прямые m и n никогда не пересекаются, т. е. они параллельны.
Мы надеемся, что решения NCERT для класса 9Математика Глава 5 Введение в геометрию Евклида Пример 5.1 поможет вам. Если у вас есть какие-либо вопросы относительно решений NCERT для математики класса 9. Глава 5. Введение в геометрию Евклида, пример 5.1, оставьте комментарий ниже, и мы свяжемся с вами в ближайшее время.
Искусство решения проблем
Онлайн-курсы по математике
Присоединяйтесь к нашим живым интерактивным математическим занятиям с опытными преподавателями и талантливыми сверстниками.
Зарегистрироваться сейчас
Книги по математике
Получите важные стратегии решения проблем, необходимые для успеха в колледже и карьере.
Купить
Как видно в
Добро пожаловать в мир AoPS Online: мир, наполненный сложными проблемами, для решения которых требуются творческий подход и настойчивость. Мир, в котором студенты учатся у впечатляющих наставников и образцовых инструкторов. Мир, наполненный вдохновляющими сверстниками, разделяющими их любовь к учебе.
Наша продвинутая учебная программа по математике позволяет учащимся максимально раскрыть свой потенциал. А связи, которые учащиеся устанавливают в классе AoPS и онлайн-сообществе, сохраняются на всю жизнь.
Каждый урок, который я проходил с AoPS, был фантастическим. Все делают большую работу, помогая учащимся добиться успеха, получая удовольствие от процесса изучения математики. Мне нравится, что сами студенты всегда готовы помочь друг другу.

– Мэтью
После прохождения курса AoPS Introduction to Geometry у меня появилось больше уверенности в математике. В процессе решения более сложных задач, чем я когда-либо мог себе представить, я также начал рассматривать геометрию как искусство. Я получаю удовольствие от математики все больше и больше!
— онлайн-студент AoPS
- Курсы
AoPS представляют собой прекрасный баланс задач и рекомендаций, постоянно напрягающих студентов и предлагающих им бороться с проблемами в своем собственном темпе, пока они не достигнут прозрения. Браво! Я бы хотел, чтобы AoPS существовал, когда я учился в старшей школе.
– Онлайн-родитель AoPS
Мой инструктор был великолепен. Она всегда была готова дать совет и знала, сколько советов нужно дать, чтобы проблемы оставались выполнимыми, но при этом приносили удовлетворение.
— онлайн-студент AoPS
Мой сын поглощает ваши уроки. Он всегда любил математику, но сейчас не может ею насытиться.
 Его прокачивают каждую среду. Способ предоставить лучший образовательный продукт, который этот папа нашел где угодно!
Его прокачивают каждую среду. Способ предоставить лучший образовательный продукт, который этот папа нашел где угодно!– Джон С.
Сочетание видео, учебников, онлайн-задач и задач из книг было фантастическим для наших мальчиков. Мне нравится, что они могут делать это в своем собственном темпе, и насколько они мотивированы теперь, когда сами несут ответственность за свое обучение.
— Онлайн-родитель AoPS
Все члены команд Международной математической олимпиады США 2015–2022 гг. являются выпускниками AoPS.
Категории онлайн-курсов по математике
Онлайн-курсы AoPS проводятся еженедельно в нашем интерактивном онлайн-классе. Опытные инструкторы проводят группы через увлекательные и сложные задачи, а студенты работают со сверстниками, творчески решая проблемы вместе.
5–10 классы и старше
От алгебры до геометрии
Узнать больше
8–12 классы и старше
Алгебра от среднего до предварительного исчисления
Подробнее
9–12 классы и старше
Исчисление к олимпиадной геометрии
Подробнее
9–12 классы
Всемирная онлайн-олимпиада Обучение по математике,
Физика и химия
Подробнее
6–12 классы
Подготовка к математическим олимпиадам
Узнать больше
Классы 6–12+
Курсы программирования
Подробнее
Книги по математике
AoPS предлагает учебники по математике для продвинутых пользователей как в онлайн-формате, так и в мягкой обложке. Наша комплексная учебная программа по математике охватывает как предалгебру, так и подготовку к соревнованиям по математике.
Наша комплексная учебная программа по математике охватывает как предалгебру, так и подготовку к соревнованиям по математике.
Просмотреть все
Введение в математикуПолная вводная учебная программа по математике для учащихся 5–10 классов, которая подробно охватывает стандартную серию преалгебры/алгебры/геометрии, а также важные отдельные математические темы.
Посмотреть
Математика для среднего и продвинутого уровняУчебники по математике для начинающих, которые подготовят учащихся 8–12 классов к продвинутым математическим предметам в средней школе, колледже и карьере в областях STEM.
Посмотреть
Подготовка к соревнованиям по математике Уже более 25 лет победители математических соревнований полагались на руководства по решению задач AoPS для подготовки к соревнованиям. Подходит для 6–12 классов и написана обладателями медалей в MATHCOUNTS, AMC, AIME и USAMO.
Просмотр
Другие программы AoPS
Art of Problem Solving предлагает еще две многогранные программы. Beast Academy — это онлайн-учебная программа по математике, основанная на комиксах, для учащихся в возрасте от 6 до 13 лет. А Академия AoPS предлагает нашу методологию учащимся 2–12 классов на небольших очных занятиях в местных кампусах.
Благодаря нашим трем программам AoPS предлагает самый полный курс математики с отличием в мире. Посмотрите полное сравнение наших программных предложений.
Бесплатные ресурсы для учащихся
Искусство решения проблем предлагает широкий выбор бесплатных ресурсов для заядлых специалистов по решению проблем, в том числе сотни видеороликов и интерактивных инструментов, таких как Alcumus, наша популярная система адаптивного обучения.
Alcumus — наша бесплатная адаптивная обучающая система. Он предлагает учащимся индивидуальный подход к обучению, приспосабливаясь к их успеваемости, чтобы решать задачи, которые бросят им вызов. Alcumus соответствует нашим онлайн-курсам и учебникам по вводной математике, средней алгебре и предварительному исчислению.
Alcumus соответствует нашим онлайн-курсам и учебникам по вводной математике, средней алгебре и предварительному исчислению.
НАЧАТЬ ОБУЧЕНИЕ
Наша видеотека содержит сотни видеороликов с участием основателя AoPS Ричарда Ручика. Многие из видеороликов связаны с нашими книгами и классами «Преалгебра», «Введение в алгебру» и «Введение в счет и вероятность».
ПОСМОТРЕТЬ СЕЙЧАС
Тренер по MATHCOUNTS содержит тысячи задач из предыдущих школьных, региональных и национальных соревнований по MATHCOUNTS. Полные решения предоставляются для каждой проблемы, поэтому начинающие математики MATHCOUNTS могут научиться подходить даже к самым сложным вопросам.
НАЧАТЬ ОБУЧЕНИЕ
Соревнуйтесь с учащимися средних школ со всего мира с помощью For the Win! (FTW), вдохновленный раундом обратного отсчета MATHCOUNTS.
НАЧАТЬ ИГРУ
Просмотреть все ресурсы
© 2023 AoPS Incorporated
Тесты и обзоры AP | СБ | ДЕЙСТВУЙ | SOL Tests & Reviews
Перейти к основному содержанию
- Leesburg, VA
- Herndon, VA
- Reston, VA
- Chantilly, VA
- Centreville, VA
- North Potomac-Darnestown, MD
- Oakton, VA
- Vienna, VA
- Fairfax City, VA
- Tysons Corner, Вирджиния
- Вирджиния
- Лучшие национальные новости
- Просмотреть все сообщества
Это сообщение было опубликовано участником сообщества. Мнения, высказанные здесь, принадлежат автору.
Эшберн, Вирджиния | Местная классификация | Другое|
Anil Goel , сосед
Ап-тесты и обзоры на юге езды только
. Химия и AP Физика C, 1 и 2
Химия и AP Физика C, 1 и 2
Начало – конец : Сб, 4 марта – Сб, 1 мая
Полноценные практические тесты : Сб, 10:00 – 13:00
Обзоры тестов : Вс , 10:00 — 13:00
Стоимость обучения: $99/месяц/предмет
Местонахождение: 4090 Lafayette Center Dr, Suite C, Chantilly, VA 20151
ACT Math and Science at Tysons Лично или в Zoom. Попробуйте один курс за 25 долларов США
Начало-окончание : вторник, 11 марта, примерно через 4 недели от даты начала
Расписание : четверг, 18:00–20:00
Стоимость обучения: 249 долларов США (4 полноценных теста ACT и 4 обзорных теста) отделений математики и естественных наук)
Адрес: 8206 Leesburg Pike, Suite 201, Vienna, VA 22182
SAT Math at Tysons Лично или в Zoom. Попробуйте один курс за 25 долларов США
Начало — конец : вторник, 1 марта — 31 мая
Расписание : среда, 18:00 — 20:00
Стоимость обучения: 199 долларов США в месяц
Расположение: 8206 Leesburg Suite11, Leesburg Pike VA 22182
SAT Чтение, письмо и математика в Ashburn Попробуйте первую неделю за 100 долларов. Лично или через Zoom
Лично или через Zoom
Начало – Окончание : Сб 4 марта – примерно четыре месяца с даты начала
Полноценные практические тесты : Сб/Вс, 9:00 — 12:15
11-классники — 3 часа/бумажный тест. А 10- и 9-классники и займут 2 часа/Цифровой тест
Обзоры тестов: Пн, 20–21:30
Лекции : Вт 8–21:30
Местоположение:
6 100006 $100006 :
44330 Premier Plaza, Unit 220, Ashburn, VA 20147 SOL Tests & Reviews Grades 3, 4, 5, 6, 7, 8 и 9. Только лично
Расписание Ashburn and Tysons: Сб, 10:30 — 12:30
Расписание South Riding: Сб и Вс, 10:30 — 12:30 (выберите один день. Комбинация/сочетание в порядке)
Обучение: Ashburn — 75 долларов в месяц
SOL: Reading, Math, Science, Social
Местоположение: Ashburn, South Riding, and Tysons
Pre/TJ Test
Ashburn Для учащихся 7-6 классов. Выбор Zoom/лично/гибрид
Выбор Zoom/лично/гибрид
Начало : Сб, 25 февраля
Практические тесты : Сб, 8–9:30
Лекции и обзоры тестов : Среда, 8–9:30
Месяц 6 9000 $ : 44330 Premier Plaza, Unit 220, Ashburn, VA 20147
Алгебра I, II и геометрия
Школьное оборудование и помощь в тестах + Дополнение
Обучение : 150 долларов в месяц. 2 часа в неделю
Расписание : гибкий день/время
Расположение: Ashburn, South Riding и Tysons
Pre-Calc, AP Calc AB, AP Calc BC, AP Stats, Bio, Chem и Phy
School HW & Test help
Schedule : Sat 10 :30:00 — 12:30
Стоимость обучения : 190 долларов в месяц. 2 часа в неделю
Адрес: Ashburn
3, 4, 5, 6 и 7 классы
Чтение, письмо, математика и естественные науки. Школьное оборудование и помощь с тестами + Дополнение
Школьное оборудование и помощь с тестами + Дополнение
Расписание : гибкий день/время
Стоимость обучения : 100 долларов в месяц. 2 часа в неделю
Местоположение: Ashburn, South Riding, and Tysons
1:1 Заявления в колледж и эссе с Анилом (автором и издателем десяти книг)
Мы редактируем и завершаем эссе, помогаем планировать и выполнять весь процесс подачи заявления в колледж
Стоимость обучения: Первый колледж стоит 1200 долларов. После этого $370/колледж
Местонахождение: Ashburn
Целостное планирование колледжа и дорожная карта 1:1
Обучение: классы 8, 9, 10 и 11-$ 150
Местоположение: Ashburn
Спасибо
Anil goel
571-206-4803 (мы предпочитаем текстовое сообщение)
Информация@MyExAmspR .com
4090 Lafayette Centre Dr, Suite C, Chantilly.

 С. Габриелян
С. Габриелян Эванс, Д. Дули, К. Баранова, В. Копылова, Р. Мильруд
Эванс, Д. Дули, К. Баранова, В. Копылова, Р. Мильруд И., Рыбченкова Л.М.
И., Рыбченкова Л.М.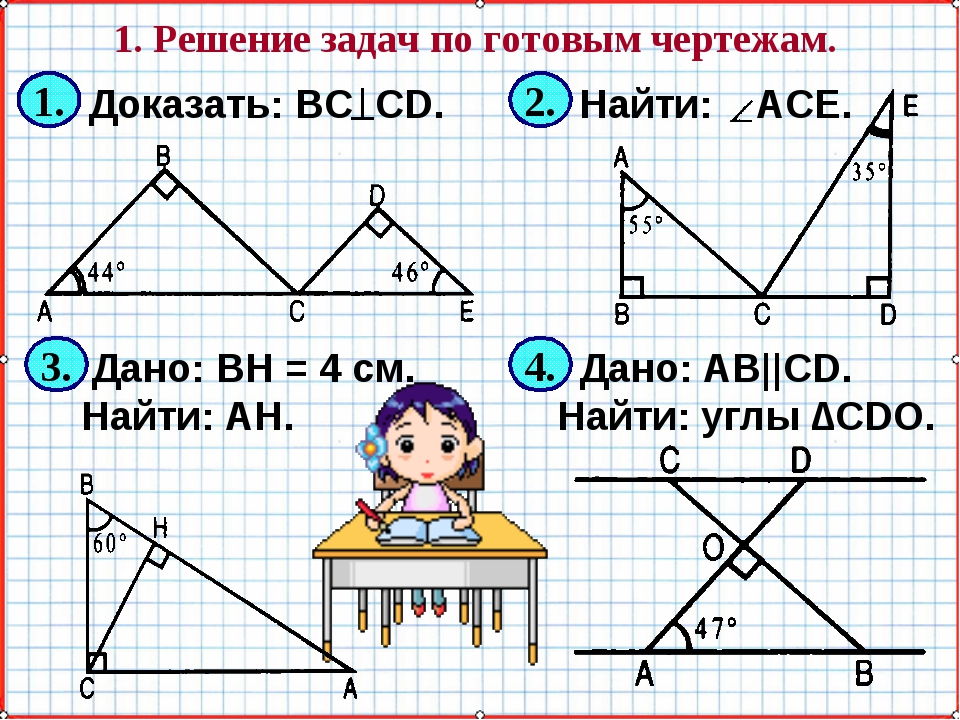 Г. Мордкович
Г. Мордкович