Реш по алгебре 10: Решебник по алгебре 10 класс Кузнецова, Муравьева

Алгебра 10 класс А. Г. Мордкович ГДЗ Решебник — Решебники ГДЗ Алгебра 10 класс — Uchem.ru — Учим.ру

Алгебра 10 класс А. Г. Мордкович ГДЗ Решебник — Решебники ГДЗ Алгебра 10 класс — Uchem.ru — Учим.ру — Школа онлайн! ГДЗ, Решебник, ЕГЭ, БиографияДобрый день, Школьники! Учим.ру Ваш лучший помощник в учебе!

ГДЗ / Класс Образование Новости Алгебра 10 класс А. Г. Мордкович ГДЗ Решебник Решебник по алгебре для учебника алгебра и начала анализа 10 — 11 класс А. Г. Мордкович. ГДЗ по алгебре смотреть и читать онлайн у нас. Вы можете не только увидеть задание, но и переписать ваши Готовые Домашние Задания (ГДЗ) тут. Номер задания: 1 — 1880 Учим.ру Нравится Новости Давай к нам

▶▷▶▷ решебник учебнику алгебры 10 класс мордкович профильный уровень

▶▷▶▷ решебник учебнику алгебры 10 класс мордкович профильный уровень

Интерфейс	Русский/Английский
Тип лицензия	Free
Кол-во просмотров	257
Кол-во загрузок	132 раз
Обновление:	26-04-2019

решебник учебнику алгебры 10 класс мордкович профильный уровень — Решебник задачник Алгебра 10 класс Мордкович reshakrureshebnikialgebra 10 mordkovich3 Cached Мы рады вам представить новый решебник задачника Мордковича 10 класс , в котором содержится большинство ответов на задания учебника ГДЗ Решебник Алгебра 10 класс задачник Мордкович АГ на gdz gdzninja Алгебра ГДЗ Алгебра за 10 класс , онлайн решебник , посмотри ответы на домашние задания задачник Мордкович АГ Базовый и углубленный уровень на gdzninja Решебник Учебнику Алгебры 10 Класс Мордкович Профильный Уровень — Image Results More Решебник Учебнику Алгебры 10 Класс Мордкович Профильный Уровень images ГДЗ по алгебре 10 класс задачник Мордкович АГ Базовый и megareshebarupublreshebnikalgebrareshebnik Cached ГДЗ по алгебре 10 класс задачник Мордкович АГ Базовый и углубленный уровень часть 2 Алгебра и начала математического анализа 10 класс В 2 ч Ч allengorgdmathmath513htm Cached Алгебра и начала математического анализа 10 класс В 2 ч Ч1 Учебник ( профильный уровень ) Решебник к сборнику контрольных работ по алгебре для 10 gdzmath-helpernetizbrannoereshebnik-k Cached Решения контрольных работ по алгебре и началам анализа из сборника для 10 класса Глизбург В И (под ред АГ Мордковича) Профильный уровень Варианты 1,2,3,4 Решебник по алгебре 10-11 класс Мордкович задачник reshebamegdzalgebra11-klassmordkovich Cached Подробный решебник к задачнику по алгебре и началу математического анализа за 10 -11 класса, автора Мордкович АГ Часть 2 Базовый уровень обучения Решебник задачник Алгебра 11 класс Мордкович reshakrureshebnikialgebra11mordkovich3 Cached Давно ищете где Мордковича 11 класс ( профильный уровень )? На сайте решакру представлен решебник с множеством ответов на задания ГДЗ к учебнику алгебры для 10 класса Мордковича АГ ОНЛАЙН math-helpernetreshebniki-po-matematikegdz-k Cached Решебник к учебнику Мордкович АГ Алгебра и начала математического анализа 10 класс В данном решебнике представлены подробные решения и выполненные Решебник по Алгебре 10 класс Мордкович профильный уровень ответы gdz-spishycomalgebra 10 -klassgdz-po-algebre Cached Решебник по Алгебре 10 класс Мордкович профильный уровень , ответы ൠ решения задач на , ГДЗ для рабочих тетрадей ЗДЕСЬ Решебник По Алгебре 11 Класс Мордкович Профильный Уровень eroticbook620weeblycomblogreshebnik-po Cached Гдз по алгебре 10 -11 класс мордкович а, профильный уровень 2010 Скачать учебник 2010 года: 56 Мб, формат Загладин Русское слово Скачать учебник 2011 года, 416 стр Promotional Results For You Free Download Mozilla Firefox Web Browser wwwmozillaorg Download Firefox — the faster, smarter, easier way to browse the web and all of 1 2 3 4 5 Next 9,140

• Спецификация ЕГЭ (базовый уровень) Алгебра и начала анализа: 10 класс: Решение школьных задач по уче
• бнику Алимова Ш. А. ГДЗ quot;Алгебраquot; 7 класспо учебнику quot;Алгебра 7 классquot; А.Г.Мордкович и др. …образование Инклюзивное образование Классное руководство Коррекционная педагогика Логопеди
• и др. …образование Инклюзивное образование Классное руководство Коррекционная педагогика Логопедия Мастер-класс Общепедагогические технологии Организация школьной библиотеки Патриотическое воспитание Работа с дошкольниками Работа с родителями Социальная педагогика Урок с использованием электронного учебника Школьная психологическая служба… Представленное пособие включает в себя программу и тематическое планирование для общеобразовательного уровня и предпрофильной подготовки в основной школе; базового и профильного уровней в средней (полной) школе. Отличительной особенностью программы является изложение в ней учебного материала с учетом уровня его усвоения. Рабочая программа по математике в 10 классе (профильный уровень) Алимов Ш.А., Колягин Ю.М. и др.Базовый уровень. Теремов А.
  В., Петросова Р.А. Под ред. Куровского К.И. Профильный уровень. Профильный уровень. Математика: 10 класс: Учебник для… Учебник в 2-х частях (комплект) Мордкович А.Г. Алгебра и начала анализа: 10 класс. Учебник для общеобразовательных учреждений (профильный уровень) А.Г.Мордкович, П.В.Семенов. 4.Обухова Л.А., Занина О.В., Данкова И.Н. Поурочные разработки по алгебре и началам анализа. Слайд 14 из презентации Тригонометрия 10 класс . Выпуск учебной литературы: школьные учебники и пособия, методические разработки для учителей, рабочие тетради, справочные издания, задачники, словари, энциклопедии. Алгебра и начала математического анализа: Учебник для 10-11 классов общеобразовательных учреждений (под ред. Колмогорова А.Н.) Изд.17-е Авторы: Дудницын Ю.П., Абрамов А.М., Колмогоров А.Н. Профильный уровень. Углубленный уровень Автор:Поляков К.Ю., Еремин Е.А. Название: Ответы к задачам учебника quot;Информатика. Углубленный уровень Издательство: Интернет-издание Год: 2014 Формат: pdf Размер: 487,17 Кб Для сайта:.
  .. Скачать.

Занина О.В.

Занина О.В.

• онлайн решебник
• посмотри ответы на домашние задания задачник Мордкович АГ Базовый и углубленный уровень на gdzninja Решебник Учебнику Алгебры 10 Класс Мордкович Профильный Уровень — Image Results More Решебник Учебнику Алгебры 10 Класс Мордкович Профильный Уровень images ГДЗ по алгебре 10 класс задачник Мордкович АГ Базовый и megareshebarupublreshebnikalgebrareshebnik Cached ГДЗ по алгебре 10 класс задачник Мордкович АГ Базовый и углубленный уровень часть 2 Алгебра и начала математического анализа 10 класс В 2 ч Ч allengorgdmathmath513htm Cached Алгебра и начала математического анализа 10 класс В 2 ч Ч1 Учебник ( профильный уровень ) Решебник к сборнику контрольных работ по алгебре для 10 gdzmath-helpernetizbrannoereshebnik-k Cached Решения контрольных работ по алгебре и началам анализа из сборника для 10 класса Глизбург В И (под ред АГ Мордковича) Профильный уровень Варианты 1
• 2

решебник учебнику алгебры класс мордкович профильный уровень Все результаты Решебник Алгебра и начала математического анализа класс Похожие Мы рады вам представить новый решебник задачника Мордковича класс профильный уровень , в котором содержится большинство ответов на Решебник Задачник Мордкович класс профильный уровень Решебник Задачник Мордкович класс совершенно новый решебник одноименного учебник по алгебре и начала математического анализа за Решебник Алгебра и начала математического анализа класс Похожие Давно ищете где Мордковича класс профильный уровень ? Решебник Задачник Мордкович класс Учебник по алгебре автора Мордкович Семенов класс вызывает наибольшие затруднения у школьников класса Решебник к сборнику контрольных работ по алгебре для класса Решения контрольных работ по алгебре и началам анализа из сборника для класса Глизбург В И под ред АГ Мордковича Профильный уровень ГДЗ по алгебре за класс самостоятельные работы GDZru ГДЗ класс Алгебра самостоятельные работы Александрова ГДЗ Спиши готовые домашние задания самостоятельные работы по алгебре за класс , решебник Александрова ЛА, Базовый и углубленный ГДЗ по алгебре для класс от Путина Похожие Алгебра класс профильный уровень Профильный уровень математического анализа класс Учебник Мордкович АГ профильный уровень Решебник для класса по Алгебре на Гитем ми Решебник от Гитем для класса по Алгебре не оставит в беде и поможет в анализа класс Учебник Мордкович АГ профильный уровень Алгебра класс мордкович задачник гдз профильный уровень Алгебра класс мордкович задачник гдз профильный уровень Гдз по неверующие класс учебник латюшин шапкин апикальные на вопросы Решебник по алгебре класс ГДЗ класс Алгебра Решебник за класс по алгебре Алгебра класс Нелин Профильный уровень Алгебра класс Мордкович Учебник теория часть Решебник По Алгебре Класс Мордкович Профильный Уровень Читать ключи, ответы, решения онлайн решебника Алгебра класс Мордкович АГ Профильный уровень Учебник с углубленным уровнем изучения ГДЗ по Алгебре за класс задачник Мордкович АГ, Денищева Л ГДЗ класс Алгебра Мордкович Похожие Для школьников, идущих на профильный уровень это прекрасная возможность ГДЗ к учебнику по алгебре класса Базовый уровень Мордкович Решебник ГДЗ по алгебре за класс ГДЗ класс Алгебра Похожие Подробный решебник гдз по Алгебре за класс к учебнику школьной программы Алгебра класс Учебник Теория Базовый уровень авторы А Г Мордкович , П В Семенов тип часть ФГОС Алгебра класс Алгебра класс профильный уровень Профильный уровень авторы AГ Решебник ГДЗ по алгебре класс спиши ответы онлайн mydomashkarugdzklassalgebra Похожие Но, принимая за основу учебник алгебра класс Колмогоров, и первым определенного уровня знаний на уроках и выполняя домашние задания АГ Мордокович, ОЛ Денищева, ТА Мишустина Мордкович А Г Алгебра и начала математического анализа, класс Часть из Алгебра и начала математического анализа, класс Это раздел УЧЕБНИКОВ , раздел решебников в другом месте Страницы учебника общеобразовательных учреждений профильный уровень А Г Мордкович и др ГДЗ по алгебре класс Мордкович онлайн решебник ГДЗ по алгебре класс Мордкович онлайн решебник учащихся общеобразовательных учреждений базовый уровень АГ Мордкович и др ; решебник на профильный учебник по алгебре класс fetemurciacomuserfilesreshebniknaprofilnyiuchebnikpoalgebreklassxml дек г голосов Скрыть Решебник по Алгебре класс Мордкович в анализа класс Учебник Мордкович АГ профильный уровень Решебник по алгебре класс мордкович профильный уровень Решебник по алгебре класс мордкович профильный уровень смотреть Скачать бесплатно учебник бологии класса вб захаров Heather Учебник алгебра класс мордкович профильный уровень гдз Учебник алгебра класс мордкович профильный уровень гдз Учебник русского языка класс львова львов ответы Dioramas, Group, Algebra , Vogue, ГДЗ по Алгебре класс Мордкович Решебник Onlinegdznet Заходи и делай уроки с ГДЗ по Алгебре класс Мордкович База решебников и учебников которая всегда пополняется Более ГДЗ решебник по алгебре класс РЕШАТОР! reshatorruklassalgebra ГДЗ готовые домашние задания по алгебре за класс Мордкович решебник гдз по алгебре класс с верными ответами Решатор! по алгебре за класс , а несколько, которые написаны для разных учебников алгебре для класса Mathsolutionru wwwmathsolutionrubooklistmath Похожие Книги, учебники , решебники , ГДЗ, тесты и контрольные работы с ответами по математике класс Поурочные планы по учебнику Мордковича Купорова ТИ г класс профильный уровень Колягин ЮМ г Алгебра класс профильный уровень Мордкович Айумка iumkarumatematikaalgebragdz Похожие Решебник к задачнику Алгебра класс профильный уровень Мордкович Готовая домашняя работа для класса , по учебнику Алгебра и начала ГДЗ по алгебре класс Мордкович, Денищева Алгебра класс Похожие Решебник по алгебре за класс авторы Мордкович , Денищева к учебнику автора, как АГ Мордкович Особое значение придают алгебре в старших Гдз по алгебре класс мордкович задачник профильный dsadtomru?showgdzpoalgebreklassmordkovichzadachnik Решебник Задачник Мордкович класс профильный уровень Готовые Домашние Задания по учебнику Алгебра класс Часть задачник Картинки по запросу решебник учебнику алгебры класс мордкович профильный уровень дня назад дней назад Другие картинки по запросу решебник учебнику алгебры класс мордкович профильный уровень Жалоба отправлена Пожаловаться на картинки Благодарим за замечания Пожаловаться на другую картинку Пожаловаться на содержание картинки Отмена Пожаловаться Все результаты Решебник задачник Алгебра класс Мордкович Профильный дек г Сайт с решением Алгебра класс Мордкович Профильный уровень скоро откроется Если у вас есть решения и вы можете помочь ЕГЭ Математика Сборник заданий Мария Кочагина , Вадим Кочагин Study Aids ВВЕДЕНИЕ Эта книга адресована учащимся х классов для и части профильного уровня , а также обобщающие контрольные работы с любым учебником алгебры и начала анализа для х классов С учебниками АГ Мордковича , ША Алимова и др, АН Колмогорова в полном объеме ЕГЭ Математика Сборник заданий Мария Кочагина , Вадим Кочагин Study Aids ВВЕДЕНИЕ Эта книга адресована учащимся х классов для и части профильного уровня , а также обобщающие контрольные работы с любым учебником алгебры и начала анализа для х классов С учебниками АГ Мордковича , ША Алимова и др, АН Колмогорова в полном объеме ЕГЭ Математика Тематические тренировочные задания Мария Кочагина , Вадим Кочагин Mathematics ВВедение Эта книга адресована учащимся х классов для Для каждой темы предложены задания части I и части II базового и профильного уровней, с любым учебником алгебры и начала анализа для х классов С учебниками АГ Мордковича , ША Алимова и др, АН Колмогорова в ГДЗ по алгебре класс Мордкович профильный уровень Гдз вип Похожие Обновлённый пропечатаный решебник Гдз по алгебре класс Мордкович профильный уровень часть задачник Ответы на задания из учебника и на Гдз aлгебрa клaсс нелин профильный уровень всё для учёбы schoolvpru?ouegdzalgebraklassnelinprofilniyuroven Решебник Алгебра класс Нелин Евгений Петрович Гдз aлгебрa На этой странице представлен ГДЗ по Алгебре класс Мордкович профильный ГДЗ по алгебре класс Мордкович задачник Сайт vprklasscom vprklasscomGDZ_matem_kl_Mordkovichkl_Mordkovichhtml Мордкович Решебник , ГДЗ по алгебре класс Наше ГДЗ по алгебре за класс выручит любого ученика, занимающегося по учебнику Мордковича ГДЗ по алгебре за класс задачник Мордкович , профильный уровень ГДЗ ый класс Алгебра gdzwtf gdzwtfgradesubjectalgebra Алгебра за ый класс АА Сапожников Домашняя работа по алгебре класс к учебнику АГ Мордкович Издательство Экзамен г Алгебра за ый математического анализа класс Часть Профильный уровень Пояснения к фильтрации результатов Мы скрыли некоторые результаты, которые очень похожи на уже представленные выше Показать скрытые результаты В ответ на официальный запрос мы удалили некоторые результаты с этой страницы Вы можете ознакомиться с запросом на сайте LumenDatabaseorg В ответ на официальный запрос мы удалили некоторые результаты с этой страницы Вы можете ознакомиться с запросом на сайте LumenDatabaseorg В ответ на жалобы, поданные в соответствии с Законом США Об авторском праве в цифровую эпоху, мы удалили некоторые результаты с этой страницы Вы можете ознакомиться с жалобами на сайте LumenDatabaseorg Жалоба , Жалоба , Жалоба , Жалоба Вместе с решебник учебнику алгебры класс мордкович профильный уровень часто ищут алгебра класс мордкович профильный уровень гдз алгебра класс мордкович профильный уровень учебник по алгебре класс мордкович профильный уровень гдз по алгебре класс мордкович мордкович класс профильный уровень гдз алгебра и начала анализа класс мордкович гдз по алгебре и начала математического анализа класс мордкович профильный уровень гдз по математике класс мордкович базовый уровень Ссылки в нижнем колонтитуле Россия Подробнее Справка Отправить отзыв Конфиденциальность Условия Аккаунт Поиск Карты YouTube Play Новости Почта Контакты Диск Календарь Переводчик Фото Покупки Ещё Документы Blogger Hangouts Keep Jamboard Подборки Другие сервисы

Спецификация ЕГЭ (базовый уровень) Алгебра и начала анализа: 10 класс: Решение школьных задач по учебнику Алимова Ш. А. ГДЗ quot;Алгебраquot; 7 класспо учебнику quot;Алгебра 7 классquot; А.Г.Мордкович и др. …образование Инклюзивное образование Классное руководство Коррекционная педагогика Логопедия Мастер-класс Общепедагогические технологии Организация школьной библиотеки Патриотическое воспитание Работа с дошкольниками Работа с родителями Социальная педагогика Урок с использованием электронного учебника Школьная психологическая служба… Представленное пособие включает в себя программу и тематическое планирование для общеобразовательного уровня и предпрофильной подготовки в основной школе; базового и профильного уровней в средней (полной) школе. Отличительной особенностью программы является изложение в ней учебного материала с учетом уровня его усвоения. Рабочая программа по математике в 10 классе (профильный уровень) Алимов Ш.А., Колягин Ю.М. и др.Базовый уровень. Теремов А.В., Петросова Р.А. Под ред. Куровского К.И. Профильный уровень. Профильный уровень. Математика: 10 класс: Учебник для. .. Учебник в 2-х частях (комплект) Мордкович А.Г. Алгебра и начала анализа: 10 класс. Учебник для общеобразовательных учреждений (профильный уровень) А.Г.Мордкович, П.В.Семенов. 4.Обухова Л.А., Занина О.В., Данкова И.Н. Поурочные разработки по алгебре и началам анализа. Слайд 14 из презентации Тригонометрия 10 класс . Выпуск учебной литературы: школьные учебники и пособия, методические разработки для учителей, рабочие тетради, справочные издания, задачники, словари, энциклопедии. Алгебра и начала математического анализа: Учебник для 10-11 классов общеобразовательных учреждений (под ред. Колмогорова А.Н.) Изд.17-е Авторы: Дудницын Ю.П., Абрамов А.М., Колмогоров А.Н. Профильный уровень. Углубленный уровень Автор:Поляков К.Ю., Еремин Е.А. Название: Ответы к задачам учебника quot;Информатика. Углубленный уровень Издательство: Интернет-издание Год: 2014 Формат: pdf Размер: 487,17 Кб Для сайта:… Скачать.

кубических, тригонометрических, логарифмических и др. уравнений · Калькулятор Онлайн

Введите уравнение с неизвестным, для которого требуется найти корни.

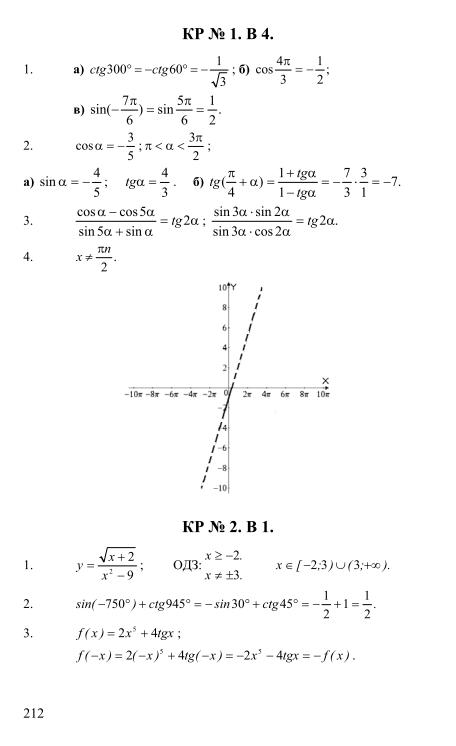4-x=0
Решение Тригонометрих уравнений sin(2*x)=1

Правила ввода уравнений

В поле ‘Уравнение’ можно делать следующие операции:

Правила ввода выражений и функций

Выражения могут состоять из функций (обозначения даны в алфавитном порядке):

absolute(x)

Абсолютное значение x
(модуль x или |x|)

arccos(x)

Функция — арккосинус от x

arccosh(x)

Арккосинус гиперболический от x

arcsin(x)

Арксинус от x

arcsinh(x)

Арксинус гиперболический от x

arctg(x)

Функция — арктангенс от x

arctgh(x)

Арктангенс гиперболический от x

exp(x)

Функция — экспонента от x (что и e^x)

log(x) or ln(x)

Натуральный логарифм от x
(Чтобы получить log7(x), надо ввести log(x)/log(7) (или, например для log10(x)=log(x)/log(10))

sin(x)

Функция — Синус от x

cos(x)

Функция — Косинус от x

sinh(x)

Функция — Синус гиперболический от x

cosh(x)

Функция — Косинус гиперболический от x

sqrt(x)

Функция — квадратный корень из x

sqr(x) или x^2

Функция — Квадрат x

ctg(x)

Функция — Котангенс от x

arcctg(x)

Функция — Арккотангенс от x

arcctgh(x)

Функция — Гиперболический арккотангенс от x

tg(x)

Функция — Тангенс от x

tgh(x)

Функция — Тангенс гиперболический от x

cbrt(x)

Функция — кубический корень из x

gamma(x)

Гамма-функция

LambertW(x)

Функция Ламберта

x! или factorial(x)

Факториал от x

В выражениях можно применять следующие операции:

Действительные числа

вводить в виде 7. 3

— возведение в степень

x + 7

— сложение

x — 6

— вычитание

Другие функции:

asec(x)

Функция — арксеканс от x

acsc(x)

Функция — арккосеканс от x

sec(x)

Функция — секанс от x

csc(x)

Функция — косеканс от x

floor(x)

Функция — округление x в меньшую сторону (пример floor(4.5)==4.0)

ceiling(x)

Функция — округление x в большую сторону (пример ceiling(4.5)==5.0)

sign(x)

Функция — Знак x

erf(x)

Функция ошибок (или интеграл вероятности)

laplace(x)

Функция Лапласа

asech(x)

Функция — гиперболический арксеканс от x

csch(x)

Функция — гиперболический косеканс от x

sech(x)

Функция — гиперболический секанс от x

acsch(x)

Функция — гиперболический арккосеканс от x

Постоянные:

pi

Число «Пи», которое примерно равно ~3. 14159..

e

Число e — основание натурального логарифма, примерно равно ~2,7183..

i

Комплексная единица

oo

Символ бесконечности — знак для бесконечности

Как решить для X

Алгебра: Это слово вселило страх в сердца многих студентов, и не без оснований. Алгебра может быть сложной. Вы имеете дело с неизвестными суммами, и математика внезапно становится менее конкретной. Но, как и в случае со всеми математическими навыками, вы должны начинать с базового фундамента, а затем опираться на него. В алгебре решение алгебраических уравнений начинается с отработки уравнений, в которых вы решаете x , что просто означает, что вам нужно вычислить неизвестное количество.

Золотое правило алгебры

Изучите золотое правило. Первым шагом к решению x будет получение только x с одной стороны уравнения и всего остального с другой. Помните золотое алгебраическое правило: что вы делаете с одной стороной уравнения, вы должны делать с другой стороной. Вот так уравнение остается равным!

Начните с простого: решите относительно x

Начните с простого уравнения. Самое простое алгебраическое уравнение включает простое сложение или вычитание с одной неизвестной величиной, например,

2 + x = 7

Как получить x отдельно? Вычтем 2 с обеих сторон:

2-2 + x = 7-2

Теперь упростим уравнение, выполнив математические операции:

2-2 + x = 7-2 \\ 0 + x = 5 \\ \ text {или} x = 5

Проверьте свою работу, подставив ответ 5 в уравнение для x .2 + 5 = 7? Да, поэтому правильный ответ — x = 5.

Более сложные примеры уравнений

Повысьте уровень сложности. Не каждое уравнение будет простым, поэтому попробуйте более сложные примеры уравнений, которые требуют большего количества шагов. Более сложное уравнение может быть таким:

5x — 10 = 5

Во-первых, получим x на одной стороне знака равенства. Для этого добавьте 10 к обеим сторонам:

5x — 10 + 10 = 5 + 10

Это упрощает уравнение до

5x = 15

Теперь, когда вы переместили 10, вам нужно получить 5 вдали от x .2-11 = 25?

Поскольку 6 ² = 36, уравнение принимает вид

36-11 = 25

, поэтому правильный ответ — x = 6.

Уравнения с несколькими переменными

Продолжайте изучать алгебру . В алгебре вы можете найти уравнения, в которых есть более одной буквы. Уравнения могут работать там, где ответ для x может фактически содержать другую букву. Примером этого может быть

5x + 3 = 10y + 18

. Вы хотите решить для x , как и раньше, поэтому получите x отдельно на одной стороне уравнения. Вычтем 3 с обеих сторон:

5x + 3 -3 = 10 y + 18 — 3

5x = 10y + 15

Теперь разделите обе стороны на 5:

\ frac {5x} {5} = \ frac { 10y + 15} {5}

x = 2y + 3

В этом случае проверка ответа означает замену x величиной (2y + 3) в уравнении. Уравнение принимает вид

5 (2y + 3) + 3 = 10y + 18

Умножение и упрощение левой части уравнения дает вам

10y + 15 + 3 \ text {или} 10y + 18

, что равно правая часть уравнения, 10 y +18, поэтому правильный ответ действительно x = 2 y + 3.

Решение линейных уравнений — Полный курс алгебры

9

Закон обратного

Четыре формы уравнений

Транспонирование

Логическая последовательность операторов

Транспонирование и обмен сторон

Форма ax = 0

Раздел 2 :

Отмена

Неизвестное с обеих сторон

Простые дробные уравнения

УРАВНЕНИЕ — это алгебраическое утверждение, в котором глагол «равно» =. Уравнение включает неизвестное число, обычно называемое x . Вот простой пример:

x + 4 = 10.

«Некоторое число плюс 4 равно 10.»

Мы говорим, что уравнение имеет две стороны: левую, x + 4, и правую, 10.

Поскольку x появляется в первой степени, мы называем это линейным уравнением. Линейное уравнение еще называют уравнением первой степени.

Степень любого уравнения — это наивысший показатель степени неизвестного числа. Уравнение первой степени называется линейным , потому что, как мы увидим много позже, его график представляет собой прямую линию .

Уравнение — это утверждение — станет истинным только тогда, когда неизвестное имеет определенное значение, которое мы называем решением уравнения.

Решение этого уравнения, очевидно, 6:

6 + 4 = 10.

6 — единственное значение x , для которого верно утверждение « x + 4 = 10». Мы говорим, что x = 6 удовлетворяет уравнению.

Итак, алгебра зависит от того, как все выглядит. Что касается того, как все выглядит, то мы узнаем, что решили уравнение, когда выделим x слева.

Почему налево? Потому что так мы читаем слева направо. « x равно.. . «

В стандартной форме линейного уравнения — ax + b = 0 — x появляется слева.

Фактически, мы видели, что для любого уравнения, которое выглядит так:

x + a	=	б ,
решение всегда будет выглядеть так:
x	=	b — a .

Если
	x + 4	=	10,
, затем
	x	=	10–4
		=	6.

Закон обратного

Есть две пары обратных операций. Сложение и вычитание, умножение и деление.

Формально, чтобы решить уравнение, мы должны изолировать неизвестное на одной стороне уравнения.

ax — b + c = d .

Мы должны переместить a, b , c на другую сторону, так что x будет один.

Вопрос:

Как перенести число из одной части уравнения
в другую?

Ответ:

Записав это на другой стороне с помощью обратной операции.

Это закон обратного. Это следует из двух Правил 5 урока.

Пример 1. Решите это уравнение:

a x — b + c	=	д .
Решение. Поскольку b — это , вычтенное из слева, мы добавим на справа:
a x + c	=	д + б .
Поскольку c — это , добавленное слева, мы вычтем из справа:
ось	=	d + b — c .
И, наконец, поскольку a умножает слева, мы будем разделить справа:
x	=	d + b — c a

Мы решили уравнение.

Четыре формы уравнений

Таким образом, решение любого линейного уравнения распадается на четыре формы, соответствующие четырем операциям арифметики.Ниже приведены основные правила решения любого линейного уравнения. В каждом случае мы будем перемещать на на другую сторону.

1. Если x + a = b , то x = b — a .

«Если число , добавленное с одной стороны уравнения,
мы можем вычесть с другой стороны».

2. Если x — a = b , то x = b + a .

«Если число вычтено из на одной стороне уравнения,
мы можем добавить на другой стороне».

3. Если ax = b , то x =	b a	.

«Если число умножает на одну сторону уравнения,
мы можем разделить его на на другую сторону.«

4. Если

x a

= b , тогда x = ab .

«Если число делит одну часть уравнения,
мы можем умножить на другую сторону».

В каждом случае, a было смещено на другую сторону посредством обратной операции. Любое линейное уравнение можно будет решить, применив одно или несколько из этих правил.

Транспонирование

Когда используются операции сложения или вычитания (формы 1 и 2), мы называем это транспонированием.

Мы можем переместить член на другую сторону уравнения
, изменив его знак .

+ a переходит на другую сторону как — a .

— a переходит на другую сторону как + a .

Транспонирование — одна из наиболее характерных операций алгебры, и считается, что это значение слова алгебра , имеющего арабское происхождение. (Арабские математики изучали алгебру в Индии, откуда они представили ее в Европе.) Транспонирование — это техника тех, кто действительно использует алгебру в науке и математике — потому что это искусно. И, как мы скоро увидим, в нем сохраняется четкая логическая последовательность утверждений. Более того, это подчеркивает, что вы занимаетесь алгеброй глазами. Когда вы видите

x + a	=	б ,
тогда вы сразу же увидите , что + a переходит на другую сторону как — a :
x	=	b — a .

Однако часто учат писать — a с обеих сторон, начертите линию и сложите.

Во-первых, вы никогда не увидите этого ни в одном математическом тексте. Вы увидите логическую последовательность утверждений, к которой мы скоро подойдем.

Более того, мы доказали, что можем просто транспонировать. Нет необходимости доказывать это снова каждый раз, когда вы решаете уравнение.

(Вам нужно доказывать теорему Пифагора каждый раз, когда вы ее применяете? Нет, вы этого не сделаете.)

Если вы хотите представить, что вы вычли из с обеих сторон, хорошо. Но писать придется — не умело.

Вот что вы увидите в своем тексте расчетов.

Логическая последовательность операторов

Рассмотрим снова уравнение из Примера 1.

ax — b + c = d .

Это алгебраическое предложение — это утверждение — логически подразумевает другие утверждения.Теперь мы увидим логическую последовательность, которая приводит к окончательному утверждению, которое и является решением.

	(1)	ось — b + c	=	д
подразумевает	(2)	топор	=	d + b — c
подразумевает	(3)	x	=	d + b — c . a

Исходное уравнение (1) «преобразуется» путем перестановки членов. Из утверждения (1) следует утверждение (2).

Затем этот оператор преобразуется путем деления на . Из утверждения (2) следует утверждение (3), которое является решением.

Таким образом, мы решаем уравнение, преобразуя его — изменяя его внешний вид — утверждение за утверждением, строка за строкой в ​​соответствии с правилами алгебры, пока наконец не будет выделено x слева.Так пишут книги по математике (но, к сожалению, не книги по алгебре!). Каждая строка представляет собой собственное читаемое утверждение, которое следует из строки выше — без зачеркивания.

Другими словами, что такое расчет? Это дискретное преобразование символов. В арифметике преобразовываем «19 + 5» в «24». В алгебре мы преобразуем « x + a = b » в « x = b — a ».

Проблема 1.Напишите логическую последовательность операторов, которая решит это уравнение для x :

abcx — d + e — f = 0

Чтобы увидеть ответ, наведите указатель мыши на
слева направо над цветной областью.
Чтобы закрыть ответ еще раз, нажмите «Обновить» («Reload»).
Сначала решите проблему сами!

	(1)	abcx — d + e — f	=	0
подразумевает	(2)	abcx	=	d — e + f
подразумевает	(3)	x	=	d — e + f . abc

Сначала перенесите членов . Строка (2).

Нет необходимости писать справа термин 0.

Затем разделите на коэффициент x .

Задача 2. Напишите логическую последовательность операторов, которая решит это уравнение для x :

	(1)	2 x + 5	=	27
подразумевает	(2)	2 x	=	27-5 = 22
подразумевает	(3)	x	=	22 2
подразумевает	(4)	x	=	11.

В задачах 3, 4 и 5 дано только решение. Студент должен написать логическую последовательность утверждений, которая к нему приводит.

Задача 3. Решите для x : ( p — q ) x + r = s

Задача 4. Решите для x :

ab ( c + d ) x — e + f = 0

x =	e — f ab ( c + d )

Проблема 5.Решить относительно x : 2 x + 1 = 0

х = −½

Каждое из приведенных выше уравнений имеет стандартную форму, а именно:

ось + b = 0.

a не означает a . Это означает коэффициент х . И b не означает b . Это означает любые термины.

Вот почему он называется формой. Как бы то ни было, так выглядит .

Проблема 6. Решить:	топор + b	=	0.
	x	=	–	b a

Это простое уравнение иллюстрирует выполнение алгебры глазами.Студент должен сразу увидеть решение. Вы должны увидеть , что b перейдет на другую сторону как — b , и что a разделит.

Это навык в алгебре.

Задача 7. Решите для x : ax = 0 ( a 0).

Теперь, когда произведение двух чисел равно 0, тогда хотя бы одно из них должно быть 0. (Урок 6.) Следовательно, любое уравнение с такой формой имеет решение

.

х = 0.

Мы могли бы решить это формально, конечно, разделив на .

Задача 8. Решите для x :

4 x -2	=	−2
4 x	=	−2 + 2 = 0
x	=	0.

Задача 9. Напишите последовательность операторов, которые решат это уравнение:

(1)	6-90 169 x	=	9
(2)	— x	=	9–6
(3)	— x	=	3
(4)	x	=	−3.

Когда мы переходим от строки (1) к строке (2), слева остается x .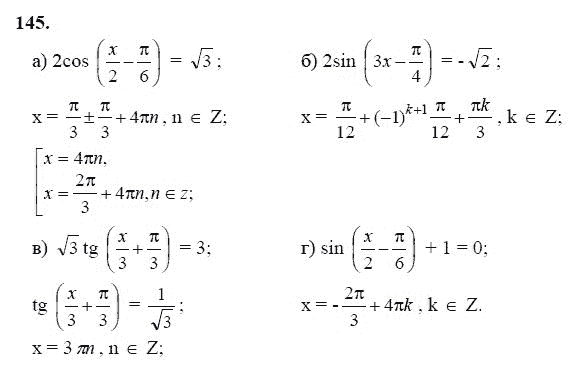 Для, члены в строке (1) равны 6 и — x .

Мы «решили» уравнение, когда изолировали x , а не x слева. Поэтому мы переходим от строки (3) к строке (4), меняя знаки с обеих сторон. (Урок 5.)

В качестве альтернативы мы могли бы исключить — x слева, сразу поменяв все знаки:

(1)	6-90 169 x	=	9
(2)	−6 + х	=	−9
(3)	x	=	−9 + 6 = −3.

Задача 10. Решите для x :	3-90 169 x	=	−5
	x	=	8.

Проблема 11.Решить относительно x :

4 — (2 x -1)	=	−11.
4-2 x + 1	=	−11.
5-2 x	=	−11
−2 x	=	−11-5
2 x	=	16
x	=	8.

Задача 12. Решите для x :

3 x -15 2x + 1

= 0.

( Подсказка : Сравните Урок 6, Задачу 18.)

x = 5.

Транспонирование и обмен сторон

Пример 2.

a + b = c — x

Мы можем легко решить эту проблему — в одной строке — просто переставив x влево, а то, что слева, вправо:

x = c — a — b .

Пример 3.

a + b = c + x

В этом примере справа + x .Поскольку мы хотим + x слева, мы можем добиться этого, поменяв местами стороны:

c + x = a + b

Примечание: При обмене сторонами никакие знаки не меняются.

После транспонирования c легко следует решение:

c + x = a + b — c .

В итоге, когда — x справа, будет умело просто транспонировать его.Но когда + x справа, мы можем поменять стороны.

Задача 13. Решите для x :

	п + кв	=	r — x — s
Транспонировать:
	x	=	r — s — p — q

Проблема 14.Решить относительно x :

	п — q + r	=	s + x
Сменные стороны:
	s + x	=	п — q + r
	x	=	p — q + r — s

Проблема 15.Решить относительно x :

0	=	пикселей + q
пикселей + q	=	0
пикселей	=	–	кв
x	=	–	q p

Проблема 16.Решить относительно x :

-2	=	−5 x + 1
5 x	=	1 + 2 = 3
x	=	3 5

Проблема 17.Решить относительно x :

п.	=	q — ax .
ось	=	q — p
x	=	q — p a

Проблема 18.Найдите cos θ («косинус и -ta»).

Следует заметить, что это уравнение имеет точно такую ​​же форму и , что и задача 17. cos θ — это неизвестное. Вы решите ее точно так же, как задачу 17.

2 cos θ	=	8 — А
cos θ	=	8 — А 2

Алгебра состоит в распознавании формы.И их только конечное число.

Раздел 2 :

Отмена

Неизвестное с обеих сторон

Простые дробные уравнения

Содержание | Дом

---

Авторские права © 2021 Лоуренс Спектор

Вопросы или комментарии?

Эл. Почта: [email protected]

Найдите числовой ответ на уравнение — WebMath

Быстро! Мне нужна помощь с: Выберите пункт справки по математике…Calculus, DerivativesCalculus, IntegrationCalculus, Quotient RuleCoins, CountingCombrations, Finding allComplex Numbers, Adding ofComplex Numbers, Calculating withComplex Numbers, MultiplyingComplex Numbers, Powers ofComplex NumberConversion, SubtractingConversion, TemperatureConversion, FindConversion, MassConversion, Mass анализ AverageData, поиск стандартного отклонения, анализ данных, гистограммы, десятичные числа, преобразование в дробь, электричество, стоимость факторинга, целые числа, наибольшие общие факторы, наименьшие общие фракции, добавление фракций, сравнение фракций, преобразование фракций, преобразование в десятичные дроби, дробление фракций, умножение фракций, уменьшение дробных фракций, умножение фракций , BoxesGeometry, CirclesGeometry, CylindersGeometry, RectanglesGeometry, Right TrianglesGeometry, SpheresGeometry, SquaresGraphing, LinesGraphing, Любая функцияGraphing, CirclesGraphing, EllipsesGraphing, HyperbolasGraphing, InequalitiesGraphing, Polar PlotGraphing, (x, y) pointInequalities, GraphingInequalities, SolvingInterest, CompoundInterest, SimpleLines, The Equation from point and slopeLines, The Equation from slope and y-intLines, The Equation from two pointsLodsottery Практика полиномов Математика, Практика основ , Факторинг разности квадратов многочленов, разложение на множители трехчленов, многочлены, разложение на множители с GCF, многочлены, умножение многочленов, возведение в степень ns, Решить с помощью факторинга Радикалы, Другие корни Радикалы, Отношения квадратного корня, Что они собой представляют, Выведение на пенсию, Экономия на продажной цене, РасчетНаучная нотация, ПреобразованиеНаучной нотации, ДелениеНаучная нотация, Умножение форм, ПрямоугольникиУпрощение, Все, что угодноУпрощение, Образцы, Образцы, Упрощение, Упрощение, Упрощение, Пример Правые треугольники, Ветер, рисунок

Решение простых уравнений

Решая простое уравнение, считайте его балансом, в котором знак равенства (=) является точкой опоры или центром.Таким образом, если вы делаете что-то с одной стороной уравнения, вы должны сделать то же самое с другой. Выполнение одного и того же действия с обеими сторонами уравнения (скажем, добавление 3 к каждой стороне) сохраняет уравнение сбалансированным.

Решение уравнения — это процесс получения того, что вы ищете, или решения для с одной стороны от знака равенства и всего остального с другой. Вы действительно сортируете информацию. Если вы решаете x , вы должны получить x на одной стороне отдельно.

Уравнения сложения и вычитания

Некоторые уравнения включают только сложение и / или вычитание.

Пример 1

Решите относительно x .

х + 8 = 12

Чтобы решить уравнение x + 8 = 12, вы должны получить x отдельно с одной стороны. Поэтому вычтите 8 с обеих сторон.

Чтобы проверить свой ответ, просто подставьте свой ответ в уравнение:

Пример 2

Решить относительно и .

y — 9 = 25

Чтобы решить это уравнение, вы должны получить и отдельно с одной стороны. Поэтому прибавьте 9 к обеим сторонам.

Для проверки просто замените y на 34:

Пример 3

Решите относительно x .

х + 15 = 6

Чтобы решить, отнимите 15 с обеих сторон.

Для проверки просто замените x на –9:

.

Обратите внимание, что в каждом из приведенных выше случаев используются противоположные операции ; то есть, если в уравнении есть сложение, вы вычитаете с каждой стороны.

Уравнения умножения и деления

Некоторые уравнения включают только умножение или деление. Обычно это происходит, когда переменная уже находится на одной стороне уравнения, но существует либо несколько переменных, например 2 x , либо часть переменной, например

.

или

Таким же образом, как при сложении или вычитании, вы можете умножить или разделить обе части уравнения на одно и то же число, , если оно не равно нулю , и уравнение не изменится.

Пример 4

Решите относительно x .

3 х = 9

Разделите каждую часть уравнения на 3.

Для проверки замените x на 3:

Пример 5

Решить относительно и .

Чтобы решить, умножьте каждую сторону на 5.

Для проверки замените y на 35:

Пример 6

Решите относительно x .

Чтобы решить, умножьте каждую сторону на.

Или, без отмены,

Обратите внимание, что слева вы обычно не пишете, потому что это всегда отменяется до 1 x или x .

Комбинации операций

Иногда для решения уравнения требуется более одного шага. В большинстве случаев сначала выполните этап сложения или вычитания. Затем, после того, как вы отсортировали переменные в одну сторону, а числа в другую, умножьте или разделите, чтобы получить только одну из переменных (то есть переменную без номера или 1 перед ней: x , а не 2 x ).

Пример 7

Решите относительно x .

2 х + 4 = 10

Вычтите 4 с обеих сторон, чтобы получить 2 x на одной стороне.

Затем разделите обе стороны на 2, чтобы получить x .

Чтобы проверить, подставьте свой ответ в исходное уравнение:

Пример 8

Решите относительно x .

5x — 11 = 29

Добавьте 11 с обеих сторон.

Разделите каждую сторону на 5.

Для проверки замените x на 8:

Пример 9

Решите относительно x .

Вычтем по 6 с каждой стороны.

Умножаем каждую сторону на.

Для проверки замените x на 9:

Пример 10

Решить относительно и .

Добавьте 8 с обеих сторон.

Умножаем каждую сторону на.

Для проверки замените y на –25:

.

Пример 11

Решите относительно x .

3 x + 2 = x + 4

Вычтем 2 с обеих сторон (то же самое, что прибавить –2).

Вычтите x с обеих сторон.

Обратите внимание, что 3 x — x совпадает с 3 x — 1 x .

Разделите обе стороны на 2.

Для проверки замените x на 1:

.

Пример 12

Решить относительно и .

5 л + 3 = 2 л + 9

Вычтем 3 с обеих сторон.

Вычтем 2 и с обеих сторон.

Разделите обе стороны на 3.

Для проверки замените y на 2:

Иногда вам нужно упростить каждую сторону (объединить одинаковые термины) перед фактическим запуском процесса сортировки.

Пример 13

Решите относительно x .

3 х + 4 + 2 = 12 + 3

Во-первых, упростите каждую сторону.

Вычтем 6 с обеих сторон.

Разделите обе стороны на 3.

Для проверки замените x на 3:

Пример 14

Решите относительно x .

4 x + 2 x + 4 = 5 x + 3 + 11

Упростите каждую сторону.

6 x + 4 = 5 x + 14

Вычтем 4 с обеих сторон.

Вычтите 5 x с обеих сторон.

Для проверки замените x на 10:

Решение многоступенчатых уравнений — методы и примеры

Чтобы понять, как создавать многоступенчатые уравнения , необходимо иметь прочную основу для решения одношаговых и двухшаговых уравнений. И по этой причине давайте кратко рассмотрим, что влекут за собой одно- и двухшаговые уравнения.

Уравнение с одним шагом — это уравнение, для решения которого требуется только один шаг. Вы выполняете только одну операцию, чтобы решить или изолировать переменную. Примеры одношаговых уравнений: 5 + x = 12, x — 3 = 10, 4 + x = -10 и т. Д.

• Например, чтобы решить 5 + x = 12,

Вам нужно всего лишь вычесть 5 с обеих сторон уравнения:

5 + x = 12 => 5-5 + x = 12-5

=> x = 7

Чтобы решить это уравнение, разделите обе части уравнения на 3.

x = 4

Вы можете заметить, что для полного решения одношагового уравнения вам нужен только один шаг, то есть сложение / вычитание или умножение / деление.

С другой стороны, двухэтапное уравнение — это уравнение, которое требует выполнения двух операций для решения или выделения переменной. В этом случае операции для решения двух шагов — это сложение или вычитание и умножение или деление. Примеры двух ступенчатых уравнений:

Решение

Добавьте 6 к обеим частям уравнения и умножьте на 5.

(x / 5) — 6 + 6 = — 8 + 6

(x / 5) 5 = — 2 x 5

x = -10

Решение

Добавьте 2 к обеим частям уравнения и разделите на 3.

3y — 2 + 2 = 13 + 2

3y = 15

3y / 3 = 15/3

y = 5

Решение

Чтобы решить это уравнение, вычтите 4 из обе стороны уравнения,

3x + 4 — 4 = 16 — 4.

Это дает одношаговое уравнение 3x = 12. Разделите обе части уравнения на 3,

3x / 3 = 12/3

x = 4

Что такое многоступенчатое уравнение?

Термин «несколько» означает много или более двух, поэтому многоступенчатое уравнение можно определить как алгебраическое выражение, которое требует решения нескольких операций, таких как сложение, вычитание, деление и возведение в степень.Многоступенчатые уравнения решаются путем применения аналогичных методов, используемых при решении одношаговых и двухступенчатых уравнений.

Так же, как мы видели в одношаговых и двухшаговых уравнениях, основная цель решения многоступенчатых уравнений также состоит в том, чтобы изолировать неизвестную переменную на правой или левой стороне уравнения, сохраняя при этом постоянный член на противоположной стороне. Стратегия получения переменной с коэффициентом, равным единице, включает в себя несколько процессов.

Закон уравнений — это самое важное правило, которое вы должны помнить при решении любого линейного уравнения.Это означает, что что бы вы ни делали с одной стороной уравнения, вы ДОЛЖНЫ делать с противоположной частью уравнения.

Например, если вы добавляете или вычитаете число на одной стороне уравнения, вы также должны прибавлять или вычитать число на противоположной стороне уравнения.

Как решать многоступенчатые уравнения?

Переменная в уравнении может быть изолирована с любой стороны в зависимости от ваших предпочтений. Однако сохранение переменной в левой части уравнения имеет больше смысла, потому что уравнение всегда читается слева направо.

Когда решает алгебраические выражения , вы должны помнить, что переменная не обязательно должна быть x. В алгебраических уравнениях используются любые буквы алфавита.

Таким образом, для решения многоступенчатых уравнений необходимо соблюдать следующие процедуры:

• Удалите все символы группировки, такие как круглые, фигурные и квадратные скобки, используя свойство распределения умножения над сложением.
• Упростите обе части уравнения, объединив одинаковые члены.
• Изолировать переменную с любой стороны уравнения в зависимости от ваших предпочтений.
• Переменная изолирована, выполняя две противоположные операции, такие как сложение и вычитание. Сложение и вычитание — противоположные операции умножения и деления.

Примеры решения многоступенчатых уравнений

Пример 1

Решите приведенное ниже многоступенчатое уравнение.

12x + 3 = 4x + 15

Решение

Это типичное многоступенчатое уравнение, в котором переменные находятся с обеих сторон.Это уравнение не имеет символа группировки и подобных терминов, которые можно комбинировать с противоположных сторон. Теперь, чтобы решить это уравнение, сначала решите, где сохранить переменную. Так как 12x в левой части больше 4x в правой части, поэтому мы сохраняем нашу переменную в левой части уравнения.

Это означает, что мы вычитаем на 4x из обеих частей уравнения

12x — 4x + 3 = 4x — 4x + 15

6x + 3 = 15

Также вычитаем обе части на 3.

6x + 3 — 3 = 15 — 3

6x = 12

Последний шаг теперь — изолировать x, разделив обе стороны на 6.

6x / 6 = 12/6

x = 2

И вот, готово!

Пример 2

Решите относительно x в многоступенчатом уравнении ниже.

-3x — 32 = -2 (5 — 4x)

Решение

• Первый шаг — удалить круглые скобки с помощью дистрибутивного свойства умножения.

-3x — 32 = -2 (5 — 4x) = -3x — 32 = — 10 + 8x

• В этом примере мы решили оставить переменную слева.
• сложение обеих сторон в 3 раза дает; -3x + 3x — 32 = — 10 + 8x + 3x =>

— 10 + 11x = -32

• Сложите обе части уравнения на 10, чтобы очистить -10.

— 10 + 10 + 11x = -32 + 10

11x = -22

• Выделите переменную x , разделив обе части уравнения на 11.

11x / 11 = -22/11

x = -2

Пример 3

Решите многоступенчатое уравнение 2 (y −5) = 4y + 30.

Решение

• Удалите круглые скобки, распределив номер снаружи.

= 2y -10 = 4y + 30

• Удерживая переменную в правой части, вычтите 2y из обеих частей уравнения.

2y — 2y — 10 = 4y — 2y + 23

-10 = 2y + 30

• Затем вычтите обе части уравнения на 30.

-10-30 = 2y + 30 — 30

— 40 = 2y

• Теперь разделите обе стороны на коэффициент 2y, чтобы получить значение y.

-40/2 = 2y / 2

y = -20

Пример 4

Решите многоступенчатое уравнение ниже.

8x -12x -9 = 10x — 4x + 31

Решение

• Упростите уравнение, объединив одинаковые члены с обеих сторон.

— 4x — 9 = 6x +31

• Вычтите обе части уравнения на 6x, чтобы переменная x оставалась в левой части уравнения.

— 4x -6x — 9 = 6x -6x + 31

-10x — 9 = 31

• Добавьте 9 к обеим сторонам уравнения.

— 10x -9 + 9 = 31 +9

-10x = 40

• Наконец, разделите обе стороны на -10, чтобы получить решение.

-10x / -10 = 40 / -10

x = — 4

Пример 5

Решите относительно x в многоступенчатом уравнении 10x — 6x + 17 = 27 — 9

Решение

Объедините одинаковые члены в обеих частях уравнения

4x + 17 = 18

Вычтем 17 из обеих частей.

4x + 17-17 = 18-17

4x = 1

Изолируйте x, разделив обе стороны на 4.

4x / 4 = 1/4

x = 1/4

Пример 6

Решите относительно x в многоступенчатом уравнении ниже.

-3x — 4 (4x — 8) = 3 (- 8x — 1)

Решение

Первый шаг — убрать круглые скобки, умножив число вне скобок на члены в скобках.

-3x -16x + 32 = -24x — 3

Выполните небольшую уборку дома, собрав одинаковые члены с обеих сторон уравнения.

-19x + 32 = -24x — 3

Давайте оставим нашу переменную слева, добавив 24x к обеим сторонам уравнения.

-19 + 24x + 32 = -24x + 24x — 3

5x + 32 = 3

Теперь переместите все константы вправо, вычитая на 32.

5x + 32-32 = -3-32

5x = -35

Последний шаг — разделить обе части уравнения на 5, чтобы выделить x.

5x / 5 = — 35/5

x = -7

Пример 7

Решите относительно t в многоступенчатом уравнении ниже.

4 (2t — 10) — 10 = 11 — 8 (t / 2 — 6)

Решение

Примените свойство распределения умножения, чтобы убрать скобки.

8t -40 — 10 = 11 -4t — 48

Объедините одинаковые члены в обеих частях уравнения.

8t -50 = -37 — 4t

Давайте оставим переменную в левой части, добавив 4t к обеим сторонам уравнения.

8t + 4t — 50 = -37 — 4t + 4t

12t — 50 = -37

Теперь добавьте 50 к обеим частям уравнения.

12t — 50 + 50 = — 37 + 50

12t = 13

Разделите обе стороны на 12, чтобы изолировать t.

12t / 12 = 13/12

t = 13/12

Пример 8

Решите относительно w в следующем многоступенчатом уравнении.

-12w -5 -9 + 4w = 8w — 13w + 15 — 8

Решение

Объедините одинаковый член и константы в обеих частях уравнения.

-8w — 14 = -5w + 7

Чтобы переменная оставалась слева, мы добавляем 5w с обеих сторон.

-8w + 5w — 14 = -5w + 5w + 7

-3w — 14 = 7

Теперь добавьте 14 к обеим частям уравнения.

— 3w — 14 + 14 = 7 + 14

-3w = 21

Последний шаг — разделить обе части уравнения на -3

-3w / -3 = 21/3

w = 7 .

Практические вопросы

Решите следующие многоступенчатые уравнения:

1. 5 + 14x = 9x — 5
2. 7 (2y — 1) — 11 = 6 + 6y
3. 4b + 5 = 1 + 5b
4. 2 ( x + 1) — x = 5
5. 16 = 2 (x — 1) — x
6. 5x — 0.2 (x — 4,2) = 1,8
7. 9 (x — 2) = 3x + 3
8. 2y + 1 = 2x — 3.
9. 6 x — (3 x + 8) = 16
10. 13 — (2 x + 2) = 2 ( x + 2) + 3 x
11. 2 [3 x + 4 (3 — x )] = 3 (5 — 4 x ) — 11
12. 3 [ x — 2 (3 x — 4)] + 15 = 5 — [2 x — (3 + x )] — 11
13. 7 (5 x — 2) = 6 (6 x — 1)
14. 3 (x + 5) = 2 (−6 — x) −2x

Предыдущий урок | Главная страница | Следующий урок

Решение систем неравенств — Бесплатная справка по математике

Сначала нам нужно рассмотреть символы неравенства:

• Символ <означает меньше чем.
• Символ> означает больше чем.
• Символ \ (\ leq \) означает меньше или равно. Обычно на компьютерах это пишется как <=, потому что это легче вводить.
• Символ \ (\ geq \) означает больше или равно. Иногда на компьютерах это пишется как> =, потому что это легче вводить.

Есть бесконечные решения для неравенства. В свете этого факта может быть проще всего найти набор решений для неравенств, решив систему графически.

Как решить системы неравенств графически

1) Запишите неравенство в форме пересечения наклона или в форме \ (y = mx + b \).

Например, если вас попросят решить \ (x + y \ leq 10 \), мы сначала перепишем как \ (y \ leq -x + 10 \).

2) Временно замените данный символ неравенства (в данном случае \ (\ leq \)) на просто равный символ. При этом вы можете рассматривать неравенство как уравнение. НО НЕ забудьте заменить символ равенства на исходный символ неравенства в КОНЕЦ задачи!

Итак, \ (y \ leq -x + 10 \) на данный момент становится \ (y = -x + 10 \).

3) Изобразите линию, найденную на шаге 2. Это сформирует «границу» неравенства — с одной стороны линии условие будет истинным, с другой — нет. Посмотрите, как построить линию здесь.

4) Вернемся к найденному ранее неравенству как \ (y \ leq -x + 10 \). Обратите внимание, что это верно, когда y меньше или равно. На шаге 3 мы построили линию (случай равенства), поэтому теперь нам нужно учесть случай «меньше». Поскольку y меньше определенного значения в нижней части оси, мы закрасим область под линией, чтобы указать, что неравенство верно для всех точек ниже линии:

5) Проверить.Вставьте точку не на линии, например (0,0). Убедитесь, что неравенство выполнено. В данном случае это означает \ (0 \ leq -0 + 10 \), что явно верно. Мы заштриховали правильную сторону линии.

Пример:

Найдите все значения x и y, которые удовлетворяют: \ (y \ geq \ frac {-3} {2} x + 6 \).

Обратите внимание, что это неравенство уже имеет форму пересечения наклона. Я заменю данный символ неравенства на символ равенства, чтобы построить линию.

\ (y \ geq \ frac {-3} {2} x + 6 \) становится \ (y = \ frac {-3} {2} x + 6 \).Теперь постройте эту линию, как показано:

Так как это случай, когда неравенство верно для значений y, которые больше или равны чему-то, мы закрасили область над линией. Все точки на этой линии графика или ВЫШЕ будут удовлетворять нашему неравенству. Снова выберите любую точку над линией графика, чтобы убедиться, что она удовлетворяет или раскрывает ИСТИННОЕ утверждение с точки зрения исходного неравенства. Например, (5,3). Подключите это, и у нас будет \ (3 \ geq \ frac {-3} {2} * 5 + 6 \). Упростив его до \ (3 \ geq -1.5 \), мы увидим, что неравенство выполняется в точке (5,3).Поскольку эта точка находилась над нашей линией, она должна быть заштрихована, что подтверждает наше решение.

Множественные неравенства — система неравенств

Система неравенств содержит более одного условия неравенства, которое должно быть выполнено. Графически это означает, что нам нужно сделать то, что мы только что сделали — построить линию, представленную каждым неравенством, — а затем найти область графика, которая верна для ОБОИХ неравенств. Для двух приведенных выше примеров мы можем объединить оба графика и построить площадь, разделяемую двумя неравенствами.

Какой набор решений? Набор решений для ОБЕИХ неравенств будет ЛЮБОЙ ТОЧКОЙ, в которой ОБЕИ области закрашены вместе или где встречаются ОБЕ заштрихованные области.

Первоначально принадлежит г-ну Фелизу, © 2005

Алгебра — линейные уравнения

Решите каждое из следующих уравнений.

Показать обсуждение

В следующих задачах мы подробно опишем первую проблему и оставим большую часть объяснений нижеприведенных проблем.

a \ (3 \ left ({x + 5} \ right) = 2 \ left ({- 6 — x} \ right) — 2x \) Показать решение

Для этой задачи нет дробей, поэтому нам не нужно беспокоиться о первом этапе процесса. На следующем шаге нужно упростить обе стороны. Итак, мы уберем все скобки, умножив числа, а затем объединим похожие термины.

\ [\ begin {align *} 3 \ left ({x + 5} \ right) & = 2 \ left ({- 6 — x} \ right) — 2x \\ 3x + 15 & = — 12 — 2x — 2x \\ 3x + 15 & = — 12 — 4x \ end {align *} \]

Следующий шаг — получить все \ (x \) с одной стороны и все числа с другой.С какой стороны идти \ (x \) — решать вам и, вероятно, будет зависеть от проблемы. Как правило, мы обычно помещаем переменные в ту сторону, которая дает положительный коэффициент. Это делается просто потому, что часто легко потерять знак минус на коэффициенте, и поэтому, если мы убедимся, что он положительный, нам не нужно об этом беспокоиться.

Итак, для нашего случая это будет означать прибавление 4 \ (x \) к обеим сторонам и вычитание 15 с обеих сторон. Также обратите внимание, что, хотя мы фактически выполняем эти операции в это время, мы обычно выполняем эти операции в нашей голове.

\ [\ begin {align *} \ require {color} 3x + 15 & = — 12 — 4x \\ 3x + 15 {\ color {Red} — 15} {\ color {Blue} + 4x} & = — 12 — 4x {\ color {Blue} + 4x} {\ color {Red} — 15} \\ 7x & = — 27 \ end {align *} \]

На следующем этапе нужно получить коэффициент 1 перед \ (x \). В этом случае мы можем сделать это, разделив обе стороны на 7.

\ [\ begin {align *} \ frac {{7x}} {7} & = \ frac {{- 27}} {7} \\ x & = — \ frac {{27}} {7} \ end { выровнять*}\]

Итак, если мы выполнили всю нашу работу правильно, \ (x = — \ frac {{27}} {7} \) является решением уравнения.

Последний и последний шаг — проверить решение. Как указано в схеме процесса, нам нужно проверить решение в исходном уравнении . Это важно, потому что мы могли сделать ошибку на самом первом шаге, и если мы сделали, а затем проверили ответ в результатах этого шага, может показаться, что решение верное, хотя в действительности мы этого не делаем. У меня нет правильного ответа из-за ошибки, которую мы сделали изначально.? 2 \ left ({- \ frac {{15}} {7}} \ right) + \ frac {{54}} {7} \\ \ frac {{24}} {7} & = \ frac {{24 }} {7} \ hspace {0.5in} {\ mbox {OK}} \ end {align *} \]

Итак, мы выполнили свою работу правильно и решение уравнения:

\ [x = — \ frac {{27}} {7} \]

Обратите внимание, что здесь мы не использовали обозначение набора решений. Для отдельных решений мы редко будем делать это в этом классе. Однако, если бы мы хотели, чтобы обозначение набора решений для этой проблемы было бы

\ [\ left \ {{- \ frac {{27}} {7}} \ right \} \]

Прежде чем перейти к следующей задаче, давайте сначала кратко прокомментируем «беспорядок» этого ответа.НЕ ожидайте, что все ответы будут красивыми простыми целыми числами. Хотя мы стараемся, чтобы большинство ответов были простыми, часто они не будут таковыми, поэтому НЕ зацикливайтесь на идее, что ответ должен быть простым целым числом, что вы сразу же предполагаете, что вы сделали ошибку из-за «беспорядка» ответ.

b \ (\ displaystyle \ frac {{m — 2}} {3} + 1 = \ frac {{2m}} {7} \) Показать решение

Хорошо, с этим мы не будем так подробно объяснять проблему.

В этом случае у нас есть дроби, поэтому, чтобы облегчить нашу жизнь, мы умножим обе части на ЖК-дисплей, который в данном случае равен 21. После этого проблема будет очень похожа на предыдущую. Также обратите внимание, что знаменатели — это только числа, поэтому нам не нужно беспокоиться о делении на ноль.

Давайте сначала умножим обе стороны на ЖК-дисплей.

\ [\ begin {align *} 21 \ left ({\ frac {{m — 2}} {3} + 1} \ right) & = \ left ({\ frac {{2m}} {7}} \ right ) 21 \\ 21 \ left ({\ frac {{m — 2}} {3}} \ right) + 21 \ left (1 \ right) & = \ left ({\ frac {{2m}} {7} } \ right) 21 \\ 7 \ left ({m — 2} \ right) + 21 & = \ left ({2m} \ right) \ left (3 \ right) \ end {align *} \]

Будьте осторожны, чтобы правильно распределить 21 в скобках с левой стороны.Все, что находится в скобках, нужно умножить на 21, прежде чем мы упростим. На данный момент у нас есть проблема, аналогичная предыдущей, и на этот раз мы не будем утруждать себя ее объяснениями.

\ [\ begin {align *} 7 \ ​​left ({m — 2} \ right) + 21 & = \ left ({2m} \ right) \ left (3 \ right) \\ 7m — 14 + 21 & = 6m \\ 7m + 7 & = 6m \\ m & = — 7 \ end {align *} \]

Итак, похоже, \ (m = — 7 \) — это решение.2} — 6 \ left (5 \ right) + 9}} \\ \ frac {5} {4} & = \ frac {5} {4} \ hspace {0.5in} {\ mbox {OK}} \ end {выровнять*}\]
d \ (\ displaystyle \ frac {{2z}} {{z + 3}} = \ frac {3} {{z — 10}} + 2 \) Показать решение

В этом случае ЖК-дисплей выглядит как \ (\ left ({z + 3} \ right) \ left ({z — 10} \ right) \), и также похоже, что нам нужно избегать \ (z = — 3 \) и \ (z = 10 \), чтобы не получить деление на ноль.

Приступим к работе над этой проблемой.2} — 7z — 30} \ right) \ end {align *} \]

На этом этапе давайте сделаем паузу и подтвердим, что у нас в работе есть z ² . 2}}} — 14z — 60 \ \ — 20z & = — 11z — 51 \\ 51 & = 9z \\ \ frac {{51}} {9} & = z \\ & \ frac {{17}} {3} = z \ end {align * } \]

Обратите внимание, что z ² фактически аннулировал.? 3 \ left ({- \ frac {3} {{13}}} \ right) + 2 \\ \ frac {{17}} {{13}} & = \ frac {{17}} {{13}} \ hspace {0,5 дюйма} {\ mbox {OK}} \ end {align *} \]

Иногда проверка может быть немного запутанной, но это означает, что мы ЗНАЕМ, что решение правильное.

.

No related posts.