Практическая работа № 2. Получение и свойства соединений металлов (Практическая работа № 4. Качественные реакции на ионы металлов)
Задание 1
В математике действует правило — «от перемены мест слагаемых сумма не изменяется». Справедливо ли оно для химии? Проверьте это на примере следующего опыта.
Получите гидроксид алюминия по реакции обмена и докажите его амфотерный характер. Для этого вы можете использовать реакцию, уравнение которой
Проведите эту реакцию в двух вариантах, используя в каждом варианте одинаковые объемы исходных веществ: сначала к раствору одного из исходных веществ (реагенту) прибавляйте по каплям раствор другого реагента, затем поменяйте последовательность введения в реакцию реагентов. Наблюдайте, в каком случае выпадет осадок, а в каком — нет.
Объясните результаты и запишите уравнения проведенных реакций в молекулярной и ионной формах.
Задание 1.
Задание 2
Проведите реакции, подтверждающие качественный состав хлорида кальция. Запишите уравнения реакций в молекулярной и ионной формах.
Задание 2.
Задание 3
Осуществите превращения согласно следующей схеме1:
1 Для осуществления второго превращения используйте хлорную воду.
Напишите уравнения соответствующих реакций и рассмотрите их с позиций окисления-восстановления. Проведите качественные реакции, подтверждающие наличие продуктов реакций. Запишите уравнения реакций в молекулярной и ионной формах.
Задание 3.
Задание 4
Получите сульфат железа (II) не менее чем тремя способами. Уравнения реакций ионного обмена запишите в ионной и молекулярной формах, а реакции замещения рассмотрите с позиций окисления-восстановления.
Задание 4.
Задание 5
Проведите реакции, подтверждающие качественный состав сульфата железа (II). Запишите уравнения соответствующих реакций в молекулярной и ионной формах.
Задание 5.
5terka.com
|
Что делали |
Что наблюдали |
Уравнение реакции |
|
1. 1)В пробирку с раствором хлорида алюминия добавим по каплям раствор щелочи
2) В другую пробирку с раствором щелочи добавим раствор хлорида алюминия.
Только, после добавления избытка А1С13 выпадет осадок А1(ОН)3. 3)Докажем амфотерный характер А1(ОН)3. Для этого, полученный осадок А1(ОН)
|
Наблюдаем образование белого осадка гидроксида алюминия.
В данном случае, щелочь присутствует в избытке, поэтому А1(ОН)3 в начале не образуется, идет образование алюмината натрия
В обоих случаях наблюдаем растворение осадка гидроксида алюминия; Гидроксид алюминия растворяется, как в кислотах, так и в щелочах, поэтому он амфотерен |
А1С13 + 3NaOH(недостаток) = 3NaCl + Al(OH)3↓ Al3+ + 3Сl— + 3Na+ + 3ОН— = А1(ОН)3↓ + 3Na+ + 3Сl— А13+ + 3ОН— = Al(OH)3↓ А1С13 + 4NaOH(избыток) = NaA1О2 + 3NaCl + 2Н2О А13+ + 3Сl— + 4Na+ + 40Н— = Na++А1О2—+ 3Na+ + 3Сl—+ 2Н2О А13+ + 4ОН— = А1О2— + 2Н2О
А1(ОН)3 + 3НС1 = А1С13 + 3Н2О А1(ОН)3 +3Н++3Сl— = А13+ +3Сl—+ 3Н2О А1(ОН)3 +3Н+=А13+ + 3Н2О
А1(ОН)3 +NaOH = NaA1О2 + 2Н2О А1(ОН)3 + Na++ОН— = Na+ +А102— +2Н2О А1(ОН)3 + ОН— = А1О2— + 2Н2О |
|
2. Для доказательства качественного состава СаС12 проведем реакции, характерные для катиона кальция и хлорид-аниона. Для этого раствор СаС12 разольем на 2 пробирки. В одну из них добавим раствор карбоната натрия,
В другую пробирку прильем раствор нитрата серебра
|
Наблюдаем выделение белого осадка карбоната кальция СаСО3
Наблюдаем выделение белого творожистого осадка.
|
Na2CО3 + СаС12 = CaCО3↓ + 2NaCl 2Na+ + СО32- + Са2+ + 2Сl— = СаСО 3↓ + Na+ + 2Сl— Са2+ + СО32- = CaCО3↓ СаС12 + 2AgNО3 = Ca(NО3)2 + 2AgCl↓ Са2+ + 2Сl— +2Ag+ + 2NО3— = Ca2++ 2NО3— + 2AgCl↓ Сl— +Ag+ = AgCl↓ |
|
3. Необходимо осуществить следующие превращения:Fe → FeCI2 → FeCl3 В пробирку с железными опилками добавим раствор соляной кислоты.
Качественная реакция на ион железа (II):
Качественные реакции на ион железа (III): а) Прильем к пробирке раствор желтой кровяной соли:
|
Наблюдаем растворение железа и выделение газообразного водорода
Наблюдаем, образование темно-синего осадка, следовательно, ионы Fe2+ получены.
Наблюдаем, образование темно-синего осадка берлинской лазури, значит, в растворе присутствуют ионы железа (III). |
Fe0 + 2Н+С1 = Fe2+Cl2 + Н20↑ Fe0 — 2е = Fe2+ 2 1 восстановитель 2Н+ +2е = Н20 2 1 окислитель
K3[Fe+3(CN)6] + Fe+2C12 = 2КС1 + KFe+3[Fe+2(CN)6] красная кровяная соль 3К++[Fe(CN) 6]3-+Fe2+ +2Сl— =KFe [Fe(CN)6]↓+2K++ 3Сl— K+ + Fe2+ + [Fe(CN)6]3— = KFe [Fe(CN)6]↓
K4[Fe+2(CN)6] + Fe+3C13 = 3KCI + KFe+3lFe+2(CN)6]↓ желтая кровяная соль берлинская лазурь 4К+ + Fe3++3Сl— +[Fe(CN)6]4-=KFe [Fe(CN)6]↓+3K+ + 3Сl— К+ + Fe3+ + [Fe(CN)6]4- = KFe [Fe(CN)6]↓ |
|
Необходимо получить FeSO4 тремя различными способами: В пробирку с железными опилками прильем разбавленный раствор серной кислоты.
В пробирку с раствором медного купороса добавим железо.
|
Наблюдаем растворение железа и выделение водорода В результате реакции образуется сульфат железа.
Наблюдаем, изменение окраски раствора, из голубого раствор становится светло-зеленым, который быстро желтеет и мутнеет. В результате реакции выделяется красная медь. |
Fe° + H2+‘S04 -» Fe+2S04 + H2°↑
Cu2+SO4 + Fe° = Fe+2SO4 + Cu0↓ Голубой светло-зеленый красный Fe° -2е= Fe2+ восстановитель |
|
4. Для получения FeSО 4 осуществим следующие превращения: FeCl2→ Fe(OH)2 → FeSО4 К раствору хлорида железа прильем раствор щелочи:
К полученному, в предыдущем опыте осадку Fe(OH)2 добавим раствор серной кислоты |
В результате реакции образуется осадок гидроксида железа (II) белого цвета.
|
FeCl2 + 2NaOH = 2NaCl + Fe(OH)2↓ Fe2+ + 2Сl— + 2Na+ + 2ОH— = 2Na+ + 2Сl— + Fe(OH)2↓ Fe2+ + 2ОH— = Fe(ОH)2↓
Fe(OH)2 + H2SО4 = FeSО4 + 2Н2О Fe(OH)2 + 2Н+ + SО42- = Fe Fe(OH)2 + 2H+ = Fe2+ + 2H2О |
|
5. Для доказательства качественного состава FeSО4 разольем раствор сульфата железа в 2 пробирки. В одну из них добавим раствор красной кровяной соли:
В другую пробирку, добавим раствор хлорида бария:
|
Наблюдаем, образование темно-синего осадка, значит, в растворе присутствуют ионы железа — Fe2+.
Наблюдаем, выделение белого осадка сульфата бария BaSО4, значит, в растворе присутствуют сульфат-ионы SО42-.
|
K3[Fe+3(CN)6] + FeS04 = K2S04 + KFe [Fe(CN)6]↓ красная кровяная соль
FeSO4 + ВаС12 = FeCl2 + BaS04↓ Fe2+ + SO42- + Ba2+ + 2Сl— = Fe2+ + 2Сl— + BaSO4↓ Ba2+ + SO42- = BaSO4↓
|
uchkopilka.ru
Практическая работа №2 — МегаЛекции
Класс
Практическая работа №2
Получение и свойства соединений металлов
Вариант 1
Инструктаж по технике безопасности.
Цель работы: Опытным путем доказать амфотерность гидроксида алюминия Al(OH)3. Доказать качественный состав хлорида кальция CaCl2.
Оборудование: Штатив с пробирками.
Реактивы: Хлорид алюминия AlCl3, гидроксид натрия NaOH, соляная кислота HCl, хлорид кальция CaCl2, карбонат натрия Na2CО3, нитрат серебра AgNO3.
Ход работы
Задание 1.Получите гидроксид алюминия по реакции обмена и докажите его амфотерный характер.
Видеоопыт:http://files.school-collection.edu.ru/dlrstore/cab570ce-c96f-d970-853e-1b0a8caabb45/index.htm
Для этого к раствору хлорида алюминия приливайте по каплям раствор гидроксида натрия, затем полученный осадок разделите на две пробирки; к одной добавьте раствор соляной кислоты, к другой — гидроксида натрия. Определите: зависит ли результат реакции от порядка сливания реагентов. Для этого поменяйте последовательность введения в реакцию реагентов: к раствору гидроксида натрия приливайте раствор хлорида алюминия. Заполните таблицу.
| № опыта | Уравнения реакций в молекулярном и ионном виде | Наблюдения |
| AlCl3 + NaOH = недостаток | ||
| Al(OH)3 + HCl = | ||
| Al(OH)3 + NaOH = | ||
| NaOH + AlCl3 = избыток |
Вывод: Сформулируйте вывод самостоятельно, ответив на вопросы. В математике действует правило — «от перемены мест слагаемых сумма не изменяется». Справедливо ли оно для химии? Почему? Доказали ли мы с помощью проведенных реакций, что гидроксид алюминия – амфотерное соединение? Почему?
Задание 2. Докажите качественный состав хлорида кальция CaCl2.
Видеоопыт: http://files.school-collection.edu.ru/dlrstore/cabb0eeb-0751-b19b-e602-5c9acbec92b2/index.htm
Для доказательства качественного состава СаС12 проведите реакции, характерные для катиона кальция и хлорид-аниона. Для этого раствор СаС12 разлейте на 2 пробирки. В одну из них добавьте раствор карбоната натрия, а в другую пробирку прилейте раствор нитрата серебра. Заполните таблицу.
| № опыта | Уравнения реакций в молекулярном и ионном виде | Наблюдения |
| CaCl2 + Na2CО3 = | ||
| CaCl2 + AgNO3 = |
Вывод: Сформулируйте вывод самостоятельно, ответив на вопросы. Какое вещество служит реактивом для обнаружения Са2+? Какое вещество служит реактивом для обнаружения Сl—?
Класс
Практическая работа №2
Получение и свойства соединений металлов
Вариант 2
Инструктаж по технике безопасности.
Цель работы: Опытным путем доказать амфотерность гидроксида алюминия Al(OH)3. Доказать качественный состав сульфата желаза(II)FeSO4.
Оборудование: Штатив с пробирками.
Реактивы: Хлорид алюминия AlCl3, гидроксид натрия NaOH, соляная кислота HCl, сульфат железа(II) FeSO4, хлорид бария BaCl2, красная кровяная соль K3[Fe(CN)6].
Ход работы
Задание 1.Получите гидроксид алюминия по реакции обмена и докажите его амфотерный характер.
Видеоопыт:http://files.school-collection.edu.ru/dlrstore/cab570ce-c96f-d970-853e-1b0a8caabb45/index.htm
Для этого к раствору хлорида алюминия приливайте по каплям раствор гидроксида натрия, затем полученный осадок разделите на две пробирки; к одной добавьте раствор соляной кислоты, к другой — гидроксида натрия. Определите: зависит ли результат реакции от порядка сливания реагентов. Для этого поменяйте последовательность введения в реакцию реагентов: к раствору гидроксида натрия приливайте раствор хлорида алюминия. Заполните таблицу.
| № опыта | Уравнения реакций в молекулярном и ионном виде | Наблюдения |
| AlCl3 + NaOH = недостаток | ||
| Al(OH)3 + HCl = | ||
| Al(OH)3 + NaOH = | ||
| NaOH + AlCl3 = избыток |
Вывод: Сформулируйте вывод самостоятельно, ответив на вопросы. В математике действует правило — «от перемены мест слагаемых сумма не изменяется». Справедливо ли оно для химии? Почему? Доказали ли мы с помощью проведенных реакций, что гидроксид алюминия – амфотерное соединение? Почему?
Задание 2. Докажите качественный состав сульфата желаза(II) FeSO4.
Видеоопыты:1)http://files.school-collection.edu.ru/dlrstore/9d3df838-d4d4-c17b-be58-7558b90c827d/index.htm2)http://files.school-collection.edu.ru/dlrstore/d8932e1e-fc13-f1de-2ace-288cbf49a4db/index.htm
Для доказательства качественного состава FeSO4 проведите реакции, характерные для катиона железа Fe2+ и сульфат-аниона. Для этого раствор FeSO4 разлейте на 3 пробирки. В одну из них добавьте красную кровяную соль – гексацианоферрат(III) калия K3[Fe(CN)6], в другую — щелочь (NaOH), а в третью прилейте раствор хлорида бария BaCl2. Заполните таблицу.
| № опыта | Уравнения реакций в молекулярном и ионном виде | Наблюдения |
| FeSO4 + К3[Fe(CN)6] = | ||
| FeSO4 + NaOH = | ||
| FeSO4 + BaCl2 = |
Вывод: Сформулируйте вывод самостоятельно, ответив на вопросы. Какие вещества служит реактивом для обнаружения Fe2+? Какое вещество служит реактивом для обнаружения SO42—?
Класс
Практическая работа №2
Рекомендуемые страницы:
Читайте также:
Воспользуйтесь поиском по сайту:
megalektsii.ru
ГДЗ по химии для 9 класса О.С. Габриелян
- ГДЗ
- 1 Класс
- Математика
- Английский язык
- Русский язык
- Немецкий язык
- Информатика
- Природоведение
- Основы здоровья
- Музыка
- Литература
- Окружающий мир
- Человек и мир
- 2 Класс
- Математика
- Английский язык
- Русский язык
- Немецкий язык
- Белорусский язык
- Украинский язык
- Информатика
- Природоведение
- Основы здоровья
- Музыка
- Литература
- Окружающий мир
- Человек и мир
- Технология
- 3 Класс
- Математика
- Английский язык
- Русский язык
- Немецкий язык
- Белорусский язык
- Украинский язык
- Информатика
- Музыка
- Литература
- Окружающий мир
- Человек и мир
- Испанский язык
- 4 Класс
- Математика
- Английский язык
- Русский язык
- Немецкий язык
- Белорусский язык
resheba.me
Практические работы по математике для студентов 2 курса
Математика 2 курс
Практическая работа № 8.
Тема: Вычисление объемов тел вращения.
Цель: Отработать навыки нахождения определенного интеграла. Научиться находить объемы тел вращения.
Теоретический материал
Вычисление объема тела по известным площадям поперечных сечений.
Если площадь сечения тела плоскостью, перпендикулярной оси Ox, может быть выражена как функция от x, т.е. в виде , то объем части тела, заключенной между перпендикулярными оси Ox плоскостями x = a и x = b, находится по формуле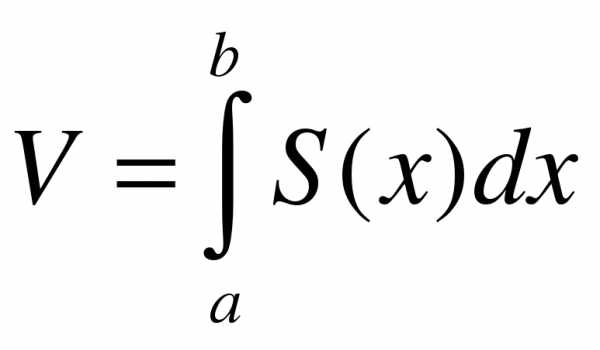 
.
Вычисление объема тела вращения.
Если криволинейная трапеция, ограниченная кривой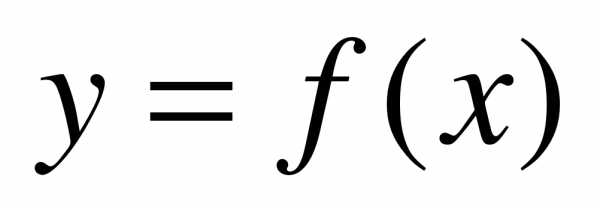 
и прямыми у = 0, х = а, x = b вращается вокруг оси Ox, то объем тела вращения вычисляется по формуле
.
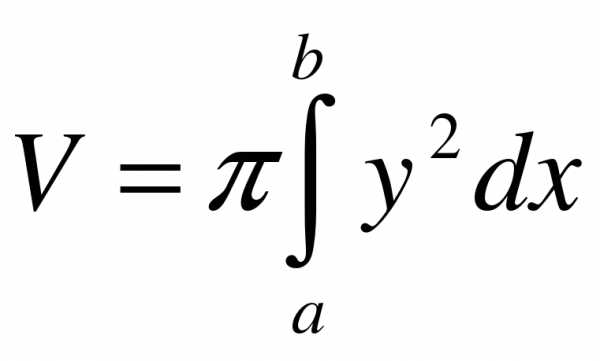Если фигура, ограниченная кривыми и и прямыми x = a, x = b, вращается вокруг оси Ox, то объем тела вращения вычисляется по формуле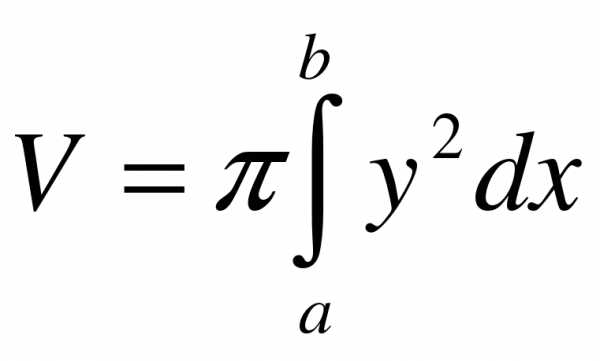 
.
Примеры.
Пример 1. Вычислить объем тела, полученного при вращении вокруг оси абсцисс фигуры, ограниченной линиями у = 2х + 1, у = х + 4, х=0 и х=1.
Р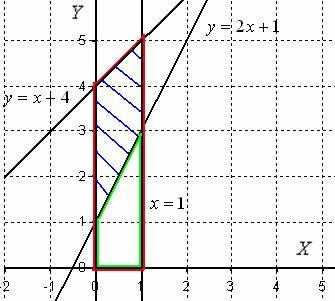
ешение: Изобразим на чертеже плоскую фигуру, ограниченную линиями у = 2х + 1, у = х + 4, х = 0 и х = 1, не забывая при этом, что уравнение х = 0 задает ось Оу.
Искомая фигура заштрихована синим цветом. Объем тела вращения вычислим как разность объемов тел.
Сначала рассмотрим фигуру, которая обведена красным цветом. При её вращении вокруг оси Ох получается усеченный конус. Обозначим объем этого усеченного конуса через V1.
Рассмотрим фигуру, которая обведена зеленым цветом. Если вращать данную фигуру вокруг оси Ох, то получится тоже усеченный конус, только чуть поменьше. Обозначим его объем через V2.
И, очевидно, разность объемов V = V1 – V2 – в точности объем искомой фигуры.
Используем формулу для нахождения объема тела вращения: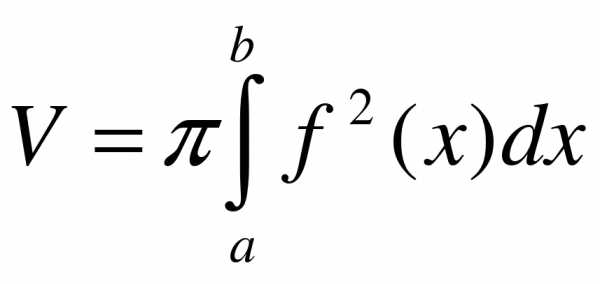 
1) Фигура, обведенная красным цветом ограничена сверху прямой y = x + 4, поэтому: .
2) Фигура, обведенная зеленым цветом ограничена сверху прямой y = 2x + 1, поэтому: .
3) Объем искомого тела вращения: .
Ответ: .
Пример 2. Вычислить объем тела, образованного вращением относительно оси Ox плоской фигуры, ограниченной линиями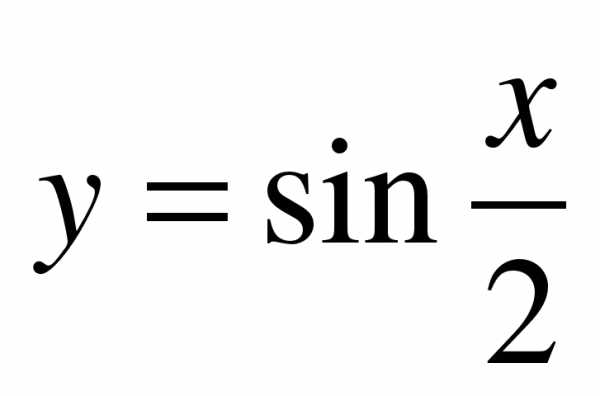 
, 
, где 
.
Р
ешение: Выполним чертеж:
Объем тела вращения вычислим как разность объемов при помощи формулы: 
.
В данном случае:
Ответ: V = π ед3. ≈ 3,14 ед3.
Пример 3. Дана плоская фигура, ограниченная линиями 
, 
, 
.
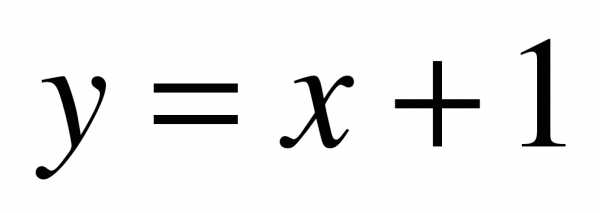1) Найти площадь плоской фигуры, ограниченной данными линиями.
2) Найти объем тела, полученного вращением плоской фигуры, ограниченной данными линиями, вокруг оси Оу.
Решение: Задача состоит из двух частей. Начнем с площади.
1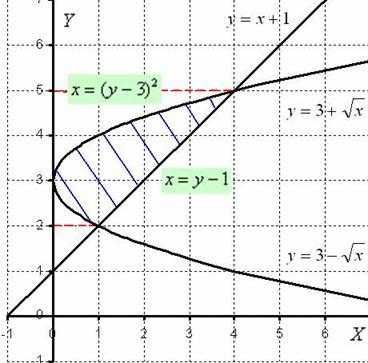
) Выполним чертёж:
Легко заметить, что функция задает верхнюю ветку параболы, а функция – нижнюю ветку параболы.
Нужная фигура, площадь которой предстоит найти, заштрихована синим цветом.
Применим более рациональный путь решения: он состоит в переходе к обратным функциям и интегрированию по оси Оу.
Для параболы:
Для прямой:
Теперь смотрим на ось Оу.
пожалуйста, периодически наклоняйте голову вправо на 90 градусов по ходу объяснений!
Нужная нам фигура лежит на отрезке [2; 5], который обозначен красным пунктиром. При этом на отрезке [2; 5] прямая х = у — 1 расположена выше параболы , а значит, площадь фигуры следует найти по формуле: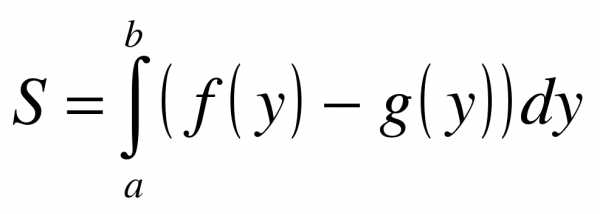 
.
! Примечание: Пределы интегрирования по оси Оу следует расставлять строго снизу вверх!
Находим площадь:
На отрезке [2; 5] , поэтому:
.
Ответ: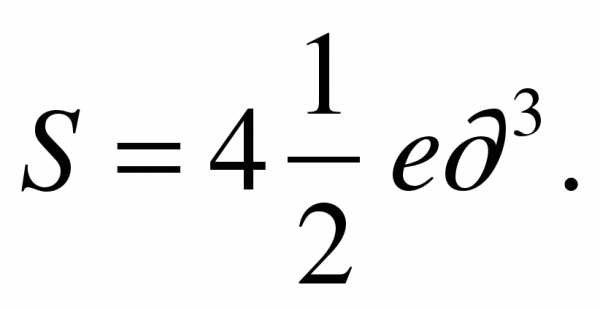 
2) Вычислим объем тела, образованного вращением данной фигуры, вокруг оси Оу.
Перерисую чертеж немного в другом оформлении.
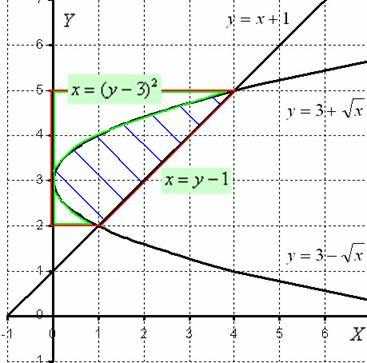
Итак, фигура, заштрихованная синим цветом, вращается вокруг оси Оу. В результате получается «зависшая бабочка», которая вертится вокруг своей оси.
Для нахождения объема тела вращения будем интегрировать по оси Оу.
Очевидно, что объем тела вращения, следует найти как разность объемов.
Вращаем фигуру, обведенную красным цветом, вокруг оси Оу, в результате получается усеченный конус. Обозначим этот объем через V1.
Вращаем фигуру, обведенную зеленым цветом, вокруг оси Оу и обозначаем через V2 объем полученного тела вращения.
Объем нашей «бабочки» равен разности объемов V = V1 – V2.
Используем формулу для нахождения объема тела вращения: 
.
Ответ:
Пример 4. Плоская фигура ограничена графиком параболы .Вычислить объем тела вращения.
Решение: Вычислим объем тела вращения, используя данную формулу:
.
Ответ:
Пример 5. Найти объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной линиями 2х – у – 2 = 0, у=0, х=3.
Решение: Выполним чертеж. Объем тела вращения:
Ответ:
Пример 6. Дана плоская фигура, ограниченная линиями x = 2, и осью Ox.
a) Перейти к обратным функциям и найти площадь плоской фигуры, ограниченной данными линиями, интегрированием по переменной y.
б) Вычислить объем тела, полученного вращением плоской фигуры, ограниченной данными линиями, вокруг оси Оу.
Р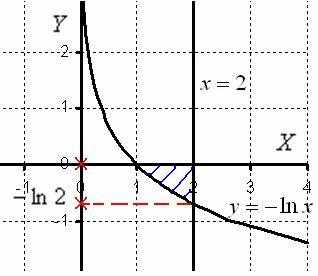
ешение:
1) Выполним чертёж.
Перейдем к обратной функции:
На отрезке [- ln 2; 0] 2 ≥ e—y, поэтому:
Ответ:
2) Вычислим объем тела, образованного вращением данной фигуры, вокруг оси Oy.
Объем тела вращения найдем как разность объемов тел вращения при помощи формулы :
Ответ:
Задания для самостоятельной работы по теме:
Вариант 1.
2. Найти объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной линиями 2х – у – 2 = 0, у=0, х=7. 3. Дана плоская фигура, ограниченная линиями x = 4, и осью Ox. a) Перейти к обратным функциям и найти площадь плоской фигуры, ограниченной данными линиями, интегрированием по переменной y. б) Вычислить объем тела, полученного вращением плоской фигуры, ограниченной данными линиями, вокруг оси Оу. | Вариант 2. 1. Плоская фигура ограничена графиком параболы .Вычислить объем тела вращения. 2. Вычислить объем тела, образованного вращением относительно оси Ox плоской фигуры, ограниченной линиями 3. Дана плоская фигура, ограниченная линиями , , . 1) Найти площадь плоской фигуры, ограниченной данными линиями. 2) Найти объем тела, полученного вращением плоской фигуры, ограниченной данными линиями, вокруг оси Оу. |
Вариант 3. 1. Плоская фигура ограничена графиком параболы .Вычислить объем тела вращения. 2 Дана плоская фигура, ограниченная линиями , , . 1) Найти площадь плоской фигуры, ограниченной данными линиями. 2) Найти объем тела, полученного вращением плоской фигуры, ограниченной данными линиями, вокруг оси Оу. 3. Вычислить объем тела, образованного вращением относительно оси Ox плоской фигуры, ограниченной линиями | Вариант 4. 1. Плоская фигура ограничена графиком параболы .Вычислить объем тела вращения. 2 Дана плоская фигура, ограниченная линиями , , . 3. Дана плоская фигура, ограниченная линиями x = 3, и осью Ox. a) Перейти к обратным функциям и найти площадь плоской фигуры, ограниченной данными линиями, интегрированием по переменной y. б) Вычислить объем тела, полученного вращением плоской фигуры, ограниченной данными линиями, вокруг оси Оу. |
Вариант5. 1. Плоская фигура ограничена графиком параболы .Вычислить объем тела вращения. 2. Найти объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной линиями 2х – у – 2 = 0, у=0, х=7 3. Дана плоская фигура, ограниченная линиями x = 6, и осью Ox. a) Перейти к обратным функциям и найти площадь плоской фигуры, ограниченной данными линиями, интегрированием по переменной y. б) Вычислить объем тела, полученного вращением плоской фигуры, ограниченной данными линиями, вокруг оси Оу. | Вариант6. 1. Плоская фигура ограничена графиком параболы .Вычислить объем тела вращения. 2. Вычислить объем тела, образованного вращением относительно оси Ox плоской фигуры, ограниченной линиями 2 Дана плоская фигура, ограниченная линиями , , . 1) Найти площадь плоской фигуры, ограниченной данными линиями. 2) Найти объем тела, полученного вращением плоской фигуры, ограниченной данными линиями, вокруг оси Оу. |
kopilkaurokov.ru
Практическая работа № 3(3). Экспериментальные задачи по распознаванию и получению веществ
В выданных вам трех пробирках (варианты 1, 2 или 3) содержатся твердые вещества, а в трех других (вариант 4) растворы веществ.
Опытным путем определите, в какой пробирке находится каждое из выданных вам веществ. Напишите уравнения соответствующих реакций в молекулярном и ионном видах.
После этой части работы выполните одну-две экспериментальные задачи из следующего перечня (по указанию учителя).
Вариант 1
а) гидроксид натрия;
б) карбонат калия;
в) хлорид бария.
Вариант 1.
Вариант 2
а) карбонат кальция;
б) сульфат натрия;
в) хлорид калия.
Вариант 2.
Вариант 3
а) нитрат бария;
б) сульфат натрия;
в) карбонат кальция.
Вариант 3.
Вариант 4
а) хлорид натрия;
б) хлорид алюминия;
в) хлорид железа (III).
Вариант 4.
Задача 1
Докажите опытным путем, что железный купорос, образец которого вам выдан, содержит примесь сульфата железа (III). Напишите уравнения соответствующих реакций в молекулярном и ионном видах.
Задача 1.
Задача 2
Получите оксид железа (III), исходя из хлорида железа (III). Напишите уравнения соответствующих реакций, а уравнение реакции с участием электролита и в ионном виде.
Задача 2.
Задача 3
Получите раствор алюмината натрия, исходя из хлорида алюминия. Запишите уравнения проделанных реакций в молекулярном и ионном видах.
Задача 3.
Задача 4
Получите сульфат железа (II), исходя из железа. Запишите уравнения проделанных реакций и разберите окислительно-восстановительные процессы.
Задача 4.
5terka.com
Урок Excel Практическая работа №2
Практическая работа №2 – Нахождение значений функции
Задание 1. Адресация и вычисления. (4 балла)
Задание 2. Формат. (1 балл)
Задание 1. Адресация и вычисления
Постановка задачи:
Вычислить значения функции
для всех х на интервале [-2,2] с шагом 0,2 при k = 10.
Заполните основную и вспомогательную таблицы для расчетов, как показано на рис. 1.
Начальное значение x
Шаг
Рис. 1
1.2. Используя функцию автозаполнения, заполните столбец А числами от 1 до 21, начиная с ячейки А2 и заканчивая ячейкой А22 аналогично тому, как заполнили блок ячеек годами и датами в работе №1.
1.3. Адресация.
Заполните столбец B значениями x:
Это означает, что в ячейку В2 заносится значение из ячейки Н2 (начальное значение x), знак $ указывает на абсолютную адресацию.
Это означает, что в этой ячейке начальное значение x будет увеличено на величину шага, которая берется из ячейки I2.
Столбец заполнится значениями X от -2 до 2 с шагом 0,2.
1.4. Поместите в ячейку C2 формулу значение которой – адрес на коэффициент k (ячейка J2). Заполните этой формулой (выбрав предварительно необходимый тип адресации в ней) блок C3:C22.
1.5. Заполните столбец D значениями функции:
Столбец заполнился как положительными, так и отрицательными значениями функции y1. Проверьте – начальное значение 3 и конечное значение 3.
1.6. Аналогичным образом заполните столбец E значениями функции:
Проверьте – все значения положительные, начальное значение 3 и конечное значение 3.
1.7. Заполните столбец F значениями функции
Проверьте! Значения функции как положительные, так и отрицательные. Начальное значение 6. Конечное значение 6.
1.8. Теперь измените исходные значения в дополнительной таблице и посмотрите за изменениями в основной.
Покажите результат преподавателю.
Задание 2. Формат
Оформите внешний вид таблицы, как показано на рис. 2. Ниже – подробнее.
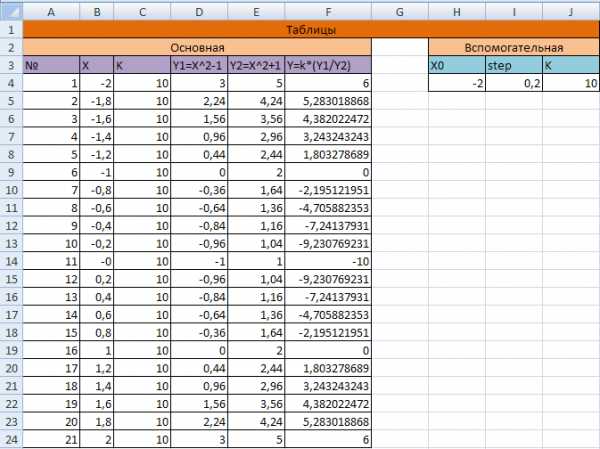
Рис. 2
2.1. Вставьте две пустые строки сверху:
ПКМ на первой строке → вставить → строку.
2.2. Объедините в первых двух строках требуемые ячейки (см. рис. 2):
Выделить нужные ячейки
Объединить ячейки
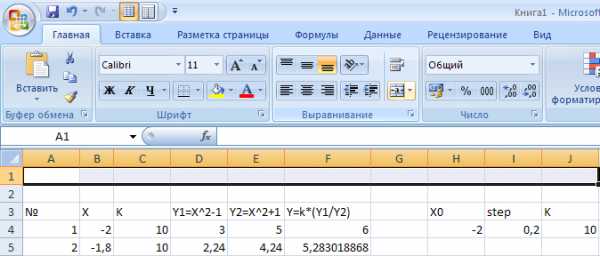
2.3. В полученные ячейки занесите заголовки таблиц (см. рис. 2).
2.4. Сделайте выделение у границ таблицы:
Выделить нужные ячейки, нажав клавишу Ctrl → ПКМ по выделенным ячейкам → Формат ячеек → Граница → Отметить «внешние» и «внутренние» → Ok.
2.4. Сделайте заливку ячеек таблицы (см. рис. 2):
Выделить нужные ячейки, нажав клавишу Ctrl → ПКМ по выделенным ячейкам → Формат ячеек → Заливка → Выбрать цвет → Ok.
2.5. Сохраните свою работу под именем work2_1 – она вам потребуется для дальнейших практических работ.
Покажите результат преподавателю.
videouroki.net