Ответы по геометрии 7 9 атанасян: ГДЗ по Геометрии за 7-9 класс: Атанасян. Решебник с пояснениями

Расположение точек на прямой. Вопрос 2 практическое задание § 1 Геометрия 7-9 класс Атанасян Л.С. – Рамблер/класс

Расположение точек на прямой. Вопрос 2 практическое задание § 1 Геометрия 7-9 класс Атанасян Л.С. – Рамблер/класс

Интересные вопросы

Школа

Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?

Новости

Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?

Школа

Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?

Школа

Когда в 2018 году намечено проведение основного периода ЕГЭ?

Новости

Будет ли как-то улучшаться система проверки и организации итоговых сочинений?

Вузы

Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?

Отметьте три точки А, В и С, не лежащие на одной прямой, и проведите прямые АВ, ВС и СА.

ответы

Вот как выглядит

 

ваш ответ

Можно ввести 4000 cимволов

отправить

дежурный

Нажимая кнопку «отправить», вы принимаете условия  пользовательского соглашения

похожие темы

Экскурсии

Мякишев Г.Я.

Досуг

Химия

похожие вопросы 5

Докажите, что треугольники подобны. Вопросы и задачи 64, Геометрия, 10-11 класс, Атанасян Л.С.

Привет. Запуталась при решении, нужна помощь знатоков!!!
 
Три прямые, проходящие через одну точку и не лежащие в одной (Подробнее…)

ГДЗГеометрия11 класс10 классАтанасян Л.С.

Самостоятельная работа 19. Вариант 2. № 2 ГДЗ Геометрия 9 класс Зив Б.Г. Помогите доказать, используя параллельный перенос

Используя параллельный перенос, докажите, что углы при основании равнобедренной трапеции равны между собой.

 

ГДЗЭкзаменыГеометрия9 классЗив Б. Г.

ГДЗ Тема 21 Физика 7-9 класс А.В.Перышкин Задание №476 Изобразите силы, действующие на тело.

Привет всем! Нужен ваш совет, как отвечать…
Изобразите силы, действующие на тело, когда оно плавает на поверхности жидкости. (Подробнее…)

ГДЗФизикаПерышкин А.В.Школа7 класс

Васильевых. 50 вариантов ответов по русскому языку. Вариант 31 ч.2 Задание 9 ОГЭ Русский язык 9 класс Однородные обособленные приложения

    Среди предложений 27-32: 
 
   (27) Нет-нет да и набирала Анюта, когда была дома одна и было грустно, Митрошин номер, и (Подробнее…)

ГДЗРусский языкОГЭ9 классВасильевых И.П.

ЕГЭ-2017 Цыбулько И. П. Русский язык ГДЗ. Вариант 13. 18. Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)…

18.
Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)
в предложении должна(-ы) стоять запятая(-ые). (Подробнее…)

ГДЗЕГЭРусский языкЦыбулько И.П.

«Исходные геометрические сведения», «Треугольник и окружность», «Параллельные прямые», «Треугольник. Соотношение углов и сторон»

Программа по геометрии наполнена разнообразной тематикой. Студентам необходимо усвоить огромное количество материала за короткий промежуток времени. Неудивительно, что в седьмом классе часто встречаются серьезные пробелы в знаниях, которые растут как снежный ком. Задача родителей и учителя – своевременно выявить и устранить проблемы в изучении материала.

ассистент

Элементы геометрия уже знакомый семиклассник в предыдущие годы обучения, когда математика включала в себя основы знаний по двум дисциплинам — алгебре и геометрии. Но теперь дело вышло на новый, предельно высокий уровень сложности. Помочь школьнику разобраться в нюансах предмета и надежно подготовиться к любым контрольным работам призвана качественная учебная литература — книга-решение к учебнику «Геометрия 7 класс Тесты Фаркова к экзамену по учебнику Атанасяна» .

Что такое пособие

Решебник не только подсказывает ученику правильный ответ, но и объясняет алгоритм решения, обучает правильному варианту записи упражнения. Кратко о содержании сборника тестов:

• Исходная геометрическая информация.
• Треугольники.
• Параллельные линии.
• Отношения между углами и сторонами треугольника.
• Прямоугольный треугольник.

Регулярная работа с пособием позволит школьнику усвоить этот сложный предмет и надежно подготовиться к контрольным работам на уроках.

Тест Параллельные прямые 7 класс (по учебнику

Атанасяна ). Пособие адресовано родителям, которые смогут проконтролировать правильность выполнения решения, а при необходимости помочь детям в реализации. домашнее задание по геометрии. Ответы на тест даны в конце статьи.

Контрольная работа рассчитана на одно занятие (45 минут) и позволяет проводить дифференцированный контроль знаний , так как задания распределяются по три уровня сложности А, Б и С. Уровень А соответствует обязательным требованиям к программному обеспечению, В — средний уровень сложности, В — для учащихся с повышенным интересом к математике, а также для использования в классах, школах, гимназии и лицеи с углубленным изучением математики. Для каждого уровня есть две эквивалентные опции, расположенные рядом.

Контрольная по геометрии 7 класс

«КА-3. ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ»

1. Контрольная работа по геометрии 7 класс. КА-3.

Вариант А1.
∠2 = 119°, ∠3 = 82°
а) Найти ∠4

2. Из точек А в В, лежащих по одну из сторон данного острого угла, проведены перпендикуляры АС и BD ко второй
а) Докажите, что AC||BD
б) Найдите ∠ABD, если ∠CAB = 125°
3. На сторонах AB и BC треугольника ABC отмечены точки D и E соответственно. Докажите, что если ∠BDE = ∠BAC, то ∠BED = ∠BCA.

Вариант A2
1. На этом рисунке ∠1 = 112°, ∠2 = 68°, ∠3 = 63°.
а) Найдите ∠4.
б) Сколько углов, равных ∠4, изображено на рисунке? Отметьте эти углы.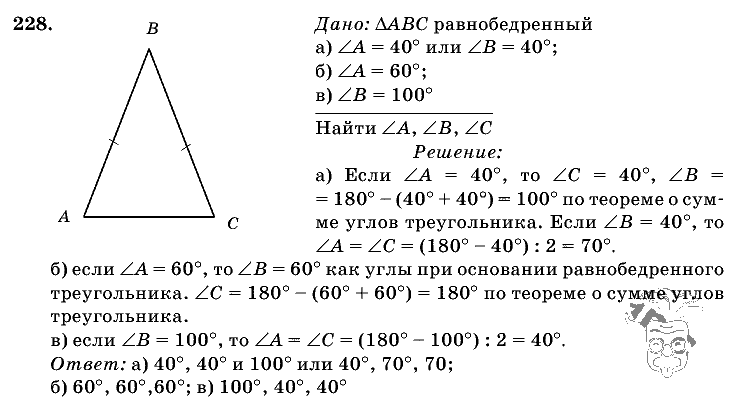
2. Из точек С и D, лежащих на одной из сторон данного острого угла, проводят перпендикуляры к этой стороне, пересекающие вторую сторону угла в точках А и В соответственно.
а) Докажите, что AC||BD.
б) Найдите ∠CAB, если ∠ABD = 55°.
3. На сторонах AB и BC треугольника ABC отмечены точки D и E соответственно. Докажите, что если ∠BED = ∠BCA, то ∠BDE = ∠BAC.

2. Контрольная работа по геометрии 7 класс. КА-3. Варианты В1 и В2.

3. Контрольная работа по геометрии 7 класс. КА-3. Варианты В1 и В2.

Тест Параллельные прямые 7 класс. ОТВЕТЫ

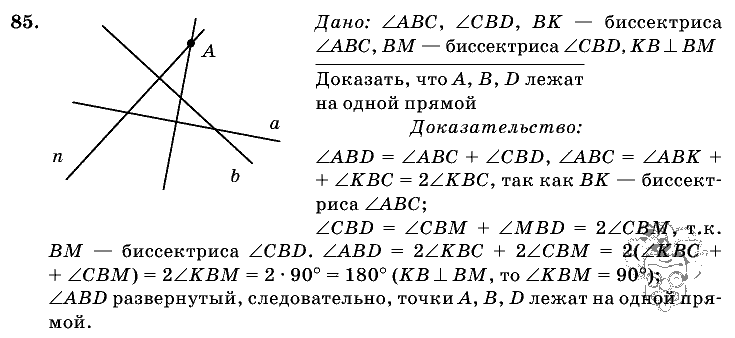
Вариант А1 : 1-а) 61°, 1-б) еще три угла, 2-а) AC⟂CD, BD⟂CD ⇒ AC||BD , 2-б) 55°.

Вариант А2: 1-а) 63°, 1-б) еще три угла, 2-а) AC⟂AB, BD⟂AB ⇒ AC||BD, 2-b) 125°.

Опция B1 : 1-b) 64°, 2-a) 38°, 2-b) 102°.

Вариант B2: 1-б) 26°, 2-а) 25°, 2-б) 119°.

Опция IN 1 : 1) 158°, 2-a) 50°, 2-b) 40°.

Опция B2: 1) 107°, 2-а) 50°, 2-б) 40°.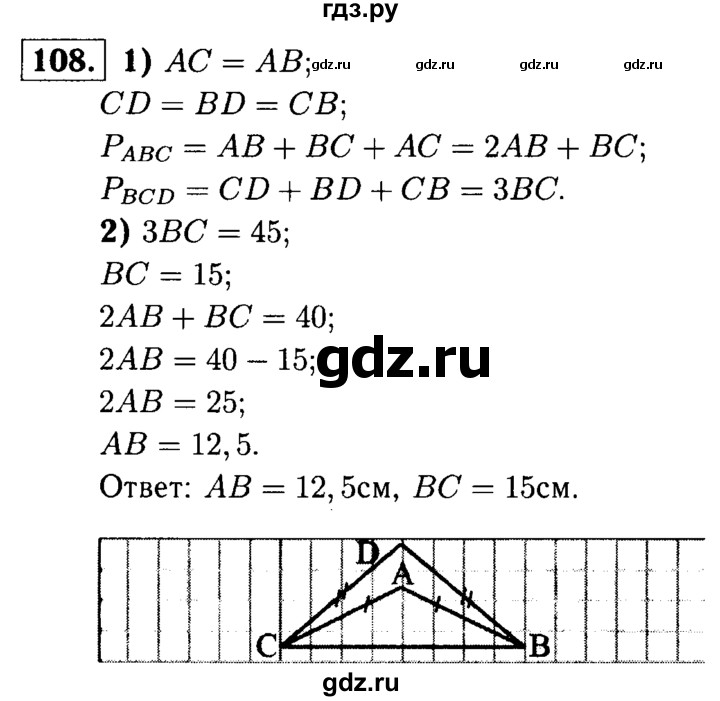

Источник : Ершова А.П., Голобородько В.В., Ершова А.С. – Самостоятельная и контрольная работа по алгебре и геометрии за 7 класс. 8-е изд., испр. и доп. — М.: ИЛЕКСА, — 2013.

8-е изд., перераб. и доп. — М.: 2015. — 126с. М.: 2009. — 126с.

Пособие является необходимым дополнением к школьным учебникам по геометрии для 7 класса, рекомендовано Министерством образования и науки Российской Федерации и включено в Федеральный перечень учебников. Пособие содержит тематические тесты, которые по структуре напоминают измерительные материалы для проведения ОГЭ по математике. Тесты ориентированы на учебник Л. С. Атанасяна и др. «Геометрия. 7-9 классы», но могут быть использованы учителями, работающими по другим учебникам. Все тесты выполнены в 4-х вариантах. а также члены аттестационных комиссий по аттестации школ.

Формат: pdf(2015, 126с.)

Размер: 1,5 МБ

Смотреть, скачать: диск.гугл

Формат: pdf(2009, 126с. )

Размер: 6.4 МБ

Смотреть, скачать: диск.гугл

СОДЕРЖАНИЕ
Введение 7
Инструкция для студентов 10
Тема I. Исходные геометрические сведения 11
Вариант 1 11
Часть 1 11
Часть 2 12
Часть 3 14
Опция II 15
Часть 1 15
Часть 2 16
Часть 3 18
Опция III 19
Часть 1 19

Часть 2 20
Часть 3 22
Опция IV 23
Часть 1 23
Часть 2 24
Часть 3 26
Тема II. Треугольники 27
Опция 1 27
Часть 1 27
Часть 2 29
Часть 3 31
Опция II 32
Часть 1 32
Часть 2 34
Часть 3 35
Опция III 36
Часть 1 36
Часть 2 38
Часть 3 39
Вариант IV 40
Часть 1 40
Часть 2 42
Часть 3 44
Тема III. Параллельные линии 45
Опция 1 45
Часть 1 45
Часть 2 47
Часть 3 49
Опция II 50
Часть 1 50
Часть 2 52
Часть 3 54
Опция III 55
Часть 1 55
Часть 2 57
Части. 3 59
Вариант IV 60
Часть 1 60
Часть 2 62
Часть 3 64
Тема IV. Отношения между углами и сторонами треугольника 65
Вариант 1 65
Часть 1 65
Часть 2 67
Часть 3 69
Вариант II 70
Часть 1 70
Часть 2 72
Часть 3 73
Опция III 74
Часть 1 74
Часть 2 76
Часть 3 77
Опция IV 78
Часть 1 78
Часть 2 80
Часть 3 81
Тема V. Прямоугольный треугольник. Построение треугольника из трех элементов 82
Вариант I 82
Часть 1 82
Часть 2 85
Часть 3 86
Вариант II 87
Часть 1 87
Часть 2 89
Часть 3 90
Вариант III 91
Часть 1 91
Часть 2 94
Часть 3 95
Вариант IV 96
Часть 1 96
Часть 2 99
Часть 3 100

Вариант I 103
Вариант II 104
Вариант III 105
Вариант IV 106
Тема II. Треугольники 107
Вариант I 107
Вариант II 108
Вариант III 109
Вариант IV 110
Тема III. Параллельные линии 111
Вариант I 111
Вариант II 112
Вариант III 113
Вариант IV 114
Тема IV. Отношения между углами и сторонами треугольника 115
Вариант I 115
Вариант II 117
Вариант III 118
Вариант IV 120
Тема V. Прямоугольный треугольник. Построение треугольника из трех элементов 122
Вариант I 122
Вариант II 123
Вариант III 124
Вариант IV 125

Задания по планиметрии включены как в число заданий ЕГЭ по математике, так и в число заданий ОГЭ (ГИА-9) по математике.
Лучшее средство для подготовки учащихся к ЕГЭ и ОГЭ – это преподавание математики, в том числе геометрии, хорошим учителем по хорошему учебнику. Одним из таких учебников является Л.С. Атанасяна и др. «Геометрия. 7-9 классы. К сожалению, заданий, аналогичных геометрическим задачам, предлагаемым в части 1 ОГЭ и части Б ЕГЭ по математике, там недостаточно.
Настоящее пособие предназначено как для проверки уровня знаний учащихся по геометрии, так и для подготовки учащихся к предстоящим формам аттестации.

Поэтому тематические тесты, разработанные в пособии, могут предлагаться наряду с тестами и другими средствами диагностики уровня образованности учащихся и в качестве итоговой работы по теме (без предложения тестов в этом случае). Пособие содержит задания с выбором ответа (Часть 1), задания с кратким ответом (Часть 2). Также содержит по одной задаче (Часть 3), на которую нужно дать развернутый ответ. В качестве заданий уровня С предлагаются задания повышенной сложности, аналогичные заданиям второй части ГИА по математике. Задачи такого рода обычно предлагаются в качестве последних экзаменационных заданий.
Предлагаемые тесты составлены в четырех вариантах по каждой теме курса геометрии 7 класса применительно к учебнику геометрии для учащихся 7-9 классов авторов Л.С. Атанасяна и др., хотя с некоторой корректировкой эти тесты могут быть предложены и студентам, обучающимся по учебникам А.В. Погорелов и И.Ф. Шарыгин.
Продолжительность этих тестов 35-40 минут. Но если учитель считает, что задание из части С не следует включать в тест, то время на тест можно сократить до 20-25 минут.

Пособие предназначено для проверки уровня знаний учащихся по курсу геометрии 7 класса и для подготовки к сдаче ЕГЭ по математике. Он содержит тематические тесты, которые по структуре напоминают измерительные материалы к ЕГЭ по математике. Тесты ориентированы на учебник Л.С. Атанасяна и др. «Геометрия. 7-9 классы», но может быть использована учителями, работающими по другим учебникам. Все тесты производятся в 4-х вариантах.
Пособие предназначено для учителей математики; его могут использовать учащиеся 7 классов для подготовки к зачетам и контрольным работам, а также члены аттестационных комиссий по аттестации школ.

Примеры.
В равнобедренном треугольнике ABC с основанием AC отрезок BD является высотой треугольника. Тогда BD тоже
а) биссектриса треугольника;
б) медиана треугольника;
в) перпендикуляр, проведенный из точки В к линии АС, а также медиана и биссектриса треугольника;
г) медиана и биссектриса треугольника.

Периметр равнобедренного треугольника равен 41 см, а сторона на 3,5 см меньше основания. Тогда основание треугольника будет
а) 12 см;
б) 16 см;
в) 15,5 см;
г) 12,5 см.

Если треугольник равнобедренный, то
а) он также равносторонний;
б) любая его медиана является биссектрисой и высотой;
в) углы при основании будут равны;
г) тоже прямоугольной формы. 11
Вариант 10061 Опция II 15
Часть 1 15
Часть 2 16
Часть 3 18
Опция III 19
Часть 1 19
Часть 2 20
Часть 3 22
Опция IV 23
Часть 1 23
Часть 2 24
Часть 3 26
Тема 2. Треугольники 27
Опция 1 27
Часть 1 27
Часть 2 29
Часть 3 31
Опция II 32
Часть 1 32
Часть 2 34
Часть 3 35
Опция III 36
Часть 1 36
Часть 2 38
Часть 3 39
Вариант IV 40
Часть 1 40
Часть 2 42
Часть 3 44
Тема III. Параллельные линии 45
Опция 1 45
Часть 1 45
Часть 2 47
Часть 3 49
Опция II 50
Часть 1 50
Часть 2 52
Часть 3 54
Опция III 55
Часть 1 55
Часть 2 57
Части.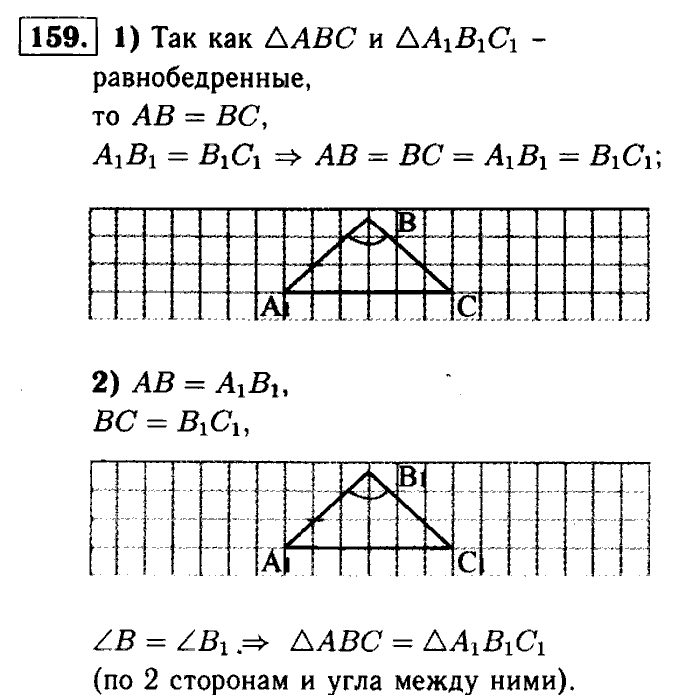 3 59
Вариант IV 60
Часть 1 60
Часть 2 62
Часть 3 64
Тема IV. Отношения между углами и сторонами треугольника 65
Вариант 1 65
Часть 1 65
Часть 2 67
Часть 3 69
Опция II 70
Часть 1 70
Часть 2 72
Часть 3 73
Опция III 74
Часть 1 74
Часть 2 76
Часть 3 77
Вариант IV 78
Часть 1 78
Часть 2 809006. 3 81
Тема V. Прямоугольный треугольник. Построение треугольника из трех элементов 82
Вариант 1 82
Часть! 82
Часть 2 85
Часть 3 86
Вариант II 87
Часть 1 87
Часть 2 89
Часть 3 90
Вариант III 91
Часть 1 91
Часть 2 94
Часть 3 95
Опция IV 96
Часть 1 96
Часть 2 99
Часть 3 100
Ответы и руководящие принципы 101
Образец Ответ Студента 101
Тема I. Начальная геометрическая информация 103
Опция 1 103
. II 104
Вариант III 105
Вариант IV 106
Тема II. Треугольники 107
Вариант I 107
Вариант II 108
Вариант III 109
Вариант IV 110
Тема III. Параллельные линии 111
Вариант I 111
Вариант II. 112
Вариант III 113
Вариант IV 114
Тема IV. Отношения между углами и сторонами треугольника 115
Вариант I 115
Вариант II 117
Вариант III 118
Вариант IV 120
Тема V. Прямоугольный треугольник. Построение треугольника из трех элементов 122
Вариант I 122
Вариант II. 123
Вариант III 124
Вариант IV 125.

Бесплатно скачать электронную книгу в удобном формате, смотреть и читать:
Скачать книгу Тесты по геометрии, 7 класс, к учебнику Атанасяна, Фаркова А.В., 2009 — fileskachat.com, скачать быстро и бесплатно.

Скачать pdf
Ниже вы можете купить эту книгу по лучшей сниженной цене с доставкой по России.

Контрольные темы: «Исходные геометрические сведения», «Треугольник и окружность», «Параллельные прямые», «Треугольник.

Соотношение углов и сторон»

Контрольная работа №1 на тему: «Прямая на плоскости. Углы »

Вариант I

а) точка С, лежащая на луче ВА;
б) точка D, не лежащая на прямой АВ;
в) точку Е, не лежащую на прямой АВ, и провести через эту точку прямую, пересекающую АВ.

2. Решить проблему.
а) Один из углов, образованных при пересечении двух прямых, равен 123 0 . Найдите остальные углы.
б) Один из соседних углов в пять раз больше другого. Найдите эти углы.

а) MN, если CD=6 см, CN=4 см, CM=2 см.
b) CN, если CM=3 см, MD=7 см, ND=1 см.

4. Биссектриса угла и прямая, пересекающая стороны угла, образуют угол α. Найдите исходный угол, если известно, что данная прямая перпендикулярна одной из сторон.

5. Угол COD=124 0 , луч OE является биссектрисой угла COD, а луч OF делит один из полученных углов в отношении 3:1. Найдите получившиеся углы.

Вариант II.
1. Проведите линию AB и отметьте точки:
а) точка С, лежащая на отрезке АВ.
б) точку F, не лежащую на прямой АВ.
в) точку Е, не лежащую на прямой АВ, и провести через эту точку прямую, пересекающую АВ.

2. Решить проблему.
а) Один из углов, образованных при пересечении двух прямых, равен 144 0 . Найдите остальные углы.
б) Один из смежных углов в 9 раз меньше другого. Найдите эти углы.

3. На отрезке CD последовательно отмечены точки M и N. Найдите длину отрезка:
а) MN, если CD=8 см, CN=5 см, CM=1 см.
б) CN, если CM=4 см, MD=9 см, ND=2 см.

4. Прямая перпендикулярна одной из сторон угла и образует с линией, проведенной из вершины угла, угол α. Найдите исходный угол.

5. Угол COD=144 0 , лучи OE и OF делят этот угол на три равных. Биссектриса OM проведена в углу ЕOF. Найдите углы COM, MOD, EOM, MOF, COF.

Тест №2 на тему: «Треугольники»

Вариант I

а) AH — медиана.
б) BM — медиана.
в) AH — высота.
г) BM — биссектриса.
д) $\bigtriangleup ABC$ равнобедренный.

2. Периметр $\bigtriangleup ABC$ равен 12см, сторона AC=5см, BC=4см. Известно, что AB=CD, ∠DCA=30°, ∠BAH=150°.
а) Докажите, что $\bigtriangleup ABC=\bigtriangleup DCA$.

3. В $\bigtriangleup ABC$ AB=AC, AH — биссектриса, ∠ABC=57&deg. Найдите углы $\bigtriangleup ABC$.

4. В окружности с центром в точке O проведены хорды AC и BE, так что ∠AOB=∠COE.
Докажите: а) АС=ВЕ; б) AE — диаметр окружности.

5. $\bigtriangleup ABC$ равнобедренный (BC=AC). Точка D взята внутри треугольника так, что BD=AD, ∠ADB=120°, ∠A=60°. Найдите ∠BDC и ∠DAC.

Вариант II.
1. Используя картинку, выберите правильный ответ:
а) AH — биссектриса.
б) BM — медиана.
в) AH — высота.
г) BM — биссектриса.
д) $\bigtriangleup ABC$ остроугольный.

2. Периметр $\bigtriangleup ABC$ равен 18 см, сторона AC=6см, BC=5см. Известно, что AB=CD, ∠DCA=60°, ∠BAH=120°.
а) Докажите, что $\bigtriangleup ABC$=$\bigtriangleup DCA$.
б) Найдите длины сторон $\bigtriangleup DCA$.

3. В $\bigtriangleup ABC$ AB=AC, AH высота, ∠ABC=38&град. Найдите углы $\bigtriangleup ABC$.

4. В окружности с центром в точке O проведены хорды AF и VM так, что ∠AOF=∠BOM.
Докажите: а) АВ=FM; б) АМ — диаметр окружности.

5. $\bigtriangleup ABC$ равнобедренный (BC=AC). Точка D взята внутри треугольника, поэтому BD=AD, ∠ADB=120°; ∠А=60°. Найдите ∠BDC и ∠DAC.

Тест №3 на тему: «Параллельные прямые»

Вариант I

2. На рисунке ∠1=126°, а||б. Найдите ∠2, ∠3, ∠4.

3. Прямые AB и CD пересекаются в точке O. Докажите, что если AD||BC и OD=CO, то $\bigtriangleup AOD= \bigtriangleup COB$.

4. $\bigtriangleup ABC$ равнобедренный, MP||BC, MP||KH, ∠B=70°, AM:MB=1:2, MK:KB=1:3, AB=6 см. Найдите: ∠A , ∠AKH, ∠KHA, HC.

5. $\bigtriangleup ABC$ равнобедренный (AB=AC), AH – высота, ∠C=52° ∠MBA=76°. Докажите, что MB||AC.

Вариант II.
1. Используя рисунок, докажите, что a||b и c||d.

2. На рисунке ∠1=132°, a||b. Найдите ∠2, ∠3, ∠4.

3. Прямые AB и CD пересекаются в точке O. Докажите, что если AC||BD и AO=OB, то $\bigtriangleup AOC= \bigtriangleup ODB$.

4. $\bigtriangleup ABC$ равнобедренный, MP||BC, MP||KH, ∠B=80°, AM:MB=1:3, MK:KB=1:5, AB=8см. Найдите: ∠A, ∠AKH, ∠KHA, HC.

5. Дан $\bigtriangleup ABC$, AH высота, ∠B=38° ∠MBA=104°. Докажите, что MB||AC.

Тест № 4 на тему: «Отношения между углами и сторонами треугольника»

Вариант I
а) $\bigtriangleup ABC$ — равнобедренный;
б) $\bigtriangleup ABC$ — тупой;
c) ∠C=80°
d) ∠2 является внешним для $\bigtriangleup ABC$.

2. В равнобедренном $\bigtriangleup ABC$ с основанием AC высота AH, ∠B=45&град. Найдите все возможные внутренние углы треугольника $\bigtriangleup ABC$.

3. В $\bigtriangleup ABC$ ∠B на 30&deg больше, чем ∠A, а ∠C в $1\frac(1)(3) $раз больше, чем ∠A. Найдите углы $\bigtriangleup ABC$.

4. Используя данные на рисунке, найдите AB.

5. В равностороннем $\bigtriangleup ABC$ проведена высота AH. На стороне АВ отмечена точка М. Через эту точку проведен перпендикуляр к стороне AC, который пересекает ее в точке N. AH и MN пересекаются в точке O. Найдите углы четырехугольника MBHO.

Вариант II.
1. Используя рисунок, выберите правильные утверждения:
а) ВС=АС;
б) $\bigtriangleup ABC$ — прямоугольная;
c) ∠A=67°
d) внешний угол к ∠A=153°.

2. В равнобедренном $\bigtriangleup ABC$ с основанием AC высота AH, ∠B=50&град. Найдите все возможные внутренние углы треугольника $\bigtriangleup ABC$.

3. В $\bigtriangleup ABC$ ∠B больше ∠A на 12&deg, а ∠C в 2 раза больше ∠A. Найдите углы $\bigtriangleup ABC$.

4. Используя данные на рисунке, найдите БК.

5. В равностороннем $\bigtriangleup ABC$ проведена высота AH. На стороне АВ отмечена точка М. Через эту точку проведена прямая, пересекающая сторону AC в точке N. AH и MN пересекаются в точке O. ∠MNA=60&deg. Найдите углы четырехугольника MBHO.

Контрольная № 5 (окончательная)

Вариант I

2. В равностороннем $\bigtriangleup ABC$ на биссектрисе BH взята точка O так, что ON⊥BC; OM⊥AB (N∈BC, M∈AB). Докажите, что $\bigtriangleup AOM= \bigtriangleup NOC$. Найдите углы этих треугольников.

3. В окружности с центром в точке O хорды AB и CD пересекаются в точке N. ∠CNB=150°; CD⊥OB; СО⊥АВ. Найдите ∠COB.

4. В $\bigtriangleup ABC$ AB=BC точки K и E отмечены на сторонах AB и AC так, что KE||BC, KH — биссектриса ∠BKE; ∠ВХ=32°. Найдите углы $\bigtriangleup ABC$.

5. Докажите, что если два отрезка равны и точка пересечения делится в одинаковом отношении, то отрезки, соединяющие концы этих отрезков, параллельны.

Вариант II.
1. Найдите по рисунку равнобедренные треугольники:

2. В равностороннем $\bigtriangleup ABC$ взята точка O на высоте BH так, что ON⊥BC; OM⊥AB (N∈BC, M∈AB). Докажите, что $\bigtriangleup MOB= \bigtriangleup NOB$. Найдите углы $\bigtriangleup ABC$.

3. В окружности с центром в точке О хорды AB и CD пересекаются в точке N. ∠И=120°; CD⊥OB; СО⊥АВ. Найдите ∠COB.

4. В $\bigtriangleup ABC$ AB=BC точки M и N отмечены на сторонах AB и AC так, что MN||BC, NH — биссектриса ∠MNC; ∠HNC=53°. Найдите углы $\bigtriangleup ABC$.

5. Докажите, что если два отрезка пересекаются посередине, то отрезки, соединяющие концы этих отрезков, параллельны.

Вариант I
1. 3 и 4.
2. 67,5°; 22,5°; 45°; 90°; 90°; 45°.
3. 45°; 75°; 60°.
4.АВ=8.
5. 150°; 60°; 90°; 60°.

Вариант II.
1. 1 и 3.
2. 40°; 25°; 65°; 90°; 90°; 50°.
3. 42°; 84°; 54°.
4.БК=8.
5. 120°; 60°; 90°; 60°.

Ответы на контрольную работу № 5 (итоговая)
Вариант I
1. а, в.
2. 60°; 30°; 90°.
3. 30°.
4. 32°; 32°; 116°.

Вариант II.
1. а, в.
2. 30°; 30°; 120°.
3. 60°.
4. 32°; 74°; 74°.

Средняя линия трапеции атанасяна предлежания. Срединная линия трапеции

Тема «Средняя линия трапеции» относится к одной из важных тем курса геометрии. Эта фигура довольно часто встречается в различных задачах, как и ее средняя линия. Задания, содержащие данные по этой теме, часто встречаются в итоговых контрольно-аттестационных работах. Знания по этой теме также могут пригодиться при обучении в средних и высших учебных заведениях.

Хотя в теме заявлена ​​фигура трапеция, рассмотрение данной темы может проходить в ходе изучения темы «Векторы» и «Использование векторов при решении задач». Это можно понять, взглянув на слайд презентации.

Здесь автор определяет срединную линию как отрезок, соединяющий середины сторон. Причем здесь также отмечается, что срединная линия трапеции параллельна ее основаниям, а также равна их полусумме. Именно в ходе доказательства этого утверждения пригодятся знания, связанные с векторами. Применяя правила сложения векторов по рисунку, приведенному в качестве иллюстрации условия, получаются равенства. У этих равенств одна и та же левая сторона, и она является средней линией трапеции, заданной в виде вектора. Складывая эти равенства, мы получаем большое выражение в правой части равенства.

слайды 1-2 (Тема презентации «Средняя линия трапеции», определение средней линии трапеции)

Если внимательно рассмотреть, то в двух случаях мы получим сложение противоположных векторов, в результате чего получится ноль . Тогда остается, что двойной вектор, содержащий среднюю линию трапеции, равен сумме векторов, содержащих основания. Разделив это равенство на 2, получается, что вектор, содержащий среднюю линию, равен половине суммы векторов, содержащих основания.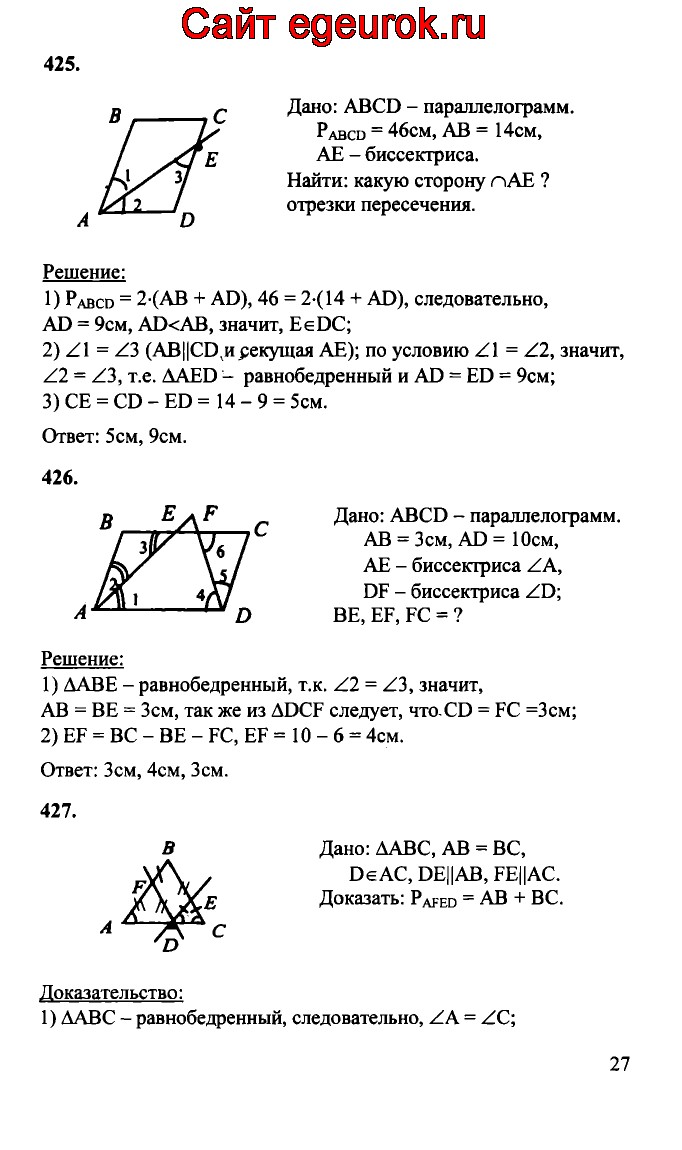 Теперь идет сравнение векторов. Получается, что все эти векторы одинаково направлены. Это означает, что знаки векторов можно смело опускать. И тогда получается, что средняя линия самой трапеции равна половине суммы оснований.

Презентация содержит один слайд, содержащий большой объем информации. Здесь дано определение средней линии трапеции, а также указано ее основное свойство. В курсе геометрии это свойство является теоремой. Итак, здесь теорема доказывается с использованием знания понятия векторов и действий над ними.

Преподаватель может дополнить эту презентацию своими примерами и заданиями, но здесь публикуется все, что требуется для среднего уровня знаний по данному предмету. При этом автор оставил возможность учителю пофантазировать, доработать то, что он сам хочет, чтобы создать соответствующую атмосферу на уроке. Не забывайте и о самом настроении на урок. Тогда с помощью этой презентации вы точно сможете добиться желаемого результата.

«Урок площади трапеции» — В основании прямоугольная трапеция 5см.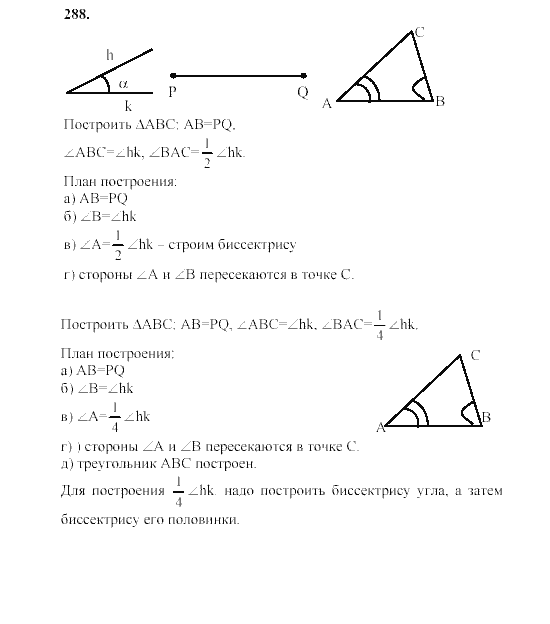 и 17см., а меньшая сторона 10см. Учитель подводит итоги, задавая вопросы: Кто набрал 5, 4, 3 балла? В каждом случае формулируется теорема, которая доказана. Решение задачи. Как рассчитать площадь трапеции? Какие элементы плоских фигур используются в формулах площади?

«Задачи по теореме Пифагора» — №21 Находка: X. №18 Находка: X. №27 Находка: X. Задания по готовым рисункам («Теорема Пифагора»). #23 Найти: X. #25 Найти: X. #26 Найти: X. #13 Найти: X. #20 Найти: X. #19Находка: X. #14 Находка: X. Вы выполнили все предложенные задания. #29 Находка: X. #28 Находка: X. #30 Находка: X. #22 Находка: X.

«Теорема Фалеса» — Фалес широко известен как геометр. Астрономия. Милетский материалист. Проведем через точку B2 прямую EF, параллельную прямой A1A3. Из равенства треугольников следует равенство сторон В1В2=В2В3. Теорема Фалеса. Считается, что Фалес первым изучил движение солнца по небесной сфере. Треугольники B2B1F и B2B1E равны по второму знаку равенства треугольников.

«Теорема синусов» — Стороны треугольника пропорциональны синусам противоположных углов.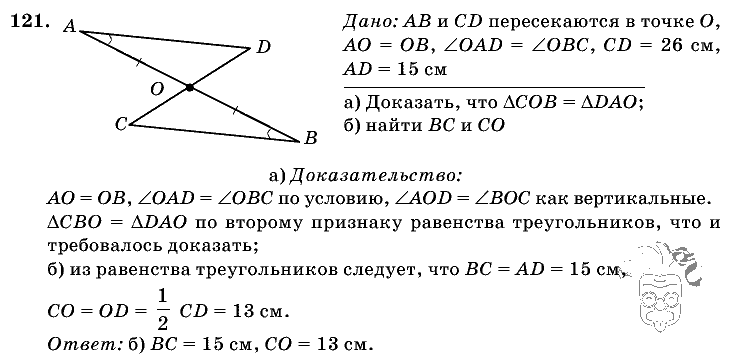 Решение: Устная работа: Ответы на задания по рисункам: Проверка домашнего задания. Тема урока: Теорема синусов. Теорема синусов:

«Урок теоремы Пифагора» — Определить вид треугольника: Знакомство с теоремой. Доказательство теоремы. Разогревать. Теорема Пифагора. И найти лестницу длиной 125 футов. План урока: Исторический экскурс. Показ картинок. Решение простых задач. Вычислите высоту CF трапеции ABCD. Доказательство. Определить тип четырехугольника КМНП.

«Теорема Пифагора 8 класс» — ЦИФРЫ. Деление чисел на четные и нечетные, простые и составные. Дано: прямоугольный треугольник a,b катеты c — гипотенуза. Высота. Доказательство Бхаскари. Пифагорейские открытия в математике. Дано: Прямоугольный треугольник, a, b — катеты, c — гипотенуза. Докажите: c2 = a2 + b2. Меньшая сторона прямоугольного треугольника.

Определение: Средняя линия треугольника — это отрезок, соединяющий середины двух его сторон. АК = КС БЭ = СЕ КЭ — средняя линия АВС Определение: средней линией трапеции называется отрезок, соединяющий середины ее боковых сторон. A BC K N E AN = HB KE = CE NOT — средняя линия ABSK A B C K E Сколько средних линий в треугольнике? Сколько средних линий в трапеции?

Срединная линия треугольника Теорема. Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны. А В М К Дано: АВС, МК — средняя линия Доказательство: Так как по условию МК средняя линия, то АМ = МБ = ½ АВ, СК = КВ = ½ ВС, Отсюда, ВМ АВ ВК ВС 1 2 В — общий для АВС и МВК, значит, АВС и МВК подобны по второму признаку сходства, следовательно, ВМС = А, значит МС АС. Докажите: MK AS, MK = ½ AS MK AS 1 2 Из подобия треугольников также следует, что, т. е. MK = ½ AS.

Решить проблему F R N ? А Б

Доказательство: Проведем A 1 B 1 A B C A1A1 B1B1 O C1C1 По условию AA 1, BB 1 медианы, значит BA 1 = CA 1, AB 1 = CB 1, то есть A 1 B 1 есть средняя линия. Отсюда А 1 В 1 АВ, следовательно, 1 = 2, 3 = 4. Следовательно, треугольники АОВ и А 1 ОВ 1 подобны в двух углах. Следовательно, их стороны пропорциональны: АО БО АВ А1ОА1О В1ОВ1О А1В1А1В1 По свойству средней линии треугольника АВ = 2 А 1 В 1 , т.е. АО БО АВ А1ОА1О В1ОВ1О А1В1А1В1 2 1 Аналогично, СО С1ОС1О 2 1 Получаем: C1OC1O АОБОКО A1OA1OB1OB1O 2 1

Срединная линия трапеции Теорема. Средняя линия трапеции параллельна основаниям и равна половине их суммы. А Б В К М Р ​​Дано: АБСК — трапеция МП — средняя линия Доказать: МП АК, МП ВС МП = Доказательство: О , тогда ВС АК, а, следовательно, ВС МЕ АК Так как МП — средняя линия, то АМ = МБ, КР = СР E Следовательно, MP лежит на ME, что означает MP AK, MP BC. Заходим в ВК. По теореме Фалеса О — середина ВК, значит МО — средняя линия АВК, ОР — средняя линия ВСК МП = МО + ИЛИ = ½ АК + ½ ВС = ½ (АК + ВС ) = т.е. в точке P.

Чтобы использовать предварительный просмотр презентаций, создайте учетную запись Google (аккаунт) и войдите в нее: https://accounts.google.com

Подписи к слайдам:

Средняя строка (8 класс)

Средняя строка треугольник

Средняя линия треугольника. Определение: Отрезок, соединяющий середины двух сторон треугольника, называется СРЕДНЕЙ ЛИНИЕЙ ТРЕУГОЛЬНИКА.

Теорема Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны. то есть: KM ║ AC KM = ½ AC A B C K M

Решите задачу устно: A B C K M 7 см Дано: M K — ср. линия Найти: AC?

Работаем в парах:

Решим задачу: Дано: MN — ср. линия Найти: P ∆ ABC M N A B C 3 4 3, 5

Работать в парах:

Срединная линия трапеции

Напомним: Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие не параллельны A D B C BC || AD — основания AB łł CD — стороны

Срединная линия трапеции. Определение: Средняя линия трапеции — это отрезок, соединяющий середины ее сторон. A D B C M N MN — средняя линия трапеции ABCD

Теорема о средней линии трапеции Средняя линия трапеции параллельна ее основаниям и равна половине их суммы. то есть: M N ║BC║A D M N = ½ (BC+A D) M N A D B C

Решить устно: M N A D B C 6,3 см 18,7 см?

Решите устно в парах: Дано: АВ = 16 см; CD = 18 см; М Н = 15 см.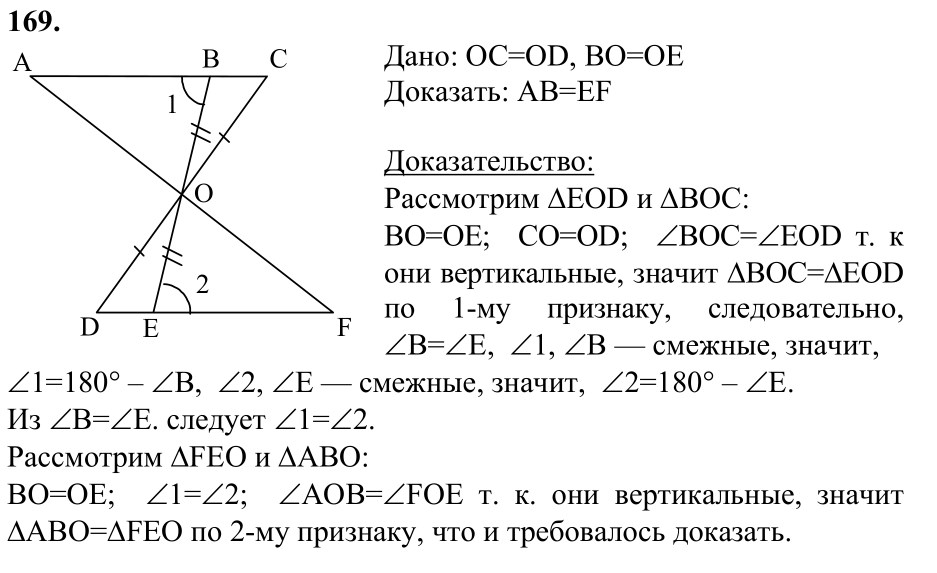 Найти: Р ABCD = ? M N A D B C

Самостоятельная работа Задача: Средняя линия трапеции 5см. Найдите основания трапеции, если известно, что нижнее основание в 1,5 раза больше верхнего. Решение: A D B C 5 см Пусть BC = X см, тогда AD = 1,5X см BC+AD = 10 см X + 1,5X = 10 X = 4 Итак: BC = 4 см AD = 6 см

СПАСИБО ЗА УРОК!!!

Презентация разработана учителем математики ГБОУ СОШ № 467 г. Санкт-Петербурга Колпинского района Лугвиной Натальей Анатольевной

На тему: методические разработки, презентации и конспекты

Занятие по обобщению и закреплению знаний на тему «Средняя линия треугольника. Срединная линия трапеции» в 8 классе с использованием ИКТ….

Рабочая тетрадь — индивидуальное творческое задание для учащегося. который предполагает самостоятельную работу с текстом по теме «Трапеция. Срединная линия трапеции», применение знаний при решении задач. …

резюме другие презентации

«Построение правильных многоугольников» — ?=60?. 180?. Геометрия. знак равно н. n — 2. Работа выполнена учителем математики МОУ «Гимназия № 11» Лисицыной Е.Ф.

«Теорема Фалеса» — Теорема Фалеса. Геометрическая теорема названа в честь Фалеса. Астрономия. Проведем через точку B2 прямую EF, параллельную прямой A1A3. Считается, что Фалес первым изучил движение Солнца по небесной сфере. Презентация по геометрии Ученики 9Класс «А» Сорогина Полина. Милетский материалист. Геометрия. По свойству параллелограмма A1A2=FB2, A2A3=B2E. Фалес широко известен как геометр. А так как A1A2=A2A3, то FB2=B2E.

«Разложение вектора на два неколлинеарных» — Пусть p коллинеарно b. Доказательство: Разложение вектора на два неколлинеарных вектора. Доказательство. Пусть a и b — неколлинеарные векторы. Лемма: Если векторы a и b коллинеарны и a? 0, то существует число k такое, что b = ka. Докажем, что любой вектор p можно разложить на векторы a и b. Геометрия 9 класс. Тогда р = уb, где у — некоторое число.

«Правильные многоугольники 9 класс» — Урок геометрии в 9 классе.