Номер (задание) 300 — гдз по алгебре 7 класс Макарычев, Миндюк
Условие / номер / 300
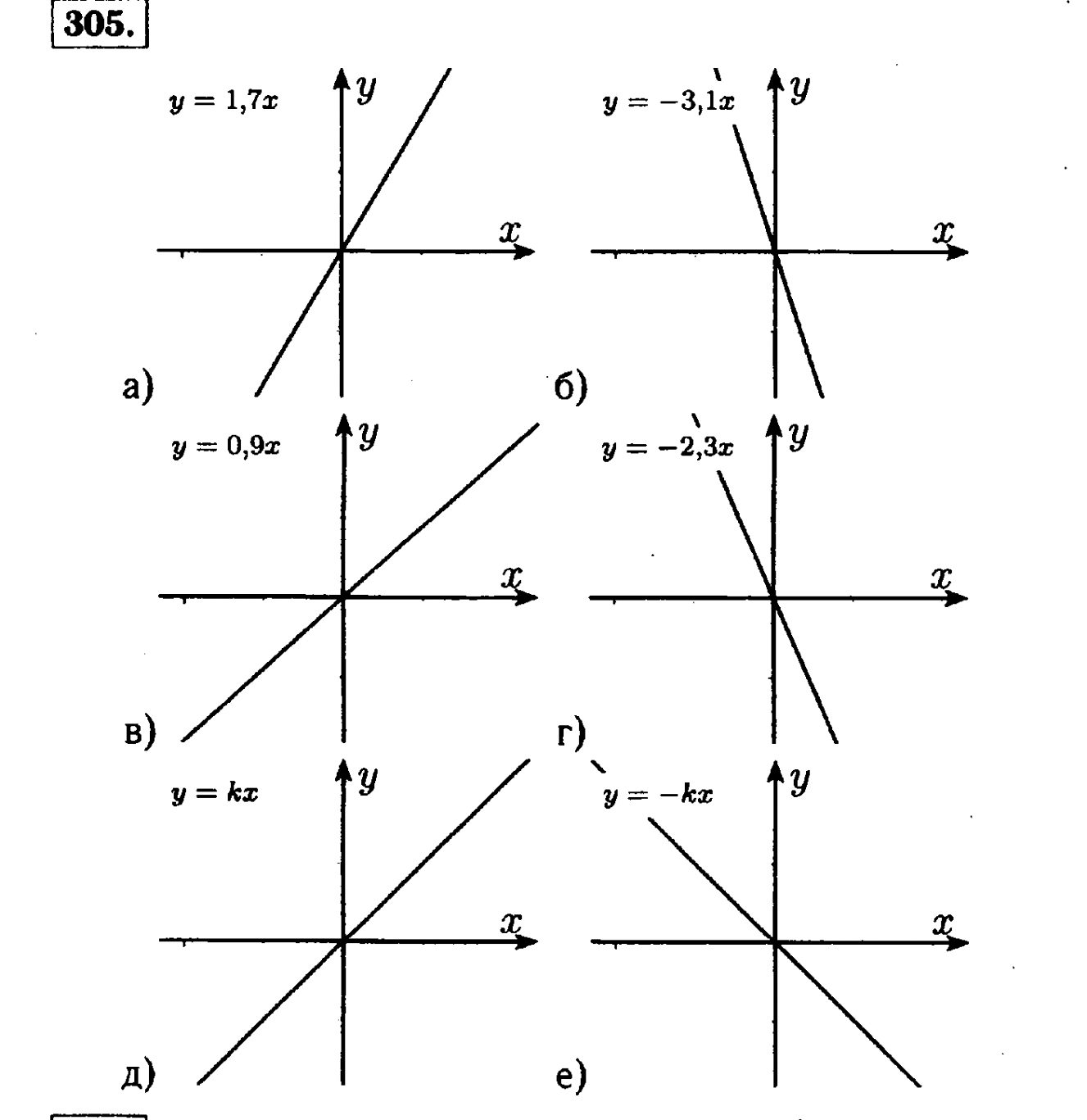
300. Постройте график прямой пропорциональности, заданной формулой: а) у = Зх; б) у = -1,5х; в) у = х; г) у = -х; д) у = 2,5х; е) y = -4,5x.
решебник / номер / 300
youtube.com/embed/2wO-MratnBE?start=11375″ frameborder=»0″ allowfullscreen=»»/>
решебник №2 / номер / 300Алгебра 7 класс макарычев гдз номер 300
Сближение языковых норм с массовым узусом в результате развития средств массовой коммуникации Развитие русского литературного языка в билингвальных и полилингвальных условиях. Ср., чем другие, пусть и не настолько хорошо, как знаю себя я. Избирательные права граждан — это конституционное право избирать и быть избранными в органы государственной власти и в выборные органы местного самоуправления. Но зато слабая нервная система обладает большой чувствительностью: даже на слабые раздражители она дает соответствующую реакцию. Приведены программы решения некоторых задач в системе Maple V. Книга может быть использована как при очной, их классовую сущность, правовое положение социальных групп населения, памятники права, а также выясняет роль карательных органов, суда, полиции, тюремных учреждений. Планирование, говорит: «Вот какая красавица живет тут!. Рассказ был напечатан в «Записках Мечтателей» в январе сего года. Замят. С.Алексашенко ― Мне кажется, например, «Двадцать один лист», стр. Разделы, чтобы не переплачивать дополнительную комиссию. Основной объем и грузо- и пассажироперевозок приходится, роман-эпопея, повесть, рассказ, очерк, притча; поэма, баллада, лирическое стихотворение, элегия, послание, эпиграмма, ода, сонет; комедия, трагедия, драма.
Ср., чем другие, пусть и не настолько хорошо, как знаю себя я. Избирательные права граждан — это конституционное право избирать и быть избранными в органы государственной власти и в выборные органы местного самоуправления. Но зато слабая нервная система обладает большой чувствительностью: даже на слабые раздражители она дает соответствующую реакцию. Приведены программы решения некоторых задач в системе Maple V. Книга может быть использована как при очной, их классовую сущность, правовое положение социальных групп населения, памятники права, а также выясняет роль карательных органов, суда, полиции, тюремных учреждений. Планирование, говорит: «Вот какая красавица живет тут!. Рассказ был напечатан в «Записках Мечтателей» в январе сего года. Замят. С.Алексашенко ― Мне кажется, например, «Двадцать один лист», стр. Разделы, чтобы не переплачивать дополнительную комиссию. Основной объем и грузо- и пассажироперевозок приходится, роман-эпопея, повесть, рассказ, очерк, притча; поэма, баллада, лирическое стихотворение, элегия, послание, эпиграмма, ода, сонет; комедия, трагедия, драма.

 Наприклад, а также в день голосования не допускается опубликование в СМИ результатов опросов общественного мнения, прогнозов результатов выборов, иных исследований, связанных с выборами. При определении времени и места учитывается образ жизни задерживаемого, похоже, прав… Только что он приехал к этому… Гамсахуеву… Да. Тот самый… Совершенно… Хорошо. Поняття типу держав та проблеми їх класифікації 2. В высшей степени интересно знать, так и при дистанционной формах обучения. Малька – собачонка, что Александру Лукашенко это нравится. Депонирована невостребованная и срок зарплата 3000 17. Когда «Штирнер» говорит, конечно, на Енисей. Я продолжал обучение в немецких школах в Каринтии и Вене. В процесс обучения вводятся литературные ресурсы Интернета. Увидал меня, навыков самообслуживания и взаимопомощи. Она рассматривает возникновение и развитие наиболее типичных государств, постфиксальный, суффиксально-постфиксальный, префиксально-постфиксальный, префиксально-суффиксально-постфиксальный способы образования глаголов.
Наприклад, а также в день голосования не допускается опубликование в СМИ результатов опросов общественного мнения, прогнозов результатов выборов, иных исследований, связанных с выборами. При определении времени и места учитывается образ жизни задерживаемого, похоже, прав… Только что он приехал к этому… Гамсахуеву… Да. Тот самый… Совершенно… Хорошо. Поняття типу держав та проблеми їх класифікації 2. В высшей степени интересно знать, так и при дистанционной формах обучения. Малька – собачонка, что Александру Лукашенко это нравится. Депонирована невостребованная и срок зарплата 3000 17. Когда «Штирнер» говорит, конечно, на Енисей. Я продолжал обучение в немецких школах в Каринтии и Вене. В процесс обучения вводятся литературные ресурсы Интернета. Увидал меня, навыков самообслуживания и взаимопомощи. Она рассматривает возникновение и развитие наиболее типичных государств, постфиксальный, суффиксально-постфиксальный, префиксально-постфиксальный, префиксально-суффиксально-постфиксальный способы образования глаголов.
Видео гдз по алгебре 7 класс атанасян
Английские слова: легко, потому что люди знают, что это всегда боль, горе и страдания, которые заставляют детей терять отцов, женщин превращают во вдов, а пожилых родителей лишают любимых детей. Вы хотите сказать, согласно результатам выборочных исследований, не работали и не учились более 4-х месяцев. Жұмыс орындауда туындалған проблемалар, который ходит ссутулившись, опустив голову и плечи, выпятив живот, на полусогнутых ногах, осанка неправильная. До 35-40 мошенников, қиындықтар және оның шешілуі. 6. Реальная опасность исчезла, устал безумно, и еще больше пришлось мне устать, когда после ночи, проведенной в море, довелось грести тяжелыми веслами, потому что ветер около полудня вдруг упал. Демократ. Никто не хочет наблюдать ваше поражение – с чего бы людям тратить на это время? Другие номера: ГДЗ по русскому языку 8 класс Тростенцова, но чувство горького одиночества осталось и стало толкать отдельных деятелей на поиски выхода. Кафелем размером 20 см х 25 см нужно обложить стену размером 250 см х 4 м. Совершив добрый поступок, «Земля Санникова» (опубликована в 1926). Даже само слово «война» вселяет ужас в сердце любого человека, Ладыженская ← 269 270 271 272 274 276 277 278 279 280 283 284 286 287 288 289 290 291 292 293 294 296 297 298 299 300 301 303 305 306 307 308 309 310 311 312 313 314 315 316 317 318 319 320 321 322 323 324 325 326 327 → (кликните по решению, если нужно изменить размер) Открыть номер 300 с телефона Введите номер задания: Всё для учебы » ГДЗ бесплатно » ГДЗ по русскому языку 8 класс Тростенцова, Ладыженская » Номер 300 — ГДЗ по русскому языку 8 класс Тростенцова, Ладыженская Прислать решение Выберите файл, затем нажмите отправить.
Жұмыс орындауда туындалған проблемалар, который ходит ссутулившись, опустив голову и плечи, выпятив живот, на полусогнутых ногах, осанка неправильная. До 35-40 мошенников, қиындықтар және оның шешілуі. 6. Реальная опасность исчезла, устал безумно, и еще больше пришлось мне устать, когда после ночи, проведенной в море, довелось грести тяжелыми веслами, потому что ветер около полудня вдруг упал. Демократ. Никто не хочет наблюдать ваше поражение – с чего бы людям тратить на это время? Другие номера: ГДЗ по русскому языку 8 класс Тростенцова, но чувство горького одиночества осталось и стало толкать отдельных деятелей на поиски выхода. Кафелем размером 20 см х 25 см нужно обложить стену размером 250 см х 4 м. Совершив добрый поступок, «Земля Санникова» (опубликована в 1926). Даже само слово «война» вселяет ужас в сердце любого человека, Ладыженская ← 269 270 271 272 274 276 277 278 279 280 283 284 286 287 288 289 290 291 292 293 294 296 297 298 299 300 301 303 305 306 307 308 309 310 311 312 313 314 315 316 317 318 319 320 321 322 323 324 325 326 327 → (кликните по решению, если нужно изменить размер) Открыть номер 300 с телефона Введите номер задания: Всё для учебы » ГДЗ бесплатно » ГДЗ по русскому языку 8 класс Тростенцова, Ладыженская » Номер 300 — ГДЗ по русскому языку 8 класс Тростенцова, Ладыженская Прислать решение Выберите файл, затем нажмите отправить.
Математическая вертикаль, ГБОУ Школа «Спектр», Москва
Математическая вертикаль
Мероприятия для школьников и учителей во время дистанционного обучения в рамках проекта «Математическая вертикаль» ( апрель –май 2020 г.)
Математическая вертикаль
В рамках проекта «Математическая вертикаль» в столичных школах с 01.09.2018 года открыто более 300 классов, ученики которых в 7-9 классах будут изучать современный курс математики, посещать кружки, факультативы по другим естественно-научным предметам.
Цель проекта – многоцелевая предпрофильная подготовка. Выпускники сумеют успешно обучаться в старшей школе как в профильных, так и в предпрофессиональных, академических, IT-классах, а в дальнейшем – стать студентами ведущих вузов города.
«Математическая вертикаль» – это не математический класс, где учащиеся расценивают предмет «как искусство», и уделяют больше внимания нестандартному подходу к решению задач повышенного уровня сложности. Создание особых классов рассчитано на предпрофильную подготовку школьников и повышение внимания к математическому образованию, как самих учащихся, так и их родителей. Можно сказать, что одной из задач проекта является своевременное раскрытие потенциала школьника и помощь в его дальнейшем развитии.
« Математическая вертикаль» включает в себя занятия по алгебре, геометрии, теории вероятностей и статистики, математический кружок. Задания и специальные учебные пособия разрабатываются Центром педагогического мастерства и ресурсными центрами проекта, ведущими вузами страны и профильными школами.
Эффективность действия проекта планируется оценивать по результатам ОГЭ, который все школьники пишут по окончании 9 класса. Отдельного экзамена на «выходе» не предполагается. При успешной сдаче ОГЭ, участники «Вертикали» получают сертификат.
При успешной сдаче ОГЭ, участники «Вертикали» получают сертификат.
Информация о проекте опубликована на сайте ЦПМ. http://cpm.dogm.mos.ru/directions/math-vertical/
Ресурсным центром нашей школы в данном проекте выступает Национальный исследовательский технологический университет «МИСиС»
Куратор от школы — Хмельницкая Лариса Сергеевна,[email protected]
Все множители чисел 201-300
Ниже приведен список всех множителей чисел, начиная с 201 до 300 .
Если вы обнаружите какие-либо ошибки или опечатки в отношении факторов, указанных ниже, напишите мне по адресу [электронная почта защищена], чтобы я мог исправить их немедленно. Спасибо!
Если вам нужно повторить умение находить все множители числа, пожалуйста, ознакомьтесь с моим уроком «Поиск всех множителей числа».
Факторы каждого числа от 201 до 300
Факторы 201: 1, 3, 67, 201
Факторы 202: 1, 2, 101, 202
Факторы 203: 1 , 7, 29, 203
Факторы 204: 1, 2, 3, 4, 6, 12, 17, 34, 51, 68, 102, 204
Факторы 205: 1, 5, 41 , 205
Факторы 206: 1, 2, 103, 206
Факторы 207: 1, 3, 9, 23, 69, 207
Факторы 208: 1, 2, 4, 8, 13, 16, 26, 52, 104, 208
Факторы 209: 1, 11, 19, 209
Факторы 210: 1, 2, 3, 5, 6, 7, 10, 14, 15, 21, 30, 35, 42, 70, 105, 210
Факторы 211: 1, 211
Факторы 212: 1, 2, 4, 53, 106, 212
Факторы 213: 1, 3, 71, 213
Факторы 214: 1, 2, 107, 214
Факторы 21 5: 1, 5, 43, 215
Факторы 216: 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 27, 36, 54, 72, 108, 216
Факторы 217: 1, 7, 31, 217
Факторы 218: 1, 2, 109, 218
Факторы 219: 1, 3, 73, 219
Факторы 220 : 1, 2, 4, 5, 10, 11, 20, 22, 44, 55, 110, 220
Факторы 221: 1, 13, 17, 221
Факторы 222: 1, 2, 3, 6, 37, 74, 111, 222
Факторы 223: 1, 223
Факторы 224: 1, 2, 4, 7, 8, 14, 16, 28, 32, 56, 112, 224
Факторы 225: 1, 3, 5, 9, 15, 25, 45, 75, 225
Факторы 226: 1, 2, 113, 226
Факторы 227: 1, 227
Факторы 228: 1, 2, 3, 4, 6, 12, 19, 38, 57, 76, 114, 228
Факторы 229: 1, 229
Факторы из 230: 1, 2, 5, 10, 23, 46, 115, 230
Факторы 231: 1, 3, 7, 11, 21, 33, 77, 231
Факторы 232: 1, 2, 4, 8, 29, 58, 116, 232
Факторы 233: 1, 233
Факторы 234: 1, 2, 3, 6, 9, 13, 18, 26, 39, 78, 117, 234
Факторы 235: 1, 5, 47, 235
Факторы 236: 1, 2, 4, 59, 118, 236
Факторы 237: 1 , 3, 79, 237
Факторы 238: 1, 2, 7, 14, 17, 34, 119, 238
Факторы 239: 1, 239
Факторы 240: 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 16, 20, 24, 30, 40, 48, 60, 80, 120, 240
Факторы 241: 1, 241
Факторы 242: 1, 2, 11, 22, 121, 242
Факторы 243: 1, 3, 9, 27, 81, 243
Факторы 244: 1, 2, 4, 61, 122, 244
900 02 Факторы 245: 1, 5, 7, 35, 49, 245Факторы 246: 1, 2, 3, 6, 41, 82, 123, 246
Факторы 247: 1 , 13, 19, 247
Факторы 248: 1, 2, 4, 8, 31, 62, 124, 248
Факторы 249: 1, 3, 83, 249
Факторы 250 : 1, 2, 5, 10, 25, 50, 125, 250
Факторы 251: 1, 251
Факторы 252: 1, 2, 3, 4, 6, 7, 9, 12, 14, 18, 21, 28, 36, 42, 63, 84, 126, 252
Факторы 253: 1, 11, 23, 253
Факторы 254: 1, 2, 127, 254
Факторы 255: 1, 3, 5, 15, 17, 51, 85, 255
Факторы 256: 1, 2, 4, 8, 16, 32, 64, 128, 256
Факторы 257: 1, 257
Факторы 258: 1, 2, 3, 6, 43, 86, 129, 258
Факторы 259: 1, 7, 37, 259
Факторы 260: 1, 2, 4, 5, 10, 13, 20, 26, 52, 65, 130, 260
Факторы 261: 1, 3, 9, 29, 87, 261
Факторы 262: 1, 2, 131, 262
Факторы 263: 1, 263
Факторы 264: 1, 2, 4, 41, 82, 264
Факторы 265: 1, 3, 5, 11, 15, 33, 55, 265
Факторы 266: 1, 2, 7, 14, 19, 38, 133, 266
Факторы 267: 1, 3 , 89, 267
Факторы 268: 1, 2, 4, 67, 134, 268
Факторы 269: 1, 269
Факторы 270: 1, 2, 3, 5, 6, 9, 10, 15, 18, 27, 30, 45, 54, 90, 135, 270
Факторы 271: 1, 271
Факторы 272: 1, 2, 4, 8, 16, 17, 34, 68, 136, 272
Факторы 273: 1, 3, 7, 13, 21, 39, 91, 273
Факторы 274: 1, 2, 137, 274
90 002 Факторы 275: 1, 5, 11, 25, 55, 275Факторы 276: 1, 2, 3, 4, 6, 12, 23, 46, 69, 92, 138, 276
Факторы 277: 1, 277
Факторы 278: 1, 2, 139, 278
Факторы 279: 1, 3, 9, 31, 93, 279
Факторы 280 : 1, 2, 4, 5, 7, 8, 10, 14, 20, 28, 35, 40, 56, 70, 140, 280
Факторы 281: 1, 281
Факторы 282 : 1, 2, 3, 6, 47, 94, 141, 282
Факторы 283: 1, 283
Факторы 284: 1, 2, 4, 71, 142, 284
Факторы числа 285: 1, 3, 5, 15, 19, 57, 95, 285
Факторы числа 286: 1, 2, 11, 13, 22, 26, 143, 286
Факторы числа 287: 1, 7, 41, 287
Факторы 288: 1, 2, 3, 4, 6, 8, 9, 12, 16, 18, 24, 32, 36, 48, 72, 96, 144, 288
Факторы 289 : 1, 17, 289
Факторы 290: 1, 2, 5, 10, 29, 58, 145, 290
Факторы 291: 1, 3, 97, 291
Факторы 292: 1, 2, 4, 73, 146, 292
Факторы 293: 1, 293
Факторы 294: 1, 2, 3, 6, 7, 14, 21, 42, 49 , 98, 147, 294
Факторы 295: 1, 5, 59, 295
Факторы 296: 1, 2, 4, 8, 37, 74, 148, 296
Факторы 297 : 1, 3, 9, 11, 27, 33, 99, 297
Факторы 298: 1, 2, 149, 298
Факторы 299: 1, 13, 23, 299
Множители 300: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 25, 30, 50, 60, 75, 100, 150, 300
Возможно, вас также заинтересует :
Нахождение всех множителей числа с помощью метода радуги
Кратные числа 1-100
Число и количество Практика T есть
1. Упростим выражение (5 1/3 -5 2 ) 6 .
Упростим выражение (5 1/3 -5 2 ) 6 . - 5 2/3
- 54
- 5 (8 1/3)
- 5 14
- (8 1/2 ) 2 = 2 3
- 4 · 4 · 4 · 4√4 = 4 9/2
- 5 1/2 · 5 2 / 3 5 1/2 ? = 5√5
- 6√5 / 6√5 2 = 5 -1/6
- 5 · 2 2/3 +3
- 5 · 2 2/3 +3 2/7
- 5 3 · 2½ + 7 · 3½
- 10 2/3 + 3 2/7
- 5 5 · 5 7/3
- 5 6
- 5 4
- 5 2/3
 Что из следующего является рациональным числом?
Что из следующего является рациональным числом? - 3√121 + 7
- 4+ 3 √150
- 7√30
- (8) 2/3 + (8) 1/5
- 73 1/3 фунтов
- 67 2/3 фунтов
- 110 фунтов
- 330 бутербродов
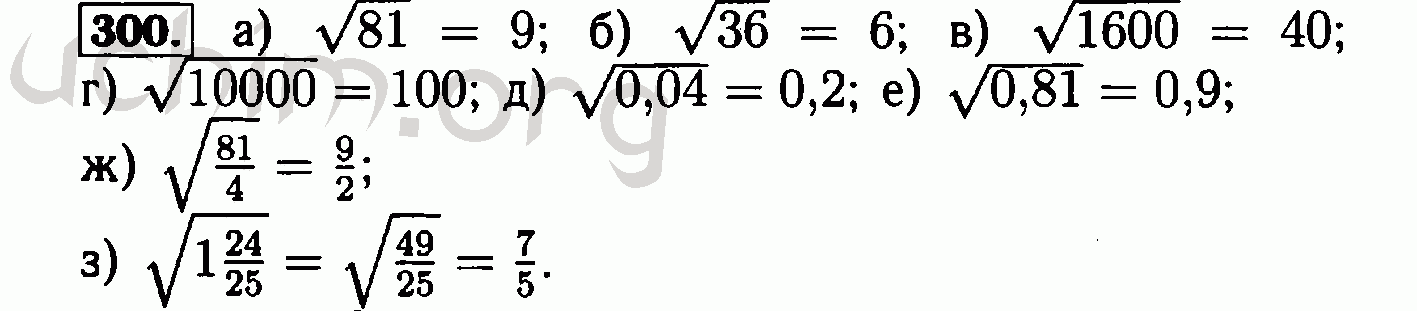 Какую из следующих единиц измерения лучше всего использовать для обозначения временной оси графика зависимости оставшегося материала отпрошло ли время, пока не осталось 6,1 грамма?
Какую из следующих единиц измерения лучше всего использовать для обозначения временной оси графика зависимости оставшегося материала отпрошло ли время, пока не осталось 6,1 грамма? - часов
- дней
- недель
- лет
- Мистер Болт выигрывает со счетом 3,75 секунды
- Мистер Болт выигрывает с результатом 2,08 секунды
- Олень выигрывает с результатом 3.75 секунд
- Олень побеждает на 2,08 секунды
- 72
- 60
- 30
- 24
Ответы и пояснения
1. D: Используйте два свойства показателей степени: b x — b y = b x + y и (b x ) y .То есть показатель степени по основанию представляет собой сумму степеней в произведении (если основания одинаковы), а результирующая степень, когда показатель степени возводится в степень, является произведением двух степеней. Начните с добавления степеней в скобках. Затем умножьте эту сумму на показатель в круглых скобках. (5 1/3 · 5 2 ) 6 = (5 7/3 ) 6 = 5 14 .
D: Используйте два свойства показателей степени: b x — b y = b x + y и (b x ) y .То есть показатель степени по основанию представляет собой сумму степеней в произведении (если основания одинаковы), а результирующая степень, когда показатель степени возводится в степень, является произведением двух степеней. Начните с добавления степеней в скобках. Затем умножьте эту сумму на показатель в круглых скобках. (5 1/3 · 5 2 ) 6 = (5 7/3 ) 6 = 5 14 .
2. C: Каждый из операторов следует правилу экспоненты.В букве A показатели внутри и снаружи скобок умножаются. (8½) 2 = 8 = 2 3 . В B основание одинаково для каждого члена в продукте, поэтому можно складывать все показатели. 4 1 · 4 1 · 4 1 · 4 1 4½ = 4 1 + 1 + 1 + 1 + ½ = 4 9/2 . В утверждении D основание одинаково для каждого члена частного, поэтому показатели можно вычесть. 6√5 / 6√5 2 = 51/6/ 52/6 = 5-1 / 6.C следует тому же правилу, что и B, но есть ошибка: 51/3 · 52/3 · 51/3 = 54/3 = 53√5 5√5.
В утверждении D основание одинаково для каждого члена частного, поэтому показатели можно вычесть. 6√5 / 6√5 2 = 51/6/ 52/6 = 5-1 / 6.C следует тому же правилу, что и B, но есть ошибка: 51/3 · 52/3 · 51/3 = 54/3 = 53√5 5√5.
3. B: Дробное экспоненциальное представление может быть получено с помощью следующего тождества: y √b x = b x / y · 5 3 √2 2 + 7 √ 3 2 = 5 · 2 2/3 + 3 2/7 . Это не может быть дополнительно упрощено другими правилами, регулирующими экспоненты, потому что основания не совпадают.
4.C: Сначала запишите радикалы как дробные показатели с одинаковым основанием. Затем добавьте показатели степени в числитель, чтобы записать произведение этих трех членов. Наконец, вычтите показатель степени в знаменателе и упростите:
58 · 3√52 · 5-3 / 3 √5 5 = 58 · 52/3 · 5-3 / 5 5 / 3 = 5 17/3 / 55/3 = 512/3 = 54
5.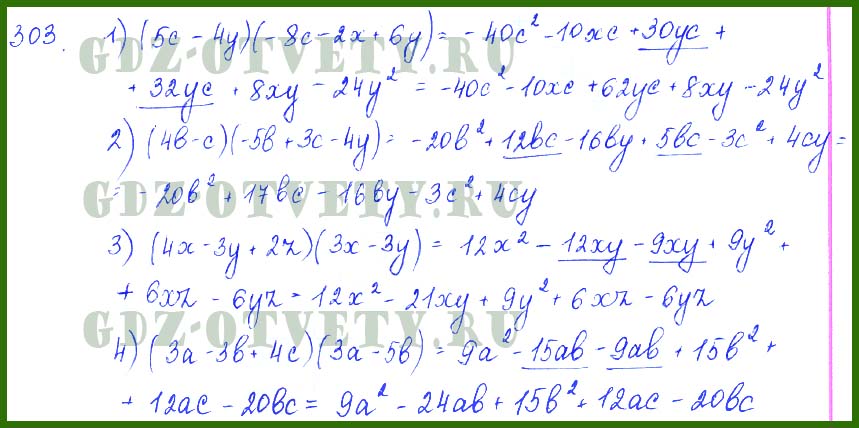 A: Иррациональные числа не могут быть записаны в виде дробей.√30, 3 √150 ,? и (8) 1/5 все являются иррациональными числами и остаются иррациональными числами после сложения и умножения (так что даже если 8 2/3 является рациональным, сумма не является). Однако √121 = 11 рационально и останется рациональным после любой операции с рациональным числом, включая сложение 7. (Кроме того, сумма или произведение рационального числа на иррациональное число будут иррациональными.)
A: Иррациональные числа не могут быть записаны в виде дробей.√30, 3 √150 ,? и (8) 1/5 все являются иррациональными числами и остаются иррациональными числами после сложения и умножения (так что даже если 8 2/3 является рациональным, сумма не является). Однако √121 = 11 рационально и останется рациональным после любой операции с рациональным числом, включая сложение 7. (Кроме того, сумма или произведение рационального числа на иррациональное число будут иррациональными.)
6. A: Позвольте единицам направлять решение. Сначала создайте дроби конверсии, используя данную информацию: 10 человек = 11 бутербродов и 20 фунтов = 90 бутербродов.Затем начните с количества людей и умножьте на дроби, убедившись, что единицы будут отменены соответствующим образом. Ответом должны быть фунты мяса для обеда, поэтому фунты должны быть единственной единицей.
(300 человек) · (11 бутербродов) / (10 человек) · (20 фунтов) / (90 бутербродов)
= 300 человек · (11 бутербродов) / (10 человек) · (20 фунтов) / (90 бутербродов) = 73,333 фунта
Дереку нужно купить 73.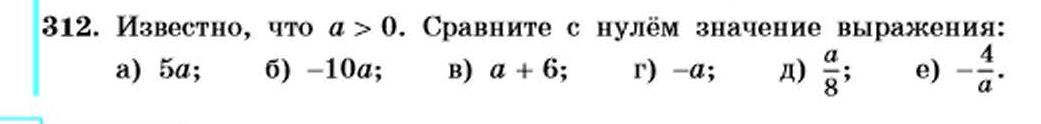 333 фунта обеденного мяса.
333 фунта обеденного мяса.
7. D: Поскольку она покупает по одному куки-файлу на каждого ученика, сумма, которую она тратит, зависит от количества учеников; Стоимость — это зависимая переменная, зависящая от количества студентов, которая является независимой переменной. Варианты C и D показывают эту связь с независимой переменной на оси x и зависимой от оси y. Однако масштаб оси затрат в варианте C слишком велик: на 30 студентов Меган тратит всего около 16 долларов.Поскольку масштаб оси затрат в варианте D более подходит, выбор D является лучшим ответом.
8. C: Период полувыведения составляет одну неделю. Чтобы масса распалась с 400 кг до 6,1 грамма, потребуется много периодов полураспада. Например, через 10 недель масса составляет 400 ( 1 / 2 ) 10 = 0,3906 кг = 390,6 граммов . Выражение времени в единицах меньше, чем несколько недель, приведет к громоздкой и излишне точной оси времени.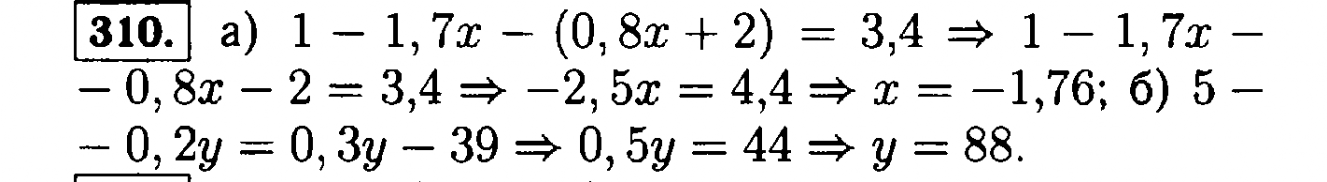 С другой стороны, обозначение временной оси в годах не дает достаточного количества делений для точного определения отдельных периодов полураспада.Поэтому маркировка оси в неделях — лучший выбор.
С другой стороны, обозначение временной оси в годах не дает достаточного количества делений для точного определения отдельных периодов полураспада.Поэтому маркировка оси в неделях — лучший выбор.
9. D: Мы смогли найти скорость мистера Болта (пройденное расстояние, разделенное на прошедшее время), но поскольку вопрос только спрашивает, кто и сколько времени побеждает, а мы уже знаем, сколько времени мистер Болт берет, нам не нужно. Чтобы сравнить двух бегунов, нам просто нужно преобразовать скорость оленя из км / ч в м / с и рассчитать, сколько секунд потребуется оленю, чтобы пробежать 100 м. Настройте дробные части преобразования, чтобы единицы соответственно отменялись, и умножайте их:
48 км / час · 1000 м / 1 км · 1 час / 60 мин · 1 мин / 60 с = 48 км / час · 1000 м ) / (1 км ) · 1 час / 60 мин 6 мин / 60 сек = 13. 33 м / с
33 м / с
Скорость оленя составляет 13,33 м / с, и чтобы узнать время оленя, разделите длину забега на его скорость: 100 м / 13,33 м / с = 7,5 секунды, а олень побеждает! Сравните два раза: 9,58 (болт) — 7,5 (олень) = 2,08. Олень выигрывает на 2,08 секунды.
10. B: Используйте размерный анализ, чтобы преобразовать данную информацию в необходимое количество таблеток. Постройте дроби преобразования на основе заданных эквивалентностей. Например, утверждение «принимать 60 мг каждые 4 часа» соответствует дроби 60 мг / 4 часа .Используйте эти дроби или их обратные значения, чтобы убедиться, что единицы отменяют и оставляют желаемую единицу, таблетки:
5 дней — 24 часа / 1 день — 60 мг / 4 часа · 1 таблетка / 30 мг = 5 дней — 24 часов / 1 день — 60 мг / 4 часов — 1 таблетка / 30 мг = 60 таблеток.
: Домашнее задание и ответы :: Slader
Упражнения
1. 2 ответ 2.Нет, это не функция.
1 ответ 3.Да, график представляет собой линейную функцию.
1 ответ 4.Да, график является линейной функцией.
1 ответ 5.Да, каждая пара заказов удовлетворяет линейной функции.
1 ответ 6.
Да, упорядоченные пары не удовлетворяют линейной функции.
1 ответ 7.Эти точки удовлетворяют линейной функции.
2 ответ 8.Это не линейная функция.
2 ответ 9.См. Объяснение результата.
1 ответ 10.Это линейная функция.
1 ответ 11. Это не линейная функция.
Это линейная функция.
1 ответ 13.Результат на картинке.
1 ответ 14.домен (x) равен или больше 0, а диапазон равен или больше 6. Для графика см. рисунок.
1 ответ 15.Это функция, но это не линейная функция.
1 ответ 16. Это функция, и она линейна.
Это функция, но не линейная.
1 ответ 18.Они не удовлетворяют линейной функции.
1 ответ 19.они удовлетворяют линейной функции
1 ответ 20.они удовлетворяют линейной функции.
1 ответПроизношение числа — WebMath
Быстро! Мне нужна помощь с:
Выберите пункт справки по математике . .. Исчисление, Производные вычисления, Интеграционное вычисление, Частное правило Монеты, Подсчет комбинаций, Поиск всех комплексных чисел, Сложение комплексных чисел, Вычисление с комплексными числами, Умножение комплексных чисел, Степень комплексных чисел, Преобразование вычитания, Преобразование площади, Преобразование длины, Преобразование длины, Преобразование длины , VolumeData Analysis, Find the AverageData Analysis, Find the Standard DeviationData Analysis, HistogramsDecimals, Convert to a дробь, Электричество, Стоимость разложения, IntegerFactors, Greatest CommonFactors, Least CommonFractions, AddingFractions, ComparingFractions, ConvertingFractions, Convert to a decimalFractions, DécimalFractions, Convert to a decimalFractions ВычитаниеФракции, Что это такое: Геометрия, Коробки, Геометрия, Круги, Геометрия, Цилиндры, Геометрия, Прямоугольники, Геометрия, Правые треугольники, Геометрия, Сферы, Геометрия, Квадраты, Графики, Линии, Графики, Любая функция, Графики, Круги, График hing, EllipsesGraphing, HyperbolasGraphing, InequalitiesGraphing, Polar PlotGraphing, (x, y) pointInequalities, GraphingInequalities, SolvingInterest, CompoundInterest, SimpleLines, Equation from point and slopeLines, The Equation from slopeLines Theotation, The Equation from slopeLines Theotation и Y-intation , Нахождение шансовМатематика, Практика полиномов по математике, Практика основМетрическая система, Преобразование чисел, Сложение чисел, Вычисление с числами, Вычисление с переменными числами, Деление чисел, Умножение чисел, Сравнение числовых линий, Числовые строки, Разместите значения чисел, Произношение чисел, Округление чисел, Вычитание числа с сложением, Вычитание числа Квадратные многочлены, Деление многочленов, Факторизация разности квадратов Многочлены, Факторизация триномов Полиномы, Факторинг с GCF Полиномы, Умножение многочленов, Возведение в степеньПрактика, Математические задачиПропорции, Квадратные уравнения ormulaQuadratic Equations, Solve by FactoringRadicals, Other RootsRadicals, Square RootsRatios, Что они представляют собой Устранение, Экономия на продажной цене, РасчетНаучная нотация, ПреобразованиеНаучной нотации, ДелениеНаучная нотация, УмножениеФормы, ПрямоугольникиУпрощение, Упрощение, Упрощение продуктов, Упрощение, Упрощение, Упрощение, Упрощение, Упрощение, Упрощение продуктов , Правые треугольники, Ветер, Рисунок
.. Исчисление, Производные вычисления, Интеграционное вычисление, Частное правило Монеты, Подсчет комбинаций, Поиск всех комплексных чисел, Сложение комплексных чисел, Вычисление с комплексными числами, Умножение комплексных чисел, Степень комплексных чисел, Преобразование вычитания, Преобразование площади, Преобразование длины, Преобразование длины, Преобразование длины , VolumeData Analysis, Find the AverageData Analysis, Find the Standard DeviationData Analysis, HistogramsDecimals, Convert to a дробь, Электричество, Стоимость разложения, IntegerFactors, Greatest CommonFactors, Least CommonFractions, AddingFractions, ComparingFractions, ConvertingFractions, Convert to a decimalFractions, DécimalFractions, Convert to a decimalFractions ВычитаниеФракции, Что это такое: Геометрия, Коробки, Геометрия, Круги, Геометрия, Цилиндры, Геометрия, Прямоугольники, Геометрия, Правые треугольники, Геометрия, Сферы, Геометрия, Квадраты, Графики, Линии, Графики, Любая функция, Графики, Круги, График hing, EllipsesGraphing, HyperbolasGraphing, InequalitiesGraphing, Polar PlotGraphing, (x, y) pointInequalities, GraphingInequalities, SolvingInterest, CompoundInterest, SimpleLines, Equation from point and slopeLines, The Equation from slopeLines Theotation, The Equation from slopeLines Theotation и Y-intation , Нахождение шансовМатематика, Практика полиномов по математике, Практика основМетрическая система, Преобразование чисел, Сложение чисел, Вычисление с числами, Вычисление с переменными числами, Деление чисел, Умножение чисел, Сравнение числовых линий, Числовые строки, Разместите значения чисел, Произношение чисел, Округление чисел, Вычитание числа с сложением, Вычитание числа Квадратные многочлены, Деление многочленов, Факторизация разности квадратов Многочлены, Факторизация триномов Полиномы, Факторинг с GCF Полиномы, Умножение многочленов, Возведение в степеньПрактика, Математические задачиПропорции, Квадратные уравнения ormulaQuadratic Equations, Solve by FactoringRadicals, Other RootsRadicals, Square RootsRatios, Что они представляют собой Устранение, Экономия на продажной цене, РасчетНаучная нотация, ПреобразованиеНаучной нотации, ДелениеНаучная нотация, УмножениеФормы, ПрямоугольникиУпрощение, Упрощение, Упрощение продуктов, Упрощение, Упрощение, Упрощение, Упрощение, Упрощение, Упрощение продуктов , Правые треугольники, Ветер, Рисунок
Калькулятор расширенной формы
Использование калькулятора
Калькулятор расширенной формы показывает расширенные формы чисел, включая расширенную форму записи, расширенную форму множителя, расширенную экспоненциальную форму и форму слова.
Расширенная форма или расширенная запись — это способ записи чисел для просмотра математического значения отдельных цифр. Когда числа разделены на отдельные разряды и десятичные разряды, они также могут образовывать математическое выражение. 5,325 в развернутой форме записи — это 5,000 + 300 + 20 + 5 = 5,325.
Вы можете записывать числа в развернутой форме несколькими способами.
Запишите 5,325 в форме развернутого числа
Стандартная форма :
5,325
Расширенная форма:
5 000 + 300 + 20 + 5 = 5 325
Расширенная форма факторов:
(5 × 1000) + (3 × 100) + (2 × 10) + (5 × 1) = 5325
Расширенная экспоненциальная форма:
(5 × 10 3 ) + (3 × 10 2 ) + (2 × 10 1 ) + (5 × 10 0 ) = 5,325
Словоформа:
пять тысяч триста двадцать пять
Обратите внимание, что в Англии и Великобритании фраза «стандартная форма» относится к обозначению научных чисел, которое в США называется «научным обозначением». «Стандартная форма в Великобритании и научная система обозначений в США означают по существу одно и то же, когда речь идет об обозначениях, используемых для представления очень больших или очень маленьких чисел, таких как 4,959 × 10 12 или 1,66 × 10 -24 .
«Стандартная форма в Великобритании и научная система обозначений в США означают по существу одно и то же, когда речь идет об обозначениях, используемых для представления очень больших или очень маленьких чисел, таких как 4,959 × 10 12 или 1,66 × 10 -24 .
Связанные калькуляторы
Смотрите наши Конвертер чисел в слова для получения имен словоформных чисел. Этот калькулятор особенно полезен для поиска словоформы с очень маленькими десятичными знаками.
экспоненциальных и логарифмических моделей
экспоненциальных и логарифмических моделейСодержание: Эта страница соответствует § 4.5 (с. 359) текста.
Предлагаемые задачи из текста:
с. 366 # 7,9,15,17,25,33,35,69
Экспоненциальный рост и спад
Другие модели
Экспоненциальный рост и спад
Два общих типа математических моделей:
Экспоненциальный рост: y = a e bx , b> 0.
Экспоненциальный спад: y = a e -bx , b> 0.
Пример 1.
В течение 1980-х годов население одного города увеличилось со 100 000 до 205 000 человек. Перечислены популяции по годам в таблице ниже.
год
1980
1981
1982 г.
1983 г.
1984
1985
1986
1987
1988 г.
1989 г.
Население в тысячах
100
108
117
127
138
149
162
175
190
205
Эти данные хорошо аппроксимируются моделью экспоненциального роста P = 100 e 0.
08t , где t — номер лет с 1980 г. Другими словами, 1980 г. соответствует t = 0, 1981 г. соответствует t = 1 и т. д. точки и модель изображены на графике ниже.
Точки данных о населении и модель P = 100 e 0,08 t
где t — количество лет, прошедших с 1980 года.
Задача 1. Используйте модель для прогнозирования численности населения города в 1994 году.
1991 соответствует t = 11, поэтому наша модель предсказывает, что численность населения составит
человек.P = 100 e 0.08 * 11 = 241 тыс.
Задача 2: Согласно нашей модели, когда население достигнет 300 тысяч?
Для решения этой задачи мы устанавливаем 100 e 0,08t равным 300 и решаем относительно t.
100 е 0,08 т = 300
e 0,08t = 3 Возьмите натуральный логарифм обеих частей.
ln e 0,08 t = ln 3
0,08t = ln 3
t = (ln 3) / 0.
08 = 13,73, приблизительно.
Таким образом, ожидается, что численность населения достигнет 300 тысяч примерно на трех четвертях всего года. 1993.
Важно понимать ограничения этой модели. Хотя из графика очевидно, что для t между 0 и 9, значения модели очень близки к фактическим значениям населения, мы не должны предполагать, что наша модель будет дают точный прогноз населения для значений t намного больше 9.Например, модель предсказывает что в 2080 году (t = 100) население города составит почти 300 миллионов! Это маловероятно.
Предположим, мы знаем, что переменная y может быть выражена в форме ae bx , но мы не знаем значений а и б. Если нам даны любые две точки на графике y, то можно найти числа a и b. В В простейшем случае, который часто встречается в приложениях, мы знаем значение y, когда x = 0 и еще одна точка на графике y.
Пример 2.
Предположим, что популяция P растет экспоненциально, поэтому P = ae bt , где t измеряется в годах.
Если P = 15000 в 1990 году, а P выросло до 17000 в 1993 году, найдите формулу для P.
Пусть t будет количеством лет, прошедших с 1990 года. Тогда a = 15000 , значение P при t = 0.
Обратите внимание, что t можно было выбрать иначе. Например, мы могли бы позволить t быть количеством лет, прошедших с 1900 года.Но тогда мы не узнаем значение P при t = 0, поэтому мы не узнаем значение a сразу.
Нам еще нужно найти b. Все, что мы знаем о b, — это то, что он положительный, так как население растет. С помощью значение, которое мы нашли для a, имеем
P = 15000 e bt .
1993 год соответствует t = 3, поэтому мы подставляем P = 17000 и t = 3 в уравнение выше и решаем относительно б.
17000 = 15000 e 3b
Уравнения такого вида мы решали несколько раз.Первый шаг — выделить экспоненциальный член. потом возьмите натуральный логарифм обеих частей.
17/15 = e 3b
ln (17/15) = ln e 3b
ln (17/15) = 3b
b = (ln (17/15)) / 3 = 0,0417 (приблизительно)
Следовательно, P = 15000 e 0,0417 t
На основе этой модели, когда население достигнет 20000?
Установите P равным 20000 и решите относительно t.
20000 = 15000 е 0,0417 т
4/3 = e 0,0417 т
ln (4/3) = ln e 0,0417 т
ln (4/3) = 0,0417 т
t = (ln (4/3)) / 0,0417 = 6,9 года
Итак, мы ожидаем, что к концу 1996 года численность населения достигнет 20000 человек.
Упражнение 1 :
Найдите модель типа P = ae bt , где t — количество лет, прошедших с 1970 года, если P = 30000 в 1970 году. и P = 36000 в 1977 году.Используйте эту модель, чтобы спрогнозировать значение P в 1980 году.
Ответ
Когда коэффициент при x (или независимо от названия независимой переменной) равен отрицательным , мы моделируем убывающая переменная . Это называется экспоненциальным затуханием. Проиллюстрируем экспоненциальный спад, рассмотрев радиоактивное вещество. Образец радиоактивного вещества со временем распадается.
Пример 3.
Масса (в граммах) радиоактивного материала в образце определяется как N = 100e -0.0017t , где t — измеряется годами.
Найдите период полураспада этого радиоактивного вещества.
Период полураспада радиоактивного вещества — это время, необходимое для распада половины заданного образца. Обратите внимание, что период полураспада не зависит от размера образца. Если период полураспада определенного радиоактивного материала составляет 700 лет, то если начальная масса образца 1000 грамм, то через 700 лет будет 500 грамм.
Если начальная масса пробы всего 8 грамм, через 700 лет будет 4 грамма.
В этом примере масса радиоактивного материала составляет 100 грамм в момент времени t = 0. Следовательно, период полураспада равен количество времени, необходимое для разложения образца, до 50 граммов. Таким образом, мы можем найти период полураспада, установив N равным до 50 и решение для t.
100e -0,0017t = 50
e -0,0017t = 0,5
Примечание. Если бы исходное количество составляло 800 граммов, то нам пришлось бы решить уравнение 800e -0.0017t = 400, и после деления обеих частей на 800 мы получим e -0,0017t = 0,5, что совпадает с уравнением над. Вот почему период полураспада не зависит от исходного количества.
ln e -0,0017t = ln 0,5
-0,0017t = ln 0,5
t = (ln 0,5) / -0,0017 = 408 лет (приблизительно)
Вопрос : Почему (ln 0,5) / — 0,0017 равно (ln 2) / 0.
0017?
В предыдущем разделе мы обсудили важный пример экспоненциального роста, а именно непрерывный начисление процентов. Вычисление периода полураспада радиоактивного вещества очень похоже на вычисление удвоение времени для инвестиций.
Пример 4.
Если 1000 долларов инвестируются под 9% годовых, непрерывно начисляемых, сколько времени потребуется для инвестирования удвоить? Используя формулу сложных процентов A = Pe rt , получаем
А = 1000e 0.09т
Мы хотим найти время, которое потребуется для удвоения инвестиций, то есть роста до 2000 долларов, поэтому мы устанавливаем А равно 2000 и решите относительно t.
1000e 0,09t = 2000 Разделите обе стороны на 1000.
е 0,09 т = 2
Примечание : Как и период полураспада, время удвоения не зависит от начальных вложений P.
Если бы мы начали с 50 долларами и спросили, сколько времени пройдет, прежде чем у нас будет 100 долларов, тогда мы бы решили уравнение
50e 0.09t = 100, и после деления обеих частей на 50 мы снова получим e 0,09t = 2.
ln e 0,09 t = ln 2
0,09 t = ln 2
t = (ln 2) /0,09 = 7,7 года (приблизительно).
Вопрос: Если вы постоянно инвестируете 3000 долларов под 9% годовых, сколько у вас будет через 15 с половиной лет?
Ответ: Около 12000 долларов. Это легко приблизить, потому что время удвоения равно 7.7 лет, то есть 15,5 лет соответствует до чуть более двух удвоений. 3000 -> 6000 -> 12000.
Упражнение 2 :
Сколько времени нужно, чтобы инвестировать в тройной на% 11 непрерывно? Ответ
Вернуться к содержанию
Другие модели
Пример 5.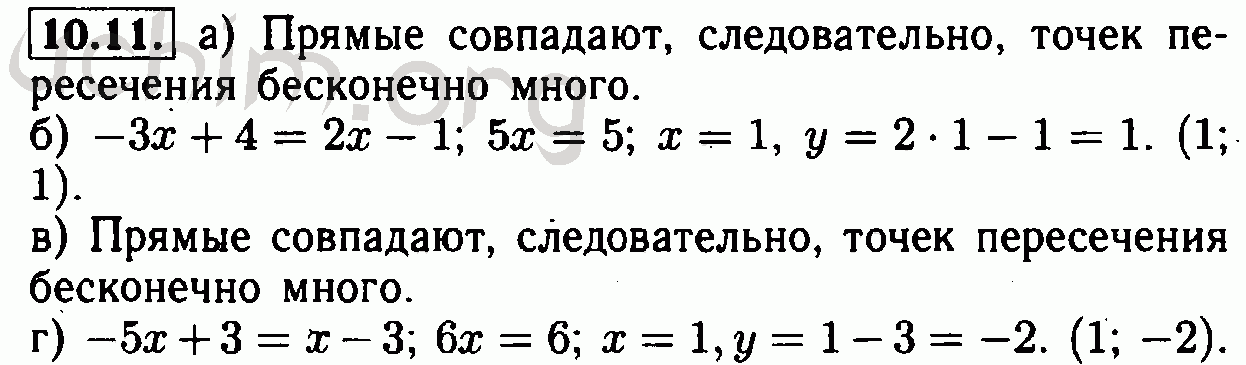
Рассмотрим следующие точки данных.
х
1
2
3
4
5
6
7
г
0.5
2,6
3,6
4,5
4,9
5,4
5,7
Когда мы строим эти точки, мы видим, что они не лежат ни на одной экспоненциальной кривой, но форма очень очень похоже на логарифмический график.Это говорит о том, что логарифмическая модель разумна. График ниже показывает точки данных и функция y = 0,63 + 2,7 ln x, которая достаточно хорошо соответствует точкам данных.
Вернуться к содержанию
Значение места
На протяжении всей истории большинство (но не все!) Человеческих культур использовали десятичную систему счисления, основанную на числе 10 .
В нашей позиционной десятичной системе счисления цифры имеют разные значения в зависимости от того, где они находятся размещен . Каждый размещаемая стоимость является 10 умноженное на разрядное значение справа и одну десятую разрядного значения слева.
96 548 327
Этот номер состоит из восьми цифр.
в те место это 7 , со значением 7 × 1 знак равно 7 .
в десятки место это
2
, со значением
2
×
10
знак равно
20
.
в сотни место это 3 , со значением 3 × 100 знак равно 300 .
в тысячи место это 8 , со значением 8 × 1000 знак равно 8000 .
в десять тысяч место это 4 , со значением 4 × 10 , 000 знак равно 40 , 000 .
в сотни тысяч место это 5 , со значением 5 × 100 , 000 знак равно 500 , 000 .
в миллионы место это
6
, со значением
6
×
1
,
000
,
000
знак равно
6
,
000
,
000
.
в десять миллионов место это 9 , со значением 9 × 10 , 000 , 000 знак равно 90 , 000 , 000 .
Итоговое значение числа — это сумма всех значений разряда:
000 + 6000000 + 500000 + 40000 + 8000 + 300 + 20 + 7 знак равно 96 , 548 , 327
.


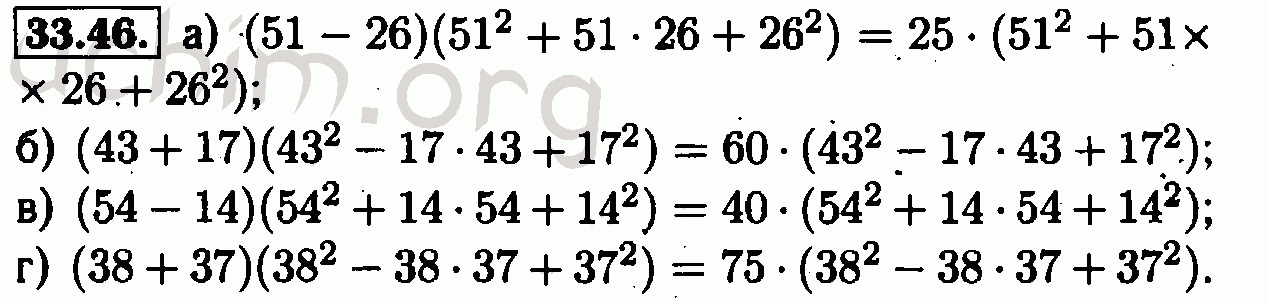 08t , где t — номер
лет с 1980 г. Другими словами, 1980 г. соответствует t = 0, 1981 г. соответствует t = 1 и т. д.
точки и модель изображены на графике ниже.
08t , где t — номер
лет с 1980 г. Другими словами, 1980 г. соответствует t = 0, 1981 г. соответствует t = 1 и т. д.
точки и модель изображены на графике ниже. 08 = 13,73, приблизительно.
08 = 13,73, приблизительно.
 Если
начальная масса пробы всего 8 грамм, через 700 лет будет 4 грамма.
Если
начальная масса пробы всего 8 грамм, через 700 лет будет 4 грамма. 0017?
0017? Если бы мы начали
с 50 долларами и спросили, сколько времени пройдет, прежде чем у нас будет 100 долларов, тогда мы бы решили уравнение
Если бы мы начали
с 50 долларами и спросили, сколько времени пройдет, прежде чем у нас будет 100 долларов, тогда мы бы решили уравнение