ГДЗ Математика 2 класс. Волкова, Моро. Проверочные работы с подробными ответами
- Главная
- ГДЗ
- 2 класс
- Математика
-
Волкова, Моро.
 Проверочные работы
Проверочные работы
Похожие ГДЗ:
Учебник часть 1, 2
Рабочая тетрадь часть 1, 2
Быстрый поиск
Список страниц
Числа от 1 до 100. Нумерация
Страница 4. Вариант 1. № 1
Страница 5. Вариант 2. № 1
Страница 6. Вариант 1. № 2
Страница 7. Вариант 2. № 2
Страница 8. Вариант 1. № 3
Страница 9. Вариант 2. № 3
Страница 10. Вариант 1. № 4
Страница 11. Вариант 2. № 4
Страница 12. Вариант 1. Тест 1
Страница 13. Вариант 2. Тест 1
Страница 14. Вариант 1. Тест 2
Страница 15.
Сложение и вычитание
Страница 16. Вариант 1. № 1
Страница 17. Вариант 2. № 1
Страница 18. Вариант 1. № 2
Страница 19. Вариант 2. № 2
Страница 20. Вариант 1. № 3
Страница 21. Вариант 2. № 3
Страница 22. Вариант 1. № 4-5
Страница 23. Вариант 2. № 4-5
Страница 24. Тест 1. Вариант 1
Страница 25. Тест 1. Вариант 2
Страница 26. Тест 2. Вариант 1
Страница 27. Тест 2. Вариант 2
Страница 28. Вариант 1. № 1
Страница 29. Вариант 2. № 1
Страница 30. Вариант 1. № 2
Страница 31.
Что узнали. Чему научились.
Страница 38. Вариант 1. Тест 1 Страница 39. Вариант 2. Тест 1 Страница 40. Вариант 1. Тест 2 Страница 41. Вариант 2. Тест 2
Сложение и вычитание (продолжение)
Страница 42. Вариант 1. № 1
Страница 43. Вариант 2. № 1
Страница 44. Вариант 1. № 2
Страница 45. Вариант 2. № 2
Страница 46. Вариант 1. № 3
Страница 47. Вариант 2. № 3
Страница 48. Вариант 1. № 4
Страница 49. Вариант 2. № 4
Страница 50. Вариант 1. Тест
Страница 51. Вариант 2. Тест
Вариант 2. № 2
Страница 46. Вариант 1. № 3
Страница 47. Вариант 2. № 3
Страница 48. Вариант 1. № 4
Страница 49. Вариант 2. № 4
Страница 50. Вариант 1. Тест
Страница 51. Вариант 2. Тест
Умножение и деление
Страница 52. Вариант 1. № 1 Страница 53. Вариант 2. № 1 Страница 54. Вариант 1. № 2 Страница 55. Вариант 2. № 2 Страница 56. Вариант 1. № 3 Страница 57. Вариант 2. № 3
Умножение и деление (продолжение)
Страница 58. Вариант 1. № 1
Страница 59. Вариант 2. № 1
Страница 60. Вариант 1. № 2
Страница 61. Вариант 2. № 2
Страница 62. Вариант 1. № 3
Страница 63. Вариант 2. № 3
Страница 64. Вариант 1. Тест 1
Страница 65. Вариант 2. Тест 1
Страница 66. Вариант 1. Тест 2
Страница 67. Вариант 2. Тест 2
Вариант 2. № 1
Страница 60. Вариант 1. № 2
Страница 61. Вариант 2. № 2
Страница 62. Вариант 1. № 3
Страница 63. Вариант 2. № 3
Страница 64. Вариант 1. Тест 1
Страница 65. Вариант 2. Тест 1
Страница 66. Вариант 1. Тест 2
Страница 67. Вариант 2. Тест 2
Страница 68. Вариант 1. Тест 1 Страница 69. Вариант 2. Тест 1 Страница 70. Вариант 1. Тест 2 Страница 71. Вариант 2. Тест 2 Страница 72. Вариант 1. Тест 3 Страница 72. Вариант 2. Тест 3
Поделись с друзьями в социальных сетях:
Описание ГДЗ
Смотреть ответы
Математика 2 класс
Проверочные работы
Авторы: Моро М. И., Волкова С.И.
И., Волкова С.И.
2015-2022 год
К списку ответов
Учебник часть 1, 2
Математика 2 класс
Моро М.И., Степанова С.В., Волкова С.И., Бантова М.А., Бельтюкова Г.В.
Рабочая тетрадь часть 1, 2
Математика 2 класс
Моро М.И., Волкова С.И.
|
Эта статья цитируется в 5 научных статьях (всего в 5 статьях) Экспоненциальные тесты, основанные на характеристике Ахсануллы и их эффективности К. Санкт-Петербургский государственный университет, Санкт-Петербург, Россия Полнотекстовый PDF (287 КБ) Ссылки: HTML Реферат: Мы строим интегральные и супремумные критерии экспоненциальности на основе характеристики экспоненциального закона, данной Ахсануллой. Мы обсуждаем предельные распределения и большие отклонения новой тестовой статистики при нулевой гипотезе и вычисляем их локальную эффективность по Бахадуру при обычных параметрических альтернативах. Даны условия локальной оптимальности новых статистик. Ключевые слова и фразы: экспоненциальный закон, проверка гипотез, характеризация, $U$- и $V$-статистика, большие уклонения, эффективность Бахадура, локальная оптимальность. Получено: 17.02.2013 Английская версия:  , том 204, выпуск 1, страницы 42–54 , том 204, выпуск 1, страницы 42–54 DOI: https://doi.org/10.1007/s10958-014-2185-4 Библиографические базы данных: Тип документа: Артикул УДК: 519.2 Язык: Русский Ссылка: К. Ю. Волкова, Я. Ю. В. Никитин, “Критерии экспоненциальности, основанные на характеристике Ахсануллы, и их эффективности”, Вероятность и статистика. Часть 19, Зап. научн. Сем. ПОМИ, 412, ПОМИ, СПб, 2013, 69–87; Дж. Матем. науч. (Нью-Йорк), 204:1 (2015), 42–54 Цитирование в формате AMSBIB Варианты соединения: Эта публикация цитируется в следующих статьях:
Ссылки на статьи в Google Scholar: русские цитаты,
английские цитаты | QR-? | ||||||||||||||||||||||||||||||||||||||||||
К.Ю. Волкова, Я. Ю. В. Никитин, “Критерии согласия для распределения степенных функций, основанные на характеризации Пури–Рубина, и их эффективности”, Вероятность и статистика. Часть 18, Зап. научн. Сем. ПОМИ, 408, ПОМИ, СПб, 2012, 115–130; Дж.
 Матем. науч. (Нью-Йорк), 199:2 (2014), 130–138
Матем. науч. (Нью-Йорк), 199:2 (2014), 130–138| Записки научных семинаров ПОМИ, 2012, том 408, страницы 115–130 (Ми знсл5496) |
Эта статья цитируется в 3 научных статьях (всего в 3 статьях)
Тесты согласия для распределения функции мощности на основе характеристики Пури-Рубина и их эффективности
К.Ю. Волкова , Я. Ю. Никитин
Санкт-Петербургский государственный университет, механико-математический факультет, Санкт-Петербург, Россия
Полнотекстовый PDF (265 КБ)
Ссылки:
HTML
Реферат: Мы строим интегральные и супремум-критерии согласия для семейства функций распределения мощности.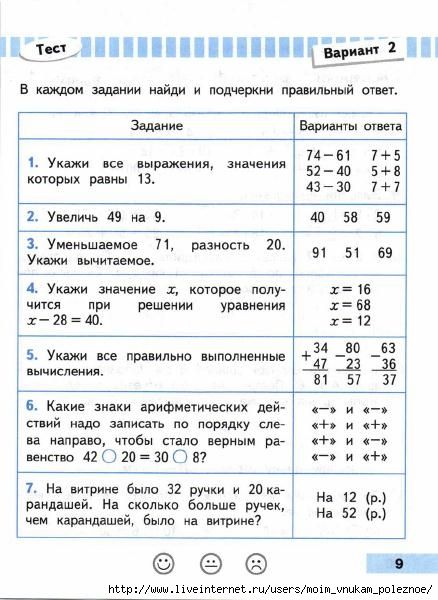 Тестовые статистики являются функционалами $U$-эмпирических процессов и основаны на классической характеристике семейства распределений степенных функций Пури и Рубина. Мы описываем логарифмическую асимптотику больших отклонений тестовой статистики при нулевой гипотезе и вычисляем их локальную эффективность по Бахадуру при обычных параметрических альтернативах. Даны условия локальной оптимальности новых статистик.
Тестовые статистики являются функционалами $U$-эмпирических процессов и основаны на классической характеристике семейства распределений степенных функций Пури и Рубина. Мы описываем логарифмическую асимптотику больших отклонений тестовой статистики при нулевой гипотезе и вычисляем их локальную эффективность по Бахадуру при обычных параметрических альтернативах. Даны условия локальной оптимальности новых статистик.
Ключевые слова и фразы: функция распределения мощности, $U$-статистика, характеризация, эффективность Бахадура, проверка гипотез, локальная оптимальность.
Поступило: 02.10.2012
Английская версия:
Журнал математических наук (Нью-Йорк), 2014 г., том 199, выпуск 2, страницы 130–138
DOI: https://doi.org/10.1007/s10958-014-1840-0
Библиографические базы данных:
Тип документа: Артикул
УДК: 519. 2
2
Язык: Русский
Ссылка: К. Ю. Волкова, Я. Ю. В. Никитин, “Критерии согласия для распределения степенных функций, основанные на характеризации Пури–Рубина, и их эффективности”, Вероятность и статистика. Часть 18, Зап. научн. Сем. ПОМИ, 408, ПОМИ, СПб, 2012, 115–130; Дж. Матем. науч. (Нью-Йорк), 199:2 (2014), 130–138
Цитирование в формате AMSBIB
\RBibitem{VolNik12}
\by К.~Ю.~Волкова, Я.~Ю.~Никитин
\paper Критерии согласия для степенной функции распределения на основе характеристики Пури--Рубина и их эффективности
\inbook Вероятность и статистика. Часть~18
\serial Зап. научн. Сем. ПОМИ
\год 2012
\том 408
\страниц 115--130
\публ ПОМИ
\публадр СПб
\mathnet{http://mi.mathnet.ru/znsl5496}
\mathscinet{http://www.ams.org/mathscinet-getitem?mr=3032212}
\transl
\jour J. Math. науч. (Нью-Йорк)
Math. науч. (Нью-Йорк)
\год 2014
\том 199
\выпуск 2
\страниц 130--138
\crossref{https://doi.org/10.1007/s10958-014-1840-0}
\scopus{https: //www.scopus.com/record/display.url?origin=inward&eid=2-s2.0-844852}
Варианты соединения:
Эта публикация цитируется в следующих статьях:
- Волкова К., “Критерии согласия распределения Парето на основе его характеристики”, Стат. Метод. Appl., 25:3 (2016), 351–373
- Я. Ю. Никитин, “Тесты, основанные на характеристиках, и их эффективность: обзор”, Acta Comment. ун-т Тарту. матем., 21:1 (2017), 3–24
- Зайцев А.Ю. Каган А.М. Никитин Я.Ю., “К истории петербургской вероятностно-статистической школы. Ив. Характеристика распределений и предельные теоремы в статистике”, Вестн.


 Проверочные работы
Проверочные работы

 mathnet.ru/znsl5652}
mathnet.ru/znsl5652} 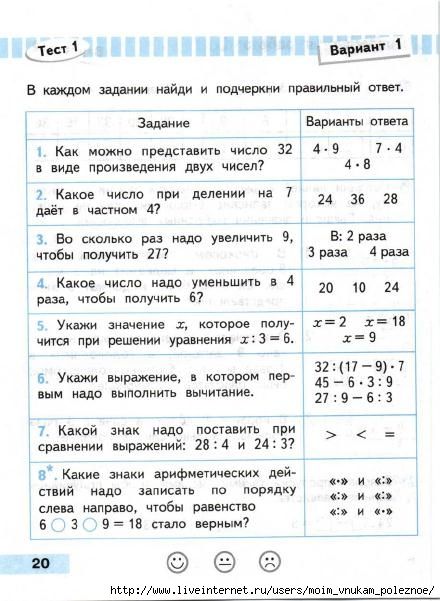 Stat. вычисл. Симул., 88:1 (2018), 108–139
Stat. вычисл. Симул., 88:1 (2018), 108–139