ГДЗ по математике 6 класс Дорофеев, Шарыгин
Решебник – незаменимое подспорье для обучения школьников 6 класса математике. Введение ФГОС ужесточает требования к учебе, а некоторым ребятам с математикой совладать сложно. Пособие, написанное квалифицированными специалистами, содержит решения к учебнику по математике Г.В. Дорофеева и соавторов, приносит заметную пользу.
ГДЗ – ученикам
Изучение готовых решений к трудным заданиям после уяснения алгоритма позволяет решать подобные самостоятельно. С ГДЗ легко можно проверить выполненные задачи, учиться без боязни насмешек соучеников и осуждения учителя. Особенно выручает решебник, если по болезни случился пропуск уроков, ведь помочь с предметом оказывается некому. При затруднениях с математикой желательно решать задания сверх заданного учителем объема, укреплять знания для будущих достойных результатов.
ГДЗ – родителям
Пособие востребовано родителями по весомым причинам. Решебник позволяет:
• эффективно контролировать ДЗ ребенка;
• установить самостоятельно его фактический уровень знаний;

Родители должны предостеречь от бессмысленного, бездумного списывания ГДЗ учеником. При изучении математики трудиться нужно напряженно, неизбежная, пугающая школьников ГИА, ждет их уже в 9 классе.
Как подготовить себя самостоятельно?
Шестиклассники завершают изучение курса классической математике, подготавливаясь к обучению в следующем, седьмом классе, двум отдельным математическим дисциплинам — геометрии и алгебре. Учитывая, что вопросы и задания из классической математики составляют значительный блок знаний, контролируемый в рамках ОГЭ и даже ЕГЭ, относиться к изучению математики в 6-м классе следует максимально вдумчиво и ответственно. Помогут реализовать эту задачу качественные учебные пособия и решебники к ним. Подбирать индивидуальный УМК следует, исходя из поставленных целей и задач:
— получить высокий результат на ВПР, диагностических по предмету;
— подготовиться к предметным математическим олимпиадам, проводимым на школьных и внешкольных площадках, иным аналогичным конкурсам.

Работая по ГДЗ, важно акцентировать внимание на таких моментах подготовки, как:
— грамотный выбор литературы — базового учебника и комплекта практикумов, справочников, контрольно-проверочных пособий к нему;
— системность, заключающаяся в планировании и исполнении намеченных планов, учете базового уровня, задач и целей шестиклассника в изучении математики;
— тщательный контроль — периодический и итоговый, для проверки достигнутых результатов, успехов в работе, корректировки планов.
В числе полезных, актуальных базовых учебников по математике за 6 класс специалисты называют книгу, составленную Дорофеевым Г. В. Задания в ней учитывают возрастные особенности шестиклассников, развивают познавательный интерес. Учебник входит в систему УМК «Учусь учиться», рассчитанную на детей и подростков возраста 3-15 лет. Подходит для школ любого типа, в том числе тех, где изучением математики занимаются углубленно.
В числе наиболее интересных и сложных тем этого сборника:
— арифметика — отношения, масштаб и их свойства, пропорции и преобразования, пропорциональные величины и действия с ними;
— понятие рациональных чисел и модуля, сравнение рациональных чисел;
— действия с рациональными числами и системы счисления.
Помимо базового учебника в помощь шестикласснику можно использовать и другие пособия и сборники этого автора, например, рабочие тетради по предмету и иные аналогичные пособия для 6-го класса.
Математика. 6 класс. Дорофеев Г.В., Шарыгин И.Ф., Суворова С.Б.
Аннотация
Содержание учебника позволяет достичь планируемых результатов обучения, предусмотренных ФГОС основного общего образования. Учебный текст разбивается на смысловые фрагменты вопросами, позволяющими проверить, как понято прочитанное. В систему упражнений включена группа заданий на повторение пройденного ранее. Задания содержат такие виды деятельности, как анализ информации, наблюдение и эксперимент, конструирование алгоритмов, поиск закономерностей, исследование и т. д. Всё это позволяет учащимся активно и осознанно овладевать универсальными учебными действиями. Каждая глава завершается рубрикой «Чему вы научились», помогающей ученику проверить себя и оценить возможность выполнения более сложных заданий.
Пример из учебника
Учебник математики для 6 класса, который вы держите в руках, устроен так же, как и учебник для 5 класса. Вместе эти две книги составляют единое целое. Надеемся, что вы уже знаете особенности учебника, научились понимать его язык. Напомним основное.
Главы делятся на пункты, и у них опять двойная нумерация: число перед точкой указывает номер главы, к которой относится данный пункт, а число после точки -номер самого пункта. Такая нумерация удобна, она часто используется в научной литературе. А если вы открыли наугад какую-либо страницу учебника, то, где вы сейчас находитесь, поможет специальная строка вверху этой страницы.
Содержание
Предисловие 3
Глава 1. Дроби и проценты
1.1. Что мы знаем о дробях 5
1. 2. Вычисления с дробями 10
2. Вычисления с дробями 10
1.3. «Многоэтажные» дроби 14
1.4. Основные задачи на дроби 17
1.5. Что такое процент 23
Чему вы научились 37
Глава 2. Прямые на плоскости и в пространстве
2.1. Пересекающиеся прямые 39
2.2. Параллельные прямые 43
2.3. Расстояние 47
Чему вы научились 51
Глава 3. Десятичные дроби
3.1. Десятичная запись дробей 53
3.2. Десятичные дроби и метрическая система мер 59
3.3. Перевод обыкновенной дроби в десятичную 62
3.4. Сравнение десятичных дробей 65
Чему вы научились 70
Глава 4. Действия с десятичными дробями
4.1. Сложение и вычитание десятичных дробей 72
4.2. Умножение и деление десятичной дроби на 10, 100, 1000, 77
4.3. Умножение десятичных дробей 81
4.4. Деление десятичных дробей 86
4.5. Деление десятичных дробей (продолжение) 91
4.6. Округление десятичных дробей 94
4.7. Задачи на движение 99
Чему вы научились ЮЗ
Глава 5. Окружность
5.
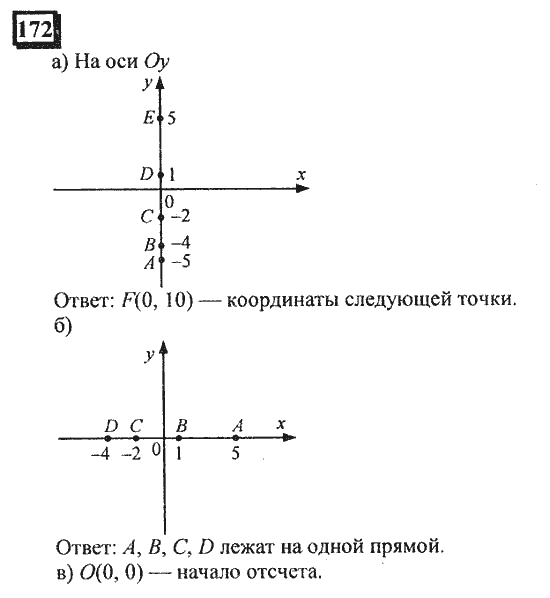
5.2. Две окружности на плоскости 108
5.3. Построение треугольника 111
5.4. Круглые тела 114
Чему вы научились 120
Глава 6. Отношения и проценты
6.1. Что такое отношение 122
6.2. Деление в данном отношении 128
6.3. «Главная» задача на проценты 131
6.4. Выражение отношения в процентах 136
Чему вы научились 143
Глава 7. Симметрия
7.1. Осевая симметрия 144
7.2. Ось симметрии фигуры 149
7.3. Центральная симметрия 155
Чему вы научились 160
Глава 8. Выражения, формулы, уравнения
8.1. О математическом языке 162
8.2. Буквенные выражения и числовые подстановки 166
8.3. Формулы. Вычисления по формулам 170
8.4. Формулы длины окружности, площади круга и объёма шара 175
8.5. Что такое уравнение 179
Чему вы научились 183
Глава 9. Целые числа
9.1. Какие числа называют целыми 185
9.2. Сравнение целых чисел 190
9.3. Сложение целых чисел 194
9.4. Вычитание целых чисел 198
9.
 5. Умножение и деление целых чисел 202
5. Умножение и деление целых чисел 202Чему вы научились 207
Глава 10. Множества. Комбинаторика
10.1. Понятие множества 208
10.2. Операции над множествами 213
10.3. Решение задач с помощью кругов Эйлера 218
10.4. Комбинаторные задачи 221
Чему вы научились 226
Глава 11. Рациональные числа
11.1. Какие числа называют рациональными 228
11.2. Сравнение рациональных чисел. Модуль числа 233
11.3. Действия с рациональными числами 238
11.4. Что такое координаты 249
11.5. Прямоугольные координаты на плоскости 253
Чему вы научились 258
Глава 12. Многоугольники и многогранники
1 12.1. Параллелограмм 260
12.2. Площади 265
12.3. Призма 270
Чему вы научились 275
Ответы 277
Предметный указатель 284
Для комфортного и реалистичного чтения учебника в онлайн режиме, встроен простой и мощный 3D плагин. Вы можете скачать учебник в PDF формате по прямой ссылке.
Главная страница // МБОУ СОШ № 36 г. Липецка
29 января 2021 завершилась II тематическая профориентационная неделя «Настройся на будущее».
Много интересных и запоминающихся мероприятий прошло с 22 по 29 января 2021:
— 25 января в рамках Единого дня профессионального самоопределения «Твой выбор» с 08.30 по 09.15 прошел единый урок
1-4 классы – «Все профессии нужны, все профессии важны», «Чем пахнут ремесла», в ходе которых ученики младших классов играли в ролевые игры, отгадывали загадки, смотрели мультфильмы о различных профессиях.
5-7 классы – «Кем быть? Каким быть?», на которых ребята ответили на вопросы тестов: «Я чувствую – значит существую. Тест эмоций», «Мой темперамент и профессия»; защитили творческие проекты «Мой идеал», «Профессии моих родителей», «Успех разный у всех. Почему?», «Профессии будущего».
8-9 классы – «Выбор профессии начинается в школе», где учащиеся ответили на вопросы анкет «Образ я и самооценка», «Профессиональный тип личности», защитили творческие проекты «Мечтать не вредно», «Моя будущая профессия».
10-11 классы – «Новое время — новые профессии», в рамках которых ученики оценивали свою готовность к избранной деятельности, защитили творческие проекты «Мои профессиональные планы»;
— 26 января состоялись индивидуально-групповые консультации с целью оказания содействия в выборе соответствующего профиля обучения с учетом индивидуальных качеств личности.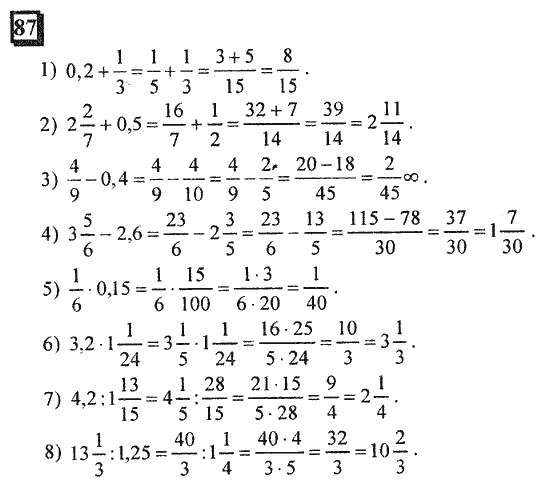 Девятиклассники также приняли участие в региональном мониторинге личностного самоопределения;
Девятиклассники также приняли участие в региональном мониторинге личностного самоопределения;
— 28 января ученики 8-9 классов посмотрели ролики ПАО НЛМК о профессиях, востребованных на предприятиях, о базовых учебных заведениях ПАО НЛМК, возможностях трудоустройства «Выбор профессии –выбор судьбы»;
прошло совещание при директоре «Роль классного руководителя в профессиональной ориентации учащихся»; состоялись родительские собрания для родителей учащихся 9, 11-х классов.
Также в течение недели прошли конкурсы:
• рисунков «Профессия моих родителей», «Кем быть», др. (1-4 классы)
• стенгазет по профориентации «Профессии по алфавиту» (5-7 классы)
• сочинений «Профессия моих родителей» (5-9 классы)
• фотографий «Профессия в кадре».
Работала выставку литературы по профориентации в школьной библиотеке.
Таким образом за прошедшие 5 дней было представлено много полезной информации, которая должна помочь подросткам сделать правильный профессии, в том числе информация о потребностях рынка труда г. Липецка, информация о потребности в профессиях и специальностях, представленных предприятиями Липецкой области, информация о новых профессиях, список 50 наиболее востребованных на рынке труда.
Липецка, информация о потребности в профессиях и специальностях, представленных предприятиями Липецкой области, информация о новых профессиях, список 50 наиболее востребованных на рынке труда.
Гдз мат 6 дорофей. Какие темы можно пройти самостоятельно на ГДЗ Дорофеева, Шарыгиной
ГДЗ по математике для 5 класса Дорофеев — онлайн-решатель, раскрывающий подробный алгоритм выполнения примеров и задач по учебнику той же группы российских ученых — Дорофеевой Г.В., Шарыгиной И.Ф., Суворовой С.Б. и др., Опубликованной в 2017. Сейчас он используется в качестве основного учебного пособия во многих средних школах России.
Математик Дорофеев — важное дополнение к учебному процессу в пятом классе
В пятом классе ученики начинают свой путь в среднем звене общеобразовательной школы, что предполагает увеличение количества предметов и их углубление.Не все дети могут легко и быстро адаптироваться к новым условиям; возникают трудности при выполнении домашних заданий.
Онлайн-решатель математики для 5 класса Дорофеев позволяет пятиклассникам самостоятельно или с помощью родителей разобраться в предмете, научиться решать примеры и задачи. На сайте Госдумы Путина предусмотрены условия для максимально удобного его использования:
- Поиск ответов и решений по номеру вакансии в таблице;
- Прикрепив к задаче 1-5 вариантов ее решения, чтобы расширить кругозор учащегося и его понимание различных формул и теорем;
- Регулярное обновление практических пособий с готовыми ответами.
Школьники и их родители могут найти готовое решение с правильным ответом на базе любого устройства — телефона, компьютера или планшета. Это позволяет детям дома, в спокойной обстановке, понимать алгоритм решения математических упражнений, а родителям — следить за успеваемостью своих детей.
ГДЗ по математике для 5 класса от Дорофеева — дроби, многоугольники, рациональные числа
В рамках домашнего задания ученик должен закрепить теоретические знания, полученные на занятиях. Что делать, если ребенок запомнил формулы, но не успел разобраться в алгоритме решения примеров и задач? Используйте онлайн-коллекции готовых домашних заданий, которые являются не базой для читерства, а образцом для домашнего задания.
Что делать, если ребенок запомнил формулы, но не успел разобраться в алгоритме решения примеров и задач? Используйте онлайн-коллекции готовых домашних заданий, которые являются не базой для читерства, а образцом для домашнего задания.
Какие упражнения дают в Госдуме по математике 5 класс Дорофеев?
- Прямая, пунктирная линия, отрезок, окружность и их длина;
- Натуральные числа, их сравнение, чтение и округление;
- Математические действия с натуральными числами и степенями;
- Использование свойств действия в расчетах;
- Углы и их размеры, многоугольники и их свойства;
- Дробные числа, действия с обыкновенными и десятичными дробями;
- Многогранники и измерение их объемов.
Онлайн-решатель основан на 4-м издании учебника Г. Дорофеева для 5 класса. Он позволяет родителям помогать пятиклассникам с арифметическими упражнениями.
ГДЗ по математике для 5 класса Дорофеев — онлайн-решатель или сборник готовых ответов, составленный на основе одноименного учебника по арифметике от известных российских авторов — Дорофеева Г. В., Шарыгина И.Ф., Суворова С.Б. и др. опубликовано в 2017 году. На его основе пятиклассникам будет легче разобраться в сложном алгоритме выполнения заданий и уравнений, а родителям — проверять успеваемость своих детей.
В., Шарыгина И.Ф., Суворова С.Б. и др. опубликовано в 2017 году. На его основе пятиклассникам будет легче разобраться в сложном алгоритме выполнения заданий и уравнений, а родителям — проверять успеваемость своих детей.
Для чего нужен решатель Дорофеева в 5 классе?
В пятом классе школьникам закладываются знания арифметики, которые станут основой для изучения алгебры и геометрии, физики и астрономии в старших классах. Поэтому крайне важно не допускать пробелов в образовании школьников. Этот факт доказывает, насколько важно использовать онлайн-решатель математики для 5 класса Дорофеева.
На основе практического руководства дети могут самостоятельно или вместе со старшими разобраться дома, в порядке выполнения сложных примеров и заданий из домашнего задания и проверить полученные ответы.Родители на основе предложенных решений всегда смогут отследить успеваемость пятиклассников по предмету.
Веб-сайт VIP-GDZ — лучший способ использовать готовое домашнее задание: просто введите номер ответа или часть его условия в поле поиска, чтобы получить решение за доли секунды.
Помимо такого значительного преимущества важно отметить:
- для каждой задачи предусмотрены подробные алгоритмы решения, а не просто готовые ответы;
- на одно упражнение можно дать несколько решений для расширения кругозора пятиклассников;
- Все решения основаны на последней версии учебника, выпущенной в 2017 году.
Школьник и родители могут использовать любой электронный гаджет для поиска ответов — будь то телефон, планшет или ноутбук.
Что изучают пятиклассники — учебник по математике Дорофеева Г.В.
Современная программа по изучению арифметики направлена на ознакомление студента с широким кругом тем, важных при дальнейшем изучении алгебры, геометрии, физики и химии.
Поэтому в Госдуме по математике для 5 класса Дорофеева можно найти задания и примеры на такие темы как:
- простые фигуры — прямая, ломаная, отрезок, окружность и их длины. ;
- понятие натурального числа, математические операции с натуральными числами и их округление;
- виды углов и их измерение;
- Понятие и типы многоугольников, свойства простых фигур на плоскости;
- действия с обыкновенными и десятичными дробями;
- Понятие многогранников и определение их объемов.

Сайт VIP GDZ — удобная возможность заниматься сложными примерами и задачами по арифметике в 5 классе без участия репетиторов и прохождения дополнительных занятий. Он учит студентов не только правильно применять арифметические формулы на практике, но и пользоваться практическими пособиями.
Научный сотрудник по математике Дорофеева Г.В., Шарыгина И.Ф. и Суворова С.Б. за 5 класс поможет вашему ребенку быстро и эффективно овладеть этим предметом.Программа, используемая авторами, полностью соответствует действующим федеральным требованиям в России (ФГОС), закрепленным в соответствующих документах.
Школьные учителя могут использовать материалы в Интернете для разработки программ работ, защищенных авторским правом, для своих учеников. ГДЗ Дорофеева поможет улучшить понимание, а подготовить к поверке и контролю работы в классе. Студенту достаточно знать данный номер примера, чтобы ознакомиться с его правильной реализацией. Также можно решать задачи и упражнения самостоятельно, и проверять окончательный ответ на панели управления для контроля.
Также можно решать задачи и упражнения самостоятельно, и проверять окончательный ответ на панели управления для контроля.
Характеристики преимущества
Важно отметить, что книга отлично подходит для детей 10-12 лет, так как была разработана профессиональными психологами и методистами специально для них. Он содержит исключительно полезный новый материал, а также снабжен упражнениями для повторения навыков, которые должны были быть сформированы в ходе начального образования.Учебник формирует культуру математического мышления, а также умение правильно и системно находить правильные алгоритмы решения практических задач определенных типов.
Использование книги по назначению
Ресебник «Дорофеев 5 класс» хорошо адаптирован для использования в качестве основного средства обучения. Ребенок может использовать его для подготовки к следующим видам образовательной деятельности:
- работа на уроке.
- контрольная и самостоятельная работа.

- тестовые и поверочные индивидуальные тесты.
- подготовка к олимпиадам.
Задания ранжируются по уровням сложности, которые соответствуют оценкам «удовлетворительно», «хорошо», «отлично». Студент сам может выбирать задания по вкусу для самостоятельной работы. Таким образом, для школьного учителя также упрощается установка текущих оценок в соответствии с успеваемостью учащихся.
Математика 6 класс
Дорофеев, Шарыгин
Образование
С каждым годом задачи, стоящие перед учащимися, усложняются, как и изучаемые предметы.Одной из самых сложных считается математика, хорошее знание которой не только очень важно для жизни, но и поможет лучше понять другие смежные предметы. Постичь мудрость этой науки можно с поверенным к учебнику «Математика 6 класс» Дорофеев, Шарыгин.
Что в него входит.
Двенадцать глав содержат более тысячи тематических заданий. В конце каждого раздела в GDZ в классе математики 6 есть упражнения для повторения и закрепления материала, которые покажут, как учащиеся поняли материал.
Нужен ли мне резольвер.
Шестиклассники этого класса должны усвоить основы алгебры и геометрии, так как вскоре им предстоит разделение по предмету. В этом плане программа довольно сложная. У некоторых ребят могут возникнуть трудности с решением уравнений, поскольку они уже не так просты, как раньше. Поэтому крайне важно убедиться, что ребенок полностью понял изучаемую тему. Ведь упустив какой-то момент, он может просто не понимать алгоритм решения и это приведет к постепенному отставанию от одноклассников.Возникает своего рода цепная реакция, когда непонимание одного приводит к неправильному пониманию всего остального. Избежать потери успеваемости ученику поможет учебник «Математика 6 класс» Дорофеева, который окажет качественную поддержку при проверке д / з.
Просвещение, 2017
- Психологи считают период поступления в вуз для ученика и родителей критическим. В начальной школе ученика находится под опекой учителя начальных классов, который находится в контакте с родителями и помогает ему в трудностях школьной жизни.
 В 5 классе нагрузка на ученика значительно увеличивается, учителей становится больше, требования дисциплины ужесточаются.
В 5 классе нагрузка на ученика значительно увеличивается, учителей становится больше, требования дисциплины ужесточаются. - В помощь ребенку по математике в трудный период приглашен решатель по учебнику Г.В. Дорофеева и соавторы. Пособие содержит решения различной сложности упражнений и контрольных задач, книга станет хорошим помощником для ученика — вы сможете самостоятельно проверить выполненную работу, выяснить ошибки, научиться выполнять типовые задания.
- Уверенно работать с натуральными числами, дробями, рисовать различные геометрические фигуры — пятикласснику надо многому научиться. При принудительном трудоустройстве взрослых ребенок остается один, делает уроки, помочь некому. Сложные требования ФГОС порой вызывают недоумение у родителей, проверяющих работу ученика. ГДЗ Учебник Дорофеева здесь становится незаменимым советчиком, волшебной палочкой. А научить ребенка грамотно пользоваться книгой, объяснить родителям бессмысленность бездумного жульничества — вполне реально.

- Переходя на средний уровень школы, пятиклассники часто сталкиваются с разного рода трудностями. В значительной степени они вызваны изменением формата представления информации, контроля и проверки знаний. Чтобы переход был максимально безболезненным и эффективным, необходимо изначально заняться регулярной и вдумчивой работой, как правило.Особенно по тем дисциплинам, которые являются обязательными для сдачи экзамена и вызывают наибольшие трудности у студентов. Среди них математика, которую можно понять, применив к ним грамотные учебники и решатели.
- Начиная обучение на ГДЗ , пятиклассники должны руководствоваться правилами:
— регулярная и системная работа. Выделяя в плане определенное количество времени на изучение отдельных тем, блоков, разделов, не нарушайте порядок. В случае возникновения затруднений можно скорректировать планы или обратиться за профессиональной помощью — к учителям-предметникам, тьюторам, руководителям подготовительных кружков и курсов;
— самоконтроль. Отслеживая динамику, сначала вместе с родителями, учителями, пятиклассники учатся контролировать свои достижения, быстро выявлять и исправлять обнаруженные недостатки, пока они не превратятся в серьезные проблемы непонимания математики;
Отслеживая динамику, сначала вместе с родителями, учителями, пятиклассники учатся контролировать свои достижения, быстро выявлять и исправлять обнаруженные недостатки, пока они не превратятся в серьезные проблемы непонимания математики;
— ответственность и повышенное внимание. Готовое домашнее задание — отличный формат, чтобы увидеть и запомнить, как правильно записывать результаты. Часто даже правильный ответ, отраженный неправильно, засчитывается как отсутствие решения и приводит к досадной потере баллов. - Среди полезных сборников, рекомендуемых многими специалистами, — комплект учебных пособий по математике для 5 класса, составленный Г. Дорофеевым. Задания, содержащиеся в авторских книгах, позволяют заниматься такими видами деятельности, формирующими математические навыки и знания, как:
— эксперимент;
— поиск закономерностей;
— строительство;
— анализ информации.
Колонка «Что вы узнали» позволит вам самостоятельно оценить усвоение материала по каждой теме, блоку тем. Для более глубокого и полного понимания материала вы можете использовать другие пособия из тех же учебных материалов, которые входят в комплект к базовому учебнику. Среди популярных — дидактических материалов, , контрольных, работ и контрольных работ, рабочие тетради, устные упражнения и другие аналогичные практические занятия.
Для более глубокого и полного понимания материала вы можете использовать другие пособия из тех же учебных материалов, которые входят в комплект к базовому учебнику. Среди популярных — дидактических материалов, , контрольных, работ и контрольных работ, рабочие тетради, устные упражнения и другие аналогичные практические занятия.
Математика для пятиклассников — правила успешного перехода в средний класс школы
(PDF) Учебный кластер КНИТУ-КАИ: обучение математике
сопровождение, методики тестирования при проверке уровня усвоения знаний. Перед преподавателем стоит
инепростая задача — найти ту тонкую грань, пропорцию «очная — заочная», при которой учащиеся
получают необходимое количество новых знаний с помощью дистанционных методов обучения.
Создание качественного электронного курса — сложная и трудоемкая задача, требующая от разработчика
знаний, усилий и времени, а также хорошее владение предметом курса и
методами обучения. предмета. Вовлечение студентов в создание электронных курсов можно рассматривать как самостоятельную задачу
, которая помогает овладеть математикой, обращать внимание на трудные моменты в обучении, а
мотивирует самостоятельную работу. Участие в создании электронного курса вместе с преподавателем
Участие в создании электронного курса вместе с преподавателем
можно рассматривать как некую известную идею «обучения через игру» [23].
Следует отметить общеизвестный факт, что сегодняшний мир не стоит на месте, а стремительно развивается
. Меняется и образовательный сегмент. Сегодня невозможно представить современное образование
без информационных и коммуникационных технологий. Технологии меняют все области нашей жизни, но
их влияние наиболее ощутимо в образовании, которое определяет будущее любого общества.Мы вступаем в эру взаимосвязанности
— от Интернета вещей до Интернета всего [26]. Студенты КНИТУ-КАИ
активно пользуются курсами дистанционного обучения. Во-первых, электронные курсы позволяют более глубоко изучить материал
, представленный преподавателем на лекциях и практических занятиях. Во-вторых, электронный курс
— это возможность качественно подготовиться к контрольным мероприятиям, сдаче теста и экзамена, а также пройти пробные
тесты в соответствующем разделе, чтобы самостоятельно проверить уровень полученных знаний.
Конечно, дистанционный курс (особенно по дисциплинам математического цикла) не может полностью заменить
аудиторные занятия, «живое» общение с преподавателем. Но в связи с эпидемией коронавируса covid-19
дистанционное обучение становится все более актуальным. В изменившихся условиях
опыт дистанционного обучения в условиях самоизоляции говорит нам, что дистанционный курс по математике
может в будущем заменить до 25-30% уроков в классе.
Дистанционные курсы в КНИТУ-КАИ создаются на платформе BlackBoard Learn [25] и доступны
учащимся в любое время дня и с любого электронного устройства с доступом в Интернет. Кстати, многие
текстовых файлов можно скачать и использовать в автономном режиме. Для удобства пользователей приложение
можно загрузить на мобильное устройство и использовать материалы курса на занятиях. Вход в систему BlackBoard
(bb.kai.ru) осуществляется с использованием логина и пароля (индивидуального для каждого студента), которые выдаются
при зачислении абитуриента в КНИТУ-КАИ.
Электронные дистанционные курсы в КНИТУ-КАИ, в частности на кафедре специальной математики,
, созданы с 2012 года. Эта работа не прекращается до сих пор: преподаватели кафедры
дополняют, видоизменяют, развивают существующие курсы и создавать новые.
Конечно, все новое не всегда вызывает положительную реакцию. Так было с введением
электронных образовательных ресурсов (ЭОР) в учебный процесс КНИТУ-КАИ:
студенты не доверяли этому нововведению, не знали, как ориентироваться в курсе и всем возможностям
платформу BlackBoard Learn, найдите необходимую информацию и пройдите тест
правильно и вовремя.Но как показала практика, и ученики, и преподаватели очень быстро включились в этот процесс
. Сегодня каждые 3-4 аудиторных занятия интерактивны.
Курсы повышения квалификации по созданию, внедрению и применению электронных курсов.
были организованы для учителей на базе Корпоративного института КНИТУ-КАИ Отметим, что создание
электронного курса «с нуля» — титанический труд для учителя, который необходимо выполнять «на рабочем месте», что есть, в
параллельно с основной нагрузкой в классе. Преподаватели кафедры специальной математики
Преподаватели кафедры специальной математики
успешно справляются с поставленной задачей, продолжают работу по модернизации созданных электронных курсов и повышают
своих профессиональных навыков в области информационно-коммуникационных технологий, регулярно проходят курсы повышения квалификации
, переподготовка и стажировки.
5. Заключение
Цифровизация — это перевод информации в цифровую форму, цифровая передача информационных данных.
Чтобы оставаться конкурентоспособными в эпоху мобильных технологий и социальных сетей, организации должны найти новые методы
для привлечения клиентов. Эти методы должны соответствовать сегодняшней цифровой реальности. Компании, которые
хотят быть на несколько шагов впереди своих конкурентов, ставят свои потребительские чувства в центр своего
Экспериментальное исследование и математическое моделирование кристаллизации сульфата аммония в кристаллизаторе с принудительной циркуляцией
org/ScholarlyArticle»> 1.Дорофеева М.И., Кольцова Е.М., Гордеев Л.С. Исследование и математическая модель истирания. Осн. Хим. Технол. , 2006, т. 40, нет. 4, стр. 401 [ Теор. Найденный. Chem. Eng . (Англ. Пер.), Т. 40, нет. 4, стр. 372].
Google ученый
Ган К., Мерсман А., Хрупкое разрушение в процессах кристаллизации, Chem. Англ. Sci. , 1999, т. 54, стр. 1273.
Статья CAS Google ученый
Neumann, A.M., Характеристики промышленных кристаллизаторов различного масштаба и типа. Диссертация , Делфт: DUP Science, 2001.
Google ученый

Либ А. и Кинд М., Определение характеристик истирания сульфата аммония и кристаллов пентаэритрита с использованием кристаллизатора с принудительной циркуляцией, Powder Technology , 2004, т. 143–144, с. 273.
Google ученый
Бермингем, С.К., Процедура проектирования и прогнозные модели для процессов кристаллизации растворов. Диссертация , Делфт: DUP Science, 2003.
Google ученый
Ган К., Мерсман А., Хрупкое разрушение в процессах кристаллизации, Chem. Англ. Sci. , 1999, т. 54, стр. 1283.
Статья CAS Google ученый
SIAM AG об ортогональных многочленах и специальных Функции
OP-SF WEB
Выписка из OP-SF NET
Тема № 8 ------------ OP-SF NET 5.6 ----------- 15 ноября 1998 г. ~~~~~~~~~~~~~ От: OP-SF NET Editors Тема: Статья У. Скорника о Вейерштрассе [В информационном бюллетене нашей группы действий появился следующий элемент: Октябрь 1998 г .; он был перепечатан с разрешения Российский информационный бюллетень "Интегральные преобразования и специальные функции"] Карл Теодор В. Вейерштрасс - Жизнь и творчество К 100-летию со дня его смерти У. Скорник Институт математики, Польская академия наук, Старомейская 8/6, 40-013 Катовице, Польша Электронная почта: skornik @ impan.gov.pl 19 февраля 1997 г. исполнилось 100 лет со дня смерти великий немецкий математик, отец классического математического анализа и теория абелевых и специальных функций, Карл Теодор Вильгельм Вейерштрасс. Он родился 31 октября 1815 года, был первым ребенком Вильгельма. Вейерштрасс, секретарь мэра Остенфельде и Теодора Vonderforst. Ничто в его ранней жизни не указывало на то, что он станет известным математик. Карл посещал католическую гимназию в Падерборне с 1829 года.
до 1834 г., когда он поступил в Боннский университет, чтобы пройти курс обучения в области государственных финансов, экономики и управления.Этот выбор далек от его собственные интересы, продиктовал его отец, в результате чего после четырех лет, потраченных на фехтование, выпивку и математику, Карл вернулся домой без сдачи экзаменов. Однако годы в Бонне были не совсем потрачено впустую. Во время пребывания там Вейерштрасс посещал лекции знаменитого геометра Плюккера, изучал "Mecanique" Селеста »Лапласа,« Fundamenta nova »Якоби и расширенный его знания по случайно найденной транскрипции лекций по эллиптическому функции Гудерманна.2 \ varphi}}, с параметром k между 0 и 1, называемым модулем эллиптического интеграл. Эллиптические функции, полученные из этого интеграла, были названы модульные функции Гудерманна. Это была новая теория, и Гудерманн был сначала после Якоби, чтобы прочитать лекции на эту тему. 2 мая 1840 года Вейерштрассу были поставлены задачи к выпускным экзаменам; один из них был поставлен Гудерманом по особому желанию его студент и заинтересованные эллиптические функции.
Осенью 1840 года Вейерштрасс представил результаты своих исследований по декомпозиции модульных функции.2. В память об Авеле, он называл их функциями Аля. Затем Вейерштрасс представил его знаменитые \ sigma-функции, которые отличаются от функций Al на множитель. Его диссертация содержала значительный новый материал и могла обеспечить академическая должность для него в Германии или где-либо еще. Неизвестно почему эта работа, высоко оцененная Гудерманом, была опубликована только 54 года назад. позже в первом томе Сборника статей Вейерштрасса. Вместо обретя математическую известность, Вейерштрасс, сдав вторую устную часть экзаменов весной 1841 г., проработал 14 лет в средней школе школьный учитель.После испытательного года в Мюнстере Вейерштрасс работал в католической церкви. гимназия (средняя школа высокого уровня) в Deutsch-Krone (Западная Пруссия) от С 1842 по 1848 год, а затем в аналогичной школе в Браунсберге (Восточная Пруссия) с 1848 по 1855 год. Он преподавал не только математику и физику, но и Немецкий язык, ботаника, география, история, гимнастика и каллиграфия.
В 1844 г. Вейерштрасс прошел курс для учителей гимнастики в Берлине. За это время он посетил знаменитого геометра Штайнера. Однако это не изменил своего положения.В Deutsch-Krone Weierstrass не имел ни доступ к математической литературе, ни возможность обмена идеи с любым другим математиком. Он чувствовал себя изолированным и наполнял свою жизнь с работой. В те годы он разработал теорию абелевых функций. которые образуют более широкий класс, чем эллиптические функции. Абелевы интегралы определяются как эллиптические интегралы формулой u = \ int (от 0 до v) R (t, \ sqrt {f (t)}) dt = I (v) где R (x, y) - рациональная функция от x и y, за исключением того, что функция f имеет очень общий тип, который включает в себя все многочлены.Инверсия тогда дает абелевы функции, так же как эллиптические функции возникают из обращение эллиптических интегралов, т.е. интегралов, где f (t) полином. Во время испытательного года Вейерштрасса в гимназии в Мюнстере он работал над тремя статьями. Первый "Darstellung einer analytischen" Funktion, deren absoluter Betrag zwischen zwei gegebenen Grenzen liegt " содержит доказательство интегральной теоремы Коши без использования двойных или поверхностные интегралы.
Он также представил серию Лорана и пришел к Теорема Лорана за два года до ее официального опубликования в Comptes Rendus Коши.В этой работе Вейерштрасс выразил сложные числа в форме r {1+ \ lambda i} \ over {1- \ lambda i}, где r - абсолютное значение, а \ lambda - действительное число, заданное как \ lambda = \ tan (\ theta / 2), где \ thet - амплитуда комплекса номер. Газета "Zur Theorie der Potenzreihen" датируется осенью 1841 года. В этой работе Вейерштрасс ввел понятие равномерной сходимости и исследовали ряды по нескольким переменным. В следующей статье «Определение analytischer Funktionen einer Veranderlichen vermittelst algebraischer Differentialgleichungen », датируемой 1842 г., он доказал теорему Коши о решении систем дифференциальных уравнений dx / dt = G_i (x_1 ,..., x_n) с начальными условиями x_i (0) = a_i, где G_i - многочлены. В В этой статье Вейерштрасс описал процесс аналитического продолжения силовой ряд. Эти статьи были опубликованы только в первом томе его Собрал статьи 1894 года, но из них ясно видно, что уже в 1842 году он полностью владел всеми методами и идеями, которые позволяли ему построить свою теорию функций.
К сожалению, его первая публикация статья "Bemerkung uber die analytischen Fakultaten" появилась в приложение к школьному отчету 1842 года в немецкой кроне и уделялось мало внимания.То же произошло и с другой статьей об Абелевах. функций, который был опубликован в 1848 году в проспекте школы Браунсберга. Вейерштрасс остался бы незамеченным, если бы летом 1853 г. во время своего пребывания в Мюнстере он прочитал мнение Гудерманна о его диссертация впервые. Уже в 1840 году Кристоф Гудерманн не не только признал редкий талант Карла, но и поместил его в ряды знаменитых первооткрыватели и предложили своему ученику работать в университете а не как учитель средней школы.Эта записка поощряла Вейерштрасс публикует свою статью «Zur Theorie der Abelschen Funktionen». Его появление в 1854 году в журнале Crelle's Journal вызвало сенсацию в математический мир. Последствия были потрясающими. Первое признание был удостоен звания почетного доктора Кенигсбергского университета. Тогда прусское министерство образования предоставило ему годовой оплачиваемый отпуск от гимназии Браунсберга, чтобы он мог сосредоточиться на своих исследованиях.
Вейерштрасс приобрел достаточно уверенности, чтобы подать заявку на эту должность в Университет в Бреслау, который был освобожден назначением Куммера профессор в Берлине.Может показаться странным, что заявление Вейерштрасса был отклонен из-за Куммера. Причина в том, что Куммер, потративший 13 лет преподавания в Бреслау, намеревался отвезти Вейерштрасса в Берлин. Он подал заявление 12 июня 1856 г. в университет в Берлине с просьбой о пост для Вейерштрасса. В этом случае он не добился успеха, но его Возможный успех дал математике в Берлине три великих имени: Вейерштрасс, Куммер и Кронекер. "Theorie der Abelschen Funktionen" Вейерштрасса опубликована в Crelle's Журнал 1856 г. содержал результаты его диссертации.Д. Гильберт рассмотрел эти результаты относительно решения обращения Якоби задача для гиперэллиптического интеграла величайшее достижение анализ. Эта публикация стала поворотным моментом в жизни Карла. Вейерштрасс. Он стал известен за рубежом, и австрийское правительство сделало запросы о нем через Александра фон Гумбольдта.
Это подтолкнуло фон Гумбольдта к действиям, и 1 июля 1856 года Вейерштрасс был назначен профессором в Промышленном институте в Берлине. В сентябре 1856 года Вейерштрасс и Куммер отправились в Вену.Вот, Граф Тун предложил Weierstrass 2000 Gulden и должность профессора в австрийском университет по своему выбору. Вейерштрасс отклонил это предложение, но оно стало Куммеру ясно, что если они хотят оставить великого математика в Германия ему снова пришлось действовать. Вскоре после этого в результате усилий Куммера Вейерштрасс был назначен доцентом Берлинского университета. В ноябре В 1856 году он стал членом Берлинской академии. С тех пор до 1890 г. читал лекции по самым разным темам, включая периодические лекции по эллиптические функции, лекции по геометрии и механике.Известный математический семинар, который он инициировал вместе с Куммером в 1861 г. привлекли международный интерес. С 1862 г. было принято делать награды лучшим участникам. Стоит отметить, что первые математико-физический семинар был основан в Кенигсберге в 1834 г.
Якоби, Нойман и Зонке, второй в Галле в 1838 году и третий в Гёттинген в 1850 году. Тяжелая рабочая нагрузка Вейерштрасса привела к ухудшению его здоровья в Декабрь 1861 г. Он вернулся к преподаванию через год, но читал лекции в сидячее положение со студентом, пишущим необходимый текст на доска.Всю оставшуюся жизнь он страдал от повторяющихся приступов бронхит и флебит, но его решимость заставляла его учить и продолжая свое исследование. В своих лекциях Вейерштрасс инициировал логическое и тщательное развитие анализа, начиная с его собственного построения действительная система счисления. Он установил понятия эпсилон-дельта в концепция непрерывности и сходимости, равномерная сходимость, абсолютная значение, окрестность (a- \ delta, a + \ delta) точки $ a $ и многие другие. Он отвергал интуитивные аргументы, которые все еще преобладали среди многих современные математики.Именно Вейерштрасс в своих лекциях по 1862 г. дал знаменитый пример непрерывного нигде не дифференцируемого функция.
В том же году он впервые в своих лекциях развил теорию функции \ gamma (u) и \ sigma (u). Его знаменитая аппроксимационная теорема появился в связи с уравнением теплопроводности и был опубликован в июле. 1885 г. в Протоколах заседаний Берлинской академии наук. Он также внес свой вклад в развитие вариационного исчисления на которую он читал в 1879 году.Однако его основные лекции были сосредоточены на Абелевы функции. Его периодически читаемые лекции включали «Введение в теорию аналитических функций», «Теория Эллиптические функции », когда-то подходивший с точки зрения дифференциальные уравнения, в другой раз с точки зрения теории функций "Применение эллиптических функций к геометрии и Механика »,« Применение абелевых функций к геометрическим задачам и вариационное исчисление ». Его лекции собрали аудиторию до 250 человек. среди них более 100 будущих профессоров, в том числе С.Ковалевский, Шварц, Фукс, Г. Миттаг-Леффлер, Л. Кенигсбергер, Х. Минковский и Кантор. Вейерштрасс оказал огромное влияние на математический мир.
Он получил высокое признание во всей Европе. Шведский математик Миттаг-Леффлер упоминает хороший анекдот. Когда он получил стипендию на учиться за границей в 1873 году он отправился в Париж, где Эрмит встретил его слова "Vous avez fait erreur, Monsieur, vous auriez du suivre les cours де Вейерштрасс в Берлине ». И, конечно же, Миттаг-Леффлер последовал примеру Эрмита. посоветовал и поехал в Берлин.Самой выдающейся ученицей Вейерштрасса была Соня Ковалевская, дочь русского артиллерийского генерала. Женщинам не разрешили учиться в России, поэтому в 1868 году она заключила брак по расчету с молодым палеонтолог Владимир Ковалевский и пара уехали учиться за границу. Сначала они поступили в Гейдельбергский университет, но через два года они разделены. Владимир поехал в Йену, а Соня поехала в Берлин в надежде посещать лекции Вейерштрасса. К сожалению, был запрет на женщин студентка Берлинского университета, и ее заявление было отклонено.Так она пошла прямо к Вейерштрассу со своими хайдельбергскими ссылками.
Он дал ей нужно было решить некоторые проблемы, и ее решения и энтузиазм впечатлили его поэтому он решил обучать ее в частном порядке. За четыре года, которые она провела в Берлине она стала его близким другом и незаменимым партнером для научные дискуссии. Мы мало что знаем о частной жизни Вейерштрасса. жизнь. Соня, однако, вторая женщина (после Марии Склодовской Кюри), которая занимал университетский пост, писатель и революционер, стал прекрасным Тема для многих биографий и романов.Вейерштрасс считал ее своим самый талантливый ученик. Фактически, во время своего пребывания в Берлине она произвела три выдающихся документа; по дифференциальным уравнениям, по абелевым интегралам и на кольцах Сатурна, и сумел получить докторскую степень от Геттингенский университет. Однако Вейерштрасс, к своему большому сожалению, мог не обеспечили ей работу в Германии, и ей пришлось вернуться в Россию. Их дружба, хотя и основывалась на чисто научном взаимодействии, стала предмет слухов. Вейерштрасс глубоко обиделся из-за настойчивых инсинуации, окружающие его ученицу и ее математические достижения.
На Вернувшись в Россию, ее интерес к математике прекратился. Она не могла работать в университет в Петербурге, потому что ее квалификация не соответствовала признал. Вернулась к семейной жизни, в 1878 году родила дочь. и вместе с мужем Владимиром пытались заработать на имении. предприниматель, но это предприятие закончилось банкротством. Вейерштрасс и Соня Ковалевски довольно регулярно переписывались из время, когда они встречались до ее смерти в 1891 году. Его письма и поддержка снова заняться математикой вдохновил ее и помог ей пройти через финансовые трудности и самоубийство мужа в 1883 году.В 1884 году Миттаг-Леффлер удалось получить ей должность преподавателя в университете в г. Стокгольм. В 1888 г. она добилась большого успеха, когда ее знаменитая статья {\ it «О вращении твердого тела вокруг неподвижной точки»} выиграли французы. Приз Академии Бордина. К сожалению, Вейерштрасс сжег все письма Сони после ее ранней смерти. Его письма, однако, сохранились и хранятся в Mittag-Leffler Институт в Дюрсхольме, Швеция.
Обширная переписка с Mittag-Leffler, Х. Шварц, Поль дю Буа-Реймон, Л.Кенигсбергер, Риман, Л. Фукс и Соня, который содержит в основном математические задачи, также освещает Жизнь Вейерштрасса. Его считали успешным, но на самом деле его жизнь был полон страданий и личных проблем. Он не женился после помолвка с Deutsch-Krone была прервана из-за неверности невеста, по словам его брата Петра. Его карьера в Берлине была едва ли началось, когда его здоровье пошатнулось. Более того, ближе к концу жизни вместо того, чтобы наслаждаться славой и признательностью, он чувствовал себя изолированным.Это было из-за конфликта с математиком и философом Леопольдом Кронекер. Вейерштрасс и Кронекер дружили более двадцати лет, делясь много плодотворных математических дискуссий и идей. К сожалению, на конце 1870-х гг. их взгляды на математику, особенно на основы математика, расходились постепенно. Работа Вейерштрасса о пределах и конвергенция привела его к разработке теории иррациональных чисел, основанной на сходящиеся последовательности рациональных чисел, которые он назвал «агрегатами».
Его студент Георг Кантор основал теорию трансфинитных чисел, которая произвела революцию в математической мысли. До Кантора математики принял понятие бесконечного в ситуации последовательности «стремящиеся к бесконечности», но не были готовы принять актуальную бесконечность как таковой. Большим достижением Кантора было введение этой точной концепции: фактически целый класс различных бесконечностей, соответствующих счетные множества, такие как натуральные числа, континуум действительных числа и так далее.Для Кронекера тип неконструктивного рассуждения использованный Вейерштрассом и Кантором был глубоко подозрительным. Его знаменитое изречение: «Бог сделал целые числа, все остальное - дело рук человека ", - произносится на Берлинский конгресс 1886 года сформулировал его философию, и он предвидел включение по существу всей математики в термины арифметика. Кронекер не скрывал своих возражений против работ Вейерштрасса и Кантора и открыто критиковал их перед студентами. Неудивительно, что этот математический конфликт превратился в личные ссоры.
К концу 1880-х годов Вейерштрасс, очевидно, признал, что его давняя дружба с Кронекер кончил, хотя сам Кронекер, казалось, не знал об этом. Вейерштрасс даже рассматривал возможность уехать из Берлина на Швейцарии, чтобы избежать продолжающегося конфликта; но, поскольку он не желал своего преемника в университете, которого выбрал Кронекер, он решил оставаться. Однако ему стало ясно, что если он не опубликует свои лекции и работы, его достижения могут быть преданы забвению.Его беспокойство, вероятно, было преувеличено, потому что его ученики были разбросаны по всем над Европой и продолжил свои исследования. Его величайшим преемником был Х. Пуанкаре в Париже. Тем не менее обстановка в Берлине была напряженной. В 1885 была создана специальная комиссия по редактированию его произведений. Сам Вейерштрасс больше не мог контролировать весь процесс, поэтому его студенты взяли на себя задачу собрать и отполировать его лекции на основе их собственных заметок или стенограмм. Вейерштрасс намеревался дать математика - обширная трактовка анализа, ясная и полная.
Так Кноблаух и Геттнер должны были подготовить теорию абелевых функций, его величайшая цель в жизни. Однако его мечта не осуществилась, и проект был крайне неудовлетворительным, по его мнению, и не соответствовал стандартам, которые он ожидал. Его тоже беспокоили отсутствие точности и опечатки. В Первый том появился в 1894 году и содержал его собрание статей. В второй был напечатан в 1895 году, но следующие пять томов были опубликованы между 1902 и 1927 годами, после его смерти. Стоит отметить, что это Вейерштрассу, что мы обязаны публикацией собрания статей Якоби, Дирихле, Штайнер и буквы Гаусса.В старости он работал редактором, чтобы пополнить свою зарплату, которой не хватало для содержать свою семью. Он жил в Берлине со своими сестрами Элис и Кларой. который вел дом, его отец, умерший в 1869 году, и внук его дяди, который он взял под опеку двухлетним ребенком в 1884 году. Он также заботился о Шесть детей Борхардта после смерти его ближайшего друга в 1880 году. В 1892 г. Вейерштрасс получил медаль Гельмгольца, а в 1895 г.
награжден медалью Копли, высшей наградой Королевского общества Лондон.В том же году он отметил свое 80-летие среди своих студенты. Последние три года жизни он провел в инвалидном кресле и умер 19. Февраль 1897 г., после воспаления легких. Рекомендации 1. Аренс, В .: Skizzen aus dem Leben Weierstrass '. Math.-naturwiss. Блаттер 4 (1907), 41-47. 2. ---: Gudermanns Urteil uber die Staatsexamensarbeit von Weierstrass. Math.-naturwiss Blatter 13 (1916), 44-46. 3. Бейкер, A.C .: Карл Теодор Вильгельм Вейерштрасс, отец современного анализ. Математика. Спектр 1996/7, т.29, № 2, 25–29. 4. Бирманн, К. Р .: Карл Вейерштрасс, Ausgewahlte Aspekte seiner Биография. Журнал Fur die reine und angewandte Mathematik, 223 (1966), 191-220. 5. Боллинг, Р.: Карл Вейерштрасс - Stationen eines Lebens. Яхресбер. Dt. Math.-Vereinigung, 96 (1994), 56-75. 6. Дорофеева, А., Чернова, М .: Карл Вейерштрасс. Математика и Кибернетика 7 (1985), Москва. 7. Flaskamp, F .: Herkunft und Lebensweg des Mathematikers Karl Вейерштрасс.
Форш. u. Fortschr.35 (1961), 236-239. 8. Хензель, К .: Gedachtnisrede auf Ernst Eduard Kummer. Festschr. Zur Feier des 100. Geburststages Эдуард Куммерс. Лейпциг и Берлин 1910 г., 1-37. 9. Гильберт, Д .: Zum Gedachtnis an Karl Weierstrass. Nachrichten v. D. Kgl. Ges. d. Wissensch. zu Gottingen 1897, 60-69. 10. ---: Uber das Unendliche. Mathematische Annalen 95 (1926), 161–185. 11. Kiepert, L .: Personliche Erinnerungen an Karl Weierstrass. Яхресбер. d. Dt. Math.-Vereinigung 35 (1926), 56-65. 12. Кочина, П.: Карл Вейерштрасс. Москва "Наука" 1985. 13. Лампе, Э .: Карл Вейерштрасс. Яхресбер. d. Dt. Math.-Vereinigung 6 (1899), 27-44. 14. ---: Zur hundertsten Wiederkehr des Geburtstages von Karl Вейерштрасс. Яхресбер. d. Dt. Math.-Vereinigung 34 (1915), 416-438. 15. фон Лилиенталь, Р .: Карл Вейерштрасс. Westfalische Lebensbilder 2 (1931), 164-179. 16. Lorey, W .: Die padagogischen Ansichten des Mathematikers Karl. Вейерштрасс. Blatter fur hoheres Schulwesen 32 (1915), 626-629.17. ---: Karl Weierstrass zum Gedachtnis.
Zeitschr. f. математика. u. натурвисс. Unterricht 46 (1915), 597-607. 18. ---: Das Studium der Mathematik an den deutschen Universitaten seit Anfang des 19. Jahrhunderts. IMUK-Abhandlungen, Bd. 3, H. 9. Leipzig und Берлин 1916 год. 19. Mittag-Leffler, G.L: Une page de la vie de Weierstrass. Compte Rendu du deuxieme international des mathematiciens. Париж, 1902, 131–153. 20. ---: Zur Biographie von Weierstrass. Acta Mathematica 35 (1912 г.), 29-65. 21.---: Die ersten 40 Jahre des Lebens von Weierstrass. Acta Mathematica 39 (1923), 1-57. 22. ---: Софи Ковалевски: Обратите внимание на biographique. Acta Mathematica 16 (1892/93), 385-395. 23. ---: Вейерштрасс и Соня Ковалевски. Acta Mathematica 39 (1923 г.), 133-198. 24. Рахманова, А .: Соня Ковалевски. Цюрих 1953 г. 25. Rothe, R .: Bericht uber den gegenwartigen Stand der Herausgabe der Mathematischen Werke von Karl Weierstrass. Яхресбер. d. Dt. Math.-Vereinigung 15 (1916), 59-62. 26. ---: Bericht uber die Herausgabe des 7.Bands der Mathematischen Верке фон Карла Вейерштрасса.
Яхресбер. d. Dt. Math.-Vereinigung 37 (1928), 198-208. 27. Runge, C .: Personliche Erinnerungen an Karl Weierstrass. Яхресбер. d. Dt. Math.-Vereiningung 35 (1926), 175-179. 28. Schubert, H .: Zum Andenken an Karl Weierstrass. Zeitschr. f. математика. u. натурвисс. Unterricht 28 (1897), 228-231. 29. Siegmund-Schultze, R .: Der Beweis des Weierstrassschen Approximationssatzes 1885 vor dem Hintergrund der Entwicklung der Fourieranalysis. Historia Mathematica 15 (1988).30. Войт К. и Линдеманн Ф .: Карл Теодор Вильгельм Вейерштрасс. Sitzungsberichte d. математико-физ. Klasse der k. б. Akademie der Wissenschaften zu Munchen 27, 1897 (1898), 402-409.
Вернуться на главную страницу из
SIAM AG на сайте Orthogonal Многочлены и специальные функции
Страница поддерживается Мартин Малдун
Кибернетика — Детали статьи
Кибернетика — Детали статьи Кибернетика Международный журнал Института теории информации и автоматизацииJournalhome содержание журнала предстоящий выпуск поиск по автору по названию по ключевому слову от MSC инструкции для авторов награда редактора редакционная коллегия распределение контакт партнеры требуют документов Логин аккаунта зарегистрироваться Забытый пароль Об асимптотиках и скоростях сходимости, связанных со слабыми предельными распределениями геометрических случайных сумм S. AsmusenApplied Probability and Queues, Springer, 2003. http://dx.doi.org/10.1007/b97236DOI: 10.1007 / b97236S. AsmusenRuin Probabilities, World Scientific, 2010. С. Бобков Г. О близости вероятностных распределений в терминах преобразования Фурье-Стилтьеса // Успехи мат. Наук. Surveys 71 (2016), 6, 1021-1079. Http://dx.doi.org/10.1070/rm9749 DOI: 10.1070 / rm9749J. Л. Бон Экспоненциальные аппроксимации геометрических сумм для надежности. Технологический университет, 2002. Л. Бон Геометрические суммы в оценке надежности регенеративных систем.В кн .: Семинар памяти Калашникова, 2002, с. 161-163. Границы ошибки Брауна для экспоненциальной аппроксимации геометрических сверток. Вероятно. 18 (1990), 3, 1388-1402. Http://dx.doi.org/10.1214/aop/1176990750 DOI: 10.1214 / aop / 1176990750F. Геометрическое приближение DalyCompound при ограничении на интенсивность отказов. Appl. Вероятн. 53 (2016), 700-714. http://dx.doi.org/10.1017/jpr.2016.35 DOI: 10.1017 / jpr.2016.35R. Добрушин Л. Лемма о пределе сложных случайных функций // Успехи матем.
AsmusenApplied Probability and Queues, Springer, 2003. http://dx.doi.org/10.1007/b97236DOI: 10.1007 / b97236S. AsmusenRuin Probabilities, World Scientific, 2010. С. Бобков Г. О близости вероятностных распределений в терминах преобразования Фурье-Стилтьеса // Успехи мат. Наук. Surveys 71 (2016), 6, 1021-1079. Http://dx.doi.org/10.1070/rm9749 DOI: 10.1070 / rm9749J. Л. Бон Экспоненциальные аппроксимации геометрических сумм для надежности. Технологический университет, 2002. Л. Бон Геометрические суммы в оценке надежности регенеративных систем.В кн .: Семинар памяти Калашникова, 2002, с. 161-163. Границы ошибки Брауна для экспоненциальной аппроксимации геометрических сверток. Вероятно. 18 (1990), 3, 1388-1402. Http://dx.doi.org/10.1214/aop/1176990750 DOI: 10.1214 / aop / 1176990750F. Геометрическое приближение DalyCompound при ограничении на интенсивность отказов. Appl. Вероятн. 53 (2016), 700-714. http://dx.doi.org/10.1017/jpr.2016.35 DOI: 10.1017 / jpr.2016.35R. Добрушин Л. Лемма о пределе сложных случайных функций // Успехи матем..jpg) АН 10 (1955), 2 (64), 157-159.http://dx.doi.org/10.4213/rm9274DOI:10.4213/rm9274W. Феллер Введение в теорию вероятностей и ее приложения. Том 2, John Wiley and Son, Inc., 1966 г. В. ГнеденкоГ. Фахим О трансфертной теореме // Докл. Акад. АН СССР 187 (1969), 1, 15-17. Гнеденко В. О некоторых теоремах устойчивости. Лекция. Notes Math. 982 (1983), 24. http://dx.doi.org/10.1007/bfb0082058 DOI: 10.1007 / bfb0082058B. В. Гнеденко Ю. Королев Случайные суммирования: предельные теоремы и приложения, CRC Press, Нью-Йорк, 1996. Т. L. HungT. L. О вероятностной метрике на основе оператора Троттера.Вьетнамский математический журнал 35: 1, (2007), 21-32.T. L. Hung О скорости сходимости в предельных теоремах для геометрических сумм. J. Sci. 2 (2013), 2, 117-130. Т. L. HungT. Н. Хау О точности аппроксимации распределения отрицательно-биномиальных случайных сумм гамма-распределением // Кибернетика, 54 (2018), 5, 921-936. Http://dx.doi.org/10.14736/kyb-2018-5- 0921ДОИ: 10.14736 / kyb-2018-5-0921В. Калашников Геометрическая сумма: границы для редких событий с приложениями, Kluwer Academic Publishers, 1997.
АН 10 (1955), 2 (64), 157-159.http://dx.doi.org/10.4213/rm9274DOI:10.4213/rm9274W. Феллер Введение в теорию вероятностей и ее приложения. Том 2, John Wiley and Son, Inc., 1966 г. В. ГнеденкоГ. Фахим О трансфертной теореме // Докл. Акад. АН СССР 187 (1969), 1, 15-17. Гнеденко В. О некоторых теоремах устойчивости. Лекция. Notes Math. 982 (1983), 24. http://dx.doi.org/10.1007/bfb0082058 DOI: 10.1007 / bfb0082058B. В. Гнеденко Ю. Королев Случайные суммирования: предельные теоремы и приложения, CRC Press, Нью-Йорк, 1996. Т. L. HungT. L. О вероятностной метрике на основе оператора Троттера.Вьетнамский математический журнал 35: 1, (2007), 21-32.T. L. Hung О скорости сходимости в предельных теоремах для геометрических сумм. J. Sci. 2 (2013), 2, 117-130. Т. L. HungT. Н. Хау О точности аппроксимации распределения отрицательно-биномиальных случайных сумм гамма-распределением // Кибернетика, 54 (2018), 5, 921-936. Http://dx.doi.org/10.14736/kyb-2018-5- 0921ДОИ: 10.14736 / kyb-2018-5-0921В. Калашников Геометрическая сумма: границы для редких событий с приложениями, Kluwer Academic Publishers, 1997. http://dx.doi.org/10.1007/978-94-017-1693-2DOI:10.1007/978-94-017-1693-2L. Б. КлебановГ. М. Мания А. Меламед Проблема Золотарёва и аналоги безгранично делимых и устойчивых распределений в схеме суммирования случайного числа случайных величин // Теория вероятн. Appl. 29 (1084), 4, 791-794. http://dx.doi.org/10.1137/1129104DOI: 10.1137 / 1129104L. Клебанов Б. Тяжелохвостые распределения // Research Gate, 2003. В. Королёв Ю.А. И. ЗейфманЗаметка о смешанных представлениях для распределений Линника и Миттаг-Леффлера и их приложениях.J. Math. Sci. 218 (2016), 3, 314-327. http://dx.doi.org/10.1007/s10958-016-3032-6DOI: 10.1007 / s10958-016-3032-6C. Королёв Ю.А. В. Дорофеева Оценки функций концентрации случайных сумм в условиях ослабленных моментов (на русск. Яз., Теор. Верят. Прим. 62 (2017), 1, 104-121). В.Ю. Королев, А.И. Зейфман и распределения Миттаг-Леффлера и их обобщения. J. Korean Statist. Soc. 46 (2017), 2, 161-181. http://dx.x.doi.org/10.1016/j.jkss.2016.07.001DOI:10.1016/j.jkss.2016.
http://dx.doi.org/10.1007/978-94-017-1693-2DOI:10.1007/978-94-017-1693-2L. Б. КлебановГ. М. Мания А. Меламед Проблема Золотарёва и аналоги безгранично делимых и устойчивых распределений в схеме суммирования случайного числа случайных величин // Теория вероятн. Appl. 29 (1084), 4, 791-794. http://dx.doi.org/10.1137/1129104DOI: 10.1137 / 1129104L. Клебанов Б. Тяжелохвостые распределения // Research Gate, 2003. В. Королёв Ю.А. И. ЗейфманЗаметка о смешанных представлениях для распределений Линника и Миттаг-Леффлера и их приложениях.J. Math. Sci. 218 (2016), 3, 314-327. http://dx.doi.org/10.1007/s10958-016-3032-6DOI: 10.1007 / s10958-016-3032-6C. Королёв Ю.А. В. Дорофеева Оценки функций концентрации случайных сумм в условиях ослабленных моментов (на русск. Яз., Теор. Верят. Прим. 62 (2017), 1, 104-121). В.Ю. Королев, А.И. Зейфман и распределения Миттаг-Леффлера и их обобщения. J. Korean Statist. Soc. 46 (2017), 2, 161-181. http://dx.x.doi.org/10.1016/j.jkss.2016.07.001DOI:10.1016/j.jkss.2016. 07.001S. KotzT. J. KozubowskiK. Подгорский The Laplace Distribution and Generalization. Springer Science and Business Media, LLC., 2001. http://dx.doi.org/10.1007/978-1-4612-0173-1DOI: 10.1007 / 978-1-4612-0173-1V . М. КругловВ. Ю. Королев Предельные теоремы для случайных сумм, Издательство Московского Университета, Москва, 1990. Ману-Аби Солим Маваки Скорость сходимости к альфа-устойчивому закону с использованием расстояния Золотарева: технический отчет. Отчет об исследованиях, HAL Archives-Ouvertes 2017.http://dx.doi.org/10.18642/jsata\_7100121914DOI:10.18642/jsata\_7100121914E. SandhyaR. Н. Пиллай О геометрической безграничной делимости. Статист Кералы. Доц. 10 (1999), 01-07.E. SandhyaR. Пиллаи Н. Теория обновления и геометрическая бесконечная делимость // Пробл. Модели 2 (2003), 1-8.В. В. Петров Предельные теоремы теории вероятностей (последовательности независимых случайных величин), Clarendon Press Oxford, 1995. http://dx.doi.org/10.1017/s001309150002335xDOI: 10.1017 / s001309150002335xW.
07.001S. KotzT. J. KozubowskiK. Подгорский The Laplace Distribution and Generalization. Springer Science and Business Media, LLC., 2001. http://dx.doi.org/10.1007/978-1-4612-0173-1DOI: 10.1007 / 978-1-4612-0173-1V . М. КругловВ. Ю. Королев Предельные теоремы для случайных сумм, Издательство Московского Университета, Москва, 1990. Ману-Аби Солим Маваки Скорость сходимости к альфа-устойчивому закону с использованием расстояния Золотарева: технический отчет. Отчет об исследованиях, HAL Archives-Ouvertes 2017.http://dx.doi.org/10.18642/jsata\_7100121914DOI:10.18642/jsata\_7100121914E. SandhyaR. Н. Пиллай О геометрической безграничной делимости. Статист Кералы. Доц. 10 (1999), 01-07.E. SandhyaR. Пиллаи Н. Теория обновления и геометрическая бесконечная делимость // Пробл. Модели 2 (2003), 1-8.В. В. Петров Предельные теоремы теории вероятностей (последовательности независимых случайных величин), Clarendon Press Oxford, 1995. http://dx.doi.org/10.1017/s001309150002335xDOI: 10.1017 / s001309150002335xW..jpg) Рудин Принципы математического анализа.Mc Graw-Hill, Inc., 1976. http://dx.doi.org/10.1017/s0013091500008889 DOI: 10.1017 / s0013091500008889 V. Золотарев М. Метрические расстояния в пространствах случайных величин и их распределения // Мат. Сб. (N.S.) 101 (143) (1976), 3, 416-454. http://dx.doi.org/10.1070/sm1976v030n03abeh002280 DOI: 10.1070 / sm1976v030n03abeh002280V. Золотарев М.Ю. Аппроксимация распределения сумм независимых переменных со значениями в бесконечномерных пространствах // Теор. Верятность. и Применен. 21 (1976), 4, 741-758. Http://dx.doi.org / 10.1137 / 1121086 DOI: 10.1137 / 1121086V. Золотарев М. Вероятностные метрики // Теор. Верятность. и Применен. 28 (1983), 2, 264-287.Кибернетика — международный журнал ÚTIA | [email protected] | дизайн chcigrafiku.cz | v2.0
Рудин Принципы математического анализа.Mc Graw-Hill, Inc., 1976. http://dx.doi.org/10.1017/s0013091500008889 DOI: 10.1017 / s0013091500008889 V. Золотарев М. Метрические расстояния в пространствах случайных величин и их распределения // Мат. Сб. (N.S.) 101 (143) (1976), 3, 416-454. http://dx.doi.org/10.1070/sm1976v030n03abeh002280 DOI: 10.1070 / sm1976v030n03abeh002280V. Золотарев М.Ю. Аппроксимация распределения сумм независимых переменных со значениями в бесконечномерных пространствах // Теор. Верятность. и Применен. 21 (1976), 4, 741-758. Http://dx.doi.org / 10.1137 / 1121086 DOI: 10.1137 / 1121086V. Золотарев М. Вероятностные метрики // Теор. Верятность. и Применен. 28 (1983), 2, 264-287.Кибернетика — международный журнал ÚTIA | [email protected] | дизайн chcigrafiku.cz | v2.0CZ — Чешская цифровая математическая библиотека: об асимптотическом поведении и скорости сходимости, связанных со слабыми предельными распределениями геометрических случайных сумм
[2] С., Асмузен: Вероятность разрушения . World Scientific, 2010. MR 1794582
[3] Г., Бобков, С.: Близость вероятностных распределений в терминах преобразования Фурье-Стилтьеса . Русская математика. Опросы 71 (2016), 6, 1021-1079. DOI 10.1070 / rm9749 | Руководство по ремонту 3588939
World Scientific, 2010. MR 1794582
[3] Г., Бобков, С.: Близость вероятностных распределений в терминах преобразования Фурье-Стилтьеса . Русская математика. Опросы 71 (2016), 6, 1021-1079. DOI 10.1070 / rm9749 | Руководство по ремонту 3588939[4] Л., Бон, Дж .: Экспоненциальные аппроксимации геометрических сумм для надежности . Технологический университет, 2002.
[5] Л., Бон, Дж .: Геометрические суммы в оценке надежности регенеративных систем . В: Семинар памяти Калашникова, 2002, с. 161-163. MR 1471479. [8] Л., Добрушин, Р.: Лемма о пределе сложных случайных функций . Успехи матем. АН 10 (1955), 2 (64), 157-159. DOI 10.4213 / rm9274 | Руководство по ремонту 0070870 [9] W., Feller ,: Введение в теорию вероятностей и ее приложения. Том 2 . John Wiley and Son, Inc., 1966. MR 0210154 [10] В., Гнеденко, Б., Г., Фахим ,: О теореме переноса . Докл. Акад. АН СССР 187 (1969), 1, 15-17. Руководство по ремонту 0251771 [12] В., Гнеденко, Б. , Ю., Королев, В .: Случайные суммирования: предельные теоремы и приложения .CRC Press, New York 1996. MR 1387113
[13] Л., Хунг, Т., Т., Л.,: О вероятностной метрике, основанной на операторе Троттера . Вьетнамский математический журнал 35: 1, (2007), 21-32. Руководство по ремонту 2317431
, Ю., Королев, В .: Случайные суммирования: предельные теоремы и приложения .CRC Press, New York 1996. MR 1387113
[13] Л., Хунг, Т., Т., Л.,: О вероятностной метрике, основанной на операторе Троттера . Вьетнамский математический журнал 35: 1, (2007), 21-32. Руководство по ремонту 2317431[14] Л., Хунг, Т .: О скорости сходимости в предельных теоремах для геометрических сумм . Юго-Восточная Азия J. Sci. 2 (2013), 2, 117-130.
[15] Л., Хунг, Т., Н., Хау, Т .: О точности аппроксимации распределения отрицательно-биномиальных случайных сумм гамма-распределением .Кибернетика 54 (2018), 5, 921-936. DOI 10.14736 / kyb-2018-5-0921 | Руководство по ремонту 3893128 [17] Б., Клебанов, Л., М., Мания, Г., А., Меламед, И .: Задача Золотарева и аналоги безгранично делимых и устойчивых распределений в схеме суммирования случайного числа случайных переменные . Теория вероятн. Appl. 29 (1084), 4, 791-794. DOI 10.1137 / 1129104 | MR 0773445 [18] Б., Клебанов, Л . : Heavy Tailed Distributions . Research Gate, 2003.
: Heavy Tailed Distributions . Research Gate, 2003.
 , Ю., Королев, В .: Предельные теоремы для случайных сумм . Издательство Московского Университета, Москва 1990. MR 1072999
[24] Солым, Маваки, Ману-Аби: Скорость сходимости к альфа-стабильному закону с использованием расстояния Золотарева: технический отчет .Отчет об исследованиях, HAL Archives-Ouvertes 2017. DOI 10.18642 / jsata \ _7100121914
, Ю., Королев, В .: Предельные теоремы для случайных сумм . Издательство Московского Университета, Москва 1990. MR 1072999
[24] Солым, Маваки, Ману-Аби: Скорость сходимости к альфа-стабильному закону с использованием расстояния Золотарева: технический отчет .Отчет об исследованиях, HAL Archives-Ouvertes 2017. DOI 10.18642 / jsata \ _7100121914[25] Э., Сандхья, Н., Пиллаи, Р .: О геометрической безграничной делимости . Дж. Статист Кералы. Доц. 10 (1999), 01-07.
[26] Э., Сандхья, Н., Пиллаи, Р .: Теория восстановления и геометрическая бесконечная делимость . ProbStat. Модели 2 (2003 г.), 1-8.
[30] М., Золотарев, В .: Аппроксимация распределения сумм независимых переменных со значениями в бесконечномерных пространствах .Теор. Верятность. и Применен. 21 (1976), 4, 741-758. DOI 10.1137 / 1121086 | Руководство по ремонту 0517338 [31] М., Золотарев, В .: Вероятностные метрики . Теор. Верятность. и Применен. 28 (1983), 2, 264-287. Руководство по ремонту 0700210
Руководство по ремонту 0700210Произошла ошибка при настройке вашего пользовательского файла cookie
Произошла ошибка при настройке вашего пользовательского файла cookieЭтот сайт использует файлы cookie для повышения производительности. Если ваш браузер не принимает файлы cookie, вы не можете просматривать этот сайт.
Настройка вашего браузера для приема файлов cookie
Существует множество причин, по которым cookie не может быть установлен правильно.Ниже приведены наиболее частые причины:
- В вашем браузере отключены файлы cookie. Вам необходимо сбросить настройки своего браузера, чтобы он принимал файлы cookie, или чтобы спросить вас, хотите ли вы принимать файлы cookie.
- Ваш браузер спрашивает вас, хотите ли вы принимать файлы cookie, и вы отказались. Чтобы принять файлы cookie с этого сайта, используйте кнопку «Назад» и примите файлы cookie.
- Ваш браузер не поддерживает файлы cookie.
 Если вы подозреваете это, попробуйте другой браузер.
Если вы подозреваете это, попробуйте другой браузер. - Дата на вашем компьютере в прошлом. Если часы вашего компьютера показывают дату до 1 января 1970 г., браузер автоматически забудет файл cookie. Чтобы исправить это, установите правильное время и дату на своем компьютере.
- Вы установили приложение, которое отслеживает или блокирует установку файлов cookie. Вы должны отключить приложение при входе в систему или уточнить у системного администратора.
Почему этому сайту требуются файлы cookie?
Этот сайт использует файлы cookie для повышения производительности, запоминая, что вы вошли в систему, когда переходите со страницы на страницу.Чтобы предоставить доступ без файлов cookie потребует, чтобы сайт создавал новый сеанс для каждой посещаемой страницы, что замедляет работу системы до неприемлемого уровня.
Что сохраняется в файлах cookie?
Этот сайт не хранит ничего, кроме автоматически сгенерированного идентификатора сеанса в cookie; никакая другая информация не фиксируется.



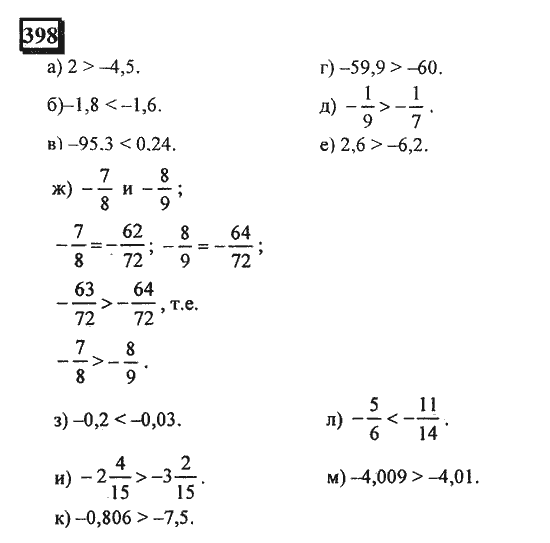 В 5 классе нагрузка на ученика значительно увеличивается, учителей становится больше, требования дисциплины ужесточаются.
В 5 классе нагрузка на ученика значительно увеличивается, учителей становится больше, требования дисциплины ужесточаются.
 Отслеживая динамику, сначала вместе с родителями, учителями, пятиклассники учатся контролировать свои достижения, быстро выявлять и исправлять обнаруженные недостатки, пока они не превратятся в серьезные проблемы непонимания математики;
Отслеживая динамику, сначала вместе с родителями, учителями, пятиклассники учатся контролировать свои достижения, быстро выявлять и исправлять обнаруженные недостатки, пока они не превратятся в серьезные проблемы непонимания математики;  Для более глубокого и полного понимания материала вы можете использовать другие пособия из тех же учебных материалов, которые входят в комплект к базовому учебнику. Среди популярных — дидактических материалов, , контрольных, работ и контрольных работ, рабочие тетради, устные упражнения и другие аналогичные практические занятия.
Для более глубокого и полного понимания материала вы можете использовать другие пособия из тех же учебных материалов, которые входят в комплект к базовому учебнику. Среди популярных — дидактических материалов, , контрольных, работ и контрольных работ, рабочие тетради, устные упражнения и другие аналогичные практические занятия..jpg) 6 ----------- 15 ноября 1998 г.
~~~~~~~~~~~~~
От: OP-SF NET Editors
Тема: Статья У. Скорника о Вейерштрассе
[В информационном бюллетене нашей группы действий появился следующий элемент:
Октябрь 1998 г .; он был перепечатан с разрешения
Российский информационный бюллетень "Интегральные преобразования и специальные функции"]
Карл Теодор В. Вейерштрасс - Жизнь и творчество
К 100-летию со дня его смерти
У. Скорник
Институт математики,
Польская академия наук,
Старомейская 8/6, 40-013
Катовице, Польша
Электронная почта: skornik @ impan.gov.pl
19 февраля 1997 г. исполнилось 100 лет со дня смерти
великий немецкий математик, отец классического математического анализа
и теория абелевых и специальных функций, Карл Теодор Вильгельм
Вейерштрасс. Он родился 31 октября 1815 года, был первым ребенком Вильгельма.
Вейерштрасс, секретарь мэра Остенфельде и Теодора
Vonderforst.
Ничто в его ранней жизни не указывало на то, что он станет известным
математик. Карл посещал католическую гимназию в Падерборне с 1829 года.
6 ----------- 15 ноября 1998 г.
~~~~~~~~~~~~~
От: OP-SF NET Editors
Тема: Статья У. Скорника о Вейерштрассе
[В информационном бюллетене нашей группы действий появился следующий элемент:
Октябрь 1998 г .; он был перепечатан с разрешения
Российский информационный бюллетень "Интегральные преобразования и специальные функции"]
Карл Теодор В. Вейерштрасс - Жизнь и творчество
К 100-летию со дня его смерти
У. Скорник
Институт математики,
Польская академия наук,
Старомейская 8/6, 40-013
Катовице, Польша
Электронная почта: skornik @ impan.gov.pl
19 февраля 1997 г. исполнилось 100 лет со дня смерти
великий немецкий математик, отец классического математического анализа
и теория абелевых и специальных функций, Карл Теодор Вильгельм
Вейерштрасс. Он родился 31 октября 1815 года, был первым ребенком Вильгельма.
Вейерштрасс, секретарь мэра Остенфельде и Теодора
Vonderforst.
Ничто в его ранней жизни не указывало на то, что он станет известным
математик. Карл посещал католическую гимназию в Падерборне с 1829 года. до 1834 г., когда он поступил в Боннский университет, чтобы пройти курс обучения
в области государственных финансов, экономики и управления.Этот выбор далек от его
собственные интересы, продиктовал его отец, в результате чего после четырех
лет, потраченных на фехтование, выпивку и математику, Карл вернулся домой
без сдачи экзаменов. Однако годы в Бонне были
не совсем потрачено впустую. Во время пребывания там Вейерштрасс
посещал лекции знаменитого геометра Плюккера, изучал "Mecanique"
Селеста »Лапласа,« Fundamenta nova »Якоби и расширенный его
знания по случайно найденной транскрипции лекций по эллиптическому
функции Гудерманна.2 \ varphi}},
с параметром k между 0 и 1, называемым модулем эллиптического
интеграл. Эллиптические функции, полученные из этого интеграла, были названы
модульные функции Гудерманна. Это была новая теория, и Гудерманн был
сначала после Якоби, чтобы прочитать лекции на эту тему.
2 мая 1840 года Вейерштрассу были поставлены задачи к выпускным экзаменам;
один из них был поставлен Гудерманом по особому желанию его
студент и заинтересованные эллиптические функции.
до 1834 г., когда он поступил в Боннский университет, чтобы пройти курс обучения
в области государственных финансов, экономики и управления.Этот выбор далек от его
собственные интересы, продиктовал его отец, в результате чего после четырех
лет, потраченных на фехтование, выпивку и математику, Карл вернулся домой
без сдачи экзаменов. Однако годы в Бонне были
не совсем потрачено впустую. Во время пребывания там Вейерштрасс
посещал лекции знаменитого геометра Плюккера, изучал "Mecanique"
Селеста »Лапласа,« Fundamenta nova »Якоби и расширенный его
знания по случайно найденной транскрипции лекций по эллиптическому
функции Гудерманна.2 \ varphi}},
с параметром k между 0 и 1, называемым модулем эллиптического
интеграл. Эллиптические функции, полученные из этого интеграла, были названы
модульные функции Гудерманна. Это была новая теория, и Гудерманн был
сначала после Якоби, чтобы прочитать лекции на эту тему.
2 мая 1840 года Вейерштрассу были поставлены задачи к выпускным экзаменам;
один из них был поставлен Гудерманом по особому желанию его
студент и заинтересованные эллиптические функции. Осенью 1840 года Вейерштрасс
представил результаты своих исследований по декомпозиции модульных
функции.2. В
память об Авеле, он называл их функциями Аля. Затем Вейерштрасс представил
его знаменитые \ sigma-функции, которые отличаются от функций Al на
множитель.
Его диссертация содержала значительный новый материал и могла обеспечить
академическая должность для него в Германии или где-либо еще. Неизвестно почему
эта работа, высоко оцененная Гудерманом, была опубликована только 54 года назад.
позже в первом томе Сборника статей Вейерштрасса. Вместо
обретя математическую известность, Вейерштрасс, сдав вторую устную часть
экзаменов весной 1841 г., проработал 14 лет в средней школе
школьный учитель.После испытательного года в Мюнстере Вейерштрасс работал в католической церкви.
гимназия (средняя школа высокого уровня) в Deutsch-Krone (Западная Пруссия) от
С 1842 по 1848 год, а затем в аналогичной школе в Браунсберге (Восточная Пруссия)
с 1848 по 1855 год. Он преподавал не только математику и физику, но и
Немецкий язык, ботаника, география, история, гимнастика и каллиграфия.
Осенью 1840 года Вейерштрасс
представил результаты своих исследований по декомпозиции модульных
функции.2. В
память об Авеле, он называл их функциями Аля. Затем Вейерштрасс представил
его знаменитые \ sigma-функции, которые отличаются от функций Al на
множитель.
Его диссертация содержала значительный новый материал и могла обеспечить
академическая должность для него в Германии или где-либо еще. Неизвестно почему
эта работа, высоко оцененная Гудерманом, была опубликована только 54 года назад.
позже в первом томе Сборника статей Вейерштрасса. Вместо
обретя математическую известность, Вейерштрасс, сдав вторую устную часть
экзаменов весной 1841 г., проработал 14 лет в средней школе
школьный учитель.После испытательного года в Мюнстере Вейерштрасс работал в католической церкви.
гимназия (средняя школа высокого уровня) в Deutsch-Krone (Западная Пруссия) от
С 1842 по 1848 год, а затем в аналогичной школе в Браунсберге (Восточная Пруссия)
с 1848 по 1855 год. Он преподавал не только математику и физику, но и
Немецкий язык, ботаника, география, история, гимнастика и каллиграфия.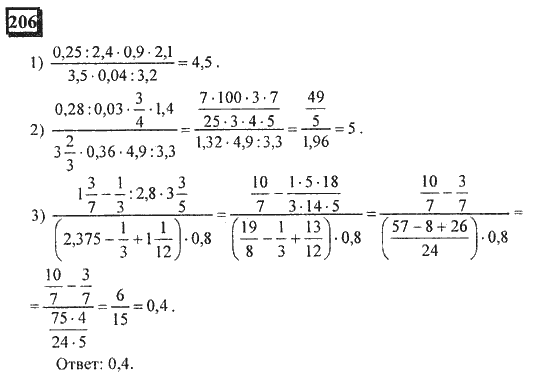 В 1844 г.
Вейерштрасс прошел курс для учителей гимнастики в Берлине.
За это время он посетил знаменитого геометра Штайнера. Однако это
не изменил своего положения.В Deutsch-Krone Weierstrass не имел ни
доступ к математической литературе, ни возможность обмена
идеи с любым другим математиком. Он чувствовал себя изолированным и наполнял свою жизнь
с работой. В те годы он разработал теорию абелевых функций.
которые образуют более широкий класс, чем эллиптические функции. Абелевы интегралы
определяются как эллиптические интегралы формулой
u = \ int (от 0 до v) R (t, \ sqrt {f (t)}) dt = I (v)
где R (x, y) - рациональная функция от x и y, за исключением того, что функция f
имеет очень общий тип, который включает в себя все многочлены.Инверсия тогда
дает абелевы функции, так же как эллиптические функции возникают из
обращение эллиптических интегралов, т.е. интегралов, где f (t)
полином.
Во время испытательного года Вейерштрасса в гимназии в Мюнстере он
работал над тремя статьями. Первый "Darstellung einer analytischen"
Funktion, deren absoluter Betrag zwischen zwei gegebenen Grenzen liegt "
содержит доказательство интегральной теоремы Коши без использования двойных
или поверхностные интегралы.
В 1844 г.
Вейерштрасс прошел курс для учителей гимнастики в Берлине.
За это время он посетил знаменитого геометра Штайнера. Однако это
не изменил своего положения.В Deutsch-Krone Weierstrass не имел ни
доступ к математической литературе, ни возможность обмена
идеи с любым другим математиком. Он чувствовал себя изолированным и наполнял свою жизнь
с работой. В те годы он разработал теорию абелевых функций.
которые образуют более широкий класс, чем эллиптические функции. Абелевы интегралы
определяются как эллиптические интегралы формулой
u = \ int (от 0 до v) R (t, \ sqrt {f (t)}) dt = I (v)
где R (x, y) - рациональная функция от x и y, за исключением того, что функция f
имеет очень общий тип, который включает в себя все многочлены.Инверсия тогда
дает абелевы функции, так же как эллиптические функции возникают из
обращение эллиптических интегралов, т.е. интегралов, где f (t)
полином.
Во время испытательного года Вейерштрасса в гимназии в Мюнстере он
работал над тремя статьями. Первый "Darstellung einer analytischen"
Funktion, deren absoluter Betrag zwischen zwei gegebenen Grenzen liegt "
содержит доказательство интегральной теоремы Коши без использования двойных
или поверхностные интегралы. Он также представил серию Лорана и пришел к
Теорема Лорана за два года до ее официального опубликования в
Comptes Rendus Коши.В этой работе Вейерштрасс выразил сложные
числа в форме
r {1+ \ lambda i} \ over {1- \ lambda i},
где r - абсолютное значение, а \ lambda - действительное число, заданное как
\ lambda = \ tan (\ theta / 2), где \ thet - амплитуда комплекса
номер. Газета "Zur Theorie der Potenzreihen" датируется осенью 1841 года.
В этой работе Вейерштрасс ввел понятие равномерной сходимости и
исследовали ряды по нескольким переменным. В следующей статье «Определение
analytischer Funktionen einer Veranderlichen vermittelst algebraischer
Differentialgleichungen », датируемой 1842 г., он доказал теорему
Коши о решении систем дифференциальных уравнений
dx / dt = G_i (x_1 ,..., x_n)
с начальными условиями x_i (0) = a_i, где G_i - многочлены. В
В этой статье Вейерштрасс описал процесс аналитического продолжения
силовой ряд. Эти статьи были опубликованы только в первом томе его
Собрал статьи 1894 года, но из них ясно видно, что уже в 1842 году он
полностью владел всеми методами и идеями, которые позволяли ему
построить свою теорию функций.
Он также представил серию Лорана и пришел к
Теорема Лорана за два года до ее официального опубликования в
Comptes Rendus Коши.В этой работе Вейерштрасс выразил сложные
числа в форме
r {1+ \ lambda i} \ over {1- \ lambda i},
где r - абсолютное значение, а \ lambda - действительное число, заданное как
\ lambda = \ tan (\ theta / 2), где \ thet - амплитуда комплекса
номер. Газета "Zur Theorie der Potenzreihen" датируется осенью 1841 года.
В этой работе Вейерштрасс ввел понятие равномерной сходимости и
исследовали ряды по нескольким переменным. В следующей статье «Определение
analytischer Funktionen einer Veranderlichen vermittelst algebraischer
Differentialgleichungen », датируемой 1842 г., он доказал теорему
Коши о решении систем дифференциальных уравнений
dx / dt = G_i (x_1 ,..., x_n)
с начальными условиями x_i (0) = a_i, где G_i - многочлены. В
В этой статье Вейерштрасс описал процесс аналитического продолжения
силовой ряд. Эти статьи были опубликованы только в первом томе его
Собрал статьи 1894 года, но из них ясно видно, что уже в 1842 году он
полностью владел всеми методами и идеями, которые позволяли ему
построить свою теорию функций. К сожалению, его первая публикация
статья "Bemerkung uber die analytischen Fakultaten" появилась в
приложение к школьному отчету 1842 года в немецкой кроне и
уделялось мало внимания.То же произошло и с другой статьей об Абелевах.
функций, который был опубликован в 1848 году в проспекте школы Браунсберга.
Вейерштрасс остался бы незамеченным, если бы летом
1853 г. во время своего пребывания в Мюнстере он прочитал мнение Гудерманна о его
диссертация впервые. Уже в 1840 году Кристоф Гудерманн не
не только признал редкий талант Карла, но и поместил его в ряды знаменитых
первооткрыватели и предложили своему ученику работать в университете
а не как учитель средней школы.Эта записка поощряла
Вейерштрасс публикует свою статью «Zur Theorie der Abelschen Funktionen».
Его появление в 1854 году в журнале Crelle's Journal вызвало сенсацию в
математический мир. Последствия были потрясающими. Первое признание
был удостоен звания почетного доктора Кенигсбергского университета.
Тогда прусское министерство образования предоставило ему годовой оплачиваемый отпуск от
гимназии Браунсберга, чтобы он мог сосредоточиться на своих исследованиях.
К сожалению, его первая публикация
статья "Bemerkung uber die analytischen Fakultaten" появилась в
приложение к школьному отчету 1842 года в немецкой кроне и
уделялось мало внимания.То же произошло и с другой статьей об Абелевах.
функций, который был опубликован в 1848 году в проспекте школы Браунсберга.
Вейерштрасс остался бы незамеченным, если бы летом
1853 г. во время своего пребывания в Мюнстере он прочитал мнение Гудерманна о его
диссертация впервые. Уже в 1840 году Кристоф Гудерманн не
не только признал редкий талант Карла, но и поместил его в ряды знаменитых
первооткрыватели и предложили своему ученику работать в университете
а не как учитель средней школы.Эта записка поощряла
Вейерштрасс публикует свою статью «Zur Theorie der Abelschen Funktionen».
Его появление в 1854 году в журнале Crelle's Journal вызвало сенсацию в
математический мир. Последствия были потрясающими. Первое признание
был удостоен звания почетного доктора Кенигсбергского университета.
Тогда прусское министерство образования предоставило ему годовой оплачиваемый отпуск от
гимназии Браунсберга, чтобы он мог сосредоточиться на своих исследованиях. Вейерштрасс приобрел достаточно уверенности, чтобы подать заявку на эту должность в
Университет в Бреслау, который был освобожден назначением Куммера
профессор в Берлине.Может показаться странным, что заявление Вейерштрасса
был отклонен из-за Куммера. Причина в том, что Куммер, потративший 13
лет преподавания в Бреслау, намеревался отвезти Вейерштрасса в Берлин. Он
подал заявление 12 июня 1856 г. в университет в Берлине с просьбой о
пост для Вейерштрасса. В этом случае он не добился успеха, но его
Возможный успех дал математике в Берлине три великих имени:
Вейерштрасс, Куммер и Кронекер.
"Theorie der Abelschen Funktionen" Вейерштрасса опубликована в Crelle's
Журнал 1856 г. содержал результаты его диссертации.Д. Гильберт
рассмотрел эти результаты относительно решения обращения Якоби
задача для гиперэллиптического интеграла величайшее достижение
анализ. Эта публикация стала поворотным моментом в жизни Карла.
Вейерштрасс. Он стал известен за рубежом, и австрийское правительство сделало
запросы о нем через Александра фон Гумбольдта.
Вейерштрасс приобрел достаточно уверенности, чтобы подать заявку на эту должность в
Университет в Бреслау, который был освобожден назначением Куммера
профессор в Берлине.Может показаться странным, что заявление Вейерштрасса
был отклонен из-за Куммера. Причина в том, что Куммер, потративший 13
лет преподавания в Бреслау, намеревался отвезти Вейерштрасса в Берлин. Он
подал заявление 12 июня 1856 г. в университет в Берлине с просьбой о
пост для Вейерштрасса. В этом случае он не добился успеха, но его
Возможный успех дал математике в Берлине три великих имени:
Вейерштрасс, Куммер и Кронекер.
"Theorie der Abelschen Funktionen" Вейерштрасса опубликована в Crelle's
Журнал 1856 г. содержал результаты его диссертации.Д. Гильберт
рассмотрел эти результаты относительно решения обращения Якоби
задача для гиперэллиптического интеграла величайшее достижение
анализ. Эта публикация стала поворотным моментом в жизни Карла.
Вейерштрасс. Он стал известен за рубежом, и австрийское правительство сделало
запросы о нем через Александра фон Гумбольдта. Это подтолкнуло фон
Гумбольдта к действиям, и 1 июля 1856 года Вейерштрасс был назначен профессором
в Промышленном институте в Берлине.
В сентябре 1856 года Вейерштрасс и Куммер отправились в Вену.Вот, Граф Тун
предложил Weierstrass 2000 Gulden и должность профессора в австрийском
университет по своему выбору. Вейерштрасс отклонил это предложение, но оно стало
Куммеру ясно, что если они хотят оставить великого математика в
Германия ему снова пришлось действовать.
Вскоре после этого в результате усилий Куммера Вейерштрасс был
назначен доцентом Берлинского университета. В ноябре
В 1856 году он стал членом Берлинской академии. С тех пор до 1890 г.
читал лекции по самым разным темам, включая периодические лекции по
эллиптические функции, лекции по геометрии и механике.Известный
математический семинар, который он инициировал вместе с Куммером в 1861 г.
привлекли международный интерес. С 1862 г. было принято делать
награды лучшим участникам. Стоит отметить, что первые
математико-физический семинар был основан в Кенигсберге в 1834 г.
Это подтолкнуло фон
Гумбольдта к действиям, и 1 июля 1856 года Вейерштрасс был назначен профессором
в Промышленном институте в Берлине.
В сентябре 1856 года Вейерштрасс и Куммер отправились в Вену.Вот, Граф Тун
предложил Weierstrass 2000 Gulden и должность профессора в австрийском
университет по своему выбору. Вейерштрасс отклонил это предложение, но оно стало
Куммеру ясно, что если они хотят оставить великого математика в
Германия ему снова пришлось действовать.
Вскоре после этого в результате усилий Куммера Вейерштрасс был
назначен доцентом Берлинского университета. В ноябре
В 1856 году он стал членом Берлинской академии. С тех пор до 1890 г.
читал лекции по самым разным темам, включая периодические лекции по
эллиптические функции, лекции по геометрии и механике.Известный
математический семинар, который он инициировал вместе с Куммером в 1861 г.
привлекли международный интерес. С 1862 г. было принято делать
награды лучшим участникам. Стоит отметить, что первые
математико-физический семинар был основан в Кенигсберге в 1834 г. Якоби, Нойман и Зонке, второй в Галле в 1838 году и третий в
Гёттинген в 1850 году.
Тяжелая рабочая нагрузка Вейерштрасса привела к ухудшению его здоровья в
Декабрь 1861 г. Он вернулся к преподаванию через год, но читал лекции в
сидячее положение со студентом, пишущим необходимый текст на
доска.Всю оставшуюся жизнь он страдал от повторяющихся приступов
бронхит и флебит, но его решимость заставляла его учить и
продолжая свое исследование. В своих лекциях Вейерштрасс инициировал логическое
и тщательное развитие анализа, начиная с его собственного построения
действительная система счисления. Он установил понятия эпсилон-дельта в
концепция непрерывности и сходимости, равномерная сходимость, абсолютная
значение, окрестность (a- \ delta, a + \ delta) точки $ a $ и многие другие.
Он отвергал интуитивные аргументы, которые все еще преобладали среди многих
современные математики.Именно Вейерштрасс в своих лекциях по
1862 г. дал знаменитый пример непрерывного нигде не дифференцируемого
функция.
Якоби, Нойман и Зонке, второй в Галле в 1838 году и третий в
Гёттинген в 1850 году.
Тяжелая рабочая нагрузка Вейерштрасса привела к ухудшению его здоровья в
Декабрь 1861 г. Он вернулся к преподаванию через год, но читал лекции в
сидячее положение со студентом, пишущим необходимый текст на
доска.Всю оставшуюся жизнь он страдал от повторяющихся приступов
бронхит и флебит, но его решимость заставляла его учить и
продолжая свое исследование. В своих лекциях Вейерштрасс инициировал логическое
и тщательное развитие анализа, начиная с его собственного построения
действительная система счисления. Он установил понятия эпсилон-дельта в
концепция непрерывности и сходимости, равномерная сходимость, абсолютная
значение, окрестность (a- \ delta, a + \ delta) точки $ a $ и многие другие.
Он отвергал интуитивные аргументы, которые все еще преобладали среди многих
современные математики.Именно Вейерштрасс в своих лекциях по
1862 г. дал знаменитый пример непрерывного нигде не дифференцируемого
функция. В том же году он впервые в своих лекциях развил теорию
функции \ gamma (u) и \ sigma (u). Его знаменитая аппроксимационная теорема
появился в связи с уравнением теплопроводности и был опубликован в июле.
1885 г. в Протоколах заседаний Берлинской академии наук.
Он также внес свой вклад в развитие вариационного исчисления на
которую он читал в 1879 году.Однако его основные лекции были сосредоточены на
Абелевы функции. Его периодически читаемые лекции включали
«Введение в теорию аналитических функций», «Теория
Эллиптические функции », когда-то подходивший с точки зрения
дифференциальные уравнения, в другой раз с точки зрения теории
функций "Применение эллиптических функций к геометрии и
Механика »,« Применение абелевых функций к геометрическим задачам и
вариационное исчисление ». Его лекции собрали аудиторию до 250 человек.
среди них более 100 будущих профессоров, в том числе С.Ковалевский, Шварц,
Фукс, Г. Миттаг-Леффлер, Л. Кенигсбергер, Х. Минковский и Кантор.
Вейерштрасс оказал огромное влияние на математический мир.
В том же году он впервые в своих лекциях развил теорию
функции \ gamma (u) и \ sigma (u). Его знаменитая аппроксимационная теорема
появился в связи с уравнением теплопроводности и был опубликован в июле.
1885 г. в Протоколах заседаний Берлинской академии наук.
Он также внес свой вклад в развитие вариационного исчисления на
которую он читал в 1879 году.Однако его основные лекции были сосредоточены на
Абелевы функции. Его периодически читаемые лекции включали
«Введение в теорию аналитических функций», «Теория
Эллиптические функции », когда-то подходивший с точки зрения
дифференциальные уравнения, в другой раз с точки зрения теории
функций "Применение эллиптических функций к геометрии и
Механика »,« Применение абелевых функций к геометрическим задачам и
вариационное исчисление ». Его лекции собрали аудиторию до 250 человек.
среди них более 100 будущих профессоров, в том числе С.Ковалевский, Шварц,
Фукс, Г. Миттаг-Леффлер, Л. Кенигсбергер, Х. Минковский и Кантор.
Вейерштрасс оказал огромное влияние на математический мир. Он
получил высокое признание во всей Европе. Шведский математик
Миттаг-Леффлер упоминает хороший анекдот. Когда он получил стипендию на
учиться за границей в 1873 году он отправился в Париж, где Эрмит встретил его
слова "Vous avez fait erreur, Monsieur, vous auriez du suivre les cours
де Вейерштрасс в Берлине ». И, конечно же, Миттаг-Леффлер последовал примеру Эрмита.
посоветовал и поехал в Берлин.Самой выдающейся ученицей Вейерштрасса была Соня Ковалевская,
дочь русского артиллерийского генерала. Женщинам не разрешили учиться
в России, поэтому в 1868 году она заключила брак по расчету с молодым
палеонтолог Владимир Ковалевский и пара уехали учиться за границу.
Сначала они поступили в Гейдельбергский университет, но через два года
они разделены. Владимир поехал в Йену, а Соня поехала в Берлин в надежде
посещать лекции Вейерштрасса. К сожалению, был запрет на женщин
студентка Берлинского университета, и ее заявление было отклонено.Так
она пошла прямо к Вейерштрассу со своими хайдельбергскими ссылками.
Он
получил высокое признание во всей Европе. Шведский математик
Миттаг-Леффлер упоминает хороший анекдот. Когда он получил стипендию на
учиться за границей в 1873 году он отправился в Париж, где Эрмит встретил его
слова "Vous avez fait erreur, Monsieur, vous auriez du suivre les cours
де Вейерштрасс в Берлине ». И, конечно же, Миттаг-Леффлер последовал примеру Эрмита.
посоветовал и поехал в Берлин.Самой выдающейся ученицей Вейерштрасса была Соня Ковалевская,
дочь русского артиллерийского генерала. Женщинам не разрешили учиться
в России, поэтому в 1868 году она заключила брак по расчету с молодым
палеонтолог Владимир Ковалевский и пара уехали учиться за границу.
Сначала они поступили в Гейдельбергский университет, но через два года
они разделены. Владимир поехал в Йену, а Соня поехала в Берлин в надежде
посещать лекции Вейерштрасса. К сожалению, был запрет на женщин
студентка Берлинского университета, и ее заявление было отклонено.Так
она пошла прямо к Вейерштрассу со своими хайдельбергскими ссылками. Он дал
ей нужно было решить некоторые проблемы, и ее решения и энтузиазм впечатлили его
поэтому он решил обучать ее в частном порядке. За четыре года, которые она провела
в Берлине она стала его близким другом и незаменимым партнером для
научные дискуссии. Мы мало что знаем о частной жизни Вейерштрасса.
жизнь. Соня, однако, вторая женщина (после Марии Склодовской Кюри), которая
занимал университетский пост, писатель и революционер, стал прекрасным
Тема для многих биографий и романов.Вейерштрасс считал ее своим
самый талантливый ученик. Фактически, во время своего пребывания в Берлине она произвела
три выдающихся документа; по дифференциальным уравнениям, по абелевым интегралам
и на кольцах Сатурна, и сумел получить докторскую степень от
Геттингенский университет. Однако Вейерштрасс, к своему большому сожалению, мог
не обеспечили ей работу в Германии, и ей пришлось вернуться в Россию.
Их дружба, хотя и основывалась на чисто научном взаимодействии, стала
предмет слухов. Вейерштрасс глубоко обиделся из-за настойчивых
инсинуации, окружающие его ученицу и ее математические достижения.
Он дал
ей нужно было решить некоторые проблемы, и ее решения и энтузиазм впечатлили его
поэтому он решил обучать ее в частном порядке. За четыре года, которые она провела
в Берлине она стала его близким другом и незаменимым партнером для
научные дискуссии. Мы мало что знаем о частной жизни Вейерштрасса.
жизнь. Соня, однако, вторая женщина (после Марии Склодовской Кюри), которая
занимал университетский пост, писатель и революционер, стал прекрасным
Тема для многих биографий и романов.Вейерштрасс считал ее своим
самый талантливый ученик. Фактически, во время своего пребывания в Берлине она произвела
три выдающихся документа; по дифференциальным уравнениям, по абелевым интегралам
и на кольцах Сатурна, и сумел получить докторскую степень от
Геттингенский университет. Однако Вейерштрасс, к своему большому сожалению, мог
не обеспечили ей работу в Германии, и ей пришлось вернуться в Россию.
Их дружба, хотя и основывалась на чисто научном взаимодействии, стала
предмет слухов. Вейерштрасс глубоко обиделся из-за настойчивых
инсинуации, окружающие его ученицу и ее математические достижения. На
Вернувшись в Россию, ее интерес к математике прекратился. Она не могла работать в
университет в Петербурге, потому что ее квалификация не соответствовала
признал. Вернулась к семейной жизни, в 1878 году родила дочь.
и вместе с мужем Владимиром пытались заработать на имении.
предприниматель, но это предприятие закончилось банкротством.
Вейерштрасс и Соня Ковалевски довольно регулярно переписывались из
время, когда они встречались до ее смерти в 1891 году. Его письма и поддержка
снова заняться математикой вдохновил ее и помог ей пройти через финансовые
трудности и самоубийство мужа в 1883 году.В 1884 году Миттаг-Леффлер
удалось получить ей должность преподавателя в университете в г.
Стокгольм. В 1888 г. она добилась большого успеха, когда ее знаменитая статья {\ it
«О вращении твердого тела вокруг неподвижной точки»} выиграли французы.
Приз Академии Бордина.
К сожалению, Вейерштрасс сжег все письма Сони после ее ранней смерти. Его
письма, однако, сохранились и хранятся в Mittag-Leffler
Институт в Дюрсхольме, Швеция.
На
Вернувшись в Россию, ее интерес к математике прекратился. Она не могла работать в
университет в Петербурге, потому что ее квалификация не соответствовала
признал. Вернулась к семейной жизни, в 1878 году родила дочь.
и вместе с мужем Владимиром пытались заработать на имении.
предприниматель, но это предприятие закончилось банкротством.
Вейерштрасс и Соня Ковалевски довольно регулярно переписывались из
время, когда они встречались до ее смерти в 1891 году. Его письма и поддержка
снова заняться математикой вдохновил ее и помог ей пройти через финансовые
трудности и самоубийство мужа в 1883 году.В 1884 году Миттаг-Леффлер
удалось получить ей должность преподавателя в университете в г.
Стокгольм. В 1888 г. она добилась большого успеха, когда ее знаменитая статья {\ it
«О вращении твердого тела вокруг неподвижной точки»} выиграли французы.
Приз Академии Бордина.
К сожалению, Вейерштрасс сжег все письма Сони после ее ранней смерти. Его
письма, однако, сохранились и хранятся в Mittag-Leffler
Институт в Дюрсхольме, Швеция. Обширная переписка с Mittag-Leffler,
Х. Шварц, Поль дю Буа-Реймон, Л.Кенигсбергер, Риман, Л. Фукс и
Соня, который содержит в основном математические задачи, также освещает
Жизнь Вейерштрасса. Его считали успешным, но на самом деле его жизнь
был полон страданий и личных проблем. Он не женился после
помолвка с Deutsch-Krone была прервана из-за неверности
невеста, по словам его брата Петра. Его карьера в Берлине была едва ли
началось, когда его здоровье пошатнулось. Более того, ближе к концу жизни
вместо того, чтобы наслаждаться славой и признательностью, он чувствовал себя изолированным.Это было
из-за конфликта с математиком и философом Леопольдом
Кронекер.
Вейерштрасс и Кронекер дружили более двадцати лет, делясь
много плодотворных математических дискуссий и идей. К сожалению, на
конце 1870-х гг. их взгляды на математику, особенно на основы
математика, расходились постепенно. Работа Вейерштрасса о пределах и
конвергенция привела его к разработке теории иррациональных чисел, основанной на
сходящиеся последовательности рациональных чисел, которые он назвал «агрегатами».
Обширная переписка с Mittag-Leffler,
Х. Шварц, Поль дю Буа-Реймон, Л.Кенигсбергер, Риман, Л. Фукс и
Соня, который содержит в основном математические задачи, также освещает
Жизнь Вейерштрасса. Его считали успешным, но на самом деле его жизнь
был полон страданий и личных проблем. Он не женился после
помолвка с Deutsch-Krone была прервана из-за неверности
невеста, по словам его брата Петра. Его карьера в Берлине была едва ли
началось, когда его здоровье пошатнулось. Более того, ближе к концу жизни
вместо того, чтобы наслаждаться славой и признательностью, он чувствовал себя изолированным.Это было
из-за конфликта с математиком и философом Леопольдом
Кронекер.
Вейерштрасс и Кронекер дружили более двадцати лет, делясь
много плодотворных математических дискуссий и идей. К сожалению, на
конце 1870-х гг. их взгляды на математику, особенно на основы
математика, расходились постепенно. Работа Вейерштрасса о пределах и
конвергенция привела его к разработке теории иррациональных чисел, основанной на
сходящиеся последовательности рациональных чисел, которые он назвал «агрегатами». Его
студент Георг Кантор основал теорию трансфинитных чисел, которая
произвела революцию в математической мысли. До Кантора математики
принял понятие бесконечного в ситуации последовательности
«стремящиеся к бесконечности», но не были готовы принять актуальную бесконечность
как таковой. Большим достижением Кантора было введение этой точной концепции:
фактически целый класс различных бесконечностей, соответствующих
счетные множества, такие как натуральные числа, континуум действительных
числа и так далее.Для Кронекера тип неконструктивного рассуждения
использованный Вейерштрассом и Кантором был глубоко подозрительным. Его знаменитое изречение: «Бог
сделал целые числа, все остальное - дело рук человека ", - произносится на
Берлинский конгресс 1886 года сформулировал его философию, и он предвидел
включение по существу всей математики в термины
арифметика.
Кронекер не скрывал своих возражений против работ Вейерштрасса и
Кантора и открыто критиковал их перед студентами. Неудивительно, что
этот математический конфликт превратился в личные ссоры.
Его
студент Георг Кантор основал теорию трансфинитных чисел, которая
произвела революцию в математической мысли. До Кантора математики
принял понятие бесконечного в ситуации последовательности
«стремящиеся к бесконечности», но не были готовы принять актуальную бесконечность
как таковой. Большим достижением Кантора было введение этой точной концепции:
фактически целый класс различных бесконечностей, соответствующих
счетные множества, такие как натуральные числа, континуум действительных
числа и так далее.Для Кронекера тип неконструктивного рассуждения
использованный Вейерштрассом и Кантором был глубоко подозрительным. Его знаменитое изречение: «Бог
сделал целые числа, все остальное - дело рук человека ", - произносится на
Берлинский конгресс 1886 года сформулировал его философию, и он предвидел
включение по существу всей математики в термины
арифметика.
Кронекер не скрывал своих возражений против работ Вейерштрасса и
Кантора и открыто критиковал их перед студентами. Неудивительно, что
этот математический конфликт превратился в личные ссоры. К концу
1880-х годов Вейерштрасс, очевидно, признал, что его давняя дружба с
Кронекер кончил, хотя сам Кронекер, казалось, не знал об этом.
Вейерштрасс даже рассматривал возможность уехать из Берлина на
Швейцарии, чтобы избежать продолжающегося конфликта; но, поскольку он не желал
своего преемника в университете, которого выбрал Кронекер, он решил
оставаться. Однако ему стало ясно, что если он не опубликует свои
лекции и работы, его достижения могут быть преданы забвению.Его беспокойство, вероятно, было преувеличено, потому что его ученики были разбросаны по всем
над Европой и продолжил свои исследования. Его величайшим преемником был Х.
Пуанкаре в Париже. Тем не менее обстановка в Берлине была напряженной. В
1885 была создана специальная комиссия по редактированию его произведений.
Сам Вейерштрасс больше не мог контролировать весь процесс, поэтому
его студенты взяли на себя задачу собрать и отполировать его лекции
на основе их собственных заметок или стенограмм. Вейерштрасс намеревался дать
математика - обширная трактовка анализа, ясная и полная.
К концу
1880-х годов Вейерштрасс, очевидно, признал, что его давняя дружба с
Кронекер кончил, хотя сам Кронекер, казалось, не знал об этом.
Вейерштрасс даже рассматривал возможность уехать из Берлина на
Швейцарии, чтобы избежать продолжающегося конфликта; но, поскольку он не желал
своего преемника в университете, которого выбрал Кронекер, он решил
оставаться. Однако ему стало ясно, что если он не опубликует свои
лекции и работы, его достижения могут быть преданы забвению.Его беспокойство, вероятно, было преувеличено, потому что его ученики были разбросаны по всем
над Европой и продолжил свои исследования. Его величайшим преемником был Х.
Пуанкаре в Париже. Тем не менее обстановка в Берлине была напряженной. В
1885 была создана специальная комиссия по редактированию его произведений.
Сам Вейерштрасс больше не мог контролировать весь процесс, поэтому
его студенты взяли на себя задачу собрать и отполировать его лекции
на основе их собственных заметок или стенограмм. Вейерштрасс намеревался дать
математика - обширная трактовка анализа, ясная и полная. Так
Кноблаух и Геттнер должны были подготовить теорию абелевых функций, его
величайшая цель в жизни. Однако его мечта не осуществилась, и проект
был крайне неудовлетворительным, по его мнению, и не соответствовал стандартам, которые он
ожидал. Его тоже беспокоили отсутствие точности и опечатки. В
Первый том появился в 1894 году и содержал его собрание статей. В
второй был напечатан в 1895 году, но следующие пять томов были опубликованы
между 1902 и 1927 годами, после его смерти. Стоит отметить, что это
Вейерштрассу, что мы обязаны публикацией собрания статей
Якоби, Дирихле, Штайнер и буквы Гаусса.В старости он
работал редактором, чтобы пополнить свою зарплату, которой не хватало для
содержать свою семью. Он жил в Берлине со своими сестрами Элис и Кларой.
который вел дом, его отец, умерший в 1869 году, и внук его дяди, который
он взял под опеку двухлетним ребенком в 1884 году. Он также заботился о
Шесть детей Борхардта после смерти его ближайшего друга в 1880 году.
В 1892 г. Вейерштрасс получил медаль Гельмгольца, а в 1895 г.
Так
Кноблаух и Геттнер должны были подготовить теорию абелевых функций, его
величайшая цель в жизни. Однако его мечта не осуществилась, и проект
был крайне неудовлетворительным, по его мнению, и не соответствовал стандартам, которые он
ожидал. Его тоже беспокоили отсутствие точности и опечатки. В
Первый том появился в 1894 году и содержал его собрание статей. В
второй был напечатан в 1895 году, но следующие пять томов были опубликованы
между 1902 и 1927 годами, после его смерти. Стоит отметить, что это
Вейерштрассу, что мы обязаны публикацией собрания статей
Якоби, Дирихле, Штайнер и буквы Гаусса.В старости он
работал редактором, чтобы пополнить свою зарплату, которой не хватало для
содержать свою семью. Он жил в Берлине со своими сестрами Элис и Кларой.
который вел дом, его отец, умерший в 1869 году, и внук его дяди, который
он взял под опеку двухлетним ребенком в 1884 году. Он также заботился о
Шесть детей Борхардта после смерти его ближайшего друга в 1880 году.
В 1892 г. Вейерштрасс получил медаль Гельмгольца, а в 1895 г. награжден медалью Копли, высшей наградой Королевского общества
Лондон.В том же году он отметил свое 80-летие среди своих
студенты. Последние три года жизни он провел в инвалидном кресле и умер 19.
Февраль 1897 г., после воспаления легких.
Рекомендации
1. Аренс, В .: Skizzen aus dem Leben Weierstrass '. Math.-naturwiss.
Блаттер 4 (1907), 41-47.
2. ---: Gudermanns Urteil uber die Staatsexamensarbeit von Weierstrass.
Math.-naturwiss Blatter 13 (1916), 44-46.
3. Бейкер, A.C .: Карл Теодор Вильгельм Вейерштрасс, отец современного
анализ. Математика. Спектр 1996/7, т.29, № 2, 25–29.
4. Бирманн, К. Р .: Карл Вейерштрасс, Ausgewahlte Aspekte seiner
Биография. Журнал Fur die reine und angewandte Mathematik, 223 (1966),
191-220.
5. Боллинг, Р.: Карл Вейерштрасс - Stationen eines Lebens. Яхресбер.
Dt. Math.-Vereinigung, 96 (1994), 56-75.
6. Дорофеева, А., Чернова, М .: Карл Вейерштрасс. Математика и
Кибернетика 7 (1985), Москва.
7. Flaskamp, F .: Herkunft und Lebensweg des Mathematikers Karl
Вейерштрасс.
награжден медалью Копли, высшей наградой Королевского общества
Лондон.В том же году он отметил свое 80-летие среди своих
студенты. Последние три года жизни он провел в инвалидном кресле и умер 19.
Февраль 1897 г., после воспаления легких.
Рекомендации
1. Аренс, В .: Skizzen aus dem Leben Weierstrass '. Math.-naturwiss.
Блаттер 4 (1907), 41-47.
2. ---: Gudermanns Urteil uber die Staatsexamensarbeit von Weierstrass.
Math.-naturwiss Blatter 13 (1916), 44-46.
3. Бейкер, A.C .: Карл Теодор Вильгельм Вейерштрасс, отец современного
анализ. Математика. Спектр 1996/7, т.29, № 2, 25–29.
4. Бирманн, К. Р .: Карл Вейерштрасс, Ausgewahlte Aspekte seiner
Биография. Журнал Fur die reine und angewandte Mathematik, 223 (1966),
191-220.
5. Боллинг, Р.: Карл Вейерштрасс - Stationen eines Lebens. Яхресбер.
Dt. Math.-Vereinigung, 96 (1994), 56-75.
6. Дорофеева, А., Чернова, М .: Карл Вейерштрасс. Математика и
Кибернетика 7 (1985), Москва.
7. Flaskamp, F .: Herkunft und Lebensweg des Mathematikers Karl
Вейерштрасс. Форш. u. Fortschr.35 (1961), 236-239.
8. Хензель, К .: Gedachtnisrede auf Ernst Eduard Kummer. Festschr. Zur
Feier des 100. Geburststages Эдуард Куммерс. Лейпциг и Берлин 1910 г.,
1-37.
9. Гильберт, Д .: Zum Gedachtnis an Karl Weierstrass. Nachrichten v. D.
Kgl. Ges. d. Wissensch. zu Gottingen 1897, 60-69.
10. ---: Uber das Unendliche. Mathematische Annalen 95 (1926), 161–185.
11. Kiepert, L .: Personliche Erinnerungen an Karl Weierstrass.
Яхресбер. d. Dt. Math.-Vereinigung 35 (1926), 56-65.
12. Кочина, П.: Карл Вейерштрасс. Москва "Наука" 1985.
13. Лампе, Э .: Карл Вейерштрасс. Яхресбер. d. Dt. Math.-Vereinigung 6
(1899), 27-44.
14. ---: Zur hundertsten Wiederkehr des Geburtstages von Karl
Вейерштрасс. Яхресбер. d. Dt. Math.-Vereinigung 34 (1915), 416-438.
15. фон Лилиенталь, Р .: Карл Вейерштрасс. Westfalische Lebensbilder 2
(1931), 164-179.
16. Lorey, W .: Die padagogischen Ansichten des Mathematikers Karl.
Вейерштрасс. Blatter fur hoheres Schulwesen 32 (1915), 626-629.17. ---: Karl Weierstrass zum Gedachtnis.
Форш. u. Fortschr.35 (1961), 236-239.
8. Хензель, К .: Gedachtnisrede auf Ernst Eduard Kummer. Festschr. Zur
Feier des 100. Geburststages Эдуард Куммерс. Лейпциг и Берлин 1910 г.,
1-37.
9. Гильберт, Д .: Zum Gedachtnis an Karl Weierstrass. Nachrichten v. D.
Kgl. Ges. d. Wissensch. zu Gottingen 1897, 60-69.
10. ---: Uber das Unendliche. Mathematische Annalen 95 (1926), 161–185.
11. Kiepert, L .: Personliche Erinnerungen an Karl Weierstrass.
Яхресбер. d. Dt. Math.-Vereinigung 35 (1926), 56-65.
12. Кочина, П.: Карл Вейерштрасс. Москва "Наука" 1985.
13. Лампе, Э .: Карл Вейерштрасс. Яхресбер. d. Dt. Math.-Vereinigung 6
(1899), 27-44.
14. ---: Zur hundertsten Wiederkehr des Geburtstages von Karl
Вейерштрасс. Яхресбер. d. Dt. Math.-Vereinigung 34 (1915), 416-438.
15. фон Лилиенталь, Р .: Карл Вейерштрасс. Westfalische Lebensbilder 2
(1931), 164-179.
16. Lorey, W .: Die padagogischen Ansichten des Mathematikers Karl.
Вейерштрасс. Blatter fur hoheres Schulwesen 32 (1915), 626-629.17. ---: Karl Weierstrass zum Gedachtnis.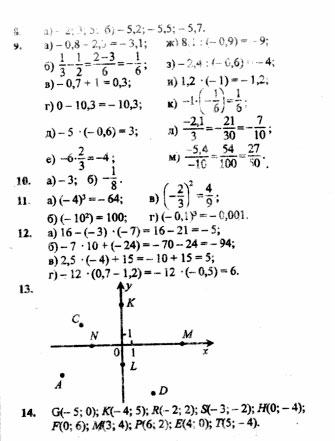 Zeitschr. f. математика. u.
натурвисс. Unterricht 46 (1915), 597-607.
18. ---: Das Studium der Mathematik an den deutschen Universitaten seit
Anfang des 19. Jahrhunderts. IMUK-Abhandlungen, Bd. 3, H. 9. Leipzig und
Берлин 1916 год.
19. Mittag-Leffler, G.L: Une page de la vie de Weierstrass. Compte Rendu
du deuxieme international des mathematiciens. Париж, 1902, 131–153.
20. ---: Zur Biographie von Weierstrass. Acta Mathematica 35 (1912 г.),
29-65.
21.---: Die ersten 40 Jahre des Lebens von Weierstrass. Acta
Mathematica 39 (1923), 1-57.
22. ---: Софи Ковалевски: Обратите внимание на biographique. Acta Mathematica 16
(1892/93), 385-395.
23. ---: Вейерштрасс и Соня Ковалевски. Acta Mathematica 39 (1923 г.),
133-198.
24. Рахманова, А .: Соня Ковалевски. Цюрих 1953 г.
25. Rothe, R .: Bericht uber den gegenwartigen Stand der Herausgabe der
Mathematischen Werke von Karl Weierstrass. Яхресбер. d. Dt.
Math.-Vereinigung 15 (1916), 59-62.
26. ---: Bericht uber die Herausgabe des 7.Bands der Mathematischen
Верке фон Карла Вейерштрасса.
Zeitschr. f. математика. u.
натурвисс. Unterricht 46 (1915), 597-607.
18. ---: Das Studium der Mathematik an den deutschen Universitaten seit
Anfang des 19. Jahrhunderts. IMUK-Abhandlungen, Bd. 3, H. 9. Leipzig und
Берлин 1916 год.
19. Mittag-Leffler, G.L: Une page de la vie de Weierstrass. Compte Rendu
du deuxieme international des mathematiciens. Париж, 1902, 131–153.
20. ---: Zur Biographie von Weierstrass. Acta Mathematica 35 (1912 г.),
29-65.
21.---: Die ersten 40 Jahre des Lebens von Weierstrass. Acta
Mathematica 39 (1923), 1-57.
22. ---: Софи Ковалевски: Обратите внимание на biographique. Acta Mathematica 16
(1892/93), 385-395.
23. ---: Вейерштрасс и Соня Ковалевски. Acta Mathematica 39 (1923 г.),
133-198.
24. Рахманова, А .: Соня Ковалевски. Цюрих 1953 г.
25. Rothe, R .: Bericht uber den gegenwartigen Stand der Herausgabe der
Mathematischen Werke von Karl Weierstrass. Яхресбер. d. Dt.
Math.-Vereinigung 15 (1916), 59-62.
26. ---: Bericht uber die Herausgabe des 7.Bands der Mathematischen
Верке фон Карла Вейерштрасса. Яхресбер. d. Dt. Math.-Vereinigung 37 (1928),
198-208.
27. Runge, C .: Personliche Erinnerungen an Karl Weierstrass. Яхресбер.
d. Dt. Math.-Vereiningung 35 (1926), 175-179.
28. Schubert, H .: Zum Andenken an Karl Weierstrass. Zeitschr. f. математика.
u. натурвисс. Unterricht 28 (1897), 228-231.
29. Siegmund-Schultze, R .: Der Beweis des Weierstrassschen
Approximationssatzes 1885 vor dem Hintergrund der Entwicklung der
Fourieranalysis. Historia Mathematica 15 (1988).30. Войт К. и Линдеманн Ф .: Карл Теодор Вильгельм Вейерштрасс.
Sitzungsberichte d. математико-физ. Klasse der k. б. Akademie der
Wissenschaften zu Munchen 27, 1897 (1898), 402-409.
Яхресбер. d. Dt. Math.-Vereinigung 37 (1928),
198-208.
27. Runge, C .: Personliche Erinnerungen an Karl Weierstrass. Яхресбер.
d. Dt. Math.-Vereiningung 35 (1926), 175-179.
28. Schubert, H .: Zum Andenken an Karl Weierstrass. Zeitschr. f. математика.
u. натурвисс. Unterricht 28 (1897), 228-231.
29. Siegmund-Schultze, R .: Der Beweis des Weierstrassschen
Approximationssatzes 1885 vor dem Hintergrund der Entwicklung der
Fourieranalysis. Historia Mathematica 15 (1988).30. Войт К. и Линдеманн Ф .: Карл Теодор Вильгельм Вейерштрасс.
Sitzungsberichte d. математико-физ. Klasse der k. б. Akademie der
Wissenschaften zu Munchen 27, 1897 (1898), 402-409.
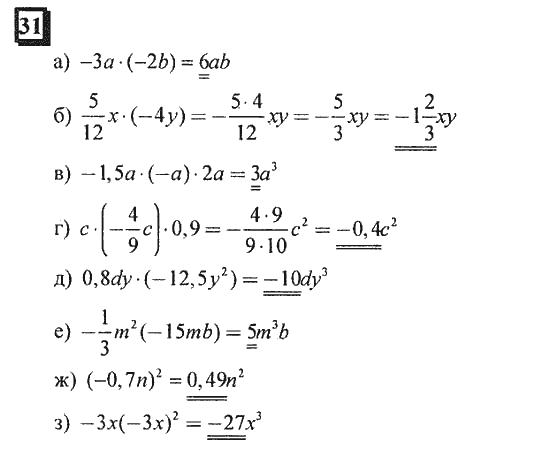 Если вы подозреваете это, попробуйте другой браузер.
Если вы подозреваете это, попробуйте другой браузер.