Математика 5 класс номер 397 398 399 зубарева мордкович ответы :: jumnanacha
14.10.2016 15:34
Уроку. ГДЗ Математика 5 класс И. И. Зубарева. Авторы: И. И. Зубарева, А. Г. Мордкович. Издательство: Мнемозина.397.398.399. Вы можете смотреть и читать гдз онлайн без скачивания на компьютере, мобильном телефоне и планшете бесплатно и без смс. Решебник по математике 5 класс Зубарева, Мордковичдомашняя работа на учебникза 2012, 2013, 2014 год ФГОС. ГДЗ по обществознанию 8 класс Хромоваответы на рабочую тетрадь. Решебник по русскому языку 5 класс Ладыженская, Баранов, Тростенцова.
Решебник ГДЗ к учебнику по Математике 5 класс Зубарева И. И., Мордкович А. Г.2015, онлайн ответы на домашнюю работу. Выбери из таблицы номера заданий с ответами и решениями по математике.397.398.399. Решить все задачи изображённые. На фото по физике 9 класс. Выберите номер задания учебника. Для тех учеников, кто затрудняется с ответом, понадобится ГДЗ. Домашние контрольные работы. ГДЗ решебник по математике 5 класс Зубарева, Мордкович Мнемозина. Приводится выполнение задач и правильный итоговый ответ.
Выберите номер задания учебника. Для тех учеников, кто затрудняется с ответом, понадобится ГДЗ. Домашние контрольные работы. ГДЗ решебник по математике 5 класс Зубарева, Мордкович Мнемозина. Приводится выполнение задач и правильный итоговый ответ.
На ГДЗ, математика, 6 классЗубарева, Мордковичонлайн решебник. Номера. Домашние работы пользователей Математика 5 класс Зубарева, Мордкович. Без ответов. Математика 6 класс Зубарева Мордкович. Кроме полного решения всех заданий и ответов, в нем есть пояснения,. С помощью решебника ГДЗ по математике для 5 класса Зубарева Мордкович 2008 ответы любой пятиклассник сможет без посторонней помощи разобраться в теме, и с помощью правильных ответов в конце решебника самостоятельно. ГДЗ по Математике 5 класс И. И. Зубарева. Актуально на 2015г. Подробный.
ГДЗ по Математика 5 класс Зубарева, Мордкович Решебник. Решебник по математике 5 класс Зубарева. ГДЗ по математике, 5 класс, Зубарева, Мордкович. Выберите номер упражнения. ГДЗ бесплатно по всем предметам.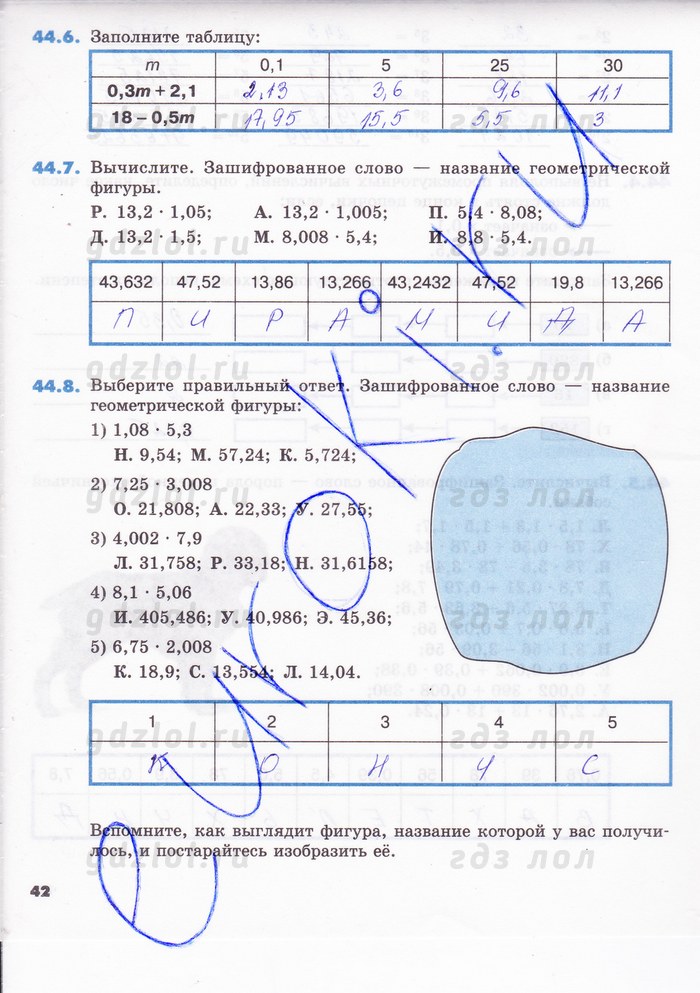
К ним. Ответы к учебнику по математике 5 класс Зубарева, Мордкович. Ответы. Другой вариант ГДЗ. ГДЗ по математике 5 класс Виленкин, Жохов, Чесноков, Шварцбурд. Решебником ГДЗ для учебника по математике Виленкин за 5 й класс. Номера . Подробные ответы к учебнику математики для 5 класса, авторов И. И. Зубарева, А. Г. ГДЗ по математике 5 класс Зубарева, Мордкович. ГДЗ решебник к учебнику по математике 5 класс Зубарева Мордкович ФГОС. Благодаря ему вы быстрее усвоите материал и подготовитесь к.
Учебнику по математике 5 класс Зубарева Мордкович. Виленкин Математика 6 класс. Заходите и находите решебники онлайн прямо на страницах нашего сайта. Выберите номер упражненияС помощью решебника ГДЗ по математике для 5 класса Зубарева Мордкович 2008 ответы любой пятиклассник сможет без посторонней помощи разобраться в теме, и с помощью правильных ответов в конце решебника самостоятельно.
Вместе с математика 5 класс номер 397 398 399 зубарева мордкович ответы часто ищут
Гдз по математике 5 класс зубарева от путина.
Гдз по математике 5 класс зубарева мордкович 2015.
Гдз по математике 5 класс зубарева мордкович контрольные задания стр 248.
Гдз по математике 5 класс зубарева 2015.
Гдз по математике зубарева 6 класс.
Гдз по русскому языку 5 класс зубарева.
За три дня лыжники прошли 256 км.
Решебник по математике 5 класс зубарева мордкович 2015
Читайте также:
Гдз по истории 7 класс история татарстана
Гдз таблитца по биологии 9 класс
Скачать поурочное планирование по русскому языку для 5 класса к учебнику баранов бесплатно и без регистрации
Математика 5 Зубарева КР-16 — Итоговая контрольная + Ответы
Администратор
Итоговая контрольная работа по математике за курс 5 класса с ответами и решениями по УМК Зубарева, Мордкович (Варианты 1, 2, 3, 4).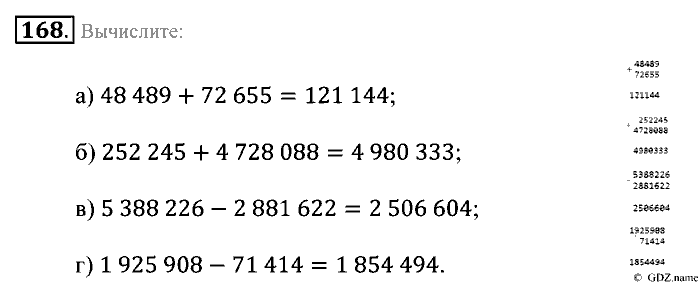 Дидактические материалы для учителей, школьников и родителей при дистанционном обучении. Математика 5 Зубарева КР-16.
Дидактические материалы для учителей, школьников и родителей при дистанционном обучении. Математика 5 Зубарева КР-16.
Математика 5 класс (Зубарева)
Итоговая контрольная работа.
КР-16. Вариант 1 (транскрипт заданий)
- Вычислите значение выражения: 0,75 • 4,6 + 91 : 1,3 – 70,5.
- Выполните действие: а) 7/9 – 1/18; б) 2/5 + 3 1/2; в) 3/10 • 4; г) 27/50 : 9.
- Решите уравнение: 8х + 3х + х = 480.
- Вычислите объём деревянного бруска, имеющего форму прямоугольного параллелепипеда, если его измерения равны 2,5 см; 4 см; 6,2 см.
- В магазин привезли 150 кг черешни. До обеда продали 20% всей черешни, а после обеда — оставшейся черешни. Сколько килограммов черешни продали после обеда?
- Постройте угол АОВ, градусная мера которого равна 60°. Отметьте точку М внутри угла. Через эту точку проведите прямую, перпендикулярную стороне ОВ угла АОВ.
ОТВЕТЫ на КР-16 В-1
Открыть РЕШЕНИЯ заданий в тетради (Вариант 1)
КР-16.
 Вариант 2
Вариант 2- Вычислите значение выражения: 3,8 • 0,65 + 128 : 1,6 – 80,07.
- Выполните действие: а) 6/7 – 1/14; б) 2/9 + 5 1/6; в) 1/20 • 8; г) 7/10 : 7.
- Решите уравнение: 7х + 2х – х = 320.
- Вычислите объём прямоугольной коробки, имеющей размеры: 5 дм; 4,8 дм; 3,5 дм.
- В течение 1 ч Петя смотрел детские телепередачи: 25% этого времени по телевизору показывали мультфильмы, а затем — остального времени — концерт детской песни. Сколько минут Петя смотрел концерт?
- Постройте угол АВС, градусная мера которого равна 75°. Отметьте точку X на стороне угла. Проведите через эту точку прямую, перпендикулярную этой стороне.
ОТВЕТЫ на КР-16 В-2
Открыть РЕШЕНИЯ заданий в тетради (Вариант 2)
Математика 5 Зубарева КР-16
. Вариант 3- Вычислите значение выражения: (6,4 – 2,15) • 0,05 + 126 : 7,5.
- Выполните действие: а) 8 3/4 + 2 1/12; б) 4 8/15 – 4 1/3; в) 3/5 • 15; г) 1/9 : 3.

- Решите уравнение: 2,5а + 4а – 4,5 = 8,5.
- Бак, имеющий форму прямоугольного параллелепипеда, вмещает 70 м3 воды. Вычислите глубину бака, если площадь его дна равна 14м
- С трёх лугов собрали сено. С первого луга — 40% всего сена, со второго — 35% всего сена. С третьего луга сена собрали на 600 кг меньше, чем со второго луга. Сколько сена собрали со всех трёх лугов вместе?
- Постройте тупоугольный треугольник: градусная мера тупого угла равна 120°. Обозначьте вершину тупого угла буквой, М из точки М проведите луч МА, перпендикулярный противолежащей стороне треугольника.
ОТВЕТЫ на КР-16 В-3
Открыть РЕШЕНИЯ заданий в тетради (Вариант 3)
КР-16. Вариант 4
- Вычислите значение выражения: (6,4 + 2,15) • 16,4 – 368 : 9,2.
- Выполните действие: а) 5 1/8 + 4 3/4; б) 11 6/10 – 10 2/5; в) 3/8 • 40; г) 1/10 : 8.

- Решите уравнение: 7,2х + 2х – 6 = 40.
- Объём зала 156 м3. Вычислите высоту зала, если площадь пола равна 52 м2.
- С поля кукурузу увезли на трёх грузовиках. На первый погрузили 35% всей кукурузы, на второй — 45% всей кукурузы, а на третий — на 2,5 т меньше, чем на второй. Сколько тонн кукурузы погрузили на все три грузовика?
- Постройте треугольник с тупым углом величиной 100°. Обозначьте вершину тупого угла буквой А. Из этой вершины проведите луч АВ, перпендикулярный противолежащей стороне треугольника.
ОТВЕТЫ на КР-16 В-4
Открыть РЕШЕНИЯ заданий в тетради (Вариант 4)
Вы смотрели: Математика 5 Зубарева КР-16. Итоговая контрольная работа по математике за 5 класс с ответами и решениями к учебнику Зубаревой, Мордковича «Математика. 5 класс» ФГОС (к новому учебнику). Дидактические материалы для учителей, школьников и родителей при дистанционном обучении.
В учебных целях использованы цитаты из пособия:
«Дидактические материалы по математике: 5 класс: к учебнику И. И. Зубаревой, А. Г. Мордковича «Математика. 5 класс». ФГОС (к новому учебнику) / В. Н. Рудницкая. — М.: Издательство «Экзамен» «. Ответы адресованы родителям, которые смогут проконтролировать правильность выполнения заданий. Цитаты представлены в учебных целях, а также для ознакомления и покупки указанного учебного пособия.
И. Зубаревой, А. Г. Мордковича «Математика. 5 класс». ФГОС (к новому учебнику) / В. Н. Рудницкая. — М.: Издательство «Экзамен» «. Ответы адресованы родителям, которые смогут проконтролировать правильность выполнения заданий. Цитаты представлены в учебных целях, а также для ознакомления и покупки указанного учебного пособия.Вернуться на страницу: Математика 5 класс (Оглавление)
Ответы
Вас могут заинтересовать…
Положительные и отрицательные числа, Модуль числа
Начальник ШМО
учителя математики _______Калашникова Ж.ЮМуниципальное бюджетное общеобразовательное учреждение
«Средняя общеобразовательная школа № 89»
Тематические контрольные работы по математике для 6-х классов
по учебнику И.И. Зубарева и А.Г. Мордкович
Составители: учителя математики:
Калашникова Жанна Юрьевна
ЗАТО Северск
2016
Содержание
Тест №1…………………………………………………… ……………………………………….
 3-6
3-6 Тест №2………………………………………………………………………………………….7-10
Тест №3……… …………………………………………………………………………………….11-14
Ответы…………………………………… ………………………………………………………..15
Тест №1 «Положительные и отрицательные числа»
Вариант 1
Укажите отрицательное дробное число:
-165
38
-7,92
67Опишите событие «На координатном луче отмечено число -5,5»
достоверно
невозможно
Случайно
Какое из четырех чисел самое большое?
8 035
80,35
0,8035
803,5
Какая из точек расположена на координатной прямой справа от точки О (0)?
M(-4)
E(-15)
K(15)
D(-1.2)
Ночью температура воздуха была -5°C. Днем на термометре было уже +3°С. Как изменилась температура воздуха?
Увеличился на 8o
Уменьшился на 2o
Уменьшился на 8o
На координатной линии отмечена точка x(-2) — центр симметрии. Укажите координаты точек, расположенных на этой прямой симметрично точке x.
(-1) и (1)
(-1) и (1)
(3) и (-3)
(0) и (-4)
Какие точки на координатной линии не симметричны относительно начала координат — точка О (0).
B(-5) и C(5)
D(0,5) и E(-0,5)
M(-3) и K(13)
A(18) и X(-18)
Какова сумма числа 0,316 + 0,4?
0,356
0,716
4,316
0,32
Рассчитать 25% от числа 0,4.
0,1
0,001
10
100
Рассчитать разницу между 9100 и 0,03
0,05
0,6
9,03
350Опция 2
Укажите отрицательное дробное число.
8,63
-1045
913-0,2
Опишите событие «На координатном луче отмечена цифра 7».
Случайное
Достоверное
Какое число наименьшее?
15,49
154,9
1,549
1549
Какая из точек расположена на координатной прямой слева от точки O(0).
А(-0,5)
В 6)
М(0,5)
К(38)
Днем термометр показывал +5°С, а вечером -2°С. Как изменилась температура воздуха?
Увеличился на 3o
Уменьшился на 7o
Уменьшился на 3o
Увеличился на 7o
На координатной линии отмечен центр симметрии — точка A (-3). Укажите координаты точек, расположенных на этой прямой симметрично точке А.
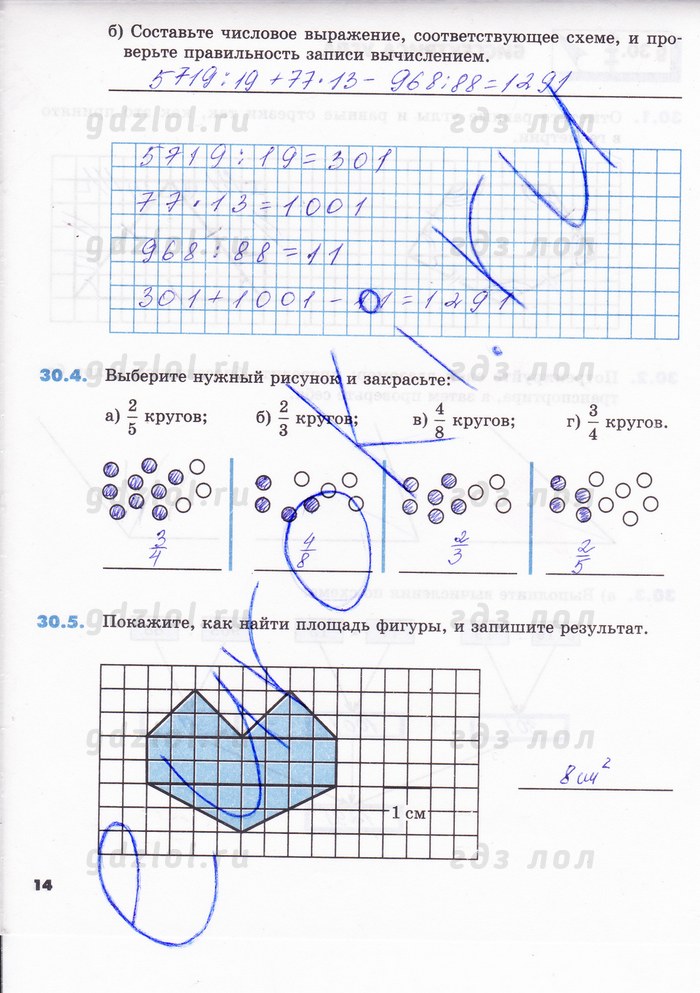
(-2) и (2)
(0) и (-5)
(-6) и (1)
(-1) и ( -5)
Какие точки координатной прямой не симметричны относительно начала координат — точка О (0).
А(6) и В(-6)
С(12) и D(-2)
М(-1) и К(1)
X(-9) и Y(9)
Чему равна сумма чисел 0,237 и 0,3
0,24
3,237
0,537
0,267
Вычислить 20% от числа 0,5
10
0,1 0,1
0,01
Рассчитать разницу между 0,07 и 31001250,5
1
425Тест №2. Абсолютное значение числа. противоположные числа.
Вариант 1
Какое из данных чисел имеет наименьший модуль
-11
1013-4,196
-4,2
Укажите неверное равенство
85=-85
-1,9=1,9
35= 3558=-58 Модуль неотрицательного числа является неотрицательным числом. Верно ли это утверждение.
Да
Не
Какое из этих чисел противоположно -34? 43-43-3434 Чему равно выражение -(-m), если m = -15
+15
-15
Вычислите значение выражения: -2,5∙4—919
-10
1
— 1
Решите уравнение: x=40-40
40
40 или -40
Какие целые числа расположены на координатной прямой между числами 2,75 и 3,9?
-2, -1, 1, 2
-1, 0, 1, 2, 3
-1, 0, 1, 2, 3, 4
-2, -1, 0, 1, 2, 3
Есть неравенство -30>-50 верно?
Не
Укажите все целые числа x, если x≤30, 1, 2
0, 1, 2, 3
0, 1, 2, 3, 4
1, 2, 3
Вариант 2
Какое число имеет наибольший модуль?
-0,6
-50,603
493550,530
Укажите неверное равенство
-1,5=1,512=12-117=117-325=-325 Может ли абсолютное значение отрицательного числа быть отрицательным числом
Да
Не
Какое из этих чисел противоположно 124?
-24
24
-124124 Чему равно выражение –(-k), если k = -9
-9
+9
Вычислить значение выражения: 2,5:-0,5+1,250
15
-2,5
2,5
Решите уравнение x=100100
-100
100 или -100
Какие целые числа расположены на координатной прямой между числами 1 и — 4,5
-4, -3, -2, -1, 0
-3, -2, -1
-5, -4, -3, -2, -1
-4, -3, -2, -1, 1
Верно ли неравенство -25Да
Не
Укажите все целые числа x, если x≤44, 3, 2
0, 1, 2, 3
1, 2, 3, 4
0, 1, 2, 3, 4
Номер теста 3. Сравнение чисел
Сравнение чисел
Опция 1
Какое из неравенств неверно?
-20 > 2
0
-16 > -7
-5
-320 -920 >
=
Верно ли, что число 0 больше любого отрицательного числа?
Да
Не
Число а неотрицательно. Как записать это утверждение в виде неравенства?
a0Введите наибольшее из заданных чисел.
0,16
-3018-0,4
0,01
При каких натуральных значениях x выполняется неравенство x≤44, 3, 2
1 , 2, 3, 4
4, 3, 2, 1
0, 1, 2, 3
При каких целых значениях у выполняется неравенство у
-1
0, -1, 1
Нет таких значений
Числа -6; -3,8; -115; 0.8 находится:
В порядке убывания
В порядке возрастания
в беспорядке
По радио передали прогноз погоды: ожидается понижение температуры до -20°С. Опишите это событие:
невозможно
достоверный
Случайный
Вариант 2
Какое из неравенств верно?
-5 > 0
6
-34 > -40
-9 Какой знак нужно поставить между данными дробями, чтобы неравенство было верным?
-1315 -715
>
=
Верно ли, что число 0 меньше любого отрицательного числа?
Да
Не
Число x не больше нуля. Как записать это утверждение в виде неравенства?
Как записать это утверждение в виде неравенства?
х≥0х>0х
-5,92
1,7
-1000
35При каких натуральных значениях a справедливо неравенство a≤3? 1, 2, 3
0, 1, 2, 3
1, 2
0, 1, 2
При каких целых значениях m выполняется неравенство m
0, -1, -2, -3, 1, 2, 3
0
Нет таких значений
Числа 1,2; -1,2; -427; -100 находится:
в беспорядке
В порядке возрастания
В порядке убывания
На линии координат отмечена точка A(5). На этой прямой случайным образом была отмечена еще одна точка B. Его координатой оказалось число, противоположное цифре 5. Опишите это событие.
Случайно
Верно
Невозможно
Ответы
Тест №1 Тест №2
№ Вариант 1 Вариант 2
1 3 4
2 2 3
3 4 3
4 3 1
5 1 2
6 4 4
7 003 2
3 8 1 2
10 4 1
No. 10 2 4
Тест #3
№ Вариант 1 Вариант 2
1 4 3
2 1 2
3 1 2
4 3 4
5 1 3
6 2 7 2 1
7 3 4 92000 урок познакомит с понятием модуля действительного числа и представит некоторые из его основных определений, а затем примеры, демонстрирующие применение различных из этих определений.
Тема: Вещественные числа
Урок: Модуль вещественных чисел
Определение 1. Расстояние от точки на координатной прямой до нуля называется модулем числа , являющегося координатой данной точки (рис. 1).
Пример 1 . Заметим, что модули противоположных чисел равны и неотрицательны, так как это расстояние, и оно не может быть отрицательным, а расстояния от чисел, симметричных относительно нуля, до начала координат равны.
Определение 2. .
Пример 2. Рассмотрим одну из задач, поставленных в предыдущем примере, для демонстрации эквивалентности введенных определений. , как мы видим, при отрицательном числе под знаком модуля добавление перед ним еще одного минуса дает неотрицательный результат, как следует из определения модуля.
Последствия. Расстояние между двумя точками с координатами на координатной прямой можно найти следующим образом независимо от взаимного расположения точек (рис. 2).
2).
1. Модуль любого числа неотрицательный
2. Модуль произведения есть произведение модулей
3. Модуль частный — это частные модули
3. Решение задачПример 3. Решить уравнение.
Решение. Воспользуемся вторым определением модуля: и запишем наше уравнение в виде системы уравнений для различных вариантов расширения модуля.
Пример 4. Решить уравнение.
Решение. Аналогично решению предыдущего примера получаем, что .
Пример 5. Решить уравнение.
Решение. Решим через следствие из первого определения модуля: . Изобразим это на числовой оси с учетом того, что искомый корень будет находиться на расстоянии 2 от точки 3 (рис. 3).
На основании рисунка получаем корни уравнения: , так как точки с этими координатами находятся на расстоянии 2 от точки 3, как и требуется в уравнении.
Ответ. .
Пример 6. Решить уравнение.
Решение. По сравнению с предыдущей задачей есть только одно осложнение — это отсутствие полного сходства с формулировкой следствия о расстоянии между числами на оси координат, так как под знаком модуля стоит знак плюс, а не знак минус . Но привести его к нужному виду несложно, что мы и сделаем:
Изобразим это на числовой оси аналогично предыдущему решению (рис. 4).
Корни уравнения .
Ответ. .
Пример 7. Решить уравнение.
Решение. Это уравнение немного сложнее предыдущего, так как неизвестное стоит на втором месте и со знаком минус, кроме того, оно еще и с числовым множителем. Для решения первой задачи воспользуемся одним из свойств модуля и получим:
Для решения второй задачи произведем замену переменных: , что приведет нас к простейшему уравнению . Согласно второму определению модуля . Подставляем эти корни в уравнение замены и получаем два линейных уравнения:
Ответ. .
4. Квадратный корень и модуль Достаточно часто в ходе решения задач с корнями возникают модули, и следует обращать внимание на ситуации, в которых они возникают.
При первом взгляде на это тождество могут возникнуть вопросы: «а зачем там модуль?» и «почему тождество ложное?». Оказывается, на второй вопрос можно привести простой контрпример: если то должно быть истинным, что эквивалентно, а это не тождество.
После этого может возникнуть вопрос: «Решает ли такое тождество проблему», но на это предложение есть и контрпример. Если тогда должно быть истинным, то что эквивалентно, и это неверное тождество.
Соответственно, если вспомнить, что квадратный корень из неотрицательного числа является неотрицательным числом, а значение модуля неотрицательно, то становится понятно, почему приведенное выше утверждение верно:
.
Пример 8. Вычислить значение выражения .
Решение. В таких задачах важно не сразу бездумно избавляться от рута, а использовать вышеуказанное тождество, т.к.
Состоит из положительных (натуральных) чисел, отрицательных чисел и нуля.
Все отрицательные числа и только они меньше нуля. На числовой оси отрицательные числа располагаются слева от нуля. Для них, как и для положительных чисел, определено отношение порядка, позволяющее сравнивать одно целое число с другим.
На числовой оси отрицательные числа располагаются слева от нуля. Для них, как и для положительных чисел, определено отношение порядка, позволяющее сравнивать одно целое число с другим.
Для каждого натурального числа n существует одно и только одно отрицательное число, обозначаемое -n , которое дополняет n до нуля: n + (− n ) = 0 . Оба номера называются напротив друг друга . Вычитание целого числа из эквивалентно прибавлению к его противоположности: -a .
Свойства отрицательных чисел
Отрицательные числа подчиняются почти тем же правилам, что и натуральные числа, но имеют некоторые особенности.
Исторический очерк
Литература
- Выгодский М.Я. Справочник по элементарной математике. — М.: АСТ, 2003. — ISBN 5-17-009554-6
- Глейзер Г.И. История математики в школе. — М.: Просвещение, 1964. — 376 с.
Ссылки
Фонд Викимедиа. 2010 .
2010 .
- Причинение вреда по неосторожности
- Неотропикс
Смотреть что такое «Неотрицательное число» в других словарях:
- Число неотрицательное , если оно больше или равно нулю.
- Число неположительное , если оно меньше или равно нулю.
- Положительные ненулевые числа и отрицательные ненулевые числа иногда (чтобы подчеркнуть, что они ненулевые) называются «строго положительными» и «строго отрицательными» соответственно.

- вращение на плоскости — например, вращение на (–90°) происходит по часовой стрелке;
- вращение в пространстве вокруг ориентированной оси обычно считается положительным, если выполняется «правило буравчика», в противном случае оно считается отрицательным.
действительное число — Вещественное или действительное число — это математическая абстракция, возникшая из-за необходимости измерения геометрических и физических величин окружающего нас мира, а также выполнения таких операций, как извлечение корня, вычисление логарифмов , решение… … Википедия
обычно небольшое неотрицательное целое число — Часть кодирования, которая представляет неограниченные неотрицательные целые значения, но где малые значения чаще встречаются (ITU T X.691). Темы… … Справочник технического переводчика
РЕАЛЬНОЕ ЧИСЛО — действительное число, положительное число, отрицательное число или нуль. Понятие числа чисел возникло путем расширения понятия рационального числа. Необходимость этого расширения обусловлена как практическим использованием математики в выражении… … Математическая энциклопедия
Простое число — Простое число — это натуральное число, имеющее ровно два различных натуральных делителя: единицу и самого себя. Все остальные натуральные числа, кроме одного, называются составными. Таким образом, все натуральные числа больше единицы… … Википедия
Все остальные натуральные числа, кроме одного, называются составными. Таким образом, все натуральные числа больше единицы… … Википедия
натуральное число — ▲ целочисленное выражение, действительное, число натуральное число неотрицательное целое; выражает количество отдельных целочисленных объектов, в которых l. агрегаты; обозначают количество действительных целых объектов; числовое выражение. четыре… Идеографический словарь русского языка
Десятичная — Десятичная дробь — это разновидность дроби, представляющая собой способ представления действительных чисел в виде, где знак дроби: либо, либо, десятичная точка, служащая разделителем между целой и дробной частями числа число… … Википедия Википедия 9(2))) символы плюс и минус задают не знак выражения, которому они предшествуют, а знак арифметической операции, поэтому знак результата может быть любым, он определяется только после вычисления выражения.
Помимо арифметики, понятие знака используется и в других разделах математики, в том числе для нечисловых математических объектов (см. ниже). Понятие знака важно и в тех разделах физики, где физические величины делятся на два класса, условно называемые положительными и отрицательными, — например, электрические заряды, положительная и отрицательная обратная связь, различные силы притяжения и отталкивания.
ниже). Понятие знака важно и в тех разделах физики, где физические величины делятся на два класса, условно называемые положительными и отрицательными, — например, электрические заряды, положительная и отрицательная обратная связь, различные силы притяжения и отталкивания.
Знак числа
Положительные и отрицательные числа
Нулю не присваивается никакого знака, т. е. + 0 (\displaystyle +0) и − 0 (\displaystyle -0) — одно и то же число в арифметике. В математическом анализе значение символов + 0 (\displaystyle +0) и − 0 (\displaystyle -0) может различаться, см. об этом Отрицательный и положительный нуль; в информатике компьютерное кодирование двух нулей (целочисленный тип) может отличаться, см. прямой код.
В связи с вышеизложенным вводятся еще несколько полезных терминов:
Та же самая терминология иногда используется для реальных функций. Например, функция называется положительной 9029.5 если все ее значения положительны, неотрицательны , если все ее значения неотрицательны и т.д. Также говорят, что функция положительна/отрицательна на данном интервале ее определения..
Пример использования функции см. в статье Квадратный корень#Комплексные числа.
Модуль (абсолютное значение) числа
Если число x (\displaystyle x) опускает знак, то результирующее значение называется модуль или абсолютное значение числа x (\displaystyle x), оно обозначается | х | . (\displaystyle |x|.) Примеры: | 3 | = 3; | − 3 | = 3. (\displaystyle |3|=3;\ |(-3)|=3.)
Для любых действительных чисел a , b (\displaystyle a,b) выполняются следующие свойства.
Знак нечисловых объектов
Знак угла
Значение угла на плоскости считается положительным, если он измерен против часовой стрелки, в противном случае — отрицательным.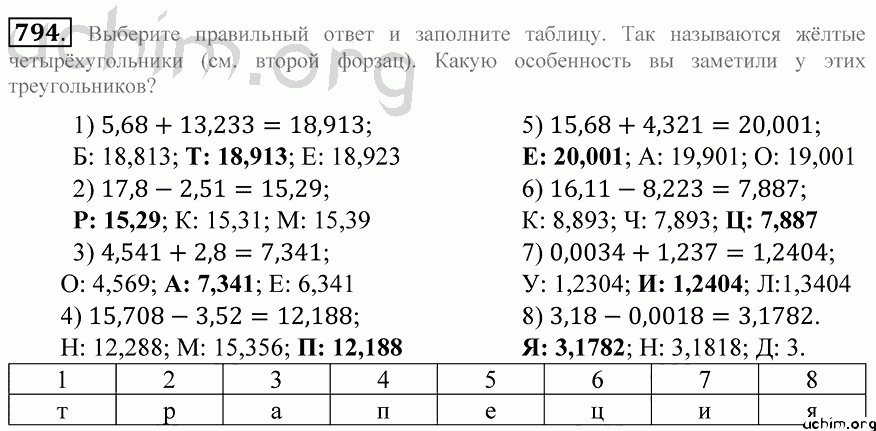 Аналогично классифицируются два случая вращения:
Аналогично классифицируются два случая вращения:
Знак направления
В аналитической геометрии и физике продвижения по заданной прямой или кривой часто условно делят на положительные и отрицательные. Такое деление может зависеть от постановки задачи или от выбранной системы координат. Например, при вычислении длины дуги кривой часто удобно приписывать этой длине знак минус в одном из двух возможных направлений.
Вход в компьютер
| старший бит | |||||||||
| 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | = | 127 |
| 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | = | 126 |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | = | 2 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | = | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | = | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | = | −1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | = | −2 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | = | −127 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | = | −128 |
| Для представления знака целого числа большинство компьютеров используют | |||||||||
по модулю числа само это число называется, если оно неотрицательно, или тем же числом с обратным знаком, если оно отрицательно.
Например, модуль 5 равен 5, а модуль -5 тоже 5.
То есть под модулем числа понимается абсолютная величина, абсолютная величина этого числа без учета его знак.
Обозначается следующим образом: |5|, | Х |, | и | и т.д.
правило :
Объяснение :
|5| = 5
Это читается так: модуль числа 5 равен 5.
|–5| = –(–5) = 5
Это читается так: модуль числа -5 равен 5.
|0| = 0
Это читается так: модуль нуля равен нулю.
Свойства модуля:
1) Модуль числа является неотрицательным числом: | и | ≥ 0 2) Модули противоположных чисел равны: | и | = |– a | 3) Квадрат модуля числа равен квадрату этого числа: | и | 2 = a2 4) Модуль произведения чисел равен произведению модулей этих чисел: | а · б | = | и | · | б | 6) Модуль частных номеров равен отношению модулей этих номеров: | и : б | = | и | : | б | 7) Модуль суммы чисел меньше или равен сумме их модулей: | а + б | ≤ | и | + | б | 8) Модуль разности чисел меньше или равен сумме их модулей: | а – б | ≤ | и | + | б | 9) Модуль суммы/разности чисел больше или равен модулю разности их модулей: | а ± б | ≥ || и | – | б || 10) Из знака модуля можно вынести постоянный положительный коэффициент: | м · и | = м · | a |, m >0 11) Степень числа можно вынести из знака модуля: | и к | = | и | k, если k существует 12) Если | и | = | б |, тогда а = ± б |
Геометрический смысл модуля.
Модуль числа — это расстояние от нуля до этого числа.
Например, снова возьмем число 5. Расстояние от 0 до 5 такое же, как и от 0 до -5 (рис. 1). А когда нам важно знать только длину отрезка, то знак не имеет не только значения, но и смысла. Однако это не совсем так: мы измеряем расстояние только положительными числами — или неотрицательными числами. Пусть значение деления нашей шкалы равно 1 см. Тогда длина отрезка от нуля до 5 равна 5 см, от нуля до -5 тоже 5 см.
На практике расстояние часто измеряют не только от нуля — точкой отсчета может быть любое число (рис. 2). Но суть от этого не меняется. Запись вида |a – b| выражает расстояние между точками a и b на числовой прямой.
Пример 1 . Решить уравнение | Х – 1| = 3.
Решение .
Смысл уравнения в том, что расстояние между точками X и 1 равно 3 (рис. 2). Следовательно, от точки 1 отсчитываем три деления влево и три деления вправо — и ясно видим оба значения X :
X 1 = –2, X 2 = 4.
Мы можем вычислить.
│ x — 1 = 3
│ x — 1 = –3
│ x = 3 + 1
│ x = –3 + 1
│ x = –3 + 1
│ x = 4
│ x = 4
│ x = 4
│ x = 4
│ x = 4
│ x = –3 + 1
│ x = –3 + 1
х = –2.
Ответ: X 1 = –2; X 2 = 4.
Пример 2 . Найдите модуль выражения:
Решение .
Давайте сначала выясним, является ли выражение положительным или отрицательным. Для этого преобразуем выражение так, чтобы оно состояло из однородных чисел. Не будем искать корень из 5 — это довольно сложно. Поступим проще: возведем 3 и 10 в корень. Затем мы сравниваем величину чисел, составляющих разницу:
3 = √9. Следовательно, 3√5 = √9 √5 = √45
10 = √100.
Мы видим, что первое число меньше второго. Это означает, что выражение отрицательное, то есть его ответ меньше нуля:
3√5 – 10
Но по правилу модуль отрицательного числа равен тому же числу с обратным знаком.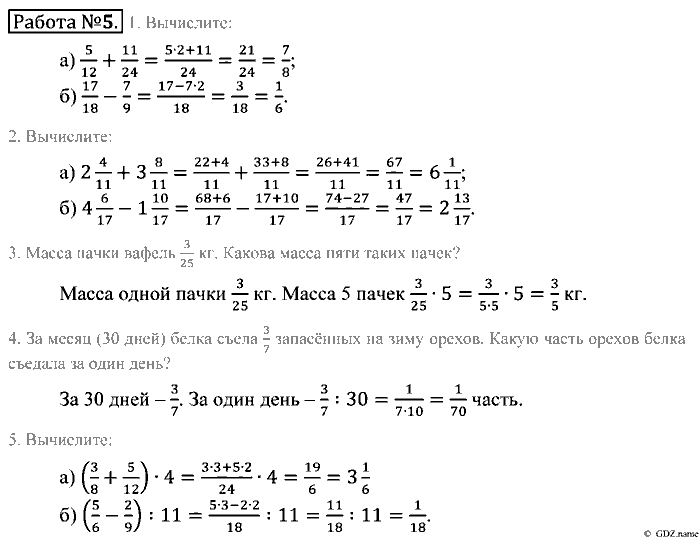 У нас есть отрицательное выражение. Поэтому необходимо изменить его знак на противоположный. Противоположностью 3√5 — 10 является -(3√5 — 10). Раскроем в нем скобки — и получим ответ:
У нас есть отрицательное выражение. Поэтому необходимо изменить его знак на противоположный. Противоположностью 3√5 — 10 является -(3√5 — 10). Раскроем в нем скобки — и получим ответ:
–(3√5 – 10) = –3√5 + 10 = 10 – 3√5.
Ответить .
Страница не найдена — ISPP
Перейти к содержимому
Д-р Мирто Пантази имеет докторскую степень в области социальной психологии, полученную в Свободном университете Брюсселя, где она в настоящее время работает над докторской диссертацией. Ранее Мирто занимал постдокторские должности в Кембриджском университете и Оксфордском институте Интернета. Она также в течение года работала аналитиком по вопросам политики в Объединенном исследовательском центре Европейской комиссии, где предоставляла поведенческие данные для разработки политики.
Научные интересы Мирто широко охватывают психологию убеждений. Сочетая методологию экспериментов и опросов, она в основном изучает, как люди проверяют информацию и почему они верят в дезинформацию. Она также интересуется убеждениями в заговоре и их связью с общественно-политическими взглядами, и она провела исследование социального влияния на общественное мнение, а также устойчивых инвестиционных решений.
Она также интересуется убеждениями в заговоре и их связью с общественно-политическими взглядами, и она провела исследование социального влияния на общественное мнение, а также устойчивых инвестиционных решений.
Д-р Слиман Халаби получил степень магистра когнитивной психологии в Тель-Авивском университете и степень доктора философии в области социальной психологии в Университете Фридриха Шиллера и в Международной исследовательской школе Макса Планка по адаптации поведения в фундаментальной Неопределенность Мир в Йене. Он работает постдоком в Университете Вупперталя в Германии. Его исследовательский интерес вращается вокруг влияния нашей социальной идентичности на взаимодействие с членами своей и чужой группы. Его докторская диссертация была посвящена промежуточным членам, которые охватывают групповое членство в группе, погруженной в межгрупповой конфликт, и тому, как промежуточные группы могут рассматриваться как угроза межгрупповым границам, а также тому, как они ориентируются в своих межгрупповых ориентациях в рамках этого конфликта. совокупность сложных отношений. В последнее время Слиман проводит исследование, в котором изучается непризнание членов группы меньшинств (путем отрицания идентичности и других «микроагрессий») и это влияет на их отношения с большинством общества. Он также исследует способы, с помощью которых члены группы большинства могут конструктивно справляться с реакцией представителей меньшинств на такой опыт, и, таким образом, тестирует вмешательства, направленные на снижение защитной реакции на критику против микроагрессии. Кроме того, Слимана интересует ролевой язык и лингвистические стили (например, акцент) в отношениях внутри и между социальными группами.
совокупность сложных отношений. В последнее время Слиман проводит исследование, в котором изучается непризнание членов группы меньшинств (путем отрицания идентичности и других «микроагрессий») и это влияет на их отношения с большинством общества. Он также исследует способы, с помощью которых члены группы большинства могут конструктивно справляться с реакцией представителей меньшинств на такой опыт, и, таким образом, тестирует вмешательства, направленные на снижение защитной реакции на критику против микроагрессии. Кроме того, Слимана интересует ролевой язык и лингвистические стили (например, акцент) в отношениях внутри и между социальными группами.
Доктор Нойнер — доцент Школы политики и глобальных исследований Университета штата Аризона. Он получил степень доктора политических наук в Мичиганском университете в 2018 году. Его исследования сосредоточены на политической психологии, политическом поведении и общественном мнении как в США, так и в сравнительном контексте. В своем текущем исследовании он заинтересован в понимании когнитивных и аффективных факторов поляризации отношения, механизмов, лежащих в основе медиа-эффектов, таких как прайминг и фрейминг, а также реакции граждан на популистские призывы.
Джессика Гейл является научным сотрудником Кентерберийского университета в Новой Зеландии и Левенского университета в Бельгии в рамках проекта, финансируемого Швейцарским национальным научным фондом. Она также является старшим научным сотрудником Лозаннского университета в Швейцарии в сотрудничестве с Национальным центром компетенций в области исследований — The Migration-Mobility Nexus. Она имеет докторскую степень по социальной психологии в университетах Лозанны и Женевы, степень магистра психологии в том же учреждении, степень бакалавра психологии в Королевском университете и степень бакалавра психологии в Трентском университете. Принимая экспериментальные и многоуровневые методологии, ее исследовательские центры культурного разнообразия, иммиграции и социальной справедливости с точки зрения межгрупповых отношений.
Доктор Ислам Боринка является лектором/доцентом в Школе психологии Дублинского университетского колледжа. Он получил докторскую степень в области социальной психологии в университетах Женевы и Лозанны в качестве получателя стипендии доктора наук в рамках индивидуального докторского проекта, спонсируемого Швейцарской федеральной комиссией по стипендиям для иностранных студентов. После этого он работал ассистентом преподавателя/исследователя в Центре Эмиля Бернхейма, Université Libre de Bruxelles (Брюссель). После этого он провел свои постдокторские исследования в Лимерикском университете (Ирландия). Его исследования сосредоточены на межгрупповых отношениях, в частности на изучении помощи, контактов и групповых норм с акцентом на эмоции, сочувствие, дегуманизацию, мета-дегуманизацию, межгрупповые извинения, предрассудки и дискриминацию во враждебном и невраждебном контексте. Он также исследует гендерные нормы, гендерные роли и поведение. Кроме того, его исследование изучает внутригрупповые процессы в отношении угроз, ожиданий и здоровья.
После этого он работал ассистентом преподавателя/исследователя в Центре Эмиля Бернхейма, Université Libre de Bruxelles (Брюссель). После этого он провел свои постдокторские исследования в Лимерикском университете (Ирландия). Его исследования сосредоточены на межгрупповых отношениях, в частности на изучении помощи, контактов и групповых норм с акцентом на эмоции, сочувствие, дегуманизацию, мета-дегуманизацию, межгрупповые извинения, предрассудки и дискриминацию во враждебном и невраждебном контексте. Он также исследует гендерные нормы, гендерные роли и поведение. Кроме того, его исследование изучает внутригрупповые процессы в отношении угроз, ожиданий и здоровья.
Рури Такидзава — аспирант по социальной психологии Женевского университета, Швейцария. Она получила степень бакалавра психологии в Университете Билефельда (Германия) и степень магистра социальных наук в Университетском колледже Лондона (Англия).
В своем исследовании Рури фокусируется на феномене стеклянной скалы , используя сочетание экспериментальных, архивных и обзорных данных. Она исследует, какое лидерство требуется в различных типах кризисов, какие ожидания возникают, когда недостаточно представленные члены группы (например, женщины и представители этнических, расовых и иммиграционных меньшинств) занимают руководящие роли в политике и организациях, и как оцениваются эти кандидаты. .
Она исследует, какое лидерство требуется в различных типах кризисов, какие ожидания возникают, когда недостаточно представленные члены группы (например, женщины и представители этнических, расовых и иммиграционных меньшинств) занимают руководящие роли в политике и организациях, и как оцениваются эти кандидаты. .
Д-р Тияна Карич имеет степень доктора социальной психологии Университета Нови-Сад, Сербия. Она работает научным сотрудником в Институте криминологических и социологических исследований в Белграде, Сербия, а с октября 2021 года она является научным сотрудником Гумбольдта в Марбургском университете имени Филиппа, Германия. В своем исследовании Тихана применяет как качественные, так и количественные методы для изучения межгрупповых отношений.
Основное направление ее исследований — межгрупповые отношения в постконфликтных обществах в отношении процессов идентичности. Тематическое исследование, которое она исследует, в основном касается Боснии и Герцеговины. Кроме того, ее интересуют предрассудки и дискриминация, а также проблемы интеграции маргинализированных групп. В последнее время она уделяет больше внимания разработке политики, основанной на фактических данных, то есть созданию доказательств для значимых социальных изменений.
В последнее время она уделяет больше внимания разработке политики, основанной на фактических данных, то есть созданию доказательств для значимых социальных изменений.
Доктор Вронски — адъюнкт-профессор политических наук Университета Миссисипи (США), чьи исследования лежат на стыке американской политики и политической психологии. Используя опросы, экспериментальные и количественные методы исследования, она исследует способы, которыми групповая идентичность и личные диспозиции формируют политическое поведение, общественное мнение и выбор избирателей. Ее исследования были опубликованы в ведущих журналах и представлены в средствах массовой информации, включая The New York Times 9.1182, Washington Post и Vox.com .
В настоящее время ее исследования сосредоточены на роли национальной и партийной идентичности, авторитаризма и эмпатии в формировании политического поведения в Соединенных Штатах. Все эти направления исследований носят явно междисциплинарный характер и объединяют теории и методологии как политологии, так и психологии. Она преподает в области американского государственного управления и методологии исследований, включая первые два семестра последовательности методов программы PhD Университета Миссисипи по политическим наукам. Вы можете следить за ней в Твиттере @julie_wronski.
Она преподает в области американского государственного управления и методологии исследований, включая первые два семестра последовательности методов программы PhD Университета Миссисипи по политическим наукам. Вы можете следить за ней в Твиттере @julie_wronski.
Даниэль получил степень бакалавра психологии в Папском католическом университете Чили. Несколько лет работал в Лаборатории социальной психологии под руководством профессора Роберто Гонсалеса и профессора Хорхе Манци. После работы там он подал заявку в PGR (аспирант) в области вычислительных социальных наук в Университете Лидса под руководством доктора Виктории Спайзер и доктора Ричарда Манна, где он работал над НЛП (обработкой естественного языка) и искусственным интеллектом. (Искусственный интеллект) для языковых проектов, связанных с социальными сетями и общественными движениями.
Вообще говоря, он заинтересован в использовании «больших данных» из цифровых источников, таких как социальные сети, Интернет вещей или просто общий цифровой след, для моделирования человеческого поведения. Мой текущий проект PhD пытается использовать публичный цифровой след в социальных сетях населения, которое в настоящее время переживает периоды социальных волнений, для извлечения их общих эмоциональных паттернов, и все это с целью построить прогностическую модель активности на основе этих параметров.
Мой текущий проект PhD пытается использовать публичный цифровой след в социальных сетях населения, которое в настоящее время переживает периоды социальных волнений, для извлечения их общих эмоциональных паттернов, и все это с целью построить прогностическую модель активности на основе этих параметров.
Фелипе получил степень бакалавра психологии в Федеральном университете Риу-Гранди-ду-Сул. Он получил степень магистра наук и является аспирантом программы для выпускников факультетов психологии Папского католического университета Риу-Гранди-ду-Сул (PUCRS), которым руководит д-р Анджело Бранделли Коста (PUCRS, Бразилия). Он является техническим редактором Revista Argentina de Ciencias del Comportamiento и управляющим редактором журнала Trends in Psychology. Он также является модератором глобальной открытой научной платформы для препринтов PsyarXiv. В настоящее время основными темами исследований являются авторитаризм, социальное доминирование и коррупция.
Ронгбо Джин — аспирант политических наук Аризонского университета в США.



