Лабораторная работа на тему определение жесткости пружины: Лабораторная работа № 2 «Измерение жесткости пружины»

Лабораторная работа № 2 «Измерение жесткости пружины»

Цель работы: найти жесткость пружины из измерений удлинения пружины при различных значениях силы тяжести

уравновешивающей силу упругости на основе закона Гука:

В каждом из опытов жесткость определяется при разных значениях силы упругости и удлинения, т. е. условия опыта меняются. Поэтому для нахождения среднего значения жесткости нельзя вычислить среднее арифметическое результатов измерений. Воспользуемся графическим способом нахождения среднего значения, который может быть применен в таких случаях. По результатам нескольких опытов построим график зависимости модуля силы упругости F_упр от модуля удлинения |x|. При построении графика по результатам опыта экспериментальные точки могут не оказаться на прямой, которая соответствует формуле

Это связано с погрешностями измерения. В этом случае график надо проводить так, чтобы примерно одинаковое число точек оказалось по разные стороны от прямой. После построения графика возьмите точку на прямой (в средней части графика), определите по нему соответствующие этой точке значения силы упругости и удлинения и вычислите жесткость k.

Она и будет искомым средним значением жесткости пружины k_ср.

Результат измерения обычно записывается в виде выражения k = = k_cp±Δk, где Δk — наибольшая абсолютная погрешность измерения. Из курса алгебры (VII класс) известно, что относительная погрешность (ε_k) равна отношению абсолютной погрешности Δk к значению величины k:

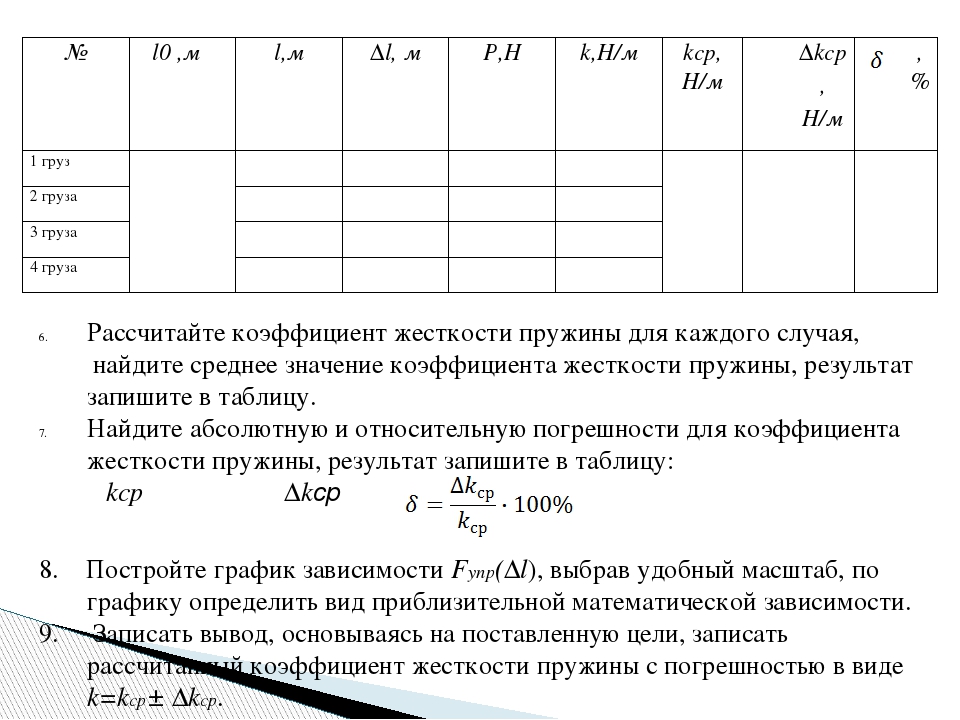
откуда Δk — ε_kk. Существует правило для расчета относительной погрешности: если определяемая в опыте величина находится в результате умножения и деления приближенных величин, входящих в расчетную формулу, то относительные погрешности складываются. В данной работе

Поэтому

Средства измерения: 1) набор грузов, масса каждого равна m₀ = 0,100 кг, а погрешность Δm₀ = 0,002 кг; 2) линейка с миллиметровыми делениями.

Материалы: 1) штатив с муфтами и лапкой; 2) спиральная пружина.

Порядок выполнения работы

1. Закрепите на штативе конец спиральной пружины (другой конец пружины снабжен стрелкой-указате-лем и крючком — рис. 176).

2. Рядом с пружиной или за ней установите и закрепите линейку с миллиметровыми делениями.

3. Отметьте и запишите то деление линейки, против которого приходится стрелка-указатель пружины.

4. Подвесьте к пружине груз известной массы и измерьте вызванное им удлинение пружины.

5. К первому грузу добавьте второй, третий и т. д. грузы, записывая каждый раз удлинение |х| пружины. По результатам измерений заполните таблицу:

Номер опыта	m, кг	mg1, Н	|х|, м

6. По результатам измерений постройте график зависимости силы упругости от удлинения и, пользуясь им, определите среднее значение жесткости пружины k_cp.

7. Рассчитайте наибольшую относительную погрешность, с которой найдено значение k_ср (из опыта с одним грузом).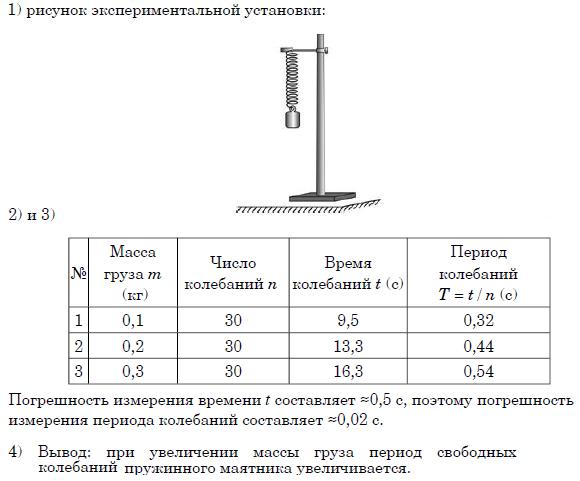 В формуле (1)

так как погрешность при измерении удлинения Δx=1 мм, то

8. Найдите

и запишите ответ в виде:

¹ Принять g≈10 м/с².

Закон Гука: «Сила упругости, возникающая при деформации тела, пропорциональна его удлинению и направлена противоположно направлению перемещения частиц тела при деформации».

Закон Гука

Жесткостью называют коэффициент пропорциональности между силой упругости и изменением длины пружины под действием приложенной к ней силы. Согласно третьему закону Ньютона, приложенная к пружине сила по модулю равна возникшей в ней силе упругости. Таким образом жесткость пружины можно выразить как:

где F — приложенная к пружине сила, а х — изменение длины пружины под ее действием. Средства измерения: набор грузов, масса каждого равна m₀ = (0,1±0,002) кг.

Линейка с миллиметровыми делениями (Δх = ±0,5 мм). Порядок выполнения работы описан в учебнике и комментариев не требует.

№ опыта	масса, кг		удлинение |х|,	К, Н/м
			м
1	0,1	1	0,036	27,78
2	0,2	2	0,074	27,03

3	0,3	3	0,112	26,79
4	0,4	4	0,155	25,81

* Ускорение свободного падения примем равным 10 м/с².

Вычисления:

Вычисление погрешности измерения:

ε_х максимально когда х — наименьшее, т.е., в нашем случае, для опыта с одним грузом

Можно записать результат измерений как:

или округляя:

т.к. в нашем случае отклонения вычисленных R₁; R₂; R₃; R₄ от R_ср велики из-за разности условий опытов принимаем

Источник:

Решебник по физике за 9 класс (И.К.Кикоин, А.К.Кикоин, 1999 год),
задача №2
к главе «ЛАБОРАТОРНЫЕ РАБОТЫ».

Все задачи

← Лабораторная работа № 1 «Измерение ускорения тела при равноускоренном движении»

Лабораторная работа № 3 «Измерение коэффициента трения скольжения» →

Лабораторная работа «Определение жесткости пружины» | Учебно-методический материал по физике (7 класс):

Лабораторная работа

«Определение жесткости пружины».

Цель работы:   Проверить справедливость закона Гука, убедиться, что сила упругости пропорциональна массе нагрузки, определить жесткость пружины.

        Приборы и материалы:    штатив с муфтами лапкой,  набор спиральных пружин,  набор грузов массой 100 г, линейка с миллиметровыми делениями.  

Краткая теория.  Цель работы – найти жесткость пружины из измерений удлинения пружины Δl при различных значениях силы тяжести F=m·g, уравновешивающей силу упругости на основе закона Гука.

В каждом из опытов жесткость определяется при разных значениях силы упругости и удлинений, т. е. условия опыта меняются. Поэтому для нахождения среднего значения жесткости нельзя вычислить среднее арифметическое результатов измерений. Значит, воспользуемся графическим способом нахождения среднего значения, который может быть применен в таких случаях: по результатам нескольких опытов построим график зависимости модуля силы упругости Fупр, от модуля удлинения Δl. 

При построении графика по результатам опыта экспериментальные точки могут не оказаться на прямой, которая соответствует формуле  .

Это связано с погрешностями измерения.

В этом случае график надо проводить так, чтобы примерно

одинаковое число точек оказалось по разные стороны от прямой.

После построения графика возьмите точку на прямой

(в средней части графика), определите по нему соответствующие

 этой точке значения силы упругости и удлинения и вычислите

жесткость  kср. Она и будет искомым средним значением

жесткости пружины.

Порядок выполнения работы.

1. Закрепите на штативе конец спиральной пружины (другой конец пружины снабжен стрелкой-указателем и крючком).        

2. Рядом с пружиной или за ней установите линейку с миллиметровыми делениями.

3. Отметьте и запишите то деление линейки, против которого приходится стрелка-указатель пружины.

4. Подвесьте к пружине груз известной массы и измерьте вызванное им удлинение пружины.

5. К первому грузу добавьте второй, третий, записывая каждый раз удлинение Δl  пружины. По результатам измерений заполните таблицу:

1 пружина	№ опыта	m, кг	F= m·g,  Н	Δl,  м	k,	kср,
	1	0,1
	2	0,2
	3	0,3
2 пружина	1	0,1
	2	0,2
	3	0,3

6. По результатам измерений постройте график зависимости силы упругости от удлинения и, пользуясь им, определите среднее значение жесткости пружины (см. теорию).

7. Вывод: 1)Проанализируйте пропорциональность модуля удлинения Δl и массы нагрузки m.

         2) Измерение каких физических величин привнесло в результат погрешность?  

         3) Подумайте, что можно предпринять, чтобы улучшить результат эксперимента.

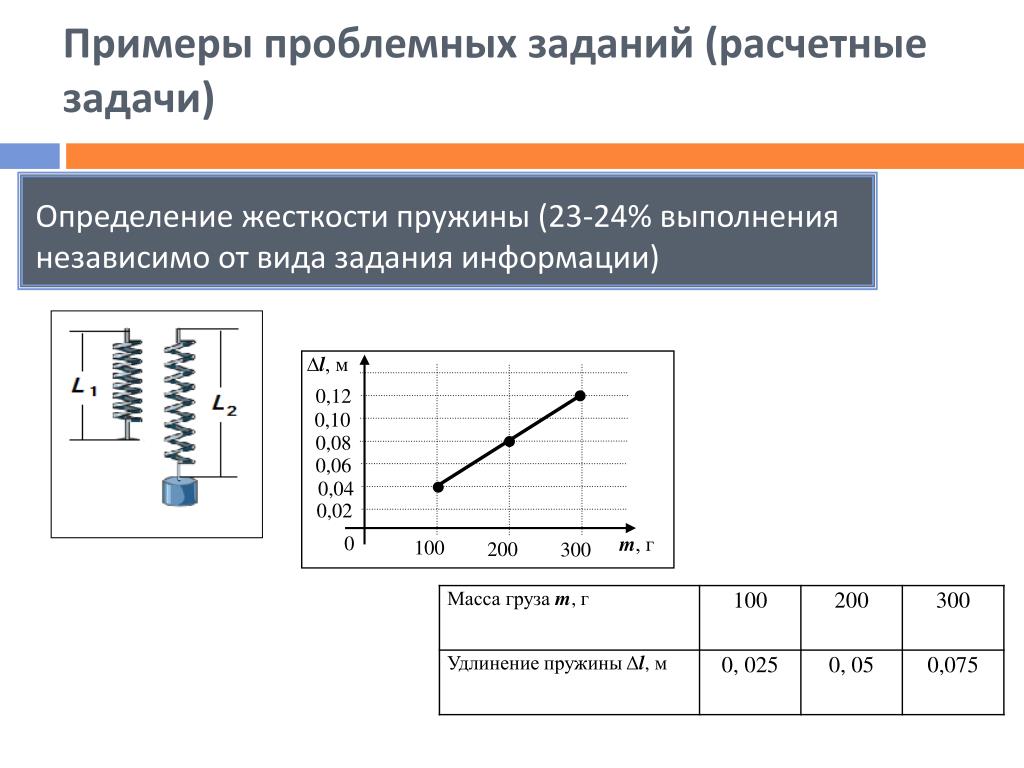
Практическая деятельность (определение постоянной силы пружины)

Пропустить до основного содержания

PAGE PATH

Практическая деятельность (определение константы силы пружины)

Практическая деятельность

В этом эксперименте вы будете измерять константу силы пружины весна. На выбор предлагается три пружины, каждая из которых имеет разную степень жесткости. Ваш учитель может попросить вас измерить постоянные пружины для всех трех или может попросить вас сосредоточиться на конкретной пружине.

Скопируйте следующие заголовки таблиц в свою лабораторную тетрадь:

Рисунок 3 Заголовки таблиц, используемые в эксперименте с системой пружинных масс.

Вы будете использовать это для записи данных, генерируемых системой массы пружины. Начальное значение представляет собой длину пружины в сантиметрах в состоянии покоя до того, как к пружине будут добавлены какие-либо веса.

Если исходное значение пружины составляет 12 см и 15,5 см после приложения груза массой 50 г, на сколько сантиметров пружина растянулась под действием приложенного груза?

После того, как вы перешли на домашнюю страницу приложения массовой системы Spring ( не делайте этого, пока внимательно не прочитаете следующие инструкции ), выберите опцию «Определение постоянной силы пружины» и приступайте к эксперименту. Ваша первая задача — выбрать пружину (у вас есть выбор: мягкая, средняя или жесткая пружина).

После того, как вы выбрали пружину, запишите начальные показания, прежде чем добавлять какие-либо грузы для ее удлинения. Затем последовательно добавляются гири, начиная с 50 г (это вес «держателя гири»), а затем добавляют еще веса с шагом в 50 г. до тех пор, пока не будет достигнута конечная масса 250 г.

После того, как вы собрали свои наблюдения, вам нужно будет создать новую таблицу в своей лабораторной тетради, где вес в граммах (г) преобразуется в значения силы в ньютонах (Н), а значения растяжения в сантиметрах (см) преобразуются в метры. (м).

Если вы не знакомы с соотношением между массой и силой, то на уровне моря 1 кг массы равен силе 9,8 Н, поэтому 100 г равен 0,98 Н.

Что такое 250 г в ньютонах?

После преобразования значений в ньютоны и метры постройте график зависимости силы от растяжения для выбранной пружины, а затем сопоставьте линию наилучшего соответствия, проходящую через точки графика, например, как показано на рисунке 4.

Рисунок 4 График, показывающий удлинение пружины в зависимости от приложенной силы.

Наклон вашего графика является мерой жесткости пружины. Данные, представленные в примере, показанном на рисунке 4, являются линейными, что означает, что предел пропорциональности не был достигнут, и поскольку соотношение между приложенной силой и удлинением пропорциональна, закон Гука можно использовать для расчета постоянной силы пружины.

Итак, если сила в 2,45 Н (эквивалент 200 г) приводит к удлинению на 1,2 м, наклон рассчитывается путем деления 2,45 Н на 1,2 м, что дает значение 1,635 Н/м.

Посмотрите на график, изображенный на рис. 4. Какая переменная нанесена на каждую ось?

Обычным соглашением при построении графика данных является построение зависимой переменной по оси Y и независимой переменной по оси X.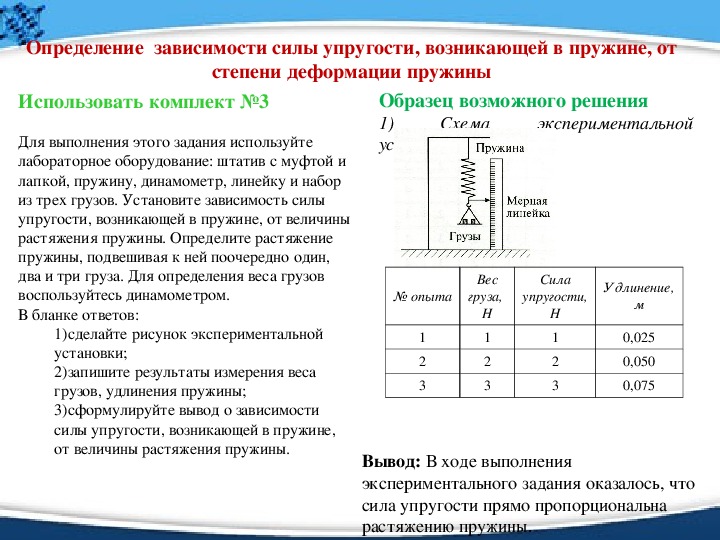 Однако, поскольку постоянная силы пружины выражается в Н/м, это соглашение меняется на противоположное при применении закона Гука: таким образом, что зависимая переменная (удлинение, м) теперь нанесена на ось абсцисс, а независимая переменная (сила, Н) — на ось у, и, следовательно, результирующий наклон выражается как Н/м.

Система пружинных грузов

Щелкните значок ниже, чтобы перейти на домашнюю страницу приложения массовой системы Spring в виртуальной лаборатории OpenSTEM Africa. Посмотрите вступительное видео перед началом эксперимента.

Предыдущий: Фон Далее: Резюме

Распечатать

стр.

Для получения дополнительной информации ознакомьтесь с нашими часто задаваемыми вопросами, которые могут оказать вам необходимую поддержку.

Есть вопрос?

Если вас что-то беспокоит на этом сайте, пожалуйста, свяжитесь с нами здесь.

Сообщить о проблеме

Лаборатория 7 — Simple Harmonic Motion

Введение

Вы когда-нибудь задумывались, почему напольные часы показывают точное время? Движение маятника представляет собой особый вид повторяющегося или периодического движения, называемого простым гармоническим движением или SHM. Положение колеблющегося объекта изменяется во времени по синусоидальному закону. Многие объекты колеблются взад и вперед. Движение ребенка на качелях можно аппроксимировать синусоидальным и, следовательно, рассматривать как простое гармоническое движение. Некоторые сложные движения, такие как турбулентные волны на воде, не считаются простым гармоническим движением. Когда объект находится в простом гармоническом движении, можно легко определить скорость, с которой он колеблется вперед и назад, а также его положение во времени.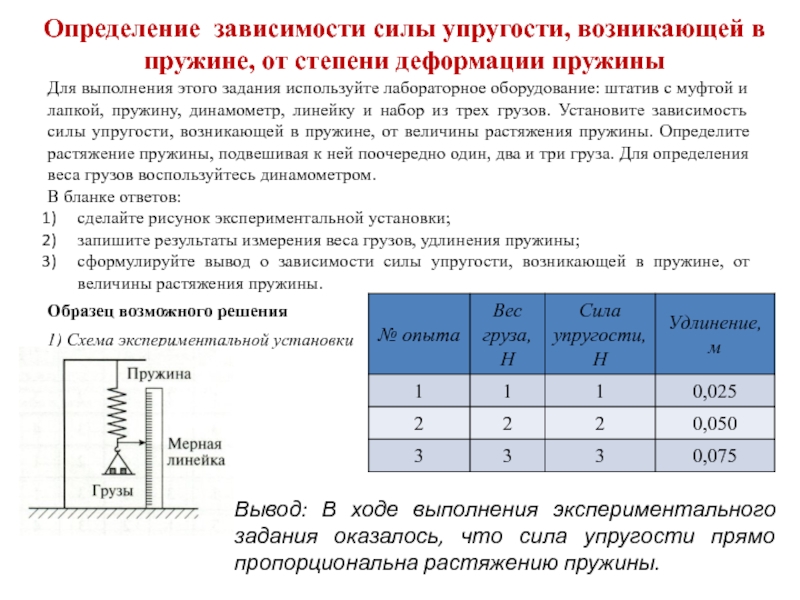 В этой лабораторной работе вы проанализируете простой маятник и систему пружинных масс, обе из которых демонстрируют простое гармоническое движение.

Обсуждение принципов

Частица, вибрирующая вертикально в простом гармоническом движении, движется вверх и вниз между двумя крайними значениями y = ± A . Максимальное смещение A называется амплитудой . Это движение показано графически на графике зависимости положения от времени на рис. 1.

Рисунок 1 : График положения, показывающий синусоидальное движение объекта в SHM

Одно полное колебание или цикл или колебание — это движение, например, от

y = −A

к

y = +A

и обратно к

9 0002 г = -А.

Интервал времени T , необходимый для совершения одного колебания, называется периодом . Родственной величиной является частота f , которая представляет собой количество колебаний, совершаемых системой в единицу времени. Частота обратна периоду и измеряется в герцах, сокращенно Гц;

1 Гц = 1 с ⁻¹ .

( 1 )

f = 1/T

Если частица колеблется вдоль оси y , то ее положение на оси y в любой данный момент времени t , отсчитываемое от начала колебания, определяется уравнением

( 2 )

y = A sin(2 π футов)

Напомним, что скорость объекта — это первая производная, а ускорение — вторая производная функции смещения по времени. Скорость v и ускорение a частицы в момент времени t определяются выражением

( 3 )

v = 2 π fA cos(2 π фута)

( 4 )

a = −(2 π f) 9 0190 2 [А грех(2 π футов)]

Обратите внимание, что скорость и ускорение также являются синусоидальными. Однако функция скорости имеет разность фаз 90° или π /2, а функция ускорения имеет разность фаз 180° или π разность фаз относительно функции смещения.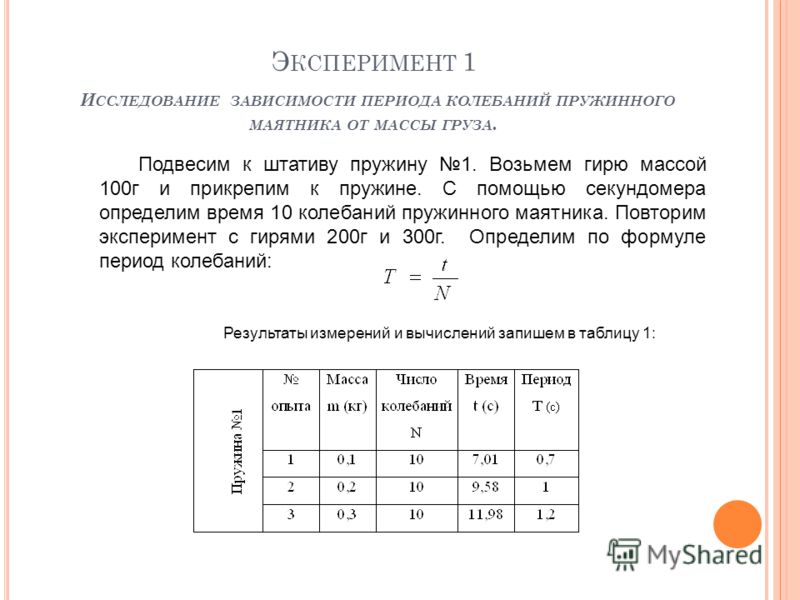 Например, когда смещение максимально положительно, скорость равна нулю, а ускорение максимально отрицательно. Замена из

уравнения. (1)

f = 1/T

в

Ур. (4)

a = −(2 π f) ² [A sin(2 π футов)]

дает

( 5 )

a = −4 π ² f ² y

Из уравнения

(5)

a = −4 π ² f ² y

мы видим, что ускорение объекта в СГМ пропорционально смещению и противоположно по знаку. Это основное свойство любого объекта, совершающего простое гармоническое движение. Рассмотрим несколько критических точек в цикле, как в случае колеблющейся системы пружина-масса. Пружинно-массовая система состоит из массы, прикрепленной к концу пружины, подвешенной к стойке. Масса немного притягивается вниз и отпускается, чтобы заставить пружину и массу колебаться в вертикальной плоскости. На рис. 2 показаны пять критических точек, когда масса пружины проходит полный цикл. Положением равновесия системы пружина-масса является положение массы, когда пружина не растянута и не сжата.

Рисунок 2 : Пять ключевых точек массы, колеблющейся на пружине.

Масса завершает полный цикл, перемещаясь из положения A в положение E. Описание каждого положения выглядит следующим образом:

• Положение A: пружина сжата; масса находится выше точки равновесия при

  y = A

  и вот-вот высвободится.
• Положение B: масса движется вниз, проходя через точку равновесия.
• Положение C: масса на мгновение покоится в самой нижней точке, прежде чем начать движение вверх.
• Положение D: масса движется вверх, когда она проходит через точку равновесия.
• Положение E: груз на мгновение останавливается в самой высокой точке, прежде чем снова начать опускаться.

Отмечая время, когда для положения, скорости и ускорения колеблющегося объекта возникают отрицательные максимальные, положительные максимальные и нулевые значения, вы можете построить график функции синуса (или косинуса). Это сделано для случая колеблющейся системы пружины и массы в таблице ниже, а три функции показаны на рис. 3. Обратите внимание, что положительное направление обычно выбирается как направление растяжения пружины. Следовательно, положительное направление в данном случае вниз и исходное положение A на рис. 2 на самом деле является отрицательным значением. Наиболее сложным для анализа параметром является ускорение. Это помогает использовать второй закон Ньютона, который говорит нам, что отрицательное максимальное ускорение возникает, когда результирующая сила является отрицательной максимальной, положительное максимальное ускорение возникает, когда результирующая сила положительна, а ускорение равно нулю, когда результирующая сила равна нулю.

9030 макс. 9 позиций

	Положение	Скорость	Ускорение
Точка A	макс. отр.	ноль	макс. позиция
точка B	ноль	макс. 9 ноль
Точка C	pos max	ноль	neg max
Точка D	ноль	отр. макс.	ноль
Точка E	отр. макс.	ноль

Рисунок 3 : Положение, скорость и ускорение в зависимости от времени

Для этого конкретного начального условия (начальное положение в точке A на рис. 2) кривая положения представляет собой косинусоидальную функцию (фактически отрицательную косинусоидальную функцию), кривая скорости представляет собой синусоидальную функцию, а кривая ускорения представляет собой просто отрицательную величину положения. изгиб.

Масса и пружина

Груз, подвешенный на конце пружины, растянет пружину на некоторое расстояние и . Сила, с которой пружина тянет вверх массу, выражается как где k — жесткость пружины, а y — растяжение пружины при приложении к ней силы F .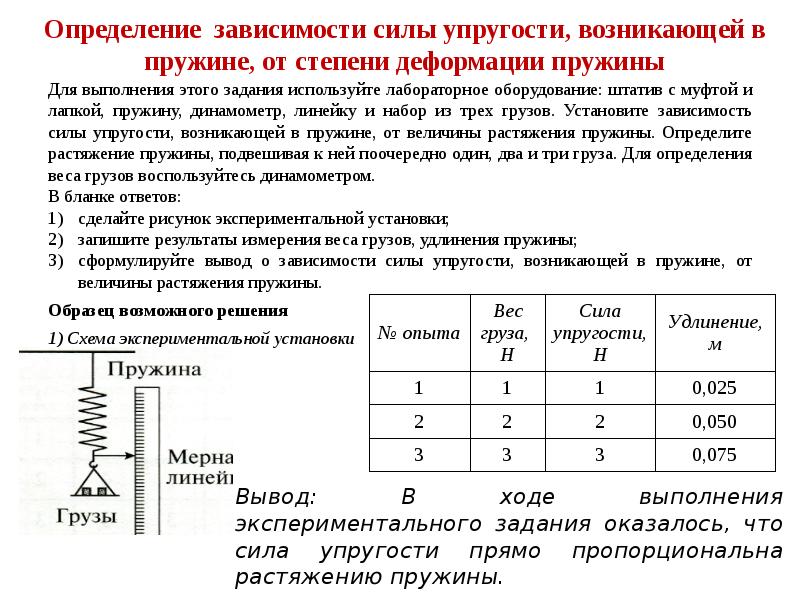 Постоянная пружины k является мерой жесткости пружины. Постоянную пружины можно определить экспериментально, позволив массе неподвижно висеть на пружине, а затем добавив дополнительную массу и записав дополнительное растяжение пружины, как показано ниже. На рис. 4а подвес груза подвешен к концу пружины. На рис. 4b к подвеске добавлена ​​дополнительная масса, и теперь пружина растянута на величину

Δy

. Эта экспериментальная установка также показана на фотографии аппарата на рис. 5.

Рисунок 4 : Установка для определения жесткости пружины

Рисунок 5 : Фото установки для определения жесткости пружины

Когда масса неподвижна, ее ускорение равно нулю. Следовательно, согласно второму закону Ньютона результирующая сила должна быть равна нулю. На массу действуют две силы; направленная вниз сила тяжести и направленная вверх сила пружины. См. диаграмму свободного тела на рис. 6 ниже.

Рисунок 6 : Схема свободного тела для системы пружины-массы

Итак, второй закон Ньютона дает нам

( 7 )

Δmg − kΔy = 0

где

Δm

— изменение массы,

Δy

— изменение растяжения пружины, вызванное изменением массы, g — ускорение свободного падения, k — постоянная пружины.

Уравнение (7)

Δmg − kΔy = 0

также можно выразить как

( 8 )

Δm = Δy

Второй закон Ньютона, примененный к этой системе, равен

мА = F = −ky.

Заменитель

Eq. (5)

a = −4 π ² f ² y

для ускорения, чтобы получить

( 9 )

м(−4 π ² f ² y) = −ky

откуда получаем выражение для частоты f и период T .

( 10 )

f =

( 11 )

T = 2 π

Используя уравнение

. (11) T = 2 π

мы можем предсказать период, если мы знаем массу пружины и константу пружины. С другой стороны, зная массу пружины и экспериментально измерив период, мы можем определить жесткость пружины. Обратите внимание, что в

Уравнение (11) T = 2 π

Связь между T и M не является линейной. График зависимости периода от массы не будет прямой линией. Если возвести в квадрат обе части уравнения

. (11) T = 2 π

, получаем

( 12 )

T ² = 4 π ²

Теперь график зависимости

T ²

от м будет представлять собой прямую линию, а константу пружины можно определить по наклону.

Простой маятник

Другой пример простого гармонического движения, который вы будете исследовать, — это простой маятник . Простой маятник состоит из груза массой м , называемого грузом маятника, прикрепленного к концу нити. Длина L простого маятника измеряется от точки подвеса струны до центра груза, как показано на рис. 7 ниже.

Рисунок 7 : Экспериментальная установка для простого маятника

Если груз отодвинуть от положения покоя на некоторый угол смещения θ , как на рис. 7, возвращающая сила вернет груз обратно в положение равновесия. Силы, действующие на груз, — это сила тяжести и сила натяжения струны. Сила натяжения струны уравновешивается той составляющей силы тяжести, которая находится на одной линии со струной (т. е. перпендикулярно движению груза). Возвращающей силой здесь является тангенциальная составляющая силы тяжести.

Рисунок 8 : Простой маятник

Применив тригонометрию к меньшему треугольнику на рис. 8, мы получим величину возвращающей силы

|F| = мг sin θ .

Эта сила зависит от массы шарика, ускорения свободного падения g и синуса угла, на который натянута нить. Снова должен применяться второй закон Ньютона, поэтому

( 13 )

мА = F = −mg sin

где отрицательный знак означает, что восстанавливающая сила действует против направления движения груза. Поскольку груз движется по дуге окружности, угловое ускорение равно

α = a/L.

Из

экв. (13)

ma = F = −mg sin θ

получаем

( 14 )

α = − sin θ

На рис. 9 синяя сплошная линия — это график θ в зависимости от sin( θ ), а прямая линия представляет собой график зависимости θ в градусах от θ в радианах. При малых углах эти две кривые почти неразличимы. Следовательно, пока смещение θ мало, мы можем использовать аппроксимацию sin θ ≅ θ .

Рисунок 9 : Графики sin θ по сравнению с θ

С этим приближением

уравнения. (14)

α = − sin θ

становится

( 15 )

α = − θ

Уравнение (15) показывает, что (угловое) ускорение пропорционально отрицательному значению (углового) смещения, и, следовательно, движение груза является простым гармоническим, и мы можем применить уравнение

. (5)

a = −4 π ² f ² y

, чтобы получить

( 16 )

α = −4 π ² f ² θ

Объединение

уравнения. (15)

α = − θ

и

Ур. (16)

α = −4 π ² f ² θ

, и упрощая, получаем

( 17 )

f =

и

( 18 )

Т = 2 π

Обратите внимание, что частота и период простого маятника не зависят от массы.

Объектив

Цель этой лабораторной работы — понять поведение объектов в простом гармоническом движении путем определения жесткости пружины системы масса-пружина и простого маятника.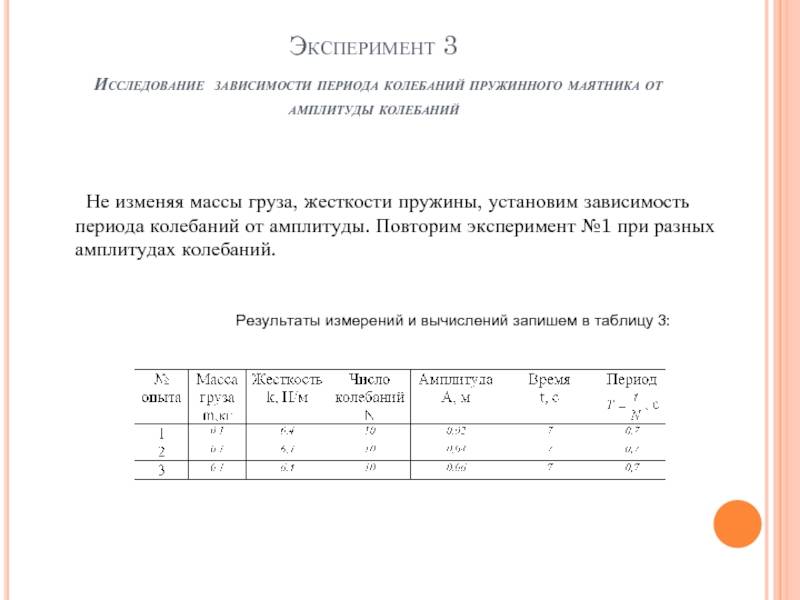

Оборудование

• Ассорти массы
• Весна
• метр палка
• Стоять
• Секундомер
• Нить
• маятниковый боб
• Транспортир
• Баланс

Процедура

Используя закон Гука, вы определите жесткость пружины, измерив растяжение пружины по мере того, как к пружине добавляются дополнительные массы. Вы определите период колебаний системы пружина-масса для различных масс и используете его для определения жесткости пружины. Затем вы сравните значения жесткости пружины, полученные двумя методами. В случае простого маятника вы измерите период колебаний для струн маятника различной длины и сравните эти значения с предсказанными значениями периода.

Процедура A. Определение жесткости пружины с использованием закона Гука

• 1

  Начиная с 50 г, добавляйте на вешалку грузы с шагом 50 г. Добавляя каждые 50 г массы, измерьте соответствующее удлинение 90 142 y 90 143 пружины, создаваемой весом этих добавленных масс. Введите эти значения в Таблицу данных 1.

• 2

  Используйте Excel для построения графика м против y . См. Приложение G.

• 3

  Используйте параметр линии тренда в Excel, чтобы определить наклон графика. Запишите это значение в рабочий лист. См. Приложение Н.

• 4

  Используйте значение наклона, чтобы определить жесткость пружины k . Запишите это значение в рабочий лист.

КПП 1:
Попросите вашего ТА проверить вашу таблицу и график Excel.

Процедура B: Определение жесткости пружины по

T ²

по сравнению с m График Мы предположили, что пружина не имеет массы, но у нее есть некоторая масса, которая повлияет на период колебаний. Теория предсказывает, а опыт подтверждает, что если к массе м в

уравнении добавить одну треть массы пружины. (11) T = 2 π

, период будет таким же, как у массы такой полной величины, колеблющейся на безмассовой пружине.

• 5

  С помощью весов измерьте массу пружины и запишите результат в рабочий лист. Добавьте одну треть этой массы к колеблющейся массе перед вычислением периода колебаний. Если масса пружины намного меньше колеблющейся массы, вам не нужно добавлять одну треть массы пружины.

• 6

  Добавьте 200 г на вешалку.

• 7

  Потяните массу вниз на короткое расстояние и отпустите, чтобы произвести устойчивое движение вверх и вниз без бокового раскачивания или поворота. По мере того, как масса движется вниз мимо точки равновесия, запустите часы и отсчитайте «ноль». Затем считайте каждый раз, когда масса перемещается вниз за точку равновесия, и на 50-м проходе останавливайте часы.

• 8

  Повторите шаг 7 еще два раза и запишите значения для трех испытаний в таблице данных 2 и определите среднее время для 50 колебаний.

• 9

  Определите период по этому среднему значению и запишите его в рабочий лист.

• 10

  Повторите шаги с 7 по 9 для трех других существенно отличающихся масс.

• 11

  Используйте Excel, чтобы построить график зависимости

  T ²

  от

  m

  .

• 12

  Используйте опцию линии тренда в Excel, чтобы определить наклон и записать это значение на листе.

• 13

  Определите жесткость пружины k по наклону и запишите это значение в рабочий лист.

• 14

  Рассчитайте процентную разницу между этим значением k и значением, полученным в процедуре А, используя закон Гука. См. Приложение Б.

КПП 2:
Попросите вашего ТА проверить значения и расчеты в вашей таблице.

Процедура C: Простой маятник

• 15

  Отрегулируйте маятник на максимально возможную длину и прочно закрепите шнур. Двухметровой палкой тщательно измерьте длину струны, включая длину маятника. С помощью штангенциркуля измерьте длину маятника. См. Приложение D. Вычтите половину этого значения из ранее измеренной длины, чтобы получить значение L , и запишите его в Таблицу данных 3 на рабочем листе.

• 16

  Используя принятое значение 9,81

  м/с ²

  для g , предскажите и запишите период маятника для этого значения L .

• 17

  Потяните маятник в сторону и отпустите. Используйте как можно меньший угол, менее 10°. Убедитесь, что боб качается вперед и назад, а не движется по кругу. С помощью секундомера измерьте время, необходимое для 50 колебаний маятника, и запишите это в таблицу данных 3.

• 18

  Повторите шаг 17 еще два раза и запишите значения для трех испытаний в таблице данных 3 и определите среднее время для 50 колебаний.

• 19

  Определите период по этому среднему значению и запишите его в рабочий лист.

  No related posts.