Лабораторная работа измерение коэффициента жесткости пружины. Лабораторная работа«Измерение жесткости пружины» методическая разработка по физике на тему
МОУ «Гимназия №6» Физический практикум 10 класс
Лабораторная работа №3
Измерение жесткости пружины
Цель работы : найти жесткость пружины из измерений удлинения пружины при различных значениях силы тяжести , уравновешивающей силу упругости
на основе закона Гука:
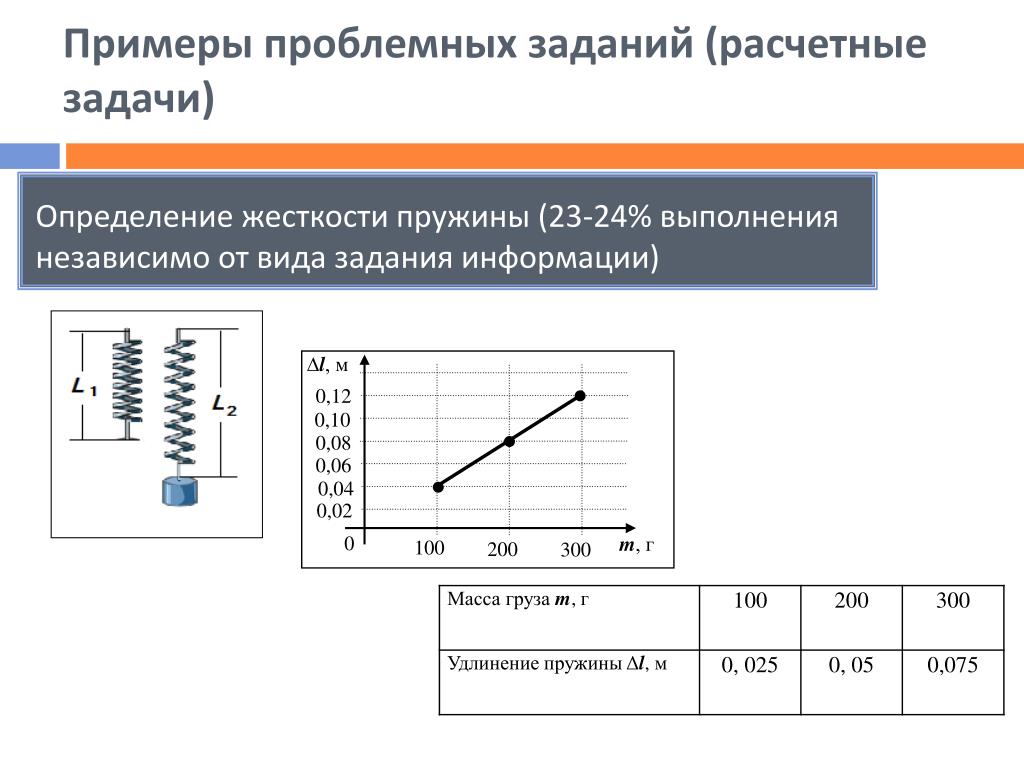
. В каждом из опытов жесткость определяется при разных значениях силы упругости и удлинения, т.е. условия опыта меняются. Поэтому для нахождения среднего значения жесткости нельзя вычислить среднее арифметическое результатов измерений. Воспользуемся графическим способом нахождения среднего значения, который может быть применен в таких случаях. По результатам нескольких опытов построим график зависимости модуля силы упругости
от модуля удлинения х . При построении графика по результатам опыта экспериментальные точки могут не оказаться на прямой, которая соответствует формуле
.
Результат измерения обычно записывается в виде выражения
, где
— наибольшая абсолютная погрешность измерения. Известно, что относительная погрешность () равна отношению абсолютной погрешности
к значению величины k :
, откуда
.
В данной работе
. Поэтому
, где
;
;
.
Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com
Подписи к слайдам:
Лабораторная работа «Измерение жесткости пружины» Учитель физики ГБОУ СОШ №145 Калининского района Санкт- Петербурга Карабашьян М.
проверить справедливость закона Гука для пружины динамометра и измерить коэффициент жесткости этой пружины. Цель работы Оборудование: набор «Механика» из комплекта L-micro- штатив с муфтой и зажимом, динамометр с заклеенной шкалой, набор грузов известной массы (по 50 г), линейка с миллиметровыми делениями.
Подготовительные вопросы Что такое сила упругости? Как вычислить силу упругости, возникающую в пружине при подвешивании к ней груза массой m кг? Что такое удлинение тела? Как измерить удлинение пружины при подвешивании к ней груза? В чем заключается закон Гука?
Правила техники безопасности Будьте осторожны при работе с растянутой пружиной. Не роняйте и не бросайте грузы.
Описание работы: Согласно закону Гука, модуль F силы упругости и модуль х удлинения пружины связаны соотношением F = kx . Измерив F и х, можно найти коэффициент жесткости k по формуле
В каждом из опытов жесткость определяется при разных значениях силы упругости и удлинения, т. е. условия опыта меняются.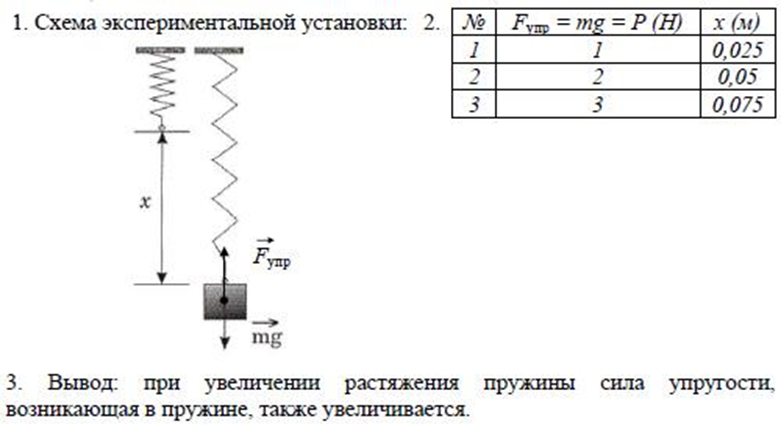 Поэтому для нахождения среднего значения жесткости нельзя вычислить среднее арифметическое результатов измерений. Воспользуемся графическим способом нахождения среднего значения, который может быть применен в таких случаях. По результатам нескольких опытов построим график зависимости модуля силы упругости F упр от модуля удлинения \ х\ . При построении графика по результатам опыта экспериментальные точки могут не оказаться на прямой, которая соответствует формуле F yпp =k\x\ . Это связано с погрешностями измерений. В этом случае график надо проводить так, чтобы примерно одинаковое число точек, оказалось, по разные стороны от прямой. После построения графика возьмите точку на прямой (в средней части графика) определите по нему соответствующие этой точке значения силы упругости и удлинения, и вычислите жесткость k . Она и будет искомым средним значением жесткости пружины k ср.
Поэтому для нахождения среднего значения жесткости нельзя вычислить среднее арифметическое результатов измерений. Воспользуемся графическим способом нахождения среднего значения, который может быть применен в таких случаях. По результатам нескольких опытов построим график зависимости модуля силы упругости F упр от модуля удлинения \ х\ . При построении графика по результатам опыта экспериментальные точки могут не оказаться на прямой, которая соответствует формуле F yпp =k\x\ . Это связано с погрешностями измерений. В этом случае график надо проводить так, чтобы примерно одинаковое число точек, оказалось, по разные стороны от прямой. После построения графика возьмите точку на прямой (в средней части графика) определите по нему соответствующие этой точке значения силы упругости и удлинения, и вычислите жесткость k . Она и будет искомым средним значением жесткости пружины k ср.
1. Закрепите на штативе конец спиральной пружины (другой конец пружины снабжен стрелкой-указателем и крючком). 2. Рядом с пружиной или за ней установите и закрепите линейку с миллиметровыми делениями. 3. Отметьте и запишите то деление линейки, против которого приходится стрелка-указатель пружины. 4. Подвесьте к пружине груз известной массы и измерьте вызванное им удлинение пружины. 5. К первому грузу добавьте второй, третий и т. д. грузы, записывая каждый раз удлинение \ х\ пружины. По результатам измерений заполните таблицу ХОД РАБОТЫ:
2. Рядом с пружиной или за ней установите и закрепите линейку с миллиметровыми делениями. 3. Отметьте и запишите то деление линейки, против которого приходится стрелка-указатель пружины. 4. Подвесьте к пружине груз известной массы и измерьте вызванное им удлинение пружины. 5. К первому грузу добавьте второй, третий и т. д. грузы, записывая каждый раз удлинение \ х\ пружины. По результатам измерений заполните таблицу ХОД РАБОТЫ:
№ опыта m, кг mg, H х, м 1 0,1 2 0,2 3 0,3 4 0,4
6. Начертите оси координат х и F, выберите удобный масштаб и нанесите полученные экспериментальные точки. 7. Оцените (качественно) справедливость закона Гука для данной пружины: находятся ли экспериментальные точки вблизи одной прямой, проходящей через начало координат. 8. По результатам измерений постройте график зависимости силы упругости от удлинения и, пользуясь им, определите среднее значение жесткости пружины k ср. 9. Рассчитайте наибольшую относительную погрешность, с которой найдено значение k cp 10.
Контрольные вопросы: Как называется зависимость между силой упругости и удлинением пружины? Пружина динамометра под действием силы 4Н удлинилась на 5 мм. Определите вес груза, под действием которого эта пружина удлиняется на 16 мм.
Лабораторные работы по физике 9 класс Генденштейн Орлов Ход работы
1 — Закрепите конец пружины в штативе. Измерьте высоту на которой находится нижний конец пружины над столом.
2 — Подвесьте к пружине груз массой 100 грамм. Измерьте высоту, на которой находится теперь нижний конец пружины над столом. Вычислите удлинение пружины.
3 — Повторите измерения, подвешивая к пружине два, три и четыре грузы массой по 100 грамм.
4 — Запишите результаты в таблицу.
5 — Начертите систему координат для построения графика зависимости силы упругости от удлинения пружины.
7 — Определите, как зависит сила упругости от удлинения пружины.
Чем больше удлинение пружины, тем больше сила упругости, то есть чем длиннее растягивается пружина, тем больше сила упругости.
8 — По построенной прямой найдите жесткость пружины.
k = Fупр /|x|k = 4/0.1 = 40 H/m
9 — Определите, зависит ли жесткость пружины от ее длины, и если зависит, то как она изменяется при уменьшении длины пружины.
Жесткость пружины не зависит от удлинения длины пружины. У каждой пружины есть k(жесткость пружины) и она постоянна, не зависит от Fупр и от ΔxПо
физике
за 9 класс (И.К.Кикоин, А.К.Кикоин, 1999 год),
задача №2
к главе «ЛАБОРАТОРНЫЕ РАБОТЫ ».
Цель работы: найти жесткость пружины из измерений удлинения пружины при различных значениях силы тяжести
уравновешивающей силу упругости на основе закона Гука:
В каждом из опытов жесткость определяется при разных значениях силы упругости и удлинения, т. е. условия опыта меняются. Поэтому для нахождения среднего значения жесткости нельзя вычислить среднее арифметическое результатов измерений. Воспользуемся графическим способом нахождения среднего значения, который может быть применен в таких случаях.
Это связано с погрешностями измерения. В этом случае график надо проводить так, чтобы примерно одинаковое число точек оказалось по разные стороны от прямой. После построения графика возьмите точку на прямой (в средней части графика), определите по нему соответствующие этой точке значения силы упругости и удлинения и вычислите жесткость k. Она и будет искомым средним значением жесткости пружины k ср.
Результат измерения обычно записывается в виде выражения k = = k cp ±Δk, где Δk — наибольшая абсолютная погрешность измерения. Из курса алгебры (VII класс) известно, что относительная погрешность (ε k) равна отношению абсолютной погрешности Δk к значению величины k:
откуда Δk — ε k k. Существует правило для расчета относительной погрешности: если определяемая в опыте величина находится в результате умножения и деления приближенных величин, входящих в расчетную формулу, то относительные погрешности складываются. В данной работе
В данной работе
Средства измерения: 1) набор грузов, масса каждого равна m 0 = 0,100 кг, а погрешность Δm 0 = 0,002 кг; 2) линейка с миллиметровыми делениями.
Материалы: 1) штатив с муфтами и лапкой; 2) спиральная пружина.
Порядок выполнения работы
1. Закрепите на штативе конец спиральной пружины (другой конец пружины снабжен стрелкой-указате-лем и крючком — рис. 176).
2. Рядом с пружиной или за ней установите и закрепите линейку с миллиметровыми делениями.
3. Отметьте и запишите то деление линейки, против которого приходится стрелка-указатель пружины.
4. Подвесьте к пружине груз известной массы и измерьте вызванное им удлинение пружины.
5. К первому грузу добавьте второй, третий и т. д. грузы, записывая каждый раз удлинение |х| пружины. По результатам измерений заполните таблицу:
6. По результатам измерений постройте график зависимости силы упругости от удлинения и, пользуясь им, определите среднее значение жесткости пружины k cp .
7. Рассчитайте наибольшую относительную погрешность, с которой найдено значение k ср (из опыта с одним грузом). В формуле (1)
так как погрешность при измерении удлинения Δx=1 мм, то
8. Найдите
и запишите ответ в виде:
1 Принять g≈10 м/с 2 .
Закон Гука: «Сила упругости, возникающая при деформации тела, пропорциональна его удлинению и направлена противоположно направлению перемещения частиц тела при деформации».
Закон Гука
Жесткостью называют коэффициент пропорциональности между силой упругости и изменением длины пружины под действием приложенной к ней силы. Согласно третьему закону Ньютона, приложенная к пружине сила по модулю равна возникшей в ней силе упругости. Таким образом жесткость пружины можно выразить как:
где F — приложенная к пружине сила, а х — изменение длины пружины под ее действием. Средства измерения: набор грузов, масса каждого равна m 0 = (0,1±0,002) кг.
Линейка с миллиметровыми делениями (Δх = ±0,5 мм). Порядок выполнения работы описан в учебнике и комментариев не требует.
Порядок выполнения работы описан в учебнике и комментариев не требует.
масса, кг | удлинение |х|, | |||
1.1-01. Закон Гука. — Лабораторная экспериментальная площадка для школьников
В данной работе Вы изучите упругое растяжение нескольких пружин под действием силы тяжести. Проведёте серию экспериментов для нахождения коэффициента жёсткости этих пружин. В ходе эксперимента увидите влияние массы пружины на растяжение и как его можно учесть при проведении эксперимента. Дополнительным заданием будет определение коэффициента жёсткости системы пружин при параллельном и последовательном соединении.
Теоретический минимум: закон Гука, сила, сила упругости, сила тяжести, ускорение свободного падения, масса, коэффициент жёсткости, деформация, упругая деформация, неупругая деформация.
Лабораторная работа рекомендуется для учащихся 8, 9 классов.
Краткое методическое описание.
Цель работы:Познакомиться с законом Гука на примере деформации пружин. Определить жёсткость двух или более пружин, проверить линейную зависимость силы упругости от удлинения пружины. Научиться проводить измерения и обрабатывать экспериментальные данные.
Порядок выполнения лабораторной работы:Задание. Измерение жёсткости пружин №1 и №2.
- Закрепить пружину №1 на стержне с крючком и отметить на шкале с помощью курсора нижний край пружины.
- Подобрать начальную массу груза, и измерить его массу вместе с держателем для груза.
- Подвесить держатель с грузом на нижний край пружины.
- Отметить вторым курсором положение нижнего края пружины после её растяжения под действием силы тяжести.
- Определить растяжение пружины и внести измеренные величины в таблицу.
Таблица 1.  Экспериментальные данные.
Экспериментальные данные.№ m, г Fт, Н x0, мм x’, мм l, 10-3м … … … … … … - Добавить груз на держатель и повторить пункты 3-5. Провести измерения для 5 разных масс.
- Построить график зависимости силы от удлинения пружины.
- По графику определить жёсткость пружины.
- Оценить погрешность измерений и полученной величины.
- Закрепить пружину №2 и повторить пункты 1-9 для второй пружины.
Дополнительное задание. Параллельное и последовательное соединение пружин.
- Закрепить параллельно пружины №1 и №2 и повторить задание «Измерение жёсткости пружин №1 и №2» для параллельного соединения пружин.

- Закрепить последовательно пружины №1 и №2 и повторить задание «Измерение жёсткости пружин №1 и №2» для последовательно соединения пружин.
- Провести расчёт жёсткости систем при последовательном и параллельном соединении пружин и сравнить результаты с экспериментальными данными.
Метки: 8 класс, 9 класс
Лабораторная работа номер 2 измерение жесткости пружины. Измерение жесткости пружины
Урок 13/33
Тема. Лабораторная работа № 2 «Измерение жесткости пружины»
Цель урока: проверить справедливость закона Гука для пружины динамометра и измерить коэффициент жесткости этой пружины
Тип урока: контроля и оценивания знаний
Оборудование: штатив с муфтой и зажимом, динамометр с заклеенной шкалой, набор грузиков известной массы (по 100 г), линейка с миллиметровыми делениями
ХОД РАБОТЫ
1. Закрепите динамометр в штативе на достаточно большой высоте.
2. Подвешивая разное количество грузиков (от одного до четырех), вычислите для каждого случая соответствующее значение F
= mg
, а также измерьте соответствующее удлинение пружины х.
3. Результаты измерений и вычислений запишите в таблицу:
4. Начертите оси координат х и F , выберите удобный масштаб и нанесите полученные во время эксперимента точки.
6. Вычислите коэффициент жесткости по формуле k = F /x , используя результаты опыта № 4 (это обеспечивает наибольшую точность).
7. Для вычисления погрешности следует использовать опыт, который мы получили во время поведення опыта № 4, потому что ему соответствует наименьшая относительная погрешность измерений. Вычислите пределы Fmin и Fmax , в которых находится истинное значение F , считая, что Fmin = F — ΔF , F = F + ΔF . Примите ΔF = 4Δm · g , где Δm — погрешность во время изготовления грузиков (для оценки можно считать, что Δm = 0,005 кг):
где Δх = 0,5 мм.
8. Пользуясь методом оценки погрешности косвенных измерений, вычислите:
9. Вычислите среднее значение kcep и абсолютную погрешность измерения Δk по формулам:
10. Вычислите относительную погрешность измерений:
11. Заполните таблицу:
Заполните таблицу:
Fmin, H | Fmax, H | xmin, м | xmax, м | kmin, Н/м | kmax, Н/м | k сэр, Н/м | ||
12. Запишите в тетради для лабораторных работ результат в виде k = kcep ± Δk , подставив в эту формулу числовые значения найденных величин.
13. Запишите в тетради для лабораторных вывод: что вы измеряли и какой получили результат.
По
физике
за 9 класс (И.К.Кикоин, А.К.Кикоин, 1999 год),
задача №2
к главе «ЛАБОРАТОРНЫЕ РАБОТЫ ».
Цель работы: найти жесткость пружины из измерений удлинения пружины при различных значениях силы тяжести
уравновешивающей силу упругости на основе закона Гука:
В каждом из опытов жесткость определяется при разных значениях силы упругости и удлинения, т. е. условия опыта меняются. Поэтому для нахождения среднего значения жесткости нельзя вычислить среднее арифметическое результатов измерений. Воспользуемся графическим способом нахождения среднего значения, который может быть применен в таких случаях. По результатам нескольких опытов построим график зависимости модуля силы упругости F упр от модуля удлинения |x|. При построении графика по результатам опыта экспериментальные точки могут не оказаться на прямой, которая соответствует формуле
е. условия опыта меняются. Поэтому для нахождения среднего значения жесткости нельзя вычислить среднее арифметическое результатов измерений. Воспользуемся графическим способом нахождения среднего значения, который может быть применен в таких случаях. По результатам нескольких опытов построим график зависимости модуля силы упругости F упр от модуля удлинения |x|. При построении графика по результатам опыта экспериментальные точки могут не оказаться на прямой, которая соответствует формуле
Это связано с погрешностями измерения. В этом случае график надо проводить так, чтобы примерно одинаковое число точек оказалось по разные стороны от прямой. После построения графика возьмите точку на прямой (в средней части графика), определите по нему соответствующие этой точке значения силы упругости и удлинения и вычислите жесткость k. Она и будет искомым средним значением жесткости пружины k ср.
Результат измерения обычно записывается в виде выражения k = = k cp ±Δk, где Δk — наибольшая абсолютная погрешность измерения.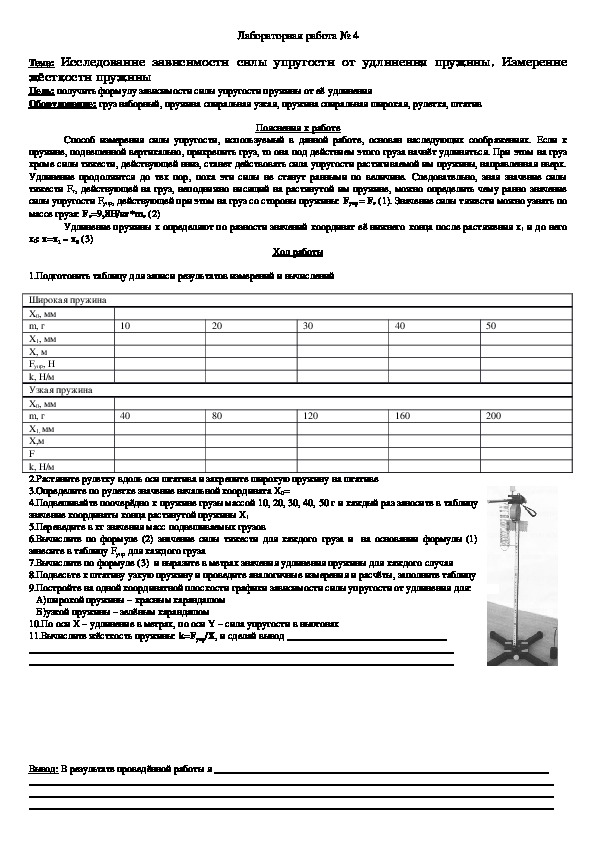 Из курса алгебры (VII класс) известно, что относительная погрешность (ε k) равна отношению абсолютной погрешности Δk к значению величины k:
Из курса алгебры (VII класс) известно, что относительная погрешность (ε k) равна отношению абсолютной погрешности Δk к значению величины k:
откуда Δk — ε k k. Существует правило для расчета относительной погрешности: если определяемая в опыте величина находится в результате умножения и деления приближенных величин, входящих в расчетную формулу, то относительные погрешности складываются. В данной работе
Средства измерения: 1) набор грузов, масса каждого равна m 0 = 0,100 кг, а погрешность Δm 0 = 0,002 кг; 2) линейка с миллиметровыми делениями.
Материалы: 1) штатив с муфтами и лапкой; 2) спиральная пружина.
Порядок выполнения работы
1. Закрепите на штативе конец спиральной пружины (другой конец пружины снабжен стрелкой-указате-лем и крючком — рис. 176).
2. Рядом с пружиной или за ней установите и закрепите линейку с миллиметровыми делениями.
3. Отметьте и запишите то деление линейки, против которого приходится стрелка-указатель пружины.
4. Подвесьте к пружине груз известной массы и измерьте вызванное им удлинение пружины.
Подвесьте к пружине груз известной массы и измерьте вызванное им удлинение пружины.
5. К первому грузу добавьте второй, третий и т. д. грузы, записывая каждый раз удлинение |х| пружины. По результатам измерений заполните таблицу:
6. По результатам измерений постройте график зависимости силы упругости от удлинения и, пользуясь им, определите среднее значение жесткости пружины k cp .
7. Рассчитайте наибольшую относительную погрешность, с которой найдено значение k ср (из опыта с одним грузом). В формуле (1)
так как погрешность при измерении удлинения Δx=1 мм, то
8. Найдите
и запишите ответ в виде:
1 Принять g≈10 м/с 2 .
Закон Гука: «Сила упругости, возникающая при деформации тела, пропорциональна его удлинению и направлена противоположно направлению перемещения частиц тела при деформации».
Закон Гука
Жесткостью называют коэффициент пропорциональности между силой упругости и изменением длины пружины под действием приложенной к ней силы. Согласно третьему закону Ньютона, приложенная к пружине сила по модулю равна возникшей в ней силе упругости. Таким образом жесткость пружины можно выразить как:
Согласно третьему закону Ньютона, приложенная к пружине сила по модулю равна возникшей в ней силе упругости. Таким образом жесткость пружины можно выразить как:
где F — приложенная к пружине сила, а х — изменение длины пружины под ее действием. Средства измерения: набор грузов, масса каждого равна m 0 = (0,1±0,002) кг.
Линейка с миллиметровыми делениями (Δх = ±0,5 мм). Порядок выполнения работы описан в учебнике и комментариев не требует.
масса, кг | удлинение |х|, | |||
цель работы: найти жесткость пружины из измерений удлинения пружины при различных значениях силы тяжести
уравновешивающей силу упругости на основе закона гука:
в каждом из опытов жесткость определяется при разных значениях силы упругости и удлинения, т. е. условия опыта меняются. поэтому для нахождения среднего значения жесткости нельзя вычислить среднее арифметическое результатов измерений. воспользуемся графическим способом нахождения среднего значения, который может быть применен в таких случаях. по результатам нескольких опытов построим график зависимости модуля силы упругости f упр от модуля удлинения |x|. при построении графика по результатам опыта экспериментальные точки могут не оказаться на прямой, которая соответствует формуле
воспользуемся графическим способом нахождения среднего значения, который может быть применен в таких случаях. по результатам нескольких опытов построим график зависимости модуля силы упругости f упр от модуля удлинения |x|. при построении графика по результатам опыта экспериментальные точки могут не оказаться на прямой, которая соответствует формуле
это связано с погрешностями измерения. в этом случае график надо проводить так, чтобы примерно одинаковое число точек оказалось по разные стороны от прямой. после построения графика возьмите точку на прямой (в средней части графика), определите по нему соответствующие этой точке значения силы упругости и удлинения и вычислите жесткость k. она и будет искомым средним значением жесткости пружины k ср.
результат измерения обычно записывается в виде выражения k = = k cp ±δk, где δk — наибольшая абсолютная погрешность измерения. из курса алгебры (vii класс) известно, что относительная погрешность (ε k) равна отношению абсолютной погрешности δk к значению величины k:
откуда δk — ε k k. существует правило для расчета относительной погрешности: если определяемая в опыте величина находится в результате умножения и деления приближенных величин, входящих в расчетную формулу, то относительные погрешности складываются. в данной работе
существует правило для расчета относительной погрешности: если определяемая в опыте величина находится в результате умножения и деления приближенных величин, входящих в расчетную формулу, то относительные погрешности складываются. в данной работе
поэтому
средства измерения: 1) набор грузов, масса каждого равна m 0 = 0,100 кг, а погрешность δm 0 = 0,002 кг; 2) линейка с миллиметровыми делениями.
материалы: 1) штатив с муфтами и лапкой; 2) спиральная пружина.
порядок выполнения работы
1. закрепите на штативе конец спиральной пружины (другой конец пружины снабжен стрелкой-указате-лем и крючком — рис. 176).
2. рядом с пружиной или за ней установите и закрепите линейку с миллиметровыми делениями.
3. отметьте и запишите то деление линейки, против которого приходится стрелка-указатель пружины.
4. подвесьте к пружине груз известной массы и измерьте вызванное им удлинение пружины.
5. к первому грузу добавьте второй, третий и т. д. грузы, записывая каждый раз удлинение |х| пружины. по результатам измерений заполните таблицу:
по результатам измерений заполните таблицу:
номер опыта | m, кг | mg 1 , н | |х|, м |
6. по результатам измерений постройте график зависимости силы упругости от удлинения и, пользуясь им, определите среднее значение жесткости пружины k cp .
7. рассчитайте наибольшую относительную погрешность, с которой найдено значение k ср (из опыта с одним грузом). в формуле (1)
так как погрешность при измерении удлинения δx=1 мм, то
8. найдите
и запишите ответ в виде:
1 принять g≈10 м/с 2 .
закон гука: «сила упругости, возникающая при деформации тела, пропорциональна его удлинению и направлена противоположно направлению перемещения частиц тела при деформации».
закон гука
жесткостью называют коэффициент пропорциональности между силой упругости и изменением длины пружины под действием приложенной к ней силы. согласно третьему закону ньютона, приложенная к пружине сила по модулю равна возникшей в ней силе упругости. таким образом жесткость пружины можно выразить как:
согласно третьему закону ньютона, приложенная к пружине сила по модулю равна возникшей в ней силе упругости. таким образом жесткость пружины можно выразить как:
где f — приложенная к пружине сила, а х — изменение длины пружины под ее действием. средства измерения: набор грузов, масса каждого равна m 0 = (0,1±0,002) кг.
линейка с миллиметровыми делениями (δх = ±0,5 мм). порядок выполнения работы описан в учебнике и комментариев не требует.
№ опыта | масса, кг | удлинение |х|, | к, н/м | |
м |
Лабораторная определение коэффициента жесткости пружины с решением. Лабораторная работа по физике «измерение жесткости пружины». III. Порядок выполнения работы
МОУ «Гимназия №6» Физический практикум 10 класс
Лабораторная работа №3
Измерение жесткости пружины
Цель работы : найти жесткость пружины из измерений удлинения пружины при различных значениях силы тяжести , уравновешивающей силу упругости
на основе закона Гука:
. В каждом из опытов жесткость определяется при разных значениях силы упругости и удлинения, т.е. условия опыта меняются. Поэтому для нахождения среднего значения жесткости нельзя вычислить среднее арифметическое результатов измерений. Воспользуемся графическим способом нахождения среднего значения, который может быть применен в таких случаях. По результатам нескольких опытов построим график зависимости модуля силы упругости
В каждом из опытов жесткость определяется при разных значениях силы упругости и удлинения, т.е. условия опыта меняются. Поэтому для нахождения среднего значения жесткости нельзя вычислить среднее арифметическое результатов измерений. Воспользуемся графическим способом нахождения среднего значения, который может быть применен в таких случаях. По результатам нескольких опытов построим график зависимости модуля силы упругости
от модуля удлинения х . При построении графика по результатам опыта экспериментальные точки могут не оказаться на прямой, которая соответствует формуле
. Это связано с погрешностями измерений. В этом случае график надо проводить так, чтобы примерно одинаковое число точек оказалось по разные стороны от прямой. После построения графика возьмите точку на прямой (в средней части графика), определите по нему соответствующие этой точке значения силы упругости и удлинения и вычислите жесткость k . Она и будет искомым средним значением жесткости пружины .
Результат измерения обычно записывается в виде выражения
, где
— наибольшая абсолютная погрешность измерения. Известно, что относительная погрешность () равна отношению абсолютной погрешности
к значению величины k :
, откуда
.
В данной работе
. Поэтому
, где
;
;
.
По
физике
за 9 класс (И.К.Кикоин, А.К.Кикоин, 1999 год),
задача №2
к главе «ЛАБОРАТОРНЫЕ РАБОТЫ ».
Цель работы: найти жесткость пружины из измерений удлинения пружины при различных значениях силы тяжести
уравновешивающей силу упругости на основе закона Гука:
В каждом из опытов жесткость определяется при разных значениях силы упругости и удлинения, т. е. условия опыта меняются. Поэтому для нахождения среднего значения жесткости нельзя вычислить среднее арифметическое результатов измерений. Воспользуемся графическим способом нахождения среднего значения, который может быть применен в таких случаях. По результатам нескольких опытов построим график зависимости модуля силы упругости F упр от модуля удлинения |x|. При построении графика по результатам опыта экспериментальные точки могут не оказаться на прямой, которая соответствует формуле
По результатам нескольких опытов построим график зависимости модуля силы упругости F упр от модуля удлинения |x|. При построении графика по результатам опыта экспериментальные точки могут не оказаться на прямой, которая соответствует формуле
Это связано с погрешностями измерения. В этом случае график надо проводить так, чтобы примерно одинаковое число точек оказалось по разные стороны от прямой. После построения графика возьмите точку на прямой (в средней части графика), определите по нему соответствующие этой точке значения силы упругости и удлинения и вычислите жесткость k. Она и будет искомым средним значением жесткости пружины k ср.
Результат измерения обычно записывается в виде выражения k = = k cp ±Δk, где Δk — наибольшая абсолютная погрешность измерения. Из курса алгебры (VII класс) известно, что относительная погрешность (ε k) равна отношению абсолютной погрешности Δk к значению величины k:
откуда Δk — ε k k. Существует правило для расчета относительной погрешности: если определяемая в опыте величина находится в результате умножения и деления приближенных величин, входящих в расчетную формулу, то относительные погрешности складываются. В данной работе
В данной работе
Средства измерения: 1) набор грузов, масса каждого равна m 0 = 0,100 кг, а погрешность Δm 0 = 0,002 кг; 2) линейка с миллиметровыми делениями.
Материалы: 1) штатив с муфтами и лапкой; 2) спиральная пружина.
Порядок выполнения работы
1. Закрепите на штативе конец спиральной пружины (другой конец пружины снабжен стрелкой-указате-лем и крючком — рис. 176).
2. Рядом с пружиной или за ней установите и закрепите линейку с миллиметровыми делениями.
3. Отметьте и запишите то деление линейки, против которого приходится стрелка-указатель пружины.
4. Подвесьте к пружине груз известной массы и измерьте вызванное им удлинение пружины.
5. К первому грузу добавьте второй, третий и т. д. грузы, записывая каждый раз удлинение |х| пружины. По результатам измерений заполните таблицу:
6. По результатам измерений постройте график зависимости силы упругости от удлинения и, пользуясь им, определите среднее значение жесткости пружины k cp .
7. Рассчитайте наибольшую относительную погрешность, с которой найдено значение k ср (из опыта с одним грузом). В формуле (1)
так как погрешность при измерении удлинения Δx=1 мм, то
8. Найдите
и запишите ответ в виде:
1 Принять g≈10 м/с 2 .
Закон Гука: «Сила упругости, возникающая при деформации тела, пропорциональна его удлинению и направлена противоположно направлению перемещения частиц тела при деформации».
Закон Гука
Жесткостью называют коэффициент пропорциональности между силой упругости и изменением длины пружины под действием приложенной к ней силы. Согласно третьему закону Ньютона, приложенная к пружине сила по модулю равна возникшей в ней силе упругости. Таким образом жесткость пружины можно выразить как:
где F — приложенная к пружине сила, а х — изменение длины пружины под ее действием. Средства измерения: набор грузов, масса каждого равна m 0 = (0,1±0,002) кг.
Линейка с миллиметровыми делениями (Δх = ±0,5 мм). Порядок выполнения работы описан в учебнике и комментариев не требует.
Порядок выполнения работы описан в учебнике и комментариев не требует.
масса, кг | удлинение |х|, | |||
Урок 13/33
Тема. Лабораторная работа № 2 «Измерение жесткости пружины»
Цель урока: проверить справедливость закона Гука для пружины динамометра и измерить коэффициент жесткости этой пружины
Тип урока: контроля и оценивания знаний
Оборудование: штатив с муфтой и зажимом, динамометр с заклеенной шкалой, набор грузиков известной массы (по 100 г), линейка с миллиметровыми делениями
ХОД РАБОТЫ
1. Закрепите динамометр в штативе на достаточно большой высоте.
2. Подвешивая разное количество грузиков (от одного до четырех), вычислите для каждого случая соответствующее значение F = mg , а также измерьте соответствующее удлинение пружины х.
3. Результаты измерений и вычислений запишите в таблицу:
4.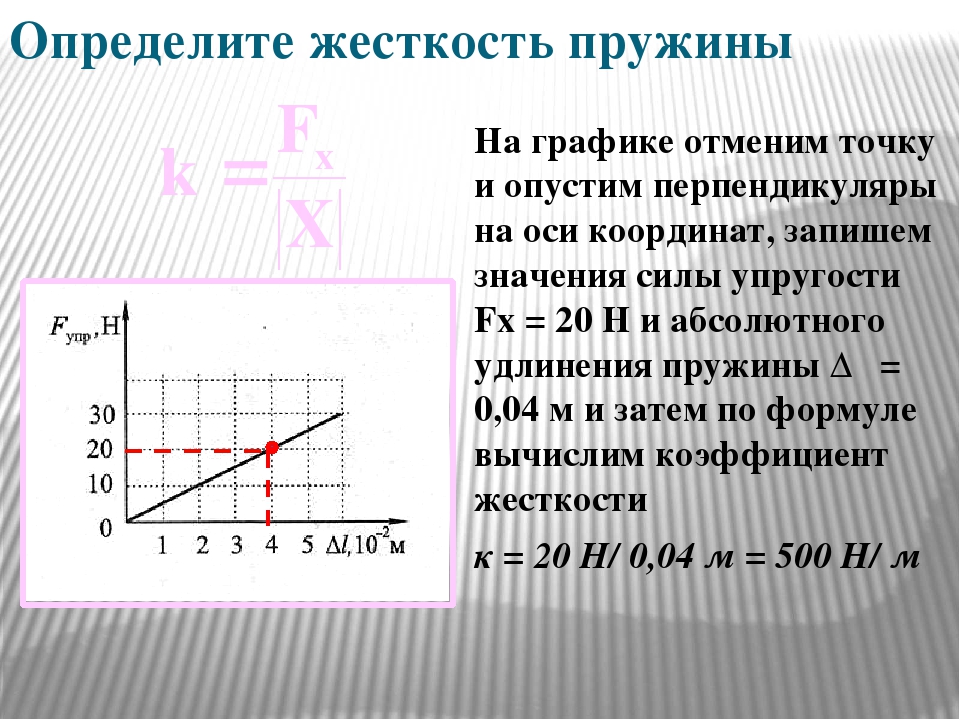 Начертите оси координат х и F
,
выберите удобный масштаб и нанесите полученные во время эксперимента точки.
Начертите оси координат х и F
,
выберите удобный масштаб и нанесите полученные во время эксперимента точки.
6. Вычислите коэффициент жесткости по формуле k = F /x , используя результаты опыта № 4 (это обеспечивает наибольшую точность).
7. Для вычисления погрешности следует использовать опыт, который мы получили во время поведення опыта № 4, потому что ему соответствует наименьшая относительная погрешность измерений. Вычислите пределы Fmin и Fmax , в которых находится истинное значение F , считая, что Fmin = F — ΔF , F = F + ΔF . Примите ΔF = 4Δm · g , где Δm — погрешность во время изготовления грузиков (для оценки можно считать, что Δm = 0,005 кг):
где Δх = 0,5 мм.
8. Пользуясь методом оценки погрешности косвенных измерений, вычислите:
9. Вычислите среднее значение kcep и абсолютную погрешность измерения Δk по формулам:
10. Вычислите относительную погрешность измерений:
11. Заполните таблицу:
Fmin, H | Fmax, H | xmin, м | xmax, м | kmin, Н/м | kmax, Н/м | k сэр, Н/м | ||
12. Запишите в тетради для лабораторных работ результат в виде k
= kcep
± Δk
, подставив в эту формулу числовые значения найденных величин.
Запишите в тетради для лабораторных работ результат в виде k
= kcep
± Δk
, подставив в эту формулу числовые значения найденных величин.
13. Запишите в тетради для лабораторных вывод: что вы измеряли и какой получили результат.
Лабораторная работа.
Определение коэффициента жесткости пружины.
Цель работы: используя экспериментальную зависимость силы упругости от абсолютного удлинения, вычислить коэффициент жёсткости пружины.
Оборудование: штатив, линейка, пружина, грузы массой по 100 г.
Теория. Под деформацией понимают изменение объема или формы тела под действием внешних сил. При изменении расстояния между частицами вещества (атомами, молекулами, ионами) изменяются силы взаимодействия между ними. При увеличении расстояния растут силы притяжения, а при уменьшении – силы отталкивания, которые стремятся вернуть тело в исходное состояния. Поэтому силы упругости имеют электромагнитную природу. Сила упругости всегда направлена к положению равновесия и стремится вернуть тело в исходное состояние. Сила упругости прямо пропорциональна абсолютному удлинению тела.
Сила упругости прямо пропорциональна абсолютному удлинению тела.
Закон Гука: Сила упругости, возникающая при деформации тела, прямо пропорциональна его удлинению (сжатию) и направлена противоположно перемещению частиц тела при деформации , F упр = кΔх , где k – коэффициент
жесткости [k] = Н/м, Δ х = Δ L – модуль удлинения тела.
Коэффициент жесткости зависит от формы и размеров тела,
а также от материала. Он численно равен силе упругости
при удлинении (сжатии) тела на 1 м.
Порядок выполнения работы.
1. Закрепить динамометр в штативе.
2. Измерить линейкой первоначальную длину пружины L 0 .
3 . Подвесить груз массой 100 г.
4. Измерить линейкой длину деформированной пружины L. Определить погрешность измерения длины: ΔƖ= 0,5дел*С 1 , где С 1 – цена деления линейки.
5. Вычислить удлинение пружины Δх = Δ L = L – L 0 .
6. На покоящийся относительно пружины груз действуют две компенсирующие друг друга силы: тяжести и упругости F т = F упр (смотри верхний рисунок )
7. Вычислить силу упругости по формуле , F упр = m g . Определить погрешность измерения силы: Δ F = 0,5дел*С 2 , где С 2 – цена деления динамометра.
8. Подвесить груз массой 200 г и повторить опыт по пунктам 4-6.
9. Подвесить груз массой 300 г и повторить опыт по пунктам 4-6.
10. Результаты занести в таблицу.
11. Вычислите коэффициент жесткости пружины для каждого измерения К= F упр / Δx и запишите в таблицу эти значения. Определите среднее значение К ср
12. Определите абсолютную погрешность измерения Δ к = ( Δ F / F упр + ΔƖ / L) * к измеренное , где Δ F – погрешность измерения силы, ΔƖ – погрешность измерения длины.
Определите абсолютную погрешность измерения Δ к = ( Δ F / F упр + ΔƖ / L) * к измеренное , где Δ F – погрешность измерения силы, ΔƖ – погрешность измерения длины.
13. Выбрать систему координат и построить график зависимости силы упругости F упр от удлинения пружины Δ L .
Таблица измерения
п/п
Начальная длина, L 0, м
Конечная длина, L , м
Абсолютное удлинение Δ x 1 =Δ L = L – L 0, м
Сила упругости, F упр, Н
Коэффициент жёсткости, К, Н/м
14. Сделайте вывод. Полученный в результате опытов коэффициент жесткости пружины можно записать: к = к ср измеренное (у каждого ученика свой коэффициент) ± Δ к (для всех разная погрешность).
Измерение жесткости пружины — презентация онлайн
1. Лабораторная работа «Измерение жесткости пружины»
2. Цель работы
проверить справедливость закона Гука дляпружины динамометра и измерить коэффициент
жесткости этой пружины.
Оборудование:
штатив с муфтой и зажимом, динамометр с
заклеенной шкалой, набор грузов известной массы
(по 100 г), линейка с миллиметровыми делениями.
Подготовительные вопросы
Что такое сила упругости?
Как вычислить силу упругости,
возникающую в пружине при подвешивании
к ней груза массой m кг?
Что такое удлинение тела?
Как измерить удлинение пружины при
подвешивании к ней груза?
В чем заключается закон Гука?
Правила техники безопасности
Будьте осторожны при работе с растянутой
пружиной.
Не роняйте и не бросайте грузы.
Описание работы:
Согласно закону Гука, модуль F силы упругости и
модуль х удлинения пружины связаны
соотношением F = kx.
 Измерив F и х, можно найти
Измерив F и х, можно найтикоэффициент жесткости k по формуле
В каждом из опытов жесткость определяется при разных значениях
силы упругости и удлинения, т. е. условия опыта меняются. Поэтому
для нахождения среднего значения жесткости нельзя вычислить
среднее арифметическое результатов измерений. Воспользуемся
графическим способом нахождения среднего значения, который
может быть применен в таких случаях. По результатам нескольких
опытов построим график зависимости модуля силы упругости Fупр от
модуля удлинения \х\. При построении графика по результатам опыта
экспериментальные точки могут не оказаться на прямой, которая
соответствует формуле Fyпp=k\x\. Это связано с погрешностями
измерений. В этом случае график надо проводить так, чтобы
примерно одинаковое число точек, оказалось, по разные стороны от
прямой. После построения графика возьмите точку на прямой (в
средней части графика) определите по нему соответствующие этой
точке значения силы упругости и удлинения, и вычислите
жесткость k.
 Она и будет искомым средним значением жесткости
Она и будет искомым средним значением жесткостипружины kср.
7. ХОД РАБОТЫ:
1. Закрепите на штативе конец спиральной пружины(другой конец пружины снабжен стрелкой-указателем и
крючком).
2. Шкалу динамометра закройте бумагой.
3. Отметьте деление, против которого находится стрелкауказатель пружины.
4. Подвесьте к пружине груз известной массы и измерьте
вызванное им удлинение пружины. Отметьте положение
стрелки-указателя динамометра.
5. К первому грузу добавьте второй, а затем третий грузы,
отмечая каждый раз положение стрелки-указателя и
записывая каждый раз удлинение \х\ пружины. По
результатам измерений заполните таблицу
6. Начертите оси координат х и F, выберите удобный
масштаб и нанесите полученные экспериментальные
точки.
7. Оцените (качественно) справедливость закона Гука для
данной пружины: находятся ли экспериментальные точки
вблизи одной прямой, проходящей через начало
координат.

8. По результатам измерений постройте график
зависимости силы упругости от удлинения и, пользуясь
им, определите среднее значение жесткости пружины kср.
9. Рассчитайте наибольшую относительную погрешность,
с которой найдено значение kcp
10. Запишите сделанный вами вывод.
№ опыта
1
m, кг
0,1
2
0,2
3
0,3
mg, H
х, м
Контрольные вопросы:
Как называется зависимость между силой
упругости и удлинением пружины?
Пружина динамометра под действием силы
4Н удлинилась на 5 мм. Определите вес
груза, под действием которого эта пружина
удлиняется на 16 мм.
Определение жёсткости пружины — Планы уроков — Каталог статей
Лабораторная работа № 4
Исследование зависимости удлинения стальной пружины от приложенной силы. Определение жёсткости пружины
Цель:
Самостоятельно поставьте цель лабораторной работы и запишите её в тетрадь для лабораторных работ.
Подумайте, зависимость каких величин вы должны получить в ходе этой лабораторной работы? Что вы определите в ходе работы?
Приборы и материалы:
Самостоятельно напишите необходимые вам приборы и материалы.
Штатив, динамометр, грузы 100 г, осциллограф, линейка, мензурка, термометр, тела неизвестной плотности, стакан с водой, секундомер, пружина неизвестной жёсткости.
Ход работы
Подготовите в тетради таблицу, которую вы будите заполнять по мере выполнения эксперимента.
Нарисовав таблицу не нужно сразу её заполнять, сначала запишите данные в черновик.
Кол-во грузов | Сила F, Н | Длина пружины ℓ, см | Удлинение x, см |
0 |
|
|
|
1 |
|
|
|
2 |
|
|
|
3 |
|
|
|
Произведите измерение необходимых величин.
Под силой понимается сила тяжести всех грузов. Вспомни формулу силы тяжести. Длина пружины измеряется линейкой. Удлинение это разница между начальной длиной и длиной в этом опыте. Обращайте внимание, если в шапке таблицы были указаны единицы измерения, то указывать рядом с величиной их повторно не надо.
Нарисуйте схему эксперимента.
Постройте график зависимости удлинения x от приложенной силы F.
Расчёты:
Запишите формулу для расчёта жёсткости, рассчитайте жёсткость.
Не забудьте перевести все единицы в систему СИ.
Вывод:
Сформулируйте и запишите вывод.
Что вы можете сказать о полученном графике? Получили ли вы входе работы жёсткость пружины? Какие трудности возникли у вас по ходу выполнения лабораторной работы? Что нового вы узнали на уроке? Где вам пригодятся полученные знания?
Критерии оценивания:
Лабораторная работа должна содержать заголовок (Номер и тему), цель работы, приборы и материалы, Ход работы и вывод.
Цель работы состоит из нескольких подцелей, которые не противоречат теме лабораторной работы.
Приборы и материалы должны содержать только необходимые и достаточные элементы для проведения лабораторной работы.
Ход работы должен содержать рисунок или схему эксперимента с показаниями прибора. При необходимости указываются расчёты. Все данные в таблицах и расчётах должны быть указаны разборчивым подчерком с указанием единиц измерения (в шапке таблицы или рядом с величиной).
Вывод — это краткий итог работы, в котором указываются полученные результаты, объяснения этих результатов, возможные причины ошибки если она есть, выдвинутые гипотезы.
Исследовательская лабораторная работа по физике
Лабораторная работа
«Определение жесткости пружины учебного динамометра»
2. 1 Цель работы: определить жесткость пружины учебного динамометра при различных значениях силы тяжести, уравновешивающей силу упругости на основе закона Гука Fупр=|k·Δx|
1 Цель работы: определить жесткость пружины учебного динамометра при различных значениях силы тяжести, уравновешивающей силу упругости на основе закона Гука Fупр=|k·Δx|
Просмотр содержимого документа
«Исследовательская лабораторная работа по физике»
Лабораторная работа
«Определение жесткости пружины учебного динамометра»
Правила техники безопасности
Долго не держать пружину в растянутом виде, т.к. может возникнуть остаточная деформация и пружина придет в негодность. Аккуратно обращаться с грузами. Не ронять!
1. Проверь себя
1.Приведите примеры упругих деформаций.
2. Сформулируйте закон Гука.
Сформулируйте закон Гука.
3.Всегда ли выполняется закон Гука? Ответ поясните.
4.Как направлена сила упругости?
5.Какая зависимость силы упругости от удлинения пружины?
2. Выполнение работы
2.1 Цель работы: определить жесткость пружины учебного динамометра при различных значениях силы тяжести, уравновешивающей силу упругости на основе закона Гука Fупр=|k·Δx|
2.2 План выполнения работы
Подвесьте к пружине динамометра груз и измерьте удлинение пружины Δх.
Найдите удлинение пружины под действием грузов 2m, 3m.
По результатам измерений постройте график зависимости силы упругости от удлинения (как практической работе № 2) и, пользуясь им, определите среднее значение жесткости пружины , используя kср = Fупр.
 / |х|
/ |х|
2.3 Необходимые средства измерения
Название прибора | Назначение прибора | Предел измерения | Цена деления |
2.4 Таблица результатов
Номер опыта | m, кг | mg, Н | |х|, м |
2. 5 Вычисления
5 Вычисления
2.6 Дополнительные задания.
По результатам измерений постройте график зависимости силы упругости от удлинения
Fупр.,Н
0 Δℓ, м
3.Вывод
4.Оцени свою работу
Самостоятельность выполнения работы (%) | Каков вклад в работу каждого члена вашей группы (%) | Оцени свою работу | Оценка учителя |
2 — Отчет лаборатории закона Гука и простого гармонического движения
Отчет лаборатории закона Гука и простого гармонического движения
Введение:
Эта лаборатория предназначена для того, чтобы мы могли определять жесткость пружины с помощью двух различных
методы и ускорение свободного падения с помощью маятника.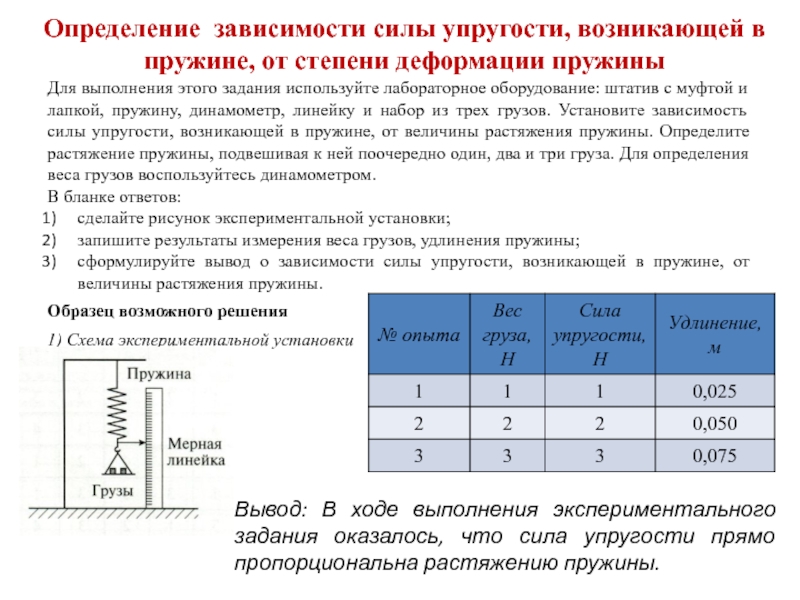 Постоянная пружины относится к тому, как
«Жесткая» пружина. Пружины эластичны, что означает, что при растяжении или сжатии они
могут вернуться в исходное состояние. Пружины, как правило, имеют более высокую жесткость пружины, и однажды
они деформированы, они являются прекрасным примером третьего закона движения Ньютона, утверждающего, что для
каждая сила имеет равную противоположную силу.Такое упругое поведение пружин можно объяснить
через закон Гука и формулу [1].
Постоянная пружины относится к тому, как
«Жесткая» пружина. Пружины эластичны, что означает, что при растяжении или сжатии они
могут вернуться в исходное состояние. Пружины, как правило, имеют более высокую жесткость пружины, и однажды
они деформированы, они являются прекрасным примером третьего закона движения Ньютона, утверждающего, что для
каждая сила имеет равную противоположную силу.Такое упругое поведение пружин можно объяснить
через закон Гука и формулу [1].
Цель:
В рамках эксперимента в первых двух частях мы определим жесткость пружины
Spring двумя разными способами. В третьей части эксперимента определим
ускорение свободного падения с помощью простого маятника.
Закон Гука помогает объяснить первые части этого эксперимента. Закон Гука гласит, что если
сила (F), прикладывается к противоположному концу закрепленного материала параллельно длине, затем в
Обычно материал либо сжимается, либо растягивается на расстояние (x).Связь этого
лучше всего можно объяснить с помощью уравнения:
F = -kx [1]
Где k сохраняется как постоянное. В этом эксперименте, поскольку в качестве материала будет использоваться пружина,
постоянную k будем называть постоянной пружины.
В этом эксперименте, поскольку в качестве материала будет использоваться пружина,
постоянную k будем называть постоянной пружины.
В третьей / последней части лаборатории мы должны определить ускорение свободного падения с помощью маятник. Согласно теории, общий период маятника может быть рассчитан через следующее уравнение
T = 2 π √ ℓ / г [2]
Где g — напряженность гравитационного поля (9.8) и ℓ будет длиной строки прикреплен к маятнику. Если масса боба никак не влияет на период маятника. Этим уравнением можно алгебраически манипулировать, чтобы иметь возможность получить ускорение свободного падения.
G = 4π 2 (ℓ / T) [3]
Процедура:
Начальная настройка
❏ Запустите компьютер и запустите программу Data Studio.
❏ Выберите «Открыть занятие». В папке механики откройте файл «Закон Гука».
❏ Осмотрите аппарат.Верхнее измерительное устройство является датчиком силы и будет
подключен к аналоговому входу A интерфейса Science Workshop. ❏ Нижний датчик является датчиком движения и подключается к цифровым входам 1 и 2,
с желтой вилкой, подключенной к входу 1.
❏ Подвесьте пружину за крюк на датчике силы.
❏ Нижний датчик является датчиком движения и подключается к цифровым входам 1 и 2,
с желтой вилкой, подключенной к входу 1.
❏ Подвесьте пружину за крюк на датчике силы.
❏ Подвесьте массовую подвеску на другом конце пружины.
Часть 1: Определение жесткости пружины
Калибровка датчиков
Сначала датчик силы
❏ Сбоку от датчика силы есть кнопка с надписью TARE.Нажмите эту кнопку; это будет ноль
датчик силы, тем самым сводя на нет силу, создаваемую пружиной и подвеской массы.
Теперь о датчике движения
❏ Щелкните кнопку запуска.
❏ Нажмите кнопку «Сохранить» пять раз, затем щелкните красное поле, чтобы остановить сбор данных.
❏ Найдите окно таблицы в нижней части дисплея. Среднее значение расстояния
от датчика до низа подвеса.
❏ Найдите панель данных в верхней левой части окна эксперимента. В рамках этого
pane — это имя переменной pos.Дважды щелкните по нему, чтобы открыть окно настройки.
❏ В нижней половине окна настройки находится заголовок экспериментальных констант. Ниже
В этом заголовке вы увидите переменную xstart и поле значения под ней. Введите среднее значение
значение, указанное в окне таблицы в этом поле.
❏ Нажмите нижнюю кнопку «Подтвердить», чтобы изменить предыдущее значение на новое, которое вы только что
вошел.
❏ Закройте окно настройки.
❏ В верхней строке меню в меню «Эксперимент» нажмите «Удалить последний запуск данных».
Получение первого набора данных: растягивание пружины
❏ Старайтесь свести к минимуму колебания массы.Хорошая техника для выполнения
это необходимо для поддержки нижней части подвески для массы одной рукой, когда вы добавляете массу
массовая вешалка. Затем медленно опустите опорную руку, чтобы подвес для грузов
постепенно опуститесь в исходное положение. Затем убери руку с дороги, прежде чем
взяв точку данных.
Прочтите весь этот шаг перед его выполнением.
❏ Изначально, когда на пружине подвешен только массодержатель, нажмите «Пуск». Контролировать
окно графика и обратите внимание на символ, который указывает, где должна быть точка данных
набор.
Ниже
В этом заголовке вы увидите переменную xstart и поле значения под ней. Введите среднее значение
значение, указанное в окне таблицы в этом поле.
❏ Нажмите нижнюю кнопку «Подтвердить», чтобы изменить предыдущее значение на новое, которое вы только что
вошел.
❏ Закройте окно настройки.
❏ В верхней строке меню в меню «Эксперимент» нажмите «Удалить последний запуск данных».
Получение первого набора данных: растягивание пружины
❏ Старайтесь свести к минимуму колебания массы.Хорошая техника для выполнения
это необходимо для поддержки нижней части подвески для массы одной рукой, когда вы добавляете массу
массовая вешалка. Затем медленно опустите опорную руку, чтобы подвес для грузов
постепенно опуститесь в исходное положение. Затем убери руку с дороги, прежде чем
взяв точку данных.
Прочтите весь этот шаг перед его выполнением.
❏ Изначально, когда на пружине подвешен только массодержатель, нажмите «Пуск». Контролировать
окно графика и обратите внимание на символ, который указывает, где должна быть точка данных
набор. В настоящее время он должен отскакивать от начала графика.
❏ Нажмите «Сохранить», чтобы получить точку данных. Не щелкайте красный квадрат, чтобы остановить данные.
❏ Осторожно добавить 100 грамм массы в вешалку для массы, чтобы она осела. Очень маленький
колебания ожидаемы и допустимы.
❏ Проверьте дисплей, чтобы увидеть, где находится символ, прежде чем нажимать кнопку «Сохранить», он должен быть
путь подобен показанному на рисунке 7-5. Не берите точку данных, если символ не горит
отслеживать. Если это так, очистите область вокруг датчика от других возможных целей.Опять же
не щелкайте красный квадрат, чтобы остановить сбор данных.
❏ Продолжайте сбор данных, добавляя к ним массу 100 грамм. Сохраняйте точку данных до десяти 100
граммовые массы на вешалке.
❏ Теперь нажмите красную кнопку.
Часть 2: Определите жесткость пружины, используя метод простого гармонического движения (SHM).
Начальная настройка
❏ Подвесьте груз весом 0,55 кг на пружине (подвеска массы плюс пять гирь по 100 грамм)
❏ В меню «Файл» выберите «Открыть действие» и откройте файл простого гармонического движения.
В настоящее время он должен отскакивать от начала графика.
❏ Нажмите «Сохранить», чтобы получить точку данных. Не щелкайте красный квадрат, чтобы остановить данные.
❏ Осторожно добавить 100 грамм массы в вешалку для массы, чтобы она осела. Очень маленький
колебания ожидаемы и допустимы.
❏ Проверьте дисплей, чтобы увидеть, где находится символ, прежде чем нажимать кнопку «Сохранить», он должен быть
путь подобен показанному на рисунке 7-5. Не берите точку данных, если символ не горит
отслеживать. Если это так, очистите область вокруг датчика от других возможных целей.Опять же
не щелкайте красный квадрат, чтобы остановить сбор данных.
❏ Продолжайте сбор данных, добавляя к ним массу 100 грамм. Сохраняйте точку данных до десяти 100
граммовые массы на вешалке.
❏ Теперь нажмите красную кнопку.
Часть 2: Определите жесткость пружины, используя метод простого гармонического движения (SHM).
Начальная настройка
❏ Подвесьте груз весом 0,55 кг на пружине (подвеска массы плюс пять гирь по 100 грамм)
❏ В меню «Файл» выберите «Открыть действие» и откройте файл простого гармонического движения. [
[
(N)
Часть 2:
- -2.840E-4.
- 6.000E-5.
- 1.092E-3 1.
- 3,424E-3 2.
- .016 3.
- .024 4.
- .034 5.
- .043 6.
- .051 7.
- .059 8.
- .067 9.
- .0192 -7.568E- Время (с) Положение (м)
.0356 -5.676E-
.0520 -3.612E-
.0685 -1.032E-
.0849 1.376E-
.1013 3.784E-
.1177 6.020E-
.1341 8.084 Е-
.1505 9.632E-
. 1669.
. 1833.
. 1997.
. 2161.
.2325 9.116E-
.2489 7.568E-
Часть 3:
Длина (см)
Общее время (сек)
т (общее время / 10) (сек)
T 2
50 14,85 1,485 2.
Часть 2:
Часть 3:
в Арлингтоне
● Маятник вычисляет значение ускорения свободного падения (g), используя принцип
кинематика простого гармонического движения простого маятника. — Международный
Бакалавриат по физике — Отмечено Teachers.com. (нет данных). Проверено 05 ноября,
2016 г., из http://www.markedbyteachers.com/international-baccalaureate/physics/
маятник-разработка-значение-ускорения-из-за-гравитации-g-с-использованием-принцип-из-
кинематика-простого-гармонического-движения-простого-маятника.html
● Робертс Д. (нет данных). Графики синуса и косинуса. Получено 7 ноября 2016 г. из
http://regentsprep.org/Regents/math/algtrig/ATT7/sinusoidal.htm
— Международный
Бакалавриат по физике — Отмечено Teachers.com. (нет данных). Проверено 05 ноября,
2016 г., из http://www.markedbyteachers.com/international-baccalaureate/physics/
маятник-разработка-значение-ускорения-из-за-гравитации-g-с-использованием-принцип-из-
кинематика-простого-гармонического-движения-простого-маятника.html
● Робертс Д. (нет данных). Графики синуса и косинуса. Получено 7 ноября 2016 г. из
http://regentsprep.org/Regents/math/algtrig/ATT7/sinusoidal.htm
Lab 7 — Простое гармоническое движение
Введение
Вы когда-нибудь задумывались, почему напольные часы показывают точное время? Движение маятника — это особый вид повторяющегося или периодического движения, называемого простым гармоническим движением , или SHM.Положение колеблющегося объекта изменяется синусоидально со временем. Многие объекты колеблются взад и вперед. Движение ребенка на качелях можно приблизительно представить как синусоидальное и, следовательно, рассматривать как простое гармоническое движение. Некоторые сложные движения, такие как турбулентные волны на воде, не считаются простым гармоническим движением. Когда объект находится в простом гармоническом движении, можно легко определить скорость, с которой он колеблется взад и вперед, а также его положение во времени.В этой лабораторной работе вы проанализируете простой маятник и систему пружина-масса, которые демонстрируют простое гармоническое движение.
Некоторые сложные движения, такие как турбулентные волны на воде, не считаются простым гармоническим движением. Когда объект находится в простом гармоническом движении, можно легко определить скорость, с которой он колеблется взад и вперед, а также его положение во времени.В этой лабораторной работе вы проанализируете простой маятник и систему пружина-масса, которые демонстрируют простое гармоническое движение.Обсуждение принципов
Частица, которая колеблется вертикально в простом гармоническом движении, перемещается вверх и вниз между двумя крайними точками y = ± A . Максимальное смещение A называется амплитудой . Это движение графически показано на графике зависимости положения от времени на рис.1.Рисунок 1 : График положения, показывающий синусоидальное движение объекта в SHM
Одно полное колебание или цикл или колебание — это движение, например, отy = −A
доy = + A
и обратно до y = −A.
1 Гц = 1 с −1 .
Если частица колеблется вдоль оси y , ее положение на оси y в любой заданный момент времени t , измеренное от начала колебания, определяется уравнением Напомним, что скорость объекта — это первая производная, а ускорение — вторая производная функции смещения по времени.Скорость v и ускорение a частицы в момент времени t задаются формулами(3)
v = 2 π fA cos (2 π фут)
(4)
a = — (2 π f) 2 [A sin (2 π футов)]
Обратите внимание, что скорость и ускорение также синусоидальны. Однако функция скорости имеет разность фаз 90 ° или π /2, а функция ускорения имеет разность фаз 180 ° или π относительно функции смещения.Например, когда смещение является положительным максимумом, скорость равна нулю, а ускорение — отрицательному максимуму. Подставляя из уравнения. (1)
Однако функция скорости имеет разность фаз 90 ° или π /2, а функция ускорения имеет разность фаз 180 ° или π относительно функции смещения.Например, когда смещение является положительным максимумом, скорость равна нулю, а ускорение — отрицательному максимуму. Подставляя из уравнения. (1)f = 1 / T
в уравнение. (4)a = — (2 π f) 2 [A sin (2 π ft)]
дает Из уравнения. (5)a = −4 π 2 f 2 y
мы видим, что ускорение объекта в SHM пропорционально смещению и противоположно по знаку. Это основное свойство любого объекта, совершающего простое гармоническое движение.Рассмотрим несколько критических точек в цикле, как в случае колебательной системы пружина-масса. Система пружина-масса состоит из массы, прикрепленной к концу пружины, подвешенной к стойке. Груз слегка опускается и отпускается, чтобы пружина и груз колебались в вертикальной плоскости. На рисунке 2 показаны пять критических точек, когда масса на пружине проходит полный цикл. Положение равновесия для системы пружина-масса — это положение массы, когда пружина не растягивается и не сжимается.
Положение равновесия для системы пружина-масса — это положение массы, когда пружина не растягивается и не сжимается.Рисунок 2 : Пять ключевых точек массы, колеблющейся на пружине.
Масса завершает полный цикл, перемещаясь из положения A в положение E. Описание каждой позиции следующее:- Положение A: пружина сжата; масса выше точки равновесия при
y =
A и вот-вот будет выпущена. - Положение B: Масса движется вниз, когда проходит через точку равновесия.
- Положение C: Масса на мгновение находится в состоянии покоя в самой нижней точке перед тем, как начать движение вверх.
- Положение D: Масса движется вверх, проходя через точку равновесия.
- Положение E: гиря на мгновение находится в состоянии покоя в наивысшей точке, прежде чем снова начать движение вниз.
 Это сделано для системы колеблющейся пружины и массы в таблице ниже, а три функции показаны на рис. 3. Обратите внимание, что положительное направление обычно выбирается как направление, в котором пружина растягивается. Следовательно, положительное направление в этом случае — вниз, и исходное положение A, на фиг. 2 фактически является отрицательным значением. Самый сложный параметр для анализа — это ускорение. Это помогает использовать второй закон Ньютона, который говорит нам, что отрицательное максимальное ускорение происходит, когда результирующая сила равна отрицательному максимуму, положительное максимальное ускорение происходит, когда результирующая сила равна положительному максимуму, и ускорение равно нулю, когда результирующая сила равна нулю.
Это сделано для системы колеблющейся пружины и массы в таблице ниже, а три функции показаны на рис. 3. Обратите внимание, что положительное направление обычно выбирается как направление, в котором пружина растягивается. Следовательно, положительное направление в этом случае — вниз, и исходное положение A, на фиг. 2 фактически является отрицательным значением. Самый сложный параметр для анализа — это ускорение. Это помогает использовать второй закон Ньютона, который говорит нам, что отрицательное максимальное ускорение происходит, когда результирующая сила равна отрицательному максимуму, положительное максимальное ускорение происходит, когда результирующая сила равна положительному максимуму, и ускорение равно нулю, когда результирующая сила равна нулю.| Положение | Скорость | Ускорение | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Точка A | отриц. Макс. | ноль | макс. Полож. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Точка B | макс. C C | макс. | ноль | макс. Отриц. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Точка D | ноль | макс. Отриц. | ноль | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Точка E | отриц. Макс. | макс. Ноль | Рисунок 3 : Положение, скорость и ускорение в зависимости отвремя Для этого конкретного начального условия (начальная позиция в точке A на рис.2) кривая положения является функцией косинуса (фактически отрицательной функцией косинуса), кривая скорости является функцией синуса, а кривая ускорения является просто отрицательной функцией положения изгиб.Масса и пружинаГруз, подвешенный на конце пружины, растянет ее на некоторое расстояние х . Сила, с которой пружина тянет вверх груз, определяется формулой Hooke ‘ s law где k — жесткость пружины, а y — растяжение пружины, когда к пружине прикладывается сила F . Константа пружины k является мерой жесткости пружины. Жесткость пружины можно определить экспериментально, позволив грузу неподвижно висеть на пружине, а затем добавив дополнительную массу и записав дополнительное растяжение пружины, как показано ниже. На рис. 4а подвеска груза подвешена к концу пружины. На рис. 4b к подвеске добавлена дополнительная масса, и теперь пружина выдвигается на величину Константа пружины k является мерой жесткости пружины. Жесткость пружины можно определить экспериментально, позволив грузу неподвижно висеть на пружине, а затем добавив дополнительную массу и записав дополнительное растяжение пружины, как показано ниже. На рис. 4а подвеска груза подвешена к концу пружины. На рис. 4b к подвеске добавлена дополнительная масса, и теперь пружина выдвигается на величинуΔy . Эта экспериментальная установка также показана на фотографии установки на рис.5.Рисунок 4 : Настройка для определения жесткости пружины Рисунок 5 : Фотография установки для определения жесткости пружины Когда масса неподвижна, ее ускорение равно нулю. Следовательно, согласно второму закону Ньютона результирующая сила должна быть равна нулю. На массу действуют две силы; сила тяжести, направленная вниз, и сила пружины, направленная вверх. См. Диаграмму свободного тела на рис.6 ниже. См. Диаграмму свободного тела на рис.6 ниже.Рисунок 6 : Схема свободного тела для системы пружина-масса Итак, второй закон Ньютона дает нам гдеΔm — изменение массы, аΔy — изменение растяжения пружины, вызванное изменением массы, g — ускорение свободного падения, а k — жесткость пружины. Уравнение (7)Δmg — kΔy = 0 также можно выразить как Второй закон Ньютона, примененный к этой системе, равенma = F = −ky. Заменить из ур. (5)a = −4 π 2 f 2 y , чтобы получить ускорение(9) м (−4 π 2 f 2 y) = −ky откуда получаем выражение для частоты f и периода T .(10) f =(11) Т = 2 π (11) T = 2 π (11) T = 2 π T 2 от м будет прямой, и жесткость пружины может быть определена по наклону.Простой маятникДругой пример простого гармонического движения, который вы исследуете, — это простой маятник . Простой маятник состоит из массы м , называемой бобом маятника, прикрепленной к концу струны. Длина L простого маятника измеряется от точки подвешивания струны до центра боба, как показано на Рис. 7 ниже. Длина L простого маятника измеряется от точки подвешивания струны до центра боба, как показано на Рис. 7 ниже.Рисунок 7 : Экспериментальная установка для простого маятника Если боб перемещен из положения покоя на некоторый угол смещения θ , как показано на рис. 7, возвращающая сила вернет боб обратно в положение равновесия. Силы, действующие на боб, — это сила тяжести и сила натяжения струны.Сила натяжения струны уравновешивается составляющей силы тяжести, которая находится на одной линии со струной (т.е. перпендикулярна движению боба). Возвратной силой здесь является тангенциальная составляющая гравитационной силы.Рисунок 8 : Простой маятник Когда мы применяем тригонометрию к меньшему треугольнику на рис. 8, мы получаем величину возвращающей силы | F | = мг sin θ . Эта сила зависит от массы боба, ускорения свободного падения g и синуса угла, на который натянута струна. Снова должен применяться второй закон Ньютона, поэтому Снова должен применяться второй закон Ньютона, поэтому(13) ма = F = −mg sin θ где отрицательный знак означает, что возвращающая сила действует противоположно направлению движения боба. Поскольку боб движется по дуге окружности, угловое ускорение определяется какα = a / L. Из уравнения. (13)ma = F = −mg sin θ получаем На рис. 9 синяя сплошная линия представляет собой график зависимости θ от sin ( θ ), а прямая линия представляет собой график θ в градусах по сравнению с θ в радианах.Для малых углов эти две кривые почти неразличимы. Следовательно, пока смещение θ мало, мы можем использовать приближение sin θ ≅ θ .Рисунок 9 : Графики sin θ в сравнении с θ В этом приближении уравнение. (14) становится Уравнение (15) показывает, что (угловое) ускорение пропорционально отрицательному значению (углового) смещения, и, следовательно, движение боба является простым гармоническим, и мы можем применить уравнение. (5) (5)a = −4 π 2 f 2 y , чтобы получить Комбинируя уравнение. (15) и уравнение. (16)α = −4 π 2 f 2 θ , и, упрощая, получаем(17) f =(18) Т = 2 πЦельЦель этой лабораторной работы — понять поведение объектов в простом гармоническом движении путем определения жесткости пружины системы пружина-масса и простого маятника.Оборудование
ПроцедураИспользуя закон Гука, вы определите жесткость пружины, измерив ее растяжение по мере того, как к пружине добавляются дополнительные массы. Вы определите период колебаний системы пружина-масса для разных масс и используете его для определения жесткости пружины. Затем вы сравните значения жесткости пружины, полученные двумя способами. В случае простого маятника вы измеряете период колебаний для различной длины струны маятника и сравниваете эти значения с предсказанными значениями периода. Вы определите период колебаний системы пружина-масса для разных масс и используете его для определения жесткости пружины. Затем вы сравните значения жесткости пружины, полученные двумя способами. В случае простого маятника вы измеряете период колебаний для различной длины струны маятника и сравниваете эти значения с предсказанными значениями периода.Процедура A: Определение постоянной пружины с использованием закона Гука
КПП 1: Процедура B: Определение жесткости пружины изT 2 по сравнению с м График Мы предположили, что пружина безмассовая, но у нее есть некоторая масса, которая влияет на период колебаний.Теория предсказывает, а опыт подтверждает, что если одна треть массы пружины была добавлена к массе м в формуле. (11) T = 2 π
КПП 2: Процедура C: Простой маятник
КПП 3: Авторские права © 2010 Advanced Instructional Systems, Inc. Dynamics — эксперимент по закону ГукаDynamics — эксперимент по закону ГукаНазначение:
Обсуждение:Всем известно, что когда вы прикладываете силу к пружине или резинка, она тянется.Ученый спросит: «Как сила что вы применяете в отношении степени растяжки? »Этот вопрос был ответил Роберт Гук, современник Ньютона, и ответ стал называться законом Гука. Закон Гука, хотите верьте, хотите нет, но очень важный и широко используемый закон в физике и технике. Его приложения идут далеко помимо пружин и резинок. Вы можете исследовать закон Гука, измерив, сколько известных сил
растянуть пружину.Удобный способ применения точно известной силы
— позволить весу известной массы быть силой, используемой для растяжения
весна. Оснащение:
Указания по безопасности:
Процедура:
Результатов:
Выводы:Закон Гука гласит, что растяжение пружины прямо пропорционально приложенной силе. (Инженеры говорят: «Стресс — это пропорционально деформации ». В символах F = kx, где F — сила, x — растяжение, а k — постоянная пропорциональности. Если Гука Закон верен, тогда график зависимости силы от растяжения будет прямая линия. Подтверждают ли ваши результаты закон Гука или противоречат ему? Пожалуйста
разрабатывать. Вопросы:Осмотрите пружинные весы. Это простое устройство для измерения силы измеряя величину, на которую сила растягивает пружину.
адаптировано из Робинсона, Лаборатория концептуальной физики Руководство , Addison-Wesley, Experiment 15, Tug-of-War последнее обновление 6 ноября 2002 г., автор: JL Stanbrough Весна прочь! — Деятельность — TeachEngineeringБыстрый просмотрУровень оценки: 8 (7-9) Требуемое время: 45 минут Расходные материалы на группу: 1 доллар США.00 Для этого занятия также требуется набор лабораторного оборудования длительного пользования (многоразового использования), часть которого уже может быть доступна в вашей лаборатории; ориентировочно 206 долларов на группу — или — использовать один комплект оборудования со всем классом и заставить все группы работать с одними и теми же данными; подробности см. в Списке материалов. Размер группы: 3 Зависимость действий: Тематические области: Алгебра Подпишитесь на нашу рассылку новостейРезюмеЭта лаборатория демонстрирует закон Гука с использованием пружин и масс.Учащиеся пытаются определить константу пропорциональности или значение k для пружины. Они делают это, вычисляя изменение длины пружины при добавлении к ней различных масс. Также вводится понятие предела упругости пружины, и студенты проверяют, не был ли предел упругости пружины достигнут во время лабораторных испытаний. После сбора данных они находят среднее значение коэффициента k пружины, измеряя наклоны между каждой из своих точек данных. Затем они применяют то, что узнали о пружинах, к тому, как инженеры могут использовать эти знания при разработке игрушек, которые позволяют детям прыгать в воздухе на 2-3 фута. Инженерное соединениеКонцепция закона Гука относится ко многим интересным приложениям в машиностроении и технике безопасности. В этом упражнении учащимся предлагается подумать о типе игрушки, которую они узнали, и к которой может иметь отношение закон Гука. Пого-палка приходит на ум из-за пружины. Инженеры должны учитывать вес пользователя и жесткость пружины, чтобы создать максимально безопасный отскок. Цели обученияПосле этого занятия студенты должны уметь:
Образовательные стандарты Каждый урок или задание TeachEngineering соотносится с одной или несколькими науками K-12,
образовательные стандарты технологии, инженерии или математики (STEM). Все 100000+ стандартов K-12 STEM, охватываемых TeachEngineering , собираются, обслуживаются и упаковываются Сетью стандартов достижений (ASN) , проект D2L (www.achievementstandards.org). В ASN стандарты имеют иерархическую структуру: сначала по источникам; например , по штатам; внутри источника по типу; например , естественные науки или математика; внутри типа по подтипу, затем по классу, и т. д. . Общие основные государственные стандарты — математика
Какое альтернативное выравнивание вы предлагаете для этого контента? Список материаловКаждой группе необходимо:
Эти материалы доступны на веб-сайте PASCO в разделе физики средней школы в рамках простой установки гармонического движения. Примечание. Если недостаточно комплектов оборудования для групп из двух или трех учеников в каждой, разделите класс на несколько групп, которые соответствуют количеству имеющихся комплектов оборудования. Если доступен только один комплект оборудования, попросите учащихся по очереди проводить измерения, а затем попросите всех собрать и вычислить k-значения, используя одни и те же данные. Поделиться со всем классом:
Больше подобной программыЗакон напряжений, деформаций и Гука Студенты знакомятся с законом Гука, а также с отношениями стресс-напряжение.В ходе занятия, состоящего из двух частей, учащиеся: 1) изучают закон Гука путем экспериментального определения неизвестной жесткости пружины, а затем 2) применяют полученные знания для создания графика деформации, изображающего опухоль . Студенты используют оборудование для сбора данных, чтобы узнать о силе и смещении в отношении простых и сложных машин.Взаимосвязь между силой, приложенной к материалу, и ее результирующим смещением является отличительным свойством материала, которое измеряется для оценки материала … Упругая потенциальная энергия пружин — это велико! Учащиеся исследуют потенциальную энергию, содержащуюся в пружинах (упругую потенциальную энергию), в рамках этапа исследования и проверки.Урок включает в себя сухую лабораторию, в которой используются пого-палки для закрепления концепций потенциальной энергии пружины, кинетической энергии и гравитационной энергии, а также сохранения . Студенты изучают закон Гука, работая в небольших группах на своих лабораторных скамьях.Они собирают данные о смещении пружин с неизвестной константой пружины k путем добавления различных масс известного веса. Предварительные знанияУмело найти наклон линии. Введение / Мотивация В этом модуле мы узнали все о линейных функциях, в том числе о важных характеристиках, а также о том, как построить их график в различных формах.Вспомните нашу главную задачу, в которой мы пытаемся найти оптимальное уравнение, соответствующее данным исследовательской лаборатории. Мы можем вычислить постоянную упругой пружины пружины, добавив подвесные массы к концу пружины и измерив изменение длины пружины. Затем мы исследуем возможности инженерных приложений с инженерами-механиками, используя закон Гука для создания забавных и безопасных игрушек. ПроцедураДо начала деятельности Подготовьте настройку занятия, следуя этим инструкциям:
Со студентами
ОценкаВстроенная оценка деятельности
Оценка после операции
Примечание. Если учащиеся испытывают трудности, научите их думать о пого-палке (F = k x), поэтому чем больше сила, тем больше будет изменение длины пружины. Авторские права© 2013 Регенты Университета Колорадо; оригинал © 2007 Университет ВандербильтаАвторыОбри МаккелвиПрограмма поддержкиVU Bioengineering RET Program, Школа инженерии, Университет ВандербильтаБлагодарностиСодержание этой учебной программы по цифровой библиотеке было разработано в рамках грантов №№ RET Национального научного фонда.0338092 и 0742871. Однако это содержание не обязательно отражает политику NSF, и вам не следует предполагать, что оно одобрено федеральным правительством. Последнее изменение: 23 января 2021 г. Лабораторное определение коэффициента жесткости пружины с помощью раствора. Лабораторная работа по физике «Измерение жесткости пружины». III. Заказ на работуМОУ «Гимназия №6» Физическая мастерская 10 класс Лабораторная работа №1. Измерение жесткости пружины Цель : найти жесткость пружины по измерениям удлинения пружины при различных значениях силы тяжести, уравновешивающей силу упругости Результат измерения обычно записывается в виде выражения В той работе Физика для 9 класса (И.К. Кикоин, А.К. Кикоин, 1999), Цель работы: найти жесткость пружины по измерениям удлинения пружины при различных значениях силы тяжести. Уравновешивающая сила упругости по закону Гука: В каждом из экспериментов жесткость равна определяется при разных значениях силы упругости и удлинения, т. Это связано с ошибками измерения.В этом случае график нужно нарисовать так, чтобы примерно одинаковое количество точек находилось по разные стороны от прямой. После построения графика возьмите точку на прямой (в середине графика), определите по ней значения силы упругости и удлинения, соответствующие этой точке, и вычислите жесткость k. Это будет желаемое среднее значение жесткости пружины k ср. Результат измерения обычно записывают в виде выражения k = = k cp ± Δk, где Δk — наибольшая абсолютная погрешность измерения. , откуда Δk — ε k k. Существует правило расчета относительной погрешности: если значение, определенное в эксперименте, является результатом умножения и деления приблизительных значений, включенных в формулу расчета, то относительные погрешности складываются. В работе Средства измерения: 1) набор гирь, масса каждой равна m 0 = 0.100 кг, а погрешность Δm 0 = 0,002 кг; 2) линейка с миллиметровыми делениями. Материалы: 1) тренога с муфтами и ножкой; 2) спиральная пружина. Заказ на работу 1. Закрепите конец винтовой пружины на штативе (другой конец пружины снабжен стрелкой и крючком — рис. 176). 2. Поместите и закрепите линейку с миллиметровыми отметками рядом с пружиной или позади нее. 3. Отметьте и запишите деление линейки, на которое указывает стрелка-указатель пружины. 4. Подвесьте известную массу на пружине и измерьте полученное удлинение пружины. 5. Добавьте второй, третий и т. Д. Грузики к первому грузику, каждый раз записывая удлинение | х | пружины. По результатам измерений заполните таблицу: 6. По результатам измерений построить график зависимости силы упругости от удлинения и по нему определить среднее значение жесткости пружины k cp. 7. Вычислите наибольшую относительную погрешность, с которой находится значение k av (из эксперимента с одной нагрузкой).В формуле (1) так как погрешность измерения удлинения Δx = 1 мм, то 8. Найдите и запишите ответ в виде: 1 Возьмем g≈10 м / с 2 Закон Гука: «Сила упругости, возникающая при деформации тела, пропорциональна его удлинению и направлена противоположно направлению движения частиц тела во время деформации». Закон Гука Жесткость — это коэффициент пропорциональности между силой упругости и изменением длины пружины под действием приложенной к ней силы.Согласно третьему закону Ньютона сила, приложенная к пружине, равна по модулю упругой силе, возникшей в ней. , где F — сила, приложенная к пружине, а x — изменение длины пружины под ее действием. Измерительные приборы: набор гирь, масса каждой m 0 = (0,1 ± 0,002) кг. Линейка с миллиметровыми делениями (Δх = ± 0,5 мм). Порядок работы описан в учебнике и не требует комментариев.
Урок 13/33 Тема. Лабораторная работа № 2 «Измерение жесткости пружины» Цель занятия: проверить справедливость закона Гука для пружины динамометра и измерить коэффициент жесткости этой пружины Тип урока: контроль и оценка знаний Оборудование: штатив с гильзой и зажимом, динамометр с пломбированной шкалой, набор гирь известной массы (по 100 г), линейка с делениями миллиметра ПРОГРЕСС 1. 2. Подвесив разное количество грузов (от одного до четырех), рассчитайте для каждого случая соответствующее значение F = мг, а также измерьте соответствующее удлинение пружины x. 3. Запишите результаты измерений и расчетов в таблицу: 4. Нарисуйте оси x и F, выберите удобный масштаб и нанесите точки, полученные в ходе эксперимента. 6. Рассчитайте коэффициент жесткости по формуле k = F / x, используя результаты эксперимента № .4 (это обеспечивает наибольшую точность). 7. Для расчета погрешности следует использовать опыт, полученный нами при ведении эксперимента № 4, так как он соответствует наименьшей относительной ошибке измерения. Вычислить пределы Fmin и Fmax, в которых находится истинное значение F, полагая, что Fmin = F — ΔF, F = F + ΔF. Возьмем ΔF = 4Δm · г, где Δm — погрешность при изготовлении гирь (для прикидки можно считать, что Δm = 0,005 кг): где Δх = 0. 8. Используя метод оценки погрешности косвенных измерений, вычислить: 9. Рассчитайте среднее значение kcep и абсолютную погрешность измерения Δk по формулам: 10. Рассчитайте относительную погрешность измерения: 11. Заполните таблицу:
12.Запишите в тетрадь для лабораторных работ результат в виде k = kcep ± Δk, подставив числовые значения найденных величин в эту формулу. 13. Запишите в блокнот для лабораторных выводов: что вы измерили и какой результат получили. Лабораторная работа. Определение коэффициента жесткости пружины. Цель: Используя экспериментальную зависимость силы упругости от абсолютного удлинения, рассчитайте коэффициент жесткости пружины. Оснащение: штатив, линейка, пружина, гири весом по 100 гр. Теория. Под деформацией понимается изменение объема или формы тела под действием внешних сил. Когда расстояние между частицами вещества (атомами, молекулами, ионами) изменяется, силы взаимодействия между ними изменяются. С увеличением расстояния силы притяжения растут, а с уменьшением — силы отталкивания, которые стремятся вернуть тело в исходное состояние.Следовательно, упругие силы имеют электромагнитную природу. Сила упругости всегда направлена к положению равновесия и стремится вернуть тело в исходное состояние. Сила упругости прямо пропорциональна абсолютному удлинению тела. Закон Гука: Сила упругости, возникающая при деформации тела, прямо пропорциональна его удлинению (сжатию) и направлена противоположно движению частиц тела при деформации , Ф контроль = кΔх , где k — коэффициент жесткости [k] = Н / м, Δ х = Δ L — модуль удлинения тела. Коэффициент жесткости зависит от формы и размера корпуса, , а также от материала. Численно она равна силе упругости при удлинении (сжатии) тела на 1 м. Порядок работы. 1. Закрепите динамометр на штативе. 2. Измерьте исходную длину пружины линейкой L 0 . 3 … Подвешиваем груз 100 гр. 4. Измерьте длину деформированной пружины линейкой L. Определите погрешность измерения длины: ΔƖ = 0,5 дел * C 1 , г. Где ОТ 1 — цена деления линейки. 5. Рассчитать удлинение пружины Δх = Δ L = L — L 0 . 6. На вес, покоящийся относительно пружины, действуют две компенсирующие друг друга силы: сила тяжести и упругость F т = Ф контроль (см. 7. Рассчитайте силу упругости по формуле, Ф контроль = кв.м. г . Определить погрешность измерения силы: Δ Ф = 0.5 дел * C 2 , г. Где ОТ 2 — цена деления динамометра. 8. Подвесьте груз весом 200 г и повторите эксперимент в точках 4-6. 9. Подвесьте гирю 300 г и повторите эксперимент в точках 4-6. 10. Введите результаты в таблицу. 11. Рассчитайте коэффициент жесткости пружины для каждого измерения К = Ф контроль / Δx и запишите эти значения в таблицу.Определить среднее значение от ДО ср 12. Определите абсолютную погрешность измерения Δ к = ( Δ Ф / Ф контроль + ΔƖ / л) * С по измерено , г. 13. Выберите систему координат и постройте график зависимости упругой силы F контроль от растяжения пружины Δ L . Таблица размеров p / p Начальная длина, L 0, м Длина торца, L, м Абсолютное удлинение Δx 1 = Δ L = L — L 0, м Прочность упругости, F контроль, H Коэффициент жесткости, К, Н / м 14. Сделайте вывод. Коэффициент жесткости пружины, полученный в результате экспериментов, можно записать: k = k ср измерено (у каждого ученика свой коэффициент) ± Δ С по (ошибка у всех разная). Работа, потенциальная энергия и кинетическая энергияВВЕДЕНИЕ Этот эксперимент был разработан для исследования взаимосвязи между работой, потенциальной энергией и кинетической энергией. Предварительные вопросы: 1. Поднимите книгу с пола на стол. Вы работали? Чтобы ответить на этот вопрос, подумайте, приложили ли вы силу, параллельную перемещению книги. Да, я поднял книгу с пола на стол.Мои руки приложили силу, параллельную перемещению книги. 2. Какая средняя сила действовала на книгу при подъеме? Могли бы вы поднять книгу с постоянной силой? При ответе на вопрос игнорируйте самое начало и конец движения. Среднее усилие на книгу превышало 9,8 Н. Кроме того, книгу можно было поднимать с постоянной силой, и это можно было легко сделать с помощью компьютерных манипуляций. 3. Удерживая один конец неподвижным, натяните резиновую ленту. Вы работали с резинкой? Чтобы ответить на этот вопрос, подумайте, приложили ли вы силу, параллельную перемещению подвижного конца резинки. Да, я работал с резиновой лентой, потому что была приложена сила, параллельная смещению подвижного конца резиновой ленты. 4. Постоянно ли прикладывается сила при растяжении резиновой ленты? Если нет, то в какой точке растяжения сила меньше всего.В какой момент сила наибольшая? Приложенная сила не была постоянной, начало растяжения имело наименьшее приложенное усилие, а конец растяжения — наибольшее приложенное усилие. Таблица данных:
Анализ / ВОПРОСЫ: 1. В Части I работа, которую вы проделали, поднимая массу, не изменила ее кинетическую энергию. Затем работа должна была изменить потенциальную энергию массы. Рассчитайте увеличение гравитационной потенциальной энергии, используя следующее уравнение. Сравните это (используйте разницу в%) со средней работой для Части I и с площадью под действием силы против графика положения : где D h — расстояние, на которое была поднята масса.Запишите свои значения в таблицу данных. Соответствует ли работа, совершаемая с массой, изменению потенциальной энергии гравитации? Должен ли он? Работа над массой соответствует изменению потенциальной энергии гравитации. Используя приведенное выше уравнение, ∆U г = 0,784 Дж, в то время как выполненная работа эквивалентна 0,763 Дж, разница всего 2,8%. Площадь под графиком «сила — положение» оценивается в 0,761, почти такая же разница в 3,02%. 2. Если вы измените скорость руки при подъеме груза, изменится ли график положения силы и ? Или он и дальше будет соответствовать мг D h ? Изменение скорости поднимающей руки не изменяет корреляцию между площадью в F и положением и mgDh, смещение будет одинаковым в любом случае. 3. В Части II вы проделали работу, чтобы растянуть пружину. График силы против положения зависит от конкретной пружины, которую вы использовали, но для большинства пружин будет прямая линия.Это соответствует закону Гука, или F = — kx , где F — сила, прикладываемая к пружине , когда она растягивается на расстояние x . k — жесткость пружины, измеряемая в Н / м. Какова жесткость пружины? Из вашего графика, следует ли весна закону Гука? Как вы думаете, он всегда будет следовать закону Гука, как бы вы его ни распространили? Почему наклон вашего графика положительный, а закон Гука имеет знак минус? Жесткость пружины — 21. 4. Упругая потенциальная энергия, запасаемая пружиной, определяется как D PE = ½ kx 2 , где x — расстояние.Сравните работу, которую вы измерили, чтобы растянуть пружину до 10 см, 20 см и максимальное растяжение, с запасенной потенциальной энергией, предсказанной этим выражением. Должны ли они быть похожими? Примечание: Используйте согласованные единицы . Запишите свои значения в таблицу данных. Разница в работе по растяжению пружины (значения DPE = ½ kx2 и интегрированная площадь) на 10 см, 20 см и 29,2 см составила 23,6%, 11,46% и 7,99% соответственно. 5. В Части III вы проделали работу по ускорению тележки. В этом случае работа пошла на изменение кинетической энергии. Поскольку пружина не задействована и тележка перемещается по ровной поверхности, потенциальная энергия не изменяется. Как ваша работа по сравнению с изменением кинетической энергии? Здесь, поскольку начальная скорость равна нулю, D KE = ½ mv 2 , где m — это общая масса тележки и любые дополнительные веса, и v — конечная скорость.Запишите свои значения в таблицу данных. Выполненная работа отличается от изменения кинетической энергии на 74,3%. Такое расхождение могло быть связано с тем, что тележка была собрана без датчика силы, который был довольно значительным. ЗАКЛЮЧЕНИЕ Этот эксперимент был превосходен для исследования взаимосвязи между работой, кинетической и потенциальной энергией. Также было интересно подсчитать процент расхождения между компьютерными вычислениями и нашими ручными вычислениями. M-6 ЗАКОН КРЮКАЗаметки для инструктора Бернард / Эпп, 4-е изд., Эксперимент 16, хорошо это рассматривает. Если пружина не растягивается сверх предела упругости, она подчиняется закону Гука: где F — сила, приложенная к концу пружины, а y — величина пружины. простирается от его нерастянутой длины. Это закон, которому пружина ведет себя идеально. эластичным образом. [Ниже я переписываю Бернарда / Эпп]
Спрингс: Латунная пружина имеет длину около 16 см и массу около 170 г. Стальная пружина имеет длину около 20 см и массу 240 г. Предельная нагрузка на конические пружины: Сталь: 1,5 кг Эти значения не превышают пределы упругости пружин. Приведенные выше данные взяты из отчета студенческой лаборатории, исправленные из-за ошибки студента в вычисление периодов. Чтобы понять динамику ошибок, ручная подгонка была выполнена выбор наклона и пересечения для минимизации квадратов отклонений. В динамическом случае это было сделано двумя способами (1) с использованием квадрата периода в качестве независимой переменной и (2) с использованием масса как независимая переменная (предпочтительный метод, потому что ошибки незначительны в масса). Статический метод был проанализирован следующим образом: F = mg = k (x-x o ), затем x = x o + (g / k) m, где наклон s = g / k, точка пересечения x o В первом анализе динамического случая использовалось T 2 = (4π 2 / k) (m + m eq ), затем m = —
м экв + T 2 (k / 4π 2 ). Второй анализ динамического случая использовал T 2 = (4π 2 / k) m eq + (4π 2 / k) m.Угловой коэффициент s = 4π 2 / k. Пересечение: I = (4π 2 / k) m eq , поэтому м экв = л / с. Результаты для динамического случая, полученные двумя методами, хорошо согласуются, что дает Жесткость латунной пружины составляет 10 147 дин / см. Массовый эквивалент пружины 44,85 грамма, что составляет 27% от массы пружины. Статическое определение пружины константа дала k = 9800 дин / см, что на 2,5% меньше динамического значения. Для стальной пружины 54 000 дин / см. Массовый эквивалент 86 г, что составляет 36%. его массы. Статическое определение жесткости пружины k = 47000 дин / см, на 6% меньше. чем динамическое значение. ВОПРОСЫ Из эксперимента Чоффари 13, Простое гармоническое движение. 4. (a) В какой момент на пути его вибрации вес, подвешенный на пружине иметь наибольшее ускорение? б) Где у него наибольшая скорость? (c) Где это иметь наименьшее ускорение? (г) Где у него наименьшая скорость? [Где используется слово «наибольший», имеется в виду «наибольший размер».] a) Наибольшее ускорение в крайних положениях смещения. 8. Какая погрешность в процентах вносится в вычисленное значение периода бибрации, для нагрузка 0,2 кг и нагрузка 0,5 кг соответственно, если масса пружины равна пренебрегали?
Масса латунной пружины 170 г.При нагрузке 0,2 кг м = 200 г + 170/3 г, погрешность 56,7 / 200 = 0,28, или 28% Это уменьшается вдвое из-за квадратного корня, поэтому ошибка составляет 14%. Для груза 0,5 кг, эффект 5,7% 9. Если добавление определенного веса в Процедуре 10 удвоит период, то какой масса прибавленного веса быть?
Exp 17 по закону Вильсона, Гука и простому гармоническому движению СОСТОЯНИЕ: балла вычитались из 10 следующим образом. Задачи с 1 по 5 оценивались в один балл. каждый. Также по одному баллу за каждое из следующего, которого нет или нет правильно: B5 График зависимости mg от y для цилиндрической пружины. Найти k (статический метод) Я также посмотрел, сделали ли студенты следующее: 1. Заявил и сравнил два (статическое и динамическое) измерения k и прокомментировал по сравнению. Этот должен быть в отдельном разделе отчета, например, в сводка результатов или обсуждение результатов . Не ищут эти вещи в техпаспорте »они результаты . 2. Укажите, является ли разница между двумя определениями k разумной с учетом оценочной неопределенности для каждого метода.Некоторые из вас думали, что разница была «хорошо» или «слишком большой» или другое качественное описание, но это не принесет вам очков, если вы поддерживаете это мнение количественным обсуждением присущих ошибки эксперимента. Конечно, вы не можете сказать ничего значимого об этом, если у вас есть не предвидел необходимости и провел необходимые экспериментальных исследований в лаборатория для исследования источников неопределенности.Я заметил, что многие люди рано уходят из лаборатории. Ясно, что у студентов было достаточно времени для таких исследований, но этого не произошло. ОБСУЖДЕНИЕ ОШИБОК: Анализ ошибок — это , а не простой список возможных источников ошибок. Некоторые из вас слишком быстро приписывают «плохие» результаты «эффектам трения». Это грубый отговорка, чтобы избежать размышлений и детального анализа ситуации. Тебе это не сойдет с рук если вы не можете продемонстрировать, что трение могло быть причиной в конкретном случае на рука.В этом эксперименте трение никак не может повлиять на статическое определение k. Трение вызывает уменьшение амплитуды «почти периодического» движения с времени, но имеет крайне малое влияние на частоту , и поэтому не может быть обвиняется в плохих результатах этого эксперимента. Некоторые из вас не умеют правильно пользоваться калькуляторами. Вопрос 5 можно было бы сделать «в голове» с отвечает ровно -10, -10 и +10.Тогда почему я увидел значения 9,98, 9,86 и даже 9,46? И почему я увидел эти глупые значения на нескольких листах бумаги? Я знаю Причина: обширный плагиат от чужих расчетов. Я вижу много доказательств копирование совершенно неправильных ответов. Вы знаете, что вы должны делать свою работу, и я намерен спуститься трудно на такой плагиат в будущем. Вы были предупреждены. ВОПРОСЫ: 1. Интерпретировать перехвата.Очевидно, автор хотел, чтобы вы сделали больше, чем задайте значений перехватов, иначе он бы не использовал слово «интерпретировать». Найдите слово в словаре! Это означает «объяснять» или «придавать значение» или «относиться к чему-то другому». Даже если это конкретное слово не использовалось, или даже если это вопрос не появился в отчете, вы должны постоянно искать физическое значение уравнения, графики, константы и т. д. по мере их возникновения. В данном случае график Force vs.смещение, точка пересечения на оси силы (где смещение равно нулю), безусловно, будет зависеть от того, какую конкретную точку вы выбрали в качестве нулевой смещения «и то, что вы выбрали в качестве» нулевой силы «(т. е. включили ли вы вес вешалка в силе, или нет). Если вы строго следовали инструкции, вы измерили смещение из положения подвески пустого груза, но с учетом веса подвески в сила. Таким образом, точка пересечения на оси силы будет представлять вес подвески.В пересечение оси смещения указывало бы на смещение, если бы подвеска была невесомой (отрицательное смещение). 2. Доказать означает математический вывод результата из основных принципы. Вас попросили доказать, что площадь под кривой представляет проделанную работу. Для вычислить проделанная работа не доказательство. Вы найдете это доказательство сделанным в той или иной форме в вашем учебнике, а если нет, то в каком-то другом учебнике, так что никому нет оправдания не делаю этого. 3. Удивительно, но многие из вас думали, что ускорение не может быть максимальным. ровно , когда скорость была равна нулю. Это свидетельствует о серьезном недоразумении этих важных количеств. Ускорение максимальное, а скорость нулевая, ровно при максимальном литраже. Скорость максимальная, а ускорение равен нулю ровно в центральной точке движения, где смещение равно нуль. 4. а) y = 10 cos (2πt / T) см Некоторые из вас забыли, что t измеряется с момента, когда вы отпустили (или нажали) объект). 5. Для ситуации а) y = 10 cos (2πt / T) а) у = -10 см 6. [Без очков] Измерьте углы и смещения от положения равновесия маятник.Для малых смещений смещение дуги примерно равно горизонтальное смещение, и составляет -Rθ, где R — длина струны маятника. Нарисуйте векторную диаграмму, правильно показывающую дугу, и покажите, что тангенциальная составляющая силы тяжести mg на опоре равна mg sin θ. Для малых углов sin θ составляет приблизительно θ радиан. Итак, ускорение по дуга приблизительно равна mgθ / m = gθ. Следовательно, формула для периода: T = 2π [- (- Rθ) / gθ] 1/2 = 2π [R / g] 1/2 © 1997, 2004 Дональд Э.Симанек. . | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 Экспериментальные данные.
Экспериментальные данные.
 / |х|
/ |х| Запишите это значение на листе.
Запишите это значение на листе.


 и Государственный университет Северной Каролины. | Кредиты
и Государственный университет Северной Каролины. | Кредиты Сила может быть рассчитана из W = mg. Протяженность
пружину можно измерить, отметив положение конца
пружина до и во время приложения силы.
Сила может быть рассчитана из W = mg. Протяженность
пружину можно измерить, отметив положение конца
пружина до и во время приложения силы. с несколькими книгами, чтобы масса не стягивала с
стол.
с несколькими книгами, чтобы масса не стягивала с
стол.




 Для диаграмм рассеяния, которые предполагают линейную связь, неформально подгоните прямую линию и неформально оцените соответствие модели, судя о близости точек данных к линии.
(Оценка
8) Подробнее
Для диаграмм рассеяния, которые предполагают линейную связь, неформально подгоните прямую линию и неформально оцените соответствие модели, судя о близости точек данных к линии.
(Оценка
8) Подробнее Опишите шаблоны, такие как кластеризация, выбросы, положительная или отрицательная связь, линейная связь и нелинейная связь.
(Оценка
8) Подробнее
Опишите шаблоны, такие как кластеризация, выбросы, положительная или отрицательная связь, линейная связь и нелинейная связь.
(Оценка
8) Подробнее (Оценки
9 —
12) Подробнее
(Оценки
9 —
12) Подробнее Оцените скорость изменения по графику.
(Оценки
9 —
12) Подробнее
Оцените скорость изменения по графику.
(Оценки
9 —
12) Подробнее (Оценки
6 —
8) Подробнее
(Оценки
6 —
8) Подробнее См. Http://www.pasco.com/physhigh/
См. Http://www.pasco.com/physhigh/ ..
.. ..
..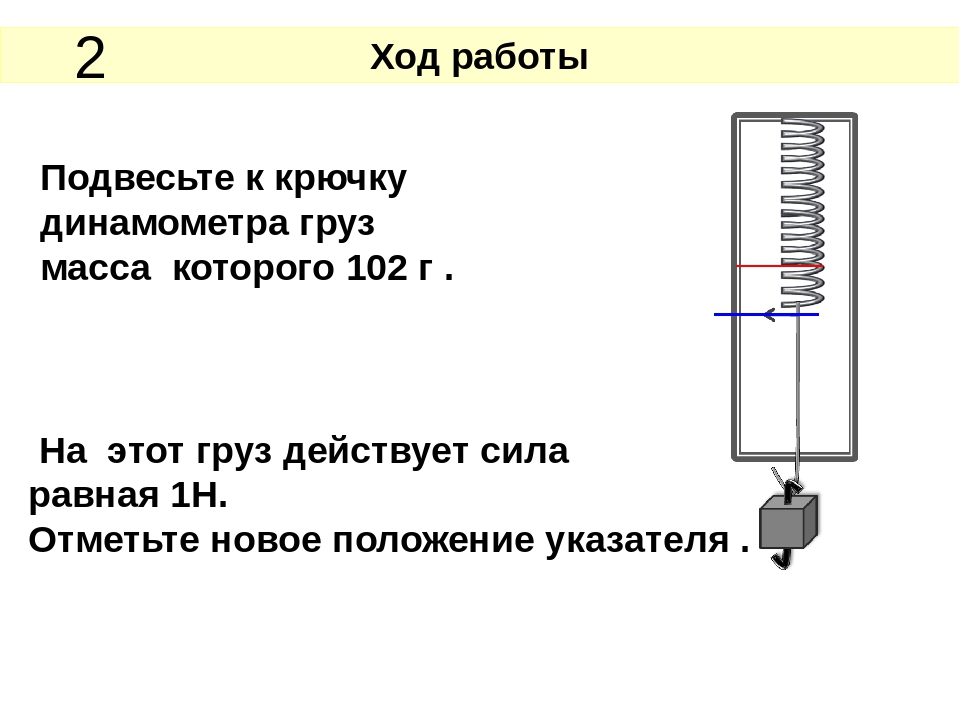 В этом упражнении вы узнаете о реальных приложениях, таких как исследования, из которых берутся данные контрольных вопросов.
В этом упражнении вы узнаете о реальных приложениях, таких как исследования, из которых берутся данные контрольных вопросов. В качестве альтернативы можно отрегулировать размер группы в соответствии с количеством доступного оборудования.
В качестве альтернативы можно отрегулировать размер группы в соответствии с количеством доступного оборудования. Это среднее значение k, константа пропорциональности, для пружины на основании закона Гука: y = k x .
Это среднее значение k, константа пропорциональности, для пружины на основании закона Гука: y = k x .

 3
3  После построения графика возьмите точку на прямой (в середине графика), определите по ней значения силы упругости и удлинения, соответствующие этой точке и вычислите жесткость k … будет желаемым средним значением жесткости пружины.
После построения графика возьмите точку на прямой (в середине графика), определите по ней значения силы упругости и удлинения, соответствующие этой точке и вычислите жесткость k … будет желаемым средним значением жесткости пружины. е.е. меняются условия эксперимента. Следовательно, чтобы найти среднее значение жесткости, нельзя рассчитать среднее арифметическое результатов измерений. Мы будем использовать графический метод нахождения среднего значения, которое может быть применено в таких случаях. По результатам нескольких экспериментов построим график зависимости модуля упругой силы F eln от модуля удлинения | х |. При построении графика по результатам эксперимента экспериментальные точки могут не находиться на прямой линии, соответствующей формуле
е.е. меняются условия эксперимента. Следовательно, чтобы найти среднее значение жесткости, нельзя рассчитать среднее арифметическое результатов измерений. Мы будем использовать графический метод нахождения среднего значения, которое может быть применено в таких случаях. По результатам нескольких экспериментов построим график зависимости модуля упругой силы F eln от модуля удлинения | х |. При построении графика по результатам эксперимента экспериментальные точки могут не находиться на прямой линии, соответствующей формуле Из курса алгебры (VII класс) известно, что относительная погрешность (ε k) равна отношению абсолютной ошибки Δk к значению k:
Из курса алгебры (VII класс) известно, что относительная погрешность (ε k) равна отношению абсолютной ошибки Δk к значению k:
 Таким образом, жесткость пружины может быть выражена как:
Таким образом, жесткость пружины может быть выражена как: Установите динамометр на штатив на достаточно большой высоте.
Установите динамометр на штатив на достаточно большой высоте. 5 мм.
5 мм.

 верхний рисунок)
верхний рисунок) где Δ Ф — погрешность измерения силы, ΔƖ — погрешность измерения длины.
где Δ Ф — погрешность измерения силы, ΔƖ — погрешность измерения длины. Применяя уравнения, изученные в классе физики, можно было сравнить их со значениями, измеренными компьютерным программным обеспечением. Примерами, использованными в эксперименте, были тележка, пружина и груз.
Применяя уравнения, изученные в классе физики, можно было сравнить их со значениями, измеренными компьютерным программным обеспечением. Примерами, использованными в эксперименте, были тележка, пружина и груз.
 350
350 0190
0190
 24 J. Из графика видно, что пружина подчиняется закону Гука, хотя и имеет положительный наклон. Пружина не всегда будет следовать закону Гука, есть точка растяжения, где пружина будет представлена как F напряжение . Наклон графика положительный, потому что он измеряет работу, выполняемую нашей рукой, а не пружиной. Работа, выполняемая нашей рукой, была одинаковой по величине и противоположной по направлению движения пружины.
24 J. Из графика видно, что пружина подчиняется закону Гука, хотя и имеет положительный наклон. Пружина не всегда будет следовать закону Гука, есть точка растяжения, где пружина будет представлена как F напряжение . Наклон графика положительный, потому что он измеряет работу, выполняемую нашей рукой, а не пружиной. Работа, выполняемая нашей рукой, была одинаковой по величине и противоположной по направлению движения пружины. 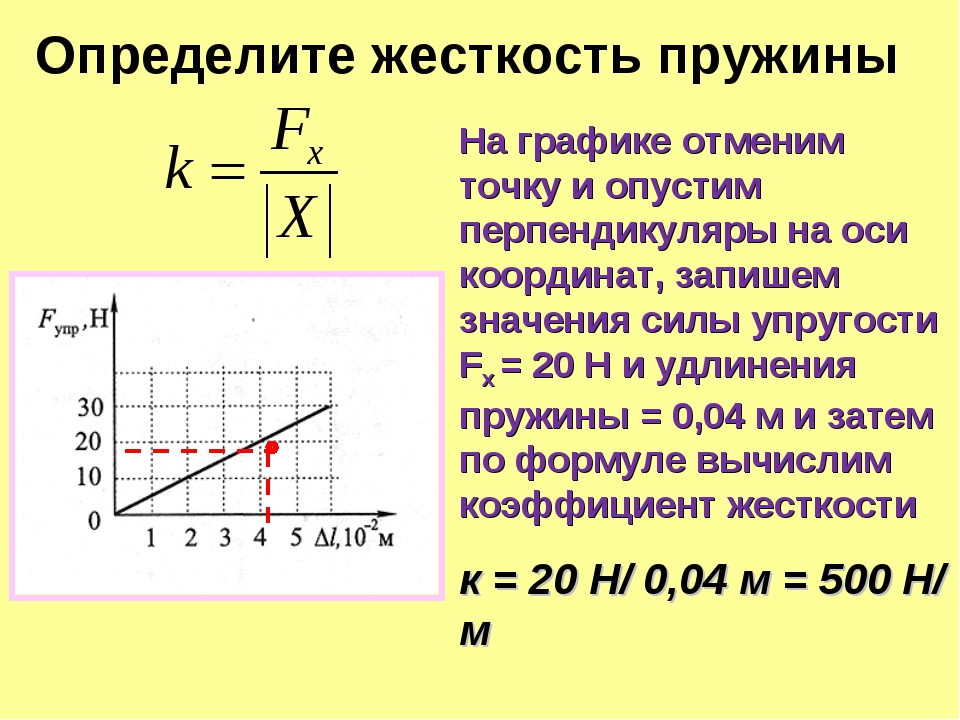 Уравнение потенциальной энергии имело более близкие значения, когда пружина была растянута дальше.У них должны быть похожие значения, потому что интеграция составляет прибл. равно 10x 2 (наклон графика был 21,241), или примерно ½ kx 2 .
Уравнение потенциальной энергии имело более близкие значения, когда пружина была растянута дальше.У них должны быть похожие значения, потому что интеграция составляет прибл. равно 10x 2 (наклон графика был 21,241), или примерно ½ kx 2 . 
 Таким образом, верхние катушки поддерживают большую массу.
чем нижние. Кроме того, натяжение пружины неравномерно по ее длине, но является наибольшим.
вверху, а самый маленький внизу.Эти соображения также влияют на вибрационное поведение.
пружины, и мы не включили их в уравнение 2. Когда берется собственная масса пружины
с учетом периода весны составляет:
Таким образом, верхние катушки поддерживают большую массу.
чем нижние. Кроме того, натяжение пружины неравномерно по ее длине, но является наибольшим.
вверху, а самый маленький внизу.Эти соображения также влияют на вибрационное поведение.
пружины, и мы не включили их в уравнение 2. Когда берется собственная масса пружины
с учетом периода весны составляет: 2 x Devs.2 разработчиков. от м Девс.
50,48 20,90 0,62 0,386 30,3 88,8337 54,241659 14,1501 0,6088244 0,0001507
90,48 24,80 0,64 0,403 34,3 90,988 58,728825 1008,14 0,7254428 0,0081799
130,48 28,80 0,83 0,694 38,4 91,2476 133,42947 8,69939 0,8257525 5,253E-05
170,48 32,60 0,92 0,842 42,4 95,374 171,39705 0,84098 0.23 5.142E-06
210,48 36,60 1,01 1,010 46,4 95,6399 214,67642 17,61 0,9965276 7,178E-05
250,48 40,20 1,08 1,164 50,4 103,901 254,30994 14,6684 1,0717589 5,243E-05
290,48 44,40 1,15 1,318 54,4 100,135 293.80133 11,0312 1,1420452 3,546E-05
330,48 48,00 1,21 1,469 58,4 108,584 332,68091 4,84399 1,2082496 1,483E-05
370,48 52,00 1,28 1,627 62,4 108,868 373,21336 7,47128 1,2710103 2,016E-05
410.2 vs м
x = xo + sm y = yo + s’m
Крутизна, с: 0,10034 1E-06 с ‘: 257 0,1 с’ ‘: 0,00389
xo: 25,26 0,001 лет: -44,9 0,1 zo: 0,1743
SSQDEV (x) 1201.
2 x Devs.2 разработчиков. от м Девс.
50,48 20,90 0,62 0,386 30,3 88,8337 54,241659 14,1501 0,6088244 0,0001507
90,48 24,80 0,64 0,403 34,3 90,988 58,728825 1008,14 0,7254428 0,0081799
130,48 28,80 0,83 0,694 38,4 91,2476 133,42947 8,69939 0,8257525 5,253E-05
170,48 32,60 0,92 0,842 42,4 95,374 171,39705 0,84098 0.23 5.142E-06
210,48 36,60 1,01 1,010 46,4 95,6399 214,67642 17,61 0,9965276 7,178E-05
250,48 40,20 1,08 1,164 50,4 103,901 254,30994 14,6684 1,0717589 5,243E-05
290,48 44,40 1,15 1,318 54,4 100,135 293.80133 11,0312 1,1420452 3,546E-05
330,48 48,00 1,21 1,469 58,4 108,584 332,68091 4,84399 1,2082496 1,483E-05
370,48 52,00 1,28 1,627 62,4 108,868 373,21336 7,47128 1,2710103 2,016E-05
410.2 vs м
x = xo + sm y = yo + s’m
Крутизна, с: 0,10034 1E-06 с ‘: 257 0,1 с’ ‘: 0,00389
xo: 25,26 0,001 лет: -44,9 0,1 zo: 0,1743
SSQDEV (x) 1201. 2 x Devs.2 разработчиков. от м Девс.
50,48 20,20 0,33 0,106 20,1 0,01479 58,544375 65,0341 0,3141272 0,0001182
90,48 21,00 0,36 0,132 20,9 0,01916 94,666541 17,5271 0,3570713 4,262E-05
130,48 21,90 0,40 0,160 21,6 0,06513 132,44 3,8416 0,3953782 2,136E-05
170,48 22,40 0,44 0,197 22,4 0,00078 182, 154,451 0.4302881 0,000188
210,48 23,30 0,47 0,220 23,2 0,00789 214,54374 16,514 0,462571 4,778E-05
250,48 24,00 0,50 0,248 24,0 3,1E-05 251,37781 0,80607 0,4927432 2,275E-05
290,48 24,90 0,52 0,274 24,8 0,01498 287,52268 8,74572 0,5211716 5,705E-06
330,48 25,40 0,55 0,305 25,6 0,02586 329,8225 0,4323 0,5481276 1,9E-05
370,48 26,40 0,57 0,327 26,3 0,00314 358,7551 137,473 0,5738187 5,713E-06
410.2 vs м
x = xo + sm y = yo + s’m
Наклон, с: 0,01958 с ‘: 1359 с’ ‘: 0,0007206
xo: 19,09 лет: -85 zo: 0,0623
SSQDEV (x) 0,19679 SSQDEV: 945.
2 x Devs.2 разработчиков. от м Девс.
50,48 20,20 0,33 0,106 20,1 0,01479 58,544375 65,0341 0,3141272 0,0001182
90,48 21,00 0,36 0,132 20,9 0,01916 94,666541 17,5271 0,3570713 4,262E-05
130,48 21,90 0,40 0,160 21,6 0,06513 132,44 3,8416 0,3953782 2,136E-05
170,48 22,40 0,44 0,197 22,4 0,00078 182, 154,451 0.4302881 0,000188
210,48 23,30 0,47 0,220 23,2 0,00789 214,54374 16,514 0,462571 4,778E-05
250,48 24,00 0,50 0,248 24,0 3,1E-05 251,37781 0,80607 0,4927432 2,275E-05
290,48 24,90 0,52 0,274 24,8 0,01498 287,52268 8,74572 0,5211716 5,705E-06
330,48 25,40 0,55 0,305 25,6 0,02586 329,8225 0,4323 0,5481276 1,9E-05
370,48 26,40 0,57 0,327 26,3 0,00314 358,7551 137,473 0,5738187 5,713E-06
410.2 vs м
x = xo + sm y = yo + s’m
Наклон, с: 0,01958 с ‘: 1359 с’ ‘: 0,0007206
xo: 19,09 лет: -85 zo: 0,0623
SSQDEV (x) 0,19679 SSQDEV: 945. 397 SSQDEV 0,0006658
k = 50051,1 дин / см k = 53651,2 дин / см 54785,481
m (экв) = 85 г m (экв) = 86.455731
397 SSQDEV 0,0006658
k = 50051,1 дин / см k = 53651,2 дин / см 54785,481
m (экв) = 85 г m (экв) = 86.455731  Наклон s = k / 4π 2 , точка пересечения — m eq .
Наклон s = k / 4π 2 , точка пересечения — m eq .