Контрольная работа по теме системы уравнений: Контрольная работа по теме Системы уравнений

Контрольная работа на тему: системы линейных уравнений

Оглавление:

Системы линейных уравнений

Задание: Решение систем линейных уравнений по правилу Крамера и методом Гаусса.

Цель: формирование умения решать системы линейных уравнений по правилу Крамера и методом Гаусса.

Задание для самостоятельной внеаудиторной работы:

5.1. Изучите теоретические основы решения системы линейных уравнений по правилу Крамера и методом Гаусса.

5.2. Решите систему уравнений, используя правило Крамера:

5.3. Решите систему линейных уравнений по методу Гаусса:

5.4. Фирма для перевозки грузов может заказывать машины трех видов. Если она закажет по одной машине каждого вида, то перевезёт 12 тонн груза. Если закажет по две машины первого и второго вида и одну машину третьего вида, то перевезёт 19 тонн груза. Если же фирма закажет по две машины первого и третьего вида и одну машину второго вида, то перевезёт 20 тонн груза. Какова грузоподъемность каждого вида машин?

Методические указания по выполнению работы:

Для решения систем линейных уравнений применяют правило Крамера и метод Гаусса.

1. Правило Крамера решения системы линейных уравнений с неизвестными.

Система линейных уравнений с неизвестными имеет единственное решение, если определитель , составленный из коэффициентов при неизвестных, отличен от нуля:

где — определитель, полученный из определителя заменой столбца коэффициентов при столбцом свободных членов;

— определитель, полученный из определителя заменой столбца коэффициентов при столбцом свободных членов;

— определитель, полученный из определителя заменой столбца коэффициентов при столбцом свободных членов.

Пример 1.

Решите систему уравнений по правилу Крамера:

Решение:

Составим определитель из коэффициентов при неизвестных и вычислим его:

Определитель отличен от 0, следовательно, система имеет единственное решение. Для его нахождения вычислим , и :

По правилу Крамера найдем неизвестные:

Замечание. Для проверки правильности решения системы уравнений необходимо подставить найденные значения неизвестных в каждое из уравнений данной системы. При этом, если все уравнения обратятся в тождества, то система решена верно.

Истинно.

Итак, решение системы найдено правильно.

Ответ:

2. Метод Гаусса решения систем линейных уравнений

1. Составьте расширенную матрицу системы — матрицу, состоящую из коэффициентов при неизвестных и столбца свободных членов.
2. С помощью элементарных преобразований приведите полученную матрицу к ступенчатому виду.
3. Восстановите систему линейных уравнений, равносильную исходной, начиная с последнего уравнения, и найдите значения неизвестных.

Метод Гаусса является более универсальным, чем правило Крамера, так как позволяет находить решения в следующих случаях:

1. число уравнений не равно числу неизвестных.
2. если в правиле Крамера .

Ответ на вопрос о существовании и количестве решений системы линейных уравнений дает теорема Кронекера-Капелли (критерий совместности системы линейных уравнений): система линейных уравнений с неизвестными совместна тогда и только тогда, когда ранг основной матрицы (матрицы, составленной из коэффициентов при неизвестных) равен рангу расширенной матрицы , причем:

1. если (ранг матрицы равен числу неизвестных), то система имеет единственное решение;
2. если (ранг матрицы меньше числа неизвестных), то система имеет бесконечное множество решений.

Все возможные случаи решения системы линейных уравнений (одно решение, нет решений, множество решений) разобраны в примерах 2-4.

Пример 2.

Решите систему уравнений методом Гаусса:

Решение:

Выпишем расширенную матрицу системы и приведем её к ступенчатому виду:

Поменяем местами первую и третью строки матрицы, что равносильно перестановке первого и третьего уравнений системы. Это позволит нам избежать появления дробных коэффициентов
при последующих вычислениях.

Первую строку полученной матрицы умножаем последовательно на (-2) и (-3) и сложим соответственно со второй и третьей строками, при этом будет иметь вид:

Для упрощения вычислений умножим третью строку на (-0,1) и поменяем ее местами со второй строкой. Тогда получим:

Далее, умножая вторую строку матрицы на 9 и складывая с третьей, окончательно получим:

Восстановим из полученной матрицы систему уравнений, равносильную данной, начиная с последнего уравнения:

Из последнего уравнения находим: .

Подставим во второе уравнение системы: .

После подстановки и в первое уравнение получим: ; . Итак, .

Проверка:

Следовательно, решение системы найдено верно.

Ответ: .

Пример 3.

Найдите все решения системы линейных уравнений:

Решение:

Составим расширенную матрицу системы и приведем ее к ступенчатому виду.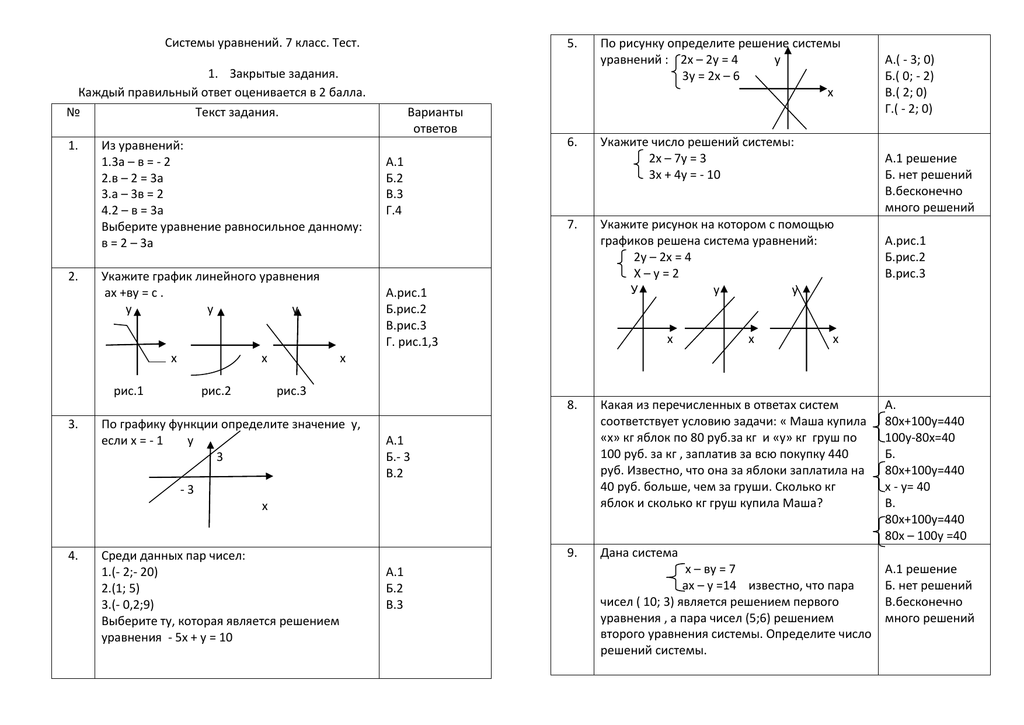

Домножим первую строку на (-2) и сложим ее со второй строкой:

Сложим первую и третью строки:

Домножим вторую строку на 2 и сложим ее с третьей строкой:

Вычеркнем нулевую строку:

Видим, что ранг основной матрицы равен рангу расширенной матрицы и равен двум. Следовательно, в силу критерия Кронеккера-Капелли, система имеет решения. Так как ранг матрицы (два) меньше числа неизвестных (три), то система имеет бесчисленное множество решений. Найдем эти решения.

Восстановим систему уравнений, равносильную исходной:

Пусть — свободная переменная, которая может принимать любые числовые значения. Выразим из первого уравнения : .

Подставим данное выражение во второе уравнение:

Такое решение будем называть общим решением системы. Запишем общее решение системы в виде тройки чисел: .

Ответ: .

Пример 4.

Докажите, что система линейных уравнений не имеет решений:

Решение:

Составим расширенную матрицу системы и приведем ее к ступенчатому виду.

Домножим первую строку на (-3) и сложим ее со второй строкой:

Домножим первую строку на 2 и сложим ее с третьей строкой:

Сложим вторую и третью строки:

Видим, что ранг основной матрицы (2) не равен рангу расширенной матрицы (3). Следовательно, в силу критерия Кронеккера-Капелли, система не имеет решений.

На этой странице вы сможете посмотреть все остальные темы готовых контрольных работ по высшей математике:

Готовые контрольные работы по высшей математике

Обратите внимание на похожие контрольные работы возможно они вам будут полезны:

контрольная работа по алгебре 8 класс на тему: «Система уравнений»

Главная / Старшие классы / Алгебра

Скачать

24.5 КБ, 1274714.doc Автор: Воробьева Юлия Викторовна, 14 Ноя 2015

урок-контрольная работа

Автор: Воробьева Юлия Викторовна

Похожие материалы

Тип	Название материала	Автор	Опубликован
документ	контрольная работа по алгебре 8 класс на тему: «Система уравнений»	Воробьева Юлия Викторовна	14 Ноя 2015
документ	Контрольная работа по алгебре на тему » Арифметическая прогрессия» 9 класс	Шангареева Фарида Максютовна	8 Фев 2016
документ	Контрольная работа №9 по алгебре для 7 класса по теме «Системы линейных уравнений»	Баринова Елена Валерьевна	8 Фев 2016
документ	Контрольная работа по алгебре 8 класс (входной контроль)	Сивец Людмила Васильевна	21 Мар 2015
документ	полугодовая контрольная работа по алгебре 8 класс	Кныш Александра Михайловна	21 Мар 2015
документ	Годовая контрольная работа по алгебре, 8 класс	Рубцова Ирина Геннадьевна	31 Мар 2015
разное	контрольная работа по алгебре №1 8 класс	Петренко Людмила Валентиновна	1 Апр 2015
разное	итоговая контрольная работа по алгебре 8 класс	Вихлянцева Марина Петровна	1 Апр 2015
документ	Контрольная работа по алгебре за I полугодие 8 класс	Савина Наталия Борисовна	1 Апр 2015
разное	контрольная работа по алгебре, 8 класс( за 2 четверть)	Съедина Лидия Николаевна	1 Апр 2015
документ	Контрольная работа по алгебре, 8 класс	Аникина Ольга Борисовна	21 Апр 2015
документ	Контрольная работа №2 по алгебре 8 класс	Задворнова Татьяна Николаевна	14 Фев 2016
документ	Итоговая контрольная работа по алгебре 8 класс	Кулешова Татьяна Викторовна	14 Янв 2016
документ	7 класс, алгебра, обучающая самостоятельная работа по алгебре по теме: «Решение уравнений и задач на составление уравнений»	Козлова Наталья Павловна	21 Мар 2015
документ	Контрольная работа по алгебре по теме «Рациональные уравнения», 8 класс	Токарева Инна Александровна	31 Мар 2015
документ	Контрольная работа по алгебре 8 класс по теме «Применение свойств квадратного корня»	Токарева Тамара Ивановна	1 Апр 2015
документ	Контрольная работа по алгебре 8 класс по теме «Применение свойст квадратного корня»	Токарева Тамара Ивановна	1 Апр 2015
документ	Контрольная работа №6 по алгебре, 8 класс «Квадратное неравенство» Учебник Ш. А.Алимова.	Мирошниченко Наталья Григорьевна	15 Окт 2015
документ	Итоговая контрольная работа по алгебре 7 класс	Колодкина Наталья Владимировна	8 Фев 2016
документ	Контрольная работа по алгебре и началам анализа по теме: «Логарифмическая функция», 10 класс	Кочухова Ирина Михайловна	8 Фев 2016
документ	Контрольная работа по алгебре на повторение, 10 класс	Россамахина Ирина Юрьевна	21 Мар 2015
документ	урок-контрольная работа 8 класс на тему: «Система уравнений»	Воробьева Юлия Викторовна	14 Ноя 2015
документ	Итоговая контрольная работа по алгебре 8 класс,по математике 5 класс	Загитова Гульфия Анатольевна	20 Сен 2015
разное	решебник по алгебре 7 класс домашняя контрольная работа 2	tronarukeh2980	11 Мая 2015
документ	Контрольная работа №1 по алгебре. 8 класс по учебнику А Г. Мерзляка В.Б.Полонского	Задворнова Татьяна Николаевна	21 Дек 2015
документ	Контрольная работа №8 по алгебре для 7 класса по теме «Преобразование целых выражений»	Баринова Елена Валерьевна	8 Фев 2016
документ	Контрольная работа по алгебре за первое полугодие. 8 класс. УМК Макарычев и др.	Сильченкова Светлана Николаевна	9 Апр 2015
документ	Контрольная работа по алгебре. 8 класс (углубленное изучение). Квадратные уравнения	Глушкова Светлана Юрьевна	15 Окт 2015
документ	Итогова контрольная работа по алгебре в 8 классе.	Перфильева Валентина Анатольевна	21 Мар 2015
документ	Годовая контрольная работа по алгебре в 8 классах	Штанина Светлана Николаевна	1 Апр 2015
документ	Итоговая контрольная работа по алгебре для 8 класса	Атлашкина Наталья Альбертовна	15 Окт 2015
документ	Входная контрольная работа по алгебре для 8 класса	Петрякова Олеся Сергеевна	26 Окт 2015
документ	Административная контрольная работа по алгебре для 8 класса (декабрь)	Агеева Юлия Владимировна	7 Дек 2015
документ	Контрольная работа для 8 класса по алгебре «Квадратные уравнения»	Северюхина Ксения Николаевна	21 Мар 2015
документ	Входная контрольная по алгебре 8 класс	Толочко Жанна Геннадьевна	24 Сен 2015
документ	Контрольная работа №6 по алгебре для 7 класса по теме «Произведение многочленов»	Баринова Елена Валерьевна	8 Фев 2016
документ	Контрольная работа №5 по алгебре для 7 класса по теме «Многочлены»	Баринова Елена Валерьевна	8 Фев 2016
документ	Контрольная работа №4 по алгебре для 7 класса по теме «Степень и ее свойства. Одночлены»	Баринова Елена Валерьевна	8 Фев 2016
документ	Контрольная работа №1 по алгебре для 7 класса по теме «Преобразование выражений»	Баринова Елена Валерьевна	8 Фев 2016
документ	Контрольная работа №7 по алгебре для 7 класса по теме «Формулы сокращенного умножения»	Баринова Елена Валерьевна	8 Фев 2016

Контрольная работа по теме Сравнение методов решения систем линейных уравнений – Telegraph

💣 👉🏻👉🏻👉🏻 ВСЯ ИНФОРМАЦИЯ ДОСТУПНА ЗДЕСЬ ЖМИТЕ 👈🏻👈🏻👈🏻

Контрольная работа по алгебре 7 класс «Системы линейных . . .
Контрольная работа по алгебре 7 класс по теме: «Линейные . . .
Контрольная работа № 9 «Системы линейных уравнений»
Контрольная работа № 7 по теме «системы линейных уравнений . . .
Контрольная работа на тему «Методы решения систем линейных . . .
контрольная работа найти Решение систем линейных уравнений
Контрольная работа № 7 по теме «Системы линейных уравнений . . .
Самостоятельная работа «Системы уравнений с двумя . . .
Контрольная работа №1 «Уравнения, неравенства, системы . . .
Урок 53 . Контрольная работа № 5 с ответами (6 вариантов, 3 . . .
Престижность профессии как фактор профессионального самоопределения студентов
Реферат по теме Равные права мужчин и женщин в различных сферах жизни общества: миф или реальность
Тэо Технико Экономическое Обоснование Образец Excel
Контрольная работа по теме «Системы линейных уравнений»Вариант 1 . Решите систему уравнений методом подстановки: Решите систему уравнений методом сложения: Студент получил стипендию 600 руб . купюрами достоинством 50 руб . и 10 руб ., всего 24 купюры .
Контрольная работа № 1 по теме: «Линейные уравнения с одной переменной» . Вариант № 1 . 1 . Решите уравнение: 1) 9 х- 7 = 6х+14; 2) 3 (4 — 2х) + 6 = -2х + 4 . 2 . В одном мешке было в 3 раза больше муки, чем в другом . Когда из первого мешка взяли 4 кг муки, а во второй добавили 2 кг, то в мешках муки . . .
Контрольная работа № 9 по алгебре в 7 классе «Системы линейных уравнений» с ответами по УМК Макарычев (легкий уровень) .) . Глава vi учебника . Урок 94 поурочного планирования — Алгебра 7 Макарычев К-9 Уровень 1 (варианты 1, 2) .
Контрольная работа № 7 по теме «системы линейных уравнений» 1 вариант . х + у = — 2 . 2х + 10 = 3 — ( 6х + 2у) . Прямая y = kx + b проходит через точки А ( 3 ; 8 ) и В ( — 4 ; 1 ) . Напишите уравнение этой прямой . Для детского сада купили 8 кг конфет двух сортов по цене 2р . И 3 р . За килограмм .
Контрольная работа по математике на тему: Методы решения систем линейных уравнений Скачать контрольную бесплатно
Описание решения систем линейных уравнений методом вращений, рассмотрение теоремы Кронекера . Произведение матрицы элементарного вращения на вектор . контрольная работа, добавлен 12 .03 .2020
Контрольная работа № 7 по теме «Системы линейных уравнений с двумя переменными» (7 класс, Мерзляк А .Г . и др .) Учебник: Алгебра . 7 класс . Мерзляк А .Г ., Полонский В .Б ., Якир М .С . М .: 2015 . — 272 с . Даны четыре варианта контрольной работы, удобно вносить изменения и печатать .
Контрольная работа «Системы уравнений с двумя переменными» (9 класс) Контрольная работа № 3 к УМК Мордкович А .Г . «Алгебра 9», составлена на основе дидактических материалов «Контрольные работы по алгебре 9 класс» ,Л .А . Александрова , «Контрольные и самостоятельные работ . . .
№3 . Решить систему линейных уравнений по формуле Крамера . . ii В . №1 . Решить уравнения . 1) = 0 . 2) 0,3х(х + 13)-2х(0,9 — 0,2х) = 0 . 3) = х 2 — 11 №2 . Решить неравенства . 1) -х 2 + 2х + 3 ≥ 0 . 2) 3х 2 — 4х + 2 . 3) 1 №3 .
III . Контрольная работа в 6 вариантах . Вариант 1 . Решите уравнение 5х 2 + 10х = 0 . Решите уравнение 9x 2 — 4 = 0 . Решите уравнение х 2 — 7х + 6 = 0 . Решите уравнение 2x 2 + 3х + 4 = 0 . Один из корней уравнения х 2 + ах + 72 = 0 равен 9 .
Курсовая Работа На Тему Мировое Хозяйство: Закономерности Формирования, Тенденции И Проблемы Развития
Дипломная работа по теме Разработка макетного лабораторного стенда для изучения работы электропривода
Реферат по теме О семантических отношениях форм залога в английском языке
Методические Рекомендации Курсовой
Реферат по теме Широкополосное согласование комплексных нагрузок на основе теории связанных контуров
Отчет По Строительной Практике Образец
Какое Сочинение
Отчет По Учебной Практике Познание Ребенка
Дневник Прохождения Педагогической Практики
Сочинение 3 Класс Фгос
Реферат по теме История развития латинского языка
В Чем Заключается Достоинство Человека Сочинение
Сочинение Про Первую Мировую Войну
Менің Университетім Менің Мақтанышым Эссе
Реферат по теме Биология и глобальные проблемы современности
Источники Загрязнения Атмосферы Реферат
Реферат: Духовная сфера
Реферат по теме Воспалительные заболевания гениталий у девочек
Реферат по теме Становление демократии в Сиракузах в V веке до н. э.
Реферат по теме Психоанализ по З. Фрейду
Реферат по теме Производство бетонных работ
Реферат: Квалиметрия как наука
Курсовая работа по теме Состояние и пути активизации экспортной деятельности в РБ
Реферат На Тему Мультимедийные Технологии
Контрольная работа: Правовое регулирование занятости в Российской Федерации
Курсовая работа: Безработица и политика занятости 2
Памятка По Итоговому Сочинению 2022
Курсовая работа по теме Система нормативно-правового регулирования бухгалтерской отчетности
Реферат Про Плутон
Курсовая работа по теме Обоснование нормативов предельно допустимых выбросов (ПДВ) загрязняющих веществ в атмосферу и мероприятия по их достижению
Классификация международных правонарушений
Сочинение Как Характеризует Человека Его Нравственный Выбор
Доклад по теме Мысль как деформация космического вакуума
Дипломная работа по теме Использование компьютерных технологий на уроках физической культуры в старших классах
Клиника Отчет По Практике
Банкротство Юридических Лиц Дипломная Работа
Курсовая работа по теме Активизация мыслительной деятельности на уроках математики
Контрольная Работа По Физике Онлайн
Красивое Сочинение Про Бабушку
Грыжи Реферат Список Использованной Литературы
Административная Контрольная Работа По Химии 11 Класс
Реферат: Перикл, афинская демократия
Реферат: Great People Essay Research Paper Great PeopleOnly
Железобетонные подкрановые и обвязочные балки.
Если Бы Я Стал Депутатом Сочинение Днр
Официальный Сайт Курсовая Работа
Темы Сочинений По Истории 2022
Отчет По Гражданской Практике
Реферат: Компоненты, границы и морфологическая структура ландшафтов
Реферат: Коммерческие организации с иностранными инвестициями в Республике Беларусь
Сочинение Тема Родины В Поэзии Серебряного Века
Математика Контрольные Работы 5 Класс Герасимов Скачать
Реферат: Понятие о документе
Учебное пособие: Методические указания по выполнению контрольных работ для студентов 1 курса заочной формы обучения (контрольная работа №1)
Курсовая работа: Залежність схильності до суїциду від соціометричного статусу старшокласників
Контрольная работа по теме Основы статуса человека и гражданина в РФ
Дипломные Работы Детская Психология
Реферат по теме СМИ как феномен общественной жизни и объект исследования
Реферат по теме Пользование лесом
Контрольная работа: Биологическое загрязнение биосферы
Где Заказать Диссертацию Отзывы
Контрольная работа по теме Содержание финансово-правового регулирования общественных отношений и его истоки
Реферат по теме Відпочинок літніх людей
Курсовая работа: Анализ рынка и рыночной конъюнктуры
Пронумерованное Сочинение Шопена 4 Буквы Сканворд
Реферат: Венера
Сочинение по теме Художественный дискурс как актуализация художественного текста в сознании читателя
Доклад: Алексей Федорович Мерзляков (1778—1830)
Скачать Образец Дипломной Работы
Дипломная работа по теме Дизайн проект интерьеров экологического образовательного центра ‘Подорожник’ в национальном парке ‘Нижняя Кама’
Курсовая работа по теме Оценка информационной готовности Польши
Реферат: Рельеф и геологическое строение России
Доклад по теме Джейн Гудолл
Реферат по теме Причины нарушения коммуникации и способы их преодоления
Курсовая работа по теме Совершенствование технологии монтажа валопровода на сухогрузном теплоходе с применением оптических средств
Дипломная работа: Традиционализм и модернизм в системе ценностных ориентаций студенческой молодежи УдГУ
Контрольная Работа По Теме Химический
Дипломная работа по теме Профессия, труд и здоровье
Неолит. Общая характеристика.
Реферат: Исследование психологических особенностей наркозависимых больных среди молодежи
Органы Государственной Власти Рф Реферат
Написать Сочинение По Данному Началу 6 Класс
Нематериальные Активы Предприятия Реферат
Реферат На Тему Реки Красноярского Края
Пособие по теме Предмет і метод економічної теорії
Реферат по теме Подвижные и спортивные игры как средство рекреации и социальной адаптации инвалидов
Реферат На Тему Потребительские Рынки И Покупательское Поведение Потребителей
Реферат: The Equality Of Women In ChaucerS Wife
Реферат: The Ark Of The Covenant Essay Research
Реферат: Гигиена питания и предупреждение желудочно-кишечных заболеваний
Методы Оценки Бизнеса Реферат
Дипломная Работа На Тему Акционерные Общества Как Субъекты Гражданского Права
Вазопись Древней Греции Реферат
Реферат по теме Уровень тревожности детей
Диссертация Ценностное Познание 2022
Дипломная работа по теме Товарооборот
Контрольная работа по теме Оценка влияния повторения изученного материала перед сном на качество запоминания
Лабораторная Работа 4 Физика Перышкин
Курсовая работа по теме Економічна безпека на підприємстві
Отчет по практике по теме Анализ деятельности предприятия ООО ‘ТрансТехСервис-25’
Контрольная работа по теме Сравнение методов решения систем линейных уравнений

5.

2 – Применение систем линейных уравнений

Цели обучения

• (5.2.1) – Решение задач о затратах и ​​доходах
  • Укажите, что представляют переменные в системе линейных уравнений затрат/доходов
  • Определить и применить подходящий метод решения системы
• (5.2.2) – Решение стоимостных задач с помощью системы линейных уравнений
• (5.2.3) – Решение смешанных задач с помощью системы линейных уравнений
• (5.2.4) – Решение задач равномерного движения с помощью системы линейных уравнений

Производитель скейтбордов представляет новую линейку досок. Производитель отслеживает свои затраты, которые представляют собой сумму, которую он тратит на производство плат, и свой доход, который представляет собой сумму, которую он зарабатывает на продаже своих плат. Как компания может определить, получает ли она прибыль от своей новой линии? Сколько скейтбордов нужно произвести и продать, чтобы можно было получить прибыль?

(кредит: Томас Серенес)

Используя то, что мы узнали о системах уравнений, мы можем вернуться к проблеме изготовления скейтборда в начале раздела. Функция дохода производителя скейтбордов — это функция, используемая для расчета суммы денег, поступающей в бизнес. Его можно представить уравнением [латекс]R=xp[/латекс], где [латекс]х=[/латекс] количество и [латекс]р=[/латекс] цена. Функция дохода показана оранжевым цветом на графике ниже.

Функция стоимости — это функция, используемая для расчета затрат на ведение бизнеса. Он включает постоянные затраты, такие как арендная плата и заработная плата, и переменные затраты, такие как коммунальные услуги. Функция стоимости показана синим цветом на графике ниже. Ось [latex]x[/latex] представляет количество в сотнях единиц. Ось и представляет либо затраты, либо доход в сотнях долларов.

Точка, в которой пересекаются две линии, называется точкой безубыточности . Из графика видно, что при производстве 700 единиц стоимость составляет 3300 долларов, а выручка также составляет 3300 долларов. Другими словами, компания безубыточна, даже если она произведет и продаст 700 единиц. Они не зарабатывают и не теряют деньги.

Заштрихованная область справа от точки безубыточности представляет объемы, при которых компания получает прибыль. Заштрихованная область слева представляет объемы, по которым компания несет убытки. Функция прибыли представляет собой функцию дохода минус функция затрат, записанную как [латекс]Р\влево(х\вправо)=R\влево(х\вправо)-С\влево(х\вправо)[/латекс]. Очевидно, что знание количества, при котором затраты равны выручке, имеет большое значение для бизнеса.

Пример

Компания хочет производить велосипедные рамы. Прежде чем они начнут производство, они должны убедиться, что они могут получать прибыль от материалов и рабочей силы, которые у них есть. Их бухгалтер дал им уравнение затрат [латекс]y=0,85x+35,000[/латекс] и уравнение дохода [латекс]у=1,55х[/латекс]:

1. Интерпретация x и y для уравнения затрат
2. Интерпретация x и y для уравнения дохода

Показать раствор

Пример: нахождение точки безубыточности и функции прибыли с помощью подстановки

Учитывая функцию затрат [латекс]C\влево(х\вправо)=0,85x+35 000[/латекс] и функцию дохода [латекс]R\влево(х\вправо)=1,55x[/латекс], найдите точка безубыточности и функция прибыли.

Решение

Редко можно получить уравнения, которые четко моделируют поведение, с которым вы сталкиваетесь в бизнесе, скорее, вы столкнетесь с ситуацией, для которой вам известна ключевая информация, как в приведенном выше примере. Ниже мы суммируем три ключевых фактора, которые помогут вам преобразовать ситуацию в систему.

Как: Дана ситуация, представляющая систему линейных уравнений, напишите систему уравнений и найдите решение.

1) Определить неизвестные величины в задаче, представить их переменными.

2) Напишите систему уравнений, моделирующую условия задачи.

3) Решите систему.

4) Проверьте предлагаемое решение.

Теперь давайте попрактикуемся в применении этих ключевых факторов. В следующем примере мы определяем, сколько различных типов билетов продано, учитывая информацию об общем доходе и количестве билетов, проданных на мероприятие.

Пример: Написание и решение системы уравнений с двумя переменными

Стоимость билета в цирк составляет 25 долларов США для детей и 50 долларов США для взрослых. В определенный день посещаемость цирка составляет 2000 человек, а общий доход от продажи билетов составляет 70 000 долларов. Сколько детей и сколько взрослых купили билеты?

Решение

В этом видео-примере мы покажем, как составить систему линейных уравнений, представляющую общую стоимость посещения музея.

Try It

Билеты в цирк стоят 4 доллара для детей и 12 долларов для взрослых. Если было куплено 1650 талонов на питание на общую сумму 14 200 долларов, сколько детей и сколько взрослых купили талоны на питание?

Решение

Иногда система может сообщить о решении. В нашем следующем примере мы помогаем ответить на вопрос: «Какая компания по аренде грузовиков даст наибольшую ценность?»

Пример: построение системы линейных моделей для выбора компании по аренде грузовиков

Джамал выбирает между двумя компаниями по аренде грузовиков. Первый, Keep on Trucking, Inc., взимает авансовый платеж в размере 20 долларов, а затем 59 центов за милю. Второй, Move It Your Way, взимает авансовый платеж в размере 16 долларов, а затем 63 цента за милю. ^[1] Когда компания Keep on Trucking, Inc. станет лучшим выбором для Джамала?

Решение

Одним из применений систем уравнений являются задачи о смесях. Смешанные задачи — это задачи, в которых два разных решения смешиваются вместе, в результате чего получается новое окончательное решение. Раствор представляет собой смесь двух или более различных веществ, таких как вода и соль или уксус и масло. Большинство биохимических реакций происходят в жидких растворах, что делает их важными для понимания врачами, медсестрами и исследователями. Есть много других дисциплин, которые также используют решения.

Концентрация или крепость жидкого раствора часто выражается в процентах. Это число исходит из отношения того, сколько массы находится в определенном объеме жидкости. Например, если у вас есть 50 граммов соли в 100 мл воды, у вас есть 50% раствор соли, основанный на следующем соотношении:

[латекс]\фракция{50\текст{грамм}}}{100\текст{мл}} =0,50\frac{\text{ грамм}}{\text{мл}}=50\text{ % }[/latex]

Растворы, используемые для большинства целей, обычно поставляются производителями в готовых концентрациях, поэтому, если вам нужно пользовательская концентрация, вам нужно будет смешать две разные силы. В этом разделе мы попрактикуемся в написании уравнений, представляющих результат смешивания растворов двух разных концентраций.

Мы будем использовать следующую таблицу, чтобы решить проблемы со смесями:

	Сумма	Концентрация (%)	Всего
Решение 1
Решение 2
Окончательное решение

Чтобы продемонстрировать, почему таблица полезна при решении неизвестных количеств или концентраций раствора, рассмотрим два смешанных вместе раствора, один из которых содержит 120 мл 9% раствора, а другой 75мл 23% раствора. Если мы смешаем оба этих раствора вместе, мы получим новый объем и новую массу растворенного вещества, и с их помощью мы сможем найти новую концентрацию.

Сначала найдите общую массу твердых веществ для каждого раствора, умножив объем на концентрацию.

	Сумма	Концентрация (%)	Общая масса
Решение 1	120 мл	0,09 [латекс]\frac{\text{грамм}}{\text{мл}}[/латекс]	[латекс]\влево(120\отмена{\текст{мл}}\вправо)\влево(0,09\фракция{\текст{грамм}}{\отмена{\текст{мл}}}\вправо)=10,8\ текст{ грамм}[/латекс]
Решение 2	75 мл	0,23 [латекс]\frac{\text{грамм}}{\text{мл}}[/латекс]	[латекс]\влево(75\отмена{\текст{мл}}\вправо)\влево(0,23\гидроразрыва{\текст{грамм}}{\отменить{\текст{мл}}}\вправо)=17,25\ текст{ грамм}[/латекс]
Окончательное решение

Далее добавляем новые объемы и новые массы.

	Сумма	Концентрация (%)	Общая масса
Решение 1	120 мл	0,09 [латекс]\frac{\text{грамм}}{\text{мл}}[/латекс]	[латекс]\влево(120\отмена{\текст{мл}}\вправо)\влево(0,09\фракция{\текст{грамм}}{\отмена{\текст{мл}}}\вправо)=10,8\ текст { грамм }[/латекс]
Решение 2	75 мл	0,23 [латекс]\frac{\text{грамм}}{\text{мл}}[/латекс]	[латекс]\влево(75\отмена{\текст{мл}}\вправо)\влево(0,23\гидроразрыва{\текст{грамм}}{\отменить{\текст{мл}}}\вправо)=17,25\ текст{ грамм}[/латекс]
Окончательное решение	195 мл	[латекс]\frac{28,05\text{ грамм}}{ 195 \text{мл}}=0,14=14\text{ % }[/latex]	[латекс]10,8\текст{грамм}+17,25\текст{грамм}=28,05\текст{грамм}[/латекс]

Теперь мы использовали математические операции для описания результата смешивания двух различных растворов. Мы знаем новый объем, концентрацию и массу растворенного вещества в новом растворе. В следующих примерах вы увидите, что мы можем использовать таблицу, чтобы найти неизвестный конечный объем или концентрацию. Эти задачи могут иметь одну или две переменные. Мы начнем с задач с одной переменной, затем перейдем к задачам с двумя переменными.

Пример

У химика есть 70 мл 50% раствора метана. Сколько 80%-ного раствора она должна добавить, чтобы конечный раствор состоял из 60%-го метана?

Показать решение

Приведенная выше задача показывает, как мы можем использовать таблицу смесей, чтобы определить уравнение, которое нужно решить для неизвестного объема. В следующем примере мы начнем с двух известных концентраций и используем систему уравнений, чтобы найти два начальных объема, необходимых для достижения заданной конечной концентрации.

Пример

У фермера есть два вида молока: одно с содержанием молочного жира 24%, а другое с содержанием молочного жира 18%. Сколько каждого из них он должен использовать, чтобы в конечном итоге получить 42 галлона 20%-го молочного жира?

Показать решение

 

В следующем видео вам будет показан пример решения задачи о смеси без использования таблицы и интерпретация результатов.

Многие реальные приложения равномерного движения возникают из-за влияния потоков воды или воздуха на фактическую скорость транспортного средства. Полеты на самолетах по пересеченной местности в Соединенных Штатах обычно занимают больше времени на запад, чем на восток из-за преобладающих ветров.

Давайте посмотрим на лодку, плывущую по реке. В зависимости от того, в каком направлении движется лодка, течение воды либо замедляет ее, либо ускоряет.

На рисунках ниже показано, как течение реки влияет на скорость, с которой движется лодка. Обозначим скорость лодки в стоячей воде [latex]b[/latex] , а скорость течения реки [latex]c[/latex].

Лодка плывет вниз по течению, в том же направлении, что и течение реки. Течение помогает толкать лодку, поэтому фактическая скорость лодки больше, чем ее скорость в стоячей воде. Фактическая скорость, с которой движется лодка, равна [latex]b+c[/latex].

Теперь лодка идет вверх по течению, против течения реки. Течение идет против лодки, поэтому фактическая скорость лодки меньше, чем ее скорость в стоячей воде. Фактическая скорость лодки [латекс]b-c[/латекс].

В следующем примере мы добавим некоторые числа к этой ситуации.

ПРИМЕР

Переведите в систему уравнений и затем решите.

Речной круизный лайнер проплыл 60 миль вниз по течению за 4 часа, а затем 5 часов плыл вверх по течению, чтобы вернуться к пристани. Найдите скорость корабля в стоячей воде и скорость течения реки.

Показать ответ

В следующем видео мы представляем еще один пример задачи о равномерном движении, которую можно решить с помощью системы линейных уравнений.

---

1. Курсы получены 2 августа 2010 г. с сайтов http://www.budgettruck.com и http://www.uhaul.com/ ↵

Решение систем линейных уравнений с использованием исключения

Горячая математика

Системы линейных уравнений:

А система линейные уравнения представляет собой просто набор из двух или более линейных уравнений.

В двух переменных ( Икс а также у ) , график системы двух уравнений представляет собой пару прямых на плоскости.

Есть три возможности:

• Линии пересекаются в нулевых точках. (Прямые параллельны.)
• Линии пересекаются ровно в одной точке. (Большинство случаев.)
• Прямые пересекаются в бесконечном числе точек. (Два уравнения представляют одну и ту же прямую.)

Как решить систему линейных уравнений методом исключения (он же метод сложения, он же метод линейной комбинации)

• Шаг 1 : Прибавьте (или вычтите) число, кратное одному уравнению, к другому уравнению (или из него) таким образом, чтобы Икс -термины или у -термины отменяются.
• Шаг 2 : Затем решите для Икс (или же у , в зависимости от того, что осталось) и подставьте обратно, чтобы получить другую координату.

Откуда мы знаем, что линейное уравнение, полученное сложением первого уравнения со скалярным умножением второго, эквивалентно первому?

Возьмем пример. Рассмотрим систему

3 Икс + 2 у знак равно 3 Икс − у знак равно − 4 .

Рассмотрим уравнение, полученное умножением второго уравнения на константу м а затем добавить полученное уравнение к первому.

То есть, ( 3 Икс + 2 у ) + м ( Икс − у ) знак равно ( 3 ) + м ( − 4 ) .

Нам нужно доказать, что это уравнение эквивалентно уравнению 3 Икс + 2 у знак равно 3 .

У нас есть Икс − у знак равно − 4 ⇒ м ( Икс − у ) знак равно − 4 м .

С м ( Икс − у ) знак равно − 4 м , вычесть м ( Икс − у ) с левой стороны и − 4 м из правой части уравнения ( 3 Икс + 2 у ) + м ( Икс − у ) знак равно ( 3 ) − 4 м который сохранит равновесие.

( 3 Икс + 2 у ) + м ( Икс − у ) − м ( Икс − у ) знак равно ( 3 ) − 4 м − ( − 4 м )

Отменив общие условия, мы получим, 3 Икс + 2 у знак равно 3 что эквивалентно первому уравнению.

Поэтому системы уравнений 3 Икс + 2 у знак равно 3 Икс − у знак равно − 4 а также ( 3 Икс + 2 у ) + м ( Икс − у ) знак равно 3 + м ( − 4 ) Икс − у знак равно − 4 эквивалентны.

В общем случае для любой системы уравнений К знак равно л а также п знак равно Вопрос , можно показать, что К + м п знак равно л + м Вопрос эквивалентно К знак равно л .

Пример:

Решите систему { 4 Икс + 3 у знак равно − 2 8 Икс − 2 у знак равно 12

Умножьте первое уравнение на − 2 и добавьте результат ко второму уравнению.

− 8 Икс − 6 у знак равно 4 8 Икс − 2 у знак равно 12 _ − 8 у знак равно 16

Решить для у .

у знак равно − 2

Замена для у в любом из исходных уравнений и решить для Икс .

4 Икс + 3 ( − 2 ) знак равно − 2 4 Икс − 6 знак равно − 2 4 Икс знак равно 4 Икс знак равно 1

Решение ( 1 , − 2 ) .

9.8: Решение систем с правилом Крамера

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

1390

• OpenStax
• OpenStax

Цели обучения

• Оценить детерминанты 2 × 2.
• Используйте правило Крамера, чтобы решить систему уравнений с двумя переменными.
• Оценить 3 × 3 определителя.
• Используйте правило Крамера, чтобы решить систему из трех уравнений с тремя переменными.
• Знать свойства определителей.

Мы научились решать системы уравнений с двумя переменными и тремя переменными, а также несколькими методами: подстановкой, сложением, методом исключения Гаусса, использованием обратной матрицы и построением графика. Некоторые из этих методов легче применять, чем другие, и они более подходят в определенных ситуациях. В этом разделе мы изучим еще две стратегии решения систем уравнений.

Вычисление определителя матрицы 2 × 2

Определитель — это действительное число, которое может быть очень полезным в математике, поскольку оно имеет множество применений, например, для вычисления площади, объема и других величин. Здесь мы будем использовать определители, чтобы выяснить, является ли матрица обратимой, используя элементы квадратной матрицы, чтобы определить, существует ли решение системы уравнений. Однако, возможно, одним из наиболее интересных приложений является их использование в криптографии. Защищенные сигналы или сообщения иногда отправляются закодированными в матрице. Данные могут быть расшифрованы только с помощью обратимой матрицы и определителя. Для наших целей мы сосредоточимся на определителе как признаке обратимости матрицы. Вычисление определителя матрицы включает в себя следование определенным шаблонам, описанным в этом разделе.

НАЙТИ ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ 2 × 2

Определитель матрицы 2 × 2, заданный

\(A=\begin{bmatrix}a&b\\c&d\end{bmatrix}\)

равен определяется как

Обратите внимание на изменение обозначения. Есть несколько способов указать определитель, в том числе \(\det(A)\) и замена скобок в матрице прямыми, \(| A |\).

Пример \(\PageIndex{1}\): нахождение определителя матрицы \(2 × 2\)

Найдите определитель данной матрицы.

\(A=\begin{bmatrix}5&2\\−6&3\end{bmatrix}\)

Решение

\[\begin{align*} \det(A)&= \begin{vmatrix} 5&2\\-6&3\end{vmatrix}\\ &= 5(3)-(-6)(2)\\ &= 27 \end{align*}\]

Использование правила Крамера для решения системы из двух Уравнения с двумя переменными

Теперь мы представим последний метод решения систем уравнений, использующий определители. Известен как Правило Крамера , этот метод восходит к середине 18 века и назван в честь его новатора, швейцарского математика Габриэля Крамера (1704-1752), который представил его в 1750 году в Introduction à l’Analyse des lignes Courbes algébriques . Правило Крамера — жизнеспособный и эффективный метод поиска решений систем с произвольным числом неизвестных при условии, что у нас есть такое же количество уравнений, как и неизвестных.

Правило Крамера даст нам единственное решение системы уравнений, если она существует. Однако, если система не имеет решения или имеет бесконечное число решений, на это будет указывать нулевой определитель. Чтобы выяснить, является ли система противоречивой или зависимой, придется использовать другой метод, такой как исключение.

Чтобы понять правило Крамера, давайте внимательно посмотрим, как мы решаем системы линейных уравнений, используя основные операции со строками. Рассмотрим систему двух уравнений с двумя переменными.

\[\begin{align} a_1x+b_1y&= c_1 (1) \label{eq1}\\ a_2x+b_2y&= c_2 (2) \label{eq2}\\ \end{align}\]

Исключаем одну переменную, используя операции со строками, и решить для другой. Скажем, что мы хотим найти \(x\). Если уравнение \ref{eq2} умножается на коэффициент, противоположный коэффициенту \(y\) в уравнении \ref{eq1}, уравнение \ref{eq1} умножается на коэффициент \(y\) в уравнении \ref {eq2}, и мы добавим два уравнения, переменная \(y\) будет исключена.

\[\begin{align*} &b_2a_1x+b_2b_1y = b_2c_1 & \text{Умножить }R_1 \text{ на }b_2 \\ -&\underline{b_1a_2x-b_1b_2y=-b_1c_2} & \text{Умножить }R_2 \ text{ by }−b_1 \\ & b_2a_1x−b_1a_2x=b_2c_1−b_1c_2 \end{align*}\]

Теперь найдите \(x\).

\[\begin{align*} b_2a_1x−b_1a_2x &= b_2c_1−b_1c_2 \\ x(b_2a_1−b_1a_2) &= b_2c_1−b_1c_2 \\ x &= \dfrac{b_2c_1−b_1c_2}{b_2a_1−b_1a_2}=\ dfrac{\begin{bmatrix}c_1&b_1\\c_2&b_2\end{bmatrix}}{\begin{bmatrix}a_1&b_1\\a_2&b_2\end{bmatrix}} \end{align*}\]

Аналогично, чтобы найти \(y\), мы исключим \(x\).

\[\begin{align*} & a_2a_1x+a_2b_1y = a_2c_1 & \text{Multiply }R_1 \text{ by }a_2 \\ -& \underline{a_1a_2x-a_1b_2y=-a_1c_2} & \text{Multiply }R_2 \text{ by }-a_1 \\ & a_2b_1y-a_1b_2y =a_2c_1-a_1c_2 \end{align*}\]

Решение для \(y\) дает

\[ \begin{align*} a_2b_1y-a_1b_2y &= a_2c_1−a_1c_2 \\ y(a_2b_1−a_1b_2) &= a_2c_1−a_1c_2 \\ y &= \dfrac{a_2c_1−a_1c_2}{a_2b_1−a_1b_2}=\dfrac{a_1c_2−a_2c_1}{a_1b_2−a_2b_1}=\dfrac{ \begin{bmatrix}a_1&c_1\\a_2&c_2\end{bmatrix}}{\begin{bmatrix}a_1&b_1\\a_2&b_2\end{bmatrix}} \end{align*}\]

Обратите внимание, что знаменатель как для \(x\), так и для \(y\) является определителем матрицы коэффициентов.

Мы можем использовать эти формулы для нахождения \(x\) и \(y\), но правило Крамера также вводит новые обозначения: детерминанты. Тогда мы можем выразить \(x\) и \(y\) как частное двух определителей.

ПРАВИЛО КРАМЕРА ДЛЯ СИСТЕМ \(2×2\)

Правило Крамера — это метод, использующий определители для решения систем уравнений, в которых число уравнений равно количеству переменных.

Рассмотрим систему двух линейных уравнений с двумя переменными.

\[\begin{align*} a_1x+b_1y&= c_1\\ a_2x+b_2y&= c_2 \end{align*}\]

Решение с использованием правила Крамера дается как

\[\begin{align} x& = \dfrac{D_x}{D} = \dfrac{\begin{bmatrix}c_1&b_1\\c_2&b_2\end{bmatrix}}{\begin{bmatrix}a_1&b_1\\a_2&b_2\end{bmatrix}}\; , D\neq 0\\ y&= \dfrac{D_y}{D} = \dfrac{\begin{bmatrix}a_1&c_1\\a_2&c_2\end{bmatrix}}{\begin{bmatrix}a_1&b_1\\a_2&b_2\end{bmatrix }}\; , D\neq 0 \end{align}\]

Если мы находим \(x\), столбец \(x\) заменяется столбцом констант. Если мы ищем \(y\), столбец \(y\) заменяется постоянным столбцом.

Пример \(\PageIndex{2}\): использование правила Крамера для решения системы \(2 × 2\)

Решите следующую систему \(2 × 2\), используя правило Крамера.

\[\begin{align*} 12x+3y&= 15\\ 2x-3y&= 13 \end{align*}\]

Решение

Найдите \(x\).

\[\begin{align*} x&= \dfrac{D_x}{D}\\ &= \dfrac{\begin{bmatrix}15&3\\13&-3\end{bmatrix}}{\begin{bmatrix} 12&3\\2&-3\end{bmatrix}}\\ &= \dfrac{-45-39}{-36-6}\\ &= \dfrac{-84}{-42}\\ &= 2 \end{align*}\]

Найдите \(y\).

\[\begin{align*} y&= \dfrac{D_y}{D}\\ &= \dfrac{\begin{bmatrix}12&15\\2&13\end{bmatrix}}{\begin{bmatrix}12&3\ \2&-3\end{bmatrix}}\\ &= \dfrac{156-30}{-36-6}\\ &= -\dfrac{126}{42}\\ &= -3 \end{align *}\]

Решение: \((2,−3)\).

Упражнение \(\PageIndex{1}\)

Используйте правило Крамера для решения системы \(2 × 2\) уравнений.

\[\begin{align*} x+2y&= -11\\ -2x+y&= -13 \end{align*}\]

Ответ

\((3,−7)\)

Вычисление определителя матрицы 3 × 3

Найти определитель матрицы 2 × 2 несложно, но определить определитель матрицы 3 × 3 сложнее. Один из методов состоит в том, чтобы дополнить матрицу 3×3 повторением первых двух столбцов, получив матрицу 3×5. Затем вычисляем сумму произведений записей вниз по по каждой из трех диагоналей (слева вверху справа внизу) и вычесть произведения записей вверх по по каждой из трех диагоналей (слева снизу вверх справа). Это легче понять с визуальным и пример.

Найдите определитель матрицы 3×3.

\(A=\begin{bmatrix}a_1&b_1&c_1\\a_2&b_2&c_2\\a_3&b_3&c_3\end{bmatrix}\)

1. Дополнить \(A\) первыми двумя столбцами.

   \(\det(A)=\left| \begin{array}{ccc|cc} a_1&b_1&c_1&a_1&b_1\\a_2&b_2&c_2&a_2&b_2\\a_3&b_3&c_3&a_3&b_3\end{array} \right|\)

2. От верхнего левого угла к нижнему правому: умножьте числа по первой диагонали. Прибавьте результат к произведению записей по второй диагонали. Добавьте этот результат к произведению записей вниз по третьей диагонали.
3. Из нижнего левого угла в верхний правый: вычтите произведение записей вверх по первой диагонали. Из этого результата вычтите произведение вхождений вверх по второй диагонали. Из этого результата вычтите произведение вхождений вверх по третьей диагонали.

Алгебра выглядит следующим образом:

\(| A |=a_1b_2c_3+b_1c_2a_3+c_1a_2b_3−a_3b_2c_1−b_3c_2a_1−c_3a_2b_1\)

Пример определения {3} индекса × 3 Matrix

Найдите определитель матрицы \(3 × 3\) по данным

\(A=\begin{bmatrix}0&2&1\\3&−1&1\\4&0&1\end{bmatrix}\)

Решение

Дополните матрицу первыми двумя столбцами и следуйте формуле. Таким образом,

\[\begin{align*} | А | &= \влево| \begin{массив}{ccc|cc}0&2&1&0&2\\3&-1&1&3&-1\\4&0&1&4&0\end{массив}\right| \\ &= 0(−1)(1)+2(1)(4)+1(3)(0)−4(−1)(1)−0(1)(0)−1(3) (2) \\ &=0+8+0+4−0−6 \\ &= 6 \end{align*}\]

Упражнение \(\PageIndex{2}\)

Найдите определитель Матрица 3 × 3.

\(\det(A)=\begin{vmatrix}1&−3&7\\1&1&1\\1&−2&3\end{vmatrix}\)

Ответ

\(−10\)

Вопросы и ответы: Можно ли использовать тот же метод для нахождения определителя матрицы большего размера?

Нет, этот метод работает только для матриц 2 × 2 и 3 × 3. Для больших матриц лучше всего использовать графическую утилиту или компьютерное программное обеспечение.

Использование правила Крамера для решения системы трех уравнений с тремя переменными

Теперь, когда мы можем найти определитель матрицы \(3 × 3\), мы можем применить правило Крамера для решения системы трех уравнений с тремя переменными переменные. Правило Крамера является простым и следует шаблону, согласующемуся с правилом Крамера для матриц \(2 × 2\). Однако по мере увеличения порядка матрицы до \(3 × 3\) требуется гораздо больше вычислений.

Когда мы вычисляем, что определитель равен нулю, правило Крамера не указывает, имеет ли система решение или бесконечное число решений. Чтобы выяснить это, мы должны выполнить исключение в системе.

Рассмотрим систему уравнений \(3 × 3\).

\[\begin{align} a_1x+b_1y+c_1z &= \color{blue}d_1 \\ a_2x+b_2y+c_2z &= \color{blue}d_2 \\ a_3x+b_3y+c_3z &= \color{blue }d_3 \\ \end{align}\]

\(x=\dfrac{D_x}{D}\), \(y=\dfrac{D_y}{D}\), \(z=\dfrac{ D_z}{D}\), \(D≠0\)

где

\[D = \begin{vmatrix} a_1 & b_1 & c_1\\ a_2 & b_2 & c_2\\ a_3 & b_3 & c_3 \end{vmatrix}\; ,\; D_x = \begin{vmatrix} \color{blue}d_1 & b_1 & c_1\\ \color{blue}d_2 & b_2 & c_2\\ \color{blue}d_3 & b_3 & c_3 \end{vmatrix}\; ,\; D_y = \begin{vmatrix} a_1 & \color{blue}d_1 & c_1\\ a_2 & \color{blue}d_2 & c_2\\ a_3 & \color{blue}d_3 & c_3 \end{vmatrix}\; ,\; D_z = \begin{vmatrix} a_1 & b_1 & \color{blue}d_1\\ a_2 & b_2 & \color{blue}d_2\\ a_3 & b_3 & \color{blue}d_3 \end{vmatrix}\]

Если мы записываем определитель \(D_x\), мы заменяем столбец \(x\) постоянным столбцом. Если мы записываем определитель \(D_y\), мы заменяем их столбец y на постоянный столбец. Если мы записываем определитель \(D_z\), мы заменяем столбец \(z\) постоянным столбцом. Всегда проверяйте ответ.

Пример \(\PageIndex{4}\): решение системы \(3 × 3\) с помощью правила Крамера

Найдите решение данной системы \(3 × 3\) с помощью правила Крамера.

\[\begin{align*} x+y-z&= 6\\ 3x-2y+z&= -5\\ x+3y-2z&= 14 \end{align*}\]

Решение

Используйте правило Крамера.

\(D=\begin{vmatrix}1&1&−1\\3&−2&1\\1&3&−2\end{vmatrix}\), \(D_x=\begin{vmatrix}6&1&−1\\−5&−2&1 \\14&3&-2\end{vmatrix}\), \(D_y=\begin{vmatrix}1&6&-1\\3&-5&1\\1&14&-2\end{vmatrix}\), \(D_z=\begin{ vmatrix}1&1&6\\3&-2&-5\\1&3&14\end{vmatrix}\)

Затем

\[\begin{align*} x&= \dfrac{D_x}{D}&= \dfrac{- 3}{-3}&= 1\\ y&= \dfrac{D_y}{D}&= \dfrac{-9}{-3}&= 3\\ z&= \dfrac{D_z}{D}&= \dfrac{6}{-3}&= -2\\ \end{align*}\]

Решение \((1,3,−2)\).

Упражнение \(\PageIndex{3}\)

Используйте правило Крамера для решения матрицы \(3 × 3\).

\[\begin{align*} x-3y+7z&= 13\\ x+y+z&= 1\\ x-2y+3z&= 4 \end{align*}\]

Ответ

\(\влево(−2,\dfrac{3}{5},\dfrac{12}{5}\вправо)\)

Пример \(\PageIndex{5A}\): использование правила Крамера для решения несогласованной системы

Решите систему уравнений по правилу Крамера.

\[\begin{align} 3x-2y&= 4 \label{eq3}\\ 6x-4y&= 0 \label{eq4}\end{align}\]

Решение

Начнем с нахождения определители \(D\), \(D_x\) и \(D_y\).

\(D=\begin{vmatrix}3&−2\\6&−4\end{vmatrix}=3(−4)−6(−2)=0\)

Мы знаем, что определитель нуля означает либо система не имеет решений, либо имеет бесконечное число решений. Чтобы увидеть, какой из них, мы используем процесс исключения. Наша цель — исключить одну из переменных.

1. Умножить уравнение \ref{eq3} на \(−2\).
2. Добавьте результат к уравнению \ref{eq4}.

\[\begin{align*} &−6x+4y=−8 \\ &\;\;\;\underline{6x−4y=0} \\ &\;\;\;\;\;\ ;\;\;\;\; 0=−8 \end{align*}\]

Получаем уравнение \(0=−8\), которое неверно. Следовательно, система не имеет решений. График системы показывает две параллельные линии. См. рисунок \(\PageIndex{1}\).

Рисунок \(\PageIndex{1}\)

Пример \(\PageIndex{5B}\): использование правила Крамера для решения зависимой системы

Решите систему с бесконечным числом решений.

\[\begin{align} x-2y+3z&= 0 \label{eq5}\\ 3x+y-2z&= 0 \label{eq6}\\ 2x-4y+6z&= 0 \label{eq7} \ end{align}\]

Решение

Сначала найдем определитель. Настройте матрицу, дополненную первыми двумя столбцами.

\(\left| \begin{array}{ccc|cc}1&−2&3&1&-2\\3&1&−2&3&1\\2&−4&6&2&-4\end{array}\right|\)

Затем

\(1(1)(6)+(−2)(−2)(2)+3(3)(−4)−2(1)(3)−(−4)(−2)( 1)−6(3)(−2)=0\)

Поскольку определитель равен нулю, решения либо нет, либо существует бесконечное число решений. Мы должны выполнить исключение, чтобы узнать.

1. Умножьте уравнение \ref{eq5} на \(−2\) и добавьте результат к уравнению \ref{eq7}:

\[\begin{align*} &−2x+4y−6x=0 \ \ &\;\;\underline{2x−4y+6z=0} \\ &\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \;0=0 \end{align*}\]

2. Получение ответа \(0=0\), утверждение, которое всегда верно, означает, что система имеет бесконечное число решений. Изобразив систему, мы видим, что две плоскости одинаковы и обе пересекают третью плоскость по прямой. См. рисунок \(\PageIndex{2}\).

Рисунок \(\PageIndex{2}\)

Понимание свойств определителей

У определителей много свойств. Здесь перечислены некоторые свойства, которые могут быть полезны при вычислении определителя матрицы.

СВОЙСТВА ОПРЕДЕЛИТЕЛЕЙ

1. Если матрица имеет верхнетреугольную форму, определитель равен произведению элементов по главной диагонали.
2. При перестановке двух строк определитель меняет знак.
3. Если две строки или два столбца совпадают, определитель равен нулю. 9{−1}\) — величина, обратная определителю матрицы \(A\).
4. Если какая-либо строка или столбец умножается на константу, определитель умножается на тот же коэффициент.

Пример \(\PageIndex{6}\): Иллюстрация свойств определителей

Проиллюстрируйте каждое из свойств определителей.

Решение

Свойство 1 гласит, что если матрица имеет форму верхнего треугольника, определитель равен произведению элементов, расположенных вниз по главной диагонали.

\(A=\begin{bmatrix}1&2&3\\0&2&1\\0&0&-1\end{bmatrix}\)

Дополнить \(A\) первыми двумя столбцами.

\(A=\left[ \begin{array}{ccc|cc}1&2&3&1&2\\0&2&1&0&2\\0&0&−1&0&0\end{array}\right]\)

Затем

\[\begin{align* } \det(A)&= 1(2)(-1)+2(1)(0)+3(0)(0)-0(2)(3)-0(1)(1)+1 (0)(2)\\ &= -2 \end{align*}\]

Свойство 2 утверждает, что перестановка строк меняет знак. Учитывая

\[\begin{align*} A&=\begin{bmatrix}-1&5\\4&-3\end{bmatrix}\\ \det(A)&= (-1)(-3)-(4) (5)\\ &= 3-20\\ &= -17 \end{align*}\]

\[\begin{align*} B&= \begin{bmatrix}4&-3\\-1&5\end {bmatrix}\\ \det(B)&= (4)(5)-(-1)(-3)\\ &= 20-3\\ &= 17 \end{align*}\]

Свойство 3 утверждает, что если две строки или два столбца идентичны, определитель равен нулю.

\[\begin{align*} A&=\left[ \begin{array}{ccc|cc}1&2&2&1&2\\2&2&2&2&2\\-1&2&2&-1&2\end{массив}\right]\\ \det(A) &=1(2)(2)+2(2)(-1)+2(2)(2)+1(2)(2)-2(2)(1)-2(2)(2) \\ &=4-4+8+4-4-8\\ &=0 \end{align*}\] 9{-1})&=-2\left(-\dfrac{1}{2}\right)-\dfrac{3}{2}(1)\\ &=-\dfrac{1}{2} \ end{align*}\]

Свойство 6 гласит, что если любая строка или столбец матрицы умножается на константу, определитель умножается на тот же коэффициент. Таким образом,

\[\begin{align*} A&=\begin{bmatrix}1&2\\3&4\end{bmatrix}\\ \det(A)&=1(4)-2(3)\\ &= -2 \end{align*}\]

\[\begin{align*} B&=\begin{bmatrix}2(1)&2(2)\\3&4\end{bmatrix}\\ \det(B) &=2(4)-3(4)\\ &=-4 \end{align*}\]

Пример \(\PageIndex{7}\): использование правила Крамера и свойств определителя для решения системы

Найдите решение заданной системы \(3 × 3\).

\[\begin{align} 2x+4y+4z&=2 \label{eq8}\\ 3x+7y+7z&=-5 \label{eq9}\\ x+2y+2z&=4 \label{eq10} \end{align}\]

Решение

Используя правило Крамера, мы имеем

\(D=\begin{bmatrix}2&4&4\\3&7&7\\1&2&2\end{bmatrix}\)

Обратите внимание, что второй и третий столбцы идентичны. Согласно свойству 3 определитель будет равен нулю, поэтому решения либо нет, либо решений бесконечное множество. Мы должны выполнить исключение, чтобы узнать.

1. Умножьте уравнение \ref{eq10} на \(–2\) и добавьте результат к уравнению \ref{eq8}.

\[\begin{align*} -2x-4y-4x&=-8\\ 2x+4y+4z&=2\\ 0&=-6 \end{align*}\]

Получение оператора, который является Противоречие означает, что система не имеет решений.

Медиа

Доступ к этим онлайн-ресурсам для получения дополнительных инструкций и практики с правилом Крамера.

• Решение системы двух уравнений с помощью правила Крамера
• Решите систему из трех уравнений, используя правило Крамера

Ключевые понятия

• Определитель для \(\begin{bmatrix}a&b\\c&d\end{bmatrix}\) равен \(ad-bc\). См. пример \(\PageIndex{1}\).
• Правило Крамера заменяет столбец переменной столбцом константы. Решения: \(x=\dfrac{D_x}{D}\), \(y=\dfrac{D_y}{D}\). См. пример \(\PageIndex{2}\).
• Чтобы найти определитель матрицы \(3×3\), увеличьте первые два столбца. Сложите три диагональных элемента (слева вверху справа внизу) и вычтите три элемента по диагонали (слева внизу справа вверху). См. пример \(\PageIndex{3}\).
• Чтобы решить систему из трех уравнений с тремя переменными с помощью правила Крамера, замените столбец переменных столбцом констант для каждого требуемого решения: \(x=\dfrac{D_x}{D}\), \(y=\dfrac{ D_y}{D}\), \(z=\dfrac{D_z}{D}\).

  No related posts.