Алгебра 7 Макарычев К-3 Уровень 3
Контрольная работа № 3 по алгебре в 7 классе «Функции» с ответами по УМК Макарычев (сложный уровень). Глава II. ФУНКЦИИ И ИХ ГРАФИКИ. Урок 33 поурочного планирования — Алгебра 7 Макарычев К-3 Уровень 3 (варианты 5, 6).
Перейти: Список контрольных по алгебре в 7 классе по УМК Макарычев (Оглавление)
Другие варианты контрольной работы № 3 «Функции»:
К-3 Уровень 1 + Ответы К-3 Уровень 2 + Ответы
Контрольная работа № 3 «Функции»
Уровень 3 (сложный). Варианты 5, 6
К-3. Вариант 5 (транскрипт)
- График линейной функции у = kх + b проходит через точки А (0; –3) и В (2; 0). Постройте график функции и определите функцию (найдите k и b).
- Укажите координаты точек пересечения графика функции у = 2х2 + 3х с осями координат.

- Найдите координаты точки графика функции у = 3х – 7, если эти координаты равны. Постройте график и укажите найденную точку.
- Постройте график зависимости |у – 2х + 1| = 2.
- Найдите точку пересечения графиков функций у = 7х – 31 и у = 2х – 6.
- Постройте график зависимости |х + 1| + |х – 1| = 2.
К-3. Вариант 6 (транскрипт)
- График линейной функции у = kх + b проходит через точки A (0; 2) и В (–3; 0). Постройте график функции и определите функцию (найдите k и b).
- Укажите координаты точек пересечения графика функции у = 3х2 + 2х с осями координат.
- Найдите координаты точки графика функции у = –3х + 5, если эти координаты равны. Постройте график и укажите найденную точку.
- Постройте график зависимости |у + 2х – 2| = 1.
- Найдите точку пересечения графиков функций у = 9х – 43 и у = 3х – 7.
- Постройте график зависимости |у – 1| + |у + 1| = 2.

Решения и ответы на контрольную работу:
ОТВЕТЫ на Вариант 5
№ 1. у = 1,5х – 3.
№ 2. А (0; 0), В(–3/2; 0).
№ 3. А (3,5; 3,5).
№ 4. См. решение
№ 5. А (5; 4).
№ 6. См. решение
Смотреть РЕШЕНИЯ заданий Варианта 5
ОТВЕТЫ на Вариант 6
№ 1. у = 2/3 • х + 2 = 2х/3 + 2
№ 2. А (0; 0) и В(–2/3; 0).
№ 3. А(5/4; 5/4).
№ 4. См. решение
№ 5. А (6; 11).
№ 6. См. решение
Смотреть РЕШЕНИЯ заданий Варианта 6
Решение контрольная работа 3. вариант номер №2 по Алгебре контрольные работы за 11 класс Глизбург В.И.
Навигация Видеорешения ГдзКлассы
7 8 9 10 11 Контрольная работа по алгебре Номер 3 » линейная функция » 1. 2=17-16=1
2=17-16=1
СВ=1
tgВ=1/4 (m+n)² > (m²-n²) в 2 разаОтвет: (m+n)² = 2· (m²-n²)
Все, что существует вокруг человека и произошло без его участия, называется природой. Человек изучает ее на протяжении многих тысячелетий. Со временем знаний становилось все больше, а сами люди старались глубже постичь природу. Так начали развиваться различные естественные науки. Предметы в природе называются телами, а все, что с ними происходит — явлениями. И тех и других огромное количество, поэтому и естественных наук тоже много. Одни из них изучают вещества и явления, а другие — различные тела. Научная деятельность не только удовлетворяет любопытство, но и реализует практические цели, направленные на улучшение качества жизни человека. Читайте подробнее на: https://natworld.info/raznoe-o-prirode/nauki-izuchajushhie-prirodu-ili-estestvennye-nauki
Одни из них изучают вещества и явления, а другие — различные тела. Научная деятельность не только удовлетворяет любопытство, но и реализует практические цели, направленные на улучшение качества жизни человека. Читайте подробнее на: https://natworld.info/raznoe-o-prirode/nauki-izuchajushhie-prirodu-ili-estestvennye-nauki
© Природа Мира|NatWorld.infoCtg(π/4 — 2x) = √3
— Ctg(2x — π/4) = √3
Ctg(2x — π/4 ) = — √3
2x — π/4 = arcctg(-√3) + πn, n∈Z
2x — π/4 = 5π/6 + πn, n∈Z
2x = 5π/6 + π/6 + πn, n∈Z
2x = π + πn, n∈Z
x = π/2 + (πn)/2 n∈Z
Алгебра 8 Контрольные работы Макарычев
Алгебра 8 Контрольные работы Макарычев — контрольные работы по алгебре в 8 классе с ответами и решениями по УМК Макарычев и др. (6 вариантов, 3 уровня сложности) В учебных целях использованы цитаты из пособия «Александр Рурукин: Алгебра. 8 класс. Поурочные разработки», которое используется в комплекте с учебником «Алгебра 8 класс /
(6 вариантов, 3 уровня сложности) В учебных целях использованы цитаты из пособия «Александр Рурукин: Алгебра. 8 класс. Поурочные разработки», которое используется в комплекте с учебником «Алгебра 8 класс / Макарычев Ю.Н., Миндюк Н.Г. и др (Просвещение)».
Алгебра 8 класс. Контрольные работы
по учебнику Макарычева
Глава I. РАЦИОНАЛЬНЫЕ ДРОБИ
К-1. Контрольная работа по алгебре с ответами «Сумма и разность дробей»
Контрольная работа № 1К-2. Контрольная работа по алгебре с ответами «Рациональные дроби»
Контрольная работа № 2Глава II. КВАДРАТНЫЕ КОРНИ
К-3. Контрольная работа с ответами «Свойства квадратного арифметического корня»
Контрольная работа № 3К-4. Контрольная работа с ответами «Применение свойств квадратного корня»
Контрольная работа № 4Глава III. КВАДРАТНЫЕ УРАВНЕНИЯ
КВАДРАТНЫЕ УРАВНЕНИЯ
К-5. Контрольная по алгебре с ответами «Квадратные уравнения»
Контрольная работа № 5К-6. Контрольная с ответами «Квадратные уравнения. Дробные рациональные уравнения»
Контрольная работа № 6Глава IV. НЕРАВЕНСТВА
К-7. Контрольная работа с ответами «Числовые неравенства и их свойства»
К-8. Контрольная работа по алгебре с ответами «Неравенства»
Глава V. СТЕПЕНЬ С ЦЕЛЫМ ПОКАЗАТЕЛЕМ.
ЭЛЕМЕНТЫ СТАТИСТИКИ
К-9. Контрольная работа с ответами «Степень с целым показателем»
К-10 «Итоговая контрольная работа» за курс 8 класса с ответами и решениями
ПОЯСНЕНИЯ
По прохождении каждой темы предусмотрена контрольная работа, состоящая из заданий трех уровней сложности, которые определяются или учителем, или самим учащимся (при этом число экземпляров вариантов должно быть достаточным). Разумеется, учащиеся должны знать о различной сложности вариантов и критериях оценки контрольной работы.
Разумеется, учащиеся должны знать о различной сложности вариантов и критериях оценки контрольной работы.
Каждая контрольная работа составлена в 6 вариантах различной сложности (варианты 1, 2 самые простые, варианты 3, 4 сложнее и варианты 5, 6 самые сложные). При этом сложность вариантов нарастает не очень резко. Каждый вариант содержит 6 задач примерно одинаковой сложности (может быть, несколько сложнее две последние задачи).
При проверке вариантов 1, 2 оценка «5» ставится за правильное решение пяти задач, оценка «4» — четырех задач и оценка «3» — трех задач. Одна задача является резервной (или запасной) и дает некоторую свободу выбора учащимся. При таких же критериях оценки за решение задач вариантов 3, 4 дается дополнительно 0,5 балла, вариантов 5, 6 — 1 балл (т. е. оценку «5» можно получить за правильное решение четырех задач).
Смотреть ВСЕ КОНТРОЛЬНЫЕ в 8 классе
Вы смотрели: Алгебра 8 Контрольные работы Макарычев — контрольные работы по алгебре в 8 классе с ответами по УМК Макарычев и др.
В учебных целях использованы цитаты из пособия «Александр Рурукин: Алгебра. 8 класс. Поурочные разработки», которое используется в комплекте с учебником «Алгебра 8 класс / Макарычев Ю.Н., Миндюк Н.Г. и др (Просвещение)».Вернуться к Списку уроков Тематического планирования в 8 классе.
Контрольная Решить 3 📝 номера на нахождение производной одной и двух…
1. Сколько стоит помощь?
Цена, как известно, зависит от объёма, сложности и срочности. Особенностью «Всё сдал!» является то, что все заказчики работают со экспертами напрямую (без посредников). Поэтому цены в 2-3 раза ниже.
2. Каковы сроки?
Специалистам под силу выполнить как срочный заказ, так и сложный, требующий существенных временных затрат.
Для каждой работы определяются оптимальные сроки. Например, помощь с курсовой работой – 5-7 дней. Сообщите нам ваши сроки, и мы выполним работу не позднее указанной даты. P.S.: наши эксперты всегда стараются выполнить работу раньше срока. 3. Выполняете ли вы срочные заказы?
Да, у нас большой опыт выполнения срочных заказов.
4. Если потребуется доработка или дополнительная консультация, это бесплатно?
Да, доработки и консультации в рамках заказа бесплатны, и выполняются в максимально короткие сроки.
5. Я разместил заказ. Могу ли я не платить, если меня не устроит стоимость?
Да, конечно — оценка стоимости бесплатна и ни к чему вас не обязывает.
6. Каким способом можно произвести оплату?
Работу можно оплатить множеством способом: картой Visa / MasterCard, с баланса мобильного, в терминале, в салонах Евросеть / Связной, через Сбербанк и т.д.
7. Предоставляете ли вы гарантии на услуги?
На все виды услуг мы даем гарантию. Если эксперт не справится — мы вернём 100% суммы.
8. Какой у вас режим работы?
Мы принимаем заявки 7 дней в неделю, 24 часа в сутки.
ГДЗ за 7 класс по Алгебре М. В. Шуркова контрольные работы
В. Шуркова контрольные работы
gdz-bot.ru
НайтиНавигация по гдз
1 класс
Русский язык
Математика
Английский язык
Окружающий мир
Литература
Информатика
Музыка
Человек и мир
2 класс
Русский язык
Математика
Английский язык
Немецкий язык
Окружающий мир
Литература
Информатика
Музыка
Технология Практический тест по алгебре
(1) Развернуть после
(i) (2x + 3y + 4z) 2
(ii) (−p + 2q + 3r) 2
(iii) (2p + 3) (2p — 4) (2p −5)
(iv) (3a +1) (3a −2) (3a + 4) Решение
(1) Используя алгебраическое тождество, найдите коэффициенты при x 2 , x и константе срок без фактического расширения.
(i) (x + 5) (x + 6) (x + 7)
(ii) (2x + 3) (2x −5) (2x −6) Решение
(2) Если (x + a) (x + b) (x + c) = x 3 + 14x 2 + 59x + 70, найдите значение
(i) a + b + c
(ii) (1 / a ) + (1 / b) + (1 / c)
(iii) a 2 + b 2 + c 2
(iv) (a / bc) + (b / ac) + ( c / ab) Решение
(3) Развернуть:
(i) (3a — 4b) 3
(ii) (x + (1 / y)) 3 Решение
(2) Оцените следующее, используя идентификаторы:
(i) 98 3
(ii) 1001 3 Решение
(3) Если (x + y + z) = 9 и (xy + yz) + zx) = 26, затем найдите значение x 2 + y 2 + z 2 Решение
(4) Найдите 27a 3 + 64b 3 , если 3a + 4b = 10 и ab = 2
Решение
(5) Найдите x 3 — y 3 , если x — y = 5 и xy = 14 Решение
(6) Если a + (1 / a) = 6, затем найдите значение a 3 + 1 / a 3
Решение
(7) Если x 2 + 1 / x 2 = 23, тогда найдите значение
x + (1 / x) и x 3 + (1 / x 3 )
Решение
(8) Если (y — (1 / y)) 3 = 27, затем найдите значение
y 3 — (1 / y) 3
Решение
(9) Упростите:
(i) (2a + 3b + 4c) (4a 2 + 9b 2 + 16c 2 — 6ab — 12bc — 8ca)
(ii) (x −2y + 3z) (x 2 + 4y 2 + 9z 2 + 2xy + 6yz −3xz)
Решение
(10) Используя идентичность, оцените следующее:
(i) 7 3 — 1 0 3 + 3 3
(ii) 1 + (1/8) — (27/8) Решение
(11) Если 2x −3y −4z = 0, то найти 8x 3 — 27y 3 — 64z 3
Решение
Помимо вышеперечисленного, если вам нужны еще какие-либо сведения по математике, воспользуйтесь нашим пользовательским поиском Google здесь.
Если у вас есть какие-либо отзывы о нашей математической информации, напишите нам:
Мы всегда ценим ваши отзывы.
Вы также можете посетить следующие веб-страницы, посвященные различным вопросам математики.
ЗАДАЧИ СО СЛОВАМИ
Задачи со словами HCF и LCM
Задачи со словами на простых уравнениях
Задачи со словами на линейных уравнениях
Проблемы со словами на квадратных уравнениях
7— Ctg(2x — π/4) = √3
Ctg(2x — π/4 ) = — √3
2x — π/4 = arcctg(-√3) + πn, n∈Z
2x — π/4 = 5π/6 + πn, n∈Z
2x = 5π/6 + π/6 + πn, n∈Z
2x = π + πn, n∈Z
x = π/2 + (πn)/2 n∈Z
 (6 вариантов, 3 уровня сложности) В учебных целях использованы цитаты из пособия «Александр Рурукин: Алгебра. 8 класс. Поурочные разработки», которое используется в комплекте с учебником «Алгебра 8 класс /
(6 вариантов, 3 уровня сложности) В учебных целях использованы цитаты из пособия «Александр Рурукин: Алгебра. 8 класс. Поурочные разработки», которое используется в комплекте с учебником «Алгебра 8 класс / по учебнику Макарычева
 КВАДРАТНЫЕ УРАВНЕНИЯ
КВАДРАТНЫЕ УРАВНЕНИЯЭЛЕМЕНТЫ СТАТИСТИКИ
 Разумеется, учащиеся должны знать о различной сложности вариантов и критериях оценки контрольной работы.
Разумеется, учащиеся должны знать о различной сложности вариантов и критериях оценки контрольной работы.

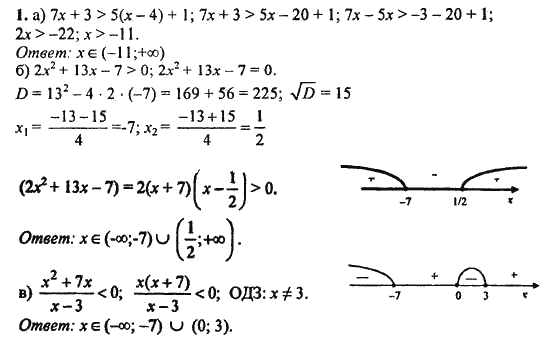
 В. Шуркова контрольные работы
В. Шуркова контрольные работы

задачи на слова 7
Проблемы со словами в поездах
Проблемы со словами по площади и периметру
Проблемы со словами при прямом и обратном изменении
Проблемы со словами по цене за единицу
Проблемы со словом при скорости единицы
задачи по сравнению ставок
Преобразование обычных единиц в текстовые задачи
Преобразование метрических единиц в текстовые задачи
Word задачи по простому проценту
Word задачи по сложным процентам
ngles
Проблемы с дополнительными и дополнительными углами в словах
Проблемы со словами с двойными фактами
Проблемы со словами тригонометрии
Проблемы со словами в процентах
Проблемы со словами в виде прибыли и убытка78 9179 Задачи
Задачи с десятичными словами
Задачи со словами о дробях
Задачи со словами о смешанных фракциях
Одношаговые задачи с уравнениями со словами
Проблемы со словами о линейных неравенствах и пропорциях 9
Задачи со словамиПроблемы со временем и рабочими словами
Задачи со словами на множествах и диаграммах Венна
Проблемы со словами на возрастах
Проблемы со словами из теоремы Пифагора
Процент числового слова проблемы
Проблемы со словами при постоянной скорости
Проблемы со словами при средней скорости
Проблемы со словами при сумме углов треугольника 180 градусов
ДРУГИЕ ТЕМЫ
Сокращения прибыли и убытков
Сокращения в процентах
Сокращения в таблице времен
Сокращения времени, скорости и расстояния
Сокращения соотношения и пропорции
000 Домен и диапазон 9173 рациональных функций функции с отверстиями
График рациональных функций
График рациональных функций с отверстиями
Преобразование повторяющихся десятичных знаков в дроби
Десятичное представление рациональных чисел
Поиск корня из длинного квадрата видение
Л. Метод CM для решения временных и рабочих задач
Метод CM для решения временных и рабочих задач
Преобразование задач со словами в алгебраические выражения
Остаток при делении 2 в степени 256 на 17
Остаток при делении степени 17 на 16 на 16
Сумма всех трехзначных чисел, делимых на 6
Сумма всех трехзначных чисел, делимых на 7
Сумма всех трехзначных чисел, делимых на 8
Сумма всех трехзначных чисел, образованных с использованием 1, 3 , 4
Сумма всех трех четырехзначных чисел, образованных ненулевыми цифрами
Сумма всех трех четырехзначных чисел, образованных с использованием 0, 1, 2, 3
Сумма всех трех четырехзначных чисел числа, образованные с использованием 1, 2, 5, 6
Matrix Рейтинг
Этот урок знакомит с концепцией матрицы с рангом и
объясняет, как ранг
матрица
раскрывается его
эшелонированная форма.
Ранг матрицы
Вы можете представить себе матрицу r x c как набор строк r векторы, каждая имеет c элементов; или вы можете представить его как набор c векторы-столбцы, каждый из которых имеет или элемента.
Ранг матрицы определяется как (а) максимальное количество линейно независимых столбца векторов в матрице или (б) максимальное количество линейно независимых строк векторов в матрице.Оба определения эквивалентны.
Для матрицы r x c матрицы,
- Если r меньше c , то максимальный ранг матрицы составляет r .
- Если r больше c , то максимальный ранг матрицы это c .
Ранг матрицы был бы равен нулю, только если бы матрица не имела элементов. Если бы матрица имела хотя бы один элемент, ее минимальный ранг был бы равен единице.
Если бы матрица имела хотя бы один элемент, ее минимальный ранг был бы равен единице.
How to Find Matrix Рейтинг
В этом разделе мы описываем метод определения ранга любой матрицы. Этот метод предполагает знакомство с эшелонированные матрицы и эшелонные преобразования.
Максимальное количество линейно независимых векторов в матрице равно к количеству ненулевых строк в его матрица эшелонов строк. Следовательно, чтобы найти ранг матрицы, мы просто преобразовать матрицу в ее форму эшелона строк и подсчитать количество ненулевые строки.
Рассмотрим матрицу A и ее ряд строк.
матрица, A исх. .Ранее мы показывали
как найти форму эшелона строки для матрицы A .
Потому что форма эшелона строки A ref имеет две ненулевые строки, мы знаем, что матрица A имеет два независимых вектора-строки; и мы знаем, что ранг матрицы A равен 2.
Вы можете убедиться, что это правильно. Ряд 1 и Ряд 2 матрицы A линейно независимый.Однако строка 3 — это линейная комбинация строк 1 и 2. В частности, строка 3 = 3 * (строка 1) + 2 * (строка 2). Следовательно, матрица A имеет только два независимых вектора-строки.
Матрицы полных рангов
Когда все векторов в матрице линейно независимый, матрица называется , полный ранг . Рассмотрим матрицы A и B ниже.
Обратите внимание, что строка 2 матрицы A является скалярным кратным
ряд 1; то есть строка 2 равна удвоенной строке 1. Следовательно, строки 1 и 2
линейно зависимый. Матрица А имеет только одну линейно независимую
строка, поэтому ее ранг равен 1. Следовательно, матрица A не имеет полного ранга.
Следовательно, строки 1 и 2
линейно зависимый. Матрица А имеет только одну линейно независимую
строка, поэтому ее ранг равен 1. Следовательно, матрица A не имеет полного ранга.
Теперь посмотрим на матрицу B . Все его строки линейно Независимо, поэтому ранг матрицы B равен 3.Матрица B является полноразмерной.
Проверьте свое понимание
Задача 1
Рассмотрим матрицу X , показанную ниже.
Какое у него звание?
(А) 0
(В) 1
(С) 2
(D) 3
(E) 4
Решение
Правильный ответ: (С).Поскольку в матрице больше нуля элементов,
его ранг должен быть больше нуля. И поскольку в нем меньше строк, чем
столбцов, его максимальный ранг равен максимальному количеству
линейно независимые строки.
И поскольку ни одна строка не зависит линейно от другой строки,
матрица имеет 2 линейно независимых строки; так что его рейтинг 2.
И поскольку в нем меньше строк, чем
столбцов, его максимальный ранг равен максимальному количеству
линейно независимые строки.
И поскольку ни одна строка не зависит линейно от другой строки,
матрица имеет 2 линейно независимых строки; так что его рейтинг 2.
Задача 2
Рассмотрим матрицу Y , показанную ниже.
Какое у него звание?
(А) 0
(В) 1
(С) 2
(D) 3
(E) 4
Решение
Правильный ответ: (С). Поскольку в матрице больше нуля элементов,
его ранг должен быть больше нуля. И поскольку в нем меньше столбцов, чем
строк, его максимальный ранг равен максимальному количеству линейно независимых
столбцы.
Столбцы 1 и 2 независимы, потому что ни один из них не может быть получен как скалярное кратное другому. Однако столбец 3 линейно зависит от столбцов 1 и 2, потому что столбец 3 равен столбцу 1 плюс столбец 2. Это оставляет матрицу максимум с двумя линейно независимые колонны; то есть столбец 1 и столбец 2. Таким образом, ранг матрицы равен 2.
| 14.1 | Графические функции синуса, косинуса и тангенса | Упражнения | п.912 |
| 14,2 | Преобразование и отражение тригонометрических графиков | Упражнения | п. 919 919 |
| Тест для уроков 14.1-14.2 | с.922 | ||
| 14,3 | Подтвердите тригонометрическую идентичность | Упражнения | п.927 |
| 14,4 | Решите тригонометрические уравнения | Упражнения | п.935 |
| Смешанный обзор | с.940 | ||
| 14,5 | Запись тригонометрических функций и моделей | Упражнения | п. 944 944 |
| Тест для уроков 14.3-14.5 | п.947 | ||
| 14,6 | Применение формул суммы и разности | Упражнения | с.952 |
| 14,7 | Применение формул двойного и полууглового углов | Упражнения | п.959 |
| Тест для уроков 14.6-14.7 | п.962 | ||
| Смешанный обзор | с. |



 2=17-16=1
2=17-16=1 Одни из них изучают вещества и явления, а другие — различные тела. Научная деятельность не только удовлетворяет любопытство, но и реализует практические цели, направленные на улучшение качества жизни человека. Читайте подробнее на: https://natworld.info/raznoe-o-prirode/nauki-izuchajushhie-prirodu-ili-estestvennye-nauki
Одни из них изучают вещества и явления, а другие — различные тела. Научная деятельность не только удовлетворяет любопытство, но и реализует практические цели, направленные на улучшение качества жизни человека. Читайте подробнее на: https://natworld.info/raznoe-o-prirode/nauki-izuchajushhie-prirodu-ili-estestvennye-nauki