Контрольная работа номер 2 рациональные дроби: КОНТРОЛЬНАЯ РАБОТА 2 — РАЦИОНАЛЬНЫЕ ДРОБИ

КОНТРОЛЬНАЯ РАБОТА 2 — РАЦИОНАЛЬНЫЕ ДРОБИ

Вариант 1

1. Представьте в виде дроби:

2. Постройте график функции у = 6/x. Какова область определения функции? При каких значениях х функция принимает отрицательные значения?

3. Докажите, что при всех значениях b ≠ ±1 значение выражения не зависит от b.

4. При каких значениях а имеет смысл выражение

Вариант 2

1. Представьте в виде дроби:

2. Постройте график функции у = -6/x. Какова область определения функции? При каких значениях х функция принимает положительные значения?

3. Докажите, что при всех значениях x ≠ ±2 значение выражения не зависит от х.

4. При каких значениях b имеет смысл выражение

Вариант 3

1. Представьте в виде дроби:

2. Постройте график функции у = 4/x. Какова область определения функции? При каких значениях х функция принимает положительные значения?

3. Докажите, что при всех значениях у ≠ ±3 значение выражения не зависит от у.

4. При каких значениях х имеет смысл выражение

Вариант 4

1. Представьте в виде дроби:

2. Постройте график функции у = -4/x. Какова область определения функции? При каких значениях х функция принимает отрицательные значения?

3. Докажите, что при всех значениях а ≠ ±5 значение выражения не зависит от а.

4. При каких значениях y имеет смысл выражение

Решение вариантов контрольной работы

Вариант 1

x	1	2	3	6	— 1	-2	-3	-6
y	6	3	2	1	-6	-3	-2	— 1

Область определения функции: (-∞; 0) и (0; +∞).

Функция принимает отрицательные значения при х є (-∞; 0).

3. Упростим данное выражение:

Таким образом, при любом значении b данное выражение равно 2, то есть не зависит от b.

4. Чтобы выражение имело смысл, должны выполняться два условия:

Ответ: a ≠ 1,5; a ≠ -1/4.

Вариант 2

x	1	2	3	6	— 1	-2	-3	-6
y	-6	-3	-2	— 1	6	3	2	1

Область определения функции: (-∞; 0) и (0; +∞).

Функция принимает положительные значения при x є (-∞; 0).

3. Упростим данное выражение:

Таким образом, при любом значении х данное выражение равно нулю, то есть не зависит от х.

4. Чтобы выражение имело смысл, должны выполниться два условия:

Ответ: b ≠ 0,5; b ≠ 1,5.

Вариант 3

x	1	2	4	— 1	-2	-4
y	4	2	1	-4	-2	— 1

Область определения функции: (-∞; 0) и (0; +∞).

Функция принимает положительные значения при х є (0; +∞).

3. Упростим выражение:

Таким образом, при любом значении у данное выражение равно 3, то есть не зависит от y.

4. Чтобы выражение имело смысл, должны выполняться два условия:

Ответ: х ≠ 2; х ≠ 4/5.

Вариант 4

x	1	2	4	— 1	-2	-4
y	-4	-2	— 1	4	2	1

Область определения функции: (-∞; 0) и (0; +∞).

Функция принимает отрицательные значения при х є (0; +∞).

3. Упростим данное выражение:

Таким образом, при любом значении a данное выражение равно 2, то есть не зависит от a.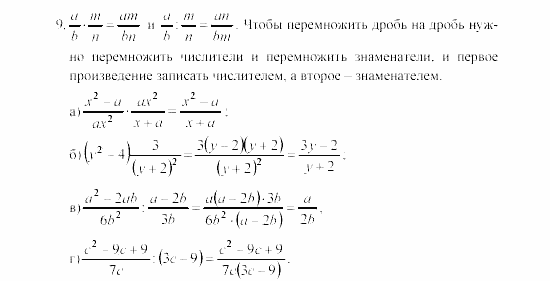

4. Чтобы выражение имело смысл, должны выполняться два условия:

Ответ:

Контрольная работа по теме «Рациональные дроби» 8 класс

Главная / Старшие классы / Алгебра

Скачать

227.11 КБ, 493952.docx Автор: Лапатин Алексей Леонидович, 21 Мар 2015

Работа рассчитана на 40 минут. Включает проверку знаний и навыков по темам «сокращение рациональных дробей», «действия с рациональными дробями», «допустимые значения переменной», «степень с отрицательным показателем», «первые представления о дробно-рациональных уравнениях».

Автор: Лапатин Алексей Леонидович

Похожие материалы

Тип	Название материала	Автор	Опубликован
документ	Контрольная работа по теме «Рациональные дроби» 8 класс	Лапатин Алексей Леонидович	21 Мар 2015
документ	Контрольная работа по теме: «Рациональные дроби» для 8 класса	Панова Анастасия Владимировна	5 Ноя 2015
документ	Контрольная работа по алгебре по теме «Рациональные уравнения», 8 класс	Токарева Инна Александровна	31 Мар 2015
документ	Контрольная работа по теме » Рациональные неравенства и их системы», 9 класс.	Микубаева Эльвира Владимировна	21 Мар 2015
документ	Самостоятельная работа по алгебре по теме «Рациональные и иррациональные числа»,8 класс	Саблина Татьяна Алексеевна	21 Мар 2015
разное	контрольная работа по теме «Однородные члены предложения» 8 класс	Есаненко Ирина Александровна	20 Ноя 2015
разное	контрольная работа по теме «Однородные члены предложения» 8 класс	Есаненко Ирина Александровна	20 Ноя 2015
документ	Контрольная работа по теме «Обыкновенные и десятичные дроби» (5 класс)	Виноградова Ирина Сергеевна	9 Апр 2015
документ	контрольная работа по теме: «Десятичные дроби. »	Гончаренко Любовь Викторовна	1 Апр 2015
документ	Контрольная работа по теме: «Дроби и проценты»	Абрамова Юлия Юрьевна	5 Сен 2015
документ	Контрольная работа по теме «Десятичные дроби»	Сметанина Любовь Борисовна	5 Апр 2015
документ	Контрольная работа по теме «Действия с десятичными дробями» Контрольная работа № 8 Контрольная работа № 8	Лыгина Ольга Владимировна	4 Апр 2015
документ	Контрольная работа по теме «Действия с десятичными дробями» Контрольная работа № 8 Контрольная работа № 8	Лыгина Ольга Владимировна	4 Апр 2015
документ	Разноуровневая проверочная работа по теме «Алгебраические дроби» 8 класс	Томадзе-Осетрова Ольга Николаевна	1 Апр 2015
документ	Контрольная работа №2 по теме «Вычисления с многозначными часлами» 5 класс учебник Мордкович. Контрольная работа №2 Контрольная работа №2 Контрольная работа №2 Контрольная работа №2 Контрольная работа №3 Контрольная работа №3 Контрольная работа	Лыгина Ольга Владимировна	21 Мар 2015
разное	Контрольная работа по теме «Имя прилагательное» 6 класс Контрольная работа по теме»Имя прилагательное » 6 класс Контрольная работа по теме»Имя прилагательное » 6 класс	Лобанова Анна Игоревна	20 Мар 2015
разное	Интерактивный тест по теме «Рациональные выражения». Алгебра 8 класс	Ковалева Инга Михайловна	1 Апр 2015
документ	8 класс, Контрольная работа по теме «Кислород», «Водород» и «Вода»	Белова Наталия Бориcовна	21 Янв 2016
документ	8 класс, Контрольная работа по теме «Классы Неорганических Веществ»	Белова Наталия Бориcовна	8 Мая 2015
документ	Контрольная работа по химии 8 класс по теме «Простые вещества» по УМК О. С.Габриеляна	Попова Елена Александровна	21 Мар 2015
документ	Урок математики в 5 классе школы VIII вида по теме: «Контрольная работа № 10 по теме «Обыкновенные дроби»»	Покидышева Ирина Ивановна	21 Мар 2015
документ	Самостоятельная работа по алгебре 9 класс по теме «Рациональные неравенства»	Ольга Михайловна Щербакова	18 Окт 2015
документ	Контрольная работа по химии 8 класс по теме «Изменения, происходящие с веществами»	Жулина Надежда Павловна	20 Мар 2015
документ	контрольная работа по химии 8 класс, по теме: «Строение вещества»	Романова Светлана Рузиятовна	21 Мар 2015
документ	Контрольная работа по геометрии 8 класс по теме «Четырехугольники»	Лапатин Алексей Леонидович	21 Мар 2015
документ	Контрольная работа по химии по теме «Атомы химических элементов» 8 класс	Савина Татьяна Викторовна	31 Мар 2015
документ	Контрольная работа по алгебре 8 класс по теме «Применение свойств квадратного корня»	Токарева Тамара Ивановна	1 Апр 2015
документ	Контрольная работа по алгебре 8 класс по теме «Применение свойст квадратного корня»	Токарева Тамара Ивановна	1 Апр 2015
документ	Контрольная работа по химии по теме «Строение атома», 8 класс	Дубанова Ольга Викторовна	4 Апр 2015
документ	Контрольная работа по химии по теме «Уравнения химических реакций», 8 класс	Дубанова Ольга Викторовна	4 Апр 2015
документ	Контрольная работа по теме «Функциональные стили речи» 8 класс ( по учебнику С. И.Львовой В.В.Львова)	Конасова Екатерина Геннадьевна	31 Мар 2015
документ	Контрольная работа по физике 8 класс по теме «Тепловые явления»	Казорина Оксана Васильевна	14 Фев 2016
документ	Контрольная работа по физике 8 класс по теме «Электрические явления»	Казорина Оксана Васильевна	14 Фев 2016
документ	Контрольная работа по теме «Главные члены предложения» 8 класс	Аверкина Светлана Владимировна	20 Мар 2015
документ	Контрольная работа по теме «Однородные члены предложения» (8 класс)	Хертек Чыжыргана Михайловна	20 Мар 2015
документ	Контрольная работа по теме «Электрические явления» 8 класс	Шапошник Ольга Николаевна	21 Мар 2015
документ	контрольная работа 8 класс по теме «Тепловые явления. Изменение агрегатных состояний вещества»	Драничникова Светлана Викторовна	21 Мар 2015
документ	Контрольная работа №1 по теме «Тепловые явления» 8 класс	Широкова Ирина Борисовна	21 Мар 2015
документ	Физика 8 класс. Контрольная работа по теме: «Количество теплоты.»	Уваров Сергей Александрович	21 Мар 2015
документ	контрольная работа по теме «Население России» 8 класс	Хабарова Надежда Васильевна	21 Мар 2015

Ершова Голобородько 8 класс самостоятельные и контрольные работы ГДЗ

Здесь представлены ответы к самостоятельным и контрольным работам по алгебре и геометрии 8 класс Ершова Голобородько. Вы можете смотреть и читать гдз онлайн (без скачивания) с компьютера и мобильных устройств.

АЛГЕБРА

Рациональные дроби
С-1. Рациональные выражения. Сокращение дробей 1 2 3 4
С-2. Сложение и вычитание дробей 1 2 3 4 5
К-1. Рациональные дроби. Сложение и вычитание дробей 1 2 3 4 5 6 7 8
С-3. Умножение и деление дробей. Возведение дроби в степень 1 2 3 4 5
С-4. Преобразование рациональных выражений 1 2 3 4 5 6
С-5*. Все действия с рациональными выражениями (домашняя самостоятельная работа)
С-6. Обратная пропорциональность и ее график 1 2 3 4 5 6
К-2. Рациональные дроби 1 2 3 4 5 6 7 8
Квадратные корни
С-7. Арифметический квадратный корень 1 2 3 4 5 6
С-8. Уравнение х2 = а. Функция у = у[х 1 2 3 4 5 6
С-9. Квадратный корень из произведения, дроби, степени 1 2 3 4
К-3. Арифметический квадратный корень и его свойства 1 2 3 4 5
С-10. Внесение и вынесение множителя в квадратных корнях 1 2 3 4
С-11. Преобразование выражений, содержащих квадратные корни 1 2 3
С-12*. Действия с квадратными корнями (домашняя самостоятельная работа)
К-4. Применение свойств арифметического квадратного корня 1 2 3 4 5 6 7 8
Квадратные уравнения
С-13. Неполные квадратные уравнения 1 2 3
С-14. Формула корней квадратного уравнения 1 2 3 4
С-15. Решение задач с помощью квадратных уравнений. Теорема Виета 1 2 3 4
С-16*. Применение свойств квадратных уравнений (домашняя самостоятельная работа)
К-5. Квадратные уравнения 1 2 3 4 5 6 7
С-17. Дробные рациональные уравнения 1 2 3 4 5
С-18. Применение дробных рациональных уравнений. Решение задач 1 2 3 4 5 6
К-6. Дробные рациональные уравнения 1 2 3 4 5 6 7 8 9
Неравенства
С-19. Свойства числовых неравенств К-7. Числовые неравенства и их свойства 1 2 3
K-7. 1 2 3 4 5 6
С-20. Линейные неравенства с одной переменной 1 2 3 4 5
С-21. Системы линейных неравенств 1 2
С-22*. Неравенства (домашняя самостоятельная работа)
К-8. Линейные неравенства и системы неравенств с одной переменной 1 2 3 4 5
С-23. Степень с отрицательным показателем 1 2
К-9. Степень с целым показателем 1 2 3
К-10. Годовая контрольная работа 1 2 3 4 5

ГЕОМЕТРИЯ (по Погорелову)

Четырехугольники
СП-1. Свойства и признаки параллелограмма 1 2 3 4
СП-2. Прямоугольник. Ромб. Квадрат 1 2 3 4
КП-1. Параллелограмм 1 2 3 4
СП-3. Теорема Фалеса. Средняя линия треугольника 1 2 3
СП-4. Трапеция. Средняя линия трапеции 1 2 3 4
СП-5*. Четырехугольники (домашняя самостоятельная работа)
КП-2. Трапеция. Средние линии треугольника и трапеции 1 2 3 4 5
Теорема Пифагора
СП-6. Теорема Пифагора 1 2 3 4 5
СП-7. Теорема, обратная теореме Пифагора. Перпендикуляр и наклонная 1 2 3 4
СП-8. Неравенство треугольника 1 2
СП-9*. Теорема Пифагора (домашняя самостоятельная работа)
КП-3. Теорема Пифагора 1 2 3 4 5 6
СП-10. Решение прямоугольных треугольников 1 2 3 4
СП-11. Свойства тригонометрических функций 1 2 3
КП-4. Прямоугольный треугольник (итоговая контрольная работа) 1 2
Декартовы координаты на плоскости
СП-12. Координаты середины отрезка. 1 2 3 4
Расстояние между точками. Уравнение окружности
СП-13. Уравнение прямой 1 2 3 4 5 6 7
СП-14*. Декартовы координаты (домашняя самостоятельная работа)
КП-5. Декартовы координаты 1 2 3 4 5 6
Движение
СП-15. Движение и его свойства. Центральная и осевая симметрии. Поворот 1 2 3
СП-16. Параллельный перенос 1 2 3
Векторы
СП-17. Понятие вектора. Равенство векторов 1 2
СП-18. Действия с векторами в координатной форме. Коллинеарные векторы 1 2
СП-19. Действия с векторами в геометрической форме 1 2 3
СП-20. Скалярное произведение 1 2 3
СП-21*. Применение параллельного переноса и векторов к решению задач (домашняя самостоятельная работа)
КП-6. Векторы 1 2 3 4
КП-7. Годовая контрольная работа 1 2 3 4 5 6 7

ГЕОМЕТРИЯ (по учебнику Атанасяна)

Четырехугольники
СА-1.Свойства и признаки параллелограмма 1 2 3
СА-2.Прямоугольник. Ромб. Квадрат 1 2 3
СА-3*. Четырехугольники (домашняя самостоятельная работа)
КА-1. Четырехугольники 1 2 3
Площадь
СА-4.Площадь прямоугольника, квадрата 9 10
СА-5.Площадь параллелограмма, ромба, треугольника 11 12
СА-6.Площадь трапеции 13 14
СА-7.Теорема Пифагора 14 15
СА-8*. Площади. Теорема Пифагора (домашняя самостоятельная работа)
КА-2. Площади. Теорема Пифагора 16 17 18
Подобные треугольники
СА-9. Определение подобных треугольников. Свойство биссектрисы угла треугольника 1 2 3 4 5 6
СА-10. Признаки подобия треугольников 1 2 3 4 5
КА-3. Подобие треугольников 1 2 3 4 5
СА-11. Применение подобия к решению задач 1 2 3
СА-12. Соотношения между сторонами и углами прямоугольного треугольника 1 2 3 4
СА-13*. Подобие и его применение (домашняя самостоятельная работа)
КА-4. Соотношения между сторонами и углами прямоугольного треугольника 1 2 3 4
Окружность
СА-14. Касательная к окружности 1 2 3 4
СА-15. Центральные и вписанные углы 1 2 3 4 5
СА-16. Теорема о произведении отрезков пересекающихся хорд. Замечательные точки треугольника 1 2 3 4
СА-17. Вписанная и описанная окружности 1 2 3 4 5
СА-18*. Задачи, связанные с окружностью (домашняя самостоятельная работа)
КА-5. Окружность 1 2 3 4 5
Векторы
СА-19. Сложение и вычитание векторов 1 2 3
СА-20. Умножение вектора на число 1 2 3
СА-21. Средняя линия трапеции 1 2 3 4
СА-22*. Векторы и их применение (домашняя самостоятельная работа)
КА-6. Векторы. Применение векторов к решению задач 1 2 3
КА-7. Годовая контрольная работа 1 2 3 4 5

Rational Expressions — SAT Math

Все ресурсы SAT Math

16 диагностических тестов 660 практических тестов Вопрос дня Карточки Learn by Concept

← Предыдущая 1 2 Следующая →

SAT Math Help » Алгебра » Выражения » Rational Expressions

Упростите выражение.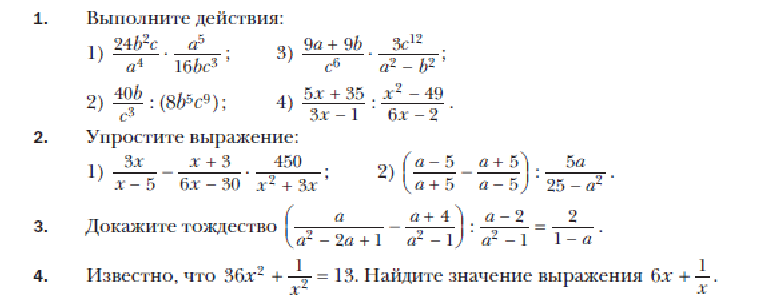

Возможные ответы:

Правильный ответ:

Объяснение:

Чтобы сложить рациональные выражения, сначала найдите наименьший общий знаменатель. Поскольку знаменатель первой дроби равен 2(x+2), ясно, что это общий знаменатель. Следовательно, умножьте числитель и знаменатель второй дроби на 2.

Это самый упрощенный вариант рационального выражения.

 

Сообщить об ошибке

Упростите следующее:

Возможные ответы:

Правильный ответ:

Объяснение:

Чтобы упростить следующее, необходимо найти общий знаменатель. В этом случае первый член должен быть умножен на (x+2) как в числителе, так и в знаменателе, а также на второй член с (x-3).

Сообщить об ошибке

Если √( ab ) = 8 и a ² = b , что такое a ?

Возможные ответы:

2

64

16

4

10

Правильный ответ:

4

Объяснение:

Если мы подставим a ² вместо b в подкоренном выражении, мы получим √( a ³ ) = 8. Это можно переписать как

7 3 a

8 = 8. Таким образом, log

_и 8 = 3/2. Подстановка вариантов ответа дает 4 как правильный ответ.

Отчет о ошибке

Возможные ответы:

–9/5

37/15

–37/15

9/5

–11/5

Правильно: Правильно: Правильный ответ:: Правильно: Правильный ответ:: Правильно: Правильный ответ:: Правильно.

–11/5

Объяснение:

Сообщить об ошибке

Если Джилл войдет, сколько времени Джилл будет идти?

Возможные ответы:

Правильный ответ:

Объяснение:

Чтобы решить эту проблему, нам нужно задать пропорцию.

Cross Multiply

Значит, Джилл придется идти пешком

Сообщить об ошибке

Если , то какое из следующих утверждений также должно быть верным?

Возможные ответы:

Правильный ответ:

Объяснение:

Сообщить об ошибке

Что из следующего эквивалентно  ? Предположим, что знаменатели всегда отличны от нуля.

Возможные ответы:

Правильный ответ:

Объяснение:

Нам нужно упростить выражение. Мы можем думать об этом как о большой дроби с числителем и знаменателем .

Чтобы упростить числитель, нам нужно объединить две дроби. При сложении или вычитании дробей мы должны иметь общий знаменатель. имеет знаменатель , и имеет знаменатель . Наименьший общий знаменатель, который имеют эти две дроби, равен . Таким образом, мы будем писать эквивалентные дроби со знаменателем .

Чтобы преобразовать дробь в знаменатель с , нам нужно будет умножить верх и низ на .

Точно так же мы умножим верхнюю и нижнюю часть на .

Теперь мы можем переписать следующим образом:

=

Вернемся к исходной дроби. Теперь мы перепишем числитель:

=

. Когда мы делим дробь на другую величину, это то же самое, что умножать дробь на обратную величину этой величины. Другими словами, .

 

=

Наконец, мы воспользуемся свойством экспонент, которое утверждает, что в общем случае .

Ответ .

Сообщить об ошибке

Упростить (4x)/(x ²  – 4) * (x + 2)/(x ²  – 2x)

Возможные ответы:

4x 904 + 8x)/(x ⁴ + 8x)

4/(x + 2) ²

4/(x – 2) ²

x/(x – 9004 9007 2) 3 2 /(x + 2)

Правильный ответ:

4/(х – 2) ²

Объяснение:

Фактор сначала. Числители не будут множиться, но первый знаменатель размножается на (x – 2)(x + 2), а второй знаменатель размножается на x(x – 2). Умножение дробей не требует общих знаменателей, поэтому теперь ищите общие множители для деления. Есть множитель x и множитель (x + 2), которые делятся, оставляя 4 в числителе и два множителя (x – 2) в знаменателе.

Отчет о ошибке

Что такое 6/8 x 20/3

Возможные ответы:

5

120/11

18/160

3/20

9/40

Правильно Ответ. : 5

Объяснение:

6/8 X 20/3 первый шаг — уменьшить 6/8 -> 3/4 (разделить верхнее и нижнее число на 2)

3/4 X 20/3 (перекрестно сократить тройки и уменьшается до 5, а 4 уменьшается до 1)

1/1 X 5/1 = 5

Сообщить об ошибке

Оцените и упростите следующий продукт:

Возможные ответы:

Правильный ответ:

Объяснение:

Процедура умножения двух рациональных выражений такая же, как и умножения любых двух дробей: найдите произведение числителей и произведение знаменателей по отдельности, а затем максимально упростите полученное частное, как показано:

Сообщить об ошибке

← Предыдущая 1 2 Следующая →

Уведомление об авторских правах 660 практических тестов Вопрос дня Карточки Learn by Concept

Решение рациональных и дробных функций

Все ресурсы SAT II Math I

6 Диагностические тесты 113 практических тестов Вопрос дня Карточки Учитесь по концепции

← Предыдущая 1 2 Следующая →

SAT II Math I Help » Функции и графики » Решающие функции » Решение рациональных и дробных функций

Упростить:

Возможные ответы:

Правильный ответ:

Объяснение:

Возведение дроби в отрицательную степень путем возведения обратной величины в степень абсолютного значения показателя степени. Затем примените свойства показателей следующим образом:

Сообщить об ошибке. Пояснение:

Чтобы упростить эту задачу, нам нужно найти наименьший общий знаменатель между двумя дробями. Для этого возьмем 5 и 8. Наименьшее общее число между этими двумя числами — 40.

Чтобы представить каждую дробь в виде знаменателя 40, нам нужно умножить следующим образом:

мы можем умножать на 8/8 и 5/5, потому что эти дроби на самом деле просто 1, записанные в другом формате.

Теперь, используя порядок операций, мы получаем следующее

Теперь у нас есть общий знаменатель, и мы можем сделать наше сложение, чтобы получить упрощенное число:

Сообщить об ошибке

Решите следующее уравнение, чтобы найти .

Возможные ответы:

Правильный ответ:

Объяснение:

Чтобы найти , мы должны сначала найти наименьший общий знаменатель. В этом случае это:

Теперь уравнение можно записать по адресу:

Решение для, мы получаем:

Сообщите о ошибке

Что является наименее распространенным номинатором и?

Возможные ответы:

Правильный ответ:

Объяснение:

При нахождении наименьшего общего знаменателя самым быстрым способом является перемножение чисел.

В этом случае и  общий коэффициент, отличный от , который равный . Мы можем разделить эти числа на получение и остаток.

Так вот, у них нет общего множителя, поэтому просто умножьте их на общий множитель. Ответ 

 

Другой подход состоит в том, чтобы перечислить множители обоих чисел и найти множитель, который появляется в обоих наборах первым.

Мы видим, что в обоих наборах стоит перед любым другим числом, поэтому это наш ответ.

Отчет о ошибке

Упростить следующее:

Возможные ответы:

Правильный ответ:

Пояснение:

Чтобы упростить сумму двух дробей, мы должны найти общий знаменатель.

Упрощая знаменатель первой дроби, получаем

, потому что знаменатель представляет собой разность двух квадратов, которая соответствует форме

Теперь мы можем переписать сумму как

Теперь гораздо проще увидеть общий знаменатель: 9004 0 905

90

Сообщить об ошибке

Решить:

Возможные ответы:

Правильный ответ:

Объяснение:

Чтобы решить это уравнение, мы должны найти наименьший общий знаменатель, чтобы сложить дроби.

Имейте в виду, что знаменатель второго члена представляет собой разность квадратов, которую можно переписать как

Это наименьший общий знаменатель.

Теперь умножаем обе части уравнения на ЖК-дисплей сверху и снизу (по сути это 1):

После сокращения членов получаем

Теперь находим x:

 

Сообщить об ошибке

Упрощение 

Возможные ответы:

Правильный ответ:

Объяснение:

Найдите наименьший общий знаменатель (НОД) и преобразуйте каждую дробь в НДО, а затем сложите. Упрощайте по мере необходимости.

Результатом является неправильная дробь, потому что числитель больше знаменателя и может быть упрощен и преобразован в смешанное числительное.

Сообщить об ошибке

Найти упрощенно результат:

Возможные ответы:

Правильный ответ:

Пояснение:

Начните с приведения обеих дробей к одному знаменателю.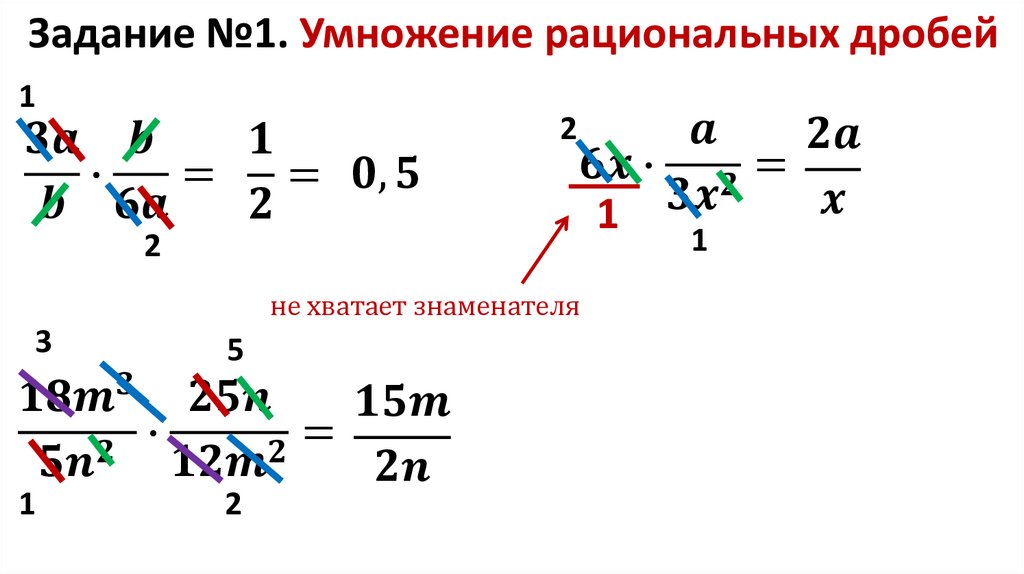 Один из вариантов:

Затем скорректируйте числители, умножив числитель каждой дроби на знаменатель другой дроби:

Затем сложите скорректированные числители:

Затем мы упростим, разделив числитель и знаменатель

что дает нам окончательный результат.

Сообщить об ошибке

Упрощение:

Возможные ответы:

Правильный ответ:

Пояснение:

Чтобы разделить дроби, нужно первую дробь умножить на обратную вторую.

Теперь умножьте числители и знаменатели вместе, затем упростите.

Сообщить об ошибке

Упрощение:

Возможные ответы:

Правильный ответ:

Пояснение:

Чтобы разделить дроби, нужно первую дробь умножить на обратную вторую.

Теперь умножьте числители и знаменатели, затем упростите.

Сообщить об ошибке

← Предыдущая 1 2 Следующая →

Уведомление об авторских правах

Все ресурсы SAT II Math I

6 Диагностические тесты 113 практических тестов Вопрос дня Карточки Learn by Concept

Рациональные числа и дроби: типы, методы и примеры

Вы готовитесь с вашим другом Максом к экзамену, и вы оба начали обсуждать, как долго вы учились. Макс сказал, что вы оба учились \(3,5\) часа, но вы считаете, что оба учились \(3\) и полчаса \((3\frac{1}{2})\). Но кто из вас прав насчет времени? Если вы оба учились на одинаковую сумму, то почему разница в количестве? Ну, и \(3.5\), и \(3\frac{1}{2}\) одинаковы. Это разные формы чисел. Один в форма рационального числа , а другая в форме дроби .

В этом разделе мы поймем понятие рациональных чисел и дробей и чем они отличаются.

Значение рациональных чисел и дробей

Рациональные числа и дробные числа — это два математических понятия, которые кажутся очень тесно связанными и чаще всего используются взаимозаменяемо. Однако в этом разделе мы познакомим вас со значением рациональных чисел и дробей, а также с различиями в их описании.

Рациональные числа — это тип вещественных чисел, которые можно записать как отношение двух целых чисел. Они выражаются в виде \(\frac{p}{q}\).

Обратите внимание, что \(p\) и \(q\) являются целыми числами, а \(q\) ненулевым. Примеры рациональных чисел: \(12, 10/12, 3/10,\) и \(0,5\). Множество рациональных чисел всегда обозначается \(\mathbb{Q}\).

Целые числа — это множество всех положительных, отрицательных чисел и нуля. Они не содержат десятичной или дробной формы.

Дроби — это числа, которые определяют часть или часть любого целого количества, записанного как отношение целых чисел. Они имеют вид \(a / b\), где \(a\) — числитель, а \(b\) — знаменатель.

Обратите внимание, что и числитель, и знаменатель являются целыми числами, а знаменатель не может быть равен нулю. Примеры дробей: \(10/32, 12/10, 4/23,\) и \(6/7\).

Целые числа представляют собой набор натуральных чисел и нуля. Это все положительные целые числа с нулем без какой-либо десятичной, дробной или отрицательной части.

Хотя дроби и рациональные числа выглядят одинаково, они не всегда одинаковы. Поскольку рациональные числа имеют целые числа и содержат отрицательные числа, их нельзя считать дробями. Поскольку дроби не включают отрицательные числа.

Рациональное число

Как определено выше, рациональное число — это тип действительного числа, который выражается в форме \(p/q\), где \(p\) и \(q\) — целые числа, а не равно \(0\). Проще говоря, можно сказать, что любая дробь с ненулевым знаменателем является рациональным числом.

Стандартная форма рациональных чисел выражается в том случае, когда они не имеют никаких общих делителей кроме одного между делимым и делителем и, следовательно, делитель положительный. Итак, стандартный вид дробей достигается за счет упрощения дробей. Например, \(3/9\) является примером рационального числа, но, кроме того, оно может делиться на \(1/3\). В форме \(1/3\) это считается стандартной формой, поскольку число больше не делится ни на какое число, кроме \(1\) и самого себя.

Помните, что число, которое вы делите, называется делимым , а число, на которое вы выполняете деление, называется делителем .

Дроби

Математическая концепция дробей используется для описания частей целого . Например, когда мы берем кусок пиццы от целого, мы говорим, что у нас есть его часть. Дроби — это числа, представленные в виде \(\frac{a}{b}\), где \(a\) и \(b\) — целые числа, а \(b\) не равно \(0\).

Дробь с числителем \(0\) равна \(0\), но дробь со знаменателем \(0\) не определена. Дробь обозначается простым «/» в форме \(a/b\), где \(a\), верхнее число называется числителем, а \(b\), нижнее число называется знаменателем. Примеры дробей: \(12/20, 5/6,\) и \(50/100\).

Доли частей круга

Различия между рациональными числами и дробями

Между рациональными числами и дробями существуют существенные различия, и они заключаются в следующем:

Рациональные числа	Дробь
1. Рациональные числа имеют вид \(p/q\), где \(p\) и \(q\) — целых чисел .	1. Рациональные числа имеют вид \(a/b\), где \(a\) и \(b\) — целых чисел .
2. Рациональные числа имеют положительных и отрицательных формы чисел.	2. Дробь имеет только положительную форму чисел.
3. Рациональные числа нельзя считать дробями.	3. Дробь можно рассматривать как рациональное число.
4. Примеры — \(-3/7, 1/3, 12\)	4. Примеры — \(4/5, 1\frac{2}{5}, 23/6\)

Типы рациональных чисел

Существует несколько типов рациональных чисел, и они следующие:

• Целые числа, например, \(-3, 5,\) и \(4\).

• Дроби вида \(p / q\), где \(p\) и \(q\) — целые числа, например, \(1/2\).

• Числа без бесконечных десятичных знаков, например, \(1/4\) от \(0,25\). Их также называют с завершающими десятичными знаками .

• Числа с бесконечными десятичными знаками, например, \(1/3\) от \(0,333….., 1,222…..\) и т. д. Они известны как некончающихся десятичных знаков. .

• Целые числа.

Типы дробей

Существует довольно много типов дробей. Если мы хотим использовать числитель и знаменатель в качестве основы, их можно рассматривать как три; правильная дробь, смешанная дробь и неправильная дробь. Тем не менее, они подразделяются на различные типы.

Правильная дробь

Правильная дробь – это дробь, у которой числитель меньше знаменателя (числитель < знаменателя). Например, \(3/4\) — правильная дробь.

Смешанная фракция

Смешанные дроби представляют собой комбинации целых чисел и правильных дробей. Они записываются как \(a\frac{m}{n}\), где \(a\) — целое число. Примером смешанной дроби является \(1\frac{2}{5}\).

Неправильная дробь

Неправильные дроби, в отличие от правильных дробей, у которых знаменатель меньше числителя. (знаменатель < числитель). Примером является \(4/3\).

Подобные дроби

Подобные дроби — это дроби, имеющие одинаковые знаменатели. Например, \(1/7\) и \(4/7\). Обе дроби здесь имеют тот же знаменатель, что и \(7\), поэтому считаются дробями.

В отличие от дробей

Эти типы дробей отличаются от подобных дробей. Они имеют разные значения в знаменателе. Примером разной дроби являются \(11/13\) и \(4/9\).

Эквивалентная дробь

Две дроби могут считаться эквивалентными после упрощения путем выполнения умножения или деления. они оба дают то же самое. Например, \(2/3\) и \(4/6\) являются эквивалентными дробями, потому что \(4/6\) можно упростить до \(2/3\).

Дроби единиц

Когда числитель дроби равен \(1\), она называется единичной дробью. Примеры: \(1/2\) (половина целого) и \(1/4\) (четверть целого).

Сложение и вычитание рациональных чисел и дробей

Знаменатель играет важную роль при сложении и умножении рациональных чисел и дробей. Давайте посмотрим, как мы можем выполнять операции сложения и вычитания над рациональными числами и дробями.

Сложение и вычитание дробей

Для сложения и вычитания дробей необходимо выполнить следующие шаги:

1. Проверить тип дроби, похожи ли они на дроби или нет.

2. Преобразовать данную дробь в подобную дробь, если они не равны. Перейдите к шагу 4, если они похожи на дроби.

3. Найдите наименьшее общее кратное для данных знаменателей. Затем умножьте на эквивалентное число все данные знаменатели, чтобы получить то же значение знаменателя.

4. Добавить/вычесть числитель, сохраняя знаменатель без изменений.

5. Если возможно, сократите полученные дроби.

Сложение и вычитание рациональных чисел

Мы используем тот же процесс для сложения и вычитания дробей рациональных чисел:

1. Преобразуем все знаменатели в положительные числа, если любой из них отрицательный.

2. Используйте LCM, чтобы сделать все знаменатели одинаковыми, если они разные.

3. Сложите/вычтите целые числа в числителе, следуя правилам целых чисел. И оставьте знаменатель как есть.

4. Упростите рациональное число.

Умножение и деление рациональных чисел и дробей

Умножение и деление рациональных чисел и дробей подчиняются тому же правилу с добавлением правил целых чисел для рациональных чисел.

Умножение рациональных чисел и дробей

Умножение рациональных чисел и дробей осуществляется по заданным правилам:

1. Умножьте числители всех заданных чисел друг на друга.

2. Умножьте знаменатели всех чисел друг на друга.

3. Упростите полученную дробь/рациональное число.

Помните, что при работе с рациональными числами всегда соблюдайте правила умножения положительных и отрицательных знаков.

Деление рациональных чисел и дробей

Деление рациональных чисел выглядит следующим образом:

1. Найдите обратную вторую дробь/рациональное число, поменяв местами числитель со знаменателем и наоборот.

2. Изменить знак деления на умножение после выполнения обратного действия.

3. Следуйте правилам умножения рациональных чисел и дробей, как указано выше.

Пример с рациональными числами и дробями

Давайте рассмотрим примеры с рациональными числами и дробями.

Определить типы дробей.

1. \(\frac{6}{7}, \frac{4}{7}\)

2. \(2\frac{3}{8}\)

3. \(\frac {12}{9}\)

Решение:

1. Как дробь — так как оба знаменателя одинаковы.

2. Смешанная дробь — Имеет дробь с целым числом.

3. Неправильная дробь — Числитель больше знаменателя.

Разделить рациональное число \(\frac{-3}{10}\) на \(\frac{7}{5}\).

Решение:

Здесь нам нужно выполнить

\[\frac{-3}{10}\div\frac{7}{5}\]

Шаг 1 — Возьмем обратное значение \(\ frac{7}{5}\)

\[\Rightarrow \frac{5}{7}\]

Шаг 2 — Изменение знака деления на умножение после получения обратной величины, которую мы имеем,

\[\ frac{-3}{10}\times \frac{5}{7}\]

Шаг 3 — Теперь мы умножаем числитель обоих чисел друг на друга и то же самое со знаменателями.

\begin{align} \frac{-3}{10}\times \frac{5}{7} &= \frac{-3\times 5}{10\times 7} \\ &=\frac{ -15}{70} \\ \end{align}

Шаг 4 — Теперь сократим полученное рациональное число.

\[\Rightarrow \frac{-15}{70} = \frac{-3}{14}\]

Вычислите данную дробь.

\[\frac{1}{3}+\frac{4}{5}\]

Решение:

Шаг 1 — Здесь обе дроби не похожи на дроби. Итак, мы преобразуем его в подобные дроби.

Шаг 2 — Считаем НОК знаменателей \(3\) и \(5\), чтобы преобразовать данные дроби в одинаковые дроби.

Следовательно, НОК \(3\) и \(5\) равен \(15\).

Шаг 3 — Теперь мы умножаем \(5\) на \(\frac{1}{3}\), чтобы получить знаменатель \(15\). Точно так же мы умножаем \(3\) на \(\frac{4}{5}\) и складываем оба полученных числителя,

\begin{align} \Rightarrow \frac{1\times 5}{3\ раз 5} + \frac{4\times 3}{5\times 3} &= \frac{5}{15}+\frac{12}{15} \\ &=\frac{5+12}{15 } \\ &=\frac{17}{15} \\ \end{align}

Здесь \(\frac{17}{15}\) уже в сокращенной форме.

Рациональные числа и дроби — основные выводы

• Рациональное число — это тип действительного числа, который выражается в форме \(p/q\), где \(p\) и \(q\) — целые числа, а не равно \(0\).

  No related posts.