Как сделать математику: Как сделать математику интересной для ребёнка: три простых шага

Как сделать математику интересной для ребёнка: три простых шага

У школьной математики плохая репутация: пропустил одну тему, недопонял другую — и уроки превращаются в страшный сон. Вроде учитель говорит по-русски, а кажется, что по-китайски. Школьники теряют интерес к предмету, с трудом сдают базовый ЕГЭ и тут же забывают о дробях и алгоритмах. А ведь математика может быть увлекательной! Рассказываем, как заинтересовать предметом закоренелого гуманитария.

Привет, учитель! Рассылка

Для тех, кто работает в школе и очень любит свою профессию

Шаг первый: рассказать о пользе математики

Математика часто представляется сферическим конём в вакууме — чем-то максимально оторванным от реальности. «Зачем мне учить таблицу умножения, есть же калькуляторы!» Знакомо? Постарайтесь донести до ребёнка идею, что в математике есть практическая польза.

Репетитор PROFI.RU Ольга Пантелеева:

«Я стараюсь соединять математику с жизненными вещами, делать её менее абстрактной. Например, с отрицательными числами проще подружиться на примере баланса телефона, а диету ученицы можно использовать как повод посчитать пропорцию. Мозг детей гораздо активнее включается в работу, если поменять объект на что-то знакомое. Если новый айфон стоил 80 тысяч, то, даже если он дважды подешевеет на 50%, цена не станет равна нулю. Понять сложную тему помогают бытовые ассоциации: замена переменных (x² заменили на y) — это как человек в халате: выглядит приличнее, чем голый, но под халатом это всё тот же человек».

Математические формулы и правила лучше всего осмысляются на примерах из жизни. Запомнить, что кратчайшим расстоянием между двумя точками является прямая, несложно. А вот понять, что это действительно значит, труднее. В книге «Математическая составляющая» приводится такой пример: «Вы хотите прогуляться по Москве. Какой путь от станции метро „Маяковская“ до станции „Курская“ короче: по Садовому кольцу или через центр, через Красную площадь?». Для поиска ответа придётся вспомнить и о кратчайшем пути между двумя точками, и о подобии фигур. Правильный ответ, кстати: пути равны.

Репетитор Олег Богданов поддерживает:

«Я часто объясняю математику через истории из жизни или бытовые ситуации. Например, однажды я пришёл к другу в гости и застал его за странным занятием: он катал велосипед по лестничной клетке. Оказалось, нужно было измерить длину дуги окружности колеса и выставить это значение на спидометр, чтобы тот показывал верную скорость. Друг не знал формулу длины дуги окружности (C = πd) и пытался высчитать длину обода колеса сложным путём через расстояние, на которое прокручивается колесо за один оборот. Знание математики подсказало бы простой путь: измерить диаметр колеса рулеткой и умножить полученное значение на число π = 3,14».

---

Шаг второй: выявить проблемы

Когда есть интерес, учиться легче. Но если проблемы всё же возникают, хорошо бы понять причины. По опыту репетиторов PROFI.RU, самая частая — неусвоенная когда-то давно тема. Как это понять? Обратите внимание на то, как ребёнок решает задачи. Возможно, ему понятен сам ход решения, но он не может, например, разобраться с десятичными дробями. Бывает, что проблема глубже, и девятиклассник застрял на уровне седьмого класса. Как бы то ни было, прежде чем двигаться дальше, нужно ликвидировать все пробелы.

Чтобы не повторять печальный опыт с новыми темами, сразу проверяйте, насколько ребёнок их усвоил. Особое внимание обращайте на незнакомые термины: учителя часто объясняют понятие один раз, а потом к нему не возвращаются. Если ребёнок непонимающе смотрит на вас при слове «парабола», нарисуйте на листке бумаги, разберите определение — так легче запомнить.

Ещё одна типичная проблема — непонимание условий задачи. Школьные учителя обычно просят записать его кратко, но яснее от этого не становится. Научите ребёнка правильно читать задание: обращать внимание на предлоги (во сколько раз и на сколько — это разные арифметические действия), не пропускать важные слова (например, когда сказано, что нужно найти процент от остатка, а не просто процент).

Хорошо работает визуализация: каждую задачу можно представить в виде схемы, обозначив на ней, что известно, а что нет

Бывает, что ребёнок всё понимает, просто не может запомнить — слишком абстрактными кажутся ему понятия. Тут на помощь снова придёт визуализация, а также мнемотехника.

Опытом делится Ольга Пантелеева:

«Я сделала две фотографии бордюра, использовав приём „восходящая“ и „нисходящая“ диагональ, чтобы было проще запомнить, в каком случае у линейной функции положительный, а в каком — отрицательный коэффициент наклона».

Это весёлые линейные функции. Они рады, что коэффициент наклона k больше нуля (Instagram @olgapmathphys)Это грустные линейные функции, они убывают, потому что у них отрицательный k. А ещё они грустят, когда ученики забывают, что k — это коэффициент наклона прямой y = k*x + b (Instagram @olgapmathphys)

Олег Богданов согласен:

«Мнемонические техники позволяют правильно и эффективно запоминать сложный материал. Например, многие ученики путают, куда направлена ось синусов — вверх или вправо? Можно запомнить это так: синус — синий, а синее небо наверху, значит, ось синусов идёт вверх. Косинус — коса, косим мы горизонтально, значит, ось косинусов ориентирована вправо. Значения тригонометрических функций можно запомнить при помощи пальцев левой руки».

---

Шаг третий: вселить уверенность

Если школьные учителя, родители, да и все вокруг долгие годы твердили, что математика ребёнку не даётся, он и сам начинает в это верить. Так формируется установка: сдать на тройку, чтобы взрослые оставили в покое. Это отношение можно преодолеть, если не подсказывать ответы, а направлять ход мыслей и хвалить за правильные решения.

Объясняет репетитор PROFI.RU Анна Владимировна Аракелова:

«Я закладываю основы, например, объясняю, как раскрывать скобки, а дальше мы решаем задачи вместе. Так, через соучастие, появляется интерес. Я стараюсь быть с учеником на равных, не давить авторитетом и знаниями. Не подсказываю, а даю намёки, говорю, в каком направлении размышлять, спрашиваю, как он сам думает, какое решение кажется правильным. Создаю между нами атмосферу соревнования. Могу, например, сказать: „Я устала, у тебя получится лучше“. Потихоньку он начинает на меня равняться и старается сделать лучше, а я усложняю задания. Всегда стараюсь хвалить, даже за что-то совсем простое: „Ух ты, как интересно ты решил задачу!“».

---

Как видите, ничего сложного! Приблизьте математику к реальному миру, превратите её изучение в игру и покажите, что в предмете нет ничего страшного. Самое главное — никогда не говорите, что математика ребёнку не даётся. Долой негативные установки! Как знать, может, вы растите скрытого математического гения?

12 простых советов тем, кто самостоятельно учит математику

В статье описаны эффективные стратегии изучения концепций высшей математики, которые пригодятся тем, кто учит математику самостоятельно.

Все бы мы хотели лучше разбираться в математике. Многие из приведенных ниже советов будут полезны тем, кто учит математику и не только.

Математика – это не только и не столько предмет вузовской программы, сколько мощный язык для представления абстрактных идей. При помощи строгих непротиворечивых наборов правил математика позволяет облечь в конкретную форму любые концепции.

К этим правилам нужно относиться с уважением, ведь развивались они на протяжении длительного времени лучшими умами. Ваш ум должен быть открыт для этого: слепое заучивание не даст результатов.  Запоминание математических фактов тем, кто учит математику, обычно происходит естественно в ходе многократного использования изученных ранее основ.

Хотя у многих людей существует страх перед математикой, исследования показывают, что восприятие учеником собственного интеллекта как развиваемого объекта приводит к хорошей динамике обучения. То есть в первую очередь нужно поверить в собственные силы. Математика доступна всем. Вы можете обучиться чему угодно, если будете иметь правильную мотивацию.

Не волнуйтесь, если вы с ходу не поняли какую-то концепцию математики. Доказано, что мозг развивается, даже когда вы делаете ошибки. Не стоит беспокоиться, если кому-то решение задач дается легче. Чаще всего это лишь дело опыта и дисциплины ума. Разбудить в себе математика помогут наши подборки книг и курсов.

Если вы изучаете математику самостоятельно, начинайте с областей, интересных лично вам. Не тратьте время на скучные для вас (но кажущиеся необходимыми) темы.

Многие из тех, кто учил или еще учит математику, сталкивались с подобной ситуацией. То, что в конкретный момент неинтересно в рамках текущей стадии обучения, становится понятным и даже увлекательным впоследствии после прохождения любопытных сейчас тем. Интерес может развиться из потребности в определенном типе знаний. Если вы увлекаетесь искусственным интеллектом, вы сразу понимаете, где пригодятся линейная алгебра, теория вероятности и т. д.

Старайтесь фокусироваться в пределах отведенного интервала времени только на одной теме. Переключаться лучше между глобальными областями, а не смежными математическими концепциями.

В памяти закрепляется именно тот материал, которым вы постоянно пользуетесь. Будет нелишним еще раз напомнить, что обучение не относится к тем вещам, которые делаются за раз одним волевым усилием. Если вы занимаетесь хотя бы понемногу каждый день, мозг воспринимает изучаемое не как случайное событие, а как необходимый для облегчения жизни материал. Это приводит к более успешному усвоению материала, чем намеренное заучивание.

Если нужен опорный материал, например, подборка формул, пользуйтесь тематическими справочниками. В том числе краткими – теми же шпаргалками, которые легко найти по запросу «[изучаемая тема] cheat sheets».

Для обучения математике нужно решать задачи. И, конечно, лучше, если это будут задачи, которые нескучно решать. На brilliant.org проделана колоссальная работа по сбору материалов из различных областей математики, представленных в различных стилях изложения.

Если задача долго не поддается решению, оставьте ее, и приступите вновь позже. Возвращайтесь к ней, пока не решите, но не уделяйте слишком много времени за один раз. В какой-то момент мозг достаточно обучится на других задачах, чтобы решить более сложную.

Если же вы ощущаете, что зашли в тупик, не стесняйтесь просить помощи, в том числе в интернете – у тех, кто еще учит математику или уже является экспертом. Увидев ситуацию другими глазами, вы откроете незнакомые прежде источники подходов к решению.

Занимайтесь ежедневно, но не слишком долго подряд, делайте перерывы. Соблюдайте баланс мыслительной работы и отдыха. Не пренебрегайте передышками и переключениями мыслей на другие вещи. В такие моменты незаметно для вас мозг продолжает обрабатывать и усваивать информацию.

Крайне важно делать разминку. Питание к тканям мозга переносит кровь, и если кровоток затруднен, учиться сложнее. Возьмите себе за правило разминаться каждые 45-50 минут: ходить по комнате, приседать, делать упражнения. Чтобы кровь могла насытиться кислородом, занимайтесь в хорошо проветриваемых помещениях.

Важна и смена обстановки. Позанимавшись полдня, прогуляйтесь или займитесь спортом, поделайте домашнюю работу.

Проучившись неделю, поезжайте отдохнуть загород. Смена обстановки дает ощущение свежести, дает по-новому взглянуть на решаемые задачи.

Не пренебрегайте питанием. Оно должно быть сбалансированным. Мыслительные процессы относятся к группе наиболее энергозатратных задач, решаемых человеческим организмом. Вы можете «мотивировать» мозг небольшими перекусами после решения заранее определенного числа задач, равномерно разбив приемы пищи в зависимости от числа и трудности заданий. Потребляйте больше полиненасыщенных жирных кислот омега-3 – они напрямую влияют на концентрацию мышления и мозговую активность. Пейте достаточно воды.

Избегайте стрессов. Один из распространенных видов стресса для организма – отсутствие сна. Недосыпы катастрофически снижают умственную производительность. Восстановиться помогает не только ночной, но и непродолжительный сон в дневное время.

Для тех, кто учит математику, существует множество средств для геймификации процесса. Среди наиболее известных – видеоигры Variant: Limits и while True: learn(), обучение в которых происходит через решение головоломок.

Если вам станет интересно как математика используется при разработке популярных игр, почитайте нашу статью.

При изучении математики важно находиться в непрерывном мыслительном потоке. Новые визуальные абстракции и способы решений можно почерпнуть из просмотра видеороликов на различные математические темы. Для этого мы подготовили подборку из 7 полезных Youtube-каналов.

Делайте записи так, чтобы получался конспект лекций, по которому мог научиться тот, кто совсем не разбирается в теме. Неплохим методологическим решением для ведения конспекта является подход, который в шутку можно назвать по первым буквам как АД ПОТ: Аналогия, Диаграмма, Пример, Объяснение, Термин.

1. Аналогия. Вначале задайтесь вопросом: встречалось ли мне раньше что-то похожее? Например, концепция электрического сопротивления похожа на концепцию движения жидкости в трубе. Свяжите получаемые знания с известными  ранее, включите их в имеющуюся картину мира. Запоминание по ассоциациям происходит более эффективно, в то время как обособленные знания наша внутренняя система «очистки мусора» удаляет первыми.
2. Диаграмма. Визуализируйте концепцию. Перед глазами должен появиться конкретный образ, на который вы сможете опираться при дальнейших рассуждениях. Это может быть рисунок, список элементов, таблица, mindmap и т. д.
3. Пример. Рассмотрите конкретный пример использования концепции, попробуйте решить задачу, получить первый опыт в применении материала.
4. Описание
   . Опишите концепцию своими словами: в чем она заключается  и для чего нужна.
5. Термин. Наконец, дайте строгое техническое определение, связывающее концепцию с другими терминами. Это формализует понимание и позволит общаться со специалистами на одном языке.

При ведении конспекта пишите и рисуйте, но не печатайте. Использование моторики стимулирует нашу творческую активность и позволяет мозгу лучше усваивать материал.  Если вы боитесь потерять записи, отсканируйте их.

Следующий совет будет полезен тем, у кого возникают трудности с «локальной» мотивацией, то есть ученикам, которым сложно проводить занятия систематически, с одинаковой периодичностью.

Делая перерыв на отдых, не стремитесь прийти к логическому завершению рассмотрения темы. Полностью используйте то конкретное время, которое вы решили потратить на занятие, но как только оно истекло, тут же прерывайтесь. Идеальный вариант – подойти к пику рассмотрения темы. Этот совет базируется на нескольких психологических предпосылках.

Во-первых, занятия в таком виде имеют строго очерченные рамки. Вы не измотаете себя и не потратите лишнее время. А, значит, будете относиться к занятиям более воодушевленно.

Во-вторых, вам будет проще войти в рабочий ритм, начиная следующее занятие. Слегка освежив знания, вы сможете быстро настроить мозг на новую деятельность. В случае же, когда начало новой темы совпадает с началом самого занятия, требуются дополнительные усилия на то, чтобы вникнуть. Это наиболее трудное место, которое лучше брать с разгону.

В-третьих, когда вы приобретете привычку регулярно размышлять о математических абстракциях, такой подход позволит развить математическую интуицию. Несмотря на то что вы прервали занятие, мозг продолжит работу и выстроит логическую цепочку размышлений самостоятельно, без поддержки учебного материала.

Что измеряется, то и улучшается. Составьте учебный план с контрольными точками. Такие рамки повышают концентрацию. Вы как бы становитесь собственным руководителем, выдающим указания. Одновременно и тем, кто учит математику, и тем, кто обучает.

Примеры подобных планов: долгосрочный план для изучения Computer Science или более специализированный по Глубокому обучению и нейронным сетям.

Многими научными исследованиями доказано, что преподавание и совместные занятия позволяют лучше выучить материал. Чтобы донести до другого человека какую-то мысль, ее нужно не только прочитать, но и осознать. Это дает дополнительную мотивацию, так как накладывает на вас обязательства. Работая в связке с приятелем или учеником, вам обоим становится проще мотивировать себя к периодическим занятиям.

В крайнем случае слушателем можете стать вы сами. Объясните пройденную тему от начала и до конца воображаемому ученику. Вы увидите, что с такого угла зрения вы смогли осознать ее более глубоко. Данный подход обязывает разобраться во всех неясных местах.

9 простых задач на математику

Ссыл­ку на эту ста­тью може­те исполь­зо­вать, что­бы про­ве­рить базо­вые мате­ма­ти­че­ские навы­ки любо­го чело­ве­ка. Кида­е­те ему ссыл­ку и про­си­те при вас (не читая реше­ния) поре­шать какие угод­но задач­ки. Все эти задач­ки уже у нас были в раз­ное вре­мя в этом году. Поэто­му если вы наш хард­кор­ный чита­тель с само­го мар­та, то може­те спо­кой­но меди­ти­ро­вать сле­ду­ю­щие пять минут, это кайф.

Таракан на стене

В ваш подъ­езд дву­мя эта­жа­ми ниже въе­ха­ли новые жиль­цы, кото­рые при­вез­ли с собой тара­ка­нов, но не при­вез­ли еды. Насе­ко­мые в поис­ках еды ста­ли полз­ти вверх по вен­ти­ля­ци­он­ной шах­те и ско­ро добе­рут­ся до вашей квар­ти­ры. Но караб­кать­ся вверх им неудоб­но: за час они под­ни­ма­ют­ся на 1 м, но сра­зу после это­го теря­ют рав­но­ве­сие и ска­ты­ва­ют­ся на ⅔ м вниз.

Вопрос: сколь­ко часов у вас есть на покуп­ку лову­шек для тара­ка­нов, если рас­сто­я­ние от вас до сосе­дей по вен­ти­ля­ци­он­ной шах­те — 7 м?

За один пол­ный час тара­кан про­пол­за­ет ⅓ м: под­ни­ма­ет­ся на метр и опус­ка­ет­ся на ⅔:

1 — ⅔ = ⅓ м — про­пол­за­ет тара­кан за час.

С дру­гой сто­ро­ны, послед­ний метр тара­кан про­пол­зёт тоже за 1 час: он добе­рёт­ся до вер­ха за 60 минут, но ска­ты­вать­ся вниз ему уже не надо, пото­му что он достиг ров­ной поверх­но­сти. Зна­чит, нуж­но узнать, сколь­ко вре­ме­ни ему пона­до­бит­ся на остав­ши­е­ся 6 м:

7 м до вас — 1 м, кото­рый он про­пол­зёт за один заход = 6 м, кото­рые тара­кан будет мед­лен­но полз­ти и скатываться.

Что­бы узнать остав­ше­е­ся вре­мя, раз­де­лим рас­сто­я­ние на скорость:

6 м / ⅓ м в час = 18 часов.

Полу­ча­ет­ся, что тара­кан про­пол­зёт 6 м за 18 часов, а остав­ший­ся метр пре­одо­ле­ет за час, пото­му что ска­ты­вать­ся уже не при­дёт­ся. Полу­ча­ем общее время:

18 + 1 = 19 часов.

Зна­чит, у вас есть 19 часов на то, что­бы купить ловуш­ки и гель от тара­ка­нов. Логика!

Долгий перелёт

Пред­ставь­те, что вам нуж­но пару раз по рабо­те сле­тать из Моск­вы во Вла­ди­во­сток и вер­нуть­ся назад. Пер­вый раз вы лети­те туда и обрат­но при пол­ном шти­ле. Во вто­рой раз при точ­но таком же пере­лё­те в оба кон­ца посто­ян­но дует запад­ный ветер оди­на­ко­вой силы: туда попут­ный, а обрат­но — лобо­вой. Как изме­нит­ся общее вре­мя полё­та во вто­ром слу­чае: умень­шит­ся, уве­ли­чит­ся или оста­нет­ся таким же, как в пер­вом случае?

Самая пер­вая реак­ция на такую зада­чу — ска­зать, что вре­мя не изме­нит­ся. Всё кажет­ся логич­ным: когда летишь туда, ветер чуть уско­ря­ет само­лёт, а когда обрат­но — точ­но так же замед­ля­ет. Но это вер­но толь­ко наполовину.

В рам­ках зада­чи при­мем ско­рость само­лё­та за 800 кило­мет­ров в час. А ветер пусть дует со ско­ро­стью 100 кило­мет­ров в час. Мы зна­ем, что в реаль­ных усло­ви­ях всё намно­го слож­нее и ско­ро­сти нель­зя скла­ды­вать напря­мую, но для упро­ще­ния допу­стим, что это воз­мож­но. Рас­сто­я­ние от Моск­вы до Вла­ди­во­сто­ка по воз­ду­ху — 6 400 километров.

Первая командировка — без ветра

Если вет­ра нет, то у нас есть толь­ко ско­рость само­лё­та, кото­рая не меня­ет­ся в обо­их слу­ча­ях. Рас­сто­я­ние тоже оди­на­ко­вое, зна­чит вре­мя полё­та будет неиз­мен­ным в путе­ше­ствии туда и обрат­но. Най­дём его:

6 400 / 800 = 8 часов.

Это зна­чит, что в без­вет­рен­ную пого­ду наш само­лёт будет лететь из Моск­вы во Вла­ди­во­сток 8 часов, и столь­ко же лететь обрат­но. В сум­ме — 16 часов.

Вторая командировка — дует постоянный ветер

Когда летишь во Вла­ди­во­сток и дует попут­ный ветер, само­лёт и в самом деле летит быст­рее: ско­рость послед­не­го скла­ды­ва­ет­ся со ско­ро­стью ветра.

800 + 100 = 900 (км/ч).

Тогда само­лёт наше рас­сто­я­ние прой­дёт за 7 часов 7 минут:

6 400 / 900 = 7,11 часа.

Когда летишь обрат­но и дует встреч­ный ветер, то ско­рость само­лё­та падает:

800 — 100 = 700 (км/ч).

И путь обрат­но он с этой ско­ро­стью про­де­ла­ет уже за 9 часов 8 минут:

6 400 / 700 = 9,14 часа.

Полу­ча­ет­ся, что общее вре­мя туда и обрат­но при таком вет­ре будет равно:

7 часов 7 минут + 9 часов 8 минут = 16 часов 15 минут.

Посто­ян­ный ветер уве­ли­чи­ва­ет общее вре­мя полё­та, и чем силь­нее ветер — тем боль­ше вре­ме­ни зай­мёт полёт.

Если ветер будет дуть в 3 раза силь­нее — 300 кило­мет­ров в час, то до Вла­ди­во­сто­ка само­лёт доле­тит за 5 часов 48 минут, а обрат­но ему потре­бу­ет­ся уже 12 часов 48 минут, что в сум­ме даст 18 часов 36 минут.

Но почему?

Пото­му что математика:

6 400 / 800 + 6 400 / 800 = 16.

6 400 / 900 + 6 400 / 700 = 16,25.

Полторы белки

Пол­то­ры бел­ки за пол­то­ры мину­ты съе­да­ют пол­то­ра оре­ха. Сколь­ко оре­хов съе­дят 9 белок за 9 минут?

Пер­вое, что хочет­ся сра­зу отве­тить — 9 оре­хов. Но это было бы слиш­ком просто.

Самое безум­ное в этой зада­че — пол­то­ры бел­ки. Давай­те от них изба­вим­ся и будем даль­ше рабо­тать уже с целы­ми животными.

Даль­ше в реше­нии будем исхо­дить из того, что бел­ки всё едят одно­вре­мен­но друг с дру­гом, неза­ви­си­мо от их коли­че­ства. В обыч­ной жиз­ни так и про­ис­хо­дит, и мы тоже будем при­дер­жи­вать­ся того же.

Узна­ем, на что спо­соб­на одна бел­ка за пол­то­ры минуты:

1,5 бел­ки за 1,5 мину­ты съе­да­ют 1,5 оре­ха → 1 бел­ка за те же 1,5 мину­ты съест 1 орех.

Теперь выяс­ним, сколь­ко оре­хов она съест за 9 минут. Для это­го нам нуж­но пол­то­ры мину­ты умно­жить на 6, а зна­чит и коли­че­ство съе­ден­но­го тоже нуж­но умно­жить на 6:

1 бел­ка за (1,5 * 6) минут съест (1 * 6) орехов

↓

1 бел­ка за 9 минут съест 6 орехов. 

Оста­лось запу­стить 9 белок одно­вре­мен­но и посчи­тать, сколь­ко оре­хов они оси­лят за те же 9 минут:

(1 * 9) белок за 9 минут съе­дят (6 * 9) орехов

↓

9 белок за 9 минут съе­дят 54 ореха!

Поче­му? Пото­му что математика!

Рекрутер и бесконечный офис

В одной круп­ной ком­па­нии появил­ся безум­ный рекру­тер, кото­рый нани­мал на рабо­ту толь­ко джу­ни­о­ров. У него был хит­рый план — запол­нить ими весь офис и полу­чить за это пре­мию от началь­ства. Что­бы это сде­лать, он каж­дый день нани­мал столь­ко же людей, сколь­ко уже рабо­та­ет в офи­се. Гру­бо гово­ря, удва­и­вал чис­ло джуниоров.

Когда он толь­ко начи­нал, в ста­ром офи­се рабо­тал толь­ко один джу­ни­ор, но 30 дней спу­стя все рабо­чие места в офи­се были пол­но­стью заня­ты напу­ган­ны­ми, ниче­го не пони­ма­ю­щи­ми джуниорами.

В новом, точ­но таком же по раз­ме­ру офи­се с пер­во­го дня рабо­та­ет в 2 раза боль­ше людей, чем на стар­те в ста­ром — целых 2 джу­ни­о­ра вме­сто одно­го. Сколь­ко вре­ме­ни уйдёт у безум­но­го рекру­те­ра на то, что­бы запол­нить новый офис и полу­чить свою квар­таль­ную премию?

Каза­лось бы, что если на стар­те в 2 раза боль­ше людей, то и новый офис запол­нит­ся быст­рее в 2 раза — за 15 дней вме­сто 30, но это не так.

Смысл в том, что, по усло­вию зада­чи, рекру­тер удва­и­ва­ет чис­ло людей каж­дый день. Это зна­чит, что в новом офи­се это удво­е­ние про­изо­шло фак­ти­че­ски на день рань­ше, чем в ста­ром, а зна­чит, и джу­ни­о­ры его пол­но­стью зай­мут толь­ко на день рань­ше — за 29 дней вме­сто 30.

Если вы люби­те точ­ные мате­ма­ти­че­ские реше­ния вме­сто рас­суж­де­ний — вот реше­ние. Сна­ча­ла посчи­та­ем, сколь­ко людей все­го вме­ща­ет каж­дый офис. Для это­го запи­шем каж­дые удво­е­ния начи­ная с одно­го джуниора:

день 1: 1 джуниор

день 2: 2 джуниора

день 3: 4 джуниора

день 4: 8 джуниоров . . .

Если выве­сти общую фор­му­лу, получим:

день 1: 2 в нуле­вой сте­пе­ни джуниоров

день 2: 2¹ джуниоров

день 3: 2² джуниоров

день 4: 2³ джуниоров

. . .

день 30: 2 в 29-й сте­пе­ни джуниоров

Полу­ча­ет­ся, что наш офис вме­ща­ет 2 в 29-й сте­пе­ни джу­ни­о­ров. Если удво­е­ние про­ис­хо­дит каж­дый день и на стар­те у нас 2 джу­ни­о­ра, то для ново­го офи­са полу­чим такое урав­не­ние, где х — коли­че­ство дней:

2 в 29-й сте­пе­ни = 2 в сте­пе­ни х

Оче­вид­но, что х = 29, а, зна­чит, на запол­не­ние все­го ново­го офи­са пона­до­бит­ся 29 дней, как мы и гово­ри­ли в начале.

Задача про бармена и гурмана

У бар­ме­на экс­клю­зив­но­го лофт-хипста-бара на ули­це Рубин­штей­на есть толь­ко два оди­на­ко­вых ста­ка­на по 150 мл. Один ста­кан — пол­ный, и в нём про­стая вода, а в дру­гом 40-градусная вод­ка, и он напо­ло­ви­ну пуст. Утро-с.

В бар зашёл посе­ти­тель и попро­сил сде­лать ему 15-градусный рас­твор спир­та. Наход­чи­вый бар­мен не рас­те­рял­ся и смог при­го­то­вить его, исполь­зуя толь­ко эти два ста­ка­на. Как он это сде­лал и какой объ­ём полу­чил­ся в итоге?

Вряд ли эта зада­ча когда-нибудь попа­дёт­ся на собе­се­до­ва­нии в ИТ-компанию, но она может при­го­дить­ся в реаль­ной жиз­ни — напри­мер, завтра.

Это вари­ант клас­си­че­ской зада­чи на пере­ли­ва­ния, толь­ко надо счи­тать ещё кре­пость рас­тво­ра и его объём.

Берём полу­пу­стой ста­кан с вод­кой и доли­ва­ем в него воды до пол­но­го. Полу­ча­ем целый ста­кан 20-градусного спир­та ((40 + 0) / 2 = 20). Во вто­ром ста­кане оста­лась поло­ви­на чистой воды, она нам сей­час пригодится.

В ста­кан с остав­шей­ся водой нали­ва­ем наш рас­твор спир­та — сно­ва до кра­ёв. В нём теперь 10 гра­ду­сов ((20 + 0) / 2 = 10). В дру­гом оста­лось пол­ста­ка­на 20-градусного спирта.

Финаль­ным эта­пом бар­мен берёт и раз­бав­ля­ет эти пол­ста­ка­на 10-градусным рас­тво­ром из пол­но­го ста­ка­на так, что­бы жид­кость сно­ва дошла до края. В ито­ге полу­ча­ет­ся 15-градусный рас­твор ((20 + 10) / 2 = 15) объ­ё­мом в 150 мл!

Популярная школьная задача

Вот вам очень про­стой мате­ма­ти­че­ский пример:

8 / 2(2 + 2)

Вы уди­ви­тесь, но боль­шин­ство людей не смо­гут пра­виль­но это посчи­тать. Посчи­тай­те сами и потом смот­ри­те пра­виль­ный ответ:

В интер­не­те мно­го спо­ров про такие при­ме­ры, поэто­му мы реши­ли разо­брать­ся, какие ошиб­ки совер­ша­ют чаще все­го и поче­му мно­гие счи­та­ют непра­виль­но. Для реше­ния нам пона­до­бят­ся три мате­ма­ти­че­ских правила:

1. То, что в скоб­ках, выпол­ня­ет­ся в первую оче­редь. Если ско­бок несколь­ко, они выпол­ня­ют­ся сле­ва направо.
2. При отсут­ствии ско­бок мате­ма­ти­че­ские дей­ствия выпол­ня­ют­ся сле­ва напра­во, сна­ча­ла умно­же­ние и деле­ние, потом — сло­же­ние и вычитание.
3. Меж­ду мно­жи­те­лем и скоб­кой (или дву­мя скоб­ка­ми) может опус­кать­ся знак умножения.

Раз­бе­рём подроб­нее, что это зна­чит в нашем случае.

1. То, что в скоб­ках, выпол­ня­ет­ся в первую оче­редь. То есть в нашем при­ме­ре, вне зави­си­мо­сти от чего угод­но, сна­ча­ла схлоп­нут­ся скобки:

8 / 2(2 + 2) → 8 / 2(4)

2. Меж­ду чис­лом и скоб­кой мож­но опу­стить знак умно­же­ния. У нас перед скоб­кой двой­ка, то есть мож­но сде­лать такую замену:

8 / 2(4) → 8 / 2 × 4

3. Мате­ма­ти­че­ские дей­ствия при отсут­ствии ско­бок выпол­ня­ют­ся сле­ва напра­во: как при чте­нии, сна­ча­ла умно­же­ние и деле­ние, потом — сло­же­ние и вычи­та­ние. Умно­же­ние и деле­ние име­ют оди­на­ко­вый при­о­ри­тет. Нет тако­го, что сна­ча­ла все­гда дела­ет­ся умно­же­ние, затем деле­ние, или наобо­рот. Со сло­же­ни­ем и вычи­та­ни­ем то же самое.

Неко­то­рые счи­та­ют, что раз мно­жи­те­ли были напи­са­ны близ­ко друг к дру­гу (когда там сто­я­ли скоб­ки), то оно выпол­ня­ет­ся в первую оче­редь, ссы­ла­ясь при этом на раз­ные мето­ди­че­ские посо­бия. На самом деле это не так, и нет тако­го скры­то­го умно­же­ния, кото­рое име­ет при­о­ри­тет над дру­гим умно­же­ни­ем или деле­ни­ем. Это такое же умно­же­ние, как и осталь­ные, и оно дела­ет­ся в общем поряд­ке — как и при­ня­то во всём мате­ма­ти­че­ском мире.

Полу­ча­ет­ся, что нам сна­ча­ла надо сло­жить 2 + 2 в скоб­ках, потом 8 раз­де­лить на 2, и полу­чен­ный резуль­тат умно­жить на то, что в скобках:

8 / 2 × (2 + 2) = 8 / 2 × 4 = 4 × 4 = 16

Кста­ти, если на айфоне запи­сать это выра­же­ние точ­но так же, как в усло­вии, теле­фон тоже даст пра­виль­ный ответ.

А инже­нер­ный каль­ку­ля­тор на Windows 10 так запи­сы­вать не уме­ет и про­пус­ка­ет первую двойку-множитель. Попро­буй­те сами 🙂

Тут в тред вры­ва­ют­ся мате­ма­ти­ки и с воп­ля­ми «Шустеф!» пояс­ня­ют криком:

«В АЛГЕБРЕ ТОТ ЖЕ ПОРЯДОК ДЕЙСТВИЙ, ЧТО И В АРИФМЕТИКЕ, но есть исклю­че­ние: в алгеб­ре знак умно­же­ния свя­зы­ва­ет ком­по­нен­ты дей­ствия силь­нее, чем знак деле­ния, поэто­му знак умно­же­ния опус­ка­ет­ся. Напри­мер, a:b·c= a: (b·c)».

Этот текст из «Мето­ди­ки пре­по­да­ва­ния алгеб­ры», курс лек­ций, Шустеф М. Ф., 1967 год. (стр. 43)

Раз в спор­ном при­ме­ре знак умно­же­ния опу­щен, то спор­ный при­мер алгеб­ра­и­че­ский, а зна­чит, сна­ча­ла умно­жа­ем 2 на 4, а потом 8 делим на 8!

Та самая цитата. 

А вот как на это отве­ча­ют те, кто дей­стви­тель­но в теме и не ленит­ся пол­но­стью посмот­реть первоисточник:

«Для устра­не­ния недо­ра­зу­ме­ний В. Л. Гон­ча­ров ука­зы­ва­ет, что пред­по­чти­тель­нее поль­зо­вать­ся в каче­стве зна­ка деле­ния чер­той и ста­вить скоб­ки [87]. П. С. Алек­сан­дров и А. Н. Кол­мо­го­ров [59] пред­ло­жи­ли изме­нить поря­док дей­ствий в ариф­ме­ти­ке и решать, напри­мер, так: 80:20×2=80:40=2 вме­сто обыч­но­го: 80:20×2=4×2=8. Одна­ко это пред­ло­же­ние не нашло поддержки».

Если апел­ли­ро­вать к Фри­де Мак­совне Шустеф, то выхо­дит, что:

1. В. Л. Гон­ча­ров гово­рит так: «Ребя­та, исполь­зуй­те чер­ту и ставь­те скоб­ки, что­бы ни у кого не было вопро­сов про приоритет».
2. Если у нас всё же бит­ва ариф­ме­ти­ки и алгеб­ры, то, по П. С. Алек­сан­дро­ву и А. Н. Кол­мо­го­ро­ву, при­мер нуж­но решать сле­ва напра­во, как обыч­но. Они, конеч­но, пред­ло­жи­ли решать такое по-другому, но науч­ное сооб­ще­ство их не поддержало.

Самое инте­рес­ное, что даль­ше в при­ме­рах Фри­да Мак­сов­на поль­зу­ет­ся как раз пра­виль­ным поряд­ком дей­ствий, объ­яс­няя реше­ние. Даже там, где есть умно­же­ние на скоб­ку с опу­щен­ным зна­ком, она выпол­ня­ет дей­ствия сле­ва направо.

Пол­ная цита­та из Шустеф, кото­рая, ока­зы­ва­ет­ся, име­ет в виду совсем не то. 

Что не так с отчётом?

Один тре­бо­ва­тель­ный HR-директор дал зада­ние мене­дже­ру: про­ве­сти опрос сре­ди веб-программистов и выяс­нить, на каком язы­ке они пишут чаще все­го — на JavaScript или на PHP. Через неде­лю мене­джер при­нёс такой отчёт:

• коли­че­ство опро­шен­ных — 300;
• уме­ет писать на JavaScript — 234;
• уме­ет писать на PHP — 213;
• уме­ют писать на обо­их язы­ках — 144;
• вооб­ще не пишут код — 0.

HR-директор посмот­рел на отчёт и ска­зал мене­дже­ру «У тебя ошиб­ка в отчё­те. Дан­ные фаль­си­фи­ци­ро­ва­ны. Ты уво­лен в свя­зи с утра­той дове­рия». За какую ошиб­ку уво­ли­ли менеджера?

Что­бы най­ти ошиб­ку, давай­те про­ве­рим циф­ры из отчё­та и срав­ним их с исход­ны­ми. Для нача­ла выяс­ним, кто уме­ет писать ТОЛЬКО на JavaScript. Что­бы это сде­лать, возь­мём тех, кто уме­ет на нём писать, и вычтем отту­да тех, кто пишет на обо­их языках:

234 − 144 = 90 (чистых JavaScript-программистов)

Точ­но так же посчи­та­ем тех, кто пишет ТОЛЬКО на PHP: возь­мём общее коли­че­ство PHP-программистов и вычтем из них тех, кто уме­ет писать на обо­их языках.

213 − 144 = 69 (чистых PHP-программистов)

А теперь сло­жим три груп­пы: тех, кто пишет толь­ко на JavaScript (90 чело­век), кто пишет толь­ко на PHP (69 чело­век) и тех, кто пишет на двух язы­ках сра­зу (144 человека).

90 + 69 + 144 = 303

Полу­чи­лось 303 чело­ве­ка, а в опро­се заяв­ле­но 300.

Понят­но, что рас­хож­де­ние в 3 чело­ве­ка не вли­я­ет на общую ста­ти­сти­ку, но для тре­бо­ва­тель­но­го HR-директора это­го было достаточно.

Программисты и часы

— Доб­рое утро. Кото­рый сей­час час?

— Сло­жи 1/4 вре­ме­ни, про­шед­ше­го с полу­но­чи до сей­час, с 1/2 от сей­час до полуночи.

— Спа­си­бо, я понял.

— Не сомневался.

Вопрос: кото­рый час?

На самом деле это очень про­стая зада­ча, если пом­нить, что в сут­ках 24 часа.

Пусть от полу­но­чи до сей­час про­шло Х вре­ме­ни. Тогда от сей­час до полу­но­чи оста­лось 24 – Х времени.

С дру­гой сто­ро­ны, если мы сло­жим чет­верть вре­ме­ни от полу­но­чи до сей­час и поло­ви­ну вре­ме­ни от сей­час до полу­но­чи, то как раз полу­чим Х — вре­мя, кото­рое сейчас:

(¼ × Х) + (½ × (24 − Х)) = Х

Рас­кры­ва­ем скобки:

Х/4 + 12 − Х/2 = Х

Пере­не­сём все Х в одну сто­ро­ну, а 12 — в другую:

Х − Х/4 + Х/2 = 12

Х + Х/4 = 12

5Х/4 = 12

5Х = 48

Х = 9,6

Полу­ча­ет­ся, что с полу­но­чи про­шло 9,6 часа, или 9 часов 36 минут.

Ответ: на часах 9:36.

Необычный автосалон

Один авто­са­лон купил подер­жан­ную маши­ну за 450 тысяч и через неде­лю про­дал её за 525 тысяч. Дирек­тор сало­на решил, что такая модель поль­зу­ет­ся спро­сом, так что он дал мене­дже­рам зада­ние — най­ти ещё одну подоб­ную маши­ну. Они нашли такую же за 550 тысяч, купи­ли её, но дирек­тор повёл себя стран­но. Он сно­ва поста­вил на неё цен­ник в 525 тысяч, и маши­на ушла за два дня. Помо­ги­те бух­гал­те­рии понять, зара­бо­тал в ито­ге салон или поте­рял часть денег?

У этой зада­чи три реше­ния: инту­и­тив­ное, поша­го­вое и бух­гал­тер­ское. Срав­ни­те подходы.

Мно­гие реша­ют эту зада­чу так:

1. Было 450 тысяч.
2. Купи­ли маши­ну и про­да­ли за 525 тысяч.
3. После про­да­жи зара­бо­та­ли 75.
4. Взя­ли в долг 25.
5. Купи­ли вто­рую маши­ну и про­да­ли сно­ва за 525.
6. Изна­чаль­но было 450, ста­ло 525, зна­чит, при­быль сно­ва соста­ви­ла 75 тысяч, а общая — 150 тысяч.
7. Отда­ём 25 дол­га, полу­ча­ем при­быль 125 тысяч.

Но это непра­виль­но. Пра­виль­но — ниже.

Давай­те раз­бе­рём эту сдел­ку по шагам, что­бы понять, сколь­ко денег было у сало­на на каж­дом этапе.

В самом нача­ле у них было 450 тысяч — запом­ним это. Эти день­ги пошли на покуп­ку пер­вой маши­ны, поэто­му на вто­ром шаге у сало­на ста­ло 0 руб­лей, но появил­ся автомобиль.

На тре­тьем шаге его про­да­ли за 525 тысяч, кото­рые и ушли в кас­су. Пока при­быль сало­на рав­на: 525 − 450 = 75 тысяч.

Вто­рая маши­на сто­и­ла на 25 тысяч доро­же, чем у них было — 550, поэто­му салон взял в долг 25 тысяч и купил её (шаг номер четы­ре). Здесь при­быль сало­на исчез­ла и появил­ся убы­ток в 25 тысяч.

Пятым шагом они про­да­ли вто­рую маши­ну за 525 тысяч, поло­жи­ли день­ги в кас­су и ста­ли раз­би­рать­ся с дол­га­ми. После того как они вер­ну­ли сум­му, кото­рую были долж­ны, у сало­на оста­лось 500 тысяч, а начи­на­ли они с сум­мы в 450 тысяч. Полу­ча­ет­ся, что они зара­бо­та­ли 500 − 450 = 50 тысяч.

Бух­гал­те­ры рабо­та­ют так: счи­та­ют все дохо­ды и рас­хо­ды, а потом нахо­дят саль­до — раз­ни­цу меж­ду ними. Сде­ла­ем то же самое.

Дохо­ды: 525 с пер­вой про­да­жи и столь­ко же со вто­рой. Полу­ча­ет­ся 525 + 525 = 1050 тысяч.

Рас­хо­ды: 450 за первую маши­ну и 550 за вто­рую. Полу­ча­ет­ся 450 + 550 = 1000 тысяч.

Саль­до: дохо­ды минус рас­хо­ды. Это 1050 − 1000 = 50 тысяч.

Как помочь ребенку полюбить математику

Общественные стереотипы делят людей на технарей и гуманитариев. Принято считать, что первые воспринимают информацию через цифры и алгоритмы, у них лучше развито логическое мышление, а вторые — познают мир при помощи чувств и образов, умеют творить и генерировать идеи. 

Впервые такое разделение происходит в школе. Если трудно с точными науками — ты гуманитарий, сколько ни старайся, всё равно ничего с математикой не выйдет.  

Раньше считалось, что человек с рождения имеет талант в определённой области, а изменить это можно, только если усиленно развивать другое направление с раннего детства.  

Такой подход уже давно неактуален. Учёные доказали: когда у человека появляется проблема, с которой раньше он не сталкивался, мозг выделяет на её решение группу нейронов. Их формирование индивидуально для каждой задачи, поэтому нельзя говорить о врождённой предрасположенности к каким-либо навыкам: при должном старании любой человек способен научиться чему угодно. Даже если ребёнку тяжело даётся устный счёт — в будущем он сможет стать великим математиком, стоит только захотеть.

В современном мире нет разделения на гуманитариев и технарей. Человек может заниматься чем хочет, а не ориентироваться на «врождённые» способности.  

Успех в том или ином предмете во многом зависит от харизмы и манеры преподавания педагога. Сплошная зубрёжка способна отбить интерес к изучению математики у школьника, даже если у ребёнка есть предрасположенность. 

В современном мире ценятся универсальные специалисты, которые умеют работать с цифрами, алгоритмами и текстами, применяют творческий подход, опираются на разнообразные умения и навыки. Например, хороший программист знает иностранные языки, а геймдизайнер должен уметь отредактировать сценарий игры и творчески проработать персонажей.

Как увлечь ребёнка математикой

Для формирования интереса к алгебре и геометрии расскажите ребёнку, чем ему будут полезны эти предметы в жизни и как их можно применять на практике. 

5 причин полюбить математику: 

• Регулярное решение уравнений и задач тренирует мозг, улучшает память, развивает внимательность и расширяет кругозор. 
• Математика в любой момент может понадобиться в повседневной жизни, например, узнать, на сколько дней хватит карманных денег. 
• Расчёты есть во многих науках, например, химии, физике, географии. Даже гуманитарные предметы — языки и литература — опираются на математические и логические законы. 
• Для тех, кто серьёзно занимается алгеброй и геометрией, в них сокрыта красота и гармония, сродни музыке — при глубоком изучении появляется любовь к математике.
  

Математика на самом деле очень простая. В ней всего два аспекта. Первый — строгость логического мышления. Неумение прослеживать причинно-следственные связи — большая проблема человечества. Из-за этого происходит множество конфликтов. Математика же позволяет определять, следует ли «А» из «Б», на уровне рефлексов. Если в задаче что-то не сказано, ты не имеешь право это предполагать, а если сказано, нельзя игнорировать. И второй — это прикладные навыки. Всё, что нас окружает, имеет инженерное происхождение. Математика помогает понять, как всё это работает.

                                                       Владимир Шарич, преподаватель математики а «Экстернате Фоксфорда»

Математика интересна, когда в ней есть творчество, а законы ясны и легки в использовании. Однако скорость усвоения материала у всех детей индивидуальна, поэтому важно уделять достаточно времени каждой теме, чтобы качественно её понять и проработать. Так, ученики «Экстерната и домашней школы Фоксфорда» могут двигаться в своём ритме. Занятия проводятся в режиме онлайн-трансляции, когда можно сразу же пообщаться с преподавателем и задать ему возникшие вопросы. Все видео сохраняются, их можно изучить в любое время и посмотреть повторно. Для ребят, которые увлечены этим предметом и хотят участвовать в олимпиадах, в «Экстернате Фоксфорда» есть математический образовательный маршрут.

5 способов полюбить математику

Главное — сделать занятия интересными. Вот несколько советов, которые помогут всей семье весело и с пользой провести время, изучая точные науки, и полюбить математику. 

Найдите математику в реальной жизни

Точные науки окружают нас повсюду, и если показать это ребёнку, то у него никогда не возникнет вопроса: «Где мне пригодятся алгебра и геометрия?». 

Начинать можно с чего-то простого: посчитать сдачу в магазине или назвать, из каких фигур состоят обычные предметы (стакан — цилиндр, кровать — прямоугольник и так далее).

Чем старше человек, тем интереснее становится математика вокруг него. Старшекласснику можно доверить ведение семейного бюджета или планирование финансов на отпуск. Всё это станет ежедневной тренировкой математического мышления.

Начните играть, чтобы полюбить математику

Компьютерные и настольные игры отлично способствуют развитию интереса к математике. Преимущество настолок в том, что это увлечение для всей семьи. Интересная математическая игра «7 на 9» понравится и детям, и взрослым. В ней каждая карта закрывается той, на которой сумма изображённых цифр выше. Это отличный способ тренировки устного счёта и быстроты реакции: кто раньше избавится от карт, тот и выиграл.

Источник: freepik.com

В интернете можно найти много бесплатных интерактивных головоломок. Например, в приложении «Math. Пазлы и математическая игра» сто уровней сложности, в каждом из которых оригинальная задача — удобная и быстрая тренировка, которая поможет увлечься математикой.

Решайте трудные задачки

Примеры в учебниках порой скучные, а тем, кто уже понял пройденную тему, могут показаться слишком лёгкими. Чтобы ребёнок не разлюбил математику, подогревайте интерес трудными, но посильными головоломками. Многие такие задачи пишутся специально для олимпиад.

Читайте книги 

Парадоксально, но литература способна повысить интерес к математике и вдохновить на собственные исследования. Младшим школьникам и подросткам подойдут художественные рассказы о математике и необычные сборники и задачники. Советуем обратить внимания на эти книги: Лев Генденштейн «Алиса в Стране математики», Владимир Левшин «Магистр Рассеянных Наук: математическая трилогия», Игорь Шарыгин «Уроки дедушки Гаврилы, или Развивающие каникулы». В каждой из них яркий герой постигает премудрости математики, и без помощи читателя ему никак не справиться.

Лев Генденштейн «Алиса в Стране математики»

Для более старшего возраста подойдут биографии известных исследователей и научно-популярные книги. Предложите своему ребёнку прочитать «Удовольствие от X» Стивена Строгаца или «Магию математики» Артура Бенджамина. 

Смотрите образовательные видео

Короткие видеолекции — удобный формат для того, чтобы полюбить математику. Советуем популярный канал на YouTube для тех, кто интересуется точными науками и готов пойти дальше школьной программы — Sibscience, его ведут настоящие учёные. Они рассказывают обо всём: от основ геометрии до теории игр и экономики. 

Также побудить интерес к математике и подготовиться к аттестациям по этому предмету помогут базовые курсы «Экстерната Фоксфорда». Выберете нужный класс обучения в каталоге, и постигайте красоту алгебры и геометрии вместе с преподавателями из лучших вузов страны!

Как делать легко математику?

         Многим кажется, что успеваемость в школе, это показатель интеллекта. Но это не совсем так. Многие подростки просто не знают как быстро и правильно делать уроки. Никто не научил, никто не показал. Вот и получается, что ты безуспешно теряешь свое время на длительное изучение, путаешься в формулах или просто бросаешь начатое на полпути, пуская все на самотек. Но как же полюбить математику? Как научиться быть королевой чисел и формул? Интересно? Тогда читаем дальше.

        Давай сначала поговорим о том, что выполнение любого домашнего задания должно начинаться с ритуала. Твоего особенного ритуала. Это может быть десять минут расслабления, а может начинаться и с приготовления рабочего места (наведи на письменном столе порядок, приготовь все необходимое). Потом нужно открыть учебник по математики и поделить задания на простые и сложные. А дальше соблюдаем простые и эффективные правила.

Читай также: «Как полюбить нелюбимые предметы в школе»

       Во-первых, ты должна усвоить некоторые правила выполнения домашнего задания: не откладывай уроки на потом (делай все день в день), не начинай делать уроки с заучивания (например, правил или формул) и изучай материал так, как собираешься отвечать на уроке. Видишь, все просто, правда? Кстати, эти правила касаются не только математики.

       Во – вторых, ты должна понять, что чтобы хорошо делать что-либо, это нужно полюбить. Вот скажи, как можно успевать по математики, не любя этот предмет? Ответ прост – никак! Говорят, что точные науки никогда не поймут творческие люди. Но как же можно изучать математику без фантазии? Ведь именно воображение учит искать нестандартное решение задачи, а это путь к раскрытию уникальных творческих способностей.

       В-третьих, ты должна понять, что математику нужно учить играя.  Это значит, что прежде чем приступать к заучиванию, ты должна понять материал. Если у тебя есть пробелы – обязательно заполни их. А дальше придумай сказку. Например, ты читаешь условие задачи и представляешь, что в каком-то государстве живет красивая и умная принцесса. Дальше просто связывай образ принцессы с условием задачи. Пытайся себе все четко и красочно представить. Увидишь, это тебя увлечет, лень отступит и тебе самой станет интересно решить пример. Выполняй задания поэтапно, не переключайся с одного (недоделав его) на другое. Не отвлекайся на какие-нибудь внешние факторы.

Читай также: «Как сделать уроки легко и интересно?»

      Ну и последнее, это мотивация. Без этого никакой настрой не поможет. Не согласна? А вот смотри, допустим, ты очень любишь рисовать и ходишь  в кружок. Допустим, у тебя занятие в субботу, но тут соседка просит тебя посидеть с ее маленьким ребенком. Рисовать ты любишь больше, поэтому, понятное дело, что ты будешь не довольна таким предложением и, скорее всего, откажешь и побежишь на урок. Ну что, если соседка тебе предложит взамен организовать мастер-класс у самого крутого и знаменитого художника? Это ведь уже другой разговор, правда? Это и есть мотивация. Мы делаем что-то, а получаем то-то.  Вот и  подумай, зачем нужна тебе эта математика.

      Поставь себе цель, ищи способы ее достижения и будь успешной! Главное помни: ты умница и у тебя все получится!

«Что делать, если не понимаешь математику?» – Яндекс.Кью

Все мы чего-нибудь не понимаем. Сначала надо понять, чем лично Вам мешает непонимание математики, а потом поставить себе конкретную цель. Может быть, достаточно худо-бедно сдать школьный экзамен, для этого особого понимания математики не требуется.

Если надо исправить застарелое школьное непонимание, а время еще есть.

Читайте учебник на один параграф вперед. Постарайтесь разобрать теорию и примеры самостоятельно. Если встречаете незнакомые слова или термины, то вернитесь назад и разберитесь, что они означают. Продвиньтесь так далеко, как только возможно, и порешайте задачи. Хорошо объединиться с товарищем и разбираться вместе. Если что-то осталось непонятным, спросите потом в классе. Цель — добиться, чтобы на следующем уроке было все понятно.

При таком способе постепенно, хотя и не скоро, заполнятся все белые пятна прошлого, после этого можно будет поставить себе другую цель.

Если надо готовиться к экзаменам, а времени в обрез.

Прорешайте 4-5 типовых вариантов и проанализируйте результаты. Все позиции в варианте разбейте на 3 группы:

1. Те задачи, которые решены во всех вариантах; возможно, с небольшими недочетами.
2. Задачи, которые решаются через раз.
3. Задачи, которые везде решены неверно или за которые не брались.

Работайте в основном над задачами из второй группы. Сейчас есть пособия, в которых отрабатывается каждая задача отдельно, вот такое надо взять. Отведите 2-3 недели на одну позицию и прорабатывайте, пока она не перейдет в первую группу.

Раз в месяц составляйте контрольную работу из задач первой группы и решайте, чтобы не забыть.

За месяц до экзамена нарешайте типовых вариантов, следя за временем.

Если вообще не понимаете, что происходит, найдите помощника — учителя, родителя, репетитора, товарища, — чтобы внимательно вас расспросил, послушал и помог составить план действий.

Как научить ребенка математике | rastishka.by

Математика — наука «не для всех». Считаете именно так? Опустили руки и решили, что «не дано» (ни вам, ни ребенку)? Рано отчаялись! Есть способы научить ребенка математике быстро и легко. В любом возрасте. Делимся наблюдениями и секретами.

www.vladtime.ru

Современное образование во многом построено на развитии аналитических способностей — это факт, творчеству уделяется совсем мало внимания. Но! О пользе развивать оба полушария головного мозга слышал, пожалуй, каждый. Все в ваших руках! Ищите нестандартные методы и решения, тогда ваш ребенок полюбит математику и не будет испытывать сложностей в школе.

Психологи сообщают неутешительную статистику.

 В школу приходит более 50% детей с творческими задатками, а уже через полгода их число снижается до 10%.

А все почему? От них требуется все делать «как учительница сказала», главный мотив — угодить учителю, маме и т.п.

Математика требует абстрактного мышления, но у младших школьников оно развито плохо.

Это данность, которую важно понять и принять. Как родителям, так и педагогу предметнику, который взял пятый класс, и на фоне старшеклассников, конечно же, чувствует колоссальную разницу.

avatars.mds.yandex.net

Родители «в шоке», ребенок «в стрессе». Как так, ОН НЕ ПОНИМАЕТ МАТЕМАТИКУ… А вот так! Он хочет понять, но не всегда может это сделать без квалифицированной помощи взрослого. А мама и папа не всегда знают, как правильно объяснить, ведь их «учили не так», да и современные учебники не всегда могут похвастаться доступностью и грамотностью изложения материала.

Итак, постараемся понять, чем мы можем помочь ребенку в математике, не дожидаясь, пока появятся проблемы в старших классах.

У ребенка проблема с математикой? Есть решение!

Чтобы привить ребенку интерес к математике и научить ее любить, не ждите начала обучения в школе. Займитесь математикой с ребенком гораздо раньше. В игре, в обычных ежедневных заботах и хлопотах, во время прогулок и походов в гости. Отвечайте на вопросы, проигрывайте нестандартные ситуации и давайте малышу «пищу для ума».

steshka.ru

ПРОБЛЕМА: Ребенок не может что-то посчитать в уме.
Причина: Он не может представить, ему нужно увидеть предметы счета, произвести с предметами какие-то действия.
Решение: Попробуйте использовать «абакус» (счеты) или другую наглядность. Это поможет ребенку «почувствовать» числа. Рисуйте графики, схемы, объясняйте «на кошках» — все, что угодно, главное — НАГЛЯДНО! И это касается любых тем в любом классе.

Просто к пяти прибавить шесть — это ни о чем, а вот к пяти ЯБЛОКАМ прибавить три ЯБЛОКА — тут все предельно ясно. Ребенок не понимает дроби? Попробуйте резать пиццу или ломать палочки. Возможно ваш путь в математику именно такой!

Если ваш малыш делает первые шаги в мире математики, начинает изучать цифры и учится считать, рекомендуем почитать:

ПРОБЛЕМА: Ребенок не может выучить таблицу умножения.
Решение: Используйте не «зубрежку», а другие методы. На самом деле, из 100 примеров выучить нужно всего 15, остальные поддаются «дрессировке». Можете попробовать ментальную арифметику. И успокойтесь. Можно не знать таблицу умножения, но успешно ее использовать. В конце концов — важна логика мышления. На крайний случай можно и сложением/вычитанием заменить.

Полезные советы вы найдете в наших статьях:

ПРОБЛЕМА: Ребенок не любит математику.
Причина: Не любят обычно то, что плохо получается, где нужно прикладывать много усилий, где не радует результат (плохие отметки), не нравится учитель.
Решение: Найдите первопричину и попробуйте исправить ситуацию.

Традиционная методика обучения математике основана на разделении материала на блоки. А вы попробуйте мыслить иначе.

Вот пример. Дошкольнику дают 3 палочки и просят составить из них квадрат. Не получается. Что делать? Дают еще одну. Из четырех палочек все получилось. Обычная ситуация из жизни. Но! В 4 классе, на теме «Периметр квадрата» этому ребенку не нужно будет вдалбливать правило, что периметр — это то-то и то-то. Он ВСПОМНИТ 4 палочки и САМ найдет решение в своей голове, ДОДУМАЕТСЯ до него. Если в математике использовать такой подход, у ребенка не возникнет проблем, он полюбит этот предмет и с радостью будет решать задачи, уравнения примеры.

Чаще используйте занимательный материал, чтобы привить ребенку интерес к математике.
Рекомендуем почитать:

«У него нет способностей к математике». Это утверждение не выдержит никакую критику, если ребенок достаточно успешен по другим предметам. Например, по иностранному у него нет проблем, а там тоже нужна логика. Значит, дело не только в способностях…

Если ребенок не уверен в себе, очень зависит от мнения окружающий (родителей, учителей), он, как правило, может испытывать бОльшие трудности, чем любознательный и уверенный в себе ученик. Постарайтесь в таком случае объяснить, что трудности — это нормально, и если систематически заниматься математикой в школе и дома, все будет хорошо.

«Эффект снежного кома» наступает тогда, когда появляются пробелы в знаниях (пропустил, не выучил, не понял и т. п.). Нужно не допускать таких ситуаций, своевременно наверстывать упущенное.

ПРОБЛЕМА: Ребенок не умеет решать задачи.
Причина: Иногда школьнику не совсем понятен смысл написанного, суть вопроса.
Решение: Для начала попробуйте «перевести» условие задачи на понятный ребенку язык. Можно рассказать его своими словами, как сказку или веселую историю. Можно зарисовать в виде схемы или даже комикса. Как только появится «эмоциональная составляющая», решение может прийти неожиданно быстро.

Как научить ребенка решать задачи: рекомендации родителям

Вопрос «Как научить ребенка решать задачи по математике» преследует некоторых родителей даже во сне. Как? Как сделать так, чтобы он наконец понял?

Решать задачи ребенку придется часто: и по математике, и по алгебре, и по геометрии, и по физике, и по химии. Поэтому стоит раз и навсегда понять, как это делать, ведь есть общие закономерности, которые применимы к любому предмету. Мама не может (и не должна!) учиться в школе ВМЕСТО сына или дочки, и уж тем более не должна делать «домашку» вместо них. Вместе — да, но не ВМЕСТО!

soroban.ua

«Решение задач — это практическое искусство, подобно плаванию, или катанию на лыжах, или игре на пианино: вы можете научиться этому, только практикуясь … если вы захотите научиться плавать, то вынуждены будете зайти в воду, а если вы захотите стать человеком, хорошо решающим задачи, вы вынуждены их решать». (Математик и педагог Д. Пойа).

Любая задача состоит из 4 составляющих:

1. Условие
2. Вопрос
3. Решение
4. Ответ

Самое главное, чему нужно научить ребенка:

• Ответ задачи скрыт в ее условии. 
• Ответ нужно списывать с вопроса.
• Ответ всегда начинается с числа.
• Ребенок должен четко знать значение «математических фраз»: «больше/меньше в… раз», «больше/меньше на…» и др.
• Ребенок должен знать понятия «слагаемое», «уменьшаемое», «вычитаемое» и т.д.

Только после этого условия задач не будут казаться такими запутанными и сложными, а решение станет простым и очевидным.  

Что нужно сделать, чтобы решить задачу по математике?

• Нужно внимательно прочитать задачу и выделить эти 4 части.

Решение любой задачи сводится к одному: по двум данным найти третье (неизвестное). Итак, что нам известно? Что мы должны найти?

• Составить краткую запись, сделать схематический рисунок или любым другим способом превратить задачу в «живую» наглядность.

Это поможет ребенку понять, что происходит в тот момент, который описан в условии задачи. Иногда можно продемонстрировать, как «Коля раскладывал тетрадки на 3 стопки…» или как «Миша разрезал яблоко на 4 части…» Разыграйте сценку, чтобы ребенок оказался сам «внутри задачи». 

• Проверьте правильность решения обратной задачей.

Не торопитесь сообщать, что «ты решил верно» или «ответ не верный». Подставьте получившиеся значения и проверьте. Возможно, не так все просто, в задаче не одно, в два или даже три действия. Пусть ребенок порассуждает сам, вы лишь направляйте.

Чтобы научить ребенка решать задачи, нужно сформировать привычку это делать, и делать это с удовольствием. А этому можно научить!

К решению любой задачи нужно подходить творчески. Не получается так — попробуйте иначе. 

• Попробуйте дать задачу, которая содержит лишние сведения. Ребенок сам почувствует, что важно, а что можно смело «опустить».
• Попробуйте нестандартные ситуации. Пусть в вашей задаче будет два или даже три варианта решения.

И самое главное! Не ждите, что вы научите ребенка решать задачи, выполнив с ним одну-две похожих. Навык нужно довести до автоматизма, задачи нужно научиться «чувствовать».

Главные выводы

• Ребенок знает не то, чему его научили, а то, с чем он столкнулся в жизни.

Поэтому в математике главное не учебный материал, а те методы, с помощью которых ребенок его осваивает.

• В обучении ребенка математике важна мотивация.

Постарайтесь поговорить со своим школьником. Объясните, что он учится не ради отметок в дневнике, не для того, чтобы угодить учительнице и порадовать маму, и даже не для того, чтобы поступить в ВУЗ. Работодателю не нужны люди, которые могут быстро умножать и делить — для этих целей есть калькулятор и «умные» бухгалтерские программы. Нужны люди, умеющие анализировать, выдвигать гипотезы, придумывать новые пути решения. 

В беседе постарайтесь уцепиться за то, чем ваш ребенок увлечен. Математику можно «прикрутить» практически к любой сфере деятельности: программисту — нужна, инженеру — нужна, строителю — нужна и т.п. Ребенок-гуманитарий скажет вам «фи», но и тут можно найти аргументы «за». Возможно, квадратные уравнения ему не особо пригодятся, но умение аналитически мыслить, которое он приобретет в результате их решения, пригодится в жизни на все 100%.

Помогите ребенку увидеть в изучении математики СМЫСЛ!

• Быстрый счет — не самоцель.

Научить ребенка быстро считать — не так важно, как научить его мыслить. Нестандартная задача поставит «обычного» ученика в тупик, а мыслящий — найдет решение.

•  Математику не нужно бояться.

Помогите ребенку преодолеть страх перед математикой. Не нагнетайте обстановку, не говорите, что это трудно, не блокируйте познавательный авантюризм.

Уважаемые читатели! Ждем ваших рассказов в комментариях о том, какие у вас отношения с математикой. Помогаете ли вы ребенку делать домашние задания, сидите вместе с ним над сложной задачей, «разжевываете» непонятное?

Как стать лучше в математике (при этом тратя меньше времени на изучение)

Несмотря на все исследования, которые показывают, что математики сделали и не родились, я не виню вас за то, что вы думаете, что вы просто плохо разбираетесь в математике, потому что математика чертовски сложно .

Чтобы построить свой математический «домик», вы должны убедиться, что каждый блок знаний идеально подходит, чтобы вы могли строить на нем, не опасаясь, что позже все это опрокинется.

И если вы откроете хотя бы одну фундаментальную тему, ваши знания рухнут перед скрежетом зубами о наборах задач и трепещущим сердцем на большом экзамене.

Итак, вопрос о деньгах таков: Как вы станете лучше в математике?

Чтобы стать лучше в математике, вам необходимо решать все более сложные математические задачи, используя стратегический психолог Андерс Эрикссон называет преднамеренной практикой в своей книге Пик: секреты новой науки опыта .

Он определяет это как «целенаправленную практику, которая знает, куда идет и как этого добиться».

Это означает, что вы должны намеренно находить проблемы, которые ставят вас в тупик, и работать над ними.А если проблема слишком сложная, сначала найдите более простую для решения.

Это один из самых важных принципов, о которых вам нужно помнить при изучении математики. В этом посте я поделюсь некоторыми советами, как это сделать.

Совет №1: разбивайте сложные проблемы на более простые

«Если вы не можете решить проблему, то вы можете решить более простую задачу: найти ее».

— Джордж Полиа , Как решить

Чтобы понять суть каждой проблемы, вы должны определить концепции, выделить их и практиковаться.Возьмем эту задачу суммирования, например:

Это относительно простая задача, которую должен уметь решать старшеклассник. Но есть часть уравнения, которая усложняет задачу:

. Для решения этой задачи требуется знание суммирования дробных показателей и .

Итак, прежде чем погрузиться в проблему, вы должны сначала убедиться, что вы понимаете суммирование и дробные показатели как таковые.

Например, вы можете взять дробную экспоненту и без нее проработать исходную задачу:

Что затем даст вам следующее решение:

Затем вы можете убрать дробную экспоненту в задаче и работать над ее усвоением. :

И поймите, что это не так уж сложно решить самостоятельно:

После того, как вы выяснили эти две концепции сами по себе, вы можете сложить их вместе, чтобы решить исходное уравнение.Посмотрите, как они все сочетаются:

Поздравляю! Вы нашли решение:

Совет № 2: Используйте простые числа

Если вы еще раз взглянете на мой пример, вы заметите, что в нем используются простые числа и низкий предел:

• Простые числа означают Мне не нужен калькулятор для выполнения операций.
• Нижний предел означает, что я не утомлю свой мозг повторяющимися операциями, которые я уже умею выполнять.

. сначала имейте простые числа.Вместо того, чтобы усложнять задачу, работа с задачами с маленькими целыми числами позволяет сосредоточиться на концепциях и принципах.

Совет № 3: Просмотрите основные концепции

Иногда, однако, ваше понимание проблемы слишком шатко. (Хорошо, давайте будем честными: это происходит в большинстве случаев. )

В таком случае пора покопаться в книге и просмотреть свои заметки в классе. (Я предполагаю, что вы делаете заметки на уровне A +. Если нет, узнайте, как делать заметки лучше здесь.)

Если вы все еще не понимаете, есть много видео на YouTube и статей, которые помогут вам. Часто у них есть пошаговые решения, показывающие, как другие люди находят свои ответы:

Наконец, попросите своего профессора или учителя о помощи. Эрикссон говорит: «Хороший учитель математики… найдет больше, чем просто ответ на проблему; он посмотрит, как именно ученик получил ответ, чтобы понять, какие мысленные представления использовал ученик. При необходимости он посоветует, как более эффективно обдумать проблему.”

Опытные учителя часто могут переформулировать или переформулировать концепции. Иногда достаточно немного другого слова, чтобы сложная концепция встала на место.

Иногда полезно увидеть пошаговое решение проблемы, над которой вы работаете, при условии, что вы сначала попытаетесь решить ее сами.

Есть три отличных инструмента для решения проблем, с которыми вы боретесь:

1. Wolfram Alpha
2. Symbolab
3. Chegg Study

Wolfram Alpha — это инструмент, который может решить практически любую математическую задачу, а также дать вам подробные решения (хотя вам понадобится премиум-версия, чтобы увидеть все шаги):

Напротив, хотя пользовательский интерфейс Symbolab более громоздкий и менее интуитивно понятный, его пошаговые решения бесплатны:

Наконец, если вы Если вам нужны решения конкретных задач в вашем учебнике, вы можете проверить Chegg Study.Он покажет вам пошаговые решения всех задач из учебника, который использует ваш класс математики:

Независимо от того, что вы выберете, убедитесь, что вы попробуете сами задачи после этого, не глядя на решения.

Это поможет вам избежать того, что Джеффри Карпик, исследователь, специализирующийся на стратегиях обучения студентов, называет иллюзией компетентности . Это когда вы чувствуете, что понимаете концепцию, потому что вы прочитали абзац несколько раз и можете быстрее его обработать

Карпик обнаружил, что вместо того, чтобы перечитывать, пытается извлечь информацию из памяти , что является наиболее эффективной формой обучения.Он выступал за такие методы, как техника Фейнмана, которые помогут вам глубоко вспомнить и запомнить концепции.

Точно так же честно спросите себя: Довел ли я свой мозг до предела, пытаясь сначала решить эту проблему? Если у вас есть, но вы все еще не можете его получить, можно найти ответ. Но после этого заставьте себя вернуться и поработать над проблемой, не просматривая свои записи и ссылки.

Опять же, весь смысл математики состоит в том, чтобы овладеть концепциями , с которыми вы работаете, чтобы вы могли строить их поверх них, а не просто выполнять домашнее задание.

Совет № 5: не торопитесь с домашним заданием

«Простое понимание того, как была решена проблема, не обязательно создает фрагмент, который вы можете легко вспомнить позже. Разве , а не , путают с «ага!» прорыва в понимании с солидным опытом! »

— Барбара Окли

Очень заманчиво поработать над домашними заданиями как можно быстрее, чтобы вернуться к игре в Civilization VI или The Witcher 3 .

Но технические предметы, такие как математика и естественные науки, требуют от вас медлительности.

Для начала, в книге профессора инженерных наук Барбары Окли A Mind for Numbers Окли предлагает применять повторений с интервалом . Вместо того, чтобы проводить долгие часы в библиотеке, она советует более короткие и частые учебные занятия, которые растягиваются на недели, а не на дни.

Этот вид медленного, преднамеренного обучения позволяет вашему мозгу прочно усвоить каждую концепцию и, что более важно, связи между ними.

Чтобы по-настоящему владеть своими инструментами, вам нужно научиться адаптировать их к различным ситуациям.

Точно так же, чтобы по-настоящему сказать, что вы освоили часть математики, вам нужно разобраться в проблемах и сразу же знать, какую формулу или процесс использовать.

Изучение математики может быть удовлетворительным

«Я не верю в идею, что есть несколько необычных людей, способных понимать математику, а остальной мир нормален. Математика — это открытие человека, и оно не сложнее, чем люди могут понять ».

— Ричард Фейнман, Omni Magazine

Стать лучше в математике — это просто, но нелегко.

Вам необходимо глубоко понять как , как концепция работает, так и , когда , чтобы использовать ее вместе с другими концепциями и операциями.

Чтобы помочь вам овладеть отдельными математическими строительными блоками, вы можете использовать справочные материалы и вспомогательные инструменты. Но в конечном итоге они могут помочь вам только пока.

Чтобы овладеть основными концепциями, вам нужно взять карандаш и бумагу и самостоятельно решать сложные задачи.

Как быстро выучить математику

Обновлено 27 ноября 2018 г.

Ли Джонсон

Математика — один из самых недолюбливаемых предметов, но в той или иной степени он нужен почти каждому. Даже если вы не занимаетесь математикой, знание того, как рассчитать 15 процентов счета, чтобы вы могли давать чаевые официантам, или умение рассчитать НДС при покупке за границей, является жизненно важным навыком в повседневной жизни. По правде говоря, у математики плохая репутация, которой она не заслуживает. Сосредоточение внимания на быстром вычислении, механическом запоминании и абстрактных задачах заставляет многих людей думать, что математика — это скучно или просто не то, что им когда-либо понадобится.

Но что, если вы ранее решили, что вам, вероятно, не понадобится математика, но теперь оказались в зависимости от нее в вашей работе? Как лучше всего выучить математику, если у вас мало знаний по этому предмету? Хотя конкретный путь, который вы выберете, во многом зависит от того, для чего вам нужна математика, есть несколько полезных советов и советов, которые могут направить вас на правильный путь.

Занимайтесь предметом

У вас гораздо больше шансов выучить математику быстро, если вы будете заниматься предметом и получать от него как можно больше удовольствия. Вам не нужно с нетерпением ждать каждого нового «Numberphile» видео или решать дифференциальные уравнения в свободное время, но чем больше вы действительно будете получать удовольствие от предмета, а не рассматривать его как рутинную работу, тем лучше. Будьте любознательны, когда узнаете что-то странное или противоречащее интуиции, используйте аналогии и юмор, чтобы сделать основные идеи более яркими, и тщательно обдумайте концепции, лежащие в основе этих идей, а не сосредотачивайтесь только на том, как рассчитывать вещи или решать проблемы.

На самом деле, может быть более практичным было бы просто попытаться избежать главных вещей, которые заставляют людей ненавидеть математику, вместо того, чтобы пытаться получать удовольствие, если это не то, что вам раньше нравилось. Доктор Джо Боулер, профессор математического образования в Стэнфорде, пишет, что сосредоточение внимания на «быстрой математике», механическое запоминание и тестирование в условиях ограниченного времени — главные препятствия, с которыми люди сталкиваются при изучении математики.

Может показаться, что это не очень быстрый метод обучения, но быстрое изучение математики означает хорошее владение основами.Если вы поймете, как это работает, вы интуитивно уловите новые идеи и увидите связи между ними, вместо того, чтобы просто вспоминать, казалось бы, бесконечный поток явно не связанных между собой фактов.

Начинайте с основ

Более сложные математические темы в значительной степени основаны на более простых, поэтому вам нужно начинать с основ — даже если вы чувствуете, что хорошо их понимаете, — прежде чем переходить к чему-то более сложному . Например, если вы надеетесь научиться математическому анализу, вы ничего не добьетесь быстро, если не будете хорошо разбираться в основах алгебры и немного тригонометрии.Перед тем как бегать, вам нужно ходить, и тот же самый базовый совет применим и к изучению математики.

Развивайте чувство числа вместо запоминания

Запоминание таблицы умножения менее важно, чем способность решать незнакомую задачу полусистемным способом. Например, вы могли запомнить, что 9 × 9 = 81, но если вы находитесь в тяжелой или стрессовой ситуации, такие факты легко забыть. «Чувство числа» — это возможность решить эту проблему с нуля простым способом.Например, умножение на 10 намного проще, поэтому вы можете решить это, вычислив 9 × 10 = 90, а затем вычтя лишние «9», которые вы включили в это вычисление (потому что вместо этого вы разработали 10 групп по девять из девяти групп по девять), чтобы получить 81.

Таким же образом, столкнувшись с проблемой типа 13 × 8, которую вы, вероятно, не запомнили, вы можете либо работать с 12 × 8 = 96, а затем добавить дополнительный восемь, или вы даже можете отметить, что 13 × 8 = 13 × 2 × 2 × 2, поэтому удвоение 13 три раза приведет вас к правильному ответу (дважды 13 равно 26, дважды это 52 и дважды это 104).

Стратегии этого типа — и подобные им — помогут вам с базовыми вычислениями намного больше, чем запоминание.

Помните о цели

Если вам нужны только базовые навыки, такие как работа с десятичными знаками и процентами, не нужно ставить себе задачу изучить геометрию или даже тригонометрию. Но если вы надеетесь заняться физикой, вам потребуются базовые знания по многим другим темам, включая алгебру, математические вычисления, векторы и многое другое. Лучший способ быстро выучить математику — выбрать кратчайший путь по нужному предмету, чтобы достичь желаемого.Убедитесь, что вы освоили все основы, но если вы спешите, вы можете позволить себе специализироваться после этого.

Ответы на практические вопросы имеют решающее значение

Математика — странный предмет, потому что, как правило, вы учитесь намного быстрее, делая это. Читать книги и смотреть примеры полезно, но это не заменяет собственно самостоятельного решения вопросов. Поэтому не пропускайте практические вопросы, включенные в вашу книгу или на веб-сайт, который вы используете: проработайте их, и если вы ошиблись, посмотрите, что вы сделали, и попытайтесь понять, почему вы ошиблись.Ошибки случаются в математике — не расстраивайтесь — но они могут указывать на пробелы в ваших знаниях, и вам следует попытаться понять, почему они произошли и что вы не совсем поняли. Если вам это нужно, просмотрите соответствующие разделы книги еще раз, пока не поймете свою ошибку.

Следите за математическим словарным запасом

Такие слова, как коэффициент и квадратичный, появляются постоянно, когда вы изучаете математику, но вам нужно понимать, что они означают, чтобы действительно добиться чего-то в своем чтении.Если вы спешите, лучший совет — записать ключевые определения и термины в блокнот, чтобы их было легче найти. Вы можете использовать онлайн-версию (см. Ресурсы), но написание определений своими словами также помогает в обучении.

Уловки и подсказки для легкого изучения математики

Развитие «чувства числа» на самом деле связано с изучением ряда стратегий для выполнения вычислений. Помимо двух упомянутых ранее, есть много советов, которые помогут легко изучить математику, и их стоит усвоить. Например, двухэтапное сложение помогает решить задачи сложения, сначала добавляя то, что легко, а затем добавляете все остальное. Итак, если вы столкнулись с 93 + 69, вы можете бороться стандартным методом (добавление 9 + 3, перенос единицы на «десятки» и т. Д.) Или обратите внимание, что 93 + 7 = 100. Итак. отнимите 7 от 69, чтобы получить 62, и прибавьте 7 к 93. Это упрощает задачу: 93 + 69 = 100 + 62 = 162. То же самое можно сделать и с вычитанием.

Есть много других подобных советов. Если у вас сложная задача умножения, например 45 × 28, если одно из чисел четное, вы можете упростить ее, разделив четное число на два и умножив второе на два.Так что вы можете написать:

Эту проблему решить немного проще. Имея немного смысла в числах, вы можете разбить это умножение на части, отметив, что:

90 × 14 = (90 × 10) + (90 × 4)

Другими словами, 14 групп по 90 равны 10. группы по 90 плюс 4 группы по 90. Понимая основы процесса умножения, вы можете найти способы упростить и решить даже, казалось бы, сложные задачи. Вы можете изучить множество подобных приемов (см. Раздел «Ресурсы»), и они очень полезны, если вам понадобится немного опыта в быстрых вычислениях без калькулятора.

Мастер решения проблем

Задачи являются ключевой частью математики, и изучение некоторых стратегий их решения может помочь вам в большинстве ситуаций. Основные советы при решении проблемы — сосредоточиться на том, что вам сказали (то есть на том, что вы знаете), какая информация вам нужна и что вы хотите найти в конце проблемы. Исключение этих ключевых фрагментов информации часто указывает вам правильное направление, когда дело доходит до уравнения для использования или общего подхода.

Это также помогает найти термины, намекающие на то, что вам нужно делать. Например, «когда значение y уменьшается на x . . . » означает «когда x вычитается из y . . . »; «Путем вычисления отношения x к y . . . » означает «путем деления x на y . . . »; и так далее.

Конечно, чем больше практических вопросов вы решите, тем лучше вы будете выполнять, но эти базовые советы действительно могут помочь вам встать на правильный путь даже при решении незнакомых проблем.

Как научить себя математике

Немногие предметы вызывают столько воспоминаний о боли и тревоге, сколько уроки математики. Запутанные символы, сложные процедуры и ужасающие графики и диаграммы.

Некоторые люди теперь даже предполагают, что изучение математики может быть травмирующим опытом, что-то пережили, а не узнали.

Жаль, что многие люди переживают болезненную историю с математикой, потому что математика невероятно полезна. Многие из лучших профессий происходят из областей науки, науки и техники, и полагаются на понимание математики.Понимание новостей и мировых событий все чаще становится уроком статистики. Наконец, математика, если ее правильно понимать, позволяет решать многие ваши собственные проблемы.

В этой статье я хотел бы объяснить, как можно научиться любой математике, будь то статистика, алгебра или алгоритмы.

Шаг первый: начните с объяснения

Первый шаг к изучению любой математики — получить предварительное объяснение темы.

Есть много мест, где вы можете получить эту информацию.Вот несколько хороших ресурсов, охватывающих широкий круг тем:

• KhanAcademy — Огромные бесплатные ресурсы видео почти по каждой математической теме
• MIT OCW — Начинают с университетского уровня, но обрабатывают много сложной математики
• Coursera — много уроков по математике

Кроме того, есть еще и специализированные ресурсы. Они, как правило, не охватывают все мыслимые темы, но часто более интересны, интуитивно понятны и полезны для тех, кто занимается:

• BetterExplained — отличные статьи, дающие интуитивное понимание исчисления, алгебры, экспонент и многого другого
• 3Blue1Brown — отличные видеоролики на YouTube, в которых подробно рассматриваются математические концепции
• Numberphile — Беседы с математиками на интересные математические темы

Где бы вы ни получили свое объяснение, ваш первый шаг — это посмотреть его один раз, чтобы вы почувствовали, что понимаете основы того, как это работает.

Что делать, если я не понимаю объяснения?

Если вы посмотрите объяснение, но не поняли его, есть две возможные проблемы:

1. У вас отсутствуют некоторые предпосылки для понимания этой части математики . Это означает, что вам нужно сделать резервную копию и пройти через это снова. Если вам кажется, что это «пошло слишком быстро» или вы не знаете, что делает учитель, вам, возможно, придется вернуться на несколько уроков назад и выучить их лучше, прежде чем продолжить.
2. Вы слишком много пытаетесь охватить, не переходя на тренировку .Хороший образец — просмотреть отрывок объяснения, а затем попробовать его самостоятельно. Если вы только смотрите, но никогда не тренируетесь, это все равно что смотреть видео о лыжах и никогда не кататься на склонах. В конце концов, объяснения потеряют смысл, потому что у вас не будет личного опыта.

Попробуйте следующее: посмотрите объяснение один раз полностью в качестве отправной точки.

Шаг второй: практические задачи

Математика — это не то, что вы смотрите и запоминаете, а то, что вы делаете.

Если вы проводите все свое время за просмотром видео, а затем решаете ряд задач, вам может быть очень трудно применить свои математические знания. Это может привести к ощущению, что вы «плохо разбираетесь в математике», даже если проблема в том, что вы используете паршивый метод для ее изучения.

Вы можете исправить это, приступив к решению проблем как можно скорее. Хорошая проблема должна казаться сложной, но не невозможной. Если вы видите решение и даже не понимаете, как оно было получено, скорее всего, вы слишком быстро двигаетесь — вернитесь назад и изучите некоторые основы, прежде чем двигаться дальше.

Что делать, если у меня нет проблем, которые нужно решать?

Если у вас нет указанных проблем, вы можете сделать несколько вещей:

• Работа над проблемами выполняется в объяснении, но не глядя на ответ.
• Создавайте собственные проблемы и пытайтесь их решить.
• Попробуйте доказать концепции в своем классе. Это продвинутая техника, но она необходима для истинного понимания более сложной математики.

Попробуйте следующее: после просмотра вашего объяснения решите достаточно задач, чтобы чувствовать себя комфортно и понимать процедуру.

Шаг третий: узнайте, почему математика работает

Интуитивное понимание очень важно для математики в отличие от других предметов. Хотя интуиция словарного запаса слов на иностранном языке может помочь, их все же необходимо запомнить. Однако запоминание математики может быть опасным, если из-за этого вы изучаете ее, не понимая.

Следующий шаг — убедить себя в том, что вы знаете, почему математика работает. Моя любимая техника для этого — техника Фейнмана, которую я демонстрирую здесь:

Техника Фейнмана требует времени, поэтому вам не нужно полностью применять ее к каждому аспекту каждой математической задачи, с которой вы сталкиваетесь. Скорее применяйте его выборочно к наиболее важным концепциям и тем, которые кажутся вам запутанными, несмотря на достаточную практику.

Попробуйте следующее: определите основные концепции математики, которую вы изучаете, и используйте технику Фейнмана, чтобы убедить себя, что вы их понимаете.

Шаг четвертый: поиграйте с математикой

Практика — это хорошо, понимание лучше, но лучше всего играть с математикой.

После того, как вы ответили на несколько заданных вам вопросов и убедились, что понимаете их, естественным продолжением будет попытка поиграть с заданной вам математикой.Как все меняется, когда вы пытаетесь изменить числа или применить это к другим задачам?

Например, предположим, что вы совсем недавно научились рассчитывать сложные проценты. Вы можете самостоятельно произвести простые расчеты процентов и понять, почему они работают. Как вы могли поиграть с этой математикой?

• Вы могли видеть, что происходит, когда увеличивается скорость начисления сложных процентов.
• Что было бы, если бы процент был отрицательным?
• Вы могли бы попытаться подсчитать свои собственные сбережения, если бы вы вложили их по разным ставкам.
• Попробуйте представить, какую часть ипотечного кредита вы платите в виде процентов по сравнению с основной суммой.

Excel — это хороший способ поиграть с математикой, поскольку вы можете вводить формулы напрямую, без необходимости выполнять столько алгебры или повторения вычислений.

Попробуйте следующее: возьмите тему математики, которую вы недавно изучили, и посмотрите, как вы можете изменять переменные, применять их к разным вещам и изменять формулы.

Шаг пятый: применение математики вне класса

В конечном счете, целью изучения математики должно быть ее использование, а не просто сдача теста.Однако для этого вам нужно освободить свое понимание от примеров из учебника и применить его к ситуациям реального мира.

Это сложнее, чем просто решить проблему. Когда вы решите проблему, вы начнете запоминать схему решения. Это часто позволяет решать проблемы, не понимая принципов их работы.

Применение математики к реальной жизни, напротив, требует распознавания ситуации, перевода ее в математику и последующего решения созданной вами проблемы.Это строго сложнее, чем решать проблемы, поэтому, если вы хотите действительно использовать то, что вы узнали, вам нужно попрактиковаться в этом.

Попробуйте следующее: возьмите тему, которую вы недавно изучали по математике, и попытайтесь найти реальную ситуацию, в которой вы могли бы ее вычислить, используя свои собственные числа или оценки, если они недоступны.

Все это звучит как слишком много работы!

Выполнение всех этих пяти шагов по каждому предмету, который вы изучаете по математике, займет много времени.Это нормально, вам не нужно делать это для каждой мелочи, которую вам нужно изучить.

Считайте это индикатором выполнения. Каждая математическая концепция, которую вы изучаете, может проходить от первого до пятого шагов, углубляя ваши знания и каждый раз повышая полезность математики. Некоторые концепции будут настолько важны, что вы захотите применить их полностью. Другие будут достаточно редки, чтобы просто посмотреть объяснение — это все, что вы можете сэкономить.

В частности, вы должны попытаться сосредоточить внимание на наиболее важных концепциях для каждой идеи.Математика имеет тенденцию быть глубокой, поэтому часто в классе полного семестра может быть только горстка действительно больших идей, а все остальные идеи являются просто различными проявлениями этой основной концепции.

Большинство курсов по математике первого года обучения, например, все сосредоточены вокруг концепции производной, где все преподается просто как различные расширения и приложения этой основной идеи. Если вы действительно понимаете, что такое производная и как она работает, эти другие части будет намного легче изучить.

10 советов по математике

Многим ученикам кажется, что знание математики — это врожденный навык, которому нельзя научиться. Но правда в том, что любой может добиться успеха в математике — им просто нужны правильные стратегии.

Джерри Бродки, доктор философии, преподавал математику более двадцати лет, от алгебры I до математического анализа. Со временем он составил список рекомендаций, которые ежегодно обсуждает с родителями на вечере «Снова в школу». Вот десять основных советов Бродки по математике.

1. Сделайте всю домашнюю работу. Никогда не думайте о домашнем задании как о выборе. Это самый важный способ, которым учащиеся практикуют и усваивают концепции, изучаемые в классе. Установите регулярное время и место, чтобы домашнее задание выполнялось автоматически.
2. Бой, чтобы не пропустить занятие. Класс математики развивается быстро, каждый день преподает новую концепцию. То, что студенты делают сегодня, способствует завтрашнему дню. Математика наказывает пропуски занятий; Чтобы не отставать, учащимся нужно найти время, чтобы вернуться и узнать, что они упустили.Поэтому, если нужно назначить встречу по желанию, постарайтесь не назначать ее во время математики.
3. Найдите друга для учебы. У всех нас есть причины для законного отсутствия. Так что найдите друга, который будет делать хорошие заметки, когда вас не будет, и позвонит вечером, чтобы рассказать вам о домашнем задании. Это хорошая практика для реального мира, где для процветания необходимо построение позитивных отношений. В более продвинутых классах рекомендуется создать учебную группу для отработки тестов.
4. Установите хорошие отношения с учителем. Учителя средней школы насчитывают до 175 учеников, поэтому важно отличаться. В течение первой недели занятий в школе представьтесь. Сообщите своему учителю, что вам интересен его класс, и вы приветствуете возможность учиться. Задавайте вопросы, которые показывают, что вы внимательны. Родители также должны представиться по электронной почте или на вечере «Обратно в школу». Учителя лучше всего отзываются о учениках, которые показывают, что им небезразличен класс.
5. Проанализируйте и поймите каждую ошибку. Наша культура стала ориентированной на совершенство, и возникает соблазн игнорировать свои ошибки. Студенты хотят пропустить ошибку, сделанную в домашнем задании или тесте, просто отпустить ее. Но важно исправить ошибки и понять, почему они были сделаны; иначе мы обречены повторить их. Найдите время, чтобы понять причину ошибки и понять, как ее исправить. Спросите учителя, если вам что-то непонятно. В продвинутых классах может быть полезно написать параграф для размышления о том, почему были сделаны ошибки.
6. Получите помощь как можно скорее. Если ученик осознает, что что-то сложно, ему следует как можно быстрее обратиться за помощью. Учителя очень внимательны к просьбам о дополнительной помощи. Устраняйте недоразумения до того, как они начнут расти как снежный ком.
7. Не проглатывайте вопросы. Вопросы — это средство обучения. Если он у вас есть, спросите. Скорее всего, многие из ваших учеников задают тот же вопрос. Сказать это вслух поможет вам, вашим одноклассникам и учителю. Задавать хорошие вопросы — это навык на всю жизнь, и школа — безопасное место для практики. Чем больше вопросов мы зададим, тем легче будет. Хороший учитель уважит все вопросы. Если вы чувствуете, что учитель смущает вас из-за того, что вы задаете вопрос, поговорите с родителями и попросите их рассказать администрации; это серьезная проблема.
8. Базовые навыки необходимы. Быстро: сколько 9 умножить на 7? Чтобы добиться успеха, учащиеся должны уметь правильно ответить на этот вопрос во сне. Таблицы умножения являются основой для большинства математических задач средней школы.Если ваш ребенок их не знает, практикуйтесь! Сделайте карточки, купите компьютерную программу и практикуйтесь, практикуйтесь, практикуйтесь.
9. Алгебра Я должен быть в совершенстве. Алгебра I имеет решающее значение для последующих курсов математики. Студенты должны овладеть такими навыками, как решение систем уравнений, построение графиков, наклон и упрощение радикалов. Не заставляйте учеников изучать алгебру I, пока их учитель не скажет, что они готовы. И если их оценка по алгебре ниже C, настоятельно рекомендуется повторно пройти курс.2 ”или 9. Ученики должны поиграть со своими калькуляторами и познакомиться с тем, как они работают.

В современном высокотехнологичном мире уроки математики приобрели новый уровень важности. Советы Бродки могут помочь каждому ученику добиться наилучших результатов на любом уровне математики. Независимо от того, какой колледж или карьеру рассматривает студент, наилучшие результаты по математике увеличат ее возможности на будущее. Наши математические игры и математические ресурсы делают математику более увлекательной, поскольку учащиеся развивают навыки числового восприятия, арифметики, геометрии и других навыков.

10 уловок для быстрого выполнения математических расчетов в голове

Не нужно быть учителем математики, чтобы знать, что многие ученики — и, вероятно, многие родители (это было давно!) — боятся математических задач, особенно если они включают большое количество. Изучение методов быстрого выполнения математики может помочь учащимся развить большую уверенность в математике, улучшить математические навыки и понимание, а также преуспеть в продвинутых курсах.

Получайте релевантные учебные материалы и обновления, доставляемые прямо в ваш почтовый ящик. Подпишитесь сегодня! Присоединиться

Если это ваша работа — обучать их, вот вам отличный урок.

Быстрые математические приемы инфографики

10 уловок для быстрой математики

Вот 10 быстрых математических стратегий, которые учащиеся (и взрослые!) Могут использовать, чтобы вычислить в уме. Освоив эти стратегии, учащиеся должны иметь возможность точно и уверенно решать математические задачи, которые они когда-то боялись решать.

1. Сложение больших чисел

Сложить в уме большие числа может быть сложно. Этот метод показывает, как упростить этот процесс, сделав все числа кратными 10. Вот пример:

644 + 238

Хотя с этими числами сложно бороться, округление их в большую сторону сделает их более управляемыми. Итак, 644 становится 650, а 238 становится 240.

Теперь сложите 650 и 240 вместе. Итого 890. Чтобы найти ответ на исходное уравнение, необходимо определить, сколько мы прибавили к числам, чтобы округлить их в большую сторону.

650 — 644 = 6 и 240 — 238 = 2

Теперь сложите 6 и 2, чтобы получить 8

Чтобы найти ответ на исходное уравнение, нужно вычесть 8 из 890.

890 — 8 = 882

Итак, ответ на 644 +238 — 882.

2. Вычитая из 1 000

Вот основное правило вычитания большого числа из 1000: вычтите все числа, кроме последнего, из 9 и вычтите последнее число из 10.

Например:

1 000–556

Шаг 1: вычтем 5 из 9 = 4

Шаг 2: вычтем 5 из 9 = 4

Шаг 3: вычтем 6 из 10 = 4

Ответ — 444.

3. 5-кратное умножение любого числа

Умножив число 5 на четное, можно быстро найти ответ.

Например, 5 x 4 =

• Шаг 1: Возьмите число, умноженное на 5, и разрежьте его пополам, в результате число 4 станет числом 2.
• Шаг 2: Добавьте ноль к числу, чтобы найти ответ. В данном случае ответ — 20.

5 х 4 = 20

При умножении нечетного числа на 5 формула немного отличается.

Например, рассмотрим 5 x 3.

• Шаг 1: вычтите единицу из числа, умноженного на 5, в этом случае число 3 становится числом 2.
• Шаг 2: Теперь уменьшите вдвое число 2, чтобы получилось число 1. Сделайте 5 последней цифрой. Произведено число 15, и это и есть ответ.

5 x 3 = 15

4. Уловки деления

Вот быстрый способ узнать, когда число может быть равномерно разделено на эти определенные числа:

• 10, если номер заканчивается на 0
• 9, когда цифры складываются и сумма делится на 9
без остатка.
• 8, если последние три цифры делятся на 8 без остатка или равны 000
• 6, если это четное число и при сложении цифр ответ делится на 3 без остатка.
• 5, если он заканчивается на 0 или 5
• 4, если оно заканчивается на 00 или двузначное число, которое делится на 4 без остатка.
• 3, когда цифры складываются и результат делится без остатка на 3
• 2, если он заканчивается на 0, 2, 4, 6 или 8

5.Умножение на 9

Это простой метод, который помогает умножить любое число на 9. Вот как это работает:

Давайте возьмем пример 9 x 3.

Шаг 1 : Вычтите 1 из числа, которое умножается на 9.

3 — 1 = 2

Число 2 — это первое число в ответе на уравнение.

Шаг 2 : Вычтите это число из числа 9.

9–2 = 7

Число 7 — второе число в ответе на уравнение.

Итак, 9 x 3 = 27

6. 10 и 11-кратные фокусы

Уловка для умножения любого числа на 10 состоит в том, чтобы добавить ноль в конец числа. Например, 62 x 10 = 620.

Существует также простой способ умножить любое двузначное число на 11. Вот оно:

11 х 25

Возьмите исходное двузначное число и поставьте между цифрами пробел. В данном примере это число 25.

2_5

Теперь сложите эти два числа и поместите результат в центр:

2_ (2 + 5) _5

2_7_5

Ответ на 11 x 25 — 275.

Если числа в центре складываются в число из двух цифр, вставьте второе число и прибавьте 1 к первому. Вот пример уравнения 11 x 88

8_ (8 +8) _8

(8 + 1) _6_8

9_6_8

Есть ответ на 11 x 88: 968

7. В процентах

Найти процентное значение числа может быть довольно сложно, но правильное понимание этого числа значительно облегчает понимание. Например, чтобы узнать, что составляет 5% от 235, воспользуйтесь этим методом:

• Шаг 1: Переместите десятичную запятую на одну позицию, 235 станет 23.5.
• Шаг 2: Разделите 23,5 на число 2, получится 11,75. Это также ответ на исходное уравнение.

8. Быстро возведите в квадрат двузначное число, которое заканчивается на 5

Давайте возьмем число 35 в качестве примера.

• Шаг 1. Умножьте первую цифру на себя плюс 1.
• Шаг 2: Поставьте 25 в конце.

35 в квадрате = [3 x (3 + 1)] & 25

[3 x (3 + 1)] = 12

12 и 25 = 1225

35 в квадрате = 1225

9.Сложное умножение

При умножении больших чисел, если одно из чисел четное, разделите первое число пополам, а затем удвойте второе число. Этот метод быстро решит проблему. Например, рассмотрим

20 х 120

Шаг 1: разделите 20 на 2, получится 10. Удвойте 120, что равно 240.

Затем умножьте свои два ответа вместе.

10 х 240 = 2400

Ответ на 20 x 120 — 2400.

10. Умножение чисел, оканчивающихся на ноль

Умножение чисел, оканчивающихся на ноль, на самом деле довольно просто.Это включает в себя умножение других чисел вместе, а затем добавление нулей в конце. Например, рассмотрим:

200 х 400

Шаг 1: Умножьте 2 на 4

2 х 4 = 8

Шаг 2: Поместите все четыре нуля после 8

80 000

200 x 400 = 80 000

Выполнение этих быстрых математических приемов может помочь как ученикам, так и учителям улучшить свои математические навыки и укрепить свои знания математики — и не бояться работать с числами в будущем.

Присоединяйтесь к Resilient Educator Подпишитесь на нашу рассылку, чтобы получать контент на свой почтовый ящик. Щелкните или коснитесь кнопки ниже.

Присоединяйтесь к Resilient Educator

Подпишитесь на нашу рассылку, чтобы получать контент на свой почтовый ящик.Щелкните или коснитесь кнопки ниже.

Присоединиться

Вы также можете прочитать

Теги: Математика и естественные науки, Математика

Как изучать математику

Показать мобильное уведомление Показать все заметки Скрыть все заметки

Похоже, вы используете устройство с «узкой» шириной экрана ( i. е. вы, вероятно, пользуетесь мобильным телефоном). Из-за особенностей математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (должна быть возможность прокручивать, чтобы увидеть их), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана.

Прежде чем я перейду к советам по изучению математики, позвольте мне сначала сказать, что все учатся по-разному, и не существует единого правильного способа учиться в математическом классе.В этом документе много советов, и есть большая вероятность, что вы не согласитесь со всеми из них или обнаружите, что не можете выполнить все из-за нехватки времени. Там нет ничего плохого. Все мы учимся по-разному, и все, что каждый может попросить от нас, — это делать все, что в наших силах. Я намерен использовать эти советы, чтобы помочь вам сделать все возможное, чтобы дать вам время, которое у вас есть.

Итак, я полагаю, что здесь есть две группы людей, читающих этот документ: те, которые довольны своей оценкой, но заинтересованы в том, что я должен сказать, и те, кто недоволен своей оценкой и хочет получить некоторые идеи по поводу как улучшить.Вот несколько быстрых комментариев для каждой из этих групп.

Если у вас есть учебный распорядок, который вас устраивает, и вы получаете желаемую оценку на уроке математики, вы можете найти это чтение интересным. Конечно, нет никаких причин менять свои учебные привычки, если вы успешно использовали их в прошлом. Однако вам может быть полезно сравнить ваши учебные привычки с представленными здесь советами.

Если вас не устраивает ваша оценка на уроке математики и вы ищете способы улучшить свою оценку, есть несколько общих замечаний, от которых я должен уйти, прежде чем приступить к советам.Большинство людей, которые плохо успевают на уроках математики, делятся на три основные категории.

Первая категория состоит из самой большой группы студентов, и это студенты, которые просто не имеют хороших привычек в учебе и / или действительно не понимают, как учиться в классе математики. Учащиеся из этой категории сочтут эти советы полезными, и хотя вы, возможно, не сможете следовать всем из них, мы надеемся, что вы сможете выполнить достаточное количество из них, чтобы улучшить свои учебные навыки.

Следующая категория — это люди, которые каждый день часами учатся, но все еще не успевают.Большинство людей из этой категории страдают от неэффективных учебных привычек, и, надеюсь, этот набор заметок поможет вам учиться более эффективно и не тратить зря время.

Последняя категория — это люди, которые просто не уделяют достаточно времени учебе. Студенты попадают в эту категорию по разным причинам. У некоторых учащихся есть работа и / или семейные обязательства, которые не позволяют им тратить время, необходимое для успешной учебы в классе математики. Честно говоря, я мало что могу сделать для вас, если это ваш случай, кроме как, надеюсь, вы станете более эффективными в учебе, прочитав это.К сожалению, подавляющее большинство студентов этой категории не осознают, что они относятся к этой категории.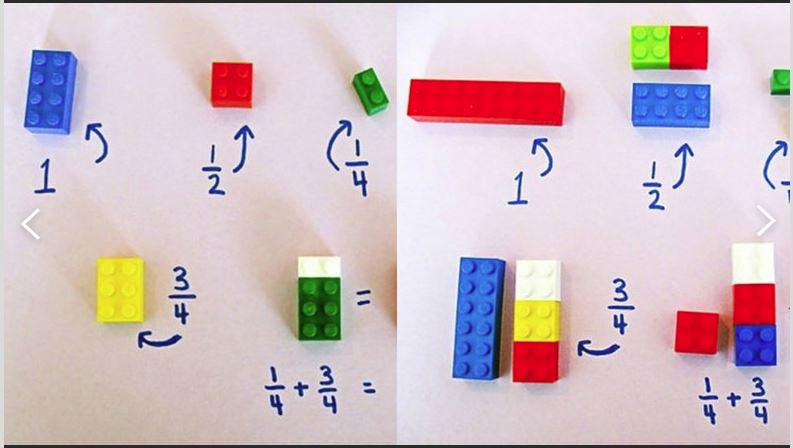 Многие не осознают, сколько времени нужно потратить на учебу, чтобы добиться успеха в классе математики. Надеюсь, что чтение этого документа поможет вам понять что вам нужно больше учиться. Многие просто не хотят тратить время на учебу, поскольку в их жизни есть другие вещи, которые для них важнее. Хотя это решение, которое вам придется принять, помните, что в конечном итоге вам придется потратить время, если вы хотите пройти курс математики.

Теперь, разобравшись со всем этим, давайте перейдем к советам. Я попытался разбить здесь подсказки и советы по конкретным областям, таким как общие советы по обучению, выполнение домашних заданий, подготовка к экзаменам, и т. Д. Однако есть три широкие общие области, в которые попадают все эти советы.

Математика — это не спорт для зрителей

Вы не можете выучить математику, просто идя в класс и наблюдая за лекцией инструктора и рабочими задачами. Чтобы изучать математику, вы должны активно участвовать в учебном процессе. Вы должны посещать занятия и уделять им внимание во время занятий. Вы должны сделать хороший набор заметок. Вам нужно работать над домашними заданиями, даже если инструктор их не назначает. Вы должны заниматься по регулярному графику, а не только накануне экзамена. Другими словами, вы должны участвовать в процессе обучения.

Реальность такова, что большинству людей действительно нужно работать, чтобы сдать урок математики, и в целом им нужно работать на уроках математики больше, чем в других классах.Если все, что вы хотите сделать, это потратить пару часов на обучение перед каждым экзаменом, вы обнаружите, что пройти большинство классов математики будет очень сложно.

Если вы не желаете активно участвовать в процессе изучения математики как в классе, так и за его пределами, у вас будут проблемы с сдачей любого урока математики.

Работа над пониманием принципов

Вы можете пройти урок истории, просто запомнив набор дат, имен и событий.Однако вы обнаружите, что для того, чтобы пройти курс математики, вам нужно будет сделать больше, чем просто запомнить набор формул. Несмотря на то, что на уроках математики, безусловно, требуется достаточно много запоминания формул, вам нужно делать больше. Вы должны понимать, как ИСПОЛЬЗОВАТЬ формулы, а это часто сильно отличается от простого их запоминания.

Некоторые формулы имеют ограничения, которые необходимо знать для их правильного использования. Например, чтобы использовать формулу корней квадратного уравнения, вы должны сначала иметь квадратичную формулу в стандартной форме.Об этом нужно помнить, иначе вы часто будете получать неправильный ответ!

Другие формулы очень общие и требуют, чтобы вы идентифицировали части проблемы, которые соответствуют частям формулы. Если вы не понимаете, как работает формула и принцип, лежащий в ее основе, часто бывает очень сложно использовать формулу. Например, в курсе математики нетрудно запомнить формулу интегрирования по частям для интегралов. Однако, если вы не понимаете, как на самом деле использовать формулу и определять соответствующие части интеграла, вы сочтете запомненную формулу бесполезной.

Математика накопительная

Вы всегда должны помнить, что курсы математики носят накопительный характер. Практически все, что вы делаете на уроке математики, будет зависеть от предметов, которые вы уже выучили. Это выходит за рамки простого знания предыдущих разделов в вашем текущем классе, чтобы помнить материал из предыдущих классов.

Вы обнаружите, что уроки алгебры в колледже будут очень трудными без тех знаний, которые вы получили на уроках алгебры в старшей школе.Вы не можете заниматься математическим анализом, не взяв (и не изучив) уроки алгебры и тригонометрии.

Итак, имея в виду эти три основные идеи, давайте перейдем к некоторым более конкретным советам по подготовке к математическому классу. Также обратите внимание, что некоторые советы представлены в нескольких разделах, так как они либо очень важны, либо просто могут относиться к нескольким общим темам.

10 лучших стратегий для улучшения своих оценок по математике

Многие учащиеся и родители просят дать им указатели и методы для лучшего изучения математики. Вот мой список из 10 лучших, применимый к любому уровню математики.

1) Если вы чего-то не понимаете, сосредоточьтесь на усвоении этой темы, прежде чем переходить к следующей теме. Звучит просто, но абсолютно необходимо. Допустим, студент изучает, например, алгебру. Кроме того, допустим, ему или ей трудно понять, как складывать и вычитать отрицательные и положительные числа. Все мы боремся с этим вначале, поскольку это проблема для большинства студентов.Некоторые учащиеся в этой ситуации, разочарованные тем, что они «не могут» изучить эту тему, переходят к следующему уроку в надежде, что они смогут понять этот.

Это рецепт катастрофы.

Математика очень похожа на обучение чтению. Если вы не знаете, как звучит ваша буква, у вас нет никакой надежды на то, что вы сможете произносить слова, конечно, вы не сможете прочитать книгу. Все математические курсы преподаются в определенной последовательности, потому что каждая тема основывается на предыдущей.Если у вас возникла проблема с темой, продолжайте работать с ней, пока вы не поймете ее и не сможете успешно решать проблемы. Посмотрите раздел DVD еще раз, посетите занятия, прочитайте книгу и примеры во второй раз или даже возьмите совершенно другую книгу, чтобы объяснить ее по-другому … но что бы вы ни делали, не переворачивайте страницу и не переходите к следующей теме. Если вы это сделаете, вы еще больше расстроитесь и, по всей вероятности, начнете терять надежду.

2) Работайте с примерами задач и проверяйте свои ответы, чтобы практиковаться на каждом уроке. Основная идея серии DVD — «учить на примере», и это самый простой способ выучить математику. После просмотра раздела на DVD и прочтения раздела в учебнике начинайте рабочие примеры с конца главы. Обязательно проработайте задачи, ответы на которые есть в конце книги, и проверьте каждую. Всегда начинайте с самой простой проблемы в своей книге, даже если вы думаете, что ее будет слишком «легко» решить. Очень важно укрепить вашу уверенность в себе.Вот почему уроки DVD начинаются с более простых задач, которые никто не сможет понять. Постепенно работайте над задачами из книги и проверяйте свой ответ на каждую из них. Проработав дюжину или больше задач из раздела (лучше две дюжины), вы готовы переходить к следующему разделу. Многие студенты хотят пропустить урок, чтобы дойти до следующего. Вы не можете просто прочитать раздел в книге по математике и стать экспертом в этом разделе. Вы должны работать над проблемами.Если вы не можете работать с проблемами, значит, вы не готовы двигаться дальше. Хорошая новость заключается в том, что рабочие задачи укрепят вашу уверенность, а уверенность — это 100% название игры в математике.

3) Начиная работать с математической задачей, не «намечайте путь от проблемы к ответу» в голове, прежде чем что-либо записывать. Я вижу это почти каждый день. Очень часто, когда кто-то смотрит на математическую задачу, он пытается «разобраться» в своей голове, прежде чем что-либо записать.Возьмем, к примеру, алгебру. Когда начинающий ученик смотрит на уравнение, он или она испытывает искушение решить уравнение в уме и ничего не записывать. Чаще всего студенты испытывают искушение делать это с помощью задач Word. Поскольку словесная проблема записана в форме предложения, принято думать, что вы можете «продумать свой путь к ответу». Я скажу вам, что я никогда, никогда не решаю математические задачи, не записывая их. Всегда.

Что вам нужно сделать, это сначала записать проблему.Затем вы начинаете решать ее, шаг за шагом. Записывайте даже простые вещи. Вам нужно убедиться, что каждый шаг, который вы записываете, совершенно законен. Другими словами, если вы, например, решаете уравнение и вычитаете «10» с обеих сторон … запишите это. Затем на СЛЕДУЮЩЕМ шаге фактически сделайте это вычитание. Затем, если вам нужно разделить обе стороны на «2», запишите ЭТО … тогда на СЛЕДУЮЩЕМ шаге фактически сделайте деление. Это дает вам бумажный след для проверки вашей работы, а также позволяет разбить проблему на куски размером с укус.Если вы можете быть уверены, что каждый маленький шаг законен, тогда вы будете в хорошей форме. Если вы попытаетесь сделать слишком много дел одновременно, что является обычным явлением, вы, вероятно, попытаетесь сделать что-то незаконное и попадете в неприятности.

4) Когда вы учитесь и делаете домашнее задание, постарайтесь найти для этого тихое место. Я был самым страшным преступником этого в школе. Раньше я все время слушал музыку, пытаясь делать уроки. Я также слушал телевизор как «фоновый шум» во время учебы.Со временем я понял, что если бы у меня было тихое место без фонового шума, я мог бы гораздо лучше сфокусироваться. Я обнаружил, что при чтении, например … мне нужно было бы прочитать что-то, возможно, 3 или 4 раза, если я слушал что-то еще, но только один раз, если бы я немного затих. Люди любят слушать музыку во время учебы, но я убежден, что если вы этого не сделаете, это будет намного эффективнее. Попробуйте найти тихое место в своем доме или в библиотеке, чтобы делать уроки, и вы сделаете свою работу намного быстрее, потому что вы сможете сосредоточиться и усвоить больше.

5) Если кто-то просит вас о помощи, постарайтесь как можно лучше объяснить ему тему. Это может показаться немного странным для этого списка . .. но есть одна универсальная правда. Те, кто может учить других, действительно понимают материал. Часто при обучении в группах один член группы отстает и не «понимает». Постарайтесь помочь этому человеку, даже если ваша собственная работа займет больше времени. Вы не только почувствуете, что помогаете кому-то добиться успеха, но и процесс перефразирования информации обратно кому-то и разбиения ее на небольшие куски улучшит ваше собственное понимание.Это поможет вам понять на фундаментальном уровне, что представляют собой камни преткновения для данной темы, что поможет вам в дальнейшем изучении математики.

6) Никогда и никогда не решайте математические задачи ручкой. Это довольно просто. Вы ошибетесь; это только вопрос времени. Когда вы это сделаете, вы захотите полностью стереть свою ошибку и переписать ее. Вам никогда не захочется что-то выцарапать и написать рядом с начертанием. Это приведет к тому, что статью будет трудно читать, а вычеркивания действительно увеличат ваше беспокойство по поводу решения этих проблем. Вам нужна чистая аккуратная бумага с чистым, хорошо продуманным решением.

7) Попробуйте использовать механический карандаш с отдельным ластиком, если можете. Механические карандаши имеют более четкие линии, а отдельный ластик позволяет стирать более аккуратно. Нет ничего хуже, чем сделать ошибку и попытаться что-то стереть, а затем размазать это по всей странице. Дешевые ластики сделают это и усложнят вам жизнь. Купите хороший механический карандаш и хороший ластик.

8) Держите свои решения аккуратными и построчно. Всегда решайте задачи вертикально, с одним шагом на каждой строке. Никогда не работайте горизонтально. Для этого может потребоваться больше бумаги, но вам будет гораздо проще следовать своим инструкциям. Что еще более важно, учитель сможет лучше следить за вашей работой, что позволит ему / ей поставить вам частичную оценку. Если есть всего 2 шага, а должно быть 10, вы не получите ни одного балла за свой мыслительный процесс. Записанные вами шаги рассказывают учителю, о чем вы думаете и как решаете проблему.

9) Не работайте поздно ночью. Я знаю, что все студенты колледжа будут смеяться над этим, но это правда. Я много-много раз пытался заниматься математикой или физикой поздно ночью, после 12 или 1 часа ночи, но вы просто оказываете себе медвежью услугу. Я часами смотрел на проблемы, потому что я просто не мог заснуть, пока не узнал, как их решить … потом я наконец заснул от сильной усталости … но когда я проснулся, мне стало так просто, как действовать дальше. проблема.Кроме того, я работал над проблемами ночью и получил неправильный ответ, и я знал, что, должно быть, у меня есть глупая ошибка в решении. Обычно я старался найти ее, но часто, когда вы устали, вы просто не можете найти глупую ошибку. На следующее утро, примерно через 5 минут, я мог заметить простую ошибку знака или даже простую ошибку умножения, которая вызвала проблему.

10) Если проблема сама собой поддается, нарисуйте ее картину. Это наиболее применимо для студентов, изучающих тригонометрию, математику и физику, но также применимо к любой проблеме со словами в базовой математике или алгебре. Пожалуйста, сделайте себе одолжение и нарисуйте картину того, что описывает проблема, даже если ваша картина проста. Мы — визуальные существа … процесс рисования ситуации заставляет нас усвоить, чего на самом деле требует проблема. Это помогает понять, как действовать дальше. Если вы изучаете физику, вы должны рисовать картинку для каждой решаемой задачи. Если вы работаете в Calculus, обязательно нарисуйте картинки для всех связанных задач с тарифами. Если вы изучаете Исчисление 2 или Исчисление 3, обязательно нарисуйте картину всех ваших трехмерных задач (трехмерные интегралы).Если вы изучаете основы математики и Дженни дает Бобу 2 карандаша, а Боб дает 1 карандаш, нарисуйте эту ситуацию. Это действительно поможет вам понять, как действовать дальше.

Помните, что в изучении математики нет серебряной пули. Для этого нужно делать что-то шаг за шагом и практиковаться. Приведенные выше советы помогут вам в изучении математики и придадут уверенности. А уверенность — это 100% -я игра в изучении математики любого уровня.