Лабораторная работа 10б класса — Лабораторная работа 10 б класса Измерение жёсткости пружины
Единственный в мире Музей Смайликов | Скачать 0.68 Mb.
|
С этим файлом связано 2 файл(ов). Среди них: kursovaya_rabota_zhikharev_206_1_Avtosokhranenny.docx, 0005_Lobok_Profsouznoe_dvizhenie_istoria_teoria_1.pdf. Показать все связанные файлы Подборка по базе: Практическая работа № 3 (1).  doc, Аммиак и соли аммония. Лабораторная работа № 6 «Качественная реа, Практическая работа.docx, Контрольная работа.docx, Практическая работа.docx, Физика1 Лабораторная работа2.docx, Лабораторная работа 3.docx, Физика1 Лабораторная работа1.docx, Культурология. Самостоятельная работа 6.3..odt, Практическая работа к теме 1.3.docxЛабораторная работа 10б класса «Измерение жёсткости пружины» Оборудование Штатив с муфтой и лапкой, пружинный динамометр, пружина, отличающаяся по толщине и длине от пружины динамометра, три груза, линейка. Порядок выполнения работы Результаты измерений записывайте в таблицу Д1.1. Укрепите динамометр на штативе. Измерьте динамометром вес первого груза, а линейкой удлинение пружины динамометра. Измерьте вес второго и третьего грузов, а также удлинение пружины динамометра в каждом случае.  Таблица Д1.1.
Результаты следующих измерений записывайте в таблицу Д1.2. Укрепите на штативе пружину, поставьте рядом линейку, запишите значение высоты, на которой находится нижний конец пружины в недеформированном состоянии. Поочерёдно подвесьте грузы и определите положение нижнего конца пружины в трёх случаях. Таблица Д1.2.
Расчёты Используя полученные данные и учитывая, что в нашем случае Fупр = P , сделайте расчёты, заполняя таблицу Д1.  3.Таблица Д1.3.
На рисунке 21 даны оси координат: по горизонтальной оси будем откладывать удлинение пружины в метрах, по вертикальной оси – вес, или силу натяжения пружины, в ньютонах. Выберите масштаб, соответствующий измеренным значениям величин.  Нанесите точки, соответствующие результатам измерений. Проведите прямую через начало координат и точки. Если они точно не ложатся на прямую, то проведите прямую так, чтобы экспериментальные точки находились по обе стороны прямой. Найдите тангенс угла наклона прямой, он будет равен жесткости пружины. Tg=0,3 Сравните найденное из вычислений среднее значение жесткости со значением, определённым по графику. Сделайте вывод. ______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________ Выполните подобные расчеты для пружины, использовавшейся во втором опыте. Таблица Д1.4.
Изобразите оси координат на следующей странице. Подобно тому как это сделано в первом опыте, нанесите точки по результатам измерений, проведите прямую и так же найдите по графику жесткость пружины.  Сделайте вывод о двух методах вычисления жесткости. ________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________ Сделайте вывод о зависимости жесткости от толщины проволоки, из которой изготовлена пружина. ________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________ Контрольные вопросы Какие погрешности возникают при измерении жесткости пружины таким способом? Какая деформация называется упругой? Почему мы не можем взять для эксперимента тяжёлые гири, а ограничиваемся лёгкими? С помощью формулы для жесткости сформулируйте, в чем состоит физический смысл для Юнга.  Почему в законе Гука следует писать знак «минус»? Почему не существует таблиц жесткости? |
Измерение жесткости пружины презентация, доклад
Лабораторная работа
«Измерение
жесткости пружины»
проверить справедливость закона Гука для пружины динамометра и измерить коэффициент жесткости этой пружины.
Цель работы
Оборудование:
штатив с муфтой и зажимом, динамометр с заклеенной шкалой, набор грузов известной массы (по 100 г), линейка с миллиметровыми делениями.
Подготовительные вопросы
Что такое сила упругости?
Как вычислить силу упругости, возникающую в пружине при подвешивании к ней груза массой m кг?
Как измерить удлинение пружины при подвешивании к ней груза?
В чем заключается закон Гука?
Правила техники безопасности
Будьте осторожны при работе с растянутой пружиной.
Не роняйте и не бросайте грузы.
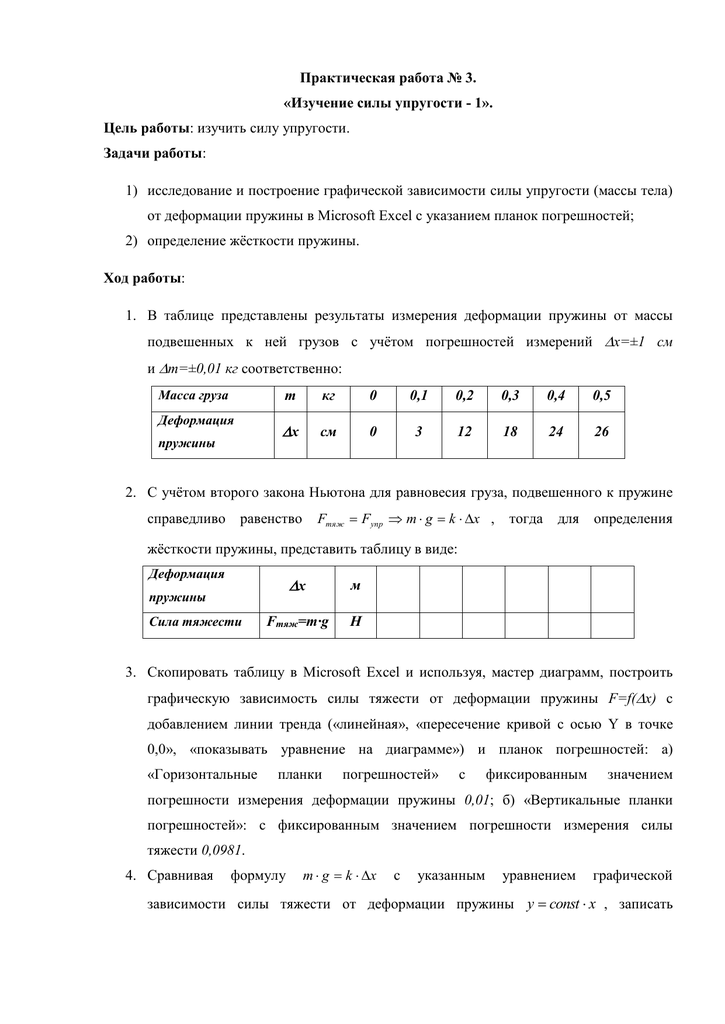
Описание работы:
Согласно закону Гука, модуль F силы упругости и модуль х удлинения пружины связаны соотношением F = kx. Измерив F и х, можно найти коэффициент жесткости k по формуле
В каждом из опытов жесткость определяется при разных значениях силы упругости и удлинения, т. е. условия опыта меняются. Поэтому для нахождения среднего значения жесткости нельзя вычислить среднее арифметическое результатов измерений. Воспользуемся графическим способом нахождения среднего значения, который может быть применен в таких случаях. По результатам нескольких опытов построим график зависимости модуля силы упругости Fупр от модуля удлинения \х\. При построении графика по результатам опыта экспериментальные точки могут не оказаться на прямой, которая соответствует формуле Fyпp=k\x\. Это связано с погрешностями измерений.
1. Закрепите на штативе конец спиральной пружины (другой конец пружины снабжен стрелкой-указателем и крючком).
2. Шкалу динамометра закройте бумагой.
3. Отметьте деление, против которого находится стрелка-указатель пружины.
4. Подвесьте к пружине груз известной массы и измерьте вызванное им удлинение пружины. Отметьте положение стрелки-указателя динамометра.
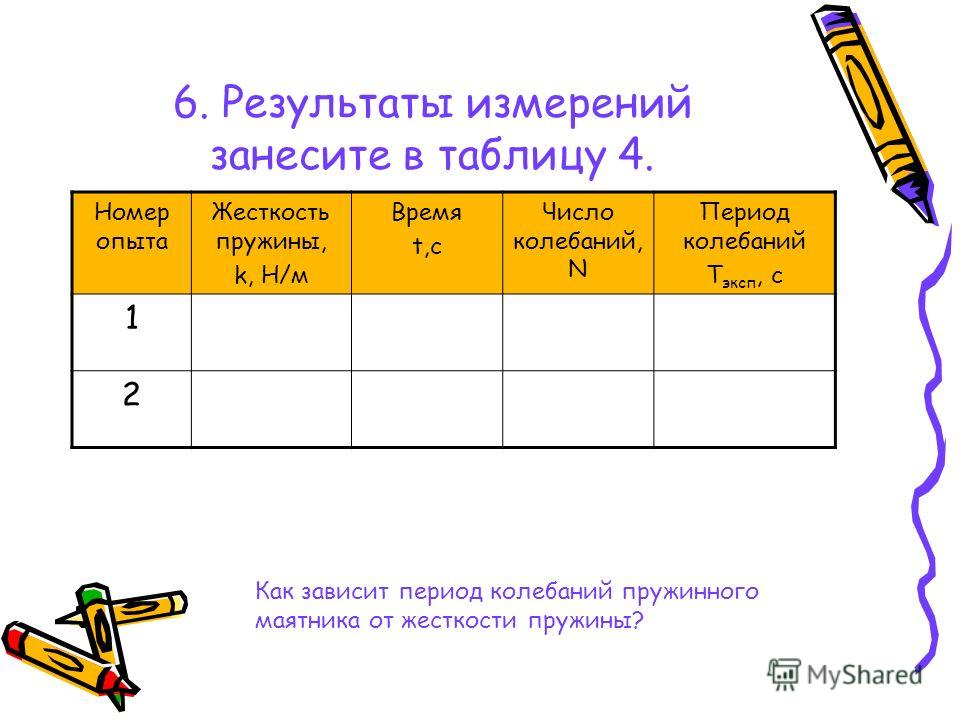
5. К первому грузу добавьте второй, а затем третий грузы, отмечая каждый раз положение стрелки-указателя и записывая каждый раз удлинение \х\ пружины. По результатам измерений заполните таблицу
ХОД РАБОТЫ:
6.
Начертите оси координат х и F, выберите удобный масштаб и нанесите полученные экспериментальные точки.
7. Оцените (качественно) справедливость закона Гука для данной пружины: находятся ли экспериментальные точки вблизи одной прямой, проходящей через начало координат.
8. По результатам измерений постройте график зависимости силы упругости от удлинения и, пользуясь им, определите среднее значение жесткости пружины kср.
9. Рассчитайте наибольшую относительную погрешность, с которой найдено значение kcp
10. Запишите сделанный вами вывод.
Контрольные вопросы:
Как называется зависимость между силой упругости и удлинением пружины?
Пружина динамометра под действием силы 4Н удлинилась на 5 мм. Определите вес груза, под действием которого эта пружина удлиняется на 16 мм.
Скачать презентацию
Макроскопические и микроскопические пружины – Процедура
Объектив
Цель
В этой лаборатории вы:
•
исследовать пружинящие свойства прямой проволоки,•
обнаружить «растяжимость» материала, не зависящую от размера и формы объекта,•
связывают макроскопическую «растяжимость» материала с микроскопической «жесткостью» межатомных связей.
Здесь приведены некоторые полезные уравнения и константы.
Вопросы для изучения
1
Твердая металлическая прямая проволока похожа на пружину? Если так, то каким образом? Если вы считаете проволоку пружиной, какова жесткость пружины по сравнению со спиральными пружинами, использованными в предыдущей лаборатории?2
Как можно выразить пружинящие свойства конкретного металла таким образом, чтобы он не зависел от размера, формы и физических размеров проволоки (модуль Юнга)?3
Как можно связать макроскопические пружинящие свойства конкретного металла с жесткостью межатомных связей этого металла (жесткость межатомной пружины).
Оборудование
- прямая металлическая проволока, натянутая на каркас, с подвесом для гирь
- миллиметровая шкала для определения положения конца проволоки
- Штангенциркуль (как читать — см. раздел «Измерение штангенциркулем» ниже)
раздел «Измерение штангенциркулем» ниже)Процедура
Пожалуйста, распечатайте рабочий лист для этой лабораторной работы. Этот лист понадобится вам для записи ваших данных.
Экспериментальная установка
Запись данных
1
Щелкните правой кнопкой мыши файл Excel ® «модуль Юнга.xls» и сохраните его в «Мои документы». Дважды щелкните файл, чтобы открыть его в Excel ® .
2
Вы должны увидеть дисплей, который включает в себя места для информации о вашей группе, измеренных значений и расчетных значений, а также место для вашего графика.
3
Вы будете записывать все свои данные и результаты анализа на лист Excel ® и отправлять их в WebAssign для быть оценены вашим TA.
Измерение штангенциркулем
В этом лабораторном упражнении вы будете использовать штангенциркуль, состоящий из двух «зубцов», один из которых прикреплен к фиксированной шкале, а другой — к скользящей (нониусной) шкале.
Чтобы измерить
ширины объекта, объект просто помещается между двумя зубьями штангенциркуля. Затем скользящий зуб перемещается до тех пор, пока объект не будет плотно зажат между зубьями. Используя обе шкалы, ширину можно прочитать с точностью до 0,005 см (или 0,05 мм). Шкалы читаются следующим образом (см. рисунок).
Рисунок 1 : Штангенциркули
4
Найдите, где нулевая отметка скользящей шкалы совпадает с фиксированной шкалой. В данном случае это чуть больше отметки 5,3 см. Итак, первое чтение 5,3 см.
5
Найдите отметку на скользящей шкале, которая наиболее точно совпадает с одной из отметок на фиксированной шкале. Здесь 5,0 и 6,0 очень близки, но 5,5 лучше всего соответствует одной из отметок на фиксированной шкале. Это значение представляет собой количество сотых долей сантиметра (или десятых долей миллиметра). Итак, второе чтение
составляет 0,055 см.
6
Сложите два значения вместе, чтобы получить общее значение: 5,3 см + 0,055 см = 5,355 см.
Чтобы попрактиковаться в чтении штангенциркуля, посетите этот веб-сайт с интерактивным апплетом Java.
На этом веб-сайте этикетка на скользящей шкале вводит в заблуждение. Шкала обозначена как «мм», что наводит пользователя на мысль, что числа на этой шкале представляют собой миллиметры. Это НЕ правильно. Как описано выше, числа на скользящей шкале представляют собой десятые доли миллиметра.
Размеры
Размеры провода
Одна из целей состоит в том, чтобы описать «растяжение» материала независимо от его размера и формы. провод. Для этого нам сначала нужно знать физические размеры провода.
1
Измерьте следующее и введите свои данные в таблицу Excel ® .
и
Вся длина провода без каких-либо грузов на немб
Диаметр проволоки с помощью штангенциркуля (см. выше раздел «Измерение штангенциркулем»)в
По измеренному диаметру провода рассчитайте площадь поперечного сечения провода.
КПП:
Сравните свои данные с другой группой, чтобы убедиться, что они разумны.
Жесткость проволоки
Чтобы определить, ведет ли прямая проволока пружину, вам нужно измерить положение конца проволоки при добавлении различного веса.
2
Устраните перегибы в проводе.
и
Добавьте 6 кг к платформе, висящей на тросе. Снимите 6 кг. Повторение. Это помогает избавиться от небольших перегибов проволоки, поэтому «прямая» проволока не действует как спиральная пружина.
Если проволока имеет перегибы, вы будете измерять упругость «скрученной» проволоки вместо жесткости прямой проволоки.
Удалите перегибы перед началом измерений.
3
Выполните следующие измерения и запишите свои данные в таблицу Excel ® .
и
Посмотрите на шкалу на приборе и убедитесь, что вы знаете, что такое деления и как читать масштаб. Вы должны уметь измерять с точностью до 0,1 мм.б
Вам нужно сделать три набора измерений, чтобы получить средние значения.и
Проведите измерения с 0 кг, затем 2 кг, 4 кг, 6 кг.II
Снимите все грузы и снова начните с нуля, проведя те же измерения еще дважды.III
Возьмите среднее значение трех наборов измерений.
в
Рассчитайте вариацию вашего измерения.и
Различия в измерениях («воспроизводимость») дают вам представление о том, насколько значимы отдельные измерения. Запишите свою оценку вариации.•
Если измерения составляют 5,5, 5,7, 5,4, 5,6, 5,8 и 5,6 мм, среднее значение равно (5,5 + 5,7 + 5,4 + 5,6 + 5,8 + 5,6)/6 = 5,6, от минимума 5,4 до максимума 5,8.•
Компактный способ сообщить это среднее значение с приблизительным отклонением составляет 5,6 ± 0,2 мм.
II
Если отклонение превышает 0,3 мм, НЕОБХОДИМО повторить измерения.•
Откажитесь от более ранних измерений, так как это, вероятно, привело к увеличению перегибов провода.
4
ПЕРЕД построением графика ваших данных обсудите следующие вопросы с членами вашей группы.
и
Если проволока действует как пружина, как, по вашему мнению, будет выглядеть график зависимости растяжения от силы?б
Как по графику определить упругость проволоки?
5
Используйте ваши данные, чтобы построить в Excel ® график зависимости растяжения провода (по оси y ) от силы, действующей на провод (по оси 9).
0236 x -ось).
и
Обе эти величины необходимо будет вычислить из ваших данных (либо вручную, либо с помощью Excel ® ).б
Из двух столбцов, представляющих растяжение и усилие, выделите ячейки с данными для 2, 4, 6 кг.
Включите в НЕ данные для 0 кг, потому что провод может перегибаться без нагрузки.
в
Выберите пункт меню «Вставить» → «Диаграмма» и выберите «XY (разброс)». (Для НЕ выберите «Линейный» график.)д
Обязательно убедитесь, что у вас есть правильные количества на правильных осях.и
Сопоставьте свои данные с «линии тренда».и
Щелкните правой кнопкой мыши одну из точек данных и выберите «Добавить линию тренда».II
Выберите «Линейный» в разделе «Тип».III
В разделе «Параметры» выберите «Отобразить уравнение на графике» — это отобразит уравнение линии, которое лучше всего соответствует вашим данным, в формеy = mx + b.
Вы можете изменить уравнение.
ф
По вашим данным определите жесткость пружины проволоки.и
ПосколькуF = K с с,
, тос = F,
, поэтому наклон вашего графика равен1/k с .
КПП:
Сравните свои измерения, расчеты и графики с другой группой, чтобы убедиться, что они разумны.
«Растяжимость» металла
Вычисление модуля Юнга — это способ измерить «упругость» или «растяжимость» металла и учесть размер и форму конкретной проволоки.
6
ПЕРЕД вычислением модуля Юнга обсудите следующие вопросы с коллегами по лаборатории и запишите свои ответы на доске.
и
Если площадь поперечного сечения проволоки увеличить вдвое, будет ли проволока растягиваться больше, меньше или на ту же величину, если на нее повесить груз массой 2 кг? Почему?и
Подумайте о том, чтобы соединить два исходных провода рядом друг с другом.II
Как это соотносится с размещением двух пружин параллельно?
б
Если бы проволока была в два раза длиннее, растянулась бы она больше, меньше или на ту же величину, когда вы подвешивали на нее груз массой 2 кг? Почему?и
Подумайте о том, чтобы соединить два исходных провода встык.II
Как это соотносится с последовательным размещением двух пружин?
в
Величина F / A называется «стресс». Каковы его единицы?д
Дробное растяжение Δ L / L 0 называется «деформацией». Каковы его единицы?
КПП:
Сравните свои ответы с другой группой.
7
Используйте измерения для вашей проволоки, чтобы определить модуль Юнга.
и
В состоянии равновесияF = k с ΔL = с,
, поэтому:
( 1 )
Y =
| (F/A) |
| (ΔL/L 0 ) |
| (k s ΔL/A) |
| ( ΔL/L 0 ) |
б
Используйте свое измерение начальной длины, расчетное значение площади поперечного сечения и значение жесткости пружины, полученное из вашего графика, чтобы определить модуль Юнга для материала, из которого сделана ваша проволока.в
Покажите свой расчет на доске и запишите результат на листе Excel ® .д
Как соотносится ваше значение модуля Юнга со значением модуля Юнга для алюминия (6,2 × 10 10 Н/м 2 ) или свинца (1,6 × 10 10 Н/м 2 )? Учитывая, что проволока латунная (сплав меди и цинка), разумна ли ваша стоимость?
КПП:
Сравните свои результаты с результатами другой группы.
Определение жесткости межатомной пружины
Модуль Юнга — это способ связать макроскопические пружинящие свойства конкретного металла с жесткостью межатомных связей этого металла (жесткость межатомной пружины).
8
ПЕРЕД определением межатомной жесткости пружины обсудите с партнерами следующее.
и
Предполагая простую модель «шарик и пружина» для нашего твердого тела, как мы можем определить длину межатомные связи, если бы мы знали плотность вещества? ( Подсказка: Вы, вероятно, недавно делали что-то подобное в своем домашнем задании.)б
Используя эту идею и следующую информацию, определите длину межатомной связи для латуни.
•
Латунь – это сплав меди и цинка.•
Атомная масса меди 64 г/моль; цинка 65 грамм/моль.•
Плотность меди 8,94 г/см 3 , цинка 7,14 г/см 3 .•
Примечание: остерегайтесь своих юнитов.
9
Используйте свой расчет длины межатомной связи и значение модуля Юнга, чтобы аппроксимировать жесткость межатомных связей,
к с, я .
и
В разделе «Растяжимость» раздела «Металл» выше мы показали:
( 2 )
Д = .
б
Для нашей модели «шарик и пружина» площадь поперечного сечения связи составляет A = d 2 , а длина в расслабленном состоянии составляет L 0 = d (если вы не уверены, почему это то есть перечитайте раздел «Межатомная жесткость пружины» из «Макроскопические и микроскопические пружины — концепции»). Таким образом:
( 3 )
Y = =
| k s,i d |
| d 2 |
в
Покажите свой расчет на доске и запишите результат на листе Excel ® .
КПП:
Сравните свои результаты с результатами другой группы.
10
Отправьте свой Excel ® и ответьте на дополнительные вопросы в WebAssign.
Как рассчитать константу пружины с помощью закона Гука
Любой физик знает, что если объект прикладывает силу к пружине, то пружина прикладывает к объекту равную и противоположную силу. Закон Гука дает силу, с которой пружина действует на прикрепленный к ней объект, с помощью следующего уравнения:F = – kx
Знак минус показывает, что эта сила направлена в противоположную сторону от силы, растягивающей или сжимающей пружину. весна. Переменные уравнения F, , который представляет силу, k, , который называется жесткостью пружины и измеряет, насколько жесткой и прочной является пружина, и x, расстояние, на которое пружина растягивается или сжимается от своего положения равновесия или покоя.
Сила, действующая на пружину, называется возвращающей силой; он всегда действует, чтобы вернуть пружину к равновесию. В законе Гука отрицательный знак силы пружины означает, что сила, действующая на пружину, противодействует смещению пружины.
Понимание пружин и направления их действия
Направление силы пружины
На предыдущем рисунке показан шарик, прикрепленный к пружине. Вы можете видеть, что если пружина не растягивается и не сжимается, она не действует на шарик. Однако если вы нажмете на пружину, она оттолкнется назад, а если вы потянете пружину, она оттянется назад.Закон Гука действителен до тех пор, пока эластичный материал, с которым вы имеете дело, остается эластичным, то есть остается в пределах своего предела эластичности . Если вы потянете пружину слишком далеко, она потеряет способность растягиваться. Пока пружина остается в пределах своего предела упругости, можно сказать, что F = – kx . Когда пружина остается в пределах своего предела упругости и подчиняется закону Гука, пружина называется идеальной пружиной .
Как найти жесткость пружины (пример задачи)
Предположим, к вам в дверь стучится группа дизайнеров автомобилей и спрашивает, не могли бы вы помочь спроектировать систему подвески.
«Конечно, — говорите вы. Вам сообщают, что машина будет иметь массу 1000 кг, и вам предстоит работать с четырьмя амортизаторами длиной по 0,5 метра каждый. Насколько сильными должны быть пружины? Если предположить, что в этих амортизаторах используются пружины, каждый из них должен выдерживать массу не менее 250 кг, что соответствует следующему весу:F = мг = (250 кг)(9,8 м/с 2 ) = 2450 Н
где F равно силе, м равно массе объекта 5 г 9057 ускорение свободного падения, 9,8 метра в секунду 2 . Пружина в амортизаторе должна, как минимум, дать вам усилие в 2450 ньютонов при максимальном сжатии 0,5 метра. Что это означает, что жесткость пружины должна быть? Чтобы выяснить , как рассчитать жесткость пружины , мы должны помнить, что говорит закон Гука:
F = – kx
Теперь нам нужно переработать уравнение, чтобы мы вычисляли недостающую метрику, которая является постоянной пружины, или k .
Глядя только на величины и, следовательно, опуская отрицательный знак, вы получаете
Время подставить числа:
Пружины, используемые в амортизаторах, должны иметь жесткость не менее 4900 ньютонов на метр. Автомобильные дизайнеры выбегают в восторге, но вы кричите им вслед: «Не забывайте, вам нужно как минимум удвоить это, если вы действительно хотите, чтобы ваша машина могла преодолевать выбоины».
Об этой статье
Эта статья из книги:
- Физика I для чайников,
Об авторе книги:
Доктор Стивен Хольцнер написал более 40 книг по физике и программированию. Он был редактором журнала PC Magazine и преподавал в Массачусетском технологическом институте и Корнелле. Он является автором книг для чайников, в том числе «Физика для чайников», и «Основы физики для чайников».