Гзд по математике 5 к мерзляк: ГДЗ по математике для 5 класса рабочая тетрадь Мерзляк Алгоритм успеха

ГДЗ проверь себя 3 математика 5 класс Мерзляк, Полонский

Решение есть!

• 1 класс
  • Математика
  • Английский язык
  • Русский язык
  • Музыка
  • Литература
  • Окружающий мир

• 2 класс
  • Математика
  • Английский язык
  • Русский язык
  • Немецкий язык
  • Информатика
  • Музыка
  • Литература
  • Окружающий мир
  • Технология

• 3 класс

✅ГДЗ по Математике 5 класс Мерзляк, Полонский ➡ Onlinegdz. net

OnlineGDZ

 

ГДЗ по математике 5 класс Мерзляк используется в огромном количестве общеобразовательных школ. Он был разработан и структурирован согласно требованиям ФГОС для учеников. Тетрадь совместима с учебником по математике за пятый класс и направлен на формирование правильных академических навыков. Кроме того, использование пособия способствует правильному и адекватному оцениванию уровню своих знаний, анализу допущенных ошибок и определению степени освоения школьной программы.

Онлайн ГДЗ по математике поможет школьникам самостоятельно или при помощи родителей сформировать план коррекции тех или иных типов задач, которые не были поняты и усвоены во время урока. Таким образом, главной целью решебника не является механическое и необдуманное списывание ответа, а самостоятельная работа над ошибками.

Структура онлайн гдз по математике авторов Мерзляк, Полонский, Якир

ГДЗ математика 5 класс Мерзляк обладает понятной, простой и интуитивной структурой. Каждый пятиклассник легко сможет найти номер задачи и правильный ответ к ней. Работать с решебником для оказания помощи в учебе могут и старшие братья или родители, что позволяет более цельно сформировать навыки математического мышления и соответственно саморазвития.

Решебник по математике 5 класс Мерзляк структурирован строго по учебнику и полностью соответствует темам, задачам и страницам. Здесь подробно разбирается каждый учебный параграф, таким образом, чтобы ученик понимал, смог найти свою ошибку и еще раз повторил пройденный материал. Это можно сделать без взрослых и нет необходимости нанимать репетиторов.

В решебнике по математике за 5 класс Мерзляка видео ответы по номерам совпадают с конкретной задачкой. Также здесь можно заранее подготовиться в предстоящей контрольной работе.

К основным преимуществам онлайн гдз можно отнести:

• Правильные ответы на задачки любой сложности;
• Возможность более легкого восприятия того или иного типа математических задач;
• Возможность самостоятельно без посторонней помощи проверить правильность домашнего задания;
• Будет полезен и для учителей и родителей;
• Позволяет в значительной мере облегчить высокую учебную нагрузку в те дни, когда задали много по разным предметам.

Видео гдз по математике 5 класс Мерзляка не предназначены для простого списывания. Они призваны помочь и поддержать ребенка в самостоятельной работе, предлагая возможность точно узнать: движется ли он в правильном направлении или есть еще над чем поработать. Таким образом, он способствует постепенному развитию аналитических и логических способностей, так как вся работа проводится индивидуально без помощи посторонних.

 

Видео решебник

Раздел I. Натуральные числа и действия над ними
Глава 1. Натуральные числа
§ 1. Ряд натуральных чисел

§ 2. Цифры. Десятичная запись натуральных чисел

§ 3. Отрезок. Длина отрезка

§ 4. Плоскость. Прямая. Луч

§ 5. Шкала. Координатный луч

§ 6. Сравнение натуральных чисел

Задание № 1 «Проверьте себя» в тестовой форме

Глава 2. Сложение и вычитание натуральных чисел
§ 7. Сложение натуральных чисел. Свойства сложения

§ 8. Вычитание натуральных чисел

§ 9. Числовые и буквенные выражения. Формулы

§ 10. Уравнение

§ 11. Угол. Обозначение углов

§ 12. Виды углов. Измерение углов

§ 13. Многоугольники. Равные фигуры

§ 14. Треугольник и его виды

§ 15. Прямоугольник. Ось симметрии фигуры

Задание № 2 «Проверьте себя» в тестовой форме

Глава 3. Умножение и деление натуральных чисел
§ 16. Умножение. Переместительное свойство умножения

§ 17. Сочетательное и распределительное свойства умножения

§ 18. Деление

§ 19. Деление с остатком

§ 20. Степень числа

§ 21. Площадь. Площадь прямоугольника

§ 22. Прямоугольный параллелепипед. Пирамида

§ 23. Объём прямоугольного параллелепипеда

§ 24. Комбинаторные задачи

Математика 5 Мерзляк СР-05 В3

Самостоятельная работа № 5 по математике в 5 классе «Сравнение натуральных чисел» с ответами. Дидактические материалы для учителей, учащихся и родителей. Представлены упражнения, из которых формируются материалы для подготовки к проверки знаний по теме, а также задания для составления самостоятельной работы. Математика 5 Мерзляк СР-05 В3.

Математика 5 класс (Мерзляк)
Самостоятельная работа № 5. Вариант 3.

СР «Сравнение натуральных чисел» (транскрипт заданий)

27. Сравните числа: 1) 148 и 259; 2) 5 003 и 3 498; 3) 25 168 и 25 170; 4) 3 456 789 и 3 456 791; 5) 4 287 546 325 и 4 287 547 211; 6) 12 000 032 009 и 12 000 041 000.

28. Расположите в порядке возрастания числа: 128, 281, 342, 173, 211.

29. Запишите все натуральные числа, которые: 1) больше 597 и меньше 602; 2) больше 428 299 и меньше 428 307; 3) больше 23 809 и меньше 23 810.

30. Запишите цифру, которую можно поставить вместо звёздочки, чтобы образовалось верное неравенство (рассмотрите все возможные случаи): 1) 5 6*9 < 5 618; 2) 7 *32 > 7 843; 3) 2 *63 < 2 452; 4) 6 *68 > 6 859.

31. Между какими двумя ближайшими натуральными числами находится число: 1) 28; 2) 653? Ответ запишите в виде двойного неравенства.

32. В записи чисел вместо нескольких цифр поставили звёздочки. Сравните эти числа: 1) 48 *** и 46 ***; 2) 2*6 и 1 ***; 3) * *1* и *99.

33. Сравните: 1) 2 879 м и 3 км; 3) 9 ц 12 кг и 908 кг. 2) 4 008 м и 4 км 4 м;

---

 

Математика 5 Мерзляк СР-05 В3.
Ответы на самостоятельную работу:

№ 27.  1) 148 < 259;   2) 5003 > 3498;   3) 25 168 < 25 170;   4) 3 456 789 < 3 456 791;   5) 4 287 546 325 < 4 287 547 211;   6) 12 000 032 009 < 12 000 041 000.

№ 28.  128 < 173 < 211 < 281 < 342.

№ 29.  1) 597 < х < 602  =>  х- = 598; 599; 600; 601.
2) 428 299 < х < 428 307  =>  х- = 428 300; 428 301; 428 302; 428 303; 428 304; 428 305; 428 306.
3) 23 809 < х < 23 810 — таких х нет.

№ 30.  1) 56*9 < 5618  =>  *= 0;
2) 7*32 > 7843  =>  *= 9;
3) 2*63 < 2452  =>  *= 0, 1, 2, 3;
4) 6*68 > 6859  =>  *= 8, 9.

№ 31.  1) 27 < 28 < 29;   2) 652 < 653 < 654.

№ 32.  1) 48*** > 46***;   2) 2*6 < 1***;   3) **1* > *99.

№ 33.  1) 2879 м < 3 км, так как 3 км = 3000 м.
2) 4008 м > 4 км 4 м, так как 4 км 4 м = 4004 м.
3) 9 ц 12 кг > 908 кг, так как 9 ц 12 кг = 912 кг.

 

---

Вы смотрели: Самостоятельная работа по математике в 5 классе «Сравнение натуральных чисел» с ответами Вариант 3. Дидактические материалы для учителей, учащихся и родителей.

Другие варианты: СР-05. Вариант 1  СР-05. Вариант 2  СР-05. Вариант 4

---

Вернуться к  Списку самостоятельных работ по математике в 5 классе УМК Мерзляк.

Перейти к  Списку контрольных работ по математике в 5 классе УМК Мерзляк.

Цитаты (упражнения) из учебного пособия «Дидактические материалы. Математика 5 класс / Мерзляк, Полонский, Рабинович, Якир — М.:Вентана-Граф» использованы на сайте исключительно в учебных целях (пп. 1 п. 1 ст. 1274 ГК РФ). Решения и ОТВЕТЫ на самостоятельную работу (нет в пособии) адресованы родителям для проверки знаний учащихся.

ГДЗ по Математике за 5 класс А.Г. Мерзляк, В.Б. Полонский ФГОС 2016

Решебники, ГДЗ

• 11 Класс
  • Русский язык
  • Английский язык
  • Немецкий язык
  • Математика
  • Алгебра
  • Геометрия
  • Физика
  • Химия
  • Биология
  • История
  • География
  • Обществознание
  • Литература
  • ОБЖ
  • Информатика
  • Белорусский язык
  • Астрономия
  • Мед. подготовка
  • Испанский язык
  • Казахский язык
• 10 Класс
  • Русский язык
  • Английский язык
  • Немецкий язык
  • Математика
  • Алгебра
  • Геометрия
  • Физика
  • Химия
  • Биология
  • История
  • География
  • Обществознание
  • Литература
  • ОБЖ
  • Информатика
  • Белорусский язык
  • Мед. подготовка
  • Французский язык
  • Испанский язык
  • Кубановедение
  • Казахский язык

Решебник ✔️ ГДЗ Математика 5 класс ⏩ А. Г. Мерзляк В. Б. Полонский М. С. Якир 2013

Математика для 5 класса существенно отличается от аналогичного предмета в более старших классах тем, что в большинстве ее задач содержание направлено на развитие научного естествоведческого мировоззрения школьников. Предмет охватывает часть арифметики, а аткже алгебру и геометрию в начальных сведениях. Решаются задачи по математике в этом классе зачастую по таблицам, схемам и чертежам. И разобраться с ними очень поможет решебник – математика, 5 класс, Мерзляк.

Для чего применять при выполнении домашнего задания решебник по математике, 5 класс, Мерзляк, Полонский, Якир

При помощи пособия этих авторов ученик сможет освоить основы математики. Причем проходить этот процесс будет намного легче и интереснее, чем без него. Но оно не рассчитано на бездумное списывание решений из подсказчика. Решебник должен использоваться только как поддержка на крайний случай, например, чтобы проверить правильность собственного развязывания задачи.

Для того, чтобы воспользоваться этим пособием по математике, достаточно ввести номер выполняемого задания в нижнее поле и нажать «ОК». Также можно выбрать номер из выпадающего списка.

Этот решебник по математике нравится очень многим школьникам и их родителям, поэтому они рекомендуют его друзьям и одноклассникам, а также делятся с ними ссылкой на него.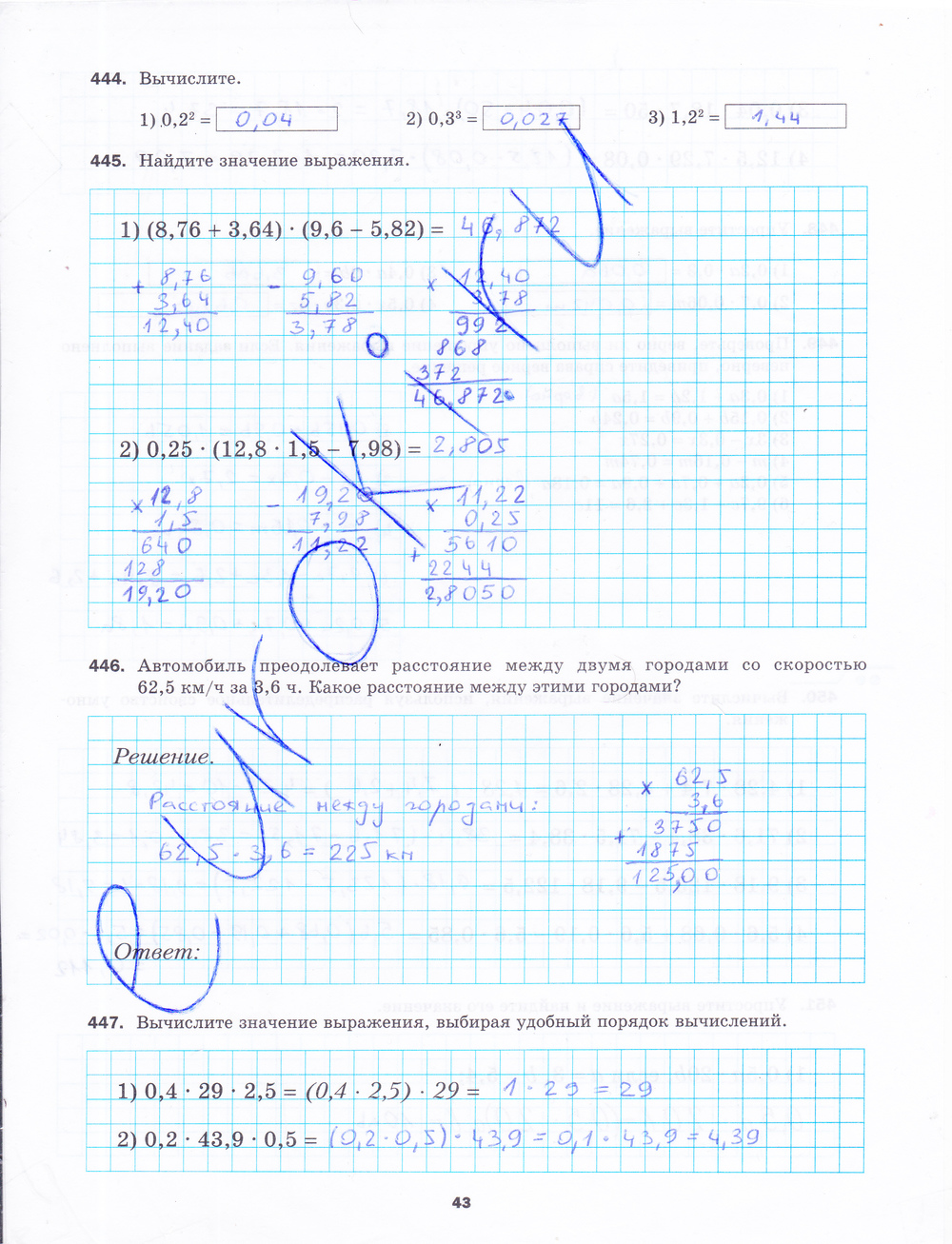

Где и как найти решебник по математике, 5 класс, Мерзляк

У нас на сайте всегда можно бесплатно воспользоваться решебником по математике под редакцией Мерзляк для 5 класса. Помимо просто полного развязывания заданий и всех ответов к ним, в пособии есть также пояснения, способные помочь школьникам, пропустившим занятия или желающим самостоятельно разобраться с новым материалом просто из любопытства.

Содержащееся на нашем сайте пособие исправлено и полностью доработано в соответствии с изменениями программы и учебника. Но, опять же, при бездумном списывании никакой решебник не добавит вам умений развязывать задачи и знаний по математике. Поэтому важно стараться решить задачу самостоятельно. Просмотреть способ решения рекомендуется только тогда, когда слишком долго не получалось сделать ее самому.

Как правильно использовать решебник по математике 5 класса, Г. Мерзляк

В средней школе пятикласснику намного труднее учиться, чем в начальной. Там он знал свою учительницу, а она знала, что от него можно потребовать и как ему лучше объяснить новый материал. А в средних классах предметы преподаются сразу несколькими педагогами. И привыкнуть к разной подаче учебного материала ребенку довольно непросто. Поэтому в этот период он может выпасть из-под контроля, завалить учебу, наполучать множество двоек. Но ему может помочь пособие с готовыми домашними заданиями, если, конечно, делать это правильно:

• Сначала нужно подобрать сборник с готовыми домашними заданиями, но только правильный – например, решебник по математике 5 класс, ФГОС, Мерзляк, Полонский, Якир.

• Книгу можно либо купить, либо скачать на нашем сайте, либо использовать ее онлайн.

• Родители должны присутствовать при выполнении домашней работы или хорошо контролировать действие ребенка, чтобы он не позволил себе просто списать задачу или уравнение, не вникая в смысл их развязывания.

• После того, как школьник развяжет задачу, родители могут проверить выполнение домашнего задания по нашему пособию.

• Позже можно разрешить ребенку самому осуществлять такую проверку, но все равно периодически нужно перепроверять, насколько осознанно он записал выполнение задачи.

• Если родители сами уже призабыли учебный материал по математике, то они волне могут восстановить свои знания с помощью нашего пособия.

Если правильно применять наш сборник по ГДЗ, то очень скоро знания вашего школьника станут достаточно прочными, чтобы работать и без этого подсказчика.

Математика 5 Мерзляк КР-03 В2

Контрольная работа № 3 по математике 5 класс «Уравнение. Угол. Многоугольники» с ответами и решениями по УМК Мерзляк, Полонский, Якир (Вариант 2). Дидактические материалы для учителей, школьников и родителей при дистанционном обучении. Математика 5 Мерзляк КР-03 В2.

Математика 5 класс (Мерзляк)
Контрольная работа № 3. Вариант 2

К-03. Вариант 2 (транскрипт заданий)

1. Запишите все углы, изображённые на рисунке 87. Измерьте угол АВК.
2. Постройте: 1) угол CDО, градусная мера которого равна 43°; 2) угол ВКА, градусная мера которого равна 135°.
3. Решите уравнение: 1) х + 38 = 64; 2) х– 479 = 164.
4. Одна сторона треугольника равна 15 дм, вторая — в 3 раза короче первой, а третья — на 12 дм длиннее второй. Вычислите периметр треугольника.
5. Решите уравнение: 1) (х + 83) – 92 = 45; 2) 62 – (х – 23) = 34.
6. Из вершины развёрнутого угла ADB (рис. 88) проведены два луча DT и DF так, что ∠ADF = 164°, ∠BDT = 148°. Вычислите величину угла TDF.
7. Какое число надо подставить вместо а, чтобы корнем уравнения 56 – (х + а) = 28 было число 23?

---

Математика 5 Мерзляк КР-03 В2
ОТВЕТЫ:

№ 1.   На рисунке изображены углы АВК, КВС, АВС. Угол АВК = 70°.

№ 2.  См.рисунок:

№ 3.   1) 26;     2) 643.

№ 4.   Ответ: Р = 37 дм.

№ 5.    1) 54;     2) 51.

№ 6.    Ответ: 132°.

№ 7.    Ответ: а = 5.

Смотреть РЕШЕНИЯ заданий в тетради

 

Математика 5 Мерзляк КР-03 В2. Контрольная работа по математике 5 класс «Уравнение. Угол. Многоугольники» с ответами и решениями по УМК Мерзляк, Полонский, Якир. Дидактические материалы для учителей, школьников и родителей при дистанционном обучении.
Другой вариант: КР-03 Вариант 1

В учебных целях использованы цитаты из пособия: «Математика 5 класс. Дидактические материалы/ А.Г. Мерзляк, В.Б. Полонский, Е.М.Рабинович и др. — М.: Вентана-Граф» . Представленная контрольная работа ориентирована на УМК Мерзляк и др. Ответы адресованы родителям, которые смогут проконтролировать правильность выполнения заданий. Цитаты представлены в учебных целях, а также для ознакомления и покупки указанного учебного пособия.

Вернуться на страницу: Контрольные работы по математике в 5 классе Мерзляк (Оглавление)

Решайте неравенства с помощью программы «Пошаговое решение математических задач»

---

Введите уравнение вместе с переменной, для которой вы хотите его решить, и нажмите кнопку «Решить».

В этой главе мы разработаем определенные методы, которые помогут решить проблемы, сформулированные на словах. Эти методы включают переписывание задач в виде символов. Например, заявленная проблема

«Найдите число, которое при добавлении к 3 дает 7»

можно записать как:

3+? = 7, 3 + n = 7, 3 + x = 1

и так далее, где символы?, N и x представляют собой число, которое мы хотим найти.Мы называем такие сокращенные версии поставленных задач уравнениями или символическими предложениями. Такие уравнения, как x + 3 = 7, являются уравнениями первой степени, поскольку переменная имеет показатель степени 1. Члены слева от знака равенства составляют левую часть уравнения; те, что справа, составляют правую часть. Таким образом, в уравнении x + 3 = 7 левый член равен x + 3, а правый член равен 7.

РЕШЕНИЕ УРАВНЕНИЙ

Уравнения могут быть истинными или ложными, так же как предложения слов могут быть истинными или ложными. Уравнение:

3 + х = 7

будет ложным, если вместо переменной подставлено любое число, кроме 4. Значение переменной, для которой верно уравнение (4 в этом примере), называется решением уравнения. Мы можем определить, является ли данное число решением данного уравнения, подставив число вместо переменной и определив истинность или ложность результата.

Пример 1 Определите, является ли значение 3 решением уравнения

4x — 2 = 3x + 1

Решение Мы подставляем значение 3 вместо x в уравнение и смотрим, совпадает ли левый член с правым.

4 (3) — 2 = 3 (3) + 1

12 — 2 = 9 + 1

10 = 10

Отв. 3 — решение.

Уравнения первой степени, которые мы рассматриваем в этой главе, имеют не более одного решения. Решения многих таких уравнений можно определить путем осмотра.

Пример 2 Найдите решение каждого уравнения путем осмотра.

а. х + 5 = 12
б. 4 · х = -20

Решения а. 7 — решение, так как 7 + 5 = 12.
b. -5 — это решение, поскольку 4 (-5) = -20.

РЕШЕНИЕ УРАВНЕНИЙ С ИСПОЛЬЗОВАНИЕМ СВОЙСТВ СЛОЖЕНИЯ И ВЫЧИСЛЕНИЯ

В разделе 3.1 мы решили несколько простых уравнений первой степени путем проверки. Однако решения большинства уравнений не сразу видны при осмотре. Следовательно, нам необходимы некоторые математические «инструменты» для решения уравнений.

ЭКВИВАЛЕНТНЫЕ УРАВНЕНИЯ

Эквивалентные уравнения — это уравнения, которые имеют идентичные решения. Таким образом,

3x + 3 = x + 13, 3x = x + 10, 2x = 10 и x = 5

эквивалентны уравнениям, потому что 5 — единственное решение каждого из них.Обратите внимание, что в уравнении 3x + 3 = x + 13 решение 5 не очевидно при осмотре, но в уравнении x = 5 решение 5 очевидно при осмотре. Решая любое уравнение, мы преобразуем данное уравнение, решение которого может быть неочевидным, в эквивалентное уравнение, решение которого легко заметить.

Следующее свойство, иногда называемое свойством сложения-вычитания , является одним из способов создания эквивалентных уравнений.

Если одинаковое количество прибавляется или вычитается из обоих элементов уравнения, полученное уравнение эквивалентно исходному уравнение.

в символах,

a — b, a + c = b + c и a — c = b — c

— эквивалентные уравнения.

Пример 1 Напишите уравнение, эквивалентное

х + 3 = 7

путем вычитания 3 из каждого члена.

Решение Если вычесть 3 из каждого члена, получим

х + 3 — 3 = 7 — 3

или

х = 4

Обратите внимание, что x + 3 = 7 и x = 4 являются эквивалентными уравнениями, поскольку решение одинаково для обоих, а именно 4.В следующем примере показано, как мы можем генерировать эквивалентные уравнения, сначала упростив один или оба члена уравнения.

Пример 2 Напишите уравнение, эквивалентное

4x- 2-3x = 4 + 6

, объединив одинаковые термины, а затем добавив по 2 к каждому члену.

Объединение одинаковых терминов дает

х — 2 = 10

Добавление 2 к каждому члену дает

х-2 + 2 = 10 + 2

х = 12

Чтобы решить уравнение, мы используем свойство сложения-вычитания, чтобы преобразовать данное уравнение в эквивалентное уравнение вида x = a, из которого мы можем найти решение путем проверки.

Пример 3 Решите 2x + 1 = x — 2.

Мы хотим получить эквивалентное уравнение, в котором все члены, содержащие x, находятся в одном члене, а все члены, не содержащие x, — в другом. Если мы сначала прибавим -1 к каждому члену (или вычтем 1 из него), мы получим

2x + 1- 1 = x — 2-1

2x = х — 3

Если мы теперь прибавим -x к каждому члену (или вычтем x из него), мы получим

2х-х = х — 3 — х

х = -3

, где решение -3 очевидно.

Решением исходного уравнения является число -3; однако ответ часто отображается в виде уравнения x = -3.

Поскольку каждое уравнение, полученное в процессе, эквивалентно исходному уравнению, -3 также является решением 2x + 1 = x — 2. В приведенном выше примере мы можем проверить решение, подставив — 3 вместо x в исходном уравнении.

2 (-3) + 1 = (-3) — 2

-5 = -5

Симметричное свойство равенства также помогает при решении уравнений. В этом объекте указано

Если a = b, то b = a

Это позволяет нам менять местами члены уравнения в любое время, не беспокоясь о каких-либо изменениях знака. Таким образом,

Если 4 = x + 2, то x + 2 = 4

Если x + 3 = 2x — 5, то 2x — 5 = x + 3

Если d = rt, то rt = d

Может быть несколько разных способов применить свойство сложения, указанное выше. Иногда один метод лучше другого, а в некоторых случаях также полезно симметричное свойство равенства.

Пример 4 Решите 2x = 3x — 9. (1)

Решение Если мы сначала добавим -3x к каждому члену, мы получим

2x — 3x = 3x — 9 — 3x

-x = -9

, где переменная имеет отрицательный коэффициент.Хотя при осмотре мы можем видеть, что решением является 9, поскольку — (9) = -9, мы можем избежать отрицательного коэффициента, добавив -2x и +9 к каждому члену уравнения (1). В этом случае получаем

2x-2x + 9 = 3x- 9-2x + 9

9 = х

, из которого решение 9 очевидно. При желании мы можем записать последнее уравнение как x = 9 по симметричному свойству равенства.

РЕШЕНИЕ УРАВНЕНИЙ С ИСПОЛЬЗОВАНИЕМ СВОЙСТВА DIVISION

Рассмотрим уравнение

3x = 12

Решение этого уравнения — 4. Также обратите внимание, что если мы разделим каждый член уравнения на 3, мы получим уравнения

, решение которого также равно 4. В общем, мы имеем следующее свойство, которое иногда называют свойством деления.

Если оба члена уравнения делятся на одно и то же (ненулевое) количество, полученное уравнение эквивалентно исходному уравнению.

в символах,

— эквивалентные уравнения.

Пример 1 Напишите уравнение, эквивалентное

-4x = 12

, разделив каждый член на -4.

Решение Разделив оба элемента на -4, получим

При решении уравнений мы используем указанное выше свойство для создания эквивалентных уравнений, в которых переменная имеет коэффициент 1.

Пример 2 Решите 3y + 2y = 20.

Сначала мы объединяем похожие термины, чтобы получить

5лет = 20

Тогда, разделив каждый член на 5, получим

В следующем примере мы используем свойство сложения-вычитания и свойство деления для решения уравнения.

Пример 3 Решить 4x + 7 = x — 2.

Решение

Сначала мы добавляем -x и -7 к каждому члену, чтобы получить

4x + 7 — x — 7 = x — 2 — x — 1

Далее, объединяя одинаковые термины, получаем

3x = -9

Наконец, мы разделим каждый член на 3, чтобы получить

РЕШЕНИЕ УРАВНЕНИЙ С СВОЙСТВОМ УМНОЖЕНИЯ

Рассмотрим уравнение

Решение этого уравнения — 12. Также обратите внимание, что если мы умножим каждый член уравнения на 4, мы получим уравнения

, решение которого также равно 12.В общем, мы имеем следующее свойство, которое иногда называют свойством умножения.

Если оба члена уравнения умножаются на одну и ту же ненулевую величину, полученное уравнение эквивалентно исходному уравнению.

в символах,

a = b и a · c = b · c (c ≠ 0)

— эквивалентные уравнения.

Пример 1 Напишите уравнение, эквивалентное

путем умножения каждого члена на 6.

Решение Умножение каждого члена на 6 дает

При решении уравнений мы используем указанное выше свойство для создания эквивалентных уравнений, не содержащих дробей.

Пример 2 Решить

Решение Сначала умножьте каждый член на 5, чтобы получить

Теперь разделите каждого члена на 3,

Пример 3 Решите

5 открытых образовательных ресурсов для K-5 Common Core Math

В Интернете существует множество открытых образовательных ресурсов по математике. На самом деле так много, что Education Week спросили: «Почему открытого контента по математике больше, чем по английскому?»

Common Core способствует значительному росту производства и курирования открытого образования, с появлением новых баз данных и источников слева и справа.Пробираться через все и находить источник, подходящий для вашего класса, может быть непосильной задачей. Имея это в виду, вот несколько ресурсов открытого образования по математике для учителей начальной школы.

Еще кое-что, что стоит проверить

• Карта общего ядра Академии Хана: найти конкретные уроки, соответствующие навыкам общего ядра, непросто. Общая основная карта Khan Academy основывается на догадках, предоставляя обзор процессов и навыков со ссылками на соответствующие уроки в Интернете.Страница ресурсов Common Core Хана — еще один отличный источник.
• Share My Lesson Общая основная база данных: Share My Lesson содержит чрезвычайно полную коллекцию согласованных планов уроков из различных источников. Мало того, что уроки разбиты по процессу и уровню подготовки, они все бесплатны, и их огромное количество из любимых источников, таких как «Улица Сезам». (Примечание. Использование Share My Lesson требует подписки на бесплатное членство.)
• Бесплатные уроки из ресурсов для преподавания математики K-5: Это еще один сайт, на котором не было работы наугад при поиске ресурсов Common Core, связанных с процессами.Здесь вы найдете исчерпывающий набор математических ресурсов для K-5, организованных по классам, и все они доступны для загрузки в формате PDF.
• Teaching Channel Серии видео по Common Core: видеоролики Teaching Channel дают потрясающий обзор Common Core на практике в классе. Для классов K-5 Teaching Channel подготовил более 70 видеороликов, охватывающих уроки математики и английского языка. Вы также найдете несколько отличных обзорных видео, которые помогут ответить на общие вопросы о внедрении новых стандартов.
• Бесплатные уроки от LearnZillion: Я уже писал о LearnZillion и раньше, но включил их базу данных открытых ресурсов в этот список, потому что в ней есть некоторые ценные уроки математики, согласованные с Общим ядром, для 2–6 классов. Не говоря уже о том, что это растущий веб-сайт, поэтому ожидайте больше 2-6 уроков в будущем, а также ресурсы для детских садов и первоклассников.

Служба проверки разметки W3C

Проверка по URI

Проверить документ онлайн:

Адрес:

Больше вариантов

Кодировка символов	(обнаруживать автоматически) utf-8 (Unicode, весь мир) utf-16 (Unicode, весь мир) iso-8859-1 (Западная Европа) iso-8859-2 (Центральная Европа) iso-8859-3 (Южная Европа) iso-8859 -4 (североевропейский) iso-8859-5 (кириллица) iso-8859-6-i (арабский) iso-8859-7 (греческий) iso-8859-8 (иврит, визуальный) iso-8859-8-i ( Иврит, логический) iso-8859-9 (турецкий) iso-8859-10 (Latin 6) iso-8859-11 (Latin / Thai) iso-8859-13 (Latin 7, Baltic Rim) iso-8859-14 (Latin 8, кельтский) iso-8859-15 (Latin 9) iso-8859-16 (Latin 10) us-ascii (базовый английский) euc-jp (японский, Unix) shift_jis (японский, Win / Mac) iso-2022-jp (Японский, электронная почта) euc-kr (корейский) ksc_5601 (корейский) gb2312 (китайский, упрощенный) gb18030 (китайский, упрощенный) big5 (китайский, традиционный) Big5-HKSCS (китайский, Гонконг) tis-620 (тайский) koi8- r (русский) koi8-u (украинский) iso-ir-111 (кириллица KOI-8) macintosh (MacRoman) windows-1250 (центральная Европа) windows-1251 (кириллица) windows-1252 (западная Европа) windows-1253 (греческий ) windows-1254 (турецкий) windows-1255 (иврит) windows-1256 (арабский) windows-1257 (бал тик обод)	Только при отсутствии
тип документа	(обнаруживать автоматически) HTML5 (экспериментальный) XHTML 1. 0 StrictXHTML 1.0 TransitionalXHTML 1.0 FramesetHTML 4.01 StrictHTML 4.01 TransitionalHTML 4.01 FramesetHTML 4.01 + RDFa 1.1HTML 3.2HTML 2.0ISO / IEC 15445: 2000 («ISO HTML») XHTML 1.1XHTML + RDFaXHTML Basic 1.0XHTML Basic 1.1XHTML Профиль печати для мобильных устройств 1.0XHTML- XHTML 1.1 плюс MathML 2.0 XHTML 1.1 плюс MathML 2.0 плюс SVG 1.1 MathML 2.0SVG 1.0SVG 1.1SVG 1.1 TinySVG 1.1 BasicSMIL 1.0SMIL 2.0	Только при отсутствии
Список сообщений последовательно сгруппировать сообщения об ошибках по типу
Показать источник	Очистите разметку с помощью HTML-Tidy
Показать контур	Проверить страницы ошибок	Подробный вывод

Подтвердить загрузкой файла

Загрузить документ для проверки:

Файл:

Больше вариантов

Кодировка символов	(обнаруживать автоматически) utf-8 (Unicode, весь мир) utf-16 (Unicode, весь мир) iso-8859-1 (Западная Европа) iso-8859-2 (Центральная Европа) iso-8859-3 (Южная Европа) iso-8859 -4 (североевропейский) iso-8859-5 (кириллица) iso-8859-6-i (арабский) iso-8859-7 (греческий) iso-8859-8 (иврит, визуальный) iso-8859-8-i ( Иврит, логический) iso-8859-9 (турецкий) iso-8859-10 (Latin 6) iso-8859-11 (Latin / Thai) iso-8859-13 (Latin 7, Baltic Rim) iso-8859-14 (Latin 8, кельтский) iso-8859-15 (Latin 9) iso-8859-16 (Latin 10) us-ascii (базовый английский) euc-jp (японский, Unix) shift_jis (японский, Win / Mac) iso-2022-jp (Японский, электронная почта) euc-kr (корейский) ksc_5601 (корейский) gb2312 (китайский, упрощенный) gb18030 (китайский, упрощенный) big5 (китайский, традиционный) Big5-HKSCS (китайский, Гонконг) tis-620 (тайский) koi8- r (русский) koi8-u (украинский) iso-ir-111 (кириллица KOI-8) macintosh (MacRoman) windows-1250 (центральная Европа) windows-1251 (кириллица) windows-1252 (западная Европа) windows-1253 (греческий ) windows-1254 (турецкий) windows-1255 (иврит) windows-1256 (арабский) windows-1257 (бал тик обод)	Только при отсутствии
тип документа	(обнаруживать автоматически) HTML5 (экспериментальный) XHTML 1. 0 StrictXHTML 1.0 TransitionalXHTML 1.0 FramesetHTML 4.01 StrictHTML 4.01 TransitionalHTML 4.01 FramesetHTML 4.01 + RDFa 1.1HTML 3.2HTML 2.0ISO / IEC 15445: 2000 («ISO HTML») XHTML 1.1XHTML + RDFaXHTML Basic 1.0XHTML Basic 1.1XHTML Профиль печати для мобильных устройств 1.0XHTML- XHTML 1.1 плюс MathML 2.0 XHTML 1.1 плюс MathML 2.0 плюс SVG 1.1 MathML 2.0SVG 1.0SVG 1.1SVG 1.1 TinySVG 1.1 BasicSMIL 1.0SMIL 2.0	Только при отсутствии
Список сообщений последовательно сгруппировать сообщения об ошибках по типу
Показать источник	Очистите разметку с помощью HTML-Tidy
Показать контур	Проверить страницы ошибок	Подробный вывод

Примечание : загрузка файлов может не работать через Интернет Проводник в некоторых версиях Windows XP Service Pack 2, см.

No related posts.