ГДЗ Алгебра Ерина 7 класс Рабочая тетрадь
Подробные решения по алгебре за 7 класс авторы Ерина, Макарычев
С каждой новой темой достигать очередной ступени в изучении алгебры в седьмом классе становится сложнее и сложнее. Не всегда даже отличники и хорошисты в состоянии справиться с выполнением того объема заданий, который требует от них нынешняя школьная программа. Что уж говорить о тех детях, которые не могут похвастаться высокими математическими достижениями, либо в силу независящих от них обстоятельств упустили ранее изучаемый материал и теперь совсем ничего не понимают в решении задач и упражнений. Специально подготовленное пособие с гдз по алгебре рабочая тетрадь за 7 класс Ерина поможет быстро справиться с освоением тематического материала и выполнением домашних заданий разного уровня сложности.
Кому и зачем могут пригодиться готовые ответы?
Выполнение домашних заданий иногда вызывает трудности у учеников. Одни из них тратят время на то, чтобы все-таки разобраться со сложной задачей. Другие же приходят на уроки неподготовленными и получают плохие оценки, чем снижают общие показатели своей успеваемости в школе. Правильно оформленные и проверенные онлайн ответы к рабочей тетради по алгебре для 7 класса автора Ериной к учебнику Макарычева – это пособие в двух частях, которое содержит целый комплекс готовых решений по всем примерам и задачам школьного курса. Оно рекомендовано Министерством образования РФ и станет полезным для пользователей разной целевой аудитории:
Другие же приходят на уроки неподготовленными и получают плохие оценки, чем снижают общие показатели своей успеваемости в школе. Правильно оформленные и проверенные онлайн ответы к рабочей тетради по алгебре для 7 класса автора Ериной к учебнику Макарычева – это пособие в двух частях, которое содержит целый комплекс готовых решений по всем примерам и задачам школьного курса. Оно рекомендовано Министерством образования РФ и станет полезным для пользователей разной целевой аудитории:
- семиклассники смогут не только списать уже готовый ответ, но и сверить правильность своего домашнего задания с тем, что представлено в издании;
- выпускникам 9 и 11 классов будет полезно вспомнить ранее изученный тематический материал и на практике потренироваться в решении сложных задач, чтобы в будущем на высокий бал написать ГИА и ЕГЭ;
- родителям теперь не придется тратить время на то, чтобы вникнуть во все тонкости алгебраических формул и разобраться с вычислениями геометрических прогрессий, используя массу учебников.
 При помощи еуроки ГДЗ они смогут легко проверить подготовку домашних заданий своими детьми, а при необходимости пояснить и пояснить упражнения, которые непонятны их ребенку;
При помощи еуроки ГДЗ они смогут легко проверить подготовку домашних заданий своими детьми, а при необходимости пояснить и пояснить упражнения, которые непонятны их ребенку; - учителям и репетиторам, которые хотят сэкономить время на подготовку проверочных заданий и максимально заинтересовать учеников к изучению такой сложной дисциплины, как алгебра.
Неоспоримые плюсы использования пособий с готовыми ответами во время учебы
Школьникам в 7 классе при изучении алгебры приходится не только знать наизусть все формулы сокращенного умножения, но и уметь их правильно применять. Также они должны разобраться с преобразованием выражений и решением уравнений с одной переменной, уметь различать основные типы функций и уметь строить их графики в декартовой системе координат. Справиться с освоением этих и других тем легче будет с решебником к рабочей тетради по алгебре за 7 класс (автор Ерина) к учебнику Макарычева, который обладает массой плюсов:
- экономит время на подготовку домашних заданий, ведь выполнение тех или иных заданий можно подсмотреть в пособии;
- экономит финансы, которые многим приходится тратить на помощь репетиторов.
 В сборнике поданы не только ответы, но и даны пояснения, представлены краткие алгоритмы действий в выполнении задач;
В сборнике поданы не только ответы, но и даны пояснения, представлены краткие алгоритмы действий в выполнении задач; - развивает самостоятельность. Ребенок сам может проконтролировать правильность выполнения домашней работы и прочитать пояснения к сложным заданиям.
Предлагаемая база решебников регулярно обновляется в соответствии с требованиями школьной программы, в них вносятся новые задания, подаются алгоритмы решения задач разного уровня сложности.
ГДЗ Алгебра Миндюк 7 класс Рабочая тетрадь
Авторы:Миндюк, Шлыкова
Изд-во:Просвещение
Вид УМК:рабочая тетрадь
Часть:1, 2
Найди ответ по номеру страницы
стр. 4стр. 5стр. 6стр. 7стр. 8стр. 9стр. 10стр. 11стр. 12стр. 13стр. 14стр. 15стр. 16стр. 17стр. 18стр. 19стр. 20стр. 21стр. 22стр. 23
стр. 24стр. 25стр. 26стр. 27стр. 28стр. 29стр. 30стр. 31стр. 32стр. 33стр. 34стр. 35стр. 36стр. 37стр. 38стр. 39стр. 40стр. 41стр. 42стр. 43
38стр. 39стр. 40стр. 41стр. 42стр. 43
стр. 44стр. 45стр. 46стр. 47стр. 48стр. 49стр. 50стр. 51стр. 52стр. 53стр. 54стр. 55стр. 56стр. 57стр. 58стр. 59стр. 60стр. 61стр. 62стр. 63
стр. 64стр. 65стр. 66стр. 67стр. 68стр. 69стр. 70стр. 71стр. 72стр. 73стр. 74стр. 75стр. 76стр. 77стр. 78стр. 79стр. 80стр. 81стр. 82стр. 83
стр. 84стр. 85стр. 86стр. 87стр. 88стр. 89стр. 90стр. 91стр. 92стр. 93стр. 94стр. 95стр. 96стр. 97стр. 98стр. 99стр. 100стр. 101стр. 102стр. 103
стр. 104стр. 105стр. 106стр. 107стр. 108стр. 109стр. 110стр. 111
Подробные решения по алгебре за 7 класс авторы Миндюк, Шлыкова
Освоить все тонкости алгебры, как школьной дисциплины, порой бывает очень сложно и практически невозможно без заученных формул, правил, таблиц и т.д. Не удивительно, что на подготовку домашних заданий у семиклассников практически всегда уходит масса времени и сил. Значительно облегчить изучение новых тем и сэкономить время на выполнение уроков поможет пособие с гдз по алгебре рабочая тетрадь за 7 класс Миндюк, которое составлено в соответствия со всеми требованиями министерства образования РФ.
Значительно облегчить изучение новых тем и сэкономить время на выполнение уроков поможет пособие с гдз по алгебре рабочая тетрадь за 7 класс Миндюк, которое составлено в соответствия со всеми требованиями министерства образования РФ.
Основные типы пользователей
Использование пособий с готовыми ответами сегодня широко распространено среди школьников разных классов. И в этом нет ничего зазорного. Важно только понимать, что онлайн решения по алгебре за 7 класс к рабочей тетради Миндюка, Шлыковой – это не шпаргалка на каждый день. Это сборник, облегчающий выполнение домашних заданий, которые взывают трудности, и рекомендован школьной программой для разных групп пользователей:
- при помощи пособия родители смогут не только проверить правильность выполнения домашних заданий своим ребенком, но и пояснить верный алгоритм решения непонятных для него задач;
- семиклассники могут быстро списать уже готовые ответы, а также сверить свои решения с тем, что представлено в издании.
 Это способствует тому, что ребенок не списывает бездумно то, что ему предлагают, а учится анализировать поданную информацию. А значит, материал в какой-то степени откладывается в его памяти и будет подсознательно применен в будущем для решения аналогичных заданий;
Это способствует тому, что ребенок не списывает бездумно то, что ему предлагают, а учится анализировать поданную информацию. А значит, материал в какой-то степени откладывается в его памяти и будет подсознательно применен в будущем для решения аналогичных заданий; - учителя, используя в своей практике такое пособие, смогут качественно подготовиться к предстоящим урокам, спланировать ход работы в классе и задания, которые будут заданы детям для домашней проработки;
- выпускникам девятых и одиннадцатых классов, которые готовятся к написанию ГИА и ЕГЭ. Материал, поданный в таком пособии, позволит вспомнить ранее изученные темы, а также применение формул для решения задач, примеров, неравенств и т.д.
Неоспоримые плюсы использования справочников
Преимущества использования онлайн справочника к рабочей тетради по алгебре за 7 класс авторов Миндюка, Шлыковой на сегодняшний день переоценить достаточно трудно. Он по праву считается настоящим помощником для школьников с разным уровнем знаний, так как позволяет не только списать готовый ответ, но и обратить внимание на алгоритмы действий в задачах и примерах.
- детальный разбор заданий на преобразование неизвестных величин в уравнениях, а также связанных с понятием квадратного корня, иррациональных чисел и алгебраических дробей;
- содержание кратких и лаконичных пояснений к заданиям, которые подразумевает соблюдение правил черчения графиков функций;
- экономию времени, ведь теперь школьнику не придется сидеть над непонятными задачами, либо ждать, пока родители помогут ему разобраться с их решением. Рассмотрев алгоритм предлагаемых действий, школьник сможет самостоятельно вникнуть в их суть и использовать полученные навыки для решения аналогичных примеров, тождеств или уравнений.
Прибегая к помощи еуроки ГДЗ, семиклассники смогут качественно подготовиться к предстоящим урокам и произвести самоконтроль своих знаний и навыков по алгебре, чтобы написать проверочные работы на хорошую оценку.
rt.representation theory — Что такое формула Янцена для определителя формы Шаповалова в случае обобщенных модулей Верма?
Не так много дополнительной литературы (особенно на английском языке) по материалу, изложенному в Jantzen 1977 Math. Анна. , но, возможно, эти замечания прояснят некоторые поднятые вами вопросы. (Глава 9 моей книги 2008 года была промежуточным компромиссом между широким изложением и записью всех мелких деталей, что потребовало бы еще большего количества обозначений, чем я уже ввел.)
Анна. , но, возможно, эти замечания прояснят некоторые поднятые вами вопросы. (Глава 9 моей книги 2008 года была промежуточным компромиссом между широким изложением и записью всех мелких деталей, что потребовало бы еще большего количества обозначений, чем я уже ввел.)
(1) Сначала я попытаюсь сфокусировать ваши вопросы в контексте (редуктивных) алгебр Ли над $\mathbb{C}$. Рассмотрим для любого $d \geq 2$ компактную группу Ли $SO(d)$, которая несколько вырождена, если только $d \geq 5$. Когда $d \geq 5$, группа (почти) проста, скажем, лиева ранга $\ell$ (размерность максимального тора). Теперь перейдем к комплексификации ее алгебры Ли, также ранга $\ell$ и простой. Здесь возможны два несколько различных случая: если $d=2\ell$ четно, то алгебра Ли имеет тип $D_\ell$, а если $d = 2\ell+1$ нечетно, то алгебра Ли имеет тип $ Б_\элл$. (Их корневые системы и группы Вейля отличаются.)
В вашей схеме отправной точкой фактически является группа $SO(d+2)$ для некоторого $d$ (скажем, $d \geq 5$, как раньше) с комплексифицированной алгеброй Ли, которая теперь называется $\mathfrak{g }$. 2-\ell$.) Для всего этого был зафиксирован базис $\ell + 1$ простых корней для системы корней и результирующие положительные корни относительно подалгебры Картана в $\mathfrak{g}$, общей с $\mathfrak{p}$. В каждом случае множество $I$ простых корней $\ell$ для производной алгебры $\mathfrak{l}$ может быть получено удалением $\alpha_1$ в нумерации Бурбаки (левый узел диаграммы Дынкина).
2-\ell$.) Для всего этого был зафиксирован базис $\ell + 1$ простых корней для системы корней и результирующие положительные корни относительно подалгебры Картана в $\mathfrak{g}$, общей с $\mathfrak{p}$. В каждом случае множество $I$ простых корней $\ell$ для производной алгебры $\mathfrak{l}$ может быть получено удалением $\alpha_1$ в нумерации Бурбаки (левый узел диаграммы Дынкина).
(2) Чтобы построить параболический модуль Верма (часто называемый «обобщенным» модулем Верма), начните с целочисленного веса $\lambda$ $\mathfrak{g}$, координаты которого относительно фундаментальных весов $\ell$ производной алгебры $\mathfrak{l}$ неотрицательны. Таким образом, $\lambda$ дает конечномерных простых модуля для $\mathfrak{l}$, который расширяется до $\mathfrak{p}$, заставляя $\mathfrak{u}$ действовать тривиально; индуцируем к $\mathfrak{g}$, чтобы получить искомый бесконечномерный параболический модуль Верма $M_I(\lambda)$.
(3) Естественная проблема состоит в том, чтобы решить, когда $M_I(\lambda)$ действительно является простым модулем. Для произвольных гирь критерии, разработанные Янценом (и обобщенные в $\S9.13$ моей книги), довольно сложны, но для обычных гирь (находящихся внутри камеры Вейля) точное условие более прямолинейно (моя Корр. 9.13(г)). Но для данной настройки все еще требуется много тщательного учета с корневыми системами. Полезно начать с гораздо более простого аналогичного примера $A_1 \hookrightarrow A_2$, который обсуждался в моей статье $\S9..5$, где снова имеется максимальная параболическая подалгебра. Здесь только 3 соответствующих камеры Вейля (из 6) и 3 простых модуля со связанными регулярными весами $\lambda$. В этом примере соответствующие параболические модули Верма имеют соответственно 2, 2, 1 композиционные факторы. В частности, обратите внимание, что вес в «средней» камере (ниже обычного доминирующего) определяет параболический модуль Верма, который не является простым, но не включает в себя параболический модуль Верма.
Для произвольных гирь критерии, разработанные Янценом (и обобщенные в $\S9.13$ моей книги), довольно сложны, но для обычных гирь (находящихся внутри камеры Вейля) точное условие более прямолинейно (моя Корр. 9.13(г)). Но для данной настройки все еще требуется много тщательного учета с корневыми системами. Полезно начать с гораздо более простого аналогичного примера $A_1 \hookrightarrow A_2$, который обсуждался в моей статье $\S9..5$, где снова имеется максимальная параболическая подалгебра. Здесь только 3 соответствующих камеры Вейля (из 6) и 3 простых модуля со связанными регулярными весами $\lambda$. В этом примере соответствующие параболические модули Верма имеют соответственно 2, 2, 1 композиционные факторы. В частности, обратите внимание, что вес в «средней» камере (ниже обычного доминирующего) определяет параболический модуль Верма, который не является простым, но не включает в себя параболический модуль Верма.
(4) В свои 19В статье 77 Янцен также адаптировал к параболическому случаю более ранние идеи, независимо развитые им и Шаповаловым. Здесь, в частности, можно (в принципе, но редко на практике) явно вычислить определитель результирующей контравариантной формы на каждом весовом пространстве. Помимо индуктивно вычисленного определителя для части Леви параболы, необходимо вычислить дополнительные множители для «остаточных» положительных корней. Даже после распаковки тяжелой нотации Янцена для всего этого, я не уверен, что смогу выполнить вычисления в этом вопросе даже для обычного веса в каждой соответствующей камере Вейля. Первый «общий» случай возникает для $B_3 \hookrightarrow B_4$ (когда $d=7$) или $D_4 \hookrightarrow D_5$ (когда $d=8$). (Но можно также рассмотреть пару меньших «вырожденных» случаев.) Прямые вычисления в любом из этих случаев выглядят громоздко.
Здесь, в частности, можно (в принципе, но редко на практике) явно вычислить определитель результирующей контравариантной формы на каждом весовом пространстве. Помимо индуктивно вычисленного определителя для части Леви параболы, необходимо вычислить дополнительные множители для «остаточных» положительных корней. Даже после распаковки тяжелой нотации Янцена для всего этого, я не уверен, что смогу выполнить вычисления в этом вопросе даже для обычного веса в каждой соответствующей камере Вейля. Первый «общий» случай возникает для $B_3 \hookrightarrow B_4$ (когда $d=7$) или $D_4 \hookrightarrow D_5$ (когда $d=8$). (Но можно также рассмотреть пару меньших «вырожденных» случаев.) Прямые вычисления в любом из этих случаев выглядят громоздко.
Словесные задачи «Расстояние» | Purplemath
Другие примеры
Purplemath
Что такое задача на «расстояние»?
Словесные задачи на «расстояние», часто также называемые задачами на «равномерную скорость», включают в себя что-то, движущееся с некоторой фиксированной и устойчивой («равномерной») скоростью («скорость», «скорость» или «скорость») или же движущееся с какая-то средняя скорость.
Всякий раз, когда вы читаете задачи на «как быстро», «как далеко» или «как долго», вы должны думать об уравнении расстояния, d = rt , где d обозначает расстояние, r обозначает скорость (постоянную или среднюю), а t обозначает время.
Содержание продолжается ниже
MathHelp.com
Проблемы со словами о расстоянии
Убедитесь, что единицы времени и расстояния совпадают с единицами скорости. Например, если они дают вам скорость в футах в секунду, то ваше время должно быть в секундах, а ваше расстояние должно быть в футах. Иногда они пытаются обмануть вас, используя неправильные единицы измерения, и вы должны уловить это и преобразовать в правильные единицы измерения.
Если вам интересно, этот тип упражнения требует, чтобы скорость была фиксированной и постоянной (то есть неизменной), чтобы работала формула d = rt . Единственный способ справиться со скоростью, которая может меняться, — это взять среднюю скорость за рассматриваемое время или расстояние. Работа непосредственно с изменяющимися скоростями будет чем-то, с чем вы столкнетесь в исчислении, так как это требует исчисления (или более продвинутых) методов.
Работа непосредственно с изменяющимися скоростями будет чем-то, с чем вы столкнетесь в исчислении, так как это требует исчисления (или более продвинутых) методов.
В чем разница между фиксированной скоростью и средней скоростью?
Упражнение с фиксированной скоростью — это упражнение, в котором машина, скажем, всегда движется ровно шестьдесят миль в час; за три часа машина проедет 180 миль. Упражнение на среднюю скорость — это упражнение, в котором автомобиль, скажем, в среднем разгоняется до сорока миль в час, но это среднее значение включает различные скорости, относящиеся к светофорам, шоссе и проселочным дорогам; за три часа машина прошла 120 миль, хотя скорость машины была непостоянной. Большинство упражнений, которые вы увидите, будут упражнениями с фиксированной скоростью, но, очевидно, они не очень «реальны». Это упрощение, которое они делают, чтобы сделать ситуацию возможной, используя только алгебраические методы.
Каков пример постановки и решения словесной задачи «расстояние»?
- 555-мильное 5-часовое путешествие на самолете было выполнено на двух скоростях.
 В первой части пути средняя скорость составляла 105 миль в час. Затем усилился попутный ветер, и оставшуюся часть пути самолет летел со средней скоростью 115 миль в час. Сколько времени самолет летел с каждой скоростью?
В первой части пути средняя скорость составляла 105 миль в час. Затем усилился попутный ветер, и оставшуюся часть пути самолет летел со средней скоростью 115 миль в час. Сколько времени самолет летел с каждой скоростью?
Существует метод подготовки и решения этих упражнений, с которым я впервые столкнулся задолго до того, как действительно выполнял их в классе. Но, как только меня познакомили с ним, я переключился, потому что это , так что намного проще.
Сначала я настроил сетку, столбцы которой были помечены переменными из формулы «расстояние», а строки были помечены задействованными «частями»:
В первой части самолет преодолел некоторое расстояние. Я не знаю, сколько, поэтому мне понадобится переменная для этого неизвестного значения. Я буду использовать переменную, которую они мне дали в уравнении расстояния:
Они дали мне скорость или скорость для этой части, поэтому я добавлю это в свою таблицу:
Во время этой первой части самолет некоторое время летал, но я не знаю, сколько времени это было. Поэтому мне нужна переменная для этого неизвестного значения; Я буду использовать переменную из уравнения расстояния:
Поэтому мне нужна переменная для этого неизвестного значения; Я буду использовать переменную из уравнения расстояния:
Во второй части самолет преодолел оставшуюся часть общего расстояния. Я не знаю точное расстояние, которое было пройдено во время этой второй части, но я знаю, что это было «сколько бы ни осталось от 555 миль после того, как первые d миль были пройдены в первой части». была оставлена после того, как [какая-то сумма] была вынута» выражается вычитанием: я беру сумму, о которой уже позаботились, и вычитаю ее из того, что было общей суммой. Добавляя это к моей таблице, я получаю:
Мне дали скорость или скорость для второй части, и я могу использовать то же самое «Сколько осталось?» строительство для того, чтобы было время для этой второй части. Итак, теперь моя таблица выглядит так:
Для строки «итого» я прибавляю (или беру информацию из отчета об упражнении):
Почему я не прибавляю в столбце «ставка»? Потому что я не могу добавлять ставки! В этом упражнении добавление скоростей показало бы, что средняя скорость за всю поездку составляет 105 + 115 = 220 миль в час. Но очевидно, что это не имеет смысла.
Но очевидно, что это не имеет смысла.
Гениальность этого табличного метода настройки заключается в том, что теперь я могу создавать уравнения из строк и столбцов. В этом упражнении есть несколько способов продолжить. Я буду работать с уравнением «расстояние», чтобы создать выражения для расстояний, пройденных в каждой части.
Умножая поперек, первая строка говорит мне, что расстояние, пройденное в первой части полета, было:
Расстояние 1-й части: 105 вторая часть полета составила:
2-я часть расстояния: 115(5 − t )
Я могу сложить эти два выражения частичного расстояния и установить их равными известному общему расстоянию:
105 t + 115(5 − t ) = 555
Это уравнение с одной переменной, которое я могу решить:
105 t + 115(5 − t ) = 555
105 т + 575 — 115 т = 555
575 − 10 т = 555
20 = 10 т
2 = t
Оглядываясь назад на свою таблицу, я вижу, что я определил t как время, которое самолет провел в воздухе на первой части своего пути.
Теперь у меня есть время для первой части полета; время было два часа. В упражнении говорилось, что вся поездка длилась пять часов, поэтому вторая часть должна была занять три часа (получено путем вычитания времени первой части из общего времени). Они не запрашивали частичные расстояния, так что у меня есть вся необходимая информация. Мой ответ:
первая часть: 2 часа
вторая часть: 3 часа
Когда я устанавливал свое уравнение, я упомянул, что есть несколько способов действовать. Каков был другой путь? Я мог бы использовать таблицу, чтобы создать выражение для каждого из двух неполных значений времени, добавить, установить результат равным заданной сумме и решить для переменной d . Поскольку уравнение расстояния d = rt , то выражения для неполных времен будут созданы путем решения уравнения для  Моя работа выглядела бы следующим образом:
Моя работа выглядела бы следующим образом:
T = D / R
Первая часть: D /105
Вторая часть: (555 — D ) /115
Добавление: d /105 + (555 − d )/115 = 5
23 д + 11 655 — 21 д = 12 075
2 d = 420
d = 210
Оглянувшись на свою таблицу, я бы увидел, что это дает мне расстояние, пройденное за первую половину полета. Оглядываясь назад на упражнение, я бы увидел, что им нужно время, а не расстояние. Таким образом, я бы вычислил время для первой части, а затем сделал вычитание, чтобы найти время для второй части. В моей работе было бы больше шагов, но мой ответ был бы таким же.
Есть три вещи, которые, я надеюсь, вы усвоили из приведенного выше примера. (1) Использование таблицы или сетки для отслеживания того, что вы делаете, может быть невероятно полезным. (2) Важно четко определить ваши переменные, чтобы вы знали (к концу), что вы имели в виду (еще в начале), чтобы вы могли правильно применить свои результаты. (3) Вы должны всегда проверять исходное упражнение, чтобы быть уверенным, что отвечаете на вопрос, который они действительно задали. (Мое значение расстояния, найденное выше, правильное, но не то, что они просили.) Но самое главное вот что:
(3) Вы должны всегда проверять исходное упражнение, чтобы быть уверенным, что отвечаете на вопрос, который они действительно задали. (Мое значение расстояния, найденное выше, правильное, но не то, что они просили.) Но самое главное вот что:
НИКОГДА НЕ ПЫТАЙТЕСЬ ДОБАВИТЬ ЦЕНЫ! Подумайте об этом: если вы едете со скоростью 20 миль в час по одной улице и со скоростью 40 миль в час по другой улице, означает ли это, что вы в среднем 60 миль в час? Конечно нет.
Могу ли я хотя бы усреднить ставки? Если бы я ехал со скоростью 20 миль в час в течение одного часа, а затем ехал бы со скоростью 60 миль в час в течение двух часов, то я бы проехал 140 миль за три часа, или чуть меньше 47 миль в час. Но 47 — это не среднее между 20 и 60.
Как видите, реальная математика, используемая для решения этого типа упражнений, часто довольно проста. Это настройка, это сложная часть. Ниже приведены еще несколько примеров, но только с показанной настройкой. Попробуйте свои силы в решении и нажмите на ссылки, чтобы получить всплывающие окна, из которых можно проверить свои уравнения и решения.
- Руководитель ехал из дома со средней скоростью 30 миль в час в аэропорт, где его ждал вертолет. Руководитель сел в вертолет и полетел в корпоративные офисы со средней скоростью 60 миль в час. Все расстояние составляло 150 миль; вся поездка заняла три часа. Найдите расстояние от аэропорта до офисов компании.
Я начну обычным способом, настроив свою таблицу:
Я пометил свои строки, чтобы было ясно, как они относятся к упражнению. Теперь мне нужно заполнить строки. Как и раньше, я не знаю ни расстояния, ни времени на участке, где ехал руководитель, поэтому я буду использовать переменные для этих неизвестных вместе с заданной скоростью.
Для летной части пути я буду использовать конструкцию «сколько осталось» вместе с заданной скоростью, чтобы заполнить вторую строку. Я также заполню итоги.
Первая строка дает мне уравнение d = 30 t . Вторая строка более беспорядочна, что дает мне уравнение:
150 − d = 60(3 − t )
Отсюда я могу пойти разными путями; Думаю, я решу это второе уравнение для переменной d , а затем приравняю результаты друг к другу.
150 − d = 60(3 − t )
150 — 60 (3 — T ) = D
Установка равных этих двух выражений для D , I GET:
30 T = 150 — 60 (3 — T )
SOLVE для для т ; интерпретировать значение; сформулируйте окончательный ответ.
- Автомобиль и автобус отправились в 14:00. из той же точки, в том же направлении. Средняя скорость автомобиля на 30 миль в час меньше, чем удвоенная скорость автобуса. За два часа автомобиль опережает автобус на 20 миль. Найдите скорость автомобиля.
Оба автомобиля проехали одинаковое количество времени.
Значения автомобиля выражаются в терминах значений шины, поэтому я буду использовать переменные для неизвестных значений шины, а затем определю автомобиль в терминах переменных шины. Это дает мне:
(Как оказалось, на этот раз мне не понадобится строка «всего».)
Это не очень полезно.

 При помощи еуроки ГДЗ они смогут легко проверить подготовку домашних заданий своими детьми, а при необходимости пояснить и пояснить упражнения, которые непонятны их ребенку;
При помощи еуроки ГДЗ они смогут легко проверить подготовку домашних заданий своими детьми, а при необходимости пояснить и пояснить упражнения, которые непонятны их ребенку;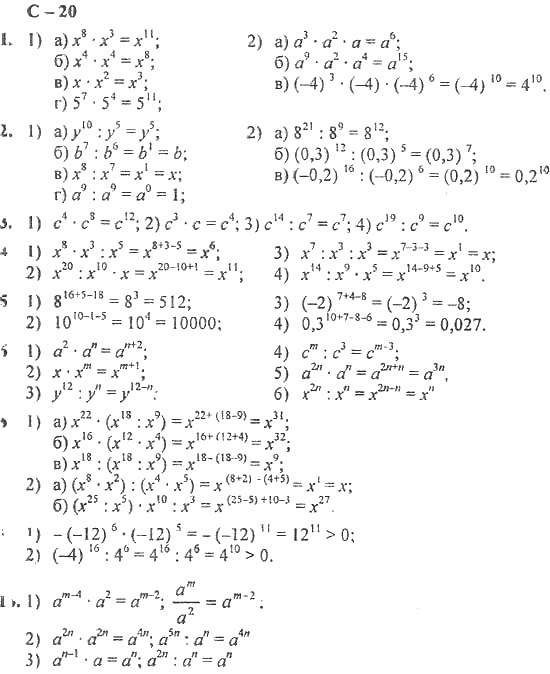 В сборнике поданы не только ответы, но и даны пояснения, представлены краткие алгоритмы действий в выполнении задач;
В сборнике поданы не только ответы, но и даны пояснения, представлены краткие алгоритмы действий в выполнении задач; Это способствует тому, что ребенок не списывает бездумно то, что ему предлагают, а учится анализировать поданную информацию. А значит, материал в какой-то степени откладывается в его памяти и будет подсознательно применен в будущем для решения аналогичных заданий;
Это способствует тому, что ребенок не списывает бездумно то, что ему предлагают, а учится анализировать поданную информацию. А значит, материал в какой-то степени откладывается в его памяти и будет подсознательно применен в будущем для решения аналогичных заданий; В первой части пути средняя скорость составляла 105 миль в час. Затем усилился попутный ветер, и оставшуюся часть пути самолет летел со средней скоростью 115 миль в час. Сколько времени самолет летел с каждой скоростью?
В первой части пути средняя скорость составляла 105 миль в час. Затем усилился попутный ветер, и оставшуюся часть пути самолет летел со средней скоростью 115 миль в час. Сколько времени самолет летел с каждой скоростью?