Гдз по алгебре онлайн: ГДЗ по алгебре 7 класс онлайн решебник с ответами

Содержание

ГДЗ (решебники) с 1 по 11 класс Онлайн

Современная школа предъявляет к ученику ряд требований, для выполнения которых необходимо уделять достаточное внимание обучению. Для того чтобы сделать этот процесс более эффективным используются различные педагогические методики и учебные пособия. Одним из наиболее популярных среди учеников пособий является ГДЗ. Очень часто оно используется наиболее упрощенным способом – для того чтобы списать правильное решение. На самом деле решебник нужен для другого, а именно – эффективного контроля за полученными знаниями.

Практика показывает, что ненавязчивый и конструктивный контроль со стороны родителей за успеваемостью ученика дает положительные результаты. У ребенка улучшается мотивационная составляющая в процессе получения знаний. Поэтому, ГДЗ нужно использовать, но делать это необходимо правильно.

Как правильно использовать готовые домашние задания

В первую очередь нужно обратить внимание на то, что данные методические пособия выпускаются после получения разрешения со стороны Министерства образования РФ. Поэтому, их нужно рассматривать как учебно-методические пособия, которые рекомендованы для использования в школе.

ГДЗ следует применять для того чтобы проверить правильно ли выполнена домашняя работа.
Перед началом выполнения домашнего задания необходимо повторить тему, по которой было оно задано.
В готовых ответах есть возможность не только свериться с правильным решением, но и получить информацию о том, какие правила и из какой темы для этого использовались.
С использованием ГДЗ можно обеспечить эффективный контроль со стороны родителей за успеваемостью своего сына или дочки.

По своему предназначению готовые домашние задания – это учебное пособие, цель которого – помогать ученикам усваивать новые знания. Простое списывание принесет только вред: школьник перестанет понимать учебный материал и полностью потеряет интерес к обучению. Поэтому, использование данного пособия должно осуществляться под присмотром учителей или родителей.

У нас вы сможете найти все ГДЗ онлайн

На нашем сайте собрано большое количество ГДЗ по различным школьным предметам: русскому языку, математике, алгебре, геометрии и другим.

Вам достаточно всего лишь зайти на сайт и найти готовые ответы по тому предмету, который вас интересует. Делаете один клик по номеру задания, и вы уже попадаете на страницу с готовым ответом.

Пользоваться нашим сайтом очень просто и удобно. Также, хотим отметить, что все его опции доступны для пользователей совершенно бесплатно.

Теперь у родителей полностью отпала необходимость покупать бумажные версии ГДЗ и тратить на это деньги. Вы можете зайти на наш сайт, используя смартфон или планшет и получить необходимую информацию.

Мы всегда готовы сделать все для того, чтобы вы могли добиваться желаемых результатов. Теперь вам будет по плечу любой диктант, контрольная и даже ЕГЭ.

Заходите на наш сайт и находите правильные ответы на все задания.

Home -Photomath

Математика еще никогда не была такой увлекательной

Наши пошаговые объяснения помогут вам освоить многие разделы математики, от арифметики и до анализа, благодаря чему вы станете увереннее в своих силах.

С чем мы можем помочь?

Математический анализ
Деление в столбик
Алгебра
Геометрия
Сложение и вычитание
Функции
Тригонометрия
Умножение
Дроби
Пределы и интегралы
Текстовые задачи
Элементарная математика
Статистика
и многое другое!

Начать обучение

Решение задач с основ

Один отец хотел помочь своим детям с домашней работой по математике. Теперь его творение помогает уже миллионам учеников по всему миру.

Родителям

Damir Sabol

основатель

Нечто большее, чем приложение

Один школьный учитель должен уделять внимание многим ученикам. В приложении Photomath, напротив, одному ученику предоставляется множество учителей.

Photomath для обучения

Более 220 млн

скачиваний

4.

Рейтинг приложения

ОБОЖАЮ это приложение. Каждый раз, когда я использую его в классе, мы с учениками поражаемся его способностям. Приложение демонстрирует несколько вариантов решения тех или иных уравнений, что дает ученикам благоприятные возможности для обучения, которые порой отсутствуют на обычном уроке.

Прекрасное приложение для решения математических задач, часто выручает в самый нужный момент!

Благодаря Photomath моего 8-летнего сына будто бы осенило: он понял, как в его случае получается правильный ответ.

Большое спасибо! Я в математическом классе, и мне это очень полезно, спасибо!

О нас пишут

Изучение алгебры с помощью онлайн-курсов, занятий и уроков

Что такое Алгебра?

Алгебра — это область математики, в которой символы используются для представления чисел в формулах и уравнениях. Понимание этих символов и того, как они работают вместе и обеспечивают структуру уравнений, позволяет математикам более эффективно писать формулы и решать математические задачи. Алгебра делится на две части: элементарная алгебра и абстрактная алгебра. Элементарная алгебра состоит из базовых алгебраических символов и уравнений, которым обучают в начальной школе. Абстрактная алгебра или современная алгебра включает изучение алгебраических структур, таких как векторные пространства и группы.

Онлайн-курсы и программы по алгебре

EdX предлагает как вводные, так и углубленные курсы по алгебре. Начните решать уравнения и изучайте основы алгебраических выражений с помощью бесплатного онлайн-курса от SchoolYourself. Курс алгебры для самостоятельного обучения научит вас работать с целыми числами, десятичными дробями и показателями степени, как оценивать степени и корни и как решать уравнения и неравенства с одной и несколькими переменными с помощью онлайн-викторин и рабочих листов по алгебре. Алгебра необходима как для средней школы, так и для колледжа, и она будет служить в качестве курса подготовки к алгебре. Решая эти задачи по алгебре, вы хорошо подготовитесь к дальнейшему изучению математики.

Для более продвинутой программы по алгебре рассмотрите курс College Algebra and Problem Solution от ASU. Этот курс для самостоятельного обучения использует систему обучения ALEKS, которая помогает адаптировать процесс обучения к индивидуальным потребностям и темпу учащихся. Узнайте, как применять алгебру к широкому кругу реальных задач и изучите важные алгебраические понятия, такие как функции, области и диапазоны. Этот курс может помочь вам подготовиться к исчислению и другим математическим курсам.

Ознакомьтесь с дополнительными онлайн-курсами и учебными пособиями по математике, которые охватывают булеву алгебру, алгебраическую геометрию, абстрактную алгебру и другие сложные темы. Многие курсы предназначены для самостоятельного изучения, поэтому вы можете записаться и учиться по собственному расписанию.

Изучение основ алгебры для начинающих с помощью онлайн-курсов

Учащиеся, которые ищут курс алгебры для начинающих, могут пройти программу SchoolYourself, которая охватывает стандартную учебную программу, обычно используемую в 1-м классе средней школы по алгебре. Во время вводного занятия вы изучите основы алгебры и примете практические задачи по алгебре о том, как решать уравнения с одной переменной и как строить графики. Этот курс от SchoolYourself — идеальное введение в алгебру для учащихся. Вы будете практиковать алгебру, узнавать о параболах и экспоненциальных функциях, о том, как решать уравнения и неравенства с одной и несколькими переменными, и многое другое

В каких работах используется алгебра?

Алгебра — это навык, применимый во многих областях и профессиях современной экономики при решении уравнений. Вы можете быть удивлены количеством рабочих мест и профессий, которые требуют практических знаний алгебры для выполнения повседневных задач. Ниже приведены несколько примеров профессий, требующих навыков алгебры, и общие задачи.

Бизнесмены, ежедневно использующие алгебру, будут бухгалтерами. Как бухгалтер, вы должны иметь возможность балансировать электронные таблицы, прогнозировать расходы и создавать отчеты о расходах для вашей компании и команды. Другим примером бизнес-профессионалов, которым необходимы практические знания алгебры, являются банкиры. Банкиры должны иметь возможность регулярно рассчитывать процентные ставки, налоги и многое другое для своих клиентов. Владельцы бизнеса также используют алгебру для расчета скорости выполнения, выручки, рентабельности и многого другого, чтобы их акционеры могли продемонстрировать потенциал роста и обеспечить финансирование и инвестиции.

Медицинские работники должны знать и понимать алгебру, чтобы назначать лекарства, выявлять отклонения от нормы, выписывать рецепты и многое другое для своих пациентов. Преобразование различных доз лекарств относительно распространено в области медицины, поэтому навыки решения задач по алгебре часто пригодятся. Особенно, когда время поджимает, а оборудования не хватает, вам нужно знать, как назначать различные лекарства, учитывая вес, возраст, дозировку и многое другое для ваших пациентов.

Инструкторы по фитнесу демонстрируют своим клиентам правильную технику упражнений. Рабочий уровень алгебры помогает инструкторам по фитнесу рассчитать идеальную тренировку для своих клиентов. Инструкторы по фитнесу рассчитывают процентное содержание жира в организме человека, рост, вес, возраст и другие параметры, чтобы разработать правильный режим тренировок. Инструкторы по фитнесу могут использовать алгебру, чтобы определить соотношение диеты и физических упражнений для достижения целей своего клиента за счет увеличения или потери веса.

Архитектура — это профессионалы, проектирующие и рисующие модели новых зданий. Точность и алгебра необходимы для этих профессионалов, чтобы получить правильные детали. Изображение высоты здания, ширины комнат, коридоров, этажей и т. д. — все это возвращает к рабочему пониманию алгебраических задач и решений.

Профессионалы-строители проектируют, проверяют и обслуживают общие системы, которые мы используем ежедневно. Некоторые из этих систем включают дороги, мосты, туннели, канализационные системы и многое другое. Как инженер-строитель, вы должны понимать алгебру, чтобы вы могли рассчитать, какой вес может выдержать мост или дорога с учетом нагрузки от транспортных средств. Еще один фактор, который необходимо учитывать инженерам-строителям, включает в себя прогнозирование того, как мост сможет выдерживать скорость ветра, землетрясения, снег и многое другое.

Зачем посещать онлайн-курсы по алгебре?

Алгебра — это практический навык, которым должны владеть многие специалисты в своей сфере деятельности. Онлайн-курсы по алгебре позволяют выбрать правильный курс, который наилучшим образом соответствует вашим потребностям. Может быть, вы хотите пройти курсы повышения квалификации, чтобы освежить свои навыки. Возможно, вы ищете более продвинутые курсы алгебры, если вы собираетесь стать архитектором и вам нужно практиковать передовые методы алгебры. Независимо от того, где вы находитесь, edX предлагает широкий спектр онлайн-курсов по алгебре, разработанных с учетом вашего плотного графика.

Курсы по алгебре на edX

Некоторые из наших курсов включают критическое мышление через решение уравнений и понимание алгебраических выражений. Другие курсы будут в значительной степени опираться на элементы, которые включают квадратные формулы, системы уравнений, полиномиальные выражения, рациональные выражения, рациональные функции, квадратные уравнения, полиномиальные функции, алгебраические операции, графики, квадратные корни, комплексные числа, линейные неравенства, абсолютные значения, отрицательные числа , распределительный закон, текстовые задачи, тригонометрия, частные дроби, линейные уравнения и многое другое. Некоторые курсы по edX заставят вас попрактиковаться в решении задач с помощью порядка операций, специальных методов, рациональных функций и многого другого. Наши курсы разработаны, чтобы помочь вам изучить алгебру с помощью пошаговых инструкций от лучших университетов.

Знаменитые умы алгебры

В истории алгебры было много известных и выдающихся умов. Совершенствование и расширение алгебраических методов и методов решения уравнений продолжали развивать область алгебры на протяжении многих лет. Прелесть алгебры в том, что она преодолевает языковые барьеры между английскими, испанскими, французскими и многими другими учеными по всему миру. Среди наиболее заметных участников открытия алгебры Никколо Фонтана Тарталья, Жозеф-Луи Лагранж, Эварист Галуа, Артур Кэли и Карл Фридрих Гаусс.

Алгебра

Показать мобильное уведомление Показать все примечания Скрыть все примечания

Уведомление для мобильных устройств

Похоже, вы используете устройство с «узкой» шириной экрана ( т. е. вы наверное на мобильном телефоне). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.

Вот мои онлайн-заметки к моему курсу алгебры, который я преподаю здесь, в Университете Ламара, хотя я должен признать, что прошли годы с тех пор, как я в последний раз читал этот курс. На данном этапе своей карьеры я в основном преподаю исчисление и дифференциальные уравнения.

Несмотря на то, что это мои «классные заметки», они должны быть доступны всем, кто хочет изучать алгебру или нуждается в освежении знаний по алгебре. Я постарался сделать заметки как можно более самодостаточными и не ссылаться ни на одну книгу. Тем не менее, они предполагают, что вы имели некоторое представление об основах алгебры в какой-то момент до этого. Хотя есть некоторый обзор показателей, факторинга и построения графиков, предполагается, что не потребуется много обзора, чтобы напомнить вам, как работают эти темы.

Вот несколько предупреждений моим ученикам, которые могут быть здесь, чтобы получить копию того, что произошло в день, который вы пропустили.

Поскольку я хотел сделать это довольно полным набором заметок для всех, кто хочет изучать алгебру, я включил некоторые материалы, которые у меня обычно не хватает времени для изучения в классе, и поскольку они меняются от семестра к семестру, они здесь не упоминаются. Вам нужно будет найти одного из своих одноклассников, чтобы узнать, есть ли в этих заметках что-то, что не было рассмотрено в классе.

Поскольку я хочу, чтобы эти заметки дали вам еще несколько примеров для прочтения, я не всегда решаю в классе те же задачи, что и в примечаниях. Точно так же, даже если я решу некоторые из задач здесь, я могу решить меньше задач в классе, чем представлено здесь.
Иногда вопросы в классе ведут по путям, которые здесь не рассматриваются. Я стараюсь предвидеть как можно больше вопросов, когда пишу их, но реальность такова, что я не могу предвидеть все вопросы. Иногда в классе задают очень хороший вопрос, который приводит к идеям, которые я здесь не включил. Вы всегда должны поговорить с кем-то, кто был в классе в тот день, когда вы пропустили, и сравнить эти записи с их заметками и посмотреть, в чем различия.

Это несколько связано с предыдущими тремя пунктами, но достаточно важно, чтобы заслужить отдельный пункт. ЭТИ ЗАПИСКИ НЕ ЗАМЕНЯЮТ ПОСЕЩЕНИЕ ЗАНЯТИЙ!! Использование этих заметок вместо урока может привести к неприятностям. Как уже отмечалось, не все в этих заметках освещается в классе, и часто материал или идеи, не указанные в этих заметках, рассматриваются в классе.

Вот список (и краткое описание) материалов, содержащихся в этом наборе заметок.

Предварительные занятия.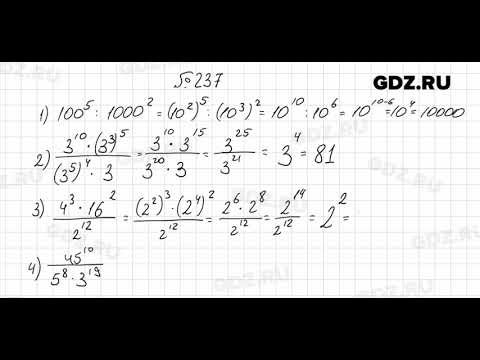 В этой главе мы сделаем краткий обзор некоторых тем, абсолютно необходимых для успешного изучения алгебры. Мы рассматриваем показатели степени (целые и рациональные), радикалы, полиномы, факторинговые полиномы, рациональные выражения и комплексные числа.

Целочисленные экспоненты. В этом разделе мы начнем рассматривать экспоненты. Мы дадим основные свойства экспонент и проиллюстрируем некоторые распространенные ошибки, которые студенты допускают при работе с экспонентами. Примеры в этом разделе мы будем ограничивать целыми показателями. Рациональные показатели будут обсуждаться в следующем разделе.
Рациональные показатели. В этом разделе мы определим, что мы подразумеваем под рациональными показателями, и распространим свойства из предыдущего раздела на рациональные показатели. Мы также обсудим, как оценивать числа, возведенные в рациональный показатель.
Радикалы. В этом разделе мы определим обозначение радикалов и свяжем радикалы с рациональными показателями.

Мы также дадим свойства радикалов и некоторые распространенные ошибки, которые студенты часто делают с радикалами. Мы также определим упрощенную радикальную форму и покажем, как рационализировать знаменатель.
Полиномы. В этом разделе мы познакомим вас с основами полиномов — темой, которая будет появляться на протяжении всего курса. Мы определим степень многочлена и обсудим, как складывать, вычитать и умножать многочлены.
Факторные полиномы. В этом разделе мы рассмотрим факторинговые полиномы — тему, которая будет появляться почти в каждой главе этого курса, поэтому крайне важно, чтобы вы ее поняли. Мы обсудим разложение наибольшего общего множителя, разложение по группам, разложение на множители квадратичных чисел и разложение на множители многочленов со степенью больше 2.
Рациональные выражения. В этом разделе мы определим рациональные выражения. Мы обсудим, как сократить рациональное выражение до минимума и как складывать, вычитать, умножать и делить рациональные выражения.

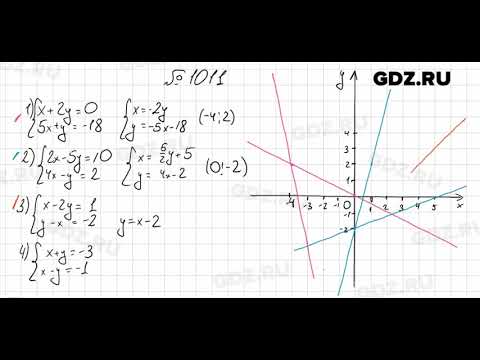
Комплексные числа. В этом разделе мы даем очень краткий обзор комплексных чисел, включая стандартную форму, их сложение, вычитание, умножение и деление.

Решение уравнений и неравенств. В этой главе мы рассмотрим одну из самых важных тем класса. Способность решать уравнения и неравенства жизненно важна для выживания в этом классе и на многих последующих математических занятиях, которые вы можете посещать. Мы обсудим решение линейных и квадратных уравнений, а также приложения. Кроме того, мы обсудим решение полиномиальных и рациональных неравенств, а также уравнений и неравенств с модулями.

Решения и наборы решений. В этом разделе мы вводим некоторые основные обозначения и идеи, связанные с решением уравнений и неравенств. Мы определяем решения для уравнений и неравенств и наборы решений.
Линейные уравнения. В этом разделе мы даем процесс решения линейных уравнений, включая уравнения с рациональными выражениями, и проиллюстрируем этот процесс несколькими примерами.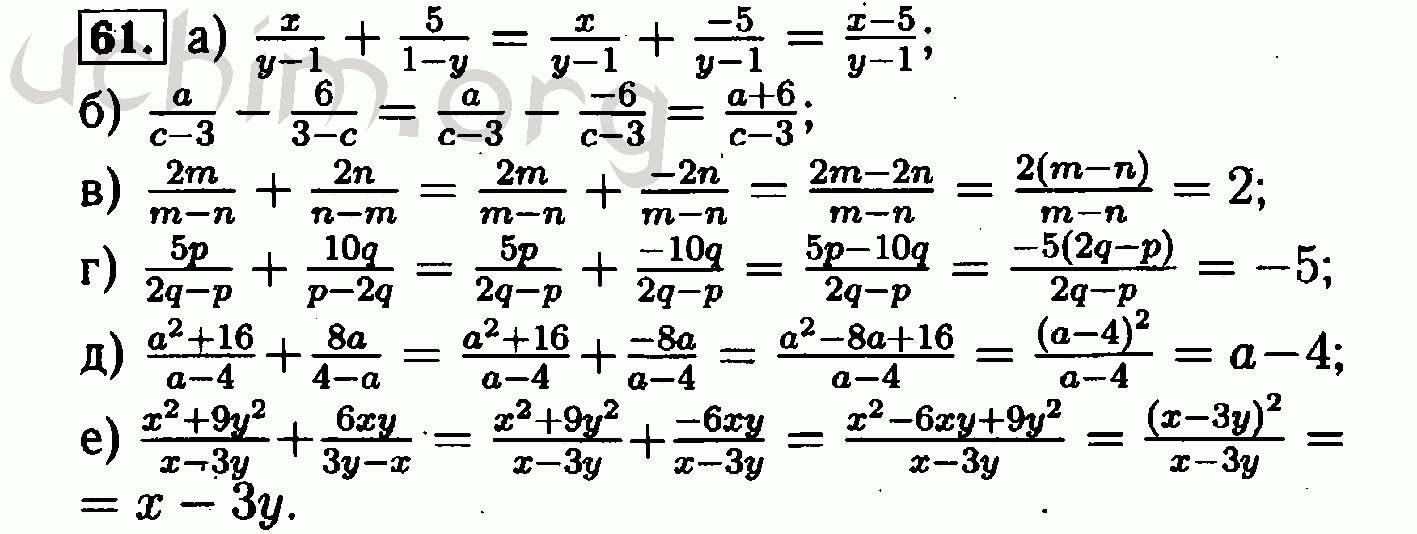 Кроме того, мы обсуждаем тонкость, связанную с решением уравнений, которую студенты часто упускают из виду.
Приложения линейных уравнений. В этом разделе мы обсуждаем процесс решения приложений в целом, хотя здесь мы сосредоточимся только на линейных уравнениях. Мы будем работать с приложениями по ценообразованию, проблемам расстояния / скорости, проблемам скорости работы и проблемам смешивания.
Уравнения с более чем одной переменной. В этом разделе мы рассмотрим решение уравнений с более чем одной переменной. В этих уравнениях будет несколько переменных, и нас попросят решить уравнение для одной из переменных. Это то, что нас будут просить делать на довольно регулярной основе.
Квадратные уравнения, часть I. В этом разделе мы начнем с решения квадратных уравнений. В частности, в этом разделе мы рассмотрим факторинг и свойство квадратного корня.
Квадратные уравнения, часть II. В этом разделе мы продолжим решать квадратные уравнения. Мы будем использовать завершение квадрата для решения квадратных уравнений в этом разделе и использовать его для вывода квадратной формулы.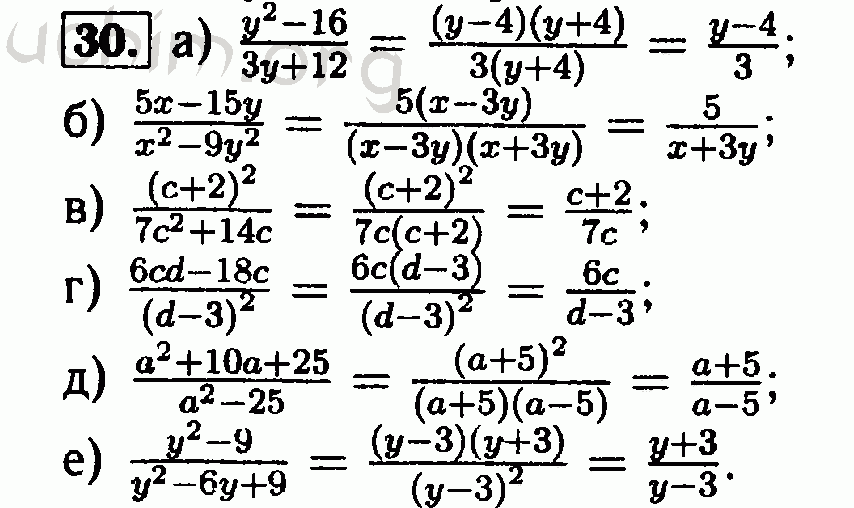 Квадратная формула — это быстрый способ, который позволит нам быстро решить любое квадратное уравнение.
Квадратные уравнения: Резюме. В этом разделе мы обобщим темы из двух последних разделов. Мы дадим процедуру определения того, какой метод использовать при решении квадратных уравнений, и определим дискриминант, который позволит нам быстро определить, какие решения мы получим при решении квадратного уравнения.
Приложения квадратных уравнений. В этом разделе мы вернемся к некоторым приложениям, которые мы видели в разделе линейных приложений, только на этот раз они будут включать решение квадратного уравнения. Включены примеры задач расстояния/скорости и задач скорости работы.
Уравнения, приводимые к квадратичной форме. Не все уравнения представляют собой то, что мы обычно считаем квадратными уравнениями. Однако некоторые уравнения при соответствующей подстановке можно превратить в квадратное уравнение. Уравнения такого типа называются квадратичными по форме. В этом разделе мы будем решать этот тип уравнения.
Уравнения с радикалами. В этом разделе мы обсудим, как решать уравнения с квадратными корнями. Как мы увидим, нам нужно быть очень осторожными с потенциальными решениями, которые мы получаем, поскольку процесс, используемый при решении этих уравнений, может привести к значениям, которые на самом деле не являются решениями уравнения.
Линейные неравенства. В этом разделе мы начнем решать неравенства. В этом разделе мы сосредоточимся на решении линейных неравенств (как одинарных, так и двойных). Мы также введем обозначение интервала.
Полиномиальные неравенства. В этом разделе мы продолжим решать неравенства. Однако в этом разделе мы отходим от линейных неравенств и переходим к решению неравенств, включающих многочлены степени не ниже 2.
Рациональные неравенства – Мы продолжаем решать неравенства в этом разделе. Теперь мы будем решать неравенства, включающие рациональные выражения, хотя, как мы увидим, процесс здесь в значительной степени идентичен процессу, используемому при решении неравенств с многочленами.
Уравнения абсолютного значения. В этом разделе мы дадим геометрическое, а также математическое определение абсолютного значения. Затем мы перейдем к решению уравнений, которые включают абсолютное значение. Мы также будем работать с примером, в котором используются два абсолютных значения.
Неравенства абсолютного значения. В этом заключительном разделе главы «Решение» мы будем решать неравенства, включающие абсолютное значение. Как мы увидим, процесс решения неравенства с \(<\) (т.е. меньше) сильно отличается от решения неравенства с \(>\) (т.е. больше).

Графики и функции. В этой главе мы рассмотрим две очень важные темы в классе алгебры. Во-первых, мы начнем обсуждение графических уравнений, введя декартову (или прямоугольную) систему координат и проиллюстрировав использование системы координат для построения линий и окружностей. Мы также формально определим функцию и обсудим графовые функции и комбинированные функции. Мы также обсудим обратные функции.

Графики. В этом разделе мы познакомимся с декартовой (или прямоугольной) системой координат. Мы определим/введем упорядоченные пары, координаты, квадранты и точки пересечения x и y. Мы проиллюстрируем эти концепции парой быстрых примеров 9.0077 Линии. В этом разделе мы обсудим графические линии. Мы введем понятие наклона и обсудим, как его найти по двум точкам на прямой. Кроме того, мы введем стандартную форму линии, а также форму точки-наклона и форму линии с пересечением наклона. Мы закончим раздел обсуждением параллельных и перпендикулярных прямых.
Круги — в этом разделе мы обсуждаем графические круги. Мы вводим стандартную форму окружности и показываем, как с помощью дополнения квадрата привести уравнение окружности к стандартной форме.
Определение функции. В этом разделе мы формально определим отношения и функции. Мы также даем «рабочее определение» функции, чтобы помочь понять, что такое функция. Мы вводим обозначения функций и работаем с несколькими примерами, иллюстрирующими, как это работает. Мы также определяем домен и диапазон функции. Кроме того, в этом разделе мы вводим кусочные функции.
Функции построения графиков. В этом разделе мы обсудим функции построения графиков, включая несколько примеров построения графиков кусочных функций.
Объединение функций. В этом разделе мы обсудим, как складывать, вычитать, умножать и делить функции. Кроме того, вводится понятие композиции функций.
Обратные функции. В этом разделе мы определяем взаимно однозначные и обратные функции. Мы также обсудим процесс, который мы можем использовать для нахождения обратной функции и проверки того, что функция, которую мы получаем в результате этого процесса, на самом деле является обратной функцией.

Общие графики. В этой главе мы рассмотрим построение графиков некоторых из наиболее распространенных функций, которые вам могут понадобиться. В этой главе мы рисуем параболы, эллипсы, гиперболы и рациональные функции. Мы также рассмотрим преобразования функций и введем понятие симметрии. 9{2}+к\).
Эллипсы. В этом разделе мы будем рисовать эллипсы. Мы представляем стандартную форму эллипса и способы ее использования для быстрого построения графика эллипса.
Гиперболы. В этом разделе мы будем рисовать гиперболы. Мы представляем стандартную форму гиперболы и то, как ее использовать для быстрого построения графика гиперболы.
Прочие функции. В этом разделе мы нарисуем несколько общих функций, которые на самом деле не требуют много работы, но потребуются в следующих разделах. Мы рассмотрим постоянную функцию, квадратный корень, абсолютное значение и простую кубическую функцию.
Преобразования. В этом разделе мы рассмотрим вертикальные и горизонтальные сдвиги графиков, а также отражения графиков относительно осей \(x\) и \(y\). В совокупности их часто называют преобразованиями, и если мы их понимаем, их часто можно использовать, чтобы позволить нам быстро построить график некоторых довольно сложных функций.
Симметрия. В этом разделе мы вводим понятие симметрии. Мы обсуждаем симметрию относительно оси x, оси y и начала координат, а также даем методы определения того, какой симметрией будет обладать график, если она вообще есть, без необходимости построения графика функции.
Рациональные функции. В этом разделе мы обсудим процесс построения графиков рациональных функций. Мы также познакомимся с понятиями вертикальных и горизонтальных асимптот, а также с тем, как определить, будут ли они иметься на графике рациональной функции.

Полиномиальные функции. В этой главе мы более подробно рассмотрим полиномиальные функции. Мы обсудим деление многочленов, нахождение нулей многочленов и построение графика многочленов. Мы также рассмотрим частичные дроби (хотя на самом деле это не касается полиномиальных функций).

Деление многочленов. В этом разделе мы рассмотрим некоторые основы деления многочленов. Мы определим остаток и делитель, используемые в процессе деления, и введем понятие синтетического деления. Мы также дадим алгоритм деления.
Нули/корни многочленов. В этом разделе мы определим ноль или корень многочлена и будет ли он простым корнем или имеет кратность \(k\). Мы также приведем Фундаментальную теорему алгебры и Факторную теорему, а также пару других полезных фактов.
Графики полиномов. В этом разделе мы опишем процесс, который позволит нам получить грубый набросок графика некоторых полиномов. Мы обсудим, как определить поведение графа на \(x\)-перехватах, и тест старшего коэффициента для определения поведения графа, когда мы допускаем неограниченное возрастание и убывание x.
Нахождение нулей многочленов. Как мы видели в предыдущем разделе, чтобы набросать график многочлена, нам нужно знать, что это за нули. Однако, если мы не можем разложить полином на множители, мы не сможем выполнить этот процесс. Итак, в этом разделе мы рассмотрим процесс с использованием теоремы о рациональном корне, который позволит нам найти некоторые нули многочлена, а в особых случаях — все нули.
Частичные дроби. В этом разделе мы рассмотрим процесс построения частичных дробей и нахождение разложения рационального выражения на неполные дроби. Здесь мы спросим, какие «меньшие» рациональные выражения мы добавили и/или вычли, чтобы получить данное рациональное выражение. Это процесс, который часто используется на некоторых более поздних уроках математики. Например, это может проявляться в исчислении и дифференциальных уравнениях.

Экспоненциальные и логарифмические функции. В этой главе мы представим две очень важные функции во многих областях: экспоненциальные и логарифмические функции. Мы рассмотрим их основные свойства, приложения и решение уравнений, включающих две функции. Если вы работаете в сфере, связанной с наукой или инженерным делом, вы столкнетесь с обеими этими функциями. 9{Икс}\).
Функции логарифмирования. В этом разделе мы познакомимся с функциями логарифмирования. Приводятся основные свойства и графики логарифмических функций. Кроме того, мы обсудим, как вычислять некоторые основные логарифмы, включая использование формулы замены основания. Мы также обсудим десятичный логарифм \(\log(x)\) и натуральный логарифм \(\ln(x)\).
Решение экспоненциальных уравнений. В этом разделе мы обсудим несколько методов решения уравнений, содержащих экспоненты.
Решение уравнений с логарифмами. В этом разделе мы обсудим несколько методов решения уравнений, содержащих логарифмы. Кроме того, как мы увидим, с одним из методов нам нужно быть осторожными с результатами метода, поскольку всегда возможно, что метод дает значения, которые на самом деле не являются решениями уравнения. Приложения
. В этом разделе мы рассмотрим несколько приложений экспоненциальных функций и приложение логарифмов. Мы смотрим на сложные проценты, экспоненциальный рост и распад и интенсивность землетрясений.

Системы уравнений. В этой главе мы рассмотрим решение систем уравнений. Мы будем решать как линейные, так и нелинейные системы уравнений. Мы также кратко рассмотрим использование расширенных матриц для решения линейных систем уравнений.

Линейные системы с двумя переменными. В этом разделе мы будем решать системы с двумя уравнениями и двумя переменными. Мы будем использовать метод подстановки и метод исключения для решения систем в этом разделе. Введем также понятия несовместных систем уравнений и зависимых систем уравнений.
Линейные системы с тремя переменными. В этом разделе мы рассмотрим несколько быстрых примеров, иллюстрирующих, как использовать метод подстановки и метод исключения, представленные в предыдущем разделе, применительно к системам из трех уравнений.
Расширенные матрицы. В этом разделе мы рассмотрим еще один метод решения систем. Введем понятие расширенной матрицы. Это позволит использовать метод исключения Гаусса-Жордана для решения систем уравнений. Мы будем использовать метод с системами двух уравнений и системами трех уравнений.
Подробнее о расширенной матрице. В этом разделе мы еще раз вернемся к случаям противоречивых и зависимых решений систем и к тому, как их идентифицировать с помощью метода расширенной матрицы.