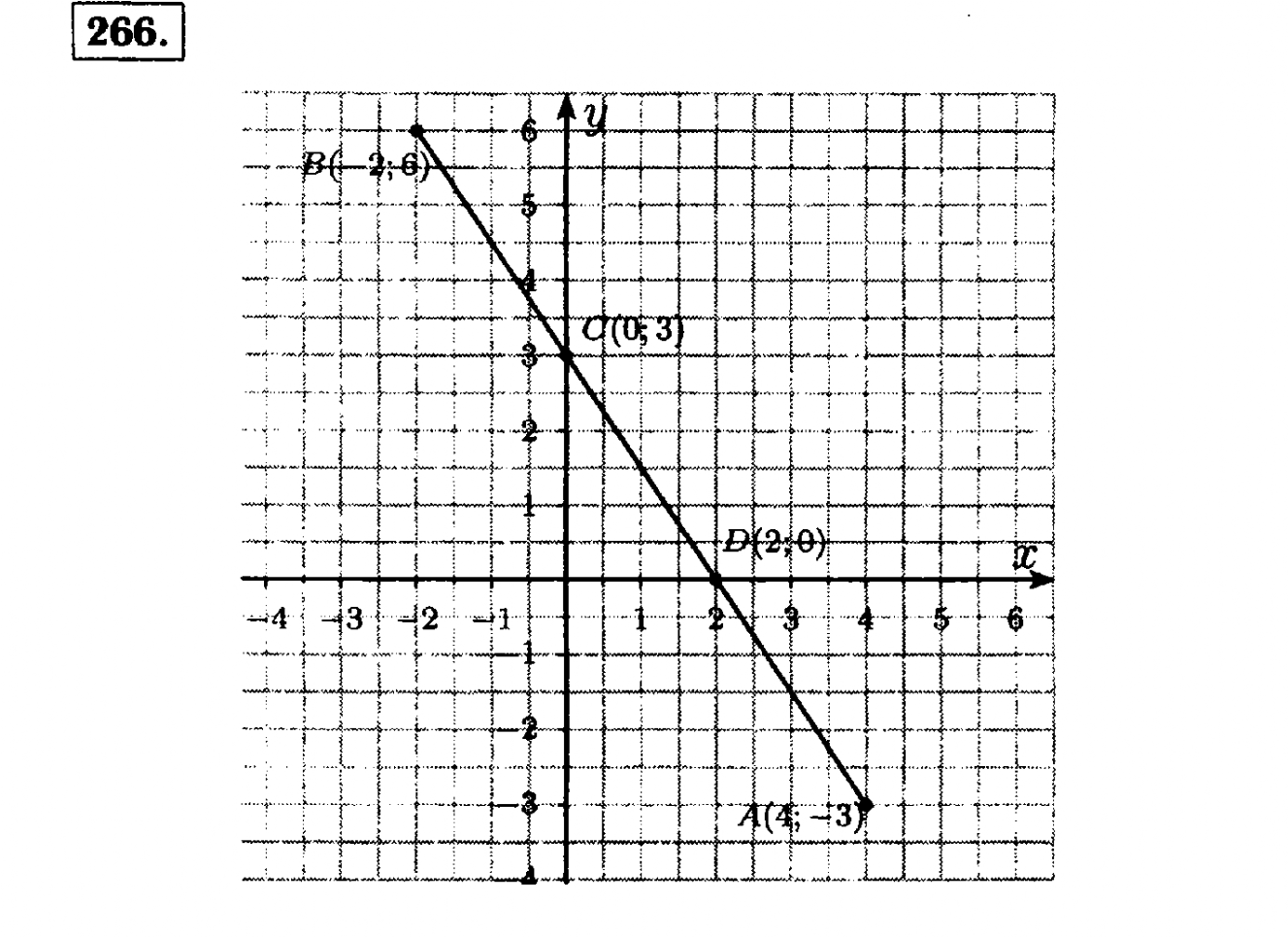
ГДЗ номер 266 алгебра 7 класс Макарычев, Миндюк
Решение есть!- 1 класс
- Математика
- Английский язык
- Русский язык
- Литература
- Окружающий мир
- 2 класс
- Математика
- Английский язык
- Русский язык
- Немецкий язык
- Информатика
- Литература
- Окружающий мир
- Технология
- 3 класс
- Математика
- Английский язык
- Русский язык
- Немецкий язык
- Информатика
- Литература
- Окружающий мир
- Казахский язык
- 4 класс
- Математика
- Английский язык
- Русский язык
- Немецкий язык
- Информатика
- Музыка
- Литература
- Окружающий мир
- Казахский язык
- 5 класс
- Математика
- Английский язык
- Русский язык
ГДЗ упражнение 266 алгебра 10‐11 класс Алимов, Колягин
Решение есть!- 1 класс
- Математика
- Английский язык
- Русский язык
- Литература
- Окружающий мир
- 2 класс
- Математика
- Английский язык
- Русский язык
- Немецкий язык
- Музыка
- Литература
- Окружающий мир
- Технология
- 3 класс
- Математика
- Английский язык
- Русский язык
- Немецкий язык
- Информатика
- Музыка
- Литература
- Окружающий мир
- Казахский язык
- 4 класс
- Математика
- Английский язык
- Русский язык
- Немецкий язык
- Информатика
- Музыка
- Литература
- Окружающий мир
- Казахский язык
- 5 класс
- Математика
- Английский язык
- Русский язык
Номер (задание) 266 — гдз по алгебре 7 класс Макарычев, Миндюк
Решебники, ГДЗ
- 1 Класс
- Математика
- Русский язык
- Английский язык
- Информатика
- Немецкий язык
- Литература
- Человек и мир
- Природоведение
- Основы здоровья
- Музыка
- Окружающий мир
- Технология
- 2 Класс
- Математика
- Русский язык
- Белорусский язык
- Английский язык
- Информатика
- Украинский язык
- Французский язык
- Немецкий язык
- Литература
- Человек и мир
Номер (задание) 266 — гдз по алгебре 9 класс Макарычев, Миндюк
Решебники, ГДЗ
- 1 Класс
- Математика
- Русский язык
- Английский язык
- Информатика
- Немецкий язык
- Литература
- Человек и мир
- Природоведение
- Основы здоровья
- Музыка
- Окружающий мир
- Технология
- 2 Класс
- Математика
- Русский язык
- Белорусский язык
Как выполнить распределение в алгебре
- Образование
- Математика
- Алгебра
- Как выполнить распределение в алгебре
Распределение предметов — это акт их равномерного распределения.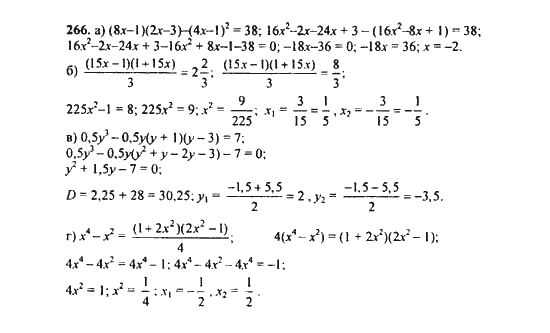 Алгебраическое распределение означает умножение каждого члена в скобках на другой член вне скобок. Чтобы распределить термин между несколькими другими терминами, вы умножаете каждый из остальных членов на первый член.
Алгебраическое распределение означает умножение каждого члена в скобках на другой член вне скобок. Чтобы распределить термин между несколькими другими терминами, вы умножаете каждый из остальных членов на первый член.
Распределение включает в себя умножение каждого отдельного термина в сгруппированном ряду терминов на термин вне группы.
a ( b + c ) = a × b + a × c
a ( b — c ) = a × b — a × c
Термин состоит из переменной (ей) и / или числа (ей), соединенных путем умножения и / или деления. Термины отделяются друг от друга сложением и / или вычитанием.
Пример 1 : Распределите число 2 над членами в скобках в выражении, 2 (4 x + 3 y — 6).
Умножьте каждый член на число (а) и / или переменную (ы) вне скобок.
2 (4 x ) + 2 (3 y ) — 2 (6)
Выполните операцию умножения в каждом члене.

8 x + 6 y — 12
Пример 2: В конкретном автосалоне пять продавцов A, B, C, D и E продали 2, 8, 6, 5 и 9 автомобилей в прошлом месяце соответственно, в общей сложности 30 вагонов (2 + 8 + 6 + 5 + 9).Владелец автосалона хочет удвоить продажи в этом месяце; он хочет, чтобы его сотрудники продали в общей сложности 60 автомобилей. Если каждый продавец удваивает то, что он продал в прошлом месяце, посмотрите, что произойдет.
Умножьте каждый член на число (а) и / или переменную (ы) вне скобок.
2 (2 + 8 + 6 + 5 + 9) = 2 (2) + 2 (8) + 2 (6) + 2 (5) + 2 (9)
Выполните операцию умножения и сложите каждый член.
4 + 16 + 12 + 10 + 18 = 60 автомобилей
Ответ, конечно же, один и тот же, независимо от того, распространяете ли вы в первую очередь или добавляете то, что указано в скобках.Вы должны сделать это суждение.
Калькуляторы линейной алгебры — eMathHelp
Калькулятор найдет обратную квадратную матрицу, используя метод исключения Гаусса, с указанными шагами.
Онлайн-калькулятор для определения величины вектора с указанными шагами.
Онлайн-калькулятор для нахождения векторного произведения двух векторов с указанными шагами.
Онлайн-калькулятор для нахождения скалярного (внутреннего) произведения двух векторов с указанными шагами.
Калькулятор найдет произведение двух матриц (если возможно) с указанными шагами.Он перемножает матрицы любого размера до 10х10.
Калькулятор найдет определитель матрицы (2×2, 3×3 и т.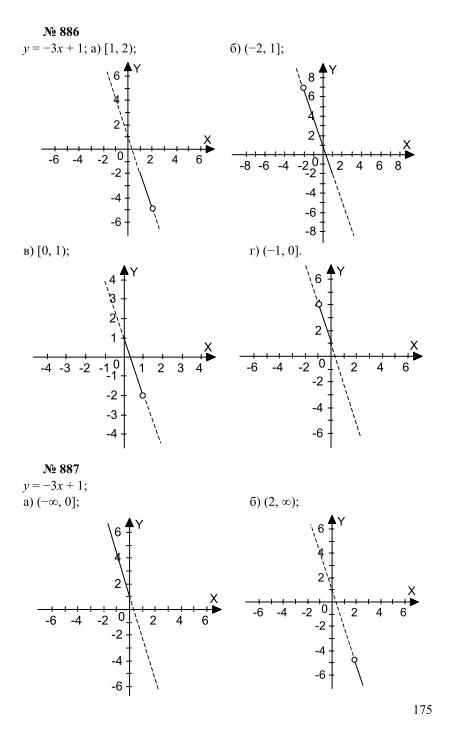 Д.) С указанными шагами.
Д.) С указанными шагами.
Калькулятор найдет эшелонированную форму строки (простую или сокращенную — RREF) данной (расширенной) матрицы (с переменными, если необходимо), с указанными шагами.
Калькулятор найдет собственные значения и собственные векторы (собственное подпространство) данной квадратной матрицы с указанными шагами.
Этот решатель будет складывать, вычитать, умножать, делить и возводить в степень две матрицы с указанными шагами. Он также найдет определитель, инверсию, rref (сокращенная форма эшелона строк), пустое пространство, ранг, собственные значения и собственные векторы.
Калькулятор найдет пустое пространство данной матрицы с указанными шагами.
Калькулятор найдет угол (в радианах и градусах) между двумя векторами и покажет результат.
Калькулятор выполнит исключение Гаусса для данной расширенной матрицы с указанными шагами.По желанию возможно полное сокращение.
Калькулятор найдет характеристический многочлен данной матрицы с указанными шагами.
Калькулятор найдет матрицу сомножителей данной квадратной матрицы с указанными шагами.
Калькулятор найдет сопряженную (сопряженную, вспомогательную) матрицу данной квадратной матрицы с указанными шагами.
Калькулятор найдет транспонирование данной матрицы с указанными шагами.
Калькулятор диагонализирует данную матрицу с указанием шагов.
Этот калькулятор ортонормирует набор векторов с помощью процесса Грама-Шмидта с указанными шагами.
90+ курсов алгебры и геометрии [2021] | Учиться онлайн бесплатно
Лучшие онлайн-курсы года
Посмотреть Закрыть Класс Центральный КурсыСубъекты
Компьютерная наука
Здоровье и медицина
Математика
Бизнес
Гуманитарные науки
Инженерное дело
Наука
Образование и обучение
Социальные науки
Арт Дизайн
Data Science
Программирование
Личное развитие
- Все предметы
Ежемесячные отчеты о курсе
- Начиная с этого месяца
- Новые онлайн-курсы
- Самостоятельный темп
- Самый популярный
Меню
Компьютерная наука
Компьютерная наука
- Искусственный интеллект
- Алгоритмы и структуры данных
- Интернет вещей
- Информационные технологии
- Кибербезопасность
- Компьютерная сеть
- Машинное обучение
- DevOps
- Глубокое обучение
- Блокчейн и криптовалюта
- Квантовые вычисления
- Посмотреть все компьютерные науки
Здоровье и медицина
Здоровье и медицина
- Питание и благополучие
- Болезни и расстройства
- Здравоохранение
- Здравоохранение
- Уход
- Анатомия
- Ветеринария
- Посмотреть все Здоровье и медицина
Математика
Математика
- Статистика и вероятность
- Основы математики
- Исчисление
- Алгебра и геометрия
- Посмотреть всю математику
Бизнес
Бизнес
- Менеджмент и лидерство
- Финансы
- Предпринимательство
- Развитие бизнеса
- Маркетинг
- Стратегический менеджмент
- Специфическая отрасль
- Бизнес-аналитика
- Бухгалтерский учет
- Отдел кадров
- Управление проектом
- Продажи
- Дизайн-мышление
Алгебра — Приложения
Онлайн-заметки ПавлаНоты Быстрая навигация Скачать
- Перейти к
- Ноты
- Проблемы с практикой
- Проблемы с назначением
- Показать / Скрыть «> Показать все решения / шаги / и т. Д.
- Скрыть все решения / шаги / и т. Д.
- Разделы
- Решение логарифмических уравнений
- Системы уравнений Введение
- Разделы
- Полиномиальные функции
- Системы уравнений
- Классы
- Алгебра
- Исчисление I
- Исчисление II
- Исчисление III
- Дифференциальные уравнения
- Дополнительно
- Алгебра и триггерный обзор
- Распространенные математические ошибки
- Праймер комплексных чисел
- Как изучать математику
- Шпаргалки и таблицы
- Разное
- Свяжитесь со мной
- Справка и настройка MathJax
- Мои студенты
- Заметки Загрузки
- Полная книга
- Текущая глава
- Текущий раздел
- Practice Problems Загрузок
- Полная книга — Только проблемы
- Полная книга — Решения
- Текущая глава — Только проблемы
- Текущая глава
Викиучебники, открытые книги для открытого мира
Предисловие [править]
Эта книга требует, чтобы вы сначала прочитали Арифметика . |
Алгебра — это раздел математики, касающийся изучения правил операций и отношений, а также возникающих из них конструкций и понятий, включая термины, многочлены, уравнения и алгебраические структуры.
Вас попросили купить арахис для вас и ваших друзей на футбольном матче. Вы собрали 12,50 долларов. Одна сумка стоит 2,75 доллара. Вы хотите знать, сколько сумок вы можете купить. Это проблема алгебры! Связанные с этим проблемы заключаются в том, сколько денег останется, и что вам следует купить или в каких пропорциях вы должны вернуть лишние деньги своим друзьям.
Алгебра помогает нам предсказывать то, чего мы еще не знаем, и определять отношения между тем, что мы делаем. Алгебра — это мощный и богатый раздел математики, который полезен в повседневной жизни, а также в бизнесе, инженерии и других технических областях.
Содержание [править]
Введение в математику [править]
- Об этой книге
- Что такое математика? — А какое мне дело?
- Кому следует прочитать эту книгу — И чего ожидать
Числа, переменные и отношения [править]
Как мы можем использовать числа и переменные, чтобы узнать неизвестную информацию?
- Обзор
- Элементарная арифметика
- Порядок операций
- Числа и переменные
- Алгебра и свойства действительных чисел
- Раздел не коммутативен
- Правила экспонент
- Корни и радикалы
- Переменные
- Наборы
- Уравнения с одной переменной
- Что такое уравнения?
- Решение уравнений с одной переменной
- Проблемы со словами
- Неравенства
- Различные типы отношений
- Обозначение интервалов и интервалы построения графиков
- Решение неравенств
Линейные функции Введение в построение графиков [править]
Математика — это метод решения задач. Вы берете информацию, которую знаете, и, манипулируя ею, используя математические принципы, вы можете найти информацию, которую не знаете. Функции — это математическая основа для решения проблем. У них есть параметры, правила и способы решения. В этом разделе вы познакомитесь с общими функциями и их использованием.
Вы берете информацию, которую знаете, и, манипулируя ею, используя математические принципы, вы можете найти информацию, которую не знаете. Функции — это математическая основа для решения проблем. У них есть параметры, правила и способы решения. В этом разделе вы познакомитесь с общими функциями и их использованием.
- Введение в линейные функции
- Функции
- Графические линейные функции
- Координатная (декартова) плоскость
- Линейные уравнения и функции
- Пересечения X и Y
- Наклон
- Стандартная форма и решающий уклон
- Графики неравенств
- Теорема Пифагора и формула расстояния
- Абсолютное значение
- Системы уравнений
- Неравенства составных и абсолютных значений
- Графические системы неравенств
- Другие типы графов
Полиномы [править]
- Полиномы
- Факторинговые многочлены
- Завершение площади
- Квадратный корень положительный (Подлежит объединению)
- Квадратичная формула
- Кубическая формула
- Биномиальная теорема
Графические полиномы [править]
- Подробнее о графике
- Графические полиномы
- Инверсии функций
- Составные и абсолютные неравенства для многочленов
- Графические системы неравенств для многочленов
Последовательности и серии [править]
- Введение в последовательности и серии
- Арифметическая прогрессия (AP)
- Геометрическая прогрессия (GP)
- Гармоническая прогрессия (HP)
Конические сечения [править]
- Конические секции
- Круг
- Эллипс
- Парабола
- Гипербола
Комплексные числа [править]
- Комплексные числа
- Подробнее о квадратичной формуле
- Подробнее о полиномах.

Элементарная вероятность и статистика [править]
- Введение в вероятность и статистику
- Вероятность
- Статистика
- Точечные диаграммы
Текущая работа по объединению [править]
ДЕЛАТЬ
Исправить алгебру для вопросов и ответов в разделе пропорций или соотношений
Сложить задачи по умножению
Добавить текстовые задачи к разделению
Добавить текстовые задачи к показателям
Добавить задачи к корням
Добавить проблемы со словами для возможных взаимосвязей как части неравенства
Добавить графику для умножения на 1 и -1 к описанию особого случая умножения на -1
Добавить описание для особого случая Возвращаясь к равенству
Пример заполнения функции половины площади
Исправить содержание, прояснить объяснение
Переместите Todos сюда… или заполните их
Почему использовать стандартную форму вместо формы пересечения наклона? Нужно больше контекста.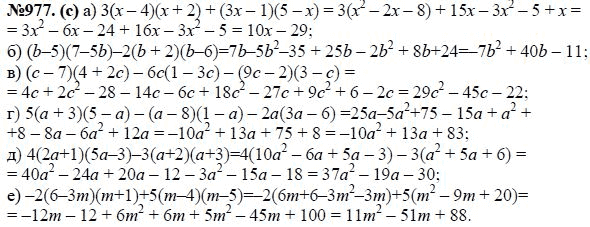
Продолжить создание ссылок между страницами.
Продолжить создание стандартного заголовка алгебры … Продолжить до содержания
Прыжок в изысканности … Конец разговорного тона. Нужно сделать дружелюбнее, проще
Подлежит объединению / несортировано
- В этой книге
- Теория
- Итерация
- Stemplots (Мы хотим этого?)
- Обсуждение: Алгебра / ToInclude
- Арифметические / числовые аксиомы (Осиротел из-за книги, должен следить за другими)
- Equalities and Inequalities (Осиротел из книги)
- Алгебра
- Квадратичные функции
- Решение уравнений
- Теория уравнений
- Перенаправить на другую книгу (почему?)
- Логарифмы
- Закрытие
Двоичные, восьмеричные и шестнадцатеричные числа
| Динарный (с основанием 10) | Шестнадцатеричный (с основанием 16) | Восьмеричный (с основанием 8) | Двоичный (с основанием 2) 5 | 0 1 2 3 4 5 6 7 8 A B C D E F | 000 001 002 003 004 005 006 007 010 011 012 013 014002 013 014 907 000016 0154 015 00000010 00000011 00000100 00000101 00000110 00000111 00001000 00001001 00001010 00001011 00001100 00001101 00001110 907 907 00001111 9055 1955 9044 9055 20 21 22 23 24 25 26 27 28 29 30 31 | 10 11 12 13 14 15 16 17 18 19 1A 907 1A 907 1D 1E 1F | 020 021 022 023 024 025 026 027 030 031 032 033 034 035
00010101 00010110 00010111 00011000 00011001 00011010 00011011 00011100 00011101 00011110 00011111 |
|---|---|---|---|
| 32 3655 9055 9055 9055 9055 9055 9055 3955 9055 9055 9055 9055 9055 9055 44 45 46 47 | 20 21 22 23 24 25 26 27 28 29 2A 2B 2C 2D 2E 2F | 904 42 040 00100000 00100101007 | 00100000 9055 00100101007 9055 9055 0010001007 9055 00101000 00101001 00101010 00101011 00101100 00101101 00101110 00101111 |
| 48 49 50 51 52 53 9055 54 907 9055 9055 9055 63 907 567 9055 | 30 31 32 33 34 35 36 37 38 39 3A 3B 3C 3D 3E 3F | 060 065 065755 055 063 070 071 072 073 074 075 076 077 | 00110000 00110001 00110010 00110011 00110100 00110101 00110 110 00110111 00111000 00111001 00111010 00111011 00111100 00111101 00111110 00111111 |
| 64 73 65 66 67 907 9055 71 78 79 | 40 41 42 43 44 45 46 47 48 49 4A 4B 4C 4D 4E 4F | 100 1047 103 102 106 107 110 111 112 113 114 115 116 117 | 01000000 01000001 01000010 01000011 0110100 01000101 01000110 01000001100 01000110 01000001100 01000110 01000001100 01001110 01001111 |
| 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 | 50 51 52 53 54 55 56 57 58 59 5A 5B 5C 5D 5E 5F 122 | 123 124 125 126 127 130 131 132 133 134 135 136 137 | 01010000 01010001 01010010 01010011 0101010055 0101010055 01011100 01011101 01011110 01011111 |
| 96 97 98 99 100 101 102 103 104 105 106 107 9055 108 1107 9055 9055 62109 9055 63 64 65 66 67 68 69 6A 6B 6C 6D 6E 6F | 140 141 142 143 144 145 146 147 150 151 152 153 154 155 156 157 | 01100000 01100001 01100010 01100011 01100100 01100101 01100110 01100111 01101000 01101001 01101010 01101011 01101100 01101101 01101110 01101111 | |
| 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 5 73 907 907 907 | 160 161 162 163 164 165 166 167 907 907 177 9055 17055 177 9055 17055 175 176 177 | 01110000 01110001 01110010 01110011 01110100 01110101 01110110 01110111 01111000 90 755 01111001 01111010 01111011 01111100 01111101 01111110 01111111 | |
| 128 129 130 131 132 133 9055 134 147 907 1407 135 132 133 9055 134 907 907 1407 135 907 | 80 81 82 83 84 85 86 87 88 89 8A 8B 8C 8D 8E 8F | 200 201 202 203 907 204 210 211 212 213 214 215 216 217 | 10000000 10000001 10000010 10000011 10000100 10000101 10000110 10000111 1000107 100011110 10000111 1000107 1000111 1055 |
| 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 | 90 91 92 93 94 95 96 97 98 99 9A 9B 9C 9D 9E 9F | ||
| 10010000 10010001 10010010 10010011 10010100 10010111 9055 10010111 9055 100755 10010111 9055 10010111 9055 10010111 9055 10011101 10011110 10011111 | |||
| 160 161 162 163 164 165 166 167 168 169 170 A2 171 907 172 907 907 1755 A1 907 172 907 1755 A4 A5 A6 A7 A8 A9 AA AB AC AD AE AF | 240 241 242 243 244 245 246 247 250 251 252 253 254 255 256 257 | 10100000 10100001 10100010 10100011 10100100 101001010101 10100100 10100101010101 10100100 101001010101 101001 10101110 10101111 | |
| 176 177 178 179 180 181 182 183 184 185 186 187 188 18955 907 907 907 907 907 907 9055 В2 B5 B6 B7 B8 B9 BA BB BC BD BE BF | 260 261 262 263 264 265 266 9055 9055 267 907 2755 2755 9055 2707 907 2755 2755 2707 907 2755 2755 275 276 277 | 10110000 10110001 10110010 10110011 10110100 10110101 10110110 10110111 10111000 90 755 10111001 10111010 10111011 10111100 10111101 10111110 10111111 | |
| 192 193 194 195 196 197 19855 907 907 907 907 907 907 19855 907 907 907 907 907 907 | C0 C1 C2 C3 C4 C5 C6 C7 C8 C9 CA CB CC CD CE CF | 300 301 304 3055 907 307 307 307 307 307 307 307 307 307 307 307 307 303 310 311 312 313 314 315 316 317 | 11000000 11000001 11000010 11000011 11000100 11000101 11000110 11000111 11001000 11001001 11001010 11001011 11001100 11001101 11001110 11001111 |
| 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 | D0 D1 D2 D3 D4 D5 D6 D7 D8 D9 DA DB DC 322 DD DE 907 9055 DF 324 325 326 327 330 331 332 333 334 335 336 337 | 11010000 11010001 11010010 11010011 11010100 11055 1101011011 11055 110101 11010101 11055 1101011 11055 110101 11011101 11011110 11011111 | |
| 224 225 226 227 228 229 230 231 232 233 234 235 236 902 902 234 235 236 902 907 E4 E5 E6 E7 E8 E9 EA EB EC ED EE EF | 340 341 342 343 344 345 346 347 350 351 352 353 354 355 356 357 | 11100000 11100001 11100010 11100011 11100100 11100101 11100110 11100111 11101000 11101001 11101010 11101011 11101100 11101101 11101110 11101111 | |
| 240 241 242 243 244 245 246 247 248 249 250 251 252 253 251 252 253 904 251 252 253 254 F5 F6 F7 F8 F9 FA FB FC FD FE FF | 360 361 362 363 364 365 366 367 907 3755 9055 9055 366 367 907 9055 375 376 377 | 11110000 11110001 11110010 11110011 11110100 11110101 11110110 11110111 11111000 90 755 11111001 11111010 11111011 11111100 11111101 11111110 11111111 |
- Denary — Денарная система счисления (десятичная) — это система счисления 9000 с основанием 10 для 9000, используемая людьми с 9000 9000.
 Восьмеричная система счисления — восьмеричная система счисления (Oct) — это система счисления с основанием 8, в которой используются цифры от 0 до 7
Восьмеричная система счисления — восьмеричная система счисления (Oct) — это система счисления с основанием 8, в которой используются цифры от 0 до 7 - Шестнадцатеричный — Шестнадцатеричная система счисления (Hex) — это система счисления с основанием 16, использующая цифры от 0 до 9 и буквы A. — F
- Двоичная — Двоичная система счисления (Bin) — это система счисления с основанием 2, использующая числа 1 и 0
Преобразование двоичного числа в десятичное
В десятичной системе счисления используется основание 10.
Динарное (десятичное) число может быть выражено как
10,5
= 1 x 10 1 + 0 x 10 0 + 5 x 10 -1
В двоичной системе счисления основание 2.
Двоичное число может быть выражено как
1011,1
= 1 x 2 3 + 0 x 2 2 + 1 x 2 1 + 1 x 2 0 + 1 x 2 -1
= 8 + 0 + 1 + 1 + 1/2
= 10.



 Восьмеричная система счисления — восьмеричная система счисления (Oct) — это система счисления с основанием 8, в которой используются цифры от 0 до 7
Восьмеричная система счисления — восьмеричная система счисления (Oct) — это система счисления с основанием 8, в которой используются цифры от 0 до 7