Деление числа в данном отношении: Деление числа в данном отношении + задачи с решением

Деление числа в данном отношении | Мел

На практике и в курсе математики довольно часто приходится делить число (величину) в данном отношении. Такие задачи решают на ЕГЭ, решали и в глубокой древности. Начнём с задачи из Древнего Египта.

Задача 1. Число и его половина составляют 9. Найдите число.

Решение. Пусть половина числа составляет 1 часть, тогда само число — 2 такие же части, так как число в 2 раза больше своей половины.

1) 1 + 2 = 3 (части) — приходится на число и его половину,

2) 9: 3 = 3 (единицы) — приходится на 1 часть, это половина числа,

3) 3 * 2 = 6 (единиц) — приходится на число.

Ответ. 6.

Изменим условие задачи на части — получим задачу на деление числа в данном отношении.

Задача 2. Разделите число 9 в отношении 2: 1. Найдите полученные числа.

Решение задачи записано выше. Сделаем вывод в виде правила, которому можно следовать при решении других задач, меняя число и члены отношения.

Чтобы число 9 разделить в отношении 2: 1, надо это число разделить на сумму членов отношения и результат умножить на каждый член отношения.

Запишем решение задачи по новому правилу.

Решение. 1) 9: (2 + 1) * 2 = 6 — большее число,

2) 9: (2 + 1) * 1 = 3 — меньшее число.

Разумеется, меньшее число можно было найти вычитанием: 9 — 6 = 3.

Ответ. 6 и 3.

Задача 3. Брат и сестра разделили 35 конфет в отношении 3: 4. Брату досталась меньшая часть. Сколько конфет досталось сестре?

Решение. 1) 35: (3 + 4) * 3 = 15 (конфет) — досталось брату,

2) 35 — 15 = 20 (конфет) — досталось сестре.

Ответ. 20 конфет.

Задача 4. Малыш и Карлсон разделили 16 плюшек в отношении 3: 5. Сколько плюшек досталось Карлсону, если Малышу досталось меньше плюшек?

Решение. 1) 16: (3 + 5) * 3 = 6 (плюшек) — досталось Малышу,

2) 16 — 6 = 10 (плюшек) — досталось Карлсону.

Ответ. 10 плюшек.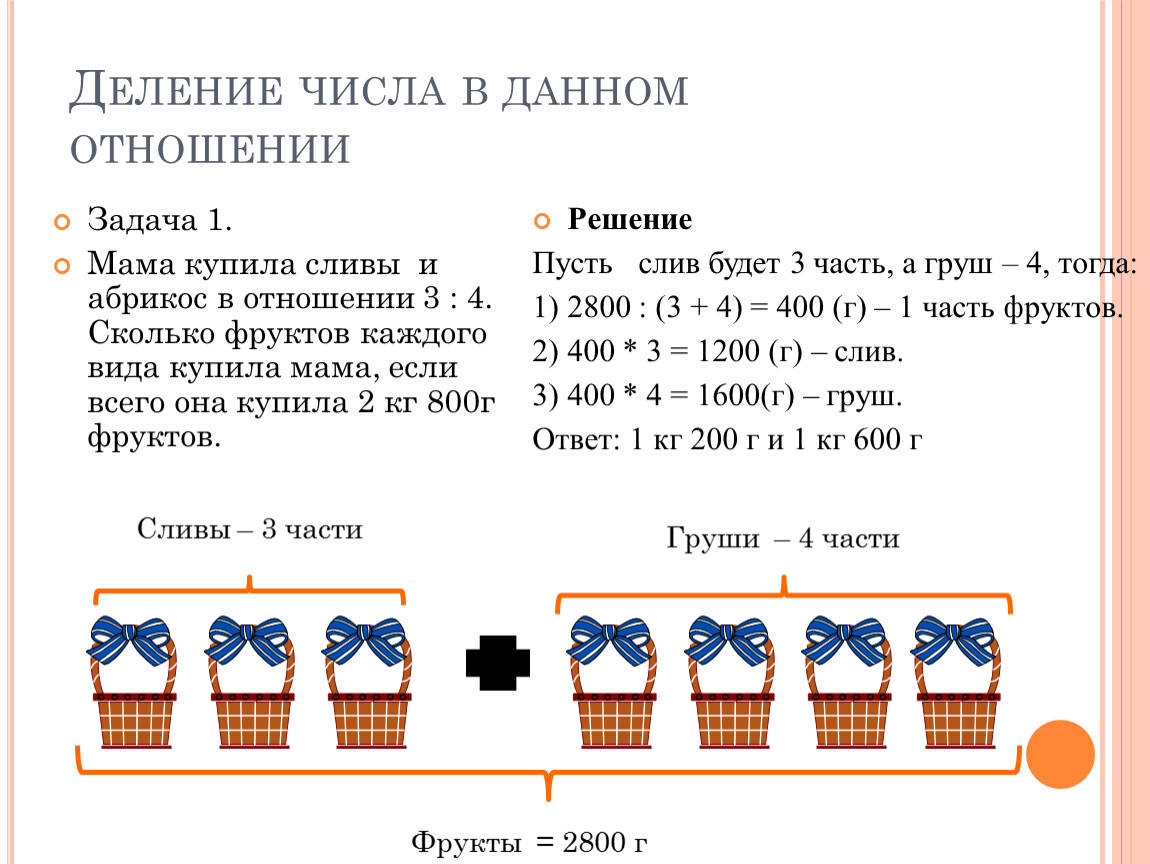

Задача для ребят постарше.

Задача 5. В треугольнике три стороны имеют длину 8, 10 и 12. На какие отрезки биссектриса треугольника делит среднюю его сторону?

Решение. Биссектриса треугольника делит его сторону на части, пропорциональные двум другим сторонам треугольника, то есть в отношении 8: 12 = 2: 3. Разделим сторону 10 в отношении 2: 3.

1) 10: (2 + 3) * 2 = 4 — длина меньшей части,

2) 10 — 4 = 6 — длина большей части.

Ответ. 4 и 6.

На ЕГЭ базового уровня в 2018 году была такая задача.

Задача 6. Маша и Медведь съели 110 печений и банку варенья, начав и закончив одновременно. Сначала Маша ела варенье, а Медведь — печенье, но в какой-то момент они поменялись. Медведь и то, и другое ест в три раза быстрее Маши. Сколько печений съел Медведь, если варенья они съели поровну?

http://fipi.ru/sites/default/files/document/1535625213/matematika_2018.pdf

Решение. Так как варенья они съели поровну, а Медведь ест варенье в 3 раза быстрее Маши, то на варенье Медведь потратил времени в 3 раза меньше, чем Маша. Печенье Медведь ел в 3 раза больше времени, чем Маша, которая в это время ела варенье. Так как скорость поедания печенья у Медведя в 3 раза больше, чем у Маши, то Медведь съел печенья в 3*3 = 9 раз больше, чем Маша. Делим 110 печений в отношении 9: 1.Медведь съел 110: (9 + 1)*9 = 99 (печений).

Ответ. 99 печений.

Авторы комментариев ФИПИ к результатам ЕГЭ отметили, что в группе хорошо подготовленных к сдаче экзамена на базовом уровне решили эту задачу менее половины выпускников, включенных в эту группу. При этом предполагалось, что задачу будут решать составлением уравнения. Как показано выше, задачу можно решить и арифметически.

Деление числа в данном отношении

Представим себе такую историю…

– Саша, чем ты занимаешься? – поинтересовался у друга Паша.

– Хочу приготовить мороженое, – ответил Саша. – Уже и рецепт нашёл, и подготовил все ингредиенты, но вот только разобраться не могу, сколько чего брать.

– А что в рецепте написано? – уточнил Паша.

– В рецепте сказано, что для приготовления мороженого нужно смешать 3 части молока, 2 части сливок и 1 часть сахара, – прочитал Саша. – А как эти части высчитать, если я хочу приготовить, например, 3 килограмма мороженого?

– И вправду, сложная задача у тебя получается, – задумался Паша. – Как эти части считать, не понятно. Но я знаю, кто нам сможет помочь!

– Ребята, прежде чем я отвечу на ваш вопрос, давайте немного разомнёмся и выполним устные задания, – предложил Мудряш.

– Давайте сверимся! – сказал Мудряш. — Посмотрите, что у вас должно было получиться!

– Ну а теперь вернёмся к вашему вопросу, – начал Мудряш. – Чтобы ответить на вопрос «Сколько каких ингредиентов нужно взять для приготовления смеси мороженого?», прежде всего нужно научиться выполнять деление числа в данном отношении. Итак, вы хотите приготовить 3 килограмма мороженого. Для удобства давайте переведём килограммы в граммы, всё же так будет легче и привычнее считать.

– Так как 1 килограмм равен 1000 грамм, – стал размышлять Саша, – значит, я хочу приготовить 3000 грамм мороженого.

– Хорошо! – согласился Мудряш. – По рецепту для приготовления мороженого нужно смешать 3 части молока, 2 части сливок и 1 часть сахара. Будем считать, что смесь мороженого состоит из  частей, имеющих одинаковые массы. Тогда как посчитать, сколько приходится на 1 часть?

– Нужно 3000 разделить на 6, – ответил Паша.

– Правильно! – сказал Мудряш. – Значит, масса одной части смеси равна 500 граммам. По рецепту молоко в смеси составляет 3 части, сливки – 2 части, а сахар – 1 часть. Посчитайте, чему же будут равны эти части.

– Тогда масса молока в смеси будет равна  и равна 1500 граммам, – принялся считать Саша. – Масса сливок будет равна  и равна 1000 грамм, а масса сахара будет равна  и равна 500 граммам.

– Получается, что для приготовления 3 килограммов мороженого нужно взять 1500 грамм молока, добавить 1000 грамм сливок, а затем добавить 500 грамм сахара? – решил уточнить Паша.

– Всё верно! – согласился Мудряш. – Из решения вашей задачи следует, что число 3000 можно представить в виде суммы трёх слагаемых – 1500, 1000 и 500, отношение которых равно . В таких случаях говорят, что число 3000 разделили в отношении . Также можно сказать, что число 3000 представили в виде суммы трёх слагаемых, пропорциональных числам 3, 2 и 1.

– И совсем несложная задача оказалась, – заметил Саша. – Теперь я без труда могу приготовить мороженое.

– Эту же задачу можно было решить и другим способом, – продолжил Мудряш. – Пусть масса одной части смеси мороженого составляет х грамм. Тогда массы молока, сливок и сахара составляют соответственно 3х грамм, 2х грамм и х грамм. Поскольку масса всей смеси мороженого равна 3000 грамм, то можем составить уравнение . Решим это уравнение. Получим, что . Отсюда . Тогда массы молока, сливок и сахара равны соответственно  грамм,  грамм и  грамм.

– Сделаем вывод, – сказал Мудряш. – Чтобы разделить число в данном отношении, можно разделить это число на сумму членов отношения, а затем результат умножить на каждый член отношения.

– А теперь, ребята, давайте посмотрим, как вы всё поняли, и выполним несколько заданий.

Задание первое: разделите числа в указанных отношениях: а) число  в отношении ;   б) число  в отношении .

Решение: нужно разделить число 12 в отношении 1 к 3. Будем считать, что всё число состоит из  частей. Значит, 1 часть равна . Тогда 3 части будут равны . Следовательно, число двенадцать можно разделить в отношении 1 к 3 так: 3 и 9.

В следующем условии нам нужно разделить число 3,5 в отношении 3 к 4. Будем считать, что всё число состоит из  частей. Тогда 1 часть равна . Отсюда 3 части числа равны . Следовательно, число 3,5 можно разделить в отношении 3 к 4 так: 1,5 и 2.

Следующее задание: два числа относятся как 4 к 7. Найдите эти числа, зная, что: их сумма равна 110, их разность равна 12.

Решение: обозначим за х одну часть. Тогда можем записать, что первое число равно 4х, второе – 7х. В первом условии сказано, что сумма этих чисел равна 110. Составим уравнение . Решим его. Получим . Отсюда . Значит, первое число равно , второе – .

Во втором условии сказано, что разность этих чисел равна 12. Составим уравнение . Решим его. Получим . Отсюда . Значит, первое число равно , второе – .

Решим задачу: стороны прямоугольника  относятся как 2 к 3. Найдите площадь этого прямоугольника, если его периметр равен 20 сантиметров.

Решение: обозначим за х длины частей, из которых состоят стороны прямоугольника. Так как периметр прямоугольника равен удвоенной сумме длин его соседних сторон, то можем составить уравнение: . Решим уравнение. Получим . Отсюда . Следовательно, одна сторона прямоугольника равна  сантиметрам, вторая –  сантиметрам. Площадь прямоугольника равна произведению длин соседних сторон. Тогда площадь прямоугольника равна  см². Запишем ответ.

И решим ещё одну задачу. Для приготовления фарфора смешивают 25 частей белой глины, 2 части песка и 1 часть гипса. Сколько нужно взять каждого материала, чтобы приготовить 504 грамма смеси?

Решение: будем считать, что вся смесь состоит из  частей, имеющих одинаковые массы. Тогда 1 часть содержит  грамм. Следовательно, чтобы приготовить 504 грамма смеси фарфора, нужно взять:  грамм белой глины,  грамм песка и  грамм гипса.

Не забудем записать ответ.

Формула деления

— Что такое формула деления? Примеры

Формула деления используется для деления числа на равные части. Символы, которые мы используем для обозначения деления,  (÷) и (/). Таким образом, «p, деленное на q», может быть записано как: (p÷q) или (p/q). Давайте посмотрим формулу деления вместе с решенными примерами в следующем разделе.

Что такое формула деления?

Формула деления — это формула деления, которая является одной из четырех основных арифметических операций. Формула деления используется для того, чтобы поровну разделить число на множество частей. Формула деления данного значения может быть выражена как

Где,

• Делимое – это число, которое нужно разделить
• Делитель — это число, которое нужно разделить на
.
• Результат — частное.

Формула деления для проверки

Давайте выясним, как мы можем проверить наш ответ деления, используя формулу деления. Например, 8 ÷ 2 = 4, остаток = 0. Другими словами, 8 = 2 × 4 + 0. Этот метод проверки может быть выражен следующим образом:

Дивиденд = (Делитель × Частное) + Остаток.

Рассмотрим еще один пример, где

• делимое = 9
• делитель = 3
• частное = 3
• остаток = 0

Подставляя значение в формулу, получаем 9 = (3×3)+0=9. Поэтому наш ответ правильный.

Хотите найти сложные математические решения за считанные секунды?

Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы. С Cuemath находите решения простыми и легкими шагами.

Записаться на бесплатный пробный урок

Примеры формулы деления

Пример 1:  Разделите, используя формулу деления, значение 500 на 50. Какое получится частное?

Решение:

Чтобы найти: частное

Делимое = 500.
Делитель = 50,
Используя формулу деления,
Дивиденд/делитель = частное
(500/50) = 10
= 10

Ответ: после деления частное будет 10.

Пример 2: 200 шоколадок были распределены поровну между 40 детьми. Сколько шоколадок дали каждому ребенку? Рассчитайте это по формуле деления.

Решение: 

Найти: Сколько шоколадок дали каждому ребенку.
Данная информация:
Всего конфет = 200 
. Всего детей = 40 
. Используя формулу деления,
Шоколадки, выданные каждому ребенку = (Всего шоколадок / Всего детей)
= (200/40)
=  5

Ответ: Каждому ребенку дали по 5 шоколадок.

Пример 3: У Лизы 4 щенка. Он купил 36 жевательных костей, чтобы накормить их поровну. Сколько костей достанется каждому щенку?

Решение:

Количество щенков у Лизы = 4.
Количество костей = 36.
Количество костей у каждого щенка = 36/4 = 9.

Ответ: Каждый щенок получит 9 костей.

Часто задаваемые вопросы о формуле дивизиона

Из каких частей состоит формула дивизиона?

Здесь представлены термины, относящиеся к делению, которые также считаются частями формулы деления.

• Дивиденд
• Делитель
• Частное
• Остаток

Что такое формула деления для проверки?

Для перепроверки нашего ответа по разделу мы склонны следовать методу проверки по разделу. Этот метод проверки может быть выражен как дивиденд = (делитель × частное) + остаток.

Как использовать формулу деления?

Обычно формула деления используется для деления числа на равные части. Рассмотрим пример.
Пример: у Суши есть 28 печений, и она хочет поровну распределить их между двумя своими детьми. Как она будет делить печенье поровну?
Решение: количество файлов cookie = 28 
. Количество детей = 2
Количество печенья у каждого ребенка = 28/2 = 14

Что такое делитель? — Факты определения и пример

Что такое Делитель?

Делитель – это число, которое делит другое число полностью или с остатком.

Делитель представлен в уравнении деления как:

Дивиденд ÷ Делитель = Частное.

При делении 20 на 4 получается 5. Здесь 4 — это число, которое полностью делит 20 на 5 частей и называется делителем. Его уравнение деления: 

Точно так же, если мы разделим 20 на 5, мы получим 4. Таким образом, и 4, и 5 являются делителями 20. 

Родственные игры

Делитель и множители

Делитель — это любое число, которое делится на другое число. Однако множитель — это делитель, который полностью делит число и не оставляет остатка. Итак, все делители числа являются его делителями. Но не все делители будут множителями.

В приведенном выше примере 4 и 5 – это множители 20. Принимая во внимание, что если мы разделим 20 на 3, это не приведет к полному разделению 20. Таким образом, 3 не является множителем 20. 

Давайте рассмотрим другой пример, 15 деление на 5 дает 3. Здесь 5 — делитель. Кроме того, при делении 15 на 3 получается 5. Здесь 3 — делитель.

Делители и множители числа 15:  1, 3, 5, 15

Связанные рабочие листы

Нахождение множителей числа 

Чтобы найти множители числа, скажем, 12, выполните указанные шаги:  

1 . Начните с 1 и запишите факты умножения так, чтобы произведение было 12, например 1 × 12.  

2. Продолжайте таким же образом находить другие факты умножения, пока не найдем пару ближайших множителей или делителей, как указано:

     1 ×12, 2×6, 3×4

3. Запишите все числа в факте умножения, так как они являются делителями 12.

4. Итак, делители или множители числа 12 равны 1, 2, 3, 4, 6 и 12. 

Разные Способы представления делителя

Существуют различные стили выражения уравнения деления. На изображениях ниже показаны различные способы записи делителя: 

Особые случаи

1. Число 1 является делителем всех чисел.

Причина : Если делитель равен 1, то частное равно делимому.

Посмотрите на приведенные примеры,  

34  1 = 34 

15  1 = 15

2. Само число всегда является одним из делителей числа.

Причина : Когда делитель совпадает с делимым, то ответ на такое деление всегда 1. 

Посмотрите на приведенные примеры,  

34  34 = 1 

15  15 = 1 900 03

3 , Когда делитель меньше числа, чем делимое, то ответом будет не целое число, а десятичное число.

Например, 510 = 0,5

Забавные факты — Если мы удвоим делитель, частное будет вдвое.

Практические задачи на делитель

1

Если 3 является делителем, какой из них даст остаток как 2?

37

47

57

67

Правильный ответ: 47
47 является правильным ответом, так как он дает остаток от 2 при делении на 3.
37 ÷ 3 = 12 Р1
47 ÷ 3 = 15 R2
57 ÷ 3 = 19
67 ÷ 3 = 22 R1

2

Какое из следующих чисел имеет наибольшее количество делителей?

44

36

29

47

Правильный ответ: 36
36 имеет наибольшее количество делителей.
Делители 44: 1, 2, 4, 11, 22, 44.
Делители 36: 1, 2, 3, 4, 6, 9, 12, 18, 36.
Делители 29: 1 и 29
Делители числа 47: 1 и 47

3

Какой наибольший общий делитель чисел 13 и 30?

3

2

1

13

Правильный ответ: 1
Делители 13: 1 и 13
Делители 30: 1, 2, 3, 10, 15, 30
Общий делитель 13 и 30 :
1 Наибольший общий делитель чисел 13 и 30: 1

4

Какое из следующих чисел НЕ является делителем 14?

1

2

4

7

Правильный ответ: 4
Коэффициенты 14: 1, 2, 7, 14.

Часто задаваемые вопросы козырек

В чем разница между делителем и делимым?

Когда мы делим два числа, то делимое число является делимым, а число, на которое мы делим, является делителем. Например, 12 конфет нужно разделить между 3 детьми. Итак, у нас есть 12 ÷ 3. Здесь 12 — делимое, а 3 — делитель.

Чем делитель отличается от множителя?

Делитель — это любое число, на которое делится другое число. Однако множитель — это делитель, который полностью делит число и не оставляет остатка.

Может ли число быть делителем самого себя?

Да, все числа делятся сами на себя. Это потому, что каждое число делится само на себя и дает 1 в качестве частного. Например, если у нас есть 12 ÷ 12, то 12 становится делителем 12, а 1 становится частным.

По какой формуле найти делитель?

Если остаток равен 0, то Делитель = Делимое ÷ Частное. Если остаток не равен 0, то Делитель = (Дивиденд — Остаток) / Частное.