Страница 58. Подведем итоги. ГДЗ к учебнику «Математика» 6 класс Бунимович, Кузнецова, Минаева
ГДЗ 1 класс
ГДЗ 10 класс
- Категория: ГДЗ Математика учебник 6 класс Бунимович, Кузнецова, Минаева ✔
Задание 1. Запишите какую−нибудь десятичную дробь с четырьмя знаками после запятой и прочитайте ее.
Ответ
8,26523 − восемь целых двадцать шесть тысяч пятьсот двадцать три стотысячных.
Задание 2. Запишите в виде суммы разрядных слагаемых:
а) натуральное число 3205;
б) десятичную дробь 0,3205.
Ответ
а) 3205 = 3000 + 200 + 5
б) 0,3205 = 0 + 0,3 + 0,002 + 0,0005
Задание 3. Запишите в виде десятичной дроби число:
а) $\frac{9}{10}$;
б) $1\frac{3}{100}$;
в) $\frac{549}{100}$.
Ответ
а) $\frac{9}{10} = 0,9$
б) $1\frac{3}{100} = 1,03$
в) $\frac{549}{100} = 5\frac{49}{100} = 5,49$
Задание 4. 1) Чему равен знаменатель обыкновенной дроби, если в ее десятичной записи содержится 2 знака после запятой? 4 знака после запятой?
2) Представьте в виде обыкновенной дроби число:
а) 0,7;
б) 0,091;
в) 1,203.
Ответ
1) Если в десятичной записи обыкновенной дроби содержится 2 знака после запятой, то знаменатель этой дроби равен 100.
Если в десятичной записи обыкновенной дроби содержится 4 знака после запятой, то знаменатель этой дроби равен 10000.2)
а) а) $0,7 = \frac{7}{10}$;
б) $0,091 = \frac{91}{1000}$;
в) $1,203 = 1\frac{203}{1000}$.
Задание 5. Запишите числа, соответствующие точками, отмеченным на координатной прямой.
Ответ
0,02; 0,05; 0,11; 0,18; 0,23; 0,29.
3} = \frac{875}{1000} = 0,875$;
$\frac{1}{5} = \frac{1 * 2}{5 * 2} = \frac{2}{10} = 0,2$.б) Если знаменатель обыкновенной дроби имеет хотя бы один простой делитель, отличный от 2 и 5, и эта дробь несократима, то ее нельзя представить в виде десятичной.
Примеры:
$\frac{1}{9} = \frac{1}{3 * 3}$;
$5\frac{5}{6} = 5\frac{5}{2 * 3}$.2) а) $\frac{1}{2} = \frac{5}{10} = 0,5$;
б) $\frac{3}{4} = \frac{75}{100} = 0,75$;
в) $\frac{1}{8} = \frac{125}{1000} = 0,125$;
г) $\frac{2}{5} = \frac{4}{10} = 0,4$;
д) $\frac{7}{20} = \frac{35}{100} = 0,35$;
е) $\frac{4}{25} = \frac{16}{100} = 0,16$.
Задание 8. Как записать десятичную дробь, равную данной десятичной дроби? Запишите три десятичной дроби, равные числу 5,070.
Ответ 7 гуру
Чтобы записать десятичную дробь, равную десятичной дроби, надо приписать к данной дроби любое количество нулей справа.
5,070 = 5,07 = 5,0700 = 5,07000000.
Задание 9. Сравните числа:
а) 1,001 и 0,9999;
б) 8,455 и 8,54;
в) 0,305 и 0,3050.
Ответ
а) 1,001 > 0,9999
б) 8,455 < 8,54
в) 0,305 = 0,3050
Задание 10. Между какими последовательными натуральными числами заключено число:
а) 9,8; б) 15,03?
Отвечая на вопрос, запишите соответствующее двойное неравенство и покажите примерное положение числа на координатной прямой.
Решение
а) Число 9,8 заключено между последовательными натуральными числами 9 и 10.
9 < 9,8 < 10б) Число 15,03 заключено между последовательными натуральными числами 15 и 16.
15 < 15,03 < 16
Задание 11. а) Выразите в метрах: 3 см; 70 см; 3 м 48 см.
б) Выразите в тоннах: 20 кг; 200 кг; 1 т 500 кг.
Решение
а) 3 см = $\frac{3}{100} = 0,03$ м;
70 см = $\frac{70}{100} = 0,7$ м;
3 м 48 см = $3\frac{48}{100} = 3,48$ м.б) 20 кг = $\frac{20}{1000} = 0,02$ т;
200 кг = $\frac{200}{1000} = 0,2$ т;
1 т 500 кг = $1\frac{500}{1000} = 1,5$ т.в) 2 к. = $\frac{2}{100} = 0,02$ р.;
90 к. = $\frac{90}{100} = 0,9$ р.;
10 р. 25 к. = $10\frac{25}{100} = 10,25$ р.
- Назад
- Вперед
умножить наподелить на
- ГДЗ
- ГДЗ Математика учебник 6 класс Бунимович, Кузнецова, Минаева
Вам может пригодиться:
учебник по математике 6 класс Бунимович.
8. Расстояние. Номер №105обществознание 6 класс бунимович
На рисунке 2 . 27 изображены три параллельные прямые. Найдите расстояние между каждой парой этих прямых.
Решение
Чтобы найти расстояние между двумя параллельными прямыми, надо отметить на одной прямой точку и от нее провести перпендикуляр ко второй прямой. Длина полученного отрезка будет расстоянием между прямыми.
Расстояние между прямыми a и b равно 7 мм.
Расстояние между прямыми b и c равно 12 мм.
Расстояние между прямыми a и c равно 19 мм.
На рисунке 2 . 27 изображены три параллельные прямые. Найдите расстояние между каждой парой этих прямых.
Чтобы найти расстояние между двумя параллельными прямыми, надо отметить на одной прямой точку и от нее провести перпендикуляр ко второй прямой. Длина полученного отрезка будет расстоянием между прямыми.
Расстояние между прямыми a и b равно 7 мм.
Расстояние между прямыми b и c равно 12 мм.
Расстояние между прямыми a и c равно 19 мм.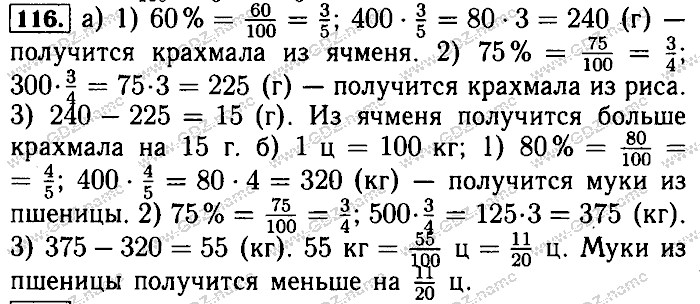
На рисунке 2.
Reshalka. com
30.05.2020 18:27:47
2020-05-30 18:27:47
Источники:
Https://reshalka. com/uchebniki/6-klass/matematika/bunimovich/139
по Математике 6 класс Бунимович Сферы » /> » /> .keyword { color: red; }
обществознание 6 класс бунимович
по математике 6 класс Арифметика. Геометрия. Бунимович поможет школьникам постичь первое знакомство с усложненной программой. Простая арифметика пройдена и вместо одной дисциплины детям придется изучать две: алгебру и геометрию. Два разных направления одной науки дадут более глубокое представление о предмете. Да, путь этот тернистый, особенно для гуманитариев. Но это не повод опускать руки и скатываться до неудовлетворительных оценок. Ведь впереди контрольные работы, олимпиады и экзамен, от результатов которого многое зависит. Даже не пропуская уроки, школьники могут иметь пробелы в знаниях, так как программа насыщена новыми терминами, понятиями и формулами.
Зачем нужно онлайн-руководство
Всегда есть соблазн просто списать решение. Но это путь в никуда, потому что в следующий раз, решая аналогичную задачу у доски или на экзамене, ребенок не сможет подсмотреть в шпаргалку. Вот почему решебник подготовлен для того, чтобы дети учились самостоятельно работать, иногда проверяя верность своего решения. Преимущества Пособия по математике 6 класс Авторы: Е. А. Бунимович, Л. В. Кузнецова, С. С. Минаева.
:Все упражнения имеют готовые ответы, что ускоряет время выполнения домашних заданий. Занимаясь с учебником и рабочей тетрадью, ученик лучше запоминает материал. Самостоятельные занятия способствуют правильному распределению времени и развитию неординарного мышления.
Что входит в решебник по математике 6 класс Бунимович
Как и основной учебник, так и дополнительные материалы разрабатываются специалистами. Рабочая тетрадь состоит из упражнений, отвечающих темам учебника.
Так же есть контрольные задания и вопросы для промежуточной проверки знаний. Учить предмет и относиться к нему с должным уважением нужно не только ради хороших оценок. Твердые и обширные знания развивают память, мышление и способность поддержать разговор на любую тему. Образование не дает полной гарантии успешности в будущем, однако широкий кругозор открывает возможности для вчерашних школьников. Так что получение знаний требует тщательного подхода и систематической работы над поставленными задачами. К тому же отпадает необходимость поиска репетитора, что существенно экономит семейный бюджет.
к задачнику по математике за 6 класс Бунимович Е. А. можно посмотреть здесь.
к тетради-тренажеру по математике за 6 класс Бунимович Е. А. можно посмотреть здесь.
к тетради-экзаменатору по математике за 6 класс Кузнецова Л. В. можно посмотреть здесь.
Что входит в решебник по математике 6 класс Бунимович.
Xn—c1acj. xn--p1ai
26.08.2018 14:56:27
2018-08-26 14:56:27
Источники:
Https://xn--c1acj.
xn--p1ai/po-matematike/6-klass/bunimovich
Решебник () по математике 6 класс Бунимович Сферы 2017-2019 » /> » /> .keyword { color: red; }
обществознание 6 класс бунимович
Математика в 6 классе продолжит изучение основ алгебры. Шестиклассника ждет более сложный, насыщенный новыми терминами, материал, который начинается с дробей и процентов, а заканчивается множеством и комбинаторикой. Масса новой информации и создает массу различных сложностей в изучении какой — либо темы. Даже не пропуская занятия порой, без посторонней помощи, сложно одолеть такой объем информации. Практика — наиболее слабое место многих шестиклассников. Поэтому, чтобы справиться с решением задач и получить необходимые знания, можно воспользоваться помощью Пособия с по математике 6 класс (авторы: Бунимович Е. А.. Кузнецова Л. В., Минаева С. С.) . Он поможет ученику запомнить формулы и правильно применять их для решение задач. Пособие соответствует требованиям ФГОС и рабочей программы Сферы для общего среднего образования.
Учебник расскажет о дробях и процентах, раскроет понятия о прямых на плоскости и в пространстве, поведает о десятичных дробях и действиях с ними. Школьник освоит понятия окружности и изображение ее на плоскости, научится выражать отношения в процентах. Шестикласснику предстоит освоить решение задач с применением выражения, формул, уравнений.
Как поможет школьнику предложенный учебно-методический комплекс по математике за 6 класс, Бунимович
При изучении сложного материала важно иметь качественного помощника, коим является решебник этих же авторов, что и основной учебник. Хотя в нем все задания имеют готовые решения, он предлагает инструмент, с помощью которого школьник научится находить разные пути и альтернативные способы решения задач. Правильное использование сборника поможет каждому шестикласснику:
- без проблем освоить новый материал; быстро и без ошибок выполнить любое задание; устранить имеющиеся проделы в знании математики; подготовиться к следующему уроку.
С помощью онлайн решебника можно быстро отыскать нужную информации по решению того или иного номера задачи. Пользоваться им можно в любое время и в любом месте, где имеется доступ к интернету и с любого компьютера. Онлайн-решебник по математике для 6 класса от Бунимовича для родителей является лучшим помощником, который поможет им раскрыть в своем ребенке его способности к изучению математики и иметь только хорошие отметки по этому предмету.
Как поможет школьнику предложенный учебно-методический комплекс по математике за 6 класс, Бунимович.
Megaresheba. ru
04.06.2019 1:53:39
2019-06-04 01:53:39
Источники:
Https://megaresheba. ru/publ/reshebnik/matematika/6_klass_bunimovich/47-1-0-2141
Стадион Бунимовича | Visual Insight
Стадион Бунимовича – Филипп Ру
Стадион Бунимович представляет собой прямоугольник, окруженный полукругами, в котором точечная частица движется с постоянной скоростью по прямым линиям, отражаясь от границы таким образом, что угол падения равен углу отражения.
Эта анимация, сделанная Филиппом Ру, показывает набор таких частиц, изначально движущихся в одном направлении. С каждым отскоком их траектории расходятся, а через какое-то время распределяются почти равномерно по всему стадиону, хотя какое-то время еще видна волна плотности, движущаяся туда-сюда.
Стадион Бунимовича фигурирует в работе Леонида Бунимовича 1979 г.:
• Леонид А. Бунимович, Об эргодических свойствах нигде не рассеивающихся бильярдов, Комм. Мат. физ. 65 (1979), 295–312.
Он показал, что движение бильярда на этом стадионе «эргодично». Это способ уточнить интуитивное предположение о том, что для бильярда со случайно выбранными начальным положением и скоростью со временем его положение почти наверняка станет равномерно распределенным по всему стадиону.
Точнее, мы можем определить фазовое пространство \(\Омега\) для стадиона Бунимовича как пространство пар положение-скорость, где скорость является единичным вектором. (Поскольку скорость бильярда не меняется, можно считать, что она нормирована на 1.
) На \(\Omega\) существует вероятностная мера, для которой временная эволюция определяет сохраняющую меру динамическую систему:
$$ T_t : \Omega \to \Omega , \qquad \qquad t \in \mathbb{R}. $$
Для динамической системы, сохраняющей меру, мы говорим, что измеримое подмножество \(A \subseteq \Omega\) равно инвариант , если для всех \(t \in \mathbb{R}\) множества \(T_t(A)\) и \(A\) отличаются только нулевым множеством, что означает, что симметричная разность \(T_t( А) \треугольник А\) имеет нулевую меру. Сохраняющая меру динамическая система является эргодической , если единственными инвариантными измеримыми подмножествами \(A \subseteq \Omega\) являются нулевые множества и дополнения нулевых множеств.
Значение этого поясняется «эргодической теоремой». Предположим, что \(T_t : \Omega \to \Omega\) является сохраняющей меру динамической системой на пространстве вероятностных мер \(\Omega,\mu\), и предположим, что \(f \colon \Omega \to \mathbb{R }\) — интегрируемая функция.
Затем мы можем определить два средних значения \(f\), «среднее по времени» и «среднее по фазовому пространству». 9t f(T_s x) \, ds .$$
Среднее по фазовому пространству: Это интеграл от \(f\) по фазовому пространству:
$$ \bar{f} = \int_\Omega f \ , д \мю(х). $$
В общем случае среднее по времени и среднее по фазовому пространству может быть разницей, а среднее по времени может не существовать. Но если \(T_t\) эргодично, то эргодическая теорема Биркгофа говорит, что
$$ \widehat{f}(x) = \bar{f} $$
почти для каждого \(x \in \Omega\ ).
Доказать, что сохраняющая меру динамическая система является эргодичной, может быть сложно. Научный руководитель Бунимовича Яков Г. Синай показал, что бильярд, движущийся по квадратному столу с отражающим диском внутри, эргодичен.
Синайский бильярд – Джордж Стаматиу
Кривизна диска увеличивает угол между слегка отличающимися траекториями. Стадион Бунимовича тоньше, потому что в нем отсутствует эта особенность: поскольку его закругленные концы выпуклые, они имеют тенденцию фокусировать отскакивающие от них бильярды.
Прямоугольная часть таблицы противодействует этому эффекту фокусировки, и в течение достаточно длительного времени наблюдается экспоненциальное увеличение расстояния между изначально близкими траекториями.
Стадион Бунимович Траектории – Якоб Шольбах
Как пишет Буминович:
Более того, более тщательный анализ этих биллиардов выявил новый механизм хаотического поведения консервативных динамических систем, названный механизмом расфокусировки . Ключевое наблюдение состоит в том, что узкий параллельный пучок лучей после фокусировки за счет отражения от границы фокусировки может пройти точку фокусировки (в линейном приближении) и стать расходящимся при условии, что свободный пробег между двумя последовательными отражениями от границы достаточно велик. . Механизм расфокусировки работает при условии, что дивергенция преобладает над конвергенцией.
Это из:
• Леонид Буминович, Динамический бильярд, Scholarpedia .
Однако этого анализа недостаточно для понимания эргодичности стадиона Бунимовича, поскольку в 1973 г. Лазуткин показал, что выпуклый бильярдный стол с бесконечно дифференцируемой границей не может быть эргодичным. На самом деле он показал это для выпуклой таблицы, граница которой имеет 553 непрерывных производных! В 1982 году Дуади показал, что 6 непрерывных производных достаточно, и предположил, что достаточно 4. Ссылки см.:
• Николай Чернов и Роберто Макарян, Введение в эргодическую теорию хаотического бильярда , 2-е изд., Импа, Рио-де-Жанейро, 2003.
О квантовых аспектах стадиона Бунимовича см.:
• Теренс Тао, Open вопрос: шрамы на стадионе Бунимовича, Что нового , 28 марта 2007 г.
Это объясняет интересный вопрос, который был рассмотрен в более поздней работе:
• Теренс Тао, Хасселл доказал наличие шрамов на стадионе Бунимовича, Что нового , 7 июля 2008 г.
Также посетите замечательную веб-страницу Карлоса Шайдеггера, на которой можно поиграть с бильярдом на стадионе Бунимовича, а также с эллиптическим столом, где их движение полностью интегрируемо:
• Карлос Шайдеггер, Бунимович
стадион.
Филипп Ру разместил свою анимацию стадиона Бунимовича в Google Фото под лицензией Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International. Джордж Стаматиу разместил свое изображение бильярда на Синае на Wikicommons под лицензией Creative Commons Attribution 2.5 Generic. Якоб Шольбах разместил свое изображение бильярдных траекторий на стадионе Бунимовича на Викикоммонсе под лицензией Attribution-ShareAlike 3.0 Unported.
Visual Insight — это место, где можно поделиться потрясающими изображениями, помогающими объяснить сложные темы математики. Я всегда ищу по-настоящему красивые изображения, поэтому, если вы знаете о них, пожалуйста, оставьте комментарий здесь и дайте мне знать!
Л. Бунимович | Ученый-семантик
Сортировка по наиболее влиятельным статьямСортировка по количеству цитированийСортировка по новизне
Об эргодических свойствах нигде не рассеивающихся биллиардов
- Бунимович Л.
Математика
- 1 октября 1979 г.
Для биллиардов в двумерных областях с границами, содержащими только фокусирующую и нейтральную регулярные компоненты и удовлетворяющих некоторым геометрическим условиям, доказано B-свойство. Некоторые примеры…
View on Springer (opens in a new tab)
Статистические свойства газа Лоренца с периодической конфигурацией рассеивателей
- Бунимович Л., Синай Ю.
Математика
191219
В предыдущей статье были построены марковские разбиения для некоторых классов дисперсных биллиардов. Используя эти разбиения, мы оцениваем затухание автокорреляционной функции скорости и доказываем… Н. Чернов
Математика
СОДЕРЖАНИЕ ??1. Введение ??2. Бильярд: необходимая информация ??3. Решетка Маркова: локальная конструкция ??4. Решетка Маркова: глобальная конструкция ??5. Оценка распада…
Просмотр через Publisher (opens in a new tab)
Где сделать отверстие для достижения максимального выхода вопрос о том, как вероятность выживания зависит от положения дыры, по-видимому, никогда не рассматривался в теории открытых динамических систем.
Мы обнаружили, что эта зависимость может быть очень…Посмотреть на Springer (откроется в новой вкладке)
Грибы и другие бильярды с разделенным фазовым пространством.
- Бунимович Л.
Физика, математика
Хаос
- 20 ноября 2001 г. дан понятный (строго изученный) бильярд в областях с фрактальной границей.
Посмотреть в PubMed (откроется в новой вкладке)
Об уравнении Больцмана для газа Лоренца. или ветровое дерево, модель. Доказано, что если ω — фиксированная конфигурация центров рассеивателей, принадлежащих множеству полной меры по отношению к… Производственные линии
- Дж. Бартольди, Л. Бунимович, Д. Эйзенштейн
Бизнес
Опер. Рез.
- 1 марта 1999 г.
Описаны все возможные асимптотики производственных линий типа «ковшовые бригады» с двумя или тремя рабочими, каждая из которых характеризуется постоянной скоростью работы. Результаты говорят о настороженности в…
Просмотр через Publisher (opens in a new tab)
Марковские разбиения для рассредоточенного бильярда
- Л. Бунимович, Ю. Синай
Математика
- 1 декабря 1980
Марковские разбиения для некоторых классов биллиардов в двумерных областях на ℝ2 или двумерном торе. Используя эти разбиения, мы представляем микроканоническое распределение…
View on Springer (opens in a new tab)
Hard Ball Systems and the Lorentz Gas
- Л. Бунимович, Д. Бураго, Л. Янг
Физика
- 2000
Часть I. Математика: 1. Д. Бураго, С. Ферлегер, А. Кононенко: Геометрический подход к полудисперсионным бильярдам.- 2. Т. Дж. Мерфи, Э. Г. Д. Коэн: О последовательности столкновений твердых сфер в…
View via Publisher (opens in a new tab)
Markov partitions for two-dimensional hyperbolic billiards
- L. Bunimovich, Y. Sinai, N. Chernov
Mathematics
- 30 June 1990
CONTENTS § 1. Основные определения и формулировки результатов § 2. Общие свойства двумерных бильярдов рассеяния § 3.
Бунимович, Ю. Синай