Алгебра 8 класс — Образовательная онлайн-платформа МЭО
Интерактивный онлайн-учебник «Алгебра 8 класс» сможет заменить традиционный учебник или дополнить его. Содержание интерактивных курсов соответствует требованиям федеральных государственных образовательных стандартов (ФГОС).
Онлайн-уроки подходят для самостоятельного изучения, репетиторам для групповых занятий, а также педагогам для работы с классом в школе или дистанционно.
Ученик познакомится с теорией, проверит полученные знания с помощью онлайн-тренажеров и интерактивных заданий, подготовится к контрольным и проверочным работам, экзаменам.
Онлайн-уроки сборника «Алгебра 8 класс» построены таким образом, что перед изучением новой темы, предлагается повторить и закрепить ранее изученный материал в курсе Алгебра 7 класс.
Такой формат занятий поможет разобраться в новой теме или подтянуть знания по предмету. Доступ к онлайн-урокам осуществляется через интернет (24/7). Это позволяет
Это позволяет
В качестве одной из составляющей курса, ученикам доступен объемный дополнительный материал, позволяющий углубить имеющиеся знания. Различные практические или тестовые задания разного уровня сложности — важная составляющих подготовки к будущим экзаменам, ОГЭ или ЕГЭ.
Программа обеспечивает достижение следующих результатов освоения образовательной программы основного общего образования:
- умение работать с математическим текстом, использовать различные языки математики, обосновывать суждения, проводить классификацию, доказывать математические утверждения;
- владение базовым понятийным аппаратом;
- умение выполнять алгебраические преобразования рациональных и иррациональных выражений;
- умение пользоваться математическими формулами и самостоятельно составлять формулы;
- умение решать линейные и квадратные уравнения, линейные неравенства;
- применять полученные умения для решения задач из математики, смежных предметов, практики;
- овладение системой функциональных понятий, функциональным языком и символикой, умение строить графики функций, описывать их свойства, использовать функционально-графические представления для описания и анализа математических задач и реальных зависимостей;
- овладение основными способами представления и анализа статистических данных;
- умение применять изученные понятия, результаты и методы при решении задач из различных разделов курса, в том числе задач, не сводящихся к непосредственному применению известных алгоритмов.

Темы:
- Алгебраические дроби
- Действительные числа. Арифметический квадратный корень
- Свойства арифметического квадратного корня
- Квадратные уравнения
- Рациональные уравнения
- Числовые неравенства и их свойства
- Неравенства с одной переменной
- Степень с целым показателем
- Стандартный вид числа
- Приближённые вычисления
- Статистика, вероятность и комбинаторика
Онлайн-уроки содержат:
- Алгебраические дроби
- Действительные числа. Арифметический квадратный корень
- Свойства арифметического квадратного корня
- Квадратные уравнения
- Рациональные уравнения
- Числовые неравенства и их свойства
- Неравенства с одной переменной
- Степень с целым показателем
- Стандартный вид числа
- Приближённые вычисления
- Статистика, вероятность и комбинаторика
|
Каталог Поиск книг Электронные приложения Авторизация Подписка на рассылку Стихи о нас Богатство Трудности эти уже превратились в смыслы. Тивикова С.К., зав. каф. начального образования НИРО Обратная связь Отправить сообщение с сайта Партнёры |
Аннотация Автор(ы): Мордкович А. Учебник написан в соответствии с ФГОС ООО и входит в завершённую линию учебников для 7—9-х классов; поддерживает разные модели изучения алгебры: базовую и углублённую. Изложение теоретического материала сопровождается подробным рассмотрением большого числа примеров, практические задания представлены на трёх уровнях сложности. В конце каждой главы приведены основные факты, а также вопросы и тест для самопроверки, дополнительные задачи и исторические сведения.
Особенностью учебников авторского коллектива под руководством А. Г. Мордковича является приоритет функционально-графического подхода в содержательно-методической линии курса алгебры, который наилучшим образом отвечает возрастным особенностям учащихся. Новизной линии учебников является изучение начал комбинаторики, статистики и теории вероятностей в интеграции с учебными темами, традиционными для школьной математики. Каждый учебник включает теоретический материал и методически обоснованную систему практических заданий, дифференцированных по трём уровням сложности, что позволяет использовать учебники в классах с разной подготовкой учеников.
Практико-ориентированный характер задач отвечает современным требованиям к изучению курса алгебры. Содержание учебников соответствует требованиям Федерального государственного образовательного стандарта основного общего образования. Они представляют собой завершенную линию учебников алгебры для 7-9-х классов Отличительная особенность – более доступное изложение материала для школьников по сравнению с традиционными учебными пособиями. ЭФУ Программа, методическое пособие и другие материалы к урокам Связанные издания:
Назад в раздел |
Операции и алгебраическое мышление — MAP Математика 8-го класса
- Войти
- Биографии репетитора
- Подготовка к тесту
СРЕДНЯЯ ШКОЛА
- ACT Репетиторство
- SAT Репетиторство
- Репетиторство PSAT
- ASPIRE Репетиторство
- ШСАТ Репетиторство
- Репетиторство STAAR
ВЫСШАЯ ШКОЛА
- Репетиторство MCAT
- Репетиторство по LSAT
- Репетиторство по GMAT
К-8
- Репетиторство AIMS
- Репетиторство по HSPT
- Репетиторство ISEE
- Репетиторство ISAT
- Репетиторство по SSAT
- Репетиторство STAAR
Поиск 50+ тестов
- Академическое обучение
репетиторство по математике
- Алгебра
- Исчисление
- Элементарная математика
- Геометрия
- Предварительный расчет
- Статистика
- Тригонометрия
репетиторство по естественным наукам
- Анатомия
- Биология
- Химия
- Физика
- Физиология
иностранные языки
- французский
- немецкий
- Латинский
- Китайский мандарин
- Испанский
начальное обучение
- Чтение
- Акустика
- Элементарная математика
прочие
- Бухгалтерия
- Информатика
- Экономика
- Английский
- Финансы
- История
- Лето
Поиск по 350+ темам
- О
- Обзор видео
- Процесс выбора наставника
- Онлайн-репетиторство
- Мобильное обучение
- Мгновенное обучение
- Как мы работаем
- Наша гарантия
- Влияние репетиторства
- Обзоры и отзывы
- Освещение в СМИ
- О преподавателях университета
Звоните прямо сейчас, чтобы записаться на обучение:
(888) 888-0446
Все математические ресурсы MAP для 8-го класса
5 практических тестов Вопрос дня Карточки Learn by Concept
MAP Помощь по математике для 8-го класса » Операции и алгебраическое мышление
Решить для
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы решить для , нам нужно изолировать в одной части уравнения.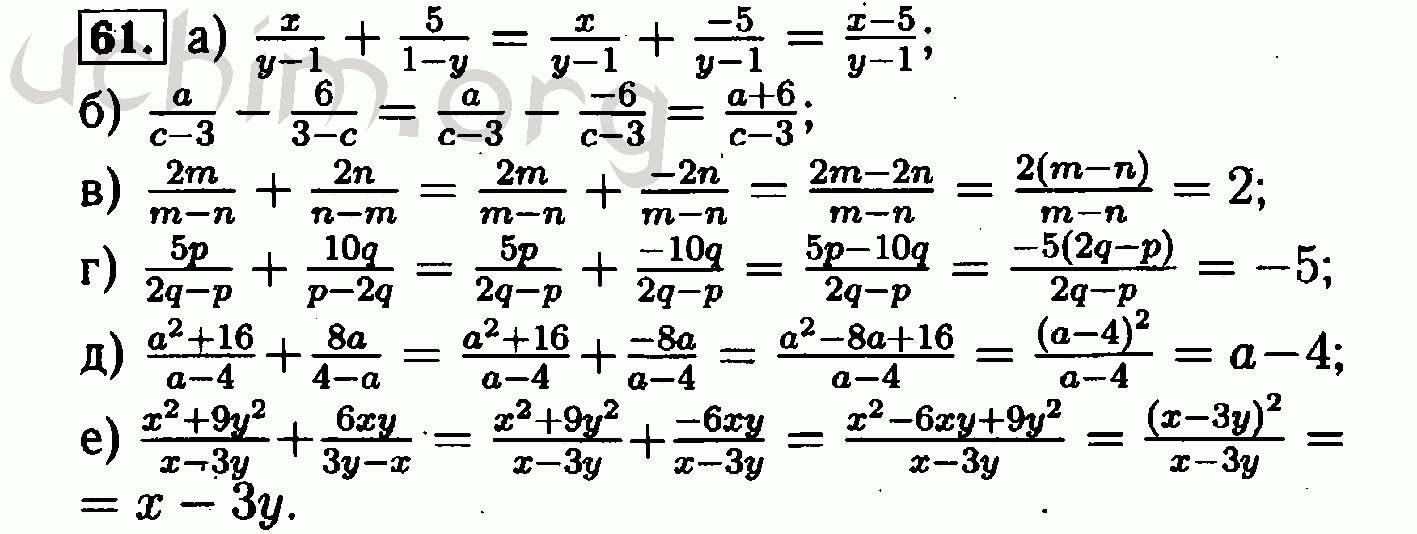
В этой задаче первое, что мы хотим сделать, это распределить:
Затем мы можем вычесть из обеих сторон:
Наконец, мы разделим 3 3
с обеих сторон:
Сообщить об ошибке
Решить:
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы решить эту задачу, нам нужно вспомнить наши правила экспоненты:
Когда наши базовые числа равны друг другу, как в этой задаче, мы можем сложить наши экспоненты вместе, используя следующую формулу:
Применим это правило к нашей задаче
Решим для показателей
Мы не можем оставить эту задачу в этом формате, потому что у нас не может быть отрицательного показателя степени. Вместо этого мы можем переместить основание и показатель степени в знаменатель дроби:
Решить задачу
Сообщить об ошибке
С помощью алгебры решить следующую систему линейных уравнений:
Возможные ответы:
Правильный ответ:
Объяснение:
Существует несколько способов решения системы линейных уравнений: графический и алгебраический.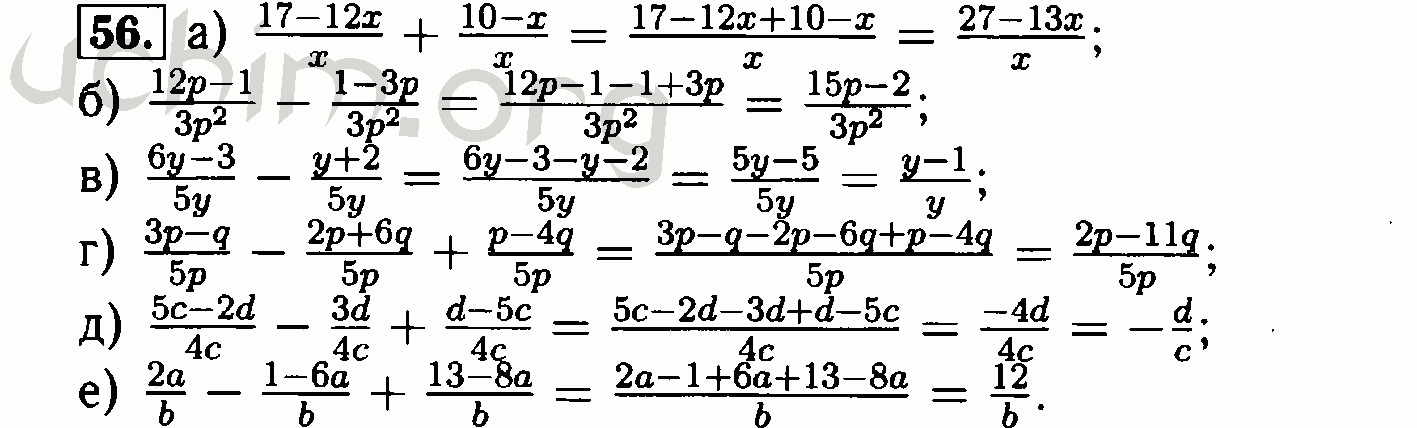 В этом уроке мы рассмотрим два способа алгебраического решения системы линейных уравнений: замена и исключение.
В этом уроке мы рассмотрим два способа алгебраического решения системы линейных уравнений: замена и исключение.
Подстановку можно использовать, решив одно из уравнений для или , а затем подставив это выражение для соответствующей переменной во втором уравнении. Вы также можете решить оба уравнения так, чтобы они были в форме , а затем приравнять оба уравнения друг к другу.
Исключение лучше всего использовать, когда одна из переменных имеет одинаковый коэффициент в обоих уравнениях, потому что тогда вы можете использовать сложение или вычитание, чтобы исключить одну из переменных и найти другую переменную.
Для этой задачи подстановка имеет смысл, потому что первое уравнение уже решено для переменной. Мы можем подставить выражение, равное , в нашего второго уравнения:
Далее нам нужно распределить и объединить одинаковые члены:
Мы ищем значение , а это значит, что нам нужно изолировать на одну сторону уравнения. Мы можем вычесть из обеих частей:
Затем разделить обе части на , чтобы найти
Помните, когда мы решаем систему линейных уравнений, мы ищем точку пересечения; таким образом, наш ответ должен иметь оба значения и .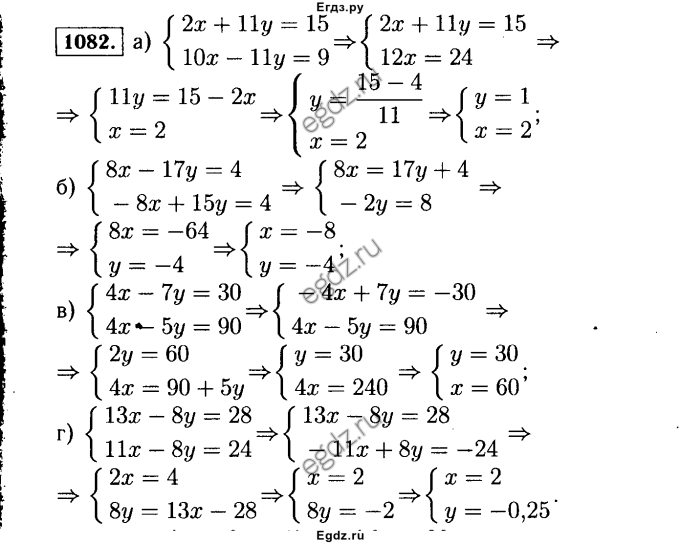
Теперь, когда у нас есть значение , мы можем подставить это значение в переменную в одном из заданных уравнений и найти
Наша точка пересечения, а решение для двух линейных уравнений —
Отчет о ошибке
Сертифицированные номера
.
Сертифицированный преподаватель
Университет Мэриленда, округ Балтимор, бакалавриат, биохимия и молекулярная биология. Медицинская школа Восточной Вирджинии, доктор философии,…
Посмотреть репетиторов
Патрисия
Сертифицированный преподаватель
SUNY New Paltz, бакалавриат, французский язык. SUNY New Paltz, магистратура, среднее образование: французский язык.
Все математические ресурсы MAP для 8-го класса
5 практических тестов Вопрос дня Карточки Learn by Concept
Математика для 8-го класса, учебная программа и онлайн-уроки по математике для 8-го класса @BYJUS
Учебная программа по математике для 8-го класса
Уравнения
Уравнения — это два математических выражения, устанавливающие равенство между двумя выражениями. Восьмиклассники, изучающие математику, изучат различные стратегии, такие как транспонирование и методы балансировки для решения уравнений.
Восьмиклассники, изучающие математику, изучат различные стратегии, такие как транспонирование и методы балансировки для решения уравнений.
Основы уравнений
Уравнение, по сути, является способом выражения равенства между двумя выражениями. В этом разделе рассказывается о свойствах и операциях, которые можно использовать для их решения.
Решение многошаговых уравнений с использованием различных операций
Некоторые уравнения невозможно решить за один шаг. В таких случаях нам нужно решить ее, используя несколько шагов, выполняя различные операции.
Решение уравнений с переменными с обеих сторон
Здесь учащиеся математики восьмого класса узнают, как решать уравнения, в которых обе стороны имеют переменные.
Переписывание уравнений и формул
Переписывание уравнений и формул помогает учащимся переводить математические текстовые задачи восьмого класса в решаемые математические уравнения. В этом разделе обсуждаются аспекты, которые необходимо учитывать при переписывании уравнений.
В этом разделе обсуждаются аспекты, которые необходимо учитывать при переписывании уравнений.
Преобразования
Манипулирование фигурами и фигурами и игра с ними превращают изучение математики в увлекательное занятие. Преобразования позволяют нам манипулировать и изучать движение геометрических фигур.
Понятие перевода
Перевод — вид преобразования, при котором геометрическая фигура перемещается на заданное расстояние в определенном направлении. Здесь студенты узнают, как переводить формы с помощью некоторых примеров.
Понятие отражения
Отражение — вид преобразования геометрических фигур. Отражение фигуры в основном является зеркальным отражением формы. Здесь учащиеся узнают значение линии отражения, наблюдая различные примеры.
Концепция вращения
Вращение — это метод преобразования, при котором фигура или объект вращается вокруг точки. В этом разделе обсуждается вращение объектов с помощью некоторых примеров из реальной жизни.
Концепция расширения
Расширение — это еще один тип геометрического преобразования, при котором размер фигуры изменяется с использованием коэффициента масштабирования. Здесь учащиеся восьмого класса узнают о концепции расширения и о том, как ее можно использовать для создания подобных фигур 9.0003
Конгруэнтные фигуры
Конгруэнтные фигуры — это геометрические фигуры одинаковой формы и размера. Другими словами, конгруэнтные фигуры обладают одинаковыми свойствами. Учащиеся узнают, как определить, конгруэнтны ли заданные две фигуры.
Похожие фигуры
Подобные фигуры — это фигуры, имеющие одинаковую форму, но разные по размеру. Восьмиклассники узнают примеры подобных фигур и их отношение к преобразованиям.
Периметры и площади подобных фигур
Периметр и площадь — термины, используемые для описания основных качеств двумерных фигур. В этом разделе учащиеся узнают о периметре и площади подобных фигур.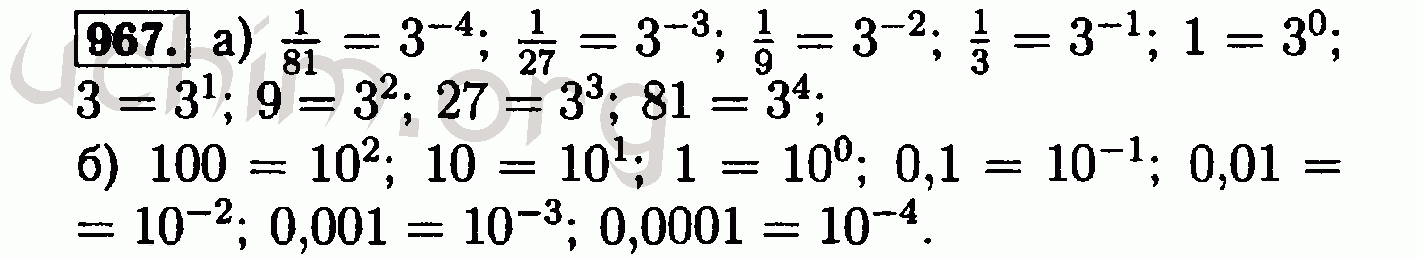
Углы и треугольники
Угол – это фигура, образованная при пересечении двух прямых или двух лучей. Угол имеет две стороны и общую вершину. Мы можем использовать комбинацию углов для построения фигур. Треугольник — это простейшая замкнутая двумерная фигура, которую можно построить.
- Сумма внутренних углов многоугольника
Параллельные прямые и секущие
Любые две прямые, которые никогда не пересекаются, называются параллельными прямыми. Третья линия, проходящая через набор параллельных прямых, называется секущей. Здесь студенты узнают некоторые интересные соотношения между углами, образованными параллельными прямыми и секущими.
Переменные внутренние углы
Углы треугольников
Треугольник – это замкнутая фигура, состоящая из трех сторон и трех углов. Комбинация углов придает треугольникам некоторые уникальные свойства. Восьмиклассники изучают эти свойства, чтобы находить отношения между углами треугольников.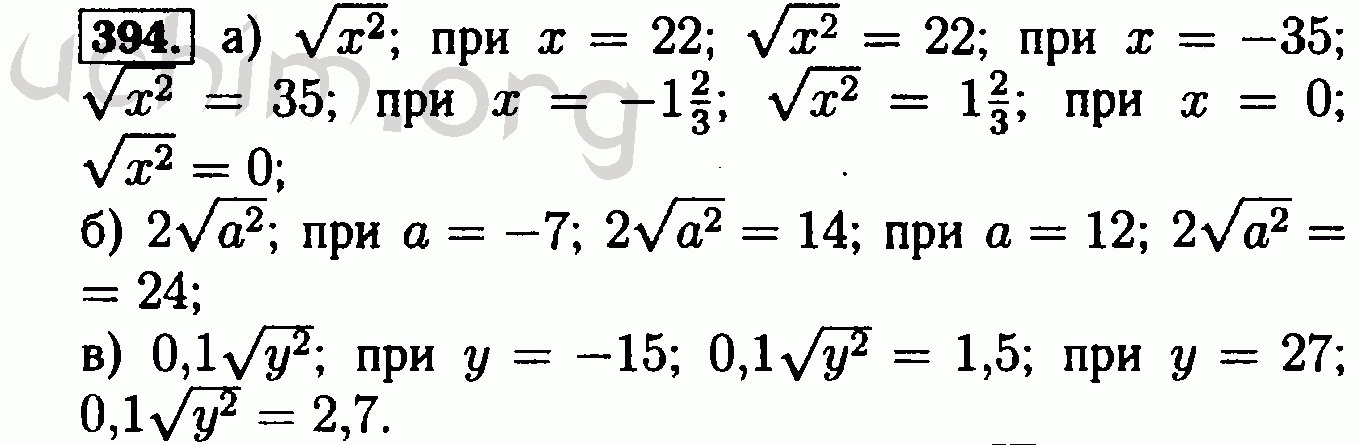
Углы многоугольников
Многоугольники представляют собой замкнутые фигуры, имеющие не менее трех прямых сторон. Треугольники, четырехугольники и пятиугольники являются примерами многоугольников. Многоугольники имеют определенный набор свойств в зависимости от их характеристик, таких как количество равных углов, количество сторон и количество параллельных сторон и т. д. Здесь учащиеся узнают об углах многоугольников с помощью математических задач восьмого класса.
Сумма внутренних углов многоугольника
Подобные треугольники
Треугольники, имеющие одинаковую форму, но разные размеры, называются подобными треугольниками. Стороны подобных треугольников пропорциональны. Здесь восьмиклассники узнают о различных методах доказательства сходства двух треугольников.
Соответствующий угол
Графики и запись линейных уравнений
Линейные уравнения — это алгебраические уравнения, в которых показатель степени равен единице. График линейного уравнения представляет собой прямую линию. Студенты узнают, как сформировать линейное уравнение и построить уравнение на графике.
График линейного уравнения представляет собой прямую линию. Студенты узнают, как сформировать линейное уравнение и построить уравнение на графике.
График линейных уравнений и пропорциональных отношений
График линейного уравнения всегда представляет собой прямую линию. Но каждое линейное уравнение будет давать разные прямые линии на миллиметровой бумаге. Учащиеся используют концепцию упорядоченных пар для построения графиков линейных уравнений и определения пропорциональных отношений.
Определение наклона линии
Наклон линии описывает крутизну линии. Мы можем вычислить наклон линии, используя различные методы. Восьмиклассники подробно узнают о каждом методе на разных страницах здесь.
Нахождение наклона линии (графическим методом)
Мы можем вычислить наклон линии по ее графику на миллиметровой бумаге. Это простой метод, который можно использовать для решения математических задач в восьмом классе.
Построение графика линейных уравнений (форма пересечения наклона)
Линейное уравнение может быть записано в различных формах. Но его график всегда представляет собой прямую линию. В этом разделе обсуждаются этапы построения графика линейного уравнения в форме пересечения наклона.
Но его график всегда представляет собой прямую линию. В этом разделе обсуждаются этапы построения графика линейного уравнения в форме пересечения наклона.
Построение графика линейных уравнений (стандартная форма)
Здесь учащиеся математики восьмого класса узнают, как построить график линейного уравнения в стандартной форме.
Написание уравнений (наклон и точка)
Учащиеся 8-го класса научатся составлять уравнение прямой, если известны ее наклон и точка на прямой.
Системы линейных уравнений
Теперь, когда учащиеся изучили основные концепции линейных уравнений, пришло время перейти к следующему, решая систему линейных уравнений. Система линейных уравнений представляет собой набор нескольких уравнений, имеющих более одной переменной.
Решение системы линейных уравнений с помощью графического метода
Существует несколько способов решения системы линейных уравнений. Восьмиклассники сначала научатся решать систему линейных уравнений с помощью графического метода. Это поможет учащимся получить четкое визуальное представление о том, что означает решение.
Это поможет учащимся получить четкое визуальное представление о том, что означает решение.
Решение систем линейных уравнений путем подстановки
Теперь, когда учащиеся знают, что означает решение системы линейных уравнений, они изучат метод подстановки для решения линейных уравнений. Этот метод решения линейных уравнений осуществляется путем записи одной переменной через другие и с помощью простых арифметических операций.
Решение систем линейных уравнений методом исключения
Следующий метод решения системы линейных уравнений заключается в исключении одной из переменных. В этом методе учащиеся научатся решать линейные уравнения, манипулируя ими с помощью простых операций, таких как сложение, вычитание, умножение и деление.
Решение специальных систем линейных уравнений
Систему линейных уравнений можно классифицировать на основе характера ее решений. В этом разделе обсуждаются факторы, определяющие характер решений системы линейных уравнений. Восьмиклассники-математики также научатся решать эти специальные системы линейных уравнений.
Восьмиклассники-математики также научатся решать эти специальные системы линейных уравнений.
Анализ данных и отображение
Данные — это совокупность информации, которая может включать числа, слова, измерения, наблюдения и т. д. Мы собираем данные, чтобы наблюдать за различными вещами в реальном мире. Но нам нужны способы отображения данных, чтобы сделать их более понятными. В этой главе восьмиклассники изучают методы анализа данных и отображения.
Отображение данных в линейной форме
В этом разделе учащиеся восьмого класса научатся отображать данные в линейной форме; т. е. путем построения линий на графике.
Отображение данных
В этом разделе учащиеся-математики восьмого класса познакомятся с различными методами отображения данных, включая пиктограммы, гистограммы, линейные графики, гистограммы, диаграммы стеблей и листьев, диаграммы с ячейками и усами, круговые диаграммы, диаграммы рассеяния и линейные сюжеты.
Функции
Функция — это выражение или правило, определяющее взаимосвязь между значением в наборе данных и значением в другом наборе данных.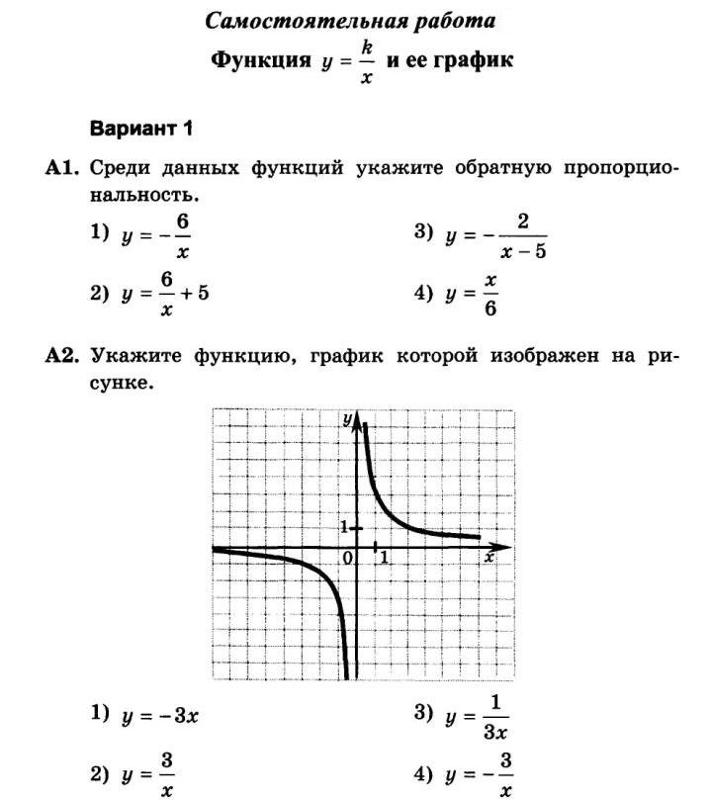 Ученикам восьмого класса важно хорошо знать функции, поскольку это фундаментальное понятие в исчислении.
Ученикам восьмого класса важно хорошо знать функции, поскольку это фундаментальное понятие в исчислении.
Отношения и функции
Отношения и функции являются важными математическими понятиями в программе 8-го класса по математике. Отношение — это просто изображение входов и выходов в виде упорядоченной пары. С другой стороны, функция — это особый тип отношения, в котором каждый вход имеет только один выход.
Различие между отношениями и функцией
Представления функций
Функция может быть представлена различными способами. Написание правила с использованием математического выражения, создание таблицы и построение графика — вот некоторые из способов представления функции. Учащиеся будут решать математические задачи восьмого класса, чтобы попрактиковаться в различных методах представления функции.
Линейные функции
Линейная функция — это функция, правило функции которой состоит из переменных, возведенных в степень единицы. График линейной функции всегда представляет собой прямую линию.
График линейной функции всегда представляет собой прямую линию.
Сравнение линейных и нелинейных функций
В этом разделе учащиеся 8-го класса изучают характеристики линейных функций и нелинейных функций. Здесь они узнают, как получать и интерпретировать линейные функции.
Анализ и набросок графиков
Мы используем графики для представления данных в понятной форме. Здесь студенты научатся анализировать и рисовать различные типы графиков.
Показатель степени и научная запись
Показатель степени представляет собой математическое представление, которое символизирует количество раз, когда число умножается само на себя. Мы можем использовать показатели степени вместо повторного умножения одного и того же числа, чтобы сократить или упростить выражения. Для упрощения термина мы можем использовать концепцию научной нотации, которая будет подробно обсуждаться позже.
- Законы экспонентов
- Разница между электроэнергией и показателем
Законы экспонентов
разница между властью и показателем
.
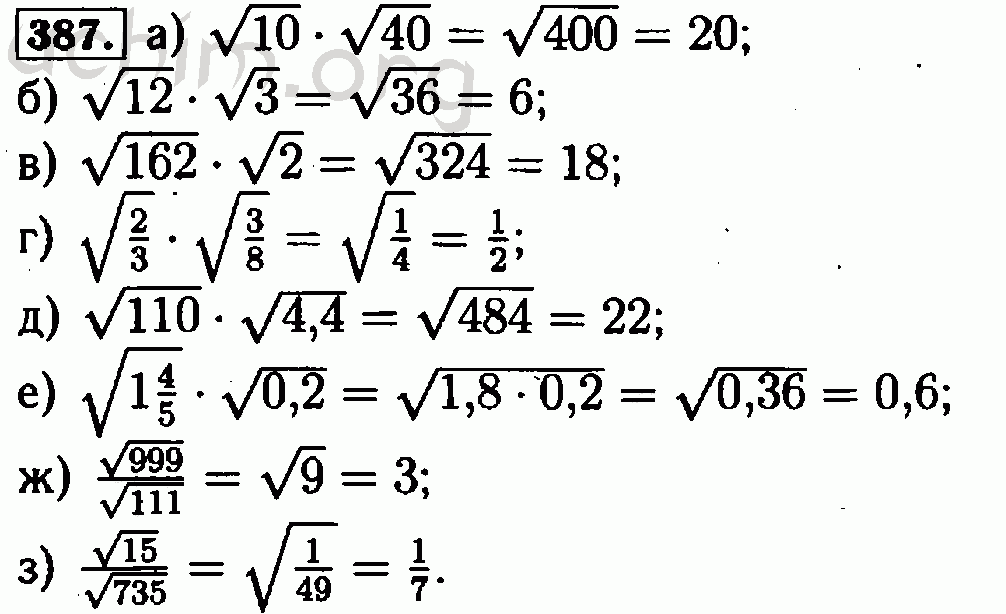 двух степеней с использованием произведения свойств степеней.
двух степеней с использованием произведения свойств степеней.Свойство отношения степеней
Здесь учащиеся изучат свойство отношения степеней, которое можно использовать для упрощения разделения двух степеней.
Нулевые и отрицательные показатели степени
Число можно увеличить до любого значения. До сих пор студенты узнали, что происходит, когда число возводится в положительную степень. Теперь учащиеся 8-го класса узнают, что означает возведение числа в ноль или в отрицательную степень.
Оценка количества
Оценка количества — важный навык, который учащиеся должны вычеркнуть из контрольного списка навыков восьмого класса. Это поможет им сэкономить время при решении математических задач.
Научное представление
Научное представление числа — это стандартный способ выражения числа с использованием степени 10. Восьмиклассники научатся использовать экспоненциальное представление для удобного представления больших и малых чисел.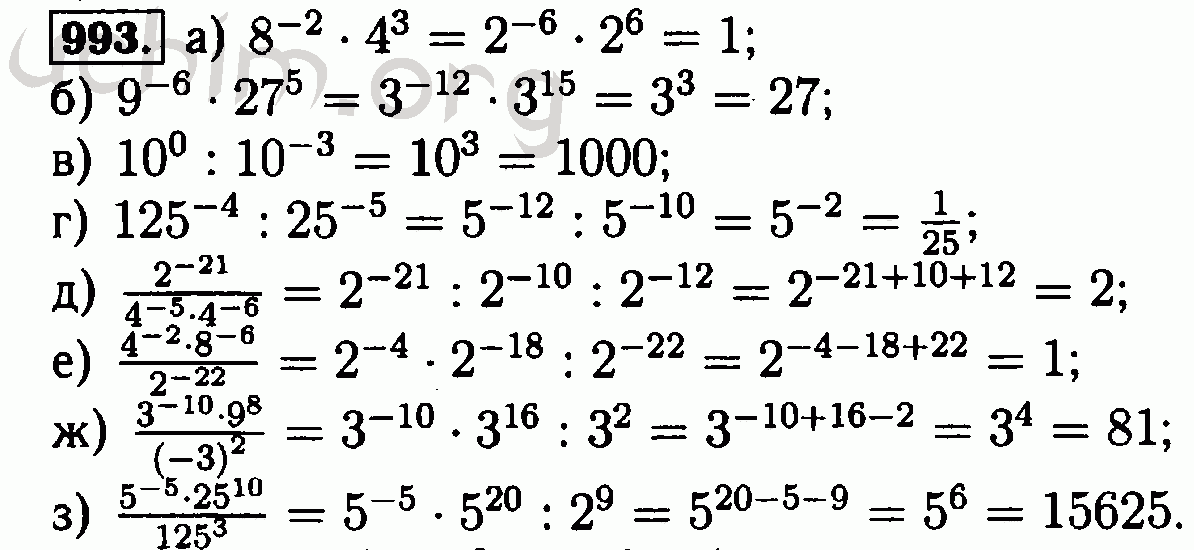 Учащиеся должны выучить эту нотацию, чтобы решать вопросы по математике и естественным наукам в старших классах.
Учащиеся должны выучить эту нотацию, чтобы решать вопросы по математике и естественным наукам в старших классах.
Операции с экспоненциальной записью
В этом разделе учащиеся 8-го класса научатся выполнять операции с экспоненциальной записью чисел.
Вещественные числа и теорема Пифагора
Множество действительных чисел включает все натуральные числа, целые числа, целые числа, дроби, рациональные числа и иррациональные числа. Восьмиклассники изучают различные типы действительных чисел. Наряду с действительными числами учащиеся также изучают теорему Пифагора, которая является важной темой в программе 8-го класса по математике.
- Квадратные корни: от 1 до 100
Квадратные корни
Здесь учащиеся 8-го класса учатся находить квадратный корень из заданного совершенного квадратного числа.
Perfect Square
Квадратные корневые уловки
квадратные корни: от 1 до 100
квадратный корень Finder
.
 треугольника, выведя соотношение между их длинами. В любом прямоугольном треугольнике площадь квадрата, стороной которого является гипотенуза, равна сумме площадей квадратов двух других сторон.
треугольника, выведя соотношение между их длинами. В любом прямоугольном треугольнике площадь квадрата, стороной которого является гипотенуза, равна сумме площадей квадратов двух других сторон.Обратная теорема Пифагора
Обратная теорема Пифагора утверждает, что если площадь квадрата, стороной которого является гипотенуза, равна сумме площадей квадратов двух других сторон, то угол, противоположный к гипотенузе — прямой угол.
Кубические корни
Кубический корень — это число, которое дает кубическое число при трехкратном умножении на само себя. Здесь ученики 8-го класса научатся находить кубические корни из чисел, с которыми они уже знакомы.
Совершенный куб чисел
Рациональные числа
Рациональное число — это число, которое может быть представлено в форме pq, где q0. В этом разделе ученики восьмого класса изучают свойства рационального числа.
Иррациональные числа
Иррациональное число — это число, которое не может быть выражено в форме pq. Студенты узнают, как распознавать иррациональное число, наблюдая за цифрами справа от десятичной точки.
Студенты узнают, как распознавать иррациональное число, наблюдая за цифрами справа от десятичной точки.
Разница между рациональными и иррациональными числами
Реальные числа
Операции на реальных числах
объем и аналогичные твердые вещества
WE используем концепцию объема для описания размера трех DIMERS
WE Researce of Trocuest Nimensional. Если быть точным, объем твердого тела – это пространство, занимаемое твердым телом. Учащиеся 8-го класса математики также узнают о концепции подобных твердых тел и связанных с ними свойствах.
- Цилиндры
- Сферы
Объемы цилиндров
Здесь учащиеся 8-го класса изучают формулу объема цилиндра. Они также будут решать математические задачи восьмого класса, чтобы тщательно изучить концепцию.
Цилиндры
Объемы конусов
Объем конуса изучается по отношению к объему цилиндра с тем же основанием. Учащиеся научатся использовать эту формулу для решения математических задач для восьмиклассников.
Учащиеся научатся использовать эту формулу для решения математических задач для восьмиклассников.
Конусы
Объемы сфер
Сфера представляет собой идеально круглую трехмерную форму, которая дает круглое поперечное сечение при разрезании по любой оси. Все точки на поверхности сферы равноудалены от ее центра.
Сферы
Площади поверхностей и объемы подобных тел
В этом разделе учащиеся 8-го класса математики научатся вычислять площадь поверхности и объем подобных тел. Учащиеся также будут решать математические задачи 8-го класса, чтобы полностью понять концепции.
Наклонной эскиз
Область нахождения и периметр различных форм
Поверхностные области и объемы
Сделайте математику для математики. your Kids
Веселые и увлекательные онлайн-рабочие листы по математике всегда помогают учащимся практиковать математические понятия в своем собственном темпе, не беспокоясь о неудачах. Это также отличный инструмент для обучения, который облегчает понимание сложных математических тем. Загрузите наши бесплатные распечатанные рабочие листы по математике здесь.
Это также отличный инструмент для обучения, который облегчает понимание сложных математических тем. Загрузите наши бесплатные распечатанные рабочие листы по математике здесь.
Часто задаваемые вопросы
Почему математика в 8 классе важна?
Большинство продвинутых понятий, преподаваемых в старших классах, будут основаны на базовых понятиях, преподаваемых в 8-м классе, поскольку 8-й класс действует как мост между средней и старшей школой. Следовательно, важно, чтобы все учащиеся овладели всеми понятиями, преподаваемыми в 8-м классе.
Как ученики могут получить хорошие оценки в 8-м классе?
Математика в 8-м классе требует много практики. Следовательно, учащиеся должны практиковать много вопросов, чтобы улучшить свои результаты по математике в восьмом классе. Учащиеся могут полагаться на концептуальные статьи и вопросы, доступные в BYJU’S Math, чтобы практиковать математические концепции восьмого класса.
Что такое квадратные и кубические корни?
Мы получаем квадратное число, когда умножаем число само на себя.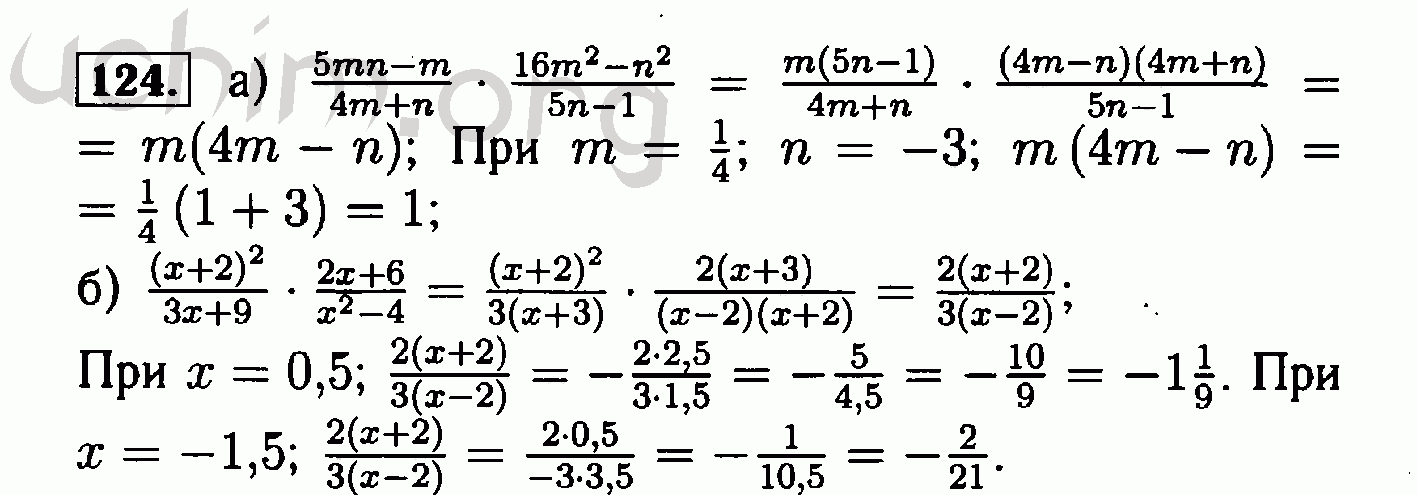



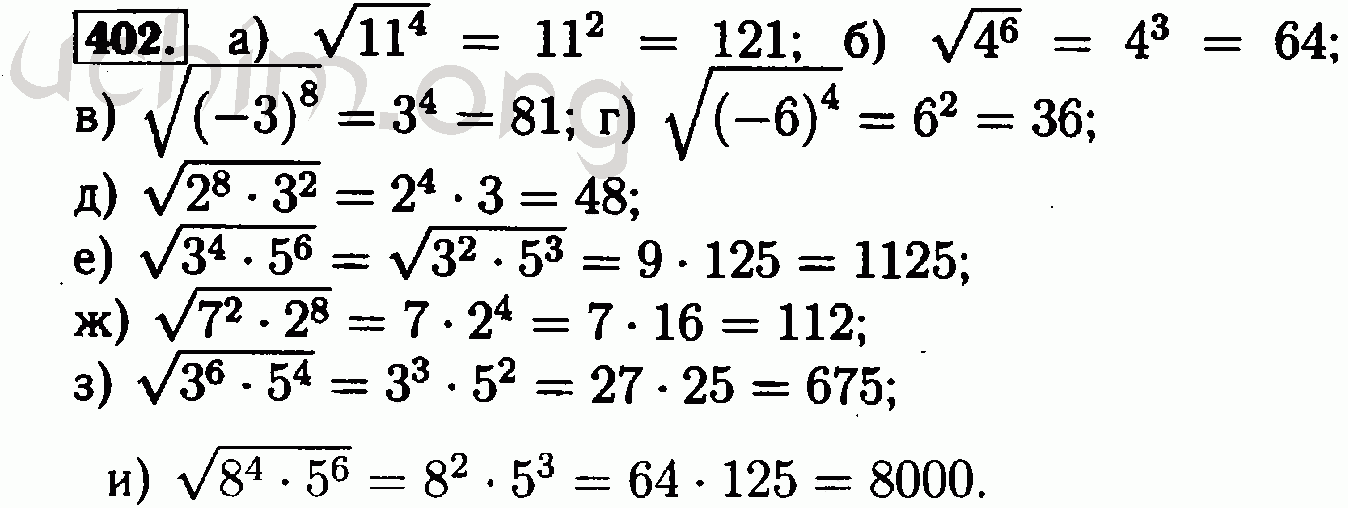 Г. / Семенов П.В. / Александрова Л.А. / Мардахаева Е.Л.
Г. / Семенов П.В. / Александрова Л.А. / Мардахаева Е.Л.
 7—9 классы. Алгебра и начала математического анализа. Базовый уровень. 10—11 классы. Примерные рабочие программы
7—9 классы. Алгебра и начала математического анализа. Базовый уровень. 10—11 классы. Примерные рабочие программы