Алгебра 7 теляковский: ГДЗ Алгебра 7 класс Макарычев

Алгебра 9 Макарычев К-6 В-1

06/01/202023/02/2022 Администратор

Контрольная работа по алгебре в 9 классе «Арифметическая прогрессия» с ответами и решениями (вариант 1). Ответы адресованы родителям, которые смогут проконтролировать правильность выполнения заданий. Алгебра 9 Макарычев К-6 В-1.

Другие варианты: К-6 Вариант 2   К-6 Вариант 3   К-6 Вариант 4

Вернуться к Списку контрольных работ (ОГЛАВЛЕНИЕ)

 

Алгебра 9 класс (Макарычев)

Контрольная работа № 6. Вариант 1

§ 9. Арифметическая прогрессия.

КР-6. Вариант 1 (транскрипт заданий)

1. Найдите тридцатый член арифметической прогрессии (а_n), если а₁ = –25 и d = 4.
2. Найдите сумму первых пятнадцати членов арифметической прогрессии (а_n), если а₁ = 2 и а₂ = 5.
3. Является ли число –6 членом арифметической прогрессии (с_n), в которой с₁ = 30 и с₇ = 21?
4. Найдите сумму первых двадцати членов последовательности, заданной формулой b_n = 2n + 1.
5. Найдите сумму всех натуральных чисел, кратных 4 и не превышающих 150.

 

Алгебра 9 Макарычев К-6 В-1

ОТВЕТЫ на контрольную работу:

№ 1. Найдите тридцатый член арифметической прогрессии (а_n), если а₁ = –25 и d = 4.

Дано: (a_n) – арифметическая прогрессия; a₁ = –25;  d = 4.
Найти: a₃₀ – ?
Решение: Формула n-го члена арифметической прогрессии: a_n = a₁ + d (n – 1), где a₁ – первый член прогрессии, d – разность прогрессии, n – количество её членов. С помощью этой формулы запишем искомый тридцатый член заданной прогрессии:
a₃₀ = a₁ + d (30 – 1) = a₁ + 29d.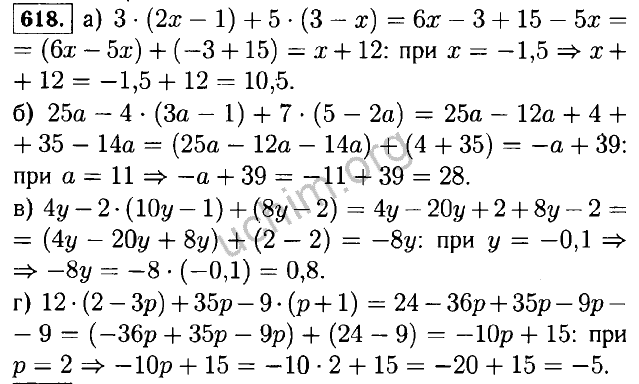 Подставим в полученное выражение известные нам по условию значения:
a₃₀ = a₁ + 29d = –25 + 29 • 4 = –25 + 116 = 91.
ОТВЕТ: a₃₀ = 91.

№ 2. Найдите сумму первых пятнадцати членов арифметической прогрессии (а_n), если а₁ = 2 и а₂ = 5.
ОТВЕТ: 345.
Решение:

№ 3. Является ли число –6 членом арифметической прогрессии (с_n), в которой с₁ = 30 и с₇ = 21?
ОТВЕТ: Да.
Решение:

№ 4. Найдите сумму первых двадцати членов последовательности, заданной формулой b_n = 2n + 1.
ОТВЕТ: 440
Решение:

№ 5. Найдите сумму всех натуральных чисел, кратных 4 и не превышающих 150.
ОТВЕТ: 2812.
Решение:

 

---

Вы смотрели: Контрольную работу по алгебре 9 класс «Арифметическая прогрессия» с ответами и решениями.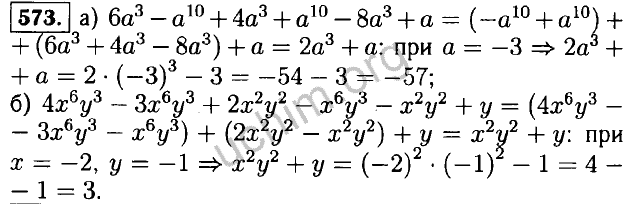 Представленная контрольная работа ориентирована на УМК Макарычева. Ответы адресованы родителям, которые смогут проконтролировать правильность выполнения заданий. Цитаты представлены в учебных целях, а также для ознакомления и покупки указанного учебного пособия. Алгебра 9 Макарычев К-6 В-1.

Другие варианты: К-6 Вариант 2   К-6 Вариант 3   К-6 Вариант 4

Вернуться к Списку контрольных работ (ОГЛАВЛЕНИЕ)

(c) В учебных целях использованы цитаты из пособия: «Алгебра. Дидактические материалы 9 класс / Макарычев, Миндюк, Крайнева — М.: Просвещение».

Ответы

Вас могут заинтересовать…

Презентация на тему «Сложение и вычитание многочленов». Презентация к занятию «Сложение и вычитание многочленов» и их степени

Цель занятия: Формирование положительных качеств личности в процессе формирования навыка по теме: «Сложение и вычитание многочленов» Задачи урока: 1 Тема: повторить правила сложения и вычитания многочленов, правила умножения, деления степеней, правила раскрытия скобок и упрощения выражений. 2. Метапредметные: адекватно использовать речь для решения различных коммуникативных задач, говорить и писать, закреплять навыки частично поисковой познавательной деятельности: осознавать проблему, делать выводы. 3. Личностные: умение вести диалог на основе равноправных отношений и взаимоуважения, самостоятельно анализировать условия достижения цели.

Устно а) 5ав б) 1,5а 0,6в в) (2ср) 2 — 1 г) 3в + в д) 7ху д) 6,7 — к Среди выражений выбрать многочлены Назовите буквы, под которыми стоят многочлены стандартного вида письменно Назовите степень каждого многочлена а) 5ав в) (2ав) 2 — 1 г) 3в + в д) 6,7 — к 3411

Многочлены. Сложение полиномов. Представьте полином в стандартной форме -4ava — 2a 2 in 2 5a 2 0.2a 2 in 3 + 2a 4 in 3 — av 13a — 8c -5a 2 — 5c 2 a 3 -1.4c 2 + 5a 2 5a 2 in — 13c 2 а -4а 2 в — 2а 2 в 2 3а 4 в 3 — ср

Расположите многочлены по степеням в порядке: 4, 3, 5, 7, 7, 2, 1. и E x A 13a — 8c -5a 2 — 5c 2 a 3 -1,4c 2 + 5a 2 5a 2 в — 13в 2 а 3 а 4 в 3 — ав л А х и л л Э Какая крылатая фраза связана с именем этого героя? в -4а 2 в — 2а 2 в 2 5а 2 в — 13в 2 а -5а 2 — 5в 2 а 3 3а 4 в 3 — аб -1.

4в 2 + 5а 2 13а — 8в

Мать Ахилла, Фетида, окунула младенца в воды подземной реки, сделав человека неуязвимым. В этом нырке она держала Ахиллеса за пятку, которая оставалась сухой и потому уязвимой. Во время Троянской войны вражеская стрела попала Ахиллесу в пятку, в результате чего он погиб. Выражение «Ахиллесова пята» в переносном смысле означает «слабое, уязвимое место».

Символически изображает голову и тело человека-Быка + льва-козла + человека-коня + человека-льва-птицу + + тело еще 3x 2 y — 2x 2 7x 2 — 5x 2 y 7x 2 y 2 — 8x 2 y 3x 2 y — 2x 2 6x 2 y -2x 2 y 2 x 2 y 2 — 3x 2 y — xy 2 7x 2 y 2 — 8x 2 y2xy 2 -6x 2 y 2 5x 2 — 2x 2 y 5x 2 y 2 — 2x 2 y x 2 года 2-3x 2×2 года 2-5x 2 года

Проверка домашнего задания 25.9 Найти сумму и разность многочленов А) р(а)=2а 5 +7а 4 +7а 3 +2а 2 +а+1 3а + 1 В) р(а) = -2а 5 + 4 + 9а 3 + а + 1 D) р (а) = -2а 5 -7а 4 -3а 3 + 4а 2 -3а (а, Ь) А )р(х;у)=57х 3 -30х 2 у+8ху 2 -3y 3 B)p(x;y)=17x 3 +3y (a,b) Решить уравнение A) 3 B) -1

Белый — самый простой (2 балла) Желтый — средней сложности (3 балла) Красный — самый сложный (4 балла) Белый (2а+5)+(3а-7)= (3а-4)+(11+ 3a)= желтый (4x 5 +2x+1)+(x 5 +x-2)= (x 11 +x 6 -3)+(2x 11 +3x 6 +1)= красный (4y 4 +2y 2 — 13)+ (4y 4 -4y 2 +13)= (18a 3 -3a 2 b-5ab 2 +2b 3)+(8a 3 +3a 2 b-5ab 2 +b 3)= 5a-2 6a+7 5x 5 +3x -1 3x 11 +4x y 4 -2y 2 26a 3 -10ab 2 +3b 3

Белый — самый простой (2 балла) Желтый — средней сложности (3 балла) Красный — самый сложный (4 балла) Белый (3а-4)-(-1-5а)= (5а-2)-(3а +4) = Желтый (2y 3 +8y-11)-(3y 3 -6y+3)= (15-7y 2)-(y 3 -y 2 -15)= Красный (y 3 -y+7)- (y 3 +5y+11)= (x 5 +x-2)-(4x 5 +2x-1)= 8a-3 2a-6 -y 3 +14y 3 -6y 2 -6y-4 -3x 5 -х- один

С6С6 С 11 С5С5 С 12 С3С3 С 10 С 13 -4х3х-7х-2х7х-3х к) 6) (с 5) 2 = (о) 3) (с 2) 6 * с = (м) 7) (с 3) 4 = (и) 4) с 7 * с 3 * с = (о) 1) 4х-8х = (д) 4)-9х + 15х + х = (и) 2) -3х + х = (л) 5) -2х + 5х = (в) 3) х 3 — (х 3 + 7х) = (к) 6) 7x 2 — (3x + 7x 2) = (e) C6PS6P C 11 O C5LS5L C 12 И C3HC3H C 10 O C 13 M -4x E 3x B -7x K -2x L 7x I — 3x D

Групповая работа В Средние века людей, умевших выполнять ЭТО АРИФМЕТИЧЕСКОЕ ДЕЙСТВИЕ, можно было пересчитать чуть ли не по пальцам. Их уважительно называли «мастерами…». Они переезжали из города в город по приглашению купцов, которые хотели привести свои счета в порядок. В Италии до сих пор сохранилась поговорка: «Это трудная задача —…». Так обычно говорят, когда сталкиваются с почти неразрешимой проблемой.

Конспект урока: «Сложение и вычитание многочленов»

Бондаренко Марина Эдуардовна, воспитатель ДОУ I-III ступеней №101 г.Донецка Донецкой области

Описание материала: конспект урока алгебры для учащиеся 7 класса на тему «Сложение и вычитание многочленов». Урок ориентирован на учебник «Алгебра, 7 класс» под редакцией С.А. Теляковского, Москва, 2016
Цель занятия:
— формирование у учащихся умения выполнять сложение и вычитание многочленов, применять изученный теоретический материал на практике
— развитие логического мышления; развитие умений и навыков в математическом плане
— формирование осознанного отношения к получению новых знаний и умений
Вид урока: изучение нового материала
На занятиях
I. Организационный момент
Приветствие учащихся, проверка готовности к уроку
II. Обновление базовых знаний
Для того, чтобы перейти к изучению нового материала, нам необходимо повторить материал предыдущего урока. А для этого проведем математический диктант.

Математический диктант
1. Как называется сумма одночленов? (многочлен)
2. Называются мономы, входящие в состав многочлена. . . (члены многочлена)
3. Если многочлен состоит из двух членов, то он называется. . . (двучленный)
4. Одночленом называется многочлен, состоящий из (один член)
5. Если члены имеют одинаковую буквенную часть, то они называются. . . ( аналогичный)
6. Если каждый член многочлена является мономом стандартного вида, и этот многочлен не содержит подобных членов, то он называется. . . (полином стандартной формы)

7. Степень полинома стандартной формы называется (наибольшая степень его монома)
Написав диктант, правильные ответы выводятся на слайд. Учащиеся ставят баллы друг другу через экспертную оценку.

III. Мотивация

Как называются выражения в скобках?
Какие действия с полиномами, написанными в скобках, нужно выполнить?
Скажите, что мы будем делать сегодня на уроке?
Итак, тема нашего урока «Сложение и вычитание многочленов»
Каковы цели нашего урока? (Ответы учащихся)

IV. Изучение нового материала
Вернемся к нашей задаче. Итак, составьте план, как сложить (группа 1) или вычесть (группа 2) многочлен.
Учащиеся предлагают план сложения (вычитания) многочленов для обсуждения.
Заключение записываем в тетрадку в виде алгоритма.

Произнося этот алгоритм, два ученика у доски записывают решение задачи. (все остальные в тетрадях)

V. Закрепление изученного материала
Какие виды заданий можно нам предложить по данной теме? (учебная работа)
— Привести к стандартной форме многочлен

— Упростить выражение
— Найти значение выражения
— Решить уравнение
Работа по мультимедиа и учебнику

№ 2 Найти значение выражения

#

6 3 Докажите, что значение выражения не зависит от переменной

#4 Решить уравнение

Далее учащимся предлагается решить самостоятельно задания из учебника, после чего следует проверка с объяснением.
№ 587, 595,
№ 597, 605
№ 602, 603
Для повторения № 612 (1-й столбец)
VI. Итоги урока
Что нового мы сегодня узнали? Чему вы научились?
Домашнее задание Выучить п.26, ответить на вопросы на стр. 134 решить № 589, 598, 606

Презентация на тему: Сложение и вычитание многочленов

Математика в переводе с древнегреческого означает изучение, знание, наука. Эта царица наук приводит разум в порядок, помогает дисциплинировать себя и, поняв ее принципы, умело применять их в жизни. Каждому, кто соприкасается с ней, она дает ясное мышление.

Пришло время наглядно вспомнить изученное ранее понятие «многочлен». Ответ прост: многочлен (или многочлен) есть сумма одночленов .

92 — 4б + 7

Теперь сделаем все наоборот, а именно научимся правильно ставить скобки после плюса или минуса.
Возьмем для примера следующий многочлен 5х — 3у + 1.
Задача: правильно расставить скобки после 5х и знаки «+» или «-«, учитывая следующие правила:

1. Если перед скобки, то термины, заключенные в скобки, записываются теми же знаками. Используем плюс.
Тогда полином будет выглядеть так: 5x — 3y + 1 = 5x + (- 3y + 1)

2. Если перед скобками ставится знак минус, то все члены, заключенные в скобки, должны быть перевернуты.

Тот же многочлен только со знаком минус 5х — 3у + 1 = 5х — (3у — 1)

слайд 5 (пример)

Как оказалось — «все гениальное просто».

Остается только сделать вывод: При сложении и вычитании многочленов мы используем один и тот же принцип, поэтому нет необходимости различать эти операции. Естественно, нет необходимости использовать два термина «сложение многочленов» и «вычитание многочленов». Невероятно, но две, казалось бы, разные противоположные функции на самом деле являются одним понятием «алгебраическая сумма многочленов».

Простейшие задачи с многочленом
Сегодня мы это сделали, друзья.
И вывод был смелый:
Что братья «плюс» и «минус»
Две стороны одной медали —
Алгебраическая сумма бытия.

Это еще раз показывает единство противоположностей, таких как да и нет, день и ночь, покой и движение, действие и противодействие. Все это наше одно огромное понятие — жизнь!

Презентация и раздаточный материал к занятию в 7 классе «Сложение и вычитание многочленов»

Цели и задачи учебного занятия:

• Учебная :
  • познакомить учащихся с правилами сложения и вычитания многочленов;
  • формировать навыки и умения сложения и вычитания многочленов, приведения слагаемых и раскрытия скобок.
• Образовательная :
  • формировать умение осуществлять мыслительные операции: выделять главное, систематизировать, анализировать;
  • развивать грамотность математического письма, память, слуховое восприятие.
• Образовательная :
  • прививать трудолюбие, усидчивость, аккуратность, аккуратность;
  • для формирования положительного отношения к предмету и интереса к знаниям.

Оборудование: учебник, доска.

Скачать:

Предварительный просмотр:

Чтобы использовать предварительный просмотр презентаций, создайте себе учетную запись (аккаунт) Google и войдите: https://accounts.google.com

Подписи к слайдам:

Сложение, вычитание многочленов. МБОУ лицей №1, г. Волжский, Волгоградской области. Учитель математики: Коротова И.В.

План урока. Теория Подготовка к УПД Практика Домашнее задание Изучение нового материала Индивидуальный опрос

Теория Моном. Одночлен стандартной формы. подобные термины. Сокращение подобных сроков. Полиномиальный. Многочлен стандартной формы. Алгоритм приведения многочлена к стандартному виду. Раскрывающие скобки, которым предшествует знак плюс (минус)

Выберите одночлены: 2 x + y; 3xу; 27аб2; гх + 4; 2м+5н; один ; 1 + к. Теория

Дайте аналогичные термины: -11ак + 8ак + 5ак; 7x 3 y 2 — 12 + 4x 2 y — 2y 2 x 3 + 6 Теория

Запишите полином в стандартной форме: 6 ab — 2 b 2 — 6 ba + 5 a 2 + 0,6 b 2 — 4 a b a + 2 a 2 b + 0,2 a 2 b 2 — 2 a 2 b 2 Теория

Открытые скобки. — (32 — 2а 2 б — 5б + 4а) + (-7 х + 8 у — 5ху + 7) Взаимная проверка

Взаимная проверка. Выделите одночлены: Отметьте 2 3 6 Приведите подобные члены: 2ak 5x 3 y 2 + 4x 2 y — 6 Запишите многочлен в стандартной форме -1.4b 2 +5a 2 -1.8a 2b 2 — 2a 2b Открытые скобки: — 32+2a 2b + 5b – 4a -7x + 8y – 5xy + 7 Итоговая оценка: план урока

Индивидуальный опрос. 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

Индивидуальный опрос. Низкий уровень 1 2 3 4 Средний уровень 1 2 3 4 Высокий уровень 1 2 3 4 Классная работа План урока

1. Низкий уровень Стандартизация полинома: Индивидуальный опрос

2. Низкий уровень Стандартизация полинома: Индивидуальный опрос

3. Низкий уровень Стандартизировать полином: Индивидуальное обследование

4. Низкий уровень Стандартизировать полином: Индивидуальное обследование

1. Средний уровень Представить полином в стандартной форме: 16a (-a 2 b) + 18a 3 b — 12aa b + 14a 2 б Индивидуальное обследование

2. Средний уровень Стандартизировать полином: 5 x (-4x 4) — 2 x 2 Z x 3 + 27 x 5 — x 6 Индивидуальное обследование

3. Средний уровень Представить полином в стандартной форме: 2y y 3 — Zu 2 4y 2 + 6y 4 — 8 y 4 — 11 Индивидуальное обследование

4. Средний уровень Представьте полином в стандартной форме: 23x 3 — 7 xx 2 y + 6x 2 x — 2 x 2 8y + 4 Индивидуальное обследование

1. Высокий уровень Выразите полином в стандартной форме: 3 a 2 b n+2 + 5 a 0,2 a b n+2 — 4 a 2 b n 0,5 b 2 + 2 a 2 b n bb Индивидуальный опрос

2. Высокий уровень Стандартизация полинома: 3,2x 2 x n x — 3,4 x n+1 2x 2 — 4,8x n+2 0,1x + x n+3 Индивидуальное обследование

3. Высокий уровень Стандартизация полинома: 0,3 y n +3 y 2 — 0,12y 2 y 0,1 y n+2 — 1,6 y n+2 yyy – 3 Индивидуальное обследование

4. Высокий уровень Стандартизация полинома: 3x n-2 x 5 -2x n 7x 2 x+4y n +1 4y 0.2y-12y n+1 0.1y 2 Индивидуальный опрос

Запишите сумму многочленов — 2 a + 5 b и — 2 b — 5 a 5y 2 + 2y — 3 и 7y 2 — 3y + 7. Запишите разность многочленов — 2а + 5б и — 2б — 5а 8у 2 + 5у + 3 и 5у 2 — 3у + 7 .

Запишите разность полиномов — 2 a + 5 b и — 2 b — 5 a 8y 2 + 5y + 3 и 5y 2 — 3y + 7.

Упростите выражение. (– 2 a + 5 b) + (– 2 b – 5 a) = Check

Упростите выражение. (5y 2 + 2y — 3) + (7y 2 — 3y + 7) = Check

Упростите выражение. (– 2 а + 5 б) + (– 2 б – 5 а) = – 2 а + 5 б – 2 б – 5 а = – 3 б – 7 а

Упростите выражение. (5у 2 + 2у — 3) + (7у 2 — 3у + 7) = 5у 2 + 2у — 3 + 7у 2 — 3у + 7 = 12у 2 — у + 4

Упростить выражение (- 2 a + 5 b) — (- 2 b — 5 a) = Проверить

Упростить выражение (8y 2 + 5y + 3) — (5y 2 — 3y + 7) = Проверить

Упростить выражение выражение (- 2 a + 5 b) — (- 2 b — 5 a) = — 2 a + 5 b + 2 b + 5 a = 7 b + 3 a

Упростим выражение (8y 2 + 5y + 3) — (5у 2 — 3у + 7) = 8у 2 + 5у + 3 — 5у 2 + 3у — 7 = 3у 2 + 8у — 4 План урока

Сложение и вычитание многочленов.

Правило сложения (вычитания) многочленов. Пусть даны два многочлена.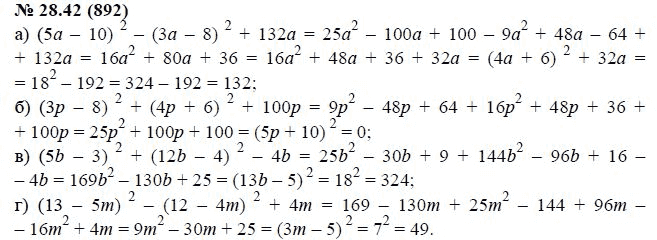 Для их добавления их пишут в скобках и ставят между ними знак плюс. При вычитании в скобках ставится знак минус. Для того чтобы найти алгебраическую сумму нескольких многочленов, нужно раскрыть скобки по соответствующему правилу и привести одинаковые члены. В результате сложения (вычитания) многочленов получается многочлен. План урока

Практические задания. № 587 (а, г) № 588 (б) Схема урока

Домашнее задание: Задание 26 № 589 (а, в) № 595 (а) № 612 (б)

а — б б а — х — y 2 x — y 3 y 3 a 0

2 a a — b b b — a a — b — b b + a 0 — x — y 2 x — y — x + 2 y 3 y 0 — 3 y x – 2 y — 2 x + y x + y

Низкий уровень Средний уровень 3 a 2 b 3 + 5 a 0,2 a b 2 — 4 a 2 b 2 0,5 b + 2 a 2 b 2 Высокий уровень 5 x n +4 2y — 10x n y 4x 4 -14 x n y 2 +18x n yy Проверка

Низкий -a b 2 Средний a 2 b 3 + 3 a 2 b 2 Высокий -30x n +4 y + 4 x n 2 План урока

Предварительный просмотр:

один . Взаимная проверка.

2. Классная работа

Ответ:	знак

один . Взаимная проверка.

2. Классная работа

Ответ:	знак

3 . Запишите в клетки каждого квадрата такие выражения, чтобы их сумма в каждом столбце, каждой строке и на каждой диагонали была равна выражению, написанному в треугольнике:

Предварительный просмотр:

Выразите полином в стандартной форме:

16a(-a 2 6) + 18a 3 6 — 12aa6 + 14a 2 6

5 x (-4x 4) — 2 x 2 W x 3 + 27 x 5 — x 6

2y y 3 — Zu 2 4y 2 + 6y 4 — 8 y 4 — 11

23x 3 — 7 xx 2 y + 6x 2 x — 2 x 2 8y + 4

3.2x 2 x n x — 3,4 х н +1 2 х 2 — 4,8 х н +2 0,1 х + х н +3.

0, 3 y n +3 y 2 — 0, 12 y 2 y 0,1 y n + 2 — 1,6 y n +2 yyy – 3

3x n-2 x 5 -2x n 7x 2 x+4y n+1 4y 0,2 у-12у н+1 0,1у 2

Предварительный просмотр:

Взаимная проверка.

Выберите одночлены:

слайд 2

План урока:

• Время организации

Учащиеся рассаживаются по командам (по 5-6 человек в каждой, парты накрываются соответственно). Каждая команда придумывает название и выбирает капитана.

• устная работа. Обновление, лобовая проверка знаний по теме

Учащиеся повторяют определение многочлена стандартной формы, правила сложения и вычитания многочленов.

• Решение проблем

Каждой команде нужно решить 4 задания, каждое оценивается в 5 баллов. Команда, выполнившая задание быстрее остальных, получает дополнительные 3 очка. Задания представлены в виде слайдов, и у каждой команды на столах распечатаны копии, куда учащиеся должны записать решения и ответы.

слайд 3

1) Представить многочлен в стандартной форме и заполнить таблицу буквами в соответствии с найденными ответами:

слайд 4

Заполнить таблицу буквами согласно найденным ответам:

слайд 5

Ответ:

• Ахиллес. Это герой древнегреческой мифологии, участник Троянской войны
• Какая крылатая фраза связана с именем этого героя?

слайд 6

• Мать Ахилла, Фетида, окунула младенца в воды подземной реки, сделав человека неуязвимым. В этом нырке она держала Ахиллеса за пятку, которая оставалась сухой и потому уязвимой. Во время Троянской войны вражеская стрела попала Ахиллесу в пятку, в результате чего он погиб.
• Выражение «Ахиллесова пята» в переносном смысле означает «слабое, уязвимое место».

Слайд 7

2) Внешний вид некоторых мифических персонажей состоит из головы и тела, взятых у разных существ. Выполнить полиномиальное сложение. Используя найденные ответы и данные таблицы, узнайте, как выглядели эти существа.

• Овал символизирует голову,
• Прямоугольник символически изображает туловище.

Слайд 8

Слайд 9

Ответ:

Слайд 10

мифический персонаж с головой быка и телом человека — минотавр. Существо с головой человека и телом лошади — кентавр. Сфинкс — персонаж с головой человека, телом льва и крыльями птицы. мифологическое существо с огнедышащей львиной пастью, телом козла и хвостом дракона — это химера. Ше’ду — крылатый бык с человеческим лицом и пятью ногами.

слайд 11

3) Запишите в клетки каждого квадрата такие выражения, чтобы их сумма в каждом столбце, каждой строке и каждой диагонали была равна выражению, написанному в треугольнике:

7: Булева алгебра — рабочая сила LibreTexts

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

937

• Tony R. Kuphaldt
• Schweitzer Engineering Laboratories via All About Circuits

Все арифметические операции, выполняемые с булевыми величинами, имеют только один из двух возможных результатов: либо 1, либо 0. В булевом мире нет таких вещей, как «2», «-1» или «1/2». Это мир, в котором все другие возможности недействительны по распоряжению. Как можно догадаться, это не та математика, которую вы хотите использовать при балансировке чековой книжки или расчете тока через резистор. Однако Клод Шеннон из Массачусетского технологического института понял, как булеву алгебру можно применить к схемам включения и выключения, где все сигналы характеризуются либо как «высокий» (1), либо как «низкий» (0).

• 7.1: Введение в булеву алгебру

• 7.2: Булева арифметика

  В булевой математике сложение эквивалентно логической функции ИЛИ, умножение эквивалентно, а дополнение эквивалентно И. логическая функция НЕ.

• 7.3: Булевы алгебраические тождества

  В математике тождество — это утверждение, истинное для всех возможных значений его переменной или переменных. Алгебраическое тождество x + 0 = x говорит нам, что все (x), добавленное к нулю, равняется исходному «чему угодно», независимо от того, какое значение может иметь это «что угодно» (x). Как и обычная алгебра, булева алгебра имеет свои уникальные тождества, основанные на бивалентных состояниях булевых переменных.

• 7.4: Булевы алгебраические свойства

  Коммутативные, ассоциативные и дистрибутивные свойства применимы к булевой алгебре.

• 7.5: Булевы правила упрощения

  Булева алгебра находит наиболее практическое применение при упрощении логических схем. Если мы переведем функцию логической схемы в символическую (булеву) форму и применим определенные алгебраические правила к полученному уравнению, чтобы уменьшить количество членов и/или арифметических операций, упрощенное уравнение можно перевести обратно в схемную форму для логической схемы, выполняющей ту же функцию с меньшим количеством компонентов.

• 7.6. Примеры упрощения схемы как XOR. В то время как функция ИЛИ эквивалентна логическому сложению, функция И — логическому умножению, а функция НЕ (инвертор) — логическому дополнению, прямого логического эквивалента для исключающего ИЛИ не существует. Однако это не помешало людям разработать символ для представления этих логических ворот.

• 7.8: Теоремы ДеМоргана

  Математик по имени ДеМорган разработал пару важных правил, касающихся групповых дополнений в булевой алгебре. Под групповым дополнением я имею в виду дополнение группы терминов, представленное длинной чертой более чем одной переменной.

• 7.9: Преобразование таблиц истинности в логические выражения

  При проектировании цифровых схем разработчик часто начинает с таблицы истинности, описывающей, что должна делать схема. Задача проектирования в значительной степени состоит в том, чтобы определить, какой тип схемы будет выполнять функцию, описанную в таблице истинности. Существуют доступные процедурные методы, и булева алгебра самым драматичным образом доказывает свою полезность.

---

Эта страница под названием 7: Булева алгебра распространяется в соответствии с лицензией GNU Free Documentation License 1.