5Terka.com — Отзывы и рекомендации
Вы находитесь здесь: Webwiki > 5terka.com Зарегистрировать здесь собственный сайт
Гото 5terka.com
Обновить запись
Сообщить о ссылке
Известность:
(ранг # 915 017)
Язык: русский
5тёрка: проверь свою домашку!
Ключевые слова: Гдз Решебник Решение Ответ
Отзывы и рейтинги 5terka.com
Оценить компанию
- Содержание
- технология
Содержание и ключевые слова
Важные и популярные веб-сайты
Веб-сайт с главной страницей «Гдз И Онлайн Решебники На Пятёрке! 5Terka. com» также размещает информацию на страницах Меню, Гдз По Классам и 7 Класс. Ниже перечислены наиболее важныe подстраницы 5terka.com :
com» также размещает информацию на страницах Меню, Гдз По Классам и 7 Класс. Ниже перечислены наиболее важныe подстраницы 5terka.com :
Актуальные темы для 5terka.com
Техническая информация
Веб-сайт 5terka.com имеет собственный веб-сервер, который обслуживает только данные веб-сайты.
Веб-страницы 5terka.com созданы с помощью языка программирования PHP. HTML-страницы созданы на основе новейшего стандарта HTML 5. В связи с отсутствием указаний по управлению устройствасбора данных Web Crawler в метаданных, содержание веб-сайта будет регистрироваться в поисковых системах.
Информация о сервере веб-сайта
| IP-адрес: | 45.128.206.165 |
Технические характеристики к технологии сайта
| ПО веб-сервера: | ddos-guard |
| Программная платформа: | PHP, Версия 7.3.16 |
| Время загрузки: | 0,63 секунд (быстрее, чем 56 % всех сайтов) |
| HTML-версия: | HTML 5 |
| Размер файла: | 134,73 KB (1291 распознанных слов в сплошном тексте) |
Безопасность и классификация
Веб-сайт не содержит сомнительной информации и может использоваться несовершеннолетними, а также в рабочей среде.
| Критерий | Оценка | |
|---|---|---|
Google Safebrowsing | безопасный | |
Разрешен для лиц младше 18 лет | ||
Безопасен для использования в рабочей среде | ||
Webwiki отзывы | нет отзыв | |
расположение сервера | Не найдено | |
| надежный 79% | ||
 Вся информация предоставляется без гарантии.
Вся информация предоставляется без гарантии.
Для администраторов сайта:
Добавить кнопки и актуальные оценки к собственному сайту!
Добавить кнопку Webviki
Похожие веб-сайты
Boomblog.ru — Обязанности менеджер по продаже шин дисков && ..
Stlegion.ru — Офисный переезд компании в Кемерово. Переезд ..
Mir-sant.ru —
Silversochi.ru — Истек срок регистрации домена silversochi.ru
Nagualapps.ru — решебник jykfqy по физике 8 класс лукашик — ..
5тёрка: проверь свою домашку!
General information
Domain Name: | 5terka. com com |
Registration Date: | 2010-02-24T16:10:36Z |
Expiration Date: | 2023-02-24T16:10:36Z |
Registrar URL: | Regtime Ltd. |
Registrar Contact: | +7 846 3733047 |
Hosted In: | |
Safety: | Safe |
Domain Extension: | .com |
IP address: |
Meta Data Analysis
Website Name:
5тёрка: проверь свою домашку!Website Description:
5тёрка: проверь свою домашку! Website Keywords:
ГДЗ, решебник, решение, ответRankings
Alexa Rank: | 50994 |
OverAll Traffic Chart | Search-Engine Traffic Chart |
Security & Safety
Google Safe Browsing: | Safe |
WOT Trustworthiness: | # |
Siteadvisor Rating: | # |
Geographics
City: | |
Country Name: | |
Latitude: | |
Longitude: |
DNS Analysis
| Host | Type | Class | TTL | Target |
5terka. com com | A | IN | 7199 | |
| 5terka.com | MX | IN | 7199 | mx.yandex.ru |
| 5terka.com | NS | IN | 7199 | ns1.nameself.com |
| 5terka.com | NS | IN | 7199 | ns2.nameself.com |
| 5terka.com | TXT | IN | 7199 | |
| 5terka.com | SOA | IN | 7199 |
SEO Analysis
Site Status | Congratulations! Your site is alive. |
Title Tag | The meta title of your page has a length of 52 characters. Most search engines will truncate meta titles to 70 characters. |
Meta Description | The meta description of your page has a length of 52 characters. |
Google Search Results Preview | 5тёрка: проверь свою домашку! |
Most Common Keywords Test | There is likely no optimal keyword density (search engine algorithms have evolved beyond
keyword density metrics as a significant ranking factor). It can be useful, however, to note which
keywords appear most often on your page and if they reflect the intended topic of your page. More
importantly, the keywords on your page should appear within natural sounding and grammatically
correct copy. -> e-mailadminterkacomadminterkacom — 1 -> ctrlenter — 1 -> terkacom — 1 |
Keyword Usage | Your most common keywords are not appearing in one or more of the meta-tags above. |
h2 Headings Status | Your pages having these h2 headigs. |
h3 Headings Status | Your pages having these h3 headigs. -> Решебники по физике -> Решебники по химии -> 9 класс -> Решебники по алгебре -> Решебники по геометрии -> Решебники по физике -> Решебники по химии -> 10 класс -> Решебники по геометрии -> Решебники по физике -> Решебники по химии -> 11 класс -> Решебники по геометрии -> Решебники по физике -> Решебники по химии |
Robots. | Your page doesn’t have «robots.txt» file |
Sitemap Test | Your page doesn’t have «sitemap.xml» file. |
Broken Links Test | Congratulations! Your page doesn’t have any broken links. |
Image Alt Test | 62 images found in your page and 2 images are without «ALT» text. |
Google Analytics | Your page not submitted to Google Analytics |
Favicon Test | Congratulations! Your website appears to have a favicon. |
Site Loading Speed Test | Your site loading time is around 1.6288840770721 seconds and the average loading speed of any website which is 5 seconds required. |
Flash Test | Congratulations! Your website does not include flash objects (an outdated technology that was sometimes used to deliver rich multimedia content). Flash content does not work well on mobile devices, and is difficult for crawlers to interpret. |
Frame Test | Congratulations! Your webpage does not use frames. |
CSS Minification | Your page having 1 external css files and out of them 1 css files are minified. |
JS Minification | Your page having 9 external js files and out of them 2 js files are minified. |
Решайте неравенства и системы с помощью программы «Пошаговое решение математических задач». В большинстве случаев можно найти точные решения. Даже если это невозможно, QuickMath может дать вам приближенные решения практически для любого требуемого уровня точности. Кроме того, вы можете нанести области, удовлетворяющие одному или нескольким неравенствам в двух переменных, четко видя, где происходят пересечения этих областей.
Что такое неравенства?
Неравенства состоят из двух или более алгебраических выражений, соединенных символами неравенства. Символы неравенства:
| < | меньше |
| > | больше |
| <= | меньше или равно |
| >= | больше или равно |
| != или <> | не равно |
Вот несколько примеров неравенств:
|
Решить
Команда Решить может быть использована для решения одного неравенства для одного
неизвестно из базовой страницы решения
или одновременно решить систему многих неравенств с одним неизвестным на странице расширенного решения. Расширенная команда позволяет указать, хотите ли вы
приблизительные числовые ответы, а также точные, и сколько цифр
точность (до 16) вам требуется.
Расширенная команда позволяет указать, хотите ли вы
приблизительные числовые ответы, а также точные, и сколько цифр
точность (до 16) вам требуется.
Множественные неравенства в расширенной секции соединяются по И. Например, неравенства 92 — 5 < 0
Другими словами, QuickMath попытается найти решения, удовлетворяющие сразу обоим неравенствам.
Перейти на страницу решения
График
Команда График из раздела Графики отображает любое неравенство, включающее
две переменные. Чтобы построить область, удовлетворяющую одному неравенству
включая x и y, перейти к основному
страница построения графика неравенства, где вы можете ввести неравенство и указать
верхний и нижний пределы x и y, которые вы хотите построить на графике
за.
Передовой
Страница построения графика неравенства позволяет вам построить объединение или пересечение
до 8 регионов на одном графике. У вас есть контроль над такими вещами, как
или не показывать оси, где оси должны располагаться и какой аспект
отношение участка должно быть. Кроме того, у вас есть возможность показать каждый
отдельный регион самостоятельно.
Кроме того, у вас есть возможность показать каждый
отдельный регион самостоятельно.
Уравнение говорит, что два выражения равны, а неравенство говорит что одно выражение больше, больше или равно, меньше или меньше или равно другому. Как и в случае с уравнениями, значение переменной для что неравенство верно, является решением неравенства, и множество всех такие решения являются множеством решений неравенства. Два неравенства с одно и то же множество решений являются эквивалентными неравенствами. Неравенства решаются с помощью следующие свойства неравенства.
СВОЙСТВА НЕРАВЕНСТВА
Для действительных чисел a, b и c:
(a)
(Одно и то же число может быть добавлено к обеим частям неравенства без изменения множество решений.)
(b)
(Обе части неравенства можно умножить на одно и то же положительное число без изменения набора решений.)
(c)
(Обе части неравенства можно умножить на одно и то же отрицательное число
без изменения множества решений, пока направление неравенства
символ перевернут. )
)
Замена < на > приводит к эквивалентным свойствам.
ПРИМЕЧАНИЕ Поскольку деление определяется как умножение, слово «умножение» может быть заменено на «деление» в частях (b) и (c) свойств. неравенства.
Обратите особое внимание на часть (c): если обе части неравенства умножается на отрицательное число, направление символа неравенства должно быть перевернутый. Например, начиная с истинного утверждения — 3 < 5 и умножая обе стороны на положительное число 2 дает
по-прежнему верное утверждение. С другой стороны, начиная с — 3 < 5 и умножение обеих частей на отрицательное число -2 дает истинный результат, только если направление символа неравенства меняется на противоположное.
Аналогичная ситуация возникает при делении обеих частей на отрицательное число. В
Подводя итог, можно сделать следующее утверждение.
При умножении или делении обеих частей неравенства на минус
число, мы должны изменить направление символа неравенства, чтобы получить
эквивалентное неравенство.
ЛИНЕЙНЫЕ НЕРАВЕНСТВА Линейное неравенство определяется аналогично линейное уравнение.
Линейное неравенство с одной переменной — это неравенство, которое можно записать в форма
где a <> 0.
Пример 1
Решите неравенство -3x + 5 > -7.
Используйте свойства неравенства. Добавление — 5 с обеих сторон дает
Теперь умножьте обе стороны на -1/3. (Мы могли бы также разделить на -3.) Так как -1/3 < 0, измените направление символа неравенства.
Исходному неравенству удовлетворяет любое действительное число меньше 4. набор решений можно записать {x|x < 4}. График набора решений показан на Рисунок 2.6, где скобки используются, чтобы показать, что 4 само по себе не принадлежит к набору решений.
Множество {x|x < 4}, множество решений неравенства в примере 1, является примером
интервала. Упрощенная запись, называемая интервальной записью, используется для
интервалы записи. В этих обозначениях интервал в примере 1 можно записать
как (-оо, 4). Символ -oo не является действительным числом; используется, чтобы показать, что
интервал включает все действительные числа меньше 4. Интервал (-оо, 4) является примером
открытый интервал, так как конечная точка 4 не является частью интервала. Примеры
другие наборы, записанные в интервальной нотации, показаны ниже. Квадратная скобка
используется, чтобы показать, что число является частью графика, а круглые скобки используются для
указывают, что число не является частью графика. Всякий раз, когда два действительных числа a и
b используются для записи интервала на следующей диаграмме, предполагается, что < б.
В этих обозначениях интервал в примере 1 можно записать
как (-оо, 4). Символ -oo не является действительным числом; используется, чтобы показать, что
интервал включает все действительные числа меньше 4. Интервал (-оо, 4) является примером
открытый интервал, так как конечная точка 4 не является частью интервала. Примеры
другие наборы, записанные в интервальной нотации, показаны ниже. Квадратная скобка
используется, чтобы показать, что число является частью графика, а круглые скобки используются для
указывают, что число не является частью графика. Всякий раз, когда два действительных числа a и
b используются для записи интервала на следующей диаграмме, предполагается, что < б.
Пример 2
Решите 4 — 3y < 7 + 2y. Запишите решение в интервальной записи и на графике.
решение на числовой прямой. Напишите следующий ряд эквивалентных
неравенства.
В нотации построителя наборов набор решений равен {y|y>=3/5}, а в интервале
обозначение множество решений (-3/5, оо). См. рис. 2.7, где показан график набора решений.
См. рис. 2.7, где показан график набора решений.
В дальнейшем решения всех неравенств будут записываться с интервалом обозначение.
ТРЕХЧАСТНЫЕ НЕРАВЕНСТВА Неравенство -2 < 5 + 3m < 20 в следующем
пример говорит, что 5 + 3m находится между -2 и 20. Это неравенство можно решить
используя расширение свойств неравенства, приведенное выше, работая со всеми
три выражения одновременно.
Решите -2 < 5 + 3m < 20.
Запишите эквивалентные неравенства следующим образом.
Решение показано на рис. 2.8
КВАДРАТНЫЕ НЕРАВЕНСТВА Решение квадратных неравенств зависит от
решение квадратных уравнений.
Квадратное неравенство — это неравенство, которое можно записать в виде
Квадратные неравенства мы обсудим в следующем разделе.
Перейти на страницу построения графиков неравенств
Калькулятор сравнения дробей
Базовый калькулятор
Сравнение дробей
Сравнение целых чисел, десятичных дробей, дробей, смешанных чисел или процентов
Операнд 1
а также
Операнд 2
Ответ:
1 3/4 < 1,875
с показателем работы
Использование данных входов:
1 3/4
1,875
Переписывание этих вводов AS DECIMAL:
1 3/
9. 875.875.875.875.875.875.875.875.
875.875.875.875.875.875.875.875.1,75
1,875
Сравнение десятичных значений, которые мы имеем:
1 3/4
1,875
1,75
<
1.875
Следовательно.0004 1 3/4 < 1,875
Поделитесь этой ссылкой для ответа: help
Вставьте эту ссылку в электронное письмо, текст или социальные сети.
Получить виджет для этого калькулятора
© Calculator Soup
Поделитесь этим калькулятором и страницей
Калькулятор Используйте
Сравните дроби, чтобы найти, какая дробь больше, а какая меньше. Вы также можете использовать этот калькулятор для сравнения смешанных чисел, сравнения десятичных дробей, сравнения целых чисел и сравнения неправильных дробей.
Как сравнивать дроби
Чтобы сравнить дроби с разными знаменателями, преобразуйте их в эквивалентные дроби с одинаковым знаменателем.
- Если у вас есть смешанные числа, преобразуйте их в неправильные дроби
- Найдите наименьший общий знаменатель (LCD) дробей
- Преобразуйте каждую дробь в ее эквивалент с ЖК-дисплеем в знаменателе
- Сравните дроби: если знаменатели совпадают, вы можете сравнить числители. Дробь с большим числителем и есть большая дробь.
Пример:
Сравните 5/6 и 3/8.
Найдите ЖК-дисплей: числа, кратные 6, равны 6, 12, 18, 24, 30 и т. д. Кратные числа 8 равны 8, 16, 24, 32 и т. д. Наименьшее общее кратное равно 24, поэтому мы используем его в качестве наименьший общий знаменатель.
Преобразуйте каждую дробь в эквивалентную ей дробь с помощью ЖК-дисплея.
Для 5/6 умножьте числитель и знаменатель на 4, чтобы получить LCD = 24 в знаменателе.

 Most search engines will truncate meta descriptions to 160 characters.
Most search engines will truncate meta descriptions to 160 characters. 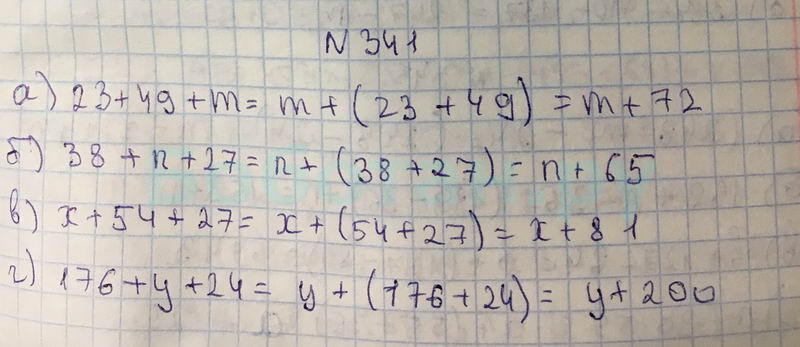 Your
primary keywords should appear in your meta-tags to help identify the topic of your webpage to
search engines.
Your
primary keywords should appear in your meta-tags to help identify the topic of your webpage to
search engines. txt Test
txt Test
 js
js