11 16 11 8 11 2: В двоичной системе сумма 11_2 + 11_8 + 11_16 равна… — Информатика и ИКТ

Тест по информатике Системы счисления 11 класс

Тест по информатике Системы счисления с ответами для учащихся 11 класса. Тест состоит из 4 вариантов в каждом по 9 заданий.

1 вариант

1. Даны числа А = В,9₁₆ и В = 13,4₈. Какое из чисел С, записанных в двоичной системе счисления, отвечает условию А

1) С = 1011,1₂
2) С = 1011,11₂
3) С = 1011,101₂
4) С = 10101,1001₂
5) нет правильного ответа.

2. Какое из чисел, записанных в шестнадцатеричной системе счисления, предшествует числу 10000₈? ­

1) 1FF
2) FFF
3) FF7
4) 7FF
5) FF1

3. Среди всех чисел, заключённых между числами 341 и 511, найдите то, которое после перевода в двоич­ную систему счисления содержит в своей записи наимень­шее количество единиц. Ответ запишите в десятичной системе счисления. Если таких чисел оказалось несколь­ко, запишите их через запятую.

4. Каково основание системы счисления, в которой 11 х 11 = 1001? Если таких оснований несколько, то пе­речислите их через запятую в порядке возрастания.

5. Определите основание системы счисления, в кото­рой справедливо равенство
21,2 + 11,2 + 22,1 = 110.
Если есть несколько вариантов ответа, то перечислите их в порядке возрастания, отделив друг от друга пробе­лом. Если такой системы счисления не существует, запи­шите в ответ число 0.

6. Запишите через запятую все основания систем счисления, в которых запись десятичного числа 29 окан­чивается цифрой 5.

7. Решите уравнение 1100₂ + 10₂ х X = 101011₂. Ответ дайте в системе счисления с основанием 8.

8. Записи некоторого числа в пятеричной и четве­ричной системах счисления различаются только порядком двух последних цифр. Укажите это число в десятичной системе счисления (если таких чисел несколько, то пере­числите их через запятую в порядке возрастания).

9. Переведите из десятичной системы счисления в шестеричную число 12,73. Ответ запишите, округлив шес­теричную дробь до трёх знаков после запятой.

2 вариант

1. Даны числа А = 13,Е₁₆ и В = 24,6₈. Какое из чи­сел С, записанных в двоичной системе счисления, отвеча­ет условию А

1) С = 10100,01₂
2) С = 10100,111₂
3) С = 10011,11₂
4) С = 10101,01₂
5) нет правильного ответа

2. Какое из чисел, записанных в шестнадцатеричной системе счисления, предшествует числу 1100₈?

1) FF1
2) 234
3) 1FF
4) 2F1
5) 23F

3. Среди всех чисел, заключённых между числами 603 и 637, найдите то, которое после перевода в двоич­ную систему счисления содержит в своей записи наиболь­шее количество нулей. Ответ запишите в десятичной сис­теме счисления. Если таких чисел оказалось несколько, запишите их через запятую.

4. Каково основание системы счисления, в которой 13 x 13 = 301? Если таких оснований несколько, то пере­числите их через запятую в порядке возрастания.

5. Определите основание системы счисления, в кото­рой справедливо равенство
31,5 + 40,6 + 65,3 = 201.
Если есть несколько вариантов ответа, то перечислите их в порядке возрастания, отделив друг от друга пробе­лом. Если такой системы счисления не существует, запи­шите в ответ число 0.

6. Запишите через запятую все основания систем счисления, в которых запись десятичного числа 33 окан­чивается цифрой 5.

7. Решите уравнение 1111₂ + 10₂ х X = 101010₂. От­вет дайте в системе счисления с основанием 8.

8. Записи некоторого числа в восьмеричной и девя­теричной системах счисления различаются только поряд­ком двух последних цифр. Укажите это число в десятич­ной системе счисления (если таких чисел несколько, то перечислите их через запятую в порядке возрастания).

9. Переведите из десятичной системы счисления в шестеричную число 21,86. Ответ запишите, округлив шес­теричную дробь до трёх знаков после запятой.

3 вариант

1. Даны числа А = 2А,3₁₆ и В = 51,1₈. Какое из чи­сел С, записанных в двоичной системе счисления, отвеча­ет условию В

1) С = 101010,01₂
2) С = 101001,001₂
3) С = 101010,0011₂
4) С = 101010,001₂
5) нет правильного ответа

2. Какое из чисел, записанных в шестнадцатеричной системе счисления, предшествует числу 1020₈

?

1) 1FF
2) F0F
3) 20F
4) 217
5) FF7

3. Среди всех чисел, заключённых между числами 515 и 560, найдите то, которое после перевода в двоич­ную систему счисления содержит в своей записи наиболь­шее количество единиц. Ответ запишите в десятичной системе счисления. Если таких чисел оказалось несколь­ко, запишите их через запятую.

4. Каково основание системы счисления, в которой 16 x 16 = 304? Если таких оснований несколько, то пере­числите их через запятую в порядке возрастания.

5. Определите основание системы счисления, в кото­рой справедливо равенство
35,4 + 23,5 + 14,2 = 72.
Если есть несколько вариантов ответа, то перечислите их в порядке возрастания, отделив друг от друга пробе­лом. Если такой системы счисления не существует, запи­шите в ответ число 0.

6. Запишите через запятую все основания систем счисления, в которых запись десятичного числа 31 окан­чивается цифрой 7.

7. Решите уравнение: 1001₂ + 10₂ х X = 101100₂. Ответ дайте в системе счисления с основанием 8.

8. Записи некоторого числа в семеричной и шесте­ричной системах счисления различаются только порядком двух последних цифр. Укажите это число в десятичной системе счисления (если таких чисел несколько, то пере­числите их через запятую в порядке возрастания).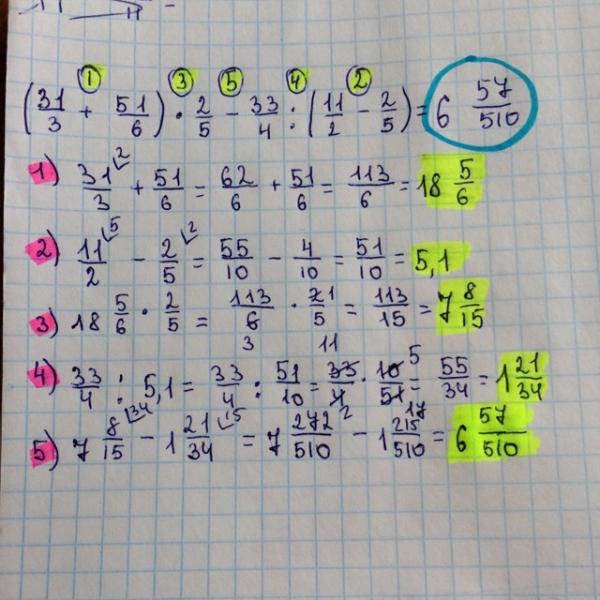

9. Переведите из десятичной системы счисления в семеричную число 12,13. Ответ запишите, округлив семе­ричную дробь до трёх знаков после запятой.

4 вариант

1. Даны числа А = 34,5₈ и В = 1С,6₁₆. Какое из чи­сел С, записанных в двоичной системе счисления, отвеча­ет условию В

1) С = 11100,01₂
2) С = 11100,111₂
3) С = 11100,1₂
4) С = 11100,011₂
5) нет правильного ответа

2. Какое из чисел, записанных в шестнадцатеричной системе счисления, предшествует числу 1000₈?

1) FF
2) FFF
3) 7FF
4) 1FF
5) FF1

3. Среди всех чисел, заключённых между числами 751 и 763, найдите то, которое после перевода в двоич­ную систему счисления содержит в своей записи наимень­шее количество нулей. Ответ запишите в десятичной системе счисления. Если таких чисел оказалось несколько, запишите их через запятую.

4. Каково основание системы счисления, в которой 19 x 19 = 309? Если таких оснований несколько, то пере­числите их через запятую в порядке возрастания.

5. Определите основание системы счисления, в кото­рой справедливо равенство
35,4 + 23,5 + 14,3 = 122.
Если есть несколько вариантов ответа, то перечислите их в порядке возрастания, отделив друг от друга пробе­лом. Если такой системы счисления не существует, запи­шите в ответ число 0.

6. Запишите через запятую все основания систем счисления, в которых запись десятичного числа 23 окан­чивается цифрой 5.

7. Решите уравнение 1101₂ + 10₂ х X = 101010₂. Ответ дайте в системе счисления с основанием 8.

8. Записи некоторого числа в семеричной и восьме­ричной системах счисления различаются только порядком двух последних цифр. Укажите это число в десятичной системе счисления (если таких чисел несколько, то пере­числите их через запятую в порядке возрастания).

9. Переведите из десятичной системы счисления в семеричную число 21,41. Ответ запишите, округлив семе­ричную дробь до трёх знаков после запятой.

Ответы на тест по информатике Системы счисления
1 вариант
1. 5
2. 2
3. 384
4. 2
5. 5
6. 6, 8, 12, 24
7. 17,4
8. 28
9. 20,422
2 вариант
1. 1
2. 5
3. 608
4. 4
5. 7
6. 7, 14, 28
7. 15,4
8. 124, 177
9. 33,510
3 вариант
1. 4
2. 3
3. 543, 559
4. 8
5. 11
6. 8, 12, 24
7. 21,4
8. 68
9. 15,063
4 вариант
1. 3
2. 4
3. 759
4. 12
5. 6
6. 6, 9, 18
7. 16,4
8. 94, 133
9. 30,261

PDF-версия
Тест Системы счисления(91 Кб, pdf)

Демоверсия ЕГЭ по информатике 2023 (Задания 11-15)

Продолжаем решать демоверсию ЕГЭ по информатике 2023.

Условия задач были взяты с сайта: https://fipi.

ru/ege/demoversii-specifikacii-kodifikatory#!/tab/151883967-5

Видеокурс — это то, с чего лучше всего начать подготовку к ЕГЭ по информатике.

Демоверсия ЕГЭ по информатике 2023 (Задания 1-5)
Демоверсия ЕГЭ по информатике 2023 (Задания 6-10)
Демоверсия ЕГЭ по информатике 2023 (Задания 16-21)
Демоверсия ЕГЭ по информатике 2023 (Задания 22-27)

Задание 11

При регистрации в компьютерной системе каждому объекту присваивается идентификатор, состоящий из 250 символов и содержащий только десятичные цифры и символы из 1650-символьного специального алфавита. В базе данных для хранения каждого идентификатора отведено одинаковое и минимально возможное целое число байт. При этом используется посимвольное кодирование идентификаторов, все символы кодируются одинаковым и минимально возможным количеством бит.

Определите объём памяти (в Кбайт), необходимый для хранения 65 536 идентификаторов. В ответе запишите только целое число – количество Кбайт.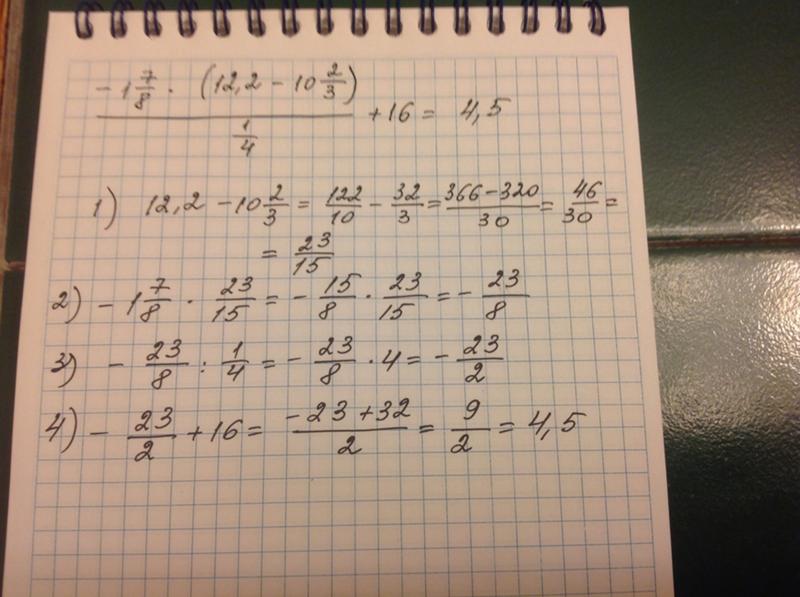

Решение:

Воспользуемся формулой для 11-ого задания из ЕГЭ по информатике.

Вместо N подставляем число 1650 + 10 = 1660 (1650 символов плюс 10 цифр). Тогда

1660 11

Т.е. 11 бит точно хватит, чтобы закодировать 1650 символов.

В идетификаторе всего 250 ячейки. Найдём сколько будет «весить» один идетификатор: 250 * 11 = 2750 бит. Узнаем, сколько байт потребуется для одного идентификатора 2772 / 8 = 344 байт (округлили в большую сторону, чтобы точно хватило).

У нас всего 65536 идентификаторов. Тогда нам потребуется 65536 * 344 = 22544384 байт. Переведём в Кб: 22544384 / 1024 = 22016 Кб.

Ответ: 22016

Задание 12

Исполнитель Редактор получает на вход строку цифр и преобразовывает её. Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки цифр.

А) заменить (v, w).

Эта команда заменяет в строке первое слева вхождение цепочки v на цепочку w. Например, выполнение команды

    заменить (111, 27)

преобразует строку 05111150 в строку 0527150.

    заменить (v, w) не меняет эту строку.

Б) нашлось (v).

Эта команда проверяет, встречается ли цепочка v в строке исполнителя Редактор. Если она встречается, то команда возвращает логическое значение «истина», в противном случае возвращает значение «ложь». Строка исполнителя при этом не изменяется.

Цикл

    ПОКА условие
      последовательность команд
    КОНЕЦ ПОКА

выполняется, пока условие истинно.

В конструкции

    ЕСЛИ условие
      ТО команда1
      ИНАЧЕ команда2
    КОНЕЦ ЕСЛИ

выполняется команда1 (если условие истинно) или команда2 (если условие ложно).

Дана программа для Редактора:

НАЧАЛО
ПОКА нашлось (>1) ИЛИ нашлось (>2) ИЛИ нашлось (>0)
  ЕСЛИ нашлось (>1)
    ТО заменить (>1, 22>)
  КОНЕЦ ЕСЛИ
  ЕСЛИ нашлось (>2)
    ТО заменить (>2, 2>)
  КОНЕЦ ЕСЛИ
  ЕСЛИ нашлось (>0)
    ТО заменить (>0, 1>)
  КОНЕЦ ЕСЛИ
КОНЕЦ ПОКА
КОНЕЦ

На вход приведённой выше программе поступает строка, начинающаяся с символа «>», а затем содержащая 39 цифр «0», n цифр «1» и 39 цифр «2», расположенных в произвольном порядке.

Определите наименьшее значение n, при котором сумма числовых значений цифр строки, получившейся в результате выполнения программы, является простым числом.

Решение:

Есть отличный разбор 12 задания в видеокурсе по подготовке к ЕГЭ по информатике.

Единица превращается в две двойки. Двойка преходим в саму себя. Ноль превращается в 1.

Изначально было 39 нулей. Значит, 39 единиц уже точно будет в строке, после выполнения программы. Так же там будет 39 двоек. Т.е., если не брать во внимание n единиц, сумма в результате будет 39 + 39 * 2 = 117.

Нужно прибавить некоторое количество чевёрок, чтобы получилось ближайшее простое число.

117 + 4*5 = 137.

Получается 5 единиц.

Ответ: 5

Задание 13

На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К, Л. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой.

Определите количество различных путей ненулевой длины, которые начинаются и заканчиваются в городе Е, не содержат этот город в качестве промежуточного пункта и проходят через промежуточные города не более одного раза.

Решение:

Решать будем примерно так же, как и классическую задачу. Основные идеи ни чем не отличаются.

В город Е входят города с числами: 16, 2 и 3. Значит, ответ получается 16 + 2 + 3 = 21.

Ответ: 21

Задание 14

Операнды арифметического выражения записаны в системе счисления с основанием 15.

123×5₁₅ + 1×233₁₅

В записи чисел переменной x обозначена неизвестная цифра из алфавита 15-ричной системы счисления. Определите наименьшее значение x, при котором значение данного арифметического выражения кратно 14. Для найденного значения x вычислите частное от деления значения арифметического выражения на 14 и укажите его в ответе в десятичной системе счисления. Основание системы счисления в ответе указывать не нужно.

Решение:

Решим с помощью программирования на языке Python.

for x in '0123456789ABCDE':
    r = int('123' + x + '5', 15) + int('1' + x + '233', 15)
    if r%14==0:
        print(r//14)
        break

Перебираем для переменной x все цифры в пятнадцатиричной системе. Вычисляем значение выражение. Функция int может перевести строку, записанную в пятнадцатиричной системе, в число.

Остаётся только найти нужное значение и остановить цикл с помощью break.

Ответ: 8767

Задание 15

Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m». Для какого наименьшего натурального числа А формула

(ДЕЛ(x, 2) → ¬ДЕЛ(x, 3)) ∨ (x + A >= 100)

тождественно истинна (т.е. принимает значение 1) при любом натуральном значении переменной x ?

Решение:

Применим шаблон из видокурса ЕГЭ по информатике.

def D(n, m):
    if n%m==0: return True
    else: return False

for A in range(1, 1000):
    k=0
    for x in range(1, 10000):
        if (not(D(x, 2)) or not(D(x, 3))) or (x + A >= 100):
            k=k+1
    if k==9999:
        print(A)

Здесь в начале пишем функцию D, которая олицетворяет функцию ДЕЛ. Потом перебираем различные натуральные значения A. Если функция для какого-то значения сработает 9999 раз, то будем считать, что такое значение A нам подходит.

Самое маленькое значение получается 74.

Ответ: 94

Демоверсия ЕГЭ по информатике 2023 (Задания 1-5)
Демоверсия ЕГЭ по информатике 2023 (Задания 6-10)
Демоверсия ЕГЭ по информатике 2023 (Задания 16-21)
Демоверсия ЕГЭ по информатике 2023 (Задания 22-27)

Калькулятор дробей

Этот калькулятор дробей выполняет базовые и расширенные операции с дробями, выражения с дробями в сочетании с целыми, десятичными и смешанными числами. Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Калькулятор помогает найти значение из операций с несколькими дробями. Решайте задачи с двумя, тремя и более дробями и числами в одном выражении.

Правила выражения с дробями:

Дроби — используйте косую черту для деления числителя на знаменатель, т.е. для пятисотых введите 5/100 . Если вы используете смешанные числа, оставьте пробел между целой и дробной частями.

Смешанные числа (смешанные числа или дроби) сохраняют один пробел между целым числом и дробью
и используют косую черту для ввода дробей, например, 1 2/3 . Пример отрицательной смешанной дроби: -5 1/2 .
Поскольку косая черта одновременно является знаком дробной строки и деления, используйте двоеточие (:) в качестве оператора деления дробей, т. е. 1/2 : 1/3 .
Decimals (десятичные числа) вводятся с десятичной точкой . и они автоматически преобразуются в дроби — т.е. 1,45 .

Math Symbols

Symbol	Symbol name	Symbol Meaning	Example
+	plus sign	addition	1/2 + 1/3
—	знак минус	вычитание	1 1/2 — 2/3
*	asterisk	multiplication	2/3 * 3/4 ​​
×	times sign	multiplication	2 /3 × 5/6
:	division sign	division	1/2 : 3
/	division slash	division	1/3 / 5 1/2 • сложение дробей и смешанных чисел: 8/5 + 6 2/7 • деление целых чисел и дробей: 5 ÷ 1/2 • сложные дроби: 5/8 : 2 2/3 • десятичная дробь: 0,625 • Преобразование дроби в десятичную: 1/4 • Преобразование дроби в процент: 1/8 % • сравнение дробей: 1/4 2/3 • умножение дроби на целое число: 6 * 3/4 ​​ • квадратный корень дроби: sqrt(1/16) • уменьшение или упрощение дроби (упрощение) — деление числителя и знаменателя дроби на одно и то же ненулевое число — эквивалентная дробь: 4/22 • выражение со скобками: 1/3 * (1/2 — 3 3/8) • составная дробь: 3/4 от 5/7 • кратные дроби: 2/3 от 3/5 • разделить, чтобы найти частное: 3/5 ÷ 2/3 Калькулятор следует известным правилам для порядка операций . Наиболее распространенные мнемоники для запоминания этого порядка операций: PEMDAS — Скобки, Экспоненты, Умножение, Деление, Сложение, Вычитание. BEDMAS — Скобки, Экспоненты, Деление, Умножение, Сложение, Вычитание BODMAS — Скобки, Порядок, Деление, Умножение, Сложение, Вычитание. GEMDAS — Символы группировки — скобки (){}, возведения в степень, умножение, деление, сложение, вычитание. MDAS — Умножение и деление имеют тот же приоритет, что и сложение и вычитание. Правило MDAS является частью порядка операций правила PEMDAS. Будьте осторожны; всегда выполняйте умножение и деление перед сложением и вычитанием . Некоторые операторы (+ и -) и (* и /) имеют одинаковый приоритет и должны оцениваться слева направо. Упрощение 12 Упрощение {1/3 + 1/12} ÷ {2/3 — 5/8} В столовой В классной комнате Джейкоба 18 учеников. Шесть учеников приносят обед в школу. Остальные обедают в столовой. Проще говоря, какая часть студентов обедает в столовой? Дробями Муравей поднимается на 2/5 шеста за первый час и на 1/4 шеста за следующий час. Какую часть шеста преодолевает муравей за два часа? А класс IV.А В классе 15 девочек и 30 мальчиков. Какая часть класса представляет мальчиков? Зденек Зденек набрал 15 литров воды из 100-литровой полной бочки. Напишите долю того, какую часть воды Зденека он собрал. Вычислить выражение Вычислить значение выражения z/3 — 2 z/9 + 1/6, для z = 2 Младенцы Двое взрослых, двое детей и четверо младенцев едут в автобусе. Какую часть населения составляют младенцы? Дети 9 В комнате 11 детей. Шесть детей — девочки. Какую часть детей составляют девочки? Ферма 6 На ферме 20 животных. Есть четыре курицы. Какую часть животных составляют куры? Выразите ответ дробью в простейшей форме. Женитьба Женитьба имела 1 1/2 дюжины яиц в холодильнике. Использовала 1/3 яйца. Какая часть яиц использовалась? Энди набрал Энди неправильно ответил на пять из 15 вопросов в тесте по математике. На какую часть вопроса Энди ответил правильно? more math problems » decimals fractions triangle ΔABC percentage % permille ‰ prime factors complex numbers LCM GCD LCD combinatorics equations статистика … все математические калькуляторы Что такое Aperture? | Понимание диафрагмы камеры от Nikon Новичок Узнайте, как диафрагма влияет на конечное изображение. Глоссарий Что такое диафрагма в фотографии? Диафрагма — это отверстие диафрагмы объектива, через которое проходит свет. Он откалиброван в шагах диафрагмы и обычно записывается в виде чисел, таких как 1,4, 2, 2,8, 4, 5,6, 8, 11 и 16. Более низкие значения ступеней диафрагмы обеспечивают большую экспозицию, поскольку они представляют большую диафрагму, в то время как более высокие значения диафрагмы стопы дают меньшую экспозицию, потому что они представляют собой меньшие апертуры. Поначалу это может показаться немного противоречивым, но станет яснее, когда вы будете делать снимки с разными значениями диафрагмы. Обязательно сначала ознакомьтесь с руководством, чтобы узнать, как установить приоритет диафрагмы для вашей камеры, а затем попробуйте поэкспериментировать, чтобы освоиться с изменением диафрагмы и распознать влияние различных апертур на конечное изображение.   Влияние диафрагмы на глубину резкости Глубина резкости — это зона приемлемой резкости перед и позади объекта, на котором сфокусирован объектив. Проще говоря: насколько резкой или размытой является область позади вашего объекта. Чем меньше диафрагма, тем больше отверстие в объективе, тем меньше глубина резкости, тем размытее фон. Чем выше значение f/stop — тем меньше отверстие в объективе — тем больше глубина резкости — тем четче фон. Как диафрагма влияет на скорость затвора Использование низкой диафрагмы означает, что в объектив попадает больше света, и поэтому затвор не должен оставаться открытым слишком долго, чтобы сделать правильную экспозицию, что приводит к более быстрой скорости затвора. Опять же, верно и обратное: использование высокой диафрагмы означает, что в объектив попадает меньше света, и поэтому затвор должен оставаться открытым немного дольше, что приводит к более медленной скорости затвора. Где найти диафрагму на объективе Nikon Все объективы имеют максимальную диафрагму, и на всех объективах NIKKOR максимально возможная диафрагма указана на корпусе объектива. На некоторых зум-объективах указано что-то вроде f/3,5–5,6 на корпусе объектива или 1:3,5–5,6 (внизу справа). Эти числа, 3,5 и 5,6, относятся к максимальной диафрагме или самой широкой диафрагме, которую объектив может достичь для каждого конца диапазона увеличения. Некоторые объективы более высокого класса могут поддерживать наибольшую диафрагму во всем диапазоне увеличения, поэтому подробно указано только одно число (внизу слева). Как выбрать диафрагму Теперь, когда мы знаем, как управлять глубиной резкости, что определяет выбор, который мы делаем при выборе диафрагмы? Мы используем фокус и глубину резкости, чтобы привлечь внимание к тому, что важно на фотографии, и используем отсутствие фокуса, чтобы свести к минимуму отвлекающие факторы, которые нельзя исключить из композиции. Хотя правил нет, есть некоторые рекомендации по выбору приоритета диафрагмы. Диафрагма для портретов Для классической портретной съемки мы отделяем наш объект от окружения с помощью «выборочной фокусировки». Выбор большой диафрагмы (меньшее значение f/stop, например, f2.8) создает очень малую глубину резкости, когда в фокусе находится только объект или только его часть. Это помогает привлечь внимание зрителя к предмету. Диафрагма для пейзажной фотографии При выборе объектива для пейзажной фотографии мы обычно хотим видеть как можно больше деталей от переднего до заднего плана; мы хотим добиться максимальной глубины резкости, выбрав маленькую диафрагму (более высокое значение f/stop, например, f/8 или f/11). No related posts. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт Copyright © 2004-2019 Карта сайта