Задачи по алгебре для 9 класса
МАТЕМАТИКА В ШКОЛЕ
Номер свидетельства СМИ ЭЛ № ФС 77 — 63677 зарегистрировано РоскомнадзоромЗадачи и примеры по темам:
Округление Сравнение Сложение Вычитание Сложение и вычитание Умножение Деление Умножение и деление Нумерация Уравнения Дроби Общие темы
Задачи и примеры по классам:
Детский сад 1 класс 2 класс 3 класс 4 класс 5 класс 6 класс 9 класс 10 класс
Уроки и презентации по классам:
1 класс 2 класс 3 класс 4 класс 5 класс 6 класс 7 класс 8 класс 9 класс 10 класс 11 класс
Тесты и тренажеры по классам
Детский сад 1 класс 2 класс 3 класс 4 класс
Контрольные работы:
1 класс:
Входная
Моро М.И.
Петерсон Л.Г.
Итоговая
2 класс:
Входная
Моро М.И.
Петерсон Л.Г.
Итоговая
3 класс:
Входная
Моро М.И.
Петерсон Л.Г.
Итоговая
4 класс:
Входная
Моро М.
И.
Итоговая
Самостоятельные работы:
1 класс: Петерсон Л.Г. Моро М.И. 2 класс: Моро М.И. 3 класс: Моро М.И. 4 класс: Моро М.И. 5 класс: Виленкина Н.Я. 6 класс: Виленкина Н.Я. 7 класс: Мордковича А.Г. Атанасяна Л.С.
Домашние задания:
1 класс: Моро М.И. 2 класс: Моро М.И. 3 класс: Моро М.И. 4 класс: Моро М.И. 5 класс: Виленкина Н.Я. 6 класс: Виленкина Н.Я. 7 класс: Мордковича А.Г.
Дата публикации: .
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Все материалы проверены антивирусной программой.
Самостоятельные работы по алгебре 9 класса к учебнику Мордковича А.Г.
Обучающие пособия и тренажеры в интернет-магазине «Интеграл» для 9 класса
Интерактивное пособие «Правила и упражнения по алгебре» для 9 класса
Мультимедийное учебное пособие для 9 класса «Алгебра за 10 минут»
Задачи на тему: « Неравенства c одной переменной. m$, числовые последовательности« | |
| Задачи на тему: «Арифметические и геометрические прогрессии« | |
| Задачи на тему: «Комбинаторика, статистика, вероятностные задачи« |
Примеры 9 класс онлайн-подготовка на Ростелеком Лицей
Тема: Системы уравнений
Урок: Примеры
1. Решение задач с алгебраическим смыслом
Ранее мы уже составляли математические модели реальных ситуаций, но только те, которые описывались линейными системами. Сейчас мы научились решать нелинейные системы. Наша задача – научиться составлять математические модели с помощью нелинейных систем уравнений.
Задача 1. Сумма двух чисел равна 12, а их произведение равно 35. Найти эти числа.
Решение:
Первый этап – переведем словесную модель на математический язык.
Пусть x и y – искомые числа. По условию
Эта нелинейная система представляет собой математическую модель реальной ситуации.
Второй этап – работа с математической моделью.
;
Ответ:
Обсудим связь полученной системы с квадратным уравнением. Воспользуемся теоремой Виета:
Это еще один способ решения системы.
Задача 2. Какое двузначное число в 4 раза больше суммы своих цифр и в 3 раза больше их произведения?
Решение:
Получим математическую модель. Пусть искомое число, x и y его цифры. сумма цифр искомого числа, произведение цифр. Составим систему.
Число двузначное, т.е.
;
Ответ: 24.
Задача 3. Если к числителю и знаменателю дроби прибавить по единице, то дробь станет равна А если сложить квадраты числителя и знаменателя исходной дроби, то получится 122. Найдите эту дробь.
Решение:
Пусть x – числитель дроби, y – знаменатель дроби, – искомая дробь.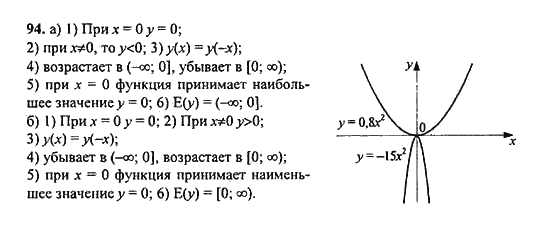
(методом подбора)
( по т.Виета) – не подходит по условию задачи.
Ответ: .
2. Решение задач с геометрическим смыслом
Задача 4. Периметр прямоугольного треугольника равен 84 см. Его гипотенуза равна 37 см. Найти площадь прямоугольного треугольника.
Решение:
Дан прямоугольный
Пусть x, y – катеты прямоугольного треугольника.
Тогда по условию задачи
Нам необходимо найти поэтому отдельно находить x и y не нужно.
Возведем в квадрат обе части первого уравнения:
Ответ:
Задача 5. Сумма катетов прямоугольного треугольника равна 49 м, гипотенуза – 41 м. Найти площадь прямоугольного треугольника.
Решение:
Пусть x, y – катеты прямоугольного треугольника. Тогда
Возведем в квадрат обе части первого уравнения, получаем:
Ответ:
3.
Заключение
Мы решили текстовые задачи, перевели русский язык на математический, получили нелинейные математические модели, решили их, и получили решения исходных задач. На следующем уроке мы рассмотрим задачи на движение.
Список рекомендованной литературы
1. Мордкович А.Г. и др. Алгебра 9 кл.: Учеб. Для общеобразоват. Учреждений.- 4-е изд. – М.: Мнемозина, 2002.-192 с.: ил.
2. Мордкович А.Г. и др. Алгебра 9 кл.: Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М.: Мнемозина, 2002.-143 с.: ил.
3. Макарычев Ю. Н. Алгебра. 9 класс : учеб. для учащихся общеобразоват. учреждений / Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, И. Е. Феоктистов. — 7-е изд., испр. и доп. — М.: Мнемозина, 2008.
4. Алимов Ш.А., Колягин Ю.М., Сидоров Ю.В. Алгебра. 9 класс. 16-е изд. — М., 2011. — 287 с.
5. Мордкович А. Г. Алгебра. 9 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А.
Г. Мордкович, П. В. Семенов. — 12-е изд., стер. — М.: 2010. — 224 с.: ил.
6. Алгебра. 9 класс. В 2 ч. Ч. 2. Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Л. А. Александрова, Т. Н. Мишустина и др.; Под ред. А. Г. Мордковича. — 12-е изд., испр. — М.: 2010.-223 с.: ил.
Рекомендованные ссылки на интернет-ресурсы
1. Раздел College.ru по математике (Источник).
2. Интернет-проект «Задачи» (Источник).
3. Образовательный портал «РЕШУ ЕГЭ» (Источник).
Рекомендованное домашнее задание
Мордкович А.Г. и др. Алгебра 9 кл.: Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М. : Мнемозина, 2002.-143 с.: ил. № 143, 146, 152, 164.
7 советов по алгебре для 9-х классов
Переход от математики 8-го класса к 9-му весьма важен, так как учащиеся начинают изучать основы остальных математических курсов в старшей школе.
Учащиеся 9 класса познакомятся с алгеброй и функциями, двумя новыми и очень важными понятиями. Если вы учитесь в 9 классе и хотите освоить алгебру, вы обратились по адресу. Вот несколько советов и рекомендаций по алгебре для 9 класса.
- Решайте задачи как можно чаще.
- Лучший способ решить любую задачу по алгебре, которая встретится вам на пути, — это попрактиковаться.
- Чем больше вы будете решать задач, тем легче вам будет решать уравнения.
- Начните с более простых задач и переходите к более сложным. Вы должны уметь решать и понимать более простые уравнения, прежде чем браться за сложные задачи.
- Ошибки делать хорошо.
- Пока вы решаете практические задачи, просматривайте свои ошибки. Делать ошибки — лучший способ учиться.
- Убедитесь, что вы исправляете свои ошибки как можно раньше, так как это поможет вам понять, как решать сложные проблемы в будущем.
- Если вы не совсем понимаете свою ошибку, обратитесь за помощью к учителю или репетитору! Правильное понимание своей ошибки поможет вам избежать повторения той же ошибки в другой задаче по алгебре.
- Ознакомьтесь с законами экспонент.
- Показатели степени вы могли видеть на предыдущих уроках математики, но в 9 классе, вы научитесь решать алгебраические выражения, включающие показатели степени.
- Это означает, что вы столкнетесь с задачами на сложение, вычитание, умножение и деление, которые добавляют к смеси показатели степени.
- Экспоненты должны следовать важным правилам, чтобы решать эти задачи без ошибок. Они называются законами экспонент.
- Практикуйтесь в решении алгебраических выражений с показателями как можно чаще. Лучше правильно понимать законы экспонент, чем запоминать их.
- Если вы будете следовать законам экспоненты и применять их к своим практическим задачам, вы легко сможете решить любое алгебраическое выражение.
- Практикуйтесь в решении полиномиальных выражений.
- Что такое многочлен? Полином — это выражение, включающее переменные и коэффициенты.
- Например, 3×2 – 5y + 2 – это полиномиальное выражение. 3 и 5 — это коэффициенты, а x и y — переменные.
- В 9 классе учащиеся узнают, как решать полиномиальные выражения, чтобы найти значение переменной.
- Давайте попробуем это со следующим полиномом: y = 5x + 15. Чтобы решить эту проблему, нам нужно изолировать x на одной стороне уравнения.
- Для начала всегда проверяйте, что выражение равно нулю. Теперь у нас есть 5x + 15 = 0.
- Наш следующий шаг заключается в перемещении константы в нулевую сторону, что дает нам
5x = –15. - Наш последний шаг требует, чтобы мы отделили 5 от переменной x. Чтобы удалить 5, нам нужно разделить его на обе части уравнения. Это дает нам x = –15 ÷ 5. Следовательно, наш окончательный ответ: x = –3.
- Помните: что бы вы ни делали с одной частью уравнения, вы должны делать и с другой.
Это дает нам x = –15 ÷ 5. Следовательно, наш окончательный ответ: x = –3.- Ознакомьтесь с порядком работы.
- 9 класс Математика включает в себя задачи с несколькими операциями в одном выражении. Это означает математическое выражение, которое включает в себя показатели степени, скобки, сложения, умножения и т. д.
- Важно понимать правила BEDMAS, если вы решаете алгебраическое выражение. «BEDMAS» означает скобки, экспоненты, деление, умножение, сложение и вычитание.
- При возникновении математической задачи с несколькими операциями вы должны начать со скобок и перейти к следующей операции.
- Если вы будете следовать порядку BEDMAS, вы сможете решить любую математическую задачу, которая встретится вам на пути.
6 . Практика работы с положительными и отрицательными числами.
- Алгебра часто включает в себя решение задач с положительными и отрицательными числами. Это часто может сбивать студентов с толку, но при достаточной практике вы быстро станете экспертом!
- Если вы визуал, попробуйте использовать числовую линейку, чтобы визуализировать положительные и отрицательные числа.
- Есть несколько правил, которым нужно следовать при сложении и вычитании положительных и отрицательных чисел.
- Прибавление отрицательного числа к положительному числу аналогично вычитанию положительного числа из другого положительного числа. Вот пример: (+8) + (–3)= (+5) — это то же самое, что (+8) — (+3) = (+5).
- Вычитание отрицательного числа из положительного равносильно добавлению положительного числа к другому положительному числу. Вот пример: (+3) – (–7) = (+10) – это то же самое, что (+3) + (+7) = (+10).
- Если знаки в уравнении одинаковые (+ и + или — и -), оно становится положительным.
- Если знаки в уравнении разные (+ и –, или – и +), оно становится отрицательным.
- Обратитесь за помощью.
- Если вы не знаете, как решить практическую задачу, обратитесь за помощью к учителю или другу.
- Лучше всего задавать вопросы, когда вы решаете математические задачи, чтобы хорошо подготовиться к викторинам и экзаменам.
- Сравните свои ответы с ответами друга. Иногда лучший способ учиться — это учить других!
- Убедитесь, что вы понимаете свои ошибки, чтобы не повторять их в будущем. Многие учащиеся допускают небольшие ошибки, которых можно избежать с помощью дополнительной практики и понимания.
Если вы будете следовать приведенным выше советам и решать математические задачи как можно чаще, у вас будет все необходимое для успешной сдачи 9 класса по алгебре. Помните, что математика в 9 классе является сложной задачей и требует много тяжелой работы, чтобы добиться успеха.
Наберитесь терпения и уверенности в своих силах! В Success Tutorial School мы предлагаем несколько программ для помощи учащимся, которые учатся или планируют поступать в 9 класс.Мат. Свяжитесь с нами, чтобы узнать больше о том, как мы можем помочь вам или вашему ребенку добиться больших успехов в математике в 9 классе.
25 мая, 2021
TOP
ALGEBRA 2 (Решение уравнений CH 4) (Математические классы миссис Бенке)
U3D0 — Решение 1DI БЛОК 3 – РЕШЕНИЕ УРАВНЕНИЙ0132 Цель обучения (буду):
В этом разделе мы будем решать уравнения первой степени, а текстовые задачи можно моделировать с помощью уравнений первой степени.
Критерии успеха (Я могу…):
- Решить простые уравнения
- Решение многошаговых уравнений
- Решение уравнений с дробями
- Преобразование формул с переменными первой степени
- Решение текстовых задач, которые можно смоделировать с помощью уравнения с одной переменной
- Решение задач с использованием процентов, соотношений, норм и пропорций
День
| Урок
| Текст Арт. | Задать. / Домашнее задание
|
| 1 | Диагностический тест U3D1 Решение простых уравнений U3D1_T_Решение простых уравнений |
4.1 |
Стр. 193-195 №3, 5, 6, 8-13, 16, 18, 20 |
| 2 | U3D2_S_Решение многошаговых уравнений U3D2_T_Решение многошаговых уравнений | 4,2
| Стр. 200-202 #2, 4 («корень» просто означает «решение»), 5а, 6а, 8, 9, 10, 13 Задача Страница 203 #18-21 Дополнительный рабочий лист по решению уравнений Тест №1 ПРАКТИКА Практика для решения викторины #1 |
| 3 | ВИКТОРИНА №1 U3D3_S – Решение уравнений с дробями, часть 1 U3D3_T – Решение уравнений с дробями I (перекрестное умножение) | 4,3 | Стр.
|
| 4 | U3D4_S – Решение уравнений с дробями, часть 2 U3D4_T – Решение уравнений с дробями II |
4,3 | Стр. 208-210 #3бд, 4бд, 11, 12, Рабочий лист 3.3 Решение уравнений с дробями Рабочий лист 3.3 Решения Страница вызова 210 #13 U3D4 Тест №2 ПРАКТИКА U3D4_Quiz#2 ПРАКТИЧЕСКИЕ Решения |
| 5 | ВИКТОРИНА №2 U3D5_S — Моделирование с помощью формул (Перестановка уравнений) U3D5_T – Моделирование с помощью формул |
4,4 |
Стр. 215-219 №1-3, 6-8, 10-12, 15, 16а Задача Стр. 219 #18, 19 U3D5_W — Рабочий лист — Дополнительная практика с уравнениями |
| 6 | U3D6_S Вопросы по истории номеров U3D6_T Вопросы по истории номеров | 4,5 | Стр. |
208-209 #1, 3ас, 4ас, 5-8