| 1. |
Деление неравенства на отрицательное число
Сложность: лёгкое |
2 |
| 2. |
Число, которое является или не является решением неравенства с модулем
|
1 |
3.
|
Линейное неравенство
Сложность: лёгкое |
3 |
| 4. |
Дробное неравенство, сводимое к линейному
Сложность: среднее |
4 |
5. |
Квадратное неравенство, сводимое к линейному (распределительный закон умножения)
Сложность: среднее |
3 |
| 6. |
Значения переменной, при которых выражение имеет смысл
Сложность: среднее |
4 |
7.
|
Область определения корня из квадратного трёхчлена
Сложность: среднее |
5 |
| 8. |
Область определения корня из дроби
Сложность: среднее |
6 |
9.
|
Значения переменной, при которых дробь имеет смысл (корень в знаменателе)
Сложность: среднее |
5 |
| 10. |
Целочисленные значения параметра
Сложность: сложное |
6 |
11.
|
Натуральное значение параметра (целые числа из множества решений)
Сложность: сложное |
6 |
| 12. |
Натуральное значение параметра (натуральные числа из множества решений)
Сложность: сложное |
6 |
| 1. |
Разность арифметической прогрессии
Сложность: лёгкое |
1 |
| 2. |
Нахождение члена и разности арифметической прогрессии
Сложность: лёгкое |
1 |
3.
|
Нахождение членов арифметической прогрессии
Сложность: лёгкое |
5 |
| 4. |
Сумма членов арифметической прогрессии
Сложность: среднее |
1 |
5.
|
Нахождение члена арифметической прогрессии, даны разность и первый член
Сложность: среднее |
3 |
| 6. |
Сумма первых членов арифметической прогрессии
Сложность: среднее |
4 |
7.-(Obshhie-metody-reshenija-uravnenij)-reshenie-56.36.jpg)
|
Разность арифметической прогрессии
Сложность: лёгкое |
2 |
| 8. |
Сумма членов арифметической прогрессии
Сложность: среднее |
2 |
9.
|
Прогрессия в текстовой задаче, вычисление высоты
Сложность: среднее |
4 |
| 10. |
Сумма натуральных чисел
Сложность: сложное |
4 |
11.
|
Вычисление разности при наименьшем значении членов прогрессии
Сложность: сложное |
4,5 |
| 12. |
Арифметическая прогрессия и трапеция
Сложность: сложное |
8 |
| 1. |
Использование свойства факториала
Сложность: лёгкое |
2 |
| 2. |
Выбор элемента из двух групп
Сложность: лёгкое |
2 |
3.
|
Выбор элемента из трёх групп
Сложность: лёгкое |
1 |
| 4. |
Действия с факториалами
Сложность: среднее |
3 |
5.
|
Число сочетаний, выбор двух элементов из группы
Сложность: среднее |
4 |
| 6. |
Составление меню
Сложность: среднее |
3 |
7.
|
Древовидная диаграмма, перестановки
Сложность: среднее |
3 |
| 8. |
Древовидная диаграмма, число размещений и сочетаний
Сложность: среднее |
2,5 |
9.
|
Количество сумм цифр на игральных кубиках
Сложность: среднее |
2 |
| 10. |
Вычисление числа треугольников
Сложность: сложное |
3 |
11.
|
Геометрическая комбинаторная задача
Сложность: сложное |
4 |
| 12. |
Анализ заданной ситуации
Сложность: сложное |
3 |
Пробный экзамен по математике 9 класс.
 1-4 варианты с ответами
1-4 варианты с ответамиРешение.
Сумма углов выпуклого четырёхугольника равна 360°. Имеем: Так как , и — общая треугольника ABD и BDC. Из равенства треугольников следует, что . Таким образом, .
Ответ: 95.
Ответ: 95
17. Короткое плечо шлагбаума имеет длину 1 м, а длинное плечо – 3 м. На какую высоту (в метрах) опустится конец короткого плеча, когда конец длинного плеча поднимается на 1,8 м?
Решение.
Найдём синус угла, на который поднимается длинное плечо:
Угол подъема длинного плеча равен углу на который опустится короткое плечо. Пусть x — высота, на которую опустится короткое плечо, имеем:
Таким образом, короткое плечо опустится на 0,6 м.
Ответ: 0,6.
Ответ: 0,6
18 На диаграмме представлено распределение количества пользователей некоторой социальной сети по странам мира. Всего в этой социальной сети 12 млн пользователей.Какое из следующих утверждений неверно?
1) Пользователей из России больше, чем пользователей из Белоруссии и Украины вместе.
2) Пользователей из Украины больше, чем пользователей Латвии.
3) Примерно две трети общего числа пользователей — из России.
4) Пользователей из Украины больше 3 миллионов.
В ответ запишите номер выбранного утверждения.
Решение.
Разъясним каждый вариант ответа:
1) Очевидно, что пользователей из России больше, чем пользователей из Украины и Белоруссии вместе.
2) Сектор «Украина» занимает большую площадь диаграммы, чем сектор «Другие страны», а т. к. «Латвия» включена в «Другие страны», имеем: пользователей из Украины больше, чем пользователей из Латвии.
3) Сектор в две трети диаграммы отсекается углом в 2·360°/3 = 240°. Очевидно, что угол, отсекающий сектор «Россия» примерно равен 240°, значит примерно две трети общего числа пользователей — из России.
4) Видно, что пользователей из Украины меньше четверти всех пользователей, значит, меньше 12/4=3 миллионов.
Ответ: 4.
Ответ: 4
19. В лыжных гонках участвуют 13 спортсменов из России, 2 спортсмена из Норвегии и 5 спортсменов из Швеции. Порядок, в котором спортсмены стартуют, определяется жребием. Найдите вероятность того, что первым будет стартовать спортсмен не из России.
Решение.
Вероятность благоприятного случая() — отношение количества благоприятных случаев к количеству всех случаев. В данной задаче благоприятным случаем является старт спортсмена не из России под номером 1. Всего благоприятных случаев 2 + 5 = 7, а количество всех случаев 13 + 2 + 5 = 20. Отношение соответственно равно
Ответ: 0,35.
Ответ: 0,35
20. Площадь трапеции можно вычислить по формуле , где — основания трапеции, — высота (в метрах). Пользуясь этой формулой, найдите высоту , если основания трапеции равны и , а её площадь .
Часть 2
Решение.
Выразим высоту трапеции из формулы площади:
Подставляя, получаем:
Ответ: 4.
Приведём другое решение.
Подставим в формулу известные значения величин:
Ответ: 4
21. Разложите на множители .
Решение.
Имеем:
.
Ответ: .
22.Два оператора, работая вместе, могут набрать текст газеты объявлений за 8 ч. Если первый оператор будет работать 3 ч, а второй 12 ч, то они выполнят только 75% всей работы. За какое время может набрать весь текст каждый оператор, работая отдельно?
23.Постройте график функции и определите, при каких значениях прямая имеет с графиком ровно три общие точки.
Решение.
Раскрывая модуль, получим, что график функции можно представить следующим образом:
Этот график изображён на рисунке:
Из графика видно, что прямая имеет с графиком функции ровно три общие точки при и
Ответ: 0; 4.
24. Диагонали и трапеции пересекаются в точке . Площади треугольников и равны соответственно и . Найдите площадь трапеции.
Решение.
Заметим, что площади двух треугольников, общей вершиной которых является точка пересечения диагоналей трапеции, а основаниями — боковые стороны, равны. Это следует, например, из того, что площади треугольников и равны (поскольку эти треугольники имеют общее основание , и их высоты, проведенные к этому основанию, равны как высоты трапеции), а . По условию, , поэтому и являются не боковыми сторонами, а основаниями трапеции. Тогда треугольники и подобны по двум углам, и отношение их площадей равно квадрату коэффициента подобия . Поэтому . Поскольку треугольники и имеют общую высоту, проведённую из вершины , то отношение их площадей равно отношению их оснований, т. е. . Значит, . Поэтому и . Но тогда .
Это следует, например, из того, что площади треугольников и равны (поскольку эти треугольники имеют общее основание , и их высоты, проведенные к этому основанию, равны как высоты трапеции), а . По условию, , поэтому и являются не боковыми сторонами, а основаниями трапеции. Тогда треугольники и подобны по двум углам, и отношение их площадей равно квадрату коэффициента подобия . Поэтому . Поскольку треугольники и имеют общую высоту, проведённую из вершины , то отношение их площадей равно отношению их оснований, т. е. . Значит, . Поэтому и . Но тогда .
Ответ: .
25.В параллелограмме ABCD диагонали AC и BD пересекаются в точке O. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника BOC.
Решение.
Проведём высоту так, чтобы она проходила через точку Углы и равны друг другу как вертикальные. Вспомним также, что диагонали делятся точкой пересечения пополам, следовательно, Рассмотрим треугольники и , они прямоугольные, имеют равные углы и равные гипотенузы, следовательно эти треугольники равны, а значит равны отрезки и . Таким образом,
Вспомним также, что диагонали делятся точкой пересечения пополам, следовательно, Рассмотрим треугольники и , они прямоугольные, имеют равные углы и равные гипотенузы, следовательно эти треугольники равны, а значит равны отрезки и . Таким образом,
Площадь параллелограмм равна а площадь треугольника
26. Основание AC равнобедренного треугольника ABC равно 10. Окружность радиуса 8 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
ВАРИАНТ № 2
Часть 1 МОДУЛЬ «АЛГЕБРА»
1. Вычислите:
Решение.
Приведём к общему знаменателю:
Ответ: 3,7.
Ответ: 3,7
2.На координатной прямой отмечены числа a, b и c:
Значение какого из следующих выражений отрицательно?
1)−a 2)a+c 3)b−c 4) c − a
Решение.
Заметим, что −2 < a < −1, 1 < b < 2 и 3 < c < 4. Тогда выражение −a положительно. Для выражения a + c верно двойное неравенство 1 < a + c < 3. Для выражения b − c верно двойное неравенство −2 < b − c < −1. Для выражения c − a верно двойное неравенство 4 < c − a < 6.
Таким образом, отрицательным является выражение b − c.
Правильный ответ указан под номером 3.
Ответ: 3
3.В какое из следующих выражений можно преобразовать дробь ?
1) 2) 3) 4)
Решение.
Упростим дробь:
Правильный ответ указан под номером 3.
Ответ: 3
4. Решите уравнение (x + 2)2 = (x − 4)2.
Решение.
Последовательно получаем:
Ответ: 1.
Приведем другое решение.
Возведем обе части уравнения в квадрат:
Приведем другое решение.
Воспользуемся формулой разности квадратов:
Ответ: 1
5.График какой из приведенных ниже функций изображен на рисунке?
1)
2)
3)
4)
Решение.
Ветви изображённой на рисунке гиперболы лежат во II и IV четверти, её график растянут вдоль оси ординат в два раза. Этим условиям соответствует вариант 1
Этим условиям соответствует вариант 1
Графику соответствует вариант под номером 1.
Ответ: 1
6. Геометрическая прогрессия задана формулой n — го члена . Укажите третий член этой прогрессии.
Решение.
По формуле n-го члена геометрической прогрессии имеем:
Ответ: 12.
Ответ: 12
7.Представьте в виде дроби выражение и найдите его значение при . В ответ запишите полученное число.
Решение.
Упростим выражение:
Найдем значение выражения при
Ответ: −10.
Ответ: -10
8.Решите неравенство:
1) 2)3) 4)
МОДУЛЬ «ГЕОМЕТРИЯ»
Решение.
Решим неравенство: Корнями уравнения являются числа -23 и 0. Поэтому
Правильный ответ указан под номером 4.
Ответ: 4
9. Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 65° и 50°. Найдите меньший угол параллелограмма.
Решение.
Сумма смежных углов параллелограмма равна 180°. Тогда величина меньшего угла параллелограмма будет равна:
Ответ:
Ответ: 65
10. В окружности с центром в точке проведены диаметры и , угол равен 25°. Найдите величину угла .
В окружности с центром в точке проведены диаметры и , угол равен 25°. Найдите величину угла .
Решение.
Углы OCD и OAB являются вписанными и опираются на одну дугу BD. Таким образом,
Ответ: 25.
Ответ: 25
11. Найдите площадь параллелограмма, изображённого на рисунке.
Решение.
Площадь параллелограмма равна произведению основания на высоту: 7 · 4 = 28.
Ответ: 28.
Ответ: 28
12. Найдите тангенс угла треугольника , изображённого на рисунке.
Решение.
Тангенс угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему. Треугольник ABC — прямоугольный, поэтому
Треугольник ABC — прямоугольный, поэтому
Ответ: 0,75.
Ответ: 0,75
13.Какие из следующих утверждений верны?
1) Каждая сторона треугольника меньше разности двух других сторон.
2) В равнобедренном треугольнике имеется не более двух равных углов.
3) Если сторона и угол одного треугольника соответственно равны стороне и углу другого треугольника, то такие треугольники равны.
4) В треугольнике ABC, для которого AB = 3, BC = 4, AC = 5, угол C наименьший.
МОДУЛЬ «РЕАЛЬНАЯ МАТЕМАТИКА»
Решение.
Проверим каждое из утверждений:
1)«Каждая сторона треугольника меньше разности двух других сторон. » — неверно, так как если имеем, что
» — неверно, так как если имеем, что
2) «В равнобедренном треугольнике имеется не более двух равных углов.» — неверно, в равнобедренном треугольнике углы при основании равны.
3)«Если сторона и угол одного треугольника соответственно равны стороне и углу другого треугольника, то такие треугольники равны.» — неверно, равенство определяется по трем элементам.
4)«В треугольнике ABC, для которого AB = 3, BC = 4, AC = 5, угол C наименьший.» — верно, в треугольнике против большего угла лежит большая сторона.
Ответ: 4.
Ответ: 4
14. Учёный Иванов выезжает из Москвы на конференцию в Санкт-Петербургский университет. Работа конференции начинается в 10:00. В таблице дано расписание ночных поездов Москва — Санкт-Петербург
Номерпоезда
Отправление из
Москвы
Прибытие в
Санкт-Петербург
026А
23:00
06:30
002А
23:55
07:55
038А
00:44
08:46
016А
01:00
08:38
Путь от вокзала до университета занимает полтора часа. Укажите номер самого позднего (по времени отправления) из московских поездов, которые подходят учёному Иванову.
Укажите номер самого позднего (по времени отправления) из московских поездов, которые подходят учёному Иванову.
1)026А 2)002А 3)038А 4) 016А
Решение.
Поскольку путь от вокзала до университета занимает полтора часа, поезд должен прибыть на вокзал не позднее 08:30. Этому условию удовлетворяют поезда под номерами: 026А и 002А. Из них позже отправляется поезд под номером 002А.
Правильный ответ указан под номером 2.
Ответ: 2
15.В таблице даны рекомендуемые суточные нормы потребления (в г/сутки) жиров, белков и углеводов детьми от 1 года до 14 лет и взрослыми.
Вещество
Дети от 1 года
до 14 лет
Мужчины
Женщины
Жиры
40—97
70—154
60—102
Белки
36—87
65—117
58—87
Углеводы
170—420
257—586
Какой вывод о суточном потреблении жиров, белков и углеводов 7-летней девочкой можно сделать, если по подсчётам диетолога в среднем за сутки она потребляет 42 г жиров, 35 г белков и 190 г углеводов? В ответе укажите номера верных утверждений.
1) Потребление жиров в норме.
2) Потребление белков в норме.
3) Потребление углеводов в норме.
Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.
Решение.
Проанализируем каждое утверждение.
1) Для семилетней девочки нормой является употребление от 40 до 97 граммов жиров в сутки, 42 грамма укладываются в этот промежуток. Первое утверждение верно.
2) Для семилетней девочки нормой является употребление от 36 до 87 граммов белков в сутки, 35 граммов не укладываются в этот промежуток. Второе утверждение неверно.
2) Для семилетней девочки нормой является употребление от 170 до 420 граммов углеводов в сутки, 190 граммов укладываются в этот промежуток. Третье утверждение верно.
Ответ: 1; 3.
Ответ: 1; 3
16.Площадь земель крестьянского хозяйства, отведённая под посадку сельскохозяйственных культур, составляет 24 га и распределена между зерновыми и овощными культурами в отношении 5:3. Сколько гектаров занимают овощные культуры?
Решение.
Овощные культуры занимают:
Ответ: 9.
Ответ: 9
17. Сколько досок длиной 3,5 м, шириной 20 см и толщиной 20 мм выйдет из четырехугольной балки длиной 105 дм, имеющей в сечении прямоугольник размером 30 см 40 см?
Решение.
Найдем объем доски : 350 · 20 · 2 = 14 000 см3. Найдем объем балки: 1050 · 30 · 40 = 1 260 000 см3.
Найдем объем балки: 1050 · 30 · 40 = 1 260 000 см3.
Поэтому количество досок равно 1 260 000 : 14 000 = 90.
Ответ: 90.
Ответ: 90
18. На диаграмме представлены семь крупнейших по площади территории (в млн км2) стран мира.
Какое из следующих утверждений неверно
1) По площади территории Австралия занимает шестое место в мире.
2) Площадь территории Бразилии составляет 7,7 млн км2.
3) Площадь Индии меньше площади Китая.
4) Площадь Канады меньше площади России на 7,1 млн км2.
В ответе запишите номер выбранного утвержденияРешение.
Проверим каждое утверждение:
1) На диаграмме видно, что Австралия — шестая по площади страна в мире. Значит первое утверждение верно.
Значит первое утверждение верно.
2) Из диаграммы видно, что площадь Бразилии — 8,5 млн км2. Второе утверждение неверно.
3) Из диаграммы видно, что площадь Индии меньше площади Китая. Третье утверждение верно.
4) Из диаграммы видно, что площадь Канады меньше площади России на 17,1-10,0=7,1 млн км2. Четвёртое утверждение верно.
Неверным является утверждение под номером 2.
Ответ: 2
Решение.
Проанализируем все утверждения.
1) Пользователей из России больше всех, тем самым, их больше чем пользователей из Украины.
2) Сектор «Беларусь» занимает большую площадь диаграммы, чем сектор «Другие страны», а т. к. «Швеция» включена в «Другие страны» пользователей из Беларуси больше чем пользователей из Швеции.
3) Сектор в треть диаграммы имеет угол 360° : 3 = 120°. Угол сектора «Украина» меньше 90°, следовательно, меньше трети пользователей сети из Украины.
4) Пользователей из России больше половины всех пользователей, значит, больше 9 : 2 = 4,5 млн, а значит, больше 4 миллионов.
Ответ:3.
Ответ: 3
19. Какова вероятность того, что случайно выбранное натуральное число от 15 до 29 делится на 5?
Решение.
Чисел от 15 до 29 — 15 штук. Среди них на 5 делится только 3 числа. Таким образом, вероятность того, что случайно выбранное натуральное число от 15 до 29 делится на 5 равна
Ответ: 0,2
20.Объём пирамиды вычисляют по формуле , где — площадь основания пирамиды, — её высота. Объём пирамиды равен 40, площадь основания 15. Чему равна высота пирамиды?
Объём пирамиды равен 40, площадь основания 15. Чему равна высота пирамиды?
Часть 2
Решение.
Выразим высоту пирамиды из формулы для ее объема:
Подставляя, получаем:
Ответ: 8.
Ответ: 8
21.Сократите дробь , если .
Решение.
Имеем:
Ответ: 1.
22.Пристани и расположены на реке, скорость течения которой на этом участке равна 3 км/ч. Лодка проходит туда и обратно без остановок со средней скоростью 8 км/ч. Найдите собственную скорость лодки.
Лодка проходит туда и обратно без остановок со средней скоростью 8 км/ч. Найдите собственную скорость лодки.
Решение.
Пусть км/ч — собственная скорость лодки. Тогда скорость движения по течению равна км/ч, а скорость движения против течения равна км/ч. Обозначим расстояние между пристанями. Время, затраченное на весь путь, равно
.
По условию средняя скорость равна 8 км/ч, а весь путь равен . Следовательно,
.
Решим это уравнение:
Получаем: или . Корень −1 не является решением задачи. Значит, скорость лодки равна 9 км/ч.
Ответ: 9 км/ч.
23.Постройте график функции
и определите, при каких значениях прямая будет иметь с графиком единственную общую точку.
Решение.
Построим график функции (см. рисунок).
Из графика видно, что прямая будет иметь с графиком функции единственную точку пересечения при принадлежащем множеству [0; 1).
Ответ: [0; 1).
24. Медианы треугольника пересекаются в точке . Найдите длину медианы, проведённой к стороне , если угол равен 47°, угол равен 133°, .
Решение.
Обозначим середину стороны за . Продлим на свою длину за точку до точки . Четырёхугольник — параллелограмм, потому что и . Значит, = 133°, поэтому четырёхугольник — вписанный. Тогда .
Ответ: 6.
25. В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём СF = АM, BE = DK. Докажите, что EFKM — параллелограмм.
Решение.
Противоположные стороны параллелограмма равны и по условию следовательно:
В параллелограмме противоположные углы равны: , Рассмотри треугольники и , в этих треугольниках , , следовательно эти треугольники равны, а значит, . Аналогично равны треугольники и а следовательно равны отрезки и Противоположные стороны четырехугольника равны, следовательно, по признаку параллелограмма, этот четырёхугольник — параллелограмм.
26.Медиана BM треугольника ABC является диаметром окружности, пересекающей сторону BC в её середине. Найдите длину стороны AC, если радиус описанной окружности треугольника ABC равен 7.
Найдите длину стороны AC, если радиус описанной окружности треугольника ABC равен 7.
ВАРИАНТ № 3
Часть 1 МОДУЛЬ «АЛГЕБРА»
1. Вычислите:
Решение.
Приведём к общему знаменателю:
Ответ: 1,03.
Ответ: 1,03
2.На координатной прямой отмечены числа и Какое из следующих утверждений неверно?
1) 2)
3) 4)
Решение.
Заметим, что и , и проверим все варианты ответа:
1) — неверно.
2) — верно, поскольку каждый множитель отрицателен.
3) — верно.
4) — верно.
Неверным является утверждение 1.
Ответ: 1
3. Какое из чисел больше: или ?
1)
2)
3)
Решение.
В силу цепочки неравенств
первое число меньше второго.
Правильный ответ указан под номером 1.
Ответ: 1
4. Найдите корни уравнения
Если корней несколько, в ответе запишите их сумму.
Решение.
Перенесём всё в уравнении в одну сторону:
По теореме, обратной теореме Виета, сумма корней равна 1, а их произведение равно −12. Тем самым, это числа −3 и 4.
Ответ: −3; 4.
Ответ: -3;4
5.Укажите соответствие между графиками функций и формулами, которые их задают.
1) 2)
3) 4)
Ответ укажите в виде последовательности цифр без пробелов и запятых в указанном порядке
АБ
В
Решение.
Определим вид графика каждой из функций.
1) уравнение прямой, которая пересекает ось абсцисс в точке 2 ; ось ординат в точке −2.
2) уравнение степенной функции с положительным дробным показателем. График проходит через точку (1; 0).
3) уравнение параболы, ветви которой направлены вверх.
4) уравнение степенной функции с положительным дробным показателем. График проходит через точку (−1; 0).
Таким образом, искомое соответствие: A — 4, Б — 3, В — 1.
Ответ: 431.
Ответ: 431
6. Последовательность задана условиями , . Найдите .
Решение.
Будем вычислять последовательно:
Данная последовательность образует арифметическую прогрессию. Найдем разность арифметической прогрессии:
Найдем разность арифметической прогрессии:
тогда
Примечание.
Зная разность и первый член арифметической прогрессии, можно найти посредственно:
Ответ: −9.
Ответ: -9
7. Сократите дробь
Решение.
Сократим дробь:
Ответ: 84.
Ответ: 84
8.На каком рисунке изображено множество решений неравенства
1)
2)
3)
4)
МОДУЛЬ «ГЕОМЕТРИЯ»
9. В равностороннем треугольнике ABC биссектрисы CN и AM пересекаются в точке P. Найдите .
В равностороннем треугольнике ABC биссектрисы CN и AM пересекаются в точке P. Найдите .
Решение.
В равностороннем треугольнике ABC все углы равны 60°. Биссектрисы CN и AM делят уголы пополам, поэтому = = Сумма углов в треугольнике равна 180°, поэтому Вертикальные углы равны, следовательно,
Ответ: 120.
Ответ: 120
10 . Треугольник ABC вписан в окружность с центром в точке O. Найдите градусную меру угла C треугольника ABC, если угол AOB равен 48°.
Решение.
Угол AOB является центральным углом, ACB — вписанным. Оба угла опираются на одну и ту же дугу, следовательно, угол AOB в два раза больше угла ACB.
Ответ: 24.
Ответ: 24
11. Сторона ромба равна 5, а диагональ равна 6. Найдите площадь ромба.
Решение.
Диагонали ромба пересекаются под углом 90° и точкой пересечения делятся пополам. Из прямоугольного треугольника, катетами которого являются половины диагоналей ромба, а гипотенузой — сторона ромба, по теореме Пифагора найдем половину неизвестной диагонали: Тогда вся неизвестная диагональ равна 8.
Площадь ромба равна половине произведения диагоналей:
Ответ: 24.
Ответ: 24
12. Найдите тангенс угла AOB, изображенного на рисунке.
Решение.
Опустим перпендикуляр BH на отрезок OA и рассмотрим прямоугольный треугольник OBH:
Ответ: 2.
Ответ: 2
13.Какие из следующих утверждений верны?
1) Вписанные углы, опирающиеся на одну и ту же хорду окружности, равны.
2) Если радиусы двух окружностей равны 5 и 7, а расстояние между их центрами равно 3, то эти окружности не имеют общих точек.
3) Если радиус окружности равен 3, а расстояние от центра окружности до прямой равно 2, то эти прямая и окружность пересекаются.
4) Если вписанный угол равен 30°, то дуга окружности, на которую опирается этот угол, равна 60°.
МОДУЛЬ «РЕАЛЬНАЯ МАТЕМАТИКА»
14. В таблице представлены нормативы по технике чтения в 3 классе.
В таблице представлены нормативы по технике чтения в 3 классе.
Какую отметку получит третьеклассник, прочитавший в апреле 68 слов за минуту?
1)«2» 2)«3» 3)«4» 4) «5»
Решение.
Проверка техники чтения происходила во втором полугодии. Из таблицы видно, что 68 прочитанных за минуту слов попадают в интервал «69 и менее» слов. Это соответствует отметке «2».
Правильный ответ указан под номером 1.
Ответ: 1
15.В таблице приведены результаты двух полуфинальных забегов на дистанцию 60 м. В финальном забеге 6 участников. Из каждого полуфинала в финал выходят два спортсмена, показавших первый и второй результаты. К ним добавляют еще двух спортсменов, показавших лучшее время среди всех остальных участников полуфиналов. Запишите в ответ номера спортсменов, не попавших в финал.
Запишите в ответ номера спортсменов, не попавших в финал.
Решение.
В полуфинале 1, лучшее время у спортсмена №4 и у спортсмена №1, таким образом, они выходят в финал.
В полуфинале 2, лучшее время у спортсмена №6 и у спортсмена №7 таким образом, они также выходят в финал.
Лучшее время из оставшихся спортсменов у спортсмена №2 и №5. таким образом таким образом, они тоже выходят в финал.
Таким образом, в финал не попали спортсмены под намерами 3 и 8.
Ответ: 38|3,8|8,3|83
16.На молочном заводе пакеты молока упаковываются по 12 штук в коробку, причём в каждой коробке все пакеты одинаковые. В партии молока, отправляемой в магазин «Уголок», коробок с полуторалитровыми пакетами молока втрое меньше, чем коробок с литровыми пакетами. Сколько литров молока в этой партии, если коробок с литровыми пакетами молока 45?
Решение.
Найдём количество коробок с полуторалитровыми пакетами молока: 45 : 3 = 15. Теперь рассчитаем количество литров молока в этой партии: 45 · 12 · 1 + 15 · 12 · 1,5 = 810 л.
Ответ: 810.
Ответ: 810
17. На каком расстоянии (в метрах) от фонаря стоит человек ростом 2 м, если длина его тени равна 1 м, высота фонаря 9 м?
Решение.
Пусть неизвестное расстояние равно х м. Рассмотрим два прямоугольных треугольника, выделенные на рисунке красным и зелёным. Они имеют общий угол и, следовательно, подобны. Поэтому отношения их катетов равны:
Тем самым, искомое расстояние равно 3,5 м.
Ответ: 3,5.
Ответ: 3,5
18.На диаграмме представлено распределение количества пользователей некоторой социальной сети по странам мира. Всего в этой социальной сети 9 млн пользователей.Какое из следующих утверждений неверно?
1) Пользователей из Беларуси меньше, чем пользователей из Украины.
2) Пользователей из России больше 4 миллионов.
3) Пользователей из Украины больше четверти общего числа пользователей.
4) Пользователей из Беларуси больше, чем пользователей из Финляндии.
В ответе запишите номер выбранного утверждения.
Решение.
Разъясним каждый вариант ответа.
1) Очевидно, что пользователей из Беларуси меньше, чем пользователей из Украины.
2) Видно, что пользователей из России больше половины всех пользователей, значит, больше 9/2 = 4,5 млн, а значит, больше 4 миллионов.
3) Сектор в четверть диаграммы отсекается углом в 360°/4 = 90°. Очевидно, что угол, отсекающий сектор «Украина» меньше 90°, значит, меньше четверти пользователей сети — из Украины.
4) Сектор «Беларусь» занимает большую площадь диаграммы, чем сектор «Другие страны», а т. к. «Финляндия» включена в «Другие страны», имеем: пользователей из Белоруссии больше, чем пользователей из Финляндии.
Ответ: 3.
Ответ: 3
19. В фирме такси в данный момент свободна 21 машина: 11 черных, 2 желтых и 8 зеленых. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчице. Найдите вероятность того, что к ней приедет зеленое такси. Полученный ответ округлите до сотых.
Найдите вероятность того, что к ней приедет зеленое такси. Полученный ответ округлите до сотых.
Решение.
Вероятность того, что приедет зеленая машина равна отношению количества зеленых машин к общему количеству машин:
Ответ: 0,38.
Ответ: 0,38
20.Площадь параллелограмма можно вычислить по формуле , где — стороны параллелограмма (в метрах). Пользуясь этой формулой, найдите площадь параллелограмма, если его стороны 10 м и 12 м и .
Часть 2
Решение.
Подставим в формулу известные значения величин:
Ответ: 60.
Ответ: 60
21.Решите систему уравнений:
Решение.
Сложим два уравнения системы:
откуда получаем или
Вычтем из первого уравнения системы второе:
Таким образом, решения систему
Ответ:
22. Две трубы наполняют бассейн за 8 часов 45 минут, а одна первая труба наполняет бассейн за 21 часов. За сколько часов наполняет бассейн одна вторая труба?
Решение.
По условию первая труба за одну минуту наполняет часть бассейна, а две трубы вместе за одну минуту наполняют часть бассейна. Таким образом, одна вторая труба за минуту наполняет часть бассейна, то есть она наполнит весь бассейн за 15 часов.
Ответ: 15.
23.При каком значении прямая имеет с параболой ровно одну общую точку? Найдите координаты этой точки. Постройте в одной системе координат данную параболу и прямую при найденном значении .
Постройте в одной системе координат данную параболу и прямую при найденном значении .
Решение.
График функции изображён на рисунке.
Запишем условие общей точки:
Прямая будет иметь с параболой единственную общую точку при условии, что дискриминант полученного квадратного уравнения равен нулю: откуда Подставив значение параметра в уравнение, находим
Ответ: (-2;0).
24. Найдите угол АСО, если его сторона СА касается окружности, О — центр окружности, а дуга AD окружности, заключённая внутри этого угла, равна 140°.
Решение.
Проведём радиус OA. Треугольник AOC — прямоугольный, ∠A = 90°. ∠COA = 180° − ∠AOD = 180° − 140° = 40°; ∠ACO = 90° − 40° = 50°.
Ответ: 50.
25.Дана равнобедренная трапеция . Точка лежит на основании и равноудалена от концов другого основания. Докажите, что — середина основания .
Решение.
Треугольник равнобедренный. Поэтому .
В равнобедренной трапеции .
Отсюда следует, что . Значит, треугольники и равны по двум сторонам и углу между ними. Следовательно, .
26. Диагонали четырёхугольника , вершины которого расположены на окружности, пересекаются в точке . Известно, что = 74°, = 102°, = 112°. Найдите .
ВАРИАНТ № 4
Часть 1 МОДУЛЬ «АЛГЕБРА»
1.Найдите значение выражения .
Решение.
Вынесем общий множитель за скобки:
Ответ: −3.-reshenie-283.jpg)
Ответ: -3
2. Одна из точек, отмеченных на координатной прямой, соответствует числу . Какая это точка?
1) точкаM 2) точкаN
3) точкаP 4) точка Q
Решение.
Возведём в квадрат числа 6, 7, 8:
Число 45 лежит между числами 36 и 49 и находится ближе к числу 49, поэтому соответствует точке N.
Правильный ответ указан под номером 2.
Ответ: 2
3 Какое из чисел больше: или?
1)
2)
3)
Решение.
В силу цепочки неравенств
первое число меньше второго.
Правильный ответ указан под номером 1.
Ответ: 1
4.Найдите корни уравнения .
Если корней несколько, запишите в ответе наименьший.
5.На одном из рисунков изображен график функции . Укажите номер этого рисунка.
1)
2)
3)
4)
Решение.
График функции проходит через точку (1; 0). Этому условию удовлетворяет только график, изображённый на рисунке 4.
Таким образом, верный ответ указан под номером 4.
Ответ: 4
6. Дана арифметическая прогрессия: 33; 25; 17; … Найдите первый отрицательный член этой прогрессии.
Решение.
Для члена имеем: По формуле нахождения n-го члена арифметической прогрессии имеем:
Первое число, которое удовлетворяет этому условию, число 6. Следовательно, первым отрицательным членом прогрессии является
Таким образом, правельный ответ указан под номером 1.
Ответ: 1.
Ответ: 1
7.Найдите значение выражения при .
Решение.
Упростим выражение:
Найдем значение выражения при
Ответ: 2,5.
Ответ: 2,5
8.На каком рисунке изображено множество решений неравенства ?
1)1 2)2 3)3 4) 4
МОДУЛЬ «ГЕОМЕТРИЯ»
9.Сумма трех углов выпуклого четырехугольника равна 300°. Найдите четвертый угол. Ответ дайте в градусах.
Решение.
Так как сумма углов выпуклого четырехугольника равна 360°, четвертый угол равен 360° − 300° = 60°.
Ответ: 60.
Ответ: 60
10.Боковая сторона равнобедренного треугольника равна 5. Угол при вершине, противолежащий основанию, равен 120°. Найдите диаметр окружности, описанной около этого треугольника.
Решение.
Воспользуемся теоремой косинусов:
Здесь и — боковые стороны равнобедренного треугольника, — основание.
Диаметр описанной окружности вычислим по формуле:
Ответ: 10.
Ответ: 10
11. Найдите площадь трапеции, изображённой на рисунке.
Решение.
Площадь трапеции вычисляется по формуле где и — основания, а — высота трапеции.
Ответ: 270.
Ответ: 270
12. Найдите тангенс угла С треугольника ABC , изображённого на рисунке.
Решение.
Тангенс угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему:
Ответ: 0,75.
Ответ: 0,75
13. Какие из следующих утверждений верны?
1) Около любого правильного многоугольника можно описать не более одной окружности.
2) Центр окружности, описанной около треугольника со сторонами, равными 3, 4, 5, находится на стороне этого треугольника.
3) Центром окружности, описанной около квадрата, является точка пересечения его диагоналей.
4) Около любого ромба можно описать окружность
МОДУЛЬ «РЕАЛЬНАЯ МАТЕМАТИКА»
14. На диаграмме представлено распределение количества пользователей некоторой социальной сети по странам мира. Всего в этой социальной сети 9 млн пользователей.
Какое из следующих утверждений неверно?
1) Пользователей из Украины больше, чем пользователей из Беларуси.
2) Пользователей из Украины меньше четверти общего числа пользователей.
3) Пользователей из Беларуси больше, чем пользователей из Эстонии.
4) Пользователей из России больше 8 миллионов.
Решение.
Проверим каждое утверждение:
1) Из диаграммы видно, что число пользователей из Украины больше, чем пользователей из Беларуси. Первое утверждение верно.
2) Из диаграммы видно, что пользователей из Украины меньше четверти общего числа пользователей. Второе утверждение верно.
3) Из диаграммы видно, что пользователей из Беларуси больше, чем пользователей из «других стран», а значит, и больше, чем пользователей из Эстонии. Третье утверждение верно.
4) Из диаграммы видно, что пользователей из России примерно две трети от общего числа пользователей. Всего пользователей 9 млн, значит пользователей из России около 6 млн, что меньше 8 млн. Четвёртое утверждение неверно.
Четвёртое утверждение неверно.
Неверным является утверждение под номером 4.
Ответ: 4
15.На графике показано, сколько человек зарегистрировалось с 25 декабря 2012 года по 13 февраля 2013 года в качестве участников конференции. По горизонтали указаны числа месяцев, а по вертикали — количество человек.
Во сколько раз возросло количество зарегистрировавшихся с 4 января по 3 февраля?
Решение.
Из графика видно, что число зарегестрировавшихся на4 января состваляло 30 человек, а 3 февраля — 270. Следовательно, число зарегистрировавшихся возросло в 270 : 30 = 9 раз.
Ответ: 9.
Ответ: 9
16. На пост председателя школьного совета претендовали два кандидата. В голосовании приняли участие 120 человек. Голоса между кандидатами распределились в отношении 3:5. Сколько голосов получил победитель?
На пост председателя школьного совета претендовали два кандидата. В голосовании приняли участие 120 человек. Голоса между кандидатами распределились в отношении 3:5. Сколько голосов получил победитель?
Решение.
Пусть x голосов приходится на одну часть, тогда 5x приходится на второго кандидата, а 3x — на первого. Зная, что в голосовании участвовало 120 человек составим уравнение:
Таким образом, победитель получил:
.
Ответ: 75.
Ответ: 75
17. Какой угол (в градусах) описывает минутная стрелка за 10 мин?
Решение.
Часовыми делениями циферблат разбит на 12 круговых секторов. Угол каждого из них равен 360° : 12 = 30°. Между минутной и часовой стрелкой два часовых деления. Они образуют угол 60°.
Угол каждого из них равен 360° : 12 = 30°. Между минутной и часовой стрелкой два часовых деления. Они образуют угол 60°.
Ответ: 60.
Ответ: 60
18. Рок-магазин продаёт значки с символикой рок-групп. В продаже имеются значки пяти цветов: чёрные, синие, зелёные, серые и белые. Данные о проданных значках представлены на столбчатой диаграмме.
Определите по диаграмме, значков какого цвета было продано меньше всего. Сколько примерно процентов от общего числа значков составляют значки этого цвета?
1) 5 2) 10 3) 15 4) 20
Решение.
Из диаграммы видно, что было продано меньше всего значков зелёного цвета в количестве 150 штук. Определим сколько процентов от общего числа составляют зелёные значки:
Значит зелёных значков примерно 15% от общего числа.
Ответ: 3.
Ответ: 3
19. На тарелке лежат пирожки, одинаковые на вид: 4 с мясом, 8 с капустой и 3 с яблоками. Петя наугад выбирает один пирожок. Найдите вероятность того, что пирожок окажется с яблоками
Решение.
Всего было подготовлено 25 билетов. Среди них 16 двузначных. Таким образом, вероятность взять билет с двухзначным номером равна
Ответ: 0,64
20. Из закона всемирного тяготения
выразите массу и найдите её величину (в килограммах), если и гравитационная постоянная
Часть 2
Решение.
Выразим массу: Подставим значения переменных:
Ответ: 1000.
Ответ: 1000
21. Решите неравенство
Решение.
Умножим на 10, приведём подобные слагаемые и разложим на множители:
Произведение двух сомножителей будет меньше нуля, если сомножители имеют разный знак (см. рисунок). Таким образом, получаем ответ:
Ответ:
22. Железнодорожный состав длиной в 1 км прошёл бы мимо столба за 1 мин., а через туннель (от входа локомотива до выхода последнего вагона) при той же скорости — за 3 мин. Какова длина туннеля (в км)?
Решение.
Поезд проходит через туннель за 3 минуты, при этом за одну минуту поезд проходит мимо выхода из туннеля, следовательно, от входа локомотива в туннель до выхода проходит 2 минуты. Мимо столба поезд длиной 1 км проходит за 1 минуту, поэтому его скорость равна 1 км/мин. Значит, за 2 минуты поезд пройдет 2 км, поэтому длина туннеля равна 2 км.
Мимо столба поезд длиной 1 км проходит за 1 минуту, поэтому его скорость равна 1 км/мин. Значит, за 2 минуты поезд пройдет 2 км, поэтому длина туннеля равна 2 км.
Ответ: 2.
23.Постройте график функции и определите, при каких значениях прямая имеет с графиком ровно три общие точки.
Решение.
Раскрывая модуль, получим, что график функции можно представить следующим образом:
Этот график изображён на рисунке:
Из графика видно, что прямая имеет с графиком функции ровно три общие точки при и
Ответ: 0; 4.
24. Диагонали и трапеции пересекаются в точке . Площади треугольников и равны соответственно и . Найдите площадь трапеции.
Диагонали и трапеции пересекаются в точке . Площади треугольников и равны соответственно и . Найдите площадь трапеции.
Решение.
Заметим, что площади двух треугольников, общей вершиной которых является точка пересечения диагоналей трапеции, а основаниями — боковые стороны, равны. Это следует, например, из того, что площади треугольников и равны (поскольку эти треугольники имеют общее основание , и их высоты, проведенные к этому основанию, равны как высоты трапеции), а . По условию, , поэтому и являются не боковыми сторонами, а основаниями трапеции. Тогда треугольники и подобны по двум углам, и отношение их площадей равно квадрату коэффициента подобия . Поэтому . Поскольку треугольники и имеют общую высоту, проведённую из вершины , то отношение их площадей равно отношению их оснований, т. е. . Значит, . Поэтому и . Но тогда .
Ответ: .
25. В параллелограмме ABCD диагонали AC и BD пересекаются в точке O. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника BOC.
В параллелограмме ABCD диагонали AC и BD пересекаются в точке O. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника BOC.
Решение.
Проведём высоту так, чтобы она проходила через точку Углы и равны друг другу как вертикальные. Вспомним также, что диагонали делятся точкой пересечения пополам, следовательно, Рассмотрим треугольники и , они прямоугольные, имеют равные углы и равные гипотенузы, следовательно эти треугольники равны, а значит равны отрезки и . Таким образом,
Площадь параллелограмм равна а площадь треугольника
26. Основание AC равнобедренного треугольника ABC равно 10. Окружность радиуса 8 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
Найдите радиус окружности, вписанной в треугольник ABC.
Олимпиада по математике 9 класс, задания, уравнения, задачи с ответами
Курс математики в 9 классе посвящен достаточно серьезным темам. Ученики знакомятся с решением квадратных неравенств, понятиями множества и подмножества, числовыми функциями и прогрессиями. Участие в олимпиадах по математике для учеников 9 класса является хорошей возможностью подготовки к предстоящей ГИА.
На этой странице предложены реальные примеры олимпиадных заданий по математике. Ученикам предложены уравнения и задачи с решениями и ответами.
Данный материал может использоваться на занятиях для подготовки к олимпиаде, а также во время проведения контрольных или итоговых работ по математике. Подробные решения задач, расписанные внизу страницы помогут провести работу над ошибками и восполнить пробелы в знаниях учащихся.
Уравнения
1. Решите уравнение: − − 3 = 0
2. Решите уравнение: − + 2 = 0
Решите уравнение: − + 2 = 0
3. Решите уравнение: − + 4 = 0
4. Решите уравнение: ( + )( + + 2) = 3
5. Решите уравнение: x4 − + 18 = 0
6. Решите уравнение: ( − − 16)( − + 2) = 88
7. Решите уравнение: ( + )( + − 5) = 84
8. Решите уравнение: ( − 1)( + 1) − 4( − 11) = 0
9. Решите уравнение: + − − + + 5 = 0
10. При каких с не имеет корней уравнение: − + с = 0
Задачи
Задача №1
Можно ли представить дробь 2/7 в виде суммы двух дробей, числители которых равны 1, а знаменатели — различные целые числа?
Задача №2
Токарь и его ученик, работая одновременно, обычно выполняют задание за 4 часа. При этом производительность труда токаря в 2 раза выше производительности ученика. Получив такое же задание, и, работая по очереди, они справились с заданием за 9 часов работы. Какую часть задания выполнил ученик токаря.
Задача №3
Стрелок десять раз выстрелил по стандартной мишени и выбил 90 очков. Сколько попаданий было в семерку, восьмерку и девятку, если десяток было четыре, а других попаданий и промахов не было?
Сколько попаданий было в семерку, восьмерку и девятку, если десяток было четыре, а других попаданий и промахов не было?
Задача №4
На столе лежат 2005 монет. Двое играют в следующую игру: ходят по очереди; за ход первый может взять со стола любое нечетное число монет от 1 до 99, второй – любое четное число монет от 2 до 100. Проигрывает тот, кто не сможет сделать ход. Кто выиграет при правильной игре?
Задача №5
Имеются два сосуда, в первом из них 1 л воды, второй сосуд пустой. Последовательно проводятся переливания из первого сосуда во второй, из второго в первый и т. д., причем доля отливаемой воды составляет последовательно 1/2, 1/3, 1/4 и т. д. от количества воды в сосуде, из которого вода отливается. Сколько воды будет в сосудах после 2007 переливаний?
Ответы к уравнениям
| Уравнение | № 1 | № 2 | № 3 | № 4 | № 5 |
| Ответ | ± | нет корней | ± | -1; 3 | ±; ± |
| Уравнение | № 6 | № 7 | № 8 | № 9 | № 10 |
| Ответ | -4; 5 | -3; 4 | нет корней | ±1; ± | c > 36 |
Ответы к задачам
Задача 1
Можно. Например, 2/7=1/4+1/28.
Например, 2/7=1/4+1/28.
Задача 2
Ученик выполнит 1\2 часть задания
Задача 3
Так как стрелок попадал лишь в семерку, восьмерку и девятку в остальные шесть выстрелов, то за три выстрела (по одному разу в семерку, восьмерку и девятку) он наберет 24 очка. Тогда за оставшиеся 3 выстрела надо набрать 26 очков. Что возможно при единственной комбинации 8 + 9 + 9 = 26. Итак, в семерку стрелок попал 1 раз, в восьмерку – 2 раза, в девятку – 3 раза.
Задача 4
Опишем стратегию первого игрока. Первым ходом он должен взять со стола 85 монет. Каждым следующим, если второй игрок берет х монет, то первый игрок должен взять 101 – x монет (он всегда может это сделать, потому что если х – четное число от 2 до 100, то (101 – x) – нечетное число от 1 до 99). Так как 2005 = 101 × 19 + 85 + 1, то через 19 таких «ответов» после хода первого на столе останется 1 монета, и второй не сможет сделать ход, т. е. проиграет.
Задача 5
«Просчитав» несколько первых переливаний, нетрудно обнаружить, что после первого, третьего, пятого переливаний в обоих сосудах будет по ½ л воды. Необходимо доказать, что так будет после любого переливания с нечетным номером. Если после переливания с нечетным номером 2k-1 в сосудах было по ½ л, то при следующем переливании из второго сосуда берется 1/(2k + 1) часть, так что в первом сосуде оказывается — 1/2 + (2/2(2k + 1)) = (k + 1)/(2k + 1) (л). При следующем переливании, имеющем номер 2k + 1, из него берется 1/(2k + 2) часть и остается (k + 1)/(2k + 1)-(k + 1)/((2k + 1)(2k + 1)) = 1/2 (л). Поэтому после седьмого, девятого и вообще любого нечетного переливания в сосудах будет по ½ л воды.
Необходимо доказать, что так будет после любого переливания с нечетным номером. Если после переливания с нечетным номером 2k-1 в сосудах было по ½ л, то при следующем переливании из второго сосуда берется 1/(2k + 1) часть, так что в первом сосуде оказывается — 1/2 + (2/2(2k + 1)) = (k + 1)/(2k + 1) (л). При следующем переливании, имеющем номер 2k + 1, из него берется 1/(2k + 2) часть и остается (k + 1)/(2k + 1)-(k + 1)/((2k + 1)(2k + 1)) = 1/2 (л). Поэтому после седьмого, девятого и вообще любого нечетного переливания в сосудах будет по ½ л воды.
Другие классы
Обновлено: , автор: Валерия ТокареваТесты по алгебре Функции (9 класс)
Сложность: знаток.Последний раз тест пройден 10 часов назад.
Материал подготовлен совместно с учителем высшей категории
Опыт работы учителем математики — более 33 лет.
Вопрос 1 из 9
Дана функция f(x) = 5x3. Найдите f(2)
- Правильный ответ
- Неправильный ответ
- Вы и еще 83% ответили правильно
- 83% ответили правильно на этот вопрос
В вопросе ошибка?
Следующий вопросОтветитьВопрос 2 из 9
При каких значениях аргумента значение функции у = -0,4х + 5, равно 13?
- Правильный ответ
- Неправильный ответ
- Вы и еще 64% ответили правильно
- 64% ответили правильно на этот вопрос
В вопросе ошибка?
ОтветитьВопрос 3 из 9
Найдите область определения функции у=
- Правильный ответ
- Неправильный ответ
- Вы ответили лучше 65% участников
- 35% ответили правильно на этот вопрос
В вопросе ошибка?
ОтветитьВопрос 4 из 9
Задана функция f(x) = , найдите f(0)
- Правильный ответ
- Неправильный ответ
- Вы ответили лучше 51% участников
- 49% ответили правильно на этот вопрос
В вопросе ошибка?
ОтветитьВопрос 5 из 9
Найдите область определения функции у =
- Правильный ответ
- Неправильный ответ
- Вы и еще 66% ответили правильно
- 66% ответили правильно на этот вопрос
В вопросе ошибка?
ОтветитьВопрос 6 из 9
Найдите точки пересечения графика функции с осью абсцисс у = 3х — х2
- Правильный ответ
- Неправильный ответ
- Вы и еще 52% ответили правильно
- 52% ответили правильно на этот вопрос
В вопросе ошибка?
ОтветитьВопрос 7 из 9
Найдите координаты точек пересечения графика с осью ординат у = х2 — 2х — 3
- Правильный ответ
- Неправильный ответ
- Вы и еще 63% ответили правильно
- 63% ответили правильно на этот вопрос
В вопросе ошибка?
ОтветитьВопрос 8 из 9
Вычислите координаты точек пересечения графиков функции у = ; у = 7 — х
- Правильный ответ
- Неправильный ответ
- Вы и еще 56% ответили правильно
- 56% ответили правильно на этот вопрос
В вопросе ошибка?
ОтветитьВопрос 9 из 9
Найдите нули функции: у = 3х2 + 5х — 2
- Правильный ответ
- Неправильный ответ
- Вы и еще 54% ответили правильно
- 54% ответили правильно на этот вопрос
В вопросе ошибка?
Ответить
Доска почёта
Чтобы попасть сюда — пройдите тест.
Тесты «Функции» (9 класс) предназначены для подготовки учеников средней школы к занятиям. Вопросы проверяют умение находить значение функции и аргумента, определять области функций, работать с координатными точками. Более сложные задания проверяют умение читать и строить графики. Представленные задания разного уровня сложности, поэтому их могут использовать ученики старших классов для повторения материала и подготовки к ЕГЭ по математике. К тесту прилагаются правильные ответы, что позволяет сразу запоминать то, что «упущено».
Тест по алгебре «Свойства функции» – один из эффективных способов качественной подготовки к самостоятельным и контрольным работам, а также к текущим урокам.
Рейтинг теста
Средняя оценка: 3.3. Всего получено оценок: 647.
А какую оценку получите вы? Чтобы узнать — пройдите тест.
Тест по алгебре Неравенства (9 класс)
Сложность: новичок. Последний раз тест пройден 14 часов назад.
Последний раз тест пройден 14 часов назад.
Материал подготовлен совместно с учителем высшей категории
Опыт работы учителем математики — более 33 лет.
Вопрос 1 из 10
Решите неравенство 17 — х > 3
- Правильный ответ
- Неправильный ответ
- Вы и еще 91% ответили правильно
- 91% ответили правильно на этот вопрос
В вопросе ошибка?
Следующий вопросОтветитьВопрос 2 из 10
Решитe неравенство:
- Правильный ответ
- Неправильный ответ
- Вы и еще 83% ответили правильно
- 83% ответили правильно на этот вопрос
В вопросе ошибка?
ОтветитьВопрос 3 из 10
Решите двойное неравенство -4 < 2x -1 < 2
- Правильный ответ
- Неправильный ответ
- Вы и еще 80% ответили правильно
- 80% ответили правильно на этот вопрос
В вопросе ошибка?
ОтветитьВопрос 4 из 10
Решитe неравенство: х(х — 3)(х + 4)(х — 7) ≤ 0
- Правильный ответ
- Неправильный ответ
- Вы и еще 83% ответили правильно
- 83% ответили правильно на этот вопрос
В вопросе ошибка?
ОтветитьВопрос 5 из 10
Запишитe сумму всех целых решений неравенства:
- Правильный ответ
- Неправильный ответ
- Вы и еще 69% ответили правильно
- 69% ответили правильно на этот вопрос
В вопросе ошибка?
ОтветитьВопрос 6 из 10
Решитe систему неравенств и указать наименьшее целое решение
- Правильный ответ
- Неправильный ответ
- Вы и еще 64% ответили правильно
- 64% ответили правильно на этот вопрос
В вопросе ошибка?
ОтветитьВопрос 7 из 10
Решите неравенство: -x2 + 10x — 21 < 0
- Правильный ответ
- Неправильный ответ
- Вы и еще 77% ответили правильно
- 77% ответили правильно на этот вопрос
В вопросе ошибка?
ОтветитьВопрос 8 из 10
Решите неравенство: |x2-5x — 6| < x + 10
- Правильный ответ
- Неправильный ответ
- Вы и еще 72% ответили правильно
- 72% ответили правильно на этот вопрос
В вопросе ошибка?
ОтветитьВопрос 9 из 10
Решите неравенство 2(х — 1) > 5x — (3x + 2)
- Правильный ответ
- Неправильный ответ
- Вы и еще 69% ответили правильно
- 69% ответили правильно на этот вопрос
В вопросе ошибка?
ОтветитьВопрос 10 из 10
Решите неравенство: |x2 — 7x + 6|>x2 + x — 2
- Правильный ответ
- Неправильный ответ
- Вы и еще 65% ответили правильно
- 65% ответили правильно на этот вопрос
В вопросе ошибка?
Ответить
Доска почёта
Чтобы попасть сюда — пройдите тест.
ТОП-3 тестакоторые проходят вместе с этимРейтинг теста
Средняя оценка: 3.8. Всего получено оценок: 374.
А какую оценку получите вы? Чтобы узнать — пройдите тест.
Репетитор урока: 9 класс Алгебра
9 класс Алгебра Элейн Эрнст Шнайдер
Начальный взгляд на базовую алгебру — Урок 1
План:
Алгебра дает основы для всей высшей математики. Вы будете работать с числами и буквами (переменными), чтобы составлять предложения (выражения), которые вы можете решить. Лучший способ выучить математику — это практиковаться в ней, поэтому каждый урок будет включать в себя упражнения, использующие полученные навыки.
Место для начала:
Математические буквы называются переменными.Они могут обозначать разные числа в разное время.
Математическое предложение называется выражением. Он может включать числа, переменные, знаки работы и символы включения.
Знаки действия подсказывают, что делать с приговором. Четыре операции — это сложение, вычитание, умножение и деление.
Символы включения — круглые скобки () и квадратные скобки [].
Важное предупреждение:
Будьте очень аккуратны в своих расчетах. Многие задачи по алгебре упускаются из виду, потому что ученик неправильно понял написанное или неправильно «выстроил» столбец для вычитания или деления.Всегда дважды проверяйте операции. Вы не хотите пропустить проблему из-за того, что добавили неправильно.
Давайте начнем:
«Оценить» выражение — значит найти его значение или решить его. Первое правило изучения алгебры — «что и когда делать». Порядок, в котором выполняются операции с выражением, может полностью изменить ответ.
При оценке алгебраического выражения сначала ищите символы, которые показывают самое сокровенное произведение. Это можно выразить с помощью круглых или квадратных скобок.Если присутствуют ОБЕ круглые скобки и скобки, они обычно являются самыми внутренними и должны обрабатываться в первую очередь.
Вот пример:
24 + [46 — (2 X 11)]
24 + [46 — 22]
24 + 24
48
А теперь пора попробовать несколько.
УПРАЖНЕНИЕ:
9 — (4 X 2)
(9 — 4) X 2
(9 — 4) X (2 X 1)
48 — [42 — (3 X 9)]
63 — [8 / 2 + (14-10)]
(Примечание: 8/2 то же самое, что 8, разделенное на 2, как и в дробях.)
[800 / (200 X 4)]
28 + [10 — (4 + 2)]
(11-5) X (10 + 14)
125 / (5 X 5) (Помните цифру 5? / = делится на.)
[28 — (4 X 5)] — 4
КЛЮЧ ОТВЕТА
| Вопрос № | Ответ |
| 1… 2… 3… 4… 5… 6… 7… 8… 9… 10… | 1 10 10 33 55 1 32 144 5 4 |
Базовая алгебра — Урок 2
Схема :
На первом уроке вы узнали, что числа и переменные образуют предложения или алгебраические «выражения».«Когда вы берете информацию из предложения и превращаете ее в математическое выражение, это называется« переводом ».
Место для начала:
- При написании алгебраических выражений используйте знаки +, — и =. Для деления используйте /, точно так же, как вы знаете, что когда вы видите дробь, это означает деление верхнего числа на нижнее число.
- Для умножения запишите выражение без символа или знака между ними, поскольку символ X (умножение) можно спутать с переменной x.Например, 3 раза переменная y должна быть записана 3y. Вы также можете использовать круглые скобки для обозначения умножения. Это особенно полезно в более длинных задачах, таких как (3y) (4-2x).
- Если вы хотите умножить что-то ПОСЛЕ того, как сначала было выполнено другое выражение, используйте круглые скобки. Например, если вы хотите сложить x и y, а ЗАТЕМ умножить результат на 7, запишите это так: 7 (x + y).
- Чтобы перевести с языка на математическое выражение, внимательно прочтите предложение. Затем решите, какие операции потребуются для достижения решения.Запишите это в алгебраическое выражение.
Давайте приступим:
Вот проблема со словом:
Я запасаюсь полками в магазине футболок. Мне выдали восемь коробок футболок. В каждой коробке 25 футболок. Я приказываю взять по одной футболке из каждой коробки и отложить ее, чтобы раздать бедным. Сколько футболок мне останется поставить на полки магазинов после того, как я разберу футболки для бедных?
Вот алгебраическое выражение:
8 (25-1)
8 (24)
192
Если вы не знаете количество футболок в каждом поле, замените это значение переменной x .Тогда выражение будет выглядеть так:
8 (x — 1)
А теперь пора попробовать несколько.
Задания, включая ключ ответа:
УПРАЖНЕНИЕ:
- Кэти 21 год. Напишите алгебраическое выражение, показывающее, сколько ей будет лет через пять. Пусть x представляет этот возраст. Решайте по своему выражению лица.
- Один гамбургер стоит x центов. Напишите алгебраическое выражение, показывающее, сколько будут стоить 4 гамбургера.
- Сэнди 21 год.Ал на пять лет старше. Сколько лет Алу будет через пять лет? Пусть x представляет возраст Ала через пять лет. Решите для x.
- У меня есть десять шляп по 47,50 долларов за все. Напишите алгебраическое выражение, чтобы показать, сколько стоит одна из этих шляп, пусть y представляет ответ. Решите для y.
- У меня есть десять шляп по 47,50 долларов за все. Сколько мне нужно будет продать КАЖДУЮ шляпу, чтобы получить прибыль в 1 доллар с каждой? Задайте решение в виде алгебраического выражения.
КЛЮЧ ОТВЕТА
| Вопрос | Ответ |
| 1.. | 21 + 5 = x 26 = x |
| 2 .. | 4x |
| . | |
| 3 .. | (21 + 5 = возраст Эла сейчас) (21 + 5) + 5 = x (возраст Эла через 5 лет) |
| . | |
| 4 .. | 47,50 долл. США / 10 = y 4,75 долл. США = y |
| . | |
| 5 .. | (47,50 / 10) + 1 доллар = x 4,75 доллара + 1 доллар = x 5 долларов.75 = x |
Урок алгебры 3 — Решение для X
План:
Краткий обзор:
1. Когда вы пишете алгебраические выражения, используйте знаки +, — и =. Для деления используйте /, точно так же, как вы знаете, что когда вы видите дробь, это означает деление верхнего числа на нижнее число.
2. Для умножения запишите выражение без символа или знака между ними, так как символ X
(умножение) можно спутать с переменной x.Например, 3 раза переменная y должна быть записана 3y. Вы также можете использовать круглые скобки для обозначения умножения. Это особенно полезно в более длинных задачах, таких как (3y) (4-2x).
3. Если вы хотите умножить что-то ПОСЛЕ того, как сначала было выполнено другое выражение, используйте скобку
. Например, если вы хотите сложить x и y, а ЗАТЕМ умножить результат на 7, запишите это так: 7 (x + y).
4. Чтобы перевести с языка на математическое выражение, внимательно прочтите предложение. Затем решите, какие операции потребуются для достижения решения.Запишите это в алгебраическое выражение.
Что-то новое:
1. Чтобы убрать что-то вне скобок, выполняйте операцию по одному за раз. Например, 7 (x + y). Сначала умножьте 7 раз x. Затем умножьте 7 раз y. Результат 7х + 7у.
2. Когда вы решаете x, вы хотите «изолировать» x на одной стороне от знака равенства. Для этого используйте противоположный знак числа, которое вы хотите переместить, и проделайте то же самое с ОБЕИМИ сторонами уравнения.
Например: 8x + 2 = 50
8x + 2-2 = 50-2 (вычтите 2 с обеих сторон от знака =)
8x = 48 (разделите на 8, чтобы решить, потому что это противоположно умножению)
x = 6
А теперь забавная задача, которая заставит вас задуматься.Решить с помощью алгебры. Переведите в выражение и решите.
Ты справишься!
Задания, включая ключ ответа:
Джордж на 4 года старше Джона, который на 4 года старше Джима, который на 4 года старше Сэма, который вдвое младше Джорджа. Сколько лет каждому мальчику? Подсказка: пусть x обозначает возраст Джорджа.
Ключ ответа
Если x — возраст Джорджа, то x — 4 — возраст Джона, потому что Джордж на 4 года старше Джона. Джордж на 8 лет старше Джима, то есть Джиму на 8 лет.Джордж на 12 лет старше Сэма, поэтому возраст Сэма можно представить как
x — 12.
Мы также знаем, что Сэм вдвое старше Джорджа.
Итак, задайте выражение:
(x — 12) = 1/2 x
Чтобы найти x, вам сначала нужно преобразовать 1 / 2x в другую форму.
Умножим 1/2 на x.
x совпадает с x больше 1, если вы поместите его в дробную форму, или x / 1. Итак, когда вы умножаете 1/2 на x, это на самом деле будет выглядеть как (1/2) (x / 1). Когда вы умножаете дроби, вы умножаете числители (1) (x), а затем знаменатели (2) (1).Результат — x / 2. Теперь перепишите выражение, используя x / 2 вместо 1 / 2x.
(x-12) = x / 2
Мы узнали, что когда вы решаете выражение, вы хотите «изолировать» переменную. Для этого умножьте ОБЕИ стороны на 2.
(x-12) = x / 2
2 (x-12) = 2 (x / 2)
2x -24 = x
Теперь вам нужно получить обе переменные с одной стороны от знака равенства, поэтому вычтите 2x из ОБЕИХ сторон:
2x — 2x — 24 = x — 2x
-24 = -1x (Разделите -24 на -1, чтобы найти x)
24 = x
, следовательно, Джорджу 24 года.Возраст Джона представлен как x — 4 или 20.
Джим равен x — 8 или 16. А Сэм равен x — 12 или 12.
Вы можете дополнительно проверить задачу, умножив возраст Сэма на 2, чтобы получить возраст Джорджа, потому что проблема подсказала нам, что Сэм вдвое моложе Джорджа.
Базовая алгебра — Урок 4
Краткое содержание:
На первом уроке вы узнали, что числа и переменные образуют предложения или алгебраические «выражения». Когда вы берете информацию из предложения и превращаете ее в математическое выражение, это называется «переводом».На другом уроке вы узнали, что при написании алгебраических выражений используйте знаки +, — и =; а для деления используйте /, точно так же, как вы знаете, что когда вы видите дробь, это означает деление верхнего числа на нижнее число
. Затем, для умножения, мы научились писать выражение без символа или знака между ними (например, 3a), с X или используя круглые скобки. Круглые скобки особенно полезны в более длинных задачах, таких как (3y) (4-2x).
А что, если скобок и скобок нет? Как узнать, что делать в первую очередь? Сложить, разделить, умножить? Который из?
Когда нет других указаний относительно того, какое вычисление выполнить в первую очередь, математики следуют правилу Порядка операций.Умножение, деление, сложение, вычитание.
Хороший способ запомнить Порядок действий — подумать о моей дорогой тете Салли. M для умножения, D в Dear для Divide, A для сложения и S в Sally для вычитания.
ПОДСКАЗКА: Если в задаче есть только умножение и деление, работайте слева направо.
ПОДСКАЗКА: Если задача состоит только из вычитания и сложения, работайте слева направо.
Приступим:
13 — 2 X 5
Если бы я просто посчитал слева направо, я бы сказал, что 13 — 2 = 11.Тогда 11 умножить на 5 = 55.
Но Порядок действий говорит мне сначала умножить! Итак, 2 X 5 = 10. Затем я вычитаю 10 из 13 и получаю 3.
Как видите, то, какой порядок вы выбираете, имеет БОЛЬШУЮ разницу в ответе! Вот почему так важно соблюдать Порядок действий.
А теперь пора попробовать несколько.
Назначения, включая ключ ответа:
1. 10 — 4 + 3
2. 10 + 4 X 2
3. (5 X 4) -15 + 2
4. 12 — 2 (3 + 1 )
5.18 + 2 (3)
6. (12 — 2) (3 + 4)
7. 4 X 3 + 5
8. 24 — 6 +2
9. 24 — 6 X 2
10. 36/9 — 2
КЛЮЧ ОТВЕТА
1. 9
2. 18
3. 7
4. 4
5. 24
6. 70
7. 17
8. 20
9. 12
10. 2
Базовая алгебра — Урок 5 — Выражения из предложений
Краткое содержание:
Обзор:
На первом уроке вы узнали, что числа и переменные образуют предложения или алгебраические «выражения».«Когда вы берете информацию из предложения и превращаете ее в математическое выражение, это называется« переводом ». На другом уроке вы узнали, что при написании алгебраических выражений используйте знаки +, — и =; а для деления используйте /, точно так же, как вы знаете, что когда вы видите дробь, это означает деление верхнего числа на нижнее число
. Затем, для умножения, мы научились писать выражение без символа или знака между ними (например, 3a), с X или используя круглые скобки. Круглые скобки особенно полезны в более длинных задачах, таких как (3y) (4-2x).
Затем вы узнали, как решать задачи без скобок или скобок, используя правило Порядка операций. Умножение, деление, сложение, вычитание.
Теперь давайте используем все это, и да, верно! Мы собираемся взять английские предложения — СЛОВА — и превратить их в алгебраические выражения.
Приступим:
Вычтем семь из двадцати одного, затем прибавим три.
Алгебраическое выражение: 21 — 7 + 3
Скобки не нужны, потому что Порядок операций говорит нам, что сложение и вычитание выполняются слева направо.
А теперь пора попробовать несколько. Запомните свои термины: вычитание, сумма, произведение, деление, умножение, частное. Возможно, вам придется использовать круглые скобки для некоторых из них.
Присвоение (я), включая ключ ответа:
1. Вычтите 2 из x; затем добавьте y.
2. Вычтите сумму 2 и y из x.
3. Разделить 10 на 3; затем умножьте на 5.
4. Разделите x на произведение 3 и z.
5. Умножить x на 3; затем добавьте y.
6. Складываем x и 3; затем умножьте на y.
7. Вычтите произведение 5 и x из 7.
8. 5 больше, чем произведение 3 и ц.
9. 13 меньше частного 5, деленного на p.
10. 4 раза сумма 10 и x.
Ключ ответа
1. x — 2 + y
2. x — (2 + y)
3. 10/3 X 5
4. x / 32
5. 3x + y
6. (x + 3) y
7. 7 — 5x
8. 3c + 5
9. 5 / p -13
10. 4 (10 + x)
Базовая алгебра — Урок 6 Балансировка уравнений для решения переменных
Схема:
На последнем уроке вы научились писать выражения и находить значения выражений.
Когда два выражения могут быть записаны так, чтобы уравновесить или уравнять друг друга, это называется уравнением
. Другими словами, все, что выражено с одной стороны от знака равенства, вычисляется как то же самое значение, что и то, что находится по другую сторону от знака равенства. Другими словами, левый и правый члены уравнения «баланс».
Примеры уравнений:
5 + 7-2 = 2 (5) (ответ слева — 10, а ответ справа — 10)
100/25 = 347 — 343 (ответ: 4 слева от знака равенства и 4 также справа)
Уравнения с неизвестными переменными решаются путем уравновешивания левого и правого элементов.Например, в уравнении y + 5 = 12 я знаю, что левый член должен быть равен 12, чтобы он уравновесился с правым членом. Это означает, что y будет 7, потому что 7 + 5 = 12. Это достаточно просто, чтобы производить вычисления без формальной процедуры. Но поскольку алгебраические уравнения могут стать намного длиннее и более рассчитанными, необходима система для решения уравнений переменных и уравнений баланса.
Возьмем приведенное выше уравнение:
y + 5 = 12
Правильная процедура решения для y — это «изолировать» y.Это означает, что мы хотим, чтобы y стоял по одну сторону от знака равенства.
Теперь имейте в виду, что мы хотим, чтобы все «балансировало» по обе стороны от знака равенства. Это означает, что все, что я делаю с левым членом, я должен делать с правым членом. Итак, чтобы выделить y и решить уравнение, я должен «переместить» 5 на другую сторону от знака равенства. Для этого я должен сделать его нулевым в левой части уравнения, вычтя 5:
y + 5 = 12
y + 5-5 = 12-5
y + 0 = 12-5
y = 7
Попробуйте найти переменную, оставив все стороны равными.Помните, идея состоит в том, чтобы «сбалансировать»
уравнение, поэтому то, что вы делаете с одной стороной, вы должны делать с другой.
100/5 = y + 2
100/5 -2 = y +2 — 2
20 — 2 = y
18 = y
Теперь вам пора попробовать несколько…
Назначение (s) включая ключ ответа:
УПРАЖНЕНИЕ:
1. y — 10 = 17
2. c + 4 = 29
3. 5y = 90
4. 1/3 t = 29
5. 6y = 72
6. 1/9 г = 58
7. 4y = 100
8.12a = 132
9. r + 9 = 48
10. x + 79 = 422
ОТВЕТ КЛЮЧ:
1. 27
2. 25
3. 18
4. 87
5. 12
6. 522
7 . 25
8. 11
9. 39
10. 343
Базовая алгебра — Урок 7 Использование уравнений для решения головоломок
Краткое содержание:
На последнем уроке вы научились балансировать уравнение, делая то, что находится на одном сторона знака равенства равна тому, что находится на другой стороне. Другими словами, левый и правый члены уравнения «баланс.
Примеры уравнений:
5 + 7 — 2 = 2 (5) (ответ слева — 10, а ответ справа — 10)
100/25 = 347 — 343 (ответ равно 4 слева от знака равенства и 4 справа)
Вы также научились изолировать переменные. Уравнения с неизвестными переменными решаются путем уравновешивания левого и правого элементов. В уравнении y + 5 = 12, правильная процедура решения для y — «изолировать» y. Это означает, что мы хотим, чтобы y стоял по одну сторону от знака равенства.
Теперь имейте в виду, что мы хотим, чтобы все «балансировало» по обе стороны от знака равенства. Это означает, что все, что я делаю с левым членом, я должен делать с правым членом. Итак, чтобы выделить y и решить уравнение, я должен «переместить» 5 на другую сторону от знака равенства. Для этого я должен сделать его нулевым в левой части уравнения, вычтя 5:
y + 5 = 12
y + 5-5 = 12-5
y + 0 = 12-5
y = 7
Уравнения также можно использовать для решения головоломок.Вы должны составить уравнение, которое в цифрах «соответствует» тому, что головоломка выражает словами. Затем найдите переменную. Это будет ответ на загадку.
Почему бы вам не попробовать несколько?
Задания, включая ключ ответа:
1. Фермер Браун сказал Бобу и Сью, что они могут собирать яблоки с его дерева, но ни один из них не может брать больше 20. Некоторое время они работали, а затем Боб спросила Сью, «Вы уже выбрали свой предел?»
Сью ответила: «Еще нет.Но если бы у меня было вдвое больше, чем сейчас, плюс вдвое меньше, чем сейчас, у меня был бы свой предел ». Сколько было у Сью?
2. Маленькому мальчику посоветовали не есть виноград с лозы, опасаясь, что он съест слишком много и у него заболит живот. Пробираясь к виноградной беседке, когда его мать не смотрела, маленький мальчик ел винограда пять дней, каждый день съедая на шесть больше, чем накануне. Фактически, через пять дней маленький мальчик был настолько болен, что ему пришлось признаться матери в том, что он съел 100 ягод винограда.Сколько винограда маленький мальчик ел КАЖДЫЙ из пяти дней?
3. Насколько высокое дерево на 15 футов короче шеста в три раза выше дерева?
ОБОЗНАЧЕНИЕ ОТВЕТА:
1. Пусть x = количество яблок, которые у нее были.
2x + 1/2 x = 20
(2x в виде дроби со знаменателем 2 будет записано как 4x / 2.)
4x / 2 + 1/2 x = 20
5x / 2 = 20
5x / 2 X 2 = 20 X 2
5x = 40
5x / 5 = 40/5
x = 8 яблок
2.Пусть x = количество ягод, съеденных маленьким мальчиком в первый день
x + 6 = количество ягод, съеденных во второй день
x + 6 + 6 = количество ягод, съеденных в третий день
x + 6 + 6 + 6 = количество ягод, съеденных на четвертый день
x + 6 + 6 + 6 + 6 = количество ягод, съеденных в пятый день
Виноград на пять дней = всего 100. Следовательно, уравнение для создания:
x + (x + 6) + (x + 6 + 6) + (x + 6 + 6 + 6) + (x + 6 + 6 + 6 + 6) = 100
x + x + 6 + x + 12 + x + 18 + x + 24 = 100
5x + 60 = 100
5x + 60-60 = 100-60
5x = 40
5x / 5 = 40/5
x = 8 ягод винограда, съеденных в первый день
(Теперь поставьте 8 вместо x во всех других выражениях.)
x + 6 = 14 ягод, съеденных на второй день
x + 6 + 6 = 20 ягод винограда, съеденных на третий день
x + 6 + 6 + 6 = 26 виноградин, съеденных на четвертый день
x + 6 + 6 + 6 + 6 = 32 винограда, съеденных на пятый день
(Чтобы проверить, прибавьте 8, 14, 20, 26, ad 32. Они равны 100.)
3. Пусть y = количество футов в высоту дерева
3y будет равно количеству футов высоты столба
Составьте уравнение:
y = 3y — 15
y — 3y = 3y — 3y — 15
-2y = -15
-2y / — 2 = -15 / -2
y = 7.5 футов
3y = 22,5 фута
Урок алгебры 8 — Уравнение, лежащее в основе старого трюка
Краткое содержание:
На последнем уроке вы узнали, что уравнения можно использовать для решения головоломок. В течение многих лет математики решали следующую головоломку, удивляя своих учеников. Это не только забавный «трюк», но и основанный на здравом математическом принципе, который заставляет его работать:
Используя номер вашего дома, математик может вычислить ваш возраст!
Вот как это работает:
1.Удвойте номер дома.
2. Сложить 5.
3. Умножить на 50.
4. Сложить свой возраст.
5. Добавьте количество дней в году (365).
6. Возьмите это число и вычтите 615.
7. Представьте, что это денежная сумма, и установите десятичную точку для долларов и центов.
Ответ: доллары будут номером вашего дома, а центы — вашим возрастом.
Но теперь большой вопрос: КАК это работает? Подумайте немного, прежде чем смотреть на ответ.
ОТВЕТ:
Чтобы понять, почему головоломка работает, вы должны решить ее алгебраически.
Пусть x = номер вашего дома.
Пусть y = ваш возраст.
Пусть A = ответ
Используя пронумерованный список инструкций, сформулируйте задачу в виде алгебраического уравнения. Это будет выглядеть так:
A = 50 (2x + 5) + y + 365-615
100
A = 100x + 250 + y +365-615
100
A = 100x + y
100
A = x + y / 100
Следовательно,
x = номер дома (вы начали с этого числа.)
y / 100 = ваш возраст (когда вы делите на 100, вы перемещаете десятичную точку на два разряда влево. .)
Урок алгебры 9 — Положительные и отрицательные стороны числовой линии
Схема:
Различные типы чисел используются для обозначения разных вещей. Есть положительные числа и есть отрицательные числа. Положительные числа больше нуля, а отрицательные числа меньше нуля.
Лучший способ «увидеть» отрицательные и положительные числа — это посмотреть на числовую строку:
/ _____ / _____ / _____ / _____ / _____ / _____ / _____ / _____ / _____ / _____ / _____ / _____ / _____ / _____ /
-7… -6….. -5…. -4 …… -3 …… -2… .. -1… .. 0 …… 1 …… 2 …… 3 …… 4 …… 5 …… 6 …… 7
При использовании числовой строки вы добавляйте плюсы по мере продвижения вправо и добавляйте негативы по мере продвижения влево. Например, 3 + -2 означает, что вы начинаете с 3 и перемещаетесь на две позиции влево. Ответ: 1. Чтобы добавить положительное к отрицательному, вы работаете слева направо. Например, -4 + 3 равно -1. Вы получите это, начав с -4 и переместившись на три позиции вправо. Чтобы добавить два негатива, переместитесь влево. Например, -1 + -3 = -4.Вы придете к этому ответу, начав с -1 и отсчитав три разряда слева.
Назначения, включая ключ ответа:
Теперь попробуйте:
1. 1 + -1
2. 4 + -2
3. 2 + 4
4. -2 + -5
5. -5 + 4
6. — 3 + 5
7. -2 + -2 + -1
8. -5 + 6
9. -7 +2
10 -4 + -2 + 2
Теперь попробуйте несколько, которые выходят за рамки числовой прямой, показанной выше. Ты можешь это сделать! Просто используйте принципы, которые вы узнали.
- -15 + 13
- -39 + -40
- -23 + 20
- 2 + -11
- -13 + -4
ВЫРЕЗАТЬ ЗДЕСЬ _________________________________________________________________
ОТВЕТЫ:
1. 0
2. 2
3. 6
4. -7
5. -1
6. 2
7. -5
8. 1
9. -5
10-4
********
- -2
- -79
- -3
- -9
-17
Урок алгебры № 10 — Абсолютные значения
План:
В уроке 9 мы узнали об отрицательных и положительных числах используя числовую линию.Отрицательные значения идут слева от нуля, а положительные — справа. Чтобы сложить отрицательное и положительное, вы начинаете с одного из чисел, а затем считаете либо влево, либо вправо в зависимости от знака. Например, чтобы сложить -2 и 3, вы можете начать с -2 и считать до трех мест. В итоге вы получите 1,2 + 3 = 1
В математике есть термин, обозначающий расстояние, на которое число отсчитывается от нуля. Абсолютное значение этого члена составляет . Абсолютное значение 3 равно трем.Абсолютное значение -6 равно шести. Это означает, что по абсолютной величине -6 больше 3. Другими словами, 6 занимает больше мест в числовой строке. Посмотрите на числовую строку ниже. Красные числа представляют количество мест, необходимое для достижения -6 с нуля. Синий цвет представляет три. Вы можете видеть, что красная линия намного длиннее синей.
/ _____ / _____ / _____ / _____ / _____ / _____ / _____ / _____ / _____ / _____ / _____ / _____ /
-6… -5 …… -4… .. -3… .. -2…. .-1… .. 0.…. 1 …… 2 …… 3 …… .4 …… 5 ..…. 6
Понятие абсолютного значения важно при сложении положительных и отрицательных чисел. Например, если у вас -7 + 4, вы можете задаться вопросом, какое число использовать, чтобы начать процесс сложения. Число четыре положительное, поэтому вы можете подумать, что оно означает «больше». Любой предпочел бы иметь на своем текущем счете 4 доллара, а на счету — 7 долларов; верно?! Но для того, чтобы произвести вычисления, мы должны сосредоточиться только на абсолютном значении . Абсолютное значение семи больше абсолютного значения четырех.Поэтому мы начинаем с -7 и рассматриваем его как большее число.
Вот проблема:
-7 + 4 =
Вычтите значения. 7 — 4 = 3. Чтобы определить, какой знак использовать, вы должны учитывать абсолютное значение. Поскольку 7 больше по абсолютной величине, его знак будет преобладающим. Ответ будет -3.
-7 + 4 = -3
Предположим, у вас есть два отрицательных числа:
-7 + -2
Сложите значения. 7 + 2 = 9. Так как вы добавили абсолютные значения, ответ будет — 9.
-7 + -2 = -9
Назначения, включая ключ ответа:
Теперь вы попробуете:
- -7 + -9
- -7 + 9
- -6 + 5
- -2 + -5
- -5 + 4
- -3 + -5
- -5 + 2
- -15 + 6
- -17 +22
- -4 + -21
ОТВЕТЫ:
- -16
- 2
- -1
- -7
- -1
- -8
- -3 9010 9
- 5
-25
Урок 11 — Аддитивные инверсии
Схема:
Аддитивные инверсии — это противоположностей. Два числа противоположны, если их сумма равна нулю. Например, -8 и 8 являются аддитивными инверсиями, потому что их сумма равна нулю. Это делает их противоположностями.
Другой способ записать противоположность –8 — написать — (- 8). Вычесть отрицательную 8 — это то же самое, что сделать положительную 8 или найти ее противоположность.
То же самое можно сделать и с переменными. Например, — (- x) = x.
Используя этот принцип, добавим отрицательное число к положительному: 8 + (-3) = 8 — 3 = 5.Это может быть прочитано как 8 плюс отрицательное 3 ИЛИ 8 минус 3 ИЛИ 8 плюс напротив из 3.
В алгебре вычитание числа также можно описать как сложение его противоположности.
Например, x — y = x + (-y).
OR
8 — (-5) = 8 + 5 = 13
А теперь давайте немного изменим ситуацию. Попробуйте это:
14 — 28 = x
Как вы можете переписать это, чтобы использовать то, что вы узнали о противоположностях?
14 + (-28) = x
–14 = x
Давайте попробуем еще раз:
11 — (-3) — 4 = x
11 + 3 — 4 = x
14 — 4 = x
10 = x
Назначения, включая ключ ответа:
1.5 — 7
2. 8 — (-10)
3. — 3 — 7
4. — 7 — 9
5. 7 + (-3)
6. 25 — 250
7. 5,8 — 2,3
8. 2,3 — 5,8
9. (34 — 13) — (15 — 17)
10. 11 — 5 — [6 + (-13)]
Ключ ответа:
1. –2
2. 18
3. –10
4. –16
5. 4
6. –225
7. 3.5
8. –3.5
9. 23
10 .13
Урок алгебры 12: Умножение положительных и отрицательных
Как мы узнали на предыдущем уроке : Аддитивные инверсии — это противоположности. Два числа противоположны, если их сумма равна нулю.Например, -8 и 8 являются аддитивными инверсиями, потому что их сумма равна нулю. Это делает их противоположностями. То же самое можно сделать и с переменными. Например, — (- x) = x.
Когда этот принцип используется в умножении, возникают следующие практические правила:
1. Отрицательное умножение на отрицательное дает положительный ответ.
2. Отрицательное умножение на положительное — отрицательное.
3. Положительный результат умноженный на положительный.
Примеры
(-6) (8) = -48
(-3) (- 12) = 36
(12) (11) = 132
Теперь, что происходит, когда нужно умножить три числа ? Просто работайте последовательно, следуя усвоенным правилам.
Пример: (-5) (-4) (-20)
(20) (-20) [умножьте –5 на –4, чтобы получить положительное число 20]
-400 [умножьте положительное число 20 из последнего шага на — 20, чтобы получить –400]
А как насчет экспонентов? Просто запишите их и соблюдайте правила.
Пример: -45 = (-4) (-4) (-4) (-4) (-4)
(16) (-4) (-4) (-4)
-64 (-4 ) (-4)
256 (-4)
-1024
Упражнения:
1. (10) (-8)
2. (-5) (-26)
3. -53
4.(-2) (-3) 2
5. (-1,5) (4)
6. (-5) (22) (-2)
7. (-3) (-5) (-4)
8 . (-1) (-3) 4
9. (-1) 15
10. (-2) 2 (-3) 4
Ключ ответа:
1. –80
2. 130
3. — 125
4. –18
5. –6
6. 220
7. –60
8. –81
9. –1 *
10. 324
** Примечание. Вы узнали что-нибудь об экспонентах? Если показатель четный, ответ положительный. Если показатель нечетный, ответ отрицательный.
Gr9 по математике
В этой главе вы найдете числа, которые делают утверждения верными.Это называется решением уравнения. Вы будете решать уравнения двумя разными способами: путем проверки и «реверсирования». их. Вы обнаружите, что два уравнения могут иметь одно и то же решение. Такие уравнения называются эквивалентные уравнения. Вы также обнаружите, что не все утверждения являются алгебраическими уравнениями. Некоторые утверждения являются алгебраическими тождествами, а другие на самом деле являются алгебраическими невозможностями. Ты узнает, в чем разница между этими тремя типами утверждений.
Решение уравнений путем проверки
Шесть уравнений перечислены под таблицей.Используйте таблицу, чтобы выяснить, для какого из заданных значений \ (x \) это будет правда, что левая часть уравнения равна справа.
«В поисках» решения уравнение с использованием таблиц называется решением Инспекция .
\ (х \)
-3
–2
–1
0
1
2
3
4
\ (2x + 3 \)
-3
–1
1
3
5
7
9
11
\ (х + 4 \)
1
2
3
4
5
6
7
8
\ (9 — х \)
12
11
10
9
8
7
6
5
\ (3x- 2 \)
-11
-8
-5
-2
1
4
7
10
\ (10x — 7 \)
-37
-27
-17
-7
3
13
23
33
\ (5x + 3 \)
-12
-7
-2
3
8
13
18
23
\ (10 - 3x \)
19
16
13
10
7
4
1
-2
\ (2x + 3 = 5x + 3 \)
\ (5x + 3 = 9 -x \)
\ (2х + 3 = х + 4 \)
\ (10x- 7 = 5x + 3 \)
\ (3х — 2 = х + 4 \)
\ (9 — х = 2x + 3 \)
Два уравнения могут иметь одно и то же решение.Например, \ (5x = 10 \) и \ (x + 2 = 4 \) имеют такое же решение; \ (x = 2 \) — решение для обоих уравнения.
Два уравнения называются эквивалентно , если у них одинаковое решение.
Какое из уравнений в вопрос 1 есть такие же решения? Объяснять.
Решение уравнений с использованием аддитивных и мультипликативных обратных
В каждом случае найдите значение \ (х \):
Заполните блок-схемы.Вы должны заполнить все недостающие числа.
Чтобы найти второй входной номер вы можете сказать себе: «После того, как я добавил 7, у меня было 12. Что у меня было до того, как я добавил 7? «
Чтобы найти входной номер, соответствует 13, вы можете спросить себя: «Что у меня было до того, как я добавил 3?» а затем: «Что у меня было прежде чем я умножил на 2? «
Используйте ваши ответы на вопрос 2, чтобы проверить свои ответы на вопрос 1.
Опишите инструкции на блок-схеме 2 (б) прописью, а также символическое выражение.
Заполните блок-схему.
Эта блок-схема называется инверсия блок-схемы в вопросе 2 (b).
Сравните ввод числа и выходные числа рассматриваемых блок-схем 2 (б) и вопрос 5.Что ты заметил?
Добавьте 5 к любому числу, а затем вычтите 5 из вашего ответа. Что вы получаете?
Умножьте любое число на 10 и затем разделите ответ на 10. Что вы получите?
Если добавить число и затем вычтите то же число, вы вернетесь туда, где вы начал. Вот почему сложение и вычитание называются обратными операциями . Если вы умножите на число, а затем разделите на такое же число, вы вернетесь туда, откуда начали.Вот почему умножение и деление называются обратными операциями
Выражение \ (5x-3 \) говорит: «» умножьте на 5, затем вычесть 3 «. Эта инструкция также может быть дана с блок-схемой:
Уравнение \ (5x — 3 = 47 \) также можно записать как блок-схема:
Решите уравнения ниже. Вы можете сделать это, используя обратные операции. Вы можете напишите блок-схему, которая поможет вам увидеть операции.
\ (2x + 5 = 23 \)
\ (3х — 5 = 16 \)
\ (5x — 60 = -5 \)
\ (\ frac {1} {3} x + 11 = 19 \)
\ (10 (х + 3) = 88 \)
\ (2 (х — 13) = 14 \)
Настройка уравнений
Построение уравнений
Вы можете легко составить уравнение, которое имеет 5 в качестве решения.Вот пример:
Начните с написания раствор | \ (х = 5 \) |
прибавить 3 к обеим сторонам | \ (х +3 = 8 \) |
Умножить обе стороны на 5 | \ (5x + 15 = 40 \) |
Какое решение уравнение \ (5x + 15 = 40 \)?
Составьте собственное уравнение с решение \ (x = 3 \).
Bongile работал вроде это сделать уравнение \ (2 (x \) + 8) = 30, но он потер вне его работы:
Начните с написания раствор
\ (х \)
=
Добавьте 8 к обеим сторонам
=
15
Умножить обе стороны на 2
\ (2 (х + 8) \)
=
30
Завершите письмо Бонджила, чтобы решить уравнение \ (2 (x + 8) = 30 \).
Вот как Бонджил сделал более сложное уравнение:
Начните с написания раствор
\ (х \)
=
Умножить на 3 на обоих стороны
\ (3x \)
=
Вычтем 9 из обоих стороны
\ (3x — 9 \)
=
6
Добавьте \ (2x \) к обоим стороны
\ (5x — 9 \)
=
\ (2x + 6 \)
Что было справа сторона перед Бонжилом вычитала 9?
Каково решение \ (5x — 9 = 2х + 6 \)?
Bongile начинался с решение, и в итоге он получил уравнение.Заполните шаги что Бонджил использовал, чтобы составить уравнение, и решить уравнение:
\ (х \)
=
\ (8x \)
=
\ (8x + 3 \)
=
\ (3x + 3 \)
=
\ (35 — 5x \)
Решение уравнений
Чтобы составить уравнение, вы можно применить одну и ту же операцию с обеих сторон | Чтобы решить уравнение, , вы можете применить обратную операцию на обоих стороны | |||||
\ (х \) | = | 4 | ||||
Умножить на 8 | \ (8x \) | = | 32 | Разделить на 8 | ||
Добавить 3 | \ (8x + 3 \) | = | 35 | Вычесть 3 | ||
Вычтем \ (5x \) | \ (3x + 3 \) | = | \ (35 — 5x \) | Добавить \ (5x \) |
Используйте любой подходящий метод для решения уравнения ниже.
\ (5x + 3 = 24 — 2x \)
\ (2x + 4 = -9 \)
\ (3 — х = х- 3 \)
\ (6 (2x + 1) = 0 \)
\ (4 (1-2x) = 12-7x \)
\ (8 (1-3x) = 5 (4x + 6) \)
\ (7x- 10 = 3x + 7 \)
\ (1,6x + 7 = 3, 5x + 3,2 \)
Числовые модели и уравнения
Какие из следующих правил будут создать числовой образец, указанный во второй строке таблицы ниже?
А.Условное значение = 8 n , где n — срок номер
B. Срок действия = 6 n — 1, где n — номер термина
C. Срок действия = 6 n + 2, где n номер термина
D. Условное значение = 10 n — 2, где n — номер термина
E. Срок действия = 5 n + 3, где n — номер термина
Номер срока
1
2
3
4
5
6
7
8
9
Срок службы
8
13
18
23
28
33
38
43
48
Шестой член последовательности имеет значение 33.Какой член будет иметь значение 143? Вы можете настроить и решите уравнение, чтобы узнать.
Примените к своему ответу правило E, чтобы проверить правильный ли ваш ответ.
Напишите правило, которое будет производить образец номера во второй строке этой таблицы. Возможно, вам придется поэкспериментируйте, чтобы узнать, что это за правило.
Номер срока
1
2
3
4
5
6
7
8
9
Срок службы
5
8
11
14
17
20
23
26
29
Какой член будет иметь значение 221?
Правило для числового шаблона A равно 4 n + 11, а правило для шаблона B — \ (7n — 34 \).
Заполните приведенную ниже таблицу для двух узоры.
Номер срока
1
2
3
4
5
6
7
8
9
Образец A
Образец B
, для которых значение n является Условия двух шаблонов равны?
Уравнения и ситуации
- Рассмотрим такую ситуацию:
Снять комнату в определенном здания, необходимо внести залог в размере 400 рандов, а затем 80 рандов за день.
Сколько денег вам нужно, чтобы арендовать номер на 10 дней?
Сколько денег вам нужно, чтобы арендовать номер на 15 дней?
Что из перечисленного лучше всего описывает метод, который вы использовали для ответа на вопрос 1 (а) и (б)?
A. Общая стоимость = 400 рэндов +
рандовБ. Общая стоимость = 400 (количество дней + 80)
C. Общая стоимость = 80 \ (\ times \) количество дней + 400
Д.Общая стоимость = (80 + 400) \ (\ times \) количество дней
На сколько дней можно вы арендуете комнату, описанную в вопросе 1, если у вас есть 800 рандов платить?
Если вы хотите знать, сколько дней вы можете снять комнату, если у вас есть R720, вы можете настроить уравнение и решите его:
Вы знаете, что общая стоимость составляет 720 рандов, и вы знаете, что что вы можете рассчитать общую стоимость следующим образом:
\ (\ text {Общая стоимость} = 80x + 400 \), где \ (x \) — количество дней.Итак, \ (80x + 400 = 720 \) и \ (x = 4 \) дней.
В каждом из следующих случаев найдите неизвестное число, задав уравнение и решив Это.
Чтобы снять комнату, вы необходимо внести залог в размере 300, а затем 120 рандов в день.
На сколько дней вы можете снять комнату, если можно заплатить всего 1 740 рэндов? (Если ты возникли проблемы с настройкой уравнения, это может помочь вам сначала решить, как вы будете рассчитывать, сколько будет стоить аренда комната на 6 дней.)
Во сколько обойдется аренда комнаты? 10 дней, 11 дней и 12 дней?
На сколько дней можно снять комнату есть ли в наличии R3 300?
На сколько дней можно снять комнату если у вас есть в наличии R3 000?
Бен и Табо решают сделать некоторые расчеты с определенным числом.Бен умножает число на 5 и прибавляет 12. Табо получает тот же ответ, что и Бен когда он умножает число на 9 и вычитает 16. Что такое номер, с которым они работали?
Стоимость аренды определенный автомобиль сроком на \ (x \) дней может быть рассчитан по следующей формуле:
\ (\ text {Стоимость аренды в рандах} = 260x + 310 \)
Какая информация об аренде эту машину вы получите, если решите уравнение
\ (260x + 310 = 2 910 \)?
Сара внесла залог 320 рандов за прилавок на рынке, и она также платит 70 рандов в день аренда для ларька.Она продает фрукты и овощи в прилавок и обнаруживает, что она зарабатывает около 150 рандов каждый день. Через сколько дней она заработает столько, сколько заработала заплатили за стойло, всего?
Решение уравнений по закону экспонент
Возможно, вам придется вернуться к Главе 5 помнить законы экспонент.
Один из видов экспоненциального уравнения, с которым вы сталкиваетесь с в 9 классе имеет один или несколько терминов с базой в степени, содержащей переменную.{-3} \)
В уравнении другого типа, включающем экспоненты, переменная находится в основании.
Когда нам нужно найти неизвестное значение, задаем вопрос: «Какое число должен быть возведен в указанную степень, чтобы утверждение было правда? «
Для этих уравнений вы должны помните, что вы знаете о степенях чисел, таких как 2, 3, 4, 5 и 10.
Решение уравнений с переменной в базе
Заполните таблицу ниже и ответьте на следующие вопросы:
\ (х \)
2
3
4
5
(а)
\ (х ^ {3} \)
\ (2 ^ {3} = 8 \)
(б)
\ (х ^ {5} \)
\ (2 ^ {5} = 32 \)
(в)
\ (х ^ {4} \)
\ (2 ^ {4} = 16 \)
Для какого значения \ (x \) составляет:
\ (x ^ {3} = 64 \)
\ (x ^ {5} = 32 \)
\ (x ^ {4} = 256 \)
\ (x ^ {3} = 8 \)
\ (x ^ {4} = 16 \)
\ (x ^ {5} = 3 125 \)
Решите относительно \ (x \) и дайте причина:
\ (x ^ {3} = 216 \)
\ (x ^ {2} = 324 \)
\ (x ^ {4} = 10 000 \)
\ (8 ^ {x} = 512 \)
\ (18 ^ {x} = 324 \)
\ (6 ^ {x} = 216 \)
Ахмед умножил число на 5, прибавил 3 к ответу, а затем вычел число, которое он началось с.Ответ был 11. Какое число он начал? с участием?
Используйте любой подходящий метод для решить уравнения.
\ (3 (х-2) = 4 (х + 1) \)
\ (5 (х + 2) = -3 (2-х) \)
\ (1,5x = 0,7x — 24 \)
- \ (5 (х + 3) = 5х + 12
\)
\ (2,5х = 0,5 (х + 10) \)
\ (7 (х — 2) = 7 (2 — х) \)
\ (\ frac {1} {2} (2x-3) = 5 \)
\ (2x — 3 (3 + x) = 5x + 9 \)
Ошибка
Перейти к… Перейти к … План курсаКалендарь курсаРекомендуемые профессиональные репетиторы по математикеГлава 1 Ключ к ответу в рабочей тетрадиГлава 1 Ключ к ответу на обзорГлава 2 Обзор 2.1 Ключ к ответу на рабочем листе по моделированию квадратов и кубов2.2 Выражение числа в качестве ключа мощного ответа2.3 Разнообразное выражение числа Ключ ответа2 .4 Листы умножения и деления степеней 1 и 2 Ключ ответа 2.5 Объединение степеней Ключ ответа 2.5 Объединение степеней 2 Ключ ответа Глава 2.1 — 2.5 Проверка ключа ответа Отрицательные показатели степени Ответ 2.6 Вычисление с помощью степеней Ключ ответа Глава 2 Обзор ответа Глава 3 Обзор 3.2 Определение сходства 3.3 Масштабный коэффициент 3.4 Рисование похожих многоугольников Ключ ответа 3.4 Рисование похожего многоугольника 3.5 Решение проблем Глава 3 Обзор ответа Ключ Глава 4 Обзор 4.1 Примечания 4.1 Рабочий лист Ключ ответа 4.2 Примечания 4.3 Примечания 4.3 Ключ к ответу на листе 4.4 Примечания Глава 4 Ключ к ответу Обзор главы 5 5.1 Примечания 5.1 Ключ к ответу на листе 5.2 Примечания 5.2 Ключ к ответу на просмотр 5.3 Примечания 5.4 Введение 5.4 Ключ к ответу на листе 25 .1-5.4 Обозначение ответов на вопросы 5.6 Примечания и рабочие листы Обозначения ответов 5.7 Примечания Глава 5 Ключ к ответам при проверке Глава 5 Ключ к ответам на обзор Глава 6 Схема 6.1 Моделирование с помощью многочленов 6.3 Сбор похожих терминов 6.4 Добавление многочленов 6.4 Обозначения рабочего листа 6.5 Вычитание Многочлены 6.7 Умножение одночлена на многочлен 6.7 Деление многочлена на одночлены 6.7 Умножение и деление многочленов 6.7 Биномиальные произведения Глава 6 Обзор Таблица умножения и деления одночленов Ключевые слова Биономные продукты Рабочий лист Ответ Ключ Вопросы) Ключ свойства хорды Записанные углы и центральные углы KeyCentral Вписанный ключ свойства Ключ свойства полукруга (страница 2) Ключ свойства Tangent Radius Ключ свойства равного касания Ключ свойства тангенса Ключ от внешней точки Циклические четырехугольники KeyGeometry Unit Примечания Ответ KeyGeometry Review Package # 1 Anspter KeyGeometry Review Package # 2 Answer KeyChaometry Review Package # 1 Anspter KeyGeometry Review Package # 2 Answer KeyChapter 10 Примечания Буклет Ответ Ключевой Буклет Примечания Часть 1 Буклет t Примечания Часть 2 Ключевой буклет с ответамиОбзор финального экзамена 1Проверка финального экзамена 2Практика финального экзамена 2Практика финального экзамена 2Ключ ответа
Год 9 Математика Алгебра Рабочий лист
Введение
Факторизация — это процесс, обратный расширению, и это мощный инструмент алгебры на всех уровнях математики.Это дает нам возможность решать квадратные уравнения, упрощать сложные выражения и рисовать нелинейные отношения в 10-м классе и позже.
При факторизации мы хотим вставить скобки. Что делает факторизацию сложным, так это то, что существует много разных типов. Вам потребуется много практики, чтобы быстро распознать разные типы и освоить различные методы их применения.
Результаты программы NSW
- Этап 5.2: Факторизация алгебраических выражений путем выделения общего алгебраического множителя (ACMNA230)
- Этап 5.3: Факторизация монических и немонических квадратичных выражений (ACMNA269)
- общие множители
- группировка попарно для четырехчленных выражений
- разность двух квадратов
- полных квадратов
- квадратичных трехчленов (монических и немонических)
Предполагаемые знания
Студенты должны быть знакомы с основными алгебраическими методами, включая специальные биномиальные произведения и простую арифметику. Также потребуется знание наименьших общих кратных (LCM) и наибольших общих множителей (HCF).
1. Общие множители
Это простейшая форма факторизации, которая включает вычитание наивысшего общего множителя (HCF) из двух или более членов. Обратите внимание, что термин HCF также может быть заключен в скобки.
Шаг 1. Найдите HCF всех членов выражения.
Шаг 2: Извлеките HCF и вставьте скобки, чтобы сформировать продукт.
После исключения общего множителя у членов, оставшихся в скобках, не должно быть других общих множителей.
Примечание для студентов
Поскольку факторизация противоположна расширению, вы всегда можете проверить, правильно ли вы разложили на множители, расширив свой результат и посмотрев, совпадает ли он с тем, с чего вы начали.
2. Факторизация путем группировки в пары
Иногда может не быть HCF для каждого отдельного члена алгебраического выражения. В этих случаях мы группируем термины в пары так, чтобы первая пара терминов имела HCF, а оставшаяся пара терминов имела другой HCF.Важно правильно сгруппировать термины, чтобы добиться успешной факторизации.
После извлечения соответствующего HCF из каждой пары вы найдете еще один общий множитель. Извлеките это, чтобы получить окончательный факторизованный ответ.
Пример: факторизация путем группировки в пары
Факторизация алгебраического выражения путем группировки в пары
\ (2xy + 3yz-4x-6z \)Решение
Шаг 1. Перегруппируйте термины так, чтобы каждая пара имела HCF.
\ (= (2xy + 3yz) — (4x + 6z) \)Шаг 2: Извлеките HCF из каждой пары.
\ (= y (2x + 3z) -2 (2x + 3z) \)Шаг 3: Извлеките полученный общий множитель.
\ ((2x + 3z) (y-2) \)Примечание для студентов
Порядок написания терминов в скобках не имеет значения. \ ((a + b) (c + d) = (c + d) (a + b) \). Это пример коммутативного закона умножения.
3. Разность двух квадратов
Есть три специальных факторизующих тождества, которые помогут вам факторизовать различные типы алгебраических выражений. Первый известен как разница двух квадратов.2} + 5x + 2 = (3x + 2) (x + 1) \)
Примечание для студентов
Все три метода преподаются на уроках теории матриц, чтобы познакомить студентов с различными стратегиями факторизации немонических квадратичных трехчленов. . В разных школах преподают разные методы, но учащиеся должны выбрать метод, который лучше всего соответствует их стилю обучения, и применять стратегию до тех пор, пока они не овладеют ею.
Рабочий лист по алгебре 9-го класса — методы факторизации
Проверьте свои навыки факторизации с помощью следующих 10 упражнений!
1.2} \)
7. \ ((t-20) (t + 3) \)
8. \ (5n (m-7) (m + 3) \)
9. \ ((3x + 4) (x-5) \)
10. \ (- (4x-1) (2x + 3) \)
Хотите вывести свои математические навыки в 9 классе на новый уровень?
Хотите подготовиться к экзамену по математике? Попробуйте нашу серию «Максимум по математике для 9-го класса», том 1: Учебное пособие для подготовки к экзаменам, которое содержит примеры и вопросы по темам «Алгебраические методы и сурды и индексы».
Факторинг по алгебре
Факторы
У чисел есть множители:
И выражения (например, x 2 + 4x + 3 ) также имеют множители:
Факторинг
Факторинг (в Великобритании называется « Факторинг ») — это процесс нахождения факторов :
Факторинг: поиск того, что нужно умножить, чтобы получить выражение.
Это похоже на «разбиение» выражения на умножение более простых выражений.
Пример: множитель 2y + 6
У 2y и 6 есть общий множитель 2:
Таким образом, мы можем разложить все выражение на:
2у + 6 = 2 (у + 3)
Таким образом, 2y + 6 был «разложен на» 2 и y + 3
Факторинг также противоположен расширению:
Общий коэффициент
В предыдущем примере мы видели, что 2y и 6 имеют общий множитель 2
Но для правильной работы нам нужен самый высокий общий множитель , включая все переменные
Пример: фактор 3y
2 + 12yВо-первых, 3 и 12 имеют общий делитель 3.
Итак, мы могли бы иметь:
3 года 2 + 12 лет = 3 (год 2 + 4 года)
Но мы можем сделать лучше!
3y 2 и 12y также разделяют переменную y.
Вместе, что составляет 3 года:
- 3y 2 — 3y × y
- 12y — 3y × 4
Таким образом, мы можем разложить все выражение на:
3 года 2 + 12 лет = 3 года (y + 4)
Чек: 3y (y + 4) = 3y × y + 3y × 4 = 3y 2 + 12y
Более сложный факторинг
Факторинг может быть трудным!
До сих пор примеры были простыми, но факторизация может быть очень сложной.
Потому что нам нужно изобразить то, что мы умножили на , чтобы получить данное нам выражение!
Это все равно, что пытаться найти, какие ингредиенты
пошли на торт, чтобы сделать его таким восхитительным.
Это сложно понять!
Опыт помогает
Чем больше опыта, тем проще факторинг.
Пример: Фактор
4x 2 -9Хммм … похоже, нет общих факторов.
Но знание специальных биномиальных произведений дает нам ключ к разгадке под названием «разница квадратов» :
Потому что 4x 2 равно (2x) 2 , а 9 равно (3) 2 ,
Итак имеем:
4x 2 — 9 = (2x) 2 — (3) 2
А это можно получить по формуле разности квадратов:
(a + b) (a − b) = a 2 — b 2
Где a — 2x, а b — 3.
Итак, давайте попробуем это сделать:
(2x + 3) (2x − 3) = (2x) 2 — (3) 2 = 4x 2 — 9
Да!
Таким образом, множители 4x 2 — 9 равны (2x + 3) и (2x − 3) :
Ответ: 4x 2 -9 = (2x + 3) (2x − 3)
Как можно этому научиться? Получив много практики и зная «Самобытность»!
Запомни эти личности
Вот список общих «идентичностей» (включая «разность квадратов» , использованную выше).
Об этом стоит помнить, поскольку они могут облегчить факторинг.
| а 2 — б 2 | = | (а + б) (а-б) |
| a 2 + 2ab + b 2 | = | (а + б) (а + б) |
| а 2 — 2ab + б 2 | = | (а-б) (а-б) |
| a 3 + b 3 | = | (a + b) (a 2 −ab + b 2 ) |
| а 3 — б 3 | = | (a − b) (a 2 + ab + b 2 ) |
| a 3 + 3a 2 b + 3ab 2 + b 3 | = | (а + б) 3 |
| a 3 −3a 2 b + 3ab 2 −b 3 | = | (а − б) 3 |
Подобных гораздо больше, но это самые полезные.
Совет
Факторная форма обычно лучше всего.
При попытке факторного расчета выполните следующие действия:
- «Вынести за скобки» любые общеупотребительные термины
- Посмотрите, подходит ли он какой-либо из идентификационных данных, а также другим лицам, которые вы, возможно, знаете
- Продолжайте, пока вы больше не сможете множить
Существуют также системы компьютерной алгебры (называемые «CAS»), такие как Axiom, Derive, Macsyma, Maple, Mathematica, MuPAD, Reduce и многие другие, которые хорошо подходят для факторинга.
Другие примеры
Опыт действительно помогает, поэтому вот еще несколько примеров, которые помогут вам на этом пути:
Пример: w
4 — 16Показатель степени 4? Может быть, мы могли бы попробовать показатель степени 2:
w 4 — 16 = (w 2 ) 2 — 4 2
Да, это разница квадратов
w 4 — 16 = (w 2 + 4) (w 2 — 4)
И «(w 2 — 4)» — это еще одно различие квадратов
w 4 — 16 = (w 2 + 4) (w + 2) (w — 2)
Это все, что я могу (если я не использую мнимые числа)
Пример: 3u
4 — 24uv 3Удалить общий множитель «3u»:
3u 4 — 24uv 3 = 3u (u 3 — 8v 3 )
Тогда разница кубиков:
3u 4 — 24uv 3 = 3u (u 3 — (2v) 3 )
= 3u (u − 2v) (u 2 + 2uv + 4v 2 )
Это все, что я могу.
Пример: z
3 — z 2 — 9z + 9Попробуйте разложить на множители первые два и вторые два по отдельности:
z 2 (z − 1) — 9 (z − 1)
Вау, (z-1) есть на обоих, так что давайте воспользуемся этим:
(z 2 −9) (z − 1)
А z 2 −9 — разность квадратов
(г-3) (г + 3) (г-1)
Это все, что я могу.
А теперь побольше опыта:
[PDF] Руководство по планированию.9 класс Работа с линейными уравнениями. Паттерны и отношения (переменные и уравнения) Конкретный результат 3
1 Руководство по планированию по математике 9 класс Работа с шаблонами и связями линейных уравнений (переменные и уравнения) Спецификация …
МатематикаРуководство по планированию 9 класс Работа с линейными уравнениями Модели и отношения (переменные и уравнения) Конкретный результат 3
Это руководство по планированию можно найти в Интернете по адресу: http: // www.learnalberta.ca/content/mepg9/html/pg9_linearequations/index.html
Содержание Учебная программа Направленность ………………………. ………………………………………….. ………………………
2
Что такое руководство по планированию? ………………………………………….. ………………………………….
3
Этапы планирования … ………………………………………….. …………………………………………………
3
Шаг 1: Определите результаты для рассмотрения ………………… ………………………………………….. . Большие идеи ……………………………………….. ………………………………………….. ………….. Последовательность результатов программы обучения ………………………. ……………
4 4 5
Шаг 2: Определите доказательства обучения учащихся ……………….. …………………………….. Использование индикаторов достижений ……………………………………. …………………………….
6 6
Шаг 3: План обучения …. ………………………………………….. …………………………….. A. Оценка предшествующих знаний и навыков …….. ………………………………………….. .Пример структурированного собеседования: оценка предшествующих знаний и навыков ……….. Б. Выбор учебных стратегий …………………… ……………………………………. C. Выбор учебных заданий … ………………………………………….. ……………….. Пример упражнения 1: Какова масса каждой формы ниже? …………………. Пример задания 2: Уравнения из геометрических фигур ……………….. ………. Пример задания 3: Использование плиток алгебры для решения уравнений ………………….. Пример задания 4: Математические дебаты. ………………………………………….. .. Пример задания 5: Представление и решение задач с помощью линейных уравнений…………………………………………… ……… Пример действия 6: Анализ ошибок …………………………….. ……………………….. Пример упражнения 7: Соединение алгебры с областью …………. ……………………….. Пример действия 8: Представление вопроса по области с помощью
7 7 11 12 13 14 15 16 19
ax = b, = a и = x …………………………………. ……… Оцените уровень знаний учащихся ……………………………….. ……………………………………. Оценка всего класса / группы ……………… ………………………………………….. Индивидуальная оценка …………………………………….. ………………………………. Прикладное обучение ……….. ………………………………………….. ………………………….
23 24 24 28 28
Шаг 4: ABC
20 21 22
Шаг 5: Последующие действия по оценке ……………………………………………………………………. 29 A. Устранение пробелов в обучении ………………………………………….. ………………….. 29 B. Укрепление и расширение обучения ……………….. ………………………………….. 29 Библиография ……. ………………………………………….. ………………………………………….. ….. 31
www.LearnAlberta.ca © 2012 Alberta Education
9 класс, Паттерны и отношения (переменные и уравнения) (SO 3) Стр. 1 из 31
Руководство по планированию: 9 класс Работа с линейными уравнениями Strand : Паттерны и отношения (переменные и уравнения) Конкретный результат: 3
В данном руководстве по планированию рассматривается следующий результат программы исследований: Строка: Паттерны и отношения (переменные и уравнения) Конкретный результат:
3.Смоделируйте и решите задачи, используя линейные уравнения вида: • ax = bx = b, a ≠ 0 • a •
ax + b = c
x • a
+ b =, ca ≠ 0 • ax = b + cx • a (x + b) = c • ax + b = cx + d • a (bx + c) = d (ex + f) • ax = b, x ≠ 0, где a, b, c, d, e и f — рациональные числа.
Направленность учебной программы Этот образец нацелен на следующие изменения учебной программы: • •
Общий результат аналогичен предыдущей программе обучения. Конкретный результат состоит из следующих различий: — умножение биномов и факторизация трехчленов перенесено в класс 10 — форма линейных уравнений, представленная в этом результате, включает дополнительные формы линейных уравнений, в том числе: o ax = bxo = ab, a ≠ 0 о ах + Ь = сх + Ь = с, а ≠ 0.o a
www.LearnAlberta.ca © 2012 Alberta Education
9 класс, Модели и отношения (переменные и уравнения) (SO 3) Стр. 2 из 31
Что такое руководство по планированию? Руководства по планированию — это инструмент, который учителя могут использовать при разработке инструкций и оценок, которые направлены на развитие и углубление понимания учащимися математических понятий. Этот инструмент основан на процессе, описанном в книге «Понимание посредством дизайна» Гранта Уиггинса и Джея Мактига.
Шаги планирования Следующие шаги помогут вам с помощью Руководства по планированию: • • • • •
Шаг 1: Определите результаты для решения (стр.4) Этап 2: Определите свидетельства обучения учащихся (стр. 6) Этап 3: План обучения (стр. 7) Этап 4: Оцените обучение учащихся (стр. 24) Этап 5: Последующие действия по оценке (стр. 29)
www.LearnAlberta.ca © 2012 Alberta Education
9 класс, Паттерны и отношения (переменные и уравнения) (SO 3) Стр. 3 из 31
Шаг 1. Определите результаты для решения наводящих вопросов • • •
Что нужно сделать Я хочу, чтобы мои ученики учились? Что мои ученики в настоящее время могут понимать и делать? Что я хочу, чтобы мои ученики понимали и могли делать на основе Больших идей и конкретных результатов в программе обучения?
Большие идеи Математику иногда называют «наукой о закономерностях».«Изучение закономерностей, а затем их преобразование и представление в виде слов, символов, выражений, уравнений и графиков помогает учащимся 9-х классов лучше понимать линейные функции. Связывание функций с предыдущим обучением и реальными ситуациями облегчает обучение учащихся. Есть несколько важных больших идей которые рассматриваются в этом результате: • • • •
Алгебра — это способ представления и объяснения математических взаимосвязей, который используется для описания и анализа изменений (Small 2009, p.7). Уравнения используются для выражения отношений между двумя величинами (Ван де Валле 2001, стр. 384). Знак равенства означает, что величина в левой части уравнения совпадает с величиной в правой части. Переменная — это символ, который может обозначать любой из набора чисел или других объектов и может быть представлен прямоугольниками или буквами (Van de Walle and Lovin 2006, p. 274).
www.LearnAlberta.ca © 2012 Alberta Education
9 класс, Модели и отношения (переменные и уравнения) (SO 3) Стр. 4 из 31
Последовательность результатов программы обучения См. Http: // www.education.alberta.ca/teachers/program/math/educator/progstudy.aspx для получения полной программы обучения. Оценка 7
Оценка 8
Оценка 9
Оценка 10
Переменные и уравнения
Переменные и уравнения
Взаимосвязи и уравнения
000
000 Характеристики
000
000 Результат
Конкретный результат
Конкретный результат
3.Продемонстрировать понимание сохранения равенства посредством: • моделирования сохранения равенства, конкретно, графически и символически • применения сохранения равенства для решения уравнений.
2. Смоделируйте и решите проблемы конкретно, наглядно и символически, используя линейные уравнения вида: • ax = b • ax = b, a ≠ 0
3. Смоделируйте и решите проблемы, используя линейные уравнения вида: • ax = b • ax = b, a ≠ 0 • ax + b = c • ax + b = c, a ≠ 0 • ax = b + cx • a (x + b) = c • ax + b = cx + d • a (bx + c) = d (ex + f) a • x = b, x ≠ 0, где a, b, c, d, e и f — рациональные числа.
9. Решайте задачи, которые включают системы линейных уравнений с двумя переменными, графически и алгебраически.
4. Объясните разницу между выражением и уравнением.
• ax + b = c • ax + b = c, a ≠ 0
• a (x + b) = c, где a, b и c — целые числа.
5. Вычислить выражение, учитывая значение переменной (ей). 6. Смоделируйте и решите, конкретно, наглядно и символически, задачи, которые могут быть представлены одношаговыми линейными уравнениями вида x + a = b, где a и b — целые числа.
www.LearnAlberta.ca © 2012 Alberta Education
9 класс, Паттерны и отношения (переменные и уравнения) (SO 3) Стр. 5 из 31
Шаг 2: Определите доказательства наличия у учащихся руководящих вопросов • •
Какие доказательства буду ли я искать, чтобы узнать, что обучение произошло? Что должны продемонстрировать учащиеся, чтобы показать свое понимание математических концепций, навыков и больших идей?
Использование индикаторов успеваемости При планировании уроков и учебных мероприятий помните о текущих способах мониторинга и оценки обучения учащихся.Отправной точкой для этого планирования является рассмотрение показателей успеваемости, перечисленных в Программе обучения математике Альберты K – 9 с показателями успеваемости. Вы также можете создавать свои собственные индикаторы и использовать их для наблюдения за учениками. Следующие индикаторы могут использоваться, чтобы определить, достигли ли учащиеся этого конкретного результата. Могут ли студенты: • • • • • •
смоделировать решение данного линейного уравнения, используя конкретные или графические представления, и записать процесс? проверить с помощью подстановки, является ли данное рациональное число решением данного линейного уравнения? символически решить данное линейное уравнение? выявить и исправить ошибку в данном неправильном решении линейного уравнения? представить заданную задачу, используя линейное уравнение? решить данную проблему, используя линейное уравнение, и записать процесс?
Примеры поведения, связанного с этими индикаторами, предлагаются для некоторых действий, перечисленных в Шаге 3, Раздел C: Выбор учебных мероприятий (стр.13).
www.LearnAlberta.ca © 2012 Alberta Education
9 класс, Паттерны и взаимосвязи (переменные и уравнения) (SO 3) Стр. 6 из 31
Шаг 3. Составьте план руководящих вопросов • • •
Какие возможности обучения и опыт, который я должен предоставить, чтобы способствовать изучению результатов и позволить студентам продемонстрировать свое обучение? Какие стратегии обучения и ресурсы мне следует использовать? Как я смогу удовлетворить разнообразные учебные потребности моих студентов?
А.Оценка предшествующих знаний и навыков Прежде чем вводить новый материал, подумайте о способах оценки и развития знаний и навыков учащихся об их понимании переменных, равенстве и решении уравнений. Вы можете использовать показатели предыдущих оценок, чтобы определить, что учащиеся должны знать или понимать. Рассмотрите возможность использования открытых вопросов, чтобы более точно оценить, что студенты могут общаться и делать. 1. Переменные. Исследования показали, что учащиеся часто неправильно понимают понятие переменных.Usiskin (1988) определил три различных способа использования переменных: 1. Как конкретное неизвестное с одним значением; например, 2n + 15 = 5n + 3. Студентов часто просят найти неизвестное значение. 2. Как обобщитель паттернов; например, 2n + 5, где n может иметь бесконечное количество значений. 3. Переменные, изменяющиеся по отношению друг к другу; например, C = 2πr, где мера радиуса (r) влияет на значение длины окружности (C). Важно, чтобы у учащихся была возможность подумать о различных способах использования переменных для представления неизвестного.Студентам также может потребоваться напомнить, что другие символы, такие как прямоугольники и буквы, могут служить той же цели. Учащиеся могут быть сбиты с толку значением букв, поскольку они часто используются для обозначения различных идей в математике. Следующие ниже упражнения должны помочь диагностировать понимание учащимися использования букв и переменных. Задание 1.1: Использование букв в качестве переменных Объясните, что такое же и что отличается от того, как буква m использовалась в следующих случаях: • • •
Мартин пробежал 100 м 2 м + 15 = 23 3 м + 2.
Студенты должны начать обсуждение того, что в первом случае m представляет собой сокращение для метра, которое отличается от двух вторых вариантов использования, где m представляет собой значение.
www.LearnAlberta.ca © 2012 Alberta Education
9 класс, Паттерны и отношения (переменные и уравнения) (SO 3) Страница 7 из 31
•
Разница между вторым и третьим случаями заключается в том, что один представляет собой одно значение, а другое представляет бесконечное количество значений.Студентам также может потребоваться пояснение, что числовой коэффициент перед переменной подразумевает умножение. Попросите их показать 2 м + 15 = 23 и 3 м + 2 в другой (развернутой) форме. Они могут поделиться такими ответами, как: — 2 • m + 15 = 23 или 2 × m + 15 = 23 или 2 (m) + 15 = 23 или 15 + 2 × m = 23… — 3 • m + 2 или 3 × m + 2 или 3 (м) + 2 или 2 + 3 × м или 2 + 3 (м)…
Если учащиеся не упоминают ярлыки операций во время обсуждения, попросите их объяснить, какие операции представлены в последних двух случаи и как их можно было бы записать по-другому.Задание 1.2: Весы Весы и весы помогают учащимся разобраться в алгебраических связях, а также поощряют мышление, рассуждения, дискуссии и дискуссии. Многие из этих вопросов не содержат признаков операции, поэтому учащимся необходимо делать выводы и интерпретировать, чтобы прийти к стратегии решения уравнений. Одна форма имеет одинаковое значение или массу. Какая форма имеет наибольшую массу? Какая форма имеет наименьшую массу? Откуда вы знаете?
Идеи, заимствованные у Ван де Валле 2001, стр. 399.
Мероприятие 1.3: Строка алгебраических чисел. Материалы: •
Лента маскирующей или суммирующей ленты длиной 5 м, размеченная 20 равномерно расположенными приращениями. Эта более длинная длина позволяет учащимся стоять вдоль линии, когда они участвуют в упражнении. • Отдельные карты отмечены следующим образом: 0, 2, –2, 5, –5, 10, –10, x, y, y + 3, y — 4, x + 2, x — 2, 3x и x. 2 Инструкции: •
Поднимите карточку 0 и попросите учащегося поставить ее на линию.
Попросите учащегося объяснить, почему он решил разместить это там.Спросите класс, является ли это единственным выбором места и почему? www.LearnAlberta.ca © 2012 Alberta Education
9 класс, Паттерны и отношения (переменные и уравнения) (SO 3) Стр. 8 из 31
Как только будет достигнута договоренность о размещении нулевой карточки, попросите учащихся разместить целочисленные карточки один за другим и обсудите, как размещение первой целочисленной карты определяет интервал. Возьмите их карту и поместите ее на другой участок ближе или дальше от нуля. Например, если карта 2 размещена на четыре шага от 0, спросите учащихся: «Что теперь представляет каждый интервал?» •
В этом случае ответ должен быть 0.5.
Определите место для 2 карты. Цель состоит в том, чтобы учащиеся обсудили и поняли, что после того, как это число размещено, оно определяет положение для последующего размещения чисел. Попросите учащихся по очереди выложить оставшиеся карточки с целыми числами. •
Поднимите карточку x и попросите учащегося положить ее (Примечание: она может идти куда угодно). Задайте следующие вопросы: — Как узнать, где поставить x? — Это единственное место, где его можно разместить? — Что вы знаете о значении x?
•
Поднимите карточку x + 2 и попросите ученика положить ее.Задайте следующие вопросы: — Как узнать, где поставить x + 2? — Это единственное место, где его можно разместить? — Что вы знаете о значении x + 2? — Что произойдет, если я поставлю x + 2 на –5?
•
Продолжайте раскладывать карточки с переменными, задавайте вопросы, аналогичные приведенным выше, и спрашивайте учащихся, какие вопросы они могут задать.
•
Рассмотрите возможность добавления карточек, например 5y
•
В конце задания попросите учащихся поразмышлять или обсудить в небольших группах: — — —
y, чтобы продлить задание.2
что-то, чему они научились, или что-то, что стало яснее во время упражнения, вопрос, у них есть что-то, что все еще сбивает с толку.
Попросите учащихся поделиться своим обсуждением всей большой группой; это упражнение должно помочь оценить, на каком уровне находятся учащиеся с точки зрения их понимания числовой линии и переменных. Чтобы дифференцировать или усилить обучение в этом упражнении, вы можете показать числовую линию на прозрачной или белой доске и попросить учащихся разместить и переместить целые числа и переменные на этом носителе.
www.LearnAlberta.ca © 2012 Alberta Education
9 класс, Паттерны и отношения (переменные и уравнения) (SO 3) Стр. 9 из 31
2. Равенство Задайте своим ученикам следующий вопрос и попросите их записать их решения на бумаге. Попросите их рассказать, почему они выбрали свои ответы. 8 + 4 = + 5 Исследования показывают, что большинство учеников начальных классов не ответят на этот вопрос правильно и будут оправдывать свои ответы следующим образом: • • •
, говоря, что ответ: 8 + 4 = 12 + 5, используя все числа, чтобы найти сумму: 8 + 4 = 17 + 5, неправильно добавив еще один знак равенства: 8 + 4 = 12 + 5 = 17.
Из книги Карпентера, Франке и Леви, 2003 г., стр. 4.
3. Решение уравнений В 8-м классе учащиеся должны были ознакомиться и уметь решать форматы уравнений, показанные в упражнении ниже. Запишите каждое уравнение на индивидуальную карточку рецепта и попросите учащихся рассортировать карточки по следующим трем категориям: a. легко решить в голове б. сложнее, но можно решить в голове c. проще использовать модель или ручку и бумагу для решения. 1. 2. 3. 4. 5. 6. 7.
n + 2 = 7 3n = 21 2n + 7 = 19 4n — 8 = 6n + 2 5 = 2n — 7 n – 2 = 7 n = 21 3 8.3n — 5 = n + 1 9. 6 (n — 4) = 2x + 4 10. 5n — 2 = 9 Попросите учащихся обсудить следующие вопросы с партнером или в небольшой группе: • • •
как вы решить, какие вопросы было бы легко решить мысленно? какой процесс вы использовали для решения этих уравнений? каковы сходства и различия в методах, которые использовал каждый человек?
Если у учащегося возникают трудности с выполнением этих заданий, рассмотрите возможность дальнейшей индивидуальной оценки, такой как структурированное собеседование, чтобы определить уровень навыков и понимания учащегося.См. Образец структурированного интервью: оценка предшествующих знаний и навыков (стр. 11).
www.LearnAlberta.ca © 2012 Alberta Education
9 класс, Паттерны и отношения (переменные и уравнения) (SO 3) Стр. 10 из 31
Пример структурированного интервью: Оценка предшествующих знаний и навыков Направления Прочтите следующее ученику : «Число удваивается, а затем увеличивается на 5.» Переведите это в алгебраическое выражение и объясните ситуацию из реальной жизни, которая моделирует это выражение.
Дата: Не совсем там Учащийся не может перевести операции на английский язык.
Готов к подаче заявки Учащийся может перевести выражение в 2n + 5.
Учащийся не знает, что представляют собой один или оба знака операции, или может отменить вычитание.
Учащийся может сформулировать контекст, например: «Мне заплатили одинаковую сумму за то, что я два раза косил лужайку моего соседа, а затем, во второй раз, мой сосед дал мне бонус в размере 5 долларов.»
Учащийся не может придумать контекст или неправильно определяет контекст.
Попросите учащегося показать» Учащийся не может определить решение, используя алгебру мозаику операции слева как или символический карандаш и умножение. Бумажное решение » : Учащийся не может решить некоторые из ситуаций, включающих: • 3x = 6 отрицательных коэффициентов или констант. • 2x = –6 • –3x = 6. Учащийся не может показать • –2x = 6. деля обе части уравнения. на общий делитель.Студент может использовать одно представление более грамотно, чем другое. Попросите учащегося показать значок. Учащийся не может правильно использовать решение, используя свойство распределения плиток алгебры. или символический карандаш и бумага для решения: Наиболее распространенной ошибкой является то, что учащийся не умножает коэффициент на второе значение в • 2 (n + 1) = 8 скобках. • 2 (n + 2) = 3 (n + 3).
Ученик правильно решает вопросы с помощью плиток и умеет показывать шаги. Студент умеет переводить графические или конкретные шаги в символическое представление.
Студент грамотно пользуется распределительным свойством. Ученик показывает правильное решение, используя плитки. Учащийся показывает правильное решение, используя числа.
Учащийся не может показать правильные шаги для решений, используя плитки. Учащийся не может показать правильные шаги для решения, используя символическое представление. www.LearnAlberta.ca © 2012 Alberta Education
9 класс, Паттерны и отношения (переменные и уравнения) (SO 3) Стр. 11 из 31
Покажите ученику следующие три уравнения и попросите его: • •
объяснить почему они разные, объясните, как они решаются.- — —
Студент не умеет разъяснять различия в операциях. Учащийся не видит разницы между двумя вопросами разделения. Учащемуся сложно решить одно или несколько уравнений.
Учащийся может сформулировать, что первое уравнение включает умножение, а два других — деление. Учащийся может предсказать, что третье уравнение будет включать рациональное значение. Студент умеет решать все три ситуации.
2x = 10 x 2 = 10 2 x = 10
B.Выбор стратегии обучения. Рассмотрите следующие рекомендации по шаблонам преподавания в 9 классе. • • • •
Учащимся должны быть предоставлены регулярные возможности участвовать в беседах и обсуждать открытые вопросы, чтобы укрепить уверенность и компетентность в математике. Когда учащимся предоставляется возможность выразить свое мышление (устно или письменно), объяснить свои соображения и выслушать стратегии, используемые другими учащимися, появляется больше возможностей для углубления их понимания.Попросите учащихся смоделировать уравнения, используя весы (фактические или графические) или плитки алгебры. Конкретные материалы помогут укрепить понимание абстрактных концепций, даже если учащийся уже является способным абстрактным мыслителем. Предоставьте учащимся возможность представлять уравнения различными способами, в том числе с помощью манипуляторов, изображений, чисел и переменных. Чем более гибкими учениками будут пользоваться все эти представления, тем лучше будет их понимание.
www.LearnAlberta.ca © 2012 Alberta Education
9 класс, Модели и отношения (переменные и уравнения) (SO 3) Стр. 12 из 31
C. Выбор учебных мероприятий Следующие учебные задания являются примерами действий, которые могут быть использованы для развития понимания учащимися концепции, указанные в Шаге 1.
Примеры действий: 1. 2. 3. 4. 5. 6. 7. 8.
Какова масса каждой формы ниже? (стр. 14) Уравнения из геометрических узоров (стр. 15) Использование плиток алгебры для решения уравнений (стр.16) Математические дебаты (стр. 19) Представление и решение задач с помощью линейных уравнений (стр. 20) Анализ ошибок (стр. 21) Связь алгебры с областью (стр. 22) Представление вопроса области с помощью ax = = a и = x ( стр. 23)
По мере выполнения этих заданий со студентами усиливайте значение словаря возникающих алгебраических терминов, таких как: • • • • • •
переменный коэффициент постоянное свойство распределения упрощать оценку изолировать.
www.LearnAlberta.ca © 2012 Alberta Education
9 класс, Паттерны и отношения (переменные и уравнения) (SO 3) Стр. 13 из 31
Пример задания 1: Какова масса каждой формы ниже? Общая масса для каждой пары фигур показана на шкале под фигурами.Попросите учащихся определить массу каждой формы, если фигуры одного цвета и размера имеют одинаковую массу. Попросите их представить свой ответ как минимум двумя способами или показать как минимум две стратегии. Набор A имеет интегральные ответы, а набор B имеет рациональные ответы. Попросите учащихся сначала решить Набор А и поделиться своими стратегиями решения. Затем предоставьте им Набор B и попросите решить неизвестные. Была ли их стратегия одинаковой для обоих наборов? Многие студенты будут использовать угадывание и проверку, чтобы найти недостающие значения.Они могут выбрать представление неизвестных с помощью таких букв, как x, y и z, или они могут показать свое решение с помощью предположений и проверок. Студенты должны поделиться своим процессом решения этих вопросов с остальным классом. Разграничивайте эти действия, используя разные наборы чисел, включая натуральные и рациональные числа.
www.LearnAlberta.ca © 2012 Alberta Education
9 класс, Паттерны и отношения (переменные и уравнения) (SO 3) Стр. 14 из 31
Пример задания 2: Уравнения из геометрических паттернов (Van de Walle 2001, p.409) Попросите учащихся построить прогрессивный линейный геометрический узор, используя различные типы блоков узора. Разные группы могут работать с разными полигонами и создавать свои шаблоны в таблицах значений; затем преобразуйте эту информацию в выражение или правило, объясняющее шаблон. Например, если учащиеся строят цепочку из шестиугольников
, таблица значений должна выглядеть, как показано ниже: Количество шестиугольников 1 2 3 4
Количество сторон 6 10 14 18
Периметр 6 (2,5 см) 10 ( 2.5 см) 14 (2,5 см) 18 (2,5 см)
Попросите учащихся, использующих различные формы, изобразить свои данные на графике класса, чтобы увидеть сходства и различия между линейными функциями. Все блоки выкройки имеют стороны 2,5 см, за исключением трапеции, у которой длина стороны 5 см. После того, как учащиеся переведут свои данные в алгебраическое выражение, предложите им написать свое выражение как минимум двумя другими эквивалентными способами. Вот некоторые из возможных: • • • • • •
4n + 2 2 (2n + 1) [использование свойства распределения] 2n + 2n + 4 2n + 2n + 2 + 2 2 (n + 1) + 2 ( n + 1) [использование распределительного свойства] 4 (n — 1) + 6.
Работа со скобками часто сбивает учеников с толку, поэтому важно закрепить применение распределительных свойств.
www.LearnAlberta.ca © 2012 Alberta Education
9 класс, Паттерны и отношения (переменные и уравнения) (SO 3) Стр. 15 из 31
Пример задания 3: Использование плиток алгебры для решения уравнений Плитки алгебры помогут укрепить шаги, которые студенты должны использовать для упрощения уравнений с интегральными значениями; однако в 9-м классе им нужно будет решить уравнения с рациональными значениями, поэтому важно понимать этапы процесса решения.Использование шаблона баланса также усиливает потребность учащихся в понимании концепции равенства. Это упражнение предоставляет учащимся графический органайзер, чтобы они могли понять, используя плитки для решения вопросов, а затем применять свои алгоритмы к вопросу с рациональными значениями. Эффективный переходный инструмент для алгебраических плиток — предоставить студентам карточку с рецептами, попросить их обвести плитки на карточке, а затем вырезать отверстия для трех фигур, тем самым сделав трафарет.
Вам следует пропорционально уменьшить размер вырезов плитки (хорошее математическое задание для студентов), чтобы студенты могли сжать свои рисунки алгебраической плитки и использовать меньше бумаги при использовании шаблона.Этот метод рисования плиток повышает эффективность рисования, и ученики 9-х классов обычно ценят переход от конкретных материалов (алгебраических плиток) к графическому изображению. Кроме того, рассмотрите возможность использования веб-сайтов, на которых студенты могут изучать вопросы в электронном виде, таких как Национальная библиотека виртуальных манипуляторов по адресу http://nlvm.usu.edu/. Эти онлайн-весы генерируют алгебраические уравнения, которые студенты должны решить, и начинают с того, что учащиеся представляют уравнения наглядно на весах.Затем они выбирают вариант решения и выбирают одну из четырех операций, чтобы начать решение. Пока они продолжают решать каждый шаг уравнения, онлайн-апплет показывает тему, как графическое (конкретное), так и алгебраическое представление шагов, которые они выбрали. Этот апплет позволяет студентам заполнять только уравнения, которые имеют интегральные решения. Учащиеся также могут использовать этот апплет для создания собственных уравнений для решения. Попросите учащихся решить приведенные ниже уравнения с помощью онлайн-апплета и / или шаблона плитки алгебры выше.Важный совет: им нужно будет использовать в своих рисунках два цвета при работе с положительными и отрицательными значениями.
www.LearnAlberta.ca © 2012 Alberta Education
9 класс, Паттерны и отношения (переменные и уравнения) (SO 3) Стр. 16 из 31
Решите, используя плитки алгебры (показать все шаги) 3x = –6
Решить алгебраически (покажите все шаги и проверьте свой ответ) 3n = –6
2x + 3 = –1 2 (x — 3) = 4
2n + 3 = –1 2 (n — 3) = 4
3x + 2 = x — 4
3x + 2 = x — 4
3 (2x + 2) = 2 (2x — 4) x = 2 3 12 = 3 xx + 5 = –2 3
3 (2n + 2 ) = 2 (2n — 4) x = 2 3 12 = 3 xx + 5 = –2 3
Более сложный: Решите (покажите все шаги и проверьте свой ответ) 1 n = 12 2 0.4n + 3,6 = 12,8 3 (n — 4) = 5 4 3n — 1 = 2n — 2 4 2 3 3 0,8 (6n + 6) = 0,6 (4n — 12) x = 0,8 2 2,5 = 0,5 nx + 8,2 = 12,8 0.4
Примеры решений для 2x + 3 = –1:
Добавьте отрицательные 3 (–3) плитки с обеих сторон и создайте ноль слева. 2x + 3 + –3 = –1 + –3
2x = –4
www.LearnAlberta.ca © 2012 Alberta Education
Класс 9, Модели и отношения (переменные и уравнения) (SO 3) Стр. 17 из 31
Разделите обе части уравнения на 2.
2 x = −4 2 2
x = –2
www.LearnAlberta.ca © 2012 Alberta Education
9 класс, Паттерны и отношения (переменные и уравнения) (SO 3) Страница 18 из 31
Пример задания 4: Математические дебаты Трое учащихся обсуждают уравнение y = 1 x + 5. Студент A думает, что каждые 2 раза y изменяется на 1, x изменяется на 2. Студент B думает, что каждый раз, когда y изменяется на 1, x изменяется на 5. Студент C думает, что каждый раз, когда y изменяется на 1, x изменяется на 1. Кто, по вашему мнению, 2 2 является правильным и почему? Используйте как минимум два представления, чтобы доказать свою правоту.Поощряйте студентов составить таблицу значений и график, чтобы помочь им контекстуализировать и представить проблему другими способами. Они должны обнаружить, что и Студент A, и Студент C верны, если они посмотрят на изменение значений в таблице или на графике. x
1x + 5 2 5 5.5 6 6.5 7
0 1 2 3 4
10 8
1 2
x + 5
6 4 2 0 0
2
4
6
8
10
x
www.LearnAlberta.ca © 2012 Alberta Education
9 класс, Паттерны и отношения (переменные и уравнения) (SO 3) Страница 19 из 31
Пример задания 5: Представление и решение задач с помощью линейных уравнений Существует множество задач, которые можно решить решается с помощью линейных уравнений. Попросите учащихся решить эти уравнения, используя личную стратегию, которой затем поделятся с классом. Примеры включают: • •
• •
Возрастные проблемы — Сумма возраста Адриана и возраста его матери составляет 62 года.Мама Адриана в три раза и на четыре года старше его. Сколько им лет? Задачи с числами — 10 меньше 1 из числа 5. Какое число? 4 — вес Марио на 2 кг меньше, чем вес его сестры Джейн в два раза. Вместе они весят 97 кг. Сколько они весят? Проблемы с деньгами. На школьный спектакль было продано 680 билетов за 1 620 долларов. Билеты на переднюю половину продаются за 3 доллара, а билеты на трибуны — за 2 доллара. Сколько билетов по каждой цене продано? Проблемы с расстоянием и перемещением — у Тейлора есть 88 см обрезки вокруг треугольного знака.Две стороны треугольника на 10 см короче третьей. Если Тейлор использует всю обрезку, каковы длины сторон треугольника?
Рассмотрите возможность использования открытых задач (с обсуждением в небольших группах, а затем с разделением классов) в дополнение к более традиционным вопросам, чтобы помочь студентам расширить свой репертуар подходов к решению проблем. Вы также можете создать сценарии, в которых учащимся нужно сравнивать ситуации, чтобы прийти к решению. Например: в школе Иоланды проводится вечерний сбор средств, на котором ученики устраивают различные игры и конкурсы.Студенты могут участвовать двумя способами: 1) они могут заплатить вступительный взнос в размере 5 долларов и играть в игры по 75 центов каждый, или 2) они могут не платить вступительный взнос и играть в игры по 1,25 доллара за каждую. •
Если у Иоланды есть 15 долларов, которые она может потратить на игры в этот вечер, какой выбор позволит ей сыграть максимальное количество игр?
•
Если у Иоланды неограниченное количество денег, будет ли один вариант лучше другого?
www.LearnAlberta.ca © 2012 Alberta Education
9 класс, Паттерны и отношения (переменные и уравнения) (SO 3) Стр. 20 из 31
Пример действия 6: Анализ ошибок Анализ ошибок — эффективный способ улучшить понимание распространенные ошибки и вовлечь учащихся в мыслительную деятельность более высокого уровня.Разработайте и используйте такие вопросы, как: Mercedes допустила некоторые ошибки в своем решении вопроса. Вы можете их найти? 3 (3x + 12) = 9x + 12 = 9x — 6x +12 = 3x = 3x = 3x = 3 x =
–2 (3x — 6) –6x — 6 –6 –6 + –12 18 18 3 6
www.LearnAlberta.ca © 2012 Alberta Education
9 класс, Паттерны и отношения (переменные и уравнения) (SO 3) Стр. 21 из 31
Пример задания 7: Соединение алгебры с областью Два прямоугольника ниже имеют одинаковую площадь . Попросите учащихся найти: •
значение x площади каждого прямоугольника.
5 7x + 4
3x + 1 2
www.LearnAlberta.ca © 2012 Alberta Education
9 класс, Паттерны и отношения (переменные и уравнения) (SO 3) Страница 22 из 31
Пример задания 8: Представление вопроса по площади с помощью bb = a и = x ax = b, ax Площадь прямоугольника составляет 15,3 см2. Длина 5,1, ширина x. Покажите хотя бы три разных способа написать это уравнение. Попросите учащихся решить каждое уравнение. Предложите учащимся поделиться своими уравнениями и обсудить, какие уравнения правильно представляют проблему.Возможные правильные уравнения: • • •
5,1x = 15,3 15,3 = 5,1, x ≠ 0 x 15,3 = x 5,1
Попросите учащихся: • • •
поделиться этапами их решения, обсудить, почему все уравнения, которые представляют проблему придете к тому же решению, обсудите, почему x ≠ 0 включен во второй образец решения.
www.LearnAlberta.ca © 2012 Alberta Education
9 класс, Паттерны и отношения (переменные и уравнения) (SO 3) Стр. 23 из 31
Шаг 4: Оцените руководящие вопросы учащихся • • •
Посмотрите назад на то, что вы определили в качестве приемлемого доказательства на шаге 2.Каковы наиболее подходящие методы и действия для оценки обучения студентов? Как мне согласовать свои стратегии оценивания со стратегиями обучения?
В дополнение к постоянной оценке на протяжении уроков, рассмотрите следующие примеры действий для оценки обучения учащихся на ключевых этапах. Даются предложения по оценке всех учащихся в классе или в группах, отдельных учащихся, нуждающихся в дальнейшей оценке, и отдельных учащихся или групп в различных контекстах.A. Выходные карточки для всего класса / группы и конкретная обратная связь По мере того, как вы слушаете и наблюдаете, как ваши ученики обсуждают решения вопросов, возможности для оценки мышления учеников увеличиваются. Поскольку первые пять минут занятия и последние пять минут занятия часто являются наиболее важным временем обучения в классе, подумайте о том, чтобы использовать карточку выхода с вопросом, который касается результатов, охваченных в классе. В последние пять-десять минут урока попросите учащихся ответить на вопросы, подобные приведенным ниже: Задание 1 В чем ценность каждого неизвестного? Покажи, откуда ты знаешь.
Задание 2 Напишите три эквивалентных выражения для 4 (n + 2). Задание 3 Сравните метод решения следующих двух наборов уравнений: • •
x = 2,5 и 5 = 2,5 x 5 2 (3x + 1) = 4 (3x + 8) и –2 (3x + 1) = –4 (3x + 8)
www.LearnAlberta.ca © 2012 Alberta Education
9 класс, Паттерны и отношения (переменные и уравнения) (SO 3) Стр. 24 из 31
Задание 4 Создайте функцию в Excel. Раздайте учащимся копию графика и попросите их найти уравнение, описывающее линейную функцию.Они должны показать шаги или дать объяснение, подтверждающее их решение.
2 1,5 1 0,5
y
0 –0,5 0
5
10
15
–1 –1,5 –2 –2,5
x
Задание 5 Попросите учащихся выбрать вопрос из раздела практики своего ресурса и попросите их решить тот же вопрос, но включить одну или две ошибки. Учащиеся могут проанализировать вопросы другого учащегося, чтобы попытаться найти допущенные ошибки. Регулярное использование выходного вопроса помогает направлять ваше планирование урока и является хорошей возможностью дать учащимся короткие комментарии и отзывы.Исследования показывают, что если вы предоставите конкретную обратную связь без оценки, понимание учащимися и их успеваемость по итоговым оценкам улучшатся.
www.LearnAlberta.ca © 2012 Alberta Education
9 класс, Паттерны и отношения (переменные и уравнения) (SO 3) Стр. 25 из 31
Задание 6 Два прямоугольника ниже имеют одинаковую площадь. Попросите учащихся найти: •
значение x площади каждого прямоугольника.
6 5x — 1
3x — 3 2 Задание 7 Докажите, что 18 x = 6 и 6x = 18 являются взаимосвязанными уравнениями.Самооценка учащихся: рейтинговая шкала
Самооценка учащихся — очень эффективная стратегия оценивания. Учащиеся должны знать о целях и результатах, которых они пытаются достичь, а также о том, насколько хорошо они достигают этих целей. Самооценка включает четыре этапа: 1. Учащиеся и учитель обсуждают и совместно создают критерии оценки работы. 2. Учитель помогает ученикам определять уровни успеваемости посредством разработки рубрики или рейтинговой шкалы. 3. Учитель обучает учеников применению мер.4. Учитель дает учащимся конкретную обратную связь по поводу их самооценки. Рассмотрите возможность использования дескрипторов для дополнения или замены числовой шкалы. Например: • • •
новичок или еще не опытный или на целевом уровне продвинутый или выше и выше.
www.LearnAlberta.ca © 2012 Alberta Education
9 класс, Модели и отношения (переменные и уравнения) (SO 3) Стр. 26 из 31
Вот возможный пример самооценки. Попросите учащихся выбрать один из трех следующих уровней для каждого из критериев и прокомментировать, почему их обучение лучше всего подходит для этой категории: Я умею: • решать линейные уравнения с использованием плиток баланса или алгебры • алгебраически решать линейные уравнения численно и проверять мои ответ • преобразовать линию на графике в таблицу значений и линейное уравнение • преобразовать текстовые задачи в линейные уравнения и решить их
Новичок
Опытный Продвинутый
Комментарий
Использование технологий Существует ряд действий, которые можно выполнить используется для подкрепления и оценки обучения учащихся на веб-сайте Interactivate: Activities (Shodor) по адресу http: // www.shodor.org/interactivate/activities/. Даются примечания для студентов и преподавателей, а также предоставляется кнопка помощи для игры. Два действия в приведенных ниже ссылках позволяют учащемуся выбирать варианты для дифференциации в соответствии с: • • •
время, отведенное для достижения решения (от 10 секунд до неограниченного), структура уравнения уровня сложности, включая: — переменные с обеих сторон — использование свойство распределения — одношаговый — двухступенчатый — квадратичный (Примечание: не выбирайте, так как это результат старшей средней школы).
www.LearnAlberta.ca © 2012 Alberta Education
9 класс, Паттерны и отношения (переменные и уравнения) (SO 3) Страница 27 из 31
Первое задание — это игра, в которую могут играть два ученика, а второе — индивидуальная викторина. См. Следующие веб-сайты: • •
http://www.shodor.org/interactivate/activities/AlgebraFour/ http://www.shodor.org/interactivate/activities/AlgebraQuiz/.
B. Индивидуальная оценка. Когда у учащихся возникают трудности с концепциями или результатами, ответы на конкретные вопросы в рамках структурированного интервью могут помочь определить источник трудностей.Эти индивидуальные оценки должны помочь учителю лучше понять мышление ученика, а также дать возможность устранить недопонимание. C. Прикладное обучение. Предоставьте учащимся возможность создавать и решать задачи с линейными уравнениями, которые связаны с поездками, деньгами, возрастом или числом. Некоторые идеи, которые могут помочь учащимся приступить к созданию вопросов, заключаются в том, чтобы попросить их исследовать: • • • • •
влияние увеличения массы на длину резинки. Используя ту же резинку, ученики должны измерить ее исходную длину, а затем повесить увеличивающиеся массы на резинке и измерить изменения, как увеличение длины и ширины квадрата или прямоугольника на две или четыре единицы изменяет значение неизвестных в уравнении расхода топлива. в семейной поездке, сравнив заработок на маленьком и большом автомобиле на разных работах; е.g. автобус или официант в ресторане получают базовую зарплату плюс чаевые (студенты могут смотреть на взаимосвязь между отработанными часами и общим заработком на основе ожидаемых чаевых) данные из кафетерия или закусочных, где студенты могут создавать пропорциональные ситуации на основе потребление напитков (в литрах) для населения столовой или школы и экстраполировать эту информацию на более широкий контекст.
www.LearnAlberta.ca © 2012 Alberta Education
9 класс, Модели и взаимосвязи (переменные и уравнения) (SO 3) Стр. 28 из 31
Шаг 5: Дальнейшие действия по руководящим вопросам оценки • • •
What выводы можно сделать из оценочной информации? Насколько эффективны учебные подходы? Каковы следующие шаги в инструкции?
А.Устранение пробелов в обучении Рассмотрите следующие стратегии, чтобы помочь учащимся, испытывающим трудности: •
Начните работать с одношаговыми уравнениями, которые включают сложение, вычитание, умножение и деление, например: — n + 3 = 6 — n – 3 = 6 — 2n = 6. Попросите учащихся показать или рассказать о том, как они могут решать уравнения. Поощряйте их попробовать использовать модель баланса, плитки алгебры или изображения плиток. Послушайте и понаблюдайте, есть ли одна модель, которую им проще всего использовать.
•
Введите двухэтапные уравнения, например: — —
3n + 2 = 14 4n — 3 = 9.
Попросите учащихся показать или рассказать о том, как они могут решать уравнения. Поощряйте их попробовать использовать модель баланса, плитки алгебры или изображения плиток. Послушайте и понаблюдайте, есть ли одна модель, которую им проще всего использовать. B. Укрепление и расширение обучения Учащиеся, которые достигли или превысили результаты, получат выгоду от постоянных возможностей применить и расширить свое обучение. Эти действия должны помочь учащимся в развитии более глубокого понимания концепции и не должны приводить к результатам в последующих классах.Рассмотрите следующие стратегии. Задание 1 С учащимися в небольших группах или парах покажите вопросы по одному и предложите учащимся решать их с помощью плиток; затем используйте следующий шаблон для графической и цифровой записи шагов. Переход от конкретного к абстрактному, а затем от интегрального к рациональному, должен помочь учащимся закрепить навыки, полученные в 8-м классе, и помочь им применить полученные знания для решения уравнений с рациональными коэффициентами и константами. www.LearnAlberta.ca © 2012 Alberta Education
9 класс, Паттерны и отношения (переменные и уравнения) (SO 3) Стр. 29 из 31
Решите, используя плитки алгебры и модель баланса (показать все шаги) 3x = –9
Решить (показать все шаги и проверьте свой ответ) 3n = –9
Сложнее: Решите (покажите все шаги и проверьте свой ответ) 1 n = 12 2 –0,4n + 3,6 = 12,8
2x + 3 = –1
2n + 3 = –1
2 (x — 3) = 4
2 (n — 3) = 4
3x + 2 = x — 4
3x + 2 = x — 4
3 (2x + 2) = 2 (2x — 4)
3 (2n + 2) = 2 (2n — 4)
3 (n — 4) = 5 4 3n− 1 = 2n− 2 4 2 3 3 0.8 (6n + 6) = 0,6 (4n — 12)
x = 2 3
x = 2 3
x = 0,8 2
12 = 3 x
12 = 3 x
2,5 = 0,5 n
x + 5 = –2 3
x + 5 = –2 3
x + 8,2 = 12,8 0,4
Задание 2: Игры Используя две кости (одну для положительных чисел и одну для отрицательных), попросите учащихся бросить кости. дважды. Подставьте значение каждого кубика в два поля в левой части уравнения при первом броске и в два поля в правой части уравнения при втором броске: •
x + = x +
Учащиеся должны решить, какой цвет кристалла представляет положительные значения, а какой — отрицательные.Например, если при первой жеребьевке ученик бросает 3 и 4, это может означать –3 и 4; и если при втором броске ученик бросает 2 и 3, используйте –2 и 3. Учащиеся решают, в каком квадрате содержится какое значение кубика. Первое уравнение, которое необходимо решить, может быть следующим: •
–3x + 4 = –2x + 3
Другие форматы уравнений, которые помогают учащимся усилить концепцию вычитания отрицательных значений: • • •
x — = x + x + = x — x — = x —
www.LearnAlberta.ca © 2012 Alberta Education
9 класс, Паттерны и отношения (переменные и уравнения) (SO 3) Стр. 30 из 31
Библиография Консорциум оценки Альберты. http://www.aac.ab.ca/ (по состоянию на 18 апреля 2012 г.). Образование Альберты. Программа обучения математике K – 9 провинции Альберта с показателями успеваемости. Эдмонтон, AB: Образование Альберты, 2007. Обучение основам алгебры. Эдмонтон, AB: Образование Альберты, 2005. Бернс, Мэрилин. О преподавании математики: ресурс для классов K – 8. 2-е изд. Саусалито, Калифорния: Math Solutions Publications, 2000.Карпентер, Томас П., Меган Лоэф Франке и Линда Леви. Математическое мышление: интеграция арифметики и алгебры в начальной школе. Портсмут, Нью-Хэмпшир: Heinemann, 2003. Национальный совет учителей математики. Принципы и стандарты школьной математики. Рестон, Вирджиния: NCTM, 2000. Шустер, Лэйни и Нэнси Канавен Андерсон. Хорошие вопросы для преподавания математики: зачем их и о чем спрашивать, K – 6. Саусалито, Калифорния: Математические решения, 2005. Shodor. «Взаимодействовать: мероприятия». http://www.shodor.org/interactivate/activities/ (по состоянию на 18 апреля 2012 г.).Маленький, Мэриан. Большие идеи от доктора Смолла: Создание зоны комфорта для преподавания математики: 4–8 классы. Скарборо, О. Н.: Nelson Education, Ltd., 2009. З. Усискин «Концепции школьной алгебры и использование переменных». В А. Ф. Коксфорде (ред.), Идеи алгебры K – 12 (Рестон, Вирджиния: Национальный совет учителей математики, 1988), стр. 8–19. Государственный университет Юты. «Национальная библиотека виртуальных манипуляторов». http://nlvm.usu.edu/ (по состоянию на 18 апреля 2012 г.). Ван де Валле, Джон А. Математика в начальной и средней школе: развивающее обучение.4-е изд. Бостон, Массачусетс: Addison Wesley Longman, Inc., 2001. Ван де Валль, Джон А. и Луэнн Х. Ловин. Обучение математике, ориентированной на учащихся: 5–8 классы. Бостон, Массачусетс: Pearson Education, Inc., 2006. Уитли, Грейсон Х. и Джордж Э. Абшир. Развитие математической беглости: упражнения для 5–8 классов. Таллахасси, Флорида: Обучение математике, 2002.
www.LearnAlberta.ca © 2012 Alberta Education
9 класс, Паттерны и отношения (переменные и уравнения) (SO 3) Страница 31 из 31
Функция | Примечания, видео, контроль качества и тесты | 9 класс> Математика по выбору> Алгебра: упорядоченная пара и декартово произведение
Функция
Функция Источник: astarmathsandphysics.comФункция — это особая связь, в которой каждый вход имеет один выход. Пусть A и B — два множества. AB — это множество всех упорядоченных пар (a, b) таких, что a ∈ A и b ∈ B. Пусть f: AB — непустое подмножество AB. Тогда f является отношением от A к B. Этот f называется функцией от A к B, если f связывает каждый элемент B. Итак, функция — это особый тип отношения, которое связывает каждый элемент множества A с одним и только элемент Б.
Изображение и предварительное изображение
Пусть f = {(x, y): x ∈ A, y ∈ B} — функция из A в B.Первый элемент x упорядоченной пары (x, y) называется прообразом второго элемента y под функцией f, а y называется образом x под f. Мы пишем f (x) = y, чтобы означать, что y является изображением x под f, и читается как f x is y или f x равно y. Так как y является образом x при f, следовательно, f (x) является образом x при f.
Домен, ко-домен и диапазон функции
Домен, совместный домен и диапазон Источник: www.math-only-math.comПусть f будет функцией от множества A до множества B. Тогда A называется областью области f, а B называется областью области f. Множество всех изображений элементов под f называется диапазоном f. Диапазон f обозначается f (A).
Если A = {1,2,3}, B = {1,4,9}
f = {(1,1), (2,4), (3,9)}, тогда f — функция от A до B.
Здесь,
Домен f = A = {1,2,, 3}
Ко-домен f = B = {1,4,9}
Диапазон f = f (A) = {1,4,9}
Здесь диапазон f и ко-домен f — равные множества.т.е. f (A) = B.
Снова рассмотрим функцию g, которая определяется следующим образом:
Здесь
Домен g = A = {1,2,3}
Ко-домен g = {1,2,3,4}
В этом примере диапазон g, то есть g (A), является правильным подмножеством ко-домена g, то есть B.
Следовательно, диапазон функции может быть надлежащим подмножеством ее ко-домена или равным ко-домену.
Итак, для функции f из A в B мы пишем f (A) ≤B.
Типы функций
Типы функций Источник: www.kshitij-iitjee.com- Onto function
Пусть f будет функцией от A до B. Тогда f называется функцией on, если каждый элемент B появляется как изображение хотя бы одного члена A
Здесь элемент B появляется как изображение элемента A. Итак, f относится к функции.
В этом примере диапазон f и ко-домен f равны. Таким образом, функция f называется on-функцией, если ее диапазон и ко-домен равны, т. Е. F (A) = B. - В функцию
Пусть f — функция от A до B.Тогда f называется функцией в функцию, если в B есть хотя бы один элемент, который не является изображением какого-либо элемента в функции.
Здесь диапазон f = {1,2,3} = A
Ко-домен f = {1,2,3,4} = B
Здесь диапазон f является правильным подмножеством его ко-домена.
Следовательно, функция f называется входящей функцией, если диапазон f является правильным подмножеством ее ко-области. - Функция один-к-одному
Пусть f будет функцией от A до B. Тогда f называется функцией один-к-одному, если никакие два разных элемента в A не имеют разумного представления в B. - Функция «многие к одному»
Пусть f будет функцией от A до B. Затем f вызывается функцией «многие к одному», если по крайней мере два элемента A имеют одинаковое представление в B. - Равные функции
Две функции f и g, определенные в одной области, называются равными, если f (a) = g (a) для каждого элемента a в области. - Независимая и зависимая переменная
Пусть f будет функцией от A до B, тогда переменная x, которая принимает значения в домене, называется независимой переменной, а переменная y, которая принимает значения в диапазоне, называется зависимой переменной. .
Основные характеристики функции
Пусть f — функция от A до B, тогда
- для каждого x∈A существует элемент y∈B такой, что (x, y) ∈f, то есть y является образом x под f, то есть y = f (x).
- ни один элемент A не может иметь более одного изображения в B.
- могут быть элементы B, которые не связаны ни с одним элементом A.
- различных элемента A могут иметь одно и то же изображение в B.
Тестирование функции
Тестирование функции Источник: www.coolmath.comФункцию можно проверить различными способами. Обычно мы проверяем это через определение, т.е.
а. Отношение называется функцией, если все элементы домена должны иметь изображение в ко-домену. В противном случае это не будет функция.
Функцию также можно проверить с помощью теста, известного как тест вертикальной линии. Для этого теста в любой точке графика рисуется вертикальная линия. Если вертикальная линия разрезает график только в одной точке, это функция, а если она разрезает более чем в одной точке, то это не функция.
Представление функции
- Форма реестра
В этой форме функция представлена набором всех упорядоченных пар, которые принадлежат данной функции.
Например, пусть A = {0,2,3,5,7} и
B = {0,2,4,5,7,9,10,15}, и f будет функцией «меньше чем». от A до B. тогда
f = {(0,2) (2,4) (3,5) (5,7) (7,9)} - Форма конструктора наборов
В этой форме функция представлена как {(): xA, yB, x … y}, пробел должен быть заменен правилом, которое связывает x и y.
Например, пусть A = {2,5,7,8}, B = {-3,0,1,2,3,4} и f = {(2, -3), (5,0) , (7,2), (8,3)} тогда, поскольку f в форме построителя множеств может быть записано как
f = {(): x∈A, y∈B, x is more than y} - По формуле
В этой форме формула может использоваться для представления функции.
Например, уравнение y = 3x + 1 представляет функцию, где x принимает все значения из набора натуральных чисел N, а значения y получаются с помощью приведенного выше уравнения. - По таблице
В этой форме таблица может использоваться для представления функции.
Например, приведенная ниже таблица представляет функцию:x 1 2 3 4 5 6 7 y 1 4 9 16 25 36 49 - Стрелочная диаграмма
В этой форме функция представлена в виде стрелок от первых компонентов ко вторым компонентам всех упорядоченных пар, которые принадлежат данной функции.

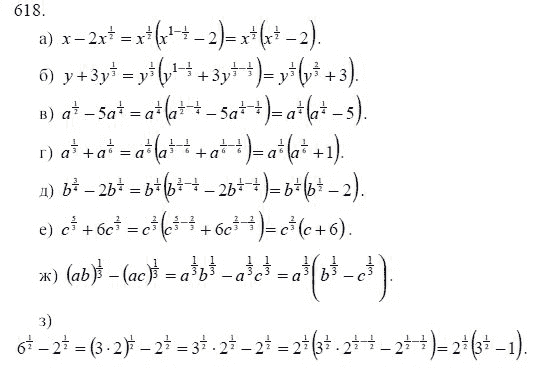 Свойства арифметической прогрессии. Алгебра, 9 класс: уроки, тесты, задания.
Свойства арифметической прогрессии. Алгебра, 9 класс: уроки, тесты, задания. Комбинаторные задачи. Алгебра, 9 класс: уроки, тесты, задания.
Комбинаторные задачи. Алгебра, 9 класс: уроки, тесты, задания.