Ответы по геометрии 9 класс: ГДЗ по геометрии 9 класс от Путина: решебники

Содержание

Готовые домашние задания (ГДЗ) для 9 класса Геометрия ⏩ Ответы на рабочие тетради, решебники учебников ⭐ Моя Школа

Самые популярные книги

В 9 классе школьная программа достаточно сложная, много точных предметов, интересных и сложных. Поскольку обучение в школе рассчитано на средний результат у детей, некоторым школьникам плохо даётся алгебра или геометрия. Как быть, если учебник и учитель дают недостаточно знаний и навыков? Помогут готовые домашние задания. Возьмем пример – ГДЗ, геометрия, 9 класс – и объясним, в чем его польза.

Решебник по геометрии, 9 класс – что представляет из себя

Если вспомнить, все списывали в школе, за исключением отличников. Но редко кому удаётся на протяжении всего школьного обучения получать высшие баллы по всем предметам. Поэтому дети списывают: на контрольных, перед уроками домашние задания. Во втором случае на это уходит много времени, иногда даже вся перемена. А ведь сделать уроки с решебником можно и дома.

мПо своей сути, готовые домашние задания – это методичка, где собраны в правильном порядке решения и ответы на упражнения из учебника. К каждой задаче есть комментарии, приведены правила, теоремы.

Раньше приходилось приобретать решебники в бумажном варианте. Теперь есть интернет, где легко можно найти нужную методичку. Необязательно даже скачивать, ведь сложности в геометрии могут быть редкими. В таких случаях и стоит заглядывать в решебник, найти свою ошибку и проанализировать.

«ГДЗ, 9 класс геометрия» онлайн – верный помощник старшеклассника

Итак, решебник может найти каждый школьник. Пользуется им он неправильно и тайком, просто бездумно списывая домашние задания, или вдумчиво и нечасто – зависит от родителей. Надо объяснять ребенку, что решебник – не шпаргалка.

Задачи по геометрии (9 класс) с решением сократят время подготовки к урокам

В старших классах половину буднего дня подросток сидит за партой, а вторую половину приходится тратить на выполнение домашних заданий. Почти не остаётся времени на отдых, личные дела, игры, общение с друзьями. Всё это приводит к стрессам, усталости, нежеланию учиться и делать уроки. Чтобы не допускать такого, стоит разрешить в особо тяжелые учебные дни пользоваться дома решебниками.

К тому же большинство детей посещают спортивные кружки, различные курсы. Некоторые готовятся к олимпиадам и соревнованиям. В такие дни мало того, что не делаются уроки, так еще и пропускаются занятия в школе. Чтобы не отстать от сверстников, пригодятся готовые домашние задания.

Бесплатный репетитор и родительская помощь

Если ребенок отстаёт по алгебре и геометрии, родители часто отправляют его к репетитору, который берет немалые деньги. Однако почему бы не подтягивать школьника самому по предметам. Можно задавать ему упражнения, и пусть решает сам, учиться логически мыслить, запоминает материал. Если будут сложности, родители всегда смогут его проконсультировать, пользуясь решебником.

Исходя из всего, от методичек есть явная польза:

помощь отстающим по учебе
нет потребности в репетиторе
«Геометрия, 9 класс, ГДЗ» скачать может любой и бесплатно

родительский контроль над успеваемостью

Тесты с ответами по геометрии 9 класс сборник

Сборник тестовых вопросов по геометрии 9 класс

Правильный вариант ответа отмечен знаком +

1. На рисунке представлена формула. Что можно найти по ней?

— это формула нахождения длины вектора;

— по данной формуле можно найти начало отрезка;

— это формула для вычисления конца отрезка;

+ по этой формуле можно с легкостью вычислить координаты середины вектора.

2. Чтобы найти «это», нужно взять первую координату вектора, возвести ее в квадрат. Затем вторую из координат вектора так же возвести в квадрат. Полученные значения сложить, а уже потом вычислить квадратный корень из имеющегося числа. Что нужно найти?

+ длину вектора;

— середину отрезка;

— начало вектора;

— конец вектора.

3. Чтобы узнать «эту вещь», нужно взять разность координат двух точек, возвести каждую из разностей в квадрат. После этого понадобится узнать число, полученное в результате сложения суммы квадратов. В конце потребуется вычисление квадратного корня. «Это» найдено. О чем идет речь?

— о нахождении длины отрезка;

— о формуле вычисления середины отрезка;

— о вычислении расстояния между началом и концом;

+ о расстоянии между двумя точками.

4. Требуется заполнить пустые строки в таблице. Внимание на рисунок.

+ {2; 2};

— {-2; -2};

— {0; 2};

— {2; 0}.

5. Какое из приведенных уравнений можно отнести к уравнению окружности:

6. Дано уравнение окружности (x+4)

2+(y-2)²=18 и точка К (5; 8). Нужно указать принадлежит ли точка данной окружности.

— точка лежит внутри окружности;

— точка лежит на окружности;

+ точка лежит вне окружности;

— нет верного ответа.

7. Что называется синусом угла λ из промежутка от 0°≤ λ ≤180°?

+ ордината точки;

— абсцисса точки;

— может быть, как абсцисса точки, так и ордината.

— верного ответа здесь нет.

8. Косинусом угла λ из промежутка от 0°≤ λ ≤180° является:

— это сложно сказать, требуется дополнительное построение;

— ордината точки;

+ абсцисса точки;

— и то, и другое.

9. Зная значение синуса и косинуса, можно ли вычислить тангенс угла? Если можно, то как это сделать?

— нельзя;

— можно, нужно найти отношение косинуса к синусу;

— можно, нужно взять половину косинуса;

+ можно, потребуется найти отношение синуса к косинусу.

тест 10. Среди представленных формул нужно выбрать основное тригонометрическое тождество.

+ sin² λ+cos² λ =1;

— sin³ λ+cos² λ =1;

— sin¹ λ+cos¹ λ =0;

— sin² λ=cos² λ.

11. На что нужно умножить половину произведения двух сторон треугольника при нахождении его площади?

+ на синус угла между ними;

— на синус любого угла треугольника;

— на косинус угла между ними;

— на косинус любого угла треугольника.

12. Чему пропорциональны стороны треугольника?

— косинусам противолежащих углов;

+ синусам противолежащих углов;

— тангенсам противолежащих углов;

— котангенсам противолежащих углов.

13. Какие из формулировок отражают содержание теоремы косинусов?

+ квадрат любой стороны треугольника равняется сумме квадратов двух остальных сторон минус удвоенное произведение этих сторон на косинус угла между ними;

— любая сторона треугольника равняется сумме квадратов двух остальных сторон минус удвоенное произведение этих сторон на косинус угла между ними;

— квадрат любой стороны треугольника равняется сумме квадратов двух других сторон минус произведение этих сторон на синус угла между ними;

— любая сторона треугольника равна сумме квадратов двух остальных сторон минус удвоенное произведение этих сторон на синус угла между ними.

14.

Векторы, не равные нулю, перпендикулярны, когда:

— сумма всех координат векторов равняется нулю;

— сумма произведений всех абсцисс равна нулю;

— произведение всех ординат равно нулю;

+ сумма произведений абсцисс и ординат данных векторов равняется нулю.

15. Можно ли вписать в правильный многоугольник окружность или описать возле него её? Если да, то сколько?

+ можно только одну;

— можно только две;

— нельзя;

— ни одной окружности вписать нельзя.

16. Что можно найти по данной формуле C= 2πR?

— площадь круга;

— площадь кругового сектора;

— площадь правильного многоугольника;

+ длину дуги окружности.

17. Среди рисунков нужно выбрать тот, который изображает правильные многоугольники. Они выделены цветом.

18. При движении треугольник отображается на:

— любой треугольник;

— отрезок;

+ равный ему треугольник;

— квадрат.

тест-20. Сохраняются ли расстояния при параллельном переносе?

— этого нельзя сказать – нужны дополнительные построения;

— нет;

+да;

— здесь нет верного ответа.

21. Какая плоскость называется секущей?

+ плоскость, содержащая по обе стороны точки данного геометрического тела;

— плоскость, не имеющая точек данного тела;

— плоскость, проходящая мимо геометрического тела;

— нет верного ответа.

22. В прямоугольном параллелепипеде известны длина основания, равная 3, ширина, равняющаяся 4, а также его высота, имеющая длину 6. Чему будет равен его объём?

— 12;

— 48;

-18;

+72.

23. В пирамиде известна площадь основания. Она равна 8. Известна высота пирамиды. Ее длина 3. Выбрать верный вариант ответа, содержащий объем пирамиды.

— 24;

+ 8;

— 112;

— 72.

24. Имеется цилиндр с высотой 6. Площадь его основания равна 5. Чему равен его объём?

+30;

— 5;

— 15;

— 12.

25. В конусе известна высота. Она равняется 9. Известна площадь основания. Она равна 2. Объём этого конуса равен:

+6;

— 18;

— 3;

-9.

26. В шаре известен радиус. Его величина равна 4. Каков объем шара?

— 16;

— 18;

+64;

— 32.

27. Вращением какой фигуры вокруг оси можно получить цилиндр?

+ это прямоугольник;

— эта фигура треугольник;

— сфера;

— пятиугольник.

28. Чтобы получить конус, нужно вокруг его оси вращать эту фигуру. Указать ее среди представленных.

— сферу;

— ромб;

— прямоугольник;

+треугольник.

29. Вычислить площадь круга радиуса 6.

+ 36π;

— 6π;

— 18π;

-9π.

тест_30. На мишени имеются 4 кольца. Самое маленькое имеет радиус 1. Чему равна его длина?

— 1/2π;

— 1/3π;

— π;

+2π.

31. Среди приведенных формул нужно выбрать уравнение прямой в прямоугольной системе координат.

— r²x+ey=0;

— r³+et-1=0;

-y+t²=1;

+hx+ey+q=0.

32. Среди представленных окружностей требуется выбрать ту, что соответствует уравнению x²+y²=16.

33. Нужно найти точки пересечения прямых x+2y-1=0 и 3x-2y+4=0. В приведенном решении указать этап с ошибкой.

Решение:

1) Составим систему уравнений

2) Выразим x из первого уравнения системы:

x=1-2y

3) Подставим полученное выражение во второе уравнение:

3 (1-2y)-2y+4=0

3-6y-2y+4=0

-8y=-7

y=7/8

4) Теперь находим x:

x=1-2*7/8=-3/4

Верно ли выполнено решение? Если нет, то в каком из этапов допущена ошибка?

+ все верно;

— ошибка есть в первом этапе;

— имеется недочет на втором этапе решения;

— есть ошибка в третьем пункте.

34. Нужно продолжить лемму: если векторы коллинеарны, то…

— сумма одного из них с каким-то числом будет равняться второму вектору;

+существует такое число, что умножив на него второй вектор можно получить второй;

-существуют такие числа, при умножении на которые получаются рассматриваемые векторы;

-имеется такой вектор, при умножении на который можно получить любое число.

35. На сколько данных векторов можно разложить любой вектор на плоскости?

-на три;

-на четыре;

-на пять;

+на два.

36. Какие из пар векторов называются координатными векторами?

37. Каждая координата суммы нескольких векторов равна…

+сумме соответствующих координат данных векторов;

-произведению соответствующих координат этих самых векторов;

-разности координат данных векторов;

-поделенным друг на друга координатам этих самых векторов.

38. Координата разности нескольких векторов равна…

+разности координат соответствующих векторов;

-сумме разности координат соответствующих векторов;

-произведению сумм данных координат векторов;

-сумме произведений координат соответствующих векторов.

39. Если вектор умножается на какое-то число, то что произойдет с его координатами?

-ничего не произойдет;

-они увеличатся на это число;

+они умножаться на данное число;

— они уменьшатся на это число.

тест* 40. Каждая координата вектора равна…

+разности координат его начала и конца;

-сумме координат его начала и конца;

-произведению координат его начала и конца;

-ничему не равна.

41. Чему равна координата середины отрезка?

-ничему не равна;

+половине суммы соответствующих координат его концов;

-тройной сумме соответствующих координат концов данных отрезков;

-помноженным друг на друга координатам концов отрезков.

42. Чтобы вычислить длину вектора, нужно…

-сложить обе его координаты, а затем полученную сумму возвести в квадрат;

+каждую координату вектора требуется возвести в квадрат, полученные значения сложить, а затем извлечь квадратный корень;

-одну из координат возвести в квадрат;

-извлечь квадратный корень из суммы координат вектора.

43. Расстояние между двумя точками находится очень просто. Для этого…

+потребуется первая координата конца отрезка, из которой вычитается первая координата начала отрезка, затем это значение возводится в квадрат и тоже самое проделывается со второй парой координат, полученные значения складываются и из них извлекается квадратный корень;

-нужно будет сложить все пары координат между собой, затем возвести их в квадрат и извлечь из полученного значения квадратный корень;

-потребуется каждую координату вектора возвести в квадрат и сложить полученные значения;

-необходимо взять первую пару координат, сложить их и возвести в квадрат, затем тоже проделать со второй парой координат, из полученного значения извлечь квадратный корень.

44. Среди представленных уравнений нужно выбрать то, что является уравнением окружности.

— x²+2=0;

— y=2;

+ x²+y²=0;

— x³.

45. Имеется уравнение ax+by+c=0. Какое это уравнение?

+уравнение прямой;

-уравнение окружности;

-такого уравнения нет;

-уравнение параболы.

46. Требуется продолжить высказывание: Площадь треугольника равна половине…

-суммы некоторых сторон;

-суммы некоторых сторон, умноженных на синус угла между ними;

-произведения сторон, умноженных на косинус угла между ними;

+произведения двух из его сторон на синус угла между ними.

47. Стороны треугольника пропорциональны…

+синусам противолежащих углов;

-косинусам противолежащих углов;

-косинусам прилежащих углов;

-синусам прилежащих углов.

48. Чему равен квадрат стороны треугольника?

-он равняется сумме квадратов двух других сторон, перемноженных на синус угла между ними;

+он равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними;

-он равняется сумме квадратов других сторон, умноженных на косинус угла между ними;

-он равен сумме квадратов двух других сторон.

49. Скалярным произведением векторов называется…

+произведение их длин на косинус угла между ними;

-умножение координат вектора на синус угла между ними;

-поделенное значение длины вектора на косинус угла между ними;

-произведение их длин на синус угла между ними.

тест№ 50. Сколько окружностей можно описать около любого правильного многоугольника?

-три;

-четыре;

-две;

+одну.

51. Можно ли в правильный многоугольник вписать окружность?

+да;

-нет;

-при особых обстоятельствах;

-нужно посмотреть на рисунок.

52. Что общего у вписанной в правильный многоугольник окружности и описанной около него окружности?

-ничего;

-стороны;

+центр;

-радиус.

53. Как можно вычислить площадь правильного многоугольника?

+для этого нужно знать половину радиуса вписанной в него окружности, умноженной на периметр;

-потребуется знать радиус вписанной в него окружности, помноженной на периметр;

-нужно будет знать радиус описанной вокруг него окружности, умноженной на радиус вписанной окружности;

-потребуется знать радиус описанной вокруг него окружности, умноженной на радиус половину периметра.

54. На каком из рисунков представлен цилиндр?

55. Какой из рисунков иллюстрирует конус?

56. На котором рисунке имеется пирамида?

57. Чтобы найти объем куба нужно…

-возвести в квадрат одну из его сторон;

+возвести в куб одну из его сторон;

-извлечь квадратный корень из одной из его сторон;

-одна из его сторон и будет объемом.

58. Для того, чтобы вычислить объем параллелепипеда следует…

-знать площадь основания и этого достаточно;

-знать ее высоту;

+знать площадь основания, умноженного на высоту;

-знать половину основания.

59. Чтобы найти объем пирамиды, нужно…

+умножить треть площади основания на высоту;

-умножить половину площади основания на высоту;

-умножить площадь основания на высоту;

-умножить площадь на площадь боковой поверхности.

тест» 60. Для того, чтобы найти объем шара, нужно…

-умножить число пи на радиус;

+перемножить число пи и 4/3 радиуса;

-перемножить число пи и ½ радиуса;

-перемножить число пи и 5 радиусов.

61. Что является основанием конуса?

-квадрат;

+круг;

-прямоугольник;

-треугольник.

62. Основанием параллелепипеда является…

-квадрат;

-круг;

+прямоугольник;

-треугольник.

63. Что является основанием куба?

+квадрат;

-круг;

-прямоугольник;

-треугольник.

Математика Часть II Решения для 9 класса Математика Глава 1

Математика Часть II Решения Решения для 9 класса Математика Глава 1 Основные понятия Геометрии представлены здесь с простыми пошаговыми объяснениями. Эти решения для базовых понятий в геометрии чрезвычайно популярны среди учащихся 9 класса по математике. Основные понятия в геометрии очень удобны для быстрого выполнения домашних заданий и подготовки к экзаменам. Все вопросы и ответы из сборника решений по математике, часть II, класс 9Математика Глава 1 предоставляется здесь для вас бесплатно. Вам также понравится безрекламный опыт решения Mathematics Part II Solutions Solutions от Meritnation. Все решения по математике, часть II Решения для класса 9 по математике подготовлены экспертами и на 100% точны.

Страница № 5:

Вопрос 1:

Найдите расстояния с помощью приведенной ниже числовой строки.

(i) d (B,E) (ii) d (J, A) (iii) d (P, C) (iv) d (J, H) (v) d (K, O)

(vi) d (O, E) (vii) d (P , J) (viii) d (Q, B)

Ответ:

Известно, что расстояние между двумя точками получается путем вычитания меньшей координаты из большей координаты.

(i) Координаты точек B и E равны 2 и 5 соответственно.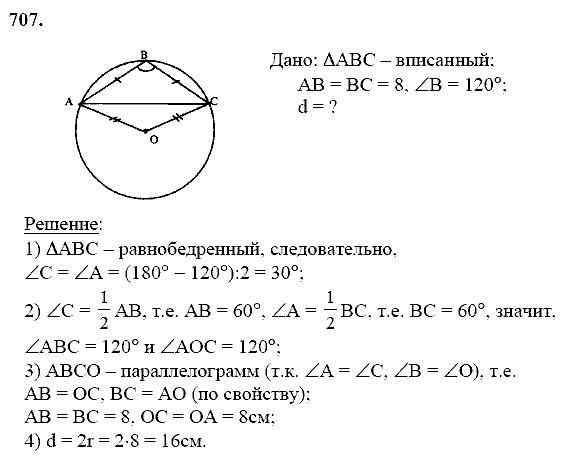 Мы знаем, что 5 > 2.
∴ d (B, E) = 5 − 2 = 3

(ii) Координаты точек J и A равны −2 и 1 соответственно. Мы знаем, что 1 > −2.
∴ d (J, A) = 1 − (−2) = 1 + 2 = 3

(iii) Координаты точек P и C равны −4 и 3 соответственно. Мы знаем, что 3 > −4.
∴ d (P, C) = 3 − (−4) = 3 + 4 = 7

(iv) Координаты точек J и H равны -2 и -1 соответственно. Мы знаем, что −1 > −2.
∴ d (J, H) = −1 − (−2) = −1 + 2 = 1

(v) Координаты точек K и O равны −3 и 0 соответственно. Мы знаем, что 0 > −3.
∴ d (K, O) = 0 − (−3) = 0 + 3 = 3

(vi) Координаты точек O и E равны 0 и 5 соответственно. Мы знаем, что 5 > 0,
∴ d (O, E) = 5 − 0 = 5

(vii) Координаты точек P и J равны −4 и −2 соответственно. Мы знаем, что −2 > −4.
∴ d (P, J) = -2 — (-4) = -2 + 4 = 2

(viii) Координаты точек Q и B равны -5 и 2 соответственно. Мы знаем, что 2 > −5.
∴ d (Q, B) = 2 − (−5) = 2 + 5 = 7

Страница № 5:

Вопрос 2:

Если координата A равна x , а координата B равна y , найдите d (A, B) .

(I) x = 1, y = 7 (II) x = 6, y = -2 (III) x = -3, y = 7

= -3, y = 7

. (iv) x = -4, y = -5 (v) x = -3, y = -6 (vi) x = 4, y = -8

9 Ответ :

(i) Координаты A и B равны x и y соответственно. Имеем x = 1 и y = 7. Мы знаем, что 7 > 1. ) Координаты A и B равны x и y соответственно. У нас x = 6 и y = −2. Мы знаем, что 6 > −2.
∴ d (A, B) = x − y = 6 − (−2) = 6 + 2 = 8 соответственно. У нас есть x = −3 и y = 7. Мы знаем, что 7 > −3.
∴ d (A, B) = y − x = 7 − (−3) = 7 + 3 = 10

(iv) Координаты точек A и B равны x 0 и 40015 соответственно. У нас есть x = −4 и y = −5. Мы знаем, что −4 > −5.
∴ d (A, B) = x − y = −4 − (−5) = −4 + 5 = 1 y соответственно. У нас есть x = −3 и y = −6. Мы знаем, что −3 > −6.
∴ d (A, B) = x — y = -3 — (-6) = -3 + 6 = 3

(vi) Координаты точек A и B равны x и y соответственно. У нас есть x = 4 и y = −8. Мы знаем, что 4 > −8.
∴ d (A, B) = x — y = 4 — (-8) = 4 + 8 = 12

Страница № 5:

Вопрос 3:

5 90 найти, какая из точек находится между двумя другими. Если точки не лежат на одной прямой, укажите это.

(i) d (P, R) = 7, d (P, Q) = 10, d (Q, R) = 3

(ii) d (R, S) = 8, d (S, T) = 6, d (R, T) = 4

(iii) d (A, T) Б) = 16, d (В, А) = 9, d (Б, В) = 7

(iv) d (Л, М) = 11, d (М, Н) ) = 12, d (N, L) = 8

(v) d (X, Y) = 15, d (Y, Z) = 7, d (X, Z) = 8

(vi) d (D, E) = 5, d (E, F) = 8, d (D, F) = 6

Ответ:

(i) Имеем, d (P, R) = 7; д (Р, Q) = 10; d (Q, R) = 3
Теперь, d (P, R) + d (Q, R) = 7 + 3
Или, d (P, R) + d ( R, Q) = 10
∴ d (P, Q) = d (P, R) + d (Q, R)
Следовательно, точки P, R и Q лежат на одной прямой.
Точка R находится между P и Q, т. е. P-R-Q.

(ii) У нас есть, d (R, S) = 8; д (С, Т) = 6; d (R, T) = 4
Теперь 8 + 6 = 14, поэтому 8 + 6 ≠ 4; 6 + 4 = 10, поэтому 6 + 4 ≠ 8 и 8 + 4 = 12, поэтому 8 + 4 ≠ 6
Так как сумма расстояний между двумя парами точек не равна расстоянию между третьей парой точек точки, поэтому заданные точки R, S и T не лежат на одной прямой.

(iii) Имеем d (A, B) = 16; д (С, А) = 9; d (B, C) = 7
Теперь d (C, A) + d (В, В) = 9 + 7
Или, d (А, В) + d (В, В) = 16
∴ d (А, В) = d (А, В) ) + d (C, B)
Значит, точки A, C и B лежат на одной прямой.
Точка C находится между A и B, т. е. A-C-B.

(iv) Имеем, d (L, M) = 11; д (М, Н) = 12; d (N, L) = 8
Итак, 11 + 12 = 23, поэтому 11 + 12 ≠ 8; 12 + 8 = 20, поэтому 12 + 8 ≠ 11 и 11 + 8 = 19, поэтому 11 + 8 ≠ 12
Так как сумма расстояний между двумя парами точек не равна расстоянию между третьей парой точек точек, поэтому заданные точки L, M и N не лежат на одной прямой.

(v) Имеем, d (X, Y) = 15; д (Y, Z) = 7; d (X, Z) = 8
Теперь, d (X, Z) + d (Y, Z) = 7 + 8
Или, d (X, Z) + d ( Z, Y) = 15
∴ d (X, Y) = d (X, Z) + d (Z, Y)
Следовательно, точки X, Z и Y лежат на одной прямой.
Точка Z находится между X и Y, т. е. X-Z-Y.

(vi) Имеем, d (D, E) = 5, d (E, F) = 8, d (D, F) = 6
Итак, 5 + 8 = 13, поэтому 5 + 8 ≠ 6; 8 + 6 = 14, поэтому 8 + 6 ≠ 5 и 5 + 6 = 11, поэтому 5 + 6 ≠ 8
. Так как сумма расстояний между двумя парами точек не равна расстоянию между третьей парой точек, поэтому заданные точки D, E и F не лежат на одной прямой.

Страница № 5:

Вопрос 4:

На числовой прямой точки A, B и C таковы, что d (A,C) = 10, d (C,B) = 8 . Найдите d (A, B), учитывая все возможности.

Ответ:

Есть только две возможности.
Случай 1: когда точка C находится между точками A и B.

Имеем d (A, C) = 10; d (C, B) = 8
Сейчас, d (A, B) = d (A, C) + d (C, B) = 10 + 8
∴ d (A , B) = 18
Случай 2: когда точка B находится между точками A и C.

Имеем d (A, C) = 10; д (С, В) = 8
Теперь, д (А, С) = д (A, B) + d (B, C)
Итак, d (A, B) = d (A, C) − d (B, C) = 10 − 8
∴ d (A, B) = 2

Страница № 5:

Вопрос 5:

Точки X, Y, Z лежат на одной прямой, так что d (X, Y) = 17, Z) = 8, найти d (X, Z) .

Ответ:

Дано, что точки X, Y и Z лежат на одной прямой.
Имеем d (X,Y) = 17; д (Y, Z) = 8,
Теперь, d (X, Z) = d (X, Y) + d (Y, Z) = 17 + 8
∴ d (X, Z) = 25

Страница № 5 :

Вопрос 6:

Нарисуйте правильный рисунок и напишите ответы на следующие вопросы.

(i) Если A — B — C и l (AC) = 11, l (BC) = 6,5, то l (AB) =?

(ii) Если R — S — T и l (ST) = 3,7, l (RS) = 2,5, то л (РТ) =?

(iii) Если X — Y — Z и l (XZ) = 3 7, l (XY) = 7 , то l (YZ) =?

Ответ:

(i)

Имеем l (AC) = 11; л (БК) = 6,5.
Итак, л (АС) = л (АВ) + л (ВС)
Итак, л (АВ) = л (АС) — л — (ВС) = 11,5
∴ l (AB) = 4,5

(ii)

Имеем, л (СТ) = 3,7; л (RS) = 2,5.
Теперь l (RT) = l (RS) + l (ST) = 3,7 + 2,5
∴ l (RT) = 5,6

(iii) 1 4 90 10,
90 (ХЗ) = 37; 1 (XY) = 7.
Теперь 1 (XZ) = 1 (XY) + 1 (YZ)
Итак, 1 (YZ) − 1 ( 1 X ) l (XY) = 37 − 7
∴ l (YZ) = 27

Страница № 5:

Вопрос 7:

Какая фигура образована тремя не лежащими на одной прямой точками?

Ответ:

Треугольник образован тремя отрезками, соединяющими три точки, не лежащие на одной прямой.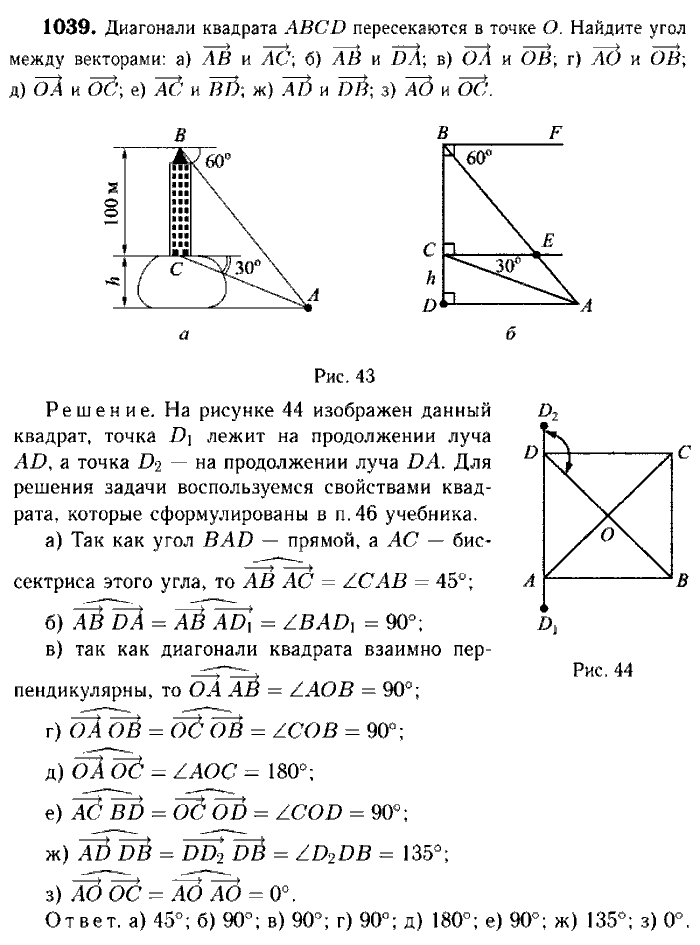

A, B и C — три неколлинеарные точки. Когда A, B и C соединяются, мы получаем ∆ABC.

Страница № 7:

Вопрос 1:

В следующей таблице показаны точки на числовой прямой и их координаты. Решите, конгруэнтны ли пары отрезков, приведенные под таблицей, или нет.

Точка	А	Б	С	Д	Е
Координата	-3	5	2	-7	9

(i) сегмент DE и сегмент AB (ii) сегмент BC и сегмент AD (iii) сегмент BE и сегмент AD

Ответ:

В данной таблице

Точка	А	Б	С	Д	Е
Координата	-3	5	2	-7	9

(i) Координаты точек D и E равны −7 и 9 соответственно. Мы знаем, что 9 > −7.
∴ l (DE) = 9 − (−7) = 9 + 7 = 16
Координаты точек A и B равны −3 и 5 соответственно. Мы знаем, что 5 > −3.
∴ l (AB) = 5 − (−3) = 5 + 3 = 8
Поскольку l (DE) ≠ l (AB), значит, сегмент DE ≇ сегмент AB.

(ii) Координаты точек B и C равны 5 и 2 соответственно. Мы знаем, что 5 > 2.
∴ l (BC) = 5 − 2 = 3
Координаты точек A и D равны −3 и −7 соответственно. Мы знаем, что −3 > −7.
∴ l (AD) = −3 − (−7) = −3 + 7 = 4
Так как l (BC) ≠ l (AD), поэтому сегмент BC ≇ сегмент AD.

(iii) Координаты точек B и E равны 5 и 9.соответственно. Мы знаем, что 9 > 5.
∴ l (BE) = 9 − 5 = 4
Координаты точек A и D равны −3 и −7 соответственно. Мы знаем, что −3 > −7.
∴ l (AD) = −3 − (−7) = −3 + 7 = 4
Поскольку l (BE) = l (AD), значит, seg BE ≅ seg AD.

Страница № 7:

Вопрос 2:

Точка M является серединой отрезка AB. Если АВ = 8, то найдите длину АМ.

Ответ:

Имеем l (AB) = 8,
Так как M является серединой отрезка AB, то
l (AM) = 12 из l (AB)
∴ l (AM) = 12 × 8 = 4
Итак, длина AM равна 4

Страница № 7:

Вопрос 3:

Точка P является серединой отрезка CD. Если CP = 2,5, найдите l (CD).

Ответ:

Имеем l (CP) = 2,5.
Поскольку P является серединой отрезка CD, то
l (CP) = 12 из l (CD)
∴ l (CD) = 2 × l (CP) = 2 × 2,5 = 5
Итак, длина CD равна 5.

Страница № 7:

Вопрос 4:

Если AB = 5 см, BP = 2 см и АП = 3,4 см, сравните отрезки.

Ответ:

Имеем l (АВ) = 5 см; л (ВР) = 2 см; l (AP) = 3,4 см
Мы знаем, что 5 > 3,4 > 2.
Итак, l (AB) > l (AP) > l (BP).
∴ сегмент AB > сегмент AP > сегмент BP.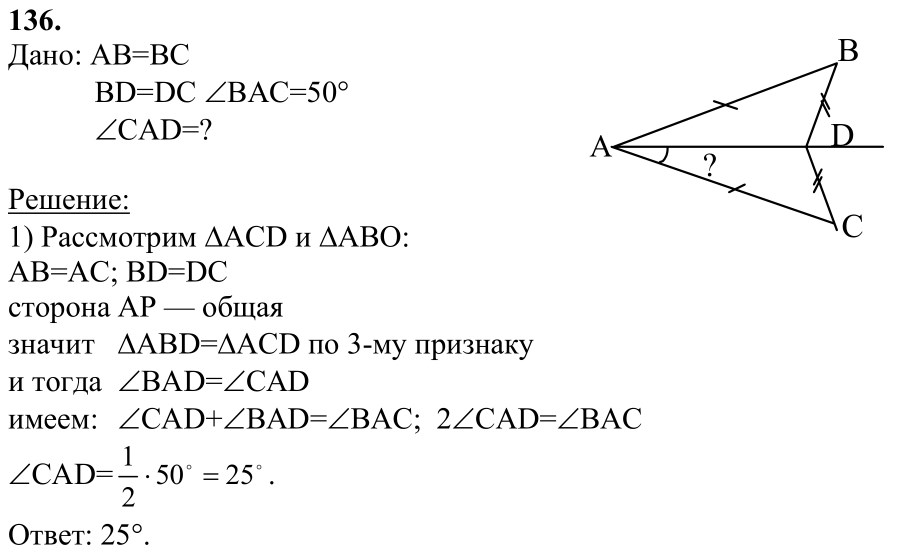

Страница № 8:

Вопрос 5:

Напишите ответы на следующие вопросы со ссылкой на данный рисунок.

(i) Напишите название луча, противоположного лучу RP.

(ii) Запишите множество пересечений луча PQ и луча RP.
(iii) Напишите объединение луча PQ и луча QR.

(iv) Укажите лучи, подмножеством которых является сегмент QR.

(v) Запишите пару противоположных лучей с общим концом R.

(vi) Запишите любые два луча с общим концом S.

(vii) Запишите множество пересечений луча SP и луча ST.

Ответ:

(i) Ray RS или Ray RT

(ii) Ray PQ

(iii) Ray QR

(iv) Ray QR, Ray Q Ray и т. д.

и Ray RT и т. д.

(vi) Ray ST и Ray SR и т. д.

(vii) Point S

Номер страницы 8:

Вопрос 6:

Ответьте на вопросы, используя заданную цифру.

(i) Укажите точки, равноудаленные от точки B.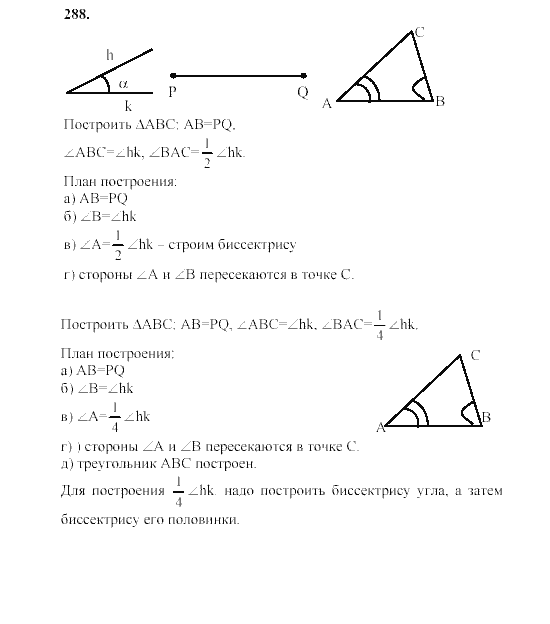

(ii) Запишите пару точек, равноудаленных от точки Q.

(iii) Найдите d (U,V), d (P,C), d (V,B), d (У, Л).

Ответ:

(i) Координаты точек B и C равны 2 и 4 соответственно. Мы знаем, что 4 > 2.
∴ d (B, C) = 4 − 2 = 2
Координаты точек B и A равны 2 и 0 соответственно. Мы знаем, что 2 > 0.
∴ d (B, A) = 2 − 0 = 2
Поскольку d (B, A) = d (B, C), то точки A и C равноудалены от точки B.
Координаты точек B и D равны 2 и 6 соответственно. Мы знаем, что 6 > 2.
∴ d (B, D) = 6 − 2 = 4
Координаты точек B и P равны 2 и −2 соответственно. Мы знаем, что 2 > −2.
∴ d (B, P) = 2 − (−2) = 2 + 2 = 4
Поскольку d (B, D) = d (B, P), то точки D и P равноудалены от точки B.

(ii) Координаты точек Q и U равны -4 и -5 соответственно. Мы знаем, что −4 > −5.
∴ d (Q, U) = −4 − (−5) = −4 + 5 = 1
Координаты точек Q и L равны −4 и −3 соответственно.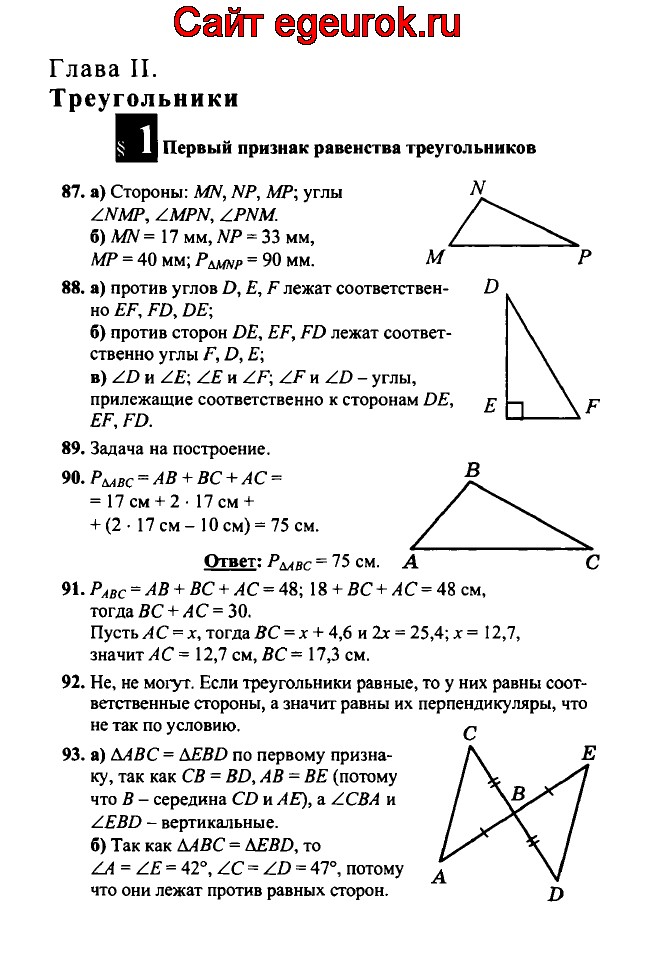 Мы знаем, что −3 > −4.
∴ d (Q, L) = −3 − (−4) = −3 + 4 = 1
Поскольку d (Q, U) = d (Q, L), то точки U и L равноудалены от точки Q.
Координаты точек Q и R равны -4 и -6 соответственно. Мы знаем, что −4 > −6.
∴ d (Q, R) = −4 − (−6) = −4 + 6 = 2
Координаты точек Q и P равны −4 и −2 соответственно. Мы знаем, что −2 > −4.
∴ d (Q, P) = −2 − (−4) = −2 + 4 = 2
Поскольку d (Q, R) = d (Q, P), то точки R и P равноудалены от точки Q.

(iii) Координаты точек U и V равны −5 и 5 соответственно. Мы знаем, что 5 > −5.
∴ d (U, V) = 5 − (−5) = 5 + 5 = 10
Координаты точек P и C равны −2 и 4 соответственно. Мы знаем, что 4 > −2.
∴ d (P, C) = 4 − (−2) = 4 + 2 = 6
Координаты точек V и B равны 5 и 2 соответственно. Мы знаем, что 5 > 2,
∴ d (V, B) = 5 − 2 = 3
Координаты точек U и L равны −5 и −3 соответственно. Мы знаем, что −3 > −5.
∴ d (U, L) = −3 − (−5) = −3 + 5 = 2

Страница № 11:

Вопрос 1:

Запишите следующие утверждения в форме «если-то».

(i) Противоположные углы параллелограмма равны.

(ii) Диагонали прямоугольника равны.

(iii) В равнобедренном треугольнике отрезок, соединяющий вершину и середину основания, перпендикулярен основанию.

Ответ:

(i) Если четырехугольник является параллелограммом, то противоположные углы этого четырехугольника равны.

(ii) Если четырехугольник является прямоугольником, то диагонали этого четырехугольника конгруэнтны.

(iii) Если треугольник равнобедренный, то отрезок, соединяющий вершину и середину основания, перпендикулярен основанию.

Страница № 11:

Вопрос 2:

Напишите обратные выражения следующих утверждений.

(i) Наклонные углы, образованные двумя параллельными прямыми и их секущей, равны.

(ii) Если пара внутренних углов, образованных секущей двух прямых, является дополнительной, то эти прямые параллельны.

(iii) Диагонали прямоугольника равны.

Ответ:

(i) Если альтернативные углы, образуемые секущей с двумя прямыми, равны, то прямые параллельны.

(ii) Если две параллельные прямые пересекаются секущей, то пара внутренних углов является дополнительной.

(iii) Если диагонали четырехугольника равны, то этот четырехугольник является прямоугольником.

Страница № 11:

Вопрос 1:

Выберите правильный вариант из ответов на приведенные ниже вопросы.

(i) Сколько средних точек имеет отрезок?

(A) только одна (B) две (C) три (D) много

(ii) Сколько точек находится на пересечении двух различных прямых?

(А) бесконечное (Б) два (В) одно (Г) ни одного

(iii) Сколько прямых определяется тремя различными точками?

(А) два (Б) три (В) один или три (Г) шесть

(iv) Найти d (А, В), если координаты А и В равны — 2 и 5 соответственно.

(A)-2 (B) 5 (C) 7 (D) 3

(v) Если P — Q — R и d (P,Q) = 2, d (P, Q) R) = 10, затем найдите d (Q,R).
(A) 12 (B) 8 (C) 96 (D) 20

Ответ:

(i) Каждый сегмент имеет одну и только одну среднюю точку.
Значит, правильный ответ — вариант (А).

(ii) Известно, что две различные прямые пересекаются в одной точке.
Следовательно, правильный ответ — вариант (С).

(iii) Рассмотрим 3 различные точки как P, Q и R.
Предположим, что точки P, Q и R лежат на одной прямой.

Итак, только одна линия определяется точками P, Q и R.
Предположим, что точки P,Q и R не лежат на одной прямой.

Итак, три линии можно определить по точкам P, Q и R.
Следовательно, правильный ответ — вариант (С).

(iv) Координаты точек A и B равны -2 и 5 соответственно. Мы знаем, что 5 > -2.
∴ d (A, B) = 5 − (−2) = 5 + 2 = 7
Следовательно, правильный ответ — вариант (C).

(v) Дано, что точка Q находится между точкой P и точкой R.

Имеем, d (P,Q) = 2; d (P,R) = 10
Теперь, d (P,R) = d (P,Q) + d (Q,R)
∴ d (Q,R) = d (P,R) − d (P,Q) = 10 − 2 = 8
Следовательно, правильный ответ — вариант (B).

Страница № 11:

Вопрос 2:

На числовой прямой координаты точек P, Q, R равны 3,- 5 и 6 соответственно. Укажите аргументированно, верны или неверны следующие утверждения.

(i) d (P,Q) + d (Q,R) = d (P,R)
(ii) d (P,R) + d (R ,Q) = d (P,Q)

(iii) d (R,P) + d (P,Q) = d (R,Q)

(iv) d (P,Q) — d (P,R) = d (Q,R)

Ответ:

Координаты точек P и Q равны 3 и −5 соответственно. Мы знаем, что 3 > −5.
Теперь, d (P, Q) = 3 − (−5) = 3 + 5 = 8
Координаты точек Q и R равны −5 и 6 соответственно.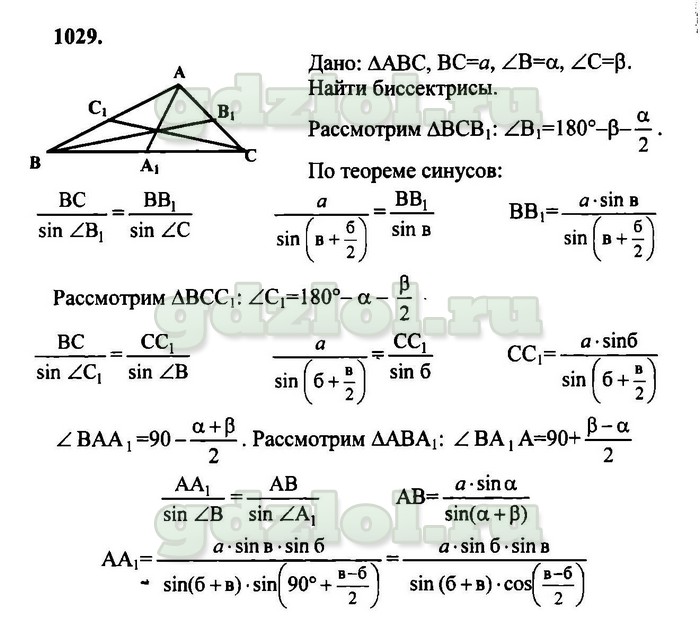 Мы знаем, что 6 > −5.
Теперь, d (Q, R) = 6 − (−5) = 6 + 5 = 11
Координаты точек P и R равны 3 и 6 соответственно. Мы знаем, что 6 > 3,
Сейчас, d (P, R) = 6 − 3 = 3

(i) d (P, Q) + d (Q, R) = 8 + 11 = 19; d (P, R) = 3
Итак, d (P, Q) + d (Q, R) ≠ d (P, R)
Следовательно, данное утверждение неверно.

(ii) d (P, R) + d (R, Q) = d (P, R) + d (Q, R) = 3 + 11 = 14; d (P, Q) = 8
Итак, d (P, R) + d (R, Q) ≠ d (P, Q)
Следовательно, данное утверждение неверно.

(iii) d (R,P) + d (P,Q) = d (P, R) + d (P,Q) = 3 + 8 = 11; d (R,Q) = d (Q, R) = 11
Итак, d (R,P) + d (P,Q) = d (R,Q)
Отсюда , данное утверждение верно.

(iv) d (P,Q) — d (P,R) = 8 − 3 = 5; d (Q,R) = 11
Итак, d (P,Q) — d (P,R) ≠ d (Q,R)
Следовательно, данное утверждение неверно.

Страница № 11:

Вопрос 3:

Ниже приведены координаты некоторых пар точек. Отсюда найдите расстояние между каждой парой.

(i) 3, 6

(ii) − 9, — 1

(iii)- 4, 5

(iv) x,- 2
(v) x + 3, x- 3
(vi) -25,-47
(vii) 80, — 85

Ответ:

(i) Пусть координаты A и B равны 3 и 6 соответственно. Мы знаем, что 6 > 3
d (A, B) = 6 − 3 = 3

(ii) Пусть координаты C и D равны -9 и -1 соответственно. Мы знаем, что −1 > −9
d (C, D) = −1 − (−9) = −1 + 9 = 8

(iii) Пусть координаты E и F равны −4 и 5 соответственно. Мы знаем, что 5 > −4
d (E, F) = 5 − (−4) = 5 + 4 = 9

(iv) Пусть координаты P и Q равны x и −2 соответственно. Предположим, что x > 0, тогда x > −2.
d (P, Q) = x — (-2) = x + 2

(v) Пусть координаты R и S равны x + 3 и x — 3 соответственно.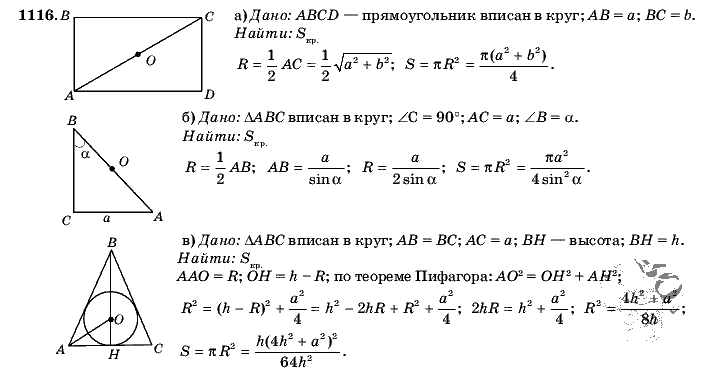 Предположим, х > 0, тогда х + 3 > х — 3
d (R, S) = ( х + 3) — ( х х 9 — 0 1) = − x + 3 = 2x

(vi) Пусть координаты L и M равны −25 и −47 соответственно. Мы знаем, что −25 > −47
d (L, M) = −25 − (−47) = −25 + 47 = 22

(vii) Пусть координаты G и H равны 80 и −85 соответственно. Мы знаем, что 80 > −85
d (G, H) = 80 − (−85) = 80 + 85 = 165

Страница № 12:

Вопрос 4:

Координата точки P на числовая строка равна -7. Найдите координаты точек на числовой прямой, которые находятся на расстоянии 8 единиц от точки P.

Ответ:

Координаты точки P на числовой прямой равны −7. Теперь будет две точки, одна слева от точки P, а другая справа от точки P на числовой прямой, которые находятся на расстоянии 8 единиц от точки P.
Пусть точка R находится справа от точки P, а точка Q — слева от точки P, каждая на расстоянии 8 единиц от точки P.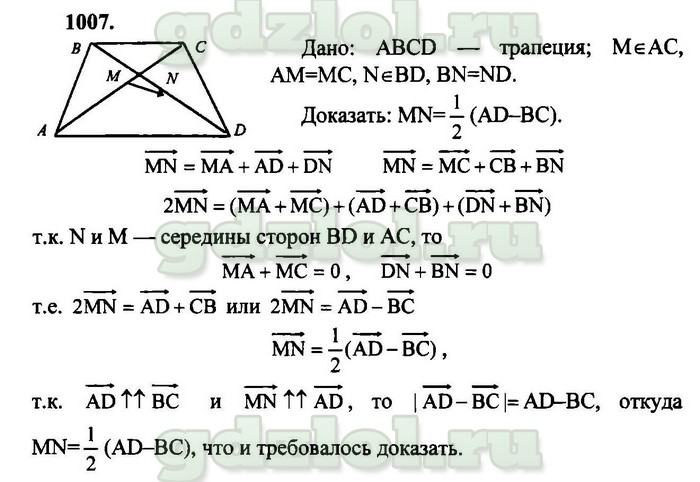
Координата точки R будет больше, а координата точки Q будет меньше по сравнению с координатой точки P.
Теперь d (P, R) = 8
Итак, координата R − координата P = 8
∴ координата точки R = 8 + координата P = 8 + (−7) = 8 − 7 = 1
Кроме того, d (Q, P) = 8
Итак, координата P − координата Q = 8
∴ координата Q = координата P − 8 = −7 − 8 = −15

Следовательно, координаты искомых точек на числовой прямой, находящихся на расстоянии 8 единиц от точки P равны 1 и -15.

Страница № 12:

Вопрос 5:

Ответьте на следующие вопросы.

(i) Если A — B — C и d (A,C) = 17, d (B,C) = 6,5, то d (A,B) = ?

(ii) Если P — Q — R и d (P, Q) = 3,4, d (Q,R)= 5,7, тогда d (P,R) = ?

Ответ:

(i)

Имеем, d (А, С) = 17; d (B, C) = 6,5
Сейчас, d (A, C) = d (A, B) + d (B, C)
Итак, d (A, B) = d (A, C) − d (B, C) = 17 − 6,5
∴ d (A, B) = 10,5

(ii)

Имеем, 5 d Q) = 3,4; d (Q, R) = 5,7
Теперь d (P, R) = d (P, Q) + d (Q, R) = 3,4 + 5,7
∴ d (P, R) = 9,1

Страница № 12:

Вопрос 6:

5 Координата-90 точка А на числовой прямой равна 1.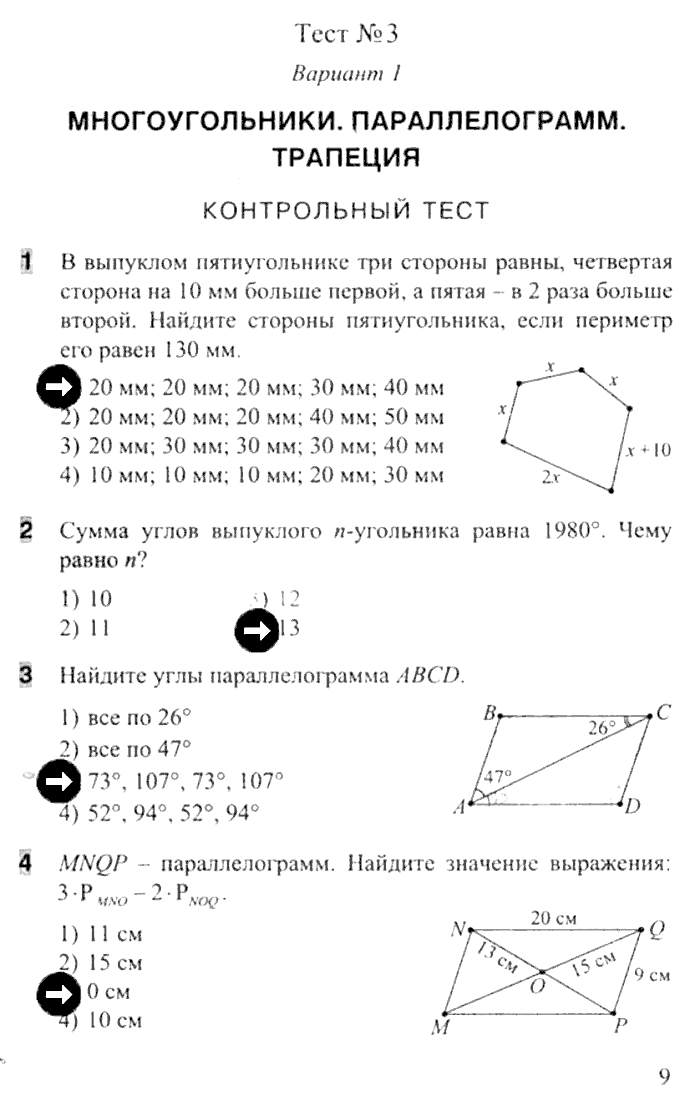 Каковы координаты точек на числовой прямой, которые находятся на расстоянии 7 единиц от А?

Ответ:

Координаты точки А на числовой прямой равны 1. Теперь будет две точки, одна слева от точки А, а другая справа от точки А на числовой прямой, которые на расстоянии 7 единиц от точки А.
Пусть точка C находится справа от точки A, а точка B — слева от точки A, каждая на расстоянии 7 единиц от точки A.
Координата точки C будет больше, а координата точки B будет меньше по сравнению с координатой точки A.
Теперь d (A, C) = 7
Итак, координата C − координата A = 7
∴ координата C = 7 + координата A = 7 + 1 = 8
Кроме того, d (B, A) = 7
Итак, координата A − координата B = 7
∴ координата B = координата A − 7 = 1 − 7 = −6

Следовательно, координаты искомых точек на числовой прямой, находящихся на расстоянии 7 единиц от точки A равны 8 и −6.

Страница № 12:

Вопрос 7:

Напишите следующие утверждения в условной форме.

(i) Каждый ромб является квадратом.

(ii) Углы в линейной паре являются дополнительными.

(iii) Треугольник – это фигура, образованная тремя сегментами.

(iv) Число, имеющее только два делителя, называется простым числом.

Ответ:

(i) Если данный четырехугольник является квадратом, то он должен быть ромбом.
(ii) Если данные два угла образуют линейную пару, то они являются дополнительными.
(iii) Если данная фигура является треугольником, то она образована тремя сегментами.
(iv) Если данное число имеет только два делителя, то это простое число.

Страница № 12:

Вопрос 8:

Напишите обратное каждому из следующих утверждений.

(i) Если сумма мер углов фигуры равна 180 ⁰ , то фигура является треугольником.

(ii) Если сумма мер двух углов равна 90 ⁰, то они дополняют друг друга.

(iii) Если соответствующие углы, образованные секущей двух прямых, равны, то эти две прямые параллельны.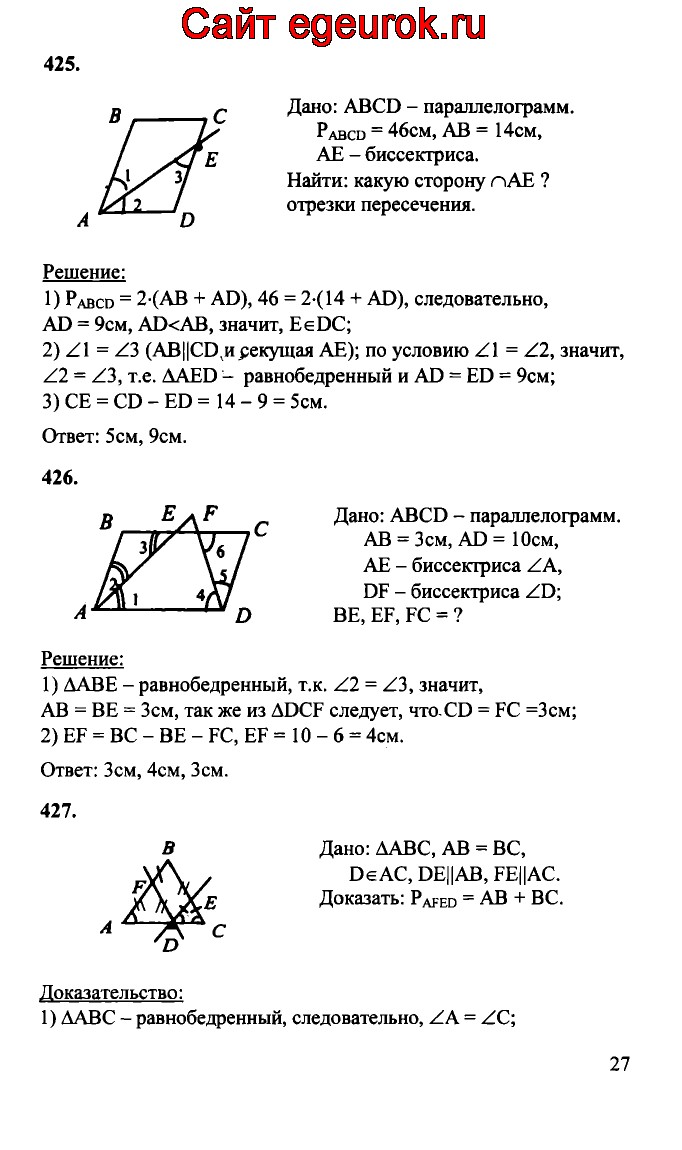

(iv) Если сумма цифр числа делится на 3, то это число делится на 3.

Ответ:

(i) Если данная фигура является треугольником, то сумма мер его углов равна 180 ⁰ .

(ii) Если данные два угла дополняют друг друга, то сумма мер двух углов равна 90 ⁰ .

(iii) Если данные две прямые параллельны, то соответствующие углы, образованные секущей двух прямых, равны.

(iv) Если данное число делится на 3, то сумма цифр этого числа делится на 3.

Страница № 12:

Вопрос 9:

Напишите антецедент (данная часть) и консеквент (часть, которую нужно доказать) в следующих утверждениях.

(i) Если все стороны треугольника равны, то равны и все его углы.

(ii) Диагонали параллелограмма делят друг друга пополам.

Ответ:

(i) Предшественник: Все стороны треугольника конгруэнтны.
Следствие: все его углы равны.

(ii) Утверждение можно записать в условной форме так: «Если данный четырехугольник является параллелограммом, то его диагонали делят друг друга пополам.
Антецедент : Данный четырехугольник является параллелограммом.
Следствие: его диагонали делят друг друга пополам.

Страница № 12:

Вопрос 10:

Нарисуйте помеченный рисунок, показывающий информацию в каждом из следующих утверждений, и напишите антецедент и консеквент.

(i) Два равносторонних треугольника подобны.

(ii) Если углы в линейной паре равны, то каждый из них прямой.

(iii) Если высоты, проведенные на двух сторонах треугольника, равны, то эти две стороны равны.

Ответ:

(i) Данное утверждение можно записать в условной форме так: «Если данные два поезда равносторонние, то они подобны».
Предшественник: данные два треугольника являются равносторонними.
Следствие: они похожи.

Здесь ∆ABC и ∆PQR — равносторонние треугольники, поэтому они подобны друг другу.

(ii) Предшественник: Углы в линейной паре конгруэнтны.
Следствие : Каждый из них является прямым углом.

Здесь ∠AOC и ∠BOC, образующие линейную пару, конгруэнтны друг другу, поэтому каждый из них является прямым углом.

(iii) Предпосылка: высоты нарисованные на двух сторонах треугольника конгруэнтны.
Следствие: эти две стороны конгруэнтны.

Здесь BL и CM — это высоты, проведенные по двум сторонам AC и AB соответственно от ∆ABC, и они конгруэнтны, поэтому сторона AB конгруэнтна стороне AC.

Рабочая тетрадь по геометрии и измерениям (9 класс, Онтарио, математика, MTh2W) 2021 Учебная программа

Эта рабочая тетрадь содержит рабочие листы Strand E: Geometry and Measurement для нового 2021 de-streamed Учебная программа по математике Онтарио для 9 класса (MTh2W) . Эта рабочая тетрадь содержит рабочие листы с пояснениями, рабочие и практические листы, викторину, исследовательское задание по геометрии / измерениям, проект дизайна поля для мини-гольфа и завершающий модульный тест.

Темы включают треугольники, четырехугольники, окружности, теорему Пифагора и вычисление периметра, площади, площади поверхности, объема и окружности. Эта рабочая тетрадь включает проверки, которые объединяют социально-эмоциональные ожидания обучения новой математической программы.

Этот блок можно распечатать для личного обучения или использовать в виртуальном обучении. Учителя, желающие использовать эту рабочую тетрадь в Интернете, могут загрузить рабочую тетрадь или отдельные страницы непосредственно на свою виртуальную учебную платформу с помощью цифрового инструмента Easel от TPT. Учителя, использующие инструмент Easel, могут собирать выполненные задания в цифровом виде.

⭐ Также доступно на французском языке: Cahier de géométrie et mesure (Mathématiques Ontario de 9e Année) Французский MTh2W

Ищу обучающих слайдов в дополнение к этому разделу? Ознакомьтесь с нашими Google Slides: Geometry and Measurement Slides for Google Slides™ (9 класс Math MTh2W)

Этот ресурс включает:

64-страничную рабочую тетрадь для Strand E: Geometry and Measurement
КЛЮЧ ПОЛНОГО ОТВЕТА

Содержание

1. Титульная страница

2. Содержание

3. Диаграмма KWL

4. Постановка целей

5. Введение в геометрию

6. Плоские и объемные фигуры

7. Практический пример: размеры хоккейной площадки

8. Вопросы из практического примера

9. Введение в измерения

10. Свойства треугольников

11. Классификация треугольников по углам

20 10 30 90 90 Классификация треугольников по длине стороны

13. Свойства углов

14. Свойства углов Практика

15. Свойства углов Практика

16. Свойства четырехугольников

17. Свойства четырехугольников Практика

18. Практика четырехсторонних свойств

19. Углы Viz

20. Углы.

26. Метрические измерения в имперские — Практика

27. Теорема Пифагора

28. Теорема Пифагора. Практика

29. Теорема Пифагора.0003

30. Пифагорская теорема Проблемы слова

31. ПИТАГОРЕВНАЯ Теорема Викторина

32. Свойства круга с использованием теоремы пифагореей

33. Расчет Периметра

34. Расчет по периметрам

35. Расчет окружающей

37. Расчет площади: круги

38. Расчет площади: треугольники

39. Расчет объема

40. Расчет площади поверхности

41. Объем и площадь поверхности Практика

42. Объем и площадь поверхности Практика

43. Расчет объема Практика

44. Расчет объемных словесных задач

45. Расчет объема объемных словесных задач

90 Объемных слов 46. Расчет объемных слов

47. Обзор исследовательского проекта по геометрии

48. Страница планирования

49. Организатор источников исследований

50. Организатор вопросов исследования

51. Организатор вопросов исследования

52. Исследовательский проект Рубрика

53. Геометрия мини -гольф. Обзор проекта по гольфу

54. План проектирования

55. План строительства

56. Расчеты проекта Mini Golf

57.