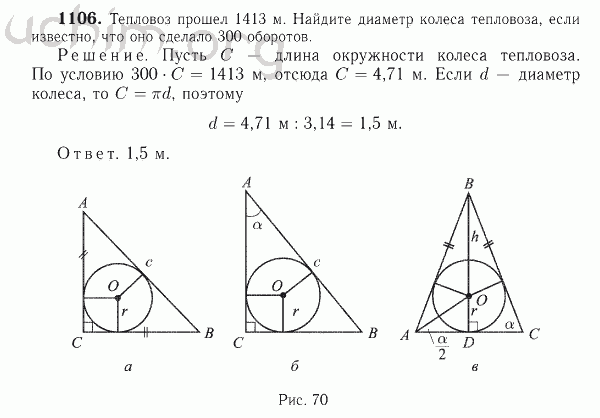
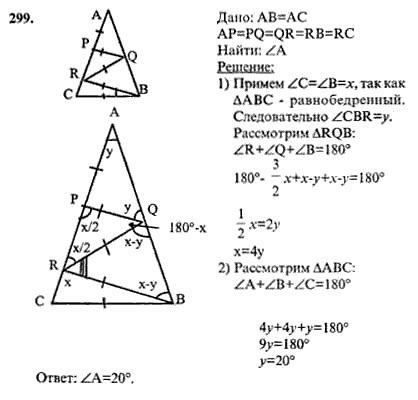
ГДЗ по геометрии для 9 класса Солтан Г.Н.
Задачи. Решения
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281 282 283 284 285 286 287 288 289 290 291 292 293 294 295 296 297 298 299 300 301 302 303 304 305 306 307 308 309 310 311 312 313 314 315 316 317 318 319 320 321 322 323 324 325 326 327 328 329 330 331 332 333 334 335 336 337 338 339 340 341 342 343 344 345 346 347 348 349 350 351 352 353 354 355 356 357 358 359 360 361 362 363 364 365 366 367 368 369 370 371 372 373 374 375 376 377 378 379 380 381 382 383 384 385 386 387 388 389 390 391 392 393 394 395 396 397 398 399 400 401 402 403 404 405 406 407 408 409 410 411 412 413 414 415 416 417 418 419 420 421 422 423 424 425 426 427 428 429 430 431 432 433 434 435 436 437 438 439 440 441 442 443 444 445 446 447 448 449 450 451 452 453Практические задания.
Решения стр.22
стр.29
стр.35
стр.39
стр.45
стр.73
стр.86
стр.104
стр.113
стр.124
стр.140
стр.153Задания для самопроверки. Решения
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53
Решения»>
Приложение 2. РешенияТ1. Понятие вектора. Коллинеарные векторы
1 2 3Т2. Сложение и вычитание векторов
1 2 3 4Т3. Умножение вектора на число
1Т4. Координаты вектора
1 2 3 4 5
Угол между векторами»>
Т5. Угол между векторами 1
2
3
4
5Т6. Применение векторов к решению задач
1 2 3 4 5 6 7Т7. Преобразование плоскости. Движение
1 2 3 4 5 6 7 8 9 10
Подобие треугольников»>
Т8. Подобие треугольников 1Т9. Признаки подобия
1 2Т10. Теорема синусов
1 2 3Т11. Теорема косинусов
1 2 3Т12. Углы вписанные в окружность
1 2
Свойства касательной и секущей, пересекающихся хорд окружности»>
Т13. Свойства касательной и секущей, пересекающихся хорд окружности 1
2Т14. Нахождение длин сторон и площадей правильных многоугольников
1 2Т15. Длина окружности дуги
1 2Т16. Площадь круга, его сектора и сегмента
1 2Т17.
Повторение курса геометрии 9 класса 1
2
3
4
5
7Геометрия Солтан 9 класс 2020 Упражнение 35 ГДЗ(дүж) решебник KZGDZ.COM
I. Векторы 1. Понятие вектора. Коллинеарные векторы Упражнение 35
← Предыдущий Следующий →
Повторение курса геометрии 8 класса.
Упражнение
6789101112131415171920212223242526272829
I. Векторы
1. Понятие вектора. Коллинеарные векторы
Упражнение
3334353637383941
2. Сложение и вычитание векторов
Упражнение
4345464950515253545556
3. Умножение вектора на число. Критерий коллинеарности двух векторов
Упражнение
6162636466676869707172
4.
Разложение вектора по двум неколлинеарным векторам.Упражнение
737475767778798081828384
5. Координаты вектора.
Упражнение
87889093949596979899100101
6. Угол между векторами. Скалярное произведение двух векторов.
Упражнение
103104105
106107108109110112113114115116117118119120
7. Применение векторов при решении задач
Упражнение
121122124126127128
8. Упражнения на повторение раздела «Векторы»
Упражнение
129131132133134135136138139140141142144145
Проверь себя!
Упражнение
148 3B148 4B148 5C
II. Преобразования плоскости.
9. Преобразование плоскости. Движение и его виды
Упражнение
149150151153154155157
10.
Применение движений к решению задачУпражнение
158159160161164165
11. Преобразования гомотетии и подобия, их свойства
Упражнение
166167168169170171172
12. Подобные треугольники
Упражнение
174175176177178179180181182183184185186187188189190
13. Подобные многоугольники
Упражнение
192193194195196197
198199200
14. Применение гомотетии и подобия при решении задач.
Упражнение
202203204205206207208
15. Упражнения на повторение раздела «Преобразования плоскости»
Упражнение
209210211212213214215216217218219220221222223224
Проверь себя!
Упражнение
225 4B225 5С
III. Решение треугольников.
16.
Теорема синусовУпражнение
226227228229230231232233234235
17. Теорема косинусов
Упражнение
236237238239240241242243244245246
18. Решение треугольников
Упражнение
247248249250251253254255256257258259
19. Углы, вписанные в окружность, и их свойства
Упражнение
260262263264265266267268269
20. Свойства касательной и секущей, пересекающихся хорд окружности
Упражнение
270271272273274275276277278279
21. Применение тригонометрии к выводу формул площадей треугольника и решению задач
Упражнение
280281282283284285286287288289290291292293294295296297298299300301302303
22. Упражнения на повторение раздела «Решение треугольников»
Упражнение
304305306307308309310311312313
Проверь себя!
Упражнение
314 4В
IV.
Окружность. Многоугольники23. Вписанные в окружность четырехугольники
Упражнение
316317318319320321
24. Описанные около окружности четырехугольники
Упражнение
322323324325326327328329330331332333334
25. Правильные многоугольники. Окружности, описанная около правильного многоугольника и вписанная в него
Упражнение
336337338339340341342
26. Нахождение длин сторон и площадей правильных многоугольников.
Упражнение
343344345346347348349
27. Длина окружности и ее дуги
Упражнение
351352353354355356357358359360361362
363364365366367368
28. Площадь круга, его сектора и сегмента
Упражнение
370371372373374375376377378379380381382383384385
29.
Упражнения на повторение раздела «Окружность. Многоугольники»Упражнение
386387388389390391392393394395396397398399400401402403404405406407408409
Повторение курса геометрии 9 класса
Упражнение
411412413414415416417418419420421422423424425426427428430431433434435436437438439440441442443444445446
447448449450451452
NCERT Solutions for Class 9 Math Chapter 3 Coordinate Geometry
NCERT Solutions Class 9 Math Chapter 3 — CBSE Free PDF Download
Решения NCERT для класса 9 по математике Глава 3 Координатная геометрия полезны для учащихся, поскольку они помогают им получить хорошие оценки на экзаменах. Мы в BYJU’S стремимся помочь учащимся с подробными решениями по главам, чтобы учащиеся легко понимали концепции. Решая вопросы из NCERT Solutions for Class 9 Maths, учащиеся смогут прояснить все свои понятия о «координатной геометрии».
Помимо этого, другие ресурсы, используемые, чтобы помочь студентам подготовиться к экзаменам CBSE и получить хорошие оценки, включают заметки NCERT, образцы работ, учебники, работы предыдущих лет, примеры вопросов и так далее.
Решения NCERT разработаны экспертами в данной области, которые собрали типовые вопросы, охватывающие все вопросы упражнений из учебника. Решения NCERT содержат подробные шаги, объясняющие все проблемы, которые подпадают под главу 3 «Координатная геометрия» учебника NCERT для класса 9. При создании решений NCERT мы следили за последним обновлением учебной программы CBSE на 2022–2023 годы, и они оформлены в соответствии с образцом экзамена Совета CBSE.
Класс 9 Математика Глава 3 Темы координатной геометрии
Из 80 баллов, выставленных на экзаменах CBSE Class 9, вопросы примерно с 6 баллами будут относиться к координатной геометрии. Кроме того, студенты могут ожидать, что по крайней мере около 2-3 вопросов из этого раздела обязательно придут на экзамен, как видно из предыдущих тенденций.
3 вопроса получили 1, 2 и 3 балла соответственно, таким образом, в сумме получается 6 баллов из единиц Координатная геометрия . Основные темы, затронутые в этой главе, включают
- 3.1 Введение
- 3.2 Декартова система
- 3.3 Нанесение точки на плоскости, если ее координаты заданы
Зачем нам учить математику 9 класса, главу 3, координатную геометрию?
Координатная геометрия — это интересный предмет, на котором учащиеся узнают о положении объекта на плоскости, узнают о координатах или концепциях декартовой плоскости и т. д. Например, «представьте ситуацию, когда вы знаете только номер улицы дома вашего друга. Вам было бы легко найти ее дом или было бы проще, если бы у вас был и номер дома, и номер улицы? Есть много других ситуаций, в которых для нахождения точки нам может потребоваться описать ее положение со ссылкой на более чем одну линию. Студенты могут узнать больше об этом из главы 3 из 9.0005 Учебники NCERT .
И здесь мы предоставляем им решения на все вопросы, касающиеся этой темы, в Решениях NCERT для математики класса 9.
Ключевые особенности решений NCERT для математики класса 9. Глава 3. Координатная геометрия
- Помощь в воспитании у учащихся правильного отношения к учебе
- Сделать основы главы очень понятными для учащихся
- Повышение эффективности за счет решения упражнений по главам
- Все вопросы собраны с подробными пояснениями
- Учащиеся могут решать эти решения в своем собственном темпе и практиковаться
Для лучшего понимания концепции координатной геометрии мы в BYJU’S также предоставили решения для других учебников. В основном они направлены на улучшение аналитических и логических способностей мышления, которые важны с точки зрения экзамена.
Загрузите PDF-файл NCERT Solutions for Class 9 Math Chapter 3 — Coordinate Geometry
Список упражнений по математике для 9 класса, глава 3
Список упражнений по координатной геометрии для 9 класса по математике, глава 3, приведен ниже.
- Упражнение 3.1 Решения 2 вопроса (1 вопрос с длинным ответом, 1 основной вопрос с 2 подвопросами под ним.)
- Упражнение 3.2 Решения 2 вопроса (1 основной вопрос с 3 подвопросами, 1 основной вопрос с 8 подвопросами.)
- Упражнение 3.3 Решения 2 вопроса (2 вопроса с длинными ответами)
Доступ к ответам на NCERT, класс 9, математика, глава 3. Координатная геометрия
Упражнение 3.1 Страница: 53
1. Как вы объясните другому человеку положение настольной лампы на вашем рабочем столе?
Решение:
Чтобы описать положение настольной лампы на рабочем столе, возьмем две линии, перпендикулярную и горизонтальную. Рассматривая стол как плоскость (оси x и y) и принимая перпендикулярные линии за ось Y и горизонтальные за ось X, соответственно, возьмите один угол стола за начало координат, где обе оси X и Y пересекаются друг с другом. Теперь длина стола — это ось Y, а ширина — ось X. От начала координат соедините линию с настольной лампой и отметьте точку.
Расстояния точки от обеих осей X и Y должны быть рассчитаны, а затем должны быть записаны в терминах координат.
Расстояние точки от оси X и оси Y равно x и y соответственно, поэтому настольная лампа будет находиться в координатах (x, y).
Здесь (х, у) = (15, 25)
2. (План улиц): В городе есть две главные дороги, которые пересекаются в центре города. Эти две дороги проходят по направлениям север-юг и восток-запад. Все остальные улицы города проходят параллельно этим дорогам на расстоянии 200 м друг от друга. В каждом направлении по 5 улиц. Используя 1 см = 200 м, нарисуйте в тетради модель города. Представляйте дороги/улицы отдельными линиями.
В вашей модели много перекрестков. Конкретный перекресток образован двумя улицами, одна из которых проходит в направлении север-юг, а другая — в направлении восток-запад. Каждый перекресток обозначается следующим образом: Если 2-я улица, идущая в направлении север-юг, и 5-я улица, идущая в направлении восток-запад, пересекаются на каком-то перекрестке, то мы будем называть этот перекресток (2, 5).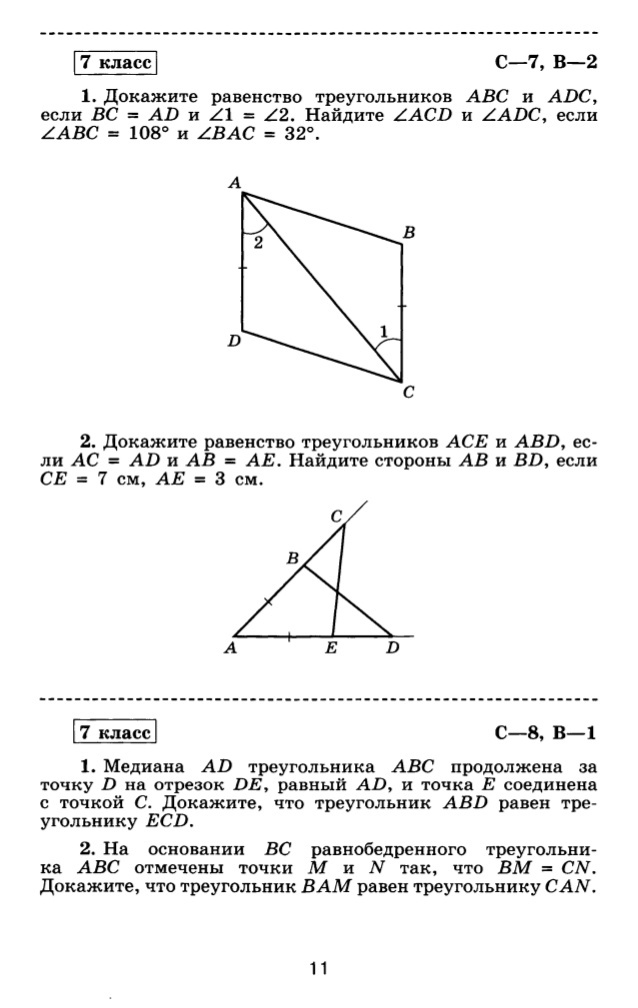
Используя это соглашение, найдите:
(i) сколько перекрестков можно назвать (4, 3)?
(ii) сколько перекрестков можно назвать (3, 4)?
Решение:
- Только одна улица может называться (4,3) (как видно из рисунка).
- Только одна улица может называться (3,4) (как видно из рисунка).
Упражнение 3.2 Страница: 60
1. Напишите ответ на каждый из следующих вопросов.
(i) Как называются горизонтальная и вертикальная линии, проведенные для определения положения любой точки на декартовой плоскости?
(ii) Как называется каждая часть плоскости, образованная этими двумя линиями?
(iii) Назовите точку пересечения этих двух линий.
Решение:
(i) Горизонтальные и вертикальные линии, проведенные для определения положения любой точки на декартовой плоскости, называются осью x и осью y соответственно.
(ii) Название каждой части плоскости, образованной этими двумя линиями, осью x и осью y, называется квадрантом.
(iii) Точка, в которой пересекаются эти две линии, называется началом координат.
2. См. рис.3.14 и напишите следующее.
я. Координаты Б.
ii. Координаты с.
iii. Точка, обозначенная координатами (–3, –5).
iv. Точка, идентифицированная координатами (2, – 4).
v. Абсцисса точки D.
VI. Ордината точки H.
vii. Координаты точки Л.
viii. Координаты точки М.
Решение:
я. Координаты B равны (−5, 2).
ii. Координаты C равны (5, −5).
III. Точка, обозначенная координатами (−3, −5), – это E.
.ив. Точка, обозначенная координатами (2, −4), – G.
. v. Абсцисса означает x координату точки D.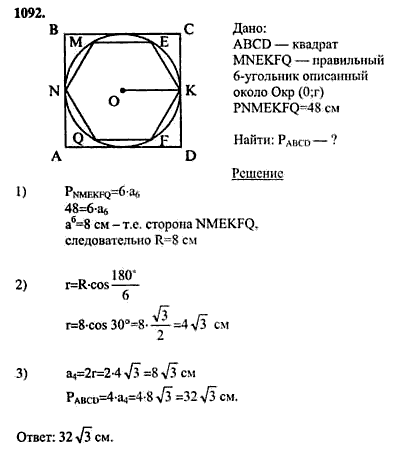
Итак, абсцисса точки D равна 6.
в.и. Ордината означает координату y точки H. Итак, ордината точки H равна -3.
vii. Координаты точки L равны (0, 5).
viii. Координаты точки M равны (−3, 0).
Упражнение 3.3 Страница: 65
1. В каком квадранте или на какой оси сделать каждую из точек (– 2, 4), (3, – 1), (– 1, 0), (1, 2) и (– 3, – 5) ложь? Проверьте свой ответ, расположив их на декартовой плоскости.
Решение:
- (– 2, 4): Второй квадрант (II-квадрант)
- (3, – 1): Четвертый квадрант (IV-квадрант)
- (– 1, 0): отрицательная ось x
- (1, 2): Первый квадрант (I-квадрант)
- (– 3, – 5): Третий квадрант (III-квадрант)
2. Нанесите на плоскость точки (x, y), указанные в следующей таблице, выбрав подходящие единицы измерения расстояния по осям.
| х | -2 | -1 | 0 | 1 | 3 |
| у | 8 | 7 | -1,25 | 3 | -1 |
Решение:
Точки, которые должны быть нанесены на (x, y), равны
я.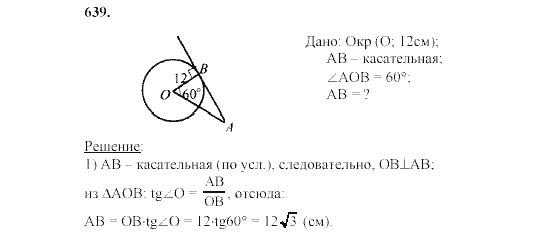
(-2, 8)
ii. (-1, 7)
III. (0, -1,25)
ив. (1, 3)
т. (3, -1)
На графике отметьте ось X и ось Y. Отметьте место встречи как О.
.Теперь пусть 1 единица = 1 см
я. (-2, 8): II- квадрант, точка пересечения воображаемых линий, которая начинается на 2 единицы левее начала координат O и на 8 единиц выше начала координат O.
ii. (-1, 7): II- квадрант, точка встречи воображаемых линий, которая начинается с 1 единицы слева от начала координат O и с 7 единиц выше начала координат O.
III. (0, -1,25): по оси X на 1,25 единицы левее исходной точки O.
ив. (1, 3): I-квадрант, точка пересечения воображаемых линий, которая начинается с 1 единицы справа от начала координат O и с 3 единиц выше начала координат O.
т. (3, -1): IV- Квадрант, точка пересечения воображаемых линий, начинающаяся на 3 единицы вправо от начала координат О и на 1 единицу ниже начала координат О.
Отказ от ответственности:
Удаленные темы — 3.
3 Нанесение точки на плоскости, если ее координаты заданы.
Часто задаваемые вопросы о решениях NCERT для класса 9Математика, глава 3
Q1
Напишите основные преимущества решений NCERT для математики класса 9, глава 3.
1. Решения, представленные в Решения NCERT для математики класса 9, глава 3 , предлагаются в виде пошагового подхода. для удобного и лучшего понимания концепций.
2. Они также предоставляют пояснительные диаграммы и таблицы для сравнительного изучения, что создает интерес к обучению.
3. Эти решения помогают учащимся приобрести хорошие знания как основных, так и продвинутых математических понятий.
4. Они также помогают учащимся быстро освоить концепции.
Q2
Чем решения NCERT для 9-го класса по математике, глава 3, полезны для учащихся 9-го класса?
NCERT Solutions for Class 9 Maths Chapter 3 может помочь учащимся развеять сомнения и лучше подготовиться к экзаменам CBSE.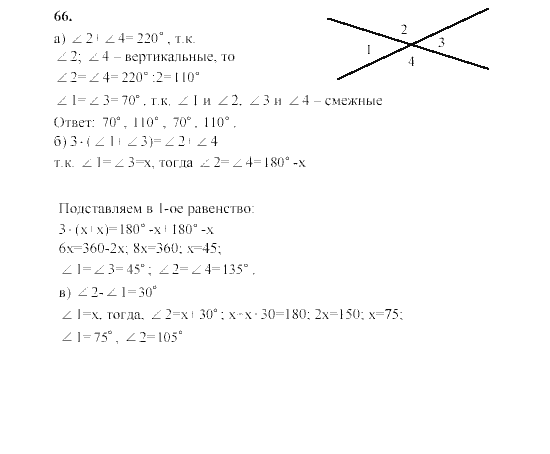
Вопросы NCERT помогают не только при подготовке к экзаменам, но и для различных конкурсных экзаменов.
Q3
Как получить высокие оценки с помощью решений NCERT для класса 9Глава 3 по математике на экзаменах CBSE?
Учащимся рекомендуется регулярно следовать NCERT Solutions for Class 9 Chapter 3, чтобы получить глубокие знания обо всех концепциях, охватываемых последней программой CBSE. Эти решения NCERT для класса 9 подготовлены нашей командой экспертов BYJU, полностью сосредоточенной на точности. Благодаря регулярному использованию этих решений учащиеся получают высокие оценки на экзаменах CBSE.
Математика Часть II Решения для 9 класса Математика Глава 1
Математика Часть II Решения Решения для 9 класса Математика Глава 1 Основные понятия геометрии представлены здесь с простыми пошаговыми объяснениями. Эти решения для базовых понятий в геометрии чрезвычайно популярны среди учащихся 9 класса по математике.
Основные понятия в геометрии очень удобны для быстрого выполнения домашних заданий и подготовки к экзаменам. Все вопросы и ответы из книги решений по математике, часть II, глава 1 по математике для класса 9, предоставляются здесь для вас бесплатно. Вам также понравится безрекламный опыт решения Mathematics Part II Solutions Solutions от Meritnation. Все решения по математике, часть II Решения для 9 классаМатематика подготовлена экспертами и на 100% точна.
Страница № 5:
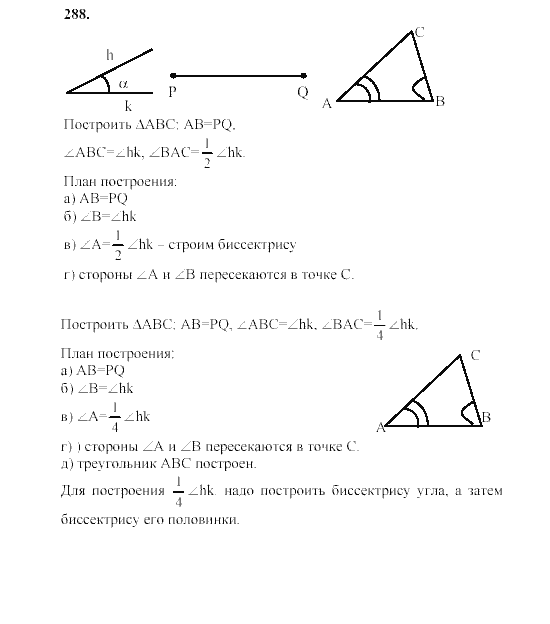
Вопрос 1:
Найдите расстояния с помощью приведенной ниже числовой строки.
(i) d (B,E) (ii) d (J, A) (iii) d (P, C) (iv) d (J, H) (v) d (K, O)
(vi) d (O, E) (vii) d (P, J) (viii) d (Q, B)
Ответ:
4
44
Известно, что расстояние между двумя точками получается путем вычитания меньшей координаты из большей координаты.
(i) Координаты точек B и E равны 2 и 5 соответственно.
Мы знаем, что 5 > 2.
∴ d (B, E) = 5 − 2 = 3
(ii) Координаты точек J и A равны −2 и 1 соответственно. Мы знаем, что 1 > −2.
∴ d (J, A) = 1 − (−2) = 1 + 2 = 3
(iii) Координаты точек P и C равны −4 и 3 соответственно. Мы знаем, что 3 > −4.
∴ d (P, C) = 3 − (−4) = 3 + 4 = 7
(iv) Координаты точек J и H равны −2 и −1 соответственно. Мы знаем, что −1 > −2.
∴ d (J, H) = −1 − (−2) = −1 + 2 = 1
(v) Координаты точек K и O равны −3 и 0 соответственно. Мы знаем, что 0 > −3.
∴ d (K, O) = 0 − (−3) = 0 + 3 = 3
(vi) Координаты точек O и E равны 0 и 5 соответственно. Мы знаем, что 5 > 0,
∴ d (O, E) = 5 − 0 = 5
(vii) Координаты точек P и J равны -4 и -2 соответственно. Мы знаем, что −2 > −4.
∴ d (P, J) = -2 — (-4) = -2 + 4 = 2
(viii) Координаты точек Q и B равны -5 и 2 соответственно. Мы знаем, что 2 > −5.
∴ d (Q, B) = 2 − (−5) = 2 + 5 = 7
Страница № 5:
Вопрос 2:
Если координата A равна x , а координата B равно y , найти d (A, B).
(i) x = 1, y = 7 (ii) x = 6, y = -2 007
(iv ) x = -4, y = -5 (v) x = -3, y = -6 (vi) x = 4, y = -8
901 Ответ:
Известно, что расстояние между двумя точками получается путем вычитания меньшей координаты из большей координаты.
(i) Координаты A и B равны x и y соответственно. Имеем x = 1 и y = 7. Мы знаем, что 7 > 1. ) Координаты A и B равны x и y соответственно. У нас есть x = 6 и y = −2. Мы знаем, что 6 > −2.
∴ d (A, B) = x — y = 6 — (-2) = 6 + 2 = 8
(iii) Координаты точек A и B равны x и y соответственно. У нас есть, x = -3 и y = 7. Мы знаем, что 7 > -3.
∴ d (A, B) = y − x = 7 − (−3) = 7 + 3 = 10
(iv) Координаты точек A и B равны x 6 9 0 61 и 0 соответственно. У нас есть x = −4 и y = -5. Мы знаем, что −4 > −5.
∴ d (A, B) = x − y = −4 − (−5) = −4 + 5 = 1
(v) Координаты точек A и B равны x и y соответственно. У нас есть x = -3 и y = -6. Мы знаем, что −3 > −6.
∴ d (A, B) = x − y = −3 − (−6) = −3 + 6 = 3
(vi) Координаты A и B равны x 60 y соответственно. У нас есть x = 4 и y = −8. Мы знаем, что 4 > −8.
∴ д (А, В) = x — y = 4 — (-8) = 4 + 8 = 12
Страница № 5:
Вопрос 3:
Из приведенной ниже информации найдите, какая из точек находится между двумя другими. Если точки не лежат на одной прямой, укажите это.
(i) d (P, R) = 7, d (P, Q) = 10, d (Q, R) = 3
(ii) 1 d 9036 S) = 8, d (S, T) = 6, d (R, T) = 4
(iii) d (A, B) = 16, d (C, A) = 9, d (B, C) = 7
(iv) d (L, M) = 11, d (M, N) = 12, d (N, L) = 8
(v) d (X, Y) = 15, d (Y, Z) = 7, d ( X, Z) = 8
(vi) d (D, E) = 5, d (E, F) = 8, d (D, F) = 6
Ответ:
(i) Имеем d (P, R) = 7; д (Р, Q) = 10; d (Q, R) = 3
Теперь, d (P, R) + d (Q, R) = 7 + 3
Или, d (P, R) + d ( R, Q) = 10
∴ d (P, Q) = d (P, R) + d (Q, R)
Следовательно, точки P, R и Q лежат на одной прямой.
Точка R находится между P и Q, т. е. P-R-Q.
(ii) У нас есть, d (R, S) = 8; д (С, Т) = 6; d (R, T) = 4
Теперь 8 + 6 = 14, поэтому 8 + 6 ≠ 4; 6 + 4 = 10, поэтому 6 + 4 ≠ 8 и 8 + 4 = 12, поэтому 8 + 4 ≠ 6
Так как сумма расстояний между двумя парами точек не равна расстоянию между третьей парой точек, то данные точки R, S и T не лежат на одной прямой.
(iii) Имеем, d (A, B) = 16; д (С, А) = 9; d (B, C) = 7
Теперь, d (C, A) + d (B, C) = 9 + 7
Или, d (A, C) + d ( C, B) = 16
∴ d (A, B) = d (A, C) + d (C, B)
Следовательно, точки A, C и B лежат на одной прямой.
Точка C находится между A и B, т. е. A-C-B.
(iv) Имеем, d (L, M) = 11; д (М, Н) = 12; d (N, L) = 8
Теперь 11 + 12 = 23, поэтому 11 + 12 ≠ 8; 12 + 8 = 20, поэтому 12 + 8 ≠ 11 и 11 + 8 = 19, поэтому 11 + 8 ≠ 12
. Так как сумма расстояний между двумя парами точек не равна расстоянию между третьей парой точек, поэтому заданные точки L, M и N не лежат на одной прямой.
(v) Имеем, d (X, Y) = 15; д (Y, Z) = 7; d (X, Z) = 8
Теперь, d (X, Z) + d (Y, Z) = 7 + 8
Или, d (X, Z) + d ( Z, Y) = 15
∴ d (X, Y) = d (X, Z) + d (Z, Y)
Следовательно, точки X, Z и Y лежат на одной прямой.
Точка Z находится между X и Y, т. е. X-Z-Y.
(vi) Имеем d (D, E) = 5, d (E, F) = 8, d (D, F) = 6
Теперь 5 + 8 = 13, поэтому 5 + 8 ≠ 6; 8 + 6 = 14, поэтому 8 + 6 ≠ 5 и 5 + 6 = 11, поэтому 5 + 6 ≠ 8
Так как сумма расстояний между двумя парами точек не равна расстоянию между третьей парой точек, то данные точки D, E и F не лежат на одной прямой.
Страница № 5:
Вопрос 4:
На числовой прямой точки A, B и C таковы, что d (A, C) = 10, d (C, B) = 8 . Найдите d (A, B), учитывая все возможности.
Ответ:
Есть только две возможности.
Случай 1: когда точка C находится между точками A и B.
Имеем, d (А, С) = 10; d (C, B) = 8
Теперь, d (A, B) = d (A, C) + d (C, B) = 10 + 8
∴ d (A , B) = 18
Случай 2: когда точка B находится между точками A и C.
Имеем d (A, C) = 10; d (C, B) = 8
Теперь, d (A, C) = d (A, B) + d (B, C)
Итак, d (A, B) = d (A, C) − d (B, C) = 10 − 8
∴ d (A, B) = 2
Страница № 5:
Вопрос 5:
Y,Z) = 8, найти d (X,Z) .
Ответ:
Дано, что точки X, Y и Z лежат на одной прямой.
Имеем d (X, Y) = 17; d (Y,Z) = 8.
Теперь d (X,Z) = d (X,Y) + d (Y,Z) = 17 + 8
∴ d ( Х, Z) = 25
Страница № 5:
Вопрос 6:
Нарисуйте правильный рисунок и напишите ответы на следующие вопросы.
(i) Если A — B — C и l (AC) = 11, l (BC) = 6,5, то l (AB) =?
(ii) Если R — S — T и l (ST) = 3,7, l (RS) = 2,5, то l (RT) =?
(iii) Если X — Y — Z и l (XZ) = 3 7, l (XY) = 7 , то l (ЯЗ) =?
Ответ:
(i)
Имеем l (AC) = 11; л (БК) = 6,5.
Итак, л (АС) = л (АВ) + л (ВС)
Итак, л (АВ) = л (АС) — л — (ВС) = 6,5.
∴ l (AB) = 4,5
(ii)
Имеем, l (ST) = 3,7; л (RS) = 2,5.
Теперь, l (RT) = l (RS) + l (ST) = 3,7 + 2,5
∴ l (RT) = 5,6
(iii)
Имеем, l (XZ) = 37; 1 (XY) = 7.
Теперь 1 (XZ) = 1 (XY) + 1 (YZ)
Итак, 1 (YZ) − 6 ( 1 X 903) l (XY) = 37 − 7
∴ l (YZ) = 27
Страница № 5:
Вопрос 7:
Какая фигура образована тремя не лежащими на одной прямой точками?
Ответ:
Треугольник образован тремя отрезками, соединяющими три не лежащие на одной прямой точки.
A, B и C — три неколлинеарные точки. Когда A, B и C соединяются, мы получаем ∆ABC.
Страница № 7:
Вопрос 1:
В следующей таблице показаны точки на числовой прямой и их координаты. Решите, конгруэнтны ли пары отрезков, приведенные под таблицей, или нет.
Точка А Б С Д Е Координата -3 5 2 -7 9
(i) сегмент DE и сегмент AB (ii) сегмент BC и сегмент AD (iii) сегмент BE и сегмент AD
Ответ:
В данной таблице
Точка А Б С Д Е Координата -3 5 2 -7 9
(i) Координаты точек D и E равны −7 и 9 соответственно. Мы знаем, что 9 > −7.
∴ l (DE) = 9 − (−7) = 9 + 7 = 16
Координаты точек A и B равны −3 и 5 соответственно. Мы знаем, что 5 > −3.
∴ l (AB) = 5 − (−3) = 5 + 3 = 8
Так как l (DE) ≠ l (AB), значит, сегмент DE ≇ сегмент AB.
(ii) Координаты точек B и C равны 5 и 2 соответственно. Мы знаем, что 5 > 2,
∴ l (BC) = 5 − 2 = 3
Координаты точек A и D равны −3 и −7 соответственно. Мы знаем, что −3 > −7.
∴ l (AD) = −3 − (−7) = −3 + 7 = 4
Поскольку l (BC) ≠ l (AD), значит, сегмент BC ≇ сегмент AD.
(iii) Координаты точек B и E равны 5 и 9 соответственно. Мы знаем, что 9 > 5.
∴ l (BE) = 9 − 5 = 4
Координаты точек A и D равны −3 и −7 соответственно. Мы знаем, что −3 > −7.
∴ l (AD) = -3 — (-7) = -3 + 7 = 4
Так как l (BE) = l (AD), поэтому seg BE ≅ seg AD.
Страница № 7:
Вопрос 2:
Точка M является серединой отрезка AB. Если АВ = 8, то найдите длину АМ.
Ответ:
Имеем l (AB) = 8.
Поскольку M — середина отрезка AB, то
l (AM) = 12 из l 1 (AB) 30 326 (AM) = 12 × 8 = 4
Итак, длина AM равна 4.
Страница № 7:
Вопрос 3:
Точка P является серединой отрезка CD. Если CP = 2,5, найдите l (CD).
Ответ:
Имеем l (CP) = 2,5.
Поскольку P является серединой отрезка CD, то
l (CP) = 12 из l (CD)
∴ l (CD) = 2 × l (CP) = 2 × 2,5 = 5
Итак, длина CD равна 5.
Страница № 7:
Вопрос 4:
Если AB = 5 см, BP = 2 см и AP = 3,4 см, сравните отрезки.
Ответ:
Имеем l (АВ) = 5 см; л (ВР) = 2 см; л (АП) = 3,4 см
Мы знаем, что 5 > 3,4 > 2.
Итак, л (АВ) > л (АП) > л (ВР).
∴ сегмент AB > сегмент AP > сегмент BP.
Страница № 8:
Вопрос 5:
Напишите ответы на следующие вопросы со ссылкой на данный рисунок.
(i) Напишите название луча, противоположного лучу RP.
(ii) Запишите множество пересечений луча PQ и луча RP.
(iii) Напишите объединение луча PQ и луча QR.
(iv) Укажите лучи, подмножеством которых является сегмент QR.
(v) Запишите пару противоположных лучей с общим концом R.
(vi) Запишите любые два луча с общим концом S.
(vii) Запишите множество пересечений луча SP и луча ST.
Ответ:
(i) Ray RS или Ray RT
(ii) Ray PQ
(iii) Ray QR
(iv) Ray QR, Ray RQ и т. д.
(v) Ray RQ и Ray RT и т. д.
(vi) Ray ST и Ray SR и т. д.
(vii) Point S
Страница № 8:
Вопрос 6:
Ответьте на вопросы, используя заданную цифру.
(i) Укажите точки, равноудаленные от точки B.
(ii) Запишите пару точек, равноудаленных от точки Q.
(iii) Найдите d (U,V), d ( П, В), д (В, Б), д (У, Л).
Ответ:
(i) Координаты точек B и C равны 2 и 4 соответственно. Мы знаем, что 4 > 2.
∴ d (B, C) = 4 − 2 = 2
Координаты точек B и A равны 2 и 0 соответственно. Мы знаем, что 2 > 0.
∴ d (B, A) = 2 − 0 = 2
Поскольку d (B, A) = d (B, C), то точки A и C равноудалены друг от друга. от точки B.
Координаты точек B и D равны 2 и 6 соответственно. Мы знаем, что 6 > 2,
∴ d (B, D) = 6 − 2 = 4
Координаты точек B и P равны 2 и −2 соответственно. Мы знаем, что 2 > −2.
∴ d (B, P) = 2 − (−2) = 2 + 2 = 4
Поскольку d (B, D) = d (B, P), то точки D и P равноудалены от точки B.
(ii) Координаты точек Q и U равны -4 и -5 соответственно. Мы знаем, что −4 > −5.
∴ d (Q, U) = −4 − (−5) = −4 + 5 = 1
Координаты точек Q и L равны −4 и −3 соответственно. Мы знаем, что −3 > −4.
∴ d (Q, L) = −3 − (−4) = −3 + 4 = 1
Поскольку d (Q, U) = d (Q, L), то точки U и L равноудалены от точки Q.
Координаты точек Q и R равны -4 и -6 соответственно. Мы знаем, что −4 > −6.
∴ d (Q, R) = −4 − (−6) = −4 + 6 = 2
Координаты точек Q и P равны −4 и −2 соответственно. Мы знаем, что −2 > −4.
∴ d (Q, P) = −2 − (−4) = −2 + 4 = 2
Поскольку d (Q, R) = d (Q, P), то точки R и P равноудалены от точки Q.
(iii) Координаты точек U и V равны −5 и 5 соответственно. Мы знаем, что 5 > −5.
∴ d (U, V) = 5 − (−5) = 5 + 5 = 10
Координаты точек P и C равны −2 и 4 соответственно. Мы знаем, что 4 > −2.
∴ d (P, C) = 4 − (−2) = 4 + 2 = 6
Координаты точек V и B равны 5 и 2 соответственно. Мы знаем, что 5 > 2.
∴ d (V, B) = 5 − 2 = 3
Координаты точек U и L равны -5 и -3 соответственно. Мы знаем, что −3 > −5.
∴ d (U, L) = −3 − (−5) = −3 + 5 = 2
Страница № 11:
Вопрос 1:
Запишите следующие утверждения в форме «если-то».
(i) Противоположные углы параллелограмма равны.
(ii) Диагонали прямоугольника равны.
(iii) В равнобедренном треугольнике отрезок, соединяющий вершину и середину основания, перпендикулярен основанию.
Ответ:
(i) Если четырехугольник является параллелограммом, то противоположные углы этого четырехугольника равны.
(ii) Если четырехугольник является прямоугольником, то диагонали этого четырехугольника конгруэнтны.
(iii) Если треугольник равнобедренный, то отрезок, соединяющий вершину и середину основания, перпендикулярен основанию.
Страница № 11:
Вопрос 2:
Напишите обратные выражения следующих утверждений.
(i) Наклонные углы, образованные двумя параллельными прямыми и их секущей, равны.
(ii) Если пара внутренних углов, образованных секущей двух прямых, является дополнительной, то эти прямые параллельны.
(iii) Диагонали прямоугольника равны.
Ответ:
(i) Если альтернативные углы, образуемые секущей с двумя прямыми, равны, то прямые параллельны.
(ii) Если две параллельные прямые пересекаются секущей, то пара внутренних углов является дополнительной.
(iii) Если диагонали четырехугольника равны, то этот четырехугольник является прямоугольником.
Страница № 11:
Вопрос 1:
Выберите правильный вариант из ответов на приведенные ниже вопросы.
(i) Сколько средних точек имеет отрезок?
(A) только одна (B) две (C) три (D) много
(ii) Сколько точек находится на пересечении двух различных прямых?
(А) бесконечный (Б) два (В) один (Г) ни один
(iii) Сколько прямых определяется тремя различными точками?
(А) два (Б) три (В) один или три (Г) шесть
(iv) Найти d (А, В), если координаты А и В равны — 2 и 5 соответственно.
(A)-2 (B) 5 (C) 7 (D) 3
(v) Если P — Q — R и d (P,Q) = 2, d (P, Q) R) = 10, тогда находим d (Q,R).
(A) 12 (B) 8 (C) 96 (D) 20
Ответ:
(i) Каждый сегмент имеет одну и только одну среднюю точку.
Значит, правильный ответ — вариант (А).
(ii) Известно, что две различные прямые пересекаются в одной точке.
Значит, правильный ответ — вариант (С).
(iii) Рассмотрим 3 различные точки как P, Q и R.
Предположим, что точки P, Q и R лежат на одной прямой.
Итак, только одна линия определяется точками P, Q и R.
Предположим, что точки P,Q и R не лежат на одной прямой.
Итак, три линии можно определить по точкам P, Q и R.
Следовательно, правильный ответ — вариант (С).
(iv) Координаты точек A и B равны -2 и 5 соответственно. Мы знаем, что 5 > -2.
∴ d (A, B) = 5 − (−2) = 5 + 2 = 7
Следовательно, правильный ответ — вариант (C).
(v) Дано, что точка Q находится между точкой P и точкой R.
Имеем, d (P,Q) = 2; d (P,R) = 10
Теперь d (P,R) = d (P,Q) + d (Q,R)
∴ d (Q,R) = d (P,R) − d (P,Q) = 10 − 2 = 8
Следовательно, правильный ответ — вариант (B).
Страница № 11:
Вопрос 2:
На числовой прямой координаты точек P, Q, R равны 3, — 5 и 6 соответственно. Укажите аргументированно, верны или неверны следующие утверждения.
(i) d (P,Q) + d (Q,R) = d (P,R)
(ii) d (P,R) + d (R) ,Q) = d (P,Q)
(iii) d (R,P) + d (P,Q) = d (R,Q)
(iv) d (P,Q) — d (P,R) = d (Q,R)
Ответ:
Координаты точек P и Q равны 3 и −5 соответственно. Мы знаем, что 3 > −5.
Теперь d (P, Q) = 3 − (−5) = 3 + 5 = 8
Координаты точек Q и R равны −5 и 6 соответственно. Мы знаем, что 6 > −5.
Теперь d (Q, R) = 6 − (−5) = 6 + 5 = 11
Координаты точек P и R равны 3 и 6 соответственно. Мы знаем, что 6 > 3,
Теперь, d (P, R) = 6 − 3 = 3
(i) d (P, Q) + d (Q, R) = 8 + 11 = 19; d (P, R) = 3
Итак, d (P, Q) + d (Q, R) ≠ d (P, R)
Следовательно, данное утверждение неверно.
(ii) d (P, R) + d (R, Q) = d (P, R) + d (Q, R) = 3 + 11 = 14; d (P, Q) = 8
Итак, d (P, R) + d (R, Q) ≠ d (P, Q)
Следовательно, данное утверждение неверно.
(iii) d (R,P) + d (P,Q) = d (P, R) + d (P,Q) = 3 + 8 = 11; d (R,Q) = d (Q, R) = 11
Итак, d (R,P) + d (P,Q) = d (R,Q)
Отсюда , данное утверждение верно.
(iv) d (P,Q) — d (P,R) = 8 − 3 = 5; d (Q, R) = 11
Итак, d (P, Q) — d (P, R) ≠ d (Q,R)
Следовательно, данное утверждение неверно.
Страница № 11:
Вопрос 3:
Координаты некоторых пар точек приведены ниже. Отсюда найдите расстояние между каждой парой.
(i) 3, 6
(ii) − 9, — 1
(iii)- 4, 5
(iv) x,- 2
(v) x + 3, x- 3
(vi) -25,-47
(vii) 80, — 85
Ответ:
(i) Пусть координаты A и B равны 3 и 6 соответственно. Мы знаем, что 6 > 3
d (A, B) = 6 − 3 = 3
(ii) Пусть координаты C и D равны -9 и -1 соответственно. Мы знаем, что −1 > −9
d (C, D) = −1 − (−9) = −1 + 9 = 8
(iii) Пусть координаты E и F равны −4 и 5 соответственно. Мы знаем, что 5 > −4
d (E, F) = 5 − (−4) = 5 + 4 = 9
(iv) Пусть координаты P и Q равны x и -2 соответственно. Предположим, что x > 0, тогда x > −2.
d (P, Q) = x — (-2) = x + 2
(v) Пусть координаты R и S равны x + 3 и x — 3 соответственно. Предположим, x > 0, тогда x + 3 > x — 3
d (R, S) = ( x + 3) — ( x + x 9 — 3 60) = − x + 3 = 2x
(vi) Пусть координаты L и M равны −25 и −47 соответственно. Мы знаем, что −25 > −47
d (L, M) = −25 − (−47) = −25 + 47 = 22
(vii) Пусть координаты G и H равны 80 и −85 соответственно. Мы знаем, что 80 > −85
d (G, H) = 80 − (−85) = 80 + 85 = 165
Страница № 12:
Вопрос 4:
Координата точки P на числовая строка равна -7. Найдите координаты точек на числовой прямой, которые находятся на расстоянии 8 единиц от точки P.
Ответ:
Координаты точки P на числовой прямой равны −7. Теперь будет две точки, одна слева от точки P, а другая справа от точки P на числовой прямой, которые находятся на расстоянии 8 единиц от точки P.
Пусть точка R находится справа от точки P, а точка Q — слева от точки P, каждая на расстоянии 8 единиц от точки P.
Координата точки R будет больше, а координата точки Q будет меньше по сравнению с координатой точки P.
Теперь d (P, R) = 8
Итак, координата R − координата P = 8
∴ координата R = 8 + координата P = 8 + (−7) = 8 − 7 = 1
Кроме того, d (Q, P) = 8
Итак, координата P — координата Q = 8
∴ координата Q = координата P − 8 = −7 − 8 = −15
Следовательно, координаты искомых точек на числовой прямой, находящихся на расстоянии 8 единиц от точки P равны 1 и -15.
Страница № 12:
Вопрос 5:
Ответьте на следующие вопросы.
(i) Если A — B — C и d (A,C) = 17, d (B,C) = 6,5, то d (A,B) = ?
(ii) Если P — Q — R и d (P, Q) = 3,4, d (Q,R)= 5,7, тогда d (P,R) = ?
Ответ:
(i)
Имеем, d (А, С) = 17; d (B, C) = 6,5
Сейчас, d (A, C) = d (A, B) + d (B, C)
Итак, d (A, B) = d (A, C) − d (B, C) = 17 − 6,5
∴ d (A, B) = 10,5
(ii)
(P, Q) = 3,4; d (Q, R) = 5,7
Теперь d (P, R) = d (P, Q) + d (Q, R) = 3,4 + 5,7
∴ d (P, R) = 9,1
Стр.
точка А на числовой прямой равна 1. Каковы координаты точек на числовой прямой, которые находятся на расстоянии 7 единиц от А? Ответ:
Координаты точки А на числовой прямой равны 1. Теперь будет две точки, одна слева от точки А, а другая справа от точки А на числовой прямой, которые на расстоянии 7 единиц от точки А.
Пусть точка C находится справа от точки A, а точка B — слева от точки A, каждая на расстоянии 7 единиц от точки A.
Координата точки C будет больше, а координата точки B будет меньше по сравнению с координатой точки A.
Теперь d (A, C) = 7
Итак, координата C − координата A = 7
∴ координата C = 7 + координата A = 7 + 1 = 8
Кроме того, d (B, A) = 7
Итак, координата A − координата B = 7
∴ координата B = координата A − 7 = 1 − 7 = −6
Следовательно, координаты искомых точек на числовой прямой, находящихся на расстоянии 7 единиц от точки A равны 8 и −6.
Страница № 12:
Вопрос 7:
Напишите следующие утверждения в условной форме.
(i) Каждый ромб является квадратом.
(ii) Углы в линейной паре являются дополнительными.
(iii) Треугольник – это фигура, образованная тремя сегментами.
(iv) Число, имеющее только два делителя, называется простым числом.
Ответ:
(i) Если данный четырехугольник является квадратом, то он должен быть ромбом.
(ii) Если данные два угла образуют линейную пару, то они являются дополнительными.
(iii) Если данная фигура является треугольником, то она образована тремя сегментами.
(iv) Если данное число имеет только два делителя, то это простое число.
Страница № 12:
Вопрос 8:
Напишите обратное каждому из следующих утверждений.
(i) Если сумма мер углов фигуры равна 180 0 , то фигура является треугольником.
(ii) Если сумма мер двух углов равна 90 0 , то они дополняют друг друга.
(iii) Если соответствующие углы, образованные секущей двух прямых, равны, то эти две прямые параллельны.
(iv) Если сумма цифр числа делится на 3, то это число делится на 3.
Ответ:
(i) Если данная фигура является треугольником, то сумма мер его углов равна 180 0 .
(ii) Если данные два угла дополняют друг друга, то сумма мер двух углов равна 90 0 .
(iii) Если данные две прямые параллельны, то соответствующие углы, образованные секущей двух прямых, равны.
(iv) Если данное число делится на 3, то сумма цифр этого числа делится на 3.
Страница № 12:
Вопрос 9:
Напишите антецедент (данная часть) и консеквент (часть, которую нужно доказать) в следующих утверждениях.
(i) Если все стороны треугольника равны, то все его углы равны.
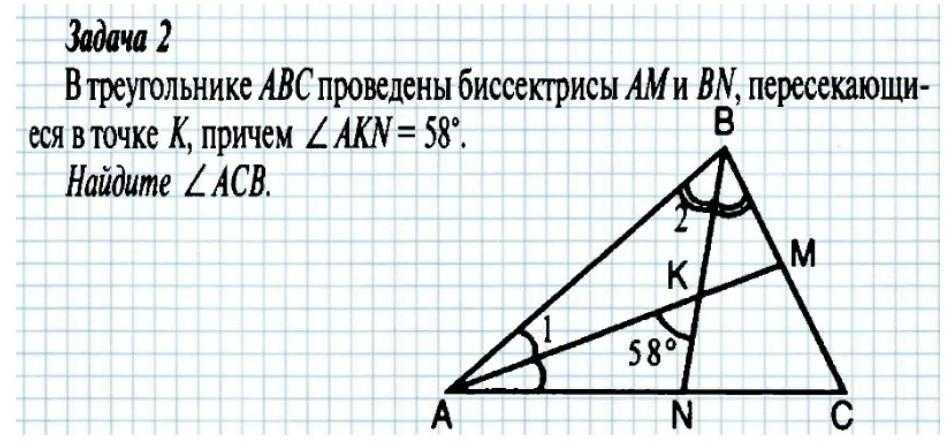
(ii) Диагонали параллелограмма делят друг друга пополам.
Ответ:
(i) Предшественник: Все стороны треугольника конгруэнтны.
Следствие: все его углы равны.
(ii) Утверждение можно записать в условной форме так: «Если данный четырехугольник является параллелограммом, то его диагонали делят друг друга пополам.
Антецедент : Данный четырехугольник является параллелограммом.
Следствие: его диагонали делят друг друга пополам.
Страница № 12:
Вопрос 10:
Нарисуйте помеченный рисунок, показывающий информацию в каждом из следующих утверждений, и запишите предшествующее и последующее.
(i) Два равносторонних треугольника подобны.
(ii) Если углы в линейной паре равны, то каждый из них прямой.
(iii) Если высоты, проведенные на двух сторонах треугольника, равны, то эти две стороны равны.
Ответ:
(i) Данное утверждение можно записать в условной форме так: «Если данные два поезда равносторонние, то они подобны».
Предшественник: Данные два треугольника равносторонние.
Следствие: они похожи.
Здесь ∆ABC и ∆PQR — равносторонние треугольники, поэтому они подобны друг другу.
(ii) Предшественник: Углы в линейной паре конгруэнтны.
Консеквент: каждый из них является прямым углом.
Здесь ∠AOC и ∠BOC, образующие линейную пару, конгруэнтны друг другу, поэтому каждый из них является прямым углом.
Мы знаем, что 5 > 2. ∴ d (B, E) = 5 − 2 = 3
∴ d (J, A) = 1 − (−2) = 1 + 2 = 3
∴ d (P, C) = 3 − (−4) = 3 + 4 = 7
∴ d (J, H) = −1 − (−2) = −1 + 2 = 1
∴ d (K, O) = 0 − (−3) = 0 + 3 = 3
∴ d (O, E) = 5 − 0 = 5
∴ d (P, J) = -2 — (-4) = -2 + 4 = 2
∴ d (Q, B) = 2 − (−5) = 2 + 5 = 7
(i) x = 1, y = 7 (ii) x = 6, y = -2 007
(iv ) x = -4, y = -5 (v) x = -3, y = -6 (vi) x = 4, y = -8
Известно, что расстояние между двумя точками получается путем вычитания меньшей координаты из большей координаты.
∴ d (A, B) = x — y = 6 — (-2) = 6 + 2 = 8
∴ d (A, B) = y − x = 7 − (−3) = 7 + 3 = 10
У нас есть x = −4 и y = -5. Мы знаем, что −4 > −5. ∴ d (A, B) = x − y = −4 − (−5) = −4 + 5 = 1
∴ d (A, B) = x − y = −3 − (−6) = −3 + 6 = 3
∴ д (А, В) = x — y = 4 — (-8) = 4 + 8 = 12
(i) d (P, R) = 7, d (P, Q) = 10, d (Q, R) = 3
(ii) 1 d 9036 S) = 8, d (S, T) = 6, d (R, T) = 4
(iii) d (A, B) = 16, d (C, A) = 9, d (B, C) = 7
(iv) d (L, M) = 11, d (M, N) = 12, d (N, L) = 8
(v) d (X, Y) = 15, d (Y, Z) = 7, d ( X, Z) = 8
(vi) d (D, E) = 5, d (E, F) = 8, d (D, F) = 6
(i) Имеем d (P, R) = 7; д (Р, Q) = 10; d (Q, R) = 3
Теперь, d (P, R) + d (Q, R) = 7 + 3
Или, d (P, R) + d ( R, Q) = 10
∴ d (P, Q) = d (P, R) + d (Q, R)
Следовательно, точки P, R и Q лежат на одной прямой.
Точка R находится между P и Q, т. е. P-R-Q.
Теперь 8 + 6 = 14, поэтому 8 + 6 ≠ 4; 6 + 4 = 10, поэтому 6 + 4 ≠ 8 и 8 + 4 = 12, поэтому 8 + 4 ≠ 6
Так как сумма расстояний между двумя парами точек не равна расстоянию между третьей парой точек, то данные точки R, S и T не лежат на одной прямой.
Теперь, d (C, A) + d (B, C) = 9 + 7
Или, d (A, C) + d ( C, B) = 16
∴ d (A, B) = d (A, C) + d (C, B)
Следовательно, точки A, C и B лежат на одной прямой.
Точка C находится между A и B, т. е. A-C-B.
Теперь 11 + 12 = 23, поэтому 11 + 12 ≠ 8; 12 + 8 = 20, поэтому 12 + 8 ≠ 11 и 11 + 8 = 19, поэтому 11 + 8 ≠ 12
.
Так как сумма расстояний между двумя парами точек не равна расстоянию между третьей парой точек, поэтому заданные точки L, M и N не лежат на одной прямой.Теперь, d (X, Z) + d (Y, Z) = 7 + 8
Или, d (X, Z) + d ( Z, Y) = 15
∴ d (X, Y) = d (X, Z) + d (Z, Y)
Следовательно, точки X, Z и Y лежат на одной прямой.
Точка Z находится между X и Y, т. е. X-Z-Y.
Теперь 5 + 8 = 13, поэтому 5 + 8 ≠ 6; 8 + 6 = 14, поэтому 8 + 6 ≠ 5 и 5 + 6 = 11, поэтому 5 + 6 ≠ 8
Так как сумма расстояний между двумя парами точек не равна расстоянию между третьей парой точек, то данные точки D, E и F не лежат на одной прямой.
Найдите d (A, B), учитывая все возможности.Случай 1: когда точка C находится между точками A и B.
Имеем, d (А, С) = 10; d (C, B) = 8
Теперь, d (A, B) = d (A, C) + d (C, B) = 10 + 8
∴ d (A , B) = 18
Случай 2: когда точка B находится между точками A и C.
Имеем d (A, C) = 10; d (C, B) = 8
Теперь, d (A, C) = d (A, B) + d (B, C)
Итак, d (A, B) = d (A, C) − d (B, C) = 10 − 8
∴ d (A, B) = 2
Дано, что точки X, Y и Z лежат на одной прямой.
Имеем d (X, Y) = 17; d (Y,Z) = 8.
Теперь d (X,Z) = d (X,Y) + d (Y,Z) = 17 + 8
∴ d ( Х, Z) = 25
(ii) Если R — S — T и l (ST) = 3,7, l (RS) = 2,5, то l (RT) =?
(iii) Если X — Y — Z и l (XZ) = 3 7, l (XY) = 7 , то l (ЯЗ) =?
(i)
Имеем l (AC) = 11; л (БК) = 6,5.
Итак, л (АС) = л (АВ) + л (ВС)
Итак, л (АВ) = л (АС) — л — (ВС) = 6,5.
∴ l (AB) = 4,5
Имеем, l (ST) = 3,7; л (RS) = 2,5.
Теперь, l (RT) = l (RS) + l (ST) = 3,7 + 2,5
∴ l (RT) = 5,6
Имеем, l (XZ) = 37; 1 (XY) = 7.
Теперь 1 (XZ) = 1 (XY) + 1 (YZ)
Итак, 1 (YZ) − 6 ( 1 X 903) l (XY) = 37 − 7
∴ l (YZ) = 27
A, B и C — три неколлинеарные точки. Когда A, B и C соединяются, мы получаем ∆ABC.
В данной таблице
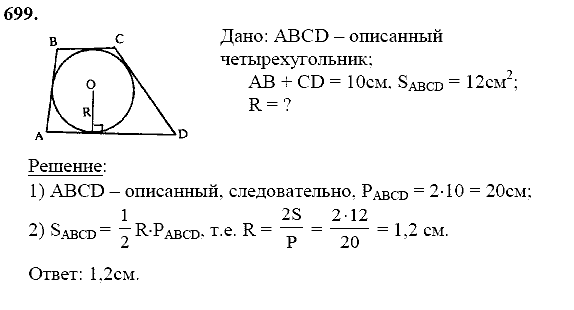Мы знаем, что 9 > −7. ∴ l (DE) = 9 − (−7) = 9 + 7 = 16
Координаты точек A и B равны −3 и 5 соответственно. Мы знаем, что 5 > −3.
∴ l (AB) = 5 − (−3) = 5 + 3 = 8
Так как l (DE) ≠ l (AB), значит, сегмент DE ≇ сегмент AB.
∴ l (BC) = 5 − 2 = 3
Координаты точек A и D равны −3 и −7 соответственно. Мы знаем, что −3 > −7.
∴ l (AD) = −3 − (−7) = −3 + 7 = 4
Поскольку l (BC) ≠ l (AD), значит, сегмент BC ≇ сегмент AD.
∴ l (BE) = 9 − 5 = 4
Координаты точек A и D равны −3 и −7 соответственно. Мы знаем, что −3 > −7.
∴ l (AD) = -3 — (-7) = -3 + 7 = 4
Так как l (BE) = l (AD), поэтому seg BE ≅ seg AD.
Если АВ = 8, то найдите длину АМ.Имеем l (AB) = 8.
Поскольку M — середина отрезка AB, то
l (AM) = 12 из l 1 (AB) 30 326 (AM) = 12 × 8 = 4
Итак, длина AM равна 4.
Имеем l (CP) = 2,5.
Поскольку P является серединой отрезка CD, то
l (CP) = 12 из l (CD)
∴ l (CD) = 2 × l (CP) = 2 × 2,5 = 5
Итак, длина CD равна 5.
Имеем l (АВ) = 5 см; л (ВР) = 2 см; л (АП) = 3,4 см
Мы знаем, что 5 > 3,4 > 2.
Итак, л (АВ) > л (АП) > л (ВР).
∴ сегмент AB > сегмент AP > сегмент BP.
(iii) Напишите объединение луча PQ и луча QR.
(i) Ray RS или Ray RT
(i) Координаты точек B и C равны 2 и 4 соответственно. Мы знаем, что 4 > 2.
∴ d (B, C) = 4 − 2 = 2
Координаты точек B и A равны 2 и 0 соответственно. Мы знаем, что 2 > 0.
∴ d (B, A) = 2 − 0 = 2
Поскольку d (B, A) = d (B, C), то точки A и C равноудалены друг от друга. от точки B.
Координаты точек B и D равны 2 и 6 соответственно. Мы знаем, что 6 > 2,
∴ d (B, D) = 6 − 2 = 4
Координаты точек B и P равны 2 и −2 соответственно. Мы знаем, что 2 > −2.
∴ d (B, P) = 2 − (−2) = 2 + 2 = 4
Поскольку d (B, D) = d (B, P), то точки D и P равноудалены от точки B.
∴ d (Q, U) = −4 − (−5) = −4 + 5 = 1
Координаты точек Q и L равны −4 и −3 соответственно.
Мы знаем, что −3 > −4. ∴ d (Q, L) = −3 − (−4) = −3 + 4 = 1
Поскольку d (Q, U) = d (Q, L), то точки U и L равноудалены от точки Q.
Координаты точек Q и R равны -4 и -6 соответственно. Мы знаем, что −4 > −6.
∴ d (Q, R) = −4 − (−6) = −4 + 6 = 2
Координаты точек Q и P равны −4 и −2 соответственно. Мы знаем, что −2 > −4.
∴ d (Q, P) = −2 − (−4) = −2 + 4 = 2
Поскольку d (Q, R) = d (Q, P), то точки R и P равноудалены от точки Q.
∴ d (U, V) = 5 − (−5) = 5 + 5 = 10
Координаты точек P и C равны −2 и 4 соответственно. Мы знаем, что 4 > −2.
∴ d (P, C) = 4 − (−2) = 4 + 2 = 6
Координаты точек V и B равны 5 и 2 соответственно. Мы знаем, что 5 > 2.
∴ d (V, B) = 5 − 2 = 3
Координаты точек U и L равны -5 и -3 соответственно.
Мы знаем, что −3 > −5. ∴ d (U, L) = −3 − (−5) = −3 + 5 = 2
(i) Если четырехугольник является параллелограммом, то противоположные углы этого четырехугольника равны.
(i) Наклонные углы, образованные двумя параллельными прямыми и их секущей, равны.
(i) Если альтернативные углы, образуемые секущей с двумя прямыми, равны, то прямые параллельны.
(A) 12 (B) 8 (C) 96 (D) 20
Значит, правильный ответ — вариант (А).
Значит, правильный ответ — вариант (С).
Предположим, что точки P, Q и R лежат на одной прямой.
Итак, только одна линия определяется точками P, Q и R.
Предположим, что точки P,Q и R не лежат на одной прямой.
Итак, три линии можно определить по точкам P, Q и R.
Следовательно, правильный ответ — вариант (С).
∴ d (A, B) = 5 − (−2) = 5 + 2 = 7
Следовательно, правильный ответ — вариант (C).
Имеем, d (P,Q) = 2; d (P,R) = 10
Теперь d (P,R) = d (P,Q) + d (Q,R)
∴ d (Q,R) = d (P,R) − d (P,Q) = 10 − 2 = 8
Следовательно, правильный ответ — вариант (B).
(i) d (P,Q) + d (Q,R) = d (P,R)
(ii) d (P,R) + d (R) ,Q) = d (P,Q)
Координаты точек P и Q равны 3 и −5 соответственно. Мы знаем, что 3 > −5.
Теперь d (P, Q) = 3 − (−5) = 3 + 5 = 8
Координаты точек Q и R равны −5 и 6 соответственно.
Мы знаем, что 6 > −5. Теперь d (Q, R) = 6 − (−5) = 6 + 5 = 11
Координаты точек P и R равны 3 и 6 соответственно. Мы знаем, что 6 > 3,
Теперь, d (P, R) = 6 − 3 = 3
Итак, d (P, Q) + d (Q, R) ≠ d (P, R)
Следовательно, данное утверждение неверно.
Итак, d (P, R) + d (R, Q) ≠ d (P, Q)
Следовательно, данное утверждение неверно.
Итак, d (R,P) + d (P,Q) = d (R,Q)
Отсюда , данное утверждение верно.
Итак, d (P, Q) — d (P, R) ≠ d (Q,R)
Следовательно, данное утверждение неверно.
(v) x + 3, x- 3
(vi) -25,-47
(vii) 80, — 85
(i) Пусть координаты A и B равны 3 и 6 соответственно. Мы знаем, что 6 > 3
d (A, B) = 6 − 3 = 3
d (C, D) = −1 − (−9) = −1 + 9 = 8
d (E, F) = 5 − (−4) = 5 + 4 = 9
d (P, Q) = x — (-2) = x + 2
Предположим, x > 0, тогда x + 3 > x — 3 d (R, S) = ( x + 3) — ( x + x 9 — 3 60) = − x + 3 = 2x
d (L, M) = −25 − (−47) = −25 + 47 = 22
d (G, H) = 80 − (−85) = 80 + 85 = 165
Пусть точка R находится справа от точки P, а точка Q — слева от точки P, каждая на расстоянии 8 единиц от точки P.
Координата точки R будет больше, а координата точки Q будет меньше по сравнению с координатой точки P.
Теперь d (P, R) = 8
Итак, координата R − координата P = 8
∴ координата R = 8 + координата P = 8 + (−7) = 8 − 7 = 1
Кроме того, d (Q, P) = 8
Итак, координата P — координата Q = 8
∴ координата Q = координата P − 8 = −7 − 8 = −15
Следовательно, координаты искомых точек на числовой прямой, находящихся на расстоянии 8 единиц от точки P равны 1 и -15.
(i) Если A — B — C и d (A,C) = 17, d (B,C) = 6,5, то d (A,B) = ?
Имеем, d (А, С) = 17; d (B, C) = 6,5
Сейчас, d (A, C) = d (A, B) + d (B, C)
Итак, d (A, B) = d (A, C) − d (B, C) = 17 − 6,5
∴ d (A, B) = 10,5
(P, Q) = 3,4; d (Q, R) = 5,7
Теперь d (P, R) = d (P, Q) + d (Q, R) = 3,4 + 5,7
∴ d (P, R) = 9,1
точка А на числовой прямой равна 1. Каковы координаты точек на числовой прямой, которые находятся на расстоянии 7 единиц от А?Пусть точка C находится справа от точки A, а точка B — слева от точки A, каждая на расстоянии 7 единиц от точки A.
Координата точки C будет больше, а координата точки B будет меньше по сравнению с координатой точки A.
Теперь d (A, C) = 7
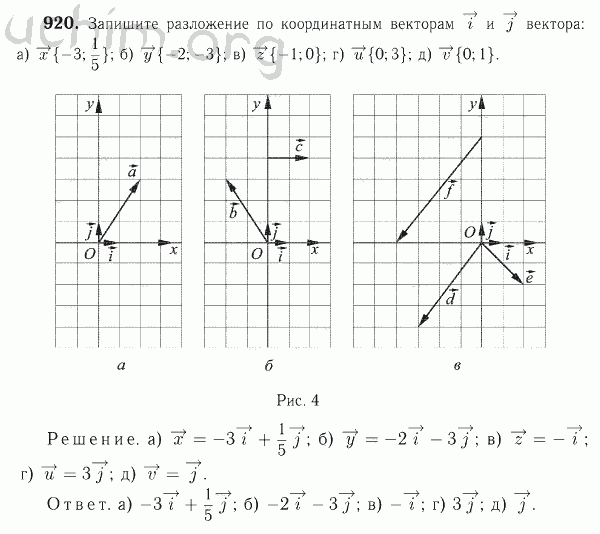
Итак, координата C − координата A = 7
∴ координата C = 7 + координата A = 7 + 1 = 8
Кроме того, d (B, A) = 7
Итак, координата A − координата B = 7
∴ координата B = координата A − 7 = 1 − 7 = −6
Следовательно, координаты искомых точек на числовой прямой, находящихся на расстоянии 7 единиц от точки A равны 8 и −6.
(i) Если данный четырехугольник является квадратом, то он должен быть ромбом.
(ii) Если данные два угла образуют линейную пару, то они являются дополнительными.
(iii) Если данная фигура является треугольником, то она образована тремя сегментами.
(iv) Если данное число имеет только два делителя, то это простое число.
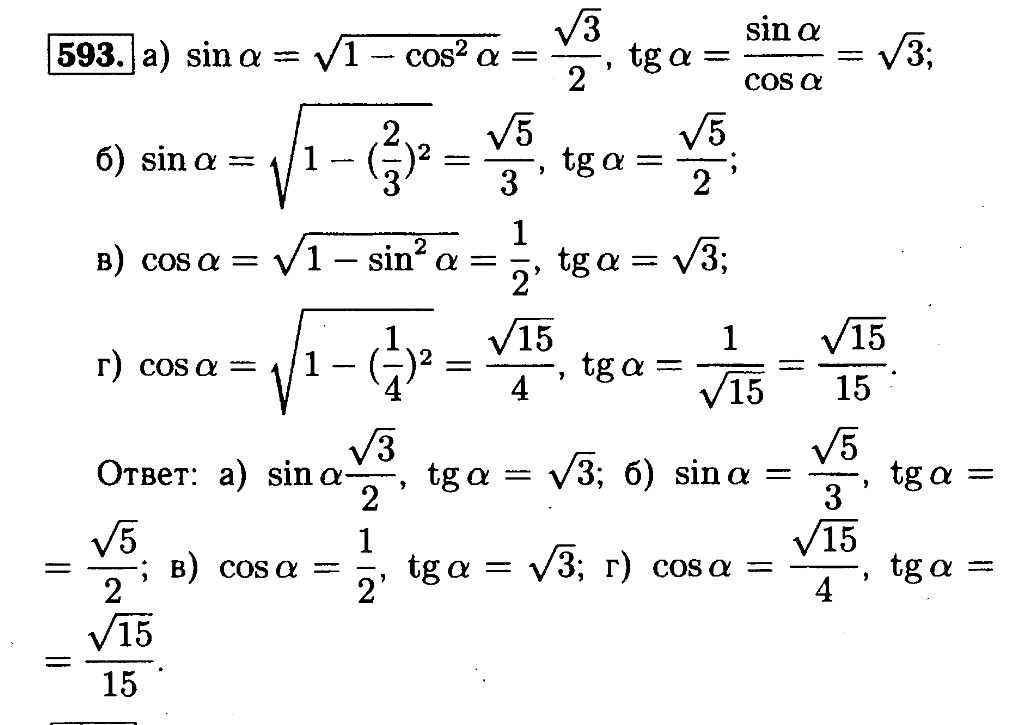
(i) Если данная фигура является треугольником, то сумма мер его углов равна 180 0 .
(i) Предшественник: Все стороны треугольника конгруэнтны.
Следствие: все его углы равны.
Антецедент : Данный четырехугольник является параллелограммом.
Следствие: его диагонали делят друг друга пополам.
(i) Два равносторонних треугольника подобны.
Предшественник: Данные два треугольника равносторонние.
Следствие: они похожи.
Здесь ∆ABC и ∆PQR — равносторонние треугольники, поэтому они подобны друг другу.
Консеквент: каждый из них является прямым углом.
Здесь ∠AOC и ∠BOC, образующие линейную пару, конгруэнтны друг другу, поэтому каждый из них является прямым углом.
