учебник для общеобразовательных учреждений ОНЛАЙН
Погорелов А.В. Геометрия. 7—9 классы : учебник для общеобразовательных учреждений/ А. В. Погорелов. — 10-е изд. — М., 2009. — 224 с. : ил.
Содержание
7 КЛАСС
§ 1. Основные свойства простейших геометрических фигур
1. Геометрические фигуры 3. 2. Точка и прямая 4. 3. Отрезок 5. 4. Измерение отрезков 5. 5. Полуплоскости 6. 6. Полупрямая 7. 7. Угол 8. 8. Откладывание отрезков и углов 10. 9. Треугольник 11. 10. Существование треугольника, равного данному 12. 11. Параллельные прямые 13. 12. Теоремы и доказательства 13. 13. Аксиомы 14. Контрольные вопросы 15. Задачи 16.
§ Смежные и вертикальные углы
14. Смежные углы 21. 15. Вертикальные углы 22. 16. Перпендикулярные прямые 23. 17. Доказательство от противного 24. 18. Биссектриса угла 25. 19. Что надо делать, чтобы успевать по геометрии 25. Контрольные вопросы 26. Задачи 26.
§ 3. Признаки равенства треугольников
20.
Первый признак равенства треугольников 28. 21. Использование аксиом при доказательстве теорем 29. 22. Второй признак равенства треугольников 30. 23. Равнобедренный треугольник 31. 24. Обратная теорема 32. 25. Высота, биссектриса и медиана треугольника 33. 26. Свойство медианы равнобедренного треугольника 33. 27. Третий признак равенства треугольников 34. 28. Как готовиться по учебнику самостоятельно 35. Контрольные вопросы 37. Задачи 37.
§ 4. Сумма углов треугольника
29. Параллельность прямых 42. 30. Углы, образованные при пересечении двух прямых секущей 42. 31. Признак параллельности прямых 43. 32. Свойство углов, образованных при пересечении параллельных прямых секущей 45. 33. Сумма углов треугольника 46. 34. Внешние углы треугольника 46. 35. Прямоугольный треугольник 47. 36. Существование и единственность перпендикуляра к прямой 48. 37. Из истории возникновения геометрии 49. Контрольные вопросы 50. Задачи 51.
§ 5. Геометрические построения
38. Окружность 55. 39.
Окружность, описанная около треугольника 55. 40. Касательная к окружности 56. 41. Окружность, вписанная в треугольник 57. 42. Что такое задачи на построение 70. 43. Построение треугольника с данными сторонами 58. 44. Построение угла, равного данному 59. 45. Построение биссектрисы угла 59. 46. Деление отрезка пополам 59. 47. Построение перпендикулярной прямой 60. 48. Геометрическое место точек 61. 49. Метод геометрических мест 61. Контрольные вопросы 62. Задачи 63.
8 КЛАСС
§ б. Четырехугольники
50. Определение четырехугольника 67. 51. Параллелограмм 68. 52. Свойство диагоналей параллелограмма 69. 53. Свойство противолежащих сторон и углов параллелограмма 70. 54. Прямоугольник 71. 55. Ромб 71. 56. Квадрат 72. 57. Теорема Фалеса 73. 58. Средняя линия треугольника 74. 59. Трапеция 75. 60. Теорема о пропорциональных отрезках 76. 61. Построение четвертого пропорционального отрезка 78. Контрольные вопросы 78. Задачи 79. § Т. Теорема Пифагора
62. Косинус угла 84. 63. Теорема Пифагора 85.
64. Египетский треугольник 86. 65. Перпендикуляр и наклонная 87. 66. Неравенство треугольника 88. 67. Соотношения между сторонами и углами в прямоугольном треугольнике 89. 68. Основные тригонометрические тождества 90. 69. Значения синуса, косинуса и тангенса некоторых углов 91.
70. Изменение синуса, косинуса и тангенса при возрастании угла 93. Контрольные вопросы 93. Задачи 94.
§ Н. Декартовы координаты на плоскости
71. Определение декартовых координат 100. 72. Координаты середины отрезка 101. 73. Расстояние между точками 102. 74. Уравнение окружности 103. 75. Уравнение прямой 104. 76. Координаты точки пересечения прямых 105. 77. Расположение прямой относительно системы координат 106. 78. Угловой коэффициент в уравнении прямой 107. 79. График линейной функции 108. 80. Пересечение прямой с окружностью 108. 81. Определение синуса, косинуса и тангенса для любого угла от 0° до 180° 109. Контрольные вопросы 110. Задачи 111.
§ 9. Движение
82. Преобразование фигур 115.
83. Свойства движения 116. 84. Симметрия относительно точки 117. 85. Симметрия относительно прямой 118. 86. Поворот 120. 87. Параллельный перенос и его свойства 120. 88. Существование и единственность параллельного переноса 122. 89. Сонаправленность полупрямых 123. 90. Равенство фигур 124. Контрольные вопросы 126. Задачи 126. §10. Векторы
91. Абсолютная величина и направление вектора 129. 92. Равенство векторов 130. 93. Координаты вектора 131. 94. Сложение векторов 132. 95. Сложение сил 134. 96. Умножение вектора на число 134.
97. Разложение вектора по двум неколлинеарным векторам 136.
98. Скалярное произведение векторов 137. 99. Разложение вектора по координатным осям 139. Контрольные вопросы 139. Задачи 140.
9 КЛАСС
§11. Подобие фигур
100. Преобразование подобия 145. 101. Свойства преобразования подобия 146. 102. Подобие фигур 147. 103. Признак подобия треугольников по двум углам 148. 104. Признак подобия треугольников по двум
сторонам и углу между ними 149.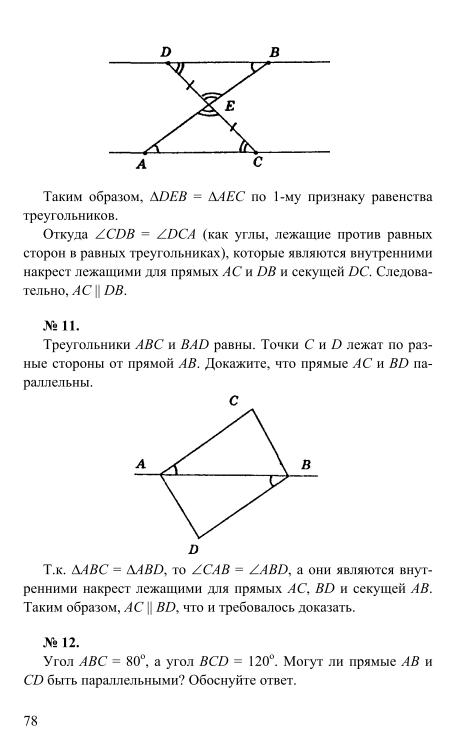
105. Признак подобия треугольников по трем сторонам 150. 106. Подобие прямоугольных треугольников 151. 107. Углы, вписанные в окружность 153.
108. Пропорциональность отрезков хорд и секущих окружности 154. Контрольные вопросы 155. Задачи 156.
§ 12. Решение треугольников
109. Теорема косинусов 161. 110. Теорема синусов 162. 111. Соотношение между углами треугольника и противолежащими сторонами 163.
112. Решение треугольников 164. Контрольные вопросы 166. Задачи 166.
§ 13. Многоугольники
113. Ломаная 168. 114. Выпуклые многоугольники 169. 115. Правильные многоугольники 171. 116. Формулы для радиусов вписанных и описанных окружностей правильных многоугольников 172. 117. Построение некоторых правильных многоугольников 173. 118. Подобие правильных выпуклых многоугольников 174. 119. Длина окружности 175.
120. Радианная мера угла 177. Контрольные вопросы 178. Задачи 179.
§ 14. Площади фигур
121. Понятие площади 182. 122. Площадь прямоугольника 183.
123. Площадь параллелограмма 184. 124. Площадь треугольника 185. 125. Формула Герона для площади треугольника 186. 126. Площадь трапеции 186. 127. Формулы для радиусов вписанной и описанной окружностей треугольника 187. 128. Площади подобных фигур 188.
129. Площадь круга 188. Контрольные вопросы 190. Задачи 191.
§ 15. Элементы стереометрии
130. Аксиомы стереометрии 195. 131. Параллельность прямых и плоскостей в пространстве 196. 132. Перпендикулярность прямых и плоскостей в пространстве 197. 133. Многогранники 200. Задачи 202. 134. Тела вращения 204. Задачи 206.
Ответы и указания к задачам 208.
Предметный указатель 219.
Геометрия для 6-10 класса (Погорелов) 1984 год
Признаки параллельности прямых 37. Сумма углов треугольника 41. Прямоугольный треугольник 43. Существование и единственность перпендикуляра к прямой 44. Вопросы для повторения 45. Упражнения 47.
§ 5. Геометрические построения
Окружность 49. Что такое задачи на построение Б1.
Построение треугольника с данными сторонами 62. Построение угла, равного данному 52. Построение биссектрисы утло 63. Деление отрезка пополам 53. Построение перпендикулярной прямой 54. Геометрическое место точек 55. Метод геометрических мест 56. Углы, в окружность 56. Вопросы для повторения 59. Упражнения 60.
7 КЛАСС
§ 6. Четырехугольники
Определение четырехугольника 65. Параллелограмм 66. Прямоугольник. Ромб. Квадрат 68. Теорема Фалеса 70. Трапеция 72. Вопросы для повторения 73. Упражнения 74.
§ 7. Теорем* Пифагора
Косно ус угла 78. Теорема Пифагор* 80. Соотношения между сторонами п углами прямоугольном треугольнике 82. Как пользоваться таблицами синусов, косинусов п тангенсов 83. Основные тригонометрические тождества 85. Значения синуса, косинуса и тангенса по- которых углов 80. Bln а, со* а и lg а при возраста она утла а 87. Неравенство треугольника 88. Вопросы для повторения 8Э. Упражнения 80.
§ 8. Декартовы координаты на плоскости
Введение координат на плоскости 84.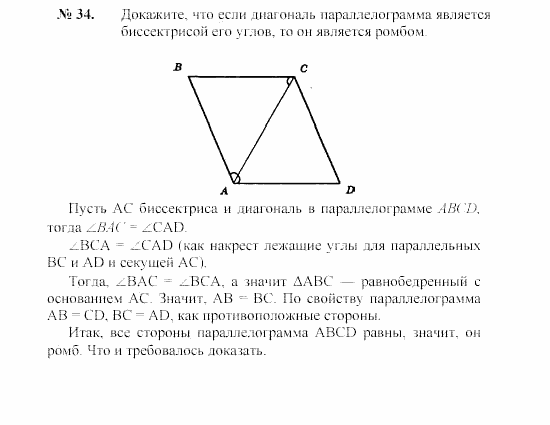
Координаты середины отрезка 80. Расстояние между точками 97. Уравнение окружности 08. Уравнение прямой 101. Расположение прямой относительно системы координат 102. Пересечение прямой с окружностью 104. Определение синуса, косинуса и тангенса для любого утла от 0° до 180’ 104. Вопросы для повторения 105. Упражнения 106.
§ 0. Преобразования фигур
Примеры преобразований фигур 109. Движение 112. Свойства движения 1Н. Равенство фигур. Преобразование подобная и его свойства 117. Подобие фигур 119. Вопросы для повторено! * 121. Упражнения
В КЛАСС
$ 10. Вех юры на плоскости
Параллельный перенос л его свойства 127. Попятив вектора 130. Абсолютная величина и направленно вектора 131. Координаты вектора 133. Сложение векторов 134. Умножение вектора на число 135. Скалярное произведение векторов 137. Вопросы для повторения 139. Упражнения 140.
$ 11. Решение треугольников
Теорема косинусов 144. Теорема синусов 145. Решение треугольников 147. Вопросы для повторения 149.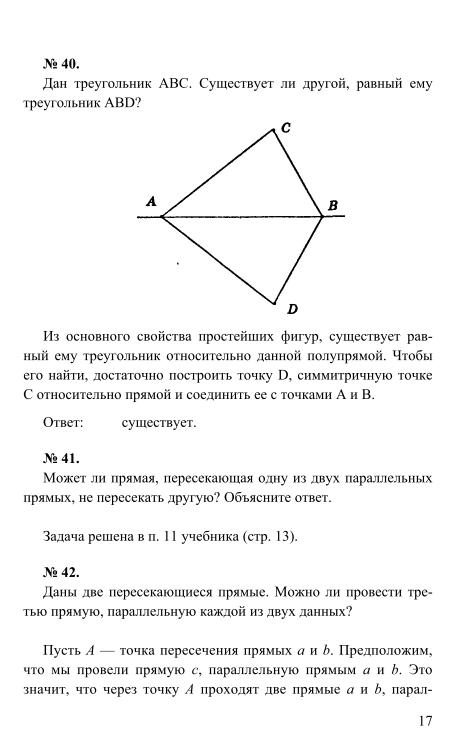
Упражнения 149.
§ 12. Многоугольники
Ломаная 151. Выпуклые многоугольники 153. Правильные многоугольники 154. Длина окружности 156. Центральный угол и дуга окружности 158. Вопроси для повторения 159. Упражнения 159.
§ 13. Площади фигур
Понятие площади 162. Площадь прямоугольника 163. Площади простейших фигур 165. Площади подобных фигур 168. Площадь круга 169. Вопросы доя повторения 171. Упражнения 172.
9 КЛАСС
СТЕРЕОМЕТРИЯ
§ 14. Аксиомы стереометрии
Некоторые следствия аксиом стереометрия 176. Вопросы для повторения 177. Упражнения 176.
§ 15. Параллельность прямых и плоскостей
Параллельные прямые о пространство 178. Параллельность прямой м плоскости 180. Параллельность плоскостей 181. Воображение пространственных фигур ив плоскости 184. Вопросы для повторения 185. Упражнения 186.
S 16. Перпендикулярность прямых на плоскости
Перпендикулярность прямых 189. Перпендикулярность прямой и плоскости 190. Перпендикуляр и наклонная 193.
Перпендикулярность плоскостей 194. Расстояние между скрещивающимися прямыми I9G. Попроси для повторения 197. Упражнения 197.
§ 17. координаты и векторы в пространстве
Введение декартовых координат в пространстве 202. Преобразовании фигур п пространстве 205. Углы между прямыми и плоскостями 207. Площадь ортогональной проекции многоугольника 210. Векторы в пространстве 211. Уравнение плоскости 212. Вопросы для повторения 213. Упражнения 214.
10 КЛАСС
§ 16. Многогранники
Многогранные углы 220. Многогранник 222. Призма 222. Построение плоских сечений 224. Па pa лл слепи лед 225. Пирамида 228. Правильные 231. Вопросы для повторения 232. Упражнении 234.
§ 19. Тела вращения
Цилиндр 239. Конус 240. Шар 243. Уравнение сферы 246. Вопроси для повторения 248. Упражнения 249.
§ 20. Объемы тел
Понятие объема 252. Объем прямоугольного параллелепипеда 253. Объем наклонного параллелепипеда 255. Объем призмы 256. Объем пирамиды 258. Объемы подобных тел 260.
Объемы цилиндра и конуса 261. Общая формула для объемов тел вращения 262. Объем шара и его частей 2G3. Вопросы для повторения 2G4. Упражнения 264.
§21. Площади поверхностей тел
Понятие площади поверхности 270. Площадь сферы 270. Боковая поверхность цилиндра 271. Вопросы для повторения 272. Упражнения 272.
Ответы и указания к упражнениям 274.
рекомендация книги по геометрии и тригонометрии для начинающих
(Примечание: это был ответ на первоначальную версию вопроса.)
Я думаю, что есть много разных ситуаций, когда человек может искать лечение геометрии или тригонометрии, которое в каком-то смысле начинается с нуля. Поэтому мой ответ будет касаться различных сценариев такого рода.
За парой исключений, я упомяну только книги на английском языке. В каждом случае указана дата первого издания на языке оригинала.
1. Вы никогда не изучали эти предметы и у вас мало знаний по математике. Вы стремитесь, в конечном счете, к более высокой способности решать проблемы.
Прочитайте следующие книги Дурелла (все они могут быть загружены с сайта Knowledge-dojo.com):
- Упрощенная геометрия (1931) или Новая геометрия для школ, этап A (1939), затем к
- Новая геометрия для школ, этап B
Эти книги использовались в Англии в основном с 1930-х по 1950-е годы. Первый этап был примерно для 11-13-летних и включал интуитивные аргументы. Второй этап, для 13—16 лет, предусматривал планомерное освоение геометрии.
Позже Дурелл написал книгу « Школьная геометрия и тригонометрия » (1949 г.), в которой унифицированно развивал геометрию и тригонометрию стадии B, но я ее не видел.
2. Вы никогда не видели этих предметов. Вы стремитесь к скромным способностям решать проблемы, сравнимым с уровнем способного ученика, который не учился сверх обычной программы средней школы в США
- Геометрия: курс средней школы (1983 г.
) Лэнга и Мерроу или Базовая геометрия (1940 г.) Биркгофа и Битли. - Тригонометрия (1999) Гельфанда и Сола или Алгебра и тригонометрия (2010) Аклера.
) Лэнга и Мерроу или Базовая геометрия (1940 г.) Биркгофа и Битли.Книга Лэнга и Мерроу обсуждает аксиоматику лишь в скромной степени, учитывая класс читателей. Базовая геометрия с самого начала использует чрезвычайно сильную систему аксиом. В обоих случаях доказательства играют важную роль, но меньшее внимание к основаниям приводит к обсуждению предметной геометрии гораздо быстрее, чем это обычно бывает в школьных учебниках, что сохраняет интерес начинающего читателя.
3. Вы уже знакомы с геометрией/тригонометрией, но хотели бы начать с более систематического изучения предмета. Вы стремитесь к высокому уровню способности решать задачи.
- Школьная геометрия (1930), Фордер.
- Тригонометрия, Часть 1: Промежуточная тригонометрия (1937), МакРоберт и Артур.
Геометрия Фордера предназначалась для детей от 13 до 16 лет в Англии.
Первый том Тригонометрия был «предназначен для использования в первокурсниках университетов и в более продвинутых классах школ» в Шотландии. Хотя предварительного знакомства с тригонометрией строго не требуется, представляется предпочтительным ознакомиться с ней хотя бы в числовой форме вплоть до решения треугольников. В противном случае может показаться, что изложению не хватает мотивации, поскольку книга подробно рассматривает аналитические аспекты, прежде чем обсуждать геометрические приложения к треугольникам и четырехугольникам.
4. Вы уже хорошо разбираетесь в геометрии, но хотели бы прочитать подробное изложение школьной геометрии с нуля. Вы стремитесь к очень высокой способности решать проблемы.
- Уроки геометрии (1898 г.), Адамар.
Эта книга переведена на многие языки, но только первый том по планиметрии имеет английскую версию. Окончательное французское издание появилось в 1949 году.
Хотя оно было написано как учебник для 15-18-летних во Франции, на практике оно было адресовано только самым лучшим из них. Математик Лоран Шварц упоминает в своей автобиографии, что эта книга повлияла на него в школьные годы.
5. Вы хотя бы минимально знакомы с геометрией и хотели бы изучать геометрию ab ovo с помощью подхода, основанного на преобразованиях, с использованием строгой системы аксиом.
- Géométrie plane (1960), Delessert.
Эта книга использовалась со способными подростками в возрасте от 13 до 16 лет в швейцарском кантоне Во. Одной из его интересных особенностей является персонаж Зосиме, который вступает в неоднократные диалоги с автором по поводу концепций аксиом и доказательств.
Как и в следующей книге Погорелова, система аксиом принимает идею числа как данность, основывается на понятии расстояния и включает в себя эквивалент аксиомы Паша о разделении плоскости любой линией на две полуплоскости (что является шагом вперед по сравнению с Евклидом в строгости).
6. Вы достаточно хорошо знаете школьную геометрию, но хотели бы посмотреть, как ее можно разработать ab ovo из строгой системы аксиом, предназначенной для использования с 12-летними детьми.
- Элементарная геометрия (1969) Погорелова.
Эта книга, изначально написанная на русском языке, на первый взгляд кажется учебником, адресованным школьникам, но на самом деле она адресована в первую очередь школьным учителям. Книга не подходит для начинающих из-за недостаточного количества упражнений, особенно легких, а также чрезмерной теоретической сложности некоторых разделов. Например, понятие площади многоугольника не постулируется, а получает правильное определение и тщательно изучается.
7. Вы хоть немного знаете линейную алгебру и хотели бы, чтобы элементарная геометрия развивалась в основном в аналитическом направлении.
- Геометрия: полный курс (1970), Педо.
Основное внимание уделяется интересной геометрии, а не основам.
Обеспечивает существенное введение в проективную геометрию.
8. Вы хотите изучать элементарную геометрию так, как, по мнению Жана Дьёдонне (из Бурбаки), ее следует преподавать 15–18-летним, начиная с аксиом векторного пространства.
- Линейная алгебра и геометрия (1964), Дьедонне.
Вы увидите много линейной алгебры, но мало треугольников, четырехугольников, окружностей или коник.
9. Вы разбираетесь в математике на университетском уровне, и вам интересно увидеть геометрию, разработанную на основе (улучшенной версии) аксиом Гильберта в краткой, удобоваримой форме . Вы также хотите познакомиться с неевклидовой геометрией.
- Лекции по основам геометрии (1959), Погорелова.
Включает главы по гиперболической и проективной геометрии, рассматриваемые с аксиоматической точки зрения. В некотором смысле это можно сравнить с урезанной версией Высшей геометрии Ефимова .
(Мое описание здесь основано на четвертом русском издании 1979 года. Английский перевод, которого я не видел, был из первого русского издания.)
10. Ваши математические способности на университетском уровне. Вы ищете подробное обсуждение основ геометрии.
- Геометрия: Евклид и не только (2000), Хартсхорн.
В книге предлагается прочитать некоторые из Элементов Евклида, в то время как она содержит комментарии и критическую точку зрения с современной точки зрения. Затем следует обширное обсуждение основ геометрии на основе различных модификаций системы аксиом из Основ Гильберта. По сравнению с лекциями Погорелова, здесь сильно акцентируется внимание на последствиях ослабления аксиом полноты и обсуждаются недавние результаты.
запрос ссылки — Почему я не могу найти современные книги по коническим сечениям и аналитической геометрии?
$\begingroup$ Я хочу изучать аналитическую геометрию, но, к сожалению, не могу найти современной книги по этому предмету.
На этом сайте нашел вопрос Хорошие книги по коническому сечению. Но всем приведенным предложениям более века. Я попробовал две главы из двух предложенных книг и больше не могу.
Мои проблемы со старыми книгами
1) Их трудно читать из-за используемого языка.
2) Приведенные задачи такие громоздкие и не дают никакого понимания. Я не ненавижу сложные задачи, но задачи в старых книгах похожи на «фактор этого полинома 5 степени».
3) Не совсем проблема, но форматирование в них действительно плохое.
Мой вопрос: почему нет новых книг на эту тему, новых средств после 1960-70-х годов, нет ли математического интереса к коническим сечениям? или просто продаж этих книг недостаточно для получения прибыли?
- геометрия
- запрос-справка
Вот некоторые английские заголовки на эту тему, написанные за последние несколько десятилетий.
- Аналитическая геометрия , Погорелов (1978, английский перевод 1980)
- Аналитическая геометрия , Испания (1963)
- Аналитическая геометрия , Вайсман (1997)
- Основы линейной алгебры и аналитической геометрии , Бугров и Никольский (1980, английский перевод 1982)
- Лекции по геометрии, семестр I: Аналитическая геометрия , Постников (1979, английский перевод 1982)
В какой-то момент, может быть, в 1960-е годы, два отдельных курса были объединены в один курс: «Исчисление и аналитическая геометрия».
В учебнике по математическому анализу, который я использовал примерно в 1970 году, обсуждались коники. В частности, вращение и перенос координат для придания конике канонического вида.
Но я думаю, что с тех пор такие вещи были значительно сокращены (или даже полностью исключены) из курса.