Геометрия Солтан 9 класс 2020 Упражнение 94 ГДЗ(дүж) решебник KZGDZ.COM
I. Векторы 5. Координаты вектора. Упражнение 94
← Предыдущий Следующий →
Повторение курса геометрии 8 класса.
Упражнение
6789101112131415171920212223242526272829
I. Векторы
1. Понятие вектора. Коллинеарные векторы
Упражнение
3334353637383941
2. Сложение и вычитание векторов
Упражнение
4345464950515253545556
3. Умножение вектора на число. Критерий коллинеарности двух векторов
Упражнение
6162636466676869707172
4. Разложение вектора по двум неколлинеарным векторам.
Упражнение
737475767778798081828384
5. Координаты вектора.
Упражнение
87889093949596979899100101
6.
 Угол между векторами. Скалярное произведение двух векторов.
Угол между векторами. Скалярное произведение двух векторов.Упражнение
103104105
106107108109110112113114115116117118119120
7. Применение векторов при решении задач
Упражнение
121122124126127128
8. Упражнения на повторение раздела «Векторы»
Упражнение
129131132133134135136138139140141142144145
Проверь себя!
Упражнение
148 3B148 4B148 5C
II. Преобразования плоскости.
9. Преобразование плоскости. Движение и его виды
Упражнение
149150151153154155157
10. Применение движений к решению задач
Упражнение
158159160161164165
11. Преобразования гомотетии и подобия, их свойства
Упражнение
166167168169170171172
12.
 Подобные треугольники
Подобные треугольникиУпражнение
174175176177178179180181182183184185186187188189190
13. Подобные многоугольники
Упражнение
192193194195196197
198199200
14. Применение гомотетии и подобия при решении задач.
Упражнение
202203204205206207208
15. Упражнения на повторение раздела «Преобразования плоскости»
Упражнение
209210211212213214215216217218219220221222223224
Проверь себя!
Упражнение
225 4B225 5С
III. Решение треугольников.
16. Теорема синусов
Упражнение
226227228229230231232233234235
17. Теорема косинусов
Упражнение
236237238239240241242243244245246
18. Решение треугольников
Упражнение
247248249250251253254255256257258259
19.
 Углы, вписанные в окружность, и их свойства
Углы, вписанные в окружность, и их свойстваУпражнение
260262263264265266267268269
20. Свойства касательной и секущей, пересекающихся хорд окружности
Упражнение
270271272273274275276277278279
21. Применение тригонометрии к выводу формул площадей треугольника и решению задач
Упражнение
280281282283284285286287288289290291292293294295296297298299300301302303
22. Упражнения на повторение раздела «Решение треугольников»
Упражнение
304305306307308309310311312313
Проверь себя!
Упражнение
314 4В
IV. Окружность. Многоугольники
23. Вписанные в окружность четырехугольники
Упражнение
316317318319320321
24. Описанные около окружности четырехугольники
Упражнение
322323324325326327328329330331332333334
25.
 Правильные многоугольники. Окружности, описанная около правильного многоугольника и вписанная в него
Правильные многоугольники. Окружности, описанная около правильного многоугольника и вписанная в негоУпражнение
336337338339340341342
26. Нахождение длин сторон и площадей правильных многоугольников.
Упражнение
343344345346347348349
27. Длина окружности и ее дуги
Упражнение
351352353354355356357358359360361362
363364365366367368
28. Площадь круга, его сектора и сегмента
Упражнение
370371372373374375376377378379380381382383384385
29. Упражнения на повторение раздела «Окружность. Многоугольники»
Упражнение
386387388389390391392393394395396397398399400401402403404405406407408409
Повторение курса геометрии 9 класса
Упражнение
411412413414415416417418419420421422423424425426427428430431433434435436437438439440441442443444445446
447448449450451452
Номер 94 — ГДЗ по Геометрии для 7-9 класса Учебник Атанасян, Позняк, Кадомцев, Бутузов (решебник)
Номер 94 — ГДЗ по Геометрии для 7-9 класса Учебник Атанасян, Позняк, Кадомцев, Бутузов (решебник) — GDZwowПерейти к содержанию
Search for:
Авторы: Атанасян Л. С., Позняк Э. Г., Кадомцев С. Б., Бутузов В.Ф.
С., Позняк Э. Г., Кадомцев С. Б., Бутузов В.Ф.
Издательство: Просвещение
Тип: Учебник
Номера
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273747576777879808182838485868788899091929394959697989910010110210310410510610710810911011111211311411511611711811912012112212312412512612712812913013113213313413513613713813914014114214314414514614714814915015115215315415515615715815916016116216316416516616716816917017117217317417517617717817918018118218318418518618718818919019119219319419519619719819920020120220320420520620720820921021121221321421521621721821922022122222322422522622722822923023123223323423523623723823924024124224324424524624724824925025125225325425525625725825926026126226326426526626726826927027127227327427527627727827928028128228328428528628728828929029129229329429529629729829930030130230330430530630730830931031131231331431531631731831932032132232332432532632732832933033133233333433533633733833934034134234334434534634734834935035135235335435535635735835936036136236336436536636736836937037137237337437537637737837938038138238338438538638738838939039139239339439539639739839940040140240340440540640740840941041141241341441541641741841942042142242342442542642742842943043143243343443543643743843944044144244344444544644744844945045145245345445545645745845946046146246346446546646746846947047147247347447547647747847948048148248348448548648748848949049149249349449549649749849950050150250350450550650750850951051151251351451551651751851952052152252352452552652752852953053153253353453553653753853954054154254354454554654754854955055155255355455555655755855956056156256356456556656756856957057157257357457557657757857958058158258358458558658758858959059159259359459559659759859960060160260360460560660760860961061161261361461561661761861962062162262362462562662762862963063163263363463563663763863964064164264364464564664764864965065165265365465565665765865966066166266366466566666766866967067167267367467567667767867968068168268368468568668768868969069169269369469569669769869970070170270370470570670770870971071171271371471571671771871972072172272372472572672772872973073173273373473573673773873974074174274374474574674774874975075175275375475575675775875976076176276376476576676776876977077177277377477577677777877978078178278378478578678778878979079179279379479579679779879980080180280380480580680780880981081181281381481581681781881982082182282382482582682782882983083183283383483583683783883984084184284384484584684784884985085185285385485585685785885986086186286386486586686786886987087187287387487587687787887988088188288388488588688788888989089189289389489589689789889990090190290390490590690790890991091191291391491591691791891992092192292392492592692792892993093193293393493593693793893994094194294394494594694794894995095195295395495595695795895996096196296396496596696796896997097197297397497597697797897998098198298398498598698798898999099199299399499599699799899910001001100210031004100510061007100810091010101110121013101410151016101710181019102010211022102310241025102610271028102910301031103210331034103510361037103810391040104110421043104410451046104710481049105010511052105310541055105610571058105910601061106210631064106510661067106810691070107110721073107410751076107710781079108010811082108310841085108610871088108910901091109210931094109510961097109810991100110111021103110411051106110711081109111011111112111311141115111611171118111911201121112211231124112511261127112811291130113111321133113411351136113711381139114011411142114311441145114611471148114911501151115211531154115511561157115811591160116111621163116411651166116711681169117011711172117311741175117611771178117911801181118211831184118511861187118811891190119111921193119411951196119711981199120012011202120312041205120612071208120912101211121212131214121512161217121812191220122112221223122412251226122712281229123012311232123312341235123612371238123912401241124212431244124512461247124812491250125112521253125412551256125712581259126012611262126312641265126612671268126912701271127212731274127512761277127812791280128112821283128412851286128712881289129012911292129312941295129612971298129913001301130213031304130513061307130813091310
Вопросы для повторения
Глава 1
123456789101112131415161718192021
Глава 2
123456789101112131415161718192021
Глава 3
123456789101112131415
Глава 4
1234567891011121314151617181920
Глава 5
1234567891011121314151617181920
Глава 6
12345678910
Глава 7
123456789101112131415161718
Глава 8
1234567891011121314151617181920212223242526
Глава 9
1234567891011121314151617181920
Глава 10
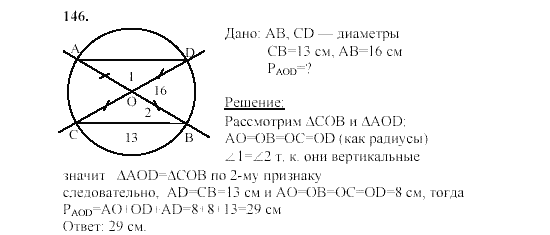
123456789101112131415161718192021
Глава 11
123456789101112131415161718192021
Глава 12
123456789101112
Глава 13
1234567891011121314151617
Глава 14
1234567891011121314151617181920212223242526
Adblockdetector
Mathematics_part_ _II_(решения) для 9 класса Math Chapter 7
Mathematics_part_ _II_(solutions) Здесь представлены решения для 9 класса Math Chapter 7 Co Ordinate Geometry с простыми пошаговыми пояснениями. Эти решения для Co Ordinate Geometry чрезвычайно популярны среди учащихся 9 класса по математике Co Ordinate Geometry Solutions пригодятся для быстрого выполнения домашних заданий и подготовки к экзаменам. Все вопросы и ответы из Книги по математике_часть__II_(решения) для 9 классаMath Chapter 7 предоставляется здесь для вас бесплатно. Вам также понравится отсутствие рекламы в Mathematics_part_ _II_(solutions) Solutions от Meritnation. Все решения Mathematics_part_ _II_(solutions) для класса 9 Math подготовлены экспертами и на 100% точны.
Эти решения для Co Ordinate Geometry чрезвычайно популярны среди учащихся 9 класса по математике Co Ordinate Geometry Solutions пригодятся для быстрого выполнения домашних заданий и подготовки к экзаменам. Все вопросы и ответы из Книги по математике_часть__II_(решения) для 9 классаMath Chapter 7 предоставляется здесь для вас бесплатно. Вам также понравится отсутствие рекламы в Mathematics_part_ _II_(solutions) Solutions от Meritnation. Все решения Mathematics_part_ _II_(solutions) для класса 9 Math подготовлены экспертами и на 100% точны.
Страница № 93:
Вопрос 1:
Укажите, в каком квадранте или на какой оси лежат следующие точки.
• A(-3, 2), • B(-5, -2), • K(3.5, 1.5), • D(2, 10),
• E(37, 35), • F(15, -18), • G(3, -7), • H(0, -5),
• M(12, 0), • N( 0, 9), • P(0, 2.5), • Q(-7, -3)
Ответ:
Координата x отрицательна, и ее y координата положительная. Следовательно, точка A(−3, 2) находится во втором квадранте.
Следовательно, точка A(−3, 2) находится во втором квадранте.
Координата x точки B(−5, −2) отрицательна, а ее координата y отрицательна. Следовательно, точка B(−5, −2) находится в третьем квадранте.
Координата x точки K(3,5, 1,5) положительна, а ее координата
Координата x D(2, 10) положительна, а ее координата y положительна. Следовательно, точка D(2, 10) находится в первом квадранте.
Координата x точки E(37, 35) положительна, а ее координата y положительна. Следовательно, точка E(37, 35) находится в первом квадранте.
Координата x F(15, −18) положительна, а ее координата y отрицательна. Следовательно, точка F(15, −18) находится в четвертом квадранте.
Координата x точки G(3, −7) положительна, а ее координата y отрицательна.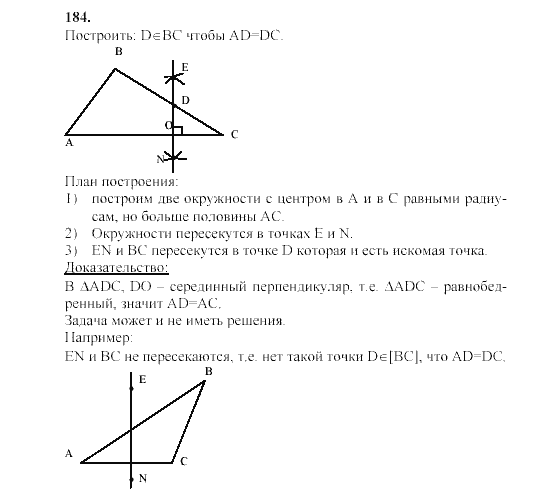 Следовательно, точка G(3, −7) находится в четвертом квадранте.
Следовательно, точка G(3, −7) находится в четвертом квадранте.
Координата x точки H(0, −5) равна нулю. Следовательно, точка H(0, −5) находится на оси Y.
Координата y M(12, 0) равна нулю. Следовательно, точка M(12, 0) находится на оси X.
Координата x N(0, 9) равна нулю. Следовательно, точка N(0, 9) находится на оси Y.
Координата x точки P(0, 2,5) равна нулю. Следовательно, точка P(0, 2,5) находится на оси Y.
Координата x точки Q(−7, −3) отрицательна, а ее координата y отрицательна. Следовательно, точка Q(−7, −3) находится в третьем квадранте.
Страница № 93:
Вопрос 2:
В каком квадранте находятся следующие точки?
(i), обе координаты которого положительны.
(ii), обе координаты которого отрицательны.
(iii), чья координата x положительна, а координата y отрицательна.
(iv) чья координата x является отрицательной, а координата y положительной.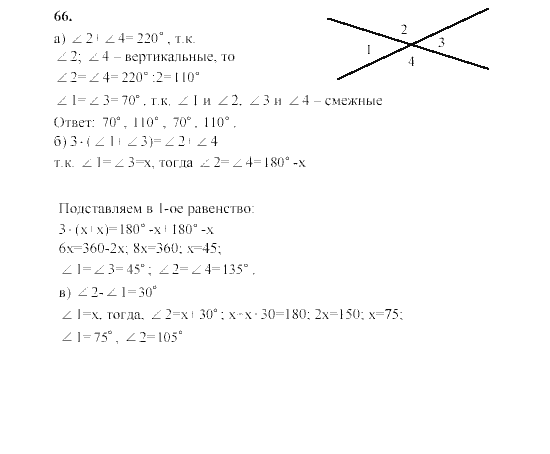
Ответ:
(i) Координата x и координата y точки положительны в первом квадранте .
(ii) Координата x и координата y точки являются отрицательными в третьем квадранте .
(iii) Координата x точки положительна, а координата y точки отрицательна в четвертом квадранте .
(iv) Координата x точки отрицательна, а координата y точки положительна во втором квадранте .
Страница № 93:
Вопрос 3:
Нарисуйте систему координат на плоскости и нанесите следующие точки.
L(-2, 4), M(5, 6), N(-3,-4), P(2,-3), Q(6,-5), S(7, 0), T(0,-5)
Ответ:
Данные точки: L(−2, 4), M(5, 6), N(−3, −4), P(2, −3), Q (6, −5), S(7, 0) и T(0, −5).
Эти точки можно изобразить в системе координат следующим образом:
Страница № 97:
Вопрос 1:
На миллиметровой бумаге нанесите точки A (3,0), B(3,3), С(0,3). Соедините A, B и B, C. Какая фигура образовалась?
Соедините A, B и B, C. Какая фигура образовалась?
Ответ:
Даны точки: A(3, 0), B(3, 3) и C(0, 3). Эти точки можно нанести на координатную плоскость следующим образом:
Координата точки x — это расстояние от оси Y, а координата точки y — это расстояние от оси X. .
Здесь OA = AB = BC = OC = 3 единицы
Следовательно, образованная фигура представляет собой квадрат.
Страница № 97:
Вопрос 2:
Напишите уравнение прямой, параллельной оси Y на расстоянии 7 единиц от нее влево.
Ответ:
Уравнение прямой, параллельной оси Y на расстоянии 7 единиц от нее слева, равно x = −7.
Страница № 97:
Вопрос 3:
Напишите уравнение прямой, параллельной оси X на расстоянии 5 единиц от нее и ниже оси X.
Ответ:
Уравнение прямой, параллельной оси X на расстоянии 5 единиц от нее и ниже оси X, равно y = −5.
Страница № 97:
Вопрос 4:
Точка Q(-3, -2) лежит на прямой, параллельной оси Y. Напишите уравнение прямой и нарисуйте ее график.
Напишите уравнение прямой и нарисуйте ее график.
Ответ:
Координата x точки — это расстояние от оси Y, а координата y — это расстояние от оси X.
Точка пересечения линии, параллельной оси Y, на расстоянии 3 единицы от нее слева от нее и линии, параллельной оси X, на расстоянии 2 единицы ниже нее, равна (−3, −2).
Уравнение прямой, параллельной оси Y на расстоянии 3 единиц от нее влево, равно x = −3.
Страница № 98:
Вопрос 5:
Ось X и линия x = -4 являются параллельными линиями. Какое расстояние между ними?
Ответ:
Отказ от ответственности : Вопрос некорректен. Вопрос должен звучать так: «Ось Y и линия x = -4 являются параллельными линиями. Каково расстояние между ними? или Ось X и линия y = -4 являются параллельными линиями. Каково расстояние между ними?»
Если вопрос «Ось Y и линия x = -4 являются параллельными линиями. Каково расстояние между ними?», то ответ будет следующим.
Каково расстояние между ними?», то ответ будет следующим.
x = -4 — это уравнение прямой, параллельной оси Y на расстоянии 4 единиц и левее оси Y.
Таким образом, расстояние между ними равно 4 единицам.0023 y = -4 — параллельные прямые. Каково расстояние между ними?», то ответ будет следующим.
y = −4 есть уравнение прямой, параллельной оси X на расстоянии 4 единиц и ниже оси X.
Таким образом, расстояние между ними составляет 4 единицы.
(и) х = 3 (ii) y -2 = 0 (iii) x + 6 = 0 (iv) y = -5
представляет собой уравнение прямой, параллельной оси Y на расстоянии 3 единиц и правее оси Y.
Таким образом, график линии x = 3 параллелен оси Y.
(ii)
y − 2 = 0
⇒ y = 2
y = 2 — уравнение прямой, параллельной оси X и на расстоянии 2 ось.
Таким образом, график прямой y − 2 = 0 параллелен оси X.
(iii)
x + 6 = 0
⇒ x = −6
x = −6 — уравнение прямой, параллельной оси Y на расстоянии 6 единиц от нее слева.
Таким образом, график прямой x + 6 = 0 параллелен оси Y.
(iv)
y = −5 — уравнение прямой, параллельной оси X на расстоянии 5 единиц и ниже оси X.
Таким образом, график линии y = -5 параллелен оси X.
Страница № 98:
Вопрос 7:
Нарисуйте на миллиметровке точки A(2, 3), B(6,-1) и C(0, 5). Если эти точки лежат на одной прямой, нарисуйте линию, включающую их. Запишите координаты точек, в которых линия пересекает оси X и оси Y.
Ответ:
Данными точками являются A(2, 3), B(6, −1) и C(0, 5).
Линия, включающая эти точки, показана ниже:
Из графика видно, что линия пересекает ось X в точке (5, 0) и ось Y в точке (0, 5).
Страница № 98:
Вопрос 8:
Изобразите графики следующих уравнений в той же системе координат.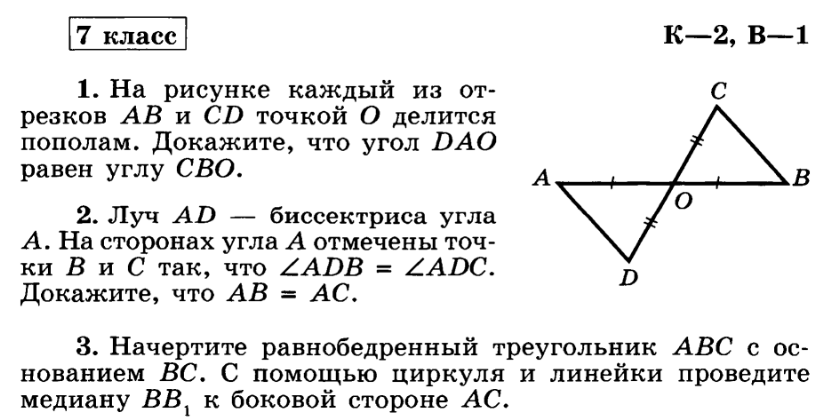 Напишите координаты точек их пересечения.
Напишите координаты точек их пересечения.
x + 4 = 0, y -1 = 0, 2 x + 3 = 0, 3 y
Ответ:
x + 4 = 0 ⇒ x = −4
x = −4 — уравнение прямой, параллельной оси Y на расстоянии 4 единиц от нее слева от нее.
y − 1 = 0 ⇒ y = 1
y = 1 — уравнение прямой, параллельной оси X на расстоянии 1 единицы и выше оси X.
2 x + 3 = 0 ⇒ x = -32
x = -32 — уравнение прямой, параллельной оси Y на расстоянии 32 единицы от нее слева от нее.
3 y − 15 = 0 ⇒ y = 153 = 5
y = 5 — уравнение прямой, параллельной оси X на расстоянии 5 единиц и выше оси X.
Из рисунка видно, что координаты точек пересечения равны -32, 1, -32, 5, (-4, 5) и (-4, 1).
Страница № 98:
Вопрос 9:
Нарисуйте графики приведенных ниже уравнений
(i) x + y = 2 (ii) 3 x — y = 0 (iii) 2 x + y
Ответ:
(i)
x + y = 2
⇒ y = 2 — x . …. (1)
…. (1)
Постановка x = 0 в (1), мы получаем
Y = 2 − 0 = 2
Подставляя x = 2 в (1), получаем
y = 2 − 2 = 0
Подставляя x = −1 в (1), получаем
y = 2 − (−1) = 2 + 1 = 3
Подставляя x = 5 в (1), получаем 3 9000
y = 2 − 5 = −3
Эти значения можно представить в таблице в виде упорядоченных пар следующим образом:
| х | 0 | 2 | −1 | 5 |
| г | 2 | 0 | 3 | −3 |
| ( x , и | (0, 2) | (2, 0) | (-1, 3) | (5, −3) |
Нанесите эти точки на миллиметровую бумагу.
Линия представляет собой график уравнения x + y = 2.
(ii)
Уравнение данной прямой 3 x — y = 0.
3 x — y = 0
⇒ y = 3 x ….. (1)
Положение x = 0 в (1), мы получаем
y = 3 × 0 = 0
Поместите x = 1 дюйм (1), мы получаем
y = 3 × 1 = 3
Положение x = = 3 × 1 = 3
. −1 в (1) получаем
y = 3 × (−1) = −3
Подставляя x = 2 в (1), получаем
y = 3 × 2 = 6
Эти значения можно представить в таблице в виде упорядоченных пар следующим образом:
| х | 0 | 1 | −1 | 2 |
| у | 0 | 3 | −3 | 6 |
| ( x , и ) | (0, 0) | (3, 0) | (-1, -3) | (2, 6) |
Нанесите эти точки на миллиметровую бумагу.
Линия представляет собой график уравнения 3 x — y = 0.
(iii)
Уравнение данной линии 2 x + y = 1.
2. x + y = 1
⇒ y = 1 − 2 x …..(1)
Подставляя x = 0 в (1), получаем
y = 1 − 2 × 0 = 1 − 0 = 1
Подставляя x 03 = 9003, получаем y = 1 − 2 × 1 = 1 − 2 = −1
Подставляя x = −1 в (1), получаем
y = 1 − 2 × (−1) = 1 + 2 = 3
Положив в (1) x = 2, получим
y = 1 − 2 × 2 = 1 – 4 = −3
Эти значения можно представить в таблице в виде упорядоченных пар следующим образом:
| х | 0 | 1 | −1 | 2 |
| у | 1 | −1 | 3 | −3 |
| ( x , и ) | (0, 1) | (1, −1) | (-1, 3) | (2, −3) |
Нанесите эти точки на миллиметровую бумагу.
Линия представляет собой график уравнения 2 x + y = 1.
Страница № 98:
Вопрос 1:
Выберите правильный альтернативный ответ на следующие вопросы.
(i) Каковы координаты точки на оси X?
(A) ( b , b ) (B) ( o , b ) (C) ( a , o ) (D) ( a , a )
(ii) Любая точка на прямой y = x равна 9 0 0 0 0 2 4 (A) ( A , A ) (B) ( O , A ) (C) ( A , O ) (D) ( A , — A )
(iii) Что представляет собой уравнение оси X?
(A) x = 0 (B) y = 0 (c) x + y = 0 (d) x = y
(iv), в которой квадрант делает точку (-4, -3). ?
(А) Первая (Б) Вторая (В) Третья (Г) Четвертая -3,5), (0,5) ?
(A) Проходит через начало координат, (B) Параллельно оси Y. (C) Параллельно оси X (D) Ничего из перечисленного
(C) Параллельно оси X (D) Ничего из перечисленного
(vi) Какая из точек P (-1,1), Q (3,-4), R(1,-1), S (-2,-3), T (-4,4) лежат в четвертом квадранте?
(A) P и T (B) Q и R (C) только S (D) P и R
Ответ:
(i)
Координата y каждой точки на X- ось равна 0. Таким образом, координаты точки на оси X равны ( a , 0).
Следовательно, правильный ответ — вариант (С).
(ii)
Помещение x = a в y = x , мы получаем
Y = A
Таким образом, любая точка на линии Y = x имеет форму ( A , A ).
Следовательно, правильный ответ — вариант (А).
(iii)
Координата y каждой точки на оси X равна 0. Следовательно, уравнение оси X равно y = 0.
Следовательно, правильный ответ — вариант ( Б).
(iv)
x 9Координата 0024 (−4, −3) отрицательна, а ее координата y отрицательна.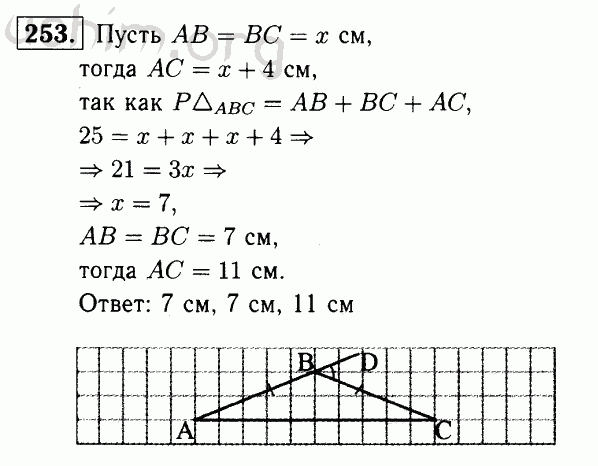 Следовательно, точка (−4, −3) лежит в третьем квадранте.
Следовательно, точка (−4, −3) лежит в третьем квадранте.
Следовательно, правильный ответ — вариант (С).
(v)
Координата y всех точек (−5, 5), (6, 5), (−3, 5) и (0, 5) равна 5. Все эти точки лежат на линия y = 5, параллельная оси X.
Таким образом, линия, включающая точки (−5, 5), (6, 5), (−3, 5) и (0, 5), параллельна оси X.
Следовательно, правильный ответ — вариант (С).
(vi)
Точка, у которой координата x положительная, а координата y отрицательная, находится в четвертом квадранте.
Таким образом, точки Q(3, −4) и R(1, −1) лежат в четвертом квадранте.
Следовательно, правильный ответ — вариант (Б).
Страница № 99:
Вопрос 2:
На данном рисунке показаны некоторые точки, с помощью которых ответьте на следующие вопросы:
(i) Запишите координаты точек Q и R.
(ii) Запишите координаты точек T и M.
(iii) Какая точка лежит в третьем квадранте?
(iv) Какие точки имеют равные координаты x и y ?
Ответ:
(i) Координата x точки — это ее расстояние от оси Y, а координата y точки — это ее расстояние от оси X.
Координаты точки Q равны (−2, 2), а координаты точки R равны (4, −1).
(ii) Координата x каждой точки по оси Y равна 0, а координата y каждой точки по оси X равна 0.
Координаты точки T равны (0, −1), а координаты точки M равны (3, 0).
(iii) Точка, координата x отрицательна, а координата y отрицательна, находится в третьем квадранте.
Таким образом, точка S(−3, −2) лежит в третьем квадранте.
(iv) Координаты точки O (0, 0).
Таким образом, O — это точка, чьи координаты x и y равны.
Страница № 99:
Вопрос 3:
Не нанося точки на график, укажите, в каком квадранте или на какой оси находится следующая точка.
(i) (5,-3) (ii) (-7, -12) (iii) (-23, 4) (iv) (-9, 5) (v) (0, -3) (vi) (-6, 0)
Ответ:
(i) Координата x точки (5, −3) положительна, а ее y отрицательная координата. Следовательно, точка (5, −3) лежит в четвертом квадранте.
(ii) Координата x точки (−7, −12) отрицательна, а ее координата y отрицательна. Следовательно, точка (−7, −12) лежит в третьем квадранте.
(iii) Координата x точки (−23, 4) отрицательна, а ее координата y положительна. Следовательно, точка (−23, 4) лежит во втором квадранте.
(iv) x координата точки (−9, 5) отрицательна, а ее y координата положительна. Следовательно, точка (−9, 5) лежит во втором квадранте.
(v) x координата точки (0, −3) равна нулю. Следовательно, точка (0, −3) лежит на оси Y.
(vi) Координата y точки (−6, 0) равна нулю. Следовательно, точка (−6, 0) лежит на оси X.
Страница № 99:
Вопрос 4:
Нанесите следующие точки в одной и той же системе координат.
A(1, 3), B(-3, -1), C(1, -4), D(-2, 3), E(0, -8), F(1, 0)
Ответ:
Даны точки: A(1, 3), B(−3, −1), C(1, −4), D(−2, 3), E(0, −8) и F (1, 0).
Эти точки можно нанести в системе координат следующим образом:
Страница № 99:
Вопрос 5:
На приведенном рядом графике линия LM параллельна оси Y.
(i) Каково расстояние линии LM от оси Y?
(ii) Запишите координаты точек P, Q и R.
(iii) В чем разница между x координатами точек L и M?
Ответ:
(i) Прямая LM параллельна оси Y и проходит через точку (3, 0).
Уравнение прямой LM равно x = 3 и находится на расстоянии 3 единиц справа от оси Y.
Таким образом, расстояние линии LM от оси Y равно 3 единицам.
(ii) Координата x точки — это ее расстояние от оси Y, а координата y — это расстояние от оси X.
Таким образом, координаты точек P, Q и R равны (3, 2), (3, −1) и (3, 0) соответственно.
(iii)
x координата точки L = 3
x координата точки M = 3
∴ Разность между x координатами точек L и M = 3 − 3 = 0
Таким образом, разница между x координаты точек L и M равны 0.
Номер страницы 99:
Вопрос 6:
Сколько существует прямых, параллельных оси X и отстоящих друг от друга на 5 единиц?
Ответ:
Уравнения прямых, параллельных оси X и находящихся на расстоянии 5 единиц от нее: y = 5 и y = −5.
Итак, имеются две прямые, параллельные оси X и отстоящие от нее на 5 единиц.
Страница № 99:
Вопрос 7:
Если « a » — действительное число, каково расстояние между осью Y и линией x = a ?
Ответ:
Прямая x = a параллельна оси Y, проходящей через ( a , 0).
Если a > 0, то линия будет на расстоянии a единиц справа от оси Y.
Если a < 0, то линия будет на расстоянии a единицы слева от оси Y.
Таким образом, расстояние между осью Y и линией x = a равно | и | единицы измерения.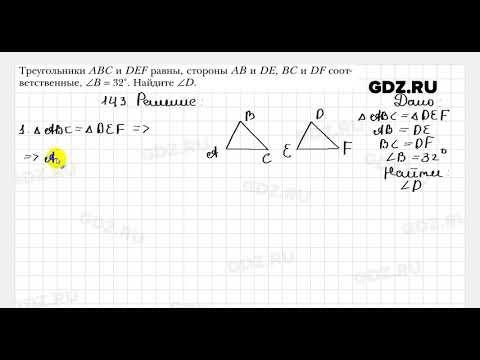
MATH-7-UNIT-5-Google SUCHE
ALLBILDERSHOPPINGNEWSMAPSVIDEOSBücher
SUCOOPTION
7 класс. Математика, блок 5-Curricaly
Access.OpenUpresources. 7.5 Арифметика рациональных чисел … Урок 1 · Интерпретация отрицательных чисел … Урок 7 · Сложение и вычитание для решения задач …
N-Gen Math 7.Unit 5.Lesson 1.The Properties of Real Numbers
www.youtube.com › смотреть
19.12.2019 · В этом уроке мы рассмотрим ассоциативные и коммутативные свойства сложения и . ..
Dauer: 18:27
Прислан: 19.12.2019
N-Gen Math 7.Unit 5.Lesson 5.Combining LikeTerms — YouTube
www.youtube.com › смотреть
227.0 · На этом уроке учащиеся повторяют понятия коэффициентов и им подобных терминов. Они то понимают…
Дата: 20:26
Прислано: 27.01.2020
Математика 7 Раздел 5 — Альта Сьерра Промежуточный — Объединенный школьный округ Кловис
altasierra. cusd.com › Math7Unit5
cusd.com › Math7Unit5
Математика Unitrational Mathematical 7 Gradeative Арифметика. Загрузить студенческое издание в формате PDF · Загрузить практическую работу учащегося в формате PDF (домашнее задание).
Глава 5 — Линейные выражения — eMATHinstruction
www.emathinstruction.com › … › N-Gen Math™ 7
Модуль 5 – Линейные выражения. Урок 1. Свойства действительных чисел. УРОК/ДОМАШНЕЕ ЗАДАНИЕ … Урок 7. Факторинг биномов. УРОК/ДОМАШНЕЕ ЗАДАНИЕ. ЛЕКЦИОН/ТАРЕЯ.
Иллюстративная математика 7 класс, раздел 5 — Учителя | IM Demo
currency.illustrativemathematics.org › учителя › 5
7.5 Арифметика рациональных чисел. В этом блоке учащиеся интерпретируют числа со знаком в контексте (например, температура, высота над уровнем моря, ввод и вывод, положение, …
Mr. Morgan’s Math Help — Unit 5 — Rational Number Arithmetic
site.google.com › illustrative-mathematics › math-7
Math 7 Unit 5 Homework. pdf · Math 7 Unit 5 Family Materials.pdf · Math 7 Модуль 5 — Полное студенческое издание.pdf.
pdf · Math 7 Unit 5 Family Materials.pdf · Math 7 Модуль 5 — Полное студенческое издание.pdf.
Веб-страница г-жи Клеменс-Брентон — Математика 7, раздел 5 — Сайты Google
site.google.com › nlesd.ca › math-7 › class-notes
NLESD Resources · Math 9 · Class Notes · Homework /Задания/Объявления. Блок 5 — Дроби, десятичные дроби и проценты. НАЗАД. Сообщить о нарушении.
[PDF] GSE Grade 7 Unit 5: Inferences — Georgia Standards
www.georgiastandards.org › frameworks › 7th-math-unit-5
Таким образом, учащиеся могут рассматривать математику как нечто большее, чем набор мнемоник или дискретные процедуры. Учащиеся демонстрируют глубокое концептуальное понимание …
Math 7 Unit 5 Percents — Digital Notes Bundle — 6 наборов Notes — TPT
www.teacherspayteachers.com › Продукт › Math-7-…
5, 75 $
Этот пакет включает в себя все мои ресурсы по математике 7 единиц 5 процентов. Это включает в себя задачи дня, цифровые заметки + заметки в формате PDF (оба варианта), мероприятия, .
