Гдз по геометрии 9 класс номер 941: Номер 941 — ГДЗ по геометрии 7-9 класс Атанасян

Содержание

Номер (задание) 941 — гдз по геометрии 7-9 класс Атанасян, Бутузов

Условие / номер / 941

941 Найдите периметр треугольника MNP, если М(4;0), N (12; -2), Р (5;-9).

Решебник №1 / номер / 941

Видеорешение / номер / 941

решебник №2 / номер / 941

решебник №3 / номер / 941

Решебник №4 / номер / 941

ГДЗ номер 941 алгебра 7 класс Макарычев, Миндюк – Telegraph

➡➡➡ ПОДРОБНЕЕ ЖМИТЕ ЗДЕСЬ!

ГДЗ номер 941 алгебра 7 класс Макарычев, Миндюк

ГДЗ (готовое домашние задание из решебника) на Номер задания №941 по учебнику Алгебра 7 класс : учебник для общеобразовательных учреждений Ю .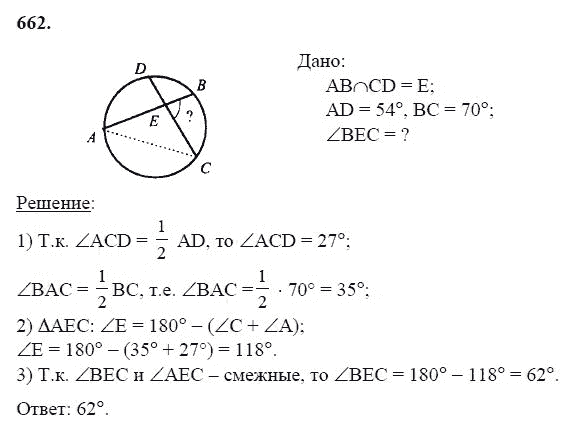 Н . Макарычев , Н .Г . Миндюк, К .И . Нешков, С .Б . Суворова; Просвещение, -2019

ГДЗ : готовые ответы по алгебре за 7 класс , решебник Ю .Н . Макарычев Углубленный уровень, онлайн решения на GDZ .RU .
ФГОС Макарычев , Миндюк , Нешков Просвещение > Задание : 941 . Изображения обложек учебников приведены на страницах данного сайта исключительно в качестве иллюстративного материала (ст . 1274 п . 1 ГДЗ алгебра 7 класс Макарычев , Миндюк, Нешков Просвещение .

ГДЗ по алгебре 7 класс Макарычев , Миндюк номер 941 . Автор ГДЗ (готовые домашние задания ), решебник онлайн по алгебре за 7 класс авторов Макарычев , Миндюк задание (номер ) 941 — вариант решения упражнения 941 .

➜ Ответ к заданию №941 — готовое решение к учебнику по Алгебре 7 класс (упражнение 941 ) . Авторы: Ю .Н . Макарычев , Н .Г . Миндюк, К .И . Нешков, С .Б . Суворова, С . А Ответы к учебнику по алгебре за 7 класс Макарычев , Миндюк , Нешков, Суворова — номер 941 . Общая оценка

Задача №941 , ГДЗ по алгебре за 7 класс к учебнику Макарычева . Ответы из решебника . Макарычев , Миндюк, Нешков . 14 . Преобразование целых выражений . Номер №941 .

Гдз по алгебре за 7 класс Макарычев , Миндюк ответ на номер № 941 . Авторы: Ю .Н . Макарычев , Н .Г . Миндюк , К .И . Нешков, С .Б . Суворова . Издательство: Просвещение год . Тип: Учебник . Подробный решебник (ГДЗ ) по Алгебре за 7 (седьмой ) класс . .

Номер № 941 из решебника ГДЗ на учебник по Алгебре 7 класса от авторов Ю .Н . Макарычев , Н .Г . Миндюк, К .И . Нешков, С .Б . Суворова .

Всё для учебы » ГДЗ бесплатно » » Номер 941 — ГДЗ по алгебре , 7 класс , Макарычев . Чтобы добавить страницу в закладки, нажмите Ctrl+D . Если страница помогла, сохраните её и поделитесь ссылкой с друзьями

Видео решение к номеру 941 по алгебре за 7 класс , авторов Ю .Н . Макарычев , Н .Г . Миндюк , К .И . Нешков, С .Б . Суворова . Более подробное гдз к этому заданию можно . .
Математический словарь . Главная ГДЗ ГДЗ по алгебре 7 класс Макарычев 1997-2001-2003 г онлайн .

Задание № 941 — Алгебра 7 класс (Макарычев ) Посмотрел видео? Пройди тест: Пройди тест Письменное решение Другие номера § 14 . Преобразование целых выражений 38 . Применение различных способов для разложения на множители 934 935 936 937 938 939 940 941 942 943 . .

Нумерация заданий совпадает с номером и темой урока школьной программы — ученик сможет самолично находить необходимую информацию ГДЗ к рабочей тетради по алгебре за 7 класс Миндюк Н .Г . можно посмотреть тут . Алгебра 7 класс углубленный уровень Макарычев изд .

Авторы: Ю .Н . Макарычев , Н .Г . Миндюк, К .И . Нешков, С .Б . Суворова . Поэтому, стоит выделить несколько плюсов, почему списывание из онлайн-решебника по алгебре для 7 класса от Макарычева Ю .Н ., Н .Г . Миндюк,К .И . Нешкова,С .Б . Суворова будет лучшим выбором

В ГДЗ к пособию авторов Макарычев , Миндюк, Нешков, Суворова делается акцент на главных понятиях предмета, а также объясняется каждая новая формула . Используя решебник для самопроверок и подсказок подросток не будет отставать от трудной школьной программы и . .

ГДЗ (готовое домашние задание из решебника) на Номер задания №941 по учебнику Алгебра 7 класс : учебник для общеобразовательных учреждений Ю .Н . Макарычев , Н .Г . Миндюк, К .И . Нешков, С .Б . Суворова; Просвещение, -2019

Авторы: Ю .Н . Макарычев , Н .Г . Миндюк, К .И . Нешков, С .Б . Суворова . Поэтому, стоит выделить несколько плюсов, почему списывание из онлайн-решебника по алгебре для 7 класса от Макарычева Ю . Н ., Н .Г . Миндюк,К .И . Нешкова,С .Б . Суворова будет лучшим выбором

ГДЗ §91 С1 физика 11 класс Мякишев, Буховцев
ГДЗ учебник 2019 / часть 2. упражнение 255 (1144) математика 6 класс Виленкин, Жохов
ГДЗ самостійні роботи / СР-4. варіант 2 геометрия 8 класс тестовый контроль знаний Гальперина
ГДЗ Unit 3 / раздел 1-8 125 английский язык 8 класс Enjoy English Биболетова, Трубанева
ГДЗ раздел 1 6 информатика 3 класс Горячев, Горина
ГДЗ § 31 31.10 алгебра 11 класс учебник, задачник Мордкович, Денищева
ГДЗ номер 220 алгебра 10‐11 класс Колмогоров, Абрамов
ГДЗ unit 1 / section 7 13 английский язык 6 класс Enjoy English Биболетова, Денисенко
ГДЗ номер 346 математика 6 класс Дорофеев, Шарыгин
ГДЗ страница 104 английский язык 5 класс Joy of English (1-й год обучения) Пахомова
ГДЗ страница 97 физика 8 класс Барьяхтар, Божинова
ГДЗ опыт 17 химия 9 класс Рудзитис, Фельдман
ГДЗ вариант 2 / тесты / Т-2 1 алгебра 7 класс дидактические материалы к учебнику Макарычева Звавич, Дяконова
ГДЗ страница 72 английский язык 5 класс Spotlight, student’s book Ваулина, Дули
ГДЗ по литературе 1 класс Климанова, Горецкий Решебник
ГДЗ упражнение 346 русский язык 6 класс Ладыженская, Баранов
ГДЗ страница 7 английский язык 4 класс Start Up! Павличенко, Доценко
ГДЗ по физике 7 класс дидактические материалы Марон, Марон Решебник
ГДЗ номер 1089 алгебра 7 класс Мерзляк, Полонский
ГДЗ часть 2 / в худшем случае 5 математика 6 класс задачник Бунимович, Кузнецова
ГДЗ страница 128 химия 9 класс рабочая тетрадь Габриелян, Сладков
ГДЗ вправа 109 алгебра 7 класс Истер
ГДЗ § 2 37 геометрия 10‐11 класс Погорелов
ГДЗ упражнение 169 русский язык 7 класс Рыбченкова, Александрова
ГДЗ часть 1. страница 8 английский язык 5 класс rainbow Афанасьева, Баранова
ГДЗ решаем устно 19 математика 5 класс Мерзляк, Полонский
ГДЗ упражнение 217 русский язык 8 класс Ладыженская, Тростенцова
ГДЗ тетрадь №1. страница 30 математика 4 класс рабочая тетрадь Гейдман, Мишарина
ГДЗ упражнение 142 русский язык 6 класс Практика Лидман-Орлова, Пименова
ГДЗ § 21 4 история 7 класс рабочая тетрадь История России Данилов, Косулина
ГДЗ часть 2 / упражнение 230 русский язык 4 класс Желтовская, Калинина
ГДЗ по английскому языку за 10 класс, решебник и ответы онлайн
ГДЗ глава 21 / § 21.5 4 химия 9 класс Гузей, Сорокин
ГДЗ раздел 2 44 информатика 3 класс Горячев, Горина
ГДЗ задание 145 информатика 9 класс рабочая тетрадь Босова, Босова
ГДЗ номер 910 алгебра 7 класс Мерзляк, Полонский
ГДЗ номер 761 алгебра 8 класс Никольский, Потапов
ГДЗ вправа 885 алгебра 8 класс Истер
ГДЗ страница 80 геометрия 8 класс рабочая тетрадь Глазков, Камаев
ГДЗ проверь себя 15 русский язык 3 класс рабочая тетрадь учусь писать без ошибок Кузнецова
ГДЗ страница 69 математика 4 класс тетрадь для контрольных работ Рудницкая, Юдачева
ГДЗ самостоятельная работа / самостоятельная работа №16 / вариант 3 5 алгебра 7 класс дидактические материалы Феоктистов
ГДЗ самостоятельные работы / С-23 / вариант 4 3 математика 5 класс дидактические материалы Потапов, Шевкин
ГДЗ раздел 1 (номер) 36 история 7 класс рабочая тетрадь Кочегаров
ГДЗ страница 42 английский язык 3 класс рабочая тетрадь Spotlight Быкова, Эванс
ГДЗ самостоятельная работа / вариант 3 28 математика 6 класс дидактические материалы Чесноков, Нешков
ГДЗ часть 2 313 математика 4 класс ИстоминаБ
ГДЗ часть №1 437 математика 6 класс Петерсон, Дорофеев
ГДЗ часть №1 / упражнение 65 математика 2 класс Александрова
ГДЗ глава 6 / упражнение 139 русский язык 5 класс Шмелев, Флоренская

ГДЗ По Истории 6

Русский Язык 10 Класс Богданова ГДЗ Часть

ГДЗ По Английскому 9 Лапицкая

Решебник Рабочая Русский 4

ГДЗ 5 Класс Номер 32

%d0%bd%d0%be%d0%bc%d0%b5%d1%80 954 %d1%80%d0%b5%d1%88%d0%b5%d0%b1%d0%bd%d0%b8%d0%ba %d0%bf%d0%be %d0%b3%d0%b5%d0%be%d0%bc%d0%b5%d1%82%d1%80%d0%b8%d0%b8 7 9 %d0%ba%d0%bb%d0%b0%d1%81%d1%81 %d0%b0%d1%82 – Corona Todays

аве мария мадонна и святые More Auction Sotheby S

Search the world’s information, including webpages, images, videos and more. google has many special features to help you find exactly what you’re looking for. Video uploaded from my mobile phone. Winscp is a free sftp, scp, amazon s3, webdav, and ftp client for windows. Date: mon, 8 mar 2021 10:42:46 0000 (utc) message id: [email protected] he de.apache.org> subject: exported from confluence mime version: 1.0. Message id: [email protected] 123> subject: exported from confluence mime version: 1.0 content type: multipart related; boundary.

аве мария мадонна и святые More Auction Sotheby S

7 идей детских игр на свежем воздухе, сделанных своими руками Все 7 идей 407 Посмотреть ещё 8 фотографий. =d0=a1=d0=bc=d0=b5=d0=bd=d0= =b0 pin =d0=ba=d0=be=d0=b4=d0=b0 =d0=92 =d0=b7=d0=b0=d0=b2=d0=b8=d1=81=d0=b8=d0=bc=d0=be=d1=81=d1=82=d0= =b8 =d0=be=d1=82 =d0=bf=d0=be=d0. =20 =d0=a7=d1=82=d0=be=d0=b1=d1=8b =d0=b8=d0=b7=d0=b1=d0=b5=d0=b6=d0=b0=d1= =82=d1=8c =d0=bc=d0=be=d1=88=d0=b5=d0=bd=d0=bd=d0=b8=d1=87=d0=b5=d1=81=d0= =ba=d0=b8=d1=85.

Самые лучшие видео приколы сентября 2011.mp4

letitbit download 19419.10a2cf849444f998e23638510f72 %25d0%25a1%25d0%25b0%25d0%25bc%25d1%258b%25d0%25b5 %25d0%25bb google url?sa=t&source=web&rct=j&url= v s.mobi amp %25d1%2581%25d0%25bb%25d0%25b0%25d0%25b9%25d0%25bc % img: lh4.googleusercontent ipls5v0sku4 wpedxnwu00i aaaaaaaaa s mtj0iublfumcondssmkb4mlr1lsksppcqcjoc w5120 h3880 Вышитый крестиком галстук к 1 сентября, схема, МК Ссылка на схемы галстуков: Ссылка на подписку петиции: yandex.ru clck jsredir?text=%d0%b2%d0%ba&from=yandex.ru%3bsuggest%3bweb&state=dtype%3dstred%2fpid%3d1%2fcid%3d71868%2fpart% скачать google imgres?imgurl=http%3a%2f%2fandrey eltsov.ru%2fwp content%2fuploads%2f2018%2f10%2f%25d0%25bf%25d0%259f% letitbit download 02307.098ceb980d66a3dec0aa63d713a4 %25d0%25a1%25d0%25b0%25d0%25bc%25d1%258b%25d0%25b5 %25d0% сыллка google url?sa=t&source=web&rct=j&url= inshot editor.ru.uptodown android%23:~:text%3dinshot%2520editor%2520%

% PDF-1.6 % 1175 0 объект> эндобдж xref 1175 81 0000000016 00000 н. 0000005133 00000 п. 0000005318 00000 н. 0000005354 00000 п. 0000005669 00000 н. 0000005796 00000 н. 0000005922 00000 н. 0000006049 00000 п. 0000006176 00000 п. 0000006303 00000 н. 0000006430 00000 н. 0000006557 00000 н. 0000006684 00000 п. 0000006811 00000 н. 0000006939 00000 п. 0000007066 00000 н. 0000007266 00000 н. 0000007748 00000 н. 0000007845 00000 н. 0000010410 00000 п. 0000011201 00000 п. 0000012018 00000 н. 0000012793 00000 п. 0000013061 00000 п. 0000013693 00000 п. 0000013796 00000 п. 0000014078 00000 п. 0000014447 00000 п. 0000014713 00000 п. 0000014891 00000 п. 0000015545 00000 п. 0000015717 00000 п. 0000017559 00000 п. 0000017867 00000 п. 0000018233 00000 п. 0000018431 00000 п. 0000027898 00000 н. 0000028512 00000 п. 0000028938 00000 п. 0000029452 00000 п. 0000030526 00000 п. 0000030743 00000 п. 0000031092 00000 п. 0000031745 00000 п. 0000032627 00000 н. 0000033313 00000 п. 0000033550 00000 п. 0000036019 00000 п. 0000036126 00000 п. 0000036534 00000 п. 0000036863 00000 п. 0000037281 00000 п. 0000037597 00000 п. 0000038787 00000 п. 0000039399 00000 п. 0000039979 00000 п. 0000040686 00000 п. 0000040853 00000 п. 0000041117 00000 п. 0000041381 00000 п. 0000041999 00000 п. 0000042641 00000 п. 0000043154 00000 п. 0000043704 00000 п. 0000044290 00000 п. 0000064061 00000 п. 0000072724 00000 н. 00000

00000 п. 0000096600 00000 п. 0000096660 00000 п. 0000096748 00000 н. 0000096835 00000 п. 0000096975 00000 п. 0000097128 00000 п. 0000097262 00000 п. 0000097396 00000 п. 0000097542 00000 п. 0000097685 00000 п. 0000097809 00000 п. 0000097921 00000 п. 0000001916 00000 н. трейлер ] >> startxref 0 %% EOF 1255 0 obj> поток xYkL [66! 1ccp.v ZW + m8t? L8_6OBZ [ng י̟ C מ ~ ׆4_ Ė? Z! Nč \ | `9rOow ‘~ aÖ / c r!> {4xm7X`ЎX | H» ym = Ց ޒ E ۃݨ VWjӹ # ,: 1 &} (lI | FqGk {vN \

рупий Aggarwal 2018 для класса 9 по математике Глава 9

Лист № 282:

Вопрос 1:

На данном рисунке AB || CD и O — это середина AD .
Покажите, что
(i) Δ AOB ≅ Δ DOC .
(ii) O — это середина г. до н.э. .

Ответ:

Дано: На данном рисунке AB || CD и O — это середина AD .

Доказать:
(i) Δ AOB ≅ Δ DOC .
(ii) O — это середина г. до н.э. .

Проба:
(i) In Δ AOB и Δ DOC ,
∠ BAO = ∠ CDO (Альтернативные внутренние углы, AB || CD )
AO = DO (дано, O является средней точкой AD )
∠ AOB = ∠ DOC (вертикально противоположные углы)

∴ По критериям соответствия ASA
Δ AOB ≅ Δ DOC

(ii) ∵ Δ AOB ≅ Δ DOC [Из (i)]
∴ BO = CO (CPCT)
Следовательно, O является средней точкой BC .

Лист № 282:

Вопрос 2:

На данном рисунке AD и BC равны перпендикулярам к отрезку линии AB . Покажите, что CD делит пополам AB .

Ответ:

Дано: На данном рисунке AD и BC равны перпендикулярам к отрезку линии AB .

Доказательство: CD делит пополам AB

Доказательство:
In Δ AOD и Δ BOC ,
∠ DAO = ∠ CBO = 90 ° (дано)
AD = BC (дано)
∠ DOA = ∠

COB (вертикально противоположные углы)

∴ По критериям конгруэнтности AAS
Δ AOD ≅ Δ BOC
∴ AO = BO (CPCT)
Следовательно, CD делит пополам AB .

Лист № 282:

Вопрос 3:

На данном рисунке две параллельные линии l и m пересекаются двумя параллельными линиями p и q .
Покажите, что Δ ABC ≅ Δ CDA .

Ответ:

Дано: На данном рисунке две параллельные линии l и m пересекаются двумя параллельными линиями p и q .

Доказать: Δ ABC ≅ Δ CDA

Проба:
In Δ ABC и Δ CDA ,

∠ BAC = ∠ DCA (Альтернативные внутренние углы, p ∥ q )
∠ BCA = ∠ DAC (Альтернативные внутренние углы, l ∥ м )
AC = CA (Общая сторона)

∴ По критериям соответствия ASA,
Δ ABC ≅ Δ CDA

Лист № 283:

Вопрос 4:

AD — это равнобедренная высота Δ ABC , в которой AB = AC .
Покажите, что (i) AD делит пополам BC , (ii) AD делит пополам ∠ A .

Ответ:

Дано: AD — это равнобедренная высота Δ ABC , в которой AB = AC .

Для доказательства: (i) AD делит пополам BC , (ii) AD делит пополам ∠ A

Доказательство:
(i) In Δ ABD и Δ ACD ,

∠ ADB = ∠ ADC = 90 ° (Дано, AD ⊥ BC )
AB = AC (Дано)
AD = AD (Общая сторона)

∴ По совпадению RHS критерии,
Δ ABD ≅ Δ ACD

∴ BD = CD (CPCT)

Следовательно, AD делит пополам BC .

(ii)
∵ Δ ABD ≅ Δ ACD [Из (i)]
∴ ∠ BAD = ∠ CAD (CPCT)
Следовательно, AD делит пополам A .

Лист № 283:

Вопрос 5:

На данном рисунке BE и CF — две равные высоты Δ ABC.
Покажите, что (i) ΔABE ≅ ΔACF, (ii) AB = AC.

Ответ:

В ABE и △ ACF имеем: BE = CF (дано) ∠BEA = ∠CFA = 90 ° ∠A = ∠A (Common) △ ABE≅ △ ACF (критерий AAS)
AB = AC (CPCT)

Лист № 283:

Вопрос 6:

Δ ABC и Δ DBC — два равнобедренных треугольника на одном основании BC , а вершины A и D находятся на одной стороне BC .Если AD продлен до пересечения BC на E , покажите, что
(i) Δ ABD ≅ Δ ACD
(ii) Δ ABE ≅ Δ ACE
(iii) AE делит пополам ∠ A , а также ∠ D
(iv) AE является серединным перпендикуляром к BC .

Ответ:

Дано: Δ ABC и Δ DBC — два равнобедренных треугольника на одном основании BC.

Для подтверждения:
(i) Δ ABD ≅ Δ ACD
(ii) Δ ABE ≅ Δ ACE
(iii) AE делит пополам ∠ A , а также ∠ D
(iv) AE — серединный перпендикуляр к BC

Доказательство:
(i) In Δ ABD и Δ ACD ,

BD = CD (Учитывая, Δ DBC — равнобедренный треугольник)
AB = AC (Дано, Δ ABC — равнобедренный треугольник)
AD = AD (Общая сторона)

∴ По критерию конгруэнтности SSS,
Δ ABD ≅ Δ ACD

Также BAD = CAD (CPCT)
или BAE = ∠ CAE….. (1)

(ii)
In Δ ABE и Δ ACE ,

AB = AC (Дано, Δ ABC — равнобедренный треугольник)
∠ BAE = ∠ CAE [Из (i)]
AE = AE (Общая сторона)

∴ По критериям соответствия SAS
Δ ABE ≅ Δ ACE

Также BE = CE (CPCT) ….. (2)
А, AEB = ∠ AEC (CPCT) ….. (3)

(iii)
В Δ BED и Δ CED ,

BD = CD (Учитывая, что Δ DBC — равнобедренный треугольник)
BE = CE [Из (2)]
DE = DE (Общая сторона)

∴ По критериям соответствия SSS
Δ BED ≅ Δ CED

Также ∠ BDE = CDE (CPCT) ….. (4)

(iv)
∵ ∠ BAE = CAE [Из (1)]
А, BDE = ∠ CDE [Из (4)]
∴ AE делит пополам ∠ A , а также ∠ D .

(v)
∵∠AEB + ∠AEC = 180 ° Линейная пара⇒∠AEB + ∠AEB = 180 ° Из 3⇒2∠AEB = 180 ° ⇒∠AEB = 180 ° 2⇒∠AEB = 90 ° …. .5

Из (2) и (5) получаем
AE — серединный перпендикуляр к BC .

Лист № 283:

Вопрос 7:

На данном рисунке, если x = y и AB = CB , то докажите, что AE = CD .

Ответ:

Рассмотрим треугольники AEB и CDB.

∠EBA = ∠DBC (Общий угол) … (i)

Далее имеем:

∠BEA = 180-y∠BDC = 180-x Так как x = y, имеем: 180-x = 180 -y ⇒∠BEA = ∠BDC … (ii)

AB = CB (Дано) … (iii)
Из (i), (ii) и (iii) имеем:
△ BDC≅ △ BEA (критерий AAS)
∴ AE = CD (CPCT)
Следовательно, доказано.

Лист № 283:

Вопрос 8:

На данном рисунке линия l — это биссектриса угла ∠ A и B — любая точка на l .Если BP и BQ перпендикуляры от B к плечам ∠ A , покажите, что
(i) Δ APB ≅ Δ AQB
(ii) BP = BQ , т.е. B равноудалена от плеч ∠ A .

Ответ:

Дано: На данном рисунке B AQ = ∠ BAP , BP ⊥ AP и BQ ⊥ AQ .

Для доказательства:
(i) Δ APB ≅ Δ AQB
(ii) BP = BQ , т.е. B равноудалена от плеч A .

Проба:
(i) In Δ APB и Δ AQB ,

∠ B AQ = ∠ BAP , (дано)
∠ APB = ∠ AQB = 90 ° (Дано, BP ⊥ AP и BQ ⊥ AQ )
AB = AB (Общая сторона)

∴ По критериям соответствия AAS
Δ APB ≅ Δ AQB

(ii)
∵ Δ APB ≅ Δ AQB [Из (i)]
∴ BP = BQ (CPCT)
Следовательно, B находится на одинаковом расстоянии от плеч A .

Лист № 283:

Вопрос 9:

ABCD — это четырехугольник, у которого диагональ AC делит пополам углы ∠ A и ∠ C . Докажите, что AB = AD и CB = CD .

Ответ:

Дано: В четырехугольнике ABCD , AC делят пополам углы ∠ A и ∠ C .

Доказать: AB = AD и CB = CD

Доказательство:
In ∆ ABC и ∆ ADC ,

∠ BAC = ∠ DAC (Учитывая, AC делит углы пополам ∠ A )
AC = AC (Общая сторона)
∠ BCA = ∠ DCA (Учитывая, AC делит углы пополам ∠ C )

∴ По критериям соответствия ASA
∆ ABC ≅∆ ADC

Следовательно, AB = AD и CB = CD .(CPCT)

Лист № 283:

Вопрос 10:

Δ ABC — это прямоугольный треугольник, расположенный под прямым углом в точке A , такой, что AB = AC , а биссектриса ∠ C пересекает сторону AB в точке D . Докажите, что AC + AD = BC.

Ответ:

Дано: В прямоугольном треугольнике Δ ABC , ∠ BAC = 90 °, AB = AC и ∠ ACD = ∠ BCD .

Доказать: AC + AD = BC

Доказательство:
Пусть AB = AC = x и AD = y .

In ∆ ABC ,

BC2 = AB2 + AC2⇒BC2 = x2 + x2⇒BC2 = 2×2⇒BC = 2×2⇒BC = x2

Итак,

BDAD = BCAC (биссектриса угла треугольник делит противоположную сторону на два сегмента, которые пропорциональны двум другим сторонам треугольника.)
⇒x-yy = x2x⇒xy-yy = 2⇒xy-1 = 2⇒xy = 2 + 1⇒y = x2 + 1
⇒y = x2 + 1 × 2-12-1⇒y = x2- 122-12⇒y = x2-x2-1⇒y = x2-x⇒x + y = x2

Следовательно, AC + AD = BC .

Лист № 284:

Вопрос 11:

На данном рисунке OA = OB и OP = OQ . Докажите, что (i) PX = QX , (ii) AX = BX .

Ответ:

Доказательство:
В △ OQA и △ OPB имеем: OQ = OP (дано) OA = OB (дано) ∠AOQ = ∠BOP (Common) △ OQA≅OPB (критерий SAS)
∠OAQ = ∠OBP (соответствующий углы конгруэнтных треугольников)
Теперь рассмотрим треугольники BQX и APX.
Дано: OA = OBOP = OQ∴ OA-OP = OB-OQ⇒AP = BQ
Далее, ∠BXQ = ∠AXP (вертикально противоположные углы)
Также мы доказали, что ∠QBX = ∠PAX.
∆BQX≅∆APX (критерий AAS)

∴ PX = QX (соответствующие стороны конгруэнтных треугольников)
Кроме того, AX = BX (соответствующие стороны конгруэнтных треугольников)
Следовательно, доказано.

Лист № 284:

Вопрос 12:

На этом рисунке ABC — равносторонний треугольник; PQ || AC и AC производятся по R , так что CR = BP. Докажите, что QR делит пополам PC .

Ответ:

Так как ∆ABC — равносторонний ∆, то ABC = ∠BCA = ∠CAB = 60 ° Поскольку PQ∥CA и PC — трансверсаль, то BPQ = ∠BCA = 60 ° Соответствующие углы Поскольку PQ∥CA и QA трансверсаль , То BQP = ∠BAC = 60 ° Соответствующие углы Далее, ∠B = 60 ° В ∆BPQ, ∠B = ∠BPQ = ∠BQP = 60 ° ∴ △ BPQ — равносторонний треугольник.т.е. BP = PQ = BQNow, BP = CR⇒PQ = CR …. 1 Учитывая △ MPQ и △ MCR, получаем: ∠PQM = ∠MRC Альтернативные внутренние углы PMQ = ∠CMR Вертикально противоположные углы PQ = CR с использованием 1 ∆MPQ≅∆MCR Критерий AAS⇒MP = MC Соответствующие части конгруэнтных треугольников равны ⇒QR делит пополам PC.

Лист № 284:

Вопрос 13:

На данном рисунке ABCD представляет собой четырехугольник, в котором AB || DC и P — это середина BC .При производстве AP и DC встречаются в Q . Докажите, что (i) AB = CQ , (ii) DQ = DC + AB .

Ответ:

В ABP и △ QCP имеем: ∠BPA = ∠CPQ (вертикально противоположный угол) ∠PAB = ∠PQC (альтернативные углы) PB = PC (P — средняя точка) △ ABP≅ △ QCP (критерий AAS)

∴ AB = CQ (CPCT)

DQ = DC + CQ ⇒DQ = DC + AB (Доказано, AB = CQ)
Следовательно, доказано.

Лист № 284:

Вопрос 14:

На данном рисунке ABCD — квадрат, а P — точка внутри него, так что PB = PD . Докажите, что CPA — прямая линия.

Ответ:

В △ PAD и △ PAB имеем: AD = AB (сторона квадрата) AP = AP (общий) PD = PB (заданный) △ PAD≅PAB (критерий SSS) ⇒∠APD = ∠APB

In △ CPD и △ CPB, имеем: CD = CB (стороны квадрата) CP = CP (общие) PD = PB (задано) △ CPD≅ △ CPB (тест SSS) ⇒∠CPD = ∠CPB

∴∠APD + ∠CPD = ∠APB + ∠CPBBut∠APD + ∠CPD + ∠APB + ∠CPB = 360 ° ⇒∠APD + ∠CPD = 180 °

Итак, CPA — прямая линия.
Значит, доказано.

Лист № 284:

Вопрос 15:

На данном рисунке O — это точка внутри квадрата ABCD , так что Δ OAB представляет собой равносторонний треугольник. Покажите, что Δ OCD — равнобедренный треугольник.

Ответ:

Дано: В квадрате ABCD Δ OAB представляет собой равносторонний треугольник.

Доказать: Δ OCD — равнобедренный треугольник.

Проба:

∵∠DAB = ∠CBA = 90 ° Углы квадрата ABCDAnd, ∠OAB = OBA = 60 ° Углы равносторонних ∆OAB∴∠DAB-∠OAB = ∠CBA-∠OBA = 90 ° -60 ° ⇒∠OAD = ∠OBC = 30 ° ….. i

Теперь, в Δ DAO и Δ CBO ,

AD = BC (Стороны квадрата ABCD )
∠ DAO = ∠ CBO [Из (i)]
AO = BO (Стороны равностороннего Δ OAB )

∴ По критериям соответствия SAS
Δ DAO ≅ Δ CBO

Итак, OD = OC (CPCT)
Следовательно, Δ OCD — равнобедренный треугольник.

Лист № 284:

Вопрос 16:

На соседнем рисунке X и Y представляют собой две точки на равных сторонах AB и AC ∆ ABC соответственно, так что AX = AY . Докажите, что CX = BY .

Ответ:

В AXC и △ AYB имеем: AC = AB (дано) AX = AY (дано) ∠BAC = ∠CAB (угол, общий для △ AXC и △ AYB) ∴ △ AXC≅ △ AYB (критерий SAS) Итак, CX = BY (CPCT)
Следовательно, доказано.

Лист № 285:

Вопрос 17:

In ∆ ABC , D — это средняя точка BC . Если DL ⊥ AB и DM ⊥ AC так, что DL = DM , докажите, что AB = AC .

Ответ:

В BDL и △ CDM имеем: BD = CD (D — средняя точка) DL = DM (дано) ∠BLD = ∠CMD (каждый по 90 °) Таким образом, BDL≅ △ CDM (критерий RHS)
⇒BL = MC (CPCT)
∴∠B = ∠C
Это делает треугольник ABC равнобедренным.
Или AB = AC
Значит, доказано.

Лист № 285:

Вопрос 18:

In ∆ ABC , AB = AC и биссектрисы ∠ B и ∠ C пересекаются в точке O . Докажите, что BO = CO и луч AO является биссектрисой ∠ A .

Ответ:

В треугольнике ABC имеем:
AB = AC (дано)
⇒∠B = ∠C⇒12∠B = 12∠C⇒OBC = ∠OCB⇒BO = CO

Теперь в △ AOB и △ AOC. , Имеем: OB = OC (доказано) AB = AC (дано) AO = AO (Common) ∴ △ AOB≅ △ AOC (критерий SSS)
i.е., BAO = ∠CAO (Соответствующие углы конгруэнтных треугольников)

Итак, это показывает, что луч AO является биссектрисой A.
Значит, доказано.

Лист № 285:

Вопрос 19:

Сегменты линии, соединяющие средние точки M и N параллельных сторон AB и DC соответственно трапеции ABCD , перпендикулярны обеим сторонам AB и DC .Докажите, что г. н.э. = г. до н.э.

Ответ:

Дано: В трапеции ABCD , M и N являются средними точками AB и DC, MN ⊥ AB и MN ⊥ DC .

Доказать: AD = BC

Строительство: Присоединитесь к CM и DM .

Проба:

In Δ CMN и Δ DMN ,

MN = MN (общие стороны)
∠ CNM = ∠ DNM = 90 ° (дано, MN ⊥ DC )
CN = DN (дано, N — средняя точка DC )

∴ По критериям соответствия SAS
Δ CMN ≅ Δ DMN

Итак, CM = DM (CPCT)….. (i)
А, CMN = ∠ DMN (CPCT)
Но, AMN = ∠ BMN = 90 ° (Дано, MN ⊥ AB )
⇒ ∠ AMN — ∠ CMN = ∠ BMN — ∠ DMN
⇒∠ AMD = ∠ BMC ….. (ii)

Теперь в Δ AMD и Δ BMC ,

DM = CM [Из (i)]
∠ AMD = ∠ BMC [From (ii)]
AM = BM (Учитывая, что M является средняя точка AB )

∴ По критериям соответствия SAS
Δ AMD ≅ Δ BMC

Следовательно, AD = BC (CPCT)

Лист № 285:

Вопрос 20:

Биссектрисы ∠ B и ∠ C равнобедренного треугольника с AB = AC пересекаются друг с другом в точке O. BO производится для соответствия AC в точке M . Докажите, что ∠ MOC = ∠ ABC .

Ответ:

Дано: Равнобедренный ∆ ABC , AB = AC ; OB и OC являются биссектрисами ∠ B и ∠ C соответственно.

Доказать: ∠ MOC = ∠ ABC

Доказательство:

In ∆ ABC ,

∵AB = AC (дано)
∴∠ ABC = ∠ ACB (Углы, противоположные равным сторонам равны)
⇒12 AB ABC = 12∠ ACB
⇒∠ OBC = ∠ OCB (Учитывая, что OB и OC являются биссектрисами ∠ B и ∠ C соответственно)….. (i)

Теперь, в ∆ OBC , MOC — это внешний угол
⇒∠ MOC = ∠ OBC + ∠ OCB (Внешний угол равен сумме двух противоположных внутренних углов)
⇒∠ MOC = ∠ OBC + ∠ OBC [Из (i)]
⇒∠ MOC = 2∠ OBC
Следовательно, ∠ MOC = ∠ ABC (Учитывая, OB — биссектриса ∠ B )

Лист № 285:

Вопрос 21:

Биссектрисы ∠ B и ∠ C равнобедренной кости Δ ABC с AB = AC пересекаются друг с другом в точке O .Покажите, что внешний угол, примыкающий к ∠ ABC , равен ∠ BOC .

Ответ:

Дано: Δ ABC , AB = AC , BO и CO являются биссектрисами 12 ABC и ∠ ACB соответственно.

Доказать: ∠ ABD = ∠ BOC

Строительство: Произвести CB до точки D .

Проба:

In Δ ABC ,

∵ AB = AC (дано)
∴ ∠ ACB = ∠ ABC (Углы, противоположные равным сторонам равны)

⇒12∠ ACB = 12∠ABC⇒∠OCB = ∠OBC ….. iGiven, BO и CO являются биссектрисами ABC и ∠ACB, соответственно

In Δ BOC ,

∠OBC + ∠OCB + ∠BOC = 180 ° По свойству суммы углов треугольника⇒∠OBC + ∠OBC + ∠BOC = 180 ° Из i⇒2∠OBC + ∠BOC = 180 ° ⇒∠ABC + ∠BOC = 180 ° BO — биссектриса угла ∠ABC….. ii

Кроме того, DBC — прямая линия.
Итак, ABC + ∠DBA = 180 ° Линейная пара ….. iii

Из (ii) и (iii) получаем
∠ABC + ∠BOC = ∠ABC + ∠DBA∴ ∠BOC = ∠DBA

Лист № 285:

Вопрос 22:

P — точка на биссектрисе ∠ ABC . Если прямая, проходящая через P , параллельная BA , пересекает BC на Q , докажите, что Δ BPQ является равнобедренным треугольником.

Ответ:

Дано: BP — биссектриса ∠ ABC и BA ∥ QP

Чтобы доказать: Δ BPQ — равнобедренный треугольник

Доказательство:

∵∠1 = ∠2 Дано, что BP является биссектрисой ABCAnd, ∠1 = ∠3 Альтернативные внутренние углы 2 = ∠3So, PQ = BQ В треугольнике стороны, противоположные равным сторонам, равны.

Но это стороны ∆BPQ.

Следовательно, ∆BPQ — равнобедренный треугольник.

Лист № 285:

Вопрос 23:

Изображение объекта, помещенного в точку A, перед плоским зеркалом LM , видно в точке B наблюдателем в точке D , как показано на рисунке. Докажите, что изображение находится за зеркалом так же далеко, как объект перед зеркалом.

Ответ:

Дано: объект помещен в точку A , изображение объекта видно в точке B , наблюдатель находится в точке D , а LM является плоским зеркалом .

Для доказательства: изображение находится за зеркалом настолько же, насколько объект находится перед зеркалом, то есть BT = AT .

Проба:

∵ LM — плоское зеркало

∴ i = r (угол падения всегда равен углу отражения) ….. (1)

Также AB∥CN (оба AB и CN перпендикулярны LM )

⇒∠TAC = ∠ACN = i (Альтернативные внутренние углы)….. (2)

И, ∠CBT = ∠NCD = r (Соответствующие углы) ….. (3)

Из (1), (2) и (3) получаем

∠ TAC = ∠CBT ….. (4)

Now,

In ∆TAC и ∆CBT, ∠TAC = ∠CBT Из 4 ATC = ∠BTC = 90 ° CT = CT Общая сторона По критериям сравнения AAS , ∆TAC≅∆CBT

Следовательно, AT = BT (CPCT)

Лист № 285:

Вопрос 24:

На следующем рисунке объясните, как можно найти реку на ширину, не переходя ее.

Ответ:

Пусть AB будет шириной реки.
М — любая точка, расположенная на берегу реки.
Пусть O будет средней точкой BM.
Движение по перпендикуляру до точки, при которой A, O и N находятся на прямой линии.
Тогда MN — требуемая ширина реки.

В OBA и △ OMN, мы имеем: OB = OM (O — средняя точка) ∠OBA = ∠OMN (каждые 90 °) ∠AOB = ∠NOM (вертикально противоположный угол) ∴ △ OBA≅ △ OMN (критерий ASA)

Таким образом, MN = AB (CPCT)
Если MN известно, можно измерить ширину реки, не пересекая ее.

Лист № 285:

Вопрос 25:

В Δ ABC, D является средней точкой стороны AC , так что BD = 12 AC . Покажите, что ∠ ABC — прямой угол.

Ответ:

Дано: В ∆ ABC , D — это средняя точка стороны AC , так что BD = 12 AC .

Доказать: ∠ ABC — прямой угол.

Доказательство:

В ∆ADB, AD = BD Дано, BD = 12AC⇒∠DAB = ∠DBA = x Пусть углы, противоположные равным сторонам равны

Аналогично, в ∆DCB, BD = CD Дано⇒∠DBC = ∠DCB = y Пусть

In ∆ABC,

∠ABC + ∠BCA + ∠CAB = 180 ° Свойство суммы углов⇒x + x + y + y = 180 ° ⇒2 (x + y) = 180 ° ⇒x + y = 90 ° ⇒∠ABC = 90 °

Следовательно, ∠ ABC — прямой угол.

Лист № 286:

Вопрос 26:

«Если две стороны и угол одного треугольника равны двум сторонам и углу другого треугольника, то два треугольника должны быть конгруэнтными.
Верно ли заявление? Почему?

Ответ:

Нет, утверждение неверно, потому что два треугольника конгруэнтны только по условию конгруэнтности SAS, но утверждение также содержит условие ASS или SSA, которые не являются каким-либо условием конгруэнтности треугольников.

Лист № 286:

Вопрос 27:

«Если два угла и сторона одного треугольника равны двум углам и стороне другого треугольника, то эти два треугольника должны быть конгруэнтными.«Верно ли заявление? Почему?

Ответ:

Да, утверждение верно, поскольку два треугольника могут совпадать по критериям соответствия AAS или ASA.

Заявление об ограничении ответственности: если соответствующие углы двух треугольников равны, то в свойстве суммирования углов третий соответствующий угол будет равен. Итак, если у нас есть два соответствующих угла и соответствующие стороны равны, то треугольники могут быть доказаны конгруэнтными критериями SAS конгруэнтности.Следовательно, критерии ASA и SAS считаются одинаковыми.

Лист № 296:

Вопрос 1:

Можно ли построить треугольник, длина сторон которого указана ниже? Обоснуйте свой ответ.
(i) 5 см, 4 см, 9 см
(ii) 8 см, 7 см, 4 см
(iii) 10 см, 5 см, 6 см
(iv) 2,5 см, 5 см, 7 см
( v) 3 см, 4 см, 8 см

Ответ:

(i) Нет, потому что сумма двух сторон треугольника не больше третьей стороны.
5 + 4 = 9

(ii) Да, потому что сумма двух сторон треугольника больше третьей стороны.
7 + 4> 8; 8 + 7> 4; 8 + 4> 7

(iii) Да, потому что сумма двух сторон треугольника больше третьей стороны.
5 + 6> 10; 10 + 6> 5; 5 + 10> 6

(iv) Да, потому что сумма двух сторон треугольника больше третьей стороны.
2,5 + 5> 7; 5 + 7> 2,5; 2.5 + 7> 5

(v) Нет, потому что сумма двух сторон треугольника не больше третьей стороны.
3 + 4 <8

Лист № 296:

Вопрос 2:

In Δ ABC , ∠ A = 50 ° и ∠ B = 60 °. Определите самую длинную и самую короткую стороны треугольника.

Ответ:

Дано: In Δ ABC , ∠ A = 50 ° и ∠ B = 60 °

In Δ ABC ,
∠ A + ∠ B + ∠ C = 180 ° (Свойство суммы углов треугольника)
⇒ 50 ° + 60 ° + ∠ C = 180 °
⇒110 ° + ∠ C = 180 °
⇒∠ C = 180 ° — 110 °
⇒∠ C = 70 °

Следовательно, самая длинная сторона будет противоположна наибольшему углу (∠ C = 70 °) i.е. АБ .
Причем, самая короткая сторона будет противоположна наименьшему углу (∠ A = 50 °), т.е. BC .

Лист № 296:

Вопрос 3:

(i) In ∆ ABC , ∠ A = 90 °. Какая его сторона самая длинная?
(ii) In ∆ ABC , A = ∠ B = 45 °. Какая его сторона самая длинная?
(iii) In ∆ ABC , ∠ A = 100 ° и ∠ C = 50 °.Какая его самая короткая сторона?

Ответ:

(i) Дано: In ∆ ABC , ∠ A = 90 °

Итак, сумма двух других углов в треугольнике ∠ B + ∠ C = 90 °

, т.е. ∠ B , C <90 °

Так как ∠ A — наибольший угол.

Итак, самая длинная сторона — г. до н.э. .

(ii) Дано: A = ∠ B = 45 °

Используя свойство суммы углов треугольника,

∠ C = 90 °

Так как ∠ C — наибольший угол.

Итак, самая длинная сторона — AB .

(iii) Дано: ∠ A = 100 ° и ∠ C = 50 °

Используя свойство суммы углов треугольника,

∠ B = 30 °

Так как ∠ A является наибольший угол.

Итак, самая короткая сторона — BC .

Лист № 297:

Вопрос 4:

В ∆ ABC сторона AB производится до D , так что BD = BC .Если ∠ B = 60 ° и ∠ A = 70 °, докажите, что (i) AD > CD и (ii) AD > AC .

Ответ:

В треугольнике CBA CBD — это внешний угол.

т.е. CBA + ∠CBD = 180 ° ⇒60 ° + ∠CBD = 180 ° ⇒ °CBD = 120 °

Треугольник BCD равнобедренный, а BC = BD.
Пусть ∠BCD = ∠BDC = x °.
В △ CBD имеем: ⇒∠BCD + ∠CBD + ∠CDB = 180 ° ⇒x + 120 ° + x = 180⇒2x = 60 ° ⇒x = 30 ° ∴∠BCD = ∠BDC = 30 °

В треугольнике ADC, C = ∠ACB + ∠BCD = 50 ° + 30 ° = 80 °
∠A = 70 ° и ∠D = 30 °

∴∠C> ∠A⇒AD> CD… (1)

Также ∠C> ∠D⇒AD> AC … (2)

Лист № 297:

Вопрос 5:

На данном рисунке ∠ B <∠ A и ∠ C <∠ D . Покажите, что AD > BC .

Ответ:

Дано: ∠ B <∠ A и ∠ C <∠ D

Доказательство: AD > BC

Доказательство:

In ∆AOB, ∠B <∠A⇒AO

В ∆COD, C <∠D⇒OD

Складывая (1) и (2), получаем AO + OD < BO + OC∴AD

Лист № 297:

Вопрос 6:

AB и CD — соответственно наименьшая и наибольшая стороны четырехугольника ABCD . Покажите, что ∠ A > ∠ C и
∠ B > ∠ D .

Ответ:

Дано: В четырехугольнике ABCD, AB и CD — соответственно наименьшая и наибольшая стороны.

Для подтверждения:
(i) ∠ A > ∠ C
(ii) ∠ B > ∠ D

Строительство: Присоединяйтесь к AC .

Доказательство:

В ∆ABC, BC> AB. Учитывая, что AB — наименьшая сторона ∠1> ∠2…1

В ∆ADC, CD> AD. Учитывая, что CD — наибольшая сторона ∠3> ∠4 … 2

Складывая 1 и 2, получаем 1 + ∠3> ∠2 + ∠4 ∴ ∠A> ∠C

(ii)

Строительство: Присоединитесь к BD .

Доказательство:

В ∆ABD, ∵ AD> AB. Учитывая, что AB — наименьшая сторона. ∠5> ∠6 … 3

В ∆CBD, ∵ CD> BC. Учитывая, что CD — наибольшая сторона. ∴ ∠7> ∠8 … 4

Складывая 3 и 4, получаем 5 + ∠7> ∠6 + ∠8∴∠B> ∠D

Лист № 297:

Вопрос 7:

В четырехугольнике ABCD покажите, что ( AB + BC + CD + DA )> ( AC + BD ).

Ответ:

Дано: Четырехугольник ABCD

Доказательство: ( AB + BC + CD + DA )> ( AC + BD )

Доказательство:

In ∆ABC, AB + BC> AC … iIn ∆CAD, CD + AD> AC … iiIn ∆BAD, AB + AD> BD … iiiIn ∆BCD, BC + CD> BD … iv

Добавление (i), (ii), (iii) и (iv) получаем

2 ( AB + BC + CD + DA ) <2 ( AC + BD )

Следовательно, ( AB + BC + CD + DA ) <( AC + BD ).

Лист № 297:

Вопрос 8:

В четырехугольнике ABCD покажите, что
AB + BC + CD + DA <2BD + AC

Ответ:

Дано: Четырехугольник ABCD
Доказать: ( AB + BC + CD + DA ) <2 ( BD + AC ).
Проба:

In ∆AOB,
OA + OB> AB ….. i
In ∆BOC,
OB + OC> BC….. ii
In ∆COD,
OC + OD> CD ….. iii
In ∆AOD,
OD + OA> AD ….. iv
Добавляя i, ii, iii и iv, мы получаем
2OA + OB + OC + OD> AB + BC + CD + DA⇒ 2OB + OD + OA + OC> AB + BC + CD + DA⇒2BD + AC> AB + BC + CD + DA

Лист № 297:

Вопрос 9:

В Δ ABC , ∠ B = 35 °, ∠ C = 65 ° и биссектриса ∠ BAC соответствует BC в X .Расположите AX , BX и CX в порядке убывания.

Ответ:

Дано: В Δ ABC , B = 35 °, ∠ C = 65 ° и биссектриса ∠ BAC соответствует BC в X .

В ∆ABX, ∵ ∠BAX> ∠ABX∴ BX> AX … i

Аналогично, в ∆ACX, ∵ ∠ACX> ∠XAC∴ AX> CX … ii

Из i и ii мы getBX> AX> CX

Лист № 297:

Вопрос 10:

На данном рисунке PQ > PR и QS и RS являются биссектрисами ∠ Q и ∠ R соответственно.Покажите, что SQ > SR .

Ответ:

Поскольку угол, противоположный длинной стороне, больше, имеем:

PQ> PR⇒∠R> ∠Q⇒12∠R> 12∠Q⇒∠SRQ> ∠RQS⇒QS> SR

∴ SQ> SR

Лист № 297:

Вопрос 11:

D — любая точка на стороне AC Δ ABC с AB = AC .Покажите, что CD < BD .

Ответ:

Дано: In ∆ ABC , AB = AC

Доказательство: CD < BD

Доказательство:

In ∆ ABC ,

Поскольку, AB = AC (дано)

Итак, ∠ABC = ∠ACB … (i)

В ∆ABC и ∆DBC, ABC> ∠DBC⇒ ∠ACB> ∠ DBC From i⇒ BD> CD Сторона, противоположная на больший угол длиннее.∴ CD

Лист № 297:

Вопрос 12:

Докажите, что в треугольнике, отличном от равностороннего, угол, противоположный самой длинной стороне, больше 23 прямого угла.

Ответ:

Дано: В ∆ ABC , BC — самая длинная сторона.

Доказать: ∠ BAC > 23 прямого угла, т.е.е., ∠ BAC > 60 °

Построить: Отметьте точку D на стороне AC так, чтобы AD = AB = BD .

Проба:

In ∆ ABD ,

∵ AD = AB = BD (По конструкции)

∴∠1 = ∠3 = ∠4 = 60 °

Now, BAC = ∠1 + ∠2 = 60 ° + ∠2, но 60 ° = 23 прямого угла Итак, BAC = 23 прямого угла + ∠2

Следовательно, ∠ BAC > 23 прямого угла.

Лист № 298:

Вопрос 13:

Докажите, что на данном рисунке
(i) CD + DA + AB > BC
(ii) CD + DA + AB + BC > 2AC.

Ответ:

Дано: Четырехугольник ABCD

Доказательство:
(i) CD + DA + AB > BC
(ii) CD + DA + AB + BC > 2AC

Доказательство:
( i)
В ∆ACD, CD + DA> CA…1 В ∆ABC, AB + CA> BC … 2
Складывая (1) и (2), получаем CD + DA + AB + CA> CA + BC∴ AB + CD + DA> BC

(ii)
В ∆CDA, CD + DA> CA … 3 В ∆BCA, BC + AB> CA … 4
Складывая (3) и (4), получаем CD + AD + BC + AB> CA + CA∴ CD + AD + BC + AB> 2CA

Лист № 298:

Вопрос 14:

Если O — точка в ∆ ABC , покажите, что:
(i) AB + AC > OB + OC
(ii) AB + BC + CA > OA + OB + OC
(iii) OA + OB + OC> 12 (AB + BC + CA)

Ответ:

Дано:
В треугольнике ABC O — любая внутренняя точка.
Мы знаем, что любой отрезок от точки O внутри треугольника до любой вершины треугольника не может быть длиннее двух сторон, прилегающих к вершине.
Таким образом, OA не может быть длиннее одновременно AB и CA (если это возможно, то O находится вне треугольника).

(i) OA не может быть длиннее одновременно AB и CA.
AB> OB … (1) AC> OC … (2) Таким образом, AB + AC> OB + OC … [Добавление ( 1) и (2)]

(ii) AB> OA …… (3) BC> OB ….. (4) CA> OC ….. (5)
Добавление вышеуказанного три уравнения, получаем:
Таким образом, AB + BC + CA> OA + OB + OC… (6)

OA не может быть длиннее одновременно AB и CA.
AB> OB ….. (5) AC> OC ….. (6) AB + AC> OB + OC .. …….. [При сложении (5) и (6)]
Таким образом, первое доказываемое уравнение оказывается правильным.

(iii) Теперь рассмотрим треугольники OAC, OBA и OBC.
У нас есть:
OA + OC> ACOA + OB> ABOB + OC> BC Сложив три вышеупомянутых уравнения, мы получаем: OA + OC + OA + OB + OB + OC> AB + AC + BC⇒2OA + OB + OC> AB + AC + BC Таким образом, OA + OB + OC> 12AB + BC + CA

Лист № 298:

Вопрос 15:

На данном рисунке AD ⊥ BC и CD > BD .Покажите, что AC > AB .

Ответ:

Дано: AD ⊥ BC и CD > BD

Для доказательства: AC > AB

Доказательство:

∠ADB = ∠ADC = 90 ° AD⊥BC. ..1∠BAD <∠DAC CD> BD … 2

In ∆ABD,

Используя свойство суммы углов треугольника,

∠B = 180 ° -∠ADB-∠BAD∠B = 90 ° — ∠ПЛОХО…3

В ∆ADC,

Используя свойство суммы углов треугольника,

∠ACD = 90 ° -∠DAC … 4

Из (2), (3) и (4) получаем

∠B> ∠C

Следовательно, AC> AB.

Лист № 298:

Вопрос 16:

На данном рисунке D — это точка на стороне BC Δ ABC , а E — такая точка, что CD = DE .Докажите, что AB + AC > BE .

Ответ:

Дано: CD = DE

Доказательство: AB + AC > BE

Доказательство:

In ∆ABC,

AB + AC> BC … 1

In ∆BED,

BD + CD> BE⇒BC> BE … 2

Из (1) и (2) получаем

AB + AC > BE

Лист № 300:

Вопрос 1:

Что из следующего не является критерием соответствия треугольников?
(a) SSA
(b) SAS
(c) ASA
(d) SSS

Ответ:

(a) SSA
SSA не является критерием соответствия треугольников.

Лист № 300:

Вопрос 2:

Если AB = QR , BC = RP и CA = PQ , то что из следующего верно?
(а) ∆ ABC ≅ ∆ PQR
(б) ∆ CBA ≅ ∆ PQR
(в) ∆ CAB ≅ ∆ PQR
(г) ∆ BCA ≅ ∆ PQR

Ответ:

∴ ∆CAB≅∆PQR

Лист № 301:

Вопрос 3:

Если ∆ ABC ≅ ∆ PQR и ∆ ABC не соответствует ∆ RPQ , то что из следующего неверно?
(а) BC = PQ
(б) AC = PR
(в) BC = QR
(г) AB = PQ

Ответ:

(a) BC = PQ

Если ∆ABC≅∆PQR и ∆ABC не конгруэнтно ∆RPQ, то
BC ≠ PQ
Следовательно, это неверно.

Лист № 301:

Вопрос 4:

In ∆ ABC , AB = AC и ∠ B = 50 °. Тогда ∠ A =?
(а) 40 °
(б) 50 °
(в) 80 °
(г) 130 °

Ответ:

В ABC имеем:
AB = AC
∠ B = 50 °
Поскольку ABC — равнобедренный треугольник, имеем:
∠C = ∠B
∠C = 50 °
В треугольнике ABC имеем :
∠A + ∠B + ∠C = 180 ° ⇒∠A + 50 + 50 = 180 ° ⇒∠A = 180 ° -100 ° ∴∠A = 80 °
Следовательно, правильный ответ — вариант (c).

Лист № 301:

Вопрос 5:

In ∆ ABC , BC = AB и ∠ B = 80 °. Тогда ∠ A =?
(а) 50 °
(б) 40 °
(в) 100 °
(г) 80 °

Ответ:

Дано: In ∆ ABC , BC = AB и ∠ B = 80 °.

In ∆ ABC ,

As, AB = BC

⇒∠A = ∠C

Пусть ∠A = ∠C = x

Используя свойство суммы углов треугольника,

∠A + ∠B + ∠ C = 180 ° ⇒x + 80 ° + x = 180 ° ⇒2x = 180 ° -80 ° ⇒2x = 100 °

⇒x = 100 ° 2⇒x = 50 ° ⇒∠A = 50 °

Следовательно, правильный вариант — (а).

Лист № 301:

Вопрос 6:

In ∆ ABC , ∠ C = ∠ A, BC = 4 см и AC = 5 см.Тогда AB =?
(а) 4 см
(б) 5 см
(в) 8 см
(г) 2,5 см

Ответ:

Дано: In ∆ ABC , ∠ C = ∠ A, BC = 4 см и AC = 5 см.

In ∆ ABC ,

As, C = ∠ A (дано)

Следовательно, BC = AB (стороны, противоположные равным углам.)

⇒BC = AB = 4 см

Следовательно, правильный вариант — (а).

Лист № 301:

Вопрос 7:

Две стороны треугольника имеют длину 4 см и 2,5 см. Длина третьей стороны треугольника не может быть
(a) 6 см
(b) 6,5 см
(c) 5,5 см
(d) 6,3 cn

Ответ:

Так как, 4 + 2,5 = 6,5

Итак, 6.5 см не может быть третьей стороной треугольника, так как сумма двух сторон треугольника всегда больше третьей стороны.

Следовательно, правильный вариант — (b).

Лист № 301:

Вопрос 8:

In ∆ ABC , если ∠ C > ∠ B , то
(a) BC > AC
(b) AB > AC
(c) AB > AC
(d) BC > AC

Ответ:

(б) AB> AC

В ∆ABC имеем:
∠C> ∠B
Сторона, противоположная большему углу, больше.
∴AB> AC

Лист № 301:

Вопрос 9:

Принято, что ∆ ABC ≅ ∆ FDE , в котором AB = 5 см, ∠ B = 40 °, ∠ A = 80 ° и FD = 5 см. Тогда что из следующего верно?
(а) ∠ D = 60 °
(б) ∠ E = 60 °
(в) ∠ F = 60 °
(г) ∠ D = 80 °

Ответ:

(b) ∠E = 60 °

∆ABC≅∆FDE
AB = 5 см, ∠B = 40 °, ∠A = 80 ° и FD = 5 см

Тогда A + ∠B + ∠C = 180 ° ⇒ 80 ° + 40 ° + ∠C = 180 ° ⇒∠C = 60 ° Также ∠C = ∠E
∴ ∠E = 60 °

Лист № 301:

Вопрос 10:

In ∆ ABC , ∠ A = 40 ° и ∠ B = 60 °.Тогда самая длинная сторона ∆ ABC равна
(a) BC
(b) AC
(c) AB
(d) не может быть определена

Ответ:

В треугольнике ABC имеем:
∠A = 40 °, ∠B = 60 ° … (Дано)
Здесь ∠A + ∠B + ∠C = 180 ° ⇒60 ° + 40 ° + ∠C = 180 ° ⇒∠C = 80 °
∴ Сторона, противоположная C, т.е. AB, является самой длинной стороной треугольника ABC.

Лист № 301:

Вопрос 11:

На этом рисунке AB > AC .Тогда что из следующего верно?
(a) AB < AD
(b) AB = AD
(c) AB > AD
(d) Не может быть определено

Ответ:

AB> AC.

∴ ∠ACB> ∠ABC

Теперь ∠ADB> ∠ACD (внешний угол) ⇒∠ADB> ∠ACB> ∠ABC⇒∠ADB> ∠ABD⇒AB> AD

Лист № 301:

Вопрос 12:

На этом рисунке AB > AC .Если BO и CO являются биссектрисами ∠ B и ∠ C соответственно, то
(a) OB < OC
(b) OB = OC
(c) O B > OC

Ответ:

AB> AC (дано)
⇒∠C> ∠B
⇒12∠C> 12∠B
⇒∠OCB> ∠OBC (Given)
⇒OB> OC

Лист № 301:

Вопрос 13:

На данном рисунке AB = AC и OB = OC .Тогда ∠ ABO : ∠ ACO =?
(a) 1: 1
(b) 2: 1
(c) 1: 2
(d) Ни один из этих

Ответ:

(a) 1: 1

В ∆OAB и ∆OAC имеем:
AB = AC (дано) OB = OC (дано) OA = OA (общая сторона)
Таким образом, ∆OAB≅OAC (критерий SSS )
т.е. ∠ABO = ∠ACO
∴ ∠ABO: ∠ACO = 1: 1

Лист № 302:

Вопрос 14:

Если высоты от двух вершин треугольника до противоположных сторон равны, то треугольник будет
(а) равносторонний
(б) равнобедренный
(в) разносторонний
(г) прямоугольный

Ответ:

(б) равнобедренный

In ∆ABC, BL∥AC.
CM∥AB такой, что BL = CM.

Для доказательства: AB = AC

In ABL и △ ACM, BL = CM (дано) ∠BAL = ∠CAM (общий угол) ∠ALB = ∠AMC (каждые 90 °) △ ABL≅ △ ACM (критерий AAS ) ∴ AB = AC (CPCT)

Лист № 302:

Вопрос 15:

В ∆ ABC и ∆ DEF указано, что AB = DE и BC = EF . Для того чтобы ∆ ABC ≅ ∆ DEF , мы должны иметь
(a) ∠ A = ∠ D
(b) ∠ B = ∠ E
(c) ∠ C = ∠ F
(d) ни один из этих

Ответ:

(b) ∠B = ∠E

В ABC и △ DEF имеем:
AB = DE (дано)
BC = EF (дано)
Для того, чтобы ABC≅DEF, мы должны иметь ∠B = ∠E.

Лист № 302:

Вопрос 16:

В ∆ ABC и ∆ DEF задано, что B = ∠ E и C = ∠ F . Для того чтобы ∆ ABC ∆ ∆ DEF , мы должны иметь
(a) AB = DF
(b) AC = DE
(c) BC = EF
(г) A = ∠ D

Ответ:

Для того, чтобы △ ABC≅ △ DEF, мы должны иметь BC = EF.
Следовательно, правильный ответ — вариант (c).

Лист № 302:

Вопрос 17:

В ∆ ABC и ∆ PQR задано, что AB = AC , C = ∠ P и ∠ B = ∠ Q . Тогда два треугольника будут
(a) равнобедренные, но не совпадающие
(b) равнобедренные и совпадающие
(c) равнобедренные, но не равнобедренные
(d) ни совпадающие, ни равнобедренные

Ответ:

(a) равнобедренный, но не конгруэнтный

AB = AC ⇒∠C = ∠B⇒∠P = ∠Q [∵∠C = ∠P и ∠B = ∠Q]
Таким образом, оба треугольника равнобедренные, но не конгруэнтны .

Лист № 302:

Вопрос 18:

Что верно?
(a) Треугольник может иметь два прямых угла.
(b) Треугольник может иметь два тупых угла.
(c) Треугольник может иметь два острых угла.
(d) Внешний угол треугольника меньше любого из внутренних противоположных углов.

Ответ:

(c) Треугольник может иметь два острых угла.
Сумма двух острых углов всегда меньше 180 ^o, таким образом удовлетворяя свойству суммы углов треугольника.
Следовательно, у треугольника может быть два острых угла.

Лист № 302:

Вопрос 19:

Заполните пропуски с помощью <или>.
(a) (Сумма любых двух сторон треугольника) …… (третья сторона)
(b) (Разница любых двух сторон треугольника) …… (третья сторона)
(c) (Сумма трех высот треугольника)…… (сумма трех сторон)
(d) (Сумма любых двух сторон треугольника) …… (удвоенная медиана третьей стороны)
(e) (Периметр треугольника ) …… (сумма трех его медиан)

Ответ:

a) Сумма любых двух сторон треугольника > третья сторона

b) Разность любых двух сторон треугольника < третья сторона

c) Сумма трех высот треугольника <сумма его три стороны

d) Сумма любых двух сторон треугольника> удвоенной медианы третьей стороны

e) Периметр треугольника> сумма трех его медиан

Лист № 302:

Вопрос 20:

Заполните пустые поля.
(a) Каждый угол равностороннего треугольника измеряет …….
(b) Медианы равностороннего треугольника равны …
(c) В прямоугольном треугольнике гипотенуза — это … сторона.
(d) Чертеж ∆ ABC с AB = 3 см, BC = 4 см и CA = 7 см это …….

Ответ:

a) Каждый угол равностороннего треугольника составляет 60 ° .

б) Медианы равностороннего треугольника равны .

c) В прямоугольном треугольнике гипотенуза — это самая длинная сторона .

d) Нарисовать △ ABC с AB = 3 см, BC = 4 см и CA = 7 см невозможно.

Просмотреть решения NCERT для всех глав класса 9

Уточненная теория четырех переменных пластин для свободных колебаний функционально градиентных пластин с произвольным градиентом

Abstract

Новинка этой статьи заключается в использовании четырех переменных уточненной теории пластин для анализа свободных колебаний пластин, изготовленных из функционально градиентных материалов с произвольным градиентом. градиент.В отличие от любой другой теории, количество задействованных неизвестных функций составляет всего четыре, по сравнению с пятью в случае других теорий деформации сдвига. Теория учитывает эффекты поперечного сдвига и параболическое распределение деформаций поперечного сдвига по толщине пластины, поэтому нет необходимости использовать поправочные коэффициенты сдвига. Предполагается, что свойства материала пластины градуируются по толщине в соответствии с простым степенным распределением с точки зрения объемных долей составляющих с произвольным градиентом.Уравнение движения прямоугольных пластин FG получено по принципу Гамильтона. Решения в замкнутой форме получаются с использованием техники Навье, а затем основные частоты находятся путем решения результатов задач на собственные значения. В случае зажатых пластин FG частоты свободных колебаний получаются путем применения метода Ритца, в котором четыре составляющие смещения принимаются как ряд простых алгебраических полиномов. Справедливость настоящей теории исследуется путем сравнения некоторых из настоящих результатов с теориями первого порядка и другими теориями более высокого порядка, описанными в литературе.Можно сделать вывод, что предложенная теория точна и проста в решении проблемы свободных колебаний пластин FG. Даны иллюстративные примеры, чтобы показать влияние различных градиентов, соотношений сторон и отношения толщины к длине на свободную вибрацию пластин FG.

Ключевые слова

A. Пластины

B. Вибрация

C. Аналитическое моделирование

Функционально классифицированные материалы

Рекомендуемые статьиЦитирующие статьи (0)

Полный текст

Цитирование статей

% PDF-1.4 % 1 0 объект > эндобдж 6 0 obj /Заголовок /Предмет / Автор /Режиссер / CreationDate (D: 202104140-00’00 ‘) / Ключевые слова () / ModDate (D: 20201130015306Z) /PTEX.Fullbanner (Это pdfTeX, версия 3.14159265-2.6-1.40.21 \ (TeX Live 2020 \) kpathsea версия 6.3.2) / В ловушке / Ложь >> эндобдж 2 0 obj > эндобдж 3 0 obj > эндобдж 4 0 obj > эндобдж 5 0 obj > эндобдж 7 0 объект > эндобдж 8 0 объект > эндобдж 9 0 объект > эндобдж 10 0 obj > эндобдж 11 0 объект > эндобдж 12 0 объект > эндобдж 13 0 объект > эндобдж 14 0 объект > эндобдж 15 0 объект > эндобдж 16 0 объект > эндобдж 17 0 объект > эндобдж 18 0 объект > эндобдж 19 0 объект > эндобдж 20 0 объект > эндобдж 21 0 объект > эндобдж 22 0 объект > эндобдж 23 0 объект > эндобдж 24 0 объект > эндобдж 25 0 объект > эндобдж 26 0 объект > эндобдж 27 0 объект > эндобдж 28 0 объект > эндобдж 29 0 объект > эндобдж 30 0 объект > эндобдж 31 0 объект > эндобдж 32 0 объект > эндобдж 33 0 объект > эндобдж 34 0 объект > эндобдж 35 0 объект > эндобдж 36 0 объект > эндобдж 37 0 объект > эндобдж 38 0 объект > эндобдж 39 0 объект > эндобдж 40 0 объект > эндобдж 41 0 объект > эндобдж 42 0 объект > эндобдж 43 0 объект > эндобдж 44 0 объект > эндобдж 45 0 объект > эндобдж 46 0 объект > эндобдж 47 0 объект > эндобдж 48 0 объект > эндобдж 49 0 объект > эндобдж 50 0 объект > эндобдж 51 0 объект > эндобдж 52 0 объект > эндобдж 53 0 объект > эндобдж 54 0 объект > эндобдж 55 0 объект > эндобдж 56 0 объект > эндобдж 57 0 объект > эндобдж 58 0 объект > эндобдж 59 0 объект > эндобдж 60 0 объект > эндобдж 61 0 объект > эндобдж 62 0 объект > эндобдж 63 0 объект > эндобдж 64 0 объект > эндобдж 65 0 объект > эндобдж 66 0 объект > эндобдж 67 0 объект > эндобдж 68 0 объект > эндобдж 69 0 объект > эндобдж 70 0 объект > эндобдж 71 0 объект > эндобдж 72 0 объект > эндобдж 73 0 объект > эндобдж 74 0 объект > эндобдж 75 0 объект > эндобдж 76 0 объект > эндобдж 77 0 объект > эндобдж 78 0 объект > эндобдж 79 0 объект > эндобдж 80 0 объект > эндобдж 81 0 объект > эндобдж 82 0 объект > эндобдж 83 0 объект > эндобдж 84 0 объект > эндобдж 85 0 объект > эндобдж 86 0 объект > эндобдж 87 0 объект > эндобдж 88 0 объект > эндобдж 89 0 объект > эндобдж 90 0 объект > эндобдж 91 0 объект > эндобдж 92 0 объект > эндобдж 93 0 объект > эндобдж 94 0 объект > эндобдж 95 0 объект > эндобдж 96 0 объект > эндобдж 97 0 объект > эндобдж 98 0 объект > эндобдж 99 0 объект > эндобдж 100 0 объект > эндобдж 101 0 объект > эндобдж 102 0 объект > эндобдж 103 0 объект > эндобдж 104 0 объект > эндобдж 105 0 объект > эндобдж 106 0 объект > эндобдж 107 0 объект > эндобдж 108 0 объект > эндобдж 109 0 объект > эндобдж 110 0 объект > эндобдж 111 0 объект > эндобдж 112 0 объект > эндобдж 113 0 объект > эндобдж 114 0 объект > эндобдж 115 0 объект > эндобдж 116 0 объект > эндобдж 117 0 объект > эндобдж 118 0 объект > эндобдж 119 0 объект > эндобдж 120 0 объект > эндобдж 121 0 объект > эндобдж 122 0 объект > эндобдж 123 0 объект > эндобдж 124 0 объект > / ProcSet [/ PDF / Text / ImageC / ImageB / ImageI] >> эндобдж 125 0 объект > поток х ڝ Xn6 ++ d,>.B @ ~ 3

У вас недостаточно прав для чтения этого закона в настоящее время

У вас недостаточно прав для чтения этого закона в настоящее время Логотип Public.Resource.Org На логотипе изображен черно-белый рисунок улыбающегося тюленя с усами. Вокруг печати находится красная круглая полоса с белым шрифтом, в верхней половине которого написано «Печать одобрения создания», а в нижней половине — «Public.Resource.Org». На внешней стороне красной круглой марки находится круг. серебряная круглая полоса с зубчатыми краями, напоминающая печать из серебряной фольги.

Public.Resource.Org

Хилдсбург, Калифорния, 95448
США

Этот документ в настоящее время недоступен для вас!

Уважаемый гражданин:

В настоящее время вам временно отказано в доступе к этому документу.

Public Resource ведет судебный процесс за ваше право читать и говорить о законе. Для получения дополнительной информации см. Досье по рассматриваемому судебному делу:
.
Американское общество испытаний и материалов (ASTM), Национальная ассоциация противопожарной защиты (NFPA), и Американское общество инженеров по отоплению, холодильной технике и кондиционированию воздуха (ASHRAE) v.Public.Resource.Org (общедоступный ресурс), DCD 1: 13-cv-01215, Объединенный окружной суд округа Колумбия [1]

Ваш доступ к этому документу, который является законом Соединенных Штатов Америки, был временно отключен, пока мы боремся за ваше право читать и говорить о законах, по которым мы решаем управлять собой как демократическим обществом.

Чтобы подать заявку на получение лицензии на ознакомление с этим законом, ознакомьтесь с Сводом федеральных правил или применимыми законами и постановлениями штата. на имя и адрес продавца.Для получения дополнительной информации о постановлениях правительства и ваших правах как гражданина в соответствии с верховенством закона , пожалуйста, прочтите мое свидетельство перед Конгрессом Соединенных Штатов. Вы можете найти более подробную информацию о нашей деятельности на общедоступных ресурсах. в нашем реестре деятельности за 2015 год. [2] [3]

Спасибо за интерес к чтению закона. Информированные граждане — фундаментальное требование для работы нашей демократии. Благодарим вас за усилия и приносим извинения за неудобства.

С уважением,

Карл Маламуд
Public.Resource.Org
7 ноября 2015 г.

Примечания

[1] http://www.archive.org/download/gov.uscourts.dcd.161410/gov.uscourts.dcd.161410.docket.html

[2] https://public.resource.org/edicts/

[3] https://public.resource.org/pro.docket.2015.html

% PDF-1.4 % 4 0 obj (Отсутствие истории и наследия) эндобдж 5 0 obj > эндобдж 8 0 объект (Гауссовское исключение сегодня) эндобдж 9 0 объект > эндобдж 12 0 объект (Устранение до Гаусса) эндобдж 13 0 объект > эндобдж 16 0 объект (« эта пчела опущена всеми, у кого есть письменное представление ») эндобдж 17 0 объект > эндобдж 20 0 объект (« Без всякого желания делать полезные вещи ») эндобдж 21 0 объект > эндобдж 24 0 объект (« Mthode des moindres Quarrs ») эндобдж 25 0 объект > эндобдж 28 0 объект (Метод Гаусса) эндобдж 29 0 объект > эндобдж 32 0 объект (Геодезия для картографии) эндобдж 33 0 объект > эндобдж 36 0 объект (Устранение после Гаусса) эндобдж 37 0 объект > эндобдж 40 0 объект (Устранение совершенствования для профессиональных компьютеров) эндобдж 41 0 объект > эндобдж 44 0 объект (Удобное обозначение Гаусса) эндобдж 45 0 объект > эндобдж 48 0 объект (Дулиттл, Легендарный компьютер) эндобдж 49 0 объект > эндобдж 52 0 объект (Механические калькуляторы) эндобдж 53 0 объект > эндобдж 56 0 объект (Холецкий: машинный алгоритм) эндобдж 57 0 объект > эндобдж 60 0 объект (Crout: « каждый элемент определяется одной непрерывной работой машины ») эндобдж 61 0 объект > эндобдж 64 0 объект (Введите матрицы) эндобдж 65 0 объект > эндобдж 68 0 объект (Теплиц: первые треугольные факторы) эндобдж 69 0 объект > эндобдж 72 0 объект (Банахевич: краковские алгоритмы) эндобдж 73 0 объект > эндобдж 76 0 объект (Фрейзер, Дункан и Коллар: элементарные матрицы) эндобдж 77 0 объект > эндобдж 80 0 объект (Дуайер: сокращенный метод Дулитла и метод квадратного корня) эндобдж 81 0 объект > эндобдж 84 0 объект (Дженсен \ (и Бодевиг \): обзоры литературы) эндобдж 85 0 объект > эндобдж 88 0 объект (Фон Нейман и Голдстайн: сочетание двух приемов) эндобдж 89 0 объект > эндобдж 92 0 объект (Гауссовская атрибуция в резюме) эндобдж 93 0 объект > эндобдж 103 0 объект > поток x ڥ ZYo ~ P4orX ~ -k9Cx 릾 y7ia2SAn; * L01 ޯ c (] {tn ^ Uy2 \ -Q? ‘~) ~ & {ldxrT «.