Гдз п алгебре 9 класс мерзляк: ГДЗ Алгебра 9 класс Мерзляк, Полонский, Якир

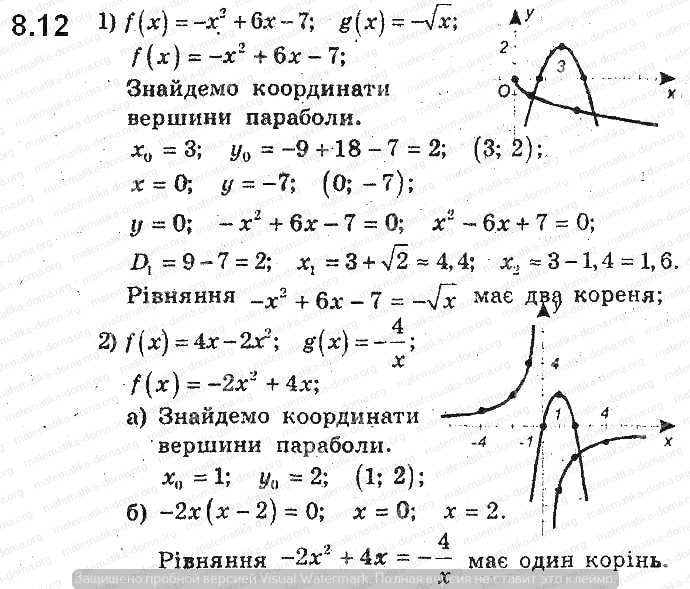
ГДЗ решебник по алгебре 9 класс Мерзляк А.Г. Полонский В.Б учебник Вентана-Граф

Алгебра 9 класс

Серия: Алгоритм успеха.

Тип пособия: Учебник

Авторы: Мерзляк, Поляков

Издательство: «Вентана-Граф»

Значимая дисциплина в жизни школьника

9 класс – сложный этап для каждого ученика, ведь по его окончанию всех ждет сдача итоговой аттестации по математике и других предметах. Большинство вопросов на этом экзамене охватывает курс алгебры и очень важно начать ее конкретно изучать прямо сейчас. Ведь по итогам ОГЭ будет решаться судьба школьника – заведение, в котором он сможет продолжить обучение и его будущая профессия. Чтобы не упустить время для изучения дисциплины, рекомендуется воспользоваться решебником «ГДЗ по алгебре 9 класс учебник Мерзляк (Вентана-Граф)». В учебнике разобрана задания на такие сложные темы как:

1. Неравенства, их свойства и действия с ними.
2. Квадратичная функция, ее график и решение уравнений.
3. Арифметическая и геометрическая прогрессии.

Используя пособие, школьник без проблем самостоятельно изучит эти темы и всегда будет готов к вопросам учителя и неожиданным проверочным работам. Это гарантировано обезопасит его от возможных затруднений с восприятием предмета в дальнейшем.

Особенности решебника

И хоть ГДЗ считается более «выгодным», чем основной учебник, раздельно они бесполезны. Но в сравнении решебник имеет большую долю преимуществ:

• более тысячи решенных заданий;
• 6 подборок упражнений для проверки своих знаний;
• 13 блоков вопросов к изученному материалу;
• 4 подборки дополнительных заданий;
• лаконичные и правильные ответы к каждому упражнению и вопросу.

С помощью пособия школьник наглядно увидит, как правильно решать те или иные задания, найдет и нивелирует пробелы в изучении дисциплины. А доскональное понимание алгебры очень важно, ведь она является базой для многих других предметов, с которыми школьник столкнется при будущем обучении в ВУЗе.

Почему именно решебник

Алгебра – сложная дисциплина в любом классе, но когда, помимо нее, школьнику нужно изучать кучу других уроков, готовиться к итоговой аттестации и не забывать, что пора определяться с будущей профессией, тяжело досконально ее понять. В такой ситуации стоит воспользоваться решебником «ГДЗ по алгебре 9 класс учебник Мерзляк А. Г. Полонский В. Б., М. С. Якир (Вентана-Граф)». Это поможет ученику заранее подготовиться к предстоящим работам в классе, найти и исправить пробелы в собственных знаниях по предмету, и этим самым сократить уровень стресса по поводу получения плохой отметки. У ребенка наконец-то появится любовь и тяга к обучению, ведь с решебником это так легко и интересно!

§1 Функция стр. 4-17

1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950

§2 Возрастание и убывание функции стр. 18-30

1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950

§3 Чётные и нечётные функции стр.

31-36

1234567891011121314151617181920212223242526

§4 Построение графиков функций y=kf(x), y=f(kx) стр. 37-45

123456789101112131415161718192021

§5 Построение графиков функций y=f(x)+b и y=f(x+a) стр. 46-60

12345678910111213141516171819202122232425262728293031323334353637

§6 Построение графиков функций y=f(|x|) и |f(x)| стр. 61-66

12345678910111213141516171819202122232425

§7 Квадратичная функция, её график и свойства стр. 67-79

12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970

§8 Решение квадратных неравенств стр. 80-87

1234567891011121314151617181920212223242526272829303132333435363738394041424344

§9 Решение неравенств методом интервалов стр.

88-104

12345678910111213141516171819202122232425262728293031323334

§10 Уравнение с двумя переменными и его график стр. 105-112

12345678910111213141516171819202122232425262728293031

§11 Графические методы решения систем уравнений с двумя переменными стр. 113-117

1234567891011121314151617181920

§12 Решение систем уравнений с двумя переменными методом подстановки и методами сложения и умножения стр. 118-126

123456789101112131415161718192021222324

§13 Метод замены переменых и другие способы решения систем уравнений с двумя переменными стр. 127-137

1234567891011121314151617181920212223242526272829303132333435

§14 Системы уравнений (неравенств) как математические модели реальных ситуаций стр. 138-147

12345678910111213141516171819202122232425262728293031

§15 Неравенства с двумя переменными стр.

148-154

123456789101112131415

§16 Системы неравенств с двумя переменными стр. 155-163

123456789101112131415161718192021222324252627

§17 Основные методы доказательства неравенств стр. 164-171

123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566

§18 Неравенства между средними величинами. Неравенство Коши — Буняковского стр. 172-191

1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768

§19 Степенная функция с натуральным показателем стр. 192-196

12345678910111213141516171819202122232425262728

§20 Обратная функция стр. 197-203

123456789101112131415

§21 Определение корня n-й степени стр.

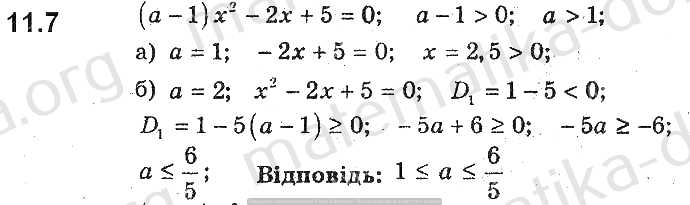204-210

12345678910111213141516171819202122232425262728

§22 Свойства корня n-й степени стр. 211-220

12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152

§23 Степень с рациональным показателем и её свойства стр. 221-231

1234567891011121314151617181920212223242526272829303132333435

§24 Числовые последовательности стр. 232-242

123456789101112131415161718192021222324252627

§25 Арифметическая прогрессия стр. 243-250

123456789101112131415161718192021222324252627282930313233343536373839404142434445464748

§26 Сумма n первых членов арифметичской прогрессии стр. 251-255

123456789101112131415161718192021222324252627282930313233343536373839404142434445

§27 Геометрическая прогрессия стр. 256-263

123456789101112131415161718192021222324252627282930313233343536

§28 Сумма n первых членов геометрической прогрессии стр.

264-267

123456789101112131415161718192021

§29 Представление о пределе последовательности. Сумма бесконечной геометрической прогрессии, у которой модуль знаменателя меньше единицы стр. 268-275

12345678910111213141516171819202122232425

§30 Суммирование стр. 276-281

12345678910111213

§31 Начальные сведения о статистике стр. 282-293

1234567891011

§32 Статистические характеристики стр. 294-305

1234567891011121314151617181920

§33 Операции над событиями стр. 306-315

1234567891011121314151617181920212223

§34 Зависимые и независимые события стр. 316-326

12345678910111213141516171819202122232425

§35 Геометрическая вероятность стр. 327-332

12345678910111213141516

§36 Схема Бернулли стр.