Физика 9 класс упражнение 13 номер 1: Упражнение 13 №1, Параграф 13

Упражнение 13-1 Физика 9 класс Перышкин С какой высоты свободно падала сосулька? – Рамблер/класс

Упражнение 13-1 Физика 9 класс Перышкин С какой высоты свободно падала сосулька? – Рамблер/класс

Интересные вопросы

Школа

Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?

Новости

Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?

Школа

Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?

Школа

Когда в 2018 году намечено проведение основного периода ЕГЭ?

Новости

Будет ли как-то улучшаться система проверки и организации итоговых сочинений?

Вузы

Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?

Поможете посчитать? 
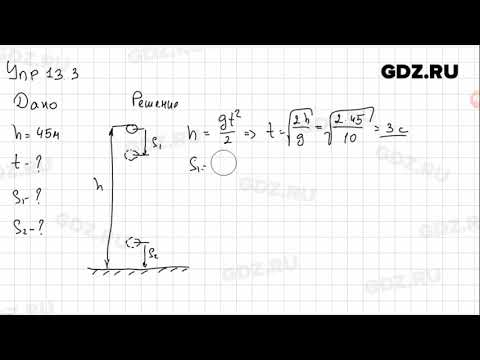
С какой высоты свободно падала сосулька, если расстояние до земли она преодолела за 4 с?

 

ответы

Дано:
t – 4c,  g = 9,8м/с2
Найти:
h — ?
Решение:
 
Ответ: h = 78,4 м.

ваш ответ

Можно ввести 4000 cимволов

отправить

дежурный

Нажимая кнопку «отправить», вы принимаете условия  пользовательского соглашения

похожие темы

Экскурсии

Мякишев Г.Я.

Досуг

Химия

похожие вопросы 5

ГДЗ Тема 21 Физика 7-9 класс А.В.Перышкин Задание №475 В обоих случаях поплавок плавает. В какую жидкость он погружается глубже?

Привет. Выручайте с ответом по физике…
Поплавок со свинцовым грузилом внизу опускают
сначала в воду, потом в масло. В обоих (Подробнее…)

ГДЗФизикаПерышкин А.В.Школа7 класс

ГДЗ Тема 21 Физика 7-9 класс А.В.Перышкин Задание №476 Изобразите силы, действующие на тело.

Привет всем! Нужен ваш совет, как отвечать…
Изобразите силы, действующие на тело, когда оно плавает на поверхности жидкости. (Подробнее…)

ГДЗФизикаПерышкин А.В.Школа7 класс

Васильевых. 50 вариантов ответов по русскому языку. Вариант 31 ч.2 Задание 13 ОГЭ Русский язык 9 класс Однородное подчинение придаточных

     Среди предложений    21-29:  
      (21) И Митрофанов услышал в этом смехе и прощение себе, и даже какое-то (Подробнее…)

ГДЗРусский языкОГЭ9 классВасильевых И.П.

16. Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)… Цыбулько И. П. Русский язык ЕГЭ-2017 ГДЗ. Вариант 13.

16.
Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)
в предложении должна(-ы) стоять запятая(-ые). (Подробнее…)

ГДЗЕГЭРусский языкЦыбулько И.П.

ЕГЭ-2017 Цыбулько И. П. Русский язык ГДЗ. Вариант 13. 18. Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)…

18.
Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)
в предложении должна(-ы) стоять запятая(-ые). (Подробнее…)

ГДЗЕГЭРусский языкЦыбулько И.П.

ГДЗ Физика Перышкин 9 класс Стр. 59

Содержание

Авторы:Перышкин, Гутник, Иванов

Год:2022

Тип:учебник

Нужно другое издание?

Содержание

• Ответы на вопросы
• Обсуди с товарищем
• Упражнение 13

Параграф 13. Свободное падение тел

Ответы на вопросы

1

. Свободным падением называют движение тел под действием силы тяжести.

2. Доказать, что свободное падение шарика, изображённого на рисунке 31, было равноускоренным можно следующим путем: модули векторов перемещения за последовательные промежутки времени будут относиться – s1: s2: s3…=1:3:5…

3. Целью опыта является найти ответ на вопрос, зависит ли ускорение свободного падения от массы падающего тела. Вывод- ускорение свободного падения одинаково для всех тел.

4. В любой момент времени все предметы имеют одинаковые мгновенные скорости, а значит, движутся с одинаковым ускорением, которое называют ускорением свободного падения и обозначают буквой g

5. В воздухе кусочек ваты падает с меньшим ускорением, чем железный шарик, потому что на падающие в воздухе тела действует сопротивление воздуха, то вата будет испытывать больше сопротивление. Из этого равнодействующая сила будет значительно меньше силы тяжести

6. Первым пришёл к выводу о том, что свободное падение является равноускоренным движением – Галилео Галилей.

Стр. 59

Обсуди с товарищем

Стр. 59

Упражнение 13

1.

Найти: \[s — \ ?\]

2.

Найти: t\(\ — \ ?\)

3.

Найти: t\(,\ s1,\ s_{n}\ — \ ?\)

4.

Найти: V\(- \ ?\)

5.

Найти: \[\text{s\ } — \ ?\]

Скачать

Ошибка или идея? Сообщить 📤

Мне не нравится на сайте, измените:Сделайте так, чтобы можно было:Решение неправильно/опечатка

Все номера

Стр. 54Стр. 59Стр. 62Стр. 63Стр. 65Стр. 170Стр. 172Стр. 173Стр. 177Стр. 178

© 2021 Copyright. Все права защищены. Правообладатель SIA Ksenokss.
Адрес: 1069, Курземес проспект 106/45, Рига, Латвия.
Тел.: +371 29-851-888 E-mail: [email protected]

Решения NCERT для математики класса 9.

Упражнение 13.1. Глава 13. Площадь поверхности и объем. Скачать PDF бесплатно.

Решения NCERT для математики класса 9. Глава 13. Площади поверхности и объемы. Решения доступны в формате PDF, и учащиеся могут легко их загрузить. Решения NCERT созданы экспертами по математике вместе с правильными геометрическими фигурами и пошаговыми пояснениями для лучшего понимания.

Сбор всех решений в Решениях NCERT для математики класса 9 соответствует последней программе NCERT и рекомендациям совета CBSE и направлен на то, чтобы помочь учащимся получить хорошие оценки на экзаменах совета.

Загрузить PDF-файл Решения NCERT для математики класса 9. Глава 13. Площади поверхностей и объемы. Упражнение 13.1

Доступ к другим решениям для упражнений по математике для 9 класса, глава 13 – Площади поверхности и объемы

Решение упражнения 13.2 (8 вопросов)

Решение упражнения 13.3 (9 вопросов)

Решение упражнения 13.4 (5 вопросов)

Решение упражнения 13. 5 (5 вопросов)

Решение упражнения 13.6 (8 вопросов)

Решение упражнения 13.7 (9 вопросов)

Решение упражнения 13.8 (10 вопросов)

Решение упражнения 13.9 (3 вопроса)

Доступ к ответам по математике NCERT, класс 9, математика, глава 13. Площади поверхности и объемы. Упражнение 13.1

1. Изготовить пластиковый ящик длиной 1,5 м, шириной 1,25 м и глубиной 65 см. Он должен быть открыт сверху. Пренебрегая толщиной пластикового листа, определить:

(i) Площадь листа, необходимая для изготовления коробки.

(ii) Стоимость листа для него, если лист размером 1 м ² стоит рупий. 20.

Решение:

Дано: длина (л) ящика = 1,5 м

Ширина (b) коробки = 1,25 м

Глубина (h) коробки = 0,65 м

(i) Коробка должна быть открыта сверху.

Требуемая площадь листа.

= 2л+2ч+фунт

= [2×1,5×0,65+2×1,25×0,65+1,5×1,25] м ²

= (1,95+1,625+1,875) м ² = 5,45 м ²

(ii) Стоимость листа за м ² площади = 20 рупий.

Стоимость листа 5,45 м ² площадь = руб (5,45×20)

= 109

рупий

2. Длина, ширина и высота помещения равны 5 м, 4 м и 3 м соответственно. Найти стоимость побелки стен помещения и потолка из расчета 7,50 руб./м

2 .

Решение:

Длина (л) помещения = 5 м

Ширина (b) помещения = 4 м

Высота (h) помещения = 3 м

Видно, что четыре стены и потолок комнаты нужно побелить.

Общая площадь побелки = Площадь стен + Площадь потолка помещения

= 2л+2ч+фунт

= [2×5×3+2×4×3+5×4]

= (30+24+20)

= 74

Площадь = 74 м ²

Также,

Стоимость побелки за м ² площади = 7,50 рупий (Данная)

Стоимость побелки 74 м ² площадь = руб. (74×7,50)

= рупий. 555

3. Пол прямоугольного зала имеет периметр 250 м. Если стоимость покраски четырех стен из расчета 10 рупий за м ² составляет 15000 рупий, найдите высоту зала.

[Подсказка: площадь четырех стен = площадь боковой поверхности]

Решение:

Пусть длина, ширина и высота прямоугольного зала равны l, b и h соответственно.

Площадь четырех стен = 2lh+2bh

= 2(l+b)ч

Периметр пола зала = 2(l+b)

= 250 м

Площадь четырех стен = 2(l+b) h = 250h·м ²

Стоимость покраски квадратного метра = 10

рупий

Стоимость покраски 250 х квадратных метров площади = рупий (250 х 10) = 2500 рупий

Однако указано, что стоимость покраски стен составляет рупий. 15000.

15000 = 2500ч

или ч = 6

Следовательно, высота зала 6 м.

4. Краски в определенной емкости достаточно, чтобы покрасить площадь, равную 9,375 м ² . Сколько кирпичей размером 22,5 см × 10 см × 7,5 см можно выкрасить из этой емкости?

Решение:

Общая площадь поверхности одного кирпича = 2(lb +bh+lb)

= [2(22,5×10+10×7,5+22,5×7,5)] см ²

= 2(225+75+168,75) см ²

= (2×468,75) см ²

= 937,5 см ²

Пусть n кирпичей можно закрасить краской из контейнера.

Площадь n кирпичей = (n×937,5) см ² = 937,5n см ²

Согласно данной инструкции, площадь, которая может быть окрашена краской контейнера = 9,375 м ² = 93750 см ²

Итак, имеем 93750 = 937,5n

n = 100

Следовательно, краской из контейнера можно закрасить 100 кирпичей.

5. Кубическая коробка имеет каждое ребро по 10 см, а другая прямоугольная коробка имеет длину 12,5 см, ширину 10 см и высоту 8 см.

(i) У какого ящика площадь боковой поверхности больше и на сколько?

(ii) У какой коробки общая площадь поверхности меньше и на сколько?

Решение:

Из постановки вопроса имеем

Ребро куба = 10см

Длина, l = 12,5 см

Ширина, b = 10см

Высота, h=8 см

(i) Найдите площадь боковой поверхности обеих фигур.

Площадь боковой поверхности кубической коробки = 4 (край) ²

= 4(10) ²

= 400 см ² …(1)

Площадь боковой поверхности прямоугольной коробки = 2[lh+bh]

= [2(12,5×8+10×8)]

= (2×180) = 360

Следовательно, площадь боковой поверхности прямоугольного ящика равна 360 см ² . …(2)

Из (1) и (2) площадь боковой поверхности кубического ящика больше, чем площадь боковой поверхности прямоугольного ящика. Разница между обеими боковыми поверхностями 40 см ² .

(Площадь боковой поверхности кубической коробки – Площадь боковой поверхности прямоугольной коробки = 400 см ² –360 см ² = 40 см ² )

(ii) Найдите общую площадь обеих фигур.

Общая площадь поверхности кубической коробки = 6(ребро) ² = 6(10 см) ² = 600 см ² …(3)

Общая площадь поверхности прямоугольного ящика

= 2[левый+черный+фунт]

= [2(12,5×8+10×8+12,5×100)]

= 610

Это означает, что общая площадь поверхности прямоугольного ящика составляет 610 см ² ..(4)

Из (3) и (4) общая площадь поверхности кубического ящика меньше, чем у прямоугольного ящика. А их разница 10см ² .

Таким образом, общая площадь поверхности кубической коробки меньше площади кубической коробки на 10 см ²

6. Небольшая комнатная теплица (гербарий) полностью состоит из стеклянных панелей (включая основание), скрепленных лентой. Его длина 30 см, ширина 25 см, высота 25 см.

(i) Какова площадь стекла?

(ii) Сколько ленты необходимо для всех 12 кромок?

Решение:

Длина теплицы, допустим l=30см

Ширина теплицы, скажем, b = 25 см

Высота теплицы, скажем, h = 25 см

(i) Общая площадь поверхности теплицы = площадь стекла = 2[lb+lh+bh]

= [2(30×25+30×25+25×25)]

= [2(750+750+625)]

= (2×2125) = 4250

Общая площадь стекла 4250 см ²

(ii)

Судя по рисунку, лента требуется вдоль сторон AB, BC, CD, DA, EF, FG, GH, HE AH, BE, DG и CF.

Общая длина ленты = 4(l+b+h)

= [4(30+25+25)] (после подстановки значений)

= 320

Следовательно, на все 12 краев требуется лента 320 см.

7. Shanti Sweets Stall размещала заказ на изготовление картонных коробок для упаковки своих сладостей. Требовались коробки двух размеров. Больший из размеров 25 см × 20 см × 5 см, а меньший из размеров 15 см × 12 см × 5 см. Для всех перекрытий требуется дополнительно 5% от общей площади поверхности. Если стоимость картона 1000 руб. 4 на 1000 см ² , найдите стоимость картона, необходимого для поставки 250 коробок каждого вида.

Решение:

Пусть l, b и h будут длиной, шириной и высотой ящика соответственно.

Большая коробка :

л = 25см

б = 20 см

ч = 5 см

Общая площадь поверхности большего ящика = 2(lb+lh+bh)

= [2(25×20+25×5+20×5)]

= [2(500+125+100)]

= 1450 см ²

Дополнительная площадь необходима для перекрытия 1450×5/100 см ²

= 72,5 см ²

С учетом всех перекрытий общая площадь большей коробки

= (1450+72,5) см ² = 1522,5 см ²

Площадь листа картона, необходимая для 250 таких больших коробок

= (1522,5×250) см ² = 380625 см ²

Меньшая коробка:

Аналогично, общая площадь поверхности меньшей коробки = [2(15×12+15×5+12×5)] см ²

= [2(180+75+60)] см ²

= (2×315) см ²

= 630 см ²

Следовательно, дополнительная площадь, необходимая для перекрытия 630×5/100 см ² = 31,5 см ²

Общая площадь поверхности 1 коробки меньшего размера с учетом всех перекрытий

= (630+31,5) см ² = 661,5 см ²

Площадь листа картона, необходимая для 250 коробок меньшего размера = (250×661,5) см ² = 165375 см ²

Короче:

Коробка	Размеры (в см)	Общая площадь поверхности (в см 2 )	Дополнительная площадь, необходимая для нахлеста (в см 2 )	Общая площадь всех перекрытий (в см 2 )	Место для 250 таких коробок (в см 2 )
Большая коробка	л = 25 б = 20 с = 5	1450	1450×5/100 = 72,5	(1450+72,5) = 1522,5	(1522,5×250) = 380625
Коробка меньшего размера	л = 15 б = 12 ч =5	630	630×5/100 = 31,5	(630+31,5) = 661,5	(250×661,5) = 165375

Всего требуется лист картона = (380625+165375) см ²

= 546000 см ²

Дано: Стоимость 1000 см ² листа картона = руб. 4

Следовательно, стоимость 546000 см ² листа картона =руб. (546000×4)/1000 = рупий. 2184

Следовательно, стоимость картона, необходимого для изготовления 250 коробок каждого вида, составит рупий. 2184.

8. Правин хотела сделать временное убежище для своей машины, соорудив коробчатую конструкцию с брезентом, закрывающим все четыре стороны и верхнюю часть машины (с передней стороной в виде створки, которую можно свернуть). Предполагая, что поля сшивания очень малы и, следовательно, незначительны, сколько брезента потребуется, чтобы сделать навес высотой 2,5 м с размерами основания 4 м × 3 м?

Решение:

Пусть l, b и h — длина, ширина и высота укрытия соответственно.

Дано:

л = 4 м

б = 3 м

ч = 2,5 м

Потребуется брезент для верхней части и четырех стенок убежища.

Используя формулу, требуемая площадь брезента = 2(lh+bh)+lb

Подставляя значения l, b и h, получаем

= [2(4×2,5+3×2,5)+4×3] м ²

= [2(10+7,5)+12]м ²

= 47 м ²

Следовательно, потребуется 47 м ² брезента.

---

Упражнение 13.1 по математике для 9 класса состоит из задач, которые охватывают такие понятия, как площадь поверхности куба и параллелепипеда. Он включает прикладной уровень задач в реальном времени, которые заставляют студентов думать и применять соответствующую формулу.

Также объясняется, как шесть прямоугольных частей используются для покрытия всей внешней поверхности прямоугольного параллелепипеда и как находится площадь поверхности прямоугольного параллелепипеда и куба.

Изучите все решения NCERT для математики класса 9, глава 13, а также другие учебные материалы и заметки, предоставленные BYJU’S. Задачи решаются подробно с соответствующими формулами и цифрами, чтобы получить хорошие оценки на экзаменах CBSE.

Ключевые особенности решений NCERT для математики класса 9. Глава 13. Площади поверхности и объем. Упражнение 13.1

• Эти решения NCERT позволяют учащимся решать и повторять все вопросы упражнения 13.1.
• Пошаговые решения, предлагаемые нашими экспертами-предметниками, помогут им получить больше оценок.
• Они следуют рекомендациям NCERT, которые помогают соответствующим образом подготовить учащихся.
• В них содержатся все важные вопросы, наиболее ожидаемые на экзамене.

Решения NCERT для главы 13, класс 9

Вы учитесь…

Получите ответы на все вопросы упражнений и примеры из главы 13, класс 9, площадь поверхности и объемы из книги NCERT. Все ответы решаются простым способом, с видео каждого вопроса

 

В этой главе мы изучим

• Боковой и Суммарный Площадь поверхности Куб и параллелепипед
• Изогнутая и общая площадь поверхности цилиндра
• Изогнутая и общая площадь поверхности прямоугольного круга Конус
• Площадь поверхности сферы
• Изогнутая и общая площадь поверхности полусферы
• Что такое Объем из твердой
• Объем Cube и Cuboid
• Объем Цилиндр
• Объем конуса
• Объем Сферы
• Объем полушария

 

Вы также можете проверить список всех формул площади поверхности и объема

 

Щелкните ссылку на упражнение или ссылку на тему ниже, чтобы начать главу.

Примечание. При нажатии на ссылку появится только первое сообщение. Другие вопросы указаны в списке со стрелками внизу

---

Серийный заказ

Пример 13.1

Пример 13.2

Пример 13.3

Пример 13.4

Пример 13.5

Пример 13.6

Пример 13.7

Пример 13.8

Примеры

Пример 13.9 (дополнительно)

---

По концепции

Площадь куба/кубоида

Объем куба/прямоугольника

Площадь цилиндра

Объем цилиндра

Площадь конуса

Объем конуса

площадь сферы

Объем сферы

Площадь полушария

Объем полушария

---

Что в нем?

Получите ответы на все вопросы с упражнениями и примеры из главы 13, класс 9, площадь поверхности и объемы из книги NCERT.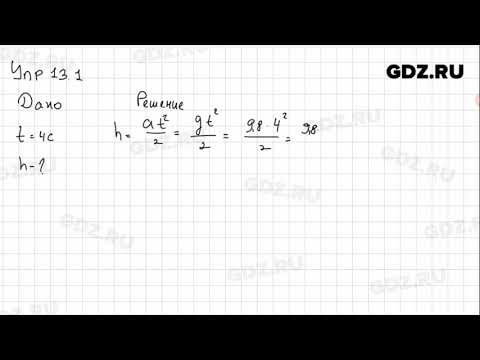 Все ответы решаются простым способом, с видео каждого вопроса

 

В этой главе мы узнаем

• Боковая сторона и Всего Площадь поверхности Куб и параллелепипед
• Изогнутая и общая площадь поверхности цилиндра
• Изогнутая и общая площадь поверхности прямоугольного круга Конус
• Площадь поверхности сферы
• Изогнутая и общая площадь поверхности полусферы
• Что такое Объем твердого тела
• Объем Cube и Cuboid
• Объем Цилиндр
• Объем конуса
• Объем Сферы
• Объем полушария

 

Вы также можете проверить список всех формул площади поверхности и объема

 

Щелкните ссылку на упражнение или ссылку на тему ниже, чтобы начать главу.