Номер (задание) 77 — гдз по алгебре 9 класс Макарычев, Миндюк
Условие / номер / 77
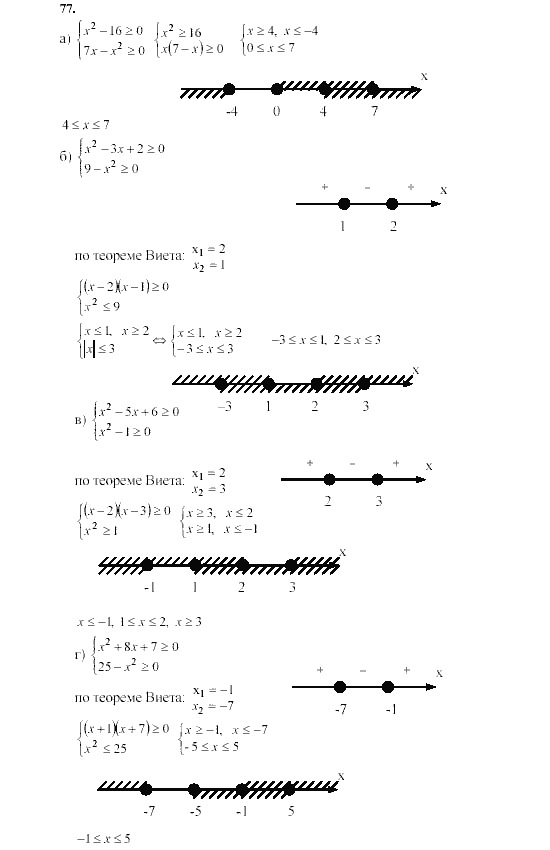
77. Разложите на множители трехчлен: а) 2х2 — 2х +1; б) -9х2 + 12х — 4; в) 16а2 + 24а + 9; г) 0,25m2 – 2m + 4.
решебник / номер / 77
youtube.com/embed/k_PoeJrxjFQ?start=21131″ frameborder=»0″ allowfullscreen=»»/>
решебник №2 / номер / 77мигом!. Учебник по алгебре, 9 класс. Макарычев Ю.А., 1999 год.
- О сайте domashka-migom.ru
- Готовые домашние задания
Выберите номер своего задания
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281 282 283 284 285 286 287 288 289 290 291 292 293 294 295 296 297 298 299 300 301 302 303 304 305 306 307 308 309 310 311 312 313 314 315 316 317 318 319 320 321 322 323 324 325 326 327 328 329 330 331 332 333 334 335 336 337 338 339 340 341 342 343 344 345 346 347 348 349 350 351 352 353 354 355 356 357 358 359 360 361 362 363 364 365 366 367 368 369 370 371 372 373 374 375 376 377 378 379 380 381 382 383 384 385 386 387 388 389 390 391 392 393 394 395 396 397 398 399 400 401 402 403 404 405 406 407 408 409 410 411 412 413 414 415 416 417 418 419 420 421 422 423 424 425 426 427 428 429 430 431 432 433 434 435 436 437 438 439 440 441 442 443 444 445 446 447 448 449 450 451 452 453 454 455 456 457 458 459 460 461 462 463 464 465 466 467 468 469 470 471 472 473 474 475 476 477 478 479 480 481 482 483 484 485 486 487 488 489 490 491 492 493 494 495 496 497 498 499 500 501 502 503 504 505 506 507 508 509 510 511 512 513 514 515 516 517 518 519 520 521 522 523 524 525 526 527 528 529 530 531 532 533 534 535 536 537 538 539 540 541 542 543 544 545 546 547 548 549 550 551 552 553 554 555 556 557 558 559 560 561 562 563 564 565 566 567 568 569 570 571 572 573 574 575 576 577 578 579 580 581 582 583 584 585 586 587 588 589 590 591 592 593 594 595 596 597 598 599 600 601 602 603 604 605 606 607 608 609 610 611 612 613 614 615 616 617 618 619 620 621 622 623 624 625 626 627 628 629 630 631 632 633 634 635 636 637 638 639 640 641 642 643 644 645 646 647 648 649 650 651 652 653 654 655 656 657 658 659 660 661 662 663 664 665 666 667 668 669 670 671 672 673 674 675 676 677 678 679 680 681 682 683 684 685 686 687 688 689 690 691 692 693 694 695 696 697 698 699 700 701 702 703 704 705 706 707 708 709 710 711 712 713 714 715 716 717 718 719 720 721 722 723 724 725 726 727 728 729 730 731 732 733 734 735 736 737 738 739 740 741 742 743 744 745 746 747 748 749 750 751 752 753 754 755 756 757 758 759 760 761 762 763 764 765 766 767 768 769 770 771 772 773 774 775 776 777 778 779 780 781 782 783 784 785 786 787 788 789 790 791 792 793 794 795 796 797 798 799 800 801 802 803 804 805 806 807 808 809 810 811 812 813 814 815 816 817 818 819 820 821 822 823 824 825 826 827 828 829 830 831 832 833 834 835 836 837 838 839 840 841 842 843 844 845 846 847 848 849 850 851 852 853 854 855 856 857 858 859 860 861 862 863 864 865 866 867 868 869 870 871 872 873 874 875 876 877 878 879 880 881 882 883 884 885 886 887 888 889 890 891 892 893 894 895 896 897 898 899 900 901 902 903 904 905 906 907 908 909 910 911 912 913 914 915 916 917 918 919 920 921 922 923 924 925 926 927 928 929 930 931 932 933 934 935 936 937 938 939 940 941 942 943 944 945 946 947 948 949 950 951 952 953 954 955 956 957 958 959 960 961 962 963 964 965 966 967 968 969 970 971 972 973 974 975 976 977 978 979 980 981 982 992 993 994 995 996 997 998 999 1000 1001 1002 1003 1004 1005 1006 1007 1008 1009 1010 1011 1012 1013 1014 1015 1016 1017 1018 1019 1020 1021 1022 1023 1024 1025 1026 1027 1028 1029 1030 1031 1032 1033 1034 1035 1036 1037 1038 1039 1040 1041 1042 1043 1044 1045 1046 1047 1048 1049 1050 1051 1052 1053 1054 1055 1056 1057 1058 1059 1060 1061 1062 1063 1064 1065 1066 1067 1068 1069 1070 1071 1072 1073 1074 1075 1076 1077 1078 1079 1080 1081 1082 1083 1084 1085 1086 1087 1088 1089 1090 1091 1092 1093 1094 1095 1096 1097 1098 1099 1100 1101 1102 1103 1104 1105 1106 1107 1108 1109 1110 1111 1112 1113 1114 1115 1116 1118 1119 1120 1121 1122 1123 1124 1125 1126 1127 1128 1129 1130 1131 1132 1133 1134 1135 1136 1137 1138 1139 1140 1141 1142 1143 1144 1145 1146 1147 1148 1149 1150 1151 1152 1153 1154 1155 1156 1157 1158 1159 1160 1161 1162 1163 1164 1165
ГДЗ решебник по задачнику алгебры 9 класс: Мордкович
Спиши ГДЗ•9 класс•Алгебра•МордковичГДЗ по алгебре за 9 класс Мордокович – это электронный сборник решений по учебнику Мордоковича А. Г., Александровой Л.А., Мишустиной Т.Н., Тульчинской Т.Е. и др. Если решение неравенства или системы равнений не привело к желаемому ответу, то решебник не только продемонстрирует правильный ответ, но и предложит алгоритм выполнения подобных заданий, который можно будет запомнить на будущее.
Г., Александровой Л.А., Мишустиной Т.Н., Тульчинской Т.Е. и др. Если решение неравенства или системы равнений не привело к желаемому ответу, то решебник не только продемонстрирует правильный ответ, но и предложит алгоритм выполнения подобных заданий, который можно будет запомнить на будущее.
Повторение
Номера
§ 1.
§ 2.
§ 3.
§ 4.
§ 5.
§ 6.
§ 7.
§ 8.
§ 9.
§ 10.
§ 11.
§ 12.
§ 13.
§ 14.
§ 15.
§ 16.
§ 17.
§ 18.
§ 19.
§ 20.
§ 21.
Итоговое повторение
Числовые выражения
Алгебраические выражения
Функции и графики
Уравнения и системы уравнений
Неравенства и системы неравенств
Задачи на составление уравнений или систем уравнений
Арифметическая и геометрическая прогрессии
ДКР 1
вариант 1
вариант 2
ДКР 2
вариант 1
вариант 2
ДКР 3
вариант 1
вариант 2
ДКР 4
вариант 1
вариант 2
ДКР 5
вариант 1
вариант 2
Готовимся к экзаменам с решебником по алгебре Мордоковича
В 9 классе нужно не только усвоить новые формулы, но и вспомнить весь материал за 5-8 классы. Что делать, если экзамены на носу, а решить не получается даже обычную домашнюю работу?
Что делать, если экзамены на носу, а решить не получается даже обычную домашнюю работу?
Решение есть – ГДЗ по алгебре для 9 класса Мордокович А.Г. В онлайн-сборнике достаточно найти нужное упражнение, разобрать и запомнить алгоритм его выполнения. Тем более, что здесь приведены решения по примерам и задачам на такие темы:
- решение систем рациональных неравенств;
- четные и нечетные числовые функции, их графики и свойства;
- решение систем уравнений и построение моделей реальных ситуаций;
- арифметическая и геометрическая прогрессии;
- простейшие задачи по комбинаторике и теории вероятности.
Если вы открыли онлайн-решебник по алгебре для 9 класса Мордокович А.Г., то не стоит бездумно списывать готовые решения: стоит подробно разобрать, как выполняется уравнение или задачка, чтобы использовать этот алгоритм на контрольных, экзаменах, при поступлении в колледж.
СПИШИ ГДЗ – понять алгебру по силам каждому
Как успевать по алгебре, если математических способностей от природы в тебе нет? Это реально, если обратиться не к увесистым сборникам теорем и формул, а к готовым домашним заданиям.
Именно в этих практических сборниках показано, как применять теоретические знания на практике: решать уравнения, задачи, примеры. На сайте СПИШИ ГДЗ ответы можно найти всего в один клик – и тем самым сэкономить свое время. Найти, разобрать и запомнить.
Какие еще преимущества мы предлагаем свои пользователям?
- бесплатный круглосуточный доступ с телефона, планшета, компьютера;
- самая свежая и актуальная база ответов;
- отсутствие видеороликов и рекламных обращений на весь экран, которые мешают пользоваться сайтом.
Ответы и решения вы можете искать и использовать без регистрации, в любое время суток. Такой алгоритм ценят не только девятиклассники, но и их родители, которым интересна успеваемость их взрослых детей.
пособие для учителей общеобразовательных организаций. Т. А. Бурмистрова
%PDF-1.6 % 442 0 obj > endobj 441 0 obj >stream application/pdf
 Сборник рабочих программ. 7-9 классы: пособие для учителей общеобразовательных организаций. Т. А. Бурмистрова
Сборник рабочих программ. 7-9 классы: пособие для учителей общеобразовательных организаций. Т. А. Бурмистрова
| ФИО | Должность | Контактный телефон | Преподаваемые дисциплины |
|---|---|---|---|
| Фатеева Нина Владимировна | Директор школы | 8 (812) 417-62-19 | |
| Заиченко Наталья Алексеевна | Научный руководитель, профессор НИУ ВШЭ, академический руководитель магистерской программы «Управление образованием» | ||
| Пуголовок Лариса Дмитриевна | Заместитель директора по воспитательной работе | 8 (812) 417-62-24 | История Обществознание ИиКСПб |
| Кондратюк Александра Владимировна | Заместитель директора по учебно-воспитательной работе, Руководитель службы сопровождения | 8 (812) 417-62-23 | |
| Сивачева Людмила Валерьевна | Заместитель директора по учебно-воспитательной работе (1-4 классы) | 8 (812) 417-62-23 | Английский язык |
| Энгель Наталья Иозеповна | Заместитель директора по учебно-воспитательной работе | 8 (812) 417-62-20 | |
| Кондратюк Ирина Павловна | Заместитель директора по естественно-научному образованию | 8 (812) 417-62-20 | Химия |
| Доброумова Ольга Викторовна | Заместитель директора по учебно-воспитательной работе (9-11 классы) | 8 (812) 417-62-20 | Алгебра и начала анализа Геометрия Математика |
| Заволокина Татьяна Николаевна | Заместитель директора по учебно-воспитательной работе (5-8 классы) | 8 (812) 417-62-20 | Русский язык Литература |
| Воронцова Юлия Михайловна | Руководитель ОДОД | ||
| Абдуллина Полина Владимировна | Учитель биологии | Биология | |
| Андреева Наталья Владимировна | Воспитатель ГПД | ||
| Аргунов Нестер Константинович | Учитель ОБЖ | ||
| Антипина Татьяна Дмитриевна | Воспитатель ГПД | ||
| Антонова Анастасия Викторовна | главный бухгалтер | ||
| Белянко Елена Алексеевна | Педагог-библиотекарь | ||
| Богачева Алла Геннадьевна | Педагог дополнительного образования | ||
| Бойкова Елена Александровна | Учитель-логопед | ||
| Вагнер Евгений Валерьевич | Учитель истории | История ИиКСПб Обществознание | |
| Васильева Анна Александровна | Учитель английского языка | Английский язык | |
| Васильева Юлия Николаевна | Учитель физической культуры | Физическая культура | |
| Воронина Екатерина Константиновна | Учитель английского языка | | |
| Галимова Эльвира Миннехатовна | Учитель русского языка и литературы | Русский язык Литература | |
| Горбачева Елена Александровна | Воспитатель ГПД | ||
| Гордейчева Дарья Романовна | Учитель начальных классов | ||
| Григораш Олеся Валерьевна | Педагог-психолог | ||
| Грицай Дмитрий Сергеевич | учитель химии | Химия Технология | |
| Грицко Юлия Юрьевна | учитель физики | Физика | |
| Грушко Елена Дмитриевна | Учитель начальных классов | ||
| Грянченко Мария Валерьевна | Учитель химии | Химия Технология |
Рабочая программа по алгебре. 9 класс.Ю.Н.Макарычев, Н.Г.Миндюк и др.
9 класс.Ю.Н.Макарычев, Н.Г.Миндюк и др.
«Согласовано» «Утверждено»
Заместитель директора по Директор МКОУ
УВР МКОУ «Протасовская «Протасовская ООШ»
ООШ» __________/Леонов А.Л./
___________/Соломатов В.С./
Приказ № ______ от
«____» _________ 2015 г. «____» _________ 2015 г.
РАБОЧАЯ ПРОГРАММА ПЕДАГОГА
Абрамовой Надежды Васильевны (категория- высшая)
по алгебре в 9 классе
Рассмотрено на заседании педагогического
совета
протокол № _________ от
«____» _____________ 2015 г.
2015 — 2016 учебный год
Пояснительная записка
Материалы рабочей программы по алгебре для 9 класса составлены на основе:
Примерной программы основного общего образования по математике,
авторской программы Миндюк Н.
 Г. по алгебре к линии Ю.Н. Макарычева и др.,
Г. по алгебре к линии Ю.Н. Макарычева и др.,федерального перечня учебников, рекомендованных Министерством образования РФ к использованию в образовательном процессе.
Базисного учебного плана общеобразовательных учреждений Российской Федерации, утверждённого приказом Минобразования РФ №1312 от 09.03.2004.
Значимость математической подготовки на ступени основного общего образования современного человека определила следующие цели обучения математике в школе:
овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;
интеллектуальное развитие учащихся, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе, свойственных математической деятельности: ясности и точности мысли, критического мышления, элементов алгоритмической культуры, пространственных представлений, способности к преодолению трудностей;
формирование представлений о математических идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;
формирование представлений о математике как форме описания и методе познания действительности;
воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, играющей особую роль в общественном развитии.

Рабочая программа конкретизирует содержание предметных тем образовательного стандарта и даёт примерное распределение учебных часов по разделам курса.
Содержание программы включает в себя минимальный объём материала, обязательного для изучения, которого должны достичь все учащиеся.
Математическое образование в основной школе складывается из следующих содержательных компонентов (точные названия блоков): арифметика; алгебра; геометрия; элементы комбинаторики, теории вероятностей, статистики и логики. В своей совокупности они отражают богатый опыт обучения математике в нашей стране, учитывают современные тенденции отечественной и зарубежной школы и позволяют реализовать поставленные перед школьным образованием цели на информационно емком и практически значимом материале. Эти содержательные компоненты, развиваясь на протяжении всех лет обучения, естественным образом переплетаются и взаимодействуют в учебных курсах.
Арифметика призвана способствовать приобретению практических навыков, необходимых для повседневной жизни. Она служит базой для всего дальнейшего изучения математики, способствует логическому развитию и формированию умения пользоваться алгоритмами.
Алгебра нацелена на формирование математического аппарата для решения задач из математики, смежных предметов, окружающей реальности. Язык алгебры подчеркивает значение математики как языка для построения математических моделей, процессов и явлений реального мира. Одной из основных задач изучения алгебры является развитие алгоритмического мышления, необходимого, в частности, для освоения курса информатики; овладение навыками дедуктивных рассуждений. Другой важной задачей изучения алгебры является получение школьниками конкретных знаний о функциях как важнейшей математической модели для описания и исследования разнообразных процессов, для формирования у учащихся представлений о роли математики в развитии цивилизации и культуры.-reshenie-178.jpg)
Геометрия – один из важнейших компонентов математического образования, необходимый для приобретения конкретных знаний о пространстве и практически значимых умений, формирования языка описания объектов окружающего мира, для развития пространственного воображения и интуиции, математической культуры, для эстетического воспитания учащихся. Изучение геометрии вносит вклад в развитие логического мышления, в формирование понятия доказательства.
Элементы логики, комбинаторики, статистики и теории вероятностей становятся обязательным компонентом школьного образования, усиливающим его прикладное и практическое значение. Этот материал необходим, прежде всего, для формирования функциональной грамотности – умений воспринимать и анализировать информацию, представленную в различных формах, понимать вероятностный характер многих реальных зависимостей, производить простейшие вероятностные расчеты. Изучение основ комбинаторики позволит учащемуся осуществлять рассмотрение случаев, перебор и подсчет числа вариантов, в том числе в простейших прикладных задачах.
При изучении статистики и теории вероятностей обогащаются представления о современной картине мира и методах его исследования, формируется понимание роли статистики как источника социально значимой информации и закладываются основы вероятностного мышления.
В ходе освоения содержания курса учащиеся получают возможность:
развить представления о числе и роли вычислений в человеческой практике; сформировать практические навыки выполнения устных, письменных, инструментальных вычислений, развить вычислительную культуру;
овладеть символическим языком алгебры, выработать формально-оперативные алгебраические умения и научиться применять их к решению математических и нематематических задач;
изучить свойства и графики элементарных функций, научиться использовать функционально-графические представления для описания и анализа реальных зависимостей;
развить пространственные представления и изобразительные умения, освоить основные факты и методы планиметрии, познакомиться с простейшими пространственными телами и их свойствами;
получить представления о статистических закономерностях в реальном мире и о различных способах их изучения, об особенностях выводов и прогнозов, носящих вероятностный характер;
развить логическое мышление и речь – умения логически обосновывать суждения, проводить несложные систематизации, приводить примеры и контрпримеры, использовать различные языки математики (словесный, символический, графический) для иллюстрации, интерпретации, аргументации и доказательства;
сформировать представления об изучаемых понятиях и методах как важнейших средствах математического моделирования реальных процессов и явлений.

Содержание рабочей программы по алгебре для 9 класса на ступени основного общего образования направлено на достижение следующих целей:
ввести понятия квадратного трехчлена, корня квадратного трехчлена, изучить формулу разложения квадратного трехчлена на множители;
расширить сведения о свойствах функций, ознакомить учащихся со свойствами и графиком квадратичной функции и степенной функции;
систематизировать и обобщить сведения о решении целых и дробных рациональных уравнений с одной переменной;
сформировать умение решать неравенства второй степени;
выработать умение решать простейшие системы, содержащие уравнение второй степени, и текстовые задачи с помощью составления таких систем;
дать понятия об арифметической и геометрической прогрессияхкак числовых последовательностях особого вида;
ознакомить учащихся с понятиями перестановки, размещения, сочетания и соответствующими формулами для подсчёта их числа; ввести понятия относительной частоты и вероятности случайного события.

В ходе преподавания алгебры в 9 классе следует обращать внимание на то, чтобы учащиеся овладевали умениями общеучебного характера, разнообразными способами деятельности, приобретали опыт:
планирования и осуществления алгоритмической деятельности, выполнения заданных и конструирования новых алгоритмов;
решения разнообразных классов задач из различных разделов курса, в том числе задач, требующих поиска пути и способов решения;
исследовательской деятельности, развития идей, проведения экспериментов, обобщения, постановки и формулирования новых задач;
ясного, точного, грамотного изложения своих мыслей в устной и письменной речи, использования различных языков математики (словесного, символического, графического), свободного перехода с одного языка на другой для иллюстрации, интерпретации, аргументации и доказательства;
проведения доказательных рассуждений, аргументации, выдвижения гипотез и их обоснования;
поиска, систематизации, анализа и классификации информации, использования разнообразных информационных источников, включая учебную и справочную литературу, современные информационные технологии.
Рабочая программа составлена к УМК по алгебре Ю.Н. Макарычева, Н.Г. Миндюк, К.И. Нешкова, С.Б.Суворова.
Изучение алгебры в 9 классе направлено на решение следующих задач:
Развитие алгоритмического мышления, необходимого для освоения курса информатики, изучения смежных дисциплин, продолжения образования;
Овладение навыками дедуктивных рассуждений;
Развитие воображения, способностей к математическому творчеству;
Получение школьниками конкретных знаний о функциях как важнейшей математической модели для описания исследования разнообразных процессов;
Формирование у учащихся представлений о роли математики в развитии цивилизации и культуры;
Овладение системой алгебраических знаний и умений, необходимых для применения в практической деятельности.
Рабочая программа выполняет функции: информационно-методическую, организационно-планирующую, контролирующую..jpg)
Согласно действующему Базисному учебному плану в основной общеобразовательной школе предусмотрено на изучение алгебры в 9 классе 136 часов при 4 часах в неделю, так как из школьного компонента добавлен 1 час. В рабочей программе будет уделено внимание графикам функции и уравнениям с модулем, параметром, расширятся способы решения задач по комбинаторике и теории вероятности; подготовке к ГИА.
Содержание курса
1. Квадратичная функция, Её свойства. Степенная функция.
Функция. Свойства функции. Квадратный трёхчлен и его корни. Разложение квадратного трёхчлена на множители. Квадратичная функция, её свойства и график. Степенная функция. Корень n-ой степени.
Параллельный перенос графиков вдоль осей координат и симметрия относительно осей.Запись корней с помощью степени с дробным показателем
Уравнения и неравенства с одной переменной.

Целое уравнение. Дробно-рациональные уравнения. Неравенства второй степени с одной переменной. Метод интервалов. Примеры решения уравнений высших степеней методом разложения на множители. Корень многочлена.Примеры решения уравнений в целых числах. Доказательство алгебраических неравенств. Примеры решения дробно-линейных неравенств.
3. Уравнения и неравенства с двумя переменными.
Уравнение с двумя переменными и его график. Системы уравнений второй степени. Решение текстовых задач с помощью систем уравнений второй степени. Неравенства второй степени и их системы. Графическая интерпретация уравнений с двумя переменными и их систем.Примеры решения нелинейных систем.
4. Прогрессии.
Арифметическая и геометрическая прогрессии. Формулы n-ого члена и суммы первых n членов прогрессии. Бесконечно убывающая геометрическая прогрессия. Сложные проценты..jpg)
5. Элементы комбинаторики и теории вероятности.
Комбинаторное правило умножения. Перестановки, размещения, сочетания. Относительная частота и вероятность случайного события. Перебор вариантов. Понятие и примеры случайных событий. Частота события. Вероятность. Представление о геометрической вероятности.
6. Итоговое повторение.
Тождественные преобразования алгебраических выражений. Решение уравнений. Решение систем уравнений. Решение текстовых задач. Решение неравенств и их систем. Прогрессии. Функции и их свойства.
Учебно-методический комплект учителя:
Учебник: Макарычев Ю.Н., Миндюк Н.Г., К.И. Нешков, С.Б. Суворовой под редакцией С.А. Теляковского; Алгебра. 9 кл.- М.: Просвещение, 2008-2012.
Л. А. Тапилина, Т. Л. Афанасьева. Поурочное планирование по алгебре к учебнику Ю. Н. Макарычева «Алгебра 9».
 Издательство «Учитель», 2009.
Издательство «Учитель», 2009.Ю.П.Дудницын, В.Л.Кронгауз . Тематические тесты по алгебре для 9 класса — М.: Просвещение, 2010
В.И.Жохов, Л.Б.Крайнева Уроки алгебры в 9 классе: книга для учителя.-М: Просвещение,2009
Ю.Н.Макарычев, Н.Г.Миндюк, Л.Б.Крайнева. Алгебра. Дидактические материалы. 9 класс- М.: Просвещение,2009-2011.
Ю.Н.Макарычев, Н.Г.Миндюк, С.Б.Суворова И.С.Шлыкова. Изучение алгебры в 7-9 классах. Пособие для учителей — М.: Просвещение,2009
Ю.Н.Макарычев, Н.Г.Миндюк, К.И.Нешков, С.Б.Суворова под редакцией С.А.Теляковского. Элементы статистики и теории вероятностей — М.: Просвещение, 2008.
Учебно-методический комплект ученика:
Учебник: Макарычев Ю.Н., Миндюк Н.Г., К.И. Нешков, С.Б. Суворовой под редакцией С.А. Теляковского; Алгебра. 9 кл.- М.: Просвещение, 2008-2012.
Ю.Н.Макарычев, Н.Г.Миндюк, Л.Б.Крайнева. Алгебра. Дидактические материалы.
 9 класс- М.: Просвещение,2009-2011.
9 класс- М.: Просвещение,2009-2011.Л.В.Кузнецова, Е.А. Бунимович, С.Б.Суворова Алгебра. Сборник заданий для подготовки к итоговой аттестации в 9 классе — М: Просвещение, 2011.
Требования к уровню подготовки учащихся.
В результате изучения алгебры 9 класса ученик должен
знать/понимать
существо понятия математического доказательства; приводить примеры доказательств;
существо понятия алгоритма; приводить примеры алгоритмов;
как используются математические формулы, уравнения и неравенства; примеры их применения для решения математических и практических задач;
как математически определенные функции могут описывать реальные зависимости; приводить примеры такого описания;
как потребности практики привели математическую науку к необходимости расширения понятия числа;
вероятностный характер многих закономерностей окружающего мира; примеры статистических закономерностей и выводов;
смысл идеализации, позволяющей решать задачи реальной действительности математическими методами, примеры ошибок, возникающих при идеализации.

Уметь
составлять буквенные выражения и формулы по условиям задач; осуществлять в выражениях и формулах числовые подстановки и выполнять соответствующие вычисления, осуществлять подстановку одного выражения в другое; выражать из формул одну переменную через остальные;
выполнять основные действия со степенями с целыми показателями, с многочленами и с алгебраическими дробями; выполнять разложение многочленов на множители; выполнять тождественные преобразования рациональных выражений;
применять свойства арифметических квадратных корней для вычисления значений и преобразований числовых выражений, содержащих квадратные корни;
решать линейные, квадратные уравнения и рациональные уравнения, сводящиеся к ним, системы двух линейных уравнений и несложные нелинейные системы;
решать линейные и квадратные неравенства с одной переменной и их системы;
решать текстовые задачи алгебраическим методом, интерпретировать полученный результат, проводить отбор решений, исходя из формулировки задачи;
изображать числа точками на координатной прямой;
определять координаты точки плоскости, строить точки с заданными координатами; изображать множество решений линейного неравенства;
распознавать арифметические и геометрические прогрессии; решать задачи с применением формулы общего члена и суммы нескольких первых членов;
находить значения функции, заданной формулой, таблицей, графиком по ее аргументу; находить значение аргумента по значению функции, заданной графиком или таблицей;
определять свойства функции по ее графику; применять графические представления при решении уравнений, систем, неравенств;
описывать свойства изученных функций, строить их графики;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
выполнения расчетов по формулам, составления формул, выражающих зависимости между реальными величинами; нахождения нужной формулы в справочных материалах;
моделирования практических ситуаций и исследования построенных моделей с использованием аппарата алгебры;
описания зависимостей между физическими величинами соответствующими формулами при исследовании несложных практических ситуаций;
интерпретации графиков реальных зависимостей между величинами.

ЭЛЕМЕНТЫ ЛОГИКИ, КОМБИНАТОРИКИ, СТАТИСТИКИ И ТЕОРИИ ВЕРОЯТНОСТЕЙ
Уметь
проводить несложные доказательства, получать простейшие следствия из известных или ранее полученных утверждений, оценивать логическую правильность рассуждений, использовать примеры для иллюстрации и контрпримеры для опровержения утверждений;
извлекать информацию, представленную в таблицах, на диаграммах, графиках; составлять таблицы, строить диаграммы и графики;
решать комбинаторные задачи путем систематического перебора возможных вариантов и с использованием правила умножения;
вычислять средние значения результатов измерений;
находить частоту события, используя собственные наблюдения и готовые статистические данные;
находить вероятности случайных событий в простейших случаях;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
выстраивания аргументации при доказательстве и в диалоге;
распознавания логически некорректных рассуждений;
записи математических утверждений, доказательств;
анализа реальных числовых данных, представленных в виде диаграмм, графиков, таблиц;
решения практических задач в повседневной и профессиональной деятельности с использованием действий с числами, процентов, длин, площадей, объемов, времени, скорости;
решения учебных и практических задач, требующих систематического перебора вариантов;
сравнения шансов наступления случайных событий, для оценки вероятности случайного события в практических ситуациях, сопоставления модели с реальной ситуацией;
понимания статистических утверждений.

Квадратичная функция
В результате изучения курса математики учащиеся должны:
знать понятие функции;
правильно употреблять функциональную терминологию, понимать ее в тексте, в речи учителя, в формулировке задач;
находить значения функций, заданных формулой, таблицей, графиком;
решать обратную задачу;
знать понятие квадратного трехчлена, формулу разложения квадратного трехчлена на множители;
выделять квадрат двучлена из квадратного трехчлена, раскладывать трехчлен на множители;
понимать функции у=ах2, у=ах2+п и у=а(х – m)2, их свойства и особенности графиков;
получать график функции y=ax2 + bx + с из графика функции у=ах2 с помощью двух параллельных переносов вдоль осей координат;
знать свойства степенной функции с натуральным показателем, схематически строить графики функций, указывать особенности графиков;
знать понятие корня п-ой степени;
вычислять корни п-ой степени (несложные задания).

Уравнения и неравенства с одной переменной
В результате изучения курса математики учащиеся должны:
знать понятие целого рационального уравнения и его степени;
владеть приемами нахождения приближенных значений корней;
владеть методом введения вспомогательной переменной;
знать о дробных рациональных уравнениях, об освобождении от знаменателя при решении уравнений;
решать неравенства второй степени с одной переменной различными методами;
решать уравнения третьей и четвертой степени с одним неизвестным с помощью разложения на множители и с помощью введения вспомогательной переменной;
решать дробные рациональные уравнения, применяя формулы сокращенного умножения и разложения квадратного трехчлена на множители;
Уравнения и неравенства с двумя переменными
В результате изучения курса математики учащиеся должны:
знать и понимать уравнение с двумя переменными и его график, уравнение окружности;
решать графически системы уравнений;
решать системы, содержащие одно уравнение первой, а другое – второй степени, системы двух уравнений второй степени с двумя переменными;
решать текстовые задачи методом составления систем уравнений;
иметь представление о решении неравенств с двумя переменными;
иметь представление о решении системы неравенств с двумя переменными;
изображать на координатной плоскости множество решений неравенств;
изображать множество решений системы неравенств с двумя переменными на координатной плоскости.

Прогрессии
В результате изучения курса математики учащиеся должны:
знать понятия последовательности, п-го члена последовательности;
использовать индексные обозначения;
понимать, что арифметическая прогрессия – числовая последовательность особого вида;
знать формулы п первых членов арифметической прогрессии;
решать задания на применение свойств арифметической прогрессии;
понимать, что геометрическая прогрессия – числовая последовательность особого вида;
знать формулы п первых членов геометрической прогрессии;
применять формулы п-го члена и суммы п первых членов геометрической прогрессии при решении задач;
решать задачи, в том числе практического содержания с непосредственным применением изучаемых формул.

Элементы статистики и теории вероятностей
В результате изучения курса математики учащиеся должны:
знать комбинаторное правило умножения, формулы числа перестановок, размещений, сочетаний;
решать упражнения и задачи, в том числе практического содержания с непосредственным применением изучаемых формул;
вычислять вероятности;
решать задачи, используя формулы комбинаторики и теории вероятностей.
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
выполнения расчетов по формулам, составления формул, выражающих зависимости между реальными величинами; нахождения нужной формулы в справочных материалах;
моделирования практических ситуаций и исследовании построенных моделей с использованием аппарата алгебры;
описания зависимостей между физическими величинами соответствующими формулами при исследовании несложных практических ситуаций;
интерпретации графиков реальных зависимостей между величинами.

Требования к уровню подготовки обучающихся в 9 классе.
В ходе преподавания алгебры в 9 классе следует обращать внимание на то, чтобы учащиеся овладевали умениями общеучебного характера, разнообразными способами деятельности, приобретали опыт:
планирования и осуществления алгоритмической деятельности, выполнения заданных и конструирования новых алгоритмов;
решения разнообразных классов задач из различных разделов курса, в том числе задач, требующих поиска пути и способов решения;
исследовательской деятельности, развития идей, проведения экспериментов, обобщения, постановки и формулирования новых задач;
ясного, точного, грамотного изложения своих мыслей в устной и письменной речи, использования различных языков математики (словесного, символического, графического), свободного перехода с одного языка на другой для иллюстрации, интерпретации, аргументации и доказательства;
проведения доказательных рассуждений, аргументации, выдвижения гипотез и их обоснования;
поиска, систематизации, анализа и классификации информации, использования разнообразных информационных источников, включая учебную и справочную литературу, современные информационные технологии.

В результате изучения курса алгебры 9 класса обучающиеся должны:
знать/понимать
существо понятия математического доказательства; примеры доказательств;
существо понятия алгоритма; примеры алгоритмов;
как используются математические формулы, уравнения и неравенства; примеры их применения для решения математических и практических задач;
как математически определенные функции могут описывать реальные зависимости; приводить примеры такого описания;
как потребности практики привели математическую науку к необходимости расширения понятия числа;
вероятностный характер многих закономерностей окружающего мира; примеры статистических закономерностей и выводов;
каким образом геометрия возникла из практических задач землемерия; примеры геометрических объектов и утверждений о них, важных для практики;
смысл идеализации, позволяющей решать задачи реальной действительности математическими методами, примеры ошибок, возникающих при идеализации.

Календарно-тематический план
№
n/n
Раздел программы, количество часов
Номер урока данного раздела
Тема урока
Раздел1.
Квадратичная функция.
(29 часов)
1
1
Функция. Область определения и область значений функции
2
2
Вычисление значения функции, заданной формулой, а также двумя и тремя формулами
3
3
График функции. Параллельный перенос графиков вдоль осей координат и симметрия относительно осей.
4
4
Интерпретация графиков реальных зависимостей
5
5
Свойства функций: нули функции, возрастающая и убывающая функции, промежутки знакопостоянства
6
6
Свойства линейных функций
7
7
Свойства обратной пропорциональности
8
8
Квадратный трёхчлен и его корни
9
9
Выделение квадрата двучлена из квадратного трёхчлена
10
10
Количество корней квадратного трёхчлена
11
11
Разложение квадратного трёхчлена на множители
12
12
Сокращение дробей с помощью разложения квадратного трёхчлена на множители
13
13
Контрольная работа № 1 по теме «Функции и их свойства. Квадратный трехчлен».
Квадратный трехчлен».
14
14
Функция у=ах², свойства функции
15
15
График функции у=ах²
16
16
Функция у=ах²+n, свойства функции
17
17
График функции у=ах² + n,
18
18
Функция у=а(x-m)², свойства функции
19
19
График функции у=а(x-m)²
20
20
Функция у= ах²+ bx+c. Область определения и область значений функции
21
21
Построение графика квадратичной функции
22
22
Функция у= ах²+ bx+c. Нули функции и промежутки знакопостоянства
Нули функции и промежутки знакопостоянства
23
23
Функция у= ах²+ bx+c. Промежутки возрастания и убывания функции
24
24
Практическое занятие по теме «Построение графика квадратичной функции»
25
25
Функция у=хⁿ
26
26
Корень n-й степени. Нахождение корня n-й степени с помощью калькулятора
27
27
Дробно — линейная функция и ее график
28
28
Степень с рациональным показателем. Запись корней с помощью степени с дробным показателем.
29
29
Контрольная работа № 2 по теме «Квадратичная функция. Степенная функция».
Степенная функция».
Раздел 2.
Уравнения и неравенства с одной переменной.
(20 часов)
30
1
Целое уравнение и его корни
31
2
Степень уравнения.
32
3
Примеры решения уравнений высших степеней методом разложения на множители. Корень многочлена.
33
4
Уравнения, приводимые к квадратным
34
5
Биквадратные уравнения. Примеры решения уравнений в целых числах.
35
6
Решение биквадратных уравнений
36
7
Дробные рациональные уравнения
37
8
Алгоритм решения дробных рациональных уравнений.
38
9
Решение дробных рациональных уравнений.
39
10
Решение дробных рациональных уравнений, используя введение новой переменной.
40
11
Решение дробных рациональных уравнений, сводя их к целым уравнениям с последующей проверкой корней.
41
12
Повторительно-обощающий урок по теме «Целое и дробные рациональные уравнения».
42
13
Неравенства второй степени с одной переменной. Доказательство алгебраических неравенств.
43
14
Решение неравенств второй степени с одной переменной.
44
15
Решение неравенств второй степени с одной переменной, используя графические представления.
45
16
Метод интервалов.
46
17
Решение неравенств методом интервалов. Примеры решения дробно-линейных неравенств
47
18
Применение метода интервалов к решению несложных рациональных неравенств
48
19
Обобщающий урок «Уравнения и неравенства с одной переменной»
49
20
Контрольная работа № 3 по теме «Уравнения и неравенства с одной переменной»
Раздел 3.
Уравнения и неравенства с двумя переменными (24 часа)
50
1
Уравнения с двумя переменными
51
2
График уравнения с двумя переменными.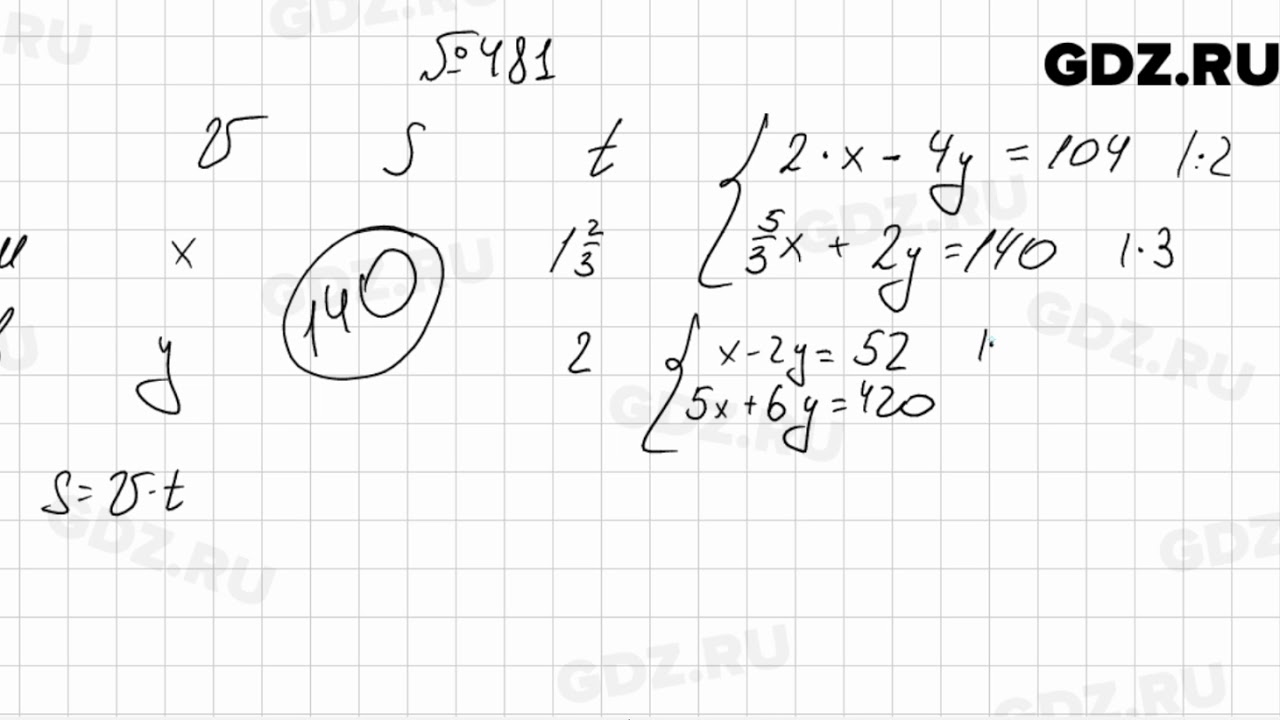
52
3
Составление уравнения с двумя переменными по заданному графику
53
4
Графическая интерпретация уравнений с двумя переменными и их систем.
54
5
Решение систем уравнений графическим способом.
55
6
Решение систем уравнений второй степени.
56
7
Решение систем, содержащих одно уравнение первой, а другое второй степени
57
8
Решение систем уравнений способом подстановки.
58
9
Решение систем уравнений способом сложения.
59
10
Решение систем уравнений.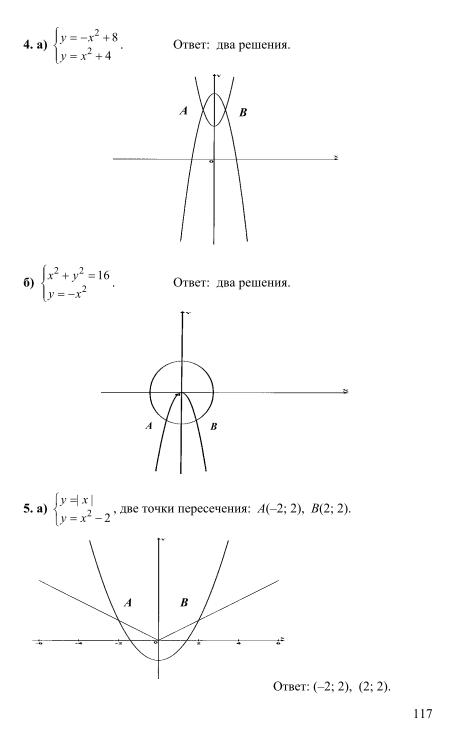
60
11
Решение систем уравнения графическим и аналитическим способами
61
12
Решение задач с помощью систем уравнений второй степени
62
13
Решение текстовых задач методом составления систем уравнений
63
14
Решение задач с помощью систем уравнений второй степени
64
15
Решение задач на движение с помощью систем уравнений второй степени
65
16
Решение задач на концентрацию и процентное содержание с помощью систем уравнений второй степени.
66
17
Неравенства с двумя переменными.
67
18
Решение неравенств с двумя переменными.
68
19
Графическое решение неравенства с двумя переменными.
69
20
Графическая интерпретация неравенств с двумя переменными и их систем.
70
21
Системы неравенств с двумя переменными.Примеры решения нелинейных систем
71
22
Решение систем неравенств с двумя переменными.
72
23
Построение решения системы неравенств с двумя переменными на координатной плоскости
73
24
Контрольная работа № 4 по теме «Уравнения и неравенства с двумя переменными».
Раздел 4.
Арифметическая и геометрическая прогрессии.
(17 часов)
74
1
Последовательности.
75
2
Основные способы задания последовательностей.
76
3
Определение арифметической прогрессии.
77
4
Формула n-го члена арифметической прогрессии
78
5
Решение упражнений на применение формулы n-го члена арифметической прогрессии
79
6
Формула суммы первых n членов арифметической прогрессии.
80
7
Решение упражнений на применение формулы суммы n первых членов арифметической прогрессии
81
8
Обобщающий урок по теме «Арифметическая прогрессия»
82
9
Контрольная работа№5 по теме «Арифметическая прогрессия»
83
10
Определение геометрической прогрессии
84
11
Формула n-го члена геометрической прогрессии. Сложные проценты.
Сложные проценты.
85
12
Решение упражнений на применение формулы n-го члена геометрической прогрессии.
86
13
Формула суммы первых n членов геометрической прогрессии.
87
14
Решение упражнений на применение формулы суммы n первых членов геометрической прогрессии.
88
15
Сумма бесконечной геометрической прогрессии при /g/ < 1
89
16
Обобщающий урок по теме «Геометрическая прогрессия»
90
17
Контрольная работа № 6 по теме «Геометрическая прогрессия».
Раздел 5.
Элементы комбинаторики и теории вероятностей
(17 часов)
91
1
Примеры комбинаторных задач. Перебор вариантов.
Перебор вариантов.
92
2
Область применения комбинаторики.
93
3
Комбинаторное правило умножения.
94
4
Применение правила комбинаторного умножения для решения задач на нахождение числа объектов или комбинаций (диагонали многоугольника, рукопожатия, число кодов, шифров, паролей и т. п.).
95
5
Перестановки
96
6
Решение упражнений на применение перестановки
97
7
Размещения
98
8
Решение упражнений на применение размещения.
99
9
Сочетания
100
10
Решение упражнений на применение сочетания.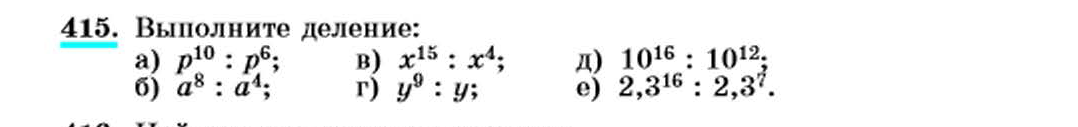
101
11
Решение комбинаторных задач.
102
12
Начальные сведения из теории вероятностей.
103
13
Частота события. Относительная частота случайного события.
104
14
Понятие и примеры случайных событий. Вычисление частоты случайного события.
105
15
Вероятность.Вероятность равновозможных событий.Представление о геометрической вероятности.
106
16
Оценка вероятности с помощью частоты, полученной опытным путём
107
17
Контрольная работа №7 по теме «Элементы комбинаторики и теории вероятностей»
Раздел 6.
Повторение.
(29 часов)
108
1
Повторение. Решение задач по курсу алгебры 7-9 классов. Вычисления.
109
2
Повторение. Преобразование алгебраических выражений
110
3
Повторение. Тождественные преобразования.
111
4
Повторение. Степень и её свойства
112
5
Повторение. Преобразование выражений со степенью
113
6
Повторение. Арифметический квадратный корень и его свойства.
114
7
Повторение. Преобразование выражений, содержащих квадратный корень
115
8
Повторение. Уравнения
Уравнения
116
9
Повторение. Системы уравнений.
117
10
Повторение. Решение систем уравнений.
118
11
Повторение. Неравенства.
119
12
Повторение. Системы неравенств.
120
13
Повторение. Функции , их свойства и графики.
121
14
Повторение. Графики функций.
122
15
Повторение. Описание зависимостей с помощью функций
123
16
Повторение. Интерпретация графиков реальных зависимостей.
124
17
Повторение.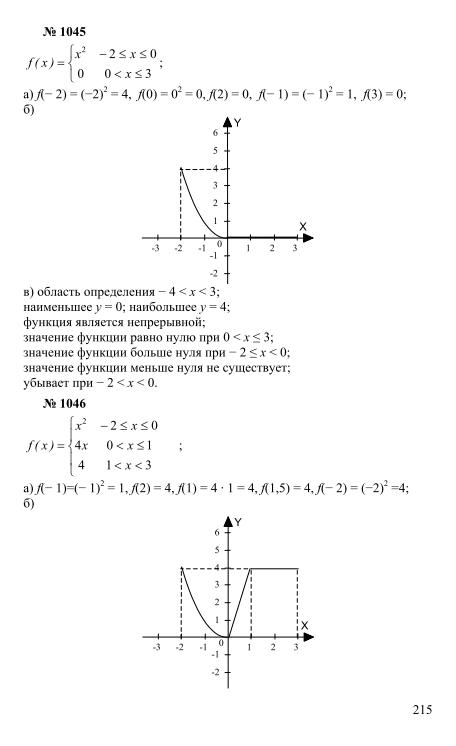 Решение задач на проценты.
Решение задач на проценты.
125
18
Повторение. Текстовые задачи. Задачи на движение
126
19
Повторение. Текстовые задачи. Задачи на работу
127
20
Повторение. Практические расчёты по формулам.
128
21
Повторение. Анализ данных, представленных графически (таблицы, графики, диаграммы)
129
22
Повторение. Основные единицы измерения величины.
130
23
Контрольная работа № 8. Итоговая работа.
131
24
Работа над ошибками. Комбинаторные задачи.
132
25
Повторение.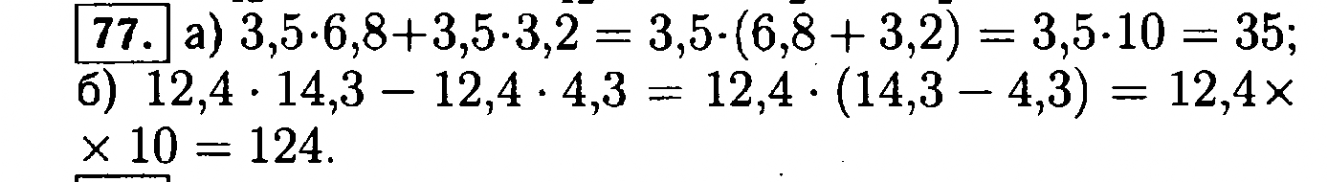 Задачи по теории вероятностей.
Задачи по теории вероятностей.
133
26
Тестовая работа по текстам ФИПИ для ГИА.
134
27
Повторение. Решение задач с помощью уравнения.
135
28
Повторение. Решение задач с помощью систем уравнений.
136
29
Повторение. Решение задач. Итоги года.
В результате изучения математики ученик должен
• существо понятия математического доказательства; приводить примеры доказательств;
• существо понятия алгоритма; приводить примеры алгоритмов;
• как используются математические формулы, уравнения и неравенства; примеры их применения для решения математических и практических задач;
• как математически определенные функции могут описывать реальные зависимости; приводить примеры такого описания;
• как потребности практики привели математическую науку к необходимости расширения понятия числа;
• вероятностный характер многих закономерностей окружающего мира; примеры статистических закономерностей и выводов;
Требования к уровню подготовки учащихся 8 класса по алгебре
В результате изучения курса алгебры ученик должен
знать/понимать
существо понятия алгоритма; приводить примеры алгоритмов;
как используются математические формулы, уравнения и неравенства; примеры их применения для решения математических и практических задач;
как определённые функции могут описывать реальные зависимости; приводить примеры такого описания;
как потребности практики привели математическую науку к необходимости расширения понятия числа;
примеры статистических закономерностей и выводов;
как решать задачи реальной действительности математическими методами.

уметь
— находить значения числовых выражений, степеней с целым показателем и корней;
— решать текстовые задачи алгебраическим методом, интерпретировать полученный результат, проводить отбор решений, исходя из формулировки задачи;
— составлять буквенные выражения и формулы по условиям задач; осуществлять в выражениях и формулах числовые подстановки и выполнять соответствующие вычисления,
— выполнять основные действия со степенями с целыми показателями и с алгебраическими дробями;
— записывать большие и малые числа с использованием целых степеней десятки;
— выполнять тождественные преобразования рациональных выражений;
— решать квадратные и рациональные уравнения, сводящиеся к ним;
— решать линейные неравенства и их системы;
— изображать множество решений линейного неравенства и системы;
— находить значения функции, заданной формулой, таблицей, графиком по её аргументу; находить значение аргумента по значению функции, заданной графиком, формулой или таблицей;
— строить графики изученных функций и определять свойства по графику;
— извлекать информацию, представленную в таблицах, на диаграммах, графиках; составлять таблицы, строить графики и диаграммы;
— проводить несложные доказательства, получать простейшие следствия из известных или ранее полученных утверждений, оценивать логическую правильность рассуждений, использовать примеры для иллюстрации и контрпримеры для опровержения утверждений;
использовать приобретённые знания и умения в практической деятельности и повседневной жизни для:
— решения несложных практических расчётных задач, в том числе с использованием при необходимости справочных материалов, калькулятора, компьютера;
— интерпретации результатов решения задач с учётом ограничений, связанных с реальными свойствами рассматриваемых процессов и явлений;
— анализа реальных числовых данных, представленных в виде диаграмм, графиков, таблиц
— понимания статистических утверждений;
— распознавания логически некорректных рассуждений;
решения практических задач в повседневной и профессиональной деятельности с использованием действий с числами, процентов, длин, площадей, объёмов, времени, скорости.

Требования к уровню подготовки обучающихся в 9 классе.
В ходе преподавания алгебры в 9 классе следует обращать внимание на то, чтобы учащиеся овладевали умениями общеучебного характера, разнообразными способами деятельности, приобретали опыт:
планирования и осуществления алгоритмической деятельности, выполнения заданных и конструирования новых алгоритмов;
решения разнообразных классов задач из различных разделов курса, в том числе задач, требующих поиска пути и способов решения;
исследовательской деятельности, развития идей, проведения экспериментов, обобщения, постановки и формулирования новых задач;
ясного, точного, грамотного изложения своих мыслей в устной и письменной речи, использования различных языков математики (словесного, символического, графического), свободного перехода с одного языка на другой для иллюстрации, интерпретации, аргументации и доказательства;
проведения доказательных рассуждений, аргументации, выдвижения гипотез и их обоснования;
поиска, систематизации, анализа и классификации информации, использования разнообразных информационных источников, включая учебную и справочную литературу, современные информационные технологии.

В результате изучения курса алгебры 9 класса обучающиеся должны:
знать/понимать
существо понятия математического доказательства; примеры доказательств;
существо понятия алгоритма; примеры алгоритмов;
как используются математические формулы, уравнения и неравенства; примеры их применения для решения математических и практических задач;
как математически определенные функции могут описывать реальные зависимости; приводить примеры такого описания;
как потребности практики привели математическую науку к необходимости расширения понятия числа;
вероятностный характер многих закономерностей окружающего мира; примеры статистических закономерностей и выводов;
каким образом геометрия возникла из практических задач землемерия; примеры геометрических объектов и утверждений о них, важных для практики;
смысл идеализации, позволяющей решать задачи реальной действительности математическими методами, примеры ошибок, возникающих при идеализации.

Перечень учебно-методического обеспечения
1.Бурмистрова Т.А. Программы общеобразовательных учреждений Алгебра. 7-9кл. М.: Просвещение. 2009.
2.ГлазковЮ.А.,.Гаиашвили М.Я. Тесты по алгебре:8класс. М.: «Экзамен». 2010.
3.ЖоховВ.И.,.Макарычев Ю.Н,.Миндюк Н.Г. Дидактические материалы по алгебре для 8кл.М.: Просвещение, 2008.
4.Макарычев Ю.Н., МиндюкН.Г. и др; под ред. Теляковского С.А. Алгебра: учебник для 8кл. М.: Просвещение. 2010.
5. Миндюк Н.Г.и др. Рабочая тетрадь.по алгебре. 8 класс. М: Просвещение.2014.
6.Миндюк Н.Г. Алгебра. Рабочие программы. Предметная линия учебников Ю.Н.Макарычева и других.7-9 классы. М.: Просвещение. 2011.
7.Черноруцкий В.В.Контрольно-измерительные материалы. Алгебра.8 класс. М: ВАКО.2013.
8.Компакт-диск. Демонстрационные таблицы. Алгебра 7-9 классы. М: Учитель.2012.
9.Видеоуроки по алгебре для 8 класса(по учебнику Ю.Н.Макарычева ).2014.
10. Ноутбук.
Ноутбук.
11.Проектор.
12.МФУ.
13.Колонки для ноутбука.
14.Таблицы по алгебре для 8 класса.
15.Компакт-диск. Комбинаторика и теория вероятностей. 7-9 классы.М: Экзамен.2011.
16.Компакт-диск . Функции и графики. 5-8 классы. М: Экзамен. 2011.
17.Компакт-диск. Уравнения и неравенства . 5-8 классы. М: Экзамен. 2011.
Список литературы
1.Безрукова О.Л. Олимпиадные задания по математике 5-11 классы.Волгоград: Учитель. 2010.
2.Дудницын Ю.П., Кронгауз В.Л. Контрольные работы по алгебре. 8 класс.М.: Экзамен.2013.
3.Жохов В.И.,Карташева Г.Д. Уроки алгебры в 8 классе. М.: Просвещение. 2009.
4.Рурукин А.Н. Поурочные разработки по алгебре. 8 класс. М.: ВАКО. 2010.
Приложение 1
Практические занятия по предмету
Плановых контрольных работ- 11.
Административных контрольных работ — 2.
0.Входная контрольная работа за курс 7 класса.
Кр№1 Сложение и вычитание рациональных дробей
Кр№2 Умножение и деление рациональных дробей
Кр№3 Квадратные корни
Кр№4 Свойства арифметического квадратного корня
Кр№5 Квадратные уравнения
Кр№6 Дробные рациональные уравнения
Кр№7 Числовые неравенства
Кр№8 Неравенства с одной переменной и их системы
Кр№9 Степень с целым показателем
Кр№10 Итоговая за курс 8 класса
Тесты — 5.
Тест 1. Рациональные дроби
Тест 2. Квадратные корни
Тест 3. Квадратные уравнения
Тест 4. Неравенства
Тест 5. Степень с целым показателем
Зачётная физкультура и аттестаты с QR-кодами: что нового принёс 2021 год в систему тамбовского образования
Почему пока не стоит торопиться родителям будущих первоклассников с заявлением в школу, зачем нужны кюар-коды на школьных аттестатах, какие дисциплины перестанут оцениваться и почему, и что ещё нового принёс наступивший год в систему отечественного образования? О нововведениях мы расспросили начальника отдела надзора в сфере образования регионального управления образования и науки Елену Афонину.
Идём в первый класс: как, когда подать документы и нужно ли готовиться к учёбе
— Елена Валерьевна, какие изменения произошли в правилах приёма детей в первый класс?
— Основное изменение коснулось даты приёма заявлений. Если раньше запись в школу была открыта уже в начале года, то в этом году приём документов начнётся с 1 апреля и продлится до 30 июня.
Распорядительный акт о приёме на обучение в первый класс издаётся только после этой даты строго в течение трёх рабочих дней после завершения приёма заявлений, а не семи дней, как раньше. Речь идёт о детях, проживающих на закреплённой к школе территории. Немаловажно то, что в приказе Министерства просвещения РФ закреплены нормы о праве преимущественного приёма детей в те учреждения, где обучаются их братья или сёстры, также документом установлены категории детей, которым предоставляются места в государственных и муниципальных школах во внеочередном и первоочередном порядке. С 6 июля начнётся приём заявлений на обучение на свободные места для детей, которые не проживают на закреплённой территории. Кроме того, расширены способы подачи заявления о приёме на обучение и обновлён перечень документов для приёма в школу.
Кроме того, расширены способы подачи заявления о приёме на обучение и обновлён перечень документов для приёма в школу.
— Какими же способами можно подать заявление?
— Конечно, можно обратиться и в саму школу. Но и не только. У родителей есть возможность оформить документы через региональный портал государственных и муниципальный услуг, отправив заявку на зачисление в электронной форме. Подать документы можно также через операторов почтовой связи заказным письмом с уведомлением о вручении. В электронной форме скан или фото заявления можно отправить по электронной почте, через информационную систему или посредством официального сайта школы в сети Интернет.
— Какие документы нужны?
— Для зачисления в школу родители или законные представители должны представить заявление, копию документа, удостоверяющего личность родителя ребёнка, копию свидетельства о рождении ребёнка, копию документа о регистрации ребёнка по месту жительства или по месту пребывания на закреплённой территории или справку о приёме документов для оформления регистрации по месту жительства.
Если у родителей есть право на первоочередной приём на обучение, то предоставляется справка с их места работы. При наличии подаётся копия заключения психолого-медико-педагогической комиссии, это нужно в случае если родители дают согласие на обучение ребёнка по адаптивной образовательной программе для детей с ограниченными возможностями здоровья.
— Проводят ли школы при приёме какие-либо испытания для будущих первоклассников, тесты, собеседования?
— Согласно Закону Российской Федерации «Об образовании», приём в первый класс государственных и муниципальных общеобразовательных учреждений запрещается проводить на конкурсной основе. Каждый ребёнок 6,5 – 8 лет, не имеющий противопоказаний по здоровью, имеет право быть зачислен в первый класс. Однако по заявлению родителей школа может принять ребёнка раньше или позже этого возраста. Причиной отказа приёма в школу может стать только отсутствие мест. Отмечу, что учреждения образования, которые занимаются подготовкой детей с выдающимися способностями, нередко проводят собеседование с детьми, желающих учиться именно у них в рамках услуги по подготовке детей к школе.
— Обязательно ли надо походить предшкольную подготовку?
— Прежде всего, отмечу, что вопрос подготовки ребёнка к школе в настоящее время успешно решается в условиях подготовительной группы в детском саду. Эта слуга есть в дошкольном образовательном учреждении, предоставляется частными центрами, в том числе за родительскую плату. Как правило, дети, посещающие детский сад или группы по подготовке детей к школе, наиболее подготовлены к дальнейшему школьному обучению. Но проходить предшкольную подготовку или нет — остаётся на усмотрение родителей. Её проходят по желанию. Хотелось бы обратить внимание родителей, что прохождение подготовки в конкретной школе не является приоритетом при поступлении.
Новинки для выпускников: кюар-коды, зачёт-незачёт, обязательный индивидуальный проект
— Елена Валерьевна, какие важные изменения произошли в системе основного общего и среднего образования?
— Основные нововведения касаются двух моментов. Приказом Министерства просвещения РФ внесены уточнения про оценивание ряда дисциплин, которые вызывали много вопросов, споров и обсуждений. Так одним из важных новшеств стало то, что по учебным предметам «Изобразительное искусство», «Музыка» и «Физическая культура» теперь допускается указание отметки «Зачтено».
Приказом Министерства просвещения РФ внесены уточнения про оценивание ряда дисциплин, которые вызывали много вопросов, споров и обсуждений. Так одним из важных новшеств стало то, что по учебным предметам «Изобразительное искусство», «Музыка» и «Физическая культура» теперь допускается указание отметки «Зачтено».
Уход на систему зачёт-незачёт по творческим предметам — в целом оправданная мера. Школьникам теперь не придётся переживать за низкую отметку из-за отсутствия музыкального слуха, свою недостаточно хорошую физическую форму. Но вопрос переходить или нет на такую систему зачёт-незачёт – остаётся за школой. Во-вторых, документ, вступивший в силу 1 января 2021 года и действующий до 1 января 2027 года, утверждает новый порядок заполнения и выдачи аттестатов об основном общем и среднем общем образовании и приложения к ним.
Новые образцы школьных аттестатов заменят образцы 2013 года. Содержание и структуру аттестата несильно изменили. Внесены уточнения про математику и индивидуальный проект. Так в случае если в учебном плане указаны предметы «Алгебра» и «Геометрия», то в графе аттестата «Наименование учебных предметов» указывается «Математика», а итоговая отметка за 9 класс по указанному учебному предмету определяется как среднее арифметическое годовых отметок по учебным предметам «Алгебра» и «Геометрия» и экзаменационной отметки выпускника. В разделе «Дополнительные сведения» аттестата указывается отметка за выполнение обучающимися индивидуального проекта, выполнение которого является обязательным требованием к результатам освоения основной образовательной программы на уровне среднего общего образования.
Так в случае если в учебном плане указаны предметы «Алгебра» и «Геометрия», то в графе аттестата «Наименование учебных предметов» указывается «Математика», а итоговая отметка за 9 класс по указанному учебному предмету определяется как среднее арифметическое годовых отметок по учебным предметам «Алгебра» и «Геометрия» и экзаменационной отметки выпускника. В разделе «Дополнительные сведения» аттестата указывается отметка за выполнение обучающимися индивидуального проекта, выполнение которого является обязательным требованием к результатам освоения основной образовательной программы на уровне среднего общего образования.
Отмечу, что основное новшество при оформлении аттестата – QR-код для прямого доступа к данным Федерального реестра сведений о документах об образовании. На обратной стороне аттестата предусмотрено белое поле в форме квадрата для нанесения машиночитаемой маркировки: двумерного матричного штрихового кода (QR-код), представляющего чёрно-белые элементы или элементы нескольких различных степеней яркости.
Он будет содержать адрес для входа в информационную систему, где можно получить информацию о выпускнике – о его фамилии, имени, отчестве, годе рождения, сведения об образовательном учреждении, выдавшем документ. Эта мера поможет подтвердить подлинность аттестата и защитить его от подделок.
Санитарные правила: расписание, нагрузка, мобильники…
— Новая коронавирусная инфекция внесла изменения во все сферы нашей жизни… В связи с этим какие новшества коснулись школ?
— Помимо Министерства просвещения РФ корректировки в привычную школьную жизнь внёс и Роспотребнадзор. Ведомство утвердило новые санитарные правила к работе школ, детских садов, лагерей и других детских учреждений, организаций общественного питания детей.
Поправки касаются режима занятий. Так уроки в школе не должны начинаться ранее восьми утра. Обучение может проходить только в две смены. Занятия второй смены могут завершаться не позднее 19 часов. Длительность уроков для 2-11 классов составляет не более 45 минут. Продолжительность перемены – не менее 10 минут. Большая перемена проводится после второго или третьего урока в 20-30 минут.
Определена допустимая учебная нагрузка. Первоклашки могут учиться только в первую смену и только в течение пяти дней. Для них в день должно быть не более четырёх уроков, при этом допускается только один раз в неделю проведение пятого урока за счёт физкультуры. А в середине третьей четверти проводятся дополнительные каникулы. Во 2-4 классах ежедневно может быть не более пяти уроков, один раз в неделю – шесть уроков — за счёт физкультуры. Проведение больше одного экзамена в день ОГЭ или ЕГЭ не разрешено.
Есть правила, касающиеся использования учеником различных электронных средств. Так интерактивную доску на уроке можно использовать детям в возрасте до десяти лет – не дольше 20 минут, старше десяти лет – до 30 минут. Работа за компьютером в 1-2 классах ограничивается 20 минутами, в 2-4 классах — 25 минутами, в 5-9 классах — 30 минутами, в 10-11 классах — 35 минутами.
Особо подчеркну, что мобильные телефоны с целью образовательной деятельности не применяются. При использовании дистанционных технологий обучения занятия завершаются не позднее 18.00. Длительность урока не должна превышать 40 минут. Конечно же, во время учебного процесса должны соблюдаться все меры профилактики заболеваний. Ученики с признаками инфекционных заболеваний к образовательному процессу не допускаются. После перенесённого заболевания ребёнок предоставляет медицинскую справку. В заключение хотелось бы отметить, что если у родителей, законных представителей ребёнка есть вопросы, касающиеся сферы образования, то можно обратиться к нам в управление образования и науки области, наш телефон: (4752) 79-23-69.
Читайте также: С этого года тамбовских первоклассников будут зачислять в школы по новым правилам
| 13.1 | Найдите вероятности и шансы | Упражнения | п.846 |
| Расширение: моделирование | п.850 | ||
| 13,2 | Найдите вероятности с помощью перестановок | Упражнения | с.853 |
| 13,3 | Найдите вероятности, используя комбинации | Упражнения | п.858 |
| 13,4 | Найдите вероятности сложных событий | Упражнения | п. 864 |
| Викторина | с.867 | ||
| Смешанный обзор | п. 870 | ||
| 13,5 | Анализировать исследования и образцы | Упражнения | п.873 |
| 13,6 | Меры использования центральной тенденции и дисперсии | Упражнения | с.877 |
| Расширение: расчет дисперсии и стандартного отклонения | п.880 | ||
| 13,7 | Интерпретация графиков и гистограмм стеблей и листьев | Упражнения | п.883 |
| 13,8 | Интерпретация графиков ящика и усов | Упражнения | с.889 |
| Викторина | п.892 | ||
| Смешанный обзор | п.894 | ||
| Обзор главы | п.896 | ||
| Глава Test | с.901 | ||
| Стандартизированная практика тестирования | п.904 | ||
| Общий обзор | п.906 |
Номер строки
Запись чисел в числовой строке позволяет легко определить
, какие числа больше или меньше
| Отрицательные числа (-) | Положительные числа (+) |
| (Линия продолжается влево и вправо бесконечно.) | |
Число слева меньше , чем число справа.
Примеры:
- 5 меньше 8
- −1 меньше 1
- −8 меньше −5
Число справа больше числа , чем число слева.
Примеры:
- 8 больше 5
- 1 больше −1
- −5 больше −8
Попробуйте эту интерактивную числовую строку (щелкните, чтобы отметить):
Вы также можете попробовать масштабируемую числовую строку.
Пример: Обед
- Джон занял 3 доллара на обед
- Вирджиния заняла 5 долларов на обед
- У Алекса было достаточно денег на обед, и у него осталось 3 доллара
Поместите этих людей в числовую линию, чтобы определить, кто самый бедный, а кто самый богатый.
Денежная задолженность — отрицательная
Наличие денег — положительная
Итак, у Джона «−3», у Вирджинии «−5», а у Алекса «+3»
Теперь легко увидеть, что:
Вирджиния беднее Джона (−5 меньше −3)
и Джон беднее Алекса (−3 меньше 3)
и Алекс, конечно же, самый богатый!
Использование числовой прямой
Мы можем использовать числовую прямую, чтобы складывать.Мы всегда движемся вправо, чтобы добавить.
Мы можем использовать числовую прямую для вычитания. Мы всегда движемся влево, чтобы вычесть.
Прочтите, как использовать числовую линию для сложения и вычитания.
Сноска: Абсолютное значение
Абсолютное значениеозначает думать только о , насколько число от нуля.
Например, «6» отстоит от нуля на 6, но «−6» отстоит от нуля на и на 6.
Таким образом, абсолютное значение 6 равно 6, а абсолютное значение −6 также равно 6
Решили? Вы умнее десятилетнего сингапурца? | Математика
Сегодня я задал вам десять вопросов на Международном сингапурском математическом конкурсе этого года.Вот вопросы и ответы. В целом у вас все получилось — умнее 10-летнего сингапурца! (С оговоркой, что у них не было ответов с несколькими вариантами ответов, а их всего десять). Единственные вопросы, на которые ваш самый популярный ответ неправильный, — это 6 и 8. (C в Q6 и B в Q8). Спасибо за участие — теперь просмотрите свои разработки …
Для учеников 5 класса:
1. Мэри отрезала 2/5 веревки. Позже она отрезала еще 14 м.Отношение длины оставшейся струны к общей отрезанной длине составляет 1: 3. Какова длина оставшейся струны?
- A. 5 м
- Б. 7 м
- В. 10 м
- Д. 14 м
Решение — C. [73 процента читателей правильно поняли]
О, Мэри! Вот как я бы решил это, используя уравнения. Пусть L будет исходной длиной строки, а R будет тем, что останется после того, как вы дважды разрежете строку.Мы знаем, что R = (L x 3/5) — 14m, и что ((L x 2/5) +14) / R = 3, или 2L / 5 + 14 = 3R. Подставляя первое уравнение во второе, получаем 2L / 5 + 14 = 9L / 5 –42. Что переставляется на: 7L / 5 = 56 или L = 40. Итак, R = 10м.
Интересно, что сингапурский метод решения другой. Это требует от нас более визуального восприятия строки: мы разрезаем ее на 2/5. Затем 14 м, и остается кусок, размер которого составляет треть от того, что было вырезано. Другими словами, у нас остается 1/4 исходной длины.Чтобы сравнить дроби 2/5, а затем 1/4, давайте изменим их на наименьший общий знаменатель, равный 20. Итак, мы отсекаем 8/20, вычитаем 14m и получаем 5/20. Давайте теперь нарисуем строку, разделенную на двадцатые части:
14 метров должны составлять 7/20 длины, что означает, что каждая двадцатая часть равна 2 метрам. Оставшийся отрезок веревки равен 5/20, то есть 10 м
2. Площади граней прямоугольной коробки составляют 84 см 2 , 70 см 2 и 30 см 2 . Какой объем коробки?
Фотография: ISMC- A.300 см 3
- Б. 420 см 3
- C. 490 см 3
- Д. 504 см 3
Решение — B . [85 процентов читателей правильно поняли]
Сначала нам нужно определить возможные длины сторон, посмотрев, какие два числа умножаются на площадь каждой грани. Грань 84 может быть 1 x 84, 2 x 42, 3 x 28, 4 x 21, 6 x 14 или 7 x 12. Грань 70 может быть 1 x 70, 2 x 35, 5 x 14 или 7 x 10.Грань 30 может быть 1 x 30, 2 x 15, 3 x 10 или 5 x 6.
- Общие множители между 84 и 70 равны 1, 2, 7 и 14.
- Общие множители между 84 и 30 равны 1, 2, 3 и 6.
Единственный способ получить 84 с каждым из этих общих множителей: 14 от верхней линии и 6 снизу. Таким образом, край, граничащий с гранями 84 и 70, имеет длину 14, а край, ограничивающий края 84 и 30, имеет длину 6. Это означает, что высота должна быть 30/6, или 70/14 = 5.Таким образом, объем 14 x 6 x 5 = 420 см.
3. Всего четыре числа. Если мы не учитываем одно число, среднее значение оставшихся трех чисел будет 45, 60, 65 или 70. Какое среднее значение всех четырех чисел?
Решение — C . [82 процента читателей правильно поняли]
Если четыре числа — A, B, C и D, то мы знаем, что
- A + B + C = 45 × 3
- A + B + D = 60 × 3
- A + C + D = 65 × 3
- B + C + D = 70 × 3
Теперь сложите их, чтобы получить 3 A + 3 B + 3 C + 3 D = (45 + 60 + 65 + 70) × 3
То есть A + B + C + D = (45 + 60 + 65 + 70) = 240 . Таким образом, их среднее значение составляет 240/4 = 60
4. Марш проходит по улицам от школы (S) до общественного центра (CC). Одна из улиц закрыта. Если марш может идти только на восток или юг, каково количество различных способов добраться до общественного центра? [10 процентов]
Фотография: ISMCРешение — B. [46 процентов читателей правильно поняли]
Есть 19 возможных способов:
5. Салли был дан набор из 5 карточек с номерами от 1 до 5 Петру также дали набор из 5 карточек с номерами от 1 до 5.Затем им завязали глаза и сказали выбрать карту из своих наборов. Сумма чисел на двух карточках была сообщена только Салли, а произведение чисел — только Питеру. Затем им было предложено угадать два числа. Вот что сказал каждый из них:
Питер: Я не знаю двух чисел.
Салли: Теперь я знаю два числа.
Питер: Я все еще не знаю двух чисел.
Салли: Позвольте помочь вам.Число, которое мне сказали, больше, чем вам сказали.
Питер: Теперь я знаю два числа.
Какие два числа?
- A. 1 и 4
- Б. 1 и 5
- C. 2 и 4
- Д. 2 и 5
Решение: A. [72 процента читателей правильно поняли]
Поскольку каждому из них были даны числа от 1 до 5, если бы Питеру сказали любое из следующих чисел, он смог бы сказать, какой были выбраны два числа:
- 1 → 1 × 1 Два числа — 1 и 1.
- 2 → 1 × 2 Два числа — 1 и 2.
- 3 → 1 × 3 Два числа — 1 и 3.
- 5 → 1 × 5 Два числа — 1 и 5.
- 6 → 2 × 3 Два числа — 2 и 3.
- 7 → 1 × 7 Два числа — 1 и 7.
- 8 → 2 × 4 Два числа — 2 и 4.
- 9 → 3 × 3 Два числа — 3 и 3.
- 10 → 2 × 5 Два числа — 2 и 5.
- 12 → 3 × 4 Два числа — 3 и 4.
- 15 → 3 × 5 Два числа — 3 и 5.
- 16 → 4 × 4 Два числа — 4 и 4.
- 20 → 4 × 5 Два числа — 4 и 5.
- 25 → 5 × 5 Два числа — 5 и 5.
(Продукты 11, 13, 14, 17, 18, 19, 21, 22, 23 и 24 не могут быть сформированы.)
Единственный неоднозначный продукт — 4, поскольку 4 может быть равно 1 × 4 или 2 × 2. Таким образом, когда Питер сказал, что он не знает чисел, Салли сможет узнать, что произведение, которое, по словам Питера, должно быть 4.Поскольку Салли сказала, что сумма, которую ей сказали, больше, чем продукт, который сказал Питеру, , два числа, которые были выбраны, должны были быть 1 и 4 (сумма = 5), а не 2 и 2 (сумма = 4).
Для учащихся 6 класса:
6. Имеется 4 ключа и 4 замка. Какое максимальное количество раз вам нужно попробовать замки, чтобы все 4 ключа совпадали с их замками?
Решение — B. [30% читателей правильно поняли]
Если вы попробуете 3 ключа на замке 1 st , вы узнаете, что 4 -й ключ совпадают.Итак, вам нужно максимум 3 попытки. Точно так же для блокировки 2 и требуется максимум 2 попытки, а для блокировки 3 rd требуется всего 1 попытка. Таким образом, необходимо 3 + 2 + 1 = 6 попыток.
7. На диаграмме (не в масштабе) наклонная линия делит площадь прямоугольника в соотношении 1: 6. Каково соотношение a : b ?
Фотография: ISMC- A. 2: 3
- Б. 1: 2
- С. 2: 5
- Д. 1: 3
Решение — C. [63 процента читателей правильно поняли]
Верхний прямоугольник имеет площадь 2 единицы 2 , нижний прямоугольник имеет площадь 6 — 1 = 5 единиц 2 . Мы знаем, что отношение площади верхнего прямоугольника к площади нижнего прямоугольника равно 2: 5. Поскольку оба прямоугольника имеют одинаковую ширину, тогда a и b также должны быть в соотношении 2: 5.
8. Сколько раз часовая и минутная стрелки часов образуют прямой угол друг с другом между 06:00 и 12:00 в один и тот же день?
Решение: A. [39 процентов читателей правильно поняли]
Время, когда часовая и минутная стрелки часов образуют прямой угол друг с другом в период с 06:00 до 12:00, составляет примерно 0617, 0649, 0722, 0754, 0828, 0900. , 0933, 1005, 1038, 1111, 1149.
Обратите внимание, что это происходит дважды в час, за исключением периода между 0800 и 1000, когда это происходит только три раза, а не четыре раза, как ожидалось. Это потому, что в 09:00 стрелки образуют прямой угол. Таким образом, с 06:00 до 12:00 это происходит (6 × 2) — 1 = 11 раз.
9. В школе 6 учеников 240 человек. Отношение количества студентов, которым нравится наука, к количеству студентов, которые не любят математику, составляет 5: 3. Отношение количества студентов, которым нравится математика, к количеству студентов, которые не любят, составляет 7: 5. Количество студентов, которым нравится и наука. и математике 86. Сколько студентов не любят и естественные науки, и математику?
Решение n — B . [75 процентов читателей правильно поняли]
Лучший способ решить эту проблему — использовать диаграмму Венна:
Теперь мы можем записать некоторые суммы:
Если количество студентов, которые любят науку, разделить на количество студентов, которые не учатся, — 5/3, затем 5/8 от общего числа любят науку, а 3/8 — нет.Поскольку общее количество студентов составляет 240, то количество тех, кто любит науку, равно (5/8) x 240 = 150
Итак, количество студентов, которым нравится только естествознания, = 150 — 86 = 64
. студентов, которым нравится математика = (7/12) x 240 = 140
Итак, количество студентов, которым нравится только , математика = 140 — 86 = 54
Таким образом, количество студентов, которым не нравятся и естественные науки, и математика, составляет 240 — (64 + 86 + 54) = 36
10.У моего учителя было 3 больших коробки конфет. В каждой коробке лежали конфеты разного цвета. Каждому ученику раздали по 5 конфет двух разных цветов. Если каждый ученик в классе получил разную комбинацию цветов, каково было наибольшее возможное количество учеников в классе?
Решение — Б. [67 процентов читателей правильно поняли]
Предположим, что это три цвета: красный, синий и желтый. Для любых двух цветов существует всего 4 различных комбинации. Итак, для красного и синего комбинации следующие:
- R R R R B
- R R R B B
- R R B B B
- R B B B B
Есть 3 способа выбрать 2 цвета из 3:
- красно-синий,
- сине-желтый
- красно-желтый
Таким образом, различные цветовые комбинации для 5 конфет составляют 4 × 3 = 12 комбинаций.Следовательно, максимально возможное количество учеников — 12.
Надеюсь, вам понравились эти головоломки. Я вернусь с еще несколькими тизерами через две недели.
Спасибо Рою Ло из Международного конкурса математиков в Сингапуре.
Фотография: Guardian FaberЕсли вам нравятся головоломки — или вы сталкиваетесь с вечной головоломкой о том, что подарить любителю головоломок на Рождество — вам может понравиться моя последняя книга « Можете ли вы решить мои проблемы?» Сборник гениальных, запутанных и совершенно интересных головоломок. Можно приобрести в книжном магазине Guardian и других магазинах.
Я задаю здесь головоломку каждые две недели по понедельникам. Если вы хотите предложить головоломку, напишите мне.
Вопросы по алгебре с ответами для 9 класса
Представлены вопросы по пропорциональной алгебре 9 класса с ответами. Включены вопросы по решению линейных и квадратных уравнений, упрощению выражений, включая выражения с дробями, нахождению наклонов прямых. Также включены решения и подробные объяснения.
Вопросы
Ответы на вышеперечисленные вопросы
|
Дополнительные ссылки и ссылки
Математика для средней школы (6, 7, 8, 9 классы) — Бесплатные вопросы и проблемы с ответамиМатематика для средней школы (10, 11 и 12 классы) — Бесплатные вопросы и проблемы с ответами
Начальная математика (4 и 5 классы) с бесплатными вопросами и проблемами с ответами Домашняя страница сообщить об этом объявлении
Как найти диапазон — Алгебра 1
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или больше ваших авторских прав, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее то информацию, описанную ниже, назначенному ниже агенту.Если репетиторы вуза предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении может быть направлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как так как ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатов), если вы искажать информацию о том, что продукт или действие нарушают ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись владельца авторских прав или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного расположения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; и Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
МАТЕМАТИКА — TACOMA
TMATH 109 Финансовые и математические основы (5) QSR
Интерпретирует повседневные финансовые события, используя количественные и алгебраические рассуждения и модели.Студенты изучают графики и уравнения линейных, экспоненциальных и логарифмических функций с акцентом на личные финансы, практикуя принятие решений и решение проблем. Темы могут включать бюджетирование, ссуды, кредитные карты, налоги, покупку в рассрочку, ипотеку, амортизацию и инвестирование. Предварительное условие: минимум 250 баллов по модифицированному тесту UWT на основе ACC-QAS или минимум 100 баллов по математическому тесту Tacoma Directed Self Placement.
Подробная информация о курсе в MyPlan: TMATH 109
TMATH 110 Вводная статистика с приложениями (5) NW, QSR
Обращается к вводным статистическим концепциям и анализу в современном обществе.Включает описательную статистику, графическое отображение данных, нормальное распределение, сбор данных, вероятность, элементы статистического вывода, проверку гипотез, а также линейную регрессию и корреляцию. Практические примеры, используемые для демонстрации статистических концепций. Предварительные условия: минимальная оценка 2,0 по TMATH 098, MATH 098, TMATH 109, TMATH 124 или MATH 124, минимальный балл 237 на экзамене по измененному размещению UWT на основе экзамена ACC-AAF или минимальный балл 200 на тесте по самооценке в Такоме.
Просмотр сведений о курсе в MyPlan: TMATH 110
TMATH 115 Предварительное исчисление I: функции (5) QSR
Знакомит с концепцией функции, ее обозначениями и подготавливает студентов к работе с кусочно-экспоненциальными, логарифмическими полиномиальные и рациональные функции. Подчеркивает вычислительные навыки, чтение графиков и решение проблем. Одна из двух частей. Можно подсчитать максимум 10 кредитов из TMATH 115, TMATH 116 и TMATH 120. Предварительные условия: минимальная оценка 2,0 по TMATH 098, MATH 098 или TMATH 109, минимальная оценка 237 по модифицированному тесту UWT на основе ACC-AAF или минимум 300 баллов по тесту Tacoma Directed Self Placement Math Test .
Подробная информация о курсе в MyPlan: TMATH 115
TMATH 116 Предварительное исчисление II: Тригонометрия (5) NW, QSR
Продолжает изучение концепции функции, ее обозначений, а также тригонометрических и обратных тригонометрических функций. Представляет параметризованные кривые, полярные координаты и комплексные числа. Делает упор на вычислительные навыки, чтение графиков и методы решения проблем. Вторая из двух частей. Можно подсчитать максимум 10 кредитов из TMATH 115, TMATH 116 и TMATH 120.Предварительные требования: минимальная оценка 2,0 по TMATH 115, минимальная оценка 263 по тесту ACC-AAF или минимум 400 баллов по тесту Tacoma Directed Self Placement Math Test.
Подробная информация о курсе в MyPlan: TMATH 116
TMATH 120 Precalculus (5) NW, QSR
Курс ускоренного обзора, охватывающий содержание TMATH 115 и TMATH 116 за один семестр. Изучает функции и обозначения функций, включая полиномиальные, рациональные, экспоненциальные, логарифмические, тригонометрические и обратные тригонометрические функции.Рекомендуемый сопреквизит: TMATH 158. Необходимое условие: минимальный балл 2,0 по TMATH 098, балл 42-120 на тестовом экзамене ACC-CL, минимальный балл 263 на тестовом экзамене ACC-AAF или минимальный балл 400 Tacoma управляемый тест по математике.
Просмотрите подробности курса в MyPlan: TMATH 120
TMATH 124 Исчисление с аналитической геометрией I (5) NW, QSR
Первая четверть в исчислении функций одной переменной. Подчеркивает дифференциальное исчисление. Акцентирует внимание на приложениях и решении проблем с использованием инструментов исчисления.Невозможно получить зачет, если кредит заработан в TMATH 122. Необходимое условие: минимальный балл 2,0 в TMATH 116 или TMATH 120, минимальный балл 68 по MPT-A, минимальный балл 75 по тесту MATHEC, минимальный балл 2 по тесту AP MATH (AB или BC), минимум 276 баллов по тесту ACC-AAF или минимум 500 баллов по тесту Tacoma Directed Self-Placement Math Test; рекомендуется: Рекомендуемый совместный реквизит: TMATH 159.
Подробная информация о курсе в MyPlan: TMATH 124
TMATH 210 Промежуточная статистика с приложениями (5) NW, QSR
Исследует промежуточные концепции статистического вывода и тестирования с использованием статистического программного обеспечения для анализа.Включает выборку и экспериментальный план, t-тесты, дискретные распределения, пропорции, ANOVA, регрессию, преобразования и тесты хи-квадрат. Анализирует наборы данных из различных дисциплин, таких как экологические и социальные науки. Включает критический обзор современных исследований. Предпосылка: минимальная оценка 2,0 в TMATH 110 Предлагается: WSp.
Подробная информация о курсе в MyPlan: TMATH 210
TMATH 316 Финансовая математика (5) QSR
Знакомит студентов с фундаментальными понятиями финансовой математики: сложный и простой процент, номинальные и эффективные ставки, настоящая и будущая стоимость, ставки дисконтирования, сила представляет интерес.Покрывает аннуитеты как постоянные, так и переменные денежные потоки, ссуды, амортизацию, рефинансирование ссуд и облигации. Исследования могут также включать временную структуру процентных ставок, спотовых ставок, арбитража, продолжительности, выпуклости и иммунизации. Предварительное условие: минимальная оценка 2,0 в TMATH 126 Предлагается: W.
Подробная информация о курсе в MyPlan: TMATH 316
TMATH 390 Probability and Statistics in Engineering and Science (5) NW, QSR
Исследует вероятность и статистику с использованием исследовательского анализа данных и интерактивные вычисления.Темы исследования, включая условную вероятность, независимость, случайные величины, функции распределения, описательную статистику, преобразования, ошибки выборки, доверительные интервалы, наименьшие квадраты и максимальное правдоподобие. Предварительное условие: минимальная оценка 2.0 в TMATH 126 или MATH 126.
Подробная информация о курсе в MyPlan: TMATH 390
TMATH 410 Регрессионное моделирование с приложениями (5) QSR
Исследует регрессионные модели с приложениями; включая множественную линейную регрессию, выбор модели, остаточный анализ, преобразования переменных и категориальные данные.Исследования могут также включать обобщенные линейные модели, нелинейную регрессию, матричную формулировку и смешанные модели. Предварительное условие: минимальная оценка 2,0 по TMATH 210 и TMATH 124 или минимальная оценка 2,0 по TMATH 390.
Подробная информация о курсе в MyPlan: TMATH 410
TMATH 412 Криптография: теория и практика (5) QSR
Охватывает «классические» криптосистемы и их криптоанализ, подход Шеннона к криптографии, включая энтропию и совершенную секретность, блочные шифры и AES.Содержит криптосистему RSA, криптографию с открытым ключом на основе дискретных логарифмов и схемы подписи. Взламывает простые шифры с помощью компьютера. Предварительное условие: минимальная оценка 2,0 в TCSS 321, TMATH 125 или TMATH 402.
Просмотреть подробности курса в MyPlan: TMATH 412
Что означает моя оценка?
Контрольный экзамен по математике на 2019 год
Экзамен по математике, 2020 г.
Аттестация по специальностям, нуждающимся в алгебре
| ALEKS SCORE | 21 или ниже ACT; Математика 520 или ниже SAT Math | 22 или выше ACT Math или 530 или выше SAT Math или 3.5 Общий HS GPA |
| 0% -9% | Математика 00020 Предалгебра | Math 10675 Алгебра для математического анализа; ИЛИ Математика 10771 Основные понятия математики I Plus; OR Math 10772 Моделирование алгебры плюс; ИЛИ |
| 10% -24% | Математика 00021 Базовая алгебра I | |
| 25% -34% | Математика 00022 Базовая алгебра II |
| ALEKS SCORE | HS GPA | ЛЮБЫЕ ДЕЙСТВИЯ ИЛИ СБОРНИК |
| 35% -44% | Math 10675 Алгебра для вычислений Boost; Math 10771 Основные понятия математики I Plus; Математика 10772 Моделирование алгебры плюс | |
| 45% -54% | 3.5 * | Math 10775 Алгебра для исчисления плюс; Math 11009 Моделирование алгебры; Математика 14001 Основные математические концепции I |
| 55% -66% | 3,5 ** | Математика 11010 Алгебра для вычислений |
| 67% -77% | Math 11012 Интуитивное исчисление; Math 11022 Тригонометрия; Математика 12011 Исчисление с предварительным исчислением | |
| 78% + | Math 12002 Аналитическая геометрия и исчисление I; Математика 12021 Исчисление для наук о жизни |
* Учащиеся с оценкой ALEKS 45–54% и средним баллом средней школы ниже , чем 3.5 могут зарегистрироваться на MATH 10675, 10771 или 10772.
* Учащиеся с показателем ALEKS 45-54% и средним баллом средней школы выше , чем 3,5, могут зарегистрироваться на MATH 10775, 11009 или 14001.
** Учащиеся с показателем ALEKS 55-66% и средним баллом средней школы ниже , чем 3,5, могут зарегистрироваться на MATH 10775, 11009 или 14001.
** Учащиеся с показателем ALEKS 55-66% и средним баллом средней школы выше , чем 3,5 могут зарегистрироваться на MATH 11010.
Аттестация по специальностям, не нуждающимся в алгебре
21 или более низкий уровень ACT по математике ИЛИ 520 или более низкий уровень SAT по математике и средний балл HS ниже 3.0 | ANY ACT Math / SAT Math ИЛИ HS GPA 3.0 или выше | 22 или выше ACT Math или 530 или выше SAT Math или 3,5 общий HS GPA |
|---|---|---|
| 0% -9%: математика 00020 Предварительная алгебра | Math 10040 Вводная статистика плюс; Математика 10050 Количественное мышление плюс | Math 10041 Вводная статистика; Math 10051 Количественное мышление; Математика 11008 Исследования в современной математике |
| 10% -24%: Математика 00021 Базовая алгебра I | ||
| 25% -34%: математика 00022 Базовая алгебра II; Math 10040: вводная статистика плюс; Математика 10050 Количественное мышление плюс | ||
| 35% -44%: математика 10041 Вводная статистика; Math 10051 Количественное мышление; Математика 11008 Исследования в современной математике |
** Студенты, желающие пройти курс, отличный от MATH 10041, MATH 10051 или MATH 11008, должны сдать экзамен ALEKS.
Версия для печати сокращенных баллов по математике
- После того, как вы завершите оценку размещения ALEKS®, ваша оценка будет сразу видна
- Если вы хотите просмотреть свой результат позже, после экзамена по размещению, вы можете сделать это, войдя в FlashLine и выбрав ALEKS® Math Placement. Когда вы войдете в систему ALEKS®, нажмите кнопку оценки, и появится ваш результат. Кроме того, ваша оценка также автоматически добавляется в ваш профиль студента штата Кент, который доступен вашему консультанту через день после того, как вы завершили экзамен .
- Вы можете улучшить свой результат, пройдя шестинедельный учебный модуль ALEKS®, а затем зарегистрировавшись для повторной оценки.Это единственный способ перейти на другой курс математики. Учащиеся, набравшие не менее 80% мастерства в своем учебном модуле, имеют отличные шансы улучшить свое положение на повторной оценке ALEKS®. Посетите канал размещения на вкладке «Инструменты для учащихся» в FlashLine, чтобы получить ссылку на учебные модули .

 9 класс.Ю.Н.Макарычев, Н.Г.Миндюк и др.
9 класс.Ю.Н.Макарычев, Н.Г.Миндюк и др.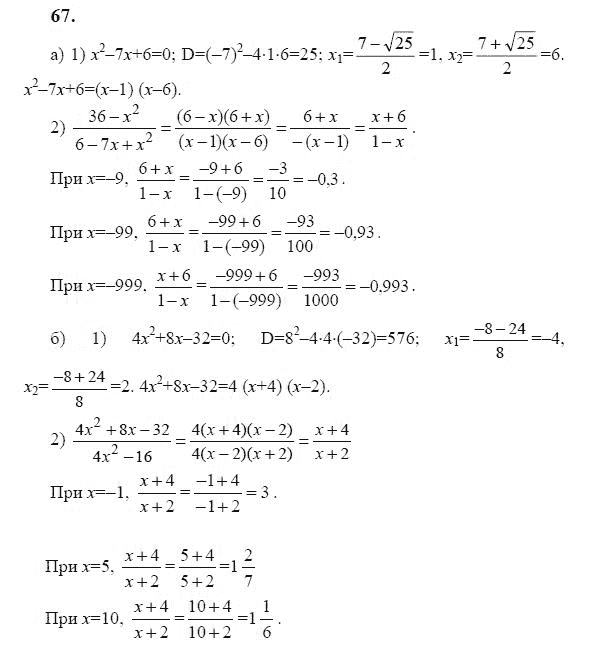 Г. по алгебре к линии Ю.Н. Макарычева и др.,
Г. по алгебре к линии Ю.Н. Макарычева и др.,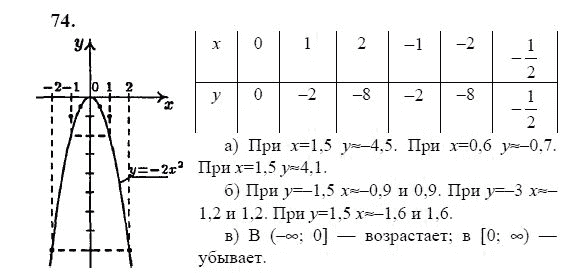


 Издательство «Учитель», 2009.
Издательство «Учитель», 2009.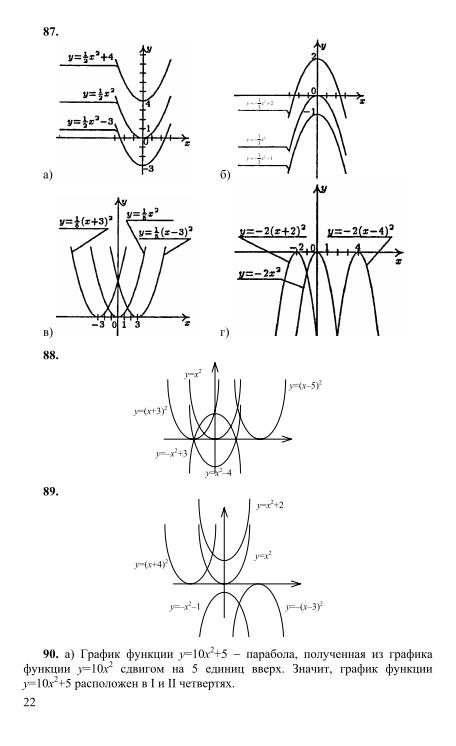 9 класс- М.: Просвещение,2009-2011.
9 класс- М.: Просвещение,2009-2011.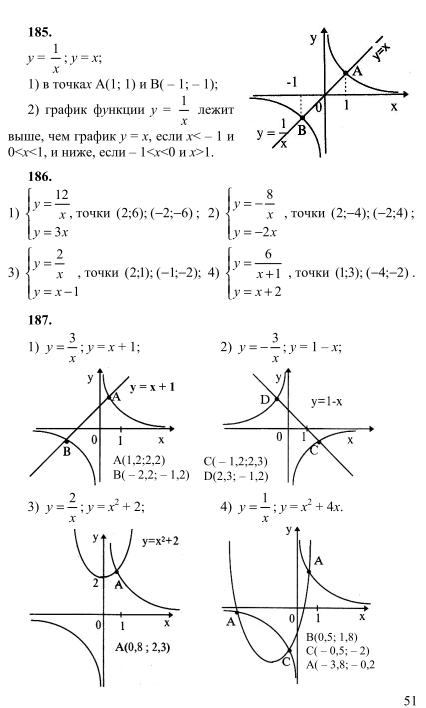
.jpg)





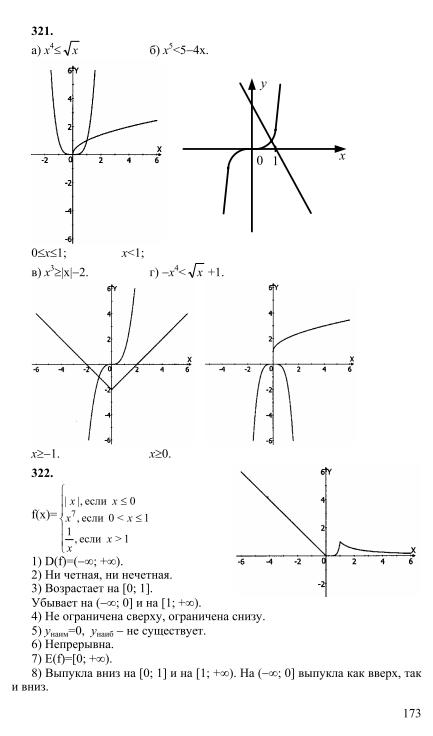
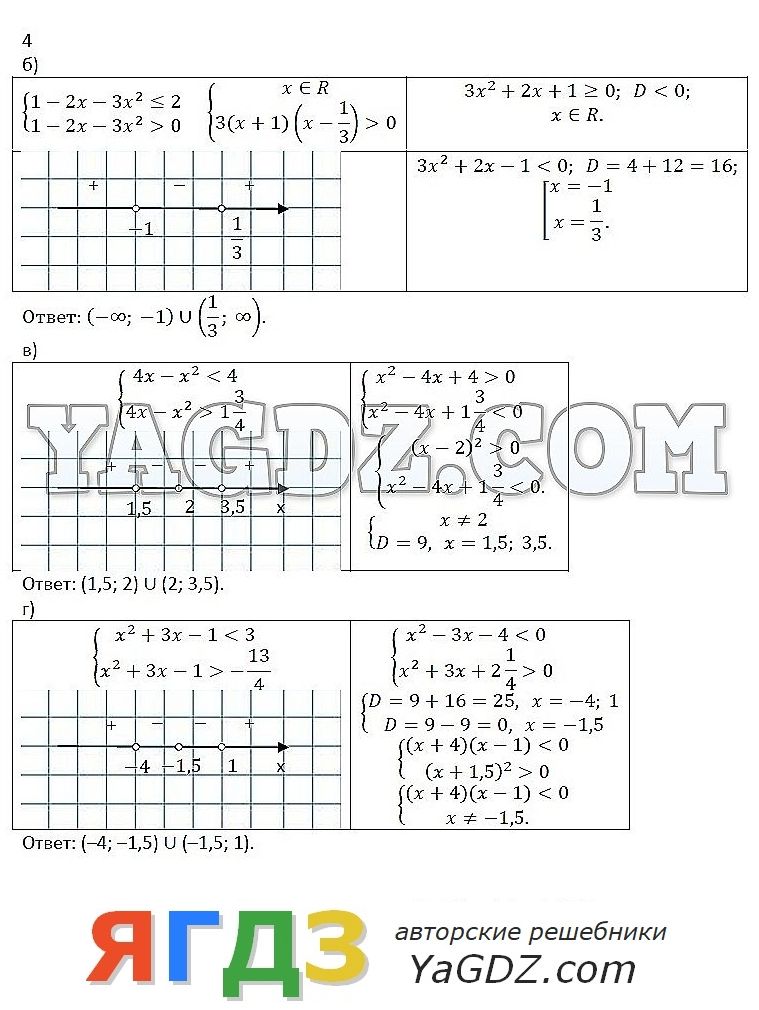
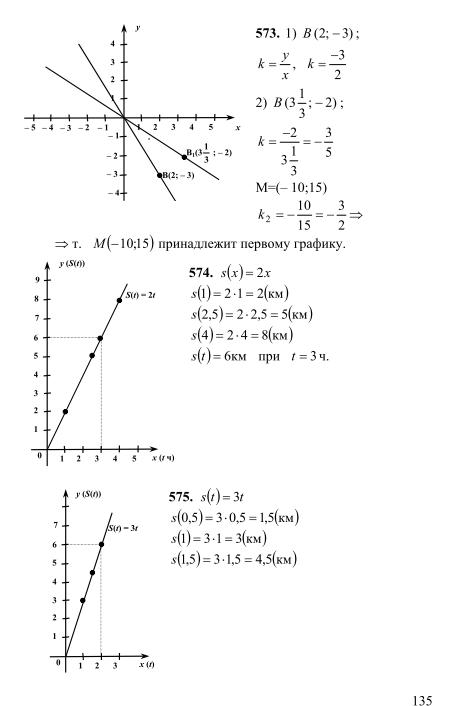


-(Chislovye-funktsii-Variant-2)-reshenie-10.jpg)