Алгебра 9 класс номер 200: Номер задания №200 — ГДЗ по Алгебре 9 класс: Макарычев Ю.Н.

Содержание

200 Алгебра 9 класс Макарычев Найдите область определения функции: – Рамблер/класс

Интересные вопросы

Школа

Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?

Новости

Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?

Школа

Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?

Школа

Когда в 2018 году намечено проведение основного периода ЕГЭ?

Новости

Будет ли как-то улучшаться система проверки и организации итоговых сочинений?

Вузы

Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?

Привет. Поможете решить?
Найдите область определения функции:

ответы

Помогу!

ваш ответ

Можно ввести 4000 cимволов

отправить

дежурный

Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения

похожие темы

ЕГЭ

10 класс

11 класс

Химия

похожие вопросы 5

150 Алгебра 9 класс Макарычев Помогите решить графически

Решите графически уравнение:
а) х3 = 2; б) х3 = 4; в) х3 = -5.

ЭкзаменыАлгебра9 классМакарычев Ю.Н.ГДЗ

Когда скорость изменения функции будет наибольшей или наименьшей? Алгебра 10-11 класс Колмогоров Упр 308

Совсем я в точных науках не сильна) Кто поможет?) Найдите значения аргумента из промежутка [-2; 5], при которых скорость изменения (Подробнее…)

ГДЗ11 классКолмогоров А.Н.Алгебра

Васильевых. 50 вариантов ответов по русскому языку. Вариант 31 ч.2 Задание 13 ОГЭ Русский язык 9 класс Однородное подчинение придаточных

Среди предложений 21-29:
(21) И Митрофанов услышал в этом смехе и прощение себе, и даже какое-то (Подробнее…)

ГДЗРусский языкОГЭ9 классВасильевых И.П.

16. Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)… Цыбулько И. П. Русский язык ЕГЭ-2017 ГДЗ. Вариант 13.

16.
Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)
в предложении должна(-ы) стоять запятая(-ые). (Подробнее…)

ГДЗЕГЭРусский языкЦыбулько И.П.

ЕГЭ-2017 Цыбулько И. П. Русский язык ГДЗ. Вариант 13. 18. Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)…

18.
Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)

в предложении должна(-ы) стоять запятая(-ые). (Подробнее…)

ГДЗЕГЭРусский языкЦыбулько И.П.

Алгебра и начала анализа, 9 класс / под ред. А. Н. Колмогорова. — 1975 // Библиотека Mathedu.Ru

Алгебра и начала анализа, 9 класс / под ред. А. Н. Колмогорова. — 1975

Обложка

Подготовка
текста

Обложка

Обложка123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139140141142143144145146147148149150151152153154155156157158159160161162163164165166167168169170171172173174175176177178179180181182183184185186187188189190191192193194195196197198199200201202203204205206207208209210211212213214215216217218219220221222223224

Содержание

Загрузка
структуры

Информация

Загрузка
описаний

Справка

Загрузка
справки

Поиск

Страниц найдено: 1

Список

Карта

Если строка в кавычках «. ..», то найдутся страницы со словосочетанием в точно такой форме.

Если слова указаны через пробел или оператор «&», то найдутся страницы, содержащие все введенные слова в одном предложении.

Если указано несколько слов через оператор «|», то найдутся страницы, содержащие любое из введенных слов.

Если указано два слова через оператор «~», то найдутся страницы, содержащие первое, но не содержащие второе слово в одном предложении.

По вашему запросу ничего не найдено.

Убедитесь, что слова написаны без ошибок или попробуйте выбрать другие значения.

null

Подождите,
пожалуйста…

Печать

Подготовка [0%]…

Отмена

Идёт
загрузка

{«root»:»text»,»url»:»kolmogorov_i_dr_algebra_i_nachala_analiza_9_1975″,»surl-package»:»\/text\/%PACKAGE%\/?query=%QUERY%»,»surl-page»:»\/text\/%PACKAGE%\/p%PAGE%\/?query=%QUERY%»,»query»:»\»\»»,»section»:»library»,»mode-gfx»:true,»mode-html»:true,»mode-prefer»:»gfx»,»layout-prefer»:»1×1″,»zoom»:{«1×1»:{«level»:100,»_w»:false,»_h»:true},»2×1″:{«level»:100,»_w»:true,»_h»:false},»html»:{«level»:100}},»textsize-prefer»:»2″,»textfont-prefer»:»a»,»tree-type»:»ajax»,»tree-state»:»visible»,»printbox-state»:»hidden»,»print-allowed»:»1″,»searchbox-state»:»hidden»,»searchbox-type»:»inline»,»goto-pageno»:null,»goto-page»:-1,»defw»:»1200″,»defh»:»1899″,»minh»:1899,»maxh»:1899,»fixeven»:null,»package»:»left»,»sitemode»:»live»,»user»:{«uuid»:»»}}

Mathematics_part_ _i_(решения) для класса 9 по математике, глава 2

Mathematics_part_ _i_(решения) Решения для класса 9 по математике, глава 2 Здесь представлены вещественные числа с простыми пошаговыми пояснениями. Эти решения для действительных чисел чрезвычайно популярны среди учащихся 9 класса по математике. Решения для действительных чисел очень удобны для быстрого выполнения домашних заданий и подготовки к экзаменам. Все вопросы и ответы из Mathematics_part_ _i_(solutions) Book of Class 9 Math Chapter 2 предоставляются здесь для вас бесплатно. Вам также понравится возможность без рекламы использовать Mathematics_part_ _i_(solutions) Solutions от Meritnation. All Mathematics_part_ _i_(solutions) Solutions for class Class 9Математика подготовлена экспертами и на 100% точна.

Страница № 21:

Вопрос 1:

Классифицируйте десятичную форму заданных рациональных чисел на завершающиеся и не прекращающиеся повторяющиеся типы.

I 135 II 211 III 2916 IV 17125 V 116

ОТВЕТ:

I 135

С тех пор 5 = 20 × 51

⇒ Знаменатель в форме 2M × 5N, где м и n находится — неотрицательные целые числа.

Итак, десятичная форма 135 будет завершающим типом.

ii 211

Поскольку 11=20×50×111

⇒ Знаменатель не имеет форму 2m×5n, где m и n — целые неотрицательные числа.

Таким образом, десятичная форма 211 будет иметь непрерывный повторяющийся тип.

iii 2916

Поскольку 16=24×50

⇒ Знаменатель имеет вид 2m×5n, где m и n — неотрицательные целые числа.

Итак, десятичная форма 2916 будет завершающим типом.

iv 17125

Поскольку 125=20×53

⇒ Знаменатель имеет вид 2m×5n, где m и n — неотрицательные целые числа.

Итак, десятичная форма 17125 будет завершающим типом.

v 116

Поскольку 6=21×50×31

⇒ Знаменатель не имеет форму 2m×5n, где m и n — неотрицательные целые числа.

Таким образом, десятичная форма 116 будет иметь непрерывный повторяющийся тип.

Страница № 21:

Вопрос 2:

Запишите следующие рациональные числа в десятичной форме.

I 127200 II 2599 III 237 IV 45 V 178

Ответ:

I 127200 = 127200 × 55 = 6351000 = 0,635

II 2599 = 44 × 2599 = 14 × 10099 = 14 × 1.010111 … = 0,2525. .. = 0,25¯

III 237 = 3,2857142857 … = 3,285714¯

IV 45 × 22 = 810 = 0,8

V 178 = 178 × 125125 = 21251000 = 2,125

Страница № 21:

Вопрос 3:

Запишите следующие рациональные числа в форме pq

i 0,6° ii 0,37¯ iii 3,17¯ iv 15,89¯ v 2,514¯

Ответ:

i . …2Вычитая 1 из 2, мы получаем 9x=6∴ x=69 Итак, 0,6°=23

ii Позвольте x=0,37¯ …1Умножая обе части на 100, мы получаем 100x=37,37¯ из вычитания 2, получаем 99x=37∴ x=3799 Итак, 0,37¯=3799

iii Пусть x=3,17¯ …1Умножая обе части на 100, получаем 100x=317,17¯ из … 2 получаем 2, вычитаем 99x=314∴ x=31499 Итак, 3,17¯=31499

iv Положим x=15,89¯ …1Умножая обе части на 100, получаем 157499so, 3,17¯ = 157499

V Let x = 2,514¯ . .. 1multiplying обе стороны на 1000, мы получаем1000x = 2514,514¯ … 2subtracting 1 из 2, мы get99x = 2512∴ x = 2512999so, 2,514¯ = 25129x = 2512

Страница № 25:

Вопрос 1:

Докажите, что 42 – иррациональное число.

Ответ:

Предположим, что 42 — рациональное число.

⇒42 = PQ, где P и Q являются целыми и Q ♠ 0.

⇒2 = P4Q

С тех пор P , Q и 4 являются целыми. Итак, p4q – рациональное число.

⇒ 2 также является рациональным числом.

, но это противоречит тому факту, что 2 — иррациональное число.

Это противоречие возникло из-за неправильного предположения, что 42 — рациональное число.

Следовательно, 42 — иррациональное число.

Страница № 25:

Вопрос 2:

Докажите, что 3 + 5 – иррациональное число.

Ответ:

Предположим, что 3 + 5 — рациональное число.

⇒3 +5 = PQ, где P и Q являются целыми числами и Q ♠ 0.

⇒5 = PQ-3 = P-3QQ

С р , Q и 3 — целые числа. Итак, p-3qq – рациональное число.

⇒ 5 также является рациональным числом.

, но это противоречит тому факту, что 5 – иррациональное число.

Это противоречие возникло из-за неправильного предположения, что 3 + 5 является рациональным числом.

Следовательно, 3 + 5 — иррациональное число.

Страница № 25:

Вопрос 3:

Представьте числа 5 и 10 на числовой прямой.

Ответ:

(i) Этапы построения для 5:

Шаг 1: Нарисуйте числовую линию. Отметьте O как ноль на числовой прямой.

Шаг 2: В точке A нарисуйте AB ⊥ OA так, чтобы AB = 1 единица.

Шаг 3. Используя точку O в качестве центра и радиус OB, нарисуйте дугу, пересекающую числовую прямую в точке P.

Таким образом, P – это точка 5 на числовой прямой.

(ii) Этапы построения числа 10:

Шаг 1: Нарисуйте числовую линию. Отметьте O как ноль на числовой прямой.

Шаг 2: В точке A нарисуйте AB ⊥ OA так, чтобы AB = 1 единица.

Шаг 3. Используя точку O в качестве центра и радиус OB, нарисуйте дугу, пересекающую числовую прямую в точке C.

Таким образом, С — это точка, обозначающая 10 на числовой прямой.

Страница № 25:

Вопрос 4:

Запишите любые три рациональных числа между двумя приведенными ниже числами.

(i) 0,3 и -0,5

(ii) -2,3 и -2,33

(iii) 5,2 и 5,3

(iv) -4,5 и -4,6

три) Рациональное числа между 0,3 и -0,5 равны -0,4, 0 и, 0,1

(ii) Три рациональных числа между -2,3 и -2,33 равны -2,31, -2,32 и -2,325

(iii) Три рациональных числа между 5,2 и 5,3: 5,21, 5,24 и 5,28

(iv) Три рациональных числа между -4,5 и -4,6: -4,51, -4,55 и -4,59 № 30:

Вопрос 1:

Укажите порядок сурдов, приведенный ниже.

I 73 II 5 12 III 104 IV 39 V 183

ОТВЕТ:

I 73 = 713

Орден SURD — 3.

II 5 12 = 5 × 1212

Орден SURD — это 2.

III 104 = 1014

Орден SURD составляет 4.

IV 39 = 3912

Орден SURD составляет 2.

V 183 = 1813

Орден SURD равен 3.

4. Страница № 30:

Вопрос 2:

Укажите, что из перечисленного является сурдами. Оправдывать.

(i) 513 (ii) 164 (iii) 815 (iv) 256 (v) 643 (vi) 227

Ответ:

(i) сурд.

(ii) Так как 164=244=2

Итак, 164 – это не сурд.

(iii) Так как, 815=345=3415=345

Итак, 815 — это сурд.

(iv) Поскольку 256=162=16

Итак, 256 не является сурдом.

(v) Так как, 643=433=4

Итак, 643 не является сурдом.

(vi) Поскольку 227=22712

Таким образом, 227 — это сурд.

Страница № 30:

Вопрос 3:

Классифицируйте данную пару сурдов на одинаковые сурды и разные сурды.

(i) 52, 513 (ii) 68, 53 (iii) 418, 7 2 (iv) 1912, 63 (v) 522,733 (vi) 55, 75

Ответ:

(i) 52, 513

Поскольку 52=4×13=213

Итак, 52, 513 подобны сурдам.

(ii) 68, 53

Так как 68=4×17=217

Итак, 68, 53 не похожи на сурды.

(iii) 418, 7 2

Так как 418=49×2=4×32=122

Итак, 418, 7 2 подобны сурдам.

(iv) 1912, 63

Так как 1912=194×3=19×23=383

Итак, 1912, 63 подобно сурдам.

(v) 522 733

Так как 522=52×11 и 733=73×11

Итак, 522 733 не похоже на сурд.

(vi) 55 , 75

Так как, 75=25×3=53

Итак, 55 , 75 подобны сурдам.

Страница № 30:

Вопрос 4:

Упростите следующие слова.

(i) 27 (ii) 50 (iii) 250 (iv) 112 (v) 168

Ответ:

(i) 27=9×3=33

(ii) 50=25×2=52

(iii) 250=25×10=510

(iv) 112=16×7=47

(v) 168=4×42=242

Страница № 30:

Вопрос 5:

Сравните следующую пару слов.

(i) 72, 53 (ii) 247,274 (iii) 27,28 (iv) 55, 72 (v) 442, 92 (vi) 53, 9 (vii) 7, 25

Ответ:

(i ) 72, 53

Так как, 72=49×2=98 и 53=25×3=75

Итак, 72 > 53

(ii) 247 274

247 < 274

, (203 iii), (203 iii)

Так как, 27=4×7=28

Итак, 27 = 28

(iv) 55, 72

Так как, 55=25×5=125 и 72=49×2=98

Итак, 55> 72

(v) 442, 92

Так как, 442=16×42=672 и 92=81×2=162

Итак, 442 > 92

(vi) 53, 9 9×

5 Так как, 53= 3=75 и 9=81

Итак, 53 < 9

(vii) 7, 25

Так как, 7=49 и 25=4×5=20

Итак, 7> 25

Страница № 30:

Вопрос 6:

Упрощение.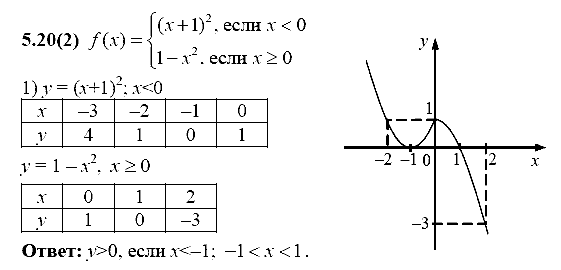

(i) 53 + 83 (ii) 95 — 45 + 125 (iii) 748 — 27 — 3 (iv)7 — 357 + 27

Ответ:

(i) 53+83=133

(ii) 95 -45+125=55+25×5=55+55=105

(iii) 748-27-3=716×3-9×3-3=7×43-33-3= 283-33-3=243

(iv) 7 -357 +27=37-357= 1557-357=1257

Страница № 30:

Вопрос 7:

Умножьте и запишите ответ в простейшей форме.

(i) 312 × 18 (ii) 312 × 715

(iii) 38 × 5 (iv) 58 × 28

×32=186

(ii) 312 × 715=34×3×715=63×715=4245=429×5=1265

(iii) 38 × 5=34×2×5=62×5=610

(iv) 58 × 28=1064=10×8=80

Страница № 30:

Вопрос 8:

Разделить, и запишите ответ в простейшей форме.

(i) 98 ÷ 2 (ii) 125 ÷ 50 (iii) 54 ÷ 27 (iv) 310 ÷ 5

Ответ:

(i) 98 ÷ 2=982=982=49=7

(ii ) 125 ÷ 50=12550=12550=52

(iii) 54 ÷ 27=5427=5427=2

(iv) 310 ÷ 5=3105=3105=62

Страница № 30: 50005

Рационализируйте знаменатель.

(i) 35 (ii) 114 =114×1414=14142=1414

(iii) 57

=57×77=5772=577

(iv) 693

=233×33=233×3=239

(v) =113×33=11332=1133

Страница № 32:

Вопрос 1:

Умножить

(i) 3 7 — 3 (ii) 5 — 7 2 :

(i)

3 7 — 3=3×7-3×3=21-9=21-3

(ii)

5 — 7 2=5×2 — 7×2=10 — 14

(iii)

32 — 3 43 — 2=32×43 — 32×2 — 3×43 + 3×2=126 — 34 — 49 + 6=136 — 3×2 — 4×3=136 — 6 — 12=136 — 18

Страница № 32:

Вопрос 2:

Рационализируйте знаменатель.

(i) 17 +2 (ii) 325 — 32 (iii) 47 + 43 (iv) 5 — 35+ 3

Ответ:

(i) 17 +2

=17+2×7-27 -2=7-272-22 a+ba-b=a2-b2=7-27-2=7-25

(ii) 325 — 32

=325-32×25+3225+32=325+32252-322 47 + 43

=47+43×7-437-43=47-4372-432 a+ba-b=a2-b2=47-4349-48=28-163

(iv) 5 — 35+ 3

=5-35+3×5-35-3=5-3252-32 a+ba-b=a2-b2=52+32-2535-2=5+3-2153=8-2153

Страница № 33:

Вопрос 1:

Найдите значение.

(i) 15 — 2 (ii) 4 — 9 (iii) 7 × -4

Ответ:

(i) 15 — 2=13=13

(ii) 4 — 9=-5=5

(iii) 7 × -4=7×4=28

Страница № 33:

Вопрос 2:

Решить.

(i) 3x — 5 = 1 (ii) 7 — 2x = 5 (iii) 8 — x2 = 5 (iv) 5 + x4 = 5

Ответ:

(i) 3x-5=1
⇒ 3x-5=±1⇒3x-5=1, или, 3x-5=-1⇒3x=1+5, или, 3x=-1+5⇒3x=6, или, 3x=4∴ x=2 , или, x=43

(ii) 7 — 2x = 5
⇒7-2x=±5⇒7-2x=5, или, 7-2x=-5⇒2x=7-5, или, 2x= 7+5⇒2x=2 или 2x=12∴x=1 или x=6

(iii) 8 — x2 = 5
⇒8-x2=±5⇒8-x2=5, или, 8-x2=-5⇒8-x=10, или, 8-x=-10⇒x =8-10, или, x=8+10∴ x=-2, или, x=18

(iv) 5 + x4 = 5
⇒5+x4=±5⇒5+x4=5, или, 5+x4=-5⇒x4=5-5, или, x4=-5-5⇒x4=0, или, x4=-10∴ x=0, или, x=-40

Страница № 34:

Вопрос 1:

Выберите правильный альтернативный ответ на приведенные ниже вопросы.

(i) Какое из следующих чисел является иррациональным?
(A) 1625 (B) 5 (C) 39 (D) 196

(ii) Какое из следующих чисел является иррациональным?

(A) 0,17 (B) 1,513 (C) 0,2746 (D) 0,101001000. ….

(iii) Десятичное расширение какого из следующих чисел является непрерывным повторяющимся?

(A) 25 (B) 316 (C) 311 (D) 13725

iv) Каждая точка на числовой прямой представляет, какое из следующих чисел?

(A) Натуральные числа (B) Иррациональные числа (C) Рациональные числа (D) Вещественные числа.

(v) Число 0,4° в форме pq равно …..
(A) 49 (B) 409 (C) 3,69 (D) 369

(vi) Чему равно n, если n не является полным квадратом количество ?
(A) Натуральное число (B) Рациональное число
(C) Иррациональное число (D) Все варианты A, B, C верны.

(vii) Что из перечисленного не является сурдом?
(A) 7 (B) 173 (C) 643 (D) 193

(viii) Каков порядок surd 53 ?
(A) 3 (B) 2 (C) 6 (D) 5

(ix) Какая из них является сопряженной парой 25 + 3 ?
(A) -25 + 3 (B) -25 — 3 (C) 23 — 5 (D) 3 + 25

(x) Значение 12 — 13 + 7 × 4 …… . …….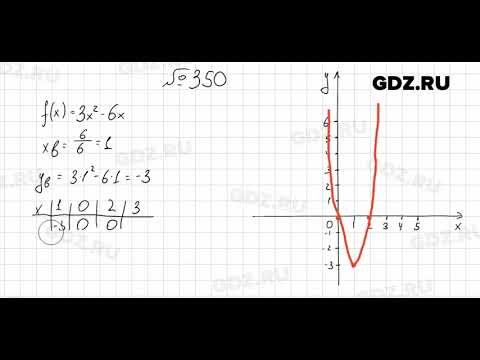
(A) -68 (B) 68 (C) -32 (D) 32

Ответ:

(i) Так как

1625 = 45 является рациональным числом; 39 – рациональное число; 196 = 14 — рациональное число; а 5 – иррациональное число.

Следовательно, правильный вариант (B).

(ii) Так как

0,17 имеет завершающее десятичное разложение, значит, это рациональное число;

1,513 имеет бесконечное повторяющееся десятичное расширение, поэтому это рациональное число;

0,2746 имеет бесконечное повторяющееся десятичное расширение, поэтому это рациональное число;

0,101001000….. имеет бесконечное неповторяющееся десятичное расширение, значит, это иррациональное число;

Следовательно, правильный вариант (D).

(iii)

(A) Так как 5 = 20×51, что в виде 2m×5n, где m и n — неотрицательные целые числа.

Итак, десятичное расширение 25 заканчивается.

(B) Так как 16 = 24×50, то есть в виде 2m×5n, где m и n — неотрицательные целые числа.

Итак, десятичное расширение 316 заканчивается.

Таким образом, десятичное расширение 311 является бесконечно повторяющимся.

(D) Так как 25 = 20×52, то есть в виде 2m×5n, где m и n — неотрицательные целые числа.

Итак, десятичное расширение 13725 заканчивается.

Следовательно, правильный вариант (C).

(iv) Поскольку каждая точка на числовой прямой представляет собой действительное число.

Следовательно, правильный вариант (D).

(v)

Пусть x=0,4¯ …iУмножая обе части на 10, получаем 10x=4,4¯ …iiВычитая i из ii, получаем9x=4⇒x=49

Следовательно, правильный вариант (A ).

(vi) Если n не является совершенным квадратным числом, то n является иррациональным числом.

Следовательно, правильный вариант (C).

(vii) Так как 643 = 4

Следовательно, правильный вариант (C).

(viii) Так как 53=513=51213=516=56

Таким образом, порядок сурда 53 равен 6.

Следовательно, правильный вариант (C).

(ix) Так как сопряженная пара (25 + 3) равна (-25 + 3).

Следовательно, правильный вариант (А).

(x) Поскольку 12-13+7×4=12-20×4=12-80=-68=68

Итак, значение 12 — 13 + 7 × 4 равно 68 .

Следовательно, правильный вариант (B).

Страница № 35:

Вопрос 2:

Запишите следующие числа в форме pq:
(i) 0,555 (ii) 29,568 (iii) 9,315 315 … (iv) 390,417211 (0) 390,417211 (0)

Ответ:

(I) 0,555

= 5551000 = 111200

(ii) 29.568

Let x = 29,568 … 1 -го с обеих сторон на 1000, мы получаем1000x = 29568.

568 … 2by Вычитание 1 из 2, мы getлять ⇒999x = 29539,x = 29539999∴ 29.568 = 2953999

(III) 9,315 315 …

с, 9,315 315 … = 9,315 LET X = 9,315. ..1Multiplying обе стороны на 1000, мы получаем 1000x = 9315.315 … 2by Вычитание 1 из 2, мы getthy ⇒ 999x = 9306,x = 9306999∴ 9,315 = 1034111

(iv) 357,417417 …

с 357,417 417 41777777777777777777777777777777777777777777777777777777.417417 …

. …=357,417. Пусть x=357,417 …1Умножая обе части на 1000, получаем 1000x=357417,417 …2Вычитая 1 из 2, мы получаем⇒999x = 357060,x = 357060999∴ 357,417 = 11

(V) 30,219

Пусть x = 30,219 … 1 -й подтереж 30189⇒x=30189999∴ 30,219=10063333

Страница № 35:

Вопрос 3:

Запишите следующие числа в десятичной форме. .

(i) -57 (ii) 911 (iii) 5 (iv) 12113 (v) 298

Ответ:

(i) -57=-0,714285

(ii) 911=0,81

(iii) 5=2,23606797…

(iv) 12113=9,307692

(v) 298=3,625

Стр.

иррациональное число.

Ответ:

Предположим, что 5 + 7 – рациональное число.

⇒ 5+7=pq, где p и q — два целых числа, а q≠0⇒ 7=pq-5=p-5qq

Поскольку p, q и 5 — целые числа, значит, p-5qq — рациональное число .

⇒ 7 также является рациональным числом.

Но это противоречит тому, что 7 – иррациональное число.

Это противоречие возникло из-за нашего предположения, что 5 + 7 — рациональное число.

Следовательно, 5 + 7 — иррациональное число.

Страница № 35:

Вопрос 5:

Напишите следующие слова в простейшей форме.

(i) 348 (ii) -5945

Ответ:

(i) 348=34×4×2=34×22=322

(ii) -5945=-599×5=-59×35 =-535

Страница № 35:

Вопрос 6:

Напишите простейшую форму рационализирующего множителя для заданных сумм.

(i) 32 (ii) 50 (iii)27 (iv) 3510 (v) 372 (vi) 411

Ответ:

i фактор.

ii Поскольку 50 = 25 × 2 = 52, то 2 — это простейшая форма рационализирующего множителя.

iii Поскольку 27=9×3=33, то 3 — это простейшая форма рационализирующего множителя.

iv Так как 3510=352×5, то 10 — это простейшая форма рационализирующего множителя.

v Так как 372=336×2=3×62=182, то 2 — это простейшая форма рационализирующего множителя.

vi Так как 411=411×1, то 11 — это простейшая форма рационализирующего множителя.

Страница № 35:

Вопрос 7:

Упрощение.

(i) 47147 + 38192 — 1575

(ii) 53+227+13

(iii) 216-56+294-36

(iv)412-75-748

8v 900 -13

Ответ:

(i) 47147 + 38192 — 1575

= 4749×3 + 3864×3 – 1525×3=47×73 + 38×83 – 15×53=43+33-3=63

(ii) 53+227+13

=53+29×3+13×33=53+63+33=113+33=333+33=3433

(iii) 216-56+294-36

=36×6-56+49×6-36×66=66-56+76-366=86-62=186-62=1762

(iv ) 412-75-748

=44×3-25×3-716×3=83-53-283=-253

(v) 248-75-13

=216×3-25×3- 13×33=83-53-33=33-33=93-33=833

Страница № 35:

Вопрос 8:

Рационализируйте знаменатель.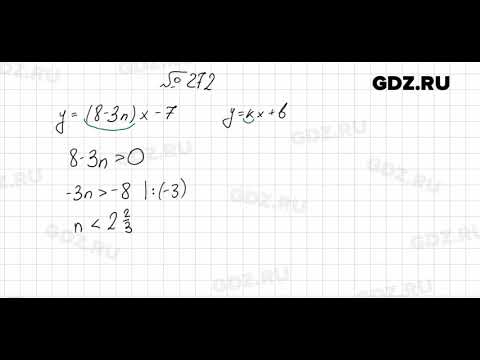

(i) 15 (ii) 237 (iii) 13-2 (iv) 135+22 (v) 1243-2

Ответ:

(i) 15

=15×55=53

2 ) 237

=237×77=273×7=2721

(iii) 13-2

=13-2×3+23+2=3+232-22 a+ba-b=a2-b2=3+ 23-2=3+2

(iv) 135+22

=135+22×35-2235-22=35-22352-222 a+ba-b=a2-b2=35-2245-8=35 -2237

(v) 1243-2

=1243-2×43+243+2=1243+2432-22 a+ba-b=a2-b2=1243+248-2=1243+246=643+ 223

Веб-расписание — SMCCD

Это веб-приложение требует включения JavaScript в вашем браузере. Пожалуйста, следуйте этому руководству (http://enable-javascript.com/), чтобы включить JavaScript в вашем браузере.

МАТЕМАТИКА 200 ЭЛЕМЕНТАРНАЯ ВЕРОЯТНОСТЬ И СТАТИСТИКА (4)
Часов/семестр: 64-72 лекции/16-18 часов по договоренности. Условие: завершение МАТЕМАТИЧЕСКОЙ 120, МАТЕМАТИЧЕСКОЙ 123 или МАТЕМАТИЧЕСКОЙ 190, или соответствующий балл вступительного теста и другие меры, если это необходимо, или эквивалент.
Основные понятия, лежащие в основе статистических методов и охватывающие описательную статистику, вероятность, распределение вероятностей, проверку гипотез, оценки и размеры выборки, корреляцию и регрессию, тесты хи-квадрат и дисперсионный анализ. Компьютерный анализ статистических данных интегрирован в курс. Включены приложения статистики к бизнесу, наукам о жизни и другим областям. Кредит на перевод: UC; ХСС (B4).

Skyline College : Карта

Количество единиц: 4

Учебник: Курс Zero Textbook Cost (ZTC) — просмотр учебников и предметов, связанных с курсами, в книжном магазине

Инструктор: Кеньятта Уэзерсби,

Большинство курсов по математике имеют предварительные условия, которые перечислены как часть описания курса в Расписании занятий. Прежде чем зарегистрироваться на курс математики, убедитесь, что вы выполнили указанные предварительные условия.

Секция инструктора	Дата встречи	Время встречи	дней	Корпус	Комната	Раздел	Описание секции
AC — Лекция и/или обсуждение Дата встречи: 18.08-12.08 Время встречи: 9:10-11:00 Дни: T, Th 1 Building 2 07 Комната: 7104 Инструктор: Кеньятта Уэзерби	18.08-12.08	9:10-11:00	Т, Чт	07	7104	переменный ток	Лекция и/или обсуждение

Критические даты для этого курса	Дата
Последний день добавления класса	30 августа 2022 г. No related posts. Навигация по записям ← Решебник по математике геометрия 7 класс: Решебник по геометрии 7 класс Казаков (2022), ГДЗ на Решеба Учебник спотлайт 8 класс читать онлайн: Spotlight 8 (Английский в фокусе. 8 класс). Учебник → Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт Поиск для: Рубрики 1 класс 10 класс 2 класс 3 класс 4 класс 5 класс 6 класс 7 класс 8 класс 9 класс ГДЗ и Решебники Разное Советы Copyright © 2004-2019 Карта сайта

Критические даты для этого курса

Дата

Последний день добавления класса

30 августа 2022 г.